The economic cost of social distancing during a pandemic: an optimal control approach in the SVIR model

Abstract

We devise a theoretical model for the optimal dynamical control of an infectious disease whose diffusion is described by the SVIR compartmental model. The control is realized through implementing social rules to reduce the disease’s spread, which often implies substantial economic and social costs. We model this trade-off by introducing a functional depending on three terms: a social cost function, the cost supported by the healthcare system for the infected population, and the cost of the vaccination campaign. Using Pontryagin’s Maximum Principle, we are able to characterize the optimal control strategy in three instances of the social cost function, the linear, quadratic, and exponential models, respectively. Finally, we present a set of results on the numerical solution of the optimally controlled system by using Italian data from the recent COVID-19 pandemics for the model calibration.

1 Introduction

For almost three years, around the world, governments have been trying to figure out the best policy to manage the pandemic caused by COVID-19. This sudden global emergency has highlighted the need to systematically address the problem of managing epidemics in a closely interconnected society. The containment measures which have been considered, from the mildest ones, such as the use of masks, to the more limiting ones, such as periods of home confinement, come naturally at the expense of losing the benefits of contact, and they may induce a persistent economic depression due to many aspects. From one side, the impossibility of carrying out all or part of the usual work activity impacts the production system as a whole. On the other hand, people become afraid of leaving their homes, thus forgoing all those activities based on “social contact”, such as purchasing goods, personal healthcare (e.g., preventive health checks), traveling, and so on. Although in almost all countries, to overcome some of these limitations, there has been increasing use of web applications for smart working, online shopping, and, to some extent, some kind of social activities; these measures entail some costs to society besides the ones strictly due to the disease itself, such as costs of treatments for infected people or for implementing a vaccinations campaign. Therefore, the development of preventive or control interventions for the disease is of central importance, as is the cost-effectiveness estimation of such measures. The definition of appropriate optimal control strategies thus becomes essential to study the planner trade-off between the direct cost due to the spread of the disease and containing the disease through social measures, which certainly implies an economic effort for the society as a whole.

In this paper, we consider the interaction between social distance interventions and the spread of a disease by using a control theoretic approach. Optimal control theory is undoubtedly the key tool to attain the trade-off between the fight against disease and the costs of social limitations imposed by a planner.

The starting point in most of the literature is the description of the spread of an infectious disease by means of the SIR model or its several modifications (see e.g. Brauer and Castillo-Chavez 2010), introduced by Kermack and McKendrick (1991), where each letter represents a compartment in which any individual of a population can be set: Susceptible (S), Infected (I), and Recovered/Removed (R). The literature on infectious disease analyzed via optimal control (see e.g. Lenhart and Workman 2007) is rapidly increasing. Behncke (2000) is one of the first attempts to systematically use a control approach in the framework of epidemiological models. In the past decades, the research was focused on measures based on selective isolation and immunization. Abakuks (1973), assuming that an infected population can be instantaneously isolated, studied how to optimally separate it, while Hethcote and Waltman (1973) proposed optimal vaccination strategies. More recently, Ledzewicz and Schattler (2011), were dealing with an optimal control problem using a model with vaccines and treatments on a growing population, while Federico et al. (2022), studied an optimal vaccination strategy in a SIRS compartmental model, using a dynamic programming approach. Gaff and Schaefer (2009) took into consideration SIR/SEIR/SIRS models where the controls are again on the vaccination rate and the cure given to the infected persons, who could also be quarantined. Bolzoni et al. (2017) analyzed the time-optimal control problems for the use of vaccination, isolation, and culling in the linear case. In Miclo et al. (2020), the authors studied a deterministic SIR model in which the social planner controls the transmission rate in order to lower its natural level so as not to overburden the health care system. In the same SIR model, Alvarez et al. (2021) conducted a numerical investigation into optimal containment policies aimed at minimizing the present discounted value of fatalities, while concurrently seeking to minimize the output costs associated with the implementation of lockdown measures. Federico and Ferrari (2021) dealt with the issue of a policymaker aiming to tame an epidemic’s spread while minimizing its associated social costs in a stochastic extension of the SIR model. Kruse and Strack (2020) extended the SIR model with a parameter controlled by the planner, which affects the rate at which the diseases are transmitted, capturing political measures such as social distancing and lockdown of institutions and businesses. While these measures reduce the spread of the disease, they often lead to economic and social costs. They modeled this trade-off by considering convex costs in the number of infected and the reduction in transmission rate. The control through lockdown policies, which affect the rate of diffusion of the disease in a SIRD model, is studied in Calvia et al. (2023) using a dynamic programming approach.

Undoubtedly, one of the most widely used preventive interventions is vaccination. Nowadays, there is extensive literature on vaccination models; see, for instance, the book by Brauer and Castillo-Chavez (2010). In order to include a vaccination strategy explicitly into the dynamical description of the disease, we rely on the model proposed by Liu et al. (2008), denoted as SVIR. Indeed, they consider vaccination in a basic SIR model by introducing a new compartment V where the vaccinees will belong before reaching immunity and, therefore, entering the compartment R of recovered individuals.

The application of an optimal control approach to a SVIR dynamical model is less considered in the literature. Ishikawa (2012) considers a stochastic version of this model and analyzes the corresponding stochastic optimal control problem for the vaccination strategy with a quadratic cost function. Witbooi et al. (2015), considered both a deterministic and stochastic optimal problem for the SVIR model, assuming the vaccination rate as control, and an additive cost functional. In Kumar and Srivastava (2017) propose and analyze a control problem in this framework by using vaccination and treatment as control policies, and a cost functional linear in the state variables, quadratic in the treatment and quartic in the vaccination policies, respectively. Similarly, Garriga et al. (2022) study the deterministic optimal control problem for a pandemic having two phases: in the first one, social restrictions are the only possible containment measures for the disease, while at a subsequent random time a vaccine becomes available. Optimal control strategies are discussed for both phases, involving one and two control variables, respectively, detailing the structure of the cost function by means of a utility function.

In this paper, we assume a deterministic SVIR dynamical model to describe the spread of an infectious disease that a social planner can control through a set of mitigation measures that aim to lower the rate of contagion in the population. The challenge is to find the optimal response balancing restrictions that will minimize the prevalence of the disease, keeping in mind the economic cost of such limitations and having at disposal an immunization instrument. We, therefore, introduce an explicit cost function to take into account the impact of such measures other than the cost of vaccination and the cost due to the infected population. Specifying the functional form of the social cost function, the linear, quadratic, and exponential instances, we are able to characterize the optimal control strategy function using Pontryagin’s Maximum Principle (see, e.g., Lenhart and Workman 2007).

Afterward, we performed a set of numerical experiments to examine the behavior of the controlled SVIR model. To solve the optimal control problem and obtain the solution efficiently, we utilized the Forward-Backward Sweep algorithm (Lenhart and Workman 2007). In our numerical experiments, we assume that a disease has spread in a population in a first period, which provides the initial conditions for subsequent analyses. The numerical simulation was conducted using fixed model parameters consistent with those observed during the recent COVID-19 pandemic. Some of these parameters were calibrated using Italian data from the initial phase of the pandemic, which featured the implementation of non-containment rules. A vaccine becomes available at a given time, and the population dynamic can be described using the SVIR model. Two scenarios were then considered for the SVIR dynamic: one involving a high-intensity vaccination campaign and the other a low-intensity campaign. Our simulations find that the optimal strategy yields compartment values for the population that are comparable to a full-control strategy but with a substantial reduction in costs, up to $70.2\%$ in one scenario. We further study the optimal control problem by varying the maximum control level: in fact, it may not be practically feasible to consider the highest possible level of control. In such situations, the decision maker may prefer a partial level of containment, eventually for a longer duration, despite the associated increase in total cost. This raises the issue of the trade-off between the length of the maximum containment period and the effectiveness/cost of the restrictions.

Our paper is structured as follows: first of all, in Sect. 2, we recall the basic SVIR model together with its main properties, then in Sect. 3, we formulate the deterministic optimal control problem, proving the existence of a solution, and characterizing the optimal control for several instances of the cost functional explicitly. Finally, by using the Forward-Backward sweep algorithm, we numerically solve the problem, and we illustrate the results obtained in several examples.

2 Outline of the basic SVIR model

The SVIR model was introduced by Liu et al. (2008) to modify the well-known SIR model in order to include a vaccination program (continuous or impulsive) in the considered population. The four groups are, therefore, the Susceptibles S, the Infected I, the Recovered R, and the Vaccinees V, representing those having begun the vaccination process, where S, V, R, and I denote the fractions of the total population belonging to each group, respectively.

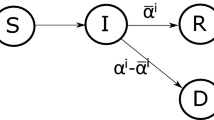
Let $\beta$ represents the transmission rate of disease when the susceptible individuals get in contact with the infected ones and let $\gamma$ be the recovery rate of the infected individuals. It is assumed that vaccinated individuals gain immunity against the disease at a rate $\gamma _1$ and that even the vaccinees have the chance to be infected at a rate $\beta _1$, which can be taken smaller than $\beta$ since after the vaccination process some immunity is acquired. Parameter $\alpha$ represents the rate at which the susceptible persons are moving in the vaccination program, and $\mu$ is the birth-death rate. Figure 1 shows how the population is moving among the four compartments S, V, I, R.

Fig. 1

The basic SVIR model graph

The framework for the continuous vaccination process can be described through the following system of first-order differential equations:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\frac{dS}{dt}(t)} =-\beta S(t)I(t) -\alpha S(t)+ \mu - \mu S(t) &{}S(0)=S_0 \\ \\ \displaystyle {\frac{dV}{dt}}(t) =\alpha S(t) - \beta _1 V(t)I(t)-\gamma _1V(t)- \mu V(t) &{}V(0)=V_0 \\ \\ \displaystyle {\frac{dI}{dt}}(t) =\beta S(t)I(t) + \beta _1 V(t)I(t)-\gamma I(t) - \mu I(t) &{}I(0)=I_0 \\ \\ \displaystyle {\frac{dR}{dt}}(t)=\gamma _1V(t)+\gamma I(t)- \mu R(t) &{}R(0)=R_0 \end{array} \right. \end{aligned}$$

(1)

where the parameters $\beta , \beta _1, \gamma , \gamma _1, \mu \in {\mathbb {R}}^+$ and $\alpha \ge 0$. Moreover, we assume that the initial data $S_0, V_0, I_0, R_0 \in {\mathbb {R}}^+$, and $S_0+V_0+I_0+R_0 = 1$. The above assumptions are stated since the model (1) represents human populations, and it can be shown that the solutions of the system are non-negative given non-negative initial values (see Liu et al. 2008). In particular, it is worth noticing that by defining $N(t) = S(t)+V(t)+I(t)+R(t)$, we immediately have from (1) that $\frac{dN}{dt}(t) = 0$: hence $N(t)=N_0 \equiv 1$, for all $t\ge 0$.

Since the first three equations in system (1) do not involve the state variable R, it is enough to study the properties of the system using only the variables S, V, and I. In Liu et al. (2008) it is shown that the model (1) has a disease free equilibrium (that is an equilibrium $(S^*, V^*, I^*)$ for which $I^* \equiv 0$)

$$\begin{aligned} E_0=\left( \frac{\mu }{\mu +\alpha }, \frac{\alpha \mu }{(\mu +\gamma _1)(\mu +\alpha )}, 0 \right) \end{aligned}$$

(2)

and an endemic equilibrium

$$\begin{aligned} E_+ = \left( \frac{\mu }{\mu +\alpha +\beta I_+}, \frac{\alpha \mu }{(\mu +\alpha +\beta I_+)(\mu +\gamma _1+\beta _1 I_+)}, I_+\right) , \end{aligned}$$

(3)

where $I_+$ is the positive root of quadratic equation, whose coefficients depend on the parameters of the model and on the basic reproduction number, given by

$$\begin{aligned} R_0^C = \frac{\mu \beta }{(\mu +\alpha )(\mu +\gamma )}+\frac{\alpha \mu \beta _1 }{(\mu +\gamma _1)(\mu +\alpha )(\mu + \gamma )}. \end{aligned}$$

(4)

The main properties of the dynamical system (1) are summarized in the two following Theorems, which are proved in Liu et al. (2008):

Theorem 1

The disease free equilibrium $E_0$, which always exists, is locally asymptotically stable if $R^C_0 <1$ and is unstable if $R^C_0>1$. System (1) has a unique positive equilibrium $E_+$ if and only if $R^C_0 >1$ and it is locally asymptotically stable when it exists.

Theorem 2

If $R^C_0 \le 1$, then the disease free equilibrium $E_0$ is globally asymptotically stable. If $R^C_0 > 1$, the endemic equilibrium $E_+$ is globally asymptotically stable in all the region of feasible model solutions except for the constant solution identically equal to $E_0$.

3 The controlled SVIR model

In this section, we introduce the controlled SVIR model, and we analyze a deterministic optimal control problem associated with it.

We consider a control variable $u(\cdot )$, which is meant to govern the social restrictions imposed by the social planner on a population until a specific time T, which is the final time of government restrictions.

The control variable u belongs to the admissible set U defined as

$$\begin{aligned} U = \left\{ u:[0,T]\rightarrow [0,{\bar{u}}]:\text{ Lebesgue } \text{ measurable }, \; {\bar{u}}\in (0,1] \right\} . \end{aligned}$$

The control variable u allows to adjust the rate of transmission of the disease, which we model as a decreasing linear function $\beta (\cdot )$. We want to design the situation where in the absence of control ($u=0$), the infectivity rate $\beta$ is high, while for increasing controls, this rate decreases. The function $\beta (u)$ captures both the infectivity of the disease and the restrictions social planner imposes to govern the speed at which the infection spreads. Furthermore we set $\beta _1= \varepsilon \beta$, where $\varepsilon$ quantifies the vaccine ineffectiveness (if $\varepsilon \equiv 0$ no vaccinated gets infected). Since the first three equations of the SVIR model do not involve the recovered people R and since R will not enter in the specification of the costs of the disease, it is enough to consider the following controlled SVIR dynamic (see Fig. 2):

Fig. 2

The controlled SVIR model graph

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\frac{dS}{dt}}(t) =-\beta (u(t))S(t)I(t) -\alpha S(t)+ \mu - \mu S(t) &{}S(0)=S_0 \\ \\ \displaystyle {\frac{dV}{dt}}(t) =\alpha S(t)-\varepsilon \beta (u(t))V(t)I(t)-\gamma _1V(t)- \mu V(t) &{}V(0)=V_0 \\ \\ \displaystyle {\frac{dI}{dt}}(t) =\beta (u(t))S(t)I(t) +\varepsilon \beta u(t)V(t)I(t)-\gamma I(t) - \mu I(t) &{}I(0)=I_0. \end{array} \right. \end{aligned}$$

(5)

Now we can formulate the optimal control problem. To this end, we introduce the following functional in order to minimize the cost of the infected population I and the cost of the vaccination, which we assume to be proportional to $\alpha S$, being the flux of individuals from S to V or, equivalently, the number of new vaccinees individuals in the unit of time. We suppose that these costs are due to hospitalization expenses for patients requiring inpatient care, with or without ICU (Intensive Care Unit), and to the arrangement of the vaccination program supply chain (e.g., the setting up and the management of a vaccination hub, of the related medical staff, and so on). Moreover, we assume that the cost of social restrictions is a function c of the control variable u such that c is a strictly increasing, convex function of the restriction policy u, and that $c(0)=0$. This means that, in the absence of control, the total costs of the disease diffusion are due to the infected individuals and the vaccination strategy. In this way, and by assuming an additive structure for the cost functional, we disentangle the costs entirely due to the disease from those due to the “restrictions” imposed on the whole society. Parameters $c_1, c_2 \in {\mathbb {R}}^+$ represent the cost of being infected and the cost of the vaccination campaign, respectively.

Hence the objective function is given by $J:U\rightarrow {\mathbb {R}}$ such that

$$\begin{aligned} J(u) =\int _{0}^{T} [c (u(t))+c_1I(t)+c_2\alpha S(t)]dt. \end{aligned}$$

(6)

Our goal is to derive the optimal strategy $u^*\in U$ and the associated state variables S, V and R to minimize (6) i.e.

$$\begin{aligned} \min _{u\in U} J(u)\qquad \hbox {subject to (5)}. \end{aligned}$$

To prove the existence of such a strategy $u^*$ we refer to Fleming and Rishel (1975), Lenhart and Workman (2007) and Kumar and Srivastava (2017).

Theorem 3

Let $\beta (\cdot )$ be a linear decreasing function and let $c(\cdot )$ be a convex, twice continuous differentiable function, such that $c'>0$ and $c(0)=0$.

Then an optimal solution $u^*$ for problem (5)–(6) exists, i.e. there exists an optimal control $u^*\in U$ such that $J(u^*)=\min J(u)$.

Proof

First of all, notice that the right-hand side functions of system (5) are Lipschitz continuous with respect to the state variables, hence Picard–Lindelof Theorem ensures that there exist solutions to (5). By definition, the set $[0,{\bar{u}}]$ is compact and convex and system (5) is linear in the control variable u, then the result follows applying Theorem 4.1 and Corollary 4.1 pp. 68–69 in Fleming and Rishel (1975). $\square$

Remark 1

Choosing in (6) a continuous function C(u, I, S), $C(\cdot ,I,S)$ convex on $[0,{\bar{u}}]$ a similar results is easily obtained, again following Corollary 4.1 pp. 68–69 in Fleming and Rishel (1975). Our choice of the particular case $C(u,I,S)= c(u)+c_1I+c_2\alpha S$ allows us to separate the costs due to social restrictions from the ones due both to of the infected population I and of the vaccination. Moreover, with this explicit choice of the integrand function, we are able to solve the problem applying numerical techniques.

In order to solve the above optimal control problem, we refer to the well-established control theory, see for instance Fleming and Rishel (1975) or Lenhart and Workman (2007). It is introduced the Hamiltonian function H and the Lagrange multipliers $\lambda _1(\cdot )$, $\lambda _2(\cdot )$ and $\lambda _3(\cdot )$ denoted also as co-states, or adjoint variables. From now on, even if the state variables S, V, I, the control variable u and the co-state variables $\lambda _1$, $\lambda _2$ and $\lambda _3$ are functions of time, we omit this dependence except where it is explicitly required.

The Hamiltonian function of the optimal control problem (5)–(6) is defined as follows

$$\begin{aligned} \begin{array}{l} H(t,S,V,I,u,\lambda _1,\lambda _2,\lambda _3) =c(u)+c_1I+c_2\alpha S+\lambda _1[-\beta (u)SI -\alpha S+ \mu - \mu S ] \\ \quad +\lambda _2[\alpha S-\varepsilon \beta (u)VI-\gamma _1V- \mu V]+ \lambda _3[\beta (u)SI +\varepsilon \beta (u)VI-\gamma I - \mu I]. \end{array}\nonumber \\ \end{aligned}$$

(7)

Theorem 4

Let $(S^*,V^*, I^*, u^*)$ be an optimal solution for problem (5)–(6), then there exist adjoint functions $\lambda _1,\lambda _2$ and $\lambda _3$ satisfying the following system of differential equations

$$\begin{aligned} \left\{ \begin{array}{l} \lambda _1' =[\beta (u^*)I^* +\alpha + \mu ]\lambda _1 - \alpha \lambda _2-\beta (u^*)I^*\lambda _3-c_2\alpha \\ \\ \lambda _2' =[\varepsilon \beta (u^*)I^* +\gamma _1+ \mu ]\lambda _2 -\varepsilon \beta (u^*)I^*\lambda _3 \\ \\ \lambda _3' =\beta (u^*)S^* \lambda _1+\varepsilon \beta (u^*)V^*\lambda _2- [\beta (u^*)S^*+\varepsilon \beta (u^*)V^*-\gamma -\mu ]\lambda _3-c_1 \end{array} \right. \end{aligned}$$

(8)

with the transversality conditions

$$\begin{aligned} \lambda _1(T)=0\qquad \lambda _2(T)=0\qquad \text{ and }\qquad \lambda _3(T)=0. \end{aligned}$$

The optimal restriction policy $u^*$ is such that

$$\begin{aligned} \displaystyle { u^*(t)\in \text{ argmin}_{u\in [0,1]} H(t,S^*,V^*,I^*,u,\lambda _1,\lambda _2,\lambda _3) }. \end{aligned}$$

(9)

Proof

Let $(S^*,V^*, I^*, u^*)$ be an optimal solution for problem (5)–(6). By Pontryagin’s Maximum Principle the costate variables $\lambda _1$, $\lambda _2$ and $\lambda _3$ satisfy system (8) whose equations are obtained evaluating the partial derivatives of the Hamiltonian function H in (7), with respect to the state variables S, V, I

$$\begin{aligned} \left\{ \begin{array}{l} \lambda _1' =-\displaystyle {\frac{\partial H}{\partial S}} \\ \\ \lambda _2' =-\displaystyle {\frac{\partial H}{\partial V}} \\ \\ \lambda _3' =-\displaystyle {\frac{\partial H}{\partial I}} \end{array} \right. \end{aligned}$$

(10)

with the transversality conditions $\lambda _1(T)=\lambda _2(T)=\lambda _3(T)=0.$ The Hamiltonian function H, defined in (7) is strictly convex with respect to the control variable u, hence the existence of a unique minimum follows (see Witbooi et al. 2015), hence

$$\begin{aligned} u^*(t)\in \text{ argmin}_{u\in [0,1]} H(t,S^*,V^*,I^*,u,\lambda _1,\lambda _2,\lambda _3). \end{aligned}$$

$\square$

Remark 2

Similar results are easily generalized using a convex function for the cost of the infected population. This more general assumption models the nonlinear impact of disease spread on the healthcare system, resulting in hospital services becoming overwhelmed.

We now further specialize the result obtained by explicitly specifying the functional form of the transmission rate $\beta (u)$ and cost function c(u). As a basic model we consider the following linear model:

$$\begin{aligned} \beta (u) = \beta _0 (1- u), \ \ \ 0 \le u \le 1, \end{aligned}$$

(11)

where $\beta _0>0$ is the specific transmission rate of the disease. In this case, we model the situation when the maximum control (i.e. $u \equiv 1$) completely “freezes” the disease diffusion.

In our practical application we consider the following functions:

• 1. $c_{quad}(u) = b u^2$, $b >0$;

• 2. $c_{exp}(u) = e^{k u}-1$, $k >0$;

• 3. $c_{lin}(u)=au$, $a>0$.

A complete characterization of the optimal controls is proved in the following.

Proposition 5

Let $\beta (u) = \beta _0 (1- u)$ and $c_{quad}(u)=b u^2$. Then the optimal control strategy $u_{quad}^*$ for problem (5)–(6) is given by

$$\begin{aligned}{} & {} u_{quad}^*(t)\nonumber \\{} & {} \quad =min\left\{ max \left[ 0,\frac{\beta _0I^*(t)[S^*(t)(\lambda _3(t)-\lambda _1(t))+ \varepsilon V^*(t)(\lambda _3(t)-\lambda _2(t))]}{2b}\right] ,{\overline{u}}\right\} \nonumber \\ \end{aligned}$$

(12)

Proof

In this case the Hamiltonian function H is defined as

$$\begin{aligned} \begin{array}{l} H(t,S,V,I,u,\lambda _1,\lambda _2,\lambda _3) \\ \quad =bu^2+c_1I+c_2\alpha S+ \lambda _1[-\beta _0(1- u) S I -\alpha S+ \mu - \mu S ] \\ \qquad +\lambda _2[\alpha S-\varepsilon \beta _0 (1- u) VI-\gamma _1V- \mu V] \\ \qquad +\lambda _3[\beta _0 (1- u) SI +\varepsilon \beta _0 (1- u) VI-\gamma I - \mu I] \end{array} \end{aligned}$$

(13)

then, imposing first-order conditions to minimize the Hamiltonian H at $S^*,I^*,V^*$

$$\begin{aligned} \displaystyle {\frac{\partial H}{\partial u}}=2bu +I^*[\beta _0 S^*(\lambda _1-\lambda _3)+ \varepsilon \beta _0 V^*(\lambda _2-\lambda _3)]=0, \end{aligned}$$

(14)

we derive the optimal restriction policy $u_{quad}^*$ (12). $\square$

Analogously to the quadratic case above, we can solve the exponential case

Proposition 6

Let $\beta (u) = \beta _0 (1- u)$ and $c_{exp}(u)=e^{k u}-1$.

If $\lambda _3(t)>\lambda _1(t)$ and $\lambda _3(t)>\lambda _2(t)$, then the optimal control strategy $u_{exp}^*(t)$ for problem (5)–(6) is given by

$$\begin{aligned} u_{exp}^*(t)= min\left\{ max \left[ 0,\frac{1}{k}\ln \frac{\beta _0 I^*(t)K(t)}{k}\right] , {\overline{u}}\right\} \end{aligned}$$

(15)

where K(t) is defined as $\displaystyle { K(t)=S^*(t)(\lambda _3(t)-\lambda _1(t))+ \varepsilon V^*(t)(\lambda _3(t)-\lambda _2(t))}$.

Remark 3

We notice that in both cases, the optimal control strategy $u^*$ depends on the shadow price differences between infected and susceptible, and infected and vaccinated (see the paper Kruse and Strack 2020). In other words, $\lambda _3-\lambda _1$ and $\lambda _3-\lambda _2$ can be interpreted as the marginal cost of having an additional susceptible person infected and as the marginal cost of having an additional vaccinated person infected, respectively.

Remark 4

It is interesting to point out that, as expected in reality, if in the optimal strategies $u_{Q}^*$ and $u_{exp}^*$ the maximum is not vanishing, then the optimal controls converges to the constant policy ${{\overline{u}}}$ as b and k tend to 0, respectively. Hence if the social planner can cut off the social cost, then the optimal policy that can be adopted is the most strict one, represented by ${{\overline{u}}}$.

Finally, we now consider the linear case: the proof of the following Proposition is reported in Appendix A and it follows the reasoning in Joshi et al. (2015).

Proposition 7

Let $\beta (u) = \beta _0 (1- u)$ and $c_{lin}(u)=au$. Then the optimal control strategy $u_{lin}^*(t)$ for problem (5)–(6) is given by

$$\begin{aligned} u_{lin}^*(t)= \left\{ \begin{array}{ll} {\bar{u}} &{} \text{ if } \frac{\partial H}{\partial u}<0 \\ \\ u_{sing}=\frac{A_2(t)}{A_1(t)} &{} \text{ if } \frac{\partial H}{\partial u}=0 \\ \\ 0 &{} \text{ if } \frac{\partial H}{\partial u}>0 \end{array} \right. \end{aligned}$$

(16)

where $A_1 (\cdot )$ and $A_2 (\cdot )$ are defined in the proof.

4 Numerical results

In this section, we utilize the optimality outcomes derived in the preceding section to investigate the controlled SVIR dynamics across various scenarios. To obtain our simulation results, we employ the Forward-Backward sweep algorithm to numerically solve the control problem, as it is a well-established indirect technique for approximating optimal control problem solutions (see Lenhart and Workman 2007, and e.g. McAsey et al. 2012 for a convergence result).

The algorithm iteratively updates the current control function $u_n(\cdot )$ by firstly solving the forward state equations (5) utilizing an ODE solver. Subsequently, the costate equations (8) are solved backward in time with the same solver, and the control is updated according to the optimality conditions. This iterative procedure leads to the generation of a new approximation of the state, costate, and control $u_{n+1}(\cdot )$. The described steps are repeatedly performed until a convergence criterion is met.

In a preliminary phase, we set up the algorithm by establishing the temporal discretization and the criterion for terminating the computation. Specifically, we selected a fixed number of time points, $N=1000$, uniformly distributed within the time horizon [0, T], and defined the stopping criterion based on the non-decreasing behavior of the cost functional. Additionally, we employed a technique of weighted averaging to update the solution iteratively, by combining the new and previous solutions. In particular, we found that the weighting constant value equal to 0.99 is a good compromise between convergence speed and smoothing properties of the obtained solution. For the linear case, where the solution is of bang-bang type, we did not used instead the averaging step, i.e. the weighting constant was set to 0. In our numerical experiments, we never observed the singularity condition (see (16)).

The proposed algorithm was implemented using the software $\text {MatLab}^{\copyright }$ (R2021b). The built-in function ode45 was utilized to efficiently solve the systems of ordinary differential equations (ODEs). After the model parameters were fixed, the computation of the optimal solution was efficiently obtained within seconds.

The parameters used in this section are summarized in Table 1, and they represent typical values of the recent COVID-19 pandemic. As a unit of time period, we take one day. In particular, we estimated the parameters $\beta _0$ and $\gamma$, by using the aggregated Italian data provided by the “Dipartimento della Protezione Civile”, available on GitHub,¹ in the early stage of the pandemic, by exploiting the procedure described in the Appendix B. Specifically, they were obtained by using data from February, $24^{th}$ to March, $15^{th}$ 2020, setting $\alpha =\gamma _1=0$ (no vaccination measures at that time).² Then, we fixed $\gamma _1^{-1}=14$, as the time to reach full protection is estimated to be around 14 days (see, e.g. WHO https://www.who.int/health-topics/coronavirus)). Hence, in our experiments, we considered a scenario where a short-lived infectious disease has spread throughout a population, and only confinement measures are available to control its spread. After a given period, a vaccine becomes available. The starting conditions for this scenario are $V_0=0$, $I_0=0.04$ and $R_0=0.12$ (corresponding to the percentage of infected and recovered Italian people in January 2022), and $S_0=1-I_0-V_0-R_0$. The time horizon was set to 240 days. Furthermore, in order to fix the value for the scenario parameter $\varepsilon$, we choose to estimate it by using the vaccine effectiveness³VE for the booster dose, averaged on the three available vaccines, ChAdOx1 nCoV-19 (Astra-Zeneca), BNT162b2 (Pfitzer-BionTech) and mRNA-1273 (Moderna), as reported in Andrews et al. (2022) (Table 3): this procedure implied the value $\varepsilon \equiv (1-VE) = 0.078$. Finally, the birth-death rate has been set equal to zero⁴, assuming that the disease has a short lifespan compared to the population’s lifetime (see e.g. Van den Driessche 2017).

As introduced in Sect. 3, the cost functional (6) is given by the sum of three terms, each related to a specific aspect of the problem: the cumulative “social cost” $J_{SC}(u) = \int _0^T c(u(t)) dt$, “infection cost” $J_{IC}(u) = \int _0^T c_1 I(t) dt$, and “vaccination cost” $J_{VC}(u) = \int _0^T c_2 \alpha S(t) dt$. In order to quantify the relative weights of each term, we rely on a quantification of the cost related to the hospitalized patients as available in the paper by Marcellusi et al. (2022) (Supplementary material), assuming that the average cost for vaccination is 15€ per person. In particular, we considered the average daily cost weighted by the total number of patients hospitalized with and without ICU and only ICU.⁵ Finally we normalized the corresponding weights in such a way $c_1=1$, implying $c_2=0.02$.

Table 1 Basic values of the parameters for the uncontrolled system

As a preliminary step of our experiments, after having fixed the cost of the infection and the cost of vaccination, we analyzed the impact of the social cost parameters on the optimal solution, by comparing it with the two limiting cases: no restrictions ($u\equiv 0$) and full restrictions ($u \equiv 1$). In general, we observed a similar qualitative behavior of the optimal strategy for the three cost functions, $c_{quad}(\cdot )$, $c_{exp}(\cdot )$, and $c_{lin}(\cdot )$, with respect to their parameter, b, k and a, respectively. Increasing these values in the instances considered, corresponds to a higher social cost for increasing controls. As expected, we immediately see that if the social cost becomes larger ($b, k, a \nearrow$), the optimal strategy collapses to the no-control strategy: it would be convenient not to adopt any restrictions if the cost of such restrictions became too expensive (see the result of such experiments in Appendix C). In particular, we noticed that the optimal policy provides a reduction of the overall cost, in all the considered scenarios.

More interestingly, we analyzed the qualitative behavior of the optimal solution in the three instances considered, comparing them with the two limiting cases given by an absence of control ($u\equiv 0$) and the maximum control ($u \equiv 1$).

4.1 Analysis of the optimal policies

For each choice of the social cost function, $c_{quad}(\cdot )$, $c_{exp}(\cdot )$, and $c_{lin}(\cdot )$, we demonstrate the effect of an optimal policy in two possible scenarios, a low-intensity ($\alpha =0.0005$) and a high-intensity ($\alpha =0.004$) vaccination campaign. In order to get comparable results among the three cost models, we set the parameters $a=b=0.04$, and $k=0.03922$, respectively. In such a way, in the given time period, the social cost with the maximum control is about the same.

In the analysis of the three cases presented, it is evident that the optimal strategy leads to a reduction in the total cost even when there is a slight increment in the cost of caring for the infected population. This outcome holds true for both low- and high-intensity vaccine campaigns, as it is demonstrated in Tables 2, 3 for the quadratic cost function, Tables 4, 5 for the exponential cost function, and Tables 6, 7 for the linear cost function, where the total cost J and the specific costs $J_{SC}$, $J_{IC}$, and $J_{VC}$, are reported. The reduction in the overall cost of the optimal strategy w.r.t. the full-control strategy is significant across all scenarios, but is most pronounced in the high-intensity case, $70.2\%$, $61.4\%$ and $61.6\%$, respectively. Moreover, it is apparent that the high-intensity vaccine campaign yields lower total costs in spite of a minor increase in related expenses ($J_{IC}$ and $J_{VC}$).

Table 2 Total costs J(u) of the strategies and the corresponding social, infection, and vaccination cost for the quadratic cost function. In parentheses the percentage value w.r.t. the total cost. Low vaccination rate scenario

Table 3 Total costs J(u) of the strategies and the corresponding social, infection and vaccination cost for the quadratic cost function. In parentheses the percentage value w.r.t. the total cost. High vaccination rate scenario

Table 4 Total costs J(u) of the strategies and the corresponding social, infection and vaccination cost for the exponential cost function. In parentheses the percentage value w.r.t. the total cost. Low vaccination rate scenario

Table 5 Total costs J(u) of the strategies and the corresponding social, infection and vaccination cost for the exponential cost function. In parentheses the percentage value w.r.t. the total cost. High vaccination rate scenario

Table 6 Total costs J(u) of the strategies and the corresponding social, infection and vaccination cost for the linear cost function. In parentheses the percentage value w.r.t. the total cost. Low vaccination rate scenario

Table 7 Total costs J(u) of the strategies and the corresponding social, infection and vaccination cost for the linear cost function. In parentheses the percentage value w.r.t. the total cost. High vaccination rate scenario

Figures 3, 4, 6, 7, 9 and 10 depict the outcomes of the dynamic model under full-control, no-control, and optimal control strategies, in the three instances considered, while Figs. 5, 8, 11 report the corresponding optimal policies $u^*$. It is evident that the optimal strategy shows compartmental dynamics that are comparable to those of the full-control strategy, while also yielding a substantial reduction in costs. Notably, in the case of the low-intensity vaccination campaign, the Susceptible compartment remains highly populated (at $70\%$, $70\%$, and $57\%$ for the three social cost functions) after 240 days, resulting in an increase in the number of infected individuals at the end of the observation period. The Infected compartment population amounts to $1.1\%$, $1.3\%,$ and $8\%$, respectively, at the final time T. This trend is particularly apparent in the linear cost case. Overall, the percentages of Recovered and Vaccinated individuals amount to $28.3\%$, $26.6\%$, and $34.74\%$, respectively. In contrast, under the high-intensity vaccine campaign scenario, the Susceptible population decreases more significantly (at $30\%$, $30\%$, and $29.1\%$ for the three social cost functions), while the Infected compartment remains consistently low (at $0.13\%$, $0.28\%$, and $0.35\%$, respectively). Furthermore, the percentages of Recovered and Vaccinated individuals increase significantly, reaching a total of $69.6\%$, $69.7\%$, and $70.6\%$ of the total population. It is noteworthy that in the quadratic cost case, Fig. 5, the optimal control policy involves the implementation of maximum control up to 15 days from the initial date, followed by a gradual decrease to zero. The rate of decrease is dependent on the intensity of the vaccination campaign. This pattern holds true for both low- and high-intensity vaccine scenarios. In the exponential cost case, Fig. 8, the maximum control value persists for a longer period of time (47 and 64 days, respectively) before rapidly decreasing to zero in the high-intensity vaccine scenario. Conversely, it remains at an intermediate level for an extended period from day 79 before reaching the minimum level after approximately 190 days from the initial date. In the linear cost case, Fig. 11, the optimal bang-bang control involves maximum control for 118 and 70 days, respectively. Notably, the number of days of maximum control is reduced in the high-intensity vaccine scenario.

Fig. 3

Compartmental dynamics corresponding to the uncontrolled system ($u\equiv 0$, dash-dotted blue line), fully controlled system ($u \equiv 1$, dashed red line) and optimally controlled system ($u^*$, black line), quadratic social cost function. High vaccination rate scenario (color figure online)

Fig. 4

Compartmental dynamics corresponding to the uncontrolled system ($u\equiv 0$, dash-dotted blue line), fully controlled system ($u \equiv 1$, dashed red line) and optimally controlled system ($u^*$, black line), quadratic social cost function. Low vaccination rate scenario (color figure online)

Fig. 5

Optimal controls for low vaccination rate (blue line) and high vaccination rate (red line) scenarios: quadratic social cost function (color figure online)

Fig. 6

Compartmental dynamics corresponding to the uncontrolled system ($u\equiv 0$, dash-dotted blue line), fully controlled system ($u \equiv 1$, dashed red line) and optimally controlled system ($u^*$, black line), exponential social cost function. High vaccination rate scenario (color figure online)

Fig. 7

Compartmental dynamics corresponding to the uncontrolled system ($u\equiv 0$, dash-dotted blue line), fully controlled system ($u \equiv 1$, dashed red line) and optimally controlled system ($u^*$, black line), exponential social cost function. Low vaccination rate scenario (color figure online)

Fig. 8

Optimal controls for low vaccination rate (blue line) and high vaccination rate (red line) scenarios: exponential social cost function (color figure online)

Fig. 9

Compartmental dynamics corresponding to the uncontrolled system ($u\equiv 0$, dash-dotted blue line), fully controlled system ($u \equiv 1$, dashed red line) and optimally controlled system ($u^*$, black line), linear social cost function. High vaccination rate scenario (color figure online)

Fig. 10

Compartmental dynamics corresponding to the uncontrolled system ($u\equiv 0$, dash-dotted blue line), fully controlled system ($u \equiv 1$, dashed red line) and optimally controlled system ($u^*$, black line), linear social cost function. Low vaccination rate scenario (color figure online)

Fig. 11

Optimal controls for low vaccination rate (blue line) and high vaccination rate (red line) scenarios: linear social cost function (color figure online)

4.2 Optimal policies with limited containment

In the second set of numerical experiments, we study the effect of reducing the maximum possible containment level ${\bar{u}}$, since there may be an inability to impose the highest level of control ${\bar{u}} \equiv 1$ for extended periods of time. In fact, the decision maker might prefer a partial level of containment, possibly for a greater number of days, in the face of increasing the total cost, while still determining similar characteristics in the population compartments, that is a trade-off between the length of the maximum containment period and the effectiveness/cost of the restrictions. We then consider the solution of the optimal control problem, assuming different levels for the value ${\bar{u}} \in \{0.4, 0.6, 0.8, 1\}$. For this experiment we report only the case of the quadratic social cost function: similar results are obtained for the other functions.

What our experiment shows is that increasing the maximum level of restriction ${\bar{u}}$ certainly generates a decrease in total cost J, in the face of a less prolonged period of maximum containment. This is observed in the case of a high-intensity vaccination campaign, see Table 8. The final population of Susceptibles and Infected is increasing with ${\bar{u}}$, while the Vaccinated and Recovered show a decreasing behavior. Notice that the change in costs and final value in the compartments going from ${\bar{u}}=0.8$ to ${\bar{u}}=$1 is very small, compared with more than doubling the number of days of maximum containment. The corresponding optimal policies are shown in Fig. 12. Similar behavior is observed in the low-intensity case, except that the number of days of maximum containment is not strictly decreasing, see Table 9 and Fig. 13 showing the corresponding optimal controls.

Table 8 Comparison of the optimally controlled system for different maximum containment levels ${\bar{u}}$ in the high-intensity vaccination scenario. Compartment values at final time

Table 9 Comparison of the optimally controlled system for different maximum containment levels ${\bar{u}}$ in the low-intensity vaccination scenario. Compartment values at final time

Fig. 12

Optimal controls for varying containment levels ${\bar{u}}$. High intensity vaccination rate scenario

Fig. 13

Optimal controls for varying containment levels ${\bar{u}}$. Low intensity vaccination rate scenario

5 Concluding remarks

In this paper, we considered the problem of optimal control of an infectious disease by modeling its diffusion through a SVIR compartmental dynamic. Differently from the classical SIR (or SIRD) model, we consider the possibility to implement a vaccination campaign to immunize the population. The control of the disease is realized by adopting political measures of containment, generally identified here as social distancing, since they may have an impact on the social behavior of the population, e.g., the use of face masks, the partial or total closure of many activities, educational structures, commercial activities, production, and/or different degrees of prohibition of movements. All these measures aim to reduce the disease’s diffusion but imply a cost for the whole society. Hence we introduced a cost functional that explicitly considers these social measures, the social cost function, other than the cost of vaccination and the cost due to the infected population. Our main result is the characterization of the solution of the optimal control of the SVIR dynamical model obtained in terms of a controlled diffusion rate to minimize the overall cost of the disease. We thoroughly describe the optimal control strategy using the Pontryagin Maximum Principle for several instances of the social cost function. Finally, we implemented the optimal controlled system using the Forward-Backward Sweep algorithm by calibrating some of the model parameters using the Italian dataset of the recent COVID-19 pandemics. In a preliminary set of experiments, we investigated the effect of social cost parameters on the optimal solution by comparing it to two extreme cases, namely the no-control and full-control strategies. The former corresponds to a situation where no social restrictions are implemented, while the latter represents a scenario where restrictions are imposed throughout the entire period under consideration. By fixing costs for treatment and vaccination, the optimal policies always allow the total cost to decrease, thereby significantly reducing the social cost in comparison to a full-control strategy, although disease-related costs may increase slightly. Moreover, the optimal policy tends to be a no-control strategy, as expected: conversely, when the social cost is negligible, the optimal strategy shifts towards a full-control strategy. Then, we analyzed the properties of the optimal policies of social restrictions in the two different scenarios, high-intensity and low-intensity vaccine campaign. Our simulations reveal in one scenario, that the optimal strategy achieves population compartment values similar to those of a full-control strategy, but at significantly lower costs, with potential savings of up to $70.2\%$. In the low-intensity vaccine campaign, the Susceptible compartment remains highly populated, up to $70\%$, possibly resulting in an increase in the number of infected individuals at the end of the observation period, stabilizing between 1.1 and $8\%$, while the Recovered and Vaccinated compartments account for a percentage of the population ranging from 26.6 to $34.74\%$. In contrast, the high-intensity vaccine campaign significantly reduces the susceptible population at about $30\%$, and keeps the Infected compartment consistently low, between 0.13 and $0.35\%$, together with about $70\%$ of Recovered and Vaccinated. The optimal control policy involves maximum control for a specific period, followed by a gradual decrease to zero or a bang-bang characterization for the linear social cost function. The duration of maximum control depends on the intensity of the vaccination campaign and the cost function. Overall, the optimal strategy in the high-intensity vaccination scenario reduces costs while maintaining the effectiveness of disease control. Furthermore, in our study of the optimal control problem, we explored the impact of varying the maximum level of control, recognizing that it may not be feasible to implement the highest possible level of control in practice. In such cases, decision makers might opt for a partial level of containment (${\bar{u}} < 1$) for an extended period, even though it could result in higher overall costs. This raises the question of balancing the duration of the maximum containment period with the effectiveness and cost of the imposed restrictions. In the case of quadratic social cost function, our experiments shows in the high-intensity vaccine campaign scenario that increasing the maximum level of restrictions produces a decrease of the total cost, in face of a less prolonged period of maximum containment, going from 15 days when the maximum level is the highest, to 94 days for the lowest. This is in line with the findings in Federico and Ferrari (2021), where the a stochastic version of the SIR model and a quadratic cost function has been considered.

As a final contribution, we highlight some possible further developments of this research. First of all, it would be natural to include in the control variables the rate of vaccination, other than the control of the rate of diffusion. The addition of a controlled vaccination campaign makes the problem more complex from a mathematical point of view, resulting in a two-dimensional constrained optimization problem. In this paper, we preferred to focus only on the impact of the social measures over the overall cost. Nevertheless, we deserve to include this variable in future research. As a second remark, in light of the recent pandemic, it would be interesting to introduce some modifications to the basic SVIR compartmental dynamical model, particularly the possibility for a recovered person to be re-infected. This could be relevant to capturing the phenomenon of virus mutations. The resulting dynamical model can be simply obtained by adding a link from the R to the I compartment. Of course, the analysis of the stability of the uncontrolled system is quite different from the one presented here, as well as the corresponding Hamiltonian function.

Finally, other essential SVIR dynamical system modifications are still under consideration to meet the peculiarities of a possible pandemic. In particular, as noticed in the numerical section based on the COVID-19 data, the cost of the pandemic can be particularly severe for its impact on hospital services becoming overwhelmed, and it is “quantifiable”. On the other hand, the cost of being “quarantined” is undoubtedly more challenging to assess. It is, therefore, reasonable to split the “I” compartment into at least three sub-compartments, e.g., Hospitalized w/o ICU, Hospitalized with ICU, and Quarantined, and to adjust the cost function accordingly, eventually adding other compartments as the Death and/or the Exposed, thus resulting in the SVIRD/SVEIR/SVEIRD models.

Appendices

Appendix A: Proof of Proposition 7

The system (5) can be written as

$$\begin{aligned} \left\{ \begin{array}{ll} S' =\beta _0(u \! - \! 1)SI -(\alpha + \mu )S+\mu &{}S(0)=S_0 \\ \\ V' =\alpha S+\varepsilon \beta _0(u \! - \! 1)VI-(\gamma _1+\mu )V &{}V(0)=V_0 \\ \\ I' =\beta _0(1-u)SI+\varepsilon \beta _0(1-u)VI- (\gamma +\mu )I &{}I(0)=I_0 \end{array} \right. \end{aligned}$$

(A1)

The Hamiltonian function H is defined as

$$\begin{aligned} \begin{array}{l} H(t,S,V,I,u) =au+c_1I+c_2\alpha S+ \lambda _1[-\beta _0(1- u) S I -\alpha S+ \mu (1- S) ]\\ \\ \quad +\lambda _2[\alpha S+\varepsilon \beta _0 (u \! - \! 1) VI-(\gamma _1+\mu )V] \\ \\ \quad +\lambda _3[\beta _0 (1- u) SI +\varepsilon \beta _0 (1- u) VI-(\gamma I + \mu )I] \end{array} \end{aligned}$$

(A2)

and the co-state system (8) can be written as

$$\begin{aligned} \left\{ \begin{array}{l} \lambda _1' =\beta _0(1-u)(\lambda _1 - \lambda _3)I+\alpha (\lambda _1 - \lambda _2)+\mu \lambda _1-c_2\alpha \\ \\ \lambda _2' =\varepsilon \beta _0(1-u)(\lambda _2 -\lambda _3)I+(\gamma _1+\mu )\lambda _2 \\ \\ \lambda _3' =\beta _0(1-u)(\lambda _1 - \lambda _3)S+\varepsilon \beta _0(1-u)(\lambda _2 -\lambda _3)V+(\gamma +\mu )\lambda _3-c_1 \end{array} \right. \end{aligned}$$

(A3)

Since the Hamiltonian is linear in the control, u is bang–bang, singular or a combination (see Joshi et al. 2015; Lenhart and Workman 2007). The singular case is attained if

$$\begin{aligned} \displaystyle {\frac{\partial H}{\partial u}}=a +\beta _0 (\lambda _1-\lambda _3)SI+ \varepsilon \beta _0 (\lambda _2-\lambda _3)VI=0, \end{aligned}$$

(A4)

on a non-trivial interval of time, else if $\frac{\partial H}{\partial u}<0$ the optimal control would be at its upper bound, while if $\frac{\partial H}{\partial u}>0$ it would be at its lower bound. So, to study the singular case, suppose $\frac{\partial H}{\partial u}=0$ on a non-trivial interval of time, calculate

$$\begin{aligned} \frac{d}{dt}\left( \frac{\partial H}{\partial u}\right) =0 \end{aligned}$$

and show that, in the above equation, the control u does not appear explicitly. Then, the value of the singular control will be obtained evaluating

$$\begin{aligned} \frac{d^2}{dt^2}\left( \frac{\partial H}{\partial u}\right) =0. \end{aligned}$$

Hence

$$\begin{aligned} \begin{array}{ll} 0 &{}= \displaystyle {\frac{d}{dt}\left( \frac{\partial H}{\partial u}\right) } =(\lambda _1'-\lambda _3')SI+(\lambda _1-\lambda _3)S'I+(\lambda _1-\lambda _3)SI' \\ \\ &{} +\varepsilon (\lambda _2'-\lambda _3')VI+\varepsilon (\lambda _2-\lambda _3)V' I+\varepsilon (\lambda _2-\lambda _3)VI'. \end{array} \end{aligned}$$

We calculate each term of the sum separately and then we add them together:

$$\begin{aligned}&(\lambda _1'-\lambda _3')SI \\&\quad = [\beta _0(1-u)(\lambda _1 - \lambda _3)I+\alpha (\lambda _1 - \lambda _2)+\mu \lambda _1-c_2\alpha - \\&\qquad - \beta _0(1-u)(\lambda _1 - \lambda _3)S-\varepsilon \beta _0(1-u)(\lambda _2 -\lambda _3)V-(\gamma +\mu )\lambda _3+c_1 ]SI \\&(\lambda _1-\lambda _3)S'I \\&\quad = [\beta _0(u \! - \! 1)SI -(\alpha + \mu )S+\mu ](\lambda _1-\lambda _3)I \\&(\lambda _1-\lambda _3)SI' \\&\quad = [\beta _0(1-u)SI+\varepsilon \beta _0(1-u)VI- (\gamma +\mu )I](\lambda _1-\lambda _3)S \\&\varepsilon (\lambda _2'-\lambda _3')VI \\&\quad = \varepsilon [\varepsilon \beta _0(1-u)(\lambda _2 -\lambda _3)I+(\gamma _1+\mu )\lambda _2 \\&\qquad -\beta _0(1-u)(\lambda _1 - \lambda _3)S-\varepsilon \beta _0(1-u)(\lambda _2 -\lambda _3)V-(\gamma +\mu )\lambda _3+c_1 ]VI \\&\varepsilon (\lambda _2-\lambda _3)V' I \\&\quad = \varepsilon [\alpha S+\varepsilon \beta _0(u \! - \! 1)VI-(\gamma _1+\mu )V](\lambda _2-\lambda _3) I \\&\varepsilon (\lambda _2-\lambda _3)VI' \\&\quad = \varepsilon [\beta _0(1-u)SI+\varepsilon \beta _0(1-u)VI- (\gamma +\mu )I](\lambda _2-\lambda _3)V. \end{aligned}$$

Hence, summing up we obtain with a little algebra

$$\begin{aligned} \begin{array}{ll} \displaystyle {\frac{d}{dt}\left( \frac{\partial H}{\partial u}\right) } &{} = [-(\gamma +\mu )\lambda _1+(\alpha +\mu )\lambda _3-\alpha \lambda _2+(c_1-\alpha c_2)]SI+\mu (\lambda _1-\lambda _3)I \\ \\ &{}\quad +\varepsilon [-(\gamma +\mu )\lambda _2+(\gamma _1+\mu )\lambda _3+c_1]VI. \end{array} \end{aligned}$$

Since the control does not appear in the previous expression, we compute the second derivative⁶:

$$\begin{aligned}{} & {} \frac{d^2}{dt^2}\left( \frac{\partial H}{\partial u}\right) \\{} & {} \quad = I' (S (c_1-\alpha c_2-\alpha \lambda _2+\alpha \lambda _3-(\gamma +\mu ) \lambda _1+\mu \lambda _3)+\varepsilon V (c_1-(\gamma +\mu ) \lambda _2\\{} & {} \qquad +(\gamma _1+\mu ) \lambda _3)+\mu (\lambda _1-\lambda _3))\\{} & {} \qquad + I (S' (c_1-\alpha c_2-\alpha \lambda _2+\alpha \lambda _3-(\gamma +\mu ) \lambda _1+\mu \lambda _3)+\varepsilon V'(c_1-(\gamma +\mu ) \lambda _2\\{} & {} \qquad +(\gamma _1 +\mu ) \lambda _3)\\{} & {} \qquad + S (-\alpha \lambda _2'+(\alpha +\mu ) \lambda _3' - ((\gamma +\mu ) \lambda _1' ) )+\varepsilon V ((\gamma _1+\mu ) \lambda _3'-(\gamma +\mu ) \lambda _2' )\\{} & {} \qquad +\mu (\lambda _1'- \lambda _3')). \end{aligned}$$

By substituting (5) and (8), we get

$$\begin{aligned}{} & {} \frac{d^2}{dt^2}\left( \frac{\partial H}{\partial u}\right) = I ((S (\alpha \! \! + \! \!\beta I\! - \!\beta I u\! + \!\mu )\! - \!\mu ) (\alpha \lambda _2\! - \!\alpha \lambda _3\! + \!\gamma \lambda _1\! - \!c_1\! + \!\alpha c_2\! \\{} & {} \quad + \!\lambda _1 \mu \! - \!\lambda _3 \mu ) \! \\{} & {} \quad +S ((\alpha \! + \!\mu ) (\gamma \lambda _3 \! - \! c_1\! + \!\lambda _3 \mu \! - \!\beta \lambda _1 S(u \! - \! 1)\! + \!\beta \lambda _3 S (u \! - \! 1) \! - \! \beta \varepsilon \lambda _2 (u \! - \! 1) V\! \\{} & {} \quad + \!\beta \varepsilon \lambda _3 (u \! - \! 1) V) \! \\{} & {} \quad -(\gamma \! + \!\mu ) (\! - \!\alpha \lambda _2\! + \!\alpha (\! - \!c_2)\! + \!\lambda _1(\alpha \! + \!I (\beta \! - \!\beta u)\! + \!\mu )\! + \!\beta I \lambda _3(u \! - \! 1))\! - \!\alpha \lambda _2(\gamma _1\! \\{} & {} \quad - \!\beta \varepsilon I (u \! - \! 1)\! + \!\mu ) \! \\{} & {} \quad +\alpha \beta \varepsilon (\! - \!I) \lambda _3(u \! - \! 1))\! + \!\mu (\! - \!\alpha \lambda _2\! + \!c_1\! - \!\alpha c_2\! + \!\lambda _1 (\alpha \! + \!I (\beta \! - \!\beta u)\! + \!\mu )\! + \!\beta I\lambda _3 (u \! - \! 1)\! \\{} & {} \quad + \!\beta \lambda _1 S(u \! - \! 1) \! \\{} & {} \quad -\lambda _3 (\gamma \! + \!\mu \! + \!\beta S (u \! - \! 1)\! + \!\beta \varepsilon u V\! - \!\beta \varepsilon V)\! + \!\varepsilon \beta \lambda _2 (u \! - \! 1)V)\! - \!(\gamma \! + \!\mu \! + \!\beta S (u \! - \! 1)\! \\{} & {} \quad + \!\beta \varepsilon u V\! - \!\beta \varepsilon V) \\{} & {} \quad \times (S (\! - \!\alpha \lambda _2\! + \!\alpha \lambda _3\! - \!\lambda _1 (\gamma \! + \!\mu )\! + \!c_1\! - \!\alpha c_2\! + \!\lambda _3 \mu )\! + \!\varepsilon V (\! - \!\lambda _2 (\gamma \! + \!\mu )\! \\{} & {} \quad + \!\lambda _3 (\gamma _1\! + \!\mu )\! + \!c_1)\! + \!\mu (\lambda _1\! - \!\lambda _3)) \! \\{} & {} \quad +\varepsilon (\! - \!\lambda _2 (\gamma \! + \!\mu )\! + \!\lambda _3 (\gamma _1\! + \!\mu )\! + \!c_1) (\alpha S\! - \!V(\gamma _1\! - \!\beta \varepsilon I (u \! - \! 1)\! + \!\mu ))\! \\{} & {} \quad + \!\varepsilon V((\gamma _1\! + \!\mu ) (\gamma \lambda _3\! - \!c_1\! + \!\lambda _3 \mu \! \\{} & {} \quad -\beta \lambda _1 S(u \! - \! 1)\! + \!\beta \lambda _3 S(u \! - \! 1)\! - \!\beta \varepsilon \lambda _2 (u \! - \! 1) V\! + \!\beta \varepsilon \lambda _3 (u \! - \! 1)V)\! - \!(\gamma \! + \!\mu ) (\gamma _1\lambda _2 \\{} & {} \quad -\beta \varepsilon I (u \! - \! 1) (\lambda _2\! - \!\lambda _3)\! + \!\lambda _2 \mu ))), \end{aligned}$$

which is linear in the control u: hence

$$\begin{aligned} \frac{d^2}{dt^2}\left( \frac{\partial H}{\partial u}\right) =A_1(t) u(t) - A_2(t) = 0 \end{aligned}$$

giving the singular control

$$\begin{aligned} u_{sing}(t) = \frac{A_2(t)}{A_1(t)}, \end{aligned}$$

if $A_1(t) \ne 0$ and $0 \le \frac{A_2(t)}{A_1(t)} \le {\bar{u}}$, where the functions $A_i$ are given by

$$\begin{aligned} A_1&= I (-\alpha \lambda _1 \mu +2 \alpha \lambda _2 \mu -\alpha \lambda _3 \mu +2 \gamma \lambda _1 \mu + c_1 (S (-\alpha (\varepsilon -2)+\gamma +\beta I\\&\quad +3 \mu -2 \beta \varepsilon V) \\&\quad + \varepsilon V (\gamma +2 \gamma _1+\beta \varepsilon I+3 \mu )-2 \mu -\beta S^2-\beta \varepsilon ^2 V^2)+\alpha c_2 (-S (\alpha +2 \gamma +\beta I\\&\quad +3 \mu -\beta \varepsilon V) \\&\quad +2 \mu +\beta S^2) - \beta I \lambda _1 \mu +\beta I \lambda _3 \mu +\alpha \beta \varepsilon I \lambda _2 S-\alpha \beta \varepsilon I \lambda _3 S-\alpha \beta I \lambda _2 S\\&\quad +\alpha \beta I \lambda _3 S-\beta \gamma I \lambda _3 S \\&\quad -\beta \gamma \varepsilon ^2 I \lambda _3 V+\beta \gamma _1 \varepsilon ^2 I \lambda _3 V+ \lambda _1 \mu ^2- \lambda _3 \mu ^2-\alpha \beta \lambda _1 S^2+\alpha \beta \lambda _2 S^2+\beta \gamma \lambda _1 S^2\\&\quad -\alpha ^2 \lambda _2 S \\&\quad +\alpha ^2 \lambda _3 S+\alpha \gamma \varepsilon \lambda _2 S-2 \alpha \gamma \lambda _2 S-\alpha \gamma _1 \varepsilon \lambda _3 S+\alpha \gamma _1 \lambda _2 S+\alpha \varepsilon \lambda _2 \mu S-\alpha \varepsilon \lambda _3 \mu S \\&\quad - 2 \alpha \lambda _2 \mu S+2 \alpha \lambda _3 \mu S-\gamma ^2 \lambda _1 S-2 \gamma \lambda _1 \mu S- \lambda _1 \mu ^2 S+ \lambda _3 \mu ^2 S\\&\quad +\beta \gamma \varepsilon \lambda _1 S V+\beta \gamma \varepsilon \lambda _2 S V \\&\quad - \beta \gamma _1 \varepsilon \lambda _1 S V+\beta \gamma \varepsilon ^2 \lambda _2 V^2-\beta \gamma _1 \varepsilon ^2 \lambda _2 V^2-\beta \varepsilon \lambda _1 \mu V-\gamma ^2 \varepsilon \lambda _2 V \\&\quad - 2 \gamma \varepsilon \lambda _2 \mu V+\gamma _1^2 \varepsilon \lambda _3 V+2 \lambda _1 \varepsilon \lambda _3 \mu V-\varepsilon \lambda _2 \mu ^2 V+\varepsilon \lambda _3 \mu ^2 V+\varepsilon \beta \lambda _2 \mu V), \end{aligned}$$

and

$$\begin{aligned} A_2&= I (\beta c_1 (I (S+\varepsilon ^2 V )-(S+\varepsilon V)^2 )+\alpha \beta c_2 S (-I+S+\varepsilon V)-\beta I \lambda _1 \mu \\&\quad +\beta I \lambda _3 \mu \\&\quad +\alpha \beta \varepsilon I \lambda _2 S-\alpha \beta \varepsilon I \lambda _3 S-\alpha \beta I \lambda _2 S+\alpha \beta I \lambda _3 S-\beta \gamma I \lambda _3 S-\beta \gamma \varepsilon ^2 I \lambda _3 V \\&\quad +\beta \gamma _1 \varepsilon ^2 I \lambda _3 V - \alpha \beta \lambda _1 S^2+\alpha \beta \lambda _2 S^2+\beta \gamma \lambda _1 S^2+\beta \gamma \varepsilon \lambda _1 S V+\beta \gamma \varepsilon \lambda _2 S V \\&\quad -\beta \gamma _1 \varepsilon \lambda _1 S V + \beta \gamma \varepsilon ^2 \lambda _2 V^2-\beta \gamma _1 \varepsilon ^2 \lambda _2 V^2-\beta \varepsilon \lambda _1 \mu V+\varepsilon \beta \lambda _2 \mu V ). \end{aligned}$$

$\square$

Appendix B: SVIR parameters estimation

The estimation of parameters for the SVIR model is typically based on a discrete-time version of (1) (where we set $\beta _1 = \epsilon \beta$), once available the observations for the compartments. By considering a discretization period $\Delta t =1$ day, and by letting $n = 0, 1, \ldots$ the discrete time instants, we consider a first-order scheme to obtain the following finite-differences model:

$$\begin{aligned} \left\{ \begin{array}{ll} S_{n+1} =S_n -\beta S_n I_n -\alpha S_n+ \mu - \mu S_n &{} S_0=s_0 \\ \\ V_{n+1} =V_n + \alpha S_n - \epsilon \beta V_n I_n-\gamma _1V_n - \mu V_n &{} V_0 = v_0 \\ \\ I_{n+1} =I_n + \beta S_n I_n + \epsilon \beta V_n I_n-\gamma I_n - \mu I_n &{} I_0=i_0 \\ \\ R_{n+1}=R_n + \gamma _1 V_n+\gamma I_n- \mu R_n &{} R_0=r_0. \end{array} \right. \end{aligned}$$

(B5)

By assuming the parameter $\mu$ as exogeneously given, the system is linear in the remaining parameters $\vartheta := (\beta , \alpha , \gamma _1, \gamma )'$. Hence, by defining

$$\begin{aligned} \Delta _n = \left( \begin{array}{c} S_{n+1}-S_n(1-\mu ) \\ V_{n+1}-V_n(1-\mu ) \\ I_{n+1} - I_n(1-\mu ) \\ R_{n+1}-R_n(1-\mu ) \end{array} \right) \ \ \ A_n = \left( \begin{array}{cccc} - S_n I_n &{} -S_n &{} 0 &{} 0 \\ \epsilon V_n I_n &{} S_n &{} -V_n &{} 0 \\ (S_n+\epsilon V_n) I_n &{} 0 &{} 0 &{} -I_n \\ 0 &{} 0 &{} V_n &{} I_n \end{array} \right) \end{aligned}$$

we can write (B5) in matrix form as $A_n \vartheta = \Delta _n$. Given the observed values of the compartments, the standard constrained regression OLS can therefore be used as the basic estimation procedure for the parameters of the model, that is

$$\begin{aligned} {\hat{\vartheta }} = \text{ argmin}_{\vartheta \ge 0} \sum _{n=1}^{T-1} \Vert \Delta _n - A_n \vartheta \Vert _2^2. \end{aligned}$$

(see e.g. Calafiore et al. 2020).

By considering the system instead with time-varying coefficients

$$\begin{aligned} \left\{ \begin{array}{ll} S_{n+1} =S_n -\beta _n S_n I_n -\alpha _n S_n+ \mu - \mu S_n &{} S_0=s_0 \\ \\ V_{n+1} =V_n + \alpha _n S_n - \epsilon \beta _n V_n I_n-\gamma _{1,n}V_n - \mu V_n &{} V_0 = v_0 \\ \\ I_{n+1} =I_n + \beta _n S_n I_n + \epsilon \beta _n V_n I_n-\gamma _n I_n - \mu I_n &{} I_0=i_0 \\ \\ R_{n+1}=R_n + \gamma _{1,n} V_n+\gamma _n I_n- \mu R_n &{} R_0=r_0, \end{array} \right. \end{aligned}$$

(B6)

we may write the discrete-time dynamic equations in a matrix form as $A_n \vartheta _n = \Delta _n$, where $\vartheta _n:= (\beta _n, \alpha _n, \gamma _{1,n}, \gamma _n)'$. When $\alpha _n = \gamma _{1,n} \equiv 0$, the system has the unique solution

$$\begin{aligned} \left\{ \begin{array}{ccc} {\hat{\beta }}_n &{} = &{} - \frac{\Delta _n^{(1)}}{S_n I_n} \\ \\ {\hat{\gamma }}_n &{} = &{} \frac{\Delta _n^{(4)}}{I_n}. \end{array} \right. \end{aligned}$$

Fig. 14

Comparison of the cost values for the three strategies, no-control, full-control, optimal control, as a function of the social cost function parameter b for the quadratic social cost function

Appendix C: Analysis of the cost functions

Fig. 15

Comparison of the cost values for the three strategies, no-control, full-control, optimal control, as a function of the exponential model of social cost function parameter k

Fig. 16

Comparison of the cost values for the three strategies, no-control, full-control, optimal control, as a function of the linear model of social cost function parameter a

In Figs. 14, 15, and 16 we plotted the values of the costs $J_{SC}, J_{IC}$ and $J_{VC}$, and the corresponding total cost J, as a function of the parameters of the social cost function, b, k, a, respectively (see Sect. 3). Our sensitivity analysis shows qualitatively similar behavior in the three cases considered: in particular, the optimal strategy always reduces the total cost compared to the two benchmark strategies, $u(t) \equiv 1$, and $u(t)\equiv 0$. Moreover, for low values of the social cost function parameter, it is possible to identify a regime in which the full-control strategy produces lower costs than the no-control strategy. As the parameter increases, the full-control strategy becomes increasingly costly, and at the same time, the optimal strategy “converges” to the no-control strategy.