On the unfairness of actuarial fair annuities

Abstract

Actuarial fairness pertains to the situation in which the price of an insurance contract is equal to its expected outcome. We show that actuarial fairness leads to “unfairness” in that annuitants with higher survival rates can choose a better payoff in the sense of second-order stochastic dominance than those with lower survival rates. To deal with this issue, we propose equal utility pricing, i.e., we determine prices such that all contracts have the same (nonlinear) utility from the viewpoint of a third party (e.g., a social planner). This approach is of particular relevance with respect to the design of group self-annuitization schemes.

1 Introduction

Actuarial fairness finds its pedigree in the seventeenth century, when, based on an analysis of gambling contracts, Johan De Witt (1625–1672) put forward the idea that the fair price of an insurance contract is obtained by computing the expected outcome. Actuarial fairness is thus fairness on average: One can expect to get back from the insurer the same amount (adjusted for time value) that has been paid as a premium. While this principle is appealing, the variability around the mean may differ from one contract to another, and it appears natural to account for differences in contracts’ variability as well. Under a fairly general setup of a financial market, we show that if all risk-averse utility maximizers agree that if one digital option has lower utility than another, while having the same expected value, then the contract with the lower utility will be strictly cheaper. We say in this case that prices are consistent with second-order stochastic dominance.

The life insurance equivalent of a digital option is a pure endowment contract, in which at a given maturity date an insured receives upon survival a fixed amount, but zero otherwise. We show, however, that there are pure endowment contracts with the same actuarial fair price, but nevertheless one is better than the other in the sense of second-order stochastic dominance, which can be seen as “unfair.” The same issue persists for annuity contracts. Specifically, we show that the payoffs to annuitants with higher survival probabilities outperform (from the viewpoint of a risk-averse utility maximizer) the payoffs to annuitants with lower survival probabilities. To this end, we consider in this paper only the case in which differences among survival probabilities result from individuals having different ages and we do not consider other reasons that justify different survival rates. For example, in Pitacco and Tabakova (2022), different premiums for annuity products result from different health status of individuals.

To remedy this problem of “unfairness,” we propose equal utility pricing. In this regard, we note that a recent online book by Sharpe (2017) points out that using expected utility theory (advocated by traditional economists) is at least instructive to see whether the traditional approaches are helpful, including the context of life insurance and retirement products. Specifically, we propose that in a first step the insurer establishes the total premium needed to insure the pool of insureds. In a second step, the individual prices are determined such that participants’ contracts exhibit equal utility per unit of premium paid, i.e., there is no interpersonal envy (Herreiner and Puppe 2009), from the viewpoint of a third party. We show that this approach is feasible and consistent with financial pricing. Further, we determine the equilibrium prices explicitly in case the insureds use power utility¹ functions to evaluate their payoffs.

Equal utility pricing is related to the concepts of the equivalent utility principle (also called the zero utility principle) and utility indifference pricing, both of which have been widely applied in insurance pricing, see, e.g., Henderson (2002) and the references therein. Considering the insurance contract from the insured’s viewpoint, the zero utility principle requires that the insurance premium be determined such that the insured is indifferent as to buying or not buying the contract. Utility indifference pricing complies with the zero utility principle and is typically coupled with the optimal dynamic asset allocation decision. In contrast to these concepts, in which equal utility is imposed on a single insured, the equal utility pricing proposed in our framework concerns various insureds. We observe the “unfairness” among insureds through actuarial fair pricing and propose a pricing that ensures fairness among insureds in terms of expected utility.

Actuarial fair pricing implicitly assumes that all probabilities used are true, i.e., the life table used in pricing reflects what is truly expected and there are no loadings (best-estimate life table). This paper aims at demonstrating the actuarial fair pricing can be perceived as unfair and provides a possible solution by applying utility-equivalent pricing. Actuarial fair pricing is, however, not applied as such in insurance practice. Indeed, life tables that are used for pricing contracts typically deviate from the best-estimate life table. Such deviations from expected values arise from various risk sources. For instance, even if the modeled best-estimate life table is perfect, the number of deaths in each time period is rarely if ever an exact match to its expected value. Moreover, there is uncertainty in the values of the model parameters of the best-estimate model (parameter risk), and there is also the issue of using an inherently wrong model, e.g., because of an incorrect specification of mortality trends (model risk). To account for these issues, the insurer typically uses a more prudent life table (incorporating implicit safety loadings). Moreover, to cover operational and solvency costs and to reward its shareholders, the insurer may also add explicit loadings. We show in Sect. 6.2 that when actuarial fair pricing is based on adjusted probabilities, consistency with second-order stochastic dominance (evaluated under true probabilities) is still violated under fairly weak conditions.

As an important application of our results, we discuss the case of group self-annuitization (Piggott et al. 2005). Here, a group of people join forces in that each of the group members agrees to invest some amount and to earn an investment return while sharing longevity risk. Specifically, at the end of some given time period, the accumulated value of the investments belonging to the dead participants is not transferred to their heirs, but is shared among the surviving participants. At each period, the surviving participants thus receive an investment return plus an additional share (mortality credit) coming from the accumulated value of the investments made by participants who do not survive. Actuarial fairness then dictates that this share is determined such that, ex ante, each participant earns the same expected return (Donnelly 2015; Sabin and Forman 2016; Fullmer and Sabin 2018). The designed pooled group annuitization with an infinite pool size is thus observationally equivalent to an annuity under the actuarial fair pricing principle. In the context of pooled group annuitization products, our results then imply that actuarially fairly pooled group annuitization products are not fair insofar as participants with higher survival rates will have a better contract payoff in the sense of second-order stochastic dominance. By contrast, our newly proposed equal utility pricing rule ensures that consistency with second-order stochastic dominance is preserved. As compared to traditional actuarial fair pricing, equal utility pricing leads to higher premiums (or lower expected benefit per unit of premium invested) for those with a lower mortality rate and lower premiums (or higher expected benefits per unit of premium invested) for those with a higher mortality rate. Under the plausible assumption that there is a negative correlation between income and mortality risk, equal utility pricing can be seen as a possible tool for reducing income inequality (Nelissen 1995; Bommier et al. 2011); social planners may use it when designing retirement products such as group self-annuitization products in which longevity risk is shared among policyholders.

The remainder of this paper is structured as follows. We introduce some preliminaries related to equivalence pricing in insurance in Sect. 2 and discuss the issues with actuarial fairness, in contrast to financial pricing, in Sect. 3. With the help of pure endowment and annuity products, we introduce in Sect. 4 the equal utility pricing rule. In Sect. 5, we compare the equivalence and equal utility pricing, using power utility. Section 6 discusses the case in which a risk loading is charged additionally to the actuarial fair premium and considers the application of the equal utility pricing rule in innovative retirement products like group self-annuitization schemes. Section 7 concludes the article.

2 Preliminaries

Let $T_{x}$ denote the random residual lifetime of an individual aged x and $K_x$ be the curtate remaining lifetime, defined as the integer part of $T_{x}$, i.e., $K_x={\lfloor }T_x{\rfloor }$. Denote by $\omega$ the maximum age one can attain and let $\mathcal {H}= \{0, 1, 2,\ldots ,\omega -x \}$ be the set containing all possible outcomes of $K_x$. Denote ${}_k p_x:=P(K_x \ge k)>0, \; k \in \mathcal {H}$.

A life annuity payoff² with payoff function $g(\cdot )$ is a random vector $g(K_x)$ of the form

$$\begin{aligned} g(K_x) = (b_1\mathbb {I}_{\{K_x\ge 1\}},\ldots , b_{\omega -x}\mathbb {I}_{\{K_x\ge \omega -x\}}), \quad b_k \ge 0, \; k=1,\ldots , \omega -x, \end{aligned}$$

(1)

where $I_A$ is the indicator fuction which gives 1 if A occurs, otherwise 0.

Hence, the benefits $b_k$ are paid out to the beneficiaries of the contract under the binding condition that the insured person is alive at time k, $k=1,\ldots ,\omega -x$. To deal with the time value of future cash flows, it is also useful to associate with each $g(K_x)$ the net present value of future random benefits, which we denote by $D(K_x)$. In this regard, we assume that discounting is done using a constant technical interest rate $\delta$, i.e., we consider discount factors of the form

$$\begin{aligned} v_k=(1+\delta )^{-k}, \quad k=1,\ldots ,\omega -x. \end{aligned}$$

(2)

Nonetheless, our results can be readily extended to the case in which the insurer uses another yield curve to make present value calculations. Hence, we express $D(K_x)$ as

$$\begin{aligned} D(K_x) = \sum _{k=1}^{\omega -x} v_k b_k\mathbb {I}_{\{K_x\ge k\}}, \quad b_k \ge 0, \; k=1,\ldots , \omega -x. \end{aligned}$$

(3)

In life insurance, the so-called equivalence principle is the basic concept on which to set premiums (Olivieri and Pitacco 2015). In essence, the principle states that at all times there must be a balance between expected income (premiums to be received) and expected loss (benefits to be paid). Apart from Section 6.2, we assume that all probabilities are on a realistic basis, i.e., we use true probabilities, and these are moreover assumed to be known in that there is no uncertainty about their levels. In this sense, possible systematic deviations are disregarded, and risks do not come from this aspect.

Definition 2.1

(Equivalence principle). Given a contract payoff function g(.), the equivalence principle sets the actuarial fair premium $\pi (g({K_x}))$ of a life insurance contract $g(K_x)$ as equal to

$$\begin{aligned} \pi (g({K_x}))&:=\pi _x(b_1,\ldots ,b_{\omega -x}) = \mathbb {E}(D(K_x))\nonumber \\&=\sum _{k=1}^{\omega -x} v_k \mathbb {E}(b_k\mathbb {I}_{\{K_x\ge k\}}) \nonumber \\&= \sum _{k=1}^{\omega -x} v_k \cdot {}_k p_x \cdot b_k. \end{aligned}$$

(4)

The actuarial fair premium $\pi (g({K_x}))$ of an insurance contract $g({K_x})$ is thus set equal to the sum of discounted expected benefits $\mathbb {E}(b_k\mathbb {I}_{\{K_x\ge k\}})$ that are paid by the insurer. All life insurance contracts $g(K_x)$ that are priced using the equivalence principle are similar in the sense that they provide the same rate of return $\delta$ for their stream of expected cash flows given as

$$\begin{aligned} (-\pi _x(b_1,\ldots ,b_{\omega -x}),\mathbb {E}(b_1\mathbb {I}_{\{K_x\ge 1\}}),\ldots ,\mathbb {E}(b_{\omega -x}\mathbb {I}_{\{K_x\ge \omega -x\}})) . \end{aligned}$$

(5)

For further details on the equivalence principle and its application in insurance pricing, see, for instance, Chapter 4 of Olivieri and Pitacco (2015), Chapter 6 of Dickson et al. (2009) or Section 4.2 of Bacinello et al. (2011).

Here are a few special cases of life annuity payoffs.

• Pure endowment at time $t=k$: The payoff $g(K_x)$ writes as

  $$\begin{aligned} g(K_x) = (0,\ldots ,0,b_k\mathbb {I}_{\{K_x\ge k\}},0,\ldots , 0), b_k >0, \end{aligned}$$

  (6)

  i.e., the amount $b_k$ will be paid provided the insured is alive at time $t=k$. In what follows, we also denote such payoff as $g(K_x) = b_k\mathbb {I}_{\{K_x\ge k\}}.$

  $$\begin{aligned} \pi _x(b_k) = \mathbb {E}(v_kb_k\mathbb {I}_{\{K_x\ge k\}})= v_k \cdot {}_k p_x \cdot b_k. \end{aligned}$$

  (7)

• Deferred life annuity: The amounts $b_k>0$, $k=m,m+1,\ldots , \omega -x$, are paid to the insured at each time $k=m,m+1, \ldots ,\omega -x$ provided he is alive at that time. We obtain that

  $$\begin{aligned} g(K_x) = (0,\ldots , 0,b_{m}\mathbb {I}_{\{K_x\ge m\}},\ldots b_{\omega -x}\mathbb {I}_{\{K_x\ge \omega -x\}}) \end{aligned}$$

  (8)

  with actuarial fair premium given as

  $$\begin{aligned} \pi _x(b_m,\ldots ,b_{\omega -x}) = \sum _{k=m}^{\omega -x} \pi _x(b_k), \end{aligned}$$

  where $\pi _x(b_k)$ is as in (7).

Note that all components of the general annuity $g(K_x)$ as defined in (1) are pure endowment payoffs $b_k\mathbb {I}_{\{K_x\ge k\}}$, $k=1,2\ldots , \omega -x$ and observe that these endowment payoffs are all increasing in the random variable $K_x$.

We define the expected utility of the general annuity product $g(K_x)$ as defined in (1) as follows:

$$\begin{aligned} V_u(g(K_x)) =\sum _{b_k>0} v_k \; {}_kp_x \; u(b_k), \end{aligned}$$

(9)

where $u: (0,\infty )\rightarrow (0,\infty )$ is an increasing concave utility function.³ Note that the utility functions we consider are finite valued, which implies that the expected utility $V_u(g(K_x))$ is well defined and finite. Individuals are assumed to maximize expected lifetime utility and to derive utility from their consumption (here, payments from retirement products) upon survival. When aggregating utility levels at different points in time, discounting is used to account for time value of consumption. Note that this definition of expected lifetime utility is based on the independence assumption between mortality and financial market risk. This approach is fairly standard in the literature on retirement products; see, e.g., Yaari (1965) and Chen et al. (2020).

Definition 2.2

(Second-order stochastic dominance). Let $g_1(K_{x_1})$ and $g_2(K_{x_2})$ denote two annuity payoffs. We say that $g_1(K_{x_1})$ dominates $g_2(K_{x_2})$ in the sense of second-order stochastic dominance, denoted as $g_1(K_{x_1}) \ge _{SSD} g_2(K_{x_2})$, if and only if for every non-decreasing concave utility function $u:(0,\infty )\rightarrow (0,\infty )$,

$$\begin{aligned} V_u(g_1(K_{x_1})))\ge V_u(g_2(K_{x_2}))). \end{aligned}$$

(10)

If, in addition, inequality (10) is strict for every strictly increasing and strictly concave utility function u, then $g_1(K_{x_1})$ is said to strictly dominate $g_2(K_{x_2})$ and we denote $g_1(K_{x_1}) >_{SSD} g_2(K_{x_2})$.

When $g_1(K_{x_1}) >_{SSD} g_2(K_{x_2})$, all non-satiated risk-averse utility maximizers thus prefer $g_1(K_{x_1})$ over $g_2(K_{x_2})$, and the preference is usually strict.

3 Issue with actuarial fairness

Hereafter, we show that two individuals might purchase a pure endowment resp. annuity contract bearing the same actuarial fair premium, but such that one contract is better than the other from the viewpoint of a risk-averse utility maximizer. This is at odds with the economic intuition that better contracts should be more expensive.

Proposition 3.1

(Unfairness of pure endowments). Consider two individuals aged $x_i$, $i=1,2$, each of whom purchases a pure endowment contract with a maturity date $1 \le k\le \text {min}\{\omega -x_1, \omega -x_2\}$,⁴

$$\begin{aligned} g_i(K_{x_i})=b_k^i \cdot \mathbb {I}_{\{K_{x_i}\ge k\}}, \quad i=1,2. \end{aligned}$$

Assume that ${}_k p_{x_1} > {}_k p_{x_2}$ and let

$$\begin{aligned} b_k^2 =\frac{{}_k p_{x_1} }{{}_k p_{x_2}} b_k^1>0. \end{aligned}$$

It holds that

• (i) $\pi _{x_1}(g_1(K_{x_1}))=\pi _{x_2}(g_2(K_{x_2}))$.

• (ii) $g_1(K_{x_1}) >_{SSD} g_2(K_{x_2})$.

Proof

By construction, $g_1(K_{x_1})$ and $g_2(K_{x_2})$ have the same mean, and the proof for (i) is thus immediate. To prove (ii), observe that $V_u(g_1(K_{x_1}))=v_k \cdot {}_k p_{x_1} \cdot u(b_k^1)$ and $V_u(g_2(K_{x_2}))=v_k \cdot {}_k p_{x_2} \cdot u(\frac{{}_k p_{x_1} }{{}_k p_{x_2}} b_k^1)$. Note that

$$\begin{aligned} v_k \cdot {}_k p_{x_1} \cdot u(b_k^1)- v_k \cdot {}_k p_{x_2} \cdot u(\frac{{}_k p_{x_1} }{{}_k p_{x_2}} b_k^1) =v_k \cdot {}_k p_{x_1} \cdot b_k^1 \left( \frac{u(b_k^1)}{b_k^1}- \frac{u(\frac{{}_k p_{x_1} }{{}_k p_{x_2}} b_k^1)}{\frac{{}_k p_{x_1} }{{}_k p_{x_2}} b_k^1} \right) . \end{aligned}$$

As $u:(0,\infty )\rightarrow (0,\infty )$ is increasing, concave and finite valued,⁵ we obtain that for every $0 <y \le z$,

$$\begin{aligned} \frac{u(y)}{y} \ge \frac{u(z)}{z}. \end{aligned}$$

(11)

The above inequality is strict when the increasingness and concavity of u are strict. This implies (ii). $\square$

Note also that if ${}_k p_{x_1} = {}_k p_{x_2}$, the payoffs are identically distributed and therefore are equally preferred.

Corollary 3.2

Consider two individuals aged $x_i$, $i=1,2$, each of whom purchases a pure endowment contract with a maturity date $1 \le k\le \text {min}\{\omega -x_1, \omega -x_2\}$,

$$\begin{aligned} g_i(K_{x_i})=b_k^i \cdot \mathbb {I}_{\{K_{x_i}\ge k\}}, \quad i=1,2. \end{aligned}$$

Assume that ${}_k p_{x_1} > {}_k p_{x_2}$ and let $b_k^i >0$, $i=1,2$. It holds that

$$\begin{aligned} \frac{g_1(K_{x_1})}{\pi _{x_1} (g_1(K_{x_1}))} >_{SSD} \frac{g_2(K_{x_2})}{\pi _{x_2} (g_2(K_{x_2}))}. \end{aligned}$$

Proof

Denote $\frac{g_1(K_{x_1})}{\pi _{x_1} (g_1(K_{x_1}))}$ as $g^*_1(K_{x_1})$ and $\frac{g_2(K_{x_2})}{\pi _{x_2} (g_2(K_{x_2}))}$ as $g^*_2(K_{x_2})$. It is then sufficient to observe that $g^*_1(K_{x_1})$ and $g^*_2(K_{x_2})$ satisfy the conditions of Proposition 3.1. $\square$

Corollary 3.2 shows that per unit of actuarial fair premium of two pure endowment contracts can always be compared in the sense of second-order stochastic dominance: From the viewpoint of a strictly risk-averse utility maximizer, the payoff corresponding to the higher survival probability, i.e., $g(K_{x_1})$, is strictly preferred over the payoff with lower survival probability, i.e., $g(K_{x_2})$.

Remark 3.3

Proposition 3.1 and Corollary 3.2 can be extended to the case in which the two payoffs have a different maturity, say $k_1$ resp. $k_2$. Specifically, let $v_{k_1}\cdot {}_{k_1} p_{x_1} > v_{k_2}\cdot {}_{k_2} p_{x_2}$ and let

$$\begin{aligned} b_k^2 =\frac{v_{k_1}\cdot {}_{k_1} p_{x_1} }{v_{k_2}\cdot {}_{k_2} p_{x_2}} b_k^1>0. \end{aligned}$$

In a similar way as in the proof for Proposition 3.1, it shows that $\pi _{x_1}(g_1(K_{x_1}))=\pi _{x_2}(g_2(K_{x_2}))$ and $g_1(K_{x_1}) >_{SSD} g_2(K_{x_2})$.                                                             $\triangle$

Proposition 3.1 can be extended to the case of annuities as follows.

Proposition 3.4

(Unfairness of annuities). Consider two individuals aged $x_i$, $i=1,2$, each of whom purchases an annuity

$$\begin{aligned} g_i(K_{x_i}) = (0,\ldots , 0,b_{m}^i\mathbb {I}_{\{K_{x_i}\ge m\}},\ldots , b_{n}^i\mathbb {I}_{\{K_{x_i}\ge n\}}), \quad b_k^i > 0, k=m,\ldots ,n, \; i=1,2, \end{aligned}$$

in which $1 \le n\le \text {min}\{\omega -x_1, \omega -x_2\}$. Assume that for all $m\le k \le n$, ${}_k p_{x_1} \ge {}_k p_{x_2}$ with at least one of the inequalities being strict, and let $b_k^2 =\frac{{}_k p_{x_1} }{{}_k p_{x_2}} b_k^1$. It holds that

• (i) $\pi _{x_1}(g_1(K_{x_1}))=\pi _{x_2}(g_2(K_{x_2}))$.

• (ii) $g_1(K_{x_1}) >_{SSD} g_2(K_{x_2}).$

Proof

Statement (i) follows from the construction of the payoffs $g(K_{x_1})$ and $g(K_{x_2})$. To prove (ii), observe that $V_u(g_1(K_{x_1}))=\sum _{b_k^1>0} v_k \cdot {}_k p_{x_1} \cdot u(b_k^1)$ and $V_u(g_2(K_{x_2}))=\sum _{b_k^1>0} v_k \cdot {}_k p_{x_2} \cdot u(\frac{{}_k p_{x_1} }{{}_k p_{x_2}} b_k^1)$. Note that

$$\begin{aligned} \sum _{k=m}^{n} v_k \cdot {}_k p_{x_1} \cdot u(b_k^1)- \sum _{k=m}^{n} v_k \cdot {}_k p_{x_2} \cdot u\left( \frac{{}_k p_{x_1} }{{}_k p_{x_2}} b_k^1\right) = \sum _{k=m}^{n} v_k \cdot {}_k p_{x_1} \cdot b_k^1 \left( \frac{u(b_k^1)}{b_k^1}- \frac{u(\frac{{}_k p_{x_1} }{{}_k p_{x_2}} b_k^1)}{\frac{{}_k p_{x_1} }{{}_k p_{x_2}} b_k^1} \right) . \end{aligned}$$

As it holds that ${}_k p_{x_1} \ge {}_k p_{x_2}$, $m\le k \le n$, the positivity and concavity of $u(\cdot )$ imply that all terms $\left( \frac{u(b_k^1)}{b_k^1}- \frac{u(\frac{{}_k p_{x_1} }{{}_k p_{x_2}} b_k^1)}{\frac{{}_k p_{x_1} }{{}_k p_{x_2}} b_k^1}\right)$ are nonnegative, which ensures the nonnegativity of the sum. This implies the statement. $\square$

Note that Proposition 3.4 can also be extended to the case of individuals having different maturity dates for the annuity payoffs they wish to receive. The results in this section show that annuity contracts may have the same actuarial fair premium, but nevertheless are such that from the viewpoint of any risk-averse observer one is always better than the other. This observation is not consistent with the paradigm that riskier assets must earn a higher expected return to give investors an incentive to hold them. The equivalent in financial markets of a pure insurance endowment contract is a so-called digital option, which pays out either nothing or a fixed amount. Hereafter, we will show that if one digital option dominates another contract in the sense of second-order stochastic dominance, then this contract will also be strictly more expensive.

To show this, consider an arbitrage-free and frictionless financial market described by a market model $S=(S_{t})_{0\le t\le T}$ in a filtered probability space $(\Omega ,\mathcal {A},(\mathcal {A} _{t})_{0\le t\le T},\mathbb {P})$. Let $r>0$ be the continuous risk-free rate, and let $\varphi := (\varphi _{t})_{0\le t\le T}=(e^{-rt}\frac{\text {d}\mathbb {Q}}{\text {d}\mathbb {P}})_{0\le t\le T}$ be a state-price density process that is adapted to the given filtration and that is used by the market participants for arbitrage-free pricing, where $\mathbb {Q}$ denotes the risk neutral pricing measure. Hence, the price of a payoff $X_k$ that matures at time k is given as

$$\begin{aligned} c(X_k)&=\mathbb {E}_\mathbb {P}(\varphi _{k}X_{k})\nonumber \\&=e^{-rk}\mathbb {E}_\mathbb {Q}(X_{k}). \end{aligned}$$

(12)

We assume that $\varphi _{t}$, ${0\le t\le T}$ is strictly continuously distributed. Roughly speaking, a low realization of $\varphi _t$ describes a good economic state, while a high realization of $\varphi _t$ represents an unfavorable economic state. Furthermore, it is well known that every investor with an increasing utility function who wishes to obtain a payoff that matures at time k will select a payoff that is decreasing in $\varphi _k$; see Dybvig (1988); Bernard et al. (2014) and Rüschendorf and Vanduffel (2020). Hence, without loss of generality, we consider payoffs that are decreasing in the state-price density.⁶

Furthermore, denote

$$\begin{aligned} p(c_k):=\mathbb {P}(\varphi _{k}\le c_k) \end{aligned}$$

and

$$\begin{aligned} q(c_k)&:=\mathbb {Q}(\varphi _{k}\le c_k)\\&=e^{rk}\mathbb {E}_\mathbb {P}(\varphi _{k}\mathbb {I}_{\varphi _k\le c_k}). \end{aligned}$$

In order to demonstrate a nifty parallel comparison to the presented insurance products, we consider digital options and multiple digital options in Propositions 3.5 and 3.6, which can be considered as an “equivalence,” respectively, to pure endowment and annuity products.

Proposition 3.5

(Digital options that are better are also more expensive). Consider two individuals, $i=1,2$, each of whom purchases a digital option with a maturity date $k>0$,

$$\begin{aligned} h_i(\varphi ):=b_k^i\mathbb {I}_{\varphi _{k}\le c_k^i}, \; i=1,2. \end{aligned}$$

Assume that $p(c_k^1)>p(c_k^2)$ and that both options have the same expected value, i.e.,

$$\begin{aligned} b_k^2 =\frac{p(c_k^1)}{p(c_k^2)}b_k^1>0 . \end{aligned}$$

It holds that

• (i) $c(h_1(\varphi )) > c(h_2(\varphi ))$.

• (ii) $h_1(\varphi ) >_{SSD} h_2(\varphi )$.

Proof

Note that $V_u(h_1(\varphi ))= v_k p(c_k^1) u(b_k^1 )$ and $V_u(h_2(\varphi ))= v_k p(c_k^2) u(\frac{p(c_k^1)}{p(c_k^2)}b_k^1)$. In a similar way as in the proof for Proposition 3.1, it shows that $h_1(\varphi ) >_{SSD} h_2(\varphi )$. By construction, $h_1(\varphi )$ and $h_2(\varphi )$ have the same expected value (with respect to the measure $\mathbb {P}$), i.e.,

$$\begin{aligned} \mathbb {E}_\mathbb {P}(h_1(\varphi ))=b_k^1 p(c_k^1)=b_k^2 p(c_k^2)=\mathbb {E}_\mathbb {P}(h_2(\varphi )). \end{aligned}$$

As for their cost, we have that

$$\begin{aligned} c(h_1(\varphi ))=e^{-rk}b_k^1 q(c_k^1), \quad c(h_2(\varphi ))=e^{-rk}b_k^2 q(c_k^2)= e^{-rk} \frac{p(c_k^1)}{p(c_k^2)}b_k^1 q(c_k^2). \end{aligned}$$

As for $c_k^1>c_k^2$, it holds that $p(c_k^1)>p(c_k^2)$, we thus only need to show that the ratio $\frac{q(c)}{p(c)}$ is increasing in c to show (i). To see this, note that q(c)/p(c) can be expressed as

$$\begin{aligned} \frac{q(c)}{p(c)}&= \frac{e^{rk}\mathbb {E}_\mathbb {P}(\varphi _{k}\mathbb {I}_{\varphi _k\le c})}{p(c)} = \frac{e^{rk}\int _0^c u f_{\varphi _{k}}(u)\textrm{d}u}{p(c)} \\&= \frac{e^{rk} c p(c)- e^{r k} \int _0^c F_{\varphi _{k}}(u)\textrm{d}u}{p(c)} = e^{r k } c - e^{r k} \frac{\int _0^c F_{\varphi _{k}}(u)\textrm{d}u}{p(c)}, \end{aligned}$$

where $f_{\varphi _{k}}(u)$ and $F_{\varphi _{k}}(u)$ are the density and distribution functions of $\varphi _k$. The first derivative of the ratio with respect to c is given by

$$\begin{aligned} \frac{\partial \frac{q(c)}{p(c)} }{\partial c}= \frac{e^{r k}}{(p(c))^2 } \cdot \frac{\partial p(c)}{\partial c} \cdot \int _0^c F_{\varphi _{k}}(u)\textrm{d}u >0. \end{aligned}$$

$\square$

Proposition 3.6

(Better financial payoffs are more expensive). Consider two individuals, $i=1,2$, each of whom purchases a vector of digital options,

$$\begin{aligned} h_i(\varphi ):=(0,\ldots , 0,b_{m}\mathbb {I}_{\varphi _m\le c_m^i},\ldots , b_{n}\mathbb {I}_{\{\varphi _n\le c_n^i\}}). \end{aligned}$$

Assume that for all $m\le k \le n$, $p(c_k^1) \ge p(c_k^2)$ with at least one of the inequalities being strict, and that $b_k^2 =\frac{p(c_k^1)}{p(c_k^2)}b_k^1>0$.

It holds that

• (i) $c(h_1(\varphi )) > c(h_2(\varphi ))$.

• (ii) $h_1(\varphi ) >_{SSD} h_2(\varphi )$.

Proof

Note that $c(h_1(\varphi ))= \sum \nolimits _{k=m}^n b_k^1 q(c_k^1 )$ and $c(h_2(\varphi ))= \sum \nolimits _{k=m}^n b_k^1 \frac{p(c_k^1)}{p(c_k^2)} q(c_k^2 )$. Due to the fact that q(c)/p(c) increases in c and that $c_k^1 > c_k^2$, we obtain straightforwardly $c(h_1(\varphi ))>c(h_2(\varphi ))$. Further, $V_u(h_1(\varphi ))= \sum \nolimits _{m}^n v_k p(c_k^1) u(b_k^1 )$ and $V_u(h_2(\varphi ))=\sum \nolimits _{m}^n v_k p(c_k^2) u(\frac{p(c_k^1)}{p(c_k^2)}b_k^1)$. In a similar way as in the proof for proposition 3.4, it shows that $h_1(\varphi ) >_{SSD} h_2(\varphi )$. $\square$

We conclude that actuarial fair pricing of life annuities does not respect a basic economic principle that payoffs that exhibit more risk should earn higher expected returns (i.e., prices are not consistent with second-order stochastic dominance) and is, in this sense, “unfair.” In the next section, we provide a solution for this problem.

4 Equal utility pricing rule

To deal with the inconsistency of the actuarial equivalence principle with respect to second-order stochastic dominance, we propose the “equal utility pricing rule.” As already mentioned in the introduction, Sharpe (2017) has pointed out that using expected utility theory is at least instructive to see whether the traditional approaches are helpful, also in the context of life insurance and retirement products. While different decision theories exist and certainly have their merits, Bernard et al. (2015) show that in finance optimal payoffs can always be rationalized in the expected utility framework. Furthermore, as pointed out by Sharpe and many others, power utility (preferences with constant relative risk aversion) is the most frequently used utility function to capture the preferences of individuals. For instance, Levy (1994) has found strong evidence to support the DARA (decreasing absolute risk aversion) hypothesis, and power utility exhibits this property. Power utility is therefore also used in our numerical section. Hence, we consider an insurer who has a portfolio with N policyholders and who charges a total premium C for the given portfolio of contract payoffs. The total premium income C can be considered as the amount the insurer aims to achieve. Further, the insurer aims to determine premiums $c^\star _i>0$ among the policyholders for obtaining their contract payoffs $g_i(K_{x_i})$ in such a manner that full allocation is obtained, i.e., it is required that

$$\begin{aligned} \sum _{i=1}^{N}{c^\star _i}=C. \end{aligned}$$

(13)

In addition to the rule of full allocation, the “equal utility condition” needs to be satisfied, i.e.,

$$\begin{aligned} V_u^i\left( \frac{g_i(K_{x_i})}{c^\star _i}\right) = V_u^j \left( \frac{g_j(K_{x_j})}{c^\star _j}\right) , \quad i,j=1,\ldots ,N, \end{aligned}$$

(14)

where $V_u^i$ is the expected utility for policyholder i, as defined in (9), $g(K_{x_i})$ the contract payoff, and $c^\star _i$ the premium/cost that individual i shall deliver at the contract-issuing time to obtain the contract payoff $g_i(K_{x_i})$. If conditions (13) and (14) are satisfied, we say that the insurance portfolio exhibits equal utility fairness (per unit of premium invested) and the $c^\star _i$, $i=1,\ldots ,N$ are called utility equilibrium prices.

Proposition 4.1

(Uniqueness of utility equilibrium prices). Consider a portfolio of N annuity payoffs

$$\begin{aligned} g_i(K_{x_i}) = (b^i_k\mathbb {I}_{\{K_{x_i}\ge k\}})_{k=1}^{\omega -x_i}, \quad b_k^i \ge 0, \; \quad i=1, \ldots , N. \end{aligned}$$

(15)

Assume that $u:(0,\infty )\rightarrow (0,\infty )$ is a strictly increasing and strictly concave utility function and that ${lim_{x\rightarrow \infty }{u(x)}=\infty }$. It holds that there exists a unique set of utility equilibrium prices $c^\star _i$, $i=1,\ldots ,N$.

Proof

Under the equal utility pricing, each individual utility equilibrium price $c^\star _i$, $i=1,\ldots N$ has to satisfy the following relation:

$$\begin{aligned} \sum \limits _{b^i_k> 0} v_k \cdot {}_kp_{x_i} \cdot u\left( \frac{b_k^i}{c^{\star }_i}\right) = \sum \limits _{b^1_k > 0} v_k \cdot {}_kp_{x_1} \cdot u\left( \frac{b_k^1}{c^{\star }_1}\right) . \end{aligned}$$

(16)

We first arbitrarily set $c_i \le \frac{C}{N}$, $i=1,\ldots ,n$. Without loss of generality (possibly after reordering the $c_i$), we can assume that $c_1$ is such that for each $c_i, i=2,\ldots , N,$ it holds that

$$\begin{aligned} \sum \limits _{b^i_k> 0} v_k {}_kp_{x_i} u\left( \frac{b_k^i}{c_i}\right) \le \sum \limits _{b^1_k > 0} v_k {}_kp_{x_1} u\left( \frac{b_k^1}{c_1}\right) . \end{aligned}$$

(17)

At first, we keep $c_1$ fixed. Then, for a given $i \in \{2,\ldots ,N\}$ in order to obtain equality in (17), the initial $c_i$ needs to become smaller. As the left-hand side in (17) is a continuous and strictly decreasing function f of $c_i$, its inverse $f^{-1}$ is also continuous and strictly decreasing, and by setting

$$\begin{aligned} c_i=f^{-1}\left( \sum \limits _{b^1_k > 0} v_k {}_kp_{x_1} u\left( \frac{b_k^1}{c_1}\right) \right) \end{aligned}$$

equality in (17) is obtained. We do this for every $i \in \{2,\ldots ,N\}$ and note that the $c_i$’s that we obtain satisfy $\sum _{i=1}^{N}{c_i}\le C$. Next, we let $c_1$ increase and note that the $c_i$, $i \in \{2,\ldots ,N\}$ that leads to equality in (17) is continuously and strictly increasing in $c_1$. Hence, by letting $c_1$ increase to a certain unique value $c^\star _1 < C$, we obtain the desired $c_i$, denoted as $c^\star _i$. $\square$

Depending on the specification of the utility function, we can determine $c^{\star }_i$ explicitly or numerically as a function of $c^{\star }_1$. Further, applying $\sum _{i=1}^N c^{\star }_i=C$, we then obtain $c_1^{\star }$ and hence also $c_i^{\star }$.

Proposition 4.2

(Utility equilibrium prices exhibiting consistency with second-order stochastic dominance). Consider a portfolio of N annuity payoffs

$$\begin{aligned} g_i(K_{x_i}) = (b^i_k\mathbb {I}_{\{K_{x_i}\ge k\}})_{k=1}^{\omega -x_i},\quad b_k^i > 0, \; \quad i=1, \ldots , N. \end{aligned}$$

(18)

Assume that $u:(0,\infty )\rightarrow (0,\infty )$ is a strictly increasing and strictly concave utility function. The equilibrium prices $c^\star _i$, $i=1,\ldots ,N$, are consistent with second-order stochastic dominance, i.e.,

$$\begin{aligned} g_i(K_{x_i}) >_{SSD} g_j(K_{x_j}) \end{aligned}$$

implies

$$\begin{aligned} c_i > c_j. \end{aligned}$$

Proof

Let

$$\begin{aligned} g_i(K_{x_i}) >_{SSD} g_j(K_{x_j}), \end{aligned}$$

then it holds that

$$\begin{aligned} V^i_u\left( g_i(K_{x_i})\right) > V^j_u\left( g_j(K_{x_j})\right) . \end{aligned}$$

Furthermore, for all $c>0$, $u(\frac{x}{c})$ will be a finite valued, strictly increasing and strictly concave utility function. Hence, it also holds that

$$\begin{aligned} V^i_u\left( \frac{g_i(K_{x_i})}{c}\right) > V^j_u\left( \frac{g_j(K_{x_j})}{c}\right) \end{aligned}$$

for all $c>0$. Consequently, the equal utility condition

$$\begin{aligned} V^i_u\left( \frac{g_i(K_{x_i})}{c_i}\right) = V^j_u\left( \frac{g_j(K_{x_j})}{c_j}\right) \end{aligned}$$

can only hold when $c_i > c_j$. $\square$

5 Equal utility versus equivalence pricing

With the help of specific utility functions, we provide here further interpretations of the results achieved in the previous sections. In particular, in this section we work out the difference between equivalence pricing and equal utility pricing.

5.1 Implications deriving from the equivalence principle

For our numerical illustration, let us consider an insurer whose portfolio consists of two types of products: either two pure endowments or two annuity products. In both settings, one contract is assigned to an individual aged $x_1$ and the other to an individual aged $x_2$. Without loss of generality, we assume that ${}_{k}p_{x_1}> {}_{k}p_{x_2}$. From Proposition 3.1, which addresses the unfairness of the equivalence principle for pure endowment, we learn that setting $b_k^2 =\frac{{}_k p_{x_1} }{{}_k p_{x_2}} b_k^1$ leads to the same actuarial fair premiums, while the contract of individual 1 stochastically dominates that of individual 2. To see this, we assume a Gompertz model (Gompertz 1825) in which the mortality rates are then given by

$$\begin{aligned} \mu _{x+t} = \frac{1}{g} e^{\frac{x+t-m}{g}}\,, \end{aligned}$$

(19)

where g is the dispersion coefficient and m is the modal age at death. The resulting survival probability is given by ${}_kp_x = e^{-\int _0^k {\mu }_{x+s}\textrm{d}s}$. We fix the parameters as follows:

$$\begin{aligned} m =&88.721, \, g =10, \, \delta =0.02, \, x_1 = 30, \, x_2 = 40, \, b_k^1 \equiv 1, k= 30, \; \omega = 120, \ \end{aligned}$$

(20)

where $\omega$ is the maximum age, and a 30-year pure endowment is considered. The discounting function in (2) is given by $v_k=(1+\delta )^{-k}$. Further, we assume $u(y)=\frac{y^{1-\gamma }}{1-\gamma }$, $\gamma \in (0,1)$.

Table 1 Given the parameters as in (20), the 30-year survival probabilities for the two individuals are given by 0.9477 and 0.8640, respectively, and for both pure endowment contracts their cost, in this case the actuarial fair premium, is given as $c_1=c_2= {{\textbf {0}}.{\textbf {5232}}}$

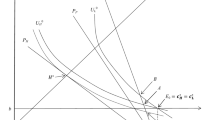
Note that in Table 1$c_1$ and $c_2$ reflect the actuarial fair premiums that are obtained under actuarial fair pricing. As we take $b_k^2 =\frac{{}_k p_{x_1} }{{}_k p_{x_2}} b_k^1$, both pure endowment contracts lead to the same price of 0.5232. However, contract type 1 (i.e., the one with a higher survival rate) leads to a higher utility level than contract type 2, which indicates the second-order stochastic dominance of contract type 1. An increase in the relative risk aversion level enlarges the difference in the utility level.

The same analysis can be carried over to the annuity product, see Proposition  3.4 and Table 2.

Table 2 Given the parameters as in (20) with $b_k^2 =\frac{{}_k p_{x_1} }{{}_k p_{x_2}} b_k^1$,$k=1,\ldots ,80$, we find that both annuity contracts have the same cost under the actuarial fairness principle, i.e., $c_1=c_2= {{\textbf {31}}.{\textbf {7825}}}$

Again, both contracts have the same price of 31.7825, but the contract of individual 1 dominates over that of the second individual in second-order stochastic dominance. An increase in the relative risk aversion level enlarges the difference in the utility level.

5.2 Implications deriving from equal expected utility pricing

In the case of the equal expected utility principle, we ensure an identical utility level for both individuals. In the case of pure endowment, for ${}_{k}p_{x_1}> {}_{k}p_{x_2}$, requiring

$$\begin{aligned} \frac{u(\frac{b_k^2}{c_2})}{u(\frac{b_k^1}{c_1})} = \frac{{}_kp_{x_1}}{{}_kp_{x_2}} \end{aligned}$$

leads to equal utility. In the case of power utility, it implies that

$$\begin{aligned} b_k^2 = b_k^ 1 \frac{c_2}{c_1} \left( \frac{{}_kp_{x_1}}{{}_kp_{x_2}}\right) ^{\frac{1}{1-\gamma }}. \end{aligned}$$

(21)

In order to conduct a reasonable comparison between the equal utility and the equivalence principle, we assume that the insurer charges a total premium identically as in the case with the equivalence principle, i.e., $C=2\cdot 0.5232=1.0464$. Further, we assume that the contract expected payment streams in these two cases are identical, i.e., $b_k^1 =1$ and $b_2^k=0.9477/0.8640 \approx 1.1085$. The two-equation system ((21) and $C=c_1+c_2$) determines the premiums $c_1$ and $c_2$ in the equal utility case (see Table 3).

Table 3 The premiums of both pure endowment contracts which show equal utility fairness (power utility case), using the parameters as in (20)

Based on Table 3, we make the following observations:

• As the total premium C is chosen to be identical as in the equivalence pricing, these two pricing principles lead to the same expected profit for the insurer.

• Moving from the equivalence pricing to equal utility pricing implies that individual 1 needs to pay more, while individual 2 can pay less, i.e., it turns out that as compared to the case in which the actuarial equivalence principle prevails, there is an implicit transfer of wealth from those with a lower mortality rate to those with a higher mortality rate.

• The lower the value of the risk aversion coefficient $\gamma$ the more the premiums under both approaches correspond to each other; indeed the lower the value of $\gamma$, the more the utility function resembles a linear function. In the case of linear utility, the equal utility principle reduces to the equivalence principle.

Table 4 illustrates the result for the annuities. Again, we have assumed that the insurer charges the total premiums as in the equivalence case, i.e., $C=2*31.7823$. Further, the $b_k^1$ and $b_k^2$ are the same benefit streams as in the equivalence case. Based on $C=c_1+c_2$ and the equal utility condition, i.e.,

$$\begin{aligned} \sum \limits _{k=1}^{\min (\omega -x_1, \omega -x_2)} v_k {}_kp_{x_1} u\left( \frac{b_k^1}{c_1}\right) = \sum \limits _{k=1}^{\min (\omega -x_1, \omega -x_2)} v_k {}_kp_{x_2} u\left( \frac{b_k^2}{c_2}\right) , \end{aligned}$$

(22)

we can compute $c_1$ and $c_2$.

Table 4 The premiums of both contract types which show equal utility fairness (power utility case), using the parameters as in (20)

In Table 4, we make similar observations to those noted in the pure endowment case. Specifically, a pricing rule based on equal utility for various policyholders suggests a higher (or a lower) price shall be charged for contract 1 (or 2).

6 Further discussion

6.1 Group self-annuitization

In this section, we show that the results obtained so far imply that group self-annuitization schemes are not fair in the sense that participants with higher survival rates receive payoffs that second order stochastically dominates those of participants with lower survival rates. For the ease of exposition, we only consider simple one-period schemes in which benefits are paid only once, namely at the end of a given time period provided the participant is alive. However, our findings also hold for general self-annuitization schemes. Hence, consider a pool of N individuals aged $x_i$, $i=1,\ldots ,N$, each investing a certain amount $c_i$ in a risk-free account earning the continuous risk-free rate $r>0$. It is also agreed that after k years only those participants who survive will receive returns on their investment, whereas the heirs of those who pass away during this period will receive nothing. The value $V_i$, $i=1,\ldots ,N$ of the investment after k years is then given as

$$\begin{aligned} V_i=\mathbb {I}_{\{K_{x_i}\ge k\}}(c_ie^{rk}+a_i B_N). \end{aligned}$$

(23)

Here, $B_N$ denotes the total amount that needs to be shared among the survivors of the pool, which is equal to the accumulated value of the investments $c_i$ corresponding to the participants who passed away, i.e.,

$$\begin{aligned} B_N=\sum _{j=1}^{N}\mathbb {I}_{\{K_{x_j} < k\}}c_je^{rk}. \end{aligned}$$

(24)

$B_N$ can be considered as the mortality credit, which can be split among the surviving participants. Further, $a_i \ge 0$ is the share that is actually received by the ith surviving participant in the case in which he survives. It is not known, ex ante, as it depends on the actual mortality that will be observed during the period under consideration. Specifically, as the total sum of the shares $a_i$, $i=1,\ldots ,N$, allocated to the survivors, needs to be equal to one (full allocation), we can express the $a_i$ as

$$\begin{aligned} a_i=\frac{\kappa _i}{\sum _{j=1}^{N}\kappa _j\mathbb {I}_{\{K_{x_j}\ge k\}}}, \end{aligned}$$

(25)

with the convention that all $a_i$ are equal to zero whenever all participants survive, i.e., when ${\sum _{j=1}^{N}\kappa _j\mathbb {I}_{\{K_{x_j}\ge k\}}}=0$. Here, the $\kappa _i > 0, i=1,\ldots ,n$ can be interpreted as the relative proportion that the i-th individual is entitled to receive upon survival.

In this contract payoff design, the participants thus obtain a (fixed) financial return, coming from the risk-free investment and a (random) return coming from the mortality credit $a_i B_N$. Note that the total return is random but always bigger than the fixed financial return. Hereafter, we show that for an infinitely large pool in which sharing is done according to the rule

$$\begin{aligned} \kappa _i=c_i\frac{{}_k q_{x_i}}{{}_k p_{x_i}}, i=1,\ldots ,N, \end{aligned}$$

where ${}_k q_{x_i}=1-{}_k p_{x_i}$, the contract payoffs correspond to pure endowments that are priced according to actuarial fair pricing (see Proposition 6.1).

In the following proposition, the notation $\overset{p}{\rightarrow }$ reflects convergence in probability (for $N {\rightarrow } \infty$).

Proposition 6.1

(Equivalence between group self-annuitization and actuarial fair pure endowments). Let $1 \le k\le \text {min}\{\omega -x_1,\ldots , \omega -x_N\}.$ Denote ${}_k q_{x_i}=1-{}_k p_{x_i}, i=1,\ldots ,N$. Let $\kappa _i, i=1,\ldots ,N,$ be given as

$$\begin{aligned} \kappa _i=c_i\frac{{}_k q_{x_i}}{{}_k p_{x_i}}, \end{aligned}$$

(26)

and assume that $c_A \le c_i \le c_B, i=1,\ldots ,N.$ It holds that

$$\begin{aligned} a_iB_N \overset{p}{\rightarrow }\ c_ie^{rk}\frac{{}_k q_{x_i}}{{}_k p_{x_i}}. \end{aligned}$$

As a consequence,

$$\begin{aligned} V_i \overset{p}{\rightarrow }\ \mathbb {I}_{\{K_{x_j}\ge k\}}b_i, \end{aligned}$$

in which $b_i=\frac{c_ie^{rk}}{{}_k p_{x_i}}$.

Proof

Noting that that the variance resp. the mean of $B_N/N$ is uniformly bounded from above resp. from below, it follows from Chebyshev’s inequality that

$$\begin{aligned} \frac{B_N}{\mathbb {E}(B_N)} \overset{p}{\rightarrow }\ 1. \end{aligned}$$

Similarly, we obtain for every $i \in \{1,\ldots ,N\}$ that

$$\begin{aligned} \frac{A_i}{\mathbb {E}(A_i)} \overset{p}{\rightarrow }\ 1, \end{aligned}$$

where we denote $A_i=1/a_i.$ Hence, from the continuous mapping theorem,

$$\begin{aligned} \frac{\mathbb {E}(A_i)}{A_i} \overset{p}{\rightarrow }\ 1, \end{aligned}$$

and using that $\overset{p}{\rightarrow }$ is preserved when taking products, we obtain that

$$\begin{aligned} \frac{\mathbb {E}(A_i)}{\mathbb {E}(B_N)}{a_iB_N} \overset{p}{\rightarrow } {1}. \end{aligned}$$

Hence, we find that

$$\begin{aligned} a_iB_N \overset{p}{\rightarrow }\ c_ie^{rk}\frac{{}_k q_{x_i}}{{}_k p_{x_i}}. \end{aligned}$$

$\square$

The above proposition shows that the payoff defined in (23) converges to a pure endowment contract with a payoff $\frac{c_ie^{rk}}{{}_k p_{x_i}}$ at maturity date k for the $i-th$ individual. As the initial investment of the ith individual is $c_i$, this means that this basic group self-annuitization product with only one payout at time k is priced according to the actuarial fairness principle; see also Donnelly (2015), Dagpunar (2021), Fullmer and Sabin (2018), and Sabin and Forman (2016), who advocate this sharing rule for allocating death benefits among survivors.

When considering a sequence of time points $k=1,\ldots , m$ where payouts are made, it shows in a similar way that a group self-annuitization with infinite pool size and with allocation rule as in (26) is asymptotically equivalent to a life annuity portfolio

$$\begin{aligned} g(K_{x_i}) = \left( \frac{c_ie^{r}}{{}_1 p_{x_i}}\mathbb {I}_{\{K_{x_i}\ge 1\}},\ldots \frac{c_ie^{r}}{{}_m p_{x_i}} \mathbb {I}_{\{K_{x_i}\ge m\}}\right) . \end{aligned}$$

(27)

Group annuitization with an infinite pool size under allocation rule (26) is thus observationally equivalent to an annuity under the fair pricing principle. The results we established in this paper imply that actuarially fairly pooled group annuitization products are not fair in the respect that participants with higher survival rates will have a better contract payoff in the sense of second-order stochastic dominance. By contrast, our newly proposed equal utility pricing rule ensures that consistency with second-order stochastic dominance is preserved. As the new rule allocates the total premium based on true probabilities and not on adjusted ones, it also enhances transparency in the annuity market.

6.2 Annuity pricing in practice

Due to tightening solvency regulations and increasing life expectancy, insurance companies will charge non-negligible risk loadings to life annuity products leading to real-world premiums that are higher than those resulting from the equivalence principle. Bauer et al. (2010) and Chen and Rach (2019) apply risk loadings by relying on the concept of risk neutral pricing. Specifically, it is then assumed that among the infinitely many risk neutral probability measures that exist in incomplete arbitrage-free markets (untradable insurance risk makes the market incomplete⁷), the insurer chooses a particular risk neutral probability measure $\mathbb {Q}$. The chosen measure $\mathbb {Q}$ then accounts for both unsystematic and systematic mortality risk. In what follows, we denote the survival curve under the pricing measure $\mathbb {Q}$ by ${}_t {\tilde{p}}_x$. Furthermore, we assume that the insurer is prudent. As only retirement products are considered, this can be achieved by imposing that

$$\begin{aligned} {}_t \tilde{p}_x \ge {}_t p_x \,, \end{aligned}$$

(28)

must hold, where ${}_t p_x$ denotes the true survival curve. Note that the choice of the pricing measure $\mathbb {Q}$ (or ${}_t\tilde{p}_x$) can depend on the pool size N. A larger pool size will lead to less longevity risk included in the retirement products, as unsystematic risk can be partly eliminated by increasing the pool size.

Given a contract payoff function $g(\cdot )$, the premium ${\tilde{\pi }}(g({K_x}))$ of a life insurance contract $g(K_x)$ is equal to

$$\begin{aligned} {\tilde{\pi }}(g({K_x}))&:={\tilde{\pi }}_x(b_1,\ldots ,b_{\omega -x}) = \mathbb {E}_{\mathbb {Q}}(D(K_x))\nonumber \\&= \sum _{k=1}^{\omega -x} v_k \mathbb {E}_{\mathbb {Q}}(b_k\mathbb {I}_{\{K_x\ge k\}}) \nonumber \\&= \sum _{k=1}^{\omega -x} v_k \cdot {}_k {\tilde{p}}_x \cdot b_k. \end{aligned}$$

(29)

Hereafter, we show that in a life insurance portfolio unfairness among policyholders may still result.

Proposition 6.2

(Unfairness of life insurance portfolios). Assume a life insurance portfolio containing two policyholders aged $x_i$, each of whom purchases a pure endowment contract with a maturity date $k_i$, $i=1,2$,

$$\begin{aligned} g_i(K_{x_i})=b_{k_i}^i \cdot \mathbb {I}_{\{K_{x_i}\ge {k_i}\}}, \quad i=1,2. \end{aligned}$$

Assume that $v_{k_1}\cdot {}_{k_1} \tilde{p}_{x_1} > v_{k_2}\cdot {}_{k_2} \tilde{p}_{x_2}$ and we take

$$\begin{aligned} b_{k_2}^2 =\frac{v_{k_1}\cdot {}_{k_1} \tilde{p}_{x_1} }{v_{k_2}\cdot {}_{k_2} \tilde{p}_{x_2}} b_{k_1}^1. \end{aligned}$$

If $\frac{{k_1} {p}_{x_1} }{{}_{k_2} {p}_{x_2}} \ge \frac{{k_1} \tilde{p}_{x_1} }{{}_{k_2} \tilde{p}_{x_2}}$, then it holds that

• (i) ${\tilde{\pi }}_{x_1}(g_1(K_{x_1}))={\tilde{\pi }}_{x_2}(g_2(K_{x_2}))$.

• (ii) $g_1(K_{x_1}) >_{SSD} g_2(K_{x_2})$.

Proof

By construction, $g_1(K_{x_1})$ and $g_2(K_{x_2})$ have the same mean under the pricing measure $\mathbb {Q}$, and the proof for (i) is thus immediate. To prove (ii), observe that $V_u(g_1(K_{x_1}))=v_{k_1} \cdot {}_{k_1} p_{x_1} \cdot u(b_k^1)$ and $V_u(g_2(K_{x_2}))=v_{k_2} \cdot {}_{k_2} p_{x_2} \cdot u(\frac{{}_{k_1} {\tilde{p}}_{x_1} }{{}_{k_2} {\tilde{p}}_{x_2}} b_k^1)$. Note that

$$\begin{aligned} v_{k_1} \cdot {}_{k_1} p_{x_1} \cdot u(b_k^1)- v_{k_2} \cdot {}_{k_2} p_{x_2} \cdot u( \frac{v_{k_1}}{v_{k_2}}\frac{{}_{k_1} \tilde{p}_{x_1} }{{}_{k_2} \tilde{p}_{x_2}} b_k^1) =v_{k_1} \cdot {}_{k_1} p_{x_1} \cdot b_k^1 \left( \frac{u(b_k^1)}{b_k^1}- \frac{u(\frac{v_{k_1} \cdot {}_{k_1} {\tilde{p}}_{x_1} }{v_{k_2} \cdot {}_{k_2} {\tilde{p}}_{x_2}} b_k^1)}{\frac{v_{k_1} \cdot {}_{k_1} p_{x_1} }{v_{k_2} \cdot {}_{k_2} p_{x_2}} b_k^1} \right) . \end{aligned}$$

The increasingness and concavity of $u(\cdot )$ imply that for every $0< y \le z_1 \le z_2$,

$$\begin{aligned} \frac{u(y)}{y} \ge \frac{u(z_1)}{z_2}. \end{aligned}$$

The above inequality is strict when the increasingness and concavity of u are strict. This implies (ii). $\square$

7 Conclusion

In this paper, in contrast to financial pricing, we demonstrate that the actuarial fair pricing principle in insurance leads to unfairness among insureds in the sense that riskier payoffs are not necessarily less expensive. Specifically, using pure endowment and life annuities as examples, we show that policyholders with higher survival rates have a better payoff than those with lower survival rates in terms of second-order stochastic dominance. To resolve this issue, we propose equal utility pricing to improve fairness among policyholders and to ensure that prices are determined such that all policyholders obtain the same utility, i.e., there is no interpersonal envy (Herreiner and Puppe 2009), from the viewpoint of a third party.

When there is no mortality risk (limiting case), our proposed equal utility condition ensures that each investor receives the same return corresponding to the financial return of the underlying investment strategy. A drawback of our approach is that there is in general no guarantee that each surviving agent always receives a positive mortality credit, as equal utility, rather than equal average return, is what matters in our setting. As an extension of our framework, one could study the pricing rule in which premiums are determined such that utilities among the members are “as equal as possible” (and no longer exactly equal as in our case) under the constraint that mortality credit returns are always non-negative.

The pricing rule can be of particular societal relevance, as social planners have genuine interest in ensuring welfare (utility) fairness [cf. see Frees and Huang (2021) addressing the importance of studying insurance discrimination for the insurance industry for decades]. Compared to traditional actuarial fair pricing, equal utility pricing leads to a transfer of wealth from those with a lower mortality rate to those with a higher mortality rate. Hence, under the plausible assumption that there is a negative correlation between income and financial risk, equal utility pricing can be considered as a possible tool for reducing income inequality (Nelissen 1995; Bommier et al. 2011). In addition, the relevance of our approach is exhibited when it comes to the fair design of innovative retirement products such as group self-annuitization products, in which longevity risk is shared among policyholders.

Making effectively retirement decisions and ensuring pension security constitute important challenges in contemporary society, both in developed industrial and developing countries [see, e.g., Cai et al. (2006), Borck (2007), and Brown (2013)]. In this context, as an extension to this article, it would be interesting to consider optimal demand for retirement products taking account of equal utility pricing, both from the individual investors’ and social planners’ point of view. In this paper, we used the expected utility theory from von Neumann and Morgenstern to assess the value (utility) of contracts. However, the idea that fairness among policyholders can be achieved by making the value of their contracts equal can also be developed under other models, such as generalized expected utility models (Quiggin 1995) or the dual theory of choice under risk (Yaari 1987). In addition, the premiums discussed in this paper are of the type single premium, i.e., a single payment is charged at the inception of the contract. In reality, insureds often make periodic payments for their life insurance and annuity products. Since a contract that is fair today is not necessarily also fair tomorrow, the extension of our results to the case of periodic premiums is not trivial. We leave such analysis to future research.