1 Introduction

Over the past two decades, the studies devoted to the search of an optimal reinsurance strategy have registered considerable advancements and relevance in the actuarial literature. A great attention has been given to the classical proportional and excess-of-loss reinsurance strategies, or both as a mixed contract (see Brachetta and Ceci 2019a, b; Brachetta and Schmidli 2020; Irgens and Paulsen 2004; Liu and Ma 2009 and references therein), which have been addressed under different optimization criteria. In many cases, the aim has been to minimize the probability of ruin (e.g. see Bai and Guo 2008; Browne 1995; Liang and Guo 2008; Promislow and Young 2005); in many others the goal has been to maximize the adjustment coefficient or the expected utility of terminal wealth (e.g. see Brachetta and Ceci 2019a, b; Centeno 2005; Liang and Guo 2011; Liang and Yuen 2016; Xu et al. 2017; Zhang et al. 2009). In all the cases the insurer’s surplus process has been modelled either as a jump process or as a diffusion approximation. (We refer to Schmidli 2018 for a valuable introduction to risk models.)

In this extremely vast literature, the recent relevant contributions Brachetta and Ceci (2019a, 2019b) and Brachetta and Schmidli (2020) deserve close attention: in these papers the problem of optimal reinsurance and investment is addressed assuming that the insurer’s surplus is affected by an exogenous stochastic factor, introduced to model the change in the number of policyholders and the risk modifications. The goal is to maximize either the wide-used expected exponential utility of terminal wealth or a member of the SAHARA class utility functions, which includes CRRA and CARA utility functions as limiting cases. Both the cases of proportional and excess-of-loss reinsurance are treated. On the other hand, restricting to the past two decades, the paper (Centeno 2005) represents one of the first contributions to consider the expected utility of terminal wealth maximization problem in the case of two dependent classes of insurance business. Afterwards, various authors considered two or more classes of dependent risks and, under different assumptions, studied the optimal dynamic reinsurance with the analogous objective to maximize the expected utility of terminal wealth. For instance, Liang and Yuen (2016) considers two classes of insurance business and assumes that the insurer’s company is allowed to invest all its surplus in a risk-free asset with interest rate r employing the variance premium principle, while in Yuen et al. (2015) a model with more than two classes of insurance business is introduced and used. Both the aforementioned papers share the goal to find the optimal proportional reinsurance. The same goal appears in Bai and Guo (2008) where the insurer is allowed to invest in a risk-free asset and n risky assets, and the risk model is of diffusion type; further, under the constraint of no-shorting, the two problems of maximizing the expected exponential utility of terminal wealth and of minimizing the probability of ruin are considered. Two other contributions, especially relevant to our work, are Gosio et al. (2016) and Liang and Guo (2011) that, with the common aim to maximize the expected utility of terminal wealth, combine the proportional and the excess-of-loss reinsurance: Liang and Guo (2011) considers independent classes of insurance business, while (Gosio et al. 2016) works with two dependent classes.

Considering a risk model with multiple dependent classes of insurance, our paper characterizes the reinsurance strategy which combines a proportional and an excess-of-loss reinsurance, and that maximizes the expected utility of wealth at a terminal finite time. We set up the model in continuous time and we assume that the claim number of the insurance classes follow a multivariate Poisson distribution. Moreover, we allow for \(n\ge 2\) dependent classes of insurance business, thus generalizing the risk model proposed in Gosio et al. (2016). Our analysis starts by deriving the rigorous control-theoretic setup where to formulate the optimal reinsurance problem. Then, invoking the dynamic programming principle, we derive the Hamilton–Jacobi–Bellman (HJB) equation for the general multiple dependent risk model problem and formulate a Verification Theorem. This provides a set of sufficient conditions for the optimality of a (candidate) admissible reinsurance strategy. Under the hypothesis that the claim size random variables are exponentially distributed and that the utility function is exponential, an educated guess on the form of the value function of the problem reduces the HJB equation to an intricate static optimization problem which we handle via the classical Karush–Kuhn–Tucker (KKT) conditions. By performing an accurate analysis of all the possible cases arising from the system of KKT conditions, we manage to explicitly determine an optimal reinsurance strategy which we prove to satisfy the conditions of the Verification Theorem. As a special case we analyse and solve the completely symmetric situation, in which all the parameters related to each class of insurance risk are the same. This study allows us to evaluate the behaviour of both the value function and the optimal strategies when the number of insurance classes increases. Further, we consider the case of two dependent classes of insurance business and relate our work to some existing literature, highlighting that our results agree with the findings of Gosio et al. (2016), when the proportional reinsurance is excluded, and of Centeno (2005), in which only the excess-of-loss reinsurance is considered. Finally, in the case \(n=2\), we provide a numerical comparative statics and discuss the effect of the parameters on the problem’s solution.

The paper is organized as follows: Sect. 2 is devoted to the model presentation; Sect. 3 contains the HJB equation and the Verification Theorem. Section 4 focuses on the case of n classes of insurance business under the assumption that the utility is exponential and the claim size random variables corresponding to each class of insurance is exponentially distributed. In particular, in Sect. 4 we present an explicit solution of the HJB equation, show its optimality by means of the Verification Theorem and analyse the special symmetric case. Section 5 presents some numerical examples to show the computed optimal solution’s behaviour under parameters’ variations when dealing with 2 classes of insurance business. Section 6 contains some final remarks and the “Appendix” collects the proof of some technical results.

2 Model formulation

In this section, under the well-known assumptions of collective risk theory, we model the total claim amount charged to the insurance company by means of the classical compound Poisson process (see Shreve 2004, Sects. 11.2–11.3).

We consider the finite time horizon [0, T], with \(0<T<+\infty \). Let \((\Omega , {\mathcal {F}}, P)\) be a complete probability space on which is given a filtration \({\mathbb {F}}:= \{{\mathcal {F}}_s\}_{0 \le s \le T}\) satisfying the usual conditions. All stochastic processes introduced below are supposed to be adapted with respect to \(\mathbb F\).

We consider \(n+1\) mutually independent Poisson processes \({\overline{N}}_0(s), {\overline{N}}_1(s),\ldots , {\overline{N}}_n(s)\) with intensities \(\theta _0, \theta _1, \ldots , \theta _n\), respectively; we denote by \(N_i(s), i=1, \ldots , n\), the Poisson process defined by

$$\begin{aligned} N_i(s):= {\overline{N}}_i(s) + {\overline{N}}_0(s) \end{aligned}$$

with intensity \(\theta _0+\theta _i\) and arrival times \(S_{ik}\). Here, the n claim number processes \(\{N_i(s), i=1, \ldots , n; s \in [0,T]\}\) represent the n classes of insurance business owned by a considered insurance company. Note that the process \(\{N_1(s), N_2(s), \ldots , N_n(s); s \in [0,T]\}\) has a multivariate Poisson distribution and the n classes of business are mutually dependent because of \({\overline{N}}_0(s)\).

For each class i of insurance risk, we let \(X_{i1}, X_{i2}, \ldots \) be a sequence of identically distributed random variables with density \(f_i\), where \(f_i\) is of class \(L^1\), \(f_i(x) =0\) for \(x \le 0\) and \(\mu _i:= \int _{0}^{\infty } x f_i(x) \textrm{d}x < +\infty \). The random variables \(X_{i1}, X_{i2}, \ldots \) represent the claim size corresponding to the ith class of insurance business, they are assumed to be independent of one another and also independent of the Poisson process \(N_i(s)\), \(s \in [0,T]\);

$$\begin{aligned} Q_i(s):= \sum _{j=1}^{N_i(s)} X_{ij} \end{aligned}$$

is the compound Poisson process with jumps of size \(X_{ij}\).

The insurance company has the possibility to reinsure each class i of insurance risk either by a pure quota-share or by an excess-of-loss strategy as follows. We let \(a_i(s) \in [0,1]\) and \(b_i(s) \in [0, +\infty ]\) be the decision variables representing the retention limits of proportional and excess-of-loss reinsurance at time s. The quantity \(\min \{ a_i(s)Q_i(s), b_i(s) \}\) will be retained by the insurer from the ith claim \(Q_i(s)\). We highlight two limit cases: \(a_i(s)=0\), for any value \(b_i(s)\in [0,+\infty ]\), refers to full reinsurance, whereas \(a_i(s)=1\) and \(b_i(s)=+\infty \) mean that no reinsurance occurs. We assume that the coefficients \(({\varvec{a}}, {\varvec{b}}):=(a_1(s), \ldots , a_n(s), b_1(s), \ldots , b_n(s))\) are the control parameters belonging to the set of admissible strategies

$$\begin{aligned} A:= & {} \{({\varvec{a}}, {\varvec{b}}): \Omega \times [0,T] \rightarrow {\mathbb {R}}^{2n} \,|\, ({\varvec{a}}, {\varvec{b}}) \text { is left-continuous},\\{} & {} \mathbb F\text {-adapted, and such that } a_i(s) \in [0,1],b_i(s) \in [0, +\infty ]\}. \end{aligned}$$

and

$$\begin{aligned} A_t:= & {} \{({\varvec{a}}, {\varvec{b}}): \Omega \times [t,T] \rightarrow \mathbb R^{2n} \,|\, ({\varvec{a}}, {\varvec{b}}) \text { is left-continuous},\\{} & {} {\mathbb {F}}\text {-adapted, and such that } a_i(s) \in [0,1],b_i(s) \in [0, +\infty ]\}. \end{aligned}$$

where \(t\in [0,T]\).

Let \(g_i: [0,1] \times [0, + \infty ] \times [0, +\infty ) \rightarrow [0, +\infty ]\), \(i=1,\ldots ,n\), be defined by

$$\begin{aligned} g_i(\alpha _i, \beta _i, \xi _i):=\left\{ \begin{array}{lll} \alpha _i \xi _i &{} &{} \text {if } \xi _i \le \displaystyle {\frac{\beta _i}{\alpha _i}}\\ \beta _i &{} &{} \text {if } \xi _i > \displaystyle {\frac{\beta _i}{\alpha _i}}, \end{array}\right. \end{aligned}$$
(2.1)

assuming, from now on, the convention \(\frac{\beta _i}{0}=+\infty \), for each \(\beta _i \in [0,+\infty ]\). The total claim amount charged to the insurance company at time s and referred to the i-type claim is

$$\begin{aligned} G^{({\varvec{a}}, {\varvec{b}})}_i(s):= \int _0^s g_i(a_i(\xi ),b_i(\xi ),\Delta Q_i(\xi )) \textrm{d}N_i(\xi ). \end{aligned}$$
(2.2)

In order to define the surplus process, we assume that all the premiums are computed according to the expected value principle and are subject to a safety loading. For each \(i \in \{1,\ldots ,n\}\), let \(\eta _i>0\) be the ith safety loading coefficient and recall that \(\mu _i\) is the expectation of \(X_{ij}\). Thus, the insurance premium rate is

$$\begin{aligned} c_i:= (1 +\eta _i)(\theta _i + \theta _0) \mu _i, \end{aligned}$$
(2.3)

and the reinsurance premium rate is

$$\begin{aligned} P^{({\varvec{a}}, {\varvec{b}})}_i(a_i(s), b_i(s)):= & {} (1+\gamma _i)(\theta _i + \theta _0) \left( \mu _i - a_i(s) \int _0^{\frac{b_i(s)}{a_i(s)}} x f_i(x) \textrm{d}x \right. \nonumber \\{} & {} \left. -b_i(s) \int _{\frac{b_i(s)}{a_i(s)}}^{+\infty } f_i(x) \textrm{d}x\right) , \end{aligned}$$
(2.4)

where, by convention, \(+\infty \cdot 0 = 0\) and we assumed \(\gamma _i>\eta _i\), i.e. reinsurance is more expensive than first insurance, a reasonable assumption in the actuarial practice, see also Liang and Guo (2011). Therefore, given the reinsurance strategy \(({\textbf{a}},{\textbf{b}})\), the inflow of premium rate over time for the insurance company is \(P^{({\varvec{a}}, {\varvec{b}})}(s):= \sum _{i=1}^n \left( c_i - P_i(a_i(s), b_i(s))\right) \), so using (2.3) and (2.4):

$$\begin{aligned} \ \ \ \ \ \ \ \ \ \ P^{({\varvec{a}}, {\varvec{b}})}(s)= & {} \sum _{i=1}^n (\theta _i + \theta _0) \left[ (\eta _i - \gamma _i) \mu _i + (1+\gamma _i) a_i(s) \int _0^{\frac{b_i(s)}{a_i(s)}} x f_i(x) \textrm{d}x\right. \nonumber \\{} & {} \left. +b_i(s) \int _{\frac{b_i(s)}{a_i(s)}}^{+\infty } f_i(x) \textrm{d}x\right] . \end{aligned}$$
(2.5)

It follows that the surplus process \(R^{({\varvec{a}}, {\varvec{b}})}\) satisfies

$$\begin{aligned} R^{({\varvec{a}}, {\varvec{b}})}(s):= R^{({\varvec{a}}, {\varvec{b}})}(0)+ \int _0^s P^{({\varvec{a}}, {\varvec{b}})}(\xi )d\xi - \sum _{i=1}^n (G^{({\varvec{a}}, {\varvec{b}})}_i(s)), \ \ \ \ \ s\in [0,T] \end{aligned}$$
(2.6)

Starting from the state x at time t, \(t \in [0,T]\), the insurer company aims to maximize the expected utility of terminal wealth using a utility function \(u: {\mathbb {R}} \rightarrow {\mathbb {R}}\), representing the preferences. Namely, we consider the performance criterion

$$\begin{aligned} J(t, x, ({\varvec{a}}, {\varvec{b}}) ):= E\left[ u(R^{({\varvec{a}}, {\varvec{b}})}(T)) \,|\, R^{({\varvec{a}}, {\varvec{b}})}(t)=x\right] , \quad t \in [0,T], \;x \in {\mathbb {R}}. \end{aligned}$$

The value function associated to the stochastic control problem is

$$\begin{aligned} V(t,x):= \sup _{({\varvec{a}}, {\varvec{b}}) \in A_t} J(t, x, ({\varvec{a}}, {\varvec{b}}) ), \end{aligned}$$
(2.7)

with terminal boundary condition \(V(T,x) = u(x)\).

We make the following assumptions on the utility function.

Assumption 2.1

The utility function \(u: {\mathbb {R}} \rightarrow {\mathbb {R}}\) satisfies the following assumptions:

  1. (i)

    u is nondecreasing;

  2. (ii)

    \(-K_0 e^{-K_1x}\le u(x)\le 0\) for some real values \(K_0, K_1 >0\) such that \(\varphi _i(K_1):=\int _0^\infty f_i(x)e^{K_1 x} \textrm{d}x<\infty \) for each \(i \in \{1,\ldots ,n\}\).

Remark 2.2

In our model the wealth may become negative. This may be interpreted by implicitly assuming the presence of a riskless asset with \(r=0\) in the market which allows the company to borrow money. Therefore, our model considers a null interest rate, simplifying a situation occurred during recent years (for instance, until recently the European Central Bank (ECB) fixed a negative Deposit facility rate). If \(r \ne 0\) the equation of the surplus process would satisfy

$$\begin{aligned} \textrm{d}R^{({\varvec{a}}, {\varvec{b}})}(s) = P^{({\varvec{a}}, {\varvec{b}})}(s)\textrm{d}s - {d}\sum _{i=1}^n G^{({\varvec{a}}, {\varvec{b}})}_i(s)+r R^{({\varvec{a}}, {\varvec{b}})}(s) \textrm{d}s, \ \ \ \ \ s\in [0,T], \end{aligned}$$

and the subsequent formulas would change accordingly. For simplicity, we consider the case \(r=0\). Moreover, as pointed out in the literature, see Brachetta and Ceci (2019a, 2019b); Liang and Young (2018), the absence of a risky asset represents no loss of generality as, under mild assumptions, the optimal reinsurance strategy turns out to depend only on the risk-free asset.

2.1 Preliminary estimates on the value function

In the following result we prove that \(J(t, x, ({\varvec{a}}, {\varvec{b}}) )\) is well-defined for each \((t,x)\in [0,T]\times {\mathbb {R}}\) and \(({\textbf{a}},{\textbf{b}})\in A_t\).

Proposition 2.3

The functional \(J(t, x, ({\varvec{a}}, {\varvec{b}}) )\) is well-defined for each \((t,x)\in [0,T]\times {\mathbb {R}}\) and \((\textbf{a},{\textbf{b}})\in A_t\) and satisfies

$$\begin{aligned} -K_0 e^{-K_1x+nTD} \le J(t, x, ({\varvec{a}}, {\varvec{b}}) ) {\le 0} \quad \forall (t,x)\in [0,T]\times {\mathbb {R}}, \; \forall ({\textbf{a}},{\textbf{b}})\in A_t, \end{aligned}$$

where

$$\begin{aligned} D:=\max \{(\theta _i+\theta _0)\left( K_1(\gamma _i - \eta _i) \mu _i+\varphi _i(K_1)-1 \right) \,|\,i \in \{1,\ldots ,n\}\} <+\infty . \end{aligned}$$

Consequently,

$$\begin{aligned} -K_0 e^{-K_1x+nTD} \le V(t, x) {\le 0} \quad \forall t \in [0,T], \forall x \in {\mathbb {R}}. \end{aligned}$$

Proof

From (2.6) the surplus process \(R^{({\varvec{a}}, {\varvec{b}})}(T)\) is

$$\begin{aligned} R^{({\varvec{a}}, {\varvec{b}})}(T) = x+ \int _t^T P^{({\varvec{a}}, {\varvec{b}})}(\xi )\textrm{d}\xi - \sum _{i=1}^n \left( G^{({\varvec{a}}, {\varvec{b}})}_i(T)- G^{({\varvec{a}}, {\varvec{b}})}_i(t)\right) . \end{aligned}$$
(2.8)

Then

$$\begin{aligned} R^{({\varvec{a}}, {\varvec{b}})}(T) \le x+ \int _t^T P^{({\varvec{a}}, {\varvec{b}})}(\xi )\textrm{d}\xi \le x+ \int _t^T \sum _{i=1}^n c_i \textrm{d}s = x+(T-t)\sum _{i=1}^n c_i \end{aligned}$$

and, using Assumption 2.1, \({u\left( R^{({\varvec{a}}, {\varvec{b}})}(T) \right) \le 0.}\) Therefore

$$\begin{aligned} J(t, x, ({\varvec{a}}, {\varvec{b}}) ) = E\left[ u \left( R^{({\varvec{a}}, {\varvec{b}})}(T)\right) \,\left| \, R^{({\varvec{a}}, {\varvec{b}})}(t)=x\right. \right] {\le 0.} \end{aligned}$$
(2.9)

Further, using (2.5) the premium rate \(P^{({\varvec{a}}, {\varvec{b}})}(s)\) can be bounded from below as follows

$$\begin{aligned} P^{({\varvec{a}}, {\varvec{b}})}(s)\ge \sum _{i=1}^n (\theta _i + \theta _0)(\eta _i - \gamma _i) \mu _i \end{aligned}$$
(2.10)

and, from (2.1) and (2.2), the ith total claim amount has the following upper bound

$$\begin{aligned} G^{({\varvec{a}}, {\varvec{b}})}_i(T) - G^{({\varvec{a}}, {\varvec{b}})}_i(t)= & {} \int _t^T g_i(a_i(\xi ), b_i(\xi ), \Delta Q_i(\xi )) dN_i(\xi )\nonumber \\\le & {} \sum _{j=N_i(t)+1}^{N_i(T)} X_{ij} \le \sum _{j=1}^{N_i(T)} X_{ij} = Q_i(T). \end{aligned}$$
(2.11)

Therefore, using (2.10) and (2.11) in (2.8) yields

$$\begin{aligned} R^{({\varvec{a}}, {\varvec{b}})}(T) \ge x+(T-t)\sum _{i=1}^n (\theta _i + \theta _0)(\eta _i - \gamma _i) \mu _i - \sum _{i=1}^n Q_i(T). \end{aligned}$$

Using again Assumption 2.1 and recalling the hypothesis \(\gamma _i>\eta _i\), it holds

$$\begin{aligned} u \left( R^{({\varvec{a}}, {\varvec{b}})}(T)\right)\ge & {} -K_0e^{-K_1x}e^{K_1 (T-t)\sum _{i=1}^n (\theta _i + \theta _0)(\gamma _i - \eta _i) \mu _i}e^{K_1\sum _{i=1}^n Q_i(T)} \\ {}\ge & {} -K_0 e^{-K_1x}\prod _{i=1}^n e^{K_1T(\theta _i+\theta _0)(\gamma _i - \eta _i) \mu _i} \prod _{i=1}^n e^{K_1 Q_i(T)}. \end{aligned}$$

Further, by applying Shreve (Shreve 2004, formula (11.3.2)) to each compound Poisson process \(Q_i(T)\) and using the hypothesis \(\varphi _i(K_1)<\infty \), it follows

$$\begin{aligned} J(t, x, ({\varvec{a}}, {\varvec{b}}) )= & {} E\left[ u \left( R^{({\varvec{a}}, {\varvec{b}})}(T)\right) \,\left| \, R^{({\varvec{a}}, {\varvec{b}})}(t)=x\right. \right] \nonumber \\ {}\ge & {} -K_0 e^{-K_1x}\prod _{i=1}^n e^{K_1T(\theta _i+\theta _0)(\gamma _i - \eta _i) \mu _i} \prod _{i=1}^n E\left[ e^{K_1 Q_i(T)}\right] \nonumber \\ {}= & {} -K_0 e^{-K_1x} \prod _{i=1}^n e^{T(\theta _i+\theta _0)(K_1(\gamma _i - \eta _i) \mu _i+\varphi _i(K_1)-1)}\nonumber \\\ge & {} -K_0 e^{-K_1x+nTD}. \end{aligned}$$
(2.12)

Recalling (2.7), the result on the value function follows from (2.9) and (2.12). \(\square \)

3 The HJB equation and the Verification Theorem

In this section we use the dynamic programming approach to write the Hamilton–Jacobi–Bellman (HJB) equation for the stochastic control problem defined in (2.7), we show that V(t, x) is its viscosity solution and formulate a Verification Theorem (see Theorem 3.2), and the latter provides a set of sufficient conditions for the optimality of a given (candidate) admissible reinsurance strategy.

Let \(C:=[0,1]^n \times [0, +\infty ]^n\); recalling (2.6), the dynamic of the surplus process \(R^{(a, b)}(s)\), \((a,b) \in C\), is:

$$\begin{aligned} dR^{(a, b)}(s) = P^{(a,b)}(s)ds - d\sum _{i=1}^n G_i^{(a,b)}(s) \end{aligned}$$
(3.1)

Let \(W \in {\mathcal {C}}^{1,1}\); following Øksendal and Sulem (2005) we write the following HJB equation:

$$\begin{aligned} \sup _{(a,b) \in C} L_t^{(a,b)} W(t,x)=0, \qquad \forall (t,x) \in [0,T)\times {\mathbb {R}}, \end{aligned}$$
(3.2)

with terminal boundary condition

$$\begin{aligned} W(T,x)=u(x), \quad x \in {\mathbb {R}}, \end{aligned}$$
(3.3)

where, by standard arguments, the infinitesimal generator is

$$\begin{aligned}{} & {} L_t^{(a,b)} W(t,x) := \frac{\partial W(t,x)}{\partial t} + P^{(a,b)}\frac{\partial W(t,x)}{\partial x} + \sum _{i=1}^n \theta _i \int _0^{+\infty } W(t, x-g_i(a_i,b_i,\xi _i))f_i(\xi _i) \textrm{d}\xi _i\nonumber \\ {}{} & {} \quad + \theta _0 \underbrace{\int _0^{+\infty } \ldots \int _0^{+\infty }}_n W \left( t, x- \sum _{i=1}^n g_i(a_i,b_i,\xi _i)\right) f_i(\xi _i) \textrm{d}\xi _i - \sum _{i=0}^n \theta _i W(t,x).\nonumber \\ \end{aligned}$$
(3.4)

Theorem 3.1

The value function V(t, x) defined in (2.7) is a viscosity solution of (3.2)–(3.3).

Proof

It is enough to apply (Øksendal and Sulem, 2005), Theorem 9.8 to the stochastic control problem (3.1) (we also refer to the book (Azcue and Muler 2014) for a valuable treatment of optimization problems in the classical collective risk model using the viscosity approach). \(\square \)

Theorem 3.2

(Verification Theorem) Let \((t,x) \in [0,T]\times {\mathbb {R}}\). Let \(W \in {\mathcal {C}}^{1,1}\) satisfy the HJB equation (3.2) with terminal boundary condition (3.3) and assume that

$$\begin{aligned} E\left[ \sup _{s\in [t,T]}\left| W\left( s, R^{({\textbf{a}},{\textbf{b}})}(s)\right) \right| \,\left| \, R^{({\varvec{a}}, {\varvec{b}})}(t)=x \right] \right. <\infty \ \ \ \ \forall ({\textbf{a}},{\textbf{b}})\in A_t. \end{aligned}$$
(3.5)

Then:

  1. (a)

    For any admissible control \(({\varvec{a}}, {\varvec{b}}) \in A_t\) it holds \(W(t,x) \ge J(t,x, ({\varvec{a}}, {\varvec{b}}))\).

  2. (b)

    If \((\mathbf{a^*}, \mathbf{b^*}) \in A_t\) is such that \(L_t^{(\mathbf{a^*}(s), \mathbf{b^*}(s))}W(s,R^{(\mathbf{a^*}, \mathbf{b^*})}(s)) =0\) for every \(s \in [t, T]\) then \(W(t,x) = J(t,x, (\mathbf{a^*}, \mathbf{b^*})).\) Hence, by item (a)

    $$\begin{aligned} W(t,x)=V(t,x) \end{aligned}$$
    (3.6)

    and \((\mathbf{a^*}, \mathbf{b^*})\) is optimal.

Proof

Let \(M>0\); we define the stopping time \(\tau _M:= \inf \{s \in [t, T] \,:\, R^{({\varvec{a}}, {\varvec{b}})}(s)\le -M\} \wedge T\). Clearly, we have \(\tau _M \xrightarrow {a.s.} T\) as \(M\rightarrow +\infty \). Ito’s formula, see also Øksendal and Sulem (2005), Theorem 1.23, applied in the time interval \([t,\tau _M]\) yields

$$\begin{aligned}{} & {} E \left[ W(\tau _M, R^{({\varvec{a}}, {\varvec{b}})}(\tau _M)) \,|\, R^{({\varvec{a}}, {\varvec{b}})}(t)=x \right] \nonumber \\{} & {} =W(t,x) + E \left[ \int _t^{\tau _M} L_t^{({\varvec{a}}(s), {\varvec{b}}(s))} W(s, R^{({\varvec{a}}, {\varvec{b}})}(s)) ds\right] . \end{aligned}$$
(3.7)

We now use the HJB equation, and then take limits as \(M \rightarrow + \infty \) to obtain, thanks to the hypothesis of uniform integrability (3.5) and the dominated convergence theorem, that:

$$\begin{aligned}{} & {} E \left[ W(T, R^{({\varvec{a}}, {\varvec{b}})}(T)) \,|\, R^{({\varvec{a}}, {\varvec{b}})}(t)=x \right] \nonumber \\{} & {} = \lim _{M\rightarrow +\infty } E[W(\tau _M, R^{({\varvec{a}}, {\varvec{b}})}(\tau _M)) \,|\, R^{({\varvec{a}}, {\varvec{b}})}(t)=x] \le W(t,x). \end{aligned}$$

Then, employing the terminal boundary condition (3.3) and the definition of \(J(t,x,({\varvec{a}}, {\varvec{b}}))\), it follows that \(J(t,x,({\varvec{a}}, {\varvec{b}})) \le W(t,x)\), so that claim (a) is proved.

In order to prove claim (b), we evaluate formula (3.7) at the admissible control \((\mathbf{a^*}, \mathbf{b^*}) \in A_t\) and get \(E \left[ W(\tau _M, R^{(\mathbf{a^*}, \mathbf{b^*})}(\tau _M)) \,|\, R^{(\mathbf{a^*}, \mathbf{b^*})}(t)=x \right] =W(t,x)\). Hence, exploiting the hypothesis of uniform integrability (3.5), we obtain again by the dominated convergence theorem that

$$\begin{aligned} W(t,x)= & {} \lim _{M \rightarrow +\infty } E \left[ W(\tau _M, R^{(\mathbf{a^*}, \mathbf{b^*})}(\tau _M)) \,|\, R^{(\mathbf{a^*}, \mathbf{b^*})}(t)=x \right] \\= & {} E \left[ W(T, R^{(\mathbf{a^*}, \mathbf{b^*})}(T)) \,|\, R^{(\mathbf{a^*}, \mathbf{b^*})}(t)=x \right] . \end{aligned}$$

The proof is thus completed. \(\square \)

4 A case study with explicit solution

In this section we consider a special case of the above problem.

Assumption 4.1

  1. (i)

    The claim size random variables \(X_{ij}\), \(i \in \{1,\ldots ,n\}\), \(j=1,2,\ldots \), corresponding to the ith class of insurance business is exponentially distributed, with density \(f_i(s):=k_i e^{-k_i s}\), \(s \ge 0\).

  2. (ii)

    \(u(x):= -\frac{1}{\beta } e^{-\beta x}\), for each \(x\in {\mathbb {R}}\), with \(0< \beta < k_i\), for each \(i=1,\ldots ,n\).

Given the structure of the problem we look for a solution of the HJB equation (3.2) of the form (see for instance Gosio et al. 2016; Liang and Guo 2011; Liang and Yuen 2016):

$$\begin{aligned} W(t,x):= -\frac{1}{\beta } e ^{-\beta (x-Z(t))}, \qquad \forall (t,x) \in [0,T]\times {\mathbb {R}} \end{aligned}$$
(4.1)

with terminal boundary condition \(W(T,x)=u(x)\), and so with \(Z(T)=0\).

We recall the notion of zth elementary symmetric polynomial in n variables \(x_1,\ldots ,x_n\) denoted by \(\sigma _z(x_1,\ldots ,x_n)\):

$$\begin{aligned} \sigma _z(x_1,\ldots ,x_n):=\sum _{1\le j_1<\cdots <j_z \le n} x_{j_1}\cdot \ldots \cdot x_{j_z}. \end{aligned}$$

Theorem 4.2

In the above setting the value function is \(V(t,x) =-\frac{1}{\beta }e^{-\beta (x-Z(t))}\) with

$$\begin{aligned} Z(t):= & {} \left[ \sum _{i=1}^n (\theta _i + \theta _0) \left( \frac{\eta _i-\gamma _i}{k_i}\right) +\sum _{i=1}^n(\theta _i + \theta _0)(1+ \gamma _i)\psi \left( k_i, b_i^*\right) \right. \\{} & {} \left. - \sum _{i=1}^n(\theta _i + \theta _0) \psi \left( k_i-\beta ,b_i^*\right) - \theta _0 \sum _{z=2}^{n} \beta ^{z-1}\sigma _z (\psi ((k_i-\beta ,b_i^*)) \,|\, i \in {\mathcal {B}})\right] \\{} & {} \times (T-t),\quad \forall (t,x) \in [0,T]\times {\mathbb {R}}, \end{aligned}$$

where \(\psi :(0, +\infty ) \times [0, \infty ) \rightarrow {\mathbb {R}}\) is defined by

$$\begin{aligned} \psi (x,y):= \frac{1-e^{-xy}}{x}, \qquad \forall x>0, \forall y \ge 0, \end{aligned}$$

and \(({\varvec{a}}^*, {\varvec{b}}^*) = (a_1^*,\ldots , a_n^*, b_1^*,\ldots , b_n^*)\), which denotes the point such that \(\Theta ({\varvec{a}}^*, {\varvec{b}}^*)=\sup _{({\varvec{a}},{\varvec{b}}) \in D}\Theta ({\varvec{a}}, {\varvec{b}})\), where \(D:=[0,1]^n \times [0,+\infty ]^n\) and

$$\begin{aligned} \Theta ({\varvec{a}},{\varvec{b}}):= & {} \sum _{i=1}^n (\theta _i + \theta _0) \left( \frac{\eta _i-\gamma _i}{k_i} +(1+ \gamma _i)\psi \left( \frac{k_i}{a_i}, b_i\right) \right) \nonumber \\ {}{} & {} - \sum _{i=1}^n(\theta _i + \theta _0) \psi \left( \frac{k_i}{a_i}-\beta ,b_i\right) +- \theta _0 \sum _{z=2}^n \beta ^{z-1}\sigma _z\nonumber \\{} & {} \times \left( \psi \left( \frac{k_1}{a_1}-\beta ,b_1\right) ,\ldots , \psi \left( \frac{k_n}{a_n}-\beta ,b_n\right) \right) \quad \forall ({\varvec{a}},{\varvec{b}}) \in D, \end{aligned}$$
(4.2)

are optimal strategies starting at any \((t,x)\in [0,T]\times {\mathbb {R}}\). For each \(i \in \{1,\ldots ,n\}\), either \(a_i^* \in (0,1]\) and \(b_i^*=0\), or \(a_i^*=1\) and \(b_i^*>0\); further, \((b_1^*,\ldots ,b_n^*) \in \prod _{i=1}^n \left[ 0,\frac{1}{\beta }\ln (1+\gamma _i)\right] \) satisfies the following system of equations:

$$\begin{aligned}{} & {} \frac{\theta _0}{\theta _i + \theta _0} \sum _{z=1}^{n-1} \beta ^z \sigma _z \left( (\psi (k_l - \beta ,b_l)\,|\, l \in \{1,\ldots ,n\} \text { and } l\ne i) \right) \nonumber \\{} & {} =(1+\gamma _i)e^{-\beta b_i} -1, \ \ i=1,\ldots ,n. \end{aligned}$$
(4.3)

Proof

In order to compute the optimal strategies we rewrite the HJB equation as an optimization problem. From (4.1), it follows that \(W(t,x) < 0\),

$$\begin{aligned} W(t, x-z) = e^{\beta z} W(t,x), \qquad \forall z \in {\mathbb {R}}, \forall (t,x) \in [0,T]\times {\mathbb {R}} \end{aligned}$$
(4.4)

and

$$\begin{aligned} \frac{\partial W}{\partial t}(t,x)= & {} \beta Z'(t) W(t,x) \qquad \forall (t,x) \in [0,T]\times {\mathbb {R}}\\ \frac{\partial W}{\partial x}(t,x)= & {} -\beta W(t,x) \qquad \forall (t,x) \in [0,T]\times {\mathbb {R}}. \end{aligned}$$

From (2.5), using \(f_i(s)=k_i e^{-k_i s}\) and \(\mu _i=\frac{1}{k_i}\) (see Assumption 4.1(a)), we have

$$\begin{aligned} P^{({\varvec{a}}, {\varvec{b}})}(t)= & {} \sum _{i=1}^n (\theta _i + \theta _0) \left[ \frac{\eta _i - \gamma _i}{k_i} +(1+\gamma _i) \left( \frac{a_i}{k_i} - \left( b_i + \frac{a_i}{k_i}\right) e^{-k_i\frac{b_i}{a_i}} +b_i e^{-k_i\frac{b_i}{a_i}}\right) \right] \nonumber \\= & {} \sum _{i=1}^n (\theta _i + \theta _0) \left[ \frac{\eta _i - \gamma _i}{k_i} +(1+\gamma _i) \frac{a_i}{k_i} \left( 1- e^{-\frac{k_i}{a_i}b_i} \right) \right] . \nonumber \\= & {} \sum _{i=1}^n (\theta _i + \theta _0) \left( \frac{\eta _i - \gamma _i}{k_i} +(1+\gamma _i) \psi \left( \frac{k_i}{a_i},b_i\right) \right) . \end{aligned}$$
(4.5)

Using formula (4.4) and recalling formula (2.1), we have:

$$\begin{aligned}{} & {} \int _0^{+\infty } W(t, x-g_i(a_i,b_i,\xi _i))f_i(\xi _i) d\xi _i \nonumber \\{} & {} \quad = W(t,x) \int _0^{+\infty } e^{\beta g_i(a_i,b_i,\xi _i)} k_i e^{-k_i \xi _i} d\xi _i \nonumber \\{} & {} \quad =W(t,x)\left( \int _0^{\frac{b_i}{a_i}} e^{\beta a_i\xi _i} k_i e^{-k_i \xi _i} d\xi _i + \int _{\frac{b_i}{a_i}}^{+\infty } e^{\beta b_i} k_i e^{-k_i \xi _i} d\xi _i\right) \nonumber \\{} & {} \quad = W(t,x) \left( 1+\frac{\beta }{\frac{k_i}{a_i}-\beta }\left( 1-e^{-\left( \frac{k_i}{a_i}-\beta \right) b_i} \right) \right) \nonumber \\{} & {} \quad = W(t,x) \left( 1+\beta \psi \left( \frac{k_i}{a_i}-\beta ,b_i\right) \right) \end{aligned}$$
(4.6)

Further, using again formula (4.4), (2.1) and the above computations, it follows:

$$\begin{aligned}{} & {} \underbrace{\int _0^{+\infty } \ldots \int _0^{+\infty }}_n W \left( t, x- \sum _{i=1}^n g_i(a_i,b_i,\xi _i)\right) f_i(\xi _i) d\xi _i \nonumber \\{} & {} \quad =\underbrace{\int _0^{+\infty } \ldots \int _0^{+\infty }}_n W(t, x) \prod _{i=1}^n e^{\beta g_i(a_i,b_i,\xi _i)}f_i(\xi _i) d\xi _i\nonumber \\{} & {} \quad = W(t,x) \prod _{i=1}^n \left( \int _0^{+\infty } e^{\beta g_i(a_i,b_i,\xi _i)} k_i e^{-k_i \xi _i}d\xi _i\right) \nonumber \\{} & {} \quad = W(t,x) \prod _{i=1}^n \left[ 1+\frac{\beta }{\frac{k_i}{a_i}-\beta }\left( 1-e^{-\left( \frac{k_i}{a_i}-\beta \right) b_i} \right) \right] \nonumber \\{} & {} \quad = W(t,x) \left[ 1+ \beta \sum _{i=1}^n \psi \left( \frac{k_i}{a_i}-\beta ,b_i\right) \right. \nonumber \\{} & {} \left. \qquad + \sum _{z=2}^n \beta ^z \sigma _z \left( \psi \left( \frac{k_1}{a_1}-\beta ,b_1\right) ,\ldots ,\psi \left( \frac{k_n}{a_n}-\beta ,b_n\right) \right) \right] . \end{aligned}$$
(4.7)

Combining (4.5), (4.6) and (4.7), the HJB equation (3.2) and the boundary condition can be rewritten as follows:

$$\begin{aligned} Z'(t) +\sup _{({\varvec{a}},{\varvec{b}}) \in D} \Theta ({\varvec{a}}, {\varvec{b}})=0\quad t \in [0,T), \; Z(T)=0, \qquad \forall (t,x) \in [0,T]\times {\mathbb {R}}\nonumber \\ \end{aligned}$$
(4.8)

\(\Theta \) is defined in (4.2) and \(\Theta |_{a_i=+\infty }({\varvec{a}}, {\varvec{b}}) =\lim _{a_i \rightarrow +\infty } \Theta ({\varvec{a}}, {\varvec{b}})\) and/or \(\Theta |_{b_j=+\infty }({\varvec{a}}, {\varvec{b}})=\lim _{b_j \rightarrow +\infty } \Theta ({\varvec{a}}, {\varvec{b}})\) for some \(i, j \in \{1,\ldots ,n\}\). We note that \(\frac{k_i}{a_i}-\beta \ge k_i-\beta >0\), for each \(i \in \{1,\ldots ,n\}\). The stationary points of \(\Theta \) in \((0,1)^n \times (0,+\infty )^n\) are computed solving the system of equations:

$$\begin{aligned} \displaystyle {\frac{\partial \Theta }{\partial a_i}}({\varvec{a}},{\varvec{b}})=\displaystyle {\frac{\partial \Theta }{\partial b_i}}({\varvec{a}},{\varvec{b}})=0, \ \ \ i =1, \ldots ,n. \end{aligned}$$
(4.9)

For each \(i \in \{1,\ldots ,n\}\) the expressions of the partial derivatives of \(\Theta \) are given by:

$$\begin{aligned} \displaystyle {\frac{\partial \Theta }{\partial a_i}}({\varvec{a}},{\varvec{b}})= & {} \displaystyle {-\frac{k_i (\theta _i+\theta _0)}{a_i^2e^{\frac{k_i}{a_i}b_i}}} \left( e^{\beta b_i} H\left( \left( \frac{{\varvec{k}}}{{\varvec{a}}}-\beta \textbf{1}\right) ^{[i]},{\varvec{b}}^{[i]}\right) \right. \nonumber \\{} & {} \left. \Phi \left( \frac{k_i}{a_i}-\beta ,b_i\right) -\left( 1+ \gamma _i\right) \Phi \left( \frac{k_i}{a_i},b_i\right) \right) \end{aligned}$$
(4.10)
$$\begin{aligned} \displaystyle {\frac{\partial \Theta }{\partial b_i}}({\varvec{a}}, {\varvec{b}})= & {} \displaystyle {\frac{(\theta _i+\theta _0)}{e^{\frac{k_i}{a_i}b_i}}} \left( (1+\gamma _i) - e^{\beta b_i} H\left( \left( \frac{{\varvec{k}}}{{\varvec{a}}}-\beta \textbf{1}\right) ^{[i]},{\varvec{b}}^{[i]}\right) \right) , \end{aligned}$$
(4.11)

where \(\displaystyle {\frac{{\varvec{k}}}{{\varvec{a}}}-\beta \textbf{1}=\left( \frac{k_1}{a_1}-\beta , \ldots ,\frac{k_n}{a_n}-\beta \right) }\), \({\varvec{b}}=(b_1,\ldots ,b_n)\) and the notation with the apex [i] indicates that the ith component has been removed, that is \(\displaystyle {\left( \frac{{\varvec{k}}}{{\varvec{a}}}-\beta \textbf{1}\right) ^{[i]}=\left( \frac{k_1}{a_1}-\beta , \ldots ,\frac{k_{i-1}}{a_{i-1}}-\beta ,\frac{k_{i+1}}{a_{i+1}}-\beta , \ldots ,\frac{k_n}{a_n} -\beta \right) }\) and \({\varvec{b}}^{[i]}=(b_1,\ldots ,b_{i-1},b_{i+1},\ldots ,b_n)\); further, \(H:(0, +\infty )^{n-1} \times [0, \infty )^{n-1}\) is defined by

$$\begin{aligned} H({\varvec{x}},{\varvec{y}}):=1+\frac{\theta _0}{\theta _i + \theta _0} \sum _{z=1}^{n-1} \beta ^z \sigma _z(\psi (x_1,y_1), \ldots , \psi (x_{n-1},y_{n-1})) \end{aligned}$$

for each \(({\varvec{x}},{\varvec{y}})=(x_1,\ldots ,x_{n-1},y_1,\ldots ,y_{n-1}) \in (0, +\infty )^{n-1} \times [0, \infty )^{n-1}\) and \(\Phi :(0,+\infty ) \times [0, +\infty ) \rightarrow {\mathbb {R}}\) is defined by

$$\begin{aligned} \Phi (x,y):= \frac{e^{xy}-xy-1 }{x^2}, \quad \forall x> 0, \forall y\ge 0. \end{aligned}$$

In \((0,1)^n \times (0,+\infty )^n\) problem (4.9) has no solutions. Indeed, for each \(i \in \{1,\ldots ,n\}\), using (4.11) equation \(\displaystyle {\frac{\partial \Theta }{\partial b_i}}({\varvec{a}},{\varvec{b}})=0\) becomes

$$\begin{aligned} e^{\beta b_i} H\left( \left( \frac{{\varvec{k}}}{{\varvec{a}}}-\beta \textbf{1}\right) ^{[i]},{\varvec{b}}^{[i]}\right) =1+\gamma _i, \qquad \forall i=1,\ldots ,n, \end{aligned}$$
(4.12)

and substituting it in \(\displaystyle {\frac{\partial \Theta }{\partial a_i}({\varvec{a}},{\varvec{b}})=0}\) yields

$$\begin{aligned} \Phi \left( \frac{k_i}{a_i}-\beta ,b_i\right) -\Phi \left( \frac{k_i}{a_i},b_i\right) =0, \end{aligned}$$

which is impossible since \(\Phi (\cdot ,b_i)\) is a strictly increasing function for each \(b_i>0\), see “Appendix”, Proposition A.1. By the previous discussion a solution \(({\varvec{a}},{\varvec{b}})=(a_1,\ldots ,a_n,b_1,\ldots ,b_n) \in D\) of system (4.12) is such that, for each i, either \(b_i=0\) and \(a_i \ge 1\), or \(b_i> 0\) and \(a_i=1\), and \((b_1,\ldots ,b_n)\) satisfies (4.3). Let \(i \in \{1,\ldots ,n\}\); we now consider the expression of \(\displaystyle {\frac{\partial \Theta }{\partial b_i}}(1,{\varvec{b}})\):

$$\begin{aligned} \displaystyle {\frac{\partial \Theta }{\partial b_i}}({\varvec{1}},{\varvec{b}})= & {} \frac{\theta _i +\theta _0}{e^{k_ib_i}}\left( 1+\gamma _i-e^{\beta b_i} -e^{\beta b_i}\frac{\theta _0}{\theta _i+\theta _0}\right. \nonumber \\{} & {} \left. \times \sum _{z=1}^{n-1} \beta ^{z} \sigma _{z} \left( \psi \left( k_l-\beta ,b_l\right) \,|\, l \ne i\right) \right) . \end{aligned}$$
(4.13)

The function \(\Theta ({\varvec{1}},{\varvec{b}})\) has maximum in \(\prod _{i=1}^n \left[ 0,\frac{1}{\beta }\ln (1+\gamma _i)\right] \) which is also a maximum in \([0,+\infty ]^n\) since \(\Theta ({\varvec{1}},{\varvec{b}})\) is strictly decreasing w.r.t. to each direction \(b_i\), \(i=1,\ldots ,n\), for \(b_i> \frac{1}{\beta }\log (1+\gamma _i)\). \(\square \)

Remark 4.3

We list some observations on Theorem 4.2. We notice that all the retention levels \(a_i^*\), \(i=1,\ldots ,n\) are useless: in fact, the reinsurer pays the quantity \(\sum _{k=1}^{N_j(t)} {\varvec{1}}_{\{X_{jk}>b_j^*\}}(X_{jk})(X_{jk} - b_j^*)\), so that the combination of a proportional and an excess-of-loss reinsurance ends with a purely excess-of-loss reinsurance.

Remark 4.4

In the special case of 2 classes of insurance business, we observe that the results of Theorem 4.2, specialized for \(n=2\), agree with the findings of Gosio et al. (2016), see formula (30),(31),(32)and Centeno (2005), see Result 2.2. Indeed, assume that \(\gamma _i<1\), for each \(i \in \{1,2\}\). If

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle {\frac{\gamma _1(\theta _1 + \theta _0)}{\theta _0}> \frac{ 1-(1+\gamma _2)^{-\frac{k_2-\beta }{\beta }} }{\frac{k_2-\beta }{\beta }}}\\ \displaystyle {\frac{\gamma _2(\theta _2 + \theta _0)}{\theta _0} > \frac{ 1-(1+\gamma _1)^{-\frac{k_1-\beta }{\beta }} }{\frac{k_1-\beta }{\beta }}} \end{array}\right. \end{aligned}$$
(4.14)

then the system of equations

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle {\frac{\theta _0}{\theta _1 + \theta _0} \frac{1-e^{-(k_2-\beta )b_2}}{\frac{k_2-\beta }{\beta }}}=(1+\gamma _1)e^{-\beta b_1} -1\\ \\ \displaystyle {\frac{\theta _0}{\theta _2+ \theta _0} \frac{1-e^{-(k_1-\beta )b_1}}{\frac{k_1-\beta }{\beta }}}=(1+\gamma _2)e^{-\beta b_2} -1 \end{array}\right. \end{aligned}$$
(4.15)

has unique solution \((b_1^*,b_2^*) \in \left( 0,\frac{1}{\beta }\ln (1+\gamma _1)\right) \times \left( 0,\frac{1}{\beta }\ln (1+\gamma _2)\right) \) and \(({\varvec{a}}^*, {\varvec{b}}^*) = (1,1, b_1^*,b_2^*)\) are optimal strategies starting at any \((t,x) \in [0,T] \times {\mathbb {R}}\). Otherwise, if

$$\begin{aligned}{} & {} \quad \text {(a)} \left\{ \begin{array}{lll} \displaystyle {\frac{\gamma _1(\theta _1 + \theta _0)}{\theta _0} \le \frac{ 1-(1+\gamma _2)^{-\frac{k_2-\beta }{\beta }} }{\frac{k_2-\beta }{\beta }}}\\ \displaystyle {\frac{\gamma _2(\theta _2 + \theta _0)}{\theta _0}> \frac{ 1-(1+\gamma _1)^{-\frac{k_1-\beta }{\beta }} }{\frac{k_1-\beta }{\beta }}} \end{array}\right. \ \ \text { or } \nonumber \\{} & {} \quad \text {(b)}\left\{ \begin{array}{lll} \displaystyle {\frac{\gamma _1(\theta _1 + \theta _0)}{\theta _0} > \frac{ 1-(1+\gamma _2)^{-\frac{k_2-\beta }{\beta }} }{\frac{k_2-\beta }{\beta }}}\\ \displaystyle {\frac{\gamma _2(\theta _2 + \theta _0)}{\theta _0} \le \frac{ 1-(1+\gamma _1)^{-\frac{k_1-\beta }{\beta }} }{\frac{k_1-\beta }{\beta }}} \end{array}\right. \end{aligned}$$
(4.16)

then \(({\varvec{a}}^*, {\varvec{b}}^*) = \left( a_1^*, 1, 0, \frac{1}{\beta }\ln (1+\gamma _2)\right) \), with \(a_1^* \in (0,1]\), or \(({\varvec{a}}^*, {\varvec{b}}^*) = \left( 1, a_2^*, \frac{1}{\beta }\ln (1+\gamma _1), 0\right) \), with \(a_2^* \in (0,1]\), are optimal strategies starting at any \((t,x) \in [0,T] \times {\mathbb {R}}\). For a proof of this facts we refer to Proposition A.2. In Sect. 5 we treat this simple case from a numerical point of view, introducing explicit examples aimed to highlight the effect of the different parameters variation on the optimal strategies.

We end the section with the analysis of the symmetric case, in which we assume that all the involved parameters are equal: \(\theta _i=\theta \), \(\eta _i=\eta \), \(\gamma _i=\gamma \), \(k_i=k\) for each \(i \in \{1,\ldots ,n\}\). This study allows us to evaluate the behaviour of both the value function and the optimal strategies when n goes to infinity. To this aim, in the involved variables we make explicit the dependence on n, so that we denote \(V=V_n\) and \(b_i=b_{n,i}\), for each \(i \in \{1,\ldots ,n\}\).

Theorem 4.5

In the symmetric case, that is when \(\theta _i=\theta \), \(\eta _i=\eta \), \(\gamma _i=\gamma \), \(k_i=k\), for each \(i \in \{1,\ldots ,n\}\), let \(b_n^* \in \left( 0, \frac{1}{\beta } \ln (1+\gamma )\right) \) be the unique solution of the equation

$$\begin{aligned} \displaystyle {\frac{\theta _0}{\theta + \theta _0} \left[ \left( 1+ \frac{1-e^{-(k-\beta )b_n}}{\frac{k-\beta }{\beta }}\right) ^{n-1}-1\right] =(1+\gamma )e^{-\beta b_n}-1}. \end{aligned}$$
(4.17)

Then the value function is \(V_n(t,x) =-\frac{1}{\beta }e^{-\beta (x-Z_n(t))}\), where \(Z_n(t)\) is given by

$$\begin{aligned} Z_n(t):= & {} \left[ n(\theta + \theta _0) \left( \frac{\eta -\gamma }{k} +(1+ \gamma )\frac{1-e^{-kb_n^*}}{k} - \frac{ 1-e^{-(k-\beta )b_n^*}}{k-\beta } \right) -\theta _0 \sum _{z=2}^{n} \beta ^{z-1}\right. \nonumber \\{} & {} \times \left. \left( {\begin{array}{c}n\\ z\end{array}}\right) \left( \frac{ 1-e^{-(k-\beta )b_n^*}}{k-\beta } \right) ^z \right] (T-t), \qquad \forall (t,x) \in [0,T]\times {\mathbb {R}} \end{aligned}$$
(4.18)

and \(({\varvec{a}}^*, {\varvec{b}}^*) = (a_{n,1}^*,\ldots , a_{n,n}^*, b_{n,1}^*,\ldots , b_{n,n}^*)\), where \(a_{n,i}^*=1\) and \(b_{n,i}^*=b_n^*\), for each \(i \in \{1,\ldots ,n\}\), is an optimal strategy starting at any \((t,x)\in [0,T]\times {\mathbb {R}}\). Further, if \(n \rightarrow +\infty \) then \(b_n^* \rightarrow 0\) and \(\lim _{n \rightarrow +\infty } V_n(t,x) = 0\).

Proof

By Theorem 4.2 and using symmetry, we obtain that \(\sup _{({\varvec{a}},{\varvec{b}}) \in D}\Theta ({\varvec{a}}, {\varvec{b}})\) is attained at \(({\varvec{a}}^*, {\varvec{b}}^*) = (1,\ldots ,1, b_n,\ldots , b_n)\) where \(b_n \in \left[ 0,\frac{1}{\beta }\ln (1+\gamma )\right] \) satisfies (4.3). Then, using equality

$$\begin{aligned}{} & {} \sum _{z=1}^{n-1} \beta ^z \sigma _z \left( (\psi (k - \beta ,b_n)\,|\,l \in \{1,\ldots ,n\} \text { and } l \ne i)\right) \\{} & {} \quad = \sum _{z=1}^{n-1} \beta ^z \sigma _z \left( \underbrace{\psi (k - \beta ,b_n), \ldots ,\psi (k - \beta ,b_n)}_{\text {(n-1) times}} \right) \\{} & {} \quad = \sum _{z=1}^{n-1} \left( {\begin{array}{c}n-1\\ z\end{array}}\right) \beta ^z \psi ^z(k- \beta ,b_n)\\{} & {} \quad =\left( 1+\beta \psi (k-\beta , b_n)\right) ^{n-1}-1\\{} & {} \quad =\left( 1+\frac{\beta }{k-\beta } \left( 1-e^{-(k-\beta )b_n}\right) \right) ^{n-1}-1, \end{aligned}$$

condition (4.3) becomes equivalent to (4.17). The unique solution of (4.17) is \(b_n^* \in \left( 0,\frac{1}{\beta } \ln (1+\gamma )\right) \) such that \(b_n^* \rightarrow 0\) when \(n \rightarrow + \infty \) (see “Appendix”, Proposition A.3). The value function is \(V_n(t,x) =-\frac{1}{\beta }e^{-\beta (x-Z_n(t))}\) where \(Z_n(t)\), deriving from Theorem 4.2, is given by (4.18). Finally \(V_n(t,x) \rightarrow 0\) when \(n \rightarrow +\infty \). \(\square \)

5 Numerical examples

In this section we consider models with two classes of insurance business and assume that the claim sizes \(X_{1j}\) and \(X_{2j}\) are exponentially distributed with parameters \(k_1\) and \(k_2\). Using the results of Theorem 4.2 and Remark 4.4, we present some numerical examples to highlight the effect of the different parameters variation on the optimal strategies.

Example 5.1

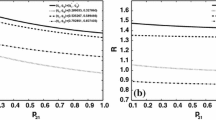
We let \(\beta =0.05\), \(\gamma _1=\gamma _2=\gamma = 0.3\), \(\theta _1=3\), \(\theta _2=4\), \(\theta _0=2\) and we consider variations of the parameters \(k_1\) and \(k_2\). In the first case \(k_1 \in [1,10]\) and \(k_2=3\); condition (4.14) holds. The results are shown in Fig. 1a. We note that the variations of \(k_1\) affect the values of both \(b_1^*\) and \(b_2^*\), but this effect is much more evident on \(b_2^*\) than on \(b_1^*\). In particular, a greater value of \(k_1\) yields greater values of \(b_2^*\) and almost constant values of \(b_1^*\). Our interpretation of the phenomenon agrees with the observations made in Yuen et al. (2015, Example 5.1): since a smaller value of \(k_1\) means to have a more risky claim size but also a greater expected value, the insurer’s optimal strategy consists to retain less. Nevertheless, our results are symmetrical with respect to the results of Yuen et al. (2015). In fact, when the claim sizes are exponentially distributed, Yuen et al. (2015) show that \(X_{1j}\) (\(X_{2j}\) respectively) has no effect on the optimal reinsurance strategy \(b_2^*\) (\(b_1^*\) respectively), while in our case \(X_{1j}\) (\(X_{2j}\) respectively) has almost no effect on the optimal reinsurance strategy \(b_1^*\) (\(b_2^*\), respectively). In the second case \(k_1=2\) and \(k_2 \in [1,10]\); condition (4.14) holds again. The results are shown in Fig. 1b which present a situation symmetrical to Fig. 1a, so all above observations hold.

Fig. 1
figure 1

The values of \(b_1^*\) (solid line), \(b_2^*\) (dashed line) and \(y=\frac{1}{\beta }\ln (1+\gamma )\) (dotted line) of Example 5.1

Full size image

Example 5.2

We let \(\beta =0.05\), \(\gamma _1=\gamma _2=\gamma =0.3\), \(k_1=2\), \(k_2=3\) and we consider variations of the parameters \(\theta _1\), \(\theta _2\) and \(\theta _0\). In the first case \(\theta _1=3\), \(\theta _2=4\) and \(\theta _0 \in [1,10]\); condition (4.14) holds. The results are shown in Fig. 2a from which we note that the variations of \(\theta _0\) affect the values of both \(b_1^*\) and \(b_2^*\). In particular, both the optimal reinsurance strategies decrease while \(\theta _0\) increases. In the second case, since the equations (4.3) only depend on the quantities \(\theta _1/\theta _0\) and \(\theta _2/\theta _0\), we let \(\theta _1=\theta _2=\theta \) and the quantity \(\theta /\theta _0 \in [0, 5]\); condition (4.14) holds again. The results are shown in Fig. 2b from which we can report the same conclusion as above (obviously when \(\theta /\theta _0\) increases, \(\theta _0\) decreases).

Fig. 2
figure 2

The values of \(b_1^*\) (solid line), \(b_2^*\) (dashed line) and \(y=\frac{1}{\beta }\ln (1+\gamma )\) (dotted line) of Example 5.2

Full size image

Example 5.3

We let \(\beta =0.05\), \(\gamma _1=0.5\), \(\gamma _2=0.1\), \(\theta _1=1\), \(\theta _2=0.1\), \(\theta _0=2\), \(k_2=3\) and we consider variations of the parameters \(k_1 \in [0.1,1]\). The results, contained in Fig. 3a, b, show that the variations of \(k_1\) affect the values of both \(b_1^*\) and \(b_2^*\) and, as already pointed out in Example 5.1, the effect is more evident on \(b_2^*\) than on \(b_1^*\).

Fig. 3
figure 3

In the case \(k_1\in [0.1,1]\), \(k_2=3\): panel a shows the values of \(b_1^*\) (solid line) and \(y=\frac{1}{\beta }\ln (1+\gamma _1)\) (dotted line); panel b shows the values of \(b_2^*\) (solid line) and \(y=\frac{1}{\beta }\ln (1+\gamma _2)\) (dotted line)

Full size image

In particular, in this case, the values of \(b_1^*\) and \(b_2^*\) are constant till a certain value \(\overline{k_1} \in (0.5, 0.6)\) of \(k_1\); then, for \(k_1>\overline{k_1}\), \(b_1^*\) slowly decreases while \(b_2^*\) decisively increases. Note that the value \(\overline{k_1}\) is the largest value of \(k_1\) satisfying (4.16)(b), so that for \(k_1 < \overline{k_1}\) the optimal solution is \(b_1^*=\frac{1}{\beta }\ln (1+\gamma _1)\) and \(b_2^*=0\), and for \(k_1 > \overline{k_1}\) the optimal solution is obtained solving the system (4.15).

6 Conclusions

In this paper we consider a risk model with multiple dependent classes of insurance business. Under the assumption that the insurance company combines the proportional and the excess-of-loss reinsurance, our aim is to maximize the expected utility of its wealth at the end of a finite time horizon. In a general setting we derive the associated HJB equation and formulate a Verification Theorem to detect the strategies optimality. In a special case with exponential utility we specialize the HJB equation and transform it into an optimization problem and, using the classical KKT conditions and a detailed discussion of its feasible solutions, we explicitly determine a reinsurance strategy and prove its optimality by the stated Verification Theorem. When only two classes of insurance business are considered, our explicit solutions agree with the results of Gosio et al. (2016), in the case the proportional reinsurance is excluded, and of Centeno (2005), in which only the excess-of-loss reinsurance is considered. This observation suggests us that the excess-of-loss reinsurance could be predominant with respect to the proportional one. The paper ends with some numerical examples to effectively show the optimal results and the impact of the different parameters’ variations on the optimal strategies. The results obtained in the paper suggest possible future developments in the field, such as the use of different claim size random variables distributions or of other principles for the premium computation, e.g. the variance principle.