Abstract
Financial performance evaluation is intimately linked to risk measurement methodologies. There exists a well-developed literature on axiomatic and operational characterization of measures of performance. Hinged on the duality between coherent risk measures and reward associated with investment strategies, we investigate representation of acceptability indices of performance using expectile-based risk measures that recently attracted a lot of attention inside the financial and actuarial community. We propose two purely expectile-based performance ratios other than the classical gain-loss ratio and the Omega ratio. We complement our analysis with elicitability of expectile-based acceptability indices and their conditional version accounting for new information flow.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Mostly used in practice to quantify market risk, value-at-risk at probability level \(\alpha \in (0,1)\) is the \(\alpha \)-quantile of the profit/loss (P &L henceafter) distribution corresponding to a single asset or a portfolio, see for example the Basel Committee on Banking Supervision (2006). But it is a well-documented fact that value-at-risk is not subadditive in general and hence it is not a coherent risk measure. Moreover it does not account for the size of losses beyond the threshold \(\alpha \), because quantiles hardly depend upon the frequency of tail losses and not on their values. On one hand, coherence is a good theoretical property satisfied instead by expected shortfall, see Artzner et al. (1999), that also accounts for extreme losses in the tail of the P &L distribution, as recognized by the recent market risk framework of the Basel Committee on Banking Supervision (2019). On the other hand from the regulatory and statistical point of view, methodologies for testing the accuracy of a risk model are essential then value-at-risk is preferred. Expected shortfall requires a huge amount of data for accurate estimation, in fact it is not elicitable as pointed out for example by Gneiting (2011). A standard risk measure that is coherent and appropriate for backtesting is the mean, but it cannot capture tail risk. Expectiles have been receiving increasing attention as risk measures in mathematical finance and actuarial science since the contribution of Kuan et al. (2009). In fact expectiles are both coherent for a threshold level range and elicitable risk measures, see Bellini et al. (2014) and the references therein. From a statistical point of view, expectiles are the least square analogue of quantiles, both being M-functionalsFootnote 1 with asymmetric convex loss function, but the latter are not coherent as risk measures. There are other advantages of using expectiles as coherent risk measures: they rely on tail expectations rather than tail probabilities, thus they are sensitive to extreme losses (in contrast to quantiles) and may lead to more prudent and reactive risk management: altering the shape of extreme losses does impact the expectiles in contrast to value-at-risk. In addition, expectiles avoid the use of regularity conditions on the underlying distribution of losses. For a detailed account of all these aspects in connection with the problem of estimation of expectiles see for example Daouia et al. (2018) and Daouia et al. (2021). Moreover, numerical evidence found in Bellini and Di Bernardino (2017) is in favor of expectiles as a reasonable alternative to value-at-risk or expected shortfall, especially when using them in portfolio management based on the gain-loss ratio.
Evaluating the performance of a financial trade is a crucial point for making informed choices among alternative investments. A popular guideline suggests that rational analysts and investors should select their portfolio according to a reward/risk criterion acting as a performance measure. Performance measurement is also a device to judge the quality of the value-added service provided by fund managers, when processing information not reflected by market prices. Needless to say, the classical Sharpe ratio is the prototypal of performance measures. Other indices have been proposed over the past four decades based on criticisms about the Sharpe ratio, concerning distributional assumptions needed for its compatibility with the mean-variance approach to portfolio selection, or the lack of consistency with arbitrage principles. Thus Bernardo and Ledoit (2000) proposed the alternative gain-loss ratio, beside Cherny and Madan (2009) elaborates on this and provides an axiomatic approach to frame performance indices meant to measure the largest nonnegative level at which the risk of loss is still acceptable. Following their approach, for a risky position X modelled by a bounded random variable, its index of acceptability is characterized as a performance measure satisfying four axioms: (increasing) monotonicity, quasi-concavity, scale invariance and Fatou property (see Sect. 3 below). Moreover, Cherny and Madan (2009) pointed out that such an index corresponds to a continuum of degrees of acceptability based on a system of acceptable bounded trades X, and Cherny and Madan (2009, Theorem 1) provides its representation through an associated system of scenarios that support the dual representation of corresponding coherent risks in such a way their expectations are positive accordingly. This is because a system of acceptable trades can be equivalently defined in term of an increasing family of coherent risk measures for which acceptability is typically given by their nonnegativity.
The contribution of this article is structured as follows. First, we propose expectile-based performance measures as special cases of acceptability indices introduced by Cherny and Madan (2009) but which generalize the gain-loss ratio and the Omega ratio used in the finance industry, see Bellini et al. (2018) and the references therein. We characterize acceptability indices of performance using the dual representation of expectiles as coherent risk measures as studied in Bellini et al. (2014). To this end we additionally give a representation of performance measures for position modelled as random variables with finite expectation. Our expectile-based performance measure leads to a more general risk-adjusted return on capital (RAROC) other than the gain-loss ratio or the Omega ratio, where the coherent risk measure is the expectile itself or the expectile-based analogue to the expected shortfall, as proposed by Daouia et al. (2020) and Daouia et al. (2021). Second, given the law-invariance of our expectile-based performance measure we also provide the corresponding Kusuoka representation. Moreover, we analyze the elicitability of the proposed performance index and highlight some practical aspects of choosing competing point forecasts. Third, we provide a conditional characterization of expectile-based performance indices whenever the coherent risk measure used is the conditional expectile as introduced by Bellini et al. (2018) as a generalization of the conditional mean.
The outline of this article is as follows. Section 2 anticipates the definition of expectile-based performance ratio and highlights the advantage of using it from an economic point of view. Section 3 sets up the definition and properties of acceptability indices for financial positions with finite expectation, then delivers the representation of coherent acceptability indices. Section 4 presents a quick review of expectiles together with their use as coherent risk measure, and provides the representation of expectile-based acceptability indices. Section 5 provides two main examples of expectile-based performance ratios. Moreover, the connection of expectile-based acceptability indices with the Omega ratio as well as the gain-loss ratio is highlighted. Section 6 is on elicitability of the expectile-based acceptability index. Section 7 develops a conditional version of expectile-based acceptability indices. Section 8 contains some concluding remarks.
2 Motivation of the paper
The framework we introduce later in this article is based on the well-understood concept of acceptability index of performance due to Cherny and Madan (2009). Originally developed for positionsFootnote 2\(X \in L^{\infty }\), given an indexed family \((\rho _x)_{x \in \mathbb {R}_+}\) of coherent risk measures increasing in x we say that a position is acceptable at the level  if and only its financial performance can be measured as
if and only its financial performance can be measured as

This establishes a natural duality between coherent risk measures and performance measures. As showed by Cherny and Madan (2009), using the dual representation of each \(\rho _x(X)\) one can obtain different acceptability indices of performance. In fact for every  the acceptability condition
the acceptability condition  is equivalently characterized by a system of acceptable trades
is equivalently characterized by a system of acceptable trades  and the supremum in (1) can be taken over \(\{x \in \mathbb {R}_+ \,|\, X \in \mathscr {A}_x\}\). Observe that \(\rho _x(X) = \inf _{\varphi \in \mathcal {S}_x} \mathsf {E}(\varphi X)\) and for each
and the supremum in (1) can be taken over \(\{x \in \mathbb {R}_+ \,|\, X \in \mathscr {A}_x\}\). Observe that \(\rho _x(X) = \inf _{\varphi \in \mathcal {S}_x} \mathsf {E}(\varphi X)\) and for each  we have \(\mathcal {S}_x\) as a set of scenarios, i.e. the class of all Radon–Nikodym derivatives \(\varphi =\frac{\mathrm {d}\mathsf {Q}}{\mathrm {d}\mathsf {P}}\) of probability measures \(\mathsf {Q}\) equivalent to the physical probability measure \(\mathsf {P}\). Choosing \(\rho _x\) as the negative of expectiles (see Sect. 4 for a formal definition) with the appropriate probability level and applying the definition of acceptability systems of X in term of the best gain-loss ratio we get
we have \(\mathcal {S}_x\) as a set of scenarios, i.e. the class of all Radon–Nikodym derivatives \(\varphi =\frac{\mathrm {d}\mathsf {Q}}{\mathrm {d}\mathsf {P}}\) of probability measures \(\mathsf {Q}\) equivalent to the physical probability measure \(\mathsf {P}\). Choosing \(\rho _x\) as the negative of expectiles (see Sect. 4 for a formal definition) with the appropriate probability level and applying the definition of acceptability systems of X in term of the best gain-loss ratio we get

Therefore, for bounded X this yields the trivial representation of expectile-based performance measure as the gain-loss ratio itself: this is not surprising since the connection between expectiles and gain-loss ratios is already known in the literature. Our first goal is to define an expectile-based performance index with domain \(L^1\) to account for potential extreme losses possibly given by heavy-tailed distributions. We keep the axiomatic approach of Cherny and Madan (2009) with appropriate modifications to account for the new domain, but as a novel approach we will make use of the dual representation of expectiles as analyzed in Bellini et al. (2014). This gives us the advantage to deduce acceptability indices other than gain-loss or Omega ratios.
Remark 1
For the mapping \(\alpha : L^{\infty } \rightarrow \mathbb {R}_+ \cup \{+\infty \}=:[0, +\infty ]\) given in Cherny and Madan (2009, Theorem 1) we adopt in our article a different name (see Sect. 3) to avoid confusion with the standard symbol used to identify the probability level for value-at-risk.
Anticipating a little our main examples of expectile-based performance ratioFootnote 3 that will be given in Sect. 5, we propose the following main alternative to the gain-loss ratio:
where \(-e_{\alpha }(X)\) is the expectile risk measure at probability level \(\alpha \), for which we usually choose the interval \((0,\tfrac{1}{2}]\), see Sect. 4 for further details. To appreciate the advantage of using this performance ratio instead of the gain-loss ratio from an economic point of view, we recall the needed asset pricing framework. Jaschke and Küchler (2001) establish a one-to-one correspondence among the partial ordering defined on the set of traded positions X (interpreted from the decision theory perspective as a preference relation), sets of acceptable positions, valuation bounds (actually good-deal bounds), coherent risk measures and price systems. Indeed, Bernardo and Ledoit (2000) introduced the gain-loss ratio as an alternative to the Sharpe ratio whose exacerbated high values yield a portfolio regarded as a quasi-arbitrage, namely a good-deal as studied also in Cochrane and Saa-Requejo (2001). This given raise to asset pricing theory based on no-good deals that postulates to restrict the Sharpe ratio and the corresponding pricing kernels. Therefore, denoting \(\mathcal {K}\) the set of (non-trivial) portfolio gains in a two-period economy and for a general probability space, the best gain-loss ratio is always attained
for a bounded and bounded away from zero state-price density Z with constants \(c,C>0\), see Bernardo and Ledoit (2000). This result is correct only for finite sample spaces \(\Omega \), in fact Biagini and Pinar (2013) showed the best gain-loss ratio is a poor performance measure in a quite general continuous-time model, after providing a refined dual representation on gain-loss free markets based on utility maximization of terminal wealth. Specifically, they assumed a filtered probability space satisfying the usual conditions and over which a semimartingale \(S=(S_t^1,\ldots ,S_t^n)_{t \in [0,T]}\) representing the underlying price processes only satisfies \(\sup _{t \in [0,T]} |S_t^i| \in L^1\), for any \(i=1,\ldots ,n\): in this way \(\mathcal {K}\) becomes the set of financial positions K replicable at zero cost through an admissible (predictable and bounded) self-financing trading strategy \(\pi =(\pi _t^1,\ldots ,\pi _t^n)_{t \in [0,T]}\), i.e. K equals the stochastic integral \((\pi \cdot S)_T:=\sum _{i=1}^n\pi _0^i S_0^i + \sum _{i=1}^n\int _0^T \pi _t^i \mathrm {d}S_t^i\), a terminal gain over the time horizon [0, T]. The main result Biagini and Pinar (2013, Theorem 2.4) yields the finiteness of the best gain-loss ratio \(\sup _{X \in \mathcal {K}, X \ne 0} \frac{\mathsf {E}(X^+)}{\mathsf {E}(X^-)}< + \infty \) if and only if the set of equivalent martingale measures is nonempty and the corresponding pricing kernels Z are Radon–Nikodým derivatives bounded and bounded away from zero, provided that the above market is gain-loss free.Footnote 4 Based on this characterization, the best gain-loss ratio is likely to be infiniteFootnote 5 and then the underlying market is not gain-loss free even if it should be arbitrage free, see Biagini and Pinar (2013, Example 2.7) where a Black–Scholes market is assumed with typical unbounded (unique) price kernel \(Z=\text {e}^{- \frac{\mu -r}{\sigma }W_T - (\frac{\mu -r}{\sigma })^2\tfrac{T}{2}}\), where r is the risk-free rate and \(\tfrac{\mu -r}{\sigma }\) is the market price of risk with a standard Brownian motion \(W=(W_t)_{t \in [0,T]}\) defined over the \(\mathsf {P}\)-augmentation of its natural filtration. In the setting of the same example, let \(K_{\epsilon }:=\mathbf {I}_{A_{\epsilon }}- c_{\epsilon }\) where \(\mathbf {I}_{\{\bullet \}}\) is the indicator of the event \(A_{\epsilon }=\{Z < \epsilon \}\) of having a very small state-price density Z for \(0<\epsilon < 1\). Assuming a zero risk-free rate \(r=0\), one considers \(\mathbf {I}_{A_{\epsilon }}\) as a cash-or-nothing digital call option on the stock price \(S_T=S_0 \text {e}^{(\mu -\frac{1}{2}\sigma ^2)T + \sigma W_T}\) with very large strike price provided that \(\epsilon \rightarrow 0\). By the market completeness, \(K_{\epsilon }\) is a trading gain where \(c_{\epsilon }=\mathsf {E}(Z \mathbf {I}_{A_{\epsilon }})\) is the replicating cost of the option that satisfies \(c_{\epsilon }< \epsilon p_{\epsilon } < 1\) and \(p_{\epsilon }\) being the probability \(\mathsf {P}(A_{\epsilon })\), since \(c_{\epsilon } < \mathsf {E}(\epsilon \mathbf {I}_{A_{\epsilon }})\). The gain-loss ratio is
which goes to \(+ \infty \) as \(\epsilon \rightarrow 0\). On the other hand, our proposed ratio
is finite because clearly \(0< p_{\epsilon }-c_{\epsilon } < + \infty \) which implies \(K_{\epsilon } \in L^1\) and by Bellini et al. (2014, Proposition 8) it also holds \(-e_{\alpha }(K_{\epsilon }) < + \infty \) for every \(\alpha \in (0,\tfrac{1}{2}]\). The same conclusion is valid (with minor modifications) in the case of a cash-or-nothing digital put option \(\mathbf {I}_{B_{\epsilon }}\) where \(B_{\epsilon }=\{Z > \epsilon \}\) and very small strike price when \(\epsilon \rightarrow 0\): one takes \(b_{\epsilon }=\mathsf {E}(Z \mathbf {I}_{B_{\epsilon }})\) with \(\tfrac{q_{\epsilon }}{\epsilon }< b_{\epsilon } < 1\) and \(\mathsf {P}(B_{\epsilon })=q_{\epsilon }\); the gain is now \(\mathbf {I}_{B_{\epsilon }}-b_{\epsilon }\) as well as its opposite \(K_{\epsilon }\), and the gain-loss ratio is bounded below by \(\tfrac{1-q_{\epsilon }}{\epsilon }\) so that it goes again to \(+\infty \) as \(\epsilon \rightarrow 0\). In a complete arbitrage-free market with unbounded price kernels, our expectile-based performance measure assigns a finite value to gains such as \(K_{\epsilon }\) while the gain-loss ratio requires a state-pricing density bounded above and bounded away from zero, thus a further advantage of our proposal is that it involves a more flexible performance measurement approach compatible with no-arbitrage asset pricing theory.
Remark 2
Dybvig and Ingersoll (1982) showed that in the CAPM framework arbitrage do exists also with bounded Sharpe ratios. On the other hand, only a bounded gain-loss ratio implies absence of arbitrage and one must impose both narrowed no-arbitrage and no-good deal bounds also in incomplete markets. While the gain-loss ratio is attractive from the perspective of determining price bounds for a specified asset pricing model or to measure funds’ performance with respect to benchmark state-price densities, it suffers from the curse of infinity in many standard models.
3 Acceptability indices on \(\varvec{L^1}\)
We review the definition of a coherent risk measure. Let \(\mathcal {X} \subset L^0\) be a linear space of financial positions containing the constants where \(L^0:=L^0(\Omega , \mathscr {F}, \mathsf {P})\) is the equivalence class of all random variables over a common atomless probability space \((\Omega , \mathscr {F}, \mathsf {P})\). Throughout this article we work with random variables \(X \in L^1\), where \(L^1:=L^1(\Omega , \mathscr {F}, \mathsf {P})\) is the equivalence class of random variables with finite first moment modelling financial positions with respect to a fixed final date. The reason why we choose the space \(L^1\) is mainly due to the findings in Filipović and Svindland (2012). Moreover, if X is a portfolio, then the restriction to \(L^1\) is not a problem from the management perspective, as empirical evidence shows losses have finite first moment. From now on all equalities, inequalities and convergence concepts concerning random variables are understood in the \(\mathsf {P}\)-a.s. sense, i.e. with probability one. Among different sign conventions for X we assume it represents P &L with losses being in the left-tail of the underlying distribution. Then, a mapping \(\rho : \mathcal {X} \rightarrow \mathbb {R}\) is a monetary risk measure if:
-
It is increasing monotone, for any \(X,Y \in \mathcal {X}\) such that
 implies
implies 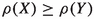 ;
; -
It is cash additive, any choice \(m \in \mathbb {R}\) implies \(\rho (X+m) = \rho (X) -m\).
If in addition \(\rho \) is
-
Positive homogeneous, \(\rho (\lambda X)=\lambda \rho (X)\) for all
 and,
and, -
Subadditive, for any \(X,Y \in \mathcal {X}\) it holds
 ,
,
then it is a coherent risk measure and a convex mapping too. The financial meaning of the above conditions is well understood. Working with positions \(X \in L^1\) requires to restate the essential properties of acceptability indices of performance. We consider acceptable P &L’s at a level \(x \in \mathbb {R}_+\) forming a convex superlevel set

which is a natural requirement for any performance measure and in particular for \(\mathsf {PERF} \equiv \textsf {a} \iota \) given in the next definition.
Definition 1
A mapping \(\textsf {a} \iota : L^1 \rightarrow [0, +\infty ]\) is an acceptability index if it satisfies the following four properties.
-
Quasi-concavity for any pair \(X,Y \in L^1\) and for every \(\lambda \in [0,1]\) such that
 and
and  one has
one has  (3)
(3) -
Monotonicity for any \(X,Y \in L^1\)
 (4)
(4) -
Scale invariance for every \(\lambda >0\) and \(X \in L^1\)
$$\begin{aligned} \textsf {a} \iota (\lambda X)= \textsf {a} \iota (X). \end{aligned}$$(5) -
Upper semi-continuity given a sequence \((X_n)_{n \in \mathbb {N}} \subset L^1\) converging to \(X \in L^1\) in the \(L^1\)-norm, \(\Vert X_n -X\Vert _1 \rightarrow 0,\) we have
 (6)
(6)which implies
 provided that
provided that  for every \(n \in \mathbb {N}\) and \(x \in \mathbb {R}_+\).
for every \(n \in \mathbb {N}\) and \(x \in \mathbb {R}_+\).
Quasi-concavity is equivalent to the convexity of any \(\mathscr {A}_x\), yielding a diversified position performs as well as its components. Acceptable positions are valued monotonically: \(\textsf {a} \iota \) is an increasing mapping and Y is at least as acceptable as X provided that the latter is dominated by the former. By scale invariance any acceptance set \(\mathscr {A}_x\) is a convex cone: the level of acceptance remains the same whenever we scale the financial positions. Eventually, the acceptability functional is required to be \(\Vert \;\Vert _1\)-upper semi-continuous and as byproduct the acceptance set \(\mathscr {A}_x\) is norm-closed in \(L^1\) for a fixed \(x \in \mathbb {R}_+\).
Remark 3
In Definition 1 there are two differences with respect to the original definition of acceptability indices given by Cherny and Madan (2009), namely the domain of \(\textsf {a} \iota \) is now \(L^1\) and the Fatou property is replaced by the upper semi-continuity of \(\textsf {a} \iota \) in the norm topology (fourth axiom above).
Now we come to the basic representation of acceptability indices on \(L^1\). To this end we provide two lemmas which we will use in the proof of the sufficiency part of Proposition 1 below. Let us define

and take the infimum over \(m \in \mathbb {R}\) of both sets  for any
for any  . Thus, \(x \mapsto \rho _{x}(X)\) increases for fixed \(X \in L^1\). Any mapping in this increasing family can be represented by acceptability indices as is established in Lemma 1 below. We refer to coherent risk measures defined on \(L^1\) that are \(\Vert \;\Vert _1\)-lower semicontinuous, i.e.
. Thus, \(x \mapsto \rho _{x}(X)\) increases for fixed \(X \in L^1\). Any mapping in this increasing family can be represented by acceptability indices as is established in Lemma 1 below. We refer to coherent risk measures defined on \(L^1\) that are \(\Vert \;\Vert _1\)-lower semicontinuous, i.e.

Lemma 1
Let \(\rho _{x}(X)\) be defined as in (7), for any \(x \in \mathbb {R}_+\) and \(X \in L^1,\) by an acceptability index \(\textsf {a} \iota .\) Then \(\rho _{x}(X)\) is a coherent risk measure on \(L^1\).
Proof
For \(m \in \mathbb {R}\) and \(x \in \mathbb {R}_+\) condition  is equivalent to \(X + m \in \mathscr {A}_x \subset L^1\) and we have that
is equivalent to \(X + m \in \mathscr {A}_x \subset L^1\) and we have that  together with \(X \in \mathscr {A}_x\) implies \(Y \in \mathscr {A}_x.\) We check monotonicity. Take \( x \in \mathbb {R}_+\) and select \(X,Y \in L^1\) such that
together with \(X \in \mathscr {A}_x\) implies \(Y \in \mathscr {A}_x.\) We check monotonicity. Take \( x \in \mathbb {R}_+\) and select \(X,Y \in L^1\) such that  By monotonicity of \(\textsf {a} \iota \) we have
By monotonicity of \(\textsf {a} \iota \) we have

Thus we deduce  and taking the infimum of both sets we get
and taking the infimum of both sets we get

To show positive homogeneity, it suffices to call for the scale invariance of \(\textsf {a} \iota .\) Next, we show subadditivity. Take \(m_1,m_2 \in \mathbb {R}\) such that  and
and  for every \(X,Y \in L^1\) and \(x \in \mathbb {R}_+.\) By quasi-concavity of \(\textsf {a} \iota ,\) for any \(\lambda \in [0,1]\) we have
for every \(X,Y \in L^1\) and \(x \in \mathbb {R}_+.\) By quasi-concavity of \(\textsf {a} \iota ,\) for any \(\lambda \in [0,1]\) we have

at the same acceptability level x. Choosing \(\lambda = \frac{1}{2}\) and using again scale invariance of the acceptability index entails

Therefore, the scalar \(m_1+m_2\) belongs to the set  and it is greater than or equal to the infimum over the same set, which in turn is just \(\rho _{x}(X+Y).\) This inequality holds true for all \(m_1\) and all \(m_2\) belonging to
and it is greater than or equal to the infimum over the same set, which in turn is just \(\rho _{x}(X+Y).\) This inequality holds true for all \(m_1\) and all \(m_2\) belonging to  and to
and to  respectively. As a consequence, taking the infimum with respect to \(m_1\) and then with respect to \(m_2\) we get
respectively. As a consequence, taking the infimum with respect to \(m_1\) and then with respect to \(m_2\) we get

To show cash invariance, we exhibit the following for every \(x \in \mathbb {R}_+\) and \(X \in L^1:\)

To check the lower semicontinuity of \(\rho _x\) in the \(\Vert \;\Vert _1\)-norm it suffices to take \(\epsilon > \liminf _{n \rightarrow + \infty } \rho _x(X_n)\) and (if necessary) passing to a subsequence to get \(X_n + \epsilon \in \mathscr {A}_x\) for all \(n \in \mathbb {N}.\) Thus,  and using the upper semi-continuity of the acceptability index we also have
and using the upper semi-continuity of the acceptability index we also have  i.e.
i.e.  and by the arbitrariness of \(\epsilon \) it holds
and by the arbitrariness of \(\epsilon \) it holds  A byproduct, \(\rho _{x}\) is a coherent risk measure on \(L^1\). \(\square \)
A byproduct, \(\rho _{x}\) is a coherent risk measure on \(L^1\). \(\square \)
Remark 4
The finiteness of \(\Vert \;\Vert _1\)-lower semicontinuous coherent risk measures on \(L^1\) is equivalent to the \(\Vert \;\Vert _1\)-continuity, see for example Rüschendorf (2013, Section 7.2.2).
We can represent acceptability indices in terms of an increasing family of coherent risk measures on \(L^1\).
Lemma 2
Let \((\rho _{x})_{x \in \mathbb {R}_+}\) be a family of coherent risk measures on \(L^1\) increasing in x. Then, the mapping \(\textsf {a} \iota : L^1 \rightarrow [0, +\infty ]\) defined as

is an acceptability index of performance (we assume \(\sup \varnothing = 0\)).
Proof
Let  then by monotonicity of the risk measures \(\rho _x\) in x we have
then by monotonicity of the risk measures \(\rho _x\) in x we have

For any  we also have
we also have  which together with the monotonicity entails
which together with the monotonicity entails  for all
for all  . As a consequence the set inclusion
. As a consequence the set inclusion

holds, and taking the supremum of both sides monotonicity of \(\textsf {a} \iota \) is proved. To check quasi-concavity of \(\textsf {a} \iota ,\) we first pick \(X,Y \in L^1\) such that  and
and  whenever \(x_0 \in (0, +\infty ).\) By definition (8) together with monotonicity of \(\rho _{x}\) we have
whenever \(x_0 \in (0, +\infty ).\) By definition (8) together with monotonicity of \(\rho _{x}\) we have  and
and  for all \(x < x_0.\) This combined with the positive homogeneity of \(\rho _{x}\) yields
for all \(x < x_0.\) This combined with the positive homogeneity of \(\rho _{x}\) yields

for every \(\lambda \in [0,1].\) Moreover, by subadditivity of \(\rho _{x}\) and again for every \(x < x_0\) we additionally have

which entails  Eventually, this combined with definition (8) yields
Eventually, this combined with definition (8) yields  and quasi-concavity follows. Scale invariance of \(\textsf {a} \iota \) follows immediately from the positive homogeneity of \(\rho _{x}.\) Finally take \((X_n)_{n \in \mathbb {N}} \subset L^1\) such that \(\Vert X_n - X\Vert _1 \rightarrow 0\) and
and quasi-concavity follows. Scale invariance of \(\textsf {a} \iota \) follows immediately from the positive homogeneity of \(\rho _{x}.\) Finally take \((X_n)_{n \in \mathbb {N}} \subset L^1\) such that \(\Vert X_n - X\Vert _1 \rightarrow 0\) and  for every \(n \in \mathbb {N}, x \in \mathbb {R}_+.\) Now, since coherent risk measures on \(L^1\) are continuous and then lower semicontinuous (this follows from, for instance, Ruszczyński and Shapiro (2006, Proposition 3.1), as byproduct we have \(\Vert \rho _x(X_n) - \rho _x(X)\Vert _1 \rightarrow 0\) and then
for every \(n \in \mathbb {N}, x \in \mathbb {R}_+.\) Now, since coherent risk measures on \(L^1\) are continuous and then lower semicontinuous (this follows from, for instance, Ruszczyński and Shapiro (2006, Proposition 3.1), as byproduct we have \(\Vert \rho _x(X_n) - \rho _x(X)\Vert _1 \rightarrow 0\) and then  because
because  which implies
which implies  \(\square \)
\(\square \)
Proposition 1
A mapping \(\textsf {a} \iota : L^1 \rightarrow [0,+ \infty ]\) is an acceptability index if and only if there exists a family of sets of scenarios \((\mathcal {S}_{x})_{x \in \mathbb {R}_+}\) increasing in x such that the representation

holds, where \(\inf \varnothing = \infty \) and \(\sup \varnothing = 0.\)
Proof
(Necessity) Let \(\textsf {a} \iota \) be given by (9). Firstly, we check property 1 of Definition 1. Pick \(X,Y \in L^1\) with  and
and  for \(z \in \mathbb {R}_+.\) For any \(y < z\) we can find a representation set \(\mathcal {S}_{y} \subset \mathcal {S}_{z}\) such that the two inequalities together with the supremum in (9) entail
for \(z \in \mathbb {R}_+.\) For any \(y < z\) we can find a representation set \(\mathcal {S}_{y} \subset \mathcal {S}_{z}\) such that the two inequalities together with the supremum in (9) entail  and
and  for the corresponding scenario \(\varphi \in \mathcal {S}_{y}.\) Taking the convex combination \(Z=\lambda X + (1- \lambda )Y,\) for any \(\lambda \in [0,1],\) and considering
for the corresponding scenario \(\varphi \in \mathcal {S}_{y}.\) Taking the convex combination \(Z=\lambda X + (1- \lambda )Y,\) for any \(\lambda \in [0,1],\) and considering  we have
we have  too, and the quasi-concavity follows by enlarging the representation set, taking the infimum of the expectations and finally taking the supremum with respect to \(x \in \mathbb {R}_+.\) Secondly, consider the sets
too, and the quasi-concavity follows by enlarging the representation set, taking the infimum of the expectations and finally taking the supremum with respect to \(x \in \mathbb {R}_+.\) Secondly, consider the sets

Now for \(X,Y \in L^1\) such that  pick \(x_0 \in A\) and observe that
pick \(x_0 \in A\) and observe that  whenever \(\varphi \in \mathcal {S}_{x_0}\) which implies \(x_0 \in B.\) On the other hand, for any \(y_0 \in B\) and using the same inequality between expectations for \(\varphi \in \mathcal {S}_{y_0}\) we can consider \(Y=0\) which implies \(\mathsf {E}(\varphi X) <0\) yielding \(y_0 \notin B.\) We conclude that \(A \subset B\) and passing to the supremum property 2 is proved. Property 3 is an easy consequence of linearity of \(\mathsf {E}(\,\cdot \,).\) To check that \(\textsf {a} \iota \) is upper-semi continuous in the \(L^1\)-norm, pick a sequence \((X_n)_{n \in \mathbb {N}} \subset L^1\) with \(X_n \in \mathscr {A}_x\) each \(n \in \mathbb {N}\) for a fixed \(x \in \mathbb {R}_+.\) Clearly
whenever \(\varphi \in \mathcal {S}_{x_0}\) which implies \(x_0 \in B.\) On the other hand, for any \(y_0 \in B\) and using the same inequality between expectations for \(\varphi \in \mathcal {S}_{y_0}\) we can consider \(Y=0\) which implies \(\mathsf {E}(\varphi X) <0\) yielding \(y_0 \notin B.\) We conclude that \(A \subset B\) and passing to the supremum property 2 is proved. Property 3 is an easy consequence of linearity of \(\mathsf {E}(\,\cdot \,).\) To check that \(\textsf {a} \iota \) is upper-semi continuous in the \(L^1\)-norm, pick a sequence \((X_n)_{n \in \mathbb {N}} \subset L^1\) with \(X_n \in \mathscr {A}_x\) each \(n \in \mathbb {N}\) for a fixed \(x \in \mathbb {R}_+.\) Clearly  Assume further \(\Vert X_n - X\Vert _1 \rightarrow 0.\) Then whatever the choice of \(y < x\) is, for any \(\varphi \in \mathcal {S}_{y}\) and any \(n \in \mathbb {N}\) we have
Assume further \(\Vert X_n - X\Vert _1 \rightarrow 0.\) Then whatever the choice of \(y < x\) is, for any \(\varphi \in \mathcal {S}_{y}\) and any \(n \in \mathbb {N}\) we have  and by the \(L^1\)-convergence
and by the \(L^1\)-convergence  too. As a consequence,
too. As a consequence,  then after passing to the supremum we have that \(\mathscr {A}_x\) is \(\Vert \;\Vert _1\)-closed and the mapping \(\textsf {a} \iota \) is then upper-semi continuous.
then after passing to the supremum we have that \(\mathscr {A}_x\) is \(\Vert \;\Vert _1\)-closed and the mapping \(\textsf {a} \iota \) is then upper-semi continuous.
(Sufficiency). Let’s assume \(\textsf {a} \iota \) is an acceptability index. Then let
with  for \(x \in \mathbb {R}_+.\) Since \(X + m \in \mathscr {A}_x\) is equivalent to
for \(x \in \mathbb {R}_+.\) Since \(X + m \in \mathscr {A}_x\) is equivalent to  by Lemma 1 each \(\rho _{x}(X)\) is a coherent risk measure of X and moreover \(x \mapsto \rho _{x}(X)\) is increasing in x. Since \(\mathscr {A}_x \subset L^1_+\) is a \(\Vert \;\Vert _1\)-closed convex cone, its polar
by Lemma 1 each \(\rho _{x}(X)\) is a coherent risk measure of X and moreover \(x \mapsto \rho _{x}(X)\) is increasing in x. Since \(\mathscr {A}_x \subset L^1_+\) is a \(\Vert \;\Vert _1\)-closed convex cone, its polar  is a \(\sigma (L^{\infty },L^1)\)-closed convex cone. A basis for this cone is \(\mathcal {S}_{x},\) i.e.
is a \(\sigma (L^{\infty },L^1)\)-closed convex cone. A basis for this cone is \(\mathcal {S}_{x},\) i.e.  By the Bipolar theorem (see for example Delbaen (2012)) we get
By the Bipolar theorem (see for example Delbaen (2012)) we get

Observe that \(\mathscr {A}_y \subset \mathscr {A}_x \) is equivalent to \((\mathscr {A}_x)^{\circ } \subset (\mathscr {A}_y)^{\circ },\) for \(0< x < y.\) Thus, X lies in some \(\mathscr {A}_{x_0}\) so that  This is in turn equivalent to
This is in turn equivalent to  which by Lemma 2 implies the desired representation (9) of the acceptability index by passing to \(\displaystyle {\inf _{\varphi \in \mathcal {S}_{x}} \mathsf {E}(\varphi X)}.\) \(\square \)
which by Lemma 2 implies the desired representation (9) of the acceptability index by passing to \(\displaystyle {\inf _{\varphi \in \mathcal {S}_{x}} \mathsf {E}(\varphi X)}.\) \(\square \)
4 Representation of expectile-based acceptability indices
Given a financial position \(X \in L^1\), the definition of expectile at a probability level \(\alpha \in (0,1)\) originally due to Newey and Powell (1987) is
also called the \(\alpha \)-expectile of X. Here \(\ell \) is the asymmetric quadratic loss function defined as

thus one could see that expectiles are asymmetric generalization of the mean and also quadratic versions of the usual quantiles. The corresponding first order condition
entails \(e_{\alpha }(X)\) as the unique minimizer, where as usual \(X^+=\max \{0,X\}\) is the positive part and \(X^-=\max \{0,-X\}\) is the negative part of a random variable.Footnote 6 Indeed, the function

is such that (after taking expectation) for \(X \in L^1\) the first order condition for the unique minimizer in Eq. (11) is given with derivative \(m \mapsto -2\,f_{X}(m),\) which implies \(f_{X}(m)=0.\) Now, by Krätschmer and Zähle (2017, Lemma A.1) the mapping \(m \mapsto f_{X}(m)\) is real-valued, continuous and strictly decreasing, thus the \(\alpha \)-expectile of a position X with finite expectation can be characterized by its inverse function as follows:
The above defines a mapping \(e_{\alpha } : L^1 \rightarrow \mathbb {R}\) whose negative \(-e_{\alpha }(X)\) is by Krätschmer and Zähle (2017, Proposition A.2) together with Bellini et al. (2014, Proposition 7(c)) a coherent risk measure for \(\alpha \in (0 ,\frac{1}{2}]\) ensures subadditivity, and which is continuous in the \(L^1\)-norm \(\Vert \;\Vert _1\) (this is especially due to Cheridito and Li (2009, Theorem 4.1)). The dual representation we use in this article is given by
where the underlying set of scenarios is

see Bellini et al. (2014, Proposition 8). Now, by Bellini et al. (2014, Proposition 7(c)) it holds \(-e_{\alpha }(X) = e_{1-\alpha }(-X)\) thus we may reformulate representation (13) for a position \(X \in L^1\) being acceptable:

Remark 5
For every \(\alpha \in (0,\frac{1}{2}]\) the set of scenarios \(\mathcal {S}_{\alpha }\) is \(\sigma (L^{\infty },L^1)\)-compact and \(\sigma (L^{\infty },L^1)\)-closed-convex in \(L^{\infty }.\) As usual we write  for the corresponding acceptance set which turns out to be a \(\Vert \;\Vert _1\)-closed convex cone in \(L^1.\) In Sect. 4 we use the duality pair \((L^1,L^{\infty })\) with \(L^1\) endowed with the \(\Vert \;\Vert _1\)-topology and \(L^{\infty }\) endowed with the \(\sigma (L^{\infty },L^1)\)-topology.
for the corresponding acceptance set which turns out to be a \(\Vert \;\Vert _1\)-closed convex cone in \(L^1.\) In Sect. 4 we use the duality pair \((L^1,L^{\infty })\) with \(L^1\) endowed with the \(\Vert \;\Vert _1\)-topology and \(L^{\infty }\) endowed with the \(\sigma (L^{\infty },L^1)\)-topology.
We call \(-e_{\alpha }(X)\) the \(\alpha \)-expectile risk measure of the position X whose relevant properties are summarized in the following lemma for ease of reference, see Newey and Powell (1987) and Bellini et al. (2014).
Lemma 3
Let \(X \in L^1\) be the terminal value of a traded position. Then:
-
(a)
\(-e_{\alpha }(X+h)=-e_{\alpha }(X)-h\), for each \(h \in \mathbb {R}\),
-
(b)
\(-e_{\alpha }(\lambda X)=-\lambda e_{\alpha }(X)\), for every \(\lambda >0\),
-
(c)
 implies
implies  , for any \(Y \in L^1\),
, for any \(Y \in L^1\), -
(d)
 , for \(\alpha \in (0,\tfrac{1}{2}]\) and every \(Y \in L^1\),
, for \(\alpha \in (0,\tfrac{1}{2}]\) and every \(Y \in L^1\), -
(e)
\(-e_{\alpha }(X)\) is strictly decreasing and continuous with respect to \(\alpha \in (0,1)\).
Remark 6
(Financial Interpretation) Since for a position \(X \in L^1\) we can write
the financial interpretation of expectiles, that especially holds for the \(\alpha \)-expectile risk measure of Lemma 3,Footnote 7 is nowadays more clear: the index of prudentiality \(\alpha \) is the ratio of expected margin shortfall to the total cost of capital requirement given by \(e_{\alpha }\); the greater the expectile, the smaller the expected loss resulting in a smaller \(\alpha \). Indeed, lower values of the probability level represent more risk aversion. This interpretation is originally due to Kuan et al. (2009) and relies on \(e_{\alpha }(X)\) being a location parameter for the distribution of X such that the average distance of X below the expectile equals the fraction \(\alpha \) of the total distance. Therefore, while quantiles are only sensitive to the ordering of the X’s values,Footnote 8 expectiles depend on the whole distribution, then \(\alpha \) associated to an expectile changes with the distribution.
Given this definition of expectile risk measure, we prove the analogous of Cherny and Madan (2009, Theorem 1) characterizing acceptability indices \(\textsf {a} \iota (X)\). The main idea of the original representation is that any acceptability index is linked to an increasing one-parameter family of sets of scenario \((\mathcal {S}_{x})_{x \in \mathbb {R}_+}\) supporting the corresponding coherent risk measure \(\rho _{x}\), thus the value \(\textsf {a} \iota (X)\) yields the largest level of acceptability x such that X is valued positively under each scenario from the associated level x.
Corollary 1
A mapping \(\textsf {a} \iota : L^1 \rightarrow [0,+ \infty ]\) is an expectile-based acceptability index if and only if there exists a family of sets of scenarios \((\mathcal {S}_{\alpha (x)})_{x \in \mathbb {R}_+}\) increasing in x such that the representation

holds, where \(\inf \varnothing = \infty \) and \(\sup \varnothing = 0.\)
Proof
We apply Proposition 1 identifying coherent risk measures \(\rho _x = -e_{\alpha (x)}\) with \(\alpha (x)=\frac{1}{1+x}\). Indeed for \(\alpha (x) \in (0,\frac{1}{2}]\) we have \(\alpha (x) \rightarrow 0\) provided \(x \rightarrow \infty \) so that \(-e_{\alpha (x)}\) increases in x. The sets of scenarios are identified with those given by (14) with the appropriate re-labeling \(\alpha \equiv \alpha (x)\). Under these conditions each \(\alpha (x)\)-expectile risk measure can be represented as the unique minimizer \(\min _{\varphi \in \mathcal {S}_{\alpha (x)}} \mathsf {E}(\varphi X)\). Moreover, expectiles are proved to be Lipschitz continuous with respect to the Wasserstain metric

where  and similarly for Y. Thus lower semicontinuity of \(\alpha (x)\)-expectile risk measures is guaranteed and we are done. \(\square \)
and similarly for Y. Thus lower semicontinuity of \(\alpha (x)\)-expectile risk measures is guaranteed and we are done. \(\square \)
Observe that Lipschitz continuity of expectiles with respect to the \(\Vert \;\Vert _1\)-norm is proved in Krätschmer and Zähle (2017, Proposition A.2), but it can also be deduced by Bellini et al. (2018, Theorem 2.3(e)) using the trivial sigma-algebra \(\{\varnothing , \Omega \},\) see Sect. 7.
Remark 7
In the Proof of Corollary 1 the used re-labeling \(\alpha =\frac{1}{1+x}\) yields  for \(x<y\) since for the corresponding expectile-based coherent risk measures we have
for \(x<y\) since for the corresponding expectile-based coherent risk measures we have  . Indeed \(\alpha \)-expectiles are strictly increasing in \(\alpha \). All this is equivalent to have a nested family of sets of scenarios \(\mathcal {S}_{\frac{1}{1+x}} \subset \mathcal {S}_{\frac{1}{1+y}}\).
. Indeed \(\alpha \)-expectiles are strictly increasing in \(\alpha \). All this is equivalent to have a nested family of sets of scenarios \(\mathcal {S}_{\frac{1}{1+x}} \subset \mathcal {S}_{\frac{1}{1+y}}\).
5 Main examples of expectile-based performance measures
With Corollary 1 in mind we are able to characterize those expectile-based performance indices other than the gain-loss ratio, for positions \(X \in L^1\). In particular, we are interested in finding the appropriate scenarios used in representation (16) such that the corresponding acceptability index is a new performance ratio. By Corollary 1 acceptability at level \(x \in \mathbb {R}_+\) of a position in term of risk and reward does correspond to a positive expectation \(\mathsf {E}(\varphi X)\) under each scenario \(\varphi \in \mathcal {S}_{\alpha (x)}\). Now, define
By convention we let \(\mathsf {RAROC}(X)=+\infty \) if the coherent \(\alpha (x)\)-expectile risk measure is  . We have the following chain of equivalences:
. We have the following chain of equivalences:

To see why the fifth equivalence holds let us use the Change of Variable formula to rewrite \(\frac{1}{1+x}\mathsf {E}(X)+ \frac{x}{1+x} \mathsf {E}(\varphi X)\) as
where the Radon–Nikodým Theorem provides each scenario \(\varphi =\frac{\mathrm {d}\mathsf {Q}}{\mathrm {d}\mathsf {P}}\) as the density of some probability measure \(\mathsf {Q}\) equivalent to \(\mathsf {P}\). As byproduct the above becomes
with density \( {\tilde{\varphi }} = \frac{\mathrm {d}{\tilde{\mathsf {Q}}}}{\mathrm {d}\mathsf {P}}\) belonging to \(\mathcal {S}_{\alpha (x)}\). In fact any set of scenarios is a \(\sigma (L^{\infty }, L^1)\)-closed convex cone, hence any of its element can be given as a Radon–Nikodým derivative corresponding to some convex combination \(\frac{1}{1+x}\mathsf {P}+ \frac{x}{1+x} \mathsf {Q}\). The second equivalence is obvious when \(\min _{\varphi \in \mathcal {S}_{\alpha (x)}} \mathsf {E}(\varphi X)<0\). If  then by our convention \(\mathsf {RAROC}(X)=+\infty \) so the inequality on the left-hand side is again satisfied with
then by our convention \(\mathsf {RAROC}(X)=+\infty \) so the inequality on the left-hand side is again satisfied with  thanks to \(\varphi \in \mathcal {S}_{\alpha (x)}\), and this implies the inequality on the right-hand side is satisfied too. As a consequence, \((\mathcal {S}_{\alpha (x)})_{x \in \mathbb {R}_+}\) supports the representation of \(\mathsf {RAROC}(X)=\textsf {a} \iota (X)\) as required by Corollary 1, provided that for every acceptability level \(x \in \mathbb {R}_+\) we let \(\mathcal {S}_{\alpha (x)}=\cap _{y >x} \mathcal {S}_{\alpha (y)}\), see Cherny and Madan (2009, Lemma 1).
thanks to \(\varphi \in \mathcal {S}_{\alpha (x)}\), and this implies the inequality on the right-hand side is satisfied too. As a consequence, \((\mathcal {S}_{\alpha (x)})_{x \in \mathbb {R}_+}\) supports the representation of \(\mathsf {RAROC}(X)=\textsf {a} \iota (X)\) as required by Corollary 1, provided that for every acceptability level \(x \in \mathbb {R}_+\) we let \(\mathcal {S}_{\alpha (x)}=\cap _{y >x} \mathcal {S}_{\alpha (y)}\), see Cherny and Madan (2009, Lemma 1).
Another expectile-based coherent risk measure recently proposed by Daouia et al. (2020, 2021) is the analogue of expected shortfall, namely the average expectile coherent risk measure defined as
Since in the current article we treat positions \(X \in L^1\) modelling P &L’s and what matter for risk measurement is the left-tail of the X’s distribution, Eq. (18) resembles the original one \(\frac{1}{1-\alpha }\int _{\alpha }^1 e_t(X) \mathrm {d}t\) with \(\alpha \in [\tfrac{1}{2},1)\) where X is typically a random variable whose values are the negative of P &L’s with extreme losses correspond to a level \(\alpha \) close to one. Coherence of the average expectile coherent risk measure is proved in Daouia et al. (2020) and easily transfers to our resembled version (18). This enable us to propose a second example of expectile-based acceptability index of performance as follows. We claim that the ratio of expectation to (18) is:

From the last equivalence and the dual representation of \(e_t(X)\), the same reasoning used in building \(\mathsf {RAROC}(X)=\frac{\mathsf {E}(X)}{-e_{\alpha (x)}(X)}\) as an expectile-based acceptability index now confirm our claim. Observe that \(t \in \text {range}(\alpha (x))\) but we do not need integration by substitution. Indeed by Corollary 1 the second expectile-based coherent risk measure must be indexed by acceptability levels \(x \in \mathbb {R}_+\).
5.1 Point estimators of expectile-based performance measures
To make statistical inference of our expectile-based \(\mathsf {RAROC}\), we consider the following procedure of non-parametric point estimation. First, from a random sample \(X_1,\ldots ,X_n\) let \(X_{(1)}, \ldots , X_{(n)}\) be the corresponding nth order statistics. The empirical counterpart of the probability level \(\alpha \in (0,\frac{1}{2}]\) is
Second, the empirical \({\tilde{\alpha }}_i\)-expectile is \({\tilde{e}}_{\alpha ,n}= X_{(i)}\) if and only if \(\alpha ={\tilde{\alpha }}_i\) for \(i=1,\ldots ,n\) with \({\tilde{\alpha }}_0=0\) and \({\tilde{\alpha }}_n=1\). In fact, its expression is
and \({\tilde{e}}_{\alpha ,n} \in [X_{(i)}, X_{(i+1)})\). Since the empirical expectile is nondecreasing in \(\alpha \) and  one get
one get
see Holzmann and Klar (2016). To emphasize the dependence on rank i we rewrite \({\tilde{e}}_{\alpha ,n(i)}\). As byproduct, to compute the nonparametric estimator
we suggest to:
-
(1)
Compute recursively each empirical level \({\tilde{\alpha }}_i\) for \(i=1,\ldots ,n\);
-
(2)
Identify the interval \( [{\tilde{\alpha }}_i, {\tilde{\alpha }}_{i+1})\);
-
(3)
Go back to the corresponding \([X_{(i)}, X_{(i+1)})\) and find the right \(-{\tilde{e}}_{\alpha ,n(i)}\).
The last step can be done by interpolation. When the population \(\mathsf {RAROC}\) is defined in term of the average expectile coherent risk measure (18) we need to compute all \({\tilde{e}}_{\alpha ,n(i)}\) in the left-tail of the empirical distribution. Therefore, we suggest to consider all the levels  for \(k=1,\ldots ,i\) yet provided by step (1) above where i is related to the interval found in step (2). Then, one repeat step (3) to get \([X_{(k)}, X_{(k+1)})\) and then the corresponding empirical expectiles \({\tilde{e}}_{\alpha ,n(k)}\). Eventually one compute the average \(- i^{-1} \alpha \sum _{k=1}^{\left\lfloor i\alpha \right\rfloor } {\tilde{e}}_{\alpha ,n(k)}\) which now replaces the denominator in \(\widetilde{\mathsf {RAROC}}_n\). Here \(\left\lfloor \, \cdot \,\right\rfloor \) is the floor function.
for \(k=1,\ldots ,i\) yet provided by step (1) above where i is related to the interval found in step (2). Then, one repeat step (3) to get \([X_{(k)}, X_{(k+1)})\) and then the corresponding empirical expectiles \({\tilde{e}}_{\alpha ,n(k)}\). Eventually one compute the average \(- i^{-1} \alpha \sum _{k=1}^{\left\lfloor i\alpha \right\rfloor } {\tilde{e}}_{\alpha ,n(k)}\) which now replaces the denominator in \(\widetilde{\mathsf {RAROC}}_n\). Here \(\left\lfloor \, \cdot \,\right\rfloor \) is the floor function.
By our main assumption \(X \in L^1\) and the well-known stylized facts about the behavior of financial return series, is reasonably to consider the class of heavy-tailed distributions corresponding to the maximum domain of attraction of the Fréchet family. We recall that Extreme Value Theory is developed around limiting distribution functions of properly normalized maxima of i.i.d. \(X_1,\ldots ,X_n\). Distributional properties of  are easily transferred to
are easily transferred to  , the latter pertaining the current context where we work with P &L’s (especially when they represent returns). Hence, we can refer to some asymptotic results of high expectiles without worry of our chosen sign convention about X. In particular, Bellini et al. (2014) showed that assuming X with heavy-tailed distribution in the Fréchet maximum domain of attraction (and then having a Paretian right-tail) it holds \(e_{\alpha }(X) < q_{\alpha }(X)\), where
, the latter pertaining the current context where we work with P &L’s (especially when they represent returns). Hence, we can refer to some asymptotic results of high expectiles without worry of our chosen sign convention about X. In particular, Bellini et al. (2014) showed that assuming X with heavy-tailed distribution in the Fréchet maximum domain of attraction (and then having a Paretian right-tail) it holds \(e_{\alpha }(X) < q_{\alpha }(X)\), where  is the \(\alpha \)-quantile of the distribution function
is the \(\alpha \)-quantile of the distribution function  , provided the tail index of the Fréchet distribution is greater than 2 and \(\alpha \in ({\bar{\alpha }},1)\) with \({\bar{\alpha }} < 1\). Passing to the negative we have
, provided the tail index of the Fréchet distribution is greater than 2 and \(\alpha \in ({\bar{\alpha }},1)\) with \({\bar{\alpha }} < 1\). Passing to the negative we have
and the expectile-based coherent risk measure is less conservative than value-at-risk. As a result, the performance ratio \(\frac{\mathsf {E}(X)}{\mathsf {VaR}_{\alpha }(X)}\) is greater than our \(\mathsf {RAROC}\)-type \(\frac{\mathsf {E}(X)}{-e_{\alpha }(X)}\), meaning more prudent performance evaluation. The same remains true when comparing the \(\mathsf {RAROC}\)-types \(\frac{\mathsf {E}(X)}{\tfrac{1}{\alpha } \int _0^{\alpha } \mathsf {VaR}_t(X) \mathrm {d}t}\) and \(\frac{\mathsf {E}(X)}{-\tfrac{1}{\alpha } \int _0^{\alpha } e_t(X) \mathrm {d}t}\), by simply taking the integrated version of (22). Recall that \(\tfrac{1}{\alpha } \int _0^{\alpha } \mathsf {VaR}_t(X) \mathrm {d}t\) is the classical expected shortfall.
5.2 The omega ratio connection
As pointed out in Delbaen (2013) and Bellini and Di Bernardino (2017), the acceptance set for the \(\alpha \)-expectile of a position \(X \in L^1\) as a coherent risk measure is

namely the acceptability of a position is given for a sufficiently high gain-loss ratio. This entails a natural link between risk and performance measures. Recall that the Omega ratio of \(X \in L^1\) with respect to a benchmark \(t \in \mathbb {R}\) is defined as

see also Remillard (2013, Section 4.4.4) for a reference at a textbook level. Since the first order condition defining expectiles can be written as  , see Bellini et al. (2018) and the references therein, there is a one-to-one relation between expectiles and Omega ratios:
, see Bellini et al. (2018) and the references therein, there is a one-to-one relation between expectiles and Omega ratios:

The Omega ratio is a widespread performance measure and the gain-loss ratio is a special case for a benchmark \(t=0.\) The advantage of its relation with expectiles is that besides the typical usage in performance measurement and especially in ranking investment funds, ordering all expectiles (in the sense of Bellini et al. (2018, Definition 6)) is equivalent to ordering all the Omega ratios (see Bellini et al. (2018, Theorem 8)) for all possible values of t. This can obviously help investors in making their risky decisions independently of the chosen benchmark in order to get the best reward.
Using the appropriate labeling \(\alpha \equiv \alpha (x)\) as in Sect. 4, Corollary 1, the acceptance set (23) can be equivalently given using the nonnegativity condition concerning expectations and expectiles. Since \(\alpha (x)=\frac{1}{1+x}\) if and only if \(x = \frac{1-\alpha }{\alpha }\), we write for \(\alpha (x) \in (0,\frac{1}{2}]\)
Now, observe that \(\alpha (x) \mapsto -e_{\alpha (x)}(X)\) is continuous and strictly increasing in \(x \in \mathbb {R}_+\) provided \(\alpha (x) \rightarrow 0\) and \(x \rightarrow \infty \). Together with the increasing family of sets of scenarios \((\mathcal {S}_{\alpha (x)})_{x \in \mathbb {R}_+}\) the acceptability \(X \in \mathscr {A}_{-e_{\alpha (x)}}\) associated to a suitable level of performance is given by

Hence we have the following:
Corollary 2
A mapping \(\textsf {a} \iota : L^1 \rightarrow [0,+ \infty ]\) is an expectile-based acceptability index if and only if there exists a family \((\mathcal {S}_{\alpha (x)})_{x \in \mathbb {R}_+}\) increasing in x such that the equivalent representation
holds, where \(\inf \varnothing = \infty \) and \(\sup \varnothing = 0.\)
Clearly, Eq. (25) can be rewritten as

To go back to the gain-loss ratio we find the right choice of scenarios, see Cherny and Madan (2009) where \(\mathsf {E}(X)\) is now replaced by \(\mathsf {E}(X^+)\). First, the special case  gives the following acceptability index of performance
gives the following acceptability index of performance
Each set of scenarios \(\mathcal {S}_{\alpha (x)}\) is for every \(x \in \mathbb {R}_+\) given by those \(\varphi \) satisfying conditions stated in Eq. (14) and in addition  for any \( X \in L^1\) with
for any \( X \in L^1\) with  . A modification of Cherny and Madan (2009, Lemma 1) yields each set of scenarios in the family \((\mathcal {S}_{\alpha (x)})_{x \in \mathbb {R}_+}\) as \(S_{\alpha (x)}= \cap _{y > x} S_{\alpha (y)}.\) Therefore, there exists a constant \(\kappa \in \mathbb {R}_+\) such that any scenario can be represented as
. A modification of Cherny and Madan (2009, Lemma 1) yields each set of scenarios in the family \((\mathcal {S}_{\alpha (x)})_{x \in \mathbb {R}_+}\) as \(S_{\alpha (x)}= \cap _{y > x} S_{\alpha (y)}.\) Therefore, there exists a constant \(\kappa \in \mathbb {R}_+\) such that any scenario can be represented as

The constant \(\kappa \) guarantees that \(\mathsf {E}(\kappa (\mathbf {I}_{\{X > 0\}} + Y))=1,\) i.e. \(\kappa = \frac{1}{\mathsf {P}(X > 0) + \mathsf {E}(Y)}.\) With all this in mind and calling for acceptability sets (1), it is easy to verify that  is equivalent to
is equivalent to  and the minimum is attained at
and the minimum is attained at  Thus we have the following chain of equivalences
Thus we have the following chain of equivalences

The last equivalence entails \(\textsf {a} \iota (X)=\mathsf {GLR}(X)\), given the chosen set of scenarios \(\mathcal {S}_{\alpha (x)}\). The optimum in the representation (26) is far from the too tolerant risk attitude given by \(e_{\frac{1}{2}}(X)=\mathsf {E}(X),\) for \(\alpha =\frac{1}{2}\) or \(x=1\). Anyway, by Corollary 2 and inequality (27) the acceptability of the trade X at the level x corresponds to the greatest nonnegative \(\alpha \)-expectile with more risk aversion produced by a greater \(\mathcal {S}_{\alpha (x)}\), since by Delbaen (2012, Example 5) any expectile can be regarded as the von Neumann-Morgenstern utility function

defined on \(\mathbb {R}\) with  for the concavity. Also, taking the supremum over \(x \in \mathbb {R}_+\) of the left-hand expression in (27) implies that \(\textsf {a} \iota (X)\) is dominated by the Omega ratio
for the concavity. Also, taking the supremum over \(x \in \mathbb {R}_+\) of the left-hand expression in (27) implies that \(\textsf {a} \iota (X)\) is dominated by the Omega ratio  or it is just equal to the Omega ratio for \(t=e_{\frac{1}{1+x}}(X)\) and \(x < +\infty .\)
or it is just equal to the Omega ratio for \(t=e_{\frac{1}{1+x}}(X)\) and \(x < +\infty .\)
Remark 8
For \(X,Y \in L^1,\) let us assume  meaning the usual stochastic order for all increasing functions \(\psi .\) This is equivalent to the expectile order
meaning the usual stochastic order for all increasing functions \(\psi .\) This is equivalent to the expectile order  defined as
defined as  for all \(\alpha \in (0,1),\) see Bellini et al. (2018, Definition 6). Let \(x_1\) be the optimum in the representation of \(\textsf {a} \iota (X)\) given by Corollary 2 and take \(t_1 = e_{\frac{1}{1+x_1}}(X).\) Thus,
for all \(\alpha \in (0,1),\) see Bellini et al. (2018, Definition 6). Let \(x_1\) be the optimum in the representation of \(\textsf {a} \iota (X)\) given by Corollary 2 and take \(t_1 = e_{\frac{1}{1+x_1}}(X).\) Thus,  since the expectile order is equivalent to the pointwise ordering of Omega ratios, see Bellini et al. (2018, Theorem 8). Writing \(x_2\) for the optimum in representation of \(\textsf {a} \iota (Y)\) given by Corollary 2, we have \(t_2=e_{\frac{1}{1+x_2}}(Y) < e_{\frac{1}{1+x_1}}(Y)\) since the expectile is strictly decreasing in \(x \in \mathbb {R}_+.\) Now we have two possibilities:
since the expectile order is equivalent to the pointwise ordering of Omega ratios, see Bellini et al. (2018, Theorem 8). Writing \(x_2\) for the optimum in representation of \(\textsf {a} \iota (Y)\) given by Corollary 2, we have \(t_2=e_{\frac{1}{1+x_2}}(Y) < e_{\frac{1}{1+x_1}}(Y)\) since the expectile is strictly decreasing in \(x \in \mathbb {R}_+.\) Now we have two possibilities:
-
(i)
 and consequently
and consequently  by the monotonicity of Omega ratios with respect to t, see Bellini et al. (2018, Theorem 2);
by the monotonicity of Omega ratios with respect to t, see Bellini et al. (2018, Theorem 2); -
(ii)
 and
and 
Only in the case (ii) the expectile order would imply  and taking the negative of the corresponding expectiles
and taking the negative of the corresponding expectiles  this corresponds to the situation when a riskier trade Y in term of the expectile risk measure need more compensation for its reward, or equivalently a trade Y preferred to a trade X in the usual stochastic order have a higher performance.
this corresponds to the situation when a riskier trade Y in term of the expectile risk measure need more compensation for its reward, or equivalently a trade Y preferred to a trade X in the usual stochastic order have a higher performance.
6 Further properties of expectile-based indices of performance
Most of the risk measures proposed by academics and used in practice are law-invariant, that is the numerical value of the risk measure is only affected by the probability distribution of the underlying financial position. They are indeed special cases of statistical functionals T(F) defined on a proper set of probability distributions \(\mathcal {M}\) over \(\mathbb {R}\) with cumulative distribution functions F. To fit in the current context, we assume F belongs to the class of all cumulative distribution functions \(\mathcal {D}^1\) on \(\mathbb {R}\) with finite first moment \(\int |x| \mathrm {d}F(x) < + \infty .\) Throughout this section we let \(e_{\alpha }(F)\) for \(X \sim F\). We give a direct representation of the proposed expectile-based acceptability index in term of the probability distribution of the financial position to assess. Following Delbaen (2012) and in particular Delbaen (2013, Theorem 7) we reformulate Corollary 1 by means of the Kusuoka representation of the \(\alpha \)-expectile as a coherent, law-invariant risk measure:
where \(\mathcal {M}_{\alpha }\) is a \(\text {weak}^{\star }\)-closed convex set of probability measures on (0, 1] such that

The integrand in the above representation is nothing but the negative of the expected shortfall,
where  is the c-quantile of F. Therefore representation (16) becomes:
is the c-quantile of F. Therefore representation (16) becomes:

for an acceptable position \(X \sim F.\) Now \((\mathcal {M}_{x})_{x \in \mathbb {R}_+}\) is an x-increasing family of sets of scenarios based on probability measures on [0, 1], supporting the representation of each \(-e_{\frac{1}{1+x}}(F),\) where as in Sect. 5.2 we let \(\alpha =\frac{1}{1+x}\). The law-invariance of any such coherent expectile-based risk measure transfers to the acceptability index \(\textsf {a} \iota (F)\). There is also a Kusuoka representation using densities. By Delbaen (2013, Theorem 2), a direct application of Fubini’s theorem entails expectiles associated to \(x \in \mathbb {R}_+\) given by
where \(\mathbf {F}_{x}\) is a convex set of convex (distortion) functions \(f:[0,1] \rightarrow [0,1]\) such that \(f(0)=0,f(1)=1\) and additionally  Notice that the density \(y \mapsto f'(y) = \int _{1-y}^1 \frac{1}{\alpha } \nu (\mathrm {d}\alpha )\) is nondecreasing, therefore
Notice that the density \(y \mapsto f'(y) = \int _{1-y}^1 \frac{1}{\alpha } \nu (\mathrm {d}\alpha )\) is nondecreasing, therefore  Taking the negative of expectiles given in (30) for a position \(X \sim F\) yields acceptability at the level \(x \in \mathbb {R}_+\) provided that the infimum in the above representation is nonnegative. In fact we have the following:
Taking the negative of expectiles given in (30) for a position \(X \sim F\) yields acceptability at the level \(x \in \mathbb {R}_+\) provided that the infimum in the above representation is nonnegative. In fact we have the following:
Corollary 3
A mapping \(\textsf {a} \iota : L^1 \rightarrow [0,+ \infty ]\) is an expectile-based acceptability index if and only if there exists a family \((\mathbf {F}_x)_{x \in \mathbb {R}_+} \subset C[0,1]\) increasing in x such that

where \(\inf \varnothing = \infty \) and \(\sup \varnothing = 0.\)
Proof
It suffices to note that \(\mathbf {F}_{x}\) is a (convex) compact (in the topology of uniform convergence) set and the infimum in (30) is attained at \({\bar{f}} \in \mathbf {F}_{x}\) with  Then for \(0< x < y\) we have by construction \(\mathbf {F}_x \subset \mathbf {F}_y\) which yields the desired result. \(\square \)
Then for \(0< x < y\) we have by construction \(\mathbf {F}_x \subset \mathbf {F}_y\) which yields the desired result. \(\square \)
6.1 Elicitability of expectile-based performance indices
Elicitability of statistical functionals, and then of law-invariant risk measures, allows the assessment and comparison of competing point forecasts by means of an error measure called scoring function which is the analogue of the loss function in statistical decision theory. This implies for risk measures the possibility to perform backtesting through the average score
where \(T_i\) are point estimates of the statistical functional for given realizations \(X_i\) of a random sample with population \(X \sim F.\) We assume scoring functions \(S : \mathbb {R}\times \mathbb {R}\rightarrow (0, + \infty )\) as defined in Bellini and Bignozzi (2015, Definition 3.1). In fact, whenever a statistical functional T(F) is elicitable then, modulo some technical conditions, it can be represented as a minimizer
where the cumulative distribution functions belong to a class \(\mathcal {D}\) such that for \(\mu \in \mathcal {M}\) we have \(F(x)=\mu (-\infty ,x].\) The above integral is nothing but the expected score \(\mathsf {E}(S(z,X))\) based on the original probability measure \(\mathsf {P},\) for example we can consider \(\mu = \mathsf {P}\circ X^{-1}.\) A statistical functional is not elicitable if is its level sets \(\{T = t\}\) are not convex for all \(t \in \mathbb {R}\), see for example Delbaen et al. (2016). In our setting, the elicitability is relative to the class \(\mathcal {M}\) or equivalently \(\mathcal {D}.\) Since the negative of expectiles are law-invariant and elicitable by Bellini and Bignozzi (2015, Theorem 4,4(b)), our aim is to show that also \(\textsf {a} \iota (F)\) is elicitableFootnote 9 too with respect to the class \(\mathcal {D}^1.\)
Corollary 4
The law-invariant acceptability index \(\textsf {a} \iota (F)\) with representation (31) is elicitable relative to the class \(\mathcal {D}^1.\)
Proof
First, observe that \(x \mapsto e_{\frac{1}{1+x}}(F)\) for fixed \(F \in \mathcal {D}^1\) is continuous in \(x \in \mathbb {R}_+\) and thus its range is the interval \([b, +\infty )\) for some \(b \in \mathbb {R}_+.\) Consider the correspondence \(\Psi : [b, +\infty ) \rightarrow 2^{\mathbb {R}_+ \times \mathbb {R}}\) defined by

for \(w=e_{\frac{1}{1+x}}(F).\) We take its restriction to the range of \(\Psi ,\) namely
We further consider a second map \(g: \Psi ([b, + \infty )) \rightarrow [0, +\infty ]\) defined by

Because the expectile is strictly decreasing in \(x \in \mathbb {R}_+,\) we have that
and the composition \(h = g \circ {\tilde{\Psi }}\) is a 1-to-1 mapping between the range \([0, + \infty )\) of the expectile and the half line \([0, + \infty ].\) By Gneiting (2011, Theorem 2.6) as a version of Osband’s revelation principle Osband (1985, p. 9) we additionally have that \(h(e_{\frac{1}{1+x}}(F))\) is elicitable for every \(x \in \mathbb {R}_+\) as the expectile is yet elicitable. Finally, taking
and applying again the above results yields the acceptability index as an elicitable statistical functional for \(F \in \mathcal {D}^1.\) \(\square \)
When the performance index is just the Omega ratio with benchmark \(t=e_{\frac{1}{1+x}}(F)\) (see Sect. 5.2, Eq. (27)) we can recover the scoring function strictly consistent with \(\textsf {a} \iota (F)\) in the case \(\mathsf {E}((X-t)^-) \ne 0\) by Gneiting (2011, Theorem 3.2(b),(c)) which is of the form
where \(\phi \) is a convex function with first derivative \(\phi '\) and
are such that \(r,s : \mathbb {R}\rightarrow (0, + \infty ).\) This only requires that \(\mathsf {E}((X-t)^+),\mathsf {E}((X-t)^-)\) and moreover \(\mathsf {E}((X-t)^+\, \phi '(X-t)),\mathsf {E}((X-t)^-\, \phi (X-t)),\mathsf {E}(X\,(X-t)^-\, \phi '(X-t))\) are all finite which is the case since \(X-t \in L^1.\)
Corollary 4 above can be rephrased as follows: the expectile-based acceptability indices \(\textsf {a} \iota (X)\) for a traded position with terminal value \(X \in L^1\) are elicitable. Consider for example the expectile-based performance ratio \(\textsf {a} \iota (X)=\tfrac{\mathsf {E}(X)}{-e_{\alpha }(X)}\) introduced in Sect. 5. Clearly, it is a statistical functionalFootnote 10 and its estimation depends on past observations of asset prices and/or returns. As a possible point estimator we considered the nonparametric statistics \({\hat{\theta }}_n:=\widetilde{\mathsf {RAROC}}_n\) given in Eq. (21), in fact other estimators \({\hat{\theta }}_n\) such asFootnote 11 maximum likelihood should be considered and this opens the question of how to choose among them, given a sample \(X_1,\ldots ,X_n\) drawn from \(X \sim F\). The discrepancy between \(\textsf {a} \iota (X)\) and \({\hat{\theta }}_n\) qualifies as estimation error and is intimately linked with the problem of forecasting, well known in financial econometrics. Now, theoretical elicitability of \(\textsf {a} \iota (X)\) means that we can assign a (strictly consistent) scoring functionFootnote 12 such that
where \(S_{\textsf {a} \iota }(z,X)\) is the score of our acceptability index. Applying the one-to-one division mapping \(g(u,v)=\tfrac{u}{v}\) to the range of the bi-variate statistical functionalFootnote 13\(\mathbf {T}(X):=(\mathsf {E}(X),-e_{\alpha }(X))\), by Gneiting (2011, Theorem 4) or Fissler and Ziegel (2016, Proposition 4.2(ii)) we get
i.e. the scoring function of our performance ratio is that of \(\mathbf {T}(X)\) before g(u, v) acts. Then it can be written as the sum of the two separate scores of \(\mathsf {E}(X)\) and \(-e_{\alpha }(X)\) respectively,
because \(\mathbf {T}(X)\) is a 2-elicitable functional, in the sense of Fissler and Ziegel (2016, Definition 2.1), with elicitable components.Footnote 14 The sample counterpart of the expected score in (33), the so called empirical score, is
namely the estimated average score where the ex-ante forecast of the acceptability indexFootnote 15 is \(z_t=\tfrac{u_t}{v_t}\), the ratio of the ex-ante forecast \(u_t\) of the mean to that of the expectile-based risk measure \(v_t\), while \(x_t\) are ex-post realizations of a time series \((X_t)_{t \in \mathbb {N}}\) of periodic returns. More extensively, we have

by identifying \(u_t=\mathsf {E}_t\) with an estimate of the expected return and \(v_t=-e_{\alpha ,t}\) with an estimate of the corresponding expectile-based risk measure at a level \(\alpha \in (0,\tfrac{1}{2}]\). Thus for competing estimation procedures we can asses the elicitation of \(\textsf {a} \iota (X)\) by ranking the corresponding empirical score (35), employing Eq. (36), and then choosing that with the lowest value. For example, we can refer to the forecast selection examples in Bellini and Di Bernardino (2017) where the competing estimation procedures are the standard Normal, the historical, and two alternative GARCH(1,1) models with Normal and with Student-t innovations, for a dataset of \(n=3818\) daily log-returns of the S &P500 Index; the author set \(\alpha =0.00145\) in order to get \(-e_{\alpha }(X)=\mathsf {VaR}_{0.01}(X)\). This approach can be easily adapted to the current framework by applying the aforementioned estimation procedures also to \(\mathsf {E}_t\) other than \(-e_{\alpha ,t}\). Indeed, one can consider additionally estimators for \(-e_{\alpha }(X)\) such as the weighted version of the empirical expectile in Daouia et al. (2021, equation (11)) which is in turn based on their definition of expectHill estimator of \(\alpha \), see Daouia et al. (2021, equation (8)). The entire procedure above can be also applied to the performance ratio \(\tfrac{\mathsf {E}(X)}{-\tfrac{1}{\alpha }\int _{0}^{\alpha } e_s(X) \mathrm {d}s}\), for which further estimation procedures can be selected out of those employed in Bellini and Di Bernardino (2017), for example one can take the extrapolated estimator of the expectile-based risk measure \(-\tfrac{1}{\alpha }\int _{0}^{\alpha } e_s(X) \mathrm {d}s\) given in Daouia et al. (2021, equation (16)).
7 Conditional expectile-based performance index
In this section we develop a conditional representation of expectile-based acceptability indices. We write \(L^p(\mathscr {F})\) for the space of all positions X with finite pth-moment which are measurable with respect to the initial information set \(\mathscr {F}.\) To account for new information and update the performance measurement we introduce a sub-\(\sigma \)-algebra \(\mathscr {G}\subset \mathscr {F}\) and also consider positions in the smaller space \(L^1(\mathscr {G}).\) Recall that we in the rest of this section all inequalities, equalities, convergence concepts and statements about solution of equations applied to random variables are meant to hold \(\mathsf {P}\)-a.s. if not stated otherwise. A conditional acceptability index is a mapping \(\textsf {a} \iota (\cdot \, | \,\mathscr {G}) : L^1(\mathscr {F}) \rightarrow L^1(\mathscr {G})\) satisfying the following conditions, where \(X,Y \in L^1(\mathscr {F})\) and \(W \in L^1(\mathscr {G})\) is a nonnegative random variable:
-
1.
Conditional quasi-concavity,
 for any \(\Lambda \in L^{\infty }(\mathscr {G})\) such that
for any \(\Lambda \in L^{\infty }(\mathscr {G})\) such that  and every W;
and every W; -
2.
Monotonicity,
 \(\Longrightarrow \)
\(\Longrightarrow \)  ;
; -
3.
Conditional scale invariance, \(\textsf {a} \iota (\Lambda X \, | \,\mathscr {G}) = \textsf {a} \iota (X \, | \,\mathscr {G})\) for any \(\Lambda \in L^{\infty }(\mathscr {G})\) such that
 ;
; -
4.
Continuity property, for any sequence \((X_n)_{n \in \mathbb {N}} \subset L^1(\mathscr {F})\) such that \(X_n \uparrow X\in L^1(\mathscr {F})\), implies
 provided that
provided that  for every \(n \in \mathbb {N}.\)
for every \(n \in \mathbb {N}.\)
To establish a representation of conditional expectile-based acceptability indices we need a modified version of conditional expectiles originally defined by Bellini et al. (2018, Definition 2). For the sake of completeness we list below this definition together with the essential properties.
Definition 2
Given \(X \in L^1(\mathscr {F})\) and \(\alpha \in (0,1),\) its conditional \(\alpha \)-expectile is the unique solution \(Z \in L^1(\mathscr {G})\) of the equation
Existence and uniqueness of \(Z=e_{\alpha }(X \, | \,\mathscr {G})\) is guaranteed by Bellini et al. (2018, Theorem 2.2). Conditional expectiles as coherent risk measures \(\rho (X \, | \,\mathscr {G})=-e_{\alpha }(X \, | \,\mathscr {G})\) for  satisfy:Footnote 16
satisfy:Footnote 16
-
1.
Conditional cash invariance, \(\rho (X + H \, | \,\mathscr {G})=\rho (X \, | \,\mathscr {G}) -H,\) for any \(H \in L^1(\mathscr {G})\);
-
2.
Monotonicity,
 implies
implies  ;
; -
3.
Conditional positive homogeneity, \(\rho (\Lambda X \, | \,\mathscr {G})= \Lambda \rho (X \, | \,\mathscr {G})\) for \(\Lambda \in L^1(\mathscr {G})\);
-
4.
Subadditivity,

To provide the analogous of Lemma 2 in Sect. 3, we introduce a slightly different definition of conditional expectiles.
Definition 3
Given \(X \in L^1(\mathscr {F})\) and a random level \(A \in L^1(\mathscr {G})\) such that they form a random vector \((A,X): \Omega \rightarrow \mathbb {R}\times (0,1),\) the randomized conditional A-expectile is the solution \(Z \in L^1(\mathscr {G})\) of the equation
Essentially, the \(\alpha \)-parameter of conditional expectile as given in Definition 2 is now a positive random variable in the conditional expected loss of Eq. (37). This can be interpreted as a risk measurement approach leading to capital requirement for a position X to asses that minimizes both risk overestimation and underestimation, conditioned on new information \(\mathscr {G}\) which also implies updating of the randomized probability level of occurrence A, see Moresco et al. (2019). We provide a short proof that the above version of conditional expectile exists as the unique solution of Eq. (37).
Lemma 4
Let \(X \in L^1(\mathscr {F})\) and \(A \in L^1(\mathscr {G})\) such that \(A(\omega ) \in (0,1)\) for every \(\omega \in \Omega .\) There exists a unique solution \(Z^{\star } \in L^1(\mathscr {G})\) of Eq. (37).
Proof
Let \(F(a,x,\omega )\) be a version of  Rewrite the conditional expectation in (37) as
Rewrite the conditional expectation in (37) as
which has a unique solution given by \(Z^{\star }(\omega ).\) The \(\mathscr {G}\)-measurability of \(Z^{\star }\) is showed as in the proof of Bellini et al. (2018, Theorem 2.2) but using the regular conditional distribution function \(F(a,x,\omega ).\) To show that \(Z^{\star }\) has finite first moment as a \(\mathscr {G}\)-measurable random variable, we proceed as in the proof of Bellini et al. (2018, Theorem 2.2) simply by considering

with 
 and analogously on
and analogously on  \(\square \)
\(\square \)
Now, our randomized version of the conditional expectile is
satisfying properties 1 to 4 of the original conditional expectile in Definition 2. This can be obtained by observing that

which can be easily deduced by equation (9) in Bellini et al. (2018, Theorem 2.2.) and its proof. The aforementioned properties are then transferred from those of the conditional shortfall risk measures introduced by Weber (2006), if in addition one considers  for the subadditivity. Nevertheless, we need two further properties of \(e_A(X \, | \,\mathscr {G}):\)
for the subadditivity. Nevertheless, we need two further properties of \(e_A(X \, | \,\mathscr {G}):\)
-
5.
 with the reverse inequality holding by a change in sign;
with the reverse inequality holding by a change in sign; -
6.
Continuity from below, \(X_n \uparrow X\) for a sequence \((X_n)_{n \in \mathbb {N}} \subset L^1(\mathscr {F}),\) implies \(e_{A}(X_n \, | \,\mathscr {G}) \uparrow e_{A}(X \, | \,\mathscr {G})\), which becomes continuity from above taking the negatives.
Property 5 is an easy generalization of the analogous monotonicity property of conditional shortfall risk measures, with respect to the parameter \(\alpha .\) Property 6 can be easily deduced by Bellini et al. (2018, Theorem 2.3(d)). We call

the randomized conditional expectile risk measure of the position X, where for the sake of consistency with the unconditional representation in Proposition 1 we have

Note that
Lemma 5
Let \(\left( \rho _W(X \, | \,\mathscr {G})\right) _{W \in L^1(\mathscr {G})}\) be an increasing family of randomized conditional expectile risk measure for \(X \in L^1.\) Then, the mapping \(\textsf {a} \iota (\cdot \, | \,\mathscr {G}) : L^1(\mathscr {F}) \rightarrow L^1(\mathscr {G})\) defined by

is a conditional acceptability index of performance (we assume \(\mathrm {ess\, sup}\varnothing = 0\)).
Although the obvious similarity between this lemma and Lemma 2, we present the proof to account for the randomization effect. Recall the all equalities and inequalities are valid \(\mathsf {P}\)-a.s.
Proof
Let  and recall Eqs. (40), (41). By the monotonicity of randomized conditional expectile risk measures we have for every \(X,Y \in L^1(\mathscr {F})\) with
and recall Eqs. (40), (41). By the monotonicity of randomized conditional expectile risk measures we have for every \(X,Y \in L^1(\mathscr {F})\) with  that
that  Thus
Thus

implies  which together with monotonicity also entails
which together with monotonicity also entails 
 Using (42) we consequently have
Using (42) we consequently have

then taking the essential supremum of both sets yields  For the quasi-concavity of \(\textsf {a} \iota (\cdot \, | \,\mathscr {G})\) we consider two random trades \(X,Y \in L^1\) such that \(\textsf {a} \iota (X \, | \,\mathscr {G})\) and \(\textsf {a} \iota (Y \, | \,\mathscr {G})\) are both
For the quasi-concavity of \(\textsf {a} \iota (\cdot \, | \,\mathscr {G})\) we consider two random trades \(X,Y \in L^1\) such that \(\textsf {a} \iota (X \, | \,\mathscr {G})\) and \(\textsf {a} \iota (Y \, | \,\mathscr {G})\) are both  for a given
for a given  satisfying (41) and (42). For all \(W \in B\) such that
satisfying (41) and (42). For all \(W \in B\) such that  combining monotonicity of the randomized conditional expectile risk measures with definition (43) we have
combining monotonicity of the randomized conditional expectile risk measures with definition (43) we have  and
and  An appeal to the conditional positive homogeneity of \(\rho _W(\cdot \, | \,\mathscr {G})\) now entails
An appeal to the conditional positive homogeneity of \(\rho _W(\cdot \, | \,\mathscr {G})\) now entails

and

for every random variable  Moreover, by subadditivity of \(\rho _W(\cdot \, | \,\mathscr {G})\) we have
Moreover, by subadditivity of \(\rho _W(\cdot \, | \,\mathscr {G})\) we have

for every \(W < W_0\) and it follows  As a by-product, definition (43) yields
As a by-product, definition (43) yields  and quasi-concavity is proved. Conditional scale invariance of \(\textsf {a} \iota ( \cdot \, | \,\mathscr {G})\) follows on B by conditional positive homogeneity of \(\rho _W( \cdot \, | \,\mathscr {G}).\) To show the continuity, pick a sequence \((X_n)_{n \in \mathbb {N}} \subset L^1(\mathscr {F})\) such that \(X_n \uparrow X\) and assume
and quasi-concavity is proved. Conditional scale invariance of \(\textsf {a} \iota ( \cdot \, | \,\mathscr {G})\) follows on B by conditional positive homogeneity of \(\rho _W( \cdot \, | \,\mathscr {G}).\) To show the continuity, pick a sequence \((X_n)_{n \in \mathbb {N}} \subset L^1(\mathscr {F})\) such that \(X_n \uparrow X\) and assume  for every \(n \in \mathbb {N}\) and \(W \in B.\) Since randomized conditional expectile risk measures are continuous from above, \(\rho _W(X_n \, | \,\mathscr {G}) \downarrow \rho _W(X \, | \,\mathscr {G})\) so that
for every \(n \in \mathbb {N}\) and \(W \in B.\) Since randomized conditional expectile risk measures are continuous from above, \(\rho _W(X_n \, | \,\mathscr {G}) \downarrow \rho _W(X \, | \,\mathscr {G})\) so that  provided that
provided that  and this combined with monotonicity of the conditional acceptability index eventually implies
and this combined with monotonicity of the conditional acceptability index eventually implies  as desired. \(\square \)
as desired. \(\square \)
As we have seen in the unconditional case, it is also possible to recover randomized conditional expectile risk measures by conditional acceptability indices. This is guaranteed by the following.
Lemma 6
Let  and define
and define

where A and W are related by Eq. (41) and \(\textsf {a} \iota (\cdot \, | \,\mathscr {G})\) is a conditional acceptability index. Then, \(\rho _W(X \, | \,\mathscr {G})\) satisfies properties 1–4 of Definition 2 together with subsequent properties 5,6.
Proof
Assume B as above. First, we check that the mapping \(W \mapsto \rho _W(\cdot \, | \,\mathscr {G})\) defined in (44) is increasing [recall Eq. (40)]. It suffices considering  and taking the essential infimum of both sets
and taking the essential infimum of both sets

To show conditional cash invariance, monotonicity, conditional positive homogeneity and subadditivity we proceed as in the Proof of Lemma 2, provided that all scalars \(x,m,\lambda , c\) are replaced by \(W,M, \Lambda , C\in L^1(\mathscr {G}),\) where in addition \(\Lambda \) is a nonnegative random variable, and the infimum is replaced by the essential infimum. To check the continuity from above of randomized conditional expectile risk measures, it suffices to proceed as in the last part of the Proof of Lemma 2 by replacing the scalar \(\epsilon \) with the random variable \(M \in L^1(\mathscr {G})\) and considering the continuity of \(\textsf {a} \iota (\cdot \, | \,\mathscr {G}).\) \(\square \)
Eventually, by Lemmas 5 and 6 together with Bellini et al. (2018, Theorem 2.4) and its proof we have our proposed conditional version of the unconditional set of scenarios (14) in Sect. 4:
Corollary 5
Let B be defined as in Lemma 5. The conditional expectile-based acceptability index can be represented as

where

is such that  implies \(\mathcal {S}_{W_1} \subset \mathcal {S}_{W_2}.\)
implies \(\mathcal {S}_{W_1} \subset \mathcal {S}_{W_2}.\)
The last condition in the definition of \(\mathcal {S}_W\) makes use of the conditional supremum \(\mathrm {ess\, sup}(\varphi \, | \,\mathscr {G})\) of each scenario, see Bellini et al. (2018) and the references therein. It is worth noting that choosing the trivial sigma-algebra \(\mathscr {G}=\{\varnothing , \Omega \},\) all the above representation results yield the unconditional representation of acceptability indices based on expectile risk measures up to replacing the continuity properties of \(\textsf {a} \iota (\cdot \, | \,\mathscr {G})\) and \(\rho _W(\cdot \, | \,\mathscr {G})\) by the original continuity properties in Sect. 3.
8 Conclusions
Given the recent increasing attention to the use of expectiles as coherent risk measures, we investigate their link to performance measurement beyond the classical gain-loss and Omega ratios. Hinged on the concept of acceptability indices of performance, we are able to drive the dual representation of expectile-based coherent risk measures to the construction of two new expectile-based performance ratios. Given the elicitability of the proposed expectile-based performance measures proved in Sect. 6.1, we suggest a proper scoring function that can easily implemented in practical forecast selection problems. Moreover, we generalize the notion of conditional expectiles and give one more representation of such performance measures when new information arrives and the probability level implicit in the piecewise loss function giving expectiles is updated accordingly.
Data Availability
The manuscript does not treat data and numerical examples.
Code Availability
No software or custom code is used in the manuscript.
Change history
27 August 2022
Missing Open Access funding information has been added in the Funding Note.
Notes
Recall that given a loss function g(x, s) which is Borel on \(\mathbb {R}\times \mathbb {R}\) an M-functional \(T(F_X)\), related to a cumulative distribution function \(F_X\) of a random variable X, is the solution of \(\int g(x,T(F_X)) \mathrm {d}F_X(x)=\min _{s \in \Theta } \int g(x,s) \mathrm {d}F_X(x)\). Here \(\Theta \) is an open subset of \(\mathbb {R}\) representing the parameter set. This is a generalization of maximum likelihood estimates.
Loosely speaking, the space \(L^{\infty }\) contains bounded random variables.
The precise concept is \(\lambda \) gain-loss free, see Biagini and Pinar (2013, Definition 2.2).
Moreover, it could be finite but with no supremum, see Biagini and Pinar (2013, Example 2.8).
Recall that \(L^1\) is a Banach lattice with respect to the cone \(L_+^1\), i.e. for all \(X,Y \in L^1\) we have \(\max \{X,Y\} \in L^1\) and
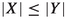 implies
implies  .
.Some authors call it expectile value-at-risk (EVaR), see for example Bellini and Di Bernardino (2017).
Namely, the ordered statistics of a sample from the X’s distribution.
In what follows we do not need to assume this class corresponds to the set of all probability measures on \(\mathbb {R}\) with compact support.
Formally it would be correctly set as \(\textsf {a} \iota (F)=\tfrac{\mathsf {E}(F)}{-e_{\alpha }(F)}\).
Observe that \({\hat{\theta }}_n\) is equivalent to the estimator \(\textsf {a} \iota (X_1,\ldots ,X_n)\).
This is similar to the risk function of statistical decision theory, i.e. \(L(\textsf {a} \iota (X),{\hat{\theta }}_n)\), for example the \(L^p\) loss \(L(x,y)=|x-y|^p\).
We have \(u=\mathsf {E}(X)\) and \(v=-e_{\alpha }(X)\), for \(-e_{\alpha }(X) \ne 0\).
It is well known that also the expectation is elicitable.
In defining the scoring function, we, without loss of generality, assume the observation domain for \(x_t\) and the action domain for \(z_t\) coincide and both are subsets of \(\mathbb {R}\).
References
Artzner, P., Delbaen, F., Eber, J.-M., Heath, D.: Coherent Measures of Risk. Math. Fin. 9(3), 203–228 (1999)
Basel Committee on Banking Supervision, In: International Convergence Of Capital Measurement and Capital Standars: A Revised Framework, Bank of International Settlements (2006)
Basel Committee on Banking Supervision, Minimum Capital Requirements for Market Risk, Bank of International Settlements (2019)
Bellini, F., Klar, B., Müller, A., Rosazza Gianin, E.: Generalized quantiles as risk measures. Insur. Math Econom. 54, 41–48 (2014)
Bellini, F., Bignozzi, V.: On elicitable risk measures. Quant. Finan. 15, 725–733 (2015)
Bellini, F., Di Bernardino, E.: Risk management with expectiles. The Europ. J. of Fin. 23(6), 487–506 (2017)
Bellini, F., Bignozzi, V., Puccetti, G.: Conditional expectiles, time consistency and mixture convexity. Insur. Math Econom. 82, 117–123 (2018)
Bellini, F., Klar, B., Müller, A.: Expectiles, omega ratios and stochastic ordering. Methodol. Comput. Appl. Probab. 20, 855–873 (2018)
Bernardo, A., Ledoit, O.: Gain, loss, and asset pricing. J. Political Econ. 108, 144–172 (2000)
Biagini, S., Pinar, M.Ç.: The best gain-loss ratio is a poor performance measure SIAM. J. Financial Math. 4(1), 228–242 (2013)
Cheridito, P., Li, T.: Risk measures on Orlicz hearts. Math. Fin. 19, 189–214 (2009)
Cherny, A., Madan, D.: New measures for performance evaluation. Rev. Financial Stud. 22(7), 2571–2606 (2009)
Cochrane, J.H., Saa-Requejo, J.: Beyond arbitrage: good-deal asset price bounds in incomplete markets. J. Political Econom. 108(1), 79–119 (2001)
Daouia, A., Girard, S., Stupfler, G.: Estimation of tail risk based on extreme expectiles. J. R. Statist. Soc. B 80(2), 263–292 (2018)
Daouia, A., Girard, S., Stupfler, G.: Tail expectile process and risk assessment. Bernoulli 26, 531–556 (2020)
Daouia, A., Girard, S., Stupfler, G.: ExpectHill estimation, extreme risk and heavy tails. J. Econom. 221, 97–117 (2021)
Delbaen, F.: Monetary Utility Functions. Osaka University CSFI Lecture Notes Series 3, Osaka University Press, Osaka (2012)
Delbaen, F.: A Remark on the Structure of Expectiles. Preprint, (2013) arXiv:1307.5881 [v1]
Delbaen, F., Bellini, F., Bignozzi, V., Ziegel, J.F.: Risk measures with the CxLS property. Finance Stoch. 20(2), 433–453 (2016)
Detlefsen, K., Scandolo, G.: Conditional and dynamic convex risk measures. Finance Stoch. 9(4), 539–561 (2005)
Dybvig, P.H., Ingersoll, J.E.: Mean-variance theory in complete markets. Jour. Busin. 55(2), 233–251 (1982)
Holzmann, H., Klar, B.: Expectile Asymptotics. Electron. J. Stat. 10, 2355–2371 (2016)
Filipović, D., Svindland, G.: The canonical model space for law-invariant convex risk measures is \(L^{1}\). Math. Fin. 22(3), 585–589 (2012)
Fissler, T., Ziegel, J.F.: Higher order elicitability and Osband’s principle. Ann. Stat. 44(4), 1680–1707 (2016)
Gneiting, T.: Making and evaluating point forecast. J. Am. Statist. Assoc. 106(494), 746–762 (2011)
Jaschke, S., Küchler, U.: Coherent risk measures and good deal bounds. Finance Stoch. 5, 181–200 (2001)
Krätschmer, V., Zähle, E.: Statistical inference for expectile-based risk measures. Scandinavian J. Stat. 44(2), 425–454 (2017)
Kuan, C.-M., Yeh, J.-H., Hsu, Y.-C.: Assessing value at risk with CARE, the conditional autoregresive expectile models. J. Econom. 150(2), 261–270 (2009)
Osband, K.H.: Providing Incentives for Better Cost Forecasting. Ph. D. Thesis. University of California, Berkeley. (1985)
Moresco, M.R., Müller, F.M., Righi, M.B.: On a robust risk measurement approach for capital determination errors minimization. Insur. Math Econom. 95, 199–211 (2019)
Newey, W.K., Powell, J.L.: Asymmetric least squares estimation and testing. Econometrica 55(4), 819–847 (1987)
Remillard, B.: Statistical Methods for Financial Engineering. CRC Press, Baco Raton (2013)
Rüschendorf, L.: Mathematical Risk Analysis. Springer Series in Operational Research and Financial Engineering, Dependence, Risk Bounds, Optimal Allocations and Portfolios (2013)
Ruszczyński, A., Shapiro, A.: Optimization of convex risk functions. Math. Oper. Res. 31(3), 433–452 (2006)
Weber, S.: Distribution-invariant risk measures. Inf. Dyn. Consist. Math. Fin. 16(2), 429–441 (2006)
Acknowledgements
The authors are grateful to one anonymous Referee for its helpful suggestions and critical comments, that help us to improve the presentation of the paper.
Funding
Open access funding provided by Università degli Studi di Catania within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The corresponding author states that there is no conflict of interest.
Ethical statement
The manuscript is not submitted to other journals. The manuscript has not been published elsewhere. Based on the well-developed framework of Acceptability Indices of Performance, the manuscript does provides a novel application using expectiles as coherent risk measures. Thus, it elaborates on this and provides additional new characterizations of expectile-based performance measures. The contribution presented is the author’s own.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rossello, D. Performance measurement with expectiles. Decisions Econ Finan 45, 343–374 (2022). https://doi.org/10.1007/s10203-022-00369-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10203-022-00369-8
Keywords
- Acceptability indices
- Expectile-based coherent risk measures
- Elicitability
- Conditional performance measure





 implies
implies 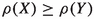 ;
; and,
and, ,
, and
and  one has
one has 


 provided that
provided that  for every
for every  implies
implies  , for any
, for any  , for
, for  and consequently
and consequently  by the monotonicity of Omega ratios with respect to t, see Bellini et al. (
by the monotonicity of Omega ratios with respect to t, see Bellini et al. ( and
and 
 for any
for any  and every W;
and every W;
 ;
; ;
; provided that
provided that  for every
for every  implies
implies  ;
;
 with the reverse inequality holding by a change in sign;
with the reverse inequality holding by a change in sign;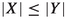 implies
implies  .
.