Abstract
The efficient market hypothesis is highly discussed in economic literature. In its strongest form, it states that there are no price trends. When weakening the non-trending assumption to arbitrary short, small, and fully unknown trends, we mathematically prove for a specific class of control-based trading strategies positive expected gains. These strategies are model free, i.e., a trader neither has to think about predictable patterns nor has to estimate market parameters such as the trend’s sign like momentum traders have to do. That means, since the trader does not have to know any trend, even trends too small to find are enough to beat the market. Adjustments for risk and comparisons with buy-and-hold strategies do not satisfactorily solve the problem. In detail, we generalize results from the literature on control-based trading strategies to market settings without specific model assumptions, but with time-varying parameters in discrete and continuous time. We give closed-form formulae for the expected gain as well as the gain’s variance and generalize control-based trading rules to a setting where older information counts less. In addition, we perform an exemplary backtesting study taking transaction costs and bid-ask spreads into account and still observe—on average—positive gains.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the 1970s, the so-called market efficiency hypothesis was highly accepted (Fama 1965, 1970). Later on, it was criticized, yet also defended (Malkiel 1989, 2005). Much of the criticism concerned so-called predictable patterns. Also, the joint hypotheses problem has to be taken into account, which states that usually market efficiency and a market model have to be tested simultaneously (Jarrow and Larsson 2012). Further, statistical inefficiency and economical inefficiency must be distinguished. When external variables are used to construct a strategy with too high returns, it may be the case that these variables are just appropriate ratios for the risk. When introducing risk-adjusted returns, excess returns are no contradiction when they go hand in hand with excess risk.
In this work, we present some results attacking the market efficiency hypothesis that do not have to deal with the joint hypothesis problem because no specific market model is assumed. The strategies under analysis neither use predictable patterns nor external variables, i.e., the typical defenses of the market efficiency hypothesis do not apply. By means of a mathematically rigorous proof, we show that the strategy contradicts the statistical efficiency of the market. A backtest with past market data also gives a strong evidence that the economical efficiency is contradicted. Risk adjustments and comparisons with other strategies do not solve the puzzle satisfactorily why it is possible to construct a market beating strategy when stochastically independent growth rates are assumed. The work at hand is technically based on a generalization of Baumann and Grüne (2017). The crucial difference to that work is that we allow for a time-varying trend (in contrast to a constant trend). This generalization does not only make the results more universal, but it constitutes the point that contradicts the efficient market hypothesis. The assumption used by Baumann and Grüne (2017) that there are assets with a constant nonzero trend (compared to the numéraire) seems to be rather unrealistic. In this work, we just assume a trend that is sometimes nonzero—and it does not matter whether the trend is positive or negative. Further, we give a closed-form formula for the gain’s variance and introduce a technique to discount older price information.
Much of the discussion on market efficiency, technical trading, and beating the market follows the idea that a trader (i) has to find a predictable pattern, (ii) has to construct a trading strategy to exploit this pattern, and (iii) has to test this new strategy against randomly selected broad index buy-and-hold strategies (Malkiel 1973). However, a new strand of research—mainly in engineering sciences and mathematics—goes another way. In the view of the respective authors, task (i) can be skipped, allowing trading strategies to be constructed directly. These strategies usually are model free and use neither predictions of patterns nor estimations of parameters. In short and using the terminology of the control community: they are constructed to be robust against the price. Instead of task (iii), which relies on real market data, (performance) properties are proven mathematically. This way, the overfitting problem (cf. Bailey et al. 2014) is avoided. The results of this work do not rely on the momentum effect as they are more general in two ways: Firstly, the main results concerning control-based trading strategies are proven mathematically while for the performance of momentum strategies there is empirical evidence. Secondly, control-based trading rules can easily deal with a sign-changing trend.
The paper is organized as follows: In Sect. 2, we briefly discuss the literature on efficient markets. In Sect. 3, the market setup as well as the trading strategies are explained and the relating literature is discussed. In Sect. 4, new results concerning special control-based trading rules, the so-called simultaneously long short (SLS) strategies, in a general market model with time-varying trends and volatilities are obtained (in detail, closed-form formulae for the expected gain and the gain’s variance). In addition, risk as well as a comparison to buy-and-hold strategies are discussed. To account for trading costs and bid-ask spreads—which are not considered in the analytical part of the work at hand—Sect. 5 is provided, in which we perform backtests on past market data using bid and ask prices. After that, in Sect. 6, the standard SLS rule is generalized to the so-called discounted SLS rule, in which old data has less influence on the strategy. Finally, in Sect. 7, we discuss the results—especially in view of the efficient market hypothesis—and conclude the paper.
2 Review of market efficiency
In this section, we briefly discuss market efficiency, its criticism, and its defense (cf. Fama 1991; Malkiel 2003). In addition, we discuss some topics where definitions are not clear, focusing on the analysis of the SLS strategy.
In its strong version, market efficiency states that either all or almost all information on the asset is reflected in the price. In the first case, no sophisticated trader and even no insider performs on average better than a simple buy-and-hold trader. Price processes are random walks around their fundamental values. When only almost all information is incorporated in the price, the costs for getting the missing information and for trading the asset are higher than the possible gain of exploiting this information (Fama 1991). The semi-strong version of the market efficiency hypothesis states that all public information is reflected in the price (Stickel 1985; Fama 1991), i.e., fundamentals and past returns are immediately incorporated. Thus, only private information can lead to excess gains. The word “immediately” has to be understood in an averaged sense, i.e., markets may overreact or underreact to new information, and markets may reflect information too early or too late, but on average all these effects balance out (Fama 1995). Last, the weak version of market efficiency states that insider trading as well as a fundamental analysis may be profitable, but a technical analysis of past returns is not. Or, a little bit weaker, when there exists a dependence of past and future returns, these anomalies are too small to be exploitable. Expressed mathematically, the weak form of the market efficiency hypothesis states that growth rates are stochastically independent or at least uncorrelated.
This work presents a technical trading strategy contradicting the weak form of the hypothesis of efficient markets, which implies a contradiction to all forms. Hence, we assume the growth rates to be stochastically independent, cf. Sects. 3.4 and 4.
One strand of criticism of the market efficiency hypothesis relies on predictable patterns. With statistical or data science methods, such patterns were found (Cross 1973; French 1980; Ariel 1987, 1990; Keim 1983; Roll 1983). However, Malkiel (2003) states that predictable patterns will self-destroy once published. Further, effects of (predictable) patterns may be too small to be exploited (Lakonishok and Smidt 1988), especially when trading costs are considered. In general, just because there is a statistical inefficiency, a trader might not be able to profit from it, hence, it may not cause an economical inefficiency. Another strand of criticism relies on stock price predictions via external variables (Rozeff 1984; Shiller 1984; Campbell and Shiller 1988; Banz 1981). But, as summarized by Fama (1991), these dependencies are either too small to be exploited or they have another reason: These variables are proxies for the risk. In the literature, one can find statements like “traders cannot expect excess returns” but also “traders can only expect excess returns when they accept excess risk.” However, it is not clear how to measure risk.
We note that there is criticism of the efficient market hypothesis from the empirical side, too (Covel 2004; Avramov et al. 2018). However, we note that empirical evidence concerning market (in)efficiency might be criticized, as all empirical results can be the result of data-dredging (p-hacking), i.e., the search for significant p values without causality. Long-term trends in assets prices found without p-hacking may be not exploitable (cf. Granger and Morgenstern 1962; Saad et al. 1998). The joint hypotheses problem states that market efficiency can (almost) always be tested only when simultaneously using a market model. Since the joint hypotheses problem is a very strong argument, we will use no market model or at least a model as general as possible (cf. Cover 1991). Event studies (Fama et al. 1969) and tests for market efficiency (Jarrow and Larsson 2012) that overcome the joint hypotheses (or bad-model) problem work with empirical data and, thus, might have the p-hacking problem.
As discussed by Carhart (1997) there is the momentum effect, relying on empirical and statistical methods: assets that performed well over the last few months will do so over the next few months, and similar for bad assets (cf. Carhart 1992; Jegadeesh and Titman 1993, 2001; Brown and Goetzmann 1995; Elton et al. 1996, 2015; Goetzmann and Ibbotson 1994; Grinblatt and Titman 1992; Hendricks et al. 1993; Jensen 1969; Wermers 1996; Fama and French 1996, 2008). Moskowitz (2010) explains why it is reasonable that assets with high momentum also have high risk. Thus, when considering risk-adjusted returns, the momentum effect might vanish. In contrast to these momentum strategies, the main performance properties of control-based strategies are shown mathematically. Further, and also in contrast to momentum strategies, control-based strategies can deal with a sign-switching trend.
Most past criticism of the efficient market hypothesis was empirical and, thus, had possibly the p-hacking problem. Theoretical critics often use a specific market model that leads to the joint hypotheses problem. To overcome the joint hypotheses problem, the p-hacking problem, and the overfitting problem (Bailey et al. 2014)—i.e., the problem that technical strategies might use too much past information to have any power for predicting the future—in the analytic part of the work at hand we present some purely theoretical criticism of the efficient market hypothesis, which uses neither past data nor any market model, except some very basic market requirements. Only in the exemplary backtesting in Sect. 5, we use past market data.
3 Market setup and simultaneously long short (SLS) trading strategies
In the control literature, there is a strand of research that seemingly is in contrast to the market efficiency hypothesis. There, by use of feedback techniques sourced and analyzed in engineering sciences as well as applied mathematics, trading strategies that are robust against noisy prices are created. In this section, we state the market setup and introduce control-based trading rules, especially the so-called simultaneously long short (SLS) rule. Furthermore, we give the most important results of the SLS literature and discuss related works.
The control theoretic way of thinking is different from classical finance: Neither fundamentals are calculated nor price patterns are searched for estimating future returns because control-based strategies do not use such estimations. Traders relying on control-based trading strategies are called feedback traders. They calculate their investment, i.e., their net asset position, which is an input variable to the system (i.e., to the financial market or actually to the trader’s portfolio) at every point in time, as a function of an output variable of the system, usually the gain. Thus, the way control-based trading rules are constructed is related to the stochastic portfolio theory (Fernholz 2002; Cuchiero et al. 2019; Pal and Wong 2016; Wong 2015; Karatzas and Ruf 2017) because both deal with functionally generated portfolios and try to be as model free as possible (i.e., esp., try to need no assumptions of model parameters).
3.1 Technical setup and construction of SLS trading rules
We consider a filtered probability space \((\varOmega ,{\mathcal {F}},{\mathbb {F}},{\mathbb {P}})\), where \({\mathbb {F}}=({\mathcal {F}}_t)_{t\in {\mathcal {T}}}\) is a filtration that fulfills the “usual hypotheses” (see Protter 2005, I.1, p. 3) and the time grid is either \({\mathcal {T}}=\{t_i=ih\ |\ i=0,\ldots ,N\}\) in the discrete time case or \({\mathcal {T}}=[0,T]\) in the continuous time case with \(T>0\) (and \(h>0\), \(N\in {\mathbb {N}}\), \(T=Nh\)).
We consider an asset market with a risk-free bond and one single risky asset. Further market requirement as well as discussions and brief justifications of these requirements are stated in Sect. 3.4.
We model the (discounted) price process p(t) of the risky asset as a positive stochastic process \({\mathcal {T}}\times \varOmega \rightarrow {\mathbb {R}}^+\) that has to be a semimartingale, i.e., esp. càdlàg, in the continuous time case. Every investment strategy of every trader \(\ell \), \(I^\ell :{\mathcal {T}}\times \varOmega \rightarrow {\mathbb {R}}\), has to be an adapted process in discrete time (i.e., \(I^\ell (t_i)\) has to fulfill that \((I^\ell (t_{i-1}))_{i=1,2,\ldots ,N+1}\) is predictable) resp. a locally bounded, predictable real-valued stochastic process in continuous time. The bond is always used to ensure the strategy to be self-financing. We calculate trader \(\ell \)’s gain/loss and the corresponding gain/loss process \(g^\ell :{\mathcal {T}}\times \varOmega \rightarrow {\mathbb {R}}\) via:
with \(n\in {\mathbb {N}}\), \(n\le N\), resp.
for \(0<t\le T\) and \(g^\ell (0)=0\). With \(\tau -\) in brackets, we denote as usual the càglàd version of the process. Note that all upcoming integrands are predictable. The stochastic integral (in continuous time) \(g^\ell (t)=\int _0^t I^\ell (\tau -)\frac{\mathrm{d}p(\tau )}{p(\tau -)}\) exists when the integrand \(\frac{I^\ell }{p}\) is locally bounded. Since p is assumed to be a positive semimartingale, i.e., esp. \(p(t)>0\ \forall t\in [0,T]\), by Itō’s formula it follows that \(t\mapsto \int _0^t\frac{1}{p(\tau -)}\mathrm{d}p(\tau )\) is again a semimartingale (in fact, \(p(t)>0\) for almost all \(t\in [0,T]\) would be enough). In this case, the existence of the stochastic integral \(g^\ell (t)=\int _0^t I^\ell (\tau -)\frac{\mathrm{d}p(\tau )}{p(\tau -)}\) follows from the fact that \(I^\ell \) is locally bounded. In turn, we will see that we choose \(I^\ell \) as \(I^\ell (t)=F(g^\ell (t))\) for some deterministic function F. Thus, we have to ask the question whether a solution of the stochastic differential equation \(\mathrm{d}g^\ell (t)=F(g^\ell (t-))\frac{\mathrm{d}p(t)}{p(t-)}\Leftrightarrow g^\ell (t)= g^\ell (0) + \int _0^t F(g^\ell (\tau -))\frac{\mathrm{d}p(\tau )}{p(\tau -)}\) for \(t\in [0,T]\) exists. Since p is a strictly positive semimartingale, i.e., \(p(t)>0\ \forall t\in [0,T]\), it follows by Itō’s formula that the process \(t\mapsto \int _0^t\frac{\mathrm{d}p(\tau )}{p(\tau -)}\) is a semimartingale. Hence, a solution of the mentioned stochastic differential equation for \(g^\ell \) exists if F is, for example, Lipschitz continuous (which is satisfied by the strategies constructed in this section) (see Protter 2005, V.3, p. 255f, Theorem 6). From this fact follows that the process \(t\mapsto I^\ell (t)=F(g^\ell (t))\) exists, too.
Note that in the discrete time case the index is shifted, i.e., for calculating \(g(t_n)\) the investment process \((I^\ell (t_i)_i\) is used up to time \(t_{n-1}\) and each \(I^\ell (t_i)\), \(i=0,1,\ldots ,n-1\), is \({\mathcal {F}}_{t_i}\)-measurable. The integral in the continuous time case is an Itō-Integral and, thus, the gain again is a (càdlàg) semimartingale.
As mentioned above, a feedback trader \(\ell \) (in this work) computes at time t the investment \(I^\ell (t)\) as a function of the trader’s own gain \(g^\ell (t)\) and—some would call this naive—of nothing else:
where F is a deterministic function (such that all integrals exist; such as a Lipschitz continuous function). Note that in general it is possible to allow for a function F that uses more information such as the whole gain process and the whole price process up to time t. However, for now, F using the gain at time t is enough—in Sect. 6 we use a more general feedback law. By construction, \((I(t_i))_{i=0,1,\ldots ,N}\) is adapted in discrete time, i.e., \((I(t_{i-1})_{i=1,2,\ldots ,N+1}\) is predictable. By definition of the càglàd version of a process (in continuous time), the integrand \(\frac{I^\ell (\tau -)}{p(\tau -)}\) is a predictable stochastic process. As discussed above, by Itō’s formula it follows that this integrand is locally bounded, too (see Protter 2005).
Now there is the question how to choose the function F. One possibility for F is the so-called linear long feedback trading rule:
where \(I^L(0)>0\) is the initial investment in the linear long rule and \(K^L>0\) is the so-called feedback parameter. That means, in this example F is chosen as affine-linear function \(F(x)=I^L(0)+K^Lx\) with positive coefficients.
In order to explain the general functioning of feedback trading, we explain the operating principle of the linear long rule from a practical point of view on the time scale \(\{0,1,2,3,\ldots \}\): At time \(t=0\), the trader invests \(I^L(0)\), i.e., the trader buys \(\frac{I^L(0)}{p(0)}\) units of stocks. At time \(t_1=1\), the trader knows the price p(1) and, thus, the gain \(g^L(1)=\frac{I^L(0)}{p(0)}\cdot (p(1)-p(0))\). This information is used by the trader to calculate the investment \(I^L(1)=I^L(0)+K^Lg^L(1)\), i.e., the trader buys or sells \(\frac{I^L(1)}{p(1)}-\frac{I^L(0)}{p(0)}\) units of stocks. At time \(t=2,3,\ldots \), the trader proceeds the same way. By doing so, the trader does neither have to estimate anything, nor does he or she have to know any future information, i.e., the strategy is non-anticipative. For the trader, there remains the question of how to choose \(I^L(0)\) and \(K^L\): for the analytical results in this work, the choice of \(I^L(0)\) does not matter in a qualitative sense. The choice of \(K^L\) is much more interesting.
In general, it is easy to see that the linear long feedback trader is a long trader in continuous time when the price process is continuous, too. This means that this trader type makes money when prices rise and loses money when prices fall. When \(K^L>1\), this strategy is a trend-following rule, i.e., the trader buys when prices rise and vice versa. Since the desired trading rule shall be robust against variations in price, the linear long rule has to be modified. For this, the linear short feedback rule is defined first:
with \(I^S(0),K^S<0\). That means, F is now chosen as the affine-linear function \(F(x)=I^S(0)+K^Sx\) with negative coefficients. When time and price are continuous, this trader is a short investor who loses money when prices rise and earns money when prices fall.
The simultaneously long short (SLS) rule is now simply defined as the superposition of the linear long and the linear short rule with the same modulus of the respective parameters, i.e., \(I^L(0)=-I^S(0)=:I_0^*>0\) and \(K^L=-K^S=:K>0\):
That means, the short side’s initial investment is \(-I^*_0\) and its feedback parameter is \(-K\). Note that the long side’s gain \(g^L\) and the short side’s gain \(g^S\) have to be calculated separately, i.e., the trader actually performs two feedback rules simultaneously. A flow diagram for the SLS rule is given in Fig. 1.
Flow diagram for the standard simultaneously long short controller with input (or disturbance) variable return on investment \(\frac{\varDelta p}{p}\) resp. \(\frac{\mathrm{d}p}{p}\) and output variable gain \(g^{SLS}\). The SLS traders’ parameters are the feedback parameter \(K>0\) and the initial-investment parameter \(I_0^*>0\)
As mentioned above, the linear long rule leads to a positive gain if prices go up and the linear short rule leads to a positive gain if prices go down (in the continuous case). When calling a strategy profitable if its expected gain is positive, the linear long rule would be profitable if the price’s trend is positive whereas the linear short rule would be profitable if the trend is negative. However, a trader using a model-free strategy should neither have to know nor to estimate the trend (or its sign). This is why the SLS rule is defined as the superposition of these two linear rules. Note again that the gains of the long and the short side have to be calculated separately. In period zero, the long side (in theory) buys assets with a value of \(I_0^*\) and the short side sells the same amount of assets, i.e., one could say that nothing happens. After that, in each period, both sides reinvest K or \(-K\) times the period gain, i.e., the trader possibly buys or sells assets (not only in theory). We note that \(I_0^*\) is not the initial investment of the SLS rule, it is the so-called initial-investment parameter. That means, the long side’s initial investment is \(I_0^*\) and the short side’s initial investment is \(-I_0^*\).
The intuition of this strategy is to systematically exploit compound effects because the profit from prices that rise, e.g., two times by 10%, is higher than the loss from prices that fall at the same rates. Note that the findings of this paper are not based on doubling-up strategies (cf. Karatzas et al. 1998) as for roulette—since the leverage (i.e., the ratio between assets and equity) of the SLS rule can be bounded (Primbs and Barmish 2012, 2017). The results of this work are also not based upon the St. Petersburg paradox.
3.2 Literature review on the performance of SLS trading rules
The following literature review will give an idea about why the SLS strategy is an interesting one. Barmish (2011) shows that for continuously differentiable, non-negative prices \(p\in {\mathcal {C}}^1\) with \(p(0)>0\) it holds
from which follows that \(g^{SLS}_{{\mathcal {C}}^1}(t)\ge 0\) for all price processes and \(g^{SLS}_{{\mathcal {C}}^1}(t)>0\) whenever \(p(t)\in (0,\infty )\setminus \{ p(0)\}\). In other words, this is an arbitrage strategy. The gain at time t is independent of the price process and only depends on the value of p(t) at time t. Since \({\mathcal {C}}^1\) prices are a rather hard assumption, Barmish and Primbs (2011, 2016) use a price process that is governed by a geometric Brownian motion (GBM)
with trend \(\mu \in {\mathbb {R}}\), volatility \(\sigma >0\), and a Wiener process, i.e., a Brownian motion, W(t). Note that the GBM is the price model used in the Black–Scholes model. Barmish and Primbs (2011, 2016) show that the SLS strategy is than not an arbitrage strategy anymore. However, for the expected gain it holds:
Since it holds true that
and
it follows especially that \({\mathbb {E}}\left[ g^{SLS}_{GBM}(t)\right] \ge 0\) and \({\mathbb {E}}\left[ g^{SLS}_{GBM}(t)\right] >0\) whenever \(\mu \ne 0\) holds. Similar results are provided by Dokuchaev and Savkin (1998a, 1998b, 2002, 2004) and Dokuchaev (2012).
When the SLS rule is analyzed using models with constant trends \(\mu \) (continuous time) resp. \(\mu _h\) (discrete time with mesh size \(h>0\)), one says that the strategy has the “robust positive expectation property” if its expected gain is (i) non-negative for all \(t\in {\mathcal {T}}\) and all parameter settings and (ii) positive for all \(t>0\) (continuous time) resp. \(t>h\) (discrete time) and for all parameter settings except for \(\mu =0\) resp. \(\mu _h=0\). In market setups with time-varying drift parameters \(\mu (t)\) resp. \(\mu _h(t)\), we say that the strategy has the robust positive expectation property if its expected gain is (i) non-negative for all \(t\in {\mathcal {T}}\) and all parameter settings and (ii) positive for T and for all parameter settings except for \(\int _0^T\mu (t)dt=0\) resp. \(\frac{1}{h}\sum _{i=1}^N\mu _h(t_i)=0\).
Primbs and Barmish (2012, 2017) show that the robust positive expectation property also holds when the trend \(\mu (t)\) as well as the volatility \(\sigma (t)\) of the GBM are time dependent. In fact, for a time-varying GBM (tvGBM) with trend \(\mu (t)\) and volatility \(\sigma (t)\) and the SLS trading rule, it holds:
Iwarere and Barmish (2014) analyze the SLS strategy when prices are governed by tree models, and Barmish and Primbs (2012) use a market model motivated by the Capital Asset Pricing Model (CAPM). Barmish (2008), Malekpour et al. (2013), and Malekpour and Barmish (2013) analyze strategies and topics related to the SLS rule, e.g., Barmish (2008) investigates a so-called saturation reset controller. Baumann (2015) and Baumann et al. (2019) mathematically analyze effects of linear long feedback strategies on market stability. O’Brien et al. (2020) analyze a generalized SLS controller with additional shape parameters in deterministic as well as GBM markets.
Baumann (2017) generalizes the results for SLS trading to prices governed by Merton’s jump diffusion model (MJDM), which is given through:
Hereby, the GBM is extended by i.i.d. jumps \((Y_i-1)>-1\) with jump intensity \(\lambda >0\), expected jump height \({\mathbb {E}}\left[ Y_i-1\right] =\kappa >0\), and a number \(N\sim {\mathcal {P}}oi(\lambda t)\) of jumps up to time t. Jumps are interesting in this context since they are known—in the fields of option pricing and hedging—for making markets incomplete (Merton 1976). Baumann (2017) shows that the expected gain of the SLS strategy is:
which is exactly the same as for the GBM. Baumann and Grüne (2019) further generalize this result to a set of price processes defined by stochastic differential equations called essentially linearly representable prices (see also Baumann 2021). Barmish and Primbs (2011) give a closed-form formula for the variance of the SLS trading rule when prices are governed by a GBM, and Baumann (2017) does this for MJDM prices as well.
Here, we mention again that the so-called linear long (short) trader is not necessarily long (short) when there are discontinuities—for example, when the price model allows for jumps, like MJDM, or when the model is in discrete time, as in the two papers discussed next. Malekpour and Barmish (2016) note an interesting and especially practical problem of the SLS rule. Price behaviors that happened a long time ago have the same impact on the SLS trading rule as if they happened a few days ago. Malekpour and Barmish (2016) introduce a new strategy called Initially Long-Short (ILS) with delay as the superposition of a linear long rule with delay \(I^{Ld}(t_n)=I_0^*+K\left( g^{Ld}(t_n)-g^{Ld}(t_{n-m})\right) \) and a linear short rule with delay \(I^{Sd}(t_n)=-I_0^*-K\left( g^{Sd}(t_n)-g^{Sd}(t_{n-m})\right) \). The strategy is defined and analyzed in a discrete time setting with a time grid \({\mathcal {T}}=\{0,1,2,\ldots \}\) with fixed time steps, e.g., days. Among other market requirements, similar to that presumed in the work at hand, the main assumption by Malekpour and Barmish (2016) is \(-1<{\mathbb {E}}\left[ \frac{p(t)-p(t-1)}{p(t-1)}\right] =\mu \ne 0\), i.e., that the expected return on investment is nonzero and constant, which is used to show that the robust positive expectation property still holds. In the ILS strategy, only the period gains of the last m days are taken into account. On the one hand, the idea of not taking into account a too-old gain is an advantage of the ILS rule. On the other hand, the hard delay definition seems to be a little bit problematic. Imagine a price history where \(m-1\) days ago an important event happened at the market. Today, this event will be taken fully into account—tomorrow, this will not be the case. This means that the strategy will change substantially only because an important event happened exactly \(m-1\) days ago, where the number m was an idiosyncratic choice of the trader. Another point to think about is that the trader is assumed to be a price-taker. However, the trader decides to trade, e.g., daily, and the expected return on investment on a daily basis is assumed to equal \(\mu \). That means the trader indirectly influences the expected return on investment by choosing a trading frequency, which at first glance seems to contradict the price-taker property. However, this is not a problem, as shown in the paper reviewed next. We will come back to the idea of not taking into account too-old information in Sect. 6.
Also Baumann and Grüne (2017) start by using a discrete time setting, but with adjustable time steps \(h>0\): \({\mathcal {T}}=\{t_i=ih\ |\ i=0,1,2,\ldots \}\). Here, it is assumed that
which is the expected return on investment (eroi). For the standard SLS strategy, the expected gain is
which is positive whenever \(\mu _h\ne 0\) and \(t>h\). Even in this setting, the conjectural contradiction to the price-taker property is given: on the one hand, the trader chooses the trading frequency h, on the other hand, the expected return on investment \(\mu _h\) has to be independent of the trader. To solve this, a (maybe more realistic) setting with an underlying continuous time price process but discrete time trades is introduced. Engineers call this a sampled-data system. The continuous time price process has to satisfy
for all \(t>s\ge 0\). This \(\mu \) is now independent of the trader’s decision on the trading time and with
the above theory is applicable. Finally, it is shown that when calculating the limits for \(h\rightarrow 0\), the results are fully in line with the known results for the GBM and MJDM. In sum, without assuming any fixed market model but only some core properties, like a nonzero expected return on investment and independent multiplicative growth of the price process, that paper shows that the SLS rule satisfies the robust positive expectation property, i.e., it yields a positive expected gain.
3.3 Further related literature
At this point, we would like to mention that there are other related theories. Of course, the seminal theory of universal portfolios of Cover (1991) should be cited here (see also Cover and Ordentlich 1996). It answers the question how to optimally allocate the resources in a multi-asset market model by means of a predictable strategy. As a benchmark, the authors use a—in some sense—best retrospectively chosen portfolio. Clearly, the best imaginable way would be to invest all resources in the asset with the highest return. However, for implementing this strategy, a trader would have to be able to look into the future. Thus, one might call this strategy “unrealistic.” Hence, as the benchmark strategy the authors choose the retrospectively best constantly rebalanced portfolio. They construct a predictable strategy approximating (for time to infinity) the benchmark’s performance. According to Cover (1991), the underlying explanation for this theory is that the growth rate of the average of exponentials is, under some conditions, approximately the same as the growth rate of the maximum.
Both the work at hand and the theory of universal portfolios are dealing with investment decisions while trying to be as model free as possible, hence, Cover (1991) allows for arbitrary price paths. However, there are some differences. Universal portfolios deal with resource allocation (in a multi-asset market), i.e., they do not allow for short selling. Consequently, the leverage is bounded to one (a trader cannot invest more than he or she has). In contrast, one basic principle of simultaneously long short trading is that a trader is allowed to do short selling. In the standard SLS literature and, thus, in this work the question is (in a single asset market) how much a trader should borrow from the bank and invest—or how much he or she should go short and put in the bank. Hence, the leverage is not bounded to one. Note that in the resource allocation setting of Cover (1991) there is an absolutely best strategy, which would require the trader to be able to look into the future, i.e., the strategy “invest all resources in the asset with the highest return” is non-predictable (resp. anticipating) and, thus, cannot be implemented. In the feedback trading setting, there is no best strategy even if a trader would be able to look into the future. (It would be: “invest an infinite amount of money if the asset goes up and disinvest an infinite amount of money if the asset goes down.”) Thus, we see that the market settings are different.
Another strand of related literature is that of stochastic portfolio theory and—as a part of this—functionally generated portfolios. These theories were established by Fernholz (1999a, 1999b) more than 20 years ago. The stochastic portfolio theory can be seen as a successor of the so-called classical portfolio theory of Markowitz (1952) (cf. Fernholz and Shay 1982). Overviews are provided by Fernholz (2002) and Fernholz and Karatzas (2009). It is descriptive—and not normative. One of its targets is to explain phenomena that can be observed on real equity markets. Thus, the stochastic portfolio theory rather differs from theories like the modern portfolio theory/dynamic asset pricing or the CAPM. In general, the stochastic portfolio theory deals with resource allocation problems (as the universal portfolios of Cover (1991) do). However, it offers insights to problems concerning arbitrage as well as market behavior and under rather general assumptions it allows to construct portfolios/trading rules with some controlled behavior. It can be used to analyze and optimize investment strategies and—as elaborated by Fernholz (1999b, 2001, 2002)—it allows to construct trading rules that outperform the so-called market portfolio by observable quantities, i.e., no intrinsic parameters have to be known. This property is also a feature of feedback-based trading strategies. Under technical conditions as integrability, (local / semi-) martingale assumptions, predictability, etc. the stochastic portfolio theory deals with topics as relative arbitrage, excess growth rates, and discount factors.
Often in stochastic portfolio theory, the capitalization (in our setting: the price) X is modeled via stochastic differential equations and Brownian motions (i.e., Wiener processes) resulting in Itō processes. However, there is also work dealing with continuous or even general semimartingales (Karatzas and Ruf 2017; Kardaras 2003; Karatzas and Kardaras 2007). Since the stochastic portfolio theory deals with resource allocations, there is more than one asset. Here, we denote the different assets with subscript i, e.g., asset i’s price \(X_i\). Usually, in the stochastic portfolio theory trading rules are given as fractions \(\pi _i\), \(i=1,2,\ldots ,n\), of the wealth \(Z_\pi \) of the trader (using strategy \(\pi \)). The wealth in time t is the initial wealth plus the gain, i.e., \(Z_\pi (t)=Z_\pi (0)+g_\pi (t)\) where \(g_\pi (t)\) is the sum of the gains resulting from trading assets \(i=1,2,\ldots ,n\). That means, the gain of a trading strategy in the stochastic portfolio theory is given by
i.e.,
Note that in stochastic portfolio theory \(\pi (t)\) is often functionally generated (see Fernholz 2002; Karatzas and Ruf 2017; Fernholz and Karatzas 2009) where—as explained by Fernholz and Karatzas (2009, Chapter III)—\(\pi (t)\) is a specific function of the market portfolio/the relative market weights \(\mu (t)=(\mu _1(t),\ldots ,\mu _n(t))=\left( \frac{X_1(t)}{\sum _{j=1}^nX_n(t)},\ldots ,\frac{X_n(t)}{\sum _{j=1}^nX_n(t)}\right) \), of a function depending on the “market price of risk,” and of a given function that fulfills some conditions. Note that portfolios and trading strategies might be adjusted for the “defect of self-financibility” and the “defect of balance” and that the function determining \(\pi \) might be “additive” or “multiplicative” (for all of these points, see Karatzas and Ruf 2017) and subject to investment or short-selling constraints (Fernholz and Karatzas 2009).
Rewriting the gain equation for a one asset market and using the formula for the traders’ wealth leads to
where X, g, \(\pi \) are one-dimensional processes with \(g_\pi (0)=0\). Put differently, it holds for the investment \(I_\pi (t)=Z_\pi (t)\pi (t)\) that
When we compare this with the linear long trader
it turns out that with \(I^*_0=Z_\pi (0)\pi (0)\) and \(K=\pi (t)\ const.\) the structure of these formulae is similar. However, whether \(\pi (t)=K\) can be chosen as constant in stochastic portfolio theory depends on self-financing constraints (cf. Duffie 2010)—which is not a problem when allowing, as we do, for investments in a bank account. Note that only for \(K=1\) the linear long rule is self-financing.
Additionally, while the linear long rule—and also the linear short rule—can be written in the form the stochastic portfolio theory uses, this is not true for the SLS rule because the SLS rule is a combination of two independent strategies. For the investment of the SLS strategy, it holds:
That means, the SLS strategy cannot be rewritten in such a way that it fits to the setting of the stochastic portfolio theory, which can also be seen easily when observing that the initial wealth of the SLS strategy is zero. This would lead to zero investments and in turn to zero gains and zero wealth for all points in time in the stochastic portfolio theory setting. Furthermore, other control-based trading strategies like the one defined and analyzed in Sect. 6 or those developed by Malekpour et al. (2013, 2018) do not fit to the stochastic portfolio theory framework, too.
Further notable work on stochastic portfolio theory and related topics is conducted by Fernholz and Karatzas (2005), Fernholz et al. (2003, 2005), and Banner et al. (2005). Pal and Wong (2016) relate functionally generated strategies to a discrete-time optimal transport problem, Schied et al. (2018) analyze path-dependent problems, and Karatzas and Ruf (2017) relate the stochastic portfolio theory to Lyapunov functions for semimartingales. Since there are very interesting results in the literature resulting from connections of universal portfolios and stochastic portfolio theory (see Cuchiero et al. 2019; Pal and Wong 2016; Wong 2015), we conjecture that the combination of universal portfolios and the stochastic portfolio theory (including Lyapunov functions) with feedback trading ideas will lead to very fruitful results when extending SLS strategies to multi-asset markets. This topic is very interesting for future work, esp., since all these theories deal with functionally generated portfolios.
3.4 Market requirements
As stated in Sect. 3.1 we consider a market with one risky asset and a risk-free bond. Note that there is work dealing with control-based trading rules in market settings with more than one asset (e.g., Deshpande and Barmish 2018). Since this work relies on a constant trend assumption, it is highly interesting for future work to analyze SLS rules for more than one risky asset with time-varying parameters. Also, the work of Cover (1991), Cover and Ordentlich (1996), Fernholz (2002), and Karatzas and Ruf (2017) investigates functionally generated portfolios in markets with more than one asset. Cover (1991) and Cover and Ordentlich (1996) analyze so-called universal (long-only) portfolios. A connection of the theories from Cover (1991), Fernholz (2002) and the work at hand will be very fruitful for future work (see also Sect. 3.3).
For the work at hand, we assume
-
a risk-free bond with
-
one interest rate for debit and credit, and
-
that the interest rate equals zero, that means that a zero coupon bond is available.
Risk-free zero-rate assets may be available on the market, cf. Treasury Bills. When this is not the case, the existence of a zero-rate risk-free bond is easily achievable: When there is any bond, we can use this bond as numéraire. That means all stock returns are somehow relative to this bond. The assumption that the interest rate is the same for debit and credit is a harder assumption than the existence of a risk-free bond, but it is actually not too hard for big traders. Note that the expected returns of all risk-neutral assets are zero. However, we assume the existence of a
-
non-risk-neutral asset
with
-
independent multiplicative growth.
Independent multiplicative growth means that there are absolutely no predictable patterns in the market. This is important since one of the aims of this work is to show that predictable patterns are not necessary to contradict the efficient market hypothesis.
The assumption of stochastically independent multiplicative growth rates is crucial for the analysis in the work at hand. It fits to the weak version of the efficient market hypothesis, however, this assumption might be debatable when SLS trading rules should be applied to real-world market data.
The results obtained in this work (and in the related literature) only hold when the asset’s trend is nonzero. Since the zero-trend case is always an exception in the results of this work (and the related work), it is important that there is an asset with a trend unequal to zero, which does not mean that the autocorrelation of the time series of returns is necessarily unequal to zero. This assumption is justifiable because we could assume that a stock market (with many risky assets) as a whole is risk-neutral (on average), but not so each single stock—and we can just pick one non-risk-neutral asset for our analysis. Additionally, it is reasonable in the sense of efficient markets that a volatile and, thus, more risky asset expects higher returns, i.e., they are positive relative to the numéraire. However, we do not need a stock with a higher expected return (compared to the bond/numéraire), only one with expected returns unequal to zero compared to the numéraire at least for short time intervals.
Next, we state some additional market requirements that are similar to those in the related SLS literature. As can be seen, the short side’s strategy requires for sure a possibility for
-
short selling, i.e., a negative investment.
Besides this market requirement, a few more assumptions are needed in the analytic parts of the work at hand:
-
costless trading, i.e., no additional costs related to buying or selling assets,
-
adequate resources, i.e., no financial constraints that could prohibit any desired transaction,
-
perfect liquidity, i.e., no bid-ask spread and no waiting time, and
-
the so-called price-taker property, i.e., no impact of the investment decisions on the price process.
We briefly justify these market requirements: short-selling and perfect liquidity should not be strong assumptions for large companies’ stocks under trade. Costless trading, in the past a strong argument of the defenders of the efficient market hypothesis to show that chartist strategies cannot work in practice (cf. Fama 1991), might be less controversial in times of flat-rate stock trading offers or when only trading over the counter. The adequate resources assumption is justified when the trader is big and rich enough, e.g., a mutual fund, and is not trading too much of the single asset under trade. The latter argument also justifies the price-taker property. With “rich” we mean that the trader has high capital, low funding constraints, and low funding costs, i.e., the trader can borrow as much as he or she wants at low interest rates resp. costs.
The key assumption is high liquidity: When trading a highly liquid stock in small amounts, it can be done over the counter. In this case, the price path is always the middle of the bid and ask prices, which allows us to assume no bid-ask spread. In the case of trading over the counter, the trader is really a price-taker and the trading costs are negligible.
In sum, for a trader with high capital and low funding costs/constraints who trades small amounts of an asset of a big underlying firm, the assumptions above can be accepted. Rich does not mean that the trader has an infinite amount of capital all the time, like it is assumed when referring to doubling-up strategies. There are papers analyzing the leverage of the SLS rule, i.e., how many times the account value a trader needs to invest. Primbs and Barmish (2012, 2017) show that this leverage can be bounded. Additionally, it is easy to see that in a discrete time model with a given time horizon (\(T<\infty \)) and bounded stock returns—like in a binomial tree model (Cox–Ross–Rubinstein; CRR)—the maximal investment is bounded, too.
Note that the market requirements stated in this section concern the analytic parts of the work at hand. In Sect. 5, we provide a backtesting study on past market data, including bid-ask spreads (i.e., imperfect liquidity), transaction costs, and interest rates. Thus, the results in Sect. 5 are empirical, not theoretical. Note that the authors of the papers discussed in Sect. 3.2 assume more or less the same market requirements as we do here.
3.5 Illustrative example
Before going to the analytic part of this work, we present a small illustrative example of how SLS trading works in a non-recombinable binomial tree with time-varying parameters on the time grid \({\mathcal {T}}=\{0,1,2\}\) (i.e., two periods). Note that for the analytical findings in Sect. 4, no values of the parameters have to be known (or estimated), though for calculating this example, parameters were chosen. The parameters, i.e., the prices and the conditional probabilities for the dynamics of the price process, can be found in Fig. 2. We compute a trend of \(\mu _1(1)=5\%\) in period one and of \(\mu _1(2)=6\%\) in period two (see Sect. 4.1). Together with the trading parameters \(I_0^*=100\) and \(K=2\), this leads to the investments and gains depicted in Fig. 2. The variable B denotes the bond, i.e., the bank account. A positive B tells how much capital the trader puts in the bank and a negative B how much capital the trader has to borrow from the bank. The expected gain is \({\mathbb {E}}\left[ g(2)\right] =0.4\cdot 8+0.1\cdot (-8)+0.4\cdot (-4)+0.1\cdot 4=1.2>0\).
In the next section, we show that the expected gain was also positive when both \(\mu _1(1)\) and \(\mu _1(2)\) were negative. The example above gives an idea how SLS trading works. When prices go up (down) several times in a row, the trader profits from compound effects of the long (short) side, ones that exceed the losses on the other side (in expectation). Another point learned by this example is that the trader does not need an infinite amount of capital: here it is bounded by 112. Even when we would add transaction costs of, e.g., 0.5 per trade, the expected gain would still be \(0.2>0\), which shows that the classical transaction costs argument of the defenders of the efficient market hypothesis is not that strong in terms of SLS trading. We will come back to the problem of transaction costs and of bid-ask spreads in Sect. 5.
4 Analysis of the simultaneously long short strategy with time-varying trends and volatilities
The main feature of control-based trading strategies is that, although market parameters like the expected return on investment are used when analyzing the strategies, the trader neither needs to know nor to estimate them. Properties of the strategies hold for almost all settings of the parameter values. The following analysis generalizes the work of Baumann and Grüne (2017) but takes into account the ideas of Primbs and Barmish (2012, 2017) who consider time-varying trends and volatilities.
Our goal is to show whether the “robust positive expectation property” as defined in Sect. 3.2 still holds in the general setting outlined in Sect. 3.1. If we can show that in continuous time for every strictly positive \({\mathbb {F}}\)-adapted semimartingale the expected trading gain of the SLS rule is non-negative for all possible (and unobservable) drifts and positive for all possible (and unobservable) drifts whenever \(\int _0^T\mu (t)\mathrm{d}t\ne 0\), it follows that the robust positive expectation property still holds (in continuous time).
After having discussed market efficiency in Sect. 2 as well as control-based and functionally generated trading strategies, especially SLS trading, in Sect. 3 we now present the analysis of the SLS rule in a general time-varying setting. This analysis is based on refinements of the trading times’ underlying time grids. In detail, we start with a stochastic price process \(p:[0,T]\times \varOmega \rightarrow {\mathbb {R}}^+\) in continuous time (with \(p(0)\in {\mathbb {R}}^+\)) that has to be a (càdlàg) semimartingale (see Sect. 3.1) and that fulfills
for all \(t>s\ge 0\) and a deterministic, Riemann integrable function \(\mu \). Especially, it holds: \(\ln \left( {\mathbb {E}}\left[ p(t)\right] \right) =\ln (p(0))+\int _0^{t}\mu (\tau )\mathrm{d}\tau \). This time-varying trend is one of the basic novelties of this work, different from the work of Baumann and Grüne (2017). Additionally and similar to Baumann and Grüne (2017), we assume that for all \(k\in {\mathbb {N}}\) and all \((s_j)_{j=0,1,\ldots ,k}\subset {\mathcal {T}}=[0,T]\) with \(0\le s_0<s_1<\ldots <s_k\le T\)
are stochastically independent. That means, the log-price has independent increments, as, e.g., Lévy processes have. We note that this assumption of stochastically independent multiplicative growth rates cannot be relaxed in the subsequent analysis and—although fitting to the weak version of the efficient market hypothesis—might seem to be rather strong when SLS trading should be applied to real-world market data. However, models used in the related literature (like the GBM or MJDM) fulfill this assumption.
Next, we draw a discrete time process \((p(t_i))_{i=0,1,2,\ldots ,N=\frac{T}{h}}\) on the equidistant time grid \(\left\{ t_i=ih\ |\ i=0,\ldots ,N=\frac{T}{h}\right\} \) with mesh size \(h>0\). Starting with the analysis of the SLS trading rule on these discrete time price processes, we will end with continuous time trading. We emphasize that the price process allows for time-varying parameters and in Sect. 4.2 the analysis takes risk-adjusted returns into account.
4.1 The robust positive expectation property
Using sampled prices as described above, we define
For the reason of non-negative prices, \(\mu _h(t)>-\frac{1}{h}\) has to hold for all \(t>0\) and \(h>0\). We note that \({\mathbb {E}}\left[ \frac{p(t_n)}{p(t_{n-1})}\right] =h\mu _h(t)+1\).
It follows that the discrete-time stochastic price process \((p(t_i))_{i=0,1,\ldots ,N}>0\) with \(p(0)\in {\mathbb {R}}^+\) fulfills the independent multiplicative growth assumption, i.e., for all \(k\in {\mathbb {N}}\) and all \(j_0<j_1<\ldots <j_k\in \{0,1,\ldots ,N\}\) (with \(t_{j_i}\in {\mathcal {T}}= \{t_i=ih\ |\ i=0,\ldots ,N\}\)) it holds that
are stochastically independent. In other words, the returns of investment must be independent. Again we note that this is the weak form of the market efficiency hypothesis. This stochastic independence also holds when applying any measurable function on the growth rates.
By the procedure done above, i.e., by starting with a continuous time process and a trend function \(\mu \) and then sampling a discrete time process, the seeming contradiction to the price-taker property is avoided. While the trader implicitly influences the trend \(\mu _h(t)\) by the choice of h, this is not true for \(\mu (t)\). Later, we calculate the limits for \(h\rightarrow 0\) for this sampled-data system and observe that the discrete time trend converges to the continuous time trend (cf. Baumann and Grüne 2017).
The robust positive expectation property does not in general hold anymore (a counter example is given later in this section). However, at least in two special cases, the robust positive expectation property is still valid. First, we note that for the expected price it holds
and
with \(0\le k<n\le N\in {\mathbb {N}}\).
We start the analysis of the SLS strategy with its long side and set \(K^L=K\) and \(I^L(0)=I^*_0\). The long side begins with investing \(I_0^*\) and adds K times the period gain in each period, i.e., (in theory) it buys as many units of the asset at the current price so that the formula \(I^L(t)=I_0^*+Kg^L(t)\) holds. By the definition of \(I^L(t_n)=I_0^*+Kg^L(t_n)\) and \(g^L(t_n)=\sum _{i=1}^n I^L(t_{i-1})\cdot \frac{p(t_i)-p(t_{i-1})}{p(t_{i-1})}\), it follows
and so
It holds
Again by the definition of \(I^L(t_n)\), it follows
and, hence,
By substituting \(I^L(0)=I_0^*\mapsto -I_0^*=I^S(0)\) and \(K^L=K\mapsto -K=K^S\), we derive the formula for the short side’s expected gain
Next, we investigate whether \({\mathbb {E}}\left[ g_t^{SLS}\right] ={\mathbb {E}}\left[ g_t^{L}+g_t^{S}\right] \) is positive or not. Unfortunately, \({\mathbb {E}}\left[ g_t^{L}+g_t^{S}\right] >0\) is not true for all t and all \(\left( \mu _h(t)\right) _t\). This can be seen by rewriting
Note that in case of a constant trend, this formula can be simplified by use of binomial coefficients as done by Baumann and Grüne (2017).
When assuming a time-varying trend in discrete time, it is easy to find an example where this sum is negative: when setting \(n=2\), i.e., \({\mathcal {T}}=\{0,h,2h\}\), with \(\mu _h(h)>0\) and \(\mu _h(2h)<0\), which is a time-varying trend, it holds that \({\mathbb {E}}\left[ g^{SLS}(2h)\right] =2KI_0^*h^2\mu _h(h)\mu _h(2h)<0\).
However, there are (at least) two special cases where \({\mathbb {E}}\left[ g^{SLS}(t)\right] \ge 0\ \forall t\in {\mathcal {T}}\) and \({\mathbb {E}}\left[ g^{SLS}(T)\right] >0\) hold. (i) When \(n>1\), \(\mu _h(t)\ge 0\) for all t and \(\mu _h(t)>0\) for at least two points in time t or when \(\mu _h(t)\le 0\) for all t and \(\mu _h(t)<0\) for at least two points in time t (since \(|\alpha |\) is even). That means, whenever \(\left( \mu _h(t_i)\right) _{i\in \{1,\ldots ,N\}}\) is non-negative (non-positive), \({\mathbb {E}}\left[ g^{SLS}(t)\right] \) is non-negative and when additionally there exists \(\nu \subset \{1,\ldots ,N\}\) with \(|\nu |\ge 2\) such that \(\left( \mu _h(t_j)\right) _{j\in \nu }\) is positive (negative), it holds that \({\mathbb {E}}\left[ g^{SLS}(T)\right] \) is positive. The settings of Baumann and Grüne (2017) and Malekpour and Barmish (2016), i.e., \(\mu _h\) resp. \(\mu \) const. and nonzero, are special cases of case (i).
(ii) When letting \(h\rightarrow 0\) (i.e., \(n=\frac{t}{h}\rightarrow \infty \)), one can use the continuously compounded interest rate formula, which is a Vito-Volterra-style product integral, to see
which is positive whenever \({\bar{\mu }}(t):=\int _0^t\mu (s)\mathrm{d}s\ne 0\). That means, in the continuous time case, we proved that the robust positive expectation property still holds. Compare Fig. 3 for a graph of the expected SLS trading gains as functions of \({\bar{\mu }}(t)\) for varying K and Fig. 4 for a contour plot of the expected SLS trading gains as a function of \(K>0\) and \({\bar{\mu }}(t)\). Note that \(\exp (x)+\exp (-x)-2\ge 0\ \forall x\) and equals zero if and only if \(x=0\). The setting of Primbs and Barmish (2012, 2017) is a special case of case (ii), and all the results using GBMs or MJDM are special cases of both case (i) (just on another time scale) and (ii). Note that by construction of the discrete time gain and investment processes with shifted index (see Sect. 3.1) the limit case for \(h\rightarrow 0\) fits to the continuous time setup established in Sect. 3.
During every time interval with positive expected returns or negative expected returns, a trader using the SLS rule can expect positive gains. Only when the expected return \(\mu \) switches from positive to negative or vice versa the trader can expect a loss. When increasing the trading frequency to continuous time trading—which is nearly a realistic assumption in times of high-frequency trading—and assuming that \(\mu (t)\) is Riemann integrable, the measure of points in time when \(\mu \) is switching its sign, goes to zero.
Mostly, in market efficiency literature, it is assumed that the price process is a random walk around its fundamental value. When allowing the fundamental value to be non-constant, and assuming it to be not too wild, i.e., \(\mu (t)\) has to be Riemann integrable, i.e., \({\bar{\mu }}(t)=\int _0^t\mu (s)\mathrm{d}s\ne 0\) exists, the SLS trader can—when trading fast enough—expect a positive gain for all t. This property of the SLS rule seems to be in contrast to the efficient market hypothesis. Malkiel (1973) suggests the comparison of a trading strategy to a randomly selected buy-and-hold portfolio for showing whether or not the strategy has excess returns. When assuming that the market has on average the same trend as the bond—(i.e., a risk-neutral market), which we assumed without loss of generality to be zero—all randomly selected buy-and-hold portfolios have an expected gain of zero, too. This means that the SLS rule is strictly better than randomly selected buy-and-hold portfolios. It is possible to compare the expected SLS gain stock-by-stock with the corresponding expected buy-and-hold gain. However, as explained, this is not a solution to the puzzle. When we randomly select some portfolio and use the SLS strategy independently on all stocks in that portfolio, we expect a positive gain. When we use the buy-and-hold strategy on each stock in that portfolio we do expect zero gain. It is clear that a buy-and-hold strategy has a positive expected gain when \({\bar{\mu }}(t)>0\) and a negative one when \({\bar{\mu }}(t)<0\). It turns out that for some special parameter settings, the buy-and-hold rule is dominant to the SLS rule. However, the expected SLS trading gain is positive for almost all parameters—the expected buy-and-hold gain is not. That means a buy-and-hold trader must know or estimate the average trend. An SLS trader has a positive expected gain without any estimation.
4.2 Risk-adjusted expected return
For sure, there are some points to think about concerning the results in Sect. 4.1. The assumption that there are short time trends in expected returns (that can be caused by changes in fundamentals) is reasonable. The argument that the trader in practice has to achieve a positive gain on average when there are trading costs, in times of over-the-counter and flat-rate trading offers, is not really a solution to the puzzle, and trading costs in a highly liquid market can be assumed to be bounded. (In Sect. 5, when performing a backtesting study on past price data, and when bid-ask spreads and trading costs are taken into account, it turns out that, nevertheless, on average, positive gains can be observed.) The same is true for the continuous trading assumption when considering high-frequency trading. However, there is one argument against the SLS rule we have to think about: the risk adjustment.
Classically, the risk argument is given by the defenders of the market efficiency hypothesis when someone finds an external variable that allows for estimating higher expected returns of an asset. Then, it is said that this external variable is just a better proxy for measuring risk, so one concludes that the asset under investigation is more risky, which allows the asset to be more profitable (on average) without being a counterexample to market efficiency. In the setting of this paper, this is not applicable since there is only one asset under analysis, and there are no external variables. Here, only different trading strategies are considered. The only way to apply the risk adjustment argument to the SLS rule is to use volatility, which we will do next. Thus, we use one common choice, which is also known as Sharpe ratio.
For calculating the standard deviation of the SLS strategy, an assumption on the volatility of the underlying price process is needed. Analogous to the definition of the trend, it is set:
Here, it follows that:
From our assumption that the price process has independent multiplicative growth rates, it follows that
are stochastically independent for all \(k\in {\mathbb {N}}\) and all \(j_0<j_1<\ldots <j_k\in \{0,1,\ldots ,N\}\) (with \(t_{j_i}\in {\mathcal {T}}=\{t_i=ih\ |\ i=0,1,\ldots ,N\}\)) since \((\cdot )^2\) is a continuous and, hence, measurable function. Note that again there is a market parameter, namely \(\sigma ^2_h(t)\), seemingly set by the trader via h (in discrete time). However, the same argument as for \(\mu _h(t)\) holds, see Sect. 3.2 (and cf. Baumann and Grüne 2017).
With these assumptions, it follows that
and
with \(0\le k < n\le N \in {\mathbb {N}}\). Again, we start the analysis of the SLS strategy with its long side with (\(K^L=K\) and \(I^L(0)=I^*_0\)). Using the definitions of \(I^L(t)\) and \(g^L(t)\) leads to
and so
It holds
Again by the definition of \(I^L(t_n)\), it follows
Once more, by substituting \(I^L(0)=I_0^*\mapsto -I_0^*=I^S(0)\) and \(K^L=K\mapsto -K=K^S\), the formula for \({\mathbb {E}}\left[ (g^S(t))^2\right] \) is
For calculating the standard deviation of the SLS strategy’s gain, the mixed expectation of the long and the short side \({\mathbb {E}}\left[ g^L(t)g^S(t)\right] \) is needed, too. It holds:
and
Thus, we calculate:
With that, it follows:
Now, by the definitions of \(I^L(t_n)\) and \(I^S(t_n)\), it follows
Now, all components needed for the calculation of
and
are known. To keep the computation simple, we calculate the limit for continuous time trading \(h\rightarrow 0\) and define \(\overline{\sigma ^2}(t):=\int _0^t\sigma ^2(s)ds\) (of course, \(\sigma ^2(t)\) has to be Riemann integrable as well). By use of the Vito-Volterra-style product integral, it follows:
Combining the results for \({\mathbb {E}}\left[ g^{SLS}(t)\right] =\frac{I_0^*}{K}(\exp (K{\bar{\mu }}(t)) +\exp (-K{\bar{\mu }}(t))-2)\) and \({\mathbb {E}}\left[ (g^{SLS}(t))^2\right] \) leads to the formula for the SLS rule’s variance:
This expression fits exactly the results obtained by Baumann (2017) for MJDM and the GBM.
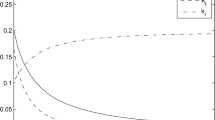
For any strategy \(\ell \), let \(rar(\ell ,t)=\frac{{\mathbb {E}}\left[ g^\ell (t)\right] }{\sqrt{Var\left( g^\ell (t)\right) }}\) be the risk-adjusted return of this strategy at time t. It is clear that rar(SLS, t) \(>0\ \forall t>0, {\bar{\mu }}(t)\ne 0\). Since we assumed a risk-free bond with zero interest rate, the risk-adjusted returns equal the so-called Sharpe ratios. We note that both the expected SLS trading gain \({\mathbb {E}}[g^{SLS}(t)]\) and the SLS strategy’s standard deviation \(\sqrt{Var\left( g^{SLS}(t)\right) }\) scale linearly in \(I^*_0\). Especially, its risk-adjusted return rar(SLS, t) is independent of \(I^*_0\). Interestingly, from the perspective of risk-adjusted returns, small values of K seem to be preferable, while large K are favorite without risk-adjustment (see Figs. 3 and 5).
Risk-adjusted return of different simultaneously long short strategies with feedback parameters \(K=\frac{1}{16},\frac{1}{8},\frac{1}{4},\frac{1}{2},1,2,4\) (from top to bottom). All returns are adjusted with the respective standard deviation. The average trend is \({\bar{\mu }}(t)\in (-1,5]\) and the average volatility is \(\overline{\sigma ^2}=1\%\). The risk-adjusted returns are independent of the parameter \(I_0^*\)
Now, the question is whether the risk-adjustment and (at the same time) the comparison to the buy-and-hold rule is the solution to the robust positive expectation property of the SLS rule in an efficient market. However, it is not. When a market as a whole (i.e., on average) is risk-neutral but not in terms of every single stock, a trader investing in a randomly selected portfolio (and this is what Malkiel (1973) suggests) can expect zero gain, therefore the risk-adjusted return is zero, too. When the trader uses the SLS rule stock-by-stock, and there is at least one single stock that is not risk-neutral (and it does not matter whether the stock’s expected return is too high or too low), the expected trading gain as well as the risk-adjusted return are positive. Indeed, it is reasonable that there are more or less volatile stocks that should have higher or lower trends, respectively.
5 Backtesting with trading fees and bid-ask spreads
In Sect. 4, we proved mathematically that the SLS strategy has positive expected returns under specific assumptions. We also discussed some of these assumptions (cf. Sect. 3.4) and investigated risk adjustments (Sect. 4.2). That means, we already presented the theoretical puzzle of market efficiency and SLS trading. This section has two targets: First, we present backtest studies of the SLS rule on real past market data. Second, in the simulations we allow for bid-ask spreads, trading costs, and different interest rates for debit and credit. This way, it might be justified to call our assumptions relatively weak.
Another point important for practice is that it may be reasonable that the trend is usually in the range of \(-5\) to 5%. It can be shown that for some positive average trends together with some \(K>1\), the expected gain of buy-and-hold rules is slightly higher than those of the SLS rules. However, for negative trends, the SLS strategies are clearly dominant to the buy-and-hold rule. This backtest study investigates which of these effects is on average more relevant in practice.
Note that we test the SLS rule stock-by-stock, i.e., individually on each stock, for 60 real-world charts. By averaging over these 60 experiments we approximate the expected trading gain. In other words, we do not use any information about the relation of these 60 charts. Note that there are trading rules constructed for more than one asset that shift money between these assets (see Cover 1991; Fernholz 2002; Deshpande and Barmish 2018). These rules might exploit some structure to improve the trading performance. However, the aim of this backtesting study is to approximate the expected SLS trading gain under real-world circumstances. We use the SLS rule stock-by-stock to get 60 paths of the SLS rule’s gain/loss function. Thus, we have a meaningful sample size to approximate the expected trading gain via Monte Carlo.
5.1 Backtesting trading dynamics—evidence from the German stock exchange
Before simulating SLS trading for different parameters on 60 stock charts (in detail: the stock charts from the years 2016 and 2017 from those firms listed in the German stock index DAX in June 2018), we have to modify the strategy in a few ways to make it applicable to real-world data. Bid and ask prices have to be used, the number of stocks held is discrete (exemplarily, we define it as an integer), trading fees lower trading gains, and a bank account with interest rates is added. That means, in detail, we define stock-by-stock on the discrete time grid \({\mathcal {T}}=\{0,1,\ldots ,T\}\) (with \(T=255\) for 2016, and \(T=252\) for 2017) with \(p^a\) being the ask price and \(p^b\) being the bid price:
-
the price \(p(t)=\frac{p^a(t)+p^b(t)}{2}\)
-
the bid-ask spread \(\zeta (t)=p^a(t)-p^b(t)\)
Now, the SLS controller internally uses the known rules (with round-operators \(\rho \) mapping real numbers to the nearest integer) but transmits to the broker only the total number of stocks to be held. That means, when, for example, the long side sends a buy signal and the short side a sell signal, only the difference is transmitted to the broker. When there is a buy or sell signal transmitted to the broker, the side causing the signal has to pay the trading costs. For example: One side gives a buy signal of 5 stocks and the other side a sell signal of 3 stocks, 2 stocks are bought and the side giving the signal 5 has to pay the fees. When both sides give signals in the same direction, each side has to pay for its own transaction proportionately.
We calculate the target investments
and
which leads in theory to a number of stocks \(\varXi \) of
and
and (theoretical) buy and sell signals \(\theta \) of
and
This leads to a total number of stocks
The buy or sell signal transmitted to the broker is:
With \(\phi >0\) being the relative broker fee and \(m>0\) being the minimal broker fee per transaction, this leads to the following transaction fees \(\gamma \):
-
When \(\theta (t)>0\) and \(|\theta ^L(t)|>|\theta ^S(t)|\) and \(\theta ^L(t)\cdot \theta ^S(t)<0\):
$$\begin{aligned} \gamma ^L(t) = \theta (t)\cdot \zeta (t)/2+\max (\theta (t)\cdot p^a(t)\cdot \phi \ ,\ m) \end{aligned}$$ -
When \(\theta (t)>0\) and \(|\theta ^L(t)|<|\theta ^S(t)|\) and \(\theta ^L(t)\cdot \theta ^S(t)<0\):
$$\begin{aligned} \gamma ^S(t) = \theta (t)\cdot \zeta (t)/2+\max (\theta (t)\cdot p^a(t)\cdot \phi \ ,\ m) \end{aligned}$$ -
When \(\theta (t)<0\) and \(|\theta ^L(t)|>|\theta ^S(t)|\) and \(\theta ^L(t)\cdot \theta ^S(t)<0\):
$$\begin{aligned} \gamma ^L(t) = -\theta (t)\cdot \zeta (t)/2+\max (-\theta (t)\cdot p^b(t)\cdot \phi \ ,\ m) \end{aligned}$$ -
When \(\theta (t)<0\) and \(|\theta ^L(t)|<|\theta ^S(t)|\) and \(\theta ^L(t)\cdot \theta ^S(t)<0\):
$$\begin{aligned} \gamma ^S(t) = -\theta (t)\cdot \zeta (t)/2+\max (-\theta (t)\cdot p^b(t)\cdot \phi \ ,\ m) \end{aligned}$$ -
When \(\theta (t)>0\) and \(\theta ^L(t)\cdot \theta ^S(t)\ge 0\):
$$\begin{aligned} \gamma ^L(t) = \theta ^L(t)\cdot \zeta (t)/2+\max (\theta (t)\cdot p^a(t)\cdot \phi \ ,\ m)\cdot \theta ^L(t)/\theta (t) \end{aligned}$$and
$$\begin{aligned} \gamma ^S(t) = \theta ^S(t)\cdot \zeta (t)/2+\max (\theta (t)\cdot p^a(t)\cdot \phi \ ,\ m)\cdot \theta ^S(t)/\theta (t) \end{aligned}$$ -
When \(\theta (t)<0\) and \(\theta ^L(t)\cdot \theta ^S(t)\ge 0\):
$$\begin{aligned} \gamma ^L(t) = -\theta ^L(t)\cdot \zeta (t)/2+\max (-\theta (t)\cdot p^b(t)\cdot \phi \ ,\ m)\cdot \theta ^L(t)/\theta (t) \end{aligned}$$and
$$\begin{aligned} \gamma ^S(t) = -\theta ^S(t)\cdot \zeta (t)/2+\max (-\theta (t)\cdot p^b(t)\cdot \phi \ ,\ m)\cdot \theta ^S(t)/\theta (t). \end{aligned}$$
These costs are used for lowering the gains. However, before calculating the gain, we have to calculate the bank account B with the interest rate \(r_c\) for credit (i.e., for capital put in the bank) and the interest rate \(r_d\) for debit (i.e., for capital borrowed from the bank). The bank account as well as the gain/loss function start with zero. The dynamics are as follows:
-
When \(B(t-1)\ge 0\) and \(\theta (t)\ge 0\):
$$\begin{aligned} B(t) = B(t-1)\cdot (1+r_c) - \theta (t)\cdot p^a(t) \end{aligned}$$ -
When \(B(t-1)<0\) and \(\theta (t)\ge 0\):
$$\begin{aligned} B(t) = B(t-1)\cdot (1+r_d) - \theta (t)\cdot p^a(t) \end{aligned}$$ -
When \(B(t-1)\ge 0\) and \(\theta (t)<0\):
$$\begin{aligned} B(t) = B(t-1)\cdot (1+r_c) - \theta (t)\cdot p^b(t) \end{aligned}$$ -
When \(B(t-1)<0\) and \(\theta (t)<0\):
$$\begin{aligned} B(t) = B(t-1)\cdot (1+r_d) - \theta (t)\cdot p^b(t). \end{aligned}$$
This leads to the theoretical trading gains of
of the long side and
of the short side. These values are used to determine next period’s investments \(I^L{(t)}\) and \(I^S{(t)}\). The real, total gain (including interest rates) is:
All in all, this leads stock-by-stock to a trading gain of \(g_T\) (minus the annual brokerage fee divided by the number of assets traded, e.g., 30 in case of the DAX).
5.2 Data, results, and criticism
The data set we use for backtesting contains 60 one-year charts with daily prices, namely the 30 stock charts indexed in the German stock index DAX in June 2018 from the years 2016 and 2017 (each with bid and ask prices) as provided by THOMSON REUTERS DATASTREAM. From the same source, we use the index data DAX 30 PERFORMANCE-PRICE-INDEX and the bond rate BUBA-YIELD-LISTD-FEDRL-SEC 3-5Y MIDDLE RATE (Thomson Reuters 2018). We chose the years 2016 and 2017 because there were no stock splits or similar for any of the shares in the backtesting study. The trading fees were taken from www.boerse-frankfurt.de/inhalt/handeln-handelskosten (Börse Frankfurt 2018), which leads to variable brokerage fees of
but a minimal fee per trade of
The harmonic mean of the bond rate is \(r=-0.5201459\%\). To make the results robust against different bond rates, we use
both divided by \(253.5=\frac{255+252}{2}\). That means, in all cases, these bond rates are bad for the trader. Even when the influence is only marginal, we choose an annual fee of 25 EUR. In Table 1, the 30 assets listed in the DAX in June 2018 are given. These assets are used for backtesting because the requirements for SLS trading state that the traded stocks should be highly liquid (and the underlying firm should be big enough), which is fulfilled for the stocks listed in the German stock index.
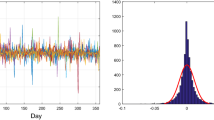
In Table 2, we present the backtesting simulation results of the SLS rule on the 60 charts (with bid-ask spread) for 2016 and 2017. The trading gains for all stocks at the end of the respective years are given, as well as the maximum amount of capital the trader has to borrow from the bank in these years for trading the respective asset (in brackets). At the end, the average trading gain per stock when SLS trading stock-by-stock is calculated, and the maximum amount of capital the trader has to borrow from the bank for trading all 30 stocks is given (which is not simply the sum of the maximal amounts for all stocks, but potentially less; in brackets). All these values are simulated for \(K=2\) and \(I_0^*=5000\). A histogram of the achieved trading gains is given in Fig. 6, and a graph for all 60 assets with the trading gains and the maximal amount of capital borrowed from the bank can be found in Fig. 7.
The trading gains are between \(-597.68\) EUR for Henkel in 2017 (with maximal 2741.03 EUR to be lent) and \(+8293.71\) EUR for Deutsche Lufthansa in 2017 (with maximal 17832.53 EUR to be lent). In total, a trader following this SLS strategy in the years under analysis for all 30 stocks in parallel does not have to borrow more than 117752.30 EUR from the bank.
To realize an excess return, the SLS rule needs a price path with a clear trend (and it does not matter whether this is an upward or a downward trend). In case of an asset with positive and negative trends—as shown in Sect. 4—the SLS trader can expect a loss. Hence, the D:HEN stock seems to have a trend with a switching sign in 2017, while the D:LHA stock seems to have a clear trend in 2017. Having a look at Fig. 8 indicates that the Lufthansa chart goes clearly in one direction (up) and the Henkel chart is (although on a higher level) more or less constant without any clear trend.
In Fig. 9, a contour plot is depicted for the average trading gains of SLS trading for varying trader parameters for the data. For small values of K as well as for small values of \(I_0^*\), the trader, on average, makes a loss. When the parameters are chosen large enough, the average gain is positive. This can be explained by the minimal transaction fee: in case of small investment amounts, the trader must pay the minimal fee for each trade, which is much higher than the relative fee. For large investments, the trader has to pay the relative fee (which is relatively smaller). In Table 3, the averaged trading gains over all stocks and years and the maximum amount of capital to be borrowed are given for varying parameters: \(K=1.5,\ 2,\) and 2.5, and \(I_0^*=2000,\ 3000,\) and 4000. These parameters are chosen because the border between positive and negative gain lies within these ranges.
To sum up, these results are a hint that the robust positive expectation property also holds for real-world data with transaction costs. In Fig. 6, the histogram for the trading gains of the SLS rule for all 60 charts are depicted. The gains are highly skewed, which is fully in line with the corresponding literature. The robust positive expectation property is a statement concerning the expected gain. Thus, for specific price paths the gain may be negative. As can be seen in Fig. 6, this is true in our backtesting study. We observe that in many cases, the SLS rule makes a small loss, however, in some cases it makes a high gain. That means, in order to realize the expected positive gain, a trader must perform SLS trading on many assets fulfilling the requirements. And this is a risk for small traders, since an SLS should not run out of money before the expected gain is realized.
There is another type of criticism of these results. When buying or selling a large amount of stocks, even a backtest simulation with bid and ask prices is not realistic since the price can change during one trade. Thus, \(I_0^*\) and K should not be too large. Another point to consider is that the DAX rose from the beginning of 2016 to the end of 2017 by a factor of 1.256. When having a look at the maximum needed capital and the gains, it might have been more profitable to invest in index mutual funds or index ETFs for the DAX (as a buy-and-hold trader). However, this would only work when the DAX goes up while SLS trading (in theory) also works when charts or the whole index goes down. We observe that a trader using the SLS rule gets rid of the risk of falling stock indices, however, he or she has to borrow a lot of money from the bank, which could cause new risks.
6 Extension: the discounted simultaneously long short strategy
As mentioned in Sect. 3.2, Malekpour and Barmish (2016) state that investment decisions should not rely (too much) on past market behavior. A controller with delay as presented by Malekpour and Barmish (2016) has the favorable feature that too old (older than \(m-1\) days) events have no influence on the strategy, but it has a questionable feature, too: an event that is \(m-1\) days old is taken fully into account today but vanishes from the calculations after m days. As an alternative controller type, we introduce the discounted SLS controller with discounting factor \(\delta \in (0,1]\) (\(\hbox {SLS}_\delta \)).
We start by defining the term discounted gain
in a discrete time grid \({\mathcal {T}}=\left\{ t_i=ih\ |\ i=0,1,\ldots ,N=\frac{T}{h}\right\} \) with \(h>0\) and terminal time T and \(f^{\ell _\delta }(0)=0\). As in Sect. 3.1, we define feedback trading strategies by use of deterministic functions F. However, in contrast to Sect. 3.1 we do not use the gain \(g^\ell \) but the discounted gain \(f^{\ell _\delta }\).
In this section, the standard SLS rule (as constructed in Sect. 3.1) is generalized to the discounted SLS rule by use of a discounting factor \(\delta \) and the corresponding discounted gain \(f^{\ell _\delta }\). Again, the price process allows for time-varying parameters. The analysis is based on a refinement of time grids. That means, the discounted SLS rule is
with
and
A flow diagram for the discounted SLS rule is given in Fig. 10. Note that for \(\delta =1\), this strategy is exactly the standard SLS strategy. The discounting factor \(\delta \) specifies to which extent past information is used for calculating the current investment (cf. other economic discounting factors like, e.g., the game theoretic discounting factor in repeated games). The higher \(\delta \) is, the more influence past information has. For \(\delta =1\), all available information is equally weighted, for \(\delta \) close to zero, only the last available information is important. Note that the interplay of an interest rate unequal to zero and the discounting factor \(\delta \) might lead to interesting results, but is regarded to future work. The discounted SLS strategy has, similar to the SLS strategy with delay, the advantage that old information is not as important as new information (when \(\delta <1\)). However, in contrast to the delay strategy, the old information loses its weight gradually, not instantaneously.
Flow diagram for the discounted simultaneously long short (\(\hbox {SLS}_\delta \)) controller with input (or disturbance) variable return on investment \(\frac{\varDelta p}{p}\) resp. \(\frac{\mathrm{d}p}{p}\) and output variable gain \(g^{SLS_\delta }\). The \(\hbox {SLS}_\delta \) traders’ parameters are \(K>0\) (feedback parameter), \(I_0^*>0\) (initial-investment parameter), and \(\delta \in (0,1]\) (discounting factor)
All market assumptions are exactly the same as in Sects. 3 and 4. In the following, we show that the robust positive expectation property holds also for the discounted SLS rule at least in two special cases, both very similar to the cases of Sect. 4. The analysis of the discounted SLS strategy is done analogously to the analysis of the standard rule, i.e., by the definitions of \(I^{L_\delta }(t_n)\) and \(f^{L_\delta }(t_n)\) it follows
and
Using the definition of \(I^{L_\delta }(t_n)\), it turns out that
By substituting \(I_0^*\mapsto -I_0^*\) and \(K\mapsto -K\), the formula for \({\mathbb {E}}\left[ f^{S_\delta }(t_n)\right] \) follows:
Next, we investigate whether \({\mathbb {E}}\left[ f^{L_\delta }(t)+f^{S_\delta }(t)\right] \) is positive / non-negative. The reader may ask why we are interested in the expected sum of the discounted gain of the short and the long side of the discounted SLS strategy. We can rewrite the undiscounted gain in the following way:
because
and, thus,
Since the expectation operator is linear, it holds:
Note that \(\delta ^{-T}\ge 1>0\ \forall 0<\delta \le 1,T>0\), that \(\delta ^h\in (0,1]\ \forall 0<\delta \le 1,h>0\), and that \(\delta ^{t_{i-1}}=\delta ^{t_{i-2}+h}=\delta ^{t_{i-2}}\cdot \delta ^h\).
Hence, we conclude: When \({\mathbb {E}}\left[ f^{L_\delta }(t_n)+f^{S_\delta }(t_n)\right] \ge 0\) for all \(n=0,\ldots ,N\) and \(>0\) for some n, then \({\mathbb {E}}\left[ g^{SLS_\delta }(t_n)\right] \ge 0\) for all \(t_n\) and \({\mathbb {E}}\left[ g^{SLS_\delta }(T)\right] >0\). This are the desired inequalities: the robust positive expectation property. Note, in the case \(\delta =1\), it holds that \({\mathbb {E}}\left[ f^{\ell _1}(t)\right] ={\mathbb {E}}\left[ g^{\ell _1}(t)\right] \).
Similar to the analysis of the standard rule, it holds that \({\mathbb {E}}\left[ f^{L_\delta }(t)+f^{S_\delta }(t)\right] \) \(>0\) is not true for all t, all \(\delta \in (0,1]\), and all \(\left( \mu _h(t)\right) _t\). This is clear since we already presented a counterexample with \(\delta =1\). This means that this is not a problem of discounting the SLS strategy, it is a problem of the time-varying trend when the time axis is non-continuous, even in the standard SLS case, i.e., when \(\delta =1\).
It holds:
The cases where \({\mathbb {E}}\left[ f^{L_\delta }(t)+f^{S_\delta }(t)\right] \ge 0\ \forall t\in {\mathcal {T}}\) and \({\mathbb {E}}\left[ f^{L_\delta }(T)+f^{S_\delta }(T)\right] >0\) hold are exactly the same as for the standard SLS rule except for the use of discounted gains instead of undiscounted ones. (i) When \(N>1\) and \(\mu _h(t_i)\ge 0\) for all \(t_i\) and \(\mu _h(t_i)>0\) for at least two points in time \(t_i\) or when \(\mu _h(t_i)\le 0\) for all \(t_i\) and \(\mu _h(t_i)<0\) for at least two points in time \(t_i\), \({\mathbb {E}}\left[ f^{L_\delta }(T)+f^{S_\delta }(T)\right] >0\) holds. Second, when letting \(h\rightarrow 0\) (i.e., \(N\rightarrow \infty \)), one can again use the Vito-Volterra-style product integral to get
which surely is non-negative and positive whenever \({\bar{\mu }}_\delta (t):=\int _0^t\delta ^{T-s}\mu (s)ds\) \(\ne 0\).
7 Discussion and conclusion
In this work, we derived closed-form formulae for an SLS trader’s expected gain (in discrete and in continuous time) and for this gain’s variance (in continuous time). We showed that in discrete time, the expected gain of the SLS strategy is both non-negative for all t and strictly positive in T when the average trend is either non-negative \((\mu _h(t_n))_n\ge 0\) for all \(0\le t_n\le T\) and positive \((\mu _h(t_n))_n>0\) for at least two points in time, or when the average trend is non-positive \((\mu _h(t_n))_n\le 0\) for all \(0\le t_n\le T\) and negative \((\mu _h(t_n))_n<0\) for at least two points in time. That means, the expected gain of the SLS rule is indeed independent of the sign of the price’s trend. Additionally, we proved that in a continuous time setting, the expected gain of the SLS strategy is non-negative for all t and positive for all t with \({\bar{\mu }}(t)\ne 0\), i.e., whenever the average trend is nonzero. We discussed risk-adjustments and provided a backtest study with real-world market data that gives strong evidence that bid-ask spreads, trading fees, and interest rates cannot explain the described robust positive expectation property. To take into account that older information should possibly have less influence on the trading strategy than newer information, we added a discounting factor in the SLS strategy.
We note that the price path itself is allowed to change its slope arbitrarily often since only the trend is of importance for the robust positive expectation property of the SLS strategy. When using the SLS rule, a trader does neither have to predict the direction of the price nor its turning point. Only if the trend—not the return—changes its sign, a trader expects a loss. When the trend path is to some extent smooth, and trading frequency is increased, the points in time where the trend changes its sign do carry less weight. The SLS rule works well even for fully unknown price trends.
The only satisfying explanation for the SLS rule’s robust positive expectation property we can give is that the risk measure is inappropriate. Skewness could be a better measure, hence, a detailed analysis of the skewness of SLS rules is an important task for future work. However, when regarding risk we could run into a problem very similar to the joint hypotheses problem: We conjecture that for various trading strategies, one can find two risk measures: one indicating that risk-adjusted returns are high, and one indicating that risk-adjusted returns are low. And, conversely, we also conjecture that for various risk measures one can find two trading strategies: one that beats the market, and one that is beaten by it. No one could say whether or not the risk measure or the market efficiency hypothesis is wrong. We guess that most traders might fear the presumably high risk related to SLS trading, and only a small fraction of traders would use this rule. Thus, the non-SLS traders would be exploited by the SLS traders. We emphasize that the robust positive expectation property is not an arbitrage possibility. It potentially needs a huge number of experiments, i.e., of trading processes, to realize, on average, a positive expected gain.
It is an important task for future work to find a closed-form formula for the skewness of the distribution of SLS gains. More fundamentally, it is also important to examine what preferences traders have regarding skewness. Another important topic for future work is the comparison of control-based strategies and momentum strategies—both empirically and theoretically. Especially controllers with saturation reset are of interest (Barmish 2008). The extension of the results concerning SLS strategies to multi-asset markets and their connection with universal portfolios, the stochastic portfolio theory, etc. (cf. Cover 1991; Deshpande and Barmish 2018; Fernholz 2002; Cuchiero et al. 2019; Pal and Wong 2016; Wong 2015; Karatzas and Ruf 2017) promises important results in the future, as does the investigation of the relationship between the discount factor of the discounted SLS strategy and the interest rate.
Change history
06 July 2023
A Correction to this paper has been published: https://doi.org/10.1007/s10203-023-00405-1
References
Ariel, R.A.: A monthly effect in stock returns. J. Financ. Econ. 18(1), 161–174 (1987)
Ariel, R.A.: High stock returns before holidays: existence and evidence on possible causes. J. Financ. 45(5), 1611–1626 (1990)
Avramov, D., Kaplanski, G., Levy, H.: Talking numbers: technical versus fundamental investment recommendations. J. Bank. Financ. 92(C), 100–114 (2018)
Bailey, D.H., Borwein, J., Lopez de Prado, M., & Zhu, Q.J.: Pseudo-mathematics and financial charlatanism: the effects of backtest overfitting on out–of–sample performance. Not. Am. Math. Soc. 61(5), 458–471 (2014)
Banner, A.D., Fernholz, R., Karatzas, I.: Atlas models of equity markets. Ann. Appl. Probab. 15(4), 2296–2330 (2005)
Banz, R.W.: The relationship between return and market value of common stocks. J. Financ. Econ. 9(1), 3–18 (1981)
Barmish, B.R.: On trading of equities: a robust control paradigm. IFAC World Congress, Seoul, Korea 1, 1621–1626 (2008)
Barmish, B.R.: On performance limits of feedback control-based stock trading strategies. In: IEEE American Control Conference (ACC), pp. 3874–3879 (2011)
Barmish, B.R., Primbs, J.A.: On arbitrage possibilities via linear feedback in an idealized Brownian motion stock market. In: IEEE Conference on Decision and Control and European Control Conference (CDC-ECC), pp. 2889–2894 (2011)
Barmish, B.R., Primbs, J.A.: On market-neutral stock trading arbitrage via linear feedback. In: IEEE American Control Conference (ACC), pp. 3693–3698 (2012)
Barmish, B.R., Primbs, J.A.: On a new paradigm for stock trading via a model-free feedback controller. IEEE Trans. Autom. Control 61(3), 662–676 (2016)
Baumann, M.H.: Effects of linear feedback trading in an interactive market model. In: American Control Conference (ACC), 2015. IEEE, pp. 3880–3885 (2015)
Baumann, M.H.: On stock trading via feedback control when underlying stock returns are discontinuous. IEEE Trans. Autom. Control 62(6), 2987–2992 (2017)
Baumann M.H.: Performance and effects of linear feedback stock trading strategies. Dissertation, University of Bayreuth, Faculty for Mathematics, Physics and Computer Science (2018)
Baumann, M.H.: A new stochastic Fubini-type theorem. On interchanging expectations and Itō integrals. Sankhya A Indian J. Stat. 83(1), 408–420 (2021)
Baumann, M.H., Grüne, L.: Simultaneously long short trading in discrete and continuous time. Syst. Control Lett. 99, 85–89 (2017)
Baumann, M.H., Grüne, L.: Positive expected feedback trading gain for all essentially linearly representable prices. In: Asian Control Conference (ASCC), pp. 150–155 (2019)
Baumann, M.H., Grüne, L., Herz, B.: Effects of control-based trading—between the poles of economics & finance and mathematics & engineering. In: International Symposium on Interdisciplinarity, Track: Interdisciplinarity in Economics, Corte (2017)
Baumann, M.H., Baumann, M., Erler, A.: Limitations of stabilizing effects of fundamentalists: facing positive feedback traders. Economics 13(1), 1–25. https://www.degruyter.com/document/doi/10.5018/economics ejournal.ja.2019-44/pdf 1-25 (2019)
Börse Frankfurt.: Das kostet das Handeln. www.boerse-frankfurt.de/inhalt/handeln-handelskosten, viewed on June 4, 2018 (2018)
Brown, S.J., Goetzmann, W.N.: Performance persistence. J. Financ. 50(2), 679–698 (1995)
Campbell, J.Y., Shiller, R.J.: Stock prices, earnings, and expected dividends. J. Financ. 43(3), 661–676 (1988)
Carhart, M.M.: Persistence in mutual fund performance re-examined. Working paper, Graduate School of Business, University of Chicago, Chicago, Ill (1992)
Carhart, M.M.: On persistence in mutual fund performance. J. Financ. 52(1), 57–82 (1997)
Covel, M.: Trend following: how great traders make millions in up or down markets. FT Press (2004)
Cover, T.M.: Universal Portfolios. Math. Financ. 1(1), 1–29 (1991)
Cover, T.M., Ordentlich, E.: Universal portfolios with side information. IEEE Trans. Inf. Theory 42(2), 348–363 (1996)
Cross, F.: The behavior of stock prices on fridays and mondays. Financ. Anal. J. 29(6), 67–69 (1973)
Cuchiero, C., Schachermayer, W., Wong, T.K.L.: Cover’s universal portfolio, stochastic portfolio theory, and the numéraire portfolio. Math. Financ. 29(3), 773–803 (2019)
Deshpande, A., Barmish, B.R.: A generalization of the robust positive expectation theorem for stock trading via feedback control. In: 2018 European Control Conference (ECC), pp. 514–520 (2018)
Dokuchaev, N.G.: Dynamic Portfolio Strategies: Quantitative Methods and Empirical Rules for Incomplete Information, vol. 47. Springer Science & Business Media (2012)
Dokuchaev, N.G., Savkin, A.V.: A hedging investment strategy with a positive average gain without market estimation. In: Proceedings of CESA’98 Symposium on Applied Mathematics and Optimization, Tunisia (1998a)
Dokuchaev, N.G., Savkin, A.V.: Asymptotic arbitrage in a stochastic financial market model. In: Computational Engineering in Systems Applications (1998b)
Dokuchaev, N.G., Savkin, A.V.: A bounded risk strategy for a market with non-observable parameters. Insur. Math. Econ. 30(2), 243–254 (2002)
Dokuchaev, N., Savkin, A.V.: Universal strategies for diffusion markets and possibility of asymptotic arbitrage. Insur. Math. Econ. 34(3), 409–419 (2004)
Duffie, D.: Dynamic asset pricing theory. Princeton University Press (2010)
Elton, E.J., Gruber, M.J., Blake, C.R.: The persistence of risk-adjusted mutual fund performance. J. Bus. 69(2), 133–157 (1996)
Elton, E.J., Gruber, M.J., Das, S., Hlavka, M.: Efficiency with costly information: a reinterpretation of evidence from managed portfolios. Rev. Financ. Stud. 6(1), 1–22 (2015)
Fama, E.F.: The behavior of stock-market prices. J. Bus. 38(1), 34–105 (1965)
Fama, E.F.: Efficient capital markets: a review of theory and empirical work. J. Financ. 25(2), 383–417 (1970)
Fama, E.F.: Efficient capital markets: II. J. Financ. 46(5), 1575–1617 (1991)
Fama, E.F.: Random walks in stock market prices. Financ. Anal. J. 51(1), 75–80 (1995)
Fama, E.F., French, K.R.: Multifactor explanations of asset pricing anomalies. J. Financ. 51(1), 55–84 (1996)
Fama, E.F., French, K.R.: Dissecting anomalies. J. Financ. 63(4), 1653–1678 (2008)
Fama, E.F., Fisher, L., Jensen, M.C., Roll, R.: The adjustment of stock prices to new information. Int. Econ. Rev. 10(1), 1–21 (1969)
Fernholz, R.: On the diversity of equity markets. J. Math. Econ. 31(3), 393–417 (1999a)
Fernholz, R.: (1999b) Portfolio generating functions. In: Quantitative Analysis in Financial Markets: Collected Papers of the New York University Mathematical Finance Seminar. World Scientific, pp. 344–367
Fernholz, R.: Equity portfolios generated by functions of ranked market weights. Financ. Stochast. 5(4), 469–486 (2001)
Fernholz, R.: Stochastic portfolio theory. Springer (2002)
Fernholz, R., Karatzas, I.: Relative arbitrage in volatility-stabilized markets. Ann. Financ. 1(2), 149–177 (2005)
Fernholz, R., Karatzas, I.: Stochastic portfolio theory: an overview. Handb. Numer. Anal. 15(89–167), 1180–91267 (2009)
Fernholz, R., Shay, B.: Stochastic portfolio theory and stock market equilibrium. J. Financ. 37(2), 615–624 (1982)
Fernholz, R., Karatzas, I., Kardaras, C.: Diversity and relative arbitrage in financial markets. Columbia University, Department of Mathematics and Statistics (2003)
Fernholz, R., Karatzas, I., Kardaras, C.: Diversity and relative arbitrage in equity markets. Financ. Stochast. 9(1), 1–27 (2005)
French, K.R.: Stock returns and the weekend effect. J. Financ. Econ. 8(1), 55–69 (1980)
Goetzmann, W.N., Ibbotson, R.G.: Do winners repeat? Patterns in mutual fund return behavior. J. Portf. Manag. 20(2), 9 (1994)
Granger, C.W.J., Morgenstern, O.: Spectral analysis of New York stock market prices. Econ. Res. Prog. Res. Memorandum 45, 1–31 (1962)
Grinblatt, M., Titman, S.: The persistence of mutual fund performance. J. Financ. 47(5), 1977–1984 (1992)
Hendricks, D., Patel, J., Zeckhauser, R.: Hot hands in mutual funds: short-run persistence of relative performance, 1974–1988. J. Financ. 48(1), 93–130 (1993)
Iwarere, S., Barmish, B.R.: On stock trading over a lattice via linear feedback. In: IFAC World Congress, vol. 19,1, pp. 7799–7804 (2014)
Jarrow, R.A., Larsson, M.: The meaning of market efficiency. Math. Financ. 22(1), 1–30 (2012)
Jegadeesh, N., Titman, S.: Returns to buying winners and selling losers: implications for stock market efficiency. J. Financ. 48(1), 65–91 (1993)
Jegadeesh, N., Titman, S.: Profitability of momentum strategies: an evaluation of alternative explanations. J. Financ. 56(2), 699–720 (2001)
Jensen, M.C.: Risk, the pricing of capital assets, and the evaluation of investment portfolios. J. Bus. 42(2), 167–247 (1969)
Karatzas, I., Kardaras, C.: The numéraire portfolio in semimartingale financial models. Financ. Stochast. 11(4), 447–493 (2007)
Karatzas, I., Ruf, J.: Trading strategies generated by Lyapunov functions. Financ. Stochast. 21, 753–787 (2017)
Karatzas, I., Shreve, S.E., Karatzas, I., Shreve, S.E.: Methods of mathematical finance, vol. 39. Springer (1998)
Kardaras, C.: Stochastic portfolio theory in semimartingale markets. Unpublished manuscript, Columbia University (2003)
Keim, D.B.: Size-related anomalies and stock return seasonality: further empirical evidence. J. Financ. Econ. 12(1), 13–32 (1983)
Lakonishok, J., Smidt, S.: Are seasonal anomalies real? A ninety-year perspective. Rev. Financ. Stud. 1(4), 403–425 (1988)
Malekpour, S., Barmish, B.R.: A Drawdown formula for stock trading via linear feedback in a market governed by Brownian motion. In: 2013 European Control Conference (ECC). IEEE, pp. 87–92 (2013)
Malekpour, S., Barmish, B.R.: On stock trading using a controller with delay: the robust positive expectation property. In: IEEE Conference on Decision and Control (CDC). IEEE, pp. 2881–2887 (2016)
Malekpour, S., Primbs, J.A., Barmish, B.R.: On stock trading using a pi controller in an idealized market: the robust positive expectation property. In: IEEE Conference on Decision and Control (CDC). IEEE, pp. 1210–1216 (2013)
Malekpour, S., Primbs, J.A., Barmish, B.R.: A generalization of simultaneous long-short stock trading to PI controllers. IEEE Trans. Autom. Control 63(10), 3531–3536 (2018)
Malkiel, B.G.: A random walk down wall street. W. W. Norton & Company (1973)
Malkiel, B.G.: Efficient market hypothesis. The new palgrave: Finance norton, New York pp 127–134 (1989)
Malkiel, B.G.: The efficient market hypothesis and its critics. J. Econ. Perspect. 17(1), 59–82 (2003)
Malkiel, B.G.: Reflections on the efficient market hypothesis: 30 years later. Financ. Rev. 40(1), 1–9 (2005)
Markowitz, H.: Portfolio selection. J. Financ. 7(1), 77–91 (1952)
Merton, R.C.: Option pricing when underlying stock returns are discontinuous. J. Financ. Econ. 3(1–2), 125–144 (1976)
Moskowitz, T.: Explanations for the momentum premium. AQR Capital Management, AQR White Paper (2010)
O’Brien, J.D., Burke, M.E., Burke, K.: A generalized framework for simultaneous long-short feedback trading. IEEE Trans. Autom. Control 66(6), 2652–2663 (2020)
Pal, S., Wong, T.K.L.: The geometry of relative arbitrage. Math. Financ. Econ. 10, 263–293 (2016)
Primbs, J.A., Barmish, B.R.: On stock trading: can a trend follower expect to win? In: SSRN Electronic Journal, Midwest Finance Association Conference (2012)
Primbs, J.A., Barmish, B.R.: On robustness of simultaneous long-short stock trading control with time-varying price dynamics. IFAC-PapersOnLine 50(1), 12267–12272 (2017)
Protter, P.E.: Stochastic integration and differential equations. Springer, Berlin (2005)
Roll, R.: Vas ist das? J. Portfolio Manag. 9(2), 18–28 (1983)
Rozeff, M.S.: Dividend yields are equity risk premiums. J. Portfolio Manag. 11(1), 68–75 (1984)
Saad, E.W., Prokhorov, D.V., Wunsch, D.C.: Comparative study of stock trend prediction using time delay, recurrent and probabilistic neural networks. IEEE Trans. Neural Netw. 9(6), 1456–1470 (1998)
Schied, A., Speiser, L., Voloshchenko, I.: Model-free portfolio theory and its functional master formula. SIAM J. Financ. Math. 9(3), 1074–1101 (2018)
Shiller, R.J.: Stock prices and social dynamics. Brook. Pap. Econ. Act. 1984(2), 457–510 (1984)
Stickel, S.E.: The effect of value line investment survey rank changes on common stock prices. J. Financ. Econ. 14(1), 121–143 (1985)
Thomson Reuters (2018) Thomson Reuters Datastream. Viewed on June 4, 2018
Wermers, R.: Momentum investment strategies of mutual funds, performance persistence, and survivorship bias. Working paper, University of Colorado at Boulder, Boulder, Col (1996)
Wong, T.K.L.: Universal portfolios in stochastic portfolio theory. arXiv:1510.02808, 1–25 (2015)
Acknowledgements
“Is Fama wrong?” This question was asked during my presentation at the International Symposium on Interdisciplinarity at the Università di Corsica Pasquale Paoli in Corte/Corti, France, in the track Interdisciplinarity in Economics (Baumann et al. 2017). This question was the motivation for the work at hand. I thank Lars Grüne (Universität Bayreuth), Bernhard Herz (Universität Bayreuth), and Michaela Baumann (Nürnberger Lebensversicherung) for their support. I thank Louisa Chen (University of Sussex), Dmitry Shevchenko (Southern Federal University Rostov-on-Don), Jakob Krause (Martin-Luther-Universität Halle-Wittenberg), and all anonymous reviewers for their helpful comments, where special thanks go to an anonymous reviewer of the Journal “Decisions in Economics and Finance” since he or she gave really helpful, constructive, and detailed comments that strengthened the readability and understandability of this work. Additionally, I thank Jane Lael for her professional editing work. This paper was presented at the Graduiertenseminar der VWL-Lehrstühle der Universität Bayreuth 2018, Schney, Lichtenfels, Germany, at the XIX Workshop on Quantitative Finance (QFW; Università degli Studi Roma Tre) 2018, Rome, Italy, at Southern Federal University Rostov-on-Don 2018, Rostov-on-Don, Russian Federation, at the 22\(^{nd}\) Annual International Conference on Macroeconomic Analysis and International Finance (ICMAIF; University of Crete) 2018, Rethymno, Crete, Greece, at the Seventeenth Annual European Economics and Finance Society Conference (EEFS; City, University of London) 2018, London, England, at the 6th International PhD Meeting in Economics (University of Macedonia) 2018, Thessaloniki, Greece, and at Martin-Luther-Universität Halle-Wittenberg 2018, Halle, Germany.
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The work of Michael Heinrich Baumann was supported by Hanns Seidel Stiftung (HSS), funded by Bundesministerium für Bildung und Forschung (BMBF). The author declares that he has no conflict of interest. Empirical data are available on THOMSON REUTERS DATASTREAM. The code is available from the author upon reasonable request.
Additional information
Parts of this work also appeared in the doctoral thesis of the author entitled “Performance and Effects of Linear Feedback Stock Trading Strategies” (University of Bayreuth, Germany, 2018) (Baumann 2018). The work of Michael H. Baumann was supported by Hanns-Seidel-Stiftung e.V. (HSS), funded by Bundesministerium für Bildung und Forschung (BMBF).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Baumann, M.H. Beating the market? A mathematical puzzle for market efficiency. Decisions Econ Finan 45, 279–325 (2022). https://doi.org/10.1007/s10203-021-00361-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10203-021-00361-8
Keywords
- Technical analysis
- Efficient market hypothesis
- Robust positive expectation property
- Simultaneously long short trading
- Control-based trading strategies