A machine learning-based price state prediction model for agricultural commodities using external factors

Abstract

In recent times of noticeable climate change the consideration of external factors, such as weather and economic key figures, becomes even more crucial for a proper valuation of derivatives written on agricultural commodities. The occurrence of remarkable price changes as a result of severe changes in these factors motivates the introduction of different price states, each describing different dynamics of the price process. In order to include external factors we propose a two-step hybrid model based on machine learning methods for clustering and classification. First, we assign price states to historical prices using K-means clustering. These price states are also assigned to the corresponding data of external factors. Second, predictions of future price states are then obtained from short-term predictions of the external factors by means of either K-nearest neighbors or random forest classification. We apply our model to real corn futures data and generate price scenarios via a Monte Carlo simulation, which we compare to Sørensen (J Futures Mark 22(5):393–426, 2002). Thereby we obtain a better approximation of the real futures prices by the simulated futures prices regarding the error measures MAE, RMSE and MAPE. From a practical point of view, these simulations can be used to support the assessment of price risks in risk management systems or as decision support regarding trading strategies under different price states.

1 Introduction

In recent years the consequences of severe natural and economic incidents have become more noticeable for the cultivation of agricultural commodities. Particularly, the severe development of climate-related factors, such as drought caused by heat waves, has direct impact on planting and harvesting conditions of agricultural commodities. Such drastic and unpredictable changes are further reflected in the price development of agricultural commodity derivatives. The crucial role of external factors¹ has been already recognized in early research on price modeling and forecasting of these derivatives. Based on several fundamentals such as stock inventories, temperature, production levels and export demand Chatrath et al. (2002); Geman and Nguyen (2005), and Hayenga et al. (1997) analyze the relation of these factors to the price development of derivatives. Furthermore, there exists a vast number of research that examines the role of reports from the United States Department of Agriculture (USDA) as being a price-driving factor themselves for a broad range of agricultural commodities. Starting from the literature in earlier years (Garcia et al. 1997; Summer and Mueller 1989) to recent work based on the current economic situation, Boudoukh et al. (2007); Karali (2012), and Karali et al. (2019) verify that these reports still represent an important source of information for the price formation of these commodities. In a more general setting, Broll and Eckwert (2008) model fundamentals as observable realizations of a random variable that are assumed to be correlated with the development of futures prices in a commodity market and thus have an impact on them.

Mathematical and statistical methods which establish the relation between fundamentals and the development of commodity prices include the formulation of stochastic price processes (Geman and Nguyen 2005; Haug 2021; Schwartz 1997; Zhu et al. 2009) as well as the construction of time series models (Garcia et al. 1997; Karali et al. 2019). More advanced stochastic models have been developed in the scope of electricity price modeling, where Benth and Meyer-Brandis (2009), Hess (2012) and Hess (2020) model fundamentals such as carbon dioxide emission costs and temperature by stochastic processes of Ornstein–Uhlenbeck type, among others. Also in the domain of electricity price modeling and forecasting, more complex statistical models can be found, where ARX-type time series are widely used in applications (Kristiansen 2012; Nogales and Conejo 2006; Weron and Misiorek 2008).

However, due to the nonlinear relation between price-driving factors and the price process, linear time series models are not able to fully capture the complex relations. For this purpose, hybrid approaches that combine classical statistical models with methods of machine learning have been developed and have recently gained attention in research pertaining to different markets. Besides the application of more sophisticated machine learning methods based on artificial neural networks (ANN) (Fan et al. 2007; González et al. 2005; Niu et al. 2010), simpler methods are as popular as their more complex counterparts. Indeed, a comparison of ANNs and support vector machines (SVM) in Sansom et al. (2003) shows better performance of SVMs in the context of electricity price forecasting. Further analysis of hybrid models, also in the scope of electricity price modeling and forecasting, can be found in Che and Wang (2010), which combines SVMs with standard (linear) time series models. With a focus on metal commodities and under consideration of price-driving factors, Kristjanpoller and Hernández (2017) analyze the performance of ANNs in combination with a GARCH model for forecasting price volatility. Finally, the use of machine learning methods as a stand-alone tool for price modeling and forecasting tasks for different markets has also been analyzed in the literature. In the context of electricity markets Fan et al. (2007) and Niu et al. (2010) introduce a two-stage machine learning approach in order to obtain short-term forecasts of day ahead electricity prices. In particular, different methods of supervised and unsupervised learning are combined in order to obtain direct price forecasts as outputs of the learning process.

We propose a two-step hybrid model that combines a well-established theoretical price model for agricultural commodities with the strengths machine learning methods offer. Based on historical data on futures prices and a selection of their price-driving factors, our approach allows for a characterization of different price behavior and development into different price states.

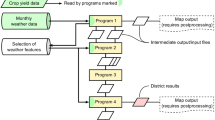
To make this more precise we explain its three major components as given in Fig. 1:

• 1. In the first step we apply a clustering algorithm to historical futures price data to identify K price states of commodity futures, see block $\textcircled {1}$ in Fig. 1. Specifically, we apply the K-means algorithm to historical futures log returns for the identification of states of log returns.² The clustering results then serve as input data for the subsequent classification and calibration tasks.

• 2. In the second component we link a selection of external factors to the commodity price states by using a classification algorithm that assigns each set of values of the external factors to a commodity price state, see block $\textcircled {2}$ in Fig. 1. More precisely, we use the identified prices states from block $\textcircled {1}$ as classes on historical data of the external factors for the training of the classification algorithm. As it is often much easier to forecast the values of the external factors, we use their forecasts as input to the selected classification model to predict the corresponding commodity price states. In our analysis we consider the two classification algorithms K-nearest neighbors (K-nn) and random forests (RF) with external data on weather and supply and demand data on corn cultivation as external factors.

• 3. In the third component, for each cluster we calibrate the parameters needed as input for the valuation formula of Sørensen (2002) for futures prices. We use the clustering results from block $\textcircled {1}$ for the state-dependent calibration of the model parameters given by an approximate version of the stochastic price model, see block $\textcircled {3}$ in Fig. 1. Finally, we combine the classification and calibration results for a Monte Carlo simulation of futures prices based on the predicted price states, see block $\textcircled {4}$ in Fig. 1. These simulated prices can also be utilized for further scenario analysis and computation of risk measures in risk controlling units of agricultural commodity businesses, which, however, is beyond the scope of this paper.

The main benefit of hybrid models that combine stochastic modeling with machine learning methods lies in the incorporation of mathematical interpretability and domain knowledge into a data-driven approach. Moreover, the two-step approach allows for exploiting the strengths of supervised and unsupervised techniques in detecting nonlinear relationships between agricultural commodity prices and their driving factors.

Hybrid models were considered in Kristjanpoller and Hernández (2017) and two-step machine learning approaches were used in Fan et al. (2007), and Niu et al. (2010). However, in the literature we did not find an approach applying clustering and classification in combination with external factors for price modeling as proposed by us.

Our work is organized as follows: We describe the hybrid and machine learning-based price state prediction model (ML price model) in detail in Sect. 2. A description of futures price data and the price-relevant factors is given in Sect. 3. The application of our model to real corn futures data and its empirical and simulation results are presented in Sect. 4. A summary of our main results concludes the final section.

2 A machine learning-based price state prediction model for the valuation of futures prices

In this section we present the procedure of the proposed two-step hybrid price state prediction model, which combines a classical stochastic price modeling approach with machine learning-based methods of clustering and classification, as explained in Introduction and illustrated in Fig. 1.

Fig. 1

Workflow of the proposed machine learning-based price state prediction model for the simulation of price paths by means of the identification and prediction of price states

2.1 Standard price model and calibration technique for the valuation of agricultural commodity futures

With $P_t, t= 0,1, \ldots , T$, denoting the spot price of agricultural commodities,³ we follow Sørensen (2002) and consider the log price process $p_t = \log (P_t)$ with dynamics given by

$$\begin{aligned} p_t = s_t + x_t + z_t. \end{aligned}$$

(1)

Here the function

$$\begin{aligned} s_t = \sum _{k = 1}^{S} (\gamma _k \cos (2\pi kt) + \gamma _k^* \sin (2\pi kt)) \end{aligned}$$

(2)

defines the deterministic seasonal component with $\gamma _k, \gamma _k^*$, $k= 1, \ldots , S$, denoting constant coefficients to be estimated. Choosing $S = 2$ as in Sørensen (2002), annual and semi-annual seasonalities are considered. Furthermore, the state variables $x_t$ and $z_t$ define stochastic processes with dynamics given by

$$\begin{aligned} dx_t&= \bigg (\mu - \frac{1}{2}\sigma ^2\bigg )dt + \sigma dW_{xt} \end{aligned}$$

(3)

$$\begin{aligned} dz_t&= -\kappa z_t dt + \nu dW_{zt}, \end{aligned}$$

(4)

where $W_{xt}$ and $W_{zt}$ denote Brownian motions correlated with constant correlation coefficient $\rho$. Hence, the state variable $x_t$ is a Brownian motion with constant drift $\mu - \frac{1}{2}\sigma ^2$ and volatility parameter $\sigma$, whereas $z_t$ follows an Ornstein–Uhlenbeck process with mean reversion level equal to zero, mean reversion speed $\kappa$ and volatility parameter $\nu$. From an economic point of view, the dynamics of $x_t$ describe long-term price changes affected by fundamental and permanent changes in the economy, e.g., given by a permanent change in supply and demand. In contrast, the dynamics of $z_t$ describe short-term price changes, which are caused by temporary changes of external factors, such as temperature and precipitation conditions.

For the valuation of derivative products, a risk neutral version of the stochastic processes is required. Specifically, a change of measure using the equivalent martingale measure Q implies an adjustment in the drifts by risk premium parameters $\lambda _x$ and $\lambda _z$. The processes are given by

$$\begin{aligned} dx_t&= \bigg (\alpha - \frac{1}{2}\sigma ^2\bigg ) dt + \sigma dW_{xt}^Q \end{aligned}$$

(5)

$$\begin{aligned} dz_t&= -(\lambda _z + \kappa z_t) dt + \nu dW_{zt}^Q, \end{aligned}$$

(6)

where $\alpha {:=}\mu - \lambda _x$ and, under Q, $dW^Q_{xt}$ and $dW^Q_{zt}$ are again increments of standard Brownian motions correlated with $dW^Q_{xt} dW^Q_{zt} = \rho dt$.

Using the relation $F_t(\tau ) = {\mathbb {E}}_t^Q(P_{\tau })$, where ${\mathbb {E}}_t^Q:={\mathbb {E}}^Q(\cdot |P_t)$ denotes the conditional expectation under Q conditional on $P_t$, the price formula is given in Sørensen (2002) by the explicit form of

$$\begin{aligned} F_t(\tau ) = \exp \left( s_\tau + A_{\tau - t} + x_t + z_t e^{-\kappa (\tau - t)}\right) , \end{aligned}$$

(7)

where $F_t(\tau )$ denotes the price of the agricultural commodity futures at time t with maturity $\tau$ and where

$$\begin{aligned} A_{\tau - t} {:=}\alpha (\tau - t) - \frac{\lambda _z - \rho \sigma \nu }{\kappa }\left( 1 - e^{-\kappa (\tau - t)}\right) + \frac{\nu ^2}{4\kappa } \left( 1 - e^{-2\kappa (\tau - t)}\right) \end{aligned}$$

(8)

is a deterministic function of the model parameters. With $f_t(\tau ) {:=}\log (F_t(\tau ))$ defining the log futures price at time t, we obtain a linear version of Eq. (7).

We use the Kalman filter maximum likelihood estimation procedure as described in Sørensen (2002) to obtain the set of model parameters

$$\begin{aligned} \Psi {:=}(\mu , \sigma , \kappa , \nu , \rho , \alpha , \lambda _z, x_0, \gamma _1, \gamma _1^*, \gamma _2, \gamma _2^*). \end{aligned}$$

(9)

For a rigorous explanation of the parameter estimation technique using the Kalman filter we refer the reader to Harvey (1990).

2.2 Identification of price states using clustering algorithms

We proceed with a detailed description of the machine learning methods that we incorporate into the existing procedure of futures valuation.

For the identification of historical price states we choose the K-means algorithm. Given a predefined number of clusters K and data $d_0, \ldots , d_T\in {\mathbb {R}}^n, n\in {\mathbb {N}}$, the algorithm groups the data into K clusters, such that dissimilarities of data within a cluster are minimized. Subsequently, we use the Euclidean distance as a dissimilarity measure. Further details regarding K-means and other clustering algorithms are given in Hastie et al. (2001).

In our application we define each cluster to represent a specific price state. Specifically, we obtain K disjoint subsets

$$\begin{aligned} C_i {:=}\{t\in \{0,\ldots , T\}| d_{t}\in \text {cluster}~i \}, \quad i = 1,\ldots , K, \end{aligned}$$

(10)

containing time points corresponding to the data points which are assigned to the cluster i. In order to obtain state-dependent model parameters for a pricing model, we suggest using the Sørensen (2002) formula for the valuation of a futures contract maturing at time $\tau$, similar to the Black-Scholes formula for European call option prices at the stock market. Therefore, we restate Eq. (7) in terms of the subsets $C_1,\ldots ,C_K$. Given a cluster $C_i$ we define the state-dependent version of Eq. (7) as

$$\begin{aligned} f_{t}(\tau , i) {:=}s_\tau (i) + A_{\tau - t}(i) + x_{t}(i) + z_{t}(i) e^{-\kappa (i)(\tau - t)} \end{aligned}$$

(11)

for a futures contract maturing at time $\tau$, $t\in C_i$ and for $i=1,\ldots ,K$. In particular, the state dependence of the functions and processes $s_\tau (i), A_{\tau - t}(i), x_{t}(i)$ and $z_{t}(i)$ are given by their corresponding state-specific parameters constituting the parameter vector

$$\begin{aligned} \Psi (i) {:=}\left( \mu (i), \sigma (i), \kappa (i), \nu (i), \rho (i), \alpha (i), \lambda _z(i), x_0(i), \gamma _1(i), \gamma _1^*(i), \gamma _2(i), \gamma _2^*(i)\right) ,\nonumber \\ \end{aligned}$$

(12)

$i = 1, \ldots , K$. Let us emphasize that we do not claim that formula (11) gives the log price formula for a futures contract. We only use it as a calibration tool in order to obtain the state-dependent parameters. This calibration procedure based on the clusters is carried out K times in order to determine these state-specific parameter vectors $\Psi (i)$.

2.3 Prediction of price states using classification algorithms

As it is our central objective to predict future price states based on observations or predictions of external factors, we aim at relating the external factors to the price states by establishing a functional relationship to historical data. Note that we do not aim at building a model that predicts the actual futures price based on the external factors.⁴ Here we focus on predicting which of the price states will be attained in the near future. This information is then used to predict the actual price values by means of the state-dependent stochastic price model and Monte Carlo simulation.

For this purpose we construct a function $\mathscr {C}:{\mathbb {R}}^{m}\mapsto \{l^1, \ldots , l^K\}$ that assigns an output class ${\mathscr {C}}(b_t)$ to an input feature vector $b_t{:=}(b_{t1}, \ldots ,b_{tm})\in {\mathbb {R}}^{m}$ for each historical time point $t= 0, \ldots , T$. Let $l_t\in \{l^1, \ldots , l^K\}$ denote the price state at time t. Our goal is to find a function ${\mathscr {C}}$ that minimizes the distance between $l_t$ and ${\mathscr {C}}(b_t)$ in an appropriate sense, resulting in a model selection and model-specific hyperparameter optimization.

Specifically, we apply the K-nearest neighbors (K-nn) and random forest (RF) classification algorithms, ${\mathscr {C}}^{\text {Knn}}$ and ${\mathscr {C}}^{\text {RF}}$, respectively. The K-nn algorithm chooses the K closest input feature vectors from the training set $D {:=}\{(b_t, l_t), t = 0,\ldots , T\}$ according to a distance measure. Then the function ${\mathscr {C}}^{\text {Knn}}$ predicts the class ${\mathscr {C}}^{\text {Knn}}(b)$ of a new feature vector b by majority vote among the classes corresponding to the K closest input feature vectors. In contrast to the simple methodology defined by K-nn, random forests constitute a more complex ensemble learning method that makes use of multiple constructions of decision trees (DT). The idea of the DT algorithm is to split the training set D into two subsets, using the best splitting criterion of the form $b_{ti} \le a$ for some $a\in {\mathbb {R}}$ and feature $i\in \{1,\ldots , m\}$. The procedure is repeated iteratively for each resulting subset until some stopping criterion is reached. Finally, the class $\mathscr {C}^{\text {RF}}(b)$ is determined by a soft voting procedure, i.e., as the class with the highest sum of predicted probabilities over all decision trees. We refer the reader to Breiman (2001) and Hastie et al. (2001) for more details regarding the RF-algorithm and the various choices of its hyperparameters.

For the training of the described classification algorithms, we use the clustering results by assigning the identified price states to the input feature vectors given by historical data of the external factors. Specifically, given the clusters $C_1, \ldots , C_K$ as defined in Eq. (10), we define the class for each input feature vector $b_t$, $t =0,\ldots ,T$, by $l_t {:=}i ~\text {if}~ t\in C_i$ for some $i\in \{1, \ldots , K\}$. With this assignment we construct a labeled set $D {:=}\{(b_t, l_t), t = 0,\ldots , T\}$, defining the training set for the classification algorithms.

3 Data and stylized facts

3.1 Futures prices and further transformations

The proposed ML price model is applied to futures contracts written on the agricultural commodity corn. Note that our method can also be applied to other agricultural commodities, where standardized derivative products exist.

We consider the time period of 2015-01-01 to 2019-12-31 of weekly observations on futures prices on corn, which are traded at the Chicago Board of Trade (CBOT). This data has been retrieved from the financial data provider Refinitiv (2020). Futures on agricultural commodities are characterized by their maturity in specific months only. In the case of corn, maturity and thus delivery of the product are only available for the months March, May, July, September and December.

For the identification of (historical) price states we consider different transformations of the original log futures prices. First, in order to obtain easily interpretable as well as reasonable price states that can be detected and distinguished by the clustering algorithm, we transform the log futures prices with maturity $\tau \in {\mathbb {N}}$ to their price changes by

$$\begin{aligned} r_t(\tau ) {:=}\log (F_t(\tau )) - \log (F_{t-1}(\tau )) = f_t(\tau ) - f_{t-1}(\tau ),\quad t\in \{1,\ldots ,\tau \}. \end{aligned}$$

(13)

Second, we follow Sørensen (2002) and define the compounded time series $\{{\tilde{f}}_t(m)\}_{t\ge 0}, m= 1, 2, \ldots$ of futures categorized with respect to their proximity to maturity. That is, given a time point t, the futures ’m-th closest to maturity’ is defined as the futures in the m-th position to mature.⁵ This transformation is particularly needed for the calibration procedure described in Sect. 2.1. We define the compounded time series of log price changes $\{{\tilde{r}}_t(m)\}_{t\ge 0}$ in an analogous way. Figures 2 and 3 depict the development of ${\tilde{f}}_t(m)$ and ${\tilde{r}}_t(m)$ for $m = 1, 5, 10$, i.e., of the futures ’1st,’ ’5th’ and ’10th closest to maturity,’ respectively. Table 1 complements the graphs with the corresponding summary statistics of the categorized futures. In this context we note that the model assumption of normally distributed log prices/log price changes is a fairly common and standard claim used in many existing works on futures price modeling and its evaluation with empirical data (Schwartz 1997; Schwartz and Smith 2000). In particular it is the underlying assumption of the model in Sørensen (2002) that we apply within our approach.

In the following we highlight some stylized facts of the price structure and behavior of agricultural commodity prices, which are crucial for an appropriate price modeling.

Fig. 2

Compounded, weekly time series of corn log futures prices, each categorized with respect to their proximity to maturity over the full sample period 2015-01-01 to 2019-12-31

Fig. 3

Compounded, weekly time series of corn log futures price changes, each categorized with respect to their proximity to maturity over the full sample period 2015-01-01 to 2019-12-31

Table 1 Summary statistics of the compounded time series of (a) log futures prices and (b) log futures price changes, each categorized according to ’m-th closest to maturity’

Yearly seasonality pattern::

In line with observations and existing works on the modeling of (agricultural) commodities (Benth and Koekebakker 2008; Brennan 1958; Fama and French 1987; Geman and Nguyen 2005; Sørensen 2002) we assume commodity prices to exhibit a yearly and sub-annual seasonal pattern. In fact, this price behavior is related to the harvest cycle of agricultural commodities. First, we can expect the price to increase before the harvest season starts, when uncertainty about the outcome is greatest. Then, during the harvest season we can expect a decrease in price fluctuations as the outcome can be better measured and estimated. Obviously, the harvest conditions and results depend strongly on external factors, such as temperature and precipitation conditions. From Fig. 2 we can observe this yearly seasonal pattern for the majority of years depicted. In particular, log prices increase at the beginning of the year and reach their highest annual value in summer, before they sharply decrease in the second half of the year. A similar observation applies to the time series of log price changes, with the highest amplitude and values in the spring and summer months.

Stronger variability for short-term futures::

 We observe stronger variability in the log prices and their changes for futures maturing in the short-term. Hereby we define short-term futures to be futures contracts with an average maturity of up to 12 months, i.e., futures within the categories up to ’5th closest to maturity.’ In both figures this is strongly visible for the compounded time series of futures ’1st closest to maturity’ and ’5th closest to maturity.’ This observation is further supported by the standard deviations in Table 1. Besides seasonality effects which may cause these fluctuations, we assume that additional, temporary changes in external factors have great impact on the magnitude of changes in the prices. As a consequence, we assume the development of futures maturing in the short-term are more strongly affected by temporary information on external factors.

Thus, for the subsequent analysis we consider only futures that are contained within the categories up to ’5th closest to maturity,’ i.e., $m\le 5$.

3.2 Introduction of external factors

For the prediction of price states we focus on the following external factors, which are commonly considered for the pricing of agricultural commodity futures (Geman and Nguyen 2005; Garcia et al. 1997; Karali 2012; Karali et al. 2019).

Weather data::

We retrieve data on temperature and precipitation from the (financial) data provider Refinitiv (2020).We consider time series data on temperature and precipitation available on a daily resolution. In addition, for each country, these measurements exist on regional levels, such that averaging of the regional data is necessary in order to obtain information in aggregated form on a country level.

Supply and demand data::

We use monthly data being published by USDA (2020b). We consider seven time series of supply data and three time series of demand data. All quantities are given in million metric tonnes.

Table 2 gives a detailed overview on the categorized external factors. Furthermore, we limit our consideration of the time series data in both categories to the most relevant corn-producing countries. Taking into account recent reports USDA (2020a), we restrict our application to data available on the countries USA, Brazil and Argentina.⁶ In total, having ten time series on country level, we end up considering 30 different time series for the subsequent prediction of price states in Sect. 4.3. For illustrational purposes Table 8 in Appendix summarizes the main descriptive statistics of the external factors for the USA. The main benefit of these factors is the availability of short-term forecasts of their values, in our case of future weather as well as supply and demand conditions.

Table 2 Overview of the categories, sub-categories and data with respect to the external factors used in the machine learning-based price state prediction model

In order to examine whether a linear relationship between the selected factors and futures prices exists, we perform a linear correlation analysis. Table 3 shows a selection of linear correlations between external factors for the USA and the compounded log futures prices in the short-term. The analysis suggests a low positive correlation between weather data and log futures prices, whereas the linear relationship between the supply and demand data and the log futures prices is characterized by low negative correlations.⁷

Consequently, we can assume that these external factors do not exhibit a strong linear relationship with the log futures prices and for that reason we do not consider linear classification algorithms or other linear statistical methods in our approach. And yet, a statistically significant nonlinear relationship may still exist. Hence, we focus on the application of nonlinear models. In fact, this might be the main benefit of the classification algorithms we are considering, which are able to detect nonlinear relationships between the futures prices and the price-driving external factors.

As we will see in Sect. 4, our model can be used for a detailed characterization of potential future price developments. In the context of classification, we will also refer to the external factors as features.

Table 3 Linear pairwise correlation analysis between log futures prices categorized by ’m-th closest to maturity’ and a selection of external factors for the USA

4 Empirical and simulation results

In this section we present the application and the corresponding results of the proposed ML price model. We apply our model to corn futures data and external factors in the full sample period 2015-01-01 to 2019-12-31. The full sample period is divided into a training sample period⁸ 2015-01-01 to 2018-12-31  and a test sample period⁹ 2019-01-01 to 2019-12-31. The training sample period is subsequently used for the identification of historical price states in Sect. 4.1, the calibration of the state dependent parameter sets in Sect. 4.2 and for the training of the classification models in Sect. 4.3. The test sample period is then used for the prediction of the unknown price states in Sect. 4.3 and based on this for the simulation of price scenarios in Sect. 4.4.

4.1 Identification of historical price states using K-means

We apply the K-means clustering algorithm to multi-dimensional historical time series of futures log price changes $\{d_t\}_{t = 0, 1,\ldots ,T}$ with

$$\begin{aligned} d_t {:=}({\tilde{r}}_t(1), {\tilde{r}}_t(2), \ldots {\tilde{r}}_t(5))\in {\mathbb {R}}^5 \end{aligned}$$

(14)

in the training sample period. For our procedure we need to choose an appropriate number $K\ge 1$ of clusters. Taking into account the computation of within sum of squared distances (WSS), the silhouette coefficient (Rousseeuw 1987) and the Bayesian information criterion (BIC) (Schwarz 1978; Pelleg and Moore 2000), we suggest $K = 2$ as the most plausible choice for our data.¹⁰

Figure 4 shows the clustering results included in the compounded time series $\{{\tilde{r}}_t(1)\}_{t = 0, 1,\ldots ,T}$ of log price changes corresponding to the compounded time series of futures ’1st closest to maturity.’¹¹ Specifically, the color of each data point shows the assignment of this time point to the two clusters. In addition, Table 4 shows the summary statistics of the different price states. In our application we identify each cluster with a specific price state described in the table. Indeed, the definition of the price states is well reflected by the corresponding average values of log price changes. The majority of the data is assigned to the cluster (red circle) which we define to be the high price state. In this state, log price changes are predominantly positive, with few time points exhibiting negative price changes. On the contrary, the low price state (blue square) contains only negative price changes. With 117 data points in the high and 90 data points in the low price state, the data set is well balanced.

Fig. 4

Compounded time series $\{{\tilde{r}}_t(1)\}_{t = 0, 1,\ldots ,T}$ of log futures price changes in the category ’1st closest to maturity,’ clustered in $K = 2$ different price states over the training sample period 2015-01-01 to 2018-12-31

4.2 Parameter calibration for different price states

We perform the calibration procedure for each of the $K = 2$ different price states we identified using K-means. For each price state the parameter estimates are given in Table 5. Additionally, in order to evaluate our model’s performance, we further run the calibration procedure for the benchmark model given in Sørensen (2002).

Table 4 Summary statistics of the $K = 2$ price states detected by K-means, based on the compounded time series $\{{\tilde{r}}_t(1)\}_{t = 0, 1,\ldots ,T}$ of log futures price changes in the category ’1st closest to maturity’ over the training sample period 2015-01-01 to 2018-12-31

Except for the long-term drift parameter $\mu$, the calibrated parameters of both models are within a similar range. The estimated mean reversion speed $\kappa$ as well as the short- and long-term volatilities $\sigma$ and $\nu$, respectively, do not differ significantly between both models. Also, both models suggest a positive correlation, with stronger values for the benchmark model and the low price state in the ML price model. The market price of risks $\alpha$ and $\lambda _z$ are close to zero and again of similar range for both models. Finally, we make the same observation for the seasonality parameters $\gamma _1, \gamma ^*_1, \gamma _2$ and $\gamma ^*_2$.¹²

Table 5 Optimal parameters from the calibration procedure of corn futures log prices, based on the benchmark model by Sørensen and the ML price model

4.3 Prediction of price states using K-nearest neighbors and random forest classification

For the prediction of price states using the K-nn and RF-algorithm we define the training set $D = \{(b_t, l_t), t = 0,\ldots , T\}$ with input feature vector $b_t\in {\mathbb {R}}^{30}$ given by the values of the aforementioned external factors and $l_t\in \{\text {Low}, \text {High}\}$ given by the definition of the two clusters. Then, based on D we train and select the classification models by hyperparameter optimization via grid search based on cross-validation (CV) methods. To be more precise, we apply several CV methods, such as K-fold cross-validation,¹³ to the classification model in order to minimize the classification error with regard to the hyperparameters over the prespecified parameter grid. For each CV method we then choose the classification model with the corresponding parametrization that has the highest CV score, given by the averaged accuracy score.¹⁴

For both classification algorithms, K-nn and RF, the respective best model along with the hyperparameters we vary by means of grid search is presented in Table 6. These specified classification models are subsequently used to make price state predictions in the defined test sample period.

Table 6 Specification of the best K-nn and random forest classification models, trained and selected on the training sample period 2015-01-01 to 2018-12-31 and using the external factors described in Sect. 3.2

Fig. 5

Prediction of price states using the K-nn and RF classification model in the test sample period 2019-01-01 to 2019-12-31. For illustrative purposes, we depict the price state prediction of the external factors with the highest feature importance

Figure 5 illustrates the price state predictions assigned to three of the features used with the highest feature importance.¹⁵ The price states are encoded by the same color scheme as in Fig. 4. Both classification models predict both price states with a similar pattern over the test sample period. Over the year, the majority of data points are assigned to the high state (red circle). Yet, both classification models predict a change of price states in the summer period (blue square). Specifically, starting from June 2019, a change from the high to the low price state is predicted, which mostly persists until the end of September 2019 (with the exception of one data point when using K-nn). Furthermore, when choosing the K-nn-model for price state prediction, there is an additional, short change of price states occurring in February 2019.

We conclude this section with a remark on the external randomness in our approach and a comparison to regime switching models.

Remark 1

It may seem that our procedure uses deterministic price states. In fact, we would like to point out that in the underlying mathematical model the external factors are represented by stochastic processes, constituting the source of randomness in the underlying theoretical price state process. The trained classifier then maps realizations of the external factors via a non-random functional relationship to the predictions of the corresponding price states.

An alternative approach could be based on Markov regime switching. Regime switching models, however, do not contain external factors. The relation to future values in regime switching models is random as one considers the conditional distribution of future values given the current state.

4.4 Simulation results and comparison of the price models

We combine the calibration and classification results for the purpose of Monte Carlo simulation of log futures prices. To this end we apply each classifier to realizations of the external factors in the test sample period, resulting in predictions of the corresponding price states. For illustrative purposes, Fig. 5 shows three paths of external factors in the test sample period and the corresponding price state predictions, which are obtained separately from the K-nn and RF-algorithm. Having assigned a price state $l_t\in \{\text {Low}, \text {High}\}$ at each day t in the test sample period by means of the classifiers, we then use the corresponding state-dependent parameter estimates given in Table 5 to simulate futures prices with the help of the price formula by Sørensen (2002). Along with the simulation of log futures prices based on our model, we also simulate price paths based on the benchmark model given in Sørensen (2002).

Fig. 6

[0.05, 0.95]-confidence band around the mean simulated price path, based on 10,000 simulation results of corn futures log prices with maturity (a) March 2019 and (b) December 2019. Simulated futures log prices based on the ML price model with K-nn (left) and RF classification (middle), as well as the benchmark model by Sørensen (2002) (right) are compared to the observed values. The simulations are generated for the test sample period 2019-01-01 to 2019-12-31

For the ML price models with K-nn and RF classification, as well as the benchmark model, Fig. 6 shows the simulated mean path along with the [0.05, 0.95]-confidence band based on 10,000 simulations of the futures contracts maturing in March 2019 and December 2019.¹⁶ Furthermore, we compare these predicted prices with the observed prices.

Considering the mean path of the simulated prices for the corn futures with maturity in March 2019 we obtain the best approximation of the observed log prices by the ML price model with K-nn classification. Together with the benchmark model it captures the downward price movement, whereas the ML price model with RF classification suggests an upward price movement. Additionally, the ML price model with K-nn classification results in a better approximation of the prices due to the price state change it predicts for February 2019. As for the corn futures maturing in December 2019, both ML price models give better approximations of the observed values than the benchmark model. This is mainly demonstrated in the summer period of 2019, where both ML price models are able to mimic the sharp price movements, again due to the predicted changes of price states. In contrast to this, the benchmark model only suggests a downward trend of prices, with difficulties in capturing the significant price movements in the summer period. Comparing only the ML price models among each other, the K-nn classification again gives a slightly better model as it gives a better approximation of the observed log-prices at the beginning of the year 2019.

Table 7 Different error measures for the ML price model with K-nn and RF classification and the benchmark model by Sørensen (2002)

In addition to the graphical analysis, in order to evaluate the models’ performance, we calculate error measures based on these 10, 000 simulated price scenarios. In particular, we compute the common error measures mean absolute error (MAE), root mean squared error (RMSE) and mean percentage absolute error (MAPE). We provide the results of the evaluation in Table 7. These error measures underline the main observations highlighted in the graphical analysis. First, the ML price model with K-nn classification performs best in terms of the error measures, irrespective of the futures’ maturity.¹⁷ Second, the performance of the ML price model with RF classification is twofold. While it has the worst RMSE-value for the corn futures with shortest maturity in March 2019, it achieves better error measures than the benchmark model for the futures with longer maturity in December 2019. Finally, we conclude that in most of the cases the benchmark model by Sørensen (2002) can be outperformed by our price model that includes applications of suitable machine learning methods. Clearly, the main benefit of our suggested model lies in the introduction of different price states, whose prediction is enabled by the incorporation of price-driving factors. Particularly, the ability to specify the parameter calibration in different price states enables a better approximation of the price dynamics in terms of simulated price paths and error measures.

5 Conclusion

We have proposed a two-step hybrid model that incorporates information on external factors into the simulation of futures prices on corn. The identification of historical price states and the availability of forecasts of the external factors enable us to predict prospective price states by means of the K-nearest neighbors and random forest algorithms.

As shown in the simulation study, our model is a useful tool to generate price scenarios, particularly in strongly fluctuating periods. Further, in terms of the numerical simulations and error measures, it represents an improvement to the benchmark model, with a more accurate price modeling of futures on corn and other agricultural commodities.

From the viewpoint of application, our hybrid model can be introduced into the risk management system of companies involved in the agricultural commodity business. Embedded into the system, price risks in different price states can be evaluated using Monte Carlo simulations based on our model. Furthermore, our model can be applied in order to develop trading strategies and decisions, which may differ depending on the current forecasts of external factors.

Further considerations of more complex clustering and classification algorithms can improve the model. In addition, a careful choice of external factors that are related to the agricultural commodity futures is another possibility to improve the model’s performance.

We conclude by emphasizing that our model is universally applicable for other markets and corresponding products. Specifically, our model is not limited to the assessment of futures prices, in that it can be applied to other (derivative) products. It is also not limited to the agricultural commodity market and can be applied to various other markets. In fact, the only assumptions needed for our approach are different empirically observable price states and the existence of forecasts of the external factors that are related to the considered product. We believe that these requirements are fulfilled in many markets of interest, in particular for energy-related sectors. As for the electricity market, our model may be used for the price modeling of short-term products, such as day ahead electricity prices or short-term futures. In this context, possible external factors expected to influence the price development are, for example, temperature as well as wind and solar power, for which forecasts are readily available.

Appendix

For illustrational purposes of the external factors we consider in the application of our model Table 8 summarizes the main descriptive statistics of the external factors for the USA.

Table 8 Summary statistics of the external factors for the USA