Speculative asset price dynamics and wealth taxes

Abstract

Based on the seminal asset-pricing model by Brock and Hommes (J Econ Dyn Control 22:1235–1274, 1998), we analytically show that higher wealth taxes increase the risky asset’s fundamental value, enlarge its local stability domain, may prevent the birth of nonfundamental steady states and, if they exist, reduce the risky asset’s mispricing. We furthermore find that higher wealth taxes may hinder the emergence of endogenous asset price oscillations and, if they exist, dampen their amplitudes. Since oscillatory price dynamics may be associated with lower mispricing than locally stable nonfundamental steady states, policymakers may not always want to suppress them by imposing (too low) wealth taxes. Overall, however, our study suggests that wealth taxes tend to stabilize the dynamics of financial markets.

1 Introduction

The detailed historical accounts offered by Galbraith (1994), Kindleberger and Aliber (2011) and Shiller (2015) reveal that the boom-bust nature of financial markets, mainly driven by the trading behavior of heterogeneous and boundedly rational speculators, may be quite harmful for the real economy. In the aftermath of financial and economic downturns, voices habitually arise requesting the imposition of a tax on speculators’ wealth to accommodate for the economic damage caused by speculators’ trading frenzy. Occasionally, these requests are associated with the hope that wealth taxes may be used to mitigate economic inequality, as outlined by Piketty (2014).¹ Unfortunately, the relationship between speculative asset price dynamics and wealth taxes has received only scant academic attention so far. One important question in this respect is whether policymakers may unintentionally render financial markets even more unstable by taxing speculators’ wealth. Based on a behavioral asset-pricing model, we find, fortunately, that a tax imposed on the wealth of speculators tends to have a stabilizing effect on the dynamics of financial markets. In particular, our analysis reveals that wealth taxes penalize speculators applying cheap destabilizing technical expectation rules more strongly than speculators relying on costly stabilizing fundamental expectation rules, thereby prompting a shift towards the use of stabilizing expectation rules. Needless to say, policymakers may generate substantial revenues by imposing wealth taxes, though this aspect is not at the core of our paper.

As a workhorse for our study, we use the seminal asset-pricing model by Brock and Hommes (1998). A key insight of their paper is that the trading behavior of boundedly rational and heterogeneous speculators, switching between a destabilizing technical and a stabilizing fundamental expectation rule, subject to their evolutionary fitness, may create complex endogenous asset price dynamics. Most notably, Brock and Hommes (1998) demonstrate that speculators’ rule selection behavior may create a rational route to randomness. Since simple technical expectation rules are cheaper than more sophisticated fundamental expectation rules, they produce higher steady-state profits. As long as speculators react only weakly to the fitness differential of their expectation rules, the market impact of the technical expectation rule remains relatively modest, allowing the asset price to converge towards its fundamental value. However, if speculators start to pay more attention to the expectation rules’ fitness differential, the technical expectation rule gains more followers and may cause the birth of locally stable nonfundamental steady states. If speculators’ intensity of choice increases even further, the popularity of the technical expectation rule continues to grow. Consequently, the nonfundamental steady states eventually become unstable and give rise to oscillatory asset price dynamics.

We extend the model by Brock and Hommes (1998) along two lines. First, we consider the eventuality of policymakers imposing a tax on speculators’ wealth. Second, we follow Hommes et al. (2005) and Anufriev and Tuinstra (2013) and allow the supply of (outside) shares of the risky asset to be positive. Assuming a positive supply of (outside) shares of the risky asset implies that the fundamental value of the risky asset entails a risk premium (which is, for simplicity, absent in the original model by Brock and Hommes 1998). Since the risk premium depends negatively on wealth taxes, higher wealth taxes increase the risky asset’s fundamental value. Moreover, the difference in the steady-state fractions of the fundamental and technical expectation rule depends positively on wealth taxes and negatively on speculators’ intensity of choice and the costs associated with using the fundamental expectation rule. As discussed above, an increase in speculators’ intensity of choice has the effect that more of them select the destabilizing technical expectation rule, rendering the risky asset’s fundamental value unstable and causing the birth of locally stable nonfundamental steady states or even the emergence of endogenous oscillatory price dynamics. Interestingly, policymakers may reverse this process and re-establish market stability by imposing higher wealth taxes. To put it plainly, policymakers may turn speculators’ rational route to randomness into a tax route to stability. As a cautionary note, however, we must add that oscillatory price dynamics may be associated with lower mispricing—defined as the deviation between the price of the risky asset and its fundamental value—than locally stable nonfundamental steady states. Hence, policymakers may not always want to suppress them by imposing (too low) wealth taxes.

In recent years, the asset-pricing model by Brock and Hommes (1998) has received great empirical support from scholars such as Boswijk et al. (2007), Anufriev and Hommes (2012), Hommes and in’t Veld (2017) and Schmitt (2020). Moreover, Brock et al. (2010), Anufriev and Tuinstra (2013), Dercole and Radi (2020) and Schmitt et al. (2020) and Schmitt and Westerhoff (2021), amongst others, have successfully used their model to address a number of relevant policy questions; see Hommes (2013) and Dieci and He (2018) for general surveys.

Of course, different forms of financial market taxes exist. Westerhoff and Dieci (2006), Mannaro et al. (2008) and Jacob Leal and Napoletano (2019) analyze how a small tax on speculators’ transactions may affect the stability of financial markets. A major difference between transaction taxes and wealth taxes is that transaction taxes aim at penalizing aggressively trading speculators, while wealth taxes essentially reduce speculators’ total investment funds. From a technical perspective, however, our paper is more related to the following papers. In particular, Anufriev et al. (2018) experimentally test the asset-pricing model by Brock and Hommes (1998) and report that a reduction in the cost of stabilizing expectation rules tends to produce more stable asset price dynamics, lending the main channel that drives our analytical insights at least some indirect empirical credit. Moreover, Schmitt and Westerhoff (2015) explore how profit taxes may shape the dynamics of the cobweb model by Brock and Hommes (1997) in which farmers switch between rational and naïve expectation rules, depending on the rules’ past profitability. Schmitt et al. (2017) show that profit taxes may also stabilize the dynamics of market entry models by reducing profit differentials between competing markets. Finally, Martin et al. (2021) explore how policymakers may stabilize the dynamics of housing markets by adjusting the tax code. As far as we are aware, however, the relationship between speculative asset price dynamics and wealth taxes has not yet been explored in this line of research. Given the relevance of this topic, we seek to make some progress in this direction.

We continue as follows. In Sect. 2, we extend the asset-pricing model by Brock and Hommes (1998) as outlined above. In Sect. 3, we present our main analytical results and illustrate them numerically. In Sect. 4, we discuss a number of more subtle issues related to the imposition of wealth taxes. In Sect. 5, we conclude our paper and point out some avenues for future research. Appendix A1 to A5 contain our main proofs and a number of additional simulations.

2 The model

Brock and Hommes (1998) assume that speculators can invest in a safe asset, paying the risk-free interest rate ${r}$, and in a risky asset, paying an uncertain dividend ${D}_{t}$. For simplicity, they specify the dividend process of the risky asset as

$${D}_{t}=\overline{D}+{\delta }_{t},$$

(1)

where ${\delta }_{t}\sim N(0,{\sigma }_{\delta }^{2})$. While the price of the safe asset is fixed, the price of the risky asset changes with respect to speculators’ trading behavior. Let ${P}_{t}$ be the price of the risky asset (ex-dividend) at time $t$. The end-of-period wealth of speculator $i$ can be expressed as

$$ W_{{t + 1}}^{i} = \left( {1 - \tau } \right)\left. {\left( {\left( {1 + r} \right)W_{t}^{i} + Z_{t}^{i} \left( {P_{{t + 1}} + D_{{t + 1}} - (1 + r} \right)P_{t} } \right) - C} \right),$$

(2)

where ${Z}_{t}^{i}$ stands for speculator $i$’s demand for the risky asset and $0\le \tau <1$ denotes the tax rate imposed by policymakers on speculators’ wealth. Parameter $C\ge 0$ represents possible (fixed) trading costs and will be discussed in more detail below.² Note that we regard all variables indexed with $t+1$ as random and assume that ${W}_{t+1}^{i}>0$ for all $i$ and $t$. Since speculators are myopic mean–variance maximizers, speculator $i$’s demand for the risky asset follows from

$$ \max _{{Z_{t}^{i} }} ~\left[ {E_{t}^{i} \left[ {W_{{t + 1}}^{i} } \right] - \frac{\lambda }{2}V_{t}^{i} \left[ {W_{{t + 1}}^{i} } \right]} \right],$$

(3)

where ${E}_{t}^{i}\left[{W}_{t+1}^{i}\right]$ and ${V}_{t}^{i}\left[{W}_{t+1}^{i}\right]$ denote his belief about the conditional expectation and conditional variance of his wealth, respectively, and parameter $\lambda >0$ stands for his risk aversion. Hence, speculator $i$’s first-order condition reads as

$$ \left( {1 - \tau } \right)\left( {E_{t}^{i} \left[ {P_{{t + 1}} } \right] + E_{t}^{i} \left[ {D_{{t + 1}} } \right] - \left( {1 + r} \right)P_{t} } \right) - \left( {1 - \tau } \right)^{2} Z_{t}^{i} \lambda V_{t}^{i} \left[ {P_{{t + 1}} + D_{{t + 1}} } \right] = 0 $$

(4)

and his optimal demand for the risky asset results in

$${Z}_{t}^{i}=\frac{{E}_{t}^{i}\left[{P}_{t+1}\right]+{E}_{t}^{i}\left[{D}_{t+1}\right]-(1+r){P}_{t}}{(1-\tau )\lambda {V}_{t}^{i}\left[{P}_{t+1}+{D}_{t+1}\right]}.$$

(5)

As indicated by (4), wealth taxes affect speculator $i$’s wealth expectations linearly, while their effect on his risk perception is quadratic. Consequently, speculator $i$’s demand for the risky asset increases in line with the tax rate.

For analytical tractability, Brock and Hommes (1998) introduce the following simplifying assumptions. There are $N$ speculators in total, believing that $E_{t}^{i} \left[ {D_{{t + 1}} } \right] = ~\overline{D}$ and ${V}_{t}^{i}\left[{P}_{t+1}+{D}_{t+1}\right]={\sigma }^{2}$. We can therefore express speculators’ aggregate demand for the risky asset as ${Z}_{t}=\sum _{i=1}^{N}{Z}_{t}^{i}=N\frac{\frac{1}{N}\sum _{i=1}^{N}{E}_{t}^{i}\left[{P}_{t+1}\right]+\overline{D}-\left(1+r\right){P}_{t}}{(1-\tau )\lambda {\sigma }^{2}}$. Moreover, denoting speculators’ average expectation about the risky asset’s next period price by ${E}_{t}\left[{P}_{t+1}\right]=\frac{1}{N}\sum _{i=1}^{N}{E}_{t}^{i}\left[{P}_{t+1}\right]$ yields

$${Z}_{t}=N\frac{{E}_{t}\left[{P}_{t+1}\right]+\overline{D}-(1+r){P}_{t}}{(1-\tau )\lambda {\sigma }^{2}}.$$

(6)

Note that speculators’ demand for the risky asset increases in line with their price and dividend expectations and decreases with the risk-free interest rate, the current price of the risky asset, their risk aversion and variance beliefs. Moreover, higher wealth taxes increase speculators’ demand for the risky asset.

Market equilibrium requires that the demand for the risky asset equals the total supply of the risky asset, that is

$${Z}_{t}={S}_{t}.$$

(7)

The total supply of the risky asset, i.e., the number of (outside) shares issued by firms, is constant, given by

$${S}_{t}=\widehat{S}=N\overline{S},$$

(8)

where $\overline{S}$ represents the (average) number of available (outside) shares of the risky asset per speculator.³ Combining (6), (7) and (8) indicates that the price of the risky asset is determined by.

$${P}_{t}=\frac{{{E}_{t}[P}_{t+1}]+\overline{D}-(1-\tau )\lambda {\sigma }^{2}\overline{S}}{1+r}+{\varepsilon }_{t},$$

(9)

where ${\varepsilon }_{t}$ reflects additional random disturbances with ${\varepsilon }_{t}\sim N\left(0,{\sigma }_{\varepsilon }^{2}\right)$. Note that (9) implies that ${P}_{t}$ increases in line with speculators’ price and dividend expectations and decreases with the risk-free interest rate, their risk aversion and variance beliefs. More importantly for our purpose, however, (9) reveals that higher wealth taxes decrease the value of risk-adjusted dividend payments, where the risk-related reduction of dividend payments is given by $(1-\tau )\lambda {\sigma }^{2}\overline{S}$. We may grasp the economic intuition behind this result by interpreting (9) as a no-arbitrage condition. Since lower risk-adjusted dividend payments make the risky asset more attractive, speculators’ demand for the risky asset increases, as indicated by (6). A higher demand for the risky asset, in turn, increases the price of the risky asset, up to the point where speculators are again indifferent between holding the risky asset and the safe asset. Recall that Brock and Hommes (1998) assume that there is a zero supply of (outside) shares of the risky asset, i.e., ${S}_{t}=0$, implying that ${P}_{t}=\frac{{{E}_{t}[P}_{t+1}]+\overline{D}}{1+r}$. Clearly, such a setup does not entail a risk premium.

In line with empirical and experimental evidence, summarized by Menkhoff and Taylor (2007) and Hommes (2011), speculators may use a technical or a fundamental expectation rule to forecast the price of the risky asset. The market shares of speculators following the technical and fundamental expectation rule are given by ${N}_{t}^{C}$ and ${N}_{t}^{F}=1-{N}_{t}^{C}$. Speculators’ average price expectations are defined by

$${{E}_{t}[P}_{t+1}]={N}_{t}^{C}{E}_{t}^{C}[{P}_{t+1}]+{N}_{t}^{F}{E}_{t}^{F}[{P}_{t+1}].$$

(10)

Speculators compute the risky asset’s fundamental value $F$ by discounting future risk-adjusted dividend payments, that is $F=\frac{\overline{D}-(1-\tau )\lambda {\sigma }^{2}\overline{S}}{r}=\frac{\overline{D}}{r}-\mathrm{R}\mathrm{P}$, where $\mathrm{R}\mathrm{P}=\frac{(1-\tau )\lambda {\sigma }^{2}\overline{S}}{r}$ denotes the risky asset’s risk premium. Note that this solution can easily be deducted from (9), assuming that ${{P}_{t}={E}_{t}[P}_{t+1}]=F$. Speculators applying the technical expectation rule, also called chartists, expect the deviation between the price of the risky asset and its fundamental value to increase. Their expectations are formalized by

$${E}_{t}^{C}\left[{P}_{t+1}\right]={P}_{t-1}+\chi ({P}_{t-1}-F),$$

(11)

where $\chi >0$ denotes the strength of chartists’ extrapolation behavior. Speculators using the fundamental expectation rule, also called fundamentalists, believe that the price of the risky asset will approach its fundamental value. As usual, their expectations are written as

$${E}_{t}^{F}\left[{P}_{t+1}\right]={P}_{t-1}+\phi (F-{P}_{t-1})$$

(12)

where $0<\phi \le 1$ indicates fundamentalists’ expected mean reversion speed. Note that both expectation rules predict the price of the risky asset for period $t+1$ at the beginning of period $t$, based on information available in period $t-1$. Consequently, speculators have to predict the price of the risky asset two periods ahead.

Brock and Hommes (1998) consider speculators switching between the technical and fundamental expectation rule with respect to their evolutionary fitness, measured in terms of past realized profits, arguing that profits are what speculators care most about.⁴ Since our goal is to explore the effects of wealth taxes, we measure the expectation rules’ evolutionary fitness via their effects on speculators’ wealth dynamics. As we will see in more detail in the sequel, what really matters to speculators is the difference in the wealth dynamics associated with their two expectation rules. Moreover, these rule-dependent wealth differences are equal among all speculators, and, for $\tau =0$, equal to the rules’ profit differentials, as in Brock and Hommes (1998). In fact, straightforward computations reveal that the difference between the fitness of the fundamental and technical expectation rule of speculator $i$ boils down to

$${A}_{t}^{F,i}-{A}_{t}^{C,i}={W}_{t-1}^{F,i}{-W}_{t-1}^{C,i}=\left(1-\tau \right)\left(\left({P}_{t-1}+{D}_{t-1}-\left(1+r\right){P}_{t-2}\right)\left({{Z}_{t-2}^{F}-{Z}_{t-2}^{C}}\right)-C\right)={A}_{t}^{F}-{A}_{t}^{C},$$

(13)

where

$${Z}_{t-2}^{C}=\frac{{E}_{t-2}^{C}\left[{P}_{t-1}\right]+\overline{D}-\left(1+r\right){P}_{t-2}}{(1-\tau )\lambda {\sigma }^{2}},$$

(14)

and

$${Z}_{t-2}^{F}=\frac{{E}_{t-2}^{F}\left[{P}_{t-1}\right]+\overline{D}-\left(1+r\right){P}_{t-2}}{(1-\tau )\lambda {\sigma }^{2}}.$$

(15)

Note that the time structure of the model implies that the last observable fitness differential of the two expectation rules depends on speculator $i$’s hypothetically experienced wealth differential in period $t-1$, had he either used the fundamental or the technical expectation rule in period $t-2$. With a slight abuse of notation, we assume in the derivation of (13) that the cost differential between using the fundamental and technical expectation rule, introduced in (2) as possible trading costs, is represented by parameter $C>0$, a term that Brock and Hommes (1998) prominently call (constant per period) information costs.⁵

Finally, the market shares of chartists and fundamentalists are modeled using the well-known discrete choice approach. Let us from now on assume that there is a continuum of speculators with mass $N$. We thus obtain for the market shares of chartists and fundamentalists

$${N}_{t}^{C}=\frac{\mathrm{e}\mathrm{x}\mathrm{p}[\beta {A}_{t}^{C}]}{\mathrm{e}\mathrm{x}\mathrm{p}\left[\beta {A}_{t}^{C}\right]+\mathrm{e}\mathrm{x}\mathrm{p}[\beta {A}_{t}^{F}]}=\frac{1}{1+\mathrm{e}\mathrm{x}\mathrm{p}[\beta {(A}_{t}^{F}-{A}_{t}^{C})]}$$

(16)

and

$$ N_{t}^{F} = \frac{{\exp \left[ {\beta A_{t}^{F} } \right]}}{{\exp \left[ {\beta A_{t}^{C} } \right] + \exp \left[ {\beta A_{t}^{F} } \right]}} = 1 - N_{t}^{C} . $$

(17)

The intensity of choice parameter $\beta >0$ measures how quickly the mass of speculators switches to the more successful expectation rule. For $\beta \to 0$, speculators do not observe any fitness differentials between the two expectation rules, implying that ${N}_{t}^{C}={N}_{t}^{F}=0.5$. For $\beta \to \infty$, speculators observe fitness differentials perfectly and all of them will choose the expectation rule that yields the higher fitness. Accordingly, the higher the intensity of choice parameter, the more speculators will select the superior expectation rule. In this sense, speculators display a boundedly rational learning behavior, an important ingredient for behavioral models to combat the lurking wilderness-of-bounded-rationality critique, as pointed out by Hommes (2013).

3 Main analytical and numerical results

In the absence of exogenous shocks, i.e., for ${\sigma }_{\delta }^{2}=0$ and ${\sigma }_{\varepsilon }^{2}=0$, the dynamics of our model is driven by the iteration of a three-dimensional nonlinear deterministic map. In fact, introducing the difference in market shares, i.e., ${m}_{t}={N}_{t}^{F}-{N}_{t}^{C}=\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}[\frac{\beta }{2}({A}_{t}^{F}-{A}_{t}^{C})]$, and noting that ${N}_{t}^{C}=(1-{m}_{t})/2$ and ${N}_{t}^{F}=(1+{m}_{t})/2$, yields the map.

$$ M: = \left\{ {\begin{array}{*{20}l} {P_{t} = \frac{1}{{1 + r}}\left\{ {\frac{{1 - m_{{t - 1}} }}{2}\chi \left( {P_{{t - 1}} - F} \right) + \frac{{1 + m_{{t - 1}} }}{2}\phi \left( {F - P_{{t - 1}} } \right) + P_{{t - 1}} + \overline{D} - (1 - \tau )\lambda \sigma ^{2} \overline{S}} \right\}} \hfill \\ {y_{t} = P_{{t - 1}} } \hfill \\ {m_{t} = \tanh \left[ {\frac{\beta }{2}\left\{ {\left( {P_{t} + \overline{D} - \left( {1 + r} \right)P_{{t - 1}} } \right)\frac{{(\chi + \phi )(F - y_{{t - 1}} )}}{{\lambda \sigma ^{2} }} - \left( {1 - \tau } \right)C} \right\}} \right]} \hfill \\ \end{array} } \right. $$

(18)

where ${y}_{t}={P}_{t-1}$ is an auxiliary variable.

Propositions 1 and 2, proven in the appendix, summarize our main results for $\overline{\mathrm{S}}=0$ and $\overline{\mathrm{S}}>0$, respectively, where an overbar denotes steady-state quantities. We are particularly interested in how an increase in parameter $\beta$ may affect the levels and stability domains of the model’s steady state(s) and how that relates to parameter $\tau$.

Proposition 1:

($\overline{S}=0$): Map (18) may possess up to three steady states, a fundamental steady state, given by ${\mathrm{F}\mathrm{S}\mathrm{S}}_{1}=\left(\overline{{P}_{1}},\overline{{y}_{1}},\overline{{m}_{1}}\right)=(\frac{\overline{D}}{r},{P}_{1},-\mathrm{tan}{\text{h}}[\frac{\left(1-\tau \right)\beta C}{2}])$, and two nonfundamental steady states, given by $\mathrm{N}\mathrm{F}{\mathrm{S}\mathrm{S}}_{\mathrm{2,3}}=\left(\overline{{P}_{\mathrm{2,3}}},\overline{{y}_{\mathrm{2,3}}},\overline{{m}_{\mathrm{2,3}}}\right)=(\overline{{P}_{1}}\pm \sqrt{\frac{\lambda {\sigma }^{2}(\left(1-\tau \right)\beta C-2\mathrm{arctan}{\text{h}}[\frac{2r+\phi -\chi }{\chi +\phi }])}{r\beta (\chi +\phi )}},\overline{{P}_{\mathrm{2,3}}},-\frac{2r+\phi -\chi }{\chi +\phi }$), with $\mathrm{N}\mathrm{F}{\mathrm{S}\mathrm{S}}_{2}\ge \mathrm{N}\mathrm{F}{\mathrm{S}\mathrm{S}}_{3}$. ${\mathrm{F}\mathrm{S}\mathrm{S}}_{1}$ always exists. Assume that $r<\chi <2r+\phi$. For $0<\beta <{\beta }^{P}:=\frac{2\mathrm{arctanh}[\frac{2r+\phi -\chi }{\chi +\phi }]}{\left(1-\tau \right)C}$, ${\mathrm{F}\mathrm{S}\mathrm{S}}_{1}$ is locally stable. At $\beta ={\beta }^{P}$, a pitchfork bifurcation occurs, causing the birth of $\mathrm{N}\mathrm{F}{\mathrm{S}\mathrm{S}}_{\mathrm{2,3}}$. For ${\beta }^{P}<\beta <{\beta }^{N}$, $\mathrm{N}\mathrm{F}{\mathrm{S}\mathrm{S}}_{\mathrm{2,3}}$ are locally stable, where $\overline{{P}_{\mathrm{2,3}}}$ are symmetrically located around $\overline{{P}_{1}}$. As parameter $\beta$ exceeds ${\beta }^{N}=\frac{\left(\phi +\chi \right)(\left(1+2r\right)-\sqrt{1+8r\left(1+r\right)})+4\left(r+\phi \right)\left(r-\chi \right)\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left[\left.\frac{2r+\phi -\chi }{\phi +\chi }\right]\right.}{2\left(1-\tau \right)C(r+\phi )(r-\chi )}$, $\mathrm{N}\mathrm{F}{\mathrm{S}\mathrm{S}}_{\mathrm{2,3}}$ become simultaneously unstable due to a Neimark–Sacker bifurcation, giving rise to oscillatory dynamics. Higher values of parameter $\beta$ increase the gaps between $\overline{{P}_{1}}$ and $\overline{{P}_{\mathrm{2,3}}}$ and $\overline{{P}_{2}}$ and $\overline{{P}_{3}}$. An increase in parameter $\tau$ causes the opposite and increases the critical bifurcation values ${\beta }^{P}$ and ${\beta }^{N}$.

Figure 1 provides a schematic representation of the levels and stability domains of the risky asset’s fundamental and nonfundamental steady-state prices as a function of parameter $\beta$. The left panels depict the main results of Proposition 1; the right panels anticipate those of Proposition 2, to be stated in the sequel. Different colors mark the risky asset’s fundamental and nonfundamental steady-state prices. Red (blue) tonalities indicate the absence (presence) of wealth taxes. Solid (dotted) lines indicate locally stable (unstable) steady states. From the top left panel to the bottom right panel, we assume (1) $\tau =0$ and $\overline{S}=0$, (2) $\tau >0$ and $\overline{S}=0$, superimposed on $\tau =0$ and $\overline{S}=0$, (3) $\tau =0$ and $\overline{S}>0$ and (iv) $\tau >0$ and $\overline{S}>0$, superimposed on $\tau =0$ and $\overline{S}>0$. Note that it may be useful to absorb the results of Proposition 2 in connection with Fig. 1, although it does not capture all possible bifurcation scenarios.

Fig. 1

Schematic representation of the levels and stability domains of the risky asset’s fundamental and nonfundamental steady state prices as a function of parameter $\beta$. Top left: $\tau =0$ and $\overline{S}=0$. Bottom left: $\tau >0$ and $\overline{S}=0$, superimposed on $\tau =0$ and $\overline{S}=0$. Top right: $\tau =0$ and $\overline{S}>0$. Bottom right: $\tau >0$ and $\overline{S}>0$, superimposed on $\tau =0$ and $\overline{S}>0$. Different colors mark the risky asset’s fundamental and nonfundamental steady-state prices, where solid (dotted) lines indicate locally stable (unstable) steady states

Proposition 2:

($\overline{\mathrm{S}}>0$): Map (18) may possess up to three steady states, a fundamental steady state, given by ${\mathrm{F}\mathrm{S}\mathrm{S}}_{1}=\left(\overline{{P}_{1}},\overline{{y}_{1}},\overline{{m}_{1}}\right)=(\frac{\overline{D}-\left(1-\tau \right)\lambda {\sigma }^{2}\overline{S}}{r},{P}_{1},-\mathrm{tan}{\text{h}}[\frac{\left(1-\tau \right)\beta C}{2}])$, and two nonfundamental steady states, given by $\mathrm{N}\mathrm{F}{\mathrm{S}\mathrm{S}}_{\mathrm{2,3}}=\left(\overline{{P}_{\mathrm{2,3}}},\overline{{y}_{\mathrm{2,3}}},\overline{{m}_{\mathrm{2,3}}}\right)=(\overline{{P}_{1}}+\frac{(1-\tau )\lambda {\sigma }^{2}\overline{S}}{2r}\pm \sqrt{{\left(\frac{(1-\tau )\lambda {\sigma }^{2}\overline{S}}{2r}\right)}^{2}+\frac{\lambda {\sigma }^{2}(\left(1-\tau \right)\beta C-2\mathrm{arctan}{\text{h}}[\frac{2r+\phi -\chi }{\chi +\phi }])}{r\beta (\chi +\phi )}},\overline{{P}_{\mathrm{2,3}}},-\frac{2r+\phi -\chi }{\chi +\phi }$), with $\mathrm{N}\mathrm{F}{\mathrm{S}\mathrm{S}}_{2}\ge \mathrm{N}\mathrm{F}{\mathrm{S}\mathrm{S}}_{3}$. ${\mathrm{F}\mathrm{S}\mathrm{S}}_{1}$ always exists. Assume that $r<\chi <2r+\phi$. For $0 < \beta {\text{ }} < \beta {\text{ }}^{P} : = \frac{{2\arctan{\text{h}}\left[ {\frac{{2r + \phi - \chi }}{{\chi + \phi }}} \right]}}{{\left( {1 - \tau } \right)C + r\left( {\chi + \phi } \right)\lambda \sigma ^{2} \left( {\frac{{\left( {1 - \tau } \right)\overline{S}}}{{2r}}} \right)^{2} }}$, ${\mathrm{F}\mathrm{S}\mathrm{S}}_{1}$ is locally stable. At $\beta {=\beta }^{S}$, a saddle-node bifurcation occurs, causing the birth of $\mathrm{N}\mathrm{F}{\mathrm{S}\mathrm{S}}_{\mathrm{2,3}}$, with $\mathrm{N}\mathrm{F}{\mathrm{S}\mathrm{S}}_{2}$ as the node and $\mathrm{N}\mathrm{F}{\mathrm{S}\mathrm{S}}_{3}$ as the saddle. For ${\beta }^{S}<\beta <{\beta }^{T}:=\frac{2\mathrm{arctan}{\text{h}}[\frac{2r+\phi -\chi }{\chi +\phi }]}{\left(1-\tau \right)C}$, ${FSS}_{1}$ remains locally stable, $\mathrm{N}\mathrm{F}{\mathrm{S}\mathrm{S}}_{2}$ is at least initially locally stable and $\mathrm{N}\mathrm{F}{\mathrm{S}\mathrm{S}}_{3}$ is unstable, with $\overline{{P}_{2}}>\overline{{P}_{3}}>\overline{{P}_{1}}$. At $\beta ={\beta }^{T}$, a transcritical bifurcation occurs, implying that $\overline{{P}_{2}}>\overline{{P}_{1}}=\overline{{P}_{3}}$. As parameter $\beta$ exceeds ${\beta }^{T}$, ${\mathrm{F}\mathrm{S}\mathrm{S}}_{1}$ becomes unstable,${\mathrm{N}\mathrm{F}\mathrm{S}\mathrm{S}}_{2}$ may still be locally stable and $\mathrm{N}{\mathrm{F}\mathrm{S}\mathrm{S}}_{3}$ is initially locally stable, with $\overline{{P}_{2}}>\overline{{P}_{1}}>\overline{{P}_{3}}$. $\mathrm{N}\mathrm{F}{\mathrm{S}\mathrm{S}}_{\mathrm{2,3}}$ eventually become unstable due to a Neimark–Sacker bifurcation as parameter $\beta$ crosses ${\beta }^{N,U}$ and ${\beta }^{N,L}$, respectively, giving rise to oscillatory dynamics, with ${\beta }^{N,U}<{\beta }^{N,L}$. When $\overline{\mathrm{S}}$ is sufficiently large, we may observe that ${\beta }^{N,U}<{\beta }^{T}$. Higher values of parameter $\beta$ increase the gaps between $\overline{{P}_{1}}$ and $\overline{{P}_{\mathrm{2,3}}}$ and $\overline{{P}_{2}}$ and $\overline{{P}_{3}}$. An increase in parameter $\tau$ causes the opposite and increases the critical bifurcation values ${\beta }^{S}$, ${\beta }^{T}$, ${\beta }^{N,U}$ and ${\beta }^{N,L}$.

In the following, we discuss the main economic implications of Propositions 1 and 2, highlighting, in particular, the role played by parameters $\tau$, $\beta$ and $\overline{S}$.

3.1 Level of the fundamental steady state

• (i) If the supply of (outside) shares of the risky asset is zero, i.e., $\overline{S}=0$, the risky asset’s risk premium vanishes and its fundamental value is given by $\overline{{P}_{1}}=F=\frac{\overline{D}}{r}$. Consequently, the risky asset’s fundamental value, corresponding to the discounted value of future dividend payments, is independent of wealth taxes and speculators’ intensity of choice.

• (ii) For $\overline{S}>0$, the risky asset’s fundamental steady state depends on wealth taxes, although not on speculators’ intensity of choice. Note first that a higher supply of (outside) shares of the risky asset increases the risky asset’s risk premium, given by $RP=\frac{(1-\tau )\lambda {\sigma }^{2}\overline{S}}{r}$, and, thereby, decreases its fundamental value $\overline{{P}_{1}}=F=\frac{\overline{D}-(1-\tau )\lambda {\sigma }^{2}\overline{S}}{r}=\frac{\overline{D}}{r}-\mathrm{R}\mathrm{P}$. Since wealth taxes (linearly) shrink the risky asset’s risk premium, $\overline{{P}_{1}}$ (linearly) increases in line with parameter $\tau$. The economic rationale behind this is as follows. Higher wealth taxes reduce the risk associated with speculators’ wealth, caused by the risky asset’s price and dividend fluctuations. Since the risky asset thus appears more attractive to speculators, their demand for the risky asset increases, creating, in turn, an increase in the price of the risky asset.

• (iii) Note that the model’s fundamental steady state implies that $\overline{{m}_{1}}=-\mathrm{tan}{\text{h}}\left[\frac{\left(1-\tau \right)\beta C}{2}\right]$, $\overline{{N}_{1}^{C}}=\frac{1}{1+\mathrm{e}\mathrm{x}\mathrm{p}[-(1-\tau )\beta C]}$ and $\overline{{N}_{1}^{F}}=\frac{1}{1+\mathrm{e}\mathrm{x}\mathrm{p}[(1-\tau )\beta C]}$. Hence, the expectation rules’ market shares at the fundamental steady state depend on the wealth tax, independently of the size of the supply of (outside) shares of the risky asset. In particular, the market share of the technical (fundamental) expectation rule decreases (increases) in line with the wealth tax. The reason for this is as follows. At the fundamental steady state, the expectation rules’ fitness differential amounts to $\overline{{A}_{1}^{F}}-\overline{{A}_{1}^{C}}=-\left(1-\tau \right)C$.⁶ Hence, higher wealth taxes reduce the fitness disadvantage of the fundamental expectation rule, making this rule relatively more attractive. For completeness, we remark that each speculator holds $\overline{S}$ shares of the risky asset at the fundamental steady state, or, stated more formally, $\overline{{Z}_{1}^{C}}=\overline{S}=\widehat{S}/N$, $\overline{{Z}_{1}^{F}}=\overline{S}=\widehat{S}/N$ and $\overline{{N_{1}^{C} }} ~N~\overline{{Z_{1}^{C} }} + \overline{{N_{1}^{F} }} ~N~\overline{{Z_{1}^{F} }} = \hat{S}$.

3.2 Stability domain of the fundamental steady state

As demonstrated in Appendix A2, the fundamental steady-state stability condition, i.e., $0<\beta <{\beta }^{P}={\beta }^{T}=\frac{2\mathrm{arctan}{\text{h}}[\frac{2r+\phi -\chi }{\chi +\phi }]}{\left(1-\tau \right)C}$, can also be written as $\overline{{N}_{1}^{C}}\chi -\overline{{N}_{1}^{F}}\phi <r$. From the latter expression, it follows immediately that the behavior of chartists is destabilizing while that of fundamentalists is stabilizing. For $\beta \to 0$, we obtain $\overline{{N}_{1}^{C}}=\overline{{N}_{1}^{C}}=0.5$ and thus $\chi <2r+\phi$. If this condition is violated, the fundamental steady state is always unstable. For $\beta \to \infty$, we have $\overline{{N}_{1}^{C}}=1$ and $\overline{{N}_{1}^{F}}=0$, implying that $\chi <r$. If this condition holds, the fundamental steady state is locally stable. In between, i.e., for $r<\chi <2r+\phi$, we can apply our propositions and conclude that an increase in speculators’ intensity of choice may compromise the stability of the fundamental steady state.⁷ However, it is also clear that policymakers can always re-establish the fundamental steady-state local stability by increasing the tax rate on speculators’ wealth. This result holds for $\overline{S}=0$ and $\overline{S}>0$.

3.3 Levels of nonfundamental steady states

• (i) For $\overline{S}=0$, we obtain $\overline{{P}_{\mathrm{2,3}}}=\overline{{P}_{1}}\pm \sqrt{\frac{\lambda {\sigma }^{2}(\left(1-\tau \right)\beta C-2\mathrm{arctan}{\text{h}}[\frac{2r+\phi -\chi }{\chi +\phi }])}{r\beta (\chi +\phi )}}$ or, alternatively, $\overline{{P}_{\mathrm{2,3}}}=\overline{{P}_{1}}\pm \sqrt{\frac{\lambda {\sigma }^{2}(\overline{{N}_{1}^{C}}\chi -\overline{{N}_{1}^{F}}\phi -r)}{r\beta (\chi +\phi )}}$. Accordingly, the model’s pitchfork bifurcation gives rise to two additional nonfundamental steady states, symmetrically located around $\overline{{P}_{1}}$. Furthermore, $\overline{{P}_{\mathrm{2,3}}}$ indicate that the risky asset’s mispricing increases with speculators’ intensity of choice, although policymakers can decrease the gap between $\overline{{P}_{\mathrm{2,3}}}$ and $\overline{{P}_{1}}$ as well as the gap between $\overline{{P}_{2}}$ and $\overline{{P}_{3}}$ by raising the wealth tax.

• (ii) For $\overline{S}>0$, however, the coordinates of $\overline{{P}_{\mathrm{2,3}}}$ display a different and, as we believe, fascinating behavior. The nonfundamental steady states are born via a saddle-node bifurcation when parameter $\beta$ passes ${\beta }^{S}$, and we have $\overline{{P}_{2}}>\overline{{P}_{3}}>\overline{{P}_{1}}$. Note that the upper (lower) nonfundamental value of the risky asset price increases (decreases) in line with parameter $\beta$. At the transcritical bifurcation, we have $(1-\tau )\beta C=2\mathrm{arctan}{\text{h}}[\frac{2r+\phi -\chi }{\chi +\phi }]$ and the square root’s second term of $\overline{{P}_{\mathrm{2,3}}}$ equals zero, resulting in $\overline{{P}_{2}}=\overline{D}/r$ and $\overline{{P}_{3}}=\overline{{P}_{1}}$, i.e., the difference between the two nonfundamental steady states is given by the risky asset’s risk premium, or, in technical terms, $\overline{{P}_{2}}-\overline{{P}_{3}}=\frac{\left(1-\tau \right)\lambda {\sigma }^{2}\overline{S}}{r}=RP$. Hence, for $\overline{S}>0$ and $\beta$ exceeding ${\beta }^{T}$, we may observe that a loss of the local stability of the model’s fundamental steady state triggers a discreet jump from $\overline{{P}_{1}}=F$ to $\overline{{P}_{2}}=\overline{D}/r$. While $\overline{{P}_{2}}$ is independent of parameters $\tau$ and $\overline{S}$ at the transcritical bifurcation, $\overline{{P}_{1}}=\overline{{P}_{3}}$ increases (decreases) with the wealth tax (supply of (outside) shares of the risky asset), thereby decreasing (increasing) the size of the jump. In contrast, $\overline{{P}_{3}}$ is not detached from $\overline{{P}_{1}}$ at the transcritical bifurcation. Furthermore, the distance between the nonfundamental steady states as well as the distance between the nonfundamental steady states and the fundamental steady state increases with the supply of (outside) shares of the risky asset and speculators’ intensity of choice, while the reverse outcome occurs when policymakers increase the wealth tax.

• (iii) Interestingly, it follows from $\overline{{m}_{\mathrm{2,3}}}=-\frac{2r+\phi -\chi }{\chi +\phi }$ that the market shares of the fundamental and technical expectation rules, given by $\overline{{N}_{\mathrm{2,3}}^{F}}=\frac{\chi -r}{\chi +\phi }$ and $\overline{{N}_{\mathrm{2,3}}^{C}}=\frac{\phi +r}{\chi +\phi }$, respectively, are independent of parameters $\overline{S}$, $\beta$ and $\tau$ and identical at the model’s nonfundamental steady states. Since $\overline{{Z}_{\mathrm{2,3}}^{C}}=\frac{\overline{S}(\chi +r)}{2r}\pm \frac{Y(\chi -r)}{(1-\tau )\lambda {\sigma }^{2}}$ and $\overline{{Z}_{\mathrm{2,3}}^{F}}=\frac{\overline{S}(r-\phi )}{2r}\pm \frac{Y(-(\phi +r))}{(1-\tau )\lambda {\sigma }^{2}}$ with $Y: = \sqrt {\left( {\frac{{(1 - \tau )\lambda \sigma ^{2} \overline{S}}}{{2r}}} \right)^{2} + \frac{{\lambda \sigma ^{2} \left( {\left( {1 - \tau } \right)\beta C - {2{\arctan}{\text{h}}}\left[ {\frac{{2r + \phi - \chi }}{{\chi + \phi }}} \right]} \right)}}{{r\beta (\chi + \phi )}}}$, we have again that $\overline{{N_{{2,3}}^{C} }} ~N~\overline{{Z_{{2,3}}^{C} }} + \overline{{N_{{2,3}}^{F} }} ~N~\overline{{Z_{{2,3}}^{F} }} = \hat{S}$. Note that chartists are too optimistic at the upper nonfundamental steady state and thus buy too much of the risky asset. In fact, the yield they obtain from holding the risky asset is below the yield they receive from investing in the risk-free asset. By contrast, fundamentalists invest less in the risky asset and hold more of the risk-free asset. Together, this reduces the fitness disadvantage of the costly fundamental expectation rule. In mathematical terms, the expectation rules’ fitness differential is given by $\overline{{A}_{\mathrm{2,3}}^{F}}-\overline{{A}_{2,3}^{C}}=-\frac{2\mathrm{arctan}{\text{h}}[\frac{2r+\phi -\chi }{\chi +\phi }]}{\beta }$, from which it becomes clear why parameters $\overline{S}$, $\beta$ and $\tau$ do not influence speculators’ choice of expectations rules at the upper nonfundamental steady state. Of course, chartists suffer from similar investment mistakes induced by their expectation rule at the lower nonfundamental steady state.

3.4 Stability domain of nonfundamental steady states and beyond

For $\overline{\mathrm{S}}=0$, the nonfundamental steady states are locally stable in the range ${\beta }^{P}<\beta <{\beta }^{N}$ and subject to a Neimark–Sacker bifurcation as parameter $\beta$ exceeds ${\beta }^{N}$. For $\overline{\mathrm{S}}>0$, the bifurcation structure is more complicated. Interval ${\beta }^{S}<\beta <{\beta }^{T}$ starts with the occurrence of a saddle-node bifurcation and we can thus conclude that the lower nonfundamental steady state, being the saddle, is unstable while the upper nonfundamental steady state, being the node, is locally stable, at least initially. Between ${\beta }^{T}<{\beta <\beta }^{N,L}$, the lower nonfundamental steady state is stable as it has exchanged its stability properties with the fundamental steady state. We can express the stability domain of the upper nonfundamental steady state by ${\beta }^{S}<{\beta <\beta }^{N,U}$. Since ${\beta }^{N,U}<{\beta }^{N,L}$, the upper nonfundamental steady state is subject to a Neimark–Sacker bifurcation for lower values of speculators’ intensity of choice than the lower nonfundamental steady state. However, ${\beta }^{N,U}$ may be larger or smaller than ${\beta }^{T}$. Importantly, the nonfundamental steady states eventually become unstable and give rise to oscillatory dynamics as the term $\left(1-\tau \right)\beta C$ increases, independently of whether the supply of (outside) shares of the risky asset is zero or positive. Hence, an increase in speculators’ intensity of choice may create endogenous asset price dynamics, while an increase in policymakers’ wealth tax may re-establish market stability.⁸ We also remark that each of the two nonfundamental steady states gives birth to a separate limit cycle when the Neimark–Sacker bifurcation occurs, i.e., there are two coexisting attractors, one originating below the fundamental steady state and one above it.

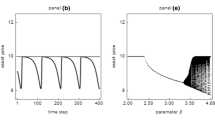
To further illustrate our propositions’ economic implications and to explore the model’s out-of-equilibrium behavior, we make use of the following base parameter setting. As in Brock and Hommes (1998), we assume that $r=0.1$, $\overline{D}=1$, ${\sigma }_{\delta }^{2}=0$, $\lambda =1$, ${\sigma }^{2}=1$, ${\sigma }_{\varepsilon }^{2}=0$, $\chi =0.2$, $\phi =1$ and $C=1$.⁹ Since our main focus rests again on parameters $\beta$, $\tau$ and $\overline{S}$, we discuss in Fig. 2 the effects of rising values of parameter $\beta$ on the properties of the risky asset’s price for different constellations of parameters $\tau$ and $\overline{S}$. The top left panel of Fig. 2 shows a bifurcation diagram for parameter $\beta$, assuming that $\tau =0$ and $\overline{S}=0$. Different colors mark the dynamics of the risky asset price for two different sets of initial conditions, selected slightly above and slightly below the model’s fundamental steady state. Obviously, the price of the risky asset converges towards its fundamental value $\overline{{P}_{1}}=F=10$ as long as the fundamental steady-state stability condition holds. At the pitchfork bifurcation, i.e., at $\beta _{{\tau = 0,~\overline{S} = 0}}^{P} = 2.398$, the fundamental steady state becomes unstable and two locally stable nonfundamental steady states are born. Depending on the initial conditions, the risky asset is then either overvalued or undervalued. Note that the risky asset’s mispricing increases in line with speculators’ intensity of choice. A Neimark–Sacker bifurcation occurs at $\beta _{{\tau = 0,~\overline{S} = 0}}^{N} = 3.331$. The two nonfundamental steady states then become unstable and give rise to two coexisting limit cycles, one located above the risky asset’s fundamental value and one below it. Note that the limit cycles’ amplitudes increase in line with speculators’ intensity of choice.

Fig. 2

Bifurcation diagrams for parameter $\beta$ and different constellations of parameters $\tau$ and $\overline{S}$. Base parameter setting, except that $\tau =0$ and $\overline{S}=0$ (top left), $\tau =0.08$ and $\overline{S}=0$ (bottom left), $\tau =0$ and $\overline{S}=0.05$ (top right) and $\tau =0.08$ and $\overline{S}=0.05$ (bottom right). Different colors mark the dynamics of the risky asset price for two different sets of initial conditions, selected slightly above and slightly below the model’s fundamental steady state

The bottom left panel of Fig. 2 repeats this experiment for $\tau =0.08$. While such a tax rate may be regarded as relatively high, it enables us to better visualize the implications of wealth taxes. Of course, similar results can be observed for lower values of parameter $\tau$, but they are less pronounced. While the risky asset’s fundamental steady state is still given with $\overline{{P}_{1}}=F=10$, the pitchfork and the Neimark–Sacker bifurcation occur at higher values of speculators’ intensity of choice, namely at $\beta _{{\tau = 0.08,~\overline{S} = 0}}^{P} = 2.606 6$ and $\beta _{{\tau = 0.08,~\overline{S} = 0}}^{N} = 3.621$. Within this interval, the risky asset’s mispricing is lower than in the absence of wealth taxes. The stabilizing effect of wealth taxes also becomes apparent by comparing the amplitudes of the risky asset’s oscillatory price behavior. For a given value of parameter $\beta$, the risky asset fluctuates less wildly when policymakers tax speculators’ wealth. We can thus conclude that wealth taxes may also stabilize the risky asset market when it is out of equilibrium.

The top right panel of Fig. 2 shows a bifurcation diagram for parameter $\beta$, assuming that $\tau =0$ and $\overline{S}=0.05$. While a positive supply of (outside) shares of the risky asset does not affect the local stability domain of the risky asset’s fundamental steady state, i.e., $\beta _{{\tau = 0,~\overline{S} = 0}}^{P} = \beta _{{\tau = 0,~\overline{S} = 0.05}}^{T} = 2.398$, the risk premium of the risky asset becomes positive, resulting in $\overline{{P}_{1}}=F=9.5$. At the transcritical bifurcation, we furthermore have that $\overline{{P}_{2}}=10$ and $\overline{{P}_{3}}=\overline{{P}_{1}}=9.5$. Note that the jump from $\overline{{P}_{1}}$ to $\overline{{P}_{2}}$ at the transcritical bifurcation is (always) given by the risk premium, that is, in our case, by $RP=0.5$. As parameter $\beta$ increases, the distance between $\overline{{P}_{1}}$ and $\overline{{P}_{2}}$, $\overline{{P}_{1}}$ and $\overline{{P}_{3}}$ and, consequently, $\overline{{P}_{2}}$ and $\overline{{P}_{3}}$ increases.¹⁰ A Neimark–Sacker bifurcation of the upper nonfundamental steady state, leading to oscillatory price dynamics above $\overline{{P}_{1}}=9.5$, occurs at $\beta _{{\tau = 0,~\overline{S} = 0.05}}^{{N,U}} = 3.074$, while the Neimark–Sacker bifurcation of the lower nonfundamental value occurs at $\beta _{{\tau = 0,~\overline{S} = 0.05}}^{{N,L}} = 3.598$, leading to oscillatory price dynamics below $\overline{{P}_{1}}=9.5$. Note that the Neimark–Sacker bifurcation for $\tau =0$ and $\overline{S}=0$ is located between these two values, i.e., $\beta _{{\tau = 0,~\overline{S} = 0.05}}^{{N,U}} < \beta _{{\tau = 0,~\overline{S} = 0}}^{N} < \beta _{{\tau = 0,~\overline{S} = 0.05}}^{{N,L}}$. As in the case of $\overline{S}=0$, an increase in speculators’ intensity of choice amplifies the limit cycles’ amplitudes and thus has to be regarded as destabilizing.

The bottom right panel of Fig. 2 reveals how the picture changes when policymakers impose a wealth tax by setting $\tau =0.08$. First, the imposition of a wealth tax increases the risky asset’s fundamental value to $\overline{{P}_{1}}=F=9.54$ and enlarges its local stability domain. Indeed, the transcritical bifurcation now occurs at $\beta _{{\tau = 0.08,~\overline{S} = 0.05}}^{T} = \beta _{{\tau = 0.08,~\overline{S} = 0}}^{P} = 2.606$, yielding, at that position, $\overline{{P}_{2}}=10$ and $\overline{{P}_{3}}=\overline{{P}_{1}}=9.54$. Between the transcritical and the Neimark–Sacker bifurcation, the nonfundamental steady states are closer to the fundamental steady state when policymakers tax speculators’ wealth. The Neimark–Sacker bifurcation occurs either at $\beta _{{\tau = 0.08,~\overline{S} = 0.05}}^{{N,U}} = 3.352$ (upper branch of the nonfundamental steady state) or at $\beta _{{\tau = 0.08,~\overline{S} = 0.05}}^{{N,L}} = 3.899$ (lower branch of the nonfundamental steady state), leading again to oscillatory price dynamics, albeit with lower amplitudes than in the absence of wealth taxes. Analog to the case $\overline{S}=0$, we have that $\beta _{{\tau = 0.08,~\overline{S} = 0.05}}^{{N,U}} < \beta _{{\tau = 0.08,~\overline{S} = 0}}^{N} < \beta _{{\tau = 0.08,~\overline{S} = 0.05}}^{{N,L}}$.

4 Discussion

Once again, we remark that policymakers may—e.g., for redistributive purposes—generate substantial revenues by taxing speculators’ wealth. However, policymakers need to understand how wealth taxes may affect the dynamics of financial markets. Our analytical and numerical results presented in the previous section highlight the stabilizing potential of wealth taxes. In this section, we discuss a number of more subtle issues associated with wealth taxes, occurring near the model’s bifurcations.

4.1 Qualitative versus quantitative effects

Qualitatively, our results suggest that wealth taxes have a stabilizing effect on the dynamics of speculative asset prices. Quantitatively, however, the stabilizing effect of wealth taxes may be regarded as weak. In the top right panel of Fig. 2, for instance, we observe for $\tau =0$ and $\overline{S}=0.05$ that the upper nonfundamental steady state becomes unstable at ${\beta }_{\tau =0,\overline{S}=0.05}^{N,U}=3.074$. To drive the risky asset’s behavior from a position slightly right of the Neimark–Sacker bifurcation, say $\beta =3.1$, to a position slightly left of the transcritical bifurcation, policymakers need to impose a wealth tax of about 23 percent (since $\left(1-\tau \right)\beta C=\left(1-0.23\right)*3.1*1=2.387<2\mathrm{arctan}{\text{h}}\left[\frac{2r+\phi -\chi }{\chi +\phi }\right]=2.3979$, the model’s fundamental steady state would then be locally stable). While the imposition of a 23 percent wealth tax seems to be unrealistic, note that lower wealth taxes contribute to a reduction of the risky asset’s mispricing, too.

However, there are market conditions where the imposition of a tiny wealth tax may have pronounced effects on the behavior of the risky asset. For instance, the upper nonfundamental steady state of the risky asset price may already imply substantial mispricing when it is born. Policymakers may suppress this mispricing by imposing a rather small wealth tax. In the top line of panels in Fig. 3, we illustrate this phenomenon in the presence of different noise levels. The magenta line depicts the evolution of the price of the risky asset in the time domain for our base parameter setting, except that $\beta =2.45$, $\overline{S}=0.05$, ${\sigma }_{\varepsilon }=0.01$ and $\tau =0$. In the absence of wealth taxes, the price of the risky asset fluctuates—after a transient period and initial conditions selected slightly above the unstable fundamental steady state $\overline{{P_{1} }} = 9.5$—around its locally stable upper nonfundamental steady state $\overline{{P}_{2}}=10.24$. Clearly, the upper (locally stable) nonfundamental steady state starts to exist as parameter $\beta$ crosses ${\beta }_{\tau =0,\overline{S}=0.05}^{S}=2.246$, while the fundamental steady state becomes unstable as parameter $\beta$ crosses ${\beta }_{\tau =0,\overline{S}=0.05}^{T}=2.398$. The cyan line shows the dynamics of the risky asset price for $\tau =0.08$ (to be able to visualize our results, we adhere to our choice of $\tau =0.08$, although smaller wealth taxes may produce similar effects). In the presence of wealth taxes, the price of the risky asset fluctuates around its new and slightly elevated locally stable fundamental steady state $\overline{{P}_{1}}=9.54$. In fact, we now have that $\beta =2.45<{\beta }_{\tau =0.08,\overline{S}=0.05}^{S}=2.454<{\beta }_{\tau =0.08,\overline{S}=0.05}^{T}=2.606$, i.e., the imposition of wealth taxes has not only stabilized the fundamental steady state, but also suppressed the saddle-node bifurcation’s emergence. The top right panel of Fig. 3, based on ${\sigma }_{\varepsilon }=0.04$, suggests that this observation is robust with respect to higher noise levels. Without question, the imposition of small wealth taxes may significantly reduce the risky asset’s mispricing if they prevent the emergence of a saddle-node bifurcation.

Fig. 3

Asset price dynamics for different constellations of parameters $\beta$, $\tau$, $\overline{S}$ and ${\sigma }_{\varepsilon }$. Base parameter setting, except that $\beta =2.45$, $\overline{S}=0.05$ and ${\sigma }_{\varepsilon }=0.01$ (top left), $\beta =2.45$, $\overline{S}=0.05$ and ${\sigma }_{\varepsilon }=0.04$ (top right), $\beta =3.6$, $\overline{S}=0$ and ${\sigma }_{\varepsilon }=0.01$ (bottom left) and $\beta =3.6$, $\overline{S}=0$ and ${\sigma }_{\varepsilon }=0.04$ (bottom right). Different colors mark the dynamics of the risky asset price for different tax rates (magenta: $\tau =0$, cyan: $\tau =0.08$)

4.2 Volatility versus mispricing

The left panels of Fig. 2 indicate that, when the imposition of wealth taxes reverses the Neimark–Sacker bifurcation, oscillatory price dynamics die out and the price of the risky asset converges towards one of the two nonfundamental steady states. While the volatility of the risky asset is zero at the nonfundamental steady states, it may display marked mispricing. Unfortunately, this constant mispricing may be larger than the average mispricing implied by the risky asset’s oscillatory price dynamics, although the latter clearly involves excess volatility. In the bottom line of panels in Fig. 3, we explore this issue in more detail. The magenta line in the bottom left panel of Fig. 3 shows how the price of the risky asset develops for our base parameter setting, except that $\beta =3.6$, $\overline{S}=0$, ${\sigma }_{\varepsilon }=0.01$ and $\tau =0$. Due to exogenous noise, the dynamics of the risky asset price is characterized by alternating bull and bear market regimes. While the volatility of the risky asset appears to be quite high, the price of the risky asset fluctuates, on average, around its fundamental value. The cyan line shows the dynamics of the risky asset price for $\tau =0.08$. While the volatility of the risky asset appears to be much lower, the price of the risky asset fluctuates, on average, above its fundamental value. This may not be in the interest of policymakers. The bottom right panel of Fig. 3, based on ${\sigma }_{\varepsilon }=0.04$, suggests that this effect may diminish for higher noise levels. Due to the quadrupling of the exogenous noise, the price of the risky asset fluctuates alternately around its upper and lower nonfundamental steady state, a fact that brings its average price much closer towards its fundamental value.

5 Conclusions

As reported by Galbraith (1994), Kindleberger and Aliber (2011) and Shiller (2015), financial markets regularly display severe bubbles and crashes, frequently associated with harmful consequences for the real economy. In the aftermath of financial and economic meltdowns, various voices from the general public regularly call for the imposition of a tax on speculators’ wealth to accommodate for the economic damage caused by speculators’ trading frenzy. The issue of economic inequality and wealth redistribution has become a heatedly discussed topic, especially since the publication of Piketty (2014). While it is obvious that policymakers may raise a substantial amount of revenue by taxing speculators’ wealth, it seems to us that the relationship between speculative asset price dynamics and wealth taxes deserves deeper academic scrutiny. In particular, policymakers need to know whether the imposition of such a tax may further endanger the stability of financial markets. If that were the case, taxing speculators’ wealth might not be a good idea.

To address this question, we extend the seminal asset-pricing model by Brock and Hommes (1998) in two directions. First, we allow policymakers to tax speculators’ wealth. Second, we consider that the supply of (outside) shares of the risky asset is positive. Overall, we find that higher wealth taxes increase the risky asset’s fundamental value by reducing its risk premium and, fortunately, tend to foster its stability. The latter result is due to the fact that wealth taxes reduce the fitness disadvantage of costly stabilizing fundamental expectation rules relative to cheap, destabilizing expectation rules, thereby promoting the use of stabilizing expectation rules. While the stabilizing effect of wealth taxes may be weak in general, the imposition of a small wealth tax may have a strong positive effect if it can prevent the emergence of a saddle-node bifurcation. If one of the risky asset’s nonfundamental steady states has just undergone a Neimark–Sacker bifurcation, however, wealth taxes may reduce the risky asset’s volatility at the expense of its mispricing. In such an environment, policymakers may not want to impose wealth taxes. To sum up, our analysis suggests that the imposition of a tax on speculators’ wealth is unlikely to pose a threat to the stability of financial markets—on the contrary, it seems that we could expect a (weak) stabilizing effect from such a policy.

We conclude our paper by pointing out a number of avenues for future research. As in Brock and Hommes (1998), we assume that speculators’ variance beliefs are constant. Since wealth taxes alter the risky asset’s dynamics, it would seem worthwhile to endogenize this model component. Gaunersdorfer (2000) and Chiarella et al. (2007) provide useful starting points for such an endeavor. Relatedly, Brock and Hommes (1998) focus on the case in which chartists believe in the persistence of bull and bear markets. Alternatively, one could consider, for instance, chartists using an expectation rule that extrapolates past price changes. Hommes (2011) provides an inspiring overview of relevant expectation rules. Furthermore, one could take into account utility functions that condition speculators’ demand for (or market impact on) the risky asset on their wealth levels, as elaborated in Chiarella et al. (2006, 2009). Taking our paper literally, we study the effects of a global wealth tax. Against this backdrop, it seems worthwhile to consider an asset-pricing model that contains a domestic and a foreign financial market to be able to study the issue of wealth-induced market interactions, crowding out effects and capital flight. Relatedly, one could explore how wealth taxes affect the dynamics of financial markets when speculators are subject to herding behavior and how this would spill over to the real economy. See Chiarella et al. (2005) and Cavalli et al. (2017, 2018) for starting points. Finally, one could study agent-based versions of our model, e.g., by following Schmitt’s (2020) agent-based adaptation of Brock and Hommes’ (1998) asset-pricing model, and keep track of speculators’ individual wealth levels, thereby being able to relax the assumption that their wealth is always positive or that the tax rate on speculators’ wealth tax is constant. Hopefully, our paper will stimulate more work in this direction and provide help to policymakers.

Appendix

In this appendix, we compute the model’s fundamental and nonfundamental steady states, study their local stability domains and present a number of additional simulations. Note that we follow a similar line of reasoning as Brock and Hommes (1998), Hommes et al. (2005) and Anufriev and Tuinstra (2013), although we extend their analysis by considering wealth taxes.

1.1 Appendix A1: The model’s fundamental and nonfundamental steady states

In order to find the model’s fundamental steady state, we set $\overline{{P}_{1}}=F={P}_{t}={P}_{t-1}={y}_{t-1}$ and $\overline{{m}_{1}}={m}_{t}={m}_{t-1}$. Map (18) then immediately reveals that the model’s fundamental steady state is given by

$$ {\text{FSS}}_{1} = \left( {\overline{{P_{1} }} ,\overline{{y_{1} }} ,\overline{{m_{1} }} } \right) = \left( {\frac{{\overline{D} - \left( {1 - \tau } \right)\lambda \sigma ^{2} \overline{S}}}{r},\frac{{\overline{D} - \left( {1 - \tau } \right)\lambda \sigma ^{2} \overline{S}}}{r},\tanh \left[ { - \frac{{\left( {1 - \tau } \right)\beta C}}{2}} \right]} \right). $$

(19)

Since $\overline{{A}_{1}^{F}}-\overline{{A}_{1}^{C}}=-\left(1-\tau \right)C$, we can directly conclude from (16) and (17) that $\overline{{N}_{1}^{C}}=\frac{1}{1+\mathrm{e}\mathrm{x}\mathrm{p}[-(1-\tau )\beta C]}$ and $\overline{{N}_{1}^{F}}=\frac{1}{1+\mathrm{e}\mathrm{x}\mathrm{p}[(1-\tau )\beta C]}$. Straightforward computations furthermore reveal that $\overline{{Z}_{1}^{C}}=\overline{S}=\widehat{S}/N$, $\overline{{Z}_{1}^{F}}=\overline{S}=\widehat{S}/N$ and $\overline{{N_{1}^{C} }} ~N~\overline{{Z_{1}^{C} }} + \overline{{N_{1}^{F} }} ~N~\overline{{Z_{1}^{F} }} = \hat{S}$.

To derive the model’s nonfundamental steady states $NF{SS}_{\mathrm{2,3}}=(\overline{{P}_{\mathrm{2,3}}},\overline{{y}_{\mathrm{2,3}}},\overline{{m}_{\mathrm{2,3}}}$), we solve the first equation of map (18) for $\overline{{m}_{\mathrm{2,3}}}={m}_{t}$ and obtain

$$\overline{{m}_{\mathrm{2,3}}}=-\frac{2r+\phi -\chi }{\chi +\phi }.$$

(20)

Substituting (20) into the third equation of map (18), and solving for $\overline{{P}_{\mathrm{2,3}}}={P}_{t}={P}_{t-1}={y}_{t-1}$ yields

$$\overline{{P}_{\mathrm{2,3}}}=\overline{{P}_{1}}+\frac{(1-\tau )\lambda {\sigma }^{2}\overline{S}}{2r}\pm \sqrt{{\left(\frac{(1-\tau )\lambda {\sigma }^{2}\overline{S}}{2r}\right)}^{2}+\frac{\lambda {\sigma }^{2}(\left(1-\tau \right)\beta C-2\mathrm{arctan}{\text{h}}[\frac{2r+\phi -\chi }{\chi +\phi }])}{r\beta (\chi +\phi )}}.$$

(21)

Of course, $\overline{{y}_{\mathrm{2,3}}}=\overline{{P}_{\mathrm{2,3}}}$. From (20), we can also conclude that $\overline{{N}_{\mathrm{2,3}}^{C}}=\frac{\phi +r}{\chi +\phi }$ and $\overline{{N}_{\mathrm{2,3}}^{F}}=\frac{\chi -r}{\chi +\phi }$. Furthermore, we have that $\overline{{A}_{\mathrm{2,3}}^{F}}-\overline{{A}_{2.3}^{C}}=-\frac{2\mathrm{arctan}{\text{h}}[\frac{2r+\phi -\chi }{\chi +\phi }]}{\beta }$. Since $\overline{{Z}_{\mathrm{2,3}}^{C}}=\frac{\overline{S}(\chi +r)}{2r}\pm \frac{Y(\chi -r)}{(1-\tau )\lambda {\sigma }^{2}}$ and $\overline{{Z}_{\mathrm{2,3}}^{F}}=\frac{\overline{S}(r-\phi )}{2r}\pm \frac{Y(-(\phi +r))}{(1-\tau )\lambda {\sigma }^{2}}$ with $Y: = \sqrt {\left( {\frac{{(1 - \tau )\lambda \sigma ^{2} \overline{S}}}{{2r}}} \right)^{2} + \frac{{\lambda \sigma ^{2} \left( {\left( {1 - \tau } \right)\beta C - {2{\arctan}{\text{h}}}\left[ {\frac{{2r + \phi - \chi }}{{\chi + \phi }}} \right]} \right)}}{{r\beta (\chi + \phi )}}}$, we can conclude that $\overline{{N_{{2,3}}^{C} }} ~N~\overline{{Z_{{2,3}}^{C} }} + \overline{{N_{{2,3}}^{F} }} ~N~\overline{{Z_{{2,3}}^{F} }} = \hat{S}$ is satisfied.

For $\overline{S}=0$, the nonfundamental steady states start to exist when parameter $\beta$ passes $\beta ^{P} : = \frac{{{2{\arctan}{\text{h}}}\left[ {\frac{{2r + \phi - \chi }}{{\chi + \phi }}} \right]}}{{\left( {1 - \tau } \right)C}}$ and $\overline{{P}_{\mathrm{2,3}}}$ are then symmetrically located around $\overline{{P}_{1}}$. For $\overline{S}>0$, the nonfundamental steady states already start to exist when parameter $\beta$ crosses $\beta ^{S} : = \frac{{{2{\arctan}{\text{h}}}\left[ {\frac{{2r + \phi - \chi }}{{\chi + \phi }}} \right]}}{{\left( {1 - \tau } \right)C + r\left( {\chi + \phi } \right)\lambda \sigma ^{2} \left( {\frac{{\left( {1 - \tau } \right)\overline{S}}}{{2r}}} \right)^{2} }} < \beta ^{T} = \beta ^{P}$. Between ${\beta }^{S}<\beta <{\beta }^{T}$, we have the ordering $\overline{{P}_{2}}>\overline{{P}_{3}}>\overline{{P}_{1}}$, while for $\beta >{\beta }^{T}$, we can conclude that $\overline{{P}_{2}}>\overline{{P}_{1}}>\overline{{P}_{3}}$. At $\beta ={\beta }^{S}$, it holds that $\overline{{P}_{2}}=\overline{{P}_{3}}=\overline{{P}_{1}}+0.5RP$. At $\beta ={\beta }^{T}$, we have that $\overline{{P}_{2}}=\overline{{P}_{1}}+RP$ and $\overline{{P}_{1}}=\overline{{P}_{3}}$.

1.2 Appendix A2: The fundamental steady-state local stability domain

To study the local stability properties of the model’s fundamental steady state, we have to evaluate the Jacobian matrix of (18) at ${FSS}_{1}$, yielding

$$J(\mathrm{F}{\mathrm{S}\mathrm{S}}_{1})=\left[\begin{array}{ccc}\frac{2+\chi -\phi +(\chi +\phi )\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}[\frac{(1-\tau )\beta C}{2}]}{2(1+r)}& 0& 0\\ 1& 0& 0\\ 0& 0& 0\end{array}\right],$$

(22)

from which we get the characteristic polynomial

$${\rm P}\left(\lambda \right)={\lambda }^{2}\left(\lambda -A\right)=0.$$

(23)

Since two eigenvalues of (23) are always equal to zero, i.e., ${\lambda }_{1}=0$ and ${\lambda }_{2}=0$, the stability of the model’s fundamental steady state hinges on the remaining (positive) eigenvalue ${\lambda }_{3}=A=\frac{2+\chi -\phi +(\chi +\phi )\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}[\frac{(1-\tau )\beta C}{2}]}{2(1+r)}$. Hence, the model’s fundamental steady state is locally stable if the third eigenvalue is smaller than one, resulting in

$$\beta <\frac{2\mathrm{arctan}{\text{h}}[\frac{2r+\phi -\chi }{\chi +\phi }]}{\left(1-\tau \right)C}.$$

(24)

Note that the left-hand side of (24) indicates for $\overline{S}=0$ the position of the pitchfork bifurcation, while for $\overline{S}>0$ it indicates the position of the transcritical bifurcation, as anticipated by the expressions ${\beta }^{P}$ and ${\beta }^{T}$ in Appendix A2.

Recall furthermore that $\overline{{m}_{1}}=\overline{{N}_{1}^{F}}-\overline{{N}_{1}^{C}}=-\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}[\frac{\left(1-\tau \right)\beta C}{2}]$ and $\overline{{N}_{1}^{F}}+\overline{{N}_{1}^{C}}=1$ so that $2\overline{{N}_{1}^{F}}=1+\overline{{m}_{1}}=1-\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}[\frac{\left(1-\tau \right)\beta C}{2}]$ and $2\overline{{N}_{1}^{C}}=1-\overline{{m}_{1}}=1+\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}[\frac{\left(1-\tau \right)\beta C}{2}]$. Since eigenvalue ${\lambda }_{3}$ can thus be expressed as ${\lambda }_{3}=\frac{2+\chi (1+\mathrm{tan}{\text{h}}\left[\frac{\left(1-\tau \right)\beta C}{2}\right])-\phi (1-\mathrm{tan}{\text{h}}\left[\frac{\left(1-\tau \right)\beta C}{2}\right])}{2(1+r)}=\frac{1+\overline{{N}_{1}^{C}}\chi -\overline{{N}_{1}^{F}}\phi }{1+r}$, we can also check the fundamental steady-state stability domain by studying $\overline{{N}_{1}^{C}}\chi -\overline{{N}_{1}^{F}}\phi <r$.

1.3 Appendix A3: The nonfundamental steady-state local stability domain for $\overline{{S}}=0$

Tedious computations reveal that the characteristic polynomial of the Jacobian matrix of map (19) computed for $\overline{S}=0$ at the nonfundamental steady states ${NFSS}_{\mathrm{2,3}}$ is given by

$${\rm P}\left(\lambda \right)={\lambda }^{3}-{\lambda }^{2}\left(1+X\right)+\lambda \left(X\left(1+r\right)\right)+rX=0,$$

(25)

where $X=-\frac{(r+\phi )(r-\chi )(\left(1-\tau \right)\beta C-{2{\arctan}{\text{h}}}\left[\frac{2r+\phi -\chi }{\chi +\phi }\right])}{r(1+r)(\chi +\phi )}$. At the pitchfork bifurcation, we have $\left(1-\tau \right)\beta C=2\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left[\frac{2r+\phi -\chi }{\chi +\phi }\right]$. Accordingly, $X=0$ and (25) yields the three eigenvalues ${\lambda }_{1}=0$, ${\lambda }_{2}=0$ and ${\lambda }_{3}=1$. If parameter $\beta$ is increased slightly, then $X$ becomes slightly positive and (25) yields three eigenvalues inside the unit circle, i.e., the nonfundamental steady states $\mathrm{N}\mathrm{F}{\mathrm{S}\mathrm{S}}_{\mathrm{2,3}}$ are initially stable. For $\beta \to \infty$, however, we observe that $X\to \infty$, implying that at least one of the eigenvalues must cross the unit circle at some critical value for $\beta$. Let us denote this value by ${\beta }^{N}$. As we have $\mathrm{{\rm P}}\left(1\right)=2Xr>0$ and $\mathrm{{\rm P}}\left(-1\right)=-2-2X<0$, we can conclude that two eigenvalues must be complex, the basis for a Neimark–Sacker bifurcation that gives rise to cyclical dynamics.¹¹ Importantly,$X$ depends on the term $\left(1-\tau \right)\beta C$. Therefore, policymakers may reverse the Neimark–Sacker bifurcation by increasing parameter $\tau$.

1.4 Appendix A4: The nonfundamental steady-state local stability domain for $\overline{{S}}>0$

Even more tedious computations reveal that the characteristic polynomial of the Jacobian matrix of map (18) computed for $\overline{S}>0$ at the nonfundamental steady states ${\mathrm{N}\mathrm{F}\mathrm{S}\mathrm{S}}_{\mathrm{2,3}}$ may be expressed by

$${\rm P}\left(\lambda \right)={\lambda }^{3}-{\lambda }^{2}\left(1+G{\overline{{D}_{\mathrm{2,3}}}}^{2}\right)+\lambda \left(G{\overline{{D}_{\mathrm{2,3}}}}^{2}\right)\left(1+r\right)-\left(G\overline{{D}_{\mathrm{2,3}}}\right)(\left(1-\tau \right)\lambda {\sigma }^{2}\overline{S}-r\overline{{D}_{\mathrm{2,3}}})=0, $$

(26)

where $\overline{{D}_{\mathrm{2,3}}}=\overline{{P}_{\mathrm{2,3}}}-\overline{{P}_{1}}=\frac{(1-\tau )\lambda {\sigma }^{2}\overline{S}}{2r}\pm \sqrt{{\left(\frac{(1-\tau )\lambda {\sigma }^{2}\overline{S}}{2r}\right)}^{2}+\frac{\lambda {\sigma }^{2}(\left(1-\tau \right)\beta C-2\mathrm{arctan}h[\frac{2r+\phi -\chi }{\chi +\phi }])}{r\beta (\chi +\phi )}}$ and $G=-\frac{\beta \left(r+\phi \right)\left(r-\chi \right)}{\left(1+r\right)\lambda {\sigma }^{2}}$. At the saddle-node bifurcation, we have $\overline{{P}_{2}}=\overline{{P}_{3}}$. Accordingly, $\overline{{D}_{\mathrm{2,3}}}=\overline{{P}_{\mathrm{2,3}}}-\overline{{P}_{1}}=\frac{(1-\tau )\lambda {\sigma }^{2}\overline{S}}{2r}$ and (26) yields the three eigenvalues ${\lambda }_{1}=1$ and $\lambda _{{2,3}} = G\frac{{\left( {\left( {1 - \tau } \right)\lambda \sigma ^{2} \overline{S}} \right)^{2} }}{{8r^{2} }} \pm \sqrt {\frac{{~G^{2} }}{4}\left( {\frac{{~(1 - \tau )\lambda \sigma ^{2} \overline{S}}}{{2r}}} \right)^{4} - G\frac{{\left( {\left( {1 - \tau } \right)\lambda \sigma ^{2} \overline{S}} \right)^{2} ~}}{{4r}}}$. If parameter $\beta$ is increased slightly, one of the nonfundamental steady states should become unstable (the saddle), while the other one should become stable (the node). In fact, it seems that between ${\beta }^{S}$ and ${\beta }^{T}$ the eigenvalue ${\lambda }_{1}$ is at least initially real and smaller than one for $\mathrm{N}\mathrm{F}{\mathrm{S}\mathrm{S}}_{2}$ and real and larger than one for $\mathrm{N}\mathrm{F}{\mathrm{S}\mathrm{S}}_{3}$.

At the transcritical bifurcation, we have $\overline{{P}_{1}}=\overline{{P}_{3}}$. Hence, $\overline{{D}_{\mathrm{2,3}}}=0$ and (26) yields the three eigenvalues ${\lambda }_{1}=1$ and ${\lambda }_{\mathrm{2,3}}=0$. As shown in Appendix A.2, the fundamental steady state becomes unstable for $\beta >{\beta }^{T}$ and $NF{SS}_{3}$ should therefore be stable for ${\beta }^{T}<\beta <{\beta }^{N,U}$. For $\beta \to \infty$, $\overline{{D}_{\mathrm{2,3}}}$ converge to $\frac{(1-\tau )\lambda {\sigma }^{2}\overline{S}}{2r}\pm \sqrt{{\left(\frac{(1-\tau )\lambda {\sigma }^{2}\overline{S}}{2r}\right)}^{2}+\frac{\left(1-\tau \right)C\lambda {\sigma }^{2}}{r(\chi +\phi )}}$, while $G$ converges to plus infinity, implying that at least one of the eigenvalues must cross the unit circle at some critical value for $\beta$. Moreover, this critical value for $\beta$ must be smaller for $\mathrm{N}\mathrm{F}{\mathrm{S}\mathrm{S}}_{2}$ than for $NF{SS}_{3}$. Denoting these values by ${\beta }^{N,U}$ and ${\beta }^{N,L}$, we have $\beta ^{{N,U}} < ~\beta ^{{N,L}}$. Furthermore, note that an increase in parameter $\overline{S}$ extends the distance between ${\beta }^{N,U}$ and ${\beta }^{N,L}$, while an increase in parameter $\tau$ causes the opposite. As we have ${\rm P}\left(1\right)=G\overline{{D}_{\mathrm{2,3}}}(2r\overline{{D}_{\mathrm{2,3}}}-\left(1-\tau \right)\lambda {\sigma }^{2}\overline{S})>0$ and ${\rm P}\left(-1\right)=-2-2(G\overline{{D}_{\mathrm{2,3}}}-G\overline{{D}_{\mathrm{2,3}}}\left(1-\tau \right)\lambda {\sigma }^{2}\overline{S})<0$, we can conclude that two eigenvalues must be complex, giving rise to a Neimark–Sacker bifurcation and oscillatory dynamics. Importantly, policymakers may reverse the Neimark–Sacker bifurcation by increasing parameter $\tau$.

1.5 Appendix A5: Coexisting attractors involving the fundamental steady state

One intriguing feature of our model’s bifurcation structure is the possibility that the risky asset possesses a locally stable fundamental steady state, which coexists with a locally stable upper nonfundamental steady state, an outcome that may occur when speculators’ intensity of choice ranges between ${\beta }^{S}<\beta <{\beta }^{T}$, as discussed in Appendix A4. Note that such a coexistence of attractors may give rise to intriguing hysteresis effects. In particular, a tiny change in a model parameter may have a drastic (jump) effect on the levels of the model’s steady states that cannot easily be reversed by a tiny correction of the same model parameter.¹² However, Appendix A4 also reveals that the critical Neimark–Sacker bifurcation value ${\beta }^{N,U}$ shrinks with the supply of (outside) shares of the risky asset. As a result, we may even observe that ${\beta }^{N,U}$ falls short of ${\beta }^{T}$ when $\overline{S}$ becomes sufficiently large.

The top left panel of Fig. 

Fig. 4

Coexisting attractors. The top line of panels shows bifurcation diagrams for parameter $\beta$, generated with our base parameter setting, except that $\overline{S}=0.15$ (top left) and $\overline{S}=0.21$ (top right). Red (blue) tonalities indicate that $\tau =0$ ($\tau =0.08$). The bottom right panel depicts simulations of the risky asset price for our base parameter setting, except that $\beta =2.35$, $\tau =0$ and $\overline{S}=0.21$, using different initial conditions. The bottom left panel visualizes the corresponding basins of attraction of the risky asset’s fundamental steady state and its limit cycle

4 shows bifurcation diagrams for parameter $\beta$, generated with our base parameter setting, except that $\overline{S}=0.15$. Red (blue) tonalities indicate that the wealth tax is equal to $\tau =0$ ($\tau =0.08$). Recall from Sect. 3 that ${\beta }^{T}$ and ${\beta }^{N,U}$ are given for $\overline{S}=0.05$ by 2.398 and 3.074 when $\tau =0$ and by 2.606 and 3.352 when $\tau =0.08$. For $\overline{S}=0.15$, however, these values are given by 2.398 and 2.594 for $\tau =0$ and by 2.606 and 2.850 for $\tau =0.08$, indicating a leftward movement of ${\beta }^{N,U}$ in the bifurcation diagrams. The top left panel of Fig. 4 repeats this exercise for $\overline{S}=0.21$. We now face a situation in which ${\beta }^{N,U}$, with 2.333, is smaller than ${\beta }^{T}$, with 2.398. The same is true for $\tau =0.08$. For convenience, we report in Table

Table 1 Critical bifurcation values for parameter $\beta$

1 all critical bifurcation values discussed in connection with Figs. 2 and 4. Once again, the stabilizing effect of wealth taxes is clearly visible.

Note that the bifurcation diagrams depicted in the top right panel of Fig. 4 indicate that the fundamental steady state coexists with a limit cycle when speculators’ intensity of choice is somewhat lower than ${\beta }^{T}$ (the aforementioned hysteresis effects may thus also involve an abrupt jump to a limit cycle). The bottom right panel of Fig. 4 confirms this finding by plotting the evolution of the risky asset’s price in the time domain for two different sets of initial conditions, using our base parameter setting, except that $\beta =2.35$, $\tau =0$ and $\overline{S}=0.21$. The bottom left panel of Fig. 4 visualizes the corresponding basins of attraction of the risky asset’s fundamental steady state and its limit cycle. Further simulation reveals that the basin of attraction of the limit cycle first shrinks and finally vanishes as policymakers increase the wealth tax. If the tax rate is set sufficiently high, the fundamental steady state even becomes the model’s unique steady state.