Abstract
We provide a lean, non-technical exposition on the pricing of path-dependent and European-style derivatives in the Cox–Ross–Rubinstein (CRR) pricing model. The main tool used in this paper for simplifying the reasoning is applying static hedging arguments. In applying the static hedging principle, we consider Arrow–Debreu securities and digital options, or backward random processes. In the last case, the CRR model is extended to an infinite state space which leads to an interesting new phenomenon not present in the classical CRR model. At the end, we discuss the paradox involving the drift parameter \(\mu \) in the Black–Scholes–Merton model pricing. We provide sensitivity analysis and an approximation of the speed of convergence for the asymptotically vanishing effect of drift in prices.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper, we provide a transparent and financially tractable approach to verifying financial derivatives pricing formulas in a lattice model.
The derivatives pricing model, originated in the seminal papers of Black and Scholes (1973) and Merton (1973) (BSM), is the cornerstone of modern derivatives pricing. However, fully understanding their approach requires rather intricate and advanced mathematical machinery. In an attempt to alleviate this burden, Cox et al. (1979) (CRR) introduced a lattice model which approximates the BSM prices with a very rapid rate of convergence as the number of time steps grows (see, for example, Leisen and Reimer 1996). The CRR model succeeds in simplifying the BSM model, and understanding it requires considerably less mathematical sophistication compared to the BSM model.
The celebrated Cox–Ross–Rubinstein binomial option pricing formula states that the price of an option is
where f denotes the payoff of the European-style derivative at maturity, N denotes the number of time steps to maturity, and r is the risk-free interest rate corresponding to each time step. The parameters u and d of the binomial model denote the sizes of up and down movements, respectively, and q can be easily calculated from the parameters of the model (see Sects. 2.2 and 3.1.1).
Lattice models, inspired by the CRR model, provide a common and well-established technique in derivatives valuation. There is a vast literature on lattice models in finance. Lattice models have been applied to the valuation of derivatives, such as financial derivatives (Babbs 2000), real options (Nembhard et al. 2002, 2003), and hybrid securities (Das and Sundaram 2007; Gamba and Trigeorgis 2007). In addition, lattice models have been used to model term structure (Heath et al. 1990), or to estimate state price density by implied trees (Rubinstein 1994). In this paper, we also study the implications of extending the state space in the CRR binomial model. Previously, the CRR model has been generalized and extended in various manners. For example, Boyle (1988) extends the model to cover the case of several state variables, and Hull and White (1993) and Kascheev (2000) extend the model to incorporate path dependency better. In addition, Chung and Shih (2007) generalize the CRR model by adding a stretch parameter. Broadie and Detemple (1996) use a combination of the CRR lattice and the Black–Scholes formula to provide new approximations to American option values.
The CRR model is easy to grasp in principle, and thus, the apparently more complicated BSM model can be understood as well by extension since it can be seen as an asymptotic limit of CRR models. However, the crucial step in the CRR paper, where their main pricing formula is actually justified, seems to be disregarded; after discussing the first two steps, Cox et al. state that they ‘now have a recursive procedure for finding the value of a call with any number of periods to go’ (Cox et al. 1979, p. 238).Footnote 1 The required backward substitution calculations become lengthy, especially for a general path-dependent payoff f, even if the idea is simple in principle. Although the CRR model was introduced as a simplified version of the BSM model and well succeeds in that, some steps of the calculations remain not that transparent at first glance, say, to a student. The rigorous arguments usually become somewhat complicated, they require probability theory, e.g. martingales, and the financial intuition may easily be lost in the details.
In fact, we have not been able to find a lean argument for the CRR pricing formula (1) in the quantitative finance literature.
Consequently, there is a rough passage starting with rudimentary considerations to the financial understanding of the BSM model. Our aim here is to further simplify the reasoning in the CRR model, essentially by using static hedging arguments. Also, we hope that our method makes the CRR model somewhat more approachable, especially from a pedagogic point of view; understanding our approach does not require mastering such heavy mathematical machinery, such as martingales, which may not be a familiar concept to an undergraduate student, for example.
Thus, the main contribution of this paper is not a novel result, but rather we will give a simple, financially oriented argument for both the classical European-style derivative and the general path-dependent option pricing formulas in the CRR model. We will apply Arrow–Debreu (AD)-type securities (Arrow and Debreu 1954) and digital options as convenient intermediate notions. These securities are financially well motivated since they can be considered as natural building blocks for other financial securities, particularly derivatives in our case. Even though the AD securities are not actively traded in the real market by themselves, traded structured products plausibly consist of such securities. Thus, these securities appear more tractable than their theoretical alternative, risk-neutral probability densities. In contrast to the AD securities, digital options are traded in the real market.
This paper is organized as follows. First, we recall the binomial model and explain various types of atomic building blocks in our model. We show how the prices of AD securities, that is, kind of elementary options on particular trajectories of the underlying security prices, arise in a rather simple way. Then, we obtain the path-dependent derivative prices by suitably aggregating these AD securities. It turns out that the classical European-style derivatives pricing formula follows easily by aggregating binary options. These, in turn, are aggregated from AD securities or, alternatively, can be priced by means of a simple backward random walk in an extended state space. In the case of an extended state space, the discounted value processes prove to exhibit an interesting aggregate time invariance, not present in the standard binomial model. At the end of the paper, we discuss the irrelevance of the trend parameter \(\mu \) in the BSM pricing, which is a bit of a paradox.
We have made an effort to explain the strategy behind the pricing of general financial derivatives in the CRR model carefully without resorting to unnecessary technical machinery. Instead of fictitious risk-neutral probabilities, we mainly consider financially tractable elementary securities. In particular, Sect. 3.2 hopefully serves as an ‘executive summary’ on the CRR pricing principles, which essentially entails all the financial reasoning behind the BSM model.
2 Preliminaries
Although we do not assume knowledge of lattice models in depth, we expect some familiarity with relevant background information; see, for example, the monographs by Copeland and Weston (1992), Luenberger (1998), Hull (2015), Föllmer and Schied (2011), or van der Hoek and Elliot (2006).
This section first introduces some notations used later in this paper and then defines the binomial model, which acts as a framework for our paper.
2.1 Some notations
In this paper, we consider a discrete-time setting \(t_n\in [0,T]\), \(n=0,\ldots ,N\), where N denotes the number of time steps, and the length of a single time step is  .
.
The price of the underlying asset at time \(t_n\) is denoted by \(S_n\). We denote by \(f:\mathbb {R}\rightarrow \mathbb {R}\) the payoff function of some financial derivative of interest. It encodes the information about the payment of the derivative. For instance, at the time of maturity \(t_N=T\), a European-style call option and a European-style put option have payoffs of the forms
respectively, where K denotes the strike price.
The indicator function becomes a beneficial notion in the payoff functions. If A is a subset of the set \(\mathscr {A}\), then the indicator function, \(\mathbf {1}_{A}:\mathscr {A}\rightarrow \{0,1\}\), is defined as
Using the notation of the indicator function, at the time of maturity \(t_N=T\), the payoff of a barrier put option, for instance, can be written in the form
where L denotes the prerequisite for the option being in-the-money.
2.2 The basic binomial model
Although we will not require much probability theory here, let us mention that our technical setup is a binomial model \((B,S,\varOmega ,\mathscr {F},\mathbb {F},\mathbf {P})\). The quartet \((\varOmega ,\mathscr {F},\mathbb {F},\mathbf {P})\) is a filtered probability space, where
is the sample space, \(\mathscr {F}\) is a \(\sigma \)-algebra representing the set of events (here we can choose \(\mathscr {F}\) to be the collection of all subsets of \(\varOmega \)), \(\mathbb {F}\) is a filtration, i.e. \(\mathbb {F}=\{\mathscr {F}_n : n=0,1,\ldots , N\}\) such that \(\mathscr {F}_n\subseteq \mathscr {F}_{n+1}\), and \(\mathbf {P}\) is a probability measure.
In addition, the binomial model involves the riskless asset \(B_n\) and one risky asset \(S_n\). The riskless asset \(B_n\) has a nominal value
where r denotes the constant risk-free rate of return. \(B_n\) corresponds to a zero-coupon bond with face value 1.
The (nominal) value of the underlying risky asset at time \(t_n, \ n=0,\ldots ,N\), is denoted by \(S_n\). In the binomial model, the asset return \((S_{n+1}-S_n)/S_n\) can only take two possible values: u (‘up’) or d (‘down’). Thus, the value of the underlying asset can jump from \(S_n\) either to the higher value \(S_n(1+u)\) or, the lower value \(S_n(1+d)\).
Therefore, the value of the risky asset S can be described as a random variable \(S:\varOmega \times \{1,\ldots ,N\}\rightarrow \mathbb {R}\) such that the initial value \(S_0\) is a given constant and
where \(\theta _i\), \(1\le i \le N\), are i.i.d. with probabilities \(\mathbf {P}(\theta _i=1)=p\) and \(\mathbf {P}(\theta _i=0)=1-p\), for some given \(0<p<1\). Note that the binomial tree defined here is recombining, meaning that moving first up and then down leads to the same state as moving first down and then up.
It is assumed that \(d<0<r<u\). The reasonable choices of d, r and u depend on the length of the time steps.
Figure 1 illustrates the binomial tree of the underlying asset S in logarithmic and real scale. The sample space essentially consists of all possible trajectories of S; see also Fig. 5.
The following theorem shows when the binomial model is arbitrage-free and defines the risk-neutral probability q, which appears in the CRR binomial option pricing formula (1), from the model parameters u, d and r. In our approach to prove the CRR formula, however, we try to eschew the concept of risk-neutral measures by finding another route to define the value of q; for more details, see Sect. 3.1.1.
Before stating the theorem, let us first remind ourselves the definitions of a martingale and a martingale measure.
Definition 1
A stochastic process \(X=(X_n)_{n\ge 0}\) on a filtered probability space \((\varOmega ,\mathscr {F},\mathbb {F}, \mathbf {P})\) is called a martingale if X is adapted and satisfies \(\mathbb {E}[|X_n|]<\infty \) for every n, and if
Definition 2
A probability measure \(\mathbf {Q}\) on \((\varOmega ,\mathscr {F}_N)\) is called a martingale measure if the discounted price process \({\overline{X}}=X/B\) is a \(\mathbf {Q}\)-martingale, i.e.
Theorem 1
The binomial model \((B,S,\varOmega ,\mathscr {F},\mathbb {F},\mathbf {P})\) is arbitrage-free if and only if \(d<r<u\). In this case, the binomial model is complete, and there is a unique martingale measure \(\mathbf {Q}\) such that
for all \(1\le i\le N\). Further, if the model is arbitrage-free, then the martingale measure \(\mathbf {Q}\) is equivalent to the probability measure \(\mathbf {P}\) and is also known as the risk-neutral measure.
Proof
See (Föllmer and Schied 2011, p. 325), for example. \(\square \)
2.3 The discounted model
To simplify the arguments, it is customary in the quantitative finance literature ‘to pass on to a discounted model’ where discounted prices appear in place of nominal prices. To perform this transition explicitly, we will do the bookkeeping in numéraire units (see, for example, Föllmer and Schied 2011, pp. 12, 294; or Hull 2015, p. 662). Expressing prices in numéraire terms is a bit like reporting inflation-adjusted prices over a time span, and it allows comparing asset prices that are quoted at different times.
Our numéraire  incorporates the currency and discounting, and it depends on time \(t_n\) as follows:
incorporates the currency and discounting, and it depends on time \(t_n\) as follows:

or, in short,

for all \(n=0,\ldots ,N\). The left-hand numéraire corresponds to time \(t_n\), and the right-hand one corresponds to time \(t_N=T\). Hence, the definition of the \(t_n\)-time numéraire can be written in an exact form as

This leads to the following dimension analysis:

That is, the net present value (NPV) of future certain cash flow  , considered as cash at the present time, is
, considered as cash at the present time, is  . In other words, the use of the numéraire saves us the bother of discounting. Hence, the CRR formula (1) can be expressed as
. In other words, the use of the numéraire saves us the bother of discounting. Hence, the CRR formula (1) can be expressed as

to denote the value of the option at time \(t_n\). Again the left-hand numéraire corresponds to cash at time \(t_n\), whereas the right-hand numéraire corresponds to future payoff at maturity \(t_N=T\). More generally, the time subscript corresponds to the time of the value process, so the terminal payoff is always expressed in  and time-\(t_n\) value of any security in
and time-\(t_n\) value of any security in  . Following this convention, we may suppress the time-step indices in the subscripts of the numéraire and, for instance, the previous formula becomes simply
. Following this convention, we may suppress the time-step indices in the subscripts of the numéraire and, for instance, the previous formula becomes simply

3 Streamlined argument for the CRR pricing formulas
This section aims to explain the idea of CRR pricing in a transparent manner.
3.1 Static hedging by Arrow–Debreu securities and digital options
Static hedging means synthesizing some required new securities (or pricing existing ones) by running a buy-and-hold strategy on some existing securities (see Derman et al. 1995; Brown and Ross 1991). The securities included long/short in the replicating portfolio are supposed to be more straightforward than the new synthesized derivative security. If it is possible to construct a portfolio whose value at the maturity of the European-style derivative exactly matches the value of this derivative, then according to ‘no free lunch’ principle, the initial price of the portfolio should be the same as the price of the new derivative. Indeed, otherwise, some very lucrative trading strategies arise where one can make money, essentially risk-free and from nothing. These are too good to be true, and over some time they should cease to exist due to extensive arbitrage activity. We refer to this sort of economic reasoning as the static hedging principle.
In the application of the static hedging principle in this paper, we consider two kinds of elementary derivatives, path-dependent ones, Arrow–Debreu (AD) securities, and path-independent ones, namely degenerate digital options. An AD security is a financial derivative whose payoff is  at the time of maturity T if the underlying asset’s evolution follows a given prescribed trajectory \(\omega \) and is
at the time of maturity T if the underlying asset’s evolution follows a given prescribed trajectory \(\omega \) and is  otherwise. AD securities may be economically more tractable than risk-neutral probabilities, even though neither of them is traded directly.
otherwise. AD securities may be economically more tractable than risk-neutral probabilities, even though neither of them is traded directly.
Regularly, a digital option is a financial derivative that pays  at maturity T if the underlying asset exceeds a given prescribed strike price K at time T, and
at maturity T if the underlying asset exceeds a given prescribed strike price K at time T, and  if it does not. For our hedging purposes, we define a restricted case of the digital option, a degenerate digital option, such that it pays
if it does not. For our hedging purposes, we define a restricted case of the digital option, a degenerate digital option, such that it pays  at maturity T if the underlying asset hits exactly a given prescribed strike price K at time T and pays
at maturity T if the underlying asset hits exactly a given prescribed strike price K at time T and pays  otherwise. Digital options are traded, and their prices can be estimated from European-style option prices. It was shown by Breeden and Litzenberger already in 1978 that, for plain vanilla calls and puts, there is an elegant model-free way to do this.
otherwise. Digital options are traded, and their prices can be estimated from European-style option prices. It was shown by Breeden and Litzenberger already in 1978 that, for plain vanilla calls and puts, there is an elegant model-free way to do this.
The following subsections first describe the properties and prices of AD securities in a one-step model. Then, they show how these single-step AD securities can be applied in the multi-step model to price both path-dependent and path-independent European-style derivatives.
3.1.1 AD securities in a 1-step 2-state model
This subsection describes the basic construction blocks, the single-step AD derivatives, which we use for the static hedging purposes in this paper.
Let us consider AD derivatives in a one-step model with times \(t_0\) and \(t_1\). The initial value of the underlying stock is \(S_0\), and at time \(t_1\), the possible values of the stock are \(S_1=S_0(1+u)\) and \(S_1=S_0(1+d)\). Let us then define the single-step AD derivatives \({AD_\uparrow }\) and \({AD_\downarrow }\) such that their payoff functions are
which are known at time \(t_1\). In other words, the derivative \({AD_\uparrow }\) pays  when the value of the underlying asset goes up, and similarly, the derivative \({AD_\downarrow }\) pays
when the value of the underlying asset goes up, and similarly, the derivative \({AD_\downarrow }\) pays  when the value of the asset goes down.
when the value of the asset goes down.
It turns out that the prices of these AD derivatives can be easily calculated by applying the static hedging argument on the asset and bonds when both long and short positions are available.
Lemma 1
The initial values of the \(AD_{\uparrow }\) and \(AD_{\downarrow }\) derivatives at time \(t_0=0\) are


Proof
To replicate the payoff of the \(AD_\uparrow \) security, we simply invest at \(t_0\) a certain amount of numéraire in the stocks,  , and a certain amount,
, and a certain amount,  , in risk-free bonds. The payoff replication conditions for \({AD_\uparrow }\) can be formalized as follows:
, in risk-free bonds. The payoff replication conditions for \({AD_\uparrow }\) can be formalized as follows:

Without loss of generality, we may assume (by splitting assets or bundling them up) that \(S_0=1\) above. Thus, we get
which can be solved by Gaussian elimination or inverting the coefficient matrix:
By recalling that  , we have the nominal value of the replicating portfolio as
, we have the nominal value of the replicating portfolio as
and thus

Here, we consider  to be the numéraire in current price and
to be the numéraire in current price and  to be the unit payoff of the derivative in NPV terms.
to be the unit payoff of the derivative in NPV terms.
Similarly, we can replicate the \(AD_{\downarrow }\) security with an investment in the stocks, \(a'S_0\), and an investment in the risk-free bonds, \(b'B_0\). In calculating this replication, we observe that we must have
Therefore, the value of the replicating portfolio is
and further

\(\square \)
Note that one may statically hedge the risk-free zero-coupon bond B with  -unit face value by combining these AD securities since their total payoff is
-unit face value by combining these AD securities since their total payoff is

the payoff of the bond, at time \(t_1\). Therefore, it makes sense that

3.2 CRR pricing using static hedging
In this subsection, we statically hedge European-style derivatives using the AD derivatives and digital options as building blocks. We first cover the case of a path-dependent derivative and then move on to a more general, path-independent derivative.
3.2.1 The path-dependent case simplified
Let us first discuss the pricing of path-dependent AD derivatives. Suppose that we want to price a path-dependent AD derivative that pays us  at time \(t_N=T\) if the evolution of the underlying asset follows precisely a given trajectory encoded in \(\omega \) (a list of ups and downs), and
at time \(t_N=T\) if the evolution of the underlying asset follows precisely a given trajectory encoded in \(\omega \) (a list of ups and downs), and  if the asset’s evolution diverts from this fixed trajectory at any time
if the asset’s evolution diverts from this fixed trajectory at any time  .
.
In pricing of this AD derivative, we utilize the one-step \(AD_{\uparrow }\) and \(AD_{\downarrow }\) derivatives presented in the previous subsection. As we recall, \(AD_{\uparrow }\) is a derivative that costs  and pays us
and pays us  if the value of the underlying asset goes up (and
if the value of the underlying asset goes up (and  otherwise). Similarly, \(AD_{\downarrow }\) is a derivative that costs
otherwise). Similarly, \(AD_{\downarrow }\) is a derivative that costs  , and whose payoff is
, and whose payoff is  if the value of the underlying goes down.
if the value of the underlying goes down.
The idea of the pricing the multi-step AD derivative is to construct a replicating portfolio from \(AD_{\uparrow }\) and \(AD_{\downarrow }\) derivatives step by step, according to the trajectory related to the AD derivative’s payoff. The construction proceeds from the time of maturity, \(t_N=T\), to the time of initiation, \(t_0\), and the idea of the construction is rather simple. Basically, at each time \(t_n, \ n\le N\), we consider the coordinate of the trajectory, \(\omega _{n+1}\), that is, the movement of the underlying asset at that time. At time \(t_n\),
-
if \(\omega _{n+1}=1\), i.e. the prescribed trajectory goes up, we synthesize a suitable number of shares of the \(AD_\uparrow \) derivative, and
-
if \(\omega _{n+1}=0\), i.e. the prescribed trajectory goes down, we synthesize a suitable number of shares of the \(AD_\downarrow \) derivative.
At time \(t_n\), this hedge will provide us with a suitable return at time \(t_{n+1}\) so that we can perform the appropriate hedge at the following time steps as well. Repeating this step-by-step hedging strategy will provide us with the static hedging portfolio, the discounted value of this portfolio, and, as a result, the discounted price of the AD derivative.
Next, we will illustrate the hedging strategy with a concrete example that prices a path-dependent AD derivative.
Example 1
Let us consider a path-dependent AD derivative that has the payoff of  if the underlying follows the fixed trajectory \(\omega \) presented in Fig. 2.
if the underlying follows the fixed trajectory \(\omega \) presented in Fig. 2.
The fixed path for the stock price movements in the example of pricing a path-dependent AD derivative (Example 1), drawn in logarithmic scale
Let us begin the hedging by considering the situation right before the maturity, at time \(t_{N-1}\). If we are not on the trajectory, then no wealth is required to cover the path-dependent AD, since it is worthless. So, let us assume we are on the trajectory. At time \(t_N=T\), we want the hedging portfolio to pay us  if the underlying stock has the fixed value \(S_N(\omega )\). Since we know that we are on the trajectory, the stock satisfies \(S_N=S_{N-1}(1+u)\), as in Fig. 2. Hence, we can hedge the derivative by buying an \(AD_{\uparrow }\) derivative which costs us
if the underlying stock has the fixed value \(S_N(\omega )\). Since we know that we are on the trajectory, the stock satisfies \(S_N=S_{N-1}(1+u)\), as in Fig. 2. Hence, we can hedge the derivative by buying an \(AD_{\uparrow }\) derivative which costs us  .
.
Let us then consider the situation two steps before the maturity, at time \(t_{N-2}\). The situation is almost the same as above, but instead of requiring the payoff of  from the hedging procedure at the next time step, we require only
from the hedging procedure at the next time step, we require only  . Indeed, with this amount of capital, we can run the previously described hedge at time \(t_{N-1}\), so that it will, in turn, pay us
. Indeed, with this amount of capital, we can run the previously described hedge at time \(t_{N-1}\), so that it will, in turn, pay us  at the time of maturity. Again, let us assume that the stock follows the prescribed trajectory and satisfies \(S_{N-1}=S_{N-2}(1+d)\). Hence, at time \(t_{N-2}\), we must perform hedging by buying q shares of \(AD_{\downarrow }\) derivatives; these will pay us
at the time of maturity. Again, let us assume that the stock follows the prescribed trajectory and satisfies \(S_{N-1}=S_{N-2}(1+d)\). Hence, at time \(t_{N-2}\), we must perform hedging by buying q shares of \(AD_{\downarrow }\) derivatives; these will pay us  each so that, at time \(t_{N-1}\), we will have the capital of
each so that, at time \(t_{N-1}\), we will have the capital of  . Thus, at time \(t_{N-2}\), the required capital is
. Thus, at time \(t_{N-2}\), the required capital is  .
.
With similar reasoning, considering the time \(t_{N-3}\), we require the capital to buy \(q(1-q)\) shares of \(AD_{\downarrow }\) derivatives, i.e. at time \(t_{N-3}\), we require the capital of \(q(1-q)^2\) in order to enable the latter phases of the hedging strategy.
We can continue this backward recursion step by step so, at time \(t_0=0\), we will have the price of the AD derivative, i.e. the amount of capital required to initiate the hedging strategy. The required initial capital of the AD derivative replication strategy then clearly becomes

where x and \(N-x\) denote the number of ‘ups’ and ‘downs’, respectively, in the fixed trajectory \(\omega \), or equivalently, the number of phases where we use single-step \(AD_{\uparrow }\) and \(AD_{\downarrow }\) derivatives, respectively.
We need to bear in mind that if the value of the underlying asset diverts from the fixed path at any time \(t_n, \ n\le N\), the path-dependent AD derivative is worthless, and therefore, the price of it is  , and also the hedging strategy ends there. On the other hand, if the evolution of the underlying follows the fixed trajectory, then the hedging strategy returns
, and also the hedging strategy ends there. On the other hand, if the evolution of the underlying follows the fixed trajectory, then the hedging strategy returns  . Consequently, the described hedging strategy yields exactly the same payoff as the path-dependent AD derivative. \(\square \)
. Consequently, the described hedging strategy yields exactly the same payoff as the path-dependent AD derivative. \(\square \)
According to the static hedging principle, we may construct any path-dependent derivative in the model by aggregating it as a suitable portfolio of AD securities \(C_\omega \). Namely, if the payoff involving trajectory \(\omega \) is \(f(\omega )\), then we may accomplish the same payoff with a portfolio including \(f(\omega )\)-many AD securities \(C_\omega \). Thus, for each \(\omega \), the weight of an AD security \(C_\omega \) in the portfolio is \(f(\omega )\). The price of the path-dependent European option \(C_f\) is then

3.2.2 The CRR pricing formula by considering combinations
Let us then discuss pricing a general path-independent European-style derivative with a payoff function f. This derivative can be easily replicated by using degenerate digital options as building blocks. The degenerate digital options, in turn, can be constructed by aggregating AD securities.
The payoff of a degenerate digital option is
where K denotes the fixed strike price, and \(S_N\) denotes the value of the underlying stock at maturity \(t_N=T\), i.e. \(S_N=S_0(1-u)^x(1+d)^{N-x}\), for some x. Thus, the payoff of  is guaranteed as long as the final value \(S_N\) equals the prescribed strike price K; it is irrelevant which particular path the value of the underlying stock follows before the maturity \(t_N=T\).
is guaranteed as long as the final value \(S_N\) equals the prescribed strike price K; it is irrelevant which particular path the value of the underlying stock follows before the maturity \(t_N=T\).
Let us consider a degenerate digital option related to a strike price \(K=S_0 (1+u)^{x_0} (1+d)^{N-x_0}\). Such a degenerate digital option can be aggregated from all such path-dependent AD derivatives connected to some trajectory consisting of exactly \(x_0\) ‘up’-moves. Therefore, the price of the degenerate digital option is

Here, the binomial coefficient \(\left( {\begin{array}{c}N\\ x_0\end{array}}\right) \) is the number of different paths that consist of exactly \(x_0\) ‘up’-moves. Alternatively, the binomial coefficient \(\left( {\begin{array}{c}N\\ x_0\end{array}}\right) \) can also be interpreted as the number of ways how the \(x_0\) ‘up’-moves can be ordered in the paths in question.
Let us next study a European-style derivative with a payoff function f. Clearly, the value of a portfolio of f(K)-many \(C_{\text {digi}, K}\) options at times \(t_0=0\) and \(t_N=T\) is

respectively. Therefore, a general European-style option payoff f can simply be matched with a portfolio of degenerate digital options in such a way that f and the payoff of the portfolio coincide exactly at maturity \(t_N=T\). According to the static hedging principle, at time \(t_0=0\), the price of the derivative equals the initial value of the hedging portfolio:

which essentially is the well-known CRR pricing formula (1).
Next, we shall illustrate the replication strategy with an example of a European call option (thus path-independent). We shall manage this by constructing the hedging strategy for suitable degenerate digital options.
Example 2
Let us consider a 2-step model and suppose that we want to price a European call option with a strike price  , and thus with a payoff \(f(\omega )=\max (S_2(\omega )-105,0)\). Let \(r=0.04\), and let the value process of the underlying satisfy
, and thus with a payoff \(f(\omega )=\max (S_2(\omega )-105,0)\). Let \(r=0.04\), and let the value process of the underlying satisfy  , \(u=0.2\), \(d=-0.1\), and \(p=1/2\), as in Fig. 3.
, \(u=0.2\), \(d=-0.1\), and \(p=1/2\), as in Fig. 3.
The value process of the underlying asset S in the binomial model described in Example 2
We shall consider each possible final state \(S_2\) individually and construct hedging portfolios for these states by using degenerate digital options.
-
1.
Let us start with the final state having the most apparent hedging strategy,
 . In this case, the value of the call is
. In this case, the value of the call is  , and since the call is out-of-the-money, we need no initial capital to hedge it.
, and since the call is out-of-the-money, we need no initial capital to hedge it. -
2.
Let us then consider the final state
 , and let us construct the hedging portfolio such that, at the time of maturity, the value of the portfolio equals the value of the call,
, and let us construct the hedging portfolio such that, at the time of maturity, the value of the portfolio equals the value of the call, 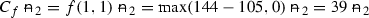 . To achieve this payoff, we need to buy f(1, 1) shares of digital options \(C_{\text {digi},S_2(1,1)}\). Each of these digital options will provide a payoff of
. To achieve this payoff, we need to buy f(1, 1) shares of digital options \(C_{\text {digi},S_2(1,1)}\). Each of these digital options will provide a payoff of  at time \(t_2\), so that, in total, our portfolio will have the desired value,
at time \(t_2\), so that, in total, our portfolio will have the desired value,  . Since there is only one possible path \(\omega =(1,1)\) from \(S_0\) to \(S_2\), the initial value of the digital option \(C_{\text {digi}, S_2(1,1)}\) is
. Since there is only one possible path \(\omega =(1,1)\) from \(S_0\) to \(S_2\), the initial value of the digital option \(C_{\text {digi}, S_2(1,1)}\) is  (38)
(38)and thus, the initial value of the hedging portfolio is
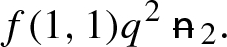 (39)
(39) -
3.
Let us consider the remaining final state,
 . Again, let us construct the hedging portfolio such that, at the time of maturity, it has the value
. Again, let us construct the hedging portfolio such that, at the time of maturity, it has the value 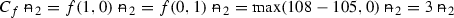 . To achieve this payoff, we need to buy f(1, 0) shares of digital option \(C_{\text {digi},S_2(1,0)}\). Note that since now there are two possible trajectories \(\omega _1=(1,0)\) and \(\omega _2=(0,1)\) from \(S_0\) to \(S_2\), the initial value of the digital option \(C_{\text {digi}, S_2(1,0)}\) is
. To achieve this payoff, we need to buy f(1, 0) shares of digital option \(C_{\text {digi},S_2(1,0)}\). Note that since now there are two possible trajectories \(\omega _1=(1,0)\) and \(\omega _2=(0,1)\) from \(S_0\) to \(S_2\), the initial value of the digital option \(C_{\text {digi}, S_2(1,0)}\) is  (40)
(40)and the initial value of the hedging portfolio is
 (41)
(41)
Since, at time \(t_0\), we do not know how the underlying stock will behave in the following time steps, we need to hedge ourselves against all possible price risks. Therefore, we will have the hedging portfolio for the call as the sum of the above hedging portfolios concerning each possible final state, that is

After substituting \(q=(r-d)/(u-d)=\left( 0.04-(-0.1)\right) /\left( 0.2-(-0.1)\right) =7/15\) and the call’s payoffs \(f(1,1)=39\) and \(f(1,0)=3\), we will have the price of the call as

which coincides with the CRR price, see (1). \(\square \)
The proof of the CRR pricing formula presented here coincides with the proof presented by Cox et al. in the sense that they both operate in a simplified model without using unnecessarily complicated machinery, such as martingales. In addition, in both proofs, the pricing of the option is based on the static hedging principle and constructing the hedging portfolio using backward recursion.
The main difference between our approach and the original approach is the components used in constructing the hedging portfolio, and thus the interpretation of the parameter q. Cox et al. form the hedging portfolio containing shares of the underlying stock and risk-free bonds. After computing the proportion of stocks and bonds in the portfolio, the parameter q is defined to simplify the notations.
Our approach first defines elementary single-time-step derivatives, \(AD_\uparrow \) and \(AD_\downarrow \), such that the parameter q equals the price of the \(AD_\uparrow \) derivative, and \(1-q\) equals the price of the \(AD_\downarrow \) derivative. Second, we use these single-step derivatives in constructing a hedging portfolio for a path-dependent AD derivative. After this, we have the price of a path-independent degenerate digital option as a sum of all such path-independent AD derivatives that lead to some specific final value. Finally, considering all possible final values, we have a price for a path-independent European-style derivative. Our approach aims to preserve the financial intuition behind the CRR pricing formula distinct, especially in the way the parameter q appears in the formula.
4 An alternative route to the CRR formula: Extending the state space and reversing the random walk
In the previous section, we derived the CRR pricing formula for a general European-style derivative using the static hedging principle on degenerate digital options. We constructed the replicating portfolio from degenerate digital options with an end state \(K=S_N\). In consequence, the price of the European-style derivative with a payoff function f equals the initial value of the replicating portfolio:

Thus, it sufficed to price each individual \(C_{\text {digi},K}\) option separately. In Sect. 3.2.2, we priced the degenerate digital option \(C_{\text {digi},K}\) by considering combinations of the corresponding AD derivatives, see formula (35). In the following subsections, we present two additional ways to price the digital option \(C_{\text {digi},K}\) by utilizing the ideas of backward recursion and a backward random walk.
First, let us extend the state space as
so that the stock may have an infinite number of possible values at each time \(t_n, \ n=0,\ldots , N\). Here, \(S_0\) is fixed. The reason we require some form of extension of the state space is to enable the branching of the backward progress of the recursion and the random walk, which are described later in the following subsections.
4.1 Backward recursion on the degenerate digital option
We will price the degenerate digital option \(C_{\text {digi},K}\) by constructing it from \(AD_{\uparrow }\) and \(AD_{\downarrow }\) derivatives. Let us begin this construction at the time of maturity, \(t_N=T\). At time \(t_N=T\), we wish to receive  if the underlying asset \(S_N\) has the value of K and
if the underlying asset \(S_N\) has the value of K and  otherwise.
otherwise.
The first steps of constructing the hedging portfolio by backward recursion are the following (see also Fig. 4):
At time \(t_{N-1}\): There are two possible states of \(S_{N-1}\) that enable the  payoff at time \(t_N\); these states satisfy \(S_N=S_{N-1}(1+d)\) or \(S_N=S_{N-1}(1+u)\). If \(S_N=S_{N-1}(1+d)\), at time \(t_{N-1}\), we require the capital to buy an \(AD_{\downarrow }\) derivative which will provide the payoff of the desired
payoff at time \(t_N\); these states satisfy \(S_N=S_{N-1}(1+d)\) or \(S_N=S_{N-1}(1+u)\). If \(S_N=S_{N-1}(1+d)\), at time \(t_{N-1}\), we require the capital to buy an \(AD_{\downarrow }\) derivative which will provide the payoff of the desired  at time \(t_N\), i.e. we require the capital of
at time \(t_N\), i.e. we require the capital of  . Similarly, if \(S_N=S_{N-1}(1+u)\), at time \(t_{N-1}\), we require the capital to buy an \(AD_{\uparrow }\) derivative which will provide the payoff of the desired
. Similarly, if \(S_N=S_{N-1}(1+u)\), at time \(t_{N-1}\), we require the capital to buy an \(AD_{\uparrow }\) derivative which will provide the payoff of the desired  at time \(t_N\), i.e. we require the capital of
at time \(t_N\), i.e. we require the capital of  .
.
At time \(t_{N-2}\): Similarly, now there are three possible states of \(S_{N-2}\) that can enable the  payoff at time \(t_N\), via the two possible states \(S_{N-1}\) described above. These states \(S_{N-2}\) satisfy
payoff at time \(t_N\), via the two possible states \(S_{N-1}\) described above. These states \(S_{N-2}\) satisfy
If \(S_N=S_{N-2}(1+d)^2\), at time \(t_{N-2}\), we require the capital to buy \(1-q\) shares of \(AD_{\downarrow }\) derivatives; these derivatives will provide a payoff of  each at time \(t_{N-1}\), so at time \(t_{N-1}\) we will have
each at time \(t_{N-1}\), so at time \(t_{N-1}\) we will have  which is the amount of capital that assures obtaining the payoff of
which is the amount of capital that assures obtaining the payoff of  at time \(t_N\). Thus, we require
at time \(t_N\). Thus, we require  . If \(S_N=S_{N-2}(1+u)^2\), with similar reasoning, at time \(t_{N-2}\), we need to have
. If \(S_N=S_{N-2}(1+u)^2\), with similar reasoning, at time \(t_{N-2}\), we need to have  to assure obtaining the desired
to assure obtaining the desired  at the time of maturity. If \(S_N=S_{N-2}(1+u)(1+d)=S_{N-2}(1+d)(1+u)\), at time \(t_{N-2}\), we require the capital to buy both \(1-q\) shares of \(AD_{\uparrow }\) derivatives and q shares of \(AD_{\downarrow }\) derivatives. Since we cannot predict which state of nature will occur at time \(t_{N-1}\), we need to provide for both. Thus, we require the capital of
at the time of maturity. If \(S_N=S_{N-2}(1+u)(1+d)=S_{N-2}(1+d)(1+u)\), at time \(t_{N-2}\), we require the capital to buy both \(1-q\) shares of \(AD_{\uparrow }\) derivatives and q shares of \(AD_{\downarrow }\) derivatives. Since we cannot predict which state of nature will occur at time \(t_{N-1}\), we need to provide for both. Thus, we require the capital of  .
.
By proceeding this replicating strategy step by step from the time of maturity to the time of initiation, \(t_0=0\), we will have the price of the digital option as in formula (35) by considering all the possible paths starting from the initial stock value \(S_0\). The first steps in constructing the hedging portfolio are represented in Fig. 4.
4.2 Backward random walk interpretation
Another way to find the price of the digital option \(C_{\text {digi},K}\) is to consider a backward random walk. This interpretation is enabled by the fact that, at each point in the state space, we have essentially the same discounted value process; this value process is represented in Fig. 5.
Let us define a random walk Y, starting from the strike price K of the digital option, as
where \(\xi \) is a biased ‘coin flip process’, i.e. \(\xi =(\xi _n)_{n\le N}\) such that \(\xi _n(\omega )=\omega _{N+1-n}\) are independent and identically distributed (i.i.d.) with
Thus, here we consider q as a probability of the event \(\xi _n=0\); the process \(\xi \) is biased in the sense that the probabilities of the two possible outcomes are not equal. This random walk can be depicted travelling backwards in time, as in Fig. 5.
Now, the price of the digital option,  , is numerically the probability that \(Y_N\) hits \(S_0\),
, is numerically the probability that \(Y_N\) hits \(S_0\),
Here, \(\xi _t\) is binomially distributed and therefore \(1-\xi _t\) is also binomially distributed. The required probability in (49) is obtained by the probability mass function of a binomially distributed random variable. Also, note that \(1-\xi _t\) satisfies
5 Some further remarks
5.1 An invariance property in the extended CRR model
In the extended CRR model in Sect. 4, at each time t, the probabilities of the backward process sum to the unity over the states, cf. Figs. 4 and 6. In other words, the replication  -values of a \(C_{\text {digi} ,K}\) option over the states do not depend on time, as the aggregate is 1.
-values of a \(C_{\text {digi} ,K}\) option over the states do not depend on time, as the aggregate is 1.
Taking this observation a bit further, if we statically hedge European-style derivatives by aggregating degenerate digital options, we also aggregate, with respective weights, the probabilities of the processes starting from different states at maturity.
Recall the extended state space in (45), and let \(V_f(s,n)\) be the value of the European-style derivative with a payoff f, at state s and time \(t_n\). By the static hedging argument (similar to Example 2), we can write the value of the derivative as a summation of the values of suitable degenerate digital options:
Here, \(V_f^{(K)}(s,n)\) denotes the time-\(t_n\) value of the degenerate digital option with a payoff \(f(K)\cdot \mathbf {1}_{\{K\}}(S_N)\). We assume that, in the summation above, the strike price K can have any discrete value among real numbers.
Proposition 1
Consider the extended model in Sect. 4, and let f be the payoff of a European-style derivative such that the infinite summation satisfies
Then, the value process of the replication strategy for \(C_f\) satisfies

Proof
By a simple calculation, we have

The first equality follows from Eq. (51). Based on the assumptions, we may change the order of summations in middle equality. The last equality holds because if the payoff of the security is 1, then the possible values at time \(t_n\), which coincide with the probabilities, sum to 1 (see Fig. 6). Similarly, since the degenerate digital option has the payoff f(K), at time \(t_n\), the sum of the possible values is \(1\cdot f(K)\). \(\square \)
The standard CRR model fails the above property. Namely, let us consider at time \(t_0=0\) the one and only state \(S_0\), and let us consider the risk-free bond with maturity at \(t_N=T\) to play the role of our derivative in this example. Then, the  -value of the bond is 1, but the sum \(\sum _K f(K) = \sum _K 1\) becomes large, as it is the number of all possible states at time \(t_N=T\).
-value of the bond is 1, but the sum \(\sum _K f(K) = \sum _K 1\) becomes large, as it is the number of all possible states at time \(t_N=T\).
On the other hand, the continuous BSM model has a similar property, namely
where we used \(y=\ln S_T\), \(x=\ln S_0\), and \(\varphi \) is the risk-neutral density function of the BSM model. Recall that the distribution is \(\mathscr {N}((r- \frac{1}{2}\sigma ^2)T, \sigma ^2 T)\) with the relevant model parameters in place.
In what follows, we will provide an example of a situation where this invariance property of the extended CRR model has an interesting implication.
Example 3
Let us consider a digital option with a payoff function
i.e. the defined digital option pays  if the underlying hits the interval \([K_1,K_2]\), and
if the underlying hits the interval \([K_1,K_2]\), and  otherwise. We assume here that the strike K can only have discrete values. As stated previously, the values \(V_f^{(K)}(s,n)\) corresponding to the strike K sum to 1 over the states at any time \(t_n, \ n=0,\ldots ,N\). By applying this property and summing all the possible values \(V_f^{(K)}(s,n)\) corresponding to all strikes K, such that \(K_1\le K\le K_2\), at time \(t_n\), we can determine the number of possible strikes in the interval \([K_1,K_2]\), since the sum must equal the number of strikes. \(\square \)
otherwise. We assume here that the strike K can only have discrete values. As stated previously, the values \(V_f^{(K)}(s,n)\) corresponding to the strike K sum to 1 over the states at any time \(t_n, \ n=0,\ldots ,N\). By applying this property and summing all the possible values \(V_f^{(K)}(s,n)\) corresponding to all strikes K, such that \(K_1\le K\le K_2\), at time \(t_n\), we can determine the number of possible strikes in the interval \([K_1,K_2]\), since the sum must equal the number of strikes. \(\square \)
5.2 Why does the trend term \(\mu \) not appear in the BSM prices?
The fact that the trend term \(\mu \) does not affect prices in the BSM pricing appears somewhat counterintuitive. There are some anecdotes on how the pricing formulas were suspected before the seminal paper of Black and Scholes was published, and even the authors first doubted their findings.
We will discuss here the irrelevance of \(\mu \) in the continuous BSM model, as seen from the lattice model asymptotics along vanishing step size. The parameter \(\mu \) cannot be excluded in the binomial framework in the formation of the risk-neutral probabilities q. On the other hand, the effect of \(\mu \) should vanish as the timescale is refined and the binomial models converge to a BSM model (in a suitable sense). Next, we will analyse the speed of convergence of the risk-neutral variance of the underlying binomial process. Recall that the asymptotic log-normal state-price density can be recovered in principle by normal approximation of the binomial distribution from the risk-neutral expectation (see (60)) and variance of the jumps, since they are i.i.d.
To this end, we will fix the following dependence of returns on the parameters:

Here, we have a time step  and the usual BSM model parameters: \(\mu >0\) is the trend of the underlying, \(\sigma >0\) the standard deviation or volatility term and \(r>0\) the short rate. Some reasonable values could be \(\mu =0.1 ,\ \sigma =0.2\) and \(r=0.04\). If \(S_t\) denotes the value of the underlying asset at time t, \(t\in [0,T]\), mimicking the BSM model, the lattice model of \(S_t\) is
and the usual BSM model parameters: \(\mu >0\) is the trend of the underlying, \(\sigma >0\) the standard deviation or volatility term and \(r>0\) the short rate. Some reasonable values could be \(\mu =0.1 ,\ \sigma =0.2\) and \(r=0.04\). If \(S_t\) denotes the value of the underlying asset at time t, \(t\in [0,T]\), mimicking the BSM model, the lattice model of \(S_t\) is

where \(\theta _t\) are i.i.d. random variables with \(\mathbf {P}(\theta _t=1)=p\) and \(\mathbf {P}(\theta _t=-1)=1-p\), for some \(0<p<1\). Here, we will use the following risk-neutral single-step probabilities as above:
Then, by simple algebra, we obtain the following identities:
Equation (60) says that, in the risk-neutral world, the expected return of the underlying asset is the risk-free return and, in particular, does not depend on \(\mu \).
The risk-neutral single-step variance of the asset return is
, and the risk-neutral variance of \(\log (S_T / S_0 )\) for small  is approximately
is approximately

where the  is the total number of steps in the time span. Indeed, we apply the fact that, for small
is the total number of steps in the time span. Indeed, we apply the fact that, for small  , the approximation
, the approximation  holds.
holds.
This reads

where the second equality follows from (60) and by thinking of the risk-neutral expectations, and the last one from (61).
To analyse the contribution of \(\mu \) on the risk-neutral variance, we shall analyse the series expansion of the above terms:

Consequently, we obtain an approximation for the risk-neutral variance:

From this form, we immediately see the BSM model variance which arises asymptotically as  :
:
The conclusion here is that, in an annual binomial model, if the time step is 1 day (\(\Delta t =1/365\)), then the effect of \(\mu \) and r on the underlying asset’s risk-neutral variance is negligible. According to (60) and (67), parameter \(\mu \) does not appear in the \(\mathbf {Q}\)-distribution, which is used in pricing options.
To conclude, we will comment on the vanishing effect of \(\mu \) on the risk-neutral probability heuristically. This is a bit of a paradox, and the above calculations give only dim insight into what is ‘really’ happening here.
Fixing small  , we have
, we have

Thus, if the parameters  , \(\sigma \) and r remain constant, the effect of changes in \(\mu \) on q is
, \(\sigma \) and r remain constant, the effect of changes in \(\mu \) on q is

This means that as \(\mu \) increases, the risk-neutral probability mass shifts down in the tree.
So, how can the risk-neutral probability measure value \(\mathbf {Q}(S_T)\) be asymptotically invariant of \(\mu \)? Clearly, the above sensitivity (69) decreases for small timescale.
Also, note that the risk-neutral density concerns explicitly the value of \(S_T\) and not the number of up jumps. Recall that in (1), the value of \(S_T\) appears rather indirectly as the number of jumps x, so let us write \(x=x(S_T)\), the number of up jumps required for a given terminal asset price \(S_T\).
Changing a down jump to an up jump results in  increase in the log-price of the asset. On the other hand, changing \(\mu \) affects uniformly every time step of the model, so the corresponding change is
increase in the log-price of the asset. On the other hand, changing \(\mu \) affects uniformly every time step of the model, so the corresponding change is
This means that if we wish to counteract the increase of \(\mu \) by changing the number of up steps, the required adjustment is

Consequently, increasing \(\mu \) shifts the risk-neutral probability mass down the tree, but it simultaneously shifts down the end node in the tree, corresponding to a fixed value \(S_T\).
6 Conclusions
This paper provides a leaner, not as technical, proof for the well-known Cox–Ross–Rubinstein pricing formula. We have made an effort to simplify the proof and make it pedagogically more approachable by emphasizing the financial intuition behind the pricing formula.
The fundamental idea of our proof is, by using the static hedging argument, to construct a replicating portfolio using Arrow–Debreu securities and degenerate digital options. We start this construction from the time of maturity and proceed backwards to time \(t_0\). In order to enable the backward recursion, we extend the state space. In this extended CRR model, there exists an interesting invariance property: at each time \(t_n, \ n=0,\ldots ,N\), the sum of the value process over the states corresponds to the sum of all possible payoffs at maturity. We show an example where this invariance property can be used in the analysis of financial derivatives. In addition to our example, the invariance property can have various applications in financial mathematics.
At the end of the paper, we discuss the paradox of the trend parameter \(\mu \) not affecting the prices of derivatives. We justify this well-known fact by showing that the risk-neutral probability \(\mathbf {Q}\) that appears in the pricing formula is independent of the parameter \(\mu \).
References
Arrow, K.J., Debreu, G.: Existence of an equilibrium for a competitive economy. Econometrica 22(3), 265–290 (1954)
Babbs, S.: Binomial valuation of lookback options. J. Econ. Dyn. Control 24, 1499–1525 (2000)
Black, F., Scholes, M.: The pricing of options and corporate liabilities. J. Polit. Econ. 81(3), 637–654 (1973)
Boyle, P.P.: A lattice framework for option pricing with two state variables. J. Financ. Quant. Anal. 23(1), 1–12 (1988)
Breeden, D.T., Litzenberger, R.H.: Prices of state-contingent claims implicit in option prices. J. Bus. 51(4), 621–651 (1978)
Broadie, M., Detemple, J.: American option valuation: new bounds, approximations, and a comparison of existing methods. Rev. Financ. Stud. 9(4), 1211–1250 (1996)
Brown, D.J., Ross, S.A.: Spanning, valuation and options. Econ. Theory 1(1), 3–12 (1991)
Chung, S.L., Shih, P.T.: Generalized Cox–Ross–Rubinstein binomial models. Manag. Sci. 53(3), 508–520 (2007)
Copeland, T.E., Weston, J.F.: Financial Theory and Corporate Policy, 3rd edn. Addison-Weasley Publishing Company, Massachusetts (1992)
Cox, J.C., Ross, S.A., Rubinstein, M.: Option pricing: a simplified approach. J. Financ. Econ. 7, 229–263 (1979)
Das, S.R., Sundaram, R.K.: An integrated model for hybrid securities. Manag. Sci. 53(9), 1439–1451 (2007)
Derman, E., Ergener, D., Kani, I.: Static options replication. J. Deriv. 2(4), 78–95 (1995)
Föllmer, H., Schied, A.: Stochastic Finance. An Introduction in Discrete Time. Third revised and extended edition. Walter de Gruyter, Berlin (2011)
Gamba, A., Trigeorgis, L.: An improved binomial lattice method for multi-dimensional options. Appl. Math. Finance 14(5), 453–475 (2007)
Heath, D., Jarrow, R., Morton, A.: Bond pricing and the term structure of interest rates: a discrete time approximation. J. Financ. Quant. Anal. 25(4), 419–440 (1990)
van der Hoek, J., Elliot, R.J.: Binomial Models in Finance. Springer, New York (2006)
Hull, J.C., White, A.: Efficient procedures for valuing European and American path-dependent options. J. Deriv. 1(1), 21–31 (1993)
Hull, J.C.: Options, Futures, and Other Derivatives, 9th edn. Pearson Education Inc., Boston (2015)
Kascheev, D.E.: On the option pricing for a generalization of the binomial model. J. Math. Sci. 99(3), 1267–1272 (2000)
Leisen, D.P.J., Reimer, M.: Binomial models for option valuation-examining and improving convergence. Appl. Math. Finance 3, 319–346 (1996)
Luenberger, D.G.: Investment Science. Oxford University Press, New York (1998)
Merton, R.C.: Theory of rational option pricing. Bell J. Econ. Manag. Sci. 4(1), 141–183 (1973)
Nembhard, H.B., Shi, L., Aktan, M.: A real options design for quality control charts. Eng. Econ. 47(1), 28–59 (2002)
Nembhard, H.B., Shi, L., Aktan, M.: A real option design for product outsourcing. Eng. Econ. 48(3), 199–217 (2003)
Rubinstein, M.: Implied binomial trees. J. Finance 49(3), 771–818 (1994)
Acknowledgements
We wish to thank the associate editor and the anonymous referees for valuable comments and suggestions that have helped us improve this article considerably.
Funding
Open access funding provided by University of Eastern Finland (UEF) including Kuopio University Hospital.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflicts of interest to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
On behalf of Minna Turunen, this work has been enabled by the working grant provided by The Finnish Cultural Foundation, North Karelia Regional fund; grant number 55172232.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Talponen, J., Turunen, M. Option pricing: a yet simpler approach. Decisions Econ Finan 45, 57–81 (2022). https://doi.org/10.1007/s10203-021-00338-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10203-021-00338-7






 . In this case, the value of the call is
. In this case, the value of the call is  , and since the call is out-of-the-money, we need no initial capital to hedge it.
, and since the call is out-of-the-money, we need no initial capital to hedge it. , and let us construct the hedging portfolio such that, at the time of maturity, the value of the portfolio equals the value of the call,
, and let us construct the hedging portfolio such that, at the time of maturity, the value of the portfolio equals the value of the call, 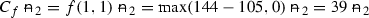 . To achieve this payoff, we need to buy f(1, 1) shares of digital options
. To achieve this payoff, we need to buy f(1, 1) shares of digital options  at time
at time  . Since there is only one possible path
. Since there is only one possible path 
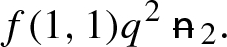
 . Again, let us construct the hedging portfolio such that, at the time of maturity, it has the value
. Again, let us construct the hedging portfolio such that, at the time of maturity, it has the value 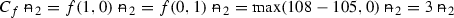 . To achieve this payoff, we need to buy f(1, 0) shares of digital option
. To achieve this payoff, we need to buy f(1, 0) shares of digital option 



