1 Introduction

In the 1990s, chaos theory was considered a promising framework to account for the dynamic evolution of industries and complex interactions among actors (Levy 1994, p. 176). More generally, Thiétart and Forgues (1995) argued that under some conditions organizations are likely to exhibit the qualitative properties of chaotic systems. This framework has been really fruitful: For instance, according to Vibert (2004), principles of chaos theory have helped organizational theorists to analyze several aspects of organizations; a list of “organizational propositions based on chaos and complexity theory” is provided in Houry (2012); small groups have been analyzed in terms of complex systems (Arrow et al. 2000). For a recent review on teams considered as complex systems, the reader may refer to Ramos-Villagrasa et al. (2018). This approach has provided insights into understanding dynamic complexity (Chia 1998; Griffin et al. 1998), exploring nonlinear causality Flatau (1995). For recent review on complexity management, see Grösser (2017). Other interesting contributions apply the principles of complexity theory to better understand the dynamic nature of emotion in organizations (Li et al. 2010). However, chaos theory—which, according to some authors (Vibert 2004; Houry 2012), can be considered belonging to functional theories according to the taxonomy provided by Burrell and Gareth (2019, p. 22)—has often remained a metaphor (Tsoukas 1991; Flatau 1995) or a source of inspiration and an alternative imagery in organization theory (Tsoukas 1998, p. 306). According to Begun (1994), one of the reasons is that the quantitative modeling of organizational systems may be more difficult than modeling natural systems. Another reason may be Thorngate (1976)’s “postulate of commensurate complexity,” i.e., the impossibility of a theory of social behavior to be simultaneously general, accurate, and simple, which has been explained by Weick (1979, p. 36) using the clock metaphor (Fig. 1).

Fig. 1
figure 1

Weick ’s metaphor (1979, p. 36) to illustrate the “postulate of commensurate complexity” (Thorngate 1976)

Full size image

In this paper, we take a step beyond the qualitative description discussed in Tsoukas (1998) and, as suggested in Tetenbaum (1998), develop a lifelike simulation testing the theory on an organizational problem in which sentiments and biases related to psychological issues influence agents’ behavior beyond the paradigm of the neoclassical Homo oeconomicus (Bischi et al. 2020). This way we are able to ground a dynamical model of a small group on data from a human interaction. This is an important step as modeling is a way of bring forth the social objects we study (Chia 1998, p. 366), with models we can discover for ourselves how complex systems work (Sterman 2002) and move beyond the metaphorical aspect mentioned above. Furthermore, considering how emotions interact with the team dynamics follows Li et al. ’s invitation to enrich our understanding of emotion in organizations as a dynamic process (2010).

For a long time, emotions in the workplace have been a neglected topic in the organizational behavior literature, even if “the workplace offers a bountiful opportunity to experience a wide range of emotions” (Muchinsky 2000, p. 803). Recently, scholars have devoted more interest to this topic with conferences and volumes about these themes, see, for example, Lord and Kanfer (2002), and Hartel et al. (2005). Once the Pandora-Box of emotions in the workplace has been opened, also “nasty” emotions (Lazarus and Lazarus 1994) such as anger, envy, and jealousy are slowly creeping in. For example, Menon and Thompson examine the toll that envy exacts on organizations, and observe how the economic crisis and the pressure about competitions between individuals collude to increase envy in the organizations: “The economic crisis has prompted people to question their own market value with more urgency and fear. The barrage of news about compensation inequalities reminds us that others enjoy huge rewards that we do not. Social networking sites tell us when our work contacts get promotions and are enjoying better vacations than our own. Anxiety about our own performance underscores our insecurities. These and other forces have recently collided to produce a perfect storm of organizational envy” (1995, p. 6).

Among emotions, envy is ubiquitous although socially undesirable (Hill and Buss 2008). According to Parrott (1991), at the heart of envy there is social comparison. As many incentives scheme in organizations are built around comparison and, indeed, social comparison is an important theme in Human Resource Practices (Baron and Kreps 1999), yet it is surprising the little attention the economics literature has devoted to envy. Nevertheless recently, with increasing frequency, economists have incorporated the concept of envy into a variety of analyses. Among the others, Nickerson and Zenger (2008) examine how social comparison and envy impose costs within firms and highlight how envy can be an important source of organizational failure. According to their approach, in the presence of differences in relative income among salient referents, social comparisons may trigger perceptions of inequity and envious emotion that individuals attempt to reduce. In their analysis, as in most of the economics literature contributions, the focus is on workers’ income deriving from wages; yet, considering only income does not take into account some important aspects of envy. In fact, according to Ben-Ze’ev “the person we envy has personal attributes (such as beauty, patience, or intelligence), possessions (such as a car), or positions (being the boss) that we lack but desire. We envy both what other people are and what they have” (2001, p. 208). Therefore, taking into account only monetary income is someway limitative. Furthermore, several other authors argue that envy is the product of comparisons with a more successful party in which one views oneself as inferior globally or in a particular domain (Leach 2008). Schoek (1966) provides several examples of envious behavior in which the comparison is not related to monetary income. According to Joseph et al. , envy is defined as “being a subjectively painful mix of discontent, frustration and hostility that occurs in response to an unfavorable social comparison on a domain of high personal self-relevance” (2008, p. 245).

Taking into account these aspects of envy that are not limited to differences of wages, we want to understand the effects of envy in a model of work group when the object of being envied is a personal attribute, such as the capacity of the other member. Therefore, in our analysis we assume that individual income is the same for each subordinate and envy may only depend on some attitude of the envious person. In order to perform the analysis, we embedded the group interaction considered in the theoretical model, ran a laboratory experiment creating the same work group conditions as in the theoretical model, and detected the most influencing variable. By analyzing the data, we selected the emerging representative behavior to be implemented in the dynamical group interactions. Then, following Thiétart and Forgues (1995)’s suggestion, we analyzed the nonlinear dynamics system and discussed the consequences based on chaos theory from the perspective of organization science, to understand how intolerance and envy may lead the effort allocations to nonefficient equilibria.

In the next section, we summarize the theoretical model which describes the decision-making process of the subordinates. Section 3 is devoted to the research hypotheses of this study. The experiment design and its analysis are presented in Sect. 4. The results of the analysis are reported in Sect. 5, while the modeling of envy and how this emotion affects the effort allocation dynamics are discussed, respectively, in Sects.  6 and 7. The last section concludes the study.

2 The model

Applications of nonlinear dynamical systems models to firms and work group behaviors can be found in the literature (Kopel et al. 2008; Guastello 2002). An important problem in work group literature is the withholding of effort (Kidwell and Bennett 1993; Bennett and Naumann 2005; Kidwell and Valentine 2009).

In this paper, we consider a model of supervised work group which has been extensively studied from the theoretical point of view (Dal Forno and Merlone 2010a, b, 2013a) and analyze the dynamics of effort allocation. Although this model is simple enough to provide a formalization of interactions, it considers several important aspects such as incentives, inequity, engagement in the task, and members’ expectations. The work group consists of a supervisor and two subordinates. Each subordinate allocates his whole capacity exerting an effort \(u_i\) in a task with the supervisor and an effort \(l_i\) in a task with the partner. We assume that the two subordinates have capacities \(C_1\) and \(C_2\), respectively. The production function of the group is the result of the joint efforts of the two subordinates in both tasks, that is, \(\left( u_1+u_2\right) ^{\alpha }\left( l_1+l_2\right) ^{\beta }\). The relative importance of the two tasks is modeled by two parameters \(\alpha \) and \(\beta \) which, from the economic point of view, are, respectively, the output elasticity with respect to the joint effort with the supervisor and with the partner. The production is zero whenever the joint effort in any of the task is zero.

The performance-contingent reward is a fixed wage w, a given linear incentive \({\bar{b}}_g\) proportional to the joint output of the team, and a given linear incentive \({\bar{b}}_i\) on the effort each agent exerts with the supervisor. Therefore, the problem the subordinates have to solve can be formalized as

$$\begin{aligned} \begin{array}{c} \displaystyle \max _{u_1,l_1}\quad w + {\bar{b}}_g \left( u_1 + u_2\right) ^\alpha \left( l_1 + l_2\right) ^\beta + {\bar{b}}_1u_1\\ \displaystyle \max _{u_2,l_2}\quad w + {\bar{b}}_g \left( u_1 + u_2\right) ^\alpha \left( l_1 + l_2\right) ^\beta + {\bar{b}}_2u_2 \end{array} \end{aligned}$$
(1)

It is not restrictive to assume \(w=0\), and null cost for the effort so far the total exerted effort does not exceed the capacity, that is, \(u_i+l_i\le C_i\); this simplifies the analysis. Furthermore, in Dal Forno and Merlone (2010a) it was proved that in such an optimization problem the optimal incentive scheme is:

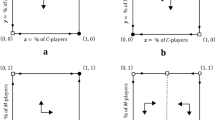
$$\begin{aligned} {\bar{b}}_g=\epsilon >0,\quad {\bar{b}}_i=0\quad \forall i=1,2. \end{aligned}$$
(2)

The supervisor can only observe the effort the subordinates exert with her and the gross production of the work group. Under these conditions, it is easy to prove that effort allocations optimize the production when the aggregated effort in the two tasks is proportional to the relative importance of the two tasks (Dal Forno and Merlone 2010a); they are represented by the continuous line in Fig. 2. This line contains all the optimal joint allocations of the two subordinates with any given capacity. Among the—not necessarily optimal—allocations, other interesting allocations can be interpreted in terms of Schelling (1960) definition of focal point. These focal joint allocations are represented by the dotted line in Fig. 2. The intersection between optimal and focal allocations provides the unique focal optimal allocation of the work group. This allocation is not only optimal but also the most natural to be chosen by subordinates. In fact, in this case their efforts are allocated proportionally to the relative importance of the two tasks and are aligned with the mutual expectations about the effort to be put in the common task.

Fig. 2
figure 2

Optimal (continuous black line) and focal (dotted line) effort allocations in the common task with parameters \(C_i=C_j=1, \alpha =0.75\), and \(\beta =0.25\). Point F indicates the focal optimal solution

Full size image

As subordinates may observe their colleague’s effort in the common task, they interact accordingly: Subordinate \(i=1,2\) allocates his effort \(l_i\) in the common task after observing the effort \(l_j\) exerted on the previous interaction by his partner. Following Dal Forno and Merlone (2013a), we consider several possible behaviors for subordinates when observing colleagues’ effort in the common task; they are represented in Fig. 3 and are formalized as follows:

$$\begin{aligned} \begin{array}{l} l_{i}\left( t+1\right) \\ \quad = \left\{ \begin{array}{ll} \frac{e_{i} }{\theta _i} \left( l_{j}\left( t\right) \right) ^{a_{i}-1}\left( C_{j}-l_{j}\left( t\right) \right) ^{{b_i}-1} &{} \text {if } a_i> 1 \, \text {and} \,b_i> 1\\ &{} \\ e_{i} \left( C_{j}-l_{j}\left( t\right) \right) ^{{b_i}-1} &{} \text {if } a_i= 1 \, \text {and} \,b_i> 1\\ &{} \\ e_{i} \left( l_{j}\left( t\right) \right) ^{a_{i}-1} &{} \text {if } a_i> 1 \, \text {and} \,b_i = 1\\ &{}\\ e_{i} &{} \text {if } a_i=b_i = 1. \end{array} \right. \end{array} \end{aligned}$$
(3)

In the equation, parameter \(e_i \in \left[ 0, 1 \right] \) is subordinate i’s engagement to the common task. Parameters \(a_i,b_i\ge 1\) determine the shape of the reaction function and model how subordinate reacts to colleague’s effort. In this way, we may have tolerant behavior when \(a_i=b_i=1\), imitative behavior when \(a_i>1\) and \(b_i=1\), compensative behavior when \(a_i=1\) and \(b_i>1\), and intolerant behavior when \(a_i,b_i>1\). Parameter

$$\begin{aligned} \begin{aligned} \theta _i =\left( C_j\frac{a_i-1}{a_i+b_i-2} \right) ^{a_i-1}\left( C_j- C_j\frac{a_i-1}{a_i+b_i-2}\right) ^{b_i-1} i=1,2 \quad a_i,b_i \ge 1 \end{aligned} \end{aligned}$$
(4)

is fixed in order to have the maximum effort equal to the engagement \(e_i\) which, for the sake of simplicity, will be considered constant through all the paper, as it does not change the results of the analysis. For a discussion about engagement, satisfaction, and business outcome, see Harter et al. (2002).

The piecewise definition of the map in equation (3) comes from considering the extremes of interval \(\left[ 0,C_j \right] \) which, when either \(a_i=1\) or \(b_i=1\) or both, could otherwise cause an indecision form; forcing \(0^0=1\), the map expression could be simpler:

$$\begin{aligned} l_{i}\left( t+1\right) = r_{i}\left( l_j\left( t\right) \right) = \frac{e_{i} }{\theta _i} \left( l_j\left( t\right) \right) ^{a_{i}-1}\left( C_j-l_j\left( t\right) \right) ^{{b_i}-1} \end{aligned}$$
(5)

with \(a_i,b_i \ge 1\) and

$$\begin{aligned} \theta _i =\left\{ \begin{array}{lr} \left( C_{j}\frac{a_i-1}{a_i+b_i-2} \right) ^{a_i-1}&{}\left( C_{j}- C_{j}\frac{a_i-1}{a_i+b_i-2}\right) ^{b_i-1} \\ &{}\quad \text {if } a_i>1 \, \text {and} \, b_i>1 \\ \\ 1&{}\text {otherwise}.\quad \quad \\ \end{array} \right. \end{aligned}$$
(6)
Fig. 3
figure 3

Subordinate i’s reaction function to observed colleague’s effort \(l_j\). With different choices of parameter values, different behaviors are obtainable: tolerance, \(a_{i}=1, b_{i}=1, e_{i}=.25\); intolerance, \(a_{i}=3.1666, b_{i}=7.5, e_{i}=.25\), and \(a_{i}=9, b_{i}=25, e_{i}=.25\); focal compensation, \(a_{i}=1, b_{i}=6, e_{i}=1\); perfect imitation, \(a_{i}=2, b_{i}=1, e_{i}=1\)

Full size image

The theoretical model we have considered provides some interesting theoretical results which rely on some assumptions; specifically, that subordinates’ efforts depend on colleagues’ efforts exerted on the previous period and the nonlinearity of their response.

In terms of Thorngate (1976)’s “postulate of commensurate complexity,” the model we have just presented can be considered a “ten o’clock research.” In order to overcome its limitations being a model both “simple” and ”general,” in the next section we will formulate the assumptions mentioned above and test them by a laboratory experiment.

3 Hypotheses

The dynamic nature of the effort allocation in a work group and the dynamical system approach for modeling both the complexity of the interactions and the different available individual reaction curves suggest that the effort allocation model can benefit from a bifurcation theory perspective. More specifically, a dynamical model based on empirical observations together with an understanding of the stability of the equilibria allows to overcome in explanation what would be obtained with a linear regression of variables for predicting the effect of incentives, wage, and production on the subordinates’ effort allocation. In particular, we consider incentives (Merlone 2002) as they are at the core of the economic model of task delegation (Laffont and Martimort 2002, p. 28), wage which, according to Houdek and Koblovsky (2017), is at the core of the standard model of worker’s decision, firm performance considered in terms of production (Farrell et al. 2012), and colleagues’ effort (Roy 1952; Adams 1965). However, as the agents cannot observe colleague’s retribution, we cannot infer any causal effect of discrimination wage—be it a voluntary act of the supervisor or not—on efforts (Gächter and Thöni 2010).

In order to pursuit this goal, three interdependent research hypotheses are associated with the study.

Hypothesis 1

The effort allocation in the two tasks depends on the incentive scheme.

We want to test the theory that, in contrast to the economic perspective which considers individuals opportunistic, agents do not necessarily react to incentives provided by the supervisor when exerting future efforts.

Hypothesis 2

The most significant variable affecting the effort allocation in a work group is the colleague’s past effort exerted in the common task.

As stated before, the effort allocation is characterized by equilibria and cyclical behaviors; likewise, there is empirical evidence of nonlinear aspects in effort allocation (Goette and Huffman 2006). Thus, we expect that a nonlinear function of the colleague’s past exerted effort might capture important marginal effects otherwise neglected. For the sake of simplicity, we consider a quadratic function.

Hypothesis 3

A model which considers the marginal effect of the colleague’s past exerted effort on the individual’s effort allocation will explain more variability than its comparable model which considers only the linear effect.

The explicative power of the bifurcation analysis is particularly helpful in understanding what happens when the intolerance and the beliefs on other’s capacity change levels. For low levels of intolerance and when the belief discrepancy from true value is small, their effect on the effort allocation is limited, while for larger values we expect to observe the occurrence of organizational misbehavior, such as effort withholding in the common task (Kidwell and Valentine 2009) which may lead the group to converge to inefficient equilibria.

4 Methods

In order to test our hypotheses, we designed an organizational experiment, in which subjects engage in a work group task to study the impact of incentives and other variables on subjects’ productivity (Camerer and Weber 2013, p. 213). With the data gathered from the experiment, we estimate variants of the following equation:

$$\begin{aligned} l_{i,t}=f\left( b_{g,t},b_{i,t}, l_{j,t-1},R_{i,t-1},P_{g,t-1}\right) \end{aligned}$$
(7)

where \(b_{g,t}\) is the incentive proportional to the output of the group, \(b_{i,t}\) is the incentive on the effort each agent exerts with the supervisor, \(l_{j,t-1}\) is the colleague’s past effort exerted in the group task, \(R_{i,t-1}\) is the performance-contingent reward, and \(P_{g,t-1}\) is the group production of the aggregated effort in the two tasks as they were all defined in the theoretical model presented in Sect. 2. The dependent variable \(l_{i,t}\) is the effort allocated in response to the group task.

4.1 Participants

Participants were 36 undergraduate students in Business Administration. There were, in total, 19 females and 17 males whose mean age was 19.72 years, ranging from 18 to 26 (s.d. \(=1.981\)). Our experiment was targeted at understanding the variables which are taken into account when deciding the effort allocation in the two tasks, and which shape the reaction function has. When considering student participants, concerns regarding external validity are often raised (Aguinis and Bradley 2014). The practice of using student samples has been debated for decades (Gordon et al. 1986); recently, Exadaktylos et al. (2013) suggest that (self-selected) students are an appropriate subject pool for the study of social behavior and (Fréchette 2015, p. 386) concludes that “overall much of the big picture seems the same whether one looks at professionals or students in laboratory experiments testing economic models.” Another important aspect is how to provide participants suitable incentives to participate to the experiment (Gneezy and Rustichini 2000). In our case, we provided both a participation and a performance incentive in terms of extra credit to those who took part to the experiment. This approach allowed us to select motivated participants and avoid the risk of side payments.

4.2 Design and procedure

The purpose of the experiment was to observe the behavior of human participants in the situation considered in the theoretical model, where the operatives have different capacity. Three different roles were considered: supervisor; hi-capacity subordinate; and low-capacity subordinate. An incentive scheme in which the production function consisted in the supervised work group production model described in Sect. 2 was introduced. The supervisor had to provide the individual incentives (privately communicated to each subordinate) and the collective incentive (publicly communicated). The experiment was run in nine weekly sessions where two different groups interacted separately. Roles were randomly attributed, and all the operatives were provided with an individual capacity, one high (\(C_i=10\)) and one low (\(C_j= 2\)), as private information. The relative importance of the two tasks (\(\alpha =0.7,\beta =0.3\)) and a base salary were common knowledge. Both private and common values were the same across all the sessions. Each period was divided into three steps:

  1. 1.

    the supervisor decided a linear incentive for the common task and the individual incentives for the task with her;

  2. 2.

    subordinates allocated their effort;

  3. 3.

    individuals’ remuneration (defined by the agent’s objective function in Eq. (1) was computed as well as the net production of the work group according to the formula

    $$\begin{aligned} \left( 1-2b_g\right) \left( u_i+u_j\right) ^\alpha \left( l_i+l_j\right) ^\beta -b_il_i-b_jl_j. \end{aligned}$$
    (8)

General written instructions were provided to the participants and are available upon request. After the participants read them, several examples were illustrated and discussed. When we were reasonably certain that participants had understood the problem, roles were randomly assigned and additional role instructions were distributed. After all participants concerns were (privately) discussed, the experiment started. The experimenter was in charge of receiving from and transmitting to the participants all the relevant information. All the variables are continuous; descriptive statistics for all variables and correlations are provided in Table 1. The correlations between some of the variables are meaningless and therefore are omitted from the table. Furthermore, in each step, for each of the five periods of the session, written motivations of participants’ decision were required. To this purpose, group members received a form to be filled during the experiment (also available upon request).

Table 1 Descriptive statistics and correlations of the observable variables in the experiment
Full size table

4.3 Analysis

The data obtained through the experiment are in the form of panel. Thus, in order to test the research hypotheses, the data were fitted individually. The independent variables were: the incentive given to the common task; the incentive given individually to perform a task with the supervisor; the individual’s past compensation; the net past production of the work group; the level of effort the colleagues exerted in the common task at the previous round. The dependent variable was the individual level of effort exerted in the common task. As the efforts were allocated after the independent variables were revealed to the agents, we can properly assess causality attributes and not only a simple association.

In order to test the research hypotheses, we tested for data poolability to investigate whether it is suitable to assume the constancy of the relationships over time. We are interested in the poolability test in the time dimension mainly because we are looking for some structural change in this relationship. Nonrejecting this assumption does not imply that each participant to the experiment had the same pattern of reaction to the colleague’s past exerted effort in the common task. Indeed, examining the 36 scatter plots of effort allocations against the past colleague’s observable effort reveals that there are several types of behaviors such as imitating, compensating, and intolerant. All these behaviors are already included in the theoretical model presented in Sect. 2 as already mentioned above and illustrated in Fig. 3.

The poolability test statistic (Chow 1960) gives \(F_{\left( 35,72\right) }=0.650\) with \(p>0.05\) when considering the colleagues’ effort and \(F_{\left( 35,72\right) }=0.647\) with \(p>0.05\) when considering the given group incentive. We could conclude that there is no evidence for a structural shift in the relation between individual effort exerted in a group task and colleagues’ past exerted effort or given incentive over the experiment stages (5 rounds) at any useful significance level. As a consequence, no panel models need to be specified, as all rounds are sufficiently homogeneous. In the rest of the paper, we will consider only data from round 3. This choice was made because by considering an intermediate round we can at least avoid a possible bias deriving from either the initial or final rounds.

We see in Table 1 that some of the independent variables considered in Eq. (7) exhibit strong correlations. There is evidence of a linear association between the observed individual retributions and group productions in the previous time period and the incentive schemes proposed. In particular, the data suggest that large-size incentives are associated with high level of past retribution; vice versa, high production levels are associated with consequent small-size incentives. From the explanation of their choices in several cases, managers provided a reward for previous turn results; the negative association is a result of Eq. (8). Furthermore, there is a strong correlation within the incentive schemes. However, the effects of observed production on the incentive schemes and how they are designed are factors to be attributed to the supervisors’ behavior only, and not to the agents.

The nature of the variables and the research hypotheses we want to test suggest that we can implement a linear multiple regressions on data from round 3. Knowing that strong associations could bias the estimate of coefficients in some variants of Eq. (7), we will consider only models in which either the incentive schemes or the organization measures will be considered, to avoid multicollinearity. As the two incentives are correlated, we will consider them separately in order to distinguish their effect on the effort allocation. This association is again the result of managers providing rewards for previous turn performance and, possibly, also to the inability to understand the role of the different incentives. This analysis is sufficient to test Hypotheses 1 and 2. In order to test Hypothesis 3, the quadratic function of the colleague’s past exerted effort will be introduced in Eq. (7) to capture the marginal effect of the social comparison. Our results are robust by using data from any other round.

5 Results

Pre hoc power analysis was used to establish the appropriate sample size for all main effects and interaction contrasts, based on the following parameters: predicted power 0.80 (Lenth 2001), and alpha 0.05.

The Pearson’s correlation test conducted on data from round 3 revealed that there are no linear associations between the incentive scheme and the allocated effort in the group task (collective incentive: \(r\left( 34\right) =0.01, p=0.961\); individual incentive: \(r\left( 34\right) =0.02, p=0.931\)). Furthermore, no other kind of association is evident from the scatter plots in Fig. 4, even after the outliers were removed. This result is not in support of Hypothesis 1, and it is in contrast to the economic perspective which considers individuals opportunistic (Osterloh and Frey 2000, p. 539), and to the empirical evidence presented in Prendergast (1999). Intrinsic motivation is considered also in economics, although it is difficult to analyze (Williamson 1985, p. 64).

Fig. 4
figure 4

Scatter plot of the relation between the incentive scheme and the effort exerted at round 3

Full size image

Table  2 reports regression estimates explaining the effort exerted by the agents. Models show estimates from regressions which include, beside the colleague’s past exerted effort, either the incentive schemes (Models (1), (2), (4), (5)) or the organization variables (Models (3), (6)). The marginal effect of the colleague’s past exerted effort is included in Models (4)–(6).

Overall, the regression results provide evidence, even if not statistically significant, that increased individual incentives results in decreased effort allocated in the collective task in response. This may be a result of incentives misalignment (Kerr 1975), as also discussed in Baron and Kreps (1999). The same evidence is stronger when considering the colleague’s exerted effort in the previous time period. Higher levels of colleague’s effort cause significant drops in effort. Controlling for the group incentive, an addition of a unitary effort of the colleague’s past exerted effort results in an average drop of about half unitary effort in the effort allocated in the common task. This indicates that a dynamic model of the effort allocation which depends only on the colleague’s past effort might provide a simpler and better fit to the data than a much more complicated model. These results support Hypothesis 2.

The scatter plot in Fig. 5 reports the observed cause/effect of the past effort exerted by the colleague on the effort allocated in response to the group task. We see that a linear association might not be the best fit to the data. Nonlinearity of the relationship is quite evident. By including the quadratic function of the colleague’s past exerted effort, Models (4)–(6) explain on average about \(10.93\%\) of the variability in the exerted effort more than their Models (1)–(3) counterparts. Controlling for either the incentives or the organization variables, there is evidence that the colleague’s past effort and its quadratic term are the only ones to be statistically significant. Because the coefficient of the colleague’s past exerted effort is negative and the coefficient of its quadratic term is positive, Models (4)–(6) imply that, at low values of the colleague’s past effort, an additional effort unit from his side has a negative effect on the effort exerted in the future; the marginal effect to exert an effort in the common task is increasing w.r.t. the colleague’s effort level, producing evidence to the compensating reaction behavior. The larger is the effort exerted in the past by the colleague, the smaller is the propensity to compensate in the common task with one’s own effort; the smaller is the colleague’s effort the larger is the propensity to compensate. At some point, the effect becomes positive, and the quadratic shape means that the effort exerted in the future is increasing as the colleague’s past exerted effort increases. The average turning point is at the effort value 4.86. It turns out that only about \(10.42\%\) of the participants had a colleague who exerted an effort greater than this value. Thus, an increase in the colleague’s past exerted effort from, say, two to three effort unit on average decreases the future effort by about 0.838 effort units. On the contrary, an increase in the colleague’s past exerted effort from, say, five to six effort units increases the future effort on average by about 0.042, an almost negligible even if positive effect. These results support Hypothesis 3.

Table 2 Predictors of level effort allocation
Full size table
Fig. 5
figure 5

Scatter plot of the relation between the colleagues’ exerted effort at round 2 and the individual effort exerted at round 3. Including the quadratic function of the colleague’s past effort (Models (4)–(6) in Table 2) provides a better fit than the models without the quadratic term (Models (1)–(3))

Full size image

Summarizing, the empirical analysis results suggest that, when modeling the effort allocations of supervised work groups, considering several variables is not parsimonious. Colleague’s behavior is the most significant determinant, and there is evidence that this causal relation is not linear, suggesting a compensative behavior. Therefore, in the remaining of the paper we will focus on the dynamics of the effort allocation of agent i to the group task when the behavior of colleague j, which is the object of social comparison, is compensating. Figure 6 illustrates different reaction functions for compensators which can be obtained from the theoretical model defined in Eq. (3) when parameter \(a_i=1\) is fixed and parameter \(b_i\) varies.

Fig. 6
figure 6

Different shapes of compensator j’s reaction function to different effort levels exerted by agent i (red lines); optimal (continuous black line) and focal (dotted line) effort allocations with \(C_i=C_j=1, \alpha =0.5\), and \(\beta =0.5\). As in Fig. 2, the intersection point \(\text {F}\) of the two black lines is the focal optimal joint allocation of subordinates’ effort (color figure online)

Full size image

6 Modeling envy

When both subordinates are compensators, the work group will reach the stable optimal and focal equilibrium. However, often real groups are characterized by instability (Fuhriman and Burlingame 1994; Arrow 1997). Furthermore, Fig. 5a shows that for low values of the colleague’s past exerted effort not all responses were compensating, as they exhibit a large variability. Among the several reasons which could contribute to explain this phenomenon, we consider the role of behaviors activated by unfavorable social comparison. According to Arnocky et al. (2016), unfavorable social comparison may activate envy. Alicke and Ethan (2008, p. 74) define envy as “a negative social comparison-based emotion, one that arises when person A compares unfavorably with person B with respect to an attribute, possession, or position that person B has and person A wants”.

As we have discussed when presenting the model, with the optimal incentive scheme the monetary compensation is the same for both subordinates despite their different capacity. Therefore, envy cannot be triggered by comparing the compensations. Rather, we therefore assume that one of the agents believes the other has higher capacity although the effort exerted in the common task by the two subordinates is the same. As a consequence, the subordinate with alleged higher capacity is able to exert a higher effort with the supervisor resulting in an unfavorable social comparison. This assumption is coherent with the definition of envy “as a painful emotion that involves the beliefs that (a) one lacks a desired object that another person has and (b) the desired object is important to the person’s self-concept or competitive position. Envy includes the motivation to reduce the pain it entails and to improve one’s relative standing” (Cohen-Charash and Larson 2016, p. 26). Furthermore, when considering the definition provided in Alicke and Ethan (2008, p. 74): “envy is a negative social comparison-based emotion, one that arises when person A compares unfavorably with person B with respect to an attribute, possession, or position that person B has and person A wants,” the comparison in our model is between the different capacities.

Let us denote \(\tilde{C}_j\ge C_i\) agent i’s belief about his colleague j’s capacity. As agent i feels envy toward his colleague because of the believed larger capacity, his effort allocation in response will not be compensative. Rather, we assume that, in order to reduce the pain, any departure of colleague’s effort from the believed optimal allocation will be punished by lowering the effort in the common task and, at the same time, freeing up more capacity which can be allocated in the task with the supervisor. To this purpose, we consider the simpler form of the reaction function defined by Eqs. (5) and (6) which we report by replacing the true colleague j’s capacity \(C_j\) with the believed capacity \(\tilde{C}_j\):

$$\begin{aligned}&l_{i}\left( t+1\right) = r_{i}\left( l_{j}\left( t\right) \right) = \frac{e_{i} }{\theta _i} \left( l_{j}\left( t\right) \right) ^{a_{i}-1}\left( \tilde{C}_{j}-l_{j}\left( t\right) \right) ^{{b_i}-1} \end{aligned}$$
(9)

with \( a_i,b_i \ge 1\) and parameter

$$\begin{aligned} \theta _i =\left\{ \begin{array}{lr} \left( \tilde{C}_{j}\frac{a_i-1}{a_i+b_i-2} \right) ^{a_i-1}&{}\left( \tilde{C}_{j}- \tilde{C}_{j}\frac{a_i-1}{a_i+b_i-2}\right) ^{b_i-1} \\ &{}\quad \text {if } a_i>1 \, \text {and} \, b_i>1 \\ \\ 1&{} \text {otherwise}.\quad \\ \end{array} \right. \end{aligned}$$
(10)

There are two aspects which are important in how we model envy. The first one is that agent i believes that colleague j has larger capacity (\(\tilde{C}_j>C_i\)); the second one is how agent i reacts to such alleged difference in capacity.

Should the alleged capacity difference have no consequence, i.e., the envious subordinate does not alter his reply, the dynamics would not be perturbed and the focal allocation would be achieved. Differently, the reaction to the belief in having a lower capacity can be modeled and calibrated by modifying the intolerance level [parameters \(a_i\) and \(b_i\) in Eqs. (9)–(10)], which shapes how subordinate i reacts to differences in the expected level effort from subordinate j—as illustrated in Fig. 7.

As it is observed in Fig. 3, with tolerance the reply is constant; by contrast, when intolerance starts growing, the reaction function becomes concave; finally, the bell-shaped line models large values of intolerance.

Both coworkers’ dynamics are nonlinear and, under some conditions, may determine chaotic behaviors, as analyzed in the next section.

Fig. 7
figure 7

Different shapes of agent i’s envious reaction. The dashed line shows the original reaction function of subordinate i; the two red continuous lines show the change in expectation and growth of intolerance in subordinate i. The blue line is colleague j’s compensating reaction function to agent i’s effort \(l_i\) (color figure online)

Full size image

7 Work group dynamics with an envious subordinate

According to Thiétart and Forgues (1995), chaos theory provides interesting insights on how groups work, such as prediction impossibility (sensitivity to initial conditions), attraction toward configurations (strange attractors), and stepwise change processes (bifurcation). Furthermore, it gives a complementary theoretical support to other existing theories. In this section, we therefore provide the dynamics analysis of the efforts allocation considering intolerance and the source of envy as bifurcation parameters, relating the results to equilibria inefficiency. As it concerns the simulations we ran, statistical power analysis is not relevant as the interaction model we consider is deterministic and not stochastic (Secchi and Seri 2017, p. 95).

When subordinates are tolerant and allocate their capacity focally, their reaction curve is constant as illustrated in Fig. 3; in this case, the only globally stable fixed point is the focal allocation which is also optimal. The same reasoning holds in case of two compensating subordinates; the focal allocation is the unique optimal stable equilibrium.

In the following, we explore the evolution of the group effort allocation in the case agent i is not compensating while his colleague j is. Rather, agent i is subject to unfavorable social comparison, believing that his colleague has a higher capacity (\(\tilde{C}_j>C_i\)) and therefore he exhibits an intolerant behavior and a shift of the expected focal point from the theoretical equilibrium F. Dependently on the expectation and the degree of intolerance (parameters \(a_i\) and \(b_i\)), the system evolves in different ways. This is described by the bifurcation diagrams in Fig. 8. The figure is obtained by fixing both agents with the same capacity \(C_i=C_j=1\), agent i’s belief about his colleague’s capacity \(\tilde{C}_j=1.8>C_i\), and letting parameters \(a_i\) and \(b_i\) vary; without loss of generalization, \(a_i\) is computed as a function of \(b_i \in \left[ 1,20\right] \) in order to keep the maximum of the reaction function at the focal point \(F\left( 0.3,0.25\right) \).

Controlling for the expected capacity \(\tilde{C}_j=1.8\), when the agent is not too intolerant to colleague’s deviation from the expected effort (i.e., low values of intolerance parameter \(b_i\)), the reaction function is concave as in Fig. 7 and there is a unique equilibrium—which is still stable—at the intersection point of the two reaction functions (blue and concave red lines). This equilibrium, even if not optimal, is not very far from the optimal allocation line (continuous black line), and this implies that the work group allocation goal can still be reasonably considered met. However, if agent i’s intolerance is not negligible (parameter \(b_i\simeq 7.17\)), the reaction function in red becomes bell-shaped and the equilibrium loses its stability. In Fig. 8, this corresponds to the first bifurcation observed, that is, when the unique line is replaced by two distinct lines, indicating that the system converges to a cycle of period two, increasingly distant from the optimal allocation line. From this point on, to an increase of the intolerance parameter \(b_i\) corresponds a cascade of period doubling bifurcation, that is, the system converges to cycles of larger and larger period.

When the agent’s intolerance is quite large (intolerance parameter \(b_i\simeq 15.35\)), there is a new contact between the two reaction functions and, besides the original equilibrium \(E_1\), there is a new equilibrium \(E_2\) with multistability. This is shown in Fig. 8 where a new branch originates and it is visible at the top-right of the left diagram in Fig. 8. As the intolerance grows further, there are three equilibria: \(E_1\) (stable), \(E_2\) (unstable), and \(E_3\) (stable) as illustrated in Fig. 9. However, the new stable equilibrium is inefficient as its distance from the efficiency line is larger than the distance of \(E_1\).

Fig. 8
figure 8

Bifurcation diagrams of subordinates j’s (left) and i’s (right) effort as intolerance \(b_i\) of subordinate i increases; other parameter values: \(C_i= 1.0, e_i= 0.25\), \(\tilde{C}_j=1.8,C_j= 1.0, a_j= 1.0, b_j= 5.8, e_j= 0.994594\), and initial condition \(l_i\left( 0\right) =0.1\), \(l_j\left( 0\right) =0.100000\)

Full size image
Fig. 9
figure 9

Envious reactions for different values of intolerance of subordinate i: \(b_i \simeq 7.168337\) and \(b_i \simeq 16.5\). Other parameter values: \(C_j= 1.0, a_j= 1.0, b_j= 5.8, e_j= 0.994594, C_i= 1.0, e_i= 0.25, \tilde{C}_j=1.8\)

Full size image

Now, we control for the intolerance degree (parameters \(a_i\simeq 2.33,b_i=5.00\)) and let the belief \(\tilde{C}_j\) about colleague j’s capacity vary (Fig. 10). We can see that there is coexistence of an equilibrium in which both subordinates work in the common task (\(l_i,l_j>0\)) and one in which the envious subordinate does not work in the common task (\(l_i=0\)). The latter equilibrium is inefficient. As the alleged capacity \(\tilde{C}_j\) increases to about 1.19, the first equilibrium loses stability. Finally, at about \(\tilde{C}_j\simeq 1.80\), the inefficient equilibrium vanishes. This is explained in Fig. 11, where we can see that with an intolerant colleague we have coexistence of three equilibria: \(E_1\) and \(E_3\) (stable), and \(E_2\) (unstable). As \(\tilde{C}_j\) increases, \(E_1\) loses stability, and for larger values of \(\tilde{C}_j, E_2\) and \(E_3\) collapse and vanish.

Fig. 10
figure 10

Bifurcation diagrams of subordinates j’s effort (left) and i’s (right) as \(\tilde{C}_j\) the believed capacity of subordinate j increases in the interval \(\left[ 1, 2\right] \) with parameters value \(C_j= 1.0, a_j= 1.0, b_j= 5.8, e_j= 0.994594, C_i= 1.0, a_i=5.8, b_i=15.4, e_i= 0.25\), and initial condition \(l_j\left( 0\right) =0.250000\), \(l_i\left( 0\right) =0.5\)

Full size image
Fig. 11
figure 11

Envious reactions for different values of the alleged capacity of subordinate j: \(\tilde{C}_j \simeq 1.188377\) and \(\tilde{C}_j \simeq 1.801603\). Other parameter values \(C_j= 1.0, a_j= 1.0, b_j= 5.8, e_j= 0.994594, C_i= 1.0, a_i=5.8, b_i=15.4, e_i= 0.25\)

Full size image

8 Discussion and conclusion

Our model of supervised work group describes a complex system where two actors interact in a double task—one to be performed jointly and one to be individually performed with the supervisor—each part of which cannot be neglected in order to achieve the organization production goal. In the absence of communication, coordination is difficult if not impossible. This absence is replaced by a flexible incentive scheme designed by the supervisor. Due to the complexity of the system, both because of the human interaction component and the presence of several variables, we decomposed the problem in three steps: (1) Which are the important variables in the effort allocation problem? (2) what kind of relationship exists between the relevant variables? and (3) taking into account the previous finding, how may the system evolve? As finding data from controlled organizational interactions is difficult, we designed and ran an experiment to explore the complex relationship between the available information and the group performance. The results support previous evidence on controversial effects of incentives, while they establish a strong causal effect of social comparison.

8.1 A dynamical model built on quantitative and qualitative data

This paper contributes to the increasing interest in expanding the available methodology repertoire of organizational theories at least in two directions. Firstly, by using the experiment we can focus on sifting through causal effects in a sufficiently controlled environment, eliminating unimportant variables and exploring how individuals respond to individual-level processes in a work group with multiple tasks. Secondly, by considering different approaches—theoretical models, experiment, empirical analysis—from different perspectives—economics, psychology, game theory—we build a dynamical model from both quantitative and qualitative data. We combine these approaches to theory making, by exploiting synergies and complementarity grounded on empirical data and formalized in theoretical models. Dynamical models as we develop here are a way to study complex social, economical, and organizational phenomena (Anderson 1999; Dooley and Van de Ven 1999; Faggini and Parziale 2012).

The resulting dynamical model allowed us to examine initial conditions, in a natural time structure, and explore how the outcomes of interest evolves and make observable the way complex interactions are realized.

8.2 Practical implications

The existence of a nonlinear relationships observed in the effort allocation of the participants at the experiment has important practical implications, as this insight may help to design intervention strategies aimed at improving the work group performance and subordinates’ well-being. Firstly, if supervisors wish to facilitate the group performance, they may consider the important factor, according to our findings, which affects the effort allocation behavior. Moreover, they might want to consider the importance of a theoretical model based on empirical results. As such, the model can help supervisors to identify the reason of the inefficient allocations existence. As shown by our model, the intolerance and the beliefs on colleagues’ capacity act as bifurcation parameters. That is, they might be responsible of different allocation dynamics found in work group behaviors. Therefore, supervisors might be advised that the extent to which subordinates perceive their colleague’s behavior in the common task will determine the emergence of sudden changes in their allocation behavior. In fact, as mentioned in Kopel et al. (2008), in complex dynamics with sensitive dependence on initial conditions, even minor interventions may suffice to prevent harmful events and to obtain better results. All these aspects may be relevant when considering group’s collective intelligence, in terms of both members’ diversity and interaction in the group (Woolley et al. 2015).

Another interesting application derives from the relationship between fair wages and productivity which has been analyzed in economics, since Akerlof ’s (1982) seminal paper. According to several contributions, e.g., Akerlof (1984), Akerlof and Yellen (1988), Cohn et al. (2015), Helpman et al. (2008), Policardo et al. (2019), an increase in wage inequality (i.e., either a decrease of lower wages or an increase in higher wages) is associated with a reduction of lower paid workers’ effort. Although subordinates cannot observe colleague’s wage, they may observe his/her effort in the common task, and when a difference is detected, it can trigger the same envious behavior aforementioned.

8.3 Limitations and future research

Some limitations must be taken into account for future research. Firstly, the experiment we considered was merely intended to test some assumptions of the theoretical model we considered; as a result, the only possible experiment which could recreate such an interaction was a laboratory experiment. Although the experiment we analyzed was only intended to offer a someway complementary perspective from the “ten o’clock research” implied in the model, the complexity of interaction should be approached also from other perspectives. A first step we recommend is designing an experiment on the field to observe work group members’ effort allocations (Dipboye and Flanagan 1979). Secondly, it is important to consider possible limitations derived from the choice of observable variables affecting the effort allocation. Other factors may influence subordinates’ decision. It might also be possible that other than compensating behaviors may emerge. In fact, the compensating is the representative behavior of the participants we considered. In further research, it would be interesting to consider further classes of behavior grounded on the experimental data as in Dal Forno and Merlone (2013b) and to extend the bifurcation analysis to groups with these classes of behaviors.

8.4 Conclusion

The present study aims to model the dynamic interaction of a supervised group. Analyzing effort allocation data from a human participant interaction, we found a nonlinear reaction to colleague’s past exerted effort. The study shows the benefit of using the experiment results to shed light on the effort allocation behavior in a nonlinear way over the traditional linear regression and confirming the existence of a compensating behavior in the considered model. Overall, the study shows that work group members take into account colleagues past exerted efforts in order to allocate their capacities in the next time period. Furthermore, the allocation behavior presents linear (decreasing) and nonlinear (marginally increasing) relationships, by confirming the existence of a compensating attitude in order to have the task accomplished. In this sense, nonlinear approaches to subordinates’ behavior can complement a more common linear approximations. Among the several reasons which could contribute to explain this phenomenon, we considered the role of behaviors activated by unfavorable social comparison (Miceli and Castelfranchi 2007). Considering how envy affects the effort allocation allowed us to understand how complex dynamics and inefficient equilibria may result in the group interaction. As our interest was to test a well-defined theory about agents’ behavior in supervised a work group (the fundamental research questions were: what do agents observe when deciding the effort allocation in the two task? and how do they react depending on the colleague’s effort in the common task?), this theory is suitable to be studied deeply with managers and subordinates in a real case study to see whether it can be applied and provide explanation about apparently irrational behaviors.