Non-compliant behaviour in public procurement: an evolutionary model with endogenous monitoring

Abstract

In recent years, the study of the evolution of non-compliant behaviour in public procurement has been widely developed due to the growing economic relevance of this phenomenon. When such a question is formalized in terms of a dynamical model, new insights can be pursued, related to the possible evolution from a situation with low dishonesty level to high dishonesty level or vice versa. The present model considers an evolutionary adaptation process explaining whether honest or dishonest behaviour prevails in society at any given time by assuming endogenous monitoring by the State. We will distinguish between a scenario in which firms converge to monomorphic configurations (all honest or all dishonest) and a scenario in which firms converge to polymorphic compositions (that is with coexistence of both groups), depending on the relevant parameters. By making use of both analytical tools and numerical simulations, the present work aims at explaining the effectiveness of economic policies to reduce or eliminate non-compliant behaviour. Social stigma is found to play a key role: if the “inner attitude toward honesty” of a country is not strong enough, then dishonesty cannot be ruled out. However, increasing both the fine level attached to dishonest behaviour and the monitoring effort by the State can reduce asymptotic dishonesty levels and escape form the dishonesty trap.

1 Introduction

Beccaria (1764) and Bentham (1789) were among the first authors to begin studying crime and criminal response in a rational way focusing on the scientific approach to criminology research. The modern theory that derives from this literature underlines how the criminal makes a decision whether to proceed with the crime after weighing up the possible risks and benefits of carrying out the crime. The criminal act will take place if the advantages appear to outweigh the potential costs. As a consequence, for a punishment to work and have a deterrent effect, the predicted utility of the crime must be less than the utility from abstention.

In Becker’s seminal paper of 1968 (Becker 1968), the main principle of the utility model states that a rational criminal has to speculate on the possible outcome. If he decides not to carry out a crime, there will be no risk involved, but obviously no criminal advantage. On the other hand, if he decides to go through with the crime, he will gain a criminal benefit but risk the consequential penalty. The predicted cost of carrying out a criminal action is a function of the probability of a criminal being caught and the degree of punishment he will receive when arrested. Following this approach, social investments in police and prisons will have an influence on the total number of crimes, while labour-market opportunities also have an impact on the relative cost of time involved in criminal offences. Regarding these offences, the most important element is deterrence. If criminals are discouraged from carrying out illegal activities in the first place, there is no need to go through the long (and expensive) process of arresting, prosecuting, sentencing or imprisonment.

The present contribution aims at considering non-compliant behaviour attached to public procurement by following the Becker’s intuition.

Public procurement refers to the process by which public authorities, such as state or local authorities, purchase works, goods or services from private companies.

Governments and public firms must procure a wide variety of public goods, services and works from the private sector: they can range from basic IT equipment to important public infrastructures (e.g. roads, railways, etc.). Public procurement is a key economic activity of governments accounting for a relevant percentage of gross domestic product (GDP): in fact, there is a need for “value for money” regarding the relevant share of public spending involved in public contracts which is estimated on average to be 15% of GDP worldwide. As stressed by Iossa “This range will increase in the next years because of the increased level of delegation to the private sector of the provision of public services, not only in traditional sectors such as transport, energy and gas, but also in new sectors, such as the prison sectors and waste”.¹

Many corruption and fraud risks are present in the public procurement procedures leading them to be considered as examples of fraudulent and dishonest behaviour. The main reason must be searched within the strict link between the public and the private sector, link which can lead to conflicts between interests often producing dishonest behaviours. To be more precise, the non-compliant aspect involved in public procurement process is mainly due to the asymmetric information which can regard both the supplier selection phase and the implementation phase (quality, costs and delays).

Illegal behaviour in public procurement can be identified in the award phase since the corrupt public official in exchange for a bribe can “pilot” the award of the contract to the firm that paid the bribe. Otherwise, especially in the case of public infrastructures, the quality of public procurement depends on the implementation phase: for this reason the possibility that the firms who provide the good through the auction can produce low-quality goods must be considered. It is therefore very important to try to ensure high-quality public procurement in order to guarantee good governance. footnoteSee, for example, Iossa and Martimort (2016).

Hence, even if the choice on the allocation of public resources may be correct, the final result can still depend on different elements, such as the design rules of the process, the choice of suppliers, the contract gain and control on the implementation phase (as we will consider in the present study). The evolution of corruption and punishments has been investigated by means of different dynamical techniques that spread from cellular automata [see, for example, Wirl (1998)] to game theory [see, for example, Povey (2014)] and focusing on different systems of the economy, from tax avoidance to strategic management [see, for example, Lorenz (2019) and Masch (2004)]. De Giovanni et al. (2019) studied the optimal control problem of a tax authority and the dynamics of compliance when individuals have to decide whether to engage in tax evasion depending on an evolutionary adaptation process. Tax evasion, evolution of compliance and regulation have been analysed also in Petrohilos-Andrianos and Xepapadeas (2016) that focused on the effect of imitation in the evolution of strategies adopted by the population.

In order to describe the evolution of non-compliant behaviour in public procurement, the model herewith presented is formalized as an evolutionary adaptation process able to establish whether compliant or non-compliant behaviour predominates in society. Furthermore, players (firms) will show either compliant (honest) or non-compliant (dishonest) behaviour according to the type of company they encounter and the rewards involved (word-of-mouth process). Following Lamantia and Pezzino (2017), we assume that honest firms which are in contact with corrupt firms may decide to change their behaviour if they realize that the reward they obtain from being corrupt is greater than the one they receive from being truthful. In addition, following Brianzoni et al. (2019), we consider the honesty propensity assumption to hold, that is all dishonest firms meeting honest ones will choose to change type if the expected utility from dishonest behaviour is not greater than the expected utility derived from honest behaviour, while not all honest firms meeting dishonest ones will choose to change type even if a higher expected utility can be reached. Differently from the previous contributions, in the present paper we focus on the behaviour of non-compliant firms when the auditing level fixed by the State is linked to the diffusion of non-compliance in the economy, i.e. the endogenous monitoring level by the State is considered. Hence, the auditing level corresponds to the enforcement effect in the model, where auditing is controlled by the probability with which a firm is monitored and penalized for the infringement once discovered. The approach of an enforcement authority will most probably affect the equilibrium and the dynamics which in turn have influence on the balance compliance decisions of the firms.

In fact, as explained in Bajari and Tadelis (2001) and Brianzoni et al. (2011), due to the varying levels of the quality of goods, difficulties appear when companies lie about the original quality of a good. Since the quality of a good is confidential information, only the State’s controllers can check the authenticity of a product. Therefore, the State can reduce or even abolish corrupt behaviour by putting in place a monitoring activity depending on several factors. For instance, Stranlund and Dhanda (1999) analysed how the probability with which a firm is monitored and the obligation to punish corruptive behaviour varies according to the different types of firms. On the other hand, Lui (1986) considers how difficult and costly it can be to monitor a corrupt official, especially if other officials are also corrupt. Finally, as analysed by Waqar (2016), the environment in which a tax inspector works also has an influence on how effective monitoring can be. Moreover, Waqar (2016) considers how equilibrium depends on the level of monitoring and the percentage of corrupt firms. By following this research line, we assume an endogenous monitoring technology, which depends on the diffusion of corruptive behaviour in society, in order to show how the endogenous audit level has an effect on equilibrium and evolution in the public procurement sector when considering non-compliant behaviours. Furthermore, we consider that different countries may have a higher or lower intrinsic attitude towards honesty. Higher intrinsic honesty derives from the fact that a greater social stigma is attributed to dishonest behaviour (as indeed it emerges from the paper by Fisman and Miguel (2007), in which the importance of considering the “culture of legality” of a country is highlighted). Clearly, this intrinsic honesty of the country is a variable on which a State can act but only in the medium–long term. Considering and comparing countries characterized by a different “attitude” towards honesty allow us to evaluate how much the efficacy of economic policies in fighting the dishonesty depends on the starting conditions and the attitude of the considered country. The economic model proposed in the present paper is formalized by a dynamical system describing the evolution of both the fraction of dishonest firms and the monitoring effort by the State over time. The final system can be differentiable or piecewise–smooth depending on the relation between production costs for honest and dishonest firms and the level of fines. By using both analytical techniques and numerical experiments, our model aims at demonstrating that the economy may converge in the long run towards monomorphic configurations, i.e. firms are all honest or all dishonest (i.e. dishonesty trap), or even to polymorphic compositions characterized by the presence of both groups. In addition, fluctuations can emerge. The transitions to different long term qualitative scenarios can be explained by considering modifications in some key ingredients of the model (such as honesty propensity, fine level, social stigma, effort put in place by the State to fight dishonest behaviour, etc.) and the related parameters (i.e. bifurcation analysis is presented). In particular, as the system can result to be continuous but not differentiable, besides the standard bifurcations occurring in smooth systems, also border-collision bifurcations (BCB) can emerge.² Starting from the initial works by Nusse and Yorke (1992) and Nusse and Yorke (1995), several contributions investigated BCB structures both in one-dim and two-dim systems [see, for instance, Panchuk et al. (2013, 2015), Banerjee et al. (2000) and Gardini et al. (2010)] and several applications in economics have been proposed [see Gardini et al. (2011, 2015)].³ Moving from standard smooth bifurcation structures to BCB sequences, the modification in qualitative dynamics as some key parameters are changed can be no more predictable, providing that economic policies aiming at fighting dishonest behaviour are difficult to be fixed.

This work conducts an analysis of the possible tools that a State can use to eliminate or at least reduce dishonest behaviour. We found that the culture of legality, i.e. the inner honesty of a country, is a necessary and sufficient condition to remove corruption: only countries with a high level of honesty will, independently of other instruments, be able to eliminate dishonest behaviour. Conversely, in countries where the culture of honesty is low, a low level of punishment for discovered dishonest behaviour leads the economy to converge in the long term towards a trap of dishonesty, i.e. a stable equilibrium in which all firms are dishonest. If the level of punishment for dishonest behaviour and the amount of public resources devoted to fighting dishonesty are high enough, the economy can converge towards an equilibrium in which there are both honest and dishonest firms. Finally, in the case in which the inner honesty is intermediate, the economy could converge towards equilibria in which both honest and dishonest firms coexist or even fluctuate. The rest of the paper is organized as follows. Section 2 presents the economic model; in Sect. 3, we show the dynamics of the system, and Sect. 4 concludes.

2 Economic set-up

In order to study the behaviour of non-compliant firms who can decide to defraud the State in a public procurement procedure, following Brianzoni et al. (2019), we consider an economy composed of three types of risk neutral players: the State, bureaucrats and firms (the number is normalized to one) and we assume that the State procures a unit of good from private firms in order to provide it free. This good can be produced at different quality levels. Although the government requires a high-quality good, a (dishonest) firm could produce a low-quality public good and lie to the authorities regarding quality.⁴ The price of the good is constant and given by $p>0$ [see Bose et al. (2008)], and therefore, firms compete with regard to quality.⁵ The production cost for a firm is such that if the good’s quality is high, the unit cost $c^h$ is also high, while if the good’s quality is low, the unit cost $c^l$ is low too. Furthermore, the production of this good is assumed to be profitable; hence, $p>c^h>c^l>0$.

Consider a reverse auction for the procurement of the public good. As a general rule, the firm offering the highest quality wins the auction, but, as we said, a firm can lie about the quality of the good produced.

Let $t=0,1,2,\ldots$, (discrete time set-up), and let $x_t\in [0,1]$ be the fraction of firms producing a low-quality good who lie about the quality (dishonest firms) at time t. Then, in order to weed out or reduce fraudulent behaviours, the State monitors firms. Denote with $q_t\in [0,1]$ the probability, at any time t, of being monitored according to the control level fixed by the State and, then, of being reported.⁶

If a dishonest firm is monitored and, hence, detected, it is punished with a constant fine $f>0$.

Taking into account the previous considerations, at any time t, the utility of an honest firm is given by

$$\begin{aligned} U_h=p-c^h, \end{aligned}$$

(1)

whereas the utility of a dishonest firm is as follows

$$\begin{aligned} U_d=\left\{ \begin{array}{ll} U_{d,NM}=p-c^l &{}\quad \hbox { if not monitored,} \\ \\ U_{d, M}= p-c^l-f &{}\quad \hbox {if monitored} \end{array}\right. . \end{aligned}$$

(2)

From (2), we obtain the expected utility for a dishonest firm that is given by:

$$\begin{aligned} E[U_d]= q_tU_{d, M}+(1-q_t)U_{d,NM}= p-c^l-fq_t\,. \end{aligned}$$

(3)

Let $\xi$ be the difference in utilities between dishonest and honest firms, then the expected $\xi$ value at time t depends on $q_t$, i.e. the monitoring level at any time t, and it is given by:

$$\begin{aligned} \delta (q_t)=E[\xi (q_t)]= E[U_d]-U_h= \varDelta _c-fq_t. \end{aligned}$$

(4)

where $\varDelta _c=c^h-c^l>0$.

Notice that $\delta (q_t)$ is a linear strictly decreasing function of the monitoring level, i.e. the difference between expected utilities decreases as the monitoring level increases, while the fine level affects its strength. Define

$$\begin{aligned} {\bar{q}}=\frac{\varDelta _c}{f}:\delta ({\bar{q}})=0 \end{aligned}$$

(5)

being the monitoring level such that the two behaviours (honest and dishonest) result to be indifferent as they produce the same expected payoffs. Then, two cases may occur:

• (LF) if $\varDelta _c\ge f$, i.e. the difference between production costs is higher than the fine, then $\delta (q_t)\ge 0$ $\forall q_t\in [0,1]$; that is, the expected payoff associated with honest behaviour cannot exceed the expected payoff associated with dishonest behaviour. We will denote this case as LF (low fine) case;

• (HF) if $\varDelta _c< f$, i.e. the difference between production costs is less than the fine, then $\delta (q_t)\ge 0$ $\forall q_t\in [0,{\bar{q}}]$ while $\delta (q_t)< 0$ $\forall q_t\in ({\bar{q}},1]$, so that the difference between expected payoff may be both positive or negative depending on the monitoring level fixed by the State at any given time. We will denote this case as a HF (high fine) case.

2.1 The evolution of non-compliant behaviour

In order to describe the evolution of non-compliant behaviour, i.e. how $x_t$ evolves over time, we consider an evolutionary game with word-of-mouth process as proposed by Dawid (1999) and Banerjee and Fudenberg (2004) and formalized by Lamantia and Pezzino (2017).

It is very important to note that the public procurement procedures are often regulated by stringent rules whereby firms discovered engaging in fraud or corruption are not allowed to participate in public procurement procedures in the future. In fact, in most countries, in order to participate in a public procurement process, firms must certify the fact that they have no links with criminal organizations or illegal conduct. For this purpose, in many countries, white lists (or complementary black lists) are provided—following the recommendations of the World Bank, The United Nations and other international organizations—which provide valuable instruments in order to select the firms that are able to participate in public procurement procedures [see, for example, Georgieva (2017) and Gaprindashvili (2015)]. In order to take into account this aspect in a simplified way, we can think about the evolutionary model in terms of a birth–death process. To be more precise, following Brianzoni et al. (2019) we can assume that at each time, the discovered non-compliant firm exits the game (i.e. exits from the white list to enter the black list) and, at the same time, it is replaced by another firm of the same kind to reconstruct the white list.

Coming back to the evolutionary process as proposed by Lamantia and Pezzino (2017), we assume agents have the possibility to make a comparison between their expected payoffs and those of the rest of society: if a firm meets a different firm manifesting the same behaviour (honest or dishonest), it gains no new information about payoff and therefore decides not to change its behaviour. Conversely, a firm could change its type (from dishonest to honest or vice versa) if it meets a firm of a different type and, after comparing their expected utilities, the firm finds it possible to increase its own expected utility by moving from one type to the other. As in Lamantia and Pezzino (2017), we assume that an honest firm which meets a dishonest one can change its behaviour iff the payoff deriving from dishonest behaviour is greater than the one deriving from honest behaviour. Hence, the probability for all honest firms changing type is defined by a non-decreasing function $\phi :{\mathbb {R}}\rightarrow [0,1]$ depending on $\delta (q_t)$.

In addition, by considering the honesty propensity assumption as first introduced by Brianzoni et al. (2019), we take into account that the mechanism governing movements of the fraction of firms from one type to another are not symmetric: while all dishonest firms meeting honest ones will choose to become honest, if the expected utility from honest behaviour is not less than the expected utility derived from dishonest behaviour, only a fraction of honest firms meeting dishonest ones will choose to change type despite a possible higher expected utility being reached. In this sense, our model allows us to consider a sort of natural propensity towards honesty. In order to consider such evidence, the assumptions on function $\phi$ are formalized by the following continuous, increasing and piecewise smooth function:

$$\begin{aligned} \phi (\delta (q_t))=\left\{ \begin{array}{ll} \phi _1(\delta (q_t))=1-\frac{1}{\alpha \delta (q_t)+1} &{}\quad \hbox {if}\,\, \delta (q_t)\ge 0 \\ \\ \phi _2(\delta (q_t))=0 &{}\quad \hbox {if}\,\, \delta (q_t)< 0 \end{array}\right. , \end{aligned}$$

(6)

where parameters $\alpha >0$ measure the propensity to become dishonest characterising the country (see Fig. 1, (a)). The probability function $\phi$, i.e. the probability (easiness) with which an honest firm can become, on the basis of an economic convenience, dishonest, is not the same among all countries but depends on the “intrinsic honesty” of each country. To take this into account, we introduced the parameter ($\alpha$) that captures the greater “easiness” with which an honest firm changes its behaviour and becomes dishonest. This parameter allows us to consider countries with a different culture of honesty which is very strictly linked to the relevance of social stigma associated, at a social level, with dishonest behaviour. Different countries attribute, at a social level, different judgment regarding dishonest behaviours, i.e. a different social stigma. A higher level of $\alpha$, as shown in Fig. 1, (a) panel, means a lower social stigma associated with dishonest behaviour, i.e. greater easiness to becoming dishonest. Therefore, in the countries characterized by a low “inner honesty", ceteris paribus, it is easier for firms to become dishonest, leading to an equilibrium with more dishonest firms. By considering the two ingredients previously underlined (i.e. the word-of-mouth mechanism as proposed by Lamantia and Pezzino (2017) and the honesty-propensity assumption as proposed by Brianzoni et al. (2019) taking into account the social stigma attached to a country), we obtain the following equation describing the evolution of the fraction of dishonest firms over time

$$\begin{aligned} x_{t+1}=F(x_t,q_t)=x_t[1+(1-x_t)(2\phi (\delta (q_t))-1)], \end{aligned}$$

(7)

where $\phi (\delta (q_t))$ is given by (6). According to such a mechanism, the fraction of dishonest firms at time t is updated by:

• adding the fraction of honest firms which meet dishonest ones and change type during the time interval because they learn than being dishonest is more convenient that being honest: $(1-x_t)x_t\phi$;

• subtracting the fraction of dishonest firms which meet honest ones and change type during the time interval because they learn that being honest is more convenient than being dishonest: $(1-x_t)x_t(1-\phi )$.

Fig. 1

a Probability function $\phi$ for different $\alpha$ values. b Monitoring level function $q_{t+1}$ as defined in (8). Blue line $\gamma = .1$, $\beta = .2$, red line $\gamma = .3$, $\beta = 1.2$, yellow line $\gamma = .8$, $\beta = 2.5$

2.2 Endogenous monitoring level

By introducing a new element with respect to previous works such as Lamantia and Pezzino (2017) and Brianzoni et al. (2019), we explain the dynamics of the monitoring level put in place by the State in order to reduce the fraction of dishonest firms. It is quite natural to assume that the monitoring level fixed by the State at any time t is a function of the level of dishonesty. Realistically, we assume that the State knows the level of dishonesty of period t and, in the following period, it sets the level of monitoring on the basis of the spread of non-compliant behaviours: the State increases the audit effort as the dishonesty level increases, i.e. the fraction of dishonest firms increases.⁷ In fact, it is plausible to assume that a State that wants to combat dishonesty, as the spread of fraud in public procurement increases, tries to counter it by increasing the level of control. Others, even more complex or more realistic schemes, can be suggested. As the present work is the first attempt to endogenize the monitoring level, we choose to start by considering the following simplifying assumption.

The monitoring level by the State evolves according to the following continuous, strictly increasing and differentiable function:

$$\begin{aligned} q_{t+1}=G(x_t)=\gamma x_t^{\beta },\;\;\gamma \in (0,1],\;\;\beta >0 \end{aligned}$$

(8)

where $\gamma$ is related to the budget constraint or to the amount of resources that want to be invested in fighting dishonest behaviour: as $\gamma$ increases, the monitoring level for any given fraction of dishonest firms in the economy increases too. On the other hand, function (8) can be linear ($\beta =1$), convex ($\beta >1$) or concave ($\beta <1$) and can be considered as a production function of the monitoring technology so that $\beta$ can be thought of as an indicator of the “productivity" of the monitoring technology. Hence, the level of monitoring can be more than proportional ($\beta <1$), proportional ($\beta =1$) or less than proportional ($\beta >1$) compared to the increase and spread of fraud in procurement (see Fig. 1b). So $\beta$ represents the “strength" with which the State counteracts the dishonesty and efficiency of this monitoring process.

2.3 The final system

Taking into account equations (6), (7) and (8), the final dynamical system $S(x_t,q_t)$ can be obtained. We distinguish between the following two cases.

In case LF, i.e. $\varDelta _c\ge f$, $\delta (q_t)\ge 0$ for all $q_t\in [0,1]$ then $\phi (\delta (q_t))=\phi _1(\delta (q_t))$ and the continuous and differentiable system $S_\mathrm{LF}:[0,1]\times [0,1]\rightarrow [0,1]\times [0,1]$ describing the evolution of both the fraction of dishonest firms and the monitoring level by the State is given by:

$$\begin{aligned} S_\mathrm{LF}(x_t,q_t):= \left\{ \begin{array}{ll} F_1(x_t,q_t)=x_t\left[ 1+(1-x_t)\frac{\alpha (\varDelta _c-fq_t)-1}{\alpha (\varDelta _c-fq_t)+1}\right] \\ \\ G(x_t)=\gamma x_t^{\beta } \end{array}\right. \end{aligned}$$

(9)

In case HF, i.e. $\varDelta _c< f$, $\delta (q_t)\ge 0$ for all $q_t\in [0,\varDelta _c/f]$, while $\delta (q_t)< 0$ for all $q_t\in (\varDelta _c/f,1]$, both $\phi _1$ and $\phi _2$ are involved. The two-dimensional piecewise smooth system $S_\mathrm{HF}:[0,1]\times [0,1]\rightarrow [0,1]\times [0,1]$ describing the evolution of both the fraction of dishonest firms and the monitoring level by the State is given by:

$$\begin{aligned} S_\mathrm{HF}(x_t,q_t)=\left\{ \begin{array}{ll} F(x_t,q_t)=\left\{ \begin{array}{ll} F_1(x_t,q_t)=x_t\left[ 1+(1-x_t)\frac{\alpha (\varDelta _c-fq_t)-1}{\alpha (\varDelta _c-fq_t)+1}\right] \;\mathrm{iff}\; q_t\in \left[ 0,\frac{\varDelta _c}{f}\right] \\ \\ F_2(x_t,q_t)=(x_t)^2\;\mathrm{iff}\; q_t\in \left( \frac{\varDelta _c}{f},1\right] \end{array}\right. \\ G(x_t)=\gamma x_t^{\beta } \end{array}\right. . \end{aligned}$$

(10)

We lastly define the general set-up as

$$\begin{aligned} S\left( x_t,q_t\right) = {\left\{ \begin{array}{ll} \begin{array}{ll} S_\mathrm{LF}\left( x_t,q_t\right) &{}\;iff\; \varDelta _c-f\ge 0\\ S_\mathrm{HF}\left( x_t,q_t\right) &{}\;iff\; \varDelta _c-f<0\\ \end{array} \end{array}\right. }. \end{aligned}$$

(11)

It is easy to see that system S is well defined as it maps the set $Q=[0,1]\times [0,1]$ into itself providing that Q is trapping and all initial conditions (i.c.) $(x_0,q_0)\in Q$ are feasible.

3 Equilibria and long-run dynamics

In this section, we describe the dynamics produced by systems $S_\mathrm{LF}$ and $S_\mathrm{HF}$ defined by (9) and (10). We shall observe that, in the phase space Q, only one or two domains are involved, as $S_\mathrm{LF}$ is defined by $F_1$ and G, while $S_\mathrm{HF}$ is defined by $F_1$ and G in $D_1=\{(x_t,q_t)\;s.t.\;0\le x_t\le 1\;and\;0\le q_t\le \varDelta _c/f\}$ and by $F_2$ and G in $D_2=\{(x_t,q_t)\;s.t.\;0\le x_t\le 1\;and\;\varDelta _c/f<q_t\le 1 \}$.

As far as the fixed points of the model are concerned, the following proposition holds.

Proposition 1

System S admits two boundary equilibria:

• $E_0=(0,0)$

• $E_1=(1,\gamma )$

and, as long as $\varDelta _c \in \left( \frac{1}{\alpha },\frac{1}{\alpha }+\gamma f\right)$, one inner equilibrium:

• $E^*=(x^*,q^*)=\left( \left( \frac{\alpha \varDelta _c-1}{\gamma \alpha f}\right) ^{\frac{1}{\beta }},\frac{\alpha \varDelta _c-1}{\alpha f}\right) \in D_1$.

Proof

Trivially, $S(0,0)=(0,0)$ and $S(1,\gamma )=(1,\gamma )$ for all parameters. Consider first that $x=F_1(x,q)$ admits the solution $q^*=\frac{\alpha \varDelta _c-1}{\alpha f}<\frac{\varDelta _c}{f}$, $\forall x\in (0,1)$. Notice that $q^*\in (0,1)$ for all $\varDelta _c\in \left( \frac{1}{\alpha },\frac{1}{\alpha }+f\right)$. By solving $q^*=\gamma x^{\beta }$, the unique solution is $x^*=\left( \frac{\alpha \varDelta _c-1}{\gamma \alpha f}\right) ^{\frac{1}{\beta }}\in (0,1)$ iff $\varDelta _c\in \left( \frac{1}{\alpha },\frac{1}{\alpha }+\gamma f\right)$. Consider also that $x=F_2(x,q)$ admits no solution.

Finally, $E^*=(x^*,q^*)$ is an interior fixed point iff $\varDelta _c \in \left( \frac{1}{\alpha },\frac{1}{\alpha }+\gamma f\right)$. $\square$

According to Proposition 3.1, we can observe three different scenarios: if the social stigma is extremely high or sufficiently low, only equilibria with monomorphic population configurations with all honest ($E_0$) or dishonest ($E_1$) firms are presented, while with intermediate levels of inner honesty propensity, a steady state characterized by the presence of both groups in the long run can emerge (i.e. polymorphic configuration). Notice that when the inner equilibrium exists, the non-compliance equilibrium level is influenced by the resources invested in monitoring activity and by the fine level: as $\gamma$ increases or f increases, the number of dishonest firms in equilibrium decreases (although the probability of being monitored, $q^*$, is not affected by changes on the invested resources). Evidently, as the propensity to become dishonest increases, the equilibrium level of $x_t$ and $q_t$ increases too. Notice that $x^*$ is also influenced by parameter $\beta$: the portion of dishonest firms in equilibrium increases as $\beta$ increases. In fact the $\beta$ parameter is linked to the effectiveness of the monitoring technology: as $\beta$ increases, the effectiveness of the monitoring function decreases and with it the level of control over dishonest behaviours which are, therefore, more widespread. Regarding the questions related to the stability of fixed points, we first consider situations with monomorphic initial configurations. As regards the state space Q, we can immediately observe that the set $I_0=(0,q_t)\cap Q$ is invariant for S and that $S(0,q_t)=(0,0), \forall q_t\in (0,1)$ and for all parameters, so that $E_0$ attracts trajectories starting from $I_0$. This means that with no dishonest firms, no monitoring activity by the State is required as corruption cannot emerge. A second question to be considered is what occurs if at the initial state all firms are dishonest, i.e. $x_0=1$. The set $I_1=(1,q_t)\cap Q$ is invariant for S and in addition $S(1,q_t)=(1,\gamma )$, i.e. the fixed point $E_1$ will attract trajectories $(x_0,q_0)\in I_1$. In such a case, the maximum monitoring level is put in place but all firms will remain dishonest. In what follows, we will consider dynamics produced by initial condition (i.c.) with $x_0\in (0,1)$ (i.e. at the initial time, both honest and dishonest firms are present) by distinguishing between the cases with low and high fine.

3.1 Low fine and simple dynamics

We focus on the continuous and smooth case defined by $S_\mathrm{LF}$ so that the bifurcation theory for smooth systems will be considered and either local and global dynamics will be discussed. We first study the local stability of fixed points. The Jacobian matrix, representing the linearization of the dynamic system $S_\mathrm{LF}$, is given by:

$$\begin{aligned} JS_\mathrm{LF}(x_t,q_t)=\left( {{\begin{array}{*{20}c} {\frac{\partial F_1}{\partial x_t} } &{} {\frac{\partial F_1}{\partial q_t} } \\ {{\frac{\partial G}{\partial x_t} } } &{} {0 } \\ \end{array}}}\right) . \end{aligned}$$

(12)

As regards the local stability of $E_0$ and $E_1$, we observe that $\frac{\partial F_1}{\partial q_t}(E_0)=\frac{\partial F_1}{\partial q_t}(E_1)=0$ so that $JS_\mathrm{LF}(E_0)$ and $JS_\mathrm{LF}(E_1)$ are triangular matrices with eigenvalues on the main diagonal. Being one eigenvalue equal to zero (the one associated with $I_0$ and $I_1$, respectively), the local stability of the two monomorphic configurations can be discussed by considering $\frac{\partial F_1}{\partial x_t}$.

First observe that $\frac{\partial F_1}{\partial x_t}(E_0)=\frac{2\alpha \varDelta _c}{\alpha \varDelta _c +1}>0$ and, in addition, $\frac{2\alpha \varDelta _c}{\alpha \varDelta _c +1}<1$ as long as $\varDelta _c<\frac{1}{\alpha }$; at $\varDelta _c=\frac{1}{\alpha }$ a transcritical bifurcation occurs, $E_0$ loses its stability and a new fixed point is created (the coexistence equilibrium $E^*$), while for all $\varDelta _c>\frac{1}{\alpha }$ $E_0$ is unstable.

Observe now that $\frac{\partial F_1}{\partial x_t}(E_1)=\frac{2}{\alpha (\varDelta _c-\gamma f) +1}>0$ being $\frac{\varDelta _c}{f}\ge 1$, and that, $\frac{2}{\alpha (\varDelta _c-\gamma f) +1}<1$ as long as $\varDelta _c>\frac{1}{\alpha }+\gamma f$; that is, $\varDelta _c$ is high enough and no inner equilibrium exists. Notice that if $\varDelta _c \in \left( \frac{1}{\alpha },\frac{1}{\alpha }+\gamma f\right)$, then both $E_0$ and $E_1$ are unstable. In this case, three equilibria coexist: unstable (saddle) $E_0$ and $E_1$, and attracting $E^*$.

About the local stability of $E^*$, we observe that the Jacobian matrix evaluated in point $E^*$ is given by

$$\begin{aligned} JS_\mathrm{LF}(E^*)=\left( {{\begin{array}{*{20}c} {1} &{} {-\frac{\alpha f x^*(1-x^*)}{2}} \\ {{\beta \gamma x^{*^{\beta -1}} } } &{} {0 } \\ \end{array}}}\right) . \end{aligned}$$

(13)

Following Lines and Medio (2001), stability conditions in terms of trace (Tr) and determinant (Det) of the Jacobian matrix evaluated at the fixed point are given by:

(i):

$1+\mathrm{Tr}(JS_\mathrm{LF}(E^*))+\mathrm{Det}(JS_\mathrm{LF}(E^*))>0,$

(ii):

$1-\mathrm{Tr}(JS_\mathrm{LF}(E^*))+\mathrm{Det}(JS_\mathrm{LF}(E^*))>0,$

(iii):

$1-\mathrm{Det}(JS_\mathrm{LF}(E^*))>0.$

Since

$$\begin{aligned} \mathrm{Tr}(JS_\mathrm{LF}(E^*))=1 \end{aligned}$$

and

$$\begin{aligned} \mathrm{Det}(JS_\mathrm{LF}(E^*))=\frac{\alpha \beta \gamma f{x^*}^{\beta }(1-x^*)}{2}>0 \end{aligned}$$

then conditions (i) and (ii) are fulfilled. Regarding condition (iii), we have to investigate whether it can be violated and a Neimark–Sacker bifurcation related to closed invariant curves may occur. In the following proposition, we prove that with low fine, i.e. $f\le \varDelta _c$, condition (iii) always holds.

Proposition 2

Let us assume: (a) $f\le \varDelta _c$ (i.e. system $S_\mathrm{LF}$ as given by (9) is considered); (b) $\varDelta _c>\frac{1}{\alpha }$ and (c) $\varDelta _c<\frac{1}{\alpha }+\gamma f$ (i.e. the interior fixed point $E^*$ exists). Then, $E^*$ is locally stable.

Proof

Conditions (i) and (ii) for the local stability are trivially verified. In order to check that also condition (iii) is verified, consider that

$$\begin{aligned} \mathrm{Det}(JS_\mathrm{LF}(E^*))=\frac{\beta }{2}(\alpha \varDelta _c-1)\left( 1-\left( \frac{\alpha \varDelta _c-1}{\gamma \alpha f}\right) ^{\frac{1}{\beta }}\right) >0 \end{aligned}$$

(14)

and that, after some algebra, condition $1-\mathrm{Det}(JS_\mathrm{LF}(E^*))>0$ holds iff

$$\begin{aligned} x^*>\frac{\beta (\alpha \varDelta _c-1)-2}{\beta (\alpha \varDelta _c-1)}. \end{aligned}$$

(15)

If $\beta (\alpha \varDelta _c-1)-2\le 0$, then, from assumptions (b) and (c), $x^*\in (0,1)$, hence the inequality in (15) is always verified, and the statement holds true.

Hence, consider the open case $\beta (\alpha \varDelta _c-1)-2> 0$, then condition (15) can be expressed in terms of f by the following equivalent inequality:

$$\begin{aligned} f<\frac{\alpha \varDelta _c-1}{\gamma \alpha }\left( \frac{\beta (\alpha \varDelta _c-1)}{\beta (\alpha \varDelta _c-1)-2}\right) ^\beta =f_\mathrm{NS}. \end{aligned}$$

(16)

From assumption (a), it must be $f\le \varDelta _c$; hence, if condition

$$\begin{aligned} f_\mathrm{NS}>\varDelta _c \end{aligned}$$

(17)

is verified, then (16) holds. In order to prove that $f_\mathrm{NS}>\varDelta _c$, we observe that, being

$$\begin{aligned} \left( \frac{\beta (\alpha \varDelta _c-1)}{\beta (\alpha \varDelta _c-1)-2}\right) ^{\beta }>1 \end{aligned}$$

then $f_\mathrm{NS}>\frac{\alpha \varDelta _c-1}{\alpha \gamma }$ so that condition

$$\begin{aligned} \varDelta _c < \frac{\alpha \varDelta _c-1}{\alpha \gamma }\Rightarrow \alpha >\frac{1}{\varDelta _c(1-\gamma )} \end{aligned}$$

(18)

is sufficient to guarantee that (17) is verified. Since condition (b) holds, i.e. $\alpha >1/\varDelta _c$, then condition (18) immediately holds true, so that condition (iii) for the stability of $E^*$ is fulfilled. $\square$

Taking into account the previous considerations and Proposition 2, the following remark concerning the local stability of fixed points of system $S_\mathrm{LF}$ can be stated.

Remark 1

Let $f\le \varDelta _c$, then the following cases may occur:

• (a) if $\varDelta _c<1/\alpha$, then $E_0$ is stable, while $E_1$ is unstable,

• (b) if $\varDelta _c=1/\alpha$, then a transcritical bifurcation occurs creating the interior equilibrium $E^*$,

• (c) if $1/\alpha<\varDelta _c<1/\alpha +\gamma f$, then $E^*$ is stable, while $E_0$ and $E_1$ are both unstable,

• (d) if $\varDelta _c=1/\alpha +\gamma f$, then $E^*$ merges with $E_1$,

• (e) if $\varDelta _c>1/\alpha +\gamma f$, then $E_1$ is stable, while $E_0$ is unstable.

Through the numerical simulations, it can be observed that local stability properties can be extended, as when a fixed point is locally stable, it is also globally stable (for all initial conditions $(x_0,q_0)\in {\mathbb {R}}^2_+$ with $x_0\ne 0$ and $x_0\ne 1$).

As regards the role of social stigma, notice that as $\alpha \rightarrow 0^+$, the equilibrium $E_0$ is always stable, while $E_1$ is unstable (case Remark 1(a)). In fact, a low $\alpha$ level means that the social stigma associated with non-compliant behaviour in the society is high, and therefore, the dishonest behaviour is, ceteris paribus, less convenient. Differently, as $\alpha \rightarrow +\infty$, then the stable fixed point is $E_1$ meaning that in the long run, the system will converge to the dishonesty trap, as the benefit deriving from dishonesty ($\varDelta _c$) is greater than the costs associated with non-compliant behaviour because the “inner honesty" of the firms is very low. In these two limiting cases, no economic policies can influence the final outcome of the economy. In order to better understand how parameters $\alpha$ and f affect the stability of the equilibria, we consider the parameters plane $(\alpha ,f)$, $\alpha>0,f>0$. The line $L=\{(\alpha ,f):f=\varDelta _c\}$ separates the plane into two regions: points below that line correspond to combinations associated with LF, i.e. $f<\varDelta _c$. In this section, we focus on this region. Notice that the line $FBC=\{(\alpha ,f):\alpha =1/\varDelta _c\}$ corresponds to the transcritical bifurcation described in Remark 1(b): parameter combinations on the left hand side imply the stability of equilibrium without dishonest firms, while when the transcritical bifurcation curve is crossed (from left to right), then the coexistence equilibrium is created and it is stable. Consider finally the curve $C=\{(\alpha ,f):\varDelta _c=1/\alpha +\gamma f\}$ corresponding to parameter combinations such that $E^*$ merges with $E_1$ (case (d) in Remark 1); the region on the left is associated with the stability of $E^*$, while the region on the right hand side is such that all dishonest firms will survive in the long term. Notice that if $\alpha$ is high enough, this final outcome cannot be avoided (see Fig. 2 panel a).

Fig. 2

Parameters $\varDelta _c=3$, $\gamma =0.9$ and $\beta =4$, i.c. (0.1, 0.1) a curves related to different long-term dynamics on the plane $(\alpha ,f)$ b 2Dim bifurcation diagram showing complex features for $f>\varDelta _c$

To summarize, consider an initial situation characterized by the presence of both honest and dishonest firms and assume that the fine is fixed by the State at low level (i.e. $\varDelta _c\ge f$). Then, even in the presence of a very strong monitoring activity by the State, the payoff associated with non-compliant behaviour is higher than the payoff associated with compliant behaviour, i.e. being dishonest is much more convenient. In order to understand if and whether non-compliant behaviour can be deleted, we proved that the equilibrium without dishonesty can be reached in the long term iff the social stigma deriving from dishonest behaviour (or the “inner attitude" towards honesty) is strong enough (i.e. $\alpha$ is small enough). In such a case, ceteris paribus, when firms belonging to different groups meet each other, although dishonest behaviour is more convenient w.r.t. honest behaviour, the fraction of honest firms moving to dishonest ones is less than the one moving in the opposite direction. More precisely, it can be shown that if $\alpha <1/{\varDelta _c}$, then $x_{t+1}<x_t$ so that the fraction of dishonest firms is decreasing over time converging towards zero. No intervention is required by the State because social stigma is an effective instrument to fight dishonesty. On the other hand, the culture of legacy of the country is not effective enough, and therefore, dishonesty cannot be eradicated. Then, we have to investigate whether some policies are possible in order to reduce the spread of dishonest behaviour, in the long term. First of all, we underline that if $\alpha$ is high enough, i.e. corruption is largely widespread in the country, then $x_t$ is a strictly increasing sequence converging in a sort of dishonesty trap in which there are only dishonest firms (even with maximum monitoring effort).

Such an unfavourable situation can be mitigated by putting in place strategies to push the economy towards a situation with coexistence of both groups. As $\alpha$ and $\varDelta _c$ must be considered as exogenous parameters, then one strategy can be to increase the fine level f (up to $\varDelta _c$), while the second one can be to increase the resources devoted to fight fraud $\gamma$ (up to 1). Investing more resources in the monitoring activity or enlarging the fine level is two policies which can reduce non-compliant behaviour in countries in which social stigma is low. Notice that without reducing $\alpha$, the equilibrium without dishonesty ($E_0$) cannot be reached. The main results described in Fig. 2 panel a are confirmed by the two-dimensional bifurcation diagram represented in Fig. 2b: different colours are associated with different long-term qualitative dynamics, while the initial condition has been fixed. Notice that only simple dynamics are exhibited in case LF, while more complex features emerge in the region above the line L. Those are associated with system $S_\mathrm{HF}$ and will be discussed in the following section.

3.2 High fine and complex dynamics

In this subsection, we consider $\frac{\varDelta _c}{f}<1$ so that the map is defined by two branches. More precisely, the map $S_\mathrm{HF}$ is given by two nonlinear systems which are defined in two half planes, $D_1=\{(x_t,q_t)\;s.t.\;0\le x_t\le 1\;and\;0\le q_t\le \varDelta _c/f\}$ and $D_2=\{(x_t,q_t)\;s.t.\;0\le x_t\le 1\;and\;\varDelta _c/f<q_t\le 1 \}$,

$$\begin{aligned} S_\mathrm{HF}\left( x_t,q_t\right) := \left\{ \begin{array}{ll} S_1(x_t,q_t),\;\;(x_t,q_t)\in D_1\\ \\ S_2(x_t,q_t),\;\;(x_t,q_t)\in D_2 \end{array}\right. \end{aligned}$$

(19)

being $S_1=(F_1,G)$ and $S_2=(F_2,G)$ (where $F_1$, $F_2$ and G are defined in (10)), while the border separating $D_1$ and $D_2$ is the set $d=\{(x_t,q_t)\in Q: q_t=\frac{\varDelta _c}{f}\}$. Notice that, being $\frac{\varDelta _c}{f}<1$, it follows that $\forall q_t\in D_1$, $\varDelta _c -q_t f\ge 0$ (i.e. $\delta (q_t)\ge 0$), while $\forall q_t\in D_2$ has $\varDelta _c -q_t f< 0$ (i.e. $\delta (q_t)< 0$).

The fixed points of system $S_\mathrm{HF}$ have been discussed in Proposition 1, where conditions for the existence of two or three equilibria have been given.

As regards the location of the fixed points on the phase space, observe that both $E_0$ and $E^*$—when it exists—belong to $D_1$. Differently, the fixed point $E_1$ belongs to $D_1$ iff $\gamma \le \varDelta _c/f$ and to $D_2$ otherwise. It is important to recall that the way through which the fraction of dishonest firms evolves over time works as a word-of-mouth mechanism, hence the same conclusions previously described for the local stability of the monomorphic equilibria along the sets $I_0$ and $I_1$ hold. As a consequence, we discuss the stability of the three steady states for i.c. $x_0\in (0,1)$ (i.e. at the initial time both honest and dishonest firms exist) in order to understand the long-term evolution of the system in the case in which the State fixes a sufficiently high fine ($f>\varDelta _c$).

We start our analysis by considering the local stability of the equilibrium $E_0$. Notice that since it belongs to $D_1$, conditions for stability of $E_0$ are the same given in Remark 1, i.e. $E_0$ is locally stable as long as $\varDelta _c<1/\alpha$, while at $\varDelta _c=1/\alpha$, a transcritical bifurcation occurs crating the interior fixed point $E^*$ and for all $\varDelta _c>1/\alpha$, the equilibrium $E_0$ remains unstable. Hence, if the difference of production costs is low and/or the inner honesty of society is high ($\alpha$ low), then the honest behaviour is more convenient than the dishonest one so that, in the long run, the only stable equilibrium will be one in which all firms find it worthwhile to be honest.

This behaviour totally replaces what occurs with low fine, provided that the social stigma, deriving from dishonest behaviour, compared to the incentive to be dishonest (i.e. $\varDelta _c$) is strong enough, and consequently, no other policies are required as compliant behaviour will prevail in the long term.

Regarding the local stability of $E_1$, the following cases may occur:

• if $\gamma < \varDelta _c/f$, then $E_1\in D_1$ and the same conditions stated in Remark 1 hold, i.e. it can be locally stable or unstable (the condition for the local stability has been previously determined, i.e. $\gamma f<\varDelta _c-1/\alpha$);

• if $\gamma > \varDelta _c/f$, then $E_1\in D_2$ and $\frac{\partial F_2}{\partial x_t}(E_1)=2$; hence, $E_1$ is unstable.

Notice that when $\gamma = \varDelta _c/f$, then $E_1$ belongs to the border d separating the two regions $D_1$ and $D_2$. To summarize the local dynamics occurring to $E_1$, we recall that $E_1$ is the situation with all dishonest firms in the system, while $\alpha$ represents the social stigma associated with non-compliant behaviour in the system. If $\alpha$ is not low enough (i.e. social stigma is at low or intermediate values), then the State, in order to reduce dishonesty, can combine two policies: investing more resources in monitoring activity (higher $\gamma$) and/or increasing the punishment, i.e. the fine level (higher f). Hence, we can think about the product $\gamma f$ as measuring the combined level of the two above-mentioned economic policies. We define the following curves in the parameter plane $(f,\gamma )$: $C_1=\{(f,\gamma )\in [\varDelta _c,+\infty )\times [0,1]:f\gamma =\varDelta _c\}$ and $C_2=\{(f,\gamma )\in [\varDelta _c,+\infty )\times [0,1]:f\gamma =\varDelta _c-1/\alpha \}$. Then, combinations between parameters such that $\gamma f<\varDelta _c$ are points below the blue curve $C_1$ in Fig. 3a corresponding to $E_1\in D_1$; when the blue curve is crossed from below, then $E_1$ enters $D_2$ and remains locally unstable, i.e. $E_1$ is a border crossing fixed point but no changes in its stability occur. On the other hand, the black curve $C_2$ is the transcritical bifurcation curve; when crossing the black curve from below, the local stability of $E_1$ is lost and the two combined policies can push the system out of the dishonesty trap. The local stability conditions of $E_1$ when the fine is fixed at a high level differ from those stated in the case of low fine. More precisely, let $\alpha$ be high enough, i.e. low attitude to honesty characterizes the country. Then, fixing a high fine level is not sufficient to reduce corruption, as this policy must be associated with an investment in monitoring activity that is strong enough and these two policy instruments must be combined to exit the dishonesty trap.

As far as the global dynamics are concerned, we finally observe that $E_0$ is stable iff $\varDelta _c<1/\alpha$, while $E_1$ is stable iff $\varDelta _c>1/\alpha +\gamma f$; moreover, the inner equilibrium $E^*$ exists only for $\varDelta _c\in \left( \frac{1}{\alpha },\frac{1}{\alpha }+\gamma f\right)$; therefore, when the monomorphic configurations are locally stable, then they are also globally stable (except for i.c. having $x_0=0$ or $x_0=1$).

While the local stability of the monomorphic configurations has been discussed, the open case is that related to the parameter values such that the inner equilibrium exists and the map is piecewise smooth (combinations above the black curve in Fig. 3a). When considering the long-term dynamics starting from a fixed initial condition, the cycle cartogram presented in Fig. 3b is shown, confirming the results previously obtained related to the stability of $E_0$, $E^*$ and $E_1$. At the same time, it can be easily observed that in the open case (parameter combinations above $C_1$), both convergence to the inner equilibrium or more complex features can be produced. We now investigate how complex behaviour can arise.

Fig. 3

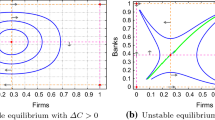
Parameters $\beta =1$ and $\alpha =2$, $\varDelta _c=3$ and i.c. (0.1, 0.1) a Regions in the plane $(f,\gamma )$ associated with convergence to the dishonesty trap; b cycle cartogram showing convergence to different attractors: the Neimark–Sacker bifurcation curve (depicted in black) opens to complexity. c The attracting closed invariant curve for $\gamma =0.5$ and $f=8.4$ (after the NS bifurcation occurring at $f_\mathrm{NS}=8.3333 \ldots$) and the three fixed points are depicted. d 1D bifurcation diagram w.r.t. f for $\gamma =0.5$

Consider conditions for the stability of the inner equilibrium $E^*$ of map $S_\mathrm{HF}$ when it exists. With this aim, we can observe that $q^*<\varDelta _c/f$; hence, the inner equilibrium $E^*$ belongs to the interior of set $D_1$ where F is defined by $F_1$. As a consequence, no border-collision bifurcations (BCB) can be related to the point $E^*$ so that $E^*$ may loose stability only through a smooth bifurcation. Being $JS_\mathrm{HF}(E^*)=JS_\mathrm{LF}(E^*)$ as given by (13), following the same steps previously described, it can be observed that $E^*$ can loose stability only via Neimark–Sacker bifurcation. The following proposition gives conditions.

Proposition 3

Let $E^*$ be the interior fixed point of system $S_\mathrm{HF}$ (i.e. $\varDelta _c<f$, $\varDelta _c>\frac{1}{\alpha }$ and (c) $\varDelta _c<\frac{1}{\alpha }+\gamma f$). Then, $f_\mathrm{NS}=\frac{\alpha \varDelta _c-1}{\gamma \alpha }\left( \frac{\beta (\alpha \varDelta _c-1)}{\beta (\alpha \varDelta _c-1)-2}\right) ^\beta >\varDelta _c$ does exist such that if $f=f_\mathrm{NS}$, point $E^*$ may undergo a Neimark–Sacker bifurcation.

Proof

(a) $f>\varDelta _c$ (i.e. system $S_\mathrm{HF}$ as given by (10) is considered); (b) $\varDelta _c>\frac{1}{\alpha }$ and (c) $\varDelta _c<\frac{1}{\alpha }+\gamma f$ (i.e. the interior fixed point $E^*$ exists), then at the steady state

$$\begin{aligned} \mathrm{Det}(JS_\mathrm{HF}(E^*))=\frac{\beta }{2}(\alpha \varDelta _c-1)\left( 1-\left( \frac{\alpha \varDelta _c-1}{\gamma \alpha f}\right) ^{\frac{1}{\beta }}\right) . \end{aligned}$$

If $f=f_\mathrm{NS}$, where

$$\begin{aligned} f_\mathrm{NS}=\frac{\alpha \varDelta _c-1}{\gamma \alpha }\left( \frac{\beta (\alpha \varDelta _c-1)}{\beta (\alpha \varDelta _c-1)-2}\right) ^\beta >\varDelta _c \end{aligned}$$

then (i) $\mathrm{Det}(JS_\mathrm{HF}(E^*))=1$, (ii) $\mathrm{Tr}(JS_\mathrm{HF}(E^*))=1$; hence, it belongs to the interval $(-2,2)$, (iii) the two non-real eigenvalues cross the unit circle at a nonzero speed when f changes and (iv) none of them may be one of the first four roots of unity (excluding cases of strong resonance). According to these conditions, a Neimark–Sacker bifurcation may occur at $f=f_\mathrm{NS}$. $\square$

Fig. 4

Parameters $\varDelta c=3$, $\gamma =0.5$, $\alpha =2$ and $\beta =1$, i.c. (0.1, 0.1) a Trajectories versus time for $f=8.4$ and i.c. (0.1, 0.1); b 1D bifurcation diagram of $q_t$ w.r.t. f, being $f_\mathrm{NS}\simeq 8.3333 \ldots$; c 2D bifurcation diagram showing a large variety of long-term dynamics for a higher value of $\alpha =10$. d 1D bifurcation diagram of $q_t$ w.r.t. $\varDelta _c$, being $f=14$ for a higher value of $\alpha =10$. e 1D bifurcation diagram of $x_t$ w.r.t. $\gamma$, being $f=14$ for a higher value of $\alpha =10$

Proposition 3 gives only a necessary condition for the occurrence of a Neimark–Sacker bifurcation as the Lyapunov coefficient has not been taken into account (see Guckenheimer and Holmes (1997) and Kuznetsov (2004)). Several numerical simulations show that the Neimark–Sacker bifurcation takes place, it is of a supercritical type and the closed invariant curve involved in such a bifurcation is stable (see Fig. 3 panel c). The Neimark–Sacker bifurcation curve in the plane $(f,\gamma )$ is depicted in red in Fig. 3a and in black in Fig. 3b. Notice that once all the parameters except f are fixed, then the $f-$value corresponding to the Neimark–Sacker bifurcation can be obtained and it is given in (3). The occurrence of this smooth bifurcation can be observed by also looking at the one dimensional bifurcation diagram w.r.t. f (Fig. 3d).

The scenario previously described shows that for some parameter configurations, if the fine level fixed by the State increases, a smooth Neimark–Sacker bifurcation occurs and immediately after this bifurcation, a stable closed invariant curve is created as shown in Fig. 3 panel c. The economy will fluctuate in the long term between configurations characterized by different fractions of dishonest firms and the monitoring level follows the same qualitative behaviour: there exists a fraction of firms changing group at each period and, consequently, the monitoring effort is updated at each period too (see Fig. 4a). Hence, fluctuations emerge for high value of the fine level.

Nevertheless, as long as situations with higher f are considered, then the attractor collides with the border and the qualitative structure of the attracting set may change due to a BCB. In Fig. 4b, the one-dimensional bifurcation diagram for the state variable $q_t$ w.r.t. f is depicted, and the blue curve represents combinations of f and $q_t$ belonging to the border d for a given fixed value of $\varDelta _c$. The collision between the attractor and the border is visible, and the new attractor seems to be very complex (very high period or chaos). In addition, it can be observed that, by still increasing f, then the situation characterized by a stable $7-$period cycle created by BCB is visible. In fact, in the present model non-smooth bifurcations may emerge due to the presence of the border d separating $D_1$ and $D_2$ where the map has a different definition. We would like to emphasize here that these bifurcations are not related to an eigenvalue of the attractor crossing the threshold values $\pm 1$, but to the collision of one attracting set with the border separating the region of different definitions on the map. The cycle cartogram in Fig. 4c shows how different periodicity regions are organized on the parameter plane and an additional study to verify its bifurcation structure is needed. In Fig. 4d, the 1-dimensional bifurcation diagram w.r.t. $\varDelta _c$ is reported, and periodicity regions and very complex attractors alternate. In Fig. 4e, the evolution of the fraction of dishonest firms is represented for increasing values of $\gamma$; in this case, $\alpha$ is high, i.e. the social stigma is not effective to fight corruption, and then, fixing a high level of fine can be a useful strategy to exit the dishonesty trap only if combined with a minimum investment level in monitoring activity. Recall that the Neimark–Sacker bifurcation occurs for $f=f_\mathrm{NS}>\varDelta _c$, therefore a decrease in the difference between production costs for low- and high-quality goods could destabilize the system.

In addition, as long as $f>\varDelta _c$, then if social stigma is at an intermediate level, the system will reach in the long run a situation where both honest and dishonest firms coexist. Differently from what occurs with low fine, both convergence to the inner equilibrium or asymptotic cycles are a possible outcome. The possibility of fluctuations arising can be explained as follows.

We consider, for example, an economic system that starts from an initial condition with a certain low level of dishonest firms. Assume that $\alpha$ is at an intermediate level then, given the difference in costs ($\varDelta _c$), it can be convenient for some firms to move from honest to dishonest. As the fraction of dishonest firms grows, the State will try to counteract this phenomenon by increasing monitoring so as to make being dishonest economically less convenient and thus reducing the spread of dishonesty. Then, the fraction of dishonest firms will be reduced and the process repeats. The first question is related to the predictability of the system. In fact, since complex dynamics are produced both from standard-smooth and non-standard non-smooth bifurcation, it is difficult to predict the long-term qualitative evolution of the system as some economic policies to reduce non-compliant behaviour are put in place. On the other hand, an important question is related to the quantitative dynamics compared to the qualitative ones. In fact, even in the presence of cycles, the punishment level f and the efforts put in place by the State to fight corruption $\gamma$ are still powerful instruments of economic policy to reduce the spread of dishonesty. Indeed as f or/and $\gamma$ increase, then a quantitative stabilization (i.e. lower levels of dishonesty during the cycle) is associated with a qualitative destabilization (more complex dynamics) as can be seen from Fig. 4b and e. Finally, these two policies alone are not sufficient to delete non-compliant behaviour, as only with self-deterrent social attitude against dishonesty, the desirable situation with all honest firms can be reached.

4 Conclusions and further developments

Table 1 Social stigma and economic policies: summarizing results

In this section, we want to summarize the main results of the present work through a table which gives a more intuitive representation of different cases. In Table 1, we have collected all the cases analysed focusing on two key ingredients of our model: the level of punishment f fixed by the State in order to discourage the dishonesty and the “inner honesty" $\alpha$. For the first parameter, we consider two different levels: low fine ($f\le \varDelta _c$) and high fine ($f>\varDelta _c$), while for the “inner honesty", we considered a low, intermediate and high level. Our analysis shows that having a high level of “inner honesty" is a necessary and sufficient condition for the system to converge towards a society in which all firms are honest. In fact, our analysis shows that the equilibrium without dishonesty can be reached in the long term iff the social stigma deriving from dishonest behaviour is strong enough (i.e. $\alpha$ is small enough). In this case, ceteris paribus, although dishonest behaviour is more worthwhile than the honest one, the amount of honest firms which change behaviour to become dishonest is less than the one moving in the opposite direction. On the other hand, when the culture of honesty in a country is not effective enough, then dishonesty cannot be eliminated. Such an unfavourable situation can be improved by putting in place strategies which drive the economy towards an equilibrium with the coexistence of both groups. In the case, in which the “inner honesty" is low, we have to consider also the level of fine: if the punishment is low, then the economy will converge to a sort of dishonesty trap in which there are only dishonest firms. The same occurs if the combination of the fine and the public resources invested in the monitoring activity is low (i.e. $f\gamma$). Differently, if the combination of the fine and the public resources invested in the monitoring activity is high, the economy can reach a stable equilibrium in which there is a coexistence of both honest and dishonest firms. In the intermediate case, the economy can avoid the dishonesty trap, reaching a stable equilibrium in which there is a coexistence of both honest and dishonest firms. As $\alpha$—at least in the short period—and $\varDelta _c$ must be considered as exogenous parameters, then the State can try to reduce the spread of dishonesty by increasing the fine level and/or the amount of public resources allocated to reduce frauds. Investing more resources in audit activity or increasing the punishment is two policies which can contain non-compliant behaviour in countries in which social stigma is low. Notice that without reducing $\alpha$, the equilibrium without dishonesty cannot be reached. From a policy point of view, increasing the culture of legality and honesty in a country would be the best strategy, but this is a process which takes a very long time, as changing the social vision of dishonesty requires investments in long-term human and social capital. We want to underline that in the present work, we have considered the question related to BCB with the main aim of giving insight in terms of economic intuition and policy suggestions, while we will leave a more in-depth mathematical oriented analysis (i.e. the bifurcation structure of the parameters space of the economically meaningful region) to future development (see, for instance, the studies on linear piecewise smooth maps by Panchuk et al. (2015, 2013)).

From an economic point of view, one of the possible extensions of the model is to insert the monitoring level in a general equilibrium analysis in which we could consider the existence of a State that finances the fight against dishonesty through fiscal revenues.