Abstract
A major challenge in regulated health insurance markets is to mitigate risk selection potential. Risk selection can occur in the presence of unpriced risk heterogeneity, which refers to predictable variation in health care spending not reflected in either premiums by insurers or risk equalization payments. This paper examines unpriced risk heterogeneity within risk groups distinguished by the sophisticated Dutch risk equalization model of 2016. Our strategy is to combine the administrative dataset used for estimation of the risk equalization model (n = 16.9 million) with information derived from a large health survey (n = 387k). The survey information allows for explaining and predicting residual spending of the risk equalization model. Based on the predicted residual spending, two metrics are used to indicate unpriced risk heterogeneity at the individual level and at the level of certain (risk) groups: the correlation coefficient between residual spending and predicted residual spending, and the mean absolute value of predicted residual spending. The analyses yield three main findings: (1) the health survey information is able to explain some residual spending of the risk equalization model, (2) unpriced risk heterogeneity exists both in morbidity and in non-morbidity groups, and (3) unpriced risk heterogeneity increases with predicted spending by the risk equalization model. These findings imply that the sophisticated Dutch risk equalization model does not completely remove unpriced risk heterogeneity. Further improvement of the model should focus on broadening and refining the current set of morbidity-based risk adjusters.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Many countries have based their health insurance system on principles of regulated competition [18]. In these systems, health insurers compete on price (i.e., the premium) and quality (e.g., in terms of the contracted provider network) within a regulatory framework set by the government. This regulatory framework aims to achieve public goals, such as individual affordability and accessibility. Common regulatory measures include standardization of the benefits package, premium-rate restrictions, open enrollment and risk equalization [7, 20].
One of the main challenges in regulated health insurance markets is to avoid risk selection [6, 11, 15, 18]. Risk selection has been defined as ‘actions by consumers and health plans to exploit unpriced risk heterogeneity and break pooling arrangements’ ([13, emphasis added). Unpriced risk heterogeneity refers to predictable variation in health care spending not reflected in either premiums by insurers, or in risk equalization payments. The extent to which ‘unpriced risk heterogeneity’ is present in regulated health insurance markets depends heavily on the specific regulations in place. On the one hand, premium-rate restrictions, standardization of the benefits package and open enrollment introduce or increase unpriced risk heterogeneity. On the other hand, risk equalization reduces unpriced risk heterogeneity by compensating insurers for predictable variation in medical spending [12, 14, 19, 29]. This paper analyzes unpriced risk heterogeneity in the Dutch health insurance market.
Minimizing unpriced risk heterogeneity is a central objective in regulated health insurance markets, because risk selection has several unfavorable effects. First, risk selection might lead to inefficient health plan design [8]. For example, insurers do not have incentives to improve (or even maintain) the quality of the contracted care for subgroups that are known to be unprofitable. Secondly, risk selection might lead to price distortions and result in inefficient sorting of consumers across health plans [4]. For example, if unprofitable individuals (e.g., those with particular pre-existing conditions) tend to sort into high-quality plans, the incremental premium for these plans does not only reflect the better quality of these plans but also captures some unpriced risk heterogeneity, which distorts consumers’ price/quality tradeoff when choosing a health plan. Thirdly, risk selection may reduce efficiency in production if it is a more effective way of reducing costs than negotiating and contracting efficient care. Finally, risk selection may reduce cross-subsidization from low-risk to high-risk individuals when these risk types are concentrated in different health plans (e.g., high- versus lower-quality plans, see previous example). Incomplete cross-subsidization might lead to compromised accessibility and affordability and violates the level playing field for insurers [19, 25, 26, 29].
Although risk equalization systems have become more sophisticated over the past decades, they still do not completely compensate for predictable variation in medical spending. Consequently, given premium-rate restrictions, unpriced risk heterogeneity is still present [1, 6, 9, 11, 15, 18, 24]. The Dutch risk equalization model, for instance, has been greatly improved over the last decade but still leads to significant under- and overcompensations on specific groups [21]. For example, in 2008, the subgroup of individuals who reported a fair or (very) poor health status in the prior year (23% of Dutch population) was undercompensated by on average 607 euros per person per year. As a result of the introduction of new risk adjusters, however, the average undercompensation for this group reduced to 390 euros in 2016. The same pattern can be observed for other subgroups. So, despite marked improvements of the Dutch model, some unpriced risk heterogeneity remains [24, 27,28,29].
The current over- and undercompensations suggest that the Dutch risk equalization model does not sufficiently identify the risk profile of individuals. More specifically, the morbidity-based risk adjusters in the risk equalization model (see below) might (1) not identify all high-risk individuals and/or (2) not homogenously classify high-risk individuals. Both issues are probably present in the Dutch risk equalization model. Take, for instance, the risk adjuster ‘pharmacy-based cost groups’ (PCGs), which classifies individuals in morbidity groups based on the use of prescribed drugs (related to chronic illness) in the prior year. For most PCGs, individuals must have used at least 181 defined daily doses (DDD) in order to be classified in a relevant PCG [29]. On the one hand, PCGs might not identify all people with a particular chronic condition because some of these people might have used less than 181 DDDs in the prior year. On the other hand, PCGs might be heterogeneous in the sense that individuals who use 365 DDDs of a specific drug may be sicker than those who used slightly more than 181 DDDs. Because of both reasons, insurers might not receive the right compensation for specific subgroups.
This paper further examines unpriced risk heterogeneity in the Dutch basic health insurance market. Since premiums for the basic health insurance in the Netherlands are community-rated per health plan, the risk equalization scheme is the main factor influencing unpriced risk heterogeneity. By studying unpriced risk heterogeneity, directions for further improvement of the risk equalization model may emerge, which in turn could further mitigate potential for risk selection. For example, unpriced risk heterogeneity within morbidity groups (as identified by the risk adjusters in the risk equalization model) might call for refinement of existing morbidity-based risk adjusters, while unpriced risk heterogeneity in non-morbidity groups (as identified by the risk adjusters in the risk equalization model) might call for a broader set of morbidity-based risk adjusters.
Identification of unpriced risk heterogeneity requires ‘external’ information on health risk, i.e., risk indicators that do not explicitly serve as risk adjusters in the risk equalization model. Since the Dutch risk equalization model is estimated by ordinary least squares (OLS) regression, the residual spending for risk classes explicitly included in the model is zero by definition, implying that the variation in spending between these classes will be compensated for completely. Of course, (some of the) variation in spending within risk classes will remain. Without external information on risk, however, it is impossible to determine to what extent this variation in spending is predictable.
In this study, the administrative data (2013) that were used to calculate the coefficients of the risk equalization model of 2016 are enriched with external data from a large health survey administered in 2012 (n ≈ 387,000). The administrative data are used to replicate the Dutch risk equalization model of 2016 and to determine individual-level residual spending. Subsequently, the health survey data are used to develop a model to explain and predict individual-level residual spending. Unpriced risk heterogeneity is then examined using two metrics: (1) the correlation between (actual) residual spending and predicted residual spending across risk classes and (2) the mean absolute value of predicted residual spending generated by this prediction model. The latter is calculated for the entire sample as well as for specific risk classes distinguished by the risk equalization model.
This study is not the first to use a large health survey to explain individual-level variation in medical spending. Ellis et al. [5] use a large health survey from Australia to assess the added value of health survey information in explaining individual-level variation in medical spending. Our study differs from Ellis et al. [5] in that it investigates the added value of health survey information in explaining variation in residual spending of the risk equalization model, the difference thus being the incorporation of a risk equalization model. Our approach is similar to that of Lamers [10] and Stam et al. [17] who also studied the added value of health survey information in explaining residual spending of the risk equalization model. The risk equalization model used in our study, however, is more advanced and incorporates more information. Another difference with Lamers [9] and Stam et al. [17] is that the sample size of our health survey is much larger: 387k versus 15k in Lamers [9] and 23k in Stam et al. [17].
The aim of this paper is twofold. The first objective is to study the added value of information derived from a health survey in explaining residual spending of the Dutch risk equalization model 2016. The second objective is to examine unpriced risk heterogeneity within risk classes distinguished by the Dutch risk equalization model.
This paper is organized as follows. In “The Dutch health insurance market” a brief description of relevant aspects of the Dutch health insurance market is given. In “Data and methods” the data and methods are explained, followed by the “Results”. “Discussion” discusses these findings and “Conclusion” concludes.
The Dutch health insurance market
This section briefly describes the most relevant aspects of the Dutch health insurance system. For a more comprehensive overview, see Van Kleef et al. [29] and Enthoven and Van de Ven [7]. Since this paper investigates unpriced risk heterogeneity under the Dutch risk equalization model of 2016, the following description focuses on the situation of 2016.
The analyses in this paper focus on the Dutch basic health insurance. In addition to the basic health insurance, there is a public insurance program for long-term care and a supplementary health insurance for health care services not included in the basic health insurance. The basic health insurance covers, among others, primary care, pharmaceutical care, inpatient and outpatient hospital care, and mental health care. For mental health care, a separate risk equalization model is applied which will not be included in the analyses. Instead, this paper focuses on the risk equalization model for curative somatic care, which comprises about 90% of total medical spending under the basic health insurance [29].
The government is responsible for the development and improvement of the risk equalization model. In practice, insurers receive a contribution based on the risk characteristics of their insured from a risk equalization fund. In addition to the community-rated premium paid to their insurer, insured pay an income-related contribution to the risk equalization fund, often through their employer [7, 22].
The risk equalization model predicts medical spending using individual risk characteristics like age and gender, region, socioeconomic status, source of income and health indicators. The latter include seven classifications related to morbidity. The first classification comprises the pharmacy-based cost groups (PCGs), consisting of 33 classes based on people’s use of medication in the previous year (see above). A person can be classified in multiple PCGs; individuals who do not reach the predetermined DDD threshold for the relevant pharmaceuticals are categorized in a separate class, i.e., ‘no PCG’ [29].
A second morbidity classification comprises the diagnoses-based cost groups (DCGs), i.e., 15 classes based on specific inpatient and outpatient hospital diagnoses from the previous year. Insured with multiple diagnoses are categorized in one class only, i.e., the one with the highest residual spending. People without any of the selected diagnoses are categorized in a separate category, i.e., ‘no DCG’ [29].
A third classification consists of the multiple-year high cost groups (MHCGs) comprising 7 classes based on the level of spending for curative somatic care in the previous 3 years. The underlying assumption is that individuals with multiple-year high costs most likely suffer from a chronic illness. Individuals are categorized in one class only, i.e., the class with the highest spending. Individuals that are not classified in one of the seven MHCG classes are classified in a separate category, i.e., ‘no MHCG’ [29].
Another classification comprises the durable medical equipment cost groups (DMECGs). This risk adjuster classifies individuals on the basis of their use of specific durable medical equipment in the previous year, related to chronic conditions and consists of 10 classes. Individuals are classified in one class only, i.e., the one with the highest residual spending. Again, those without a DMECG are classified in a separate class, i.e., ‘no DMECG’ [29].
The last three classifications are all based on prior-year spending for specific types of health care, i.e., physiotherapy, geriatric rehabilitation care and home care. The classifications based on physiotherapy and geriatric rehabilitation care spending both include 2 classes: yes/no spending in the previous year. The classification based on home care spending includes 7 classes; individuals are categorized in one class only, which is the class with the highest spending [3, 29].
Data and methods
This section describes the data and methods used (1) to study the added value of information derived from a health survey in explaining residual spending of the Dutch risk equalization model 2016 and (2) to examine unpriced risk heterogeneity within risk classes distinguished by the Dutch risk equalization model 2016.
As mentioned in “Introduction”, identification of unpriced risk heterogeneity requires ‘external’ data (i.e., information about health risk that does not serve as the basis for risk adjuster variables). The reason is twofold. First, the mean residual spending for risk classes in the risk equalization model is zero by definition, a property of OLS. This implies that the variation in spending between these classes will be compensated for completely. Of course, within risk classes variation in spending will remain, but without external information it is impossible to determine to what extent this variation in spending is predictable. Second, greater variation in spending within specific risk classes compared to others does not automatically indicate greater unpriced risk heterogeneity in these classes. This study relies on external information from a health survey conducted among a large sample of the adult Dutch population.
Two datasets are used in this study. First, we use administrative data containing individual-level information on medical spending and risk adjusters for all citizens with a basic health insurance in 2013 (n = 16.9 million). Second, health survey data from Statistics Netherlands are used containing information on physical and mental health as well as on lifestyle for 387,195 individuals. The health survey data are restricted to individuals of 19 years or older (on September 1, 2012) who do not live in an institution. The sample results from a combination of three surveys held in 2012, i.e., the elderly monitor (65 years and above), the adult monitor (19–64) and the health monitor (all ages) [30]. The two datasets are merged at the individual level using the citizen service number (i.e., personal ID number assigned to every Dutch citizen by the government). To protect individuals’ privacy, citizen service numbers were anonymized by a trusted third party before the datasets were made available for this research [24]. All analyses in this study (except the estimation of the risk equalization model) are conditional on the individuals who participated in the health survey and who successfully merged with the administrative data (see below).
We address the research objectives in four steps, which are explained in more detail below. First, we test the representativeness of the sample. Second, we develop a prediction model to explain residual spending with the information from the health survey. We use this model to make a prediction of residual spending for all individuals included in the health survey. Third, we construct several groups for analyzing within-group risk heterogeneity not explained by the risk equalization model. Finally, we apply specific metrics to examine unpriced risk heterogeneity both at the individual level and at the level of specific groups.
Step 1: testing the representativeness of the sample
In this first step, the sample is compared with the adult population in terms of population frequencies for both risk classes included in the risk equalization model and deciles of spending (Table 1 and Fig. 1). In addition, the sample is compared in terms of mean spending per decile of spending (Fig. 2).
Of the 387,195 respondents of the health survey, 384,004 respondents successfully merged with the administrative dataset. The match is not 100% due to death and migration of citizens. Unfortunately, many records in the sample contain missing values for one or more crucial items in the health survey. After removing these records, 228,944 records remained for analysis.
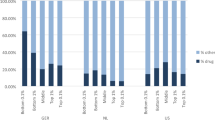
Table 1 shows the prevalence for several risk classes included in the risk equalization model. The last column presents the prevalence for the total adult population with a health plan in 2013. The adjacent column shows the prevalence for the sample after removal of the missing values. It appears that the sample is overrepresented by the young, the healthy, the higher educated and high-income people.
Figure 1 compares both groups in terms of the prevalence per decile of spending. The deciles are based on the total Dutch adult population. The bars for the sample show a different pattern than the bars for the population and indicate that the sample is overrepresented by people with low spending. As can be observed in Fig. 2, however, the average medical spending per decile of spending matches relatively well.
Recalibrating the survey data
Because the Dutch risk equalization model is estimated by OLS, the mean predicted spending equals the mean spending in the data on which the model is estimated. In other words, the mean residual spending in the population is zero. For the survey sample, however, the mean residual spending equals almost 65 euros per person per year (i.e., an overcompensation). The reasons for this deviation are that (1) the sample is relatively healthy (see Table 1 and Fig. 1) and that (2) apparently, the risk equalization model does not completely correct for this selection bias. In order to correct for this difference in mean residual spending between the sample and the population, we recalibrated the survey data by multiplying the individual-level predicted spending by a factor of 0.967 (i.e., mean spending of 1928 euros in the sample divided by the mean predicted spending of 1992 euros in the sample). After this correction, the mean residual spending in the sample equals zero. Without this correction, our measures of unpriced risk heterogeneity would be affected by the overcompensation on the sample.
Step 2: building a model to explain and predict residual spending
Next, we built a model to explain and predict residual spending from the risk equalization model. To do so, we first determined the individual-level residual spending \(e_{i}\) by calculating the difference between spending \(y_{i}\) and predicted spending by the risk equalization model \(\hat{y}_{i}\):
Secondly, we use the information from the health survey to explain variance of \(e_{i}\). This model was developed in three phases: A, B and C. In phase A, we estimated a model including all variables (i.e., 56) available in the health survey as predictors. To fully exploit the information from the health survey, in phase B we identified relevant interaction terms. As many interactions are possible, we used a classification tree analysis to identify the statistically significant interaction terms. A classification tree explores higher-order interactions to explain a binary outcome variable [16]. Buchner et al. [2] have used a similar technique to identify relevant interaction terms for the German risk equalization model. In this study, the binary outcome is having a positive (1) or negative prediction error (0) based on the model from phase A. This way, the classification tree only yields interaction terms that can explain additional variance in \(e_{i}\) (i.e., variance that is not yet explained by the model from phase A). In phase C, the interaction terms were added to the model from phase A and, using stepwise selection, statistically insignificant variables (P > 0.1) were dropped. This ultimately led to our final model, which includes 33 variables including three interaction terms (see “Appendix A”). This model is used to predict individual-level residual spending from the risk equalization model:
Step 3: constructing groups for analyzing within-group unpriced risk heterogeneity
In the third step, two types of risk groups were constructed: (1) groups based on yes/no morbidity, and (2) groups based on deciles of predicted spending by the risk equalization model (\(\hat{y}_{i}\)). Morbidity is defined as being classified in at least one of the seven morbidity-based risk adjusters of the risk equalization model (see “The Dutch health insurance market”). Non-morbidity is defined as being classified in none of the seven morbidity characteristics of the Dutch risk equalization model. The deciles of predicted spending result in ten groups based on the predicted spending \(\hat{y}_{i}\). More specifically, we determined deciles of \(\hat{y}_{i}\) for the entire adult Dutch population. These deciles thus order the individuals in the sample according to the predicted spending by the risk equalization model. This is a different way to analyze the relationship between unpriced risk heterogeneity and the risk information included in the risk equalization model.
Step 4: examining unpriced risk heterogeneity
In the final step, unpriced risk heterogeneity is examined at the individual level and at the level of the groups defined in step 3. Because the sample is overrepresented by healthy individuals, any unpriced risk heterogeneity found probably underestimates the actual unpriced risk heterogeneity. To indicate individual-level unpriced risk heterogeneity, we calculate the R2Footnote 1 and cummings prediction measure (CPM)Footnote 2 of our prediction model from step 2. In addition, we examine the distribution of the (individual-level) predicted residual spending. To indicate unpriced risk heterogeneity per group, two metrics were used. First, the correlation between the individual-level residual spending \(e_{i}\) and individual-level predicted residual spending \(\hat{e}_{i}\) per group was calculated. This correlation indicates the cohesion between residual spending and predicted residual spending. In a situation where risk equalization completely compensates for predictable variation in spending, residual spending will not be predictable. In that case, the correlation coefficient will be zero (or at least not statistically significant). Note that because we use a sample of the population, random variation is present. We are, however, interested in systematic variation. This is identified by testing for statistical significance. A statistically significant correlation coefficient indicates unpriced risk heterogeneity.
The second metric is the mean absolute value of predicted residual spending per group j:
Again, in a situation where risk equalization completely compensates for predictable variance in spending, residual spending is not predictable. In that case, the mean absolute value of predicted residual spending will be (close to) zero. A higher value of \(\left| {\bar{\hat{e}}} \right|_{j}\), indicates more unpriced risk heterogeneity. We deliberately examine the absolute values of predicted residual spending and not the relative amount of heterogeneity that can be explained by the prediction model (e.g. \(\left| {\bar{\hat{e}}} \right|_{j}\) as a percentage of \(\left| {\bar{e}} \right|_{j}\)), as incentives for risk selection are primarily determined by absolute differences between spending and revenues.
Results
This section presents the results of the empirical analyses. “Unpriced risk heterogeneity in the total sample” focusses on unpriced risk heterogeneity in the entire sample and “Unpriced risk heterogeneity within risk groups” on unpriced risk heterogeneity in specific groups. Finally, “Predicted residual spending and predicted spending” studies the relationship between unpriced risk heterogeneity and predicted spending by the risk equalization model.
Unpriced risk heterogeneity in the total sample
When explaining variance in medical spending, the prediction model constructed based on health survey variables (see “Step 2: Building a model to explain and predict residual spending”) yields an R2 of 10.2%. The same model has an R2 of 0.48% when explaining variance in residual spending of the risk equalization model of 2016. This indicates that the risk equalization model already performs well in reducing unpriced risk heterogeneity. This conclusion is reinforced when comparing the above mentioned R2 values to the R2 of the risk equalization model itself: 28.1%. This also shows that the information in the health survey is able to explain only a portion of the variance in residual spending of the Dutch risk equalization model of 2016. The same conclusion arises when we look at the CPM which equals 0.97% for the prediction model explaining variance in residual spending of the risk equalization model compared to 30.5% for the risk equalization model itself. Still, the results indicate that after risk equalization some unpriced risk heterogeneity remains.
Figure 3 shows the distribution of the predicted residual spending resulting from our prediction model (\(\hat{e}_{i}\)) in the total sample. If the risk equalization model would perfectly compensate for predictable variation in medical spending, the prediction model would not be able to predict any residual spending. This would result in a very narrow distribution. The wider the distribution, the better the model predicts residual spending and the more unpriced risk heterogeneity is present. Figure 3 indeed indicates presence of unpriced risk heterogeneity in the sample. Figure 4 shows the same distribution separately for the morbidity group and the non-morbidity group. The distribution is clearly wider for the morbidity group (panel 4a) than for the non-morbidity group (panel 4b), indicating a higher level of unpriced risk heterogeneity in the morbidity group than the non-morbidity group. This ‘width’ of the distribution can be quantified using the mean absolute value of predicted residual spending: \(\left| {\bar{\hat{e}}_{i} } \right|\).
Unpriced risk heterogeneity within risk groups
Table 2 provides information on unpriced risk heterogeneity within the morbidity and non-morbidity groups as defined in “Step 3: constructing groups for analyzing within-group unpriced risk heterogeneity”. For all groups, we find a statistically significant positive correlation between residual spending and predicted residual spending. Unsurprisingly, the average spending is higher for the morbidity group than for the non-morbidity group. The same is true for the mean absolute value of residual spending \(\left| {\bar{e}} \right|_{j}\), indicating greater unexplained spending variation in the morbidity group as compared to the non-morbidity group (i.e., heteroskedasticity). Note, however, that \(\left| {\bar{e}} \right|_{j}\) not necessarily indicates ‘unpriced risk’ because variation in residual spending is not necessarily predictable. Therefore, the mean absolute value of predicted residual spending \(\left| {\bar{\hat{e}}} \right|_{j}\) is much more interesting. This value indicates the extent to which the health survey variables in the prediction model (which are omitted from the risk equalization model itself, see “Step 2: building a model to explain and predict residual spending”) are able to explain residual spending from the risk equalization model of 2016. The last column of Table 2 shows that \(\left| {\bar{\hat{e}}} \right|_{j}\) is larger than zero for the morbidity and non-morbidity groups, indicating the presence of unpriced risk heterogeneity in both groups. The results show that \(\left| {\bar{\hat{e}}} \right|_{j}\) in the morbidity group is almost twice as high as in the non-morbidity group, implying more unpriced risk heterogeneity in the morbidity group. These findings correspond with Fig. 4. A deeper look into the constituent elements of the morbidity group (i.e., the PCGs, DCGs, etc.) reveals that the largest values of \(\left| {\bar{\hat{e}}} \right|_{j}\) are found in the classifications based on geriatric rehabilitation care spending and home care spending in the previous year.
Table 3 shows the same metrics as Table 2, only then for the ten deciles of predicted spending based on the risk equalization model 2016. As described in “Data and methods”, these deciles are based on the total adult population, which is why the prevalence in the second column does not equal 10% for each class. Kautter et al. [9] also used deciles of predicted spending in their research, but then to evaluate model performance. In this research, the purpose of the deciles of predicted spending is to order the included groups of the risk equalization model by risk class, enabling us to examine unpriced risk heterogeneity on a different level. For all risk classes, a statistically significant correlation between \(e_{i}\) and \(\hat{e}_{i}\) is found. Both the mean absolute value of residual spending \(\left| {\bar{e}} \right|_{j}\) and the mean absolute value of predicted residual spending \(\left| {\bar{\hat{e}}} \right|_{j}\) increase with predicted spending. The latter indicates more unpriced risk heterogeneity among individuals with the highest levels of predicted spending. This corresponds with the results from Table 2, which also showed that the groups with high (predicted) spending have higher levels of unpriced risk heterogeneity.
Predicted residual spending and predicted spending
Figure 5 shows the relation between unpriced risk heterogeneity and predicted spending from a different angle. On the horizontal axis, the deciles of predicted residual spending are depicted. Both the mean predicted residual spending \(\bar{\hat{e}}_{j}\) (shaded bars) and the mean predicted spending \(\bar{\hat{y}}_{j}\) (empty bars) per decile j of the risk equalization model are shown. This shows an interesting pattern: the two highest deciles of predicted residual spending also have the highest predicted spending by the risk equalization model. This suggests that for people with the highest predicted residual spending, the risk equalization model already predicts high medical spending, only not high enough.
Discussion
A major challenge in regulated health insurance markets is to avoid risk selection, which can occur in the presence of unpriced risk heterogeneity. Risk equalization models aim to mitigate unpriced risk heterogeneity by compensating insurers for predictable variation in medical spending. In this paper, we examined unpriced risk heterogeneity in the Dutch basic health insurance market. Our findings comprise three main conclusions, which are discussed below.
Health survey information indicates unpriced risk heterogeneity
We examined unpriced risk heterogeneity within risk groups included in the risk equalization model. To that end, we merged administrative data on spending and risk characteristics of 2013 for the entire adult Dutch population with rich health survey data from 2012. With the information from the health survey, a prediction model was constructed to explain and predict residual spending from the risk equalization model. The health survey information is able to explain approximately 10% of variation in individual-level medical spending. Ellis et al. [5] found a similar R2 of 10% for a model based on external health survey information to explain variance in individual-level medical spending in Australia. When explaining variation in residual spending (i.e., after application of the Dutch risk equalization model 2016), the R2 drops to 0.48%, given these data, indicating that the health survey information is able to explain a small but non-negligible share of this variation. This confirms that although the Dutch risk equalization model 2016 performs quite well, some unpriced risk heterogeneity—and thus potential for risk selection—remains. These findings are in line with previous research. Recent studies on risk heterogeneity by Newhouse et al. [15] and Van de Ven et al. [23] also show that there is still selection potential in markets with sophisticated risk equalization models. In addition, Stam et al. [17], who analyzed the predictive power of self-reported health measures for a risk equalization model that already included several morbidity characteristics (i.e., PCGs and DCGs), also found that these self-reported health measures have added value in explaining medical spending. The R2 of 0.48% found in this study is lower than the incremental change in R2 of 2%, found by Stam et al. [17]. This difference can be explained by improvements of the Dutch risk equalization model over the past decade [24, 27, 28].
Unpriced risk heterogeneity is present in both morbidity and non-morbidity groups
Our findings indicate that unpriced risk heterogeneity is present in both the morbidity group and the non-morbidity group included in the risk equalization model. In addition, our findings suggest more unpriced risk heterogeneity in the morbidity group than the non-morbidity group. In line with the latter finding, unpriced risk heterogeneity increases with predicted spending by the risk equalization model. These results lead us to the conclusion that per-person predictable profits and losses (i.e., over- and undercompensations) are larger in the morbidity group than in the non-morbidity group and increase with predicted spending. Apparently, the high-risk group identified by the morbidity indicators in the risk equalization model is to some extent heterogeneous. This calls for further refinement of these indicators, to the extent that remaining unpriced risk heterogeneity in these groups is considered a problem.
When it comes to selection potential, however, not just the per-person predictable profits and losses matter, but also the size of the relevant group. Although the per-person predictable profits and losses are smaller in the non-morbidity group compared to the morbidity group, the former group is larger. Therefore, unpriced risk heterogeneity in this group should not be neglected. It appears that the morbidity indicators do not identify all high-risk individuals and leave some of these people in the non-morbidity group, which calls for extending the set of morbidity indicators.
Relationship between predicted residual spending and predicted spending
Our findings also suggest a relationship between predicted residual spending (following from our prediction model) and predicted spending by the risk equalization model: those with the highest predicted residual spending also have high predicted spending. This shows that the risk equalization model predicts high spending for these individuals, only not high enough. One option to reduce undercompensation for specific groups is to extend the risk equalization model with new risk adjusters that identify these groups [19]. When new or better risk adjusters are not available (in the short run), another option to reduce undercompensation for specific groups is overpaying individuals on the basis of their predicted spending from the risk equalization model. Such overpayment can be realized by, for instance, the use of constrained least squares regression [8, 25].
Limitations
The findings in this paper must be viewed in the light of some limitations. First, missing values in the health survey data necessitated the exclusion of approximately 150,000 individuals from our analyses. Nonetheless, a substantial sample size of over 200,000 individuals remained. A second limitation may be overfitting as a result of the use of a classification tree to identify relevant interactions between health survey variables (to enrich our prediction model). However, our main aim in identifying interactions was to optimally use the health survey information in explaining residual spending (and thus to indicate remaining unpriced risk heterogeneity), and not to develop potential new risk adjusters to include into the risk equalization model. Moreover, adding the identified interactions to the prediction model only marginally increases the R2 of this model (i.e., from 0.45% to 0.48%), suggesting that the non-interaction variables explain the vast majority of the variation in residual spending explained by the prediction model. Thirdly, in this research the information from the health survey was used to explain variation in residual spending of the risk equalization model. Alternatively, the information from the health survey could have been added to the risk equalization model and this extended model could then have been compared to the original risk equalization model, similar to the approach of Stam et al. [17]. The reason for choosing the first approach lies in the risk of overfitting. Despite having a large sample, the number of people that would be classified in specific categories of the risk equalization model would be too small to yield trustworthy estimates.
Finally, in this research the potential for risk selection has been explored by examining the existence of unpriced risk heterogeneity. It is important to note that the potential for risk selection does not depend on the existence of unpriced risk heterogeneity alone. As recognized in the definition of risk selection by Newhouse [13], unpriced risk heterogeneity is just one of the conditions that need to be present in order for risk selection to take place. The other conditions relate to ‘actions by consumers or health plans’ [13]. This includes all possible actions by insurers, regardless of intentions, to exploit unpriced risk heterogeneity as well as the response of consumers to these actions.
Conclusion
This study examined the unpriced risk heterogeneity in the Dutch health insurance market. The analyses yield three main findings: (1) the health survey information is able to explain some residual spending of the risk equalization model, (2) unpriced risk heterogeneity exists in both morbidity and non-morbidity groups, and (3) unpriced risk heterogeneity increases with predicted spending by the risk equalization model. These findings imply that—despite its broad set of morbidity-based risk adjusters—the Dutch risk equalization model 2016 does not completely remove unpriced risk heterogeneity. Further improvement of the model should focus on broadening the current set of morbidity-based risk adjusters (to reduce unpriced risk heterogeneity in the large non-morbidity group) and on refinement of the current morbidity-based risk adjusters (to reduce unpriced risk heterogeneity in the morbidity group), if improvement for these groups is desired through risk equalization.
Notes
\(R^{2} = 1 - \frac{{\sum\nolimits_{i = 1}^{n} {(e_{i} - \hat{e}_{i} )} ^2}}{{\sum\nolimits_{i = 1}^{n} {(e_{i} - \hat{e})}^{2} }}\)
\({\text{CPM}} = 1 - \frac{{\sum\nolimits_{i = 1}^{n} {(e_{i} - \hat{e}_{i} )} }}{{\sum\nolimits_{i = 1}^{n} {(e_{i} - \hat{e})} }}\)
References
Brown, J., Duggan, M., Kuziemko, I., Woolston, W.: How does risk selection respond to risk adjustment? New evidence from the medicare advantage program. Am. Econ. Rev. 104(10), 3335–3364 (2014). https://doi.org/10.1257/aer.104.10.3335
Buchner, F., Wasem, J., Schillo, S.: Regression trees identify relevant interactions: can this improve the predictive performance of risk adjustment? J. Health Econ. 26, 74–85 (2017). https://doi.org/10.1002/hec.3277
Eijkenaar, F., van Vliet, R.C.J.A.: Improving risk equalization using information on physiotherapy diagnoses. Eur. J. Health Econ. (2017). https://doi.org/10.1007/s10198-017-0874-x
Einav, L., Finkelstein, A.: Selection in insurance markets: theory and empirics in pictures. J. Econ. Perspect. 25(1), 115–138 (2011). https://doi.org/10.1257/jep.25.1.115
Ellis, R.P., Fiebig, D.G., Johar, M.J., Jones, G., Savage, E.: Explaining health care expenditure variation: large-sample evidence using linked survey and health administrative data. Health Econ. 22, 1093–1110 (2013). https://doi.org/10.1002/hec.2916
Ellis, R.P., Jiang, S., Kuo, T.: Does service level spending show evidence of selection across health plan types? Appl. Econ. 45(13), 1701–1712 (2013). https://doi.org/10.1080/00036846.2011.636023
Enthoven, A.C., van de Ven, W.P.M.M.: Going Dutch—managed-competition health insurance in The Netherlands. N. Engl. J. Med. 357(24), 2421–2423 (2007). https://doi.org/10.1056/NEJMp078199
Glazer, J., McGuire, T.G.: Optimal risk adjustment in markets with adverse selection: an application to managed care. Am. Econ. Rev. 90(4), 1055–1071 (2000). https://doi.org/10.1016/j.jhealeco.2006.01.005
Kautter, J., Pope, G.C., Ingber, M., Freeman, S., Patterson, L., Cohen, M., Keenan, P.: The HHS-HHC risk adjustment model for individual and small group markets under the affordable care act. Medicare Medicaid Res. Rev. (2014). https://doi.org/10.5600/mmrr.004.03.a03
Lamers, L.M.: Risk-adjusted capitation based on the diagnostic cost group model: an empirical evaluation with health survey information. Health Serv. Res. 33(6), 1727–1744 (1999)
McGuire, T.G., Newhouse, J.P., Normand, S., Shi, J., Zuvekas, S.: Assessing incentives for service level selection in private health insurance exchanges. J. Health Econ. 35, 47–63 (2014). https://doi.org/10.1016/j.jhealeco.2014.01.009
McWilliams, J.M., Hsu, J., Newhouse, J.P.: New risk-adjustment system was associated with reduced favorable selection in medicare advantage. Health Aff. 31(12), 2630–2640 (2012). https://doi.org/10.1377/hlthaff.2011.1344
Newhouse, J.P.: Reimbursing health plans and health providers: efficiency in production versus selection. J. Econ. Lit. 34, 1236–1263 (1996)
Newhouse, J.P., Price, M., Huang, J., McWilliams, M., Hsu, J.: Steps to reduce favorable risk selection in medicare advantage largely succeeded, boding well for health insurance exchanges. Health Aff. 31(12), 2618–2628 (2012). https://doi.org/10.1377/hlthaff.2012.0345
Newhouse, J.P., Price, M., McWilliams, J.M., Hsu, J., McGuire, T.G.: How much favorable selection is left in medicare advantage? Am. J. Health Econ. 1(1), 1–26 (2015). https://doi.org/10.1162/ajhe_a_00001
Speybroeck, N.: Classification and regression trees. Int. J. Public Health 57, 243–246 (2012). https://doi.org/10.1007/s00038-011-0315-z
Stam, P.J.A., van Vliet, R.C.J.A., van de Ven, W.P.M.M.: Diagnostic, pharmacy-based and self-reported health measures in risk equalization models. Med. Care 48(5), 448–457 (2010). https://doi.org/10.1097/MLR.0b013e3181d559b4
van de Ven, W.P.M.M., Beck, K., Buchner, F., Chernichovsky, D., Gardiol, L., Holly, A., Lamers, L.M., Schokkaert, E., Shmueli, A., Spycher, S., van de Voorde, C., van Vliet, R.C.J.A., Wasem, J., Zmora, I.: Risk equalization and risk selection on the sickness fund insurance market in five European countries. Health Policy 65, 75–98 (2003). https://doi.org/10.1016/S0168-8510(02)00118-5
van de Ven, W.P.M.M., Ellis, R.P.: Risk adjustment in competitive health insurance markets. In: Culyer, A.J., Newhouse, J.P. (eds.) Handbook of Health Economics, pp. 755–845. Elsevier, Amsterdam (2000)
van de Ven, W.P.M.M., Beck, K., Buchner, F., Schokkaert, E., Schut, F.T., Shmueli, A., Wasem, J.: Preconditions for efficiency and affordability in competitive healthcare markets: are they fulfilled in Belgium, Germany, Israel, The Netherlands and Switzerland? Health Policy 109, 226–245 (2013). https://doi.org/10.1016/j.healthpol.2013.01.002
van de Ven, W.P.M.M.: Risk adjustment and risk equalization: what needs to be done? Health Econ. Policy Law 6, 147–156 (2011). https://doi.org/10.1017/S1744133110000319
van de Ven, W.P.M.M., Schut, F.T.: Guaranteed access to affordable coverage in individual health insurance markets’. In: Glied, S., Smith, P.C. (eds.) The Oxford Handbook of Health Economics, pp. 380–404. Oxford University Press, Oxford (2011)
van de Ven, W.P.M.M., van Vliet, R.C.J.A., van Kleef, R.C.: How can the regulator show evidence of (no) risk selection in health insurance markets? Conceptual framework and empirical evidence. Eur. J. Health Econ. 18, 167–180 (2017). https://doi.org/10.1007/s10198-016-0764-7
van Kleef, R.C., Eijkenaar, F., van Vliet, R.C.J.A.: Risicoverevening 2016: uitkomsten op subgroepen uit de gezondheidsmonitor 2012. iBMG/Erasumus Universiteit Rotterdam, Rotterdam (2017)
van Kleef, R.C., McGuire, T.G., van Vliet, R.C.J.A., van de Ven, W.P.M.M.: Improving risk equalization with constraint regression. Eur. J. Health Econ. (2016). https://doi.org/10.1007/s10198-016-0859-1
van Kleef, R.C., van de Ven, W.P.M.M., van Vliet, R.C.J.A.: Risk selection in a regulated health insurance market: a review of the concept, possibilities and effects. Expert Rev. Pharmacoecon. Outcomes Res. 13(6), 743–752 (2013). https://doi.org/10.1586/14737167.2013.841546
van Kleef, R.C., van Vliet, R.C.J.A., van de Ven, W.P.M.M.: Risicoverevening tussen zorgverzekeraars: kwantificering modelverbeteringen 1993–2011. Tijdschrift voor Gezondheidswetenschappen 5, 311–326 (2012). https://doi.org/10.1007/s12508-012-0110-0
van Kleef, R.C., van Vliet, R.C.J.A., van de Ven, W.P.M.M.: Risicoverevening 2014 voor somatische zorg: Analyse van uitkomsten op subgroepniveau. iBMG/Erasumus Universiteit Rotterdam, Rotterdam (2014)
van Kleef, R.C., Eijkenaar, F., van de Ven, W.P.M.M.: Health plan payment in the Netherlands. In McGuire, T.G., van Kleef, R.C. (eds.) Risk Adjustment, Risk Sharing and Premium Regulation in Health Insurance Markets: Theory and Practice, Elsevier Publishing, Amsterdam (2018) (forthcoming)
Volksgezondheidenzorg.info: Health monitor adults, public health services, Statistics Netherlands, and National Institute for Public health and the Environment. Volksgezondheidenzorg.info. https://bronnen.zorggegevens.nl/Bron?naam=Gezondheidsmonitor-Volwassenen%2C-GGD%E2%80%99en%2C-CBS-en-RIVM. Accessed 12 March 2018
Acknowledgements
The authors gratefully acknowledge comments on earlier versions of this article by two anonymous reviewers, René van Vliet, Wynand van de Ven, Erik Schut, Thomas McGuire and Suzanne van Veen. Furthermore, the authors would like to thank the participants of the HSI seminar series and RAN meeting 2017 for helpful discussions. The authors also gratefully acknowledge the Dutch Ministry of Health, the Dutch Association of Health Insurers and Statistics Netherlands for providing the administrative and survey data. In addition, the authors are grateful to the members of the supervisory committee for their valuable comments. Remaining errors are the responsibility of the authors.
Funding
The authors received no financial support for the research, authorship and/or publication of this article.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare to have no conflict of interest.
Appendix A: Prediction model
Appendix A: Prediction model
Variable | Coefficient |
|---|---|
Intercept | − 29 |
Fair or (very) poor general health | 453 |
Cancer in the last 12 months | 381 |
Heart condition in the last 12 months | 576 |
Stroke in the last 12 months | 1041 |
Interaction term 1* | 2439 |
Interaction term 2* | 1479 |
Severe/recurrent disease of intestines in the last 12 months | 269 |
Immigrant of the first generation | − 224 |
Other chronic illness in the last 12 months | 153 |
Sufficient physical activity according to ‘fit’ norm | − 116 |
3 self-reported conditions | 220 |
Moderate smoker | 136 |
Stroke ever | 273 |
Semi-sufficient physical activity according to ‘fit’ norm | − 82 |
Loneliness on a social level | − 129 |
OECD limitations in hearing | 210 |
High risk of incurring anxiety disorder or depression | − 294 |
Peripheral artery disease in the last 12 months | 232 |
Heavy smoker | 154 |
Psoriasis in the last 12 months | 158 |
Loneliness, moderately | 77 |
OECD limitations in mobility | 121 |
Interaction term 3* | 359 |
Diabetic | − 150 |
Sufficient physical activity according to ‘beweeg’ norm | − 138 |
Heavy drinker | 92 |
Severe/recurring dizziness in the last 12 months | 139 |
Semi-sufficient physical activity according to ‘beweeg’ norm | − 100 |
2 self-reported conditions | 67 |
Severe/recurring condition of back in the last 12 months | − 80 |
High educated | 48 |
Obese | 65 |
OECD limitations in sight | 103 |
Interaction term | N (weighted) | |
|---|---|---|
1 | Chronic illness * OECD limitations in mobility * no asthma 12 months * no low risk of incurring anxiety disorder or depression * no joint inflammation 12 months * cancer 12 months | 9966 |
2 | Chronic illness * no OECD limitations in mobility * no severe/recurring condition of neck in the last 12 months * no low risk incurring anxiety disorder or depression* no joint inflammation 12 months * other chronic illness 12 months * cancer 12 months | 26,416 |
3 | Chronic illness * no OECD limitations in mobility * no severe/recurring condition of neck in the last 12 months * high risk of incurring anxiety disorder or depression* no fair or (very) poor general health | 57,790 |
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Withagen-Koster, A.A., van Kleef, R.C. & Eijkenaar, F. Examining unpriced risk heterogeneity in the Dutch health insurance market. Eur J Health Econ 19, 1351–1363 (2018). https://doi.org/10.1007/s10198-018-0979-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10198-018-0979-x