Market structure and hospital–insurer bargaining in the Netherlands

Abstract

In 2005, competition was introduced in part of the hospital market in the Netherlands. Using a unique dataset of transactions and list prices between hospitals and insurers in the years 2005 and 2006, we estimate the influence of buyer and seller concentration on the negotiated prices. First, we use a traditional structure–conduct–performance model (SCP-model) along the lines of Melnick et al. (J Health Econ 11(3): 217–233, 1992) to estimate the effects of buyer and seller concentration on price–cost margins. Second, we model the interaction between hospitals and insurers in the context of a generalized bargaining model similar to Brooks et al. (J Health Econ 16: 417–434, 1997). In the SCP-model, we find that the market shares of hospitals (insurers) have a significantly positive (negative) impact on the hospital price–cost margin. In the bargaining model, we find a significant negative effect of insurer concentration, but no significant effect of hospital concentration. In both models, we find a significant impact of idiosyncratic effects on the market outcomes. This is consistent with the fact that the Dutch hospital sector is not yet in a long-run equilibrium.

Introduction

Until very recently, cost containment was the major issue in the institutional design in the health care sector, Schut [33]. In recent years, many countries like Netherlands and Germany have started to increase price competition for hospital services. In 2005, competition has been introduced in some segments in the Dutch health care sector (for example, some parts of the hospital care and physiotherapy). The Dutch government is also planning to introduce more incentive-based mechanisms in the currently regulated domain.

We investigate the effects of buyer and seller concentration on the price of the unregulated part of the Dutch hospital care in 2005 and 2006. We estimate two models describing the interaction between hospitals and insurers in determining the negotiated prices. In the first model, we estimate the price–cost margin as a function of the Herfindahl–Hirschmann Indices (HHIs) and the market shares of hospitals and insurers. In the second model, we use a bargaining model to describe how the gains from trade are divided between hospitals and insurers. For that purpose, we regress the bargaining share of the hospital on the concentration and market shares of both hospitals and insurers.

In this paper, we employ a traditional empirical approach in industrial organization research: the structure–conduct–performance (SCP) approach. The idea is that market structure determines the conduct of firms and that conduct then yields market performance. As a consequence, our analysis is best thought of as an empirical investigation of the intuitive idea that more concentrated markets have less price competition.¹ Unfortunately, we do not currently posses consumer demand data and are limited to aggregate industry data.²

The contributions of this paper are fourfold. First, we analyze the effect of both hospital concentration and insurer concentration on prices in a period just after the introduction of price competition in the Netherlands. This provides valuable insights into the workings of an “emerging market” where market parties have little or no prior experience with bargaining and selective contracting. We expect that Dutch market parties will exhibit a steep learning curve as they adjust their terms over time and become more astute at balancing the trade-offs in their efforts to improve their bargaining strength. As time progresses and more data become available, it will be possible to model the convergence from short-run price dynamics to a long-run equilibrium.

Second, we cover a market outside the United States. Historically, health care in most countries has been provided through government-owned providers or heavily regulated private providers. The most notable exception to this was the US. Along the lines that Cutler [12] calls, the ‘third wave of reform’, market- and incentive-oriented reforms have been implemented or are being considered in many countries (for example, Germany, UK, Switzerland, Sweden and Australia). However, there is not much empirical evidence on the effects of market reforms outside the United States. As far as we know, the existing literature has an exclusive focus on competition in the US, while we focus on the Netherlands. The institutional design of competition in the Netherlands is different from the United States, so that insurers and hospitals operate under more regulation. In the near future, the competitive segment will most likely be expanded so that our paper provides a starting point for studying the interaction between competition and regulation in an emerging market.

Third, we improve the estimation of both Melnick et al. [29] and the bargaining model based on Brooks et al. [5]. Compared to Melnick et al. [29], we use an exogenous measure of insurers’ concentration and incorporate the effects of buyer and seller concentration in a more symmetric fashion. In the bargaining model, we improve on the estimation method by regressing the ‘relative bargaining share’ instead of the ‘absolute bargaining share’ (thereby correcting for heteroskedasticity) and by employing a Tobit regression rather than OLS (taking into account the censored nature of the dependent variable).

Finally, we use a dataset that contains information about both contracted prices (i.e. the actual transaction prices) and the list prices over a number of products for a period of 2 years. To the best of our knowledge, all other papers in the literature have either list prices or transaction prices, but not both.

The paper is organized as follows. In Sect. “Price competition between hospitals in the Netherlands”, we give some background on the introduction of price competition between hospitals in the Netherlands. We continue in Sect. “Literature review” with an overview of the literature on the estimation of market power and bilateral negotiations. In Sect. “The model”, we develop our econometric models. We give a description of our dataset in Sect. “Data”. In Sect. “Estimation results”, we give the results of the estimated econometric models. Section “Discussion” contains a discussion of methods and possible extensions. Results of estimations are summarized in the appendix.

Price competition between hospitals in the Netherlands

The introduction of competition in the Dutch health care sector has been long debated. The Dutch government plans a step-by-step introduction of price competition between hospitals. For a comprehensive overview of the reform process, we refer to Helderman et al. [25].

The Dutch reforms are based on a mandatory health insurance system for all Dutch citizens combined with a model of managed competition for hospitals [16]. The health insurance package includes primary medical care and hospital care, but excludes dental and nursing home care. It involves virtually no co-payments and an optional deductible (between 0 and 500 Euro). Supplementary insurance policies (e.g. for dental and cosmetic care) are optionally available. The mandatory insurance for the basic benefits package aims at ensuring risk solidarity and universal health care access for all Dutch citizens.

The mandatory insurance is complemented by a mandatory acceptance by health insurers of all enrollees, without room for risk selection (i.e. a refusal to insure) or price discrimination. A sophisticated ex-ante risk adjustment system is in place to compensate insurance companies for actuarially predictable health expenditure differentials induced by socio-demographic factors, such as age, sex, income, location and prior health care consumption (chronic pharmaceutical dependencies and prior hospitalization). The ex-ante risk adjustment system levels the playing field for health insurers by enabling price competition on the premium rates (see [34]).

However, there is also an ex-post risk-sharing scheme in place, consisting of both a proportional risk-sharing component and an outlier risk-sharing component (see [40]). These ex-post compensations between profit- and loss-making health insurers partly dilute the ex-ante incentives for vigorous price negotiations with health care providers (for more details, see [30]).

The basic idea behind these reforms is that health insurers will start ‘managing competition’ between health care providers by negotiating price discounts from a selectively contracted network of health care providers. In this way, insurers can compete for enrollees by offering health plans that are both attractively priced, but still give a reasonably broad choice of health care providers.

Two reports by the Dutch Healthcare Authority [9] and [10]) monitoring the competitive hospital segment, however, indicated that selective contracting of hospitals has been virtually non-existent. Rather, most insurers have been contracting almost every hospital. The main reasons for this lack of selective contracting are lack of transparency of quality information, as well as the legal constraints on using co-payments for out-of-network health care. This makes patient steering to preferred providers more difficult because the benefits (higher quality) are not transparent and there is little financial downside for out-of-network care. Other characteristic features of managed care in the United States, such as utilization review by health insurers, are also still in their infancy in the Dutch health care system.

Annual health care expenditures (excluding long-term care) in the Netherlands for 2005 and 2006 amounted to approximately €2,000 per capita, half of which were funded by payroll taxes, the other half being funded by the insurance premiums. Almost half of the health care expenditures was on hospital care. Because of the large share of hospital care in total health care expenditure, the likely effects of the introduced competition on prices in the hospital care contracting market are of great interests to policy makers.

In this paper, we will study the impact of both hospital and insurer concentration and market shares on Dutch hospital prices in the competitive segment. Since measures of concentration or market share require a market definition, we have to define the relevant market (as in anti-trust cases). The relevant market consists of a geographic dimension and a product dimension. We delineate the markets for contracting the provision of elective hospital care using the Elzinga–Hogarty test on patient flow data.³

The resulting local markets have a rather strong seller (hospital) concentration with an average HHI of 2,350. The buyer (insurer) concentration on these local markets is even stronger: all HHIs on the buyers’ side are above 2,000, with an average of 4,500. These high measures of buyer concentration can be explained by the historically assigned regional legal monopoly positions of the local health plans.

The relevant product market can be defined as the set of all hospital products in the competitive segment. As in most OECD countries, a product and treatment classification is in place in the Netherlands. In 2005, a system of diagnoses treatment combinations (“DBC”) was introduced as a simultaneous product and treatment structure. A DBC ‘includes all activities and services and treatments associated with a patients demand for care from initial consultation or examination to final check-up’ [34]. In total, approximately 100,000 DBCs have been developed, of which approximately 33,000 DBCs are used in practice.⁴

The competitive segment is restricted to uncomplicated, elective care and consists of the more standardized and frequently performed (surgical) procedures such as cataract surgery, knee and hip replacements, incontinence surgery and diabetes care. It consists of 1,376 different DBCs, which cover 15 (out of 24) different medical specialties and belong to 28 different diagnoses. See Fig. 1 in the appendix for an overview of the most frequently performed procedures in the competitive segment. The composition of the initial version of the competitive segment was partly based on political reasons such as covering as many medical specialties as possible and total expenditures not exceeding 10%. For a more detailed list of the included procedures, we refer to Dutch Healthcare Authority [9] and [10].

Fig. 1

Most frequently performed procedures in the competitive segment

The revenue of the competitive segment is approximately 1.1 billion euros, which is about 8% of the total expenses on hospital care in the Netherlands. To eliminate the revenue associated with the competitive segment from the prospective budgets for the regulated segment, the Dutch Healthcare Authority estimated average unit costs for the products, based on a survey of a group of 12 hospitals and multiplied these average unit costs with the estimated volumes (see further in Sect. “Data”).

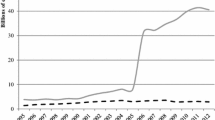
Apart from hospitals, there are also so-called Independent Treatment Centers (ZBCs) active in the market for hospital care. These ZBCs were allowed to enter the market from 1998. In recent years, the proliferation in the number of ZBCs has been in contrast to the steady concentration of hospitals (see Figs. 2, 3).

Fig. 2

Total number of ZBC’s

Fig. 3

Total number of hospitals

The total revenue of the ZBCs was estimated to be 2% of the competitive segment in 2006 [11]. Most ZBCs were established as subsidiary branches of hospitals (often on the same premises), allowing the latter to circumvent the rationing regime in the regulated segment by shifting production toward ZBCs (which are exempt from the budget regime). However, for the competitive segment, there is no government-imposed volume-rationing and the incentive to shift production toward ZBCs is absent. Effectively, ZBCs therefore exercise little competitive constraint on the prices of the incumbent hospitals in the competitive segment. Furthermore, we only possess price from ZBCs in 2006. In the remainder of this paper, we will exclude ZBCs from our analysis.

Literature review

There is a large amount of literature on the impact of buyer and seller concentration in health care markets. For good reviews, see e.g. Dranove and Satterthwaite [15] and Gaynor and Vogt [23]. Most of the previous literature is concerned with the exercise of market power on only one side of the market: either insurers’ monopsony power or hospitals’ monopoly power. Most studies follow the structure–conduct–performance (SCP) tradition and estimate a reduced form model in which price or margins are regressed on control variables (mostly cost and demand shifters) and a measure of either buyer or seller concentration.

However, to identify the effects of buyer (seller) concentration with monopsony (monopoly) power, specification of an underlying structural model is required. The new empirical industrial organisation (NEIO) models provide such accurate and direct measures of market power, but the high standards imposed on the available data and estimation methods can often prevent clean tests of these models. For example, in competitive markets, price is exogenous, but in markets with monopoly (monospony) power, price is endogenous and has to be instrumented for, e.g. with demand and cost shifters. Furthermore, the proper identification of the conduct parameter related to monopoly (monopsony) power requires a demand (supply) rotator such as the price of an outside good (or factor prices in outside industries) in order to instrument for the marginal demand (supply) appearing in the pricing equation [4]. These requirements are often not fulfilled by the data used in such studies.

There is a large literature on the unilateral impact of buyer concentration on hospital prices. Examples are Feldman and Greenberg [18], Adamache and Sloan [1], Frech [20], and Foreman et al. [19]. These studies analyze the relationship between the market share of Blue Cross/Blue Shield and the hospital discounts from list prices. All find positive relationships between Blue Cross/Blue Shield share and provider discounts. However, Staten et al. [36, 37] find no significant relationship between these variables. Melnick et al. [29] attribute the insignificant results of Staten et al. [36, 37] to the relative inexperience with selective contracting of the newly formed Blue Cross Indiana PPO. Using more recent data from the same market, they find a significant negative relation between prices and insurers’ market share.

As alluded to above, the negative relation between prices and buyers’ concentration as measured by insurers market share is not necessarily an indication of monopsony power [23]. Issues such as the market definition on the buyer’s side, endogeneity of insurers’ market share with price and the proper measurement of transaction prices (as opposed to list prices) have affected most studies to date. In summary, the bulk of empirical work has been consistent with the exercise of monopsony power by health insurers but has not tested the monopsony power hypothesis directly.

There are also a large number of studies assessing the unilateral impact of seller concentration on hospital prices. Examples are Noether [31], Melnick et al. [29], Dranove et al. [13], Lynk [27], Connor et al. [8], Simpson and Shin [35], Dranove and Ludwick [14], Keeler et al. [26], and Lynk and Neumann [28]. These studies regress hospital price on measure of seller concentration (usually a Herfindahl–Hirschmann index) and other control variables. The vast majority of these studies find that hospital concentration increases prices. Again, as with the impact of buyer concentration, the measured positive impact of seller concentration on prices has not directly been identified with the exercise of monopoly power by hospitals.

Only Staten et al. [36], Melnick et al. [29] and Gaynor et al. [21] analyze the bilateral exercise of market power. However, the first study focuses on the concentration of insurers and, as discussed earlier, has some indeterminate results. Melnick et al. [29] focuses on the concentration of hospitals. In both cases, the measurement of the concentration of the other side is not very precise. For example, Melnick et al. [29] use the Blue Cross market share of the hospital’s inpatient days as a measure of insurer concentration, rather than the share of Blue Cross in the entire local market. This measure is therefore endogenous with hospital price. Gaynor et al. [21] analyze how both hospitals’ and insurers’ concentrations, measured by HHIs on both sides of the market, are related to the prices. Their results indicate that increasing concentration of insurers significantly decreases price, while estimation of the effect of hospital concentration on price does not give any significant results.

Another stream of literature directly models the bargaining process between insurers and hospitals. Brooks et al. [5] consider a potential gain from bargaining divided by insurers and hospitals and identifies the exercises of bargaining power by both sides. They specify and estimate a cooperative Nash-bargaining model of hospital–insurer bargaining over prices. Their model is inspired by Svejnar [38], a generalization of the Harsanyi–Nash–Zeuthen bargaining model. Brooks et al. report that hospitals have relatively more bargaining power (as indicated by the magnitude of the estimated bargaining parameter) than insurers. They did not include a measure of insurers’ concentration, although they find that a greater enrollment of the population in HMOs has a positive impact on hospital bargaining power with respect to fee for service plans. There are some methodological issues with the study, however, as the authors do not take into account the censored nature of their dependent variable, raising concerns for the consistency of their estimation results. Furthermore, the model of Brooks et al. [5] is one of bilateral monopoly, rather than a bilateral oligopoly. To the best of our knowledge, for markets with bilateral market power, there are no well-specified generalizations of the Nash-bargaining model for the bilateral monopoly. This potentially reduces the applicability of the model of Brooks et al. [5] to real-word health care markets. Nevertheless, the intuitive results of their paper are very appealing.

Most of the studies cited earlier were either cross-sectional or panel studies of industry-level data. Brooks et al. [5] and Gaynor et al. [21] use patient-level data. In the more recent literature, consumer-choice models have also been employed to investigate the impact of concentration on prices. Examples are Town and Vistnes [39] and Capps et al. [6]. Town and Vistnes equate a hospital’s bargaining with the value a hospital adds to a network and find a positive impact of bargaining power on prices. Capps et al. [6] model a similar situation and measure each hospital’s market power by an aggregation of consumer’s willingness to pay to the hospital. They find a similar positive link between willingness to pay and prices. Such consumer-level studies can be used to directly simulate the impact on prices following hospital mergers, making these models relevant in anti-trust cases.

The model

SCP-model

SCP-models are based on Chamberlin’s [7] monopolistic competition theory and seek to explain firm performance through market structure conditions, such as number and size distribution of firms and entry condition in the market. The SCP-hypothesis explains the performance of firms by the structure of the market and is based on the premise that a more concentrated market indicates higher market power and consequently higher profits for all firms in the market.

The basic SCP-model can be formulated as follows (where i is a product, firm, or time index):

$$ P_{i} = f(M_{i} ,D_{i} ,C_{i} ) $$

(1)

where P is a performance measure, M a (set of) market structure variables, D a (set of) demand variables, and C a set of firm/product-specific control variables. In the health economics literature, D variables are often referred as demand shifters and C variables are referred as cost shifters.

A number of traditional concentration ratios have been used as market structure indices. The most common indicator is the Herfindahl–Hirschman index, ${\text{HHI}} = \sum\nolimits_{i = 1}^{n} {MS_{i}^{2} }$. It is determined as a sum of squared market shares. HHI gives extra weight to those hospitals that dominate the market. In a Cournot model for homogenous products, the HHI is related to the industry averaged price–cost margin and buyer demand elasticity. In SCP-models, price–cost margins are taken from the data and conduct is already determined (by the assumption of Cournot behavior), so that the coefficient of the HHI coefficient measures the buyer demand elasticity. In structural models aimed at measuring market power directly, both price–cost margins and conduct (i.e. the exercise of market power) are to be estimated. We lack the necessary data to directly estimate the conduct parameter, so that the coefficient of HHI can only serve to back up the intuition that higher hospital concentration leads to higher prices.

The main equation to be estimated on the basis of per hospital, per product and per year data is as follows (where h, i, and t index hospitals, insurers, and time, respectively)⁵:

$$ \ln {\frac{{(p_{hit} - c_{h} )}}{{p_{hit} }}} = a + s\ln (M_{hi} ) + d\ln (D_{i} ) + c\ln (C_{h} ) + d \cdot t + \varepsilon_{hit} $$

(2)

where as before M is the market share, D represents the set of variables summarizing demand shifters, and C represents the set of variables summarizing cost shifters. Following the main papers in this stream of literature, we use a log–log transformation of the model to allow for an easier economic interpretation of the coefficients in terms of elasticities: by how much does the price–cost margin increase after a 1% increase in market share?

If we take hospital market share as the only market structure variable M _hi , then the Cournot oligopoly prediction is s = 1. In case of perfect competition, an increase in hospital market share has no impact on performance and s = 0. Therefore, in interpreting the coefficient s, we will focus on its sign and significance rather than its magnitude.⁶

If collusive behavior on the part of sellers exists, then the impact of hospital market share on performance is more than proportional and one would expect s > 1. An intuitive way to test the hypothesis of coordinated market power (i.e. collusion) against the hypothesis of unilateral market power (i.e. bargaining power) would be to include both the HHI and the market share in the regression Eq. 2. If collusion is the dominant driver behind price–cost margins, one would expect this to be picked by the coefficient of the HHI, since even small firms in concentrated market would profit from the collusion. If, on the other hand, firms only exercise their individual market power, one would expect the coefficient of market share to prevail.⁷ For both sides of the market, we therefore include both the HHI and the market share in our model.

However, because the HHI can be interpreted as a weighted average market share (with the weights being equal to the market shares themselves), the simultaneous inclusion of both the HHI and market shares as explanatory variables requires a careful interpretation. While the HHI and market shares are not directly proportional to each other for moderately concentrated markets, they almost coincide for near-monopoly markets. This means that even though the simultaneous inclusion of the HHI and market share does not introduce multicollinearity, the potential nonlinear overlap for highly concentrated markets makes the unilateral and coordinated effects harder to disentangle.

To this effect, we center the market shares with respect to the HHI. After this linear transformation of our data, the coefficient of the centered market share measures the purely unilateral impact (i.e. bargaining power) of an above-average market share on market performance. On the other hand, the net coefficient of the HHI (i.e. the difference of the coefficient of the HHI itself and the coefficient of the centered market share) measures the coordinated impact of the market concentration (e.g. collusion) on the price–cost margin.

We stress that the nonlinear relationship between HHI and market shares necessitates some kind of transformation between coefficients in order to have a clear interpretation of unilateral and coordinated effects. For example, without this centering of the market shares, the unilateral effect is picked up by the net coefficient of market share (i.e. the difference of the coefficients for the market share and the HHI), whereas the coordinated effect would then be identified as the coefficient for the HHI. All our results are robust against such alternative model specifications. We chose to center the market shares because the main focus of our paper is on unilateral bargaining power.

Extension of the SCP-model to estimate effects of demand-side and supply-side concentration

In this section, we describe the model that can help to identify the effects of both buyer and seller concentration on the price of hospital care. We therefore symmetrize Eq. 2 across insurers and hospitals by including measures of concentration in both the insurance market and in the hospital market in the regression Eq. 2 described earlier. The resulting equation is as follows (where h, i, and t index hospitals, insurers, and time, respectively):

$$ \ln {\frac{{(p_{hit} - c_{h} )}}{{p_{hit} }}} = a + s\ln (M_{h} ) + b\ln (M_{i} ) + d\ln (D_{i} ) + c\ln (C_{h} ) + d \cdot t + \varepsilon_{hit} . $$

(3)

Here, the variables M _h and M _i define measures of the market structure of the hospitals and insurers in the relevant hospital care market. D _i again is a (set of) demand shifters (ranging over all insurers), and C _h is a set of hospital product-specific control variables (cost shifters).

Our prior hypotheses are that a higher concentration or market share of hospitals increases price markup, while insurer concentration or market share decreases the markup on prices for hospital care, i.e. s > 0 and d < 0. As in the previous section, we include both the HHI and the centered market shares as measures of concentration.

Following Gaynor et al. [21], we like to stress that there is no theoretical consensus on what should be a structural model for a bilateral oligopoly. Therefore, these kinds of models are based on the intuition that a higher concentration of hospitals (insurers) would lead to higher (lower) prices.

Hospital–insurer bargaining model

The Svejnar’s [38] generalization of the Harsanyi–Nash–Zeuthen bargaining model implies that the potential gain from bargaining is divided among the players so as to maximize the following expression:

$$ V = (U_{i} - \bar{U}_{i} )^{\gamma (Z)} (U_{j} - \bar{U}_{j} )^{1 - \gamma (Z)} $$

(4)

where U _i and U _j define utilities from bargaining to players i and j, respectively. Point $(\bar{U}_{i} ,\bar{U}_{j} )$ is a disagreement outcome, i.e. utilities for both players if an agreement is not reached. γ(Z) represents bargaining power of the player as a function of a set of variables Z, which reflects the set of exogenous characteristics such as market structure.

Brooks et al. [5] discussed an application of this model to the situation of hospital–insurer bargaining. In their setup, the hospital and insurer bargain over a discount from the hospital list price and arrive at a mutually agreed transaction price. Both the hospital and the insurer are assumed to be profit maximizers. The bargaining outcome is the transaction price that maximizes

$$ V = (\Uppi_{H} - \bar{\Uppi }_{H} )^{\gamma } (\Uppi_{I} - \bar{\Uppi }_{I} )^{(1 - \gamma )} $$

(5)

where $\bar{\Uppi }_{H}$ and $\bar{\Uppi }_{I}$ are the hospital and insurer disagreement profit levels, respectively, and $(\Uppi_{H} - \bar{\Uppi }_{H} )$ and $(\Uppi_{I} - \bar{\Uppi }_{I} )$ are their corresponding net gains from bargaining.

The net profit (gain) of the insurer can be written:

$$ (\Uppi_{I} - \bar{\Uppi }_{I} ) = (R - K - PN) - (R - K - P_{T} N) $$

(6)

where R is the insurer revenue, K is its cost of production, P is the contracted price, N is the number of patients insured by this insurance company and P _T is the price the insurer must pay for an episode of inpatient care if the insurer has no bargaining power.⁸ In our case, we assume that this monopoly price is equal to the list price.

The net gain of the hospital can be written:

$$ \Uppi_{H} - \bar{\Uppi }_{H} = [N(P - C)] - [N(P_{L} - C)] $$

(7)

where C is the average cost per episode of care, P and N are as previously defined, and P _L the minimum price that the hospital would accept to provide a privately insured episode of inpatient care. In our case, this monopsony price is equal to the average unit cost.

Substituting Eqs. 6 and 7 into Eq. 5 and maximizing the resulting equation with respect to P yields:

$$ P = \gamma P_{T} + (1 - \gamma )P_{L}. $$

(8)

From this, we see that the negotiated price is a weighted combination of the monopoly and monopsony prices, with the bargaining power as the weight. We can solve this equation for the bargaining power:

$$ \gamma = {\frac{{P - P_{L} }}{{P_{T} - P_{L} }}}. $$

(9)

Note that P _T  − P _L is the potential absolute gain (in euro’s) from bargaining to be divided between the hospital and the insurer, and P − P _L is the margin gained by the hospital. The measure of relative bargaining share, γ, is the share of the potential gain that a hospital keeps as a result of bargaining. If γ equals one, the hospital has complete bargaining power. On the other hand, if γ equals zero, the insurer has complete bargaining power and is able to extract a maximum discount from the hospital.

To explore how bargaining power is influenced by observable exogenous characteristics Z, we can parameterize γ:

$$ {\frac{{P - P_{L} }}{{P_{T} - P_{L} }}} = (\alpha + \beta Z). $$

(10)

If β equals zero, then α equals γ. In this case, bargaining power does not vary with Z. When γ is zero, perfect competition exists (insurers are able to extract all rents). When γ is one, the hospital uses monopoly pricing (suppliers are able to extract all rents). The Nash-bargaining solution is represented by a γ of 0.5.

The model Eq. 10 resembles the model of Brooks et al. [5]. However, they estimated the absolute gain from bargaining rather than the relative gain from bargaining, thereby introducing heteroskedasticity, since a larger hospital with average bargaining power will have both a higher absolute gain and a higher margin. Moreover, the estimation of the empirical counterparts to Eqs. 8 and 9 require data on contracted prices P, estimates of P _L and P _T , and data on exogenous factors, Z, that are theoretically related to the bargaining power underlying each transaction. Since the bargaining power has to lie within the unit interval, ordinary least squares is an inconsistent estimation method and censored regression techniques (such as a Tobit regression) have to be employed.

For the empirical estimation of the model described by Eq. 10, we use the same covariates as in the estimation of Eq. 3:

$$ {\frac{{(p_{hit} - c_{h} )}}{{(l_{ht} - c_{h} )}}} = a + s\ln (M_{h} ) + b\ln (M_{i} ) + d\ln (D_{i} ) + c\ln (C_{h} ) + d \cdot t + \varepsilon_{hit} $$

(11)

Here, we have denoted the list price with l _ht .⁹

Data

Data sources

In this section, we describe the various data sources that we employed for our estimations. Table 1 shows the different sources.

Table 1 Data sources that were employed for estimations

Per DBC, we have three price-related components: the average total costs, the contracted price, and the list price (i.e. the price that uninsured patients and patients from non-contracted insurers have to pay). We also have estimates of the associated volumes per DBC.

Because of the administrative difficulties associated with the newly introduced DBC-system, many hospitals were not yet able to calculate their own average total costs. We therefore used cost data from a sample of 12 so-called front-runner hospitals to estimate the average cost per DBC.¹⁰

The DBC-volumes in 2004 for the 12 “front-runner” hospitals were used to translate the number of admissions in 2004 (an administrative measure used in the previous registration system) into estimates for the DBC-volumes in 2005. This translation is done using a three-step multiplicative imputation procedure. First, we know per insurer–hospital pair, the number of days of stay in the regulated segment as well as the total number of days of stay per hospital in the regulated segment. This allows us to compute for each hospital the market share of each insurer in the number of days of stay in the regulated segment. Second, we have for each hospital–diagnosis pair the number of inpatient and initial outpatient admissions in the competitive segment. Since each DBC can by law contain only one inpatient admission or one initial outpatient admission per episode, we can extrapolate the relation between admissions and DBCs for the 12 front-runner hospitals to obtain estimates of volumes per hospital–DBC pair for all remaining hospitals. Third, we multiply these volumes by the hospital–insurer market shares to obtain estimates of volumes per hospital–insurer–DBC combination. We currently do not possess the actually realized DBC-volumes of 2005 or 2006 for hospitals that did not take part in the “front-runner” data collection.

Contracted prices were submitted by health insurers. Some smaller insurers did not or could not supply all their contracted prices. Since it is hard to distinguish between DBCs that were not contracted at all and contracts that were closed but not submitted, we cannot make definite statements about the coverage of our database. However, from background interviews with hospitals and health insurers [9], we learned that in 2005 most insurers contracted almost every hospital for their entire range of product. As the 10 largest insurers submitted approximately 95% of their contracted prices, we estimate to have about 75% of all contract prices in our database. Virtually, all hospitals complied with the mandatory supply of list prices to Dutch Healthcare Authority. Hospitals are also obliged to post these list prices on publicly accessible places such as in waiting rooms or on their website.

In principle, average total costs are expected to be lower than contracted prices, which in turn should lie below the list prices. However, in our database, we observe all six possible permutations from the expected pattern. Contracting below average unit costs (4.5% of our sample) can occur because hospitals offer cost-heterogeneous but medically related DBC-packages for a single-price (e.g. all DBCs related to a single diagnosis). Above list price contracting (9.1% of all observations) also occur, possibly because insurers with a small but non-negligible revenue share might not have enough bargaining power to get much of a reduction from the list price. However, they still might want to contract the hospital to avoid the expensive administrative task of processing insurance claims from individual consumers. These extra administrative costs might induce a willingness to pay toward the hospital that lies slightly above the list price. Other explanations for such odd patterns in the price data might be administrative difficulties with the relatively new DBC-system, and the inexperience in the bargaining process.

We treat these data problems by performing a multivariate outlier analysis, along the lines of Hadi [24]. Furthermore, for the remaining observations with transaction price below cost or above the list price, we use the following censoring procedure. When price is below cost, we conclude that the hospital has no bargaining power. When price is above the list price, including the rather bewildering sequence of list price < contracted price < average unit costs, we conclude that the hospital has all the bargaining power. This is equal to the treatment in Table 1 of Brooks et al. [5]. Finally, we aggregate the price–cost margins and bargaining share across all hospital products to an overall price–cost margin and bargaining. The level of analysis is therefore all 1,235 unique hospital–insurers pairs for a period of 2 years.

Market concentration and market shares

In the near future, as the DBC-system will overcome the early administrative difficulties, more complete micro-level data will become available, including average unit costs from all hospitals and zipcode locations of patients. However, since our current dataset does not contain such micro-level data, we were unable to determine the relevant product and geographic market from first principles.

On behalf of the Dutch Ministry of Health, a private company (Prismant) [32] performed such a market analysis based on micro-level data from the previous medical registration system. There are two important dimensions for the relevant market: the product market definition and the geographic market definition. Prismant distinguishes the following product markets for hospital care:

• Acute care versus elective care

• Inpatient care versus outpatient care

• Uncomplicated care versus complicated care.

The competitive segment in 2005 is restricted to uncomplicated, elective care.

We used published market share data based on patient flows (Elzinga–Hogarty (EH) test [32]).¹¹ This test takes a geographic market to be the area in which most citizens consume locally produced healthcare, and where locally produced healthcare is also mostly consumed by local citizens. The determination of geographic market by the EH-test has been subject to a lot of research and debate. For an overview of the method and the debate, we refer to Gaynor and Vogt [22] and to the FTC/DOJ report [17].

The results from the Prismant analysis include for every hospital in our database a list of hospitals that are in the same geographic market, and for all these hospitals, their market share in the relevant product market of uncomplicated, elective care. The resulting market shares have been used to compute the Herfindahl–Hirschman Index of market concentration for each geographic hospital market.

From another private data source (Vektis 2004), we obtain the local market shares of health insurers. We combine these data with the distribution of contracted health care per hospital over the various health insurers, which are obtained from a database by CTZ. This dataset contains the number of nursing days per hospital each insurer bought in the regulated segment.

To avoid issues of endogeneity in our estimation, we use the market shares of insurers per hospital in the regulated segment (where prices are fixed) as instruments for the relative shares of insurers per hospital in the competitive segment (where prices are negotiable). From these exogenous measures, we computed the relative shares of insurers in the estimated DBC-volumes obtained from the first data source in Table 1, and subsequently the HHI of insurers within the geographic hospital market.

In our models, we simultaneously include the HHI and the market share of hospitals and insurers. To cleanly separate the unilateral and the coordinated effect of market shares on prices, we first center the market shares toward a zero mean by subtracting the HHI.

All in all, we have the following variable indicating market concentration and market share:

• the HHI of hospitals in the relevant market

• the HHI of insurers in the relevant market

• the centered market share of a hospital in the relevant market

• the centered market share of an insurer in the relevant market.

Following Melnick et al. [29], we also interact market share with concentration to capture possible diminishing effects of competing firms on a given firms market power. We construct 4 dummy variables that divide the HHI along the levels of 2,000; 3,333; and 5,000.

Control variables

From our basic database, we construct the following demand and cost shifters. To capture demand shifters, we construct indicators for the relative importance of the competitive segment for a specific hospital or insurer. For a hospital, this is calculated as the ratio between the revenue of the competitive segment and the regulated segment. For insurers, this is calculated as the revenue of the insurer in a local hospital market compared to its national turnover. We also include dummies labeling the different geographic areas (provinces), and we finally also include a dummy to capture possible time effects. To avoid the basic dummy variable trap, we use the general hospitals, the province of Zuid-Holland and the year 2005 as the reference groups in the regressions.

As cost shifters, we include the following variables. First, we include dummies for hospital type (general hospitals, tertiary care hospitals, and teaching hospitals). Second, we compute a proxy for casemix of the hospital production. Normally, a casemix index is created by calculating the ratio between (total) expenditures and the number of patients. Since we do not have data on the number of patients in the competitive segment, we first calculated the unit cost of an average DBC as the ratio between the aggregate DBC-expenditures (DBC-volumes priced and average unit cost) and the aggregate DBC-volume and index this variable such that the national average is 100. We also construct size indicators that might capture economies of scale for a specific hospital or insurer. For a hospital, this is calculated as total the revenue of the competitive and regulated segment combined. For insurers, this is calculated as its national total of nursing days.

We log transformed most of our continuous variables (except for the bargaining share, the casemix index, and the importance measures) since preliminary regressions indicated that the residuals of the linear model were characterized by a much skewed distribution.¹² Furthermore, the log–log transformation of our model allows the interpretation of the influence of market concentration on prices in terms of elasticities.

Estimation results

Estimation of the SCP-model

As a performance measure in the SCP-model, we use a price markup derived from the price and cost data as a ratio of list price less estimated costs to list price. See Table 2 that provides an overview of descriptive statistics. The average price–cost margin in our sample was 6.5%. Descriptive statistics of the dependent variables and explanatory variables that have been discussed in Sect. “Market concentration and market shares” are also provided in Table 2.

Table 2 Descriptive statistics

For the estimation of the SCP-model, we regressed price–cost margins on indicators of industry performance and on the set of explanatory variables using OLS regression. The estimation results are summarized in the column Model I of Table 3. The model explains 28% of the variation of the price–cost margin. We rejected the hypothesis that we omitted variables (using the Ramsey’s RESET test).¹³

Table 3 Estimation results

The model also indicates that the concentration measures have the expected signs. Similarly to Melnick et al. [29], the concentration of hospitals (insurers) has a significant positive (negative) impact on the price–cost markup that hospitals are able to charge for their products in the competitive domain. Furthermore, teaching hospitals are able to charge significantly higher price–cost margins than general hospitals, as they get about 14% higher markups than general hospitals. See Table 3.

Interestingly, the estimation of SCP-version of the model suggests that the coefficients for the HHI on the hospital’s and insurer’s market are almost identical to the coefficients for their centered market shares.¹⁴ This means that the net impact of the HHI on either side of the market is not significantly different from zero. As we conjectured in Sect. “The model”, this might indicate that there is no coordinated market power present in our data set. Intuitively, the estimation results suggest that only unilateral market power is being exercised since higher market shares rather than a higher HHI influence the price–cost margins. It would be interesting for future research to construct a structural model that can cleanly distinguish between coordinated and unilateral market power.

Since our results indicate that market structure has only weak (though significant) impact on price–cost margins in the competitive segment of hospital care, the implications for the welfare effects of e.g. hospitals’ or insurers’ mergers are to be interpreted rather carefully. For a merger of 2 out of 5 equally sized hospitals (insurers), we predict a modest 1,5% price increase (decrease), whereas the predicted price–cost difference for a merger of 2 out of 3 equally sized market parties would amount to about 1.8%.

Estimation of the hospital–insurer bargaining model

For estimation of hospital-insurer bargaining model, we constructed a dependent variable denoting the bargaining share of the hospital. It is defined as the relative location of the contracted price on the interval between the estimated average unit costs and the list price for non-insured consumers.¹⁵ In other words, it is determined as a fraction of the total gains from trade between hospitals and insures that goes to hospitals. The average share a hospital gets from the total gains of trade is 47% (see Table 2). This would mean that on average the insurers have slightly more bargaining power, if we can reject the hypothesis that hospitals and insurers reach the Nash-bargaining solution of 0.5 (see Sect. “Hospital–insurer bargaining model” for theoretical background). Following a formal t-test based on our data, we reject the hypothesis that hospitals and insurers reached a Nash-bargaining solution.

It should also be stressed that this dependent variable is limited between 0 and 1 by construction (see Sect. “Data”). This structure of the dependent variable calls for application of limited dependent variable econometric techniques, rather than the ordinary least squares techniques of Brooks et al. [5]. The hospital–insurer bargaining model is estimated using the censored regression Tobit model. We report the estimation results for hospital–insurer bargaining model in the column Model II in Table 3.

From these results, we conclude that a higher concentration of the HHI of insurers leads to a significant increase in the insurer’s bargaining share. This impact of insurer concentration is purely picked up by the insurers HHI, with no significant coefficient for the centered market share. This would suggest that insurers bargain in a somewhat coordinated way with hospitals since a higher HHI on the insurer market leads to a higher bargaining share for the insurers. This finding is consistent with the institutionalized historical practice of collective insurer bargaining in the regulated segment.

For hospitals, however, only the centered market share has a significant coefficient, but with a negative sign. We interpret this at first sight counter-intuitive result as follows. The net coefficient of the hospital HHI (i.e. the difference of the coefficients for the hospital market HHI and the hospital market share) is significantly positive. This would suggest that hospitals also coordinate their bargaining with insurers. However, this coordinated bargaining power is significantly adjusted downward by the hospital’s own market share. This interpretation is consistent with the fact that smaller hospitals profit more from the coordinated bargaining than larger hospitals.

On average, teaching hospitals are able to obtain a better market outcome as they get about 17% more of the bargaining share than general hospitals. But the regression coefficient for the teaching dummy is not significant. This implies that although academic hospitals are able to charge significantly higher prices, they do bargain not significantly better compared to other types of hospitals.

Estimation of idiosyncratic effects in the bargaining process

As Melnick et al. [29] observe based on papers describing the situation in California just after the introduction of competition in hospital care, the market might not be in a long-run equilibrium. This suggests that idiosyncratic effects such as the bargaining skills of the individuals at the negotiating table rather than structural conditions such as the outside options might have a sizeable impact on the market outcomes. However, direct inclusion of fixed effects per hospital and insurer in our model did not improve our initial estimation results (because of the severe reduction in degrees of freedom). To test this hypothesis, we therefore performed ordinary least squares regression of the residuals of our initial regression on hospital- and insurer-specific dummies. Using an ANOVA, we found that various firm-specific dummies were jointly significantly different from zero. See Table 4.

Table 4 Idiosyncratic effects in the residual variance

We find that in the SCP-model approximately 28% of the residual variation can be explained by idiosyncratic effects of the individual hospitals and insurers, 11% by insurer-specific effects and 17% by hospital specific effects.

We also perform an ANOVA on the residuals of our initial regression. See Table 4. We find that approximately 41% of the residual variation of the bargaining model can be explained by idiosyncratic effects, 12% by insurer-specific effects and 29% by hospital specific effects.

Summary of results

The results of the SCP-model presented in the Sect. “Estimation of the SCP-model” imply that the market shares of hospitals (insurers) have a significantly positive (negative) impact on the hospital price–cost margin, i.e. only an organization’s market share matters in terms of price negotiations rather than HHI per se. Furthermore, teaching hospitals are able to charge a significantly higher price–cost margins than general hospitals as they get about 14% higher markups than general hospitals.

The results of the bargaining model presented in the Sect. “Estimation of the hospital–insurer bargaining model” imply a significant negative effect of insurer concentration on the bargaining share, but no significant effect of hospital concentration on the division of the gains from bargaining. The average share a hospital gets from the total gains of trade is 47%. This would mean that on average the insurers have slightly more bargaining power. Academic hospitals again are able to charge significantly higher prices, but they do not significantly better bargain, compared to other types of hospitals.

In summary, we find that a larger supply-side concentration leads to significantly higher price–cost margins for hospitals and that a larger demand-side concentration has a significant downward effect on hospital’s margins in the Netherlands. Moreover, we find that stronger hospital concentration does not lead to a significantly higher bargaining share for hospitals, whereas a larger concentration of insurers does have a significant downward effect on the bargaining share for hospitals. Also in both models, we find a significant impact of idiosyncratic effects on the market outcomes.

Discussion

In this paper, we estimate the impact of concentration and bargaining power on the negotiation results in the first 2 years after the institutional change in the Dutch hospital sector. This is one of the few empirical studies that investigates the bargaining process between insurers and hospitals, just after the introduction of a market-oriented reform.

Since we model the bargaining process just after an institutional change, the data base is not always very good. We do not possess individual hospital data on costs. We cannot make definite statement about the coverage of our database on contracted prices and the data show sometime odd patterns. We have tried to mitigate the effect of these data problems by performing a multivariate outlier analysis and by censoring the data.

As a first model, we use a traditional structure–conduct–performance model (SCP-model) along the lines of Melnick et al. [29] for estimation of the effects of buyer and seller concentration on price markups. Second, we model the interaction between hospitals and insurers in the context of a generalized bargaining model [5].

We realize the general problem of endogeneity that arises when estimating SCP-models. However, we partly overcome this limitation and improve the estimation by instrumenting market shares of hospitals and insurers in the regression equations estimated for both models. In particular, we instrument market shares of hospitals by lagged market shares and insurers’ market shares are instrumented by market shares of insurers in the regulated segment.

Further we noticed that in both estimated models, we find a significant impact of idiosyncratic effects on the market outcomes. This is consistent with the fact that the Dutch hospital sector is not yet in a long-run equilibrium. The institutional design of the hospital market in the Netherlands is in many ways similar to that in the United States.¹⁶ There are, however, some important differences. First, US citizens are not obliged to have health insurance, and second, US insurers do not have a mandatory acceptance for any patient at community rating. Finally, almost the entire hospital sector (at least for privately insured patients) has been without direct price regulation for several decades. The stakes in bargaining between insurers and hospitals are therefore currently far greater in the US than in the Netherlands, and US market parties have had more time than their Dutch counterparts to reach a long-run equilibrium.

Since our results indicate that market structure has only weak (though significant) impact on price–cost margins in the competitive segment of hospital care, the implications for the welfare effects of e.g., hospital or insurers mergers are to be interpreted rather carefully.

Our results from the SCP-model seem to indicate that the negotiations were not coordinated between either the hospitals or insurers. However, the bargaining model suggests some coordination between both hospitals and insurers. Our estimated models do not allow us to draw any hard conclusions on the distinction between coordinated and unilateral effects.

We expect to have more and better data in the future. Especially, we expect to gather data on the treatment volumes and patient-level data (some characteristics like sex, age, diagnosis, and zip-code), which will allow us to extend the estimated models along the lines of Capps et al. [6] and Antwi et al. [2]. These approaches will allow us to estimate a structural model of hospital competition. These structural models might also allow us to better distinguish between coordinated and unilateral market power.