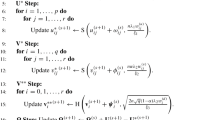Post-processing for Bayesian analysis of reduced rank regression models with orthonormality restrictions

Abstract

Orthonormality constraints are common in reduced rank models. They imply that matrix-variate parameters are given as orthonormal column vectors. However, these orthonormality restrictions do not provide identification for all parameters. For this setup, we show how the remaining identification issue can be handled in a Bayesian analysis via post-processing the sampling output according to an appropriately specified loss function. This extends the possibilities for Bayesian inference in reduced rank regression models with a part of the parameter space restricted to the Stiefel manifold. Besides inference, we also discuss model selection in terms of posterior predictive assessment. We illustrate the proposed approach with a simulation study and an empirical application.

1 Introduction

Bayesian analysis of reduced rank regression models is a well-established tool in economics, psychology, and neuroscience, see Aguilar and West (2000), Chib et al. (2006), Woolley et al. (2010), Edwards (2010), Sadtler et al. (2014), Geweke (1996), and Baştürk et al. (2017). Factor models constitute a special case of reduced rank regression models, see Man and Culpepper (2020), Chan et al. (2018), and Aßmann et al. (2016) for corresponding Bayesian approaches. The same holds for vector error correction models, which are discussed in Koop et al. (2010) from a Bayesian perspective. Eventually, Zellner et al. (2014) relate reduced rank regression models to models with instrumental variables.

Typically, reduced rank regression models require identifying restrictions to come up with interpretable estimation results. In certain setups, this has troublesome consequences, as the choice of ex-ante identifying restrictions can influence model evidence, see Chan et al. (2018). Moreover, the posterior distribution can exhibit multimodality, see Gelman and Rubin (1992), Lopes and West (2004), and Ročková and George (2016). With regard to factor models, which are a prominent class of reduced rank regression models, multimodality can occur if identification is reached by constraining the loading matrix to a positive lower triangular (PLT) matrix a priori as proposed by Geweke and Zhou (1996). More generally, if the constraints are imposed on particular elements of the loading matrix, inference results may depend on the ordering of the variables. This is likewise observed by Carvalho et al. (2008). Altogether, ex-ante identification, which is achieved by constraining the parameter space, may influence inference results for the quantities of interest, i.e., the model parameters and functions of these parameters. Hence, Chan et al. (2018) advise to refrain from this kind of identification. In this line, Aßmann et al. (2016) and Erosheva and Curtis (2017) suggest ex-post approaches to achieve directed inference on factors and loadings.¹ The post-processing algorithm proposed in Aßmann et al. (2016) addresses static and dynamic factor models whose scaling restrictions are formulated in terms of restricted moments of the prior distribution. This approach is hence not suited to handle factor models with orthonormality restrictions. If the restrictions are placed such that they reflect the classical model assumptions of Thurstone (1935), regarding zero-mean unit-scale uncorrelated factors, draws from the posterior distribution produce correlated factors with non-zero mean and non-unit scaling. This also carries over to the posterior factor estimates. As the major contribution of this paper, we provide a modified post-processing algorithm that yields perfectly orthonormal factor estimates. In fact, the modified approach allows for Bayesian inference on factors and loadings corresponding to inference on factors via principal component analysis in a frequentist setup. Furthermore, the approach can be applied not only to static factor models, but also to other reduced rank regression models with orthonormality restrictions. The new post-processing approach proposed in this paper is based on the sampler by Koop et al. (2010) for vector error correction models.

Due to cointegration, vector error correction models also belong to the class of reduced rank models. Cointegration spaces are only identified up to an arbitrary linear combination of the corresponding cointegration vectors. Several authors, e.g., Villani (2005), Kleibergen and van Dijk (1994), and Kleibergen and Paap (2002), suggest to enforce linear identifying restrictions a priori. Enforcing linear restrictions a priori, however, can likewise induce estimation results to depend on the ordering of the variables. To address this issue, several papers, e.g., Strachan (2003), Strachan and van Dijk (2003), and Strachan and Inder (2004), follow an alternative identification strategy related to the classical setup in Johansen (1988, 1991) and provide order-invariant Bayesian estimation approaches. Also, Villani (2006) argues that point estimates based on the method in Strachan (2003) may provide counterintuitive interpretations and proposes an alternative ex-post point estimator for the cointegration space. Further, resulting Bayesian estimation is typically straightforward in terms of Markov chain Monte Carlo (MCMC) techniques. Villani (2005) proposes an MCMC sampler where identification is imposed by means of linear identifying restrictions on the cointegration space implying, via a Cauchy density on the unrestricted elements, a uniform distribution of the entire cointegration space. The resulting ex-post point estimator has the drawback that inference is only feasible for the cointegration space as a whole and not for a specific cointegration vector. Thus, identifying assumptions that permit structural interpretations cannot be incorporated. Finally, Koop et al. (2010) propose an approach that is order-invariant and computationally efficient. In this approach, cointegrating vectors stem from the Stiefel manifold, and Koop et al. (2010) also suggest an MCMC sampling approach that is easy to implement. Chan et al. (2018) adapt this sampling approach to factor models, albeit with a set of identifying restrictions different from the one discussed in the following. Note that in Koop et al. (2010) the identification problem is solved up to an orthogonal transformation. The sampler by Koop et al. (2010) is the starting point for the novel ex-post identification approach in the light of orthonormality restrictions proposed in this paper.

To implement the ex-post approach, we discuss two appropriate loss functions formulated in terms of squared Frobenius norms, either involving orthogonal transformations or orthogonal complements to assess estimation loss when the parameter space is partly restricted to the Stiefel manifold. We assess similarities and differences of the loss functions and derive corresponding post-processing algorithms that fit the model setup based on the MCMC sampling approach of Koop et al. (2010). The post-processing scheme allows to employ different additional identifying assumptions to reach inference for directed factors and loadings, like e.g., Varimax or Quartimax. In the context of vector error correction models, inference is possible for single cointegration vectors and not just the entire cointegration space. The suggested ex-post identification also provides the point estimator of Villani (2006) in terms of a decision-theoretic approach under an appropriately defined loss function. In a further contribution of this paper, we assess the possibility to use posterior predictive assessment for model selection in reduced rank models. For factor models with orthonormality restrictions, Chan et al. (2018) point at possible computational difficulties when using the Savage-Dickey density ratio to determine the number of factors. The same also applies to the calculation of marginal model likelihoods for model selection. Thus, we propose to use a posterior predictive assessment approach for model selection and discuss its performance by means of a simulation study for static factor models. The simulation study confirms the possibility to identify the reduced rank dimensionality correctly.

The paper proceeds as follows. Section 2 states the considered reduced rank regression models and discusses the involved identification issues. Section 3 provides the suggested ex-post approach toward identification in reduced rank regression models and discusses two alternative loss functions. Section 4 evaluates the suggested approach via simulation and numerical experiments. Section 5 provides details regarding the selection of rank order in terms of posterior predictive assessment. Section 6 provides an empirical illustration. Section 7 concludes.

2 Model setup, identification, and estimation

Following Geweke (1996), the reduced rank regression model setup including the vector error correction and the factor model can be stated as

$$\begin{aligned} \underset{(P\times T)}{Y}=\underset{(P\times J)}{\Pi } \underset{(J\times T)}{X}\ + \underset{(P\times Q)}{\Xi } \underset{(Q\times T)}{W}\ + \underset{(P\times T)}{E}, \end{aligned}$$

(1)

where $Y=(y_1,\ldots ,y_T)$ is the $P \times T$ matrix of dependent variables. $E=(e_1,\ldots ,e_T)$ is the corresponding matrix of error terms with $\text {vec}(E)$ following a multivariate normal distribution with mean zero and covariance $I_T\otimes \Sigma$, where $\Sigma$ denotes a $P\times P$ covariance matrix.² Further, W is a $Q\times T$ matrix of explanatory variables with corresponding parameter matrix $\Xi$ of size $P\times Q$. $\Pi X$ incorporates the reduced rank structure of the model, where $\Pi$ denotes a $P\times J$ matrix and X a corresponding $J\times T$ matrix. The vector error correction model, see e.g., Villani (2006), arises when Y corresponds to first differences of observed variables, i.e., $Y=(\Delta y_1,\ldots ,\Delta y_{T})$ with appropriately chosen initial conditions for $y_0, y_{-1},\ldots y_{2-K}$ and corresponding values for $\Delta y_1, \Delta y_0,\ldots ,\Delta y_{1-K}$. Accordingly, we have $X=(y_0,\ldots ,y_{T-1})$ and W summarizing K lagged differences and exogenous variables, i.e., 

$$\begin{aligned} W=\left( \begin{array}{ccc} \Delta y_0 &{} \cdots &{} \Delta y_{T-1} \\ \vdots &{} &{} \vdots \\ \Delta y_{1-K} &{} \cdots &{} \Delta y_{T-K} \\ Z_1 &{} \cdots &{} Z_T \end{array} \right) \quad \text {and} \quad \Xi =(\Phi _1,\ldots ,\Phi _K,\phi ), \end{aligned}$$

where $Z_t$, $t=1\ldots ,T$ denotes the vectors of exogenous variables of dimension $M\times 1$ each. Hence, we have $J=P$ and $Q=KP+M$. A static factor model arises for $X=I_T$, $W=(Z_1,\ldots ,Z_T)$ and $\Xi =\phi$, $J=T$, and $Q=M$.

The reduced rank structure is captured via decomposing $\Pi =\alpha \beta '$ with $\alpha$ denoting a parameter matrix of dimension $P\times R$ and $\beta$ a parameter matrix of dimension $J \times R$, with $R\ll \min \{J,P\}$. In the case of the vector error correction model, $\alpha$ governs the adjustment back to equilibrium and $\beta 'X$ denotes the T vectors of stationary departures from the R long run equilibria, while in the case of the static factor model, $\alpha$ denotes the matrix of factor loadings and $\beta$ the matrix of factors. Then with

$$\begin{aligned} \Theta =(\text {vec}(\alpha )',\text {vec}(\beta )',\text {vec}(\Xi )',\text {vech}(\Sigma )')', \end{aligned}$$

(2)

the resulting likelihood for both models is given as

$$\begin{aligned} \mathcal {L}(Y|\Theta , X,W)= \frac{|\Sigma |^{-\frac{T}{2}}}{(2\pi )^{\frac{TP}{2}}} \exp \left\{ -\frac{1}{2}\text {tr}\left[ \left( Y - \alpha \beta ' X -\Xi W \right) '\Sigma ^{-1}\left( Y - \alpha \beta ' X -\Xi W\right) \right] \right\} . \end{aligned}$$

(3)

For $\Sigma$ and $\Xi$, we choose the commonly used conjugate priors as independent inverse Wishart and multivariate normal distributions with probability densities given as

$$\begin{aligned} \pi (\Sigma )\propto |\Omega _{\Sigma }|^{\frac{\mu _{\Sigma }}{2}} |\Sigma |^{-\frac{\mu _{\Sigma }+P+1}{2}}\exp \left\{ -\frac{1}{2} \text {tr}[\Omega _{\Sigma }\Sigma ^{-1}]\right\} \end{aligned}$$

and

$$\begin{aligned} \pi (\Xi )\propto \exp \left\{ -\frac{1}{2}\text {tr}[(\Xi -\mu _{\Xi }) \Omega _{\Xi }^{-1}(\Xi -\mu _{\Xi })']\right\} . \end{aligned}$$

The prior for $\alpha$ and $\beta$ has to address the identification problem arising in factor and cointegration analysis, as for an invertible matrix D of dimension $R\times R$, we have

$$\begin{aligned} (\alpha D)(\beta ({{}{D^{-1}}})^\prime )'=\alpha DD^{-1}\beta '. \end{aligned}$$

Thus, the likelihood is invariant under this transformation. One part of the implied identification problem is typically addressed by restricting the scaling of $\alpha$ or $\beta$, where restrictions on the scaling of $\beta$ are prominent within the literature, see Villani (2005). We follow Strachan and Inder (2004), Villani (2006), and Koop et al. (2010) and restrict the scaling of $\beta$ by assuming that $\beta '\beta =I_R$, i.e., $\beta$ is a semiorthogonal matrix and therefore has orthonormal column vectors. The corresponding prior distribution is hence defined on the Stiefel manifold.³ Moreover, $\alpha$ and $\beta$ can be replaced by $\alpha ^*=\alpha D$ and $\beta ^* = \beta D$, where D is an orthogonal matrix.⁴ Then D can be represented as $D = E_{D} \cdot \text {diag}(\text {sgn}(l_{1,1}),\text {sgn}(l_{2,2}),\ldots ,\text {sgn}(l_{R,R}))$, where $E_D$ and L result from the QR decomposition $\beta ' = E_DL'$ with $\text {sgn}(\cdot )$ providing the sign of the argument, see e.g., Golub and van Loan (2013). This reduces the number of free elements in $\beta$ by another $R(R-1)/2$. Thus, the number of free elements in $\alpha$ is RP, and the number of free elements in $\beta$ is $RJ-R(R+1)/2$. Koop et al. (2010) suggest to use a prior setup for $\alpha$ and $\beta$ given as

$$\begin{aligned} \pi (\alpha ,\beta |\Sigma )\propto |\Sigma |^{-\frac{R}{2}}\exp \left\{ -\frac{1}{2}\text {tr}\left[ \nu ^{-1}\beta 'C_{\tau }^{-1} \beta \alpha '\Sigma ^{-1}\alpha \right] \right\} \mathcal {I}(\beta '\beta =I_R), \end{aligned}$$

(4)

where $\mathcal {I}(\cdot )$ denotes the indicator matrix. This joint prior distribution corresponds to a marginal matrix angular central Gaussian distribution with parameter $C_{\tau }$ for $\beta$ and a conditional multivariate normal prior for $\alpha$ conditional on $\beta$ with expected value zero and covariance matrix $\nu (\beta 'C_{\tau }^{-1}\beta )^{-1}\otimes \Sigma$ with $\nu$ denoting a shrinkage parameter, see Appendix 1 for further details.⁵ Although this prior distribution for $\alpha$ and $\beta$ identifies the scaling of $\beta$, the so far implied posterior distribution

$$\begin{aligned} p(\Theta |Y,X,W)\propto \mathcal {L}(Y|\Theta ,X,W)\pi (\Xi )\pi (\alpha ,\beta |\Sigma )\pi (\Sigma ), \end{aligned}$$

remains invariant when D is an orthogonal matrix. To formalize, define for any orthogonal $R\times R$ matrix D the transformation

$$\begin{aligned} H(D)\Theta& = (\text {vec}(\alpha D)',\text {vec}(\beta D)',\text {vec}(\Xi )',\text {vech}(\Sigma )')'\nonumber \\&= (\text {vec}(\tilde{\alpha })',\text {vec}(\tilde{\beta } )',\text {vec}(\Xi )',\text {vech}(\Sigma )')'=\tilde{\Theta }, \end{aligned}$$

(5)

with

$$\begin{aligned} H(D) = \left( \begin{array}{cc} (D'\otimes I_{P+J}) &{} 0 \\ 0 &{} I_{P Q+ P(P+1)/2} \\ \end{array} \right) . \end{aligned}$$

(6)

Taking into account that the transformation described in Eq. (5) has no impact on the range of parameters and $d \tilde{\Theta }=|\text {det}(H(D)^{-1})|d\Theta$ with $|\text {det}(H(D)^{-1})|=1$, the marginal likelihood

$$\begin{aligned} \mathcal {M}(Y|X,W)=\int p(Y, \Theta |X,W)d\Theta =\int p(Y, \tilde{\Theta }|X,W)d\tilde{\Theta }, \end{aligned}$$

(7)

is also invariant and thus is the posterior distribution $p(\Theta |Y,X,W)=p(H(D)\Theta |Y,X,W)$. The invariance arises hence for a model setup conditional on $\beta$, in contrast to the marginalized model setup used in Aßmann et al. (2016) to assess the invariance.

The considered model setup allows for sampling from the posterior distribution using an MCMC sampler which we call the rotation-invariant sampler in the following, as it ensures that $\beta$ has zero-mean uncorrelated unit-length column vectors, but does not impose an orientation. Accordingly, we also refer to the obtained samples and the posterior distribution they originate from as rotation-invariant. To facilitate efficient closed form sampling, Koop et al. (2010) discuss a reparametrization using the transformation $A=\alpha (\alpha '\alpha )^{-\frac{1}{2}}$ and $B=\beta (\alpha '\alpha )^{\frac{1}{2}}$ with corresponding inverse functions given as $\alpha =A(B'B)^{\frac{1}{2}}$ and $\beta =B(B'B)^{-\frac{1}{2}}$ implying $\alpha \beta '=AB'$.⁶ As stated in Koop et al. (2010), this transformation yields

$$\begin{aligned} \pi (A,B|\Sigma )\propto |\Sigma |^{-\frac{R}{2}}\exp \left\{ -\frac{1}{2}\text {tr}\left[ \nu ^{-1}A'\Sigma ^{-1}AB'C_{\tau }^{-1}B\right] \right\} \mathcal {I}(A'A=I_R). \end{aligned}$$

The considered reparametrization corresponds to $\Theta _{AB}=(\text {vec}(A)',\text {vec}(B)',\text {vec}\,(\Xi )',\text {vech}(\Sigma )')'$ with posterior distribution

$$\begin{aligned} p(\Theta _{AB}|Y,X,W)\propto \mathcal {L}(Y|\Theta _{AB},X,W)\pi (\Xi )\pi (A,B|\Sigma )\pi (\Sigma ). \end{aligned}$$

(8)

Note that the posterior is also invariant when considering the reparametrization in terms of A and B and under any permutation of the P variables in Y, the corresponding rows of each $\alpha$, $\beta$, $\Xi$, and the corresponding rows and columns of $\Sigma$, see also Appendix 1. Following Koop et al. (2010) and considering the reparametrization in terms of A and B, allowing for efficient sampling, yields the following set of full conditional distributions. For the covariance matrix $\Sigma$ we have

$$\begin{aligned} f(\Sigma |Y,X,W,\alpha ,\beta ,\Xi )\propto |\Sigma |^{-\frac{\varphi _{\Sigma }+P+R+1}{2}} \exp \left\{ -\frac{1}{2}\text {tr}[\Psi _{\Sigma }\Sigma ^{-1}]\right\} , \end{aligned}$$

with $\varphi _{\Sigma }=\mu _{\Sigma }+T-1$ and $\Psi _{\Sigma }=\Omega _{\Sigma }+(Y-\alpha \beta ' X-\Xi W)(Y-\alpha \beta ' X-\Xi W)'+\frac{1}{\tau }\alpha \beta 'C_{\tau }^{-1}\beta \alpha '$. For the parameters $\Xi$, the full conditional distribution is given as

$$\begin{aligned} f(\Xi |Y,X,W,\alpha ,\beta ,\Sigma )\propto \exp \left\{ -\frac{1}{2} (\text {vec}(\Xi )-\varphi _{\Xi })'\Psi _{\Xi }^{-1}(\text {vec}(\Xi )-\varphi _{\Xi })\right\} , \end{aligned}$$

where $\Psi _{\Xi }=((WW'\otimes \Sigma ^{-1})+\Omega _{\Xi }^{-1})^{-1}$ and $\varphi _{\Xi }=\Psi _{\Xi }(\text {vec}(\Sigma ^{-1}(Y-\alpha \beta 'X)W')+\Omega _{\Xi }^{-1}\mu _{\Xi })$. For the full conditional of $\alpha$ we have

$$\begin{aligned} f(\alpha |Y,X,W,\beta ,\Xi ,\Sigma )\propto \exp \left\{ -\frac{1}{2} (\text {vec}(\alpha )-\varphi _{\alpha })'\Psi _{\alpha }^{-1}(\text {vec}(\alpha )-\varphi _{\alpha })\right\} , \end{aligned}$$

with $\Psi _{\alpha }=((\beta 'XX' \beta \otimes \Sigma ^{-1})+\frac{1}{\nu }(\beta 'C_{\tau }^{-1}\beta \otimes \Sigma ^{-1}))^{-1}$ and $\varphi _{\alpha }=\Psi _{\alpha }(\text {vec}(\Sigma ^{-1}(Y-\Xi W) X'\beta ))$. This draw of $\alpha$ is then transformed into $A=\alpha (\alpha '\alpha )^{-\frac{1}{2}}$. Given A, we have the full conditional of B as

$$\begin{aligned} f(B|Y,X,W,A,\Xi ,\Sigma )\propto \exp \left\{ -\frac{1}{2}(\text {vec} (B)-\varphi _{B})'\Psi _{B}^{-1}(\text {vec}(B)-\varphi _{B})\right\} , \end{aligned}$$

with $\Psi _{B}=((A'\Sigma ^{-1}A\otimes X'X)+(A'\Sigma ^{-1}A\otimes \frac{1}{\nu }C_{\tau }^{-1}))^{-1}$ and $\varphi _{B}=\Psi _{B}(\text {vec}(X'(Y-\Xi W)\Sigma ^{-1}A))$. The draw of B is then transformed into $\beta =B(B'B)^{-\frac{1}{2}}$. The prior hyperparameters used in estimation and simulation are documented in Table 1.

Table 1 Prior hyperparameter setting

With this sampling algorithm, a posterior sample can be obtained. However, this sample and the involved draws are subject to the identification invariance as described above. This makes estimation and inference feasible merely for quantities not subject to the identification problem, such as $\alpha \beta '$. To obtain estimates and posterior distributions for all quantities, we propose the following post-processing procedure.

3 Solving the identification problem via post-processing

In the following, we outline the post-processing approach for reduced rank models with the parameter space of $\beta$ restricted to the Stiefel manifold. The presentation follows Aßmann et al. (2016), as it is a modification of the approach for factor models involving prior moment restrictions. The modification guarantees that the estimator based on post-processing lies on the Stiefel manifold and hence satisfies the imposed orthonormality restrictions.

A loss function $L({\Theta ^*}, \Theta )$ defines a mapping of the estimators ${\Theta ^*}$ from the set of possible estimators and each of the parameter values $\Theta$ within the parameter space onto the real line. The optimal estimator in terms of minimal expected loss is then defined as

$$\begin{aligned} \hat{{\Theta }}^*=\arg \min _{{\Theta ^*}} \int _{\Theta } L({\Theta ^*},\Theta )p(\Theta |Y,X,W)d\Theta . \end{aligned}$$

To solve the identification problem, we propose to extend the loss function approach in order to discriminate between invariant losses of estimators invoked under the transformation described in Eq. (5) depending on an orthogonal matrix D. The extended loss function then takes the form

$$\begin{aligned} L(\Theta ^*,\Theta )=\min _{D}\{L_D(\Theta ^*,H(D),\Theta )\},\quad \text {s.t. } D^{\prime }D=I_R, \end{aligned}$$

with $L_D(\Theta ^*,H(D),\Theta )$ denoting for given $\Theta ^*$ the loss invoked for any transformation of $\Theta$ as described in Eq. (5).⁷ As this minimization is done for each $\Theta$, the parameter space of $\Theta$ is restricted ex-post via the corresponding first order conditions. Since the integral involved in the expected posterior loss is approximated via Monte Carlo (MC) methods, the corresponding minimization problem takes the form

$$\begin{aligned} {\{\{\hat{D}^{(s)}\}_{s=1}^S,\hat{\Theta }^*\}} = \arg \min _{\{D^{(s)}\}_{s=1}^S,\Theta ^*} \sum _{s=1}^S L_D(\Theta ^*,H(D^{(s)}),\Theta ^{(s)}), \end{aligned}$$

(9)

subject to $\beta ^{*\prime }\beta ^*=I_R$ and $D^{(s)\prime }D^{(s)}=I_R$ for all $s=1,\ldots ,S$, where $\Theta ^{(s)}$, $s=1,\ldots ,S$ denotes a sample from the rotation-invariant posterior distribution. Note that all samples taking the form $\{H(D^{(s)})\Theta ^{(s)}\}_{s=1}^S$ for arbitrary sequences of orthogonal matrices $\{D^{(s)}\}_{s=1}^S$ have the same posterior probability.

Loss functions are typically formulated in terms of squared Frobenius norms given as

$$\begin{aligned} L_D\left( \Theta ^*,H\left( D^{(s)}\right) ,\Theta ^{(s)}\right) =\text {tr} \left[ \mathcal {K}\left( \Theta ^*,H\left( D^{(s)}\right) ,\Theta ^{(s)}\right) \mathcal {K}\left( \Theta ^*,H\left( D^{(s)}\right) ,\Theta ^{(s)}\right) ^{\prime }\right] , \end{aligned}$$

(10)

where $\mathcal {K}(\cdot )$ denotes a function of the involved quantities $\Theta ^*$, $\Theta ^{(s)}$, and $H(D^{(s)})$ for $s=1\ldots ,S$.⁸ A typical choice is the Euclidean norm, which results in our first loss function

$$\begin{aligned} \mathcal {K}_{\text {EOT}}\left( \Theta ^*,H\left( D^{(s)}\right) ,\Theta ^{(s)}\right) =\left( \begin{array}{c} \text {vec}\left( \alpha ^{(s)} D^{(s)}-\alpha ^*\right) \\ \text {vec}\left( \beta ^{(s)}D^{(s)}-\beta ^*\right) \\ \text {vec}\left( \Xi ^{(s)}-\Xi ^*\right) \\ \text {vech}\left( \Sigma ^{(s)}-\Sigma ^{*}\right) \\ \end{array} \right) ^{\prime }, \end{aligned}$$

which involves an orthogonal transformation affecting the directed quantities $\alpha$ and $\beta$ and is hence labelled as EOT. Larsson and Villani (2001) discuss the properties of the Euclidean norm without involving an orthogonal transformation for assessing losses on the Stiefel manifold and suggest the use of a squared Frobenius norm involving orthogonal complements (FOC) of the quantities defined on the Stiefel manifold. This concept is incorporated in our second loss function, which is

$$\begin{aligned} \mathcal {K}_{\text {FOC}}\left( \Theta ^*,H\left( D^{(s)}\right) ,\Theta ^{(s)}\right) =\left( \begin{array}{c} \text {vec}\left( \alpha ^{(s)}D^{(s)}-\alpha ^*\right) \\ \text {vec}\left( \beta ^{*\prime }_{\perp }\beta ^{(s)}D^{(s)}\right) \\ \text {vec}\left( \Xi ^{(s)}-\Xi ^*\right) \\ \text {vech}(\Sigma ^{(s)}-\Sigma ^{*}) \end{array} \right) ^{\prime }, \end{aligned}$$

with $\perp$ denoting the orthogonal complement, i.e., the null space, of the indicated matrix. We will consider both possibilities to assess the loss, illustrate and discuss the strong similarities of the two loss functions in assessing and minimizing expected loss, and point at the implied differences with regard to handling of the orthogonal invariance. For all elements of $\Theta ^*$ not referring to $\beta$, the estimator implied by the defined loss functions takes the form of an arithmetic mean given as

$$\begin{aligned} \overline{H(D)\Theta }=\frac{1}{S}\sum _{s=1}^S H(D^{(s)})\Theta ^{(s)}. \end{aligned}$$

(11)

For $\beta$, however, the elements of $\overline{H(D)\Theta }$ do not fulfill the restriction $\beta ^{*\prime }\beta ^*=I_R$.

This restriction in combination with the considered EOT loss function turns the minimization of the posterior expected loss with regard to $\beta$ into an orthogonal Procrustes problem. The defined EOT loss functions implies

$$\begin{aligned} \hat{\beta }^*_{\text {EOT}} = \arg \min _{\beta ^*} \text {tr} \left[ -{{}{\beta ^*}}' \sum _{s=1}^S \beta ^{(s)}D^{(s)}\right] ,\quad \text {s.t.}\quad \beta ^{*\prime }\beta ^*=I_R. \end{aligned}$$

(12)

Note that the structure of the minimization problem for determining $D^{(s)}$ as arising from Eq. (10) under the EOT loss takes the form

$$\begin{aligned} \arg \min _{D^{(s)}}\text {tr}[(\bar{\Lambda }^{(s)}D^{(s)}-\bar{\Lambda }^*)'(\bar{\Lambda }^{(s)}D^{(s)}-\bar{\Lambda }^*)],\quad \text {s.t.}\quad D^{(s)\prime }D^{(s)}=I_R, \end{aligned}$$

(13)

with $\bar{\Lambda }^*$ denoting the estimator of the stacked matrix $\bar{\Lambda }=(\alpha ',\beta ')'$ and $\bar{\Lambda }^{(s)}$ denoting a draw of $\bar{\Lambda }$ from the rotation-invariant sampler. The post-processing approach as discussed here transforms the output from the rotation-invariant sampler given a fixed point, i.e., the estimator.

In case the loss is assessed in terms of the FOC loss function, the estimator is based on orthogonal complements. Hence, in this loss function, the sequence of the orthogonal transformation matrices $D^{(s)}$, $s=1,\ldots ,S$ is not linked to the corresponding sequence $\beta ^{(s)}$, $s=1,\ldots ,S$. Considering $D^{\prime }=D^{-1}$ and

$$\begin{aligned} \text {vec}(\beta ^{*\prime }_{\perp } \beta D)^{\prime } \text {vec}(\beta ^{*\prime }_{\perp }\beta D)&= \text {tr}\left[ (\beta D)^{\prime } \beta _{\perp }^*\beta _{\perp }^{*\prime }(\beta D)\right] =\text {tr}\left[ D^{\prime }\beta ^{\prime } \beta _{\perp }^*\beta _{\perp }^{*\prime }\beta D\right] \nonumber \\&= \text {tr}\left[ \beta ^{\prime }\beta _{\perp }^*\beta _{\perp }^{*\prime }\beta \right] =\text {tr}\left[ \beta ^{*\prime } \beta _{\perp } \beta _{\perp }^{\prime } \beta ^{*}\right] =\text {tr}\left[ \beta ^{*\prime } (I_R-\beta \beta ^{\prime }) \beta ^{*}\right] , \end{aligned}$$

(14)

see also Larsson and Villani (2001), the minimization problem for $\beta ^*$ in case of the FOC loss function takes the form

$$\begin{aligned} \hat{\beta }_{\text {FOC}}^*=\arg \min _{\beta ^*} \text {tr}\left[ \beta ^{*\prime } \left( \sum _{s=1}^S \beta ^{(s)}_{\perp }\beta ^{(s)\prime }_{\perp } \right) \beta ^*\right] ,\quad \text {s.t.}\quad \beta ^{*\prime }\beta ^*=I_R. \end{aligned}$$

(15)

Since

$$\begin{aligned} \text {tr}\left[ \beta ^{*\prime } \left( \sum _{s=1}^S \beta ^{(s)}_{\perp }\beta ^{(s)\prime }_{\perp } \right) \beta ^*\right] =\text {tr}\left[ \beta ^{*\prime } \left( \sum _{s=1}^S (I_R-\beta ^{(s)}\beta ^{(s)\prime })\right) \beta ^*\right] =RS-\text {tr}\left[ \beta ^{*\prime } \left( \sum _{s=1}^S \beta ^{(s)}\beta ^{(s)\prime } \right) \beta ^*\right] \end{aligned}$$

given the relations stated in Eq. (14), the minimization problem stated in (15) is equivalent to

$$\begin{aligned} \hat{\beta }_{\text {FOC}}^*=\arg \max _{\beta ^*} \text {tr}\left[ \beta ^{*\prime } \left( \sum _{s=1}^S \beta ^{(s)}\beta ^{(s)\prime }\right) \beta ^*\right] ,\quad \text {s.t.}\quad \beta ^{*\prime }\beta ^*=I_R. \end{aligned}$$

(16)

The structure of the minimization problem for determining $D^{(s)}$ as arising from Eq. (10) takes the form

$$\begin{aligned} \arg \min _{D^{(s)}}\text {tr}\left[ (\alpha ^{(s)} D^{(s)}-\alpha ^*)(\alpha ^{(s)}D^{(s)}-\alpha ^*)^{\prime }\right] , \text { s.t. } D^{(s)\prime }D^{(s)}=I_R. \end{aligned}$$

(17)

Given this, the similarities and differences between the two loss functions shall be discussed. The implied estimators for the undirected quantities $\Sigma$ and $\Xi$ are the same. The loss functions, however, have a slightly different approach toward assessing distances on the Stiefel manifold. As pointed out by Larsson and Villani (2001), the Euclidean distance not involving an orthogonal transformation between two P-dimensional vectors is strictly increasing with respect to the angle between them. For instance, the Euclidean and FOC loss functions for $R=1$ are given as $\propto 1-\cos (\eta )$ and $\propto \sin ^2(\eta ),$ respectively, where $\eta \in (0,\pi )$ denotes the angle between the two considered vectors on the Stiefel manifold. While the Euclidean loss function reaches its maximum at $\pi$, the FOC loss function increases between 0 and $\pi /2$ and decreases between $\pi /2$ and $\pi$. Thus, the situation with maximal loss for the Euclidean loss function is in fact the situation where both vectors span the same space.

This setup changes if the Euclidean loss function takes an orthogonal transformation into account, resulting in the EOT loss function. The sequence $D^{(s)}$, $s=1,\ldots ,S$ captures the information about the orientation in the $\alpha ^{(s)}$ and $\beta ^{(s)}$, respectively, thus solving the aforementioned problem in the Euclidean loss function. Consider as a simple example the case $R = 1$, where the orthogonal transformation takes the form $\pm 1$. The corresponding EOT loss function is given as $\propto \min \{1-\cos (\eta ), 1-\cos (\eta -\pi )\}$, which also increases between 0 and $\pi /2$ and decreases between $\pi /2$ and $\pi$, just like the FOC loss function. Note, however, that the FOC loss function deliberately works with quantities in which unwanted orthogonal transformations in the $\beta ^{(s)}$ cancel out, see Eq. (15).⁹ Hence, for arbitrary orthogonal transformations in the $\alpha ^{(s)}$ and $\beta ^{(s)}$, which occur in the sampling process, there is no effect on the estimator for $\beta ^*$ if the FOC loss function is used, but the estimator for $\beta ^*$ is affected by such transformations if the EOT loss function is used. However, in such a situation, the orthogonal transformations are fully captured in the sequence $D^{(s)}$, $s=1,\ldots ,S$. If the FOC loss function is used, an according sequence is also obtained, albeit only based on the $\alpha ^{(s)}$, see Eq. (17). Thus the estimator for $\alpha ^*$ changes under both loss functions for orthogonal transformations in the $\alpha ^{(s)}$ and $\beta ^{(s)}$. To summarize, the FOC loss function is able to provide an estimator for $\beta ^*$ that is entirely unaffected by orthogonal transformations in the draws, whereas the EOT loss function is able to provide estimators for $\alpha ^*$ and $\beta ^*$ that are aligned with each other such that the $D^{(s)}$, $s=1,\ldots ,S$ affect both of them in virtually the same manner.¹⁰

Both in simulation and empirical studies, the obtained estimates for $\alpha ^*$ and $\beta ^*$ undergo a final orthogonal mapping, either onto the parameters used in the simulation, or to satisfy an identification constraint, for instance, a lower triangular form with positive diagonal elements, or according to some criterion, such as Varimax. If the EOT loss function is used, the mapping involves the same orthogonal matrix for $\alpha ^*$ and $\beta ^*$. For the FOC loss function, on the other hand, the information in the $D^{(s)}$, $s=1,\ldots ,S$ affects the initial estimation of $\alpha ^*$, but not that of $\beta ^*$, which is an undirected estimator. In simulation studies, where the parameter values for $\alpha$ and $\beta$ are at hand, this simply means that the orthogonal mappings for $\alpha ^*$ and $\beta ^*$ are distinct. In applications, on the other hand, this is not possible. As the initially obtained estimates for $\alpha ^*$ and $\beta ^*$ are not aligned with each other in the first place, an orthogonal mapping that turns $\alpha ^*$ into a positive lower triangular matrix, see Sect. 2, or results in the Varimax solution for $\alpha ^*$, would yield an arbitrary estimator if applied to $\beta ^*$. If $\beta ^*$ is of interest beyond the mere cointegration space that it spans, it is therefore advisable to align the FOC estimators $\alpha ^*_{FOC}$ and $\beta ^*_{FOC}$ with each other prior to this step. Two approaches to achieve this are described below. As will be shown in the simulation study and the empirical illustration, not only the differences between the estimators for $\alpha ^*$ are negligible, but also those between the estimators for $\beta ^*$. In this sense, this paper points out that the Euclidean norm involving an orthogonal transformation is well suited for estimators defined on the Stiefel manifold. Further, the equivalence of the optimization problems stated in Eqs. (15) and (16) implies that the estimator resulting from the FOC loss function is the posterior mean cointegration space (PMCS) estimator discussed in Villani (2006).

The following paragraphs outline how a solution for the reduced rank regression models can be obtained via sequential algorithms in case of the EOT and FOC loss functions. The post-processing approach as discussed here transforms the output from the rotation-invariant sampler given a fixed point, i.e., the estimator. The algorithms need an initialization with regard to $\Theta ^*$, where we choose the last draw of the rotation-invariant sampler for convenience.

• EOT For the EOT loss function, the algorithm takes the following steps.

  • EOT 1 For given $\Theta ^*$ the minimization problem implied by Eq. (13) resembles the orthogonal Procrustes problem discussed by Kristof (1964) and Schönemann (1966), see also Golub and van Loan (2013). The solution involves the following calculations.

    • EOT 1.1 Define $\Upsilon _{D^{(s)}} = \bar{\Lambda }^{(s)\prime }\bar{\Lambda }^*$.

    • EOT 1.2 Do the singular value decomposition $\Upsilon _{D^{(s)}} = U_{D^{(s)}} M_{D^{(s)}} V_{D^{(s)}}'$, where $U_{D^{(s)}}$ and $V_{D^{(s)}}$ denote the matrix of eigenvectors of $\Upsilon _{D^{(s)}}\Upsilon _{D^{(s)}}'$ and $\Upsilon _{D^{(s)}}'\Upsilon _{D^{(s)}}$, respectively, and $M_{D^{(s)}}$ denotes a diagonal matrix of singular values, which are the square roots of the eigenvalues of $\Upsilon _{D^{(s)}}\Upsilon _{D^{(s)}}'$ and $\Upsilon _{D^{(s)}}'\Upsilon _{D^{(s)}}$. Note that the nonzero eigenvalues of $\Upsilon _{D^{(s)}}\Upsilon _{D^{(s)}}'$ and $\Upsilon _{D^{(s)}}'\Upsilon _{D^{(s)}}$ are identical.

    • EOT 1.3 Obtain the orthogonal transformation matrix as $D^{(s)}=U_{D^{(s)}}V_{D^{(s)}}'$.

      For further details on the derivation of this solution, see Schönemann (1966).

  • EOT 2 Choose $\alpha ^*$, $\Xi ^*$, and $\Sigma ^*$ as implied by Eq. (11). With regard to $\beta ^*$, the minimization problem given in Eq. (12) also takes the form of an orthogonal Procrustes problem, where the solution then involves the following calculations.

    • EOT 2.1 Define $\mathcal {S}_{\beta } = \sum _{s=1}^S \beta ^{(s)}D^{(s)}$.

    • EOT 2.2 Do the singular value decomposition $\mathcal {S}_{\beta } = U_{\beta } M_{\beta } V_{\beta }'$, where $U_{\beta }$ denotes the matrix of the eigenvectors of $\mathcal {S}_{\beta }\mathcal {S}_{\beta }'$, and $V_{\beta }$ denotes the matrix of eigenvectors of $\mathcal {S}_{\beta }'\mathcal {S}_{\beta }$. Further, $M_{\beta }$ denotes a diagonal matrix of singular values, which are the square roots of the eigenvalues of $\mathcal {S}_{\beta }'\mathcal {S}_{\beta }$, which are also the nonzero eigenvalues of $\mathcal {S}_{\beta }\mathcal {S}_{\beta }'$.

  • EOT 2.3 Obtain the semiorthogonal matrix $\beta ^*_{\text {EOT}}=U_{\beta }\mathcal {J}_{\text {EOT}}V_{\beta }'$, where the matrix $\mathcal {J}_{\text {EOT}} = [I_R~ 0_{R \times (P-R)}]'$ selects the R largest eigenvectors of $\mathcal {S}_{\beta }\mathcal {S}_{\beta }'$ based on a corresponding implicit sorting. The information from the $D^{(s)}$, $s=1,\ldots ,S$ matrices contained in $\mathcal {S}_{\beta }$ accordingly rotates the eigenvectors such that $\beta ^*_{\text {EOT}}$ is aligned with $\alpha ^*$.

• FOC For the FOC loss function, the sequential algorithm involves the following steps.

  • FOC 1 For given $\Theta ^*$ the minimization problem implied by Eq. (17) resembles again an orthogonal Procrustes problem but involves only $\alpha ^*$ and $\alpha ^{(s)}$, $s=1,\ldots ,S$. The solution involves the following calculations.

    • FOC 1.1 Define $\tilde{\Upsilon }_{D^{(s)}} = \alpha ^{(s)\prime }\alpha ^*$.

    • FOC 1.2 Do the singular value decomposition $\tilde{\Upsilon }_{D^{(s)}} = \tilde{U}_{D^{(s)}} \tilde{M}_{D^{(s)}} \tilde{V}_{D^{(s)}}'$, where $\tilde{U}_{D^{(s)}}$ and $\tilde{V}_{D^{(s)}}$ denote the matrix of eigenvectors of $\tilde{\Upsilon }_{D^{(s)}}\tilde{\Upsilon }_{D^{(s)}}'$ and $\tilde{\Upsilon }_{D^{(s)}}'\tilde{\Upsilon }_{D^{(s)}}$, respectively, and $\tilde{M}_{D^{(s)}}$ denotes a diagonal matrix of singular values, which are the square roots of the eigenvalues of $\tilde{\Upsilon }_{D^{(s)}}\tilde{\Upsilon }_{D^{(s)}}'$ and $\tilde{\Upsilon }_{D^{(s)}}'\tilde{\Upsilon }_{D^{(s)}}$. Note that the nonzero eigenvalues of $\tilde{\Upsilon }_{D^{(s)}}\tilde{\Upsilon }_{D^{(s)}}'$ and $\tilde{\Upsilon }_{D^{(s)}}'\tilde{\Upsilon }_{D^{(s)}}$ are identical.

    • FOC 1.3 Obtain the orthogonal transformation matrix as $D^{(s)}=\tilde{U}_{D^{(s)}}\tilde{V}_{D^{(s)}}'$.

  • FOC 2 Choose $\alpha ^*$, $\Xi ^*$, and $\Sigma ^*$ as implied by Eq. (11). With regard to $\beta ^*$, the minimization problem under FOC loss given in Eq. (15) is solved by the following calculations, see also Lütkepohl (1996).

    • FOC 2.1 Calculate the orthogonal complement $\beta ^{(s)}_{\perp }$ for each $s=1,\ldots ,S$ as the null space of the involved matrix, i.e., $\beta ^{(s)}_{\perp }=\text {null}(\beta ^{(s)\prime })$ for all $s=1,\ldots ,S$.

    • FOC 2.2 Define $\tilde{\mathcal {S}}_{\beta }=\sum _{s=1}^S \beta ^{(s)}_{\perp }\beta ^{(s)\prime }_{\perp }$. As discussed above, step FOC 2.2 could alternatively be based on the optimization problem stated in Eq. (16). The resulting estimator consists of the eigenvectors corresponding to the R largest eigenvalues of the matrix $\sum _{s=1}^S \beta ^{(s)}\beta ^{(s)\prime }$ and is thus the PMCS estimator of Villani (2006).

    • FOC 2.3 Do the spectral decomposition of $\tilde{\mathcal {S}}_{\beta } = \tilde{V}_{\beta } \tilde{D}_{\beta } \tilde{V}_{\beta }'$, where $\tilde{V}_{\beta }$ denotes the matrix of the eigenvectors and $\tilde{D}_{\beta }$ denotes the diagonal matrix of eigenvalues.

    • FOC 2.4 Obtain the semiorthogonal matrix $\beta ^*_{\text {FOC}}=\tilde{V}_{\beta }\mathcal {J}_{\text {FOC}}$, where the matrix $\mathcal {J}_{\text {FOC}} = [0_{R \times (P-R)}~ I_R]'$ selects the R smallest eigenvectors of $\tilde{\mathcal {S}}_{\beta }$ based on a corresponding implicit sorting.

Note that $\tilde{\mathcal {S}}_{\beta }$ in FOC 2.2 is unaffected by arbitrary orthogonal transformations of the $\beta ^{(s)}$, $s=1,\ldots ,S$. Hence, $\beta ^*_{\text {FOC}}$ is an undirected estimator, whereas $\alpha ^*$ is a directed one. It is possible, however, to obtain an orthogonal mapping that aligns the estimators for $\alpha ^*$ and $\beta ^*_{\text {FOC}}$ with each other with regard to $\Pi ^* = \frac{1}{S}\sum _{s=1}^S\alpha ^{(s)}{{}{\beta ^{(s)}}}'$. The required matrix $D_A$ can be obtained via minimizing the squared Frobenius norm, i.e.,

$$\begin{aligned} D_A = \arg \min _{D} \text {tr}\left[ (\alpha ^*(\beta ^{*}_{\text {FOC}}D)' - \Pi ^*)'(\alpha ^*(\beta ^{*}_{\text {FOC}}D)' - \Pi ^*)\right] , \end{aligned}$$

taking the form of an orthogonal Procrustes problem as well. This approach, however, only provides a directed point estimator for $\tilde{\beta }_{\text {FOC}}^*=\beta _{\text {FOC}}^*D_A$. To allow for inference, the orthogonal transformation matrices $D^{(s)}$, $s=1,\ldots ,S$ from FOC 1.3 can be used to transform the corresponding $\beta ^{(s)}$, $s=1,\ldots ,S$ matrices. This aligns each $\beta ^{(s)}$ with the corresponding $\alpha ^{(s)}$, and hence turns $\beta ^*_{FOC}$ into a directed estimator, as does the matrix $D_A$ if the orthogonal transformation matrices are not applied. The cointegration space remains the same under this transformation, so information on the orientation and on the distribution of $\beta$ is added, while none of the previously contained information is lost.

With regard to convergence of the post-processing algorithms, we have found that for arbitrary initial choices of $\Theta ^*$ taken from the rotation-invariant sampler output, less than ten iterations usually suffice to achieve convergence to a fixed point $\hat{\Theta }^*$ providing the Bayes estimator. Convergence is assumed if the sum of squared deviations between two successive $\hat{\Theta }^*$ does not exceed a predefined threshold value, where we use $10^{-9}$. In case of the EOT loss function, the iterative procedure of the algorithm suggests to use the transformed output of the rotation-invariant sample, i.e., $H(D^{(s)})\Theta ^{(s)}$, as input for the next iteration, thus reducing required computer memory capacities. In this line, De Vito et al. (2021) have found that also a single iteration may result in estimates sufficiently close to the final estimates. The post-processed posterior sample then provides the basis to calculate posterior summary statistics including uncertainty measures allowing for inference. Note that all estimation and simulation routines have been implemented in MATLAB^® and are available from the authors upon request. Within the supplementary material all necessary files to reestimate the empirical illustration are provided in form of a zip-archive.

4 Simulation and numerical experiments

To illustrate the properties of the suggested post-processing approach, we perform a simulation experiment for a vector error correction model. We show that the point estimator under EOT loss and the FOC estimator are extremely close, thus showing the adequacy of the EOT and the FOC loss functions. The results obtained from the simulation experiment are based on the following setup. We simulate $T = 500$ observations following a vector error correction model with $R = 2$ cointegrating vectors for $P = 4$ variables. Moreover, we set $K = 3$. We assume throughout the simulation study $y_0=\ldots =y_{2-K}=0$ and correspondingly $\Delta y_1=y_1$ and $\Delta y_0=\ldots ,\Delta y_{1-K}=0$ as initial conditions for the data generating process (DGP), where parameter values used within the DGP with regard to $\alpha \beta '$ and thus $\alpha$ and $\beta$ are given in the first column of Table 2 and Table 3, respectively. To obtain a sample from the posterior distribution of $\alpha$ and $\beta$, we run the rotation-invariant sampler of Koop et al. (2010) with $S =$20,000 after a burn-in phase of 5,000 iterations. Note that the rotation-invariant sampler ensures that the orthonormality restriction $\beta '\beta =I_R$ holds for each draw.

Table 2 Parameter values and estimates for $\alpha \beta '$

Table 3 Parameter values and estimates for $\alpha$ and $\beta$

Figure 1 illustrates the identification problem by showing the circular shape of the posterior distribution when plotting pairwise parameter trajectories arising from the rotation-invariant sampler of Koop et al. (2010). The $\beta$ matrices are semiorthogonal, so their columns have unit length. An illustration analogous to Fig. 1 could show this in four dimensions only, hence we add Fig. 2, which depicts the distribution of the lengths of the row vectors (upper part) and the column vectors (lower part). Note that the vector lengths are invariant under the transformation described in Eq. (5), and that the distribution of the lengths of the column vectors of $\beta$ is degenerate due to the scale restriction implied by $\beta '\beta =I_R$.

Fig. 1

Distribution of row vectors of $\alpha$ and of $\beta$ without post-processing (first and second row) and with post-processing (third and fourth row)

Fig. 2

Distribution of row vector lengths (top) and column vector lengths (bottom) of $\beta$

Since the quantity $\alpha \beta '$ is invariant under the aforementioned transformation, we can use the output from the rotation-invariant Koop et al. (2010) sampler for inference on this quantity with no post-processing required. The second column of Table 2 shows the point estimates for $\alpha \beta '$ based on the output of the rotation-invariant Koop et al. (2010) sampler, which is quite accurate. Note that in the EOT approach, the estimates for $\alpha$ and $\beta$, and indeed the entire samples from the respective posterior distributions, can be transformed by a single orthogonal matrix to satisfy identifying assumptions. In the FOC approach, this is only possible for $\alpha$, as $\beta$ is an undirected estimator. We can augment the information contained in the $D^{(s)}$ matrices, however, to obtain directed point estimates for $\beta$ and the according distributions, and then proceed in the same way as in the EOT approach. The third column shows the product of the point estimate for $\alpha$ and the transpose of the point estimate of $\beta$. We observe a substantial deviation between this result and the estimate for the invariant quantity $\alpha \beta '$ if the output from the sampler without post-processing is used. This reflects the equally imprecise estimates for $\alpha$ and $\beta$, which are not separately reported, and point out that both, sampling of $\alpha$ and $\beta$ within the rotation-invariant sampler, are sources of the orthogonal invariance. If the output is post-processed, the estimate for the invariant quantity $\alpha \beta '$ stays the same, as can be seen in the fourth column of Table 2. The product of the point estimates for $\alpha$ and $\beta$ under the two considered loss functions FOC and EOT as shown in the last two columns of Table 2, are now almost identical to the invariant estimate. This, in turn, indicates that the estimates after post-processing for $\alpha$ and $\beta$ must be much more precise than if no post-processing is applied. Further, the results obtained for the two alternative loss functions are almost identical. This underlines the conceptual similarities as discussed above. The effects of post-processing the output of the rotation-invariant sampler can also be seen by looking at the shape of the posterior distribution of $\beta$. The lower panels of Fig. 1 indicate that the posterior distributions of the rows are no longer circular. They also allow for proper inference on the elements of $\alpha$ and $\beta$.

The point estimates and highest posterior density intervals (HPDIs) in Table 3 show the results of two different transformations applied to the same output after post-processing in that respect. HPDIs were calculated using the HPDI estimation algorithm according to Chen and Shao (1999), following Chen et al. (2000). In the upper part of Table 3, we choose the transformation that minimizes the Frobenius norm of the distance between the estimates and the parameters $\alpha$ and $\beta$ used to simulate the data.

In the lower part of Table 3, on the other hand, we choose the rotation that minimizes the Frobenius norm of the distance between the EOT estimate and the FOC estimate for $\beta$.¹¹ The resulting point estimates for $\alpha$ and $\beta$ show that estimates obtained under the two alternative loss functions can both be well transformed to match the parameters of the DGP. In fact, the point estimates for the FOC and the EOT approach are very similar. The Frobenius norm of the distance for $\alpha$ is 0.1306 in both cases. The Frobenius norm of the distance for $\beta$ is 0.0172 for the FOC approach and 0.0170 for the EOT approach. More substantial differences can be found for the HPDIs, which are overall slightly narrower for $\alpha$, but wider for $\beta$ in the FOC approach, compared to the EOT approach. This is due to the fact that the FOC approach relies only on the information in $\alpha$ to determine the transformation matrices, which results in reduced variation in the draws of $\alpha$ and increased variation for the draws of $\beta$. Similar results are obtained when mapping the estimates onto the FOC estimate. The resulting Frobenius norms are necessarily identical here. Again, the HPDIs for $\alpha$ are slightly narrower in the FOC approach, and those for $\beta$ are wider.

5 Model selection via posterior predictive assessment

In a Bayesian context, model selection and specification is conceptually straightforward in terms of the marginal model likelihood $\mathcal {M}(Y|X,W)$ stated in Eq. (7), see Chib (1995) and Kass and Raftery (1995). In reduced rank regression models, model selection amounts to specifying the reduced rank dimension, i.e., the number of latent factors or the number of cointegrating vectors on the Stiefel manifold. Evaluating the marginal model likelihood for this type of model, however, involves substantial computational difficulties. Typically, the computation of the marginal model likelihood is based on the full conditional distributions including the corresponding normalizing constants, see Chib (1995) and Chib and Jeliazkov (2001). As the functional form of the involved full conditional distribution for $\beta$ is given as a Bingham-von Mises-Fisher distribution, as discussed by Chikuse (2003), Gupta and Nagar (2000) and Hoff (2009), the integrating constant required for computation of the marginal model likelihood involves Hayakawa polynomials, see Mathai et al. (1995) and Crowther (1975), or the hypergeometric function with matrix argument, see Herz (1955) and Koev and Edelman (2006). However, the analytical calculation is nontrivial and the saddlepoint approximation suggested by Kume et al. (2013), generalizing the work of Butler and Wood (2003) and Kume (2005), does not provide sufficient numerical precision for typical dimensions relevant in application contexts. The same holds for alternative numerical approaches as power posterior sampling, see Friel and Pettitt (2008), as a version of thermodynamic integration closely related to annealed importance sampling, see Neal (2001), bridge sampling, see Meng and Wong (1996), and path sampling, see Gelman and Meng (1998). Chan et al. (2018) report computational difficulties for the Savage-Dickey density ratio as well.

Given the aforementioned difficulties with common model selection approaches, we propose to make use of posterior predictive assessment, see Gelman et al. (1996), to perform model selection with regard to the dimensionality of the reduced rank structure. Note that this approach involves only invariant quantities and thus does not depend on an assumed loss function. For this purpose, a defined fraction of the data Y, e.g., within the range from 1 to 10%, are discarded. Hence, we can partition the data into discarded ($Y^{\text {DIS}}$) and remaining ($Y^{\text {REM}}$) observations, where $O=PT=O_{\text {DIS}}+O_{\text {REM}}$ where $O_{\text {DIS}}$ and $O_{\text {REM}}$ denote the number of discarded and remaining observations, respectively. The partition implies $y^ {\text {DIS}}_t=L_t^{\text {DIS}}y_t$ and $y^ {\text {REM}}_t=L_t^{\text {REM}}y_t$ for all $t=1,\ldots ,T$, where $L_t^{\text {DIS}}$ and $L_t^{\text {REM}}$, $t=1,\ldots ,T$ denote appropriately defined elimination matrices. The discarded observations are then augmented to the parameter vector and subject to sampling within the Gibbs sampling algorithm. Kaufmann and Kugler (2010) provide a similar approach for handling outlying and missing values. Posterior predictive assessment is then based on extending the Gibbs sampling scheme with the full conditional distributions of the discarded observations $Y^{\text {DIS}}$. For the factor model setup, this set of full conditional distributions is directly arising from the likelihood function given in Eq. (3). Since the likelihood in the static factor model setup (F) can be factorized as

$$\begin{aligned} \mathcal {L}_{\text {F}}(Y|\Theta ,X,W)=\prod _{t=1}^T f_{\text {F}}(y_t|\Theta ,Z_t), \end{aligned}$$

the corresponding posterior predictive distribution is given as

$$\begin{aligned} f_{\text {F}}(Y^{\text {DIS}}|Y^{\text {REM}},\Theta ,X,W)=\prod _{t=1}^T f(y_t^{\text {DIS}}|y_t^{\text {REM}},\Theta ,Z_t) \end{aligned}$$

where $f(y_t^{\text {DIS}}|y_t^{\text {REM}},\Theta ,Z_t)$ is given as multivariate normal as implied by multivariate normal distribution theory.

For the vector error correction model (VECM) setup, sampling from the set of full conditional distributions of the discarded observation values is more elaborate. First, the VECM is reformulated as a vector autoregressive model in levels $y_t$, i.e.,

$$\begin{aligned} y_t=(I+\alpha \beta '+ \Phi _1)y_{t-1}+\sum _{k=1}^K(\Phi _{k+1}-\Phi _k)y_{t-k}+e_t, \end{aligned}$$

where $\Phi _{K+1}=0$. The corresponding state space representation has $y_t^{\text {DIS}}=L_t^{\text {DIS}}y_t$ as the measurement equation, whereas the corresponding transition equation is given by

$$\begin{aligned} \tilde{Y}_t=\Gamma \tilde{Y}_{t-1}+\tilde{Z}_t\phi +\tilde{E}_t, \end{aligned}$$

where $\tilde{Y}_t=(y_t, y_{t-1},\ldots ,y_{t-K})'$,

$$\begin{aligned}\Gamma = \begin{pmatrix} I_P+\alpha \beta ' +\Phi _1 &{} \Phi _2-\Phi _1 &{} \Phi _3-\Phi _2 &{} \ldots &{} -\Phi _{K} \\ I_P &{} 0 &{} 0&{} \ldots &{} 0 \\ 0&{} I_P&{} 0 &{} &{}0 \\ \vdots &{} &{}\ddots &{} &{} \vdots \\ 0 &{} \ldots &{}0 &{} I_P&{} 0 \end{pmatrix}, \end{aligned}$$

$\tilde{Y}_{t-1}=(y_{t-1},y_{t-2},\ldots ,y_{t-K-1})'$, $\tilde{Z}_t=(Z_t, 0,\ldots 0)'$, and $\tilde{E}_t=(e_t,0,\ldots ,0)'$. A sample of all discarded values $Y^{\text {DIS}}$ in the VECM context can then be obtained by iteratively sampling from the set of full conditional distributions of $y_t$ for all $y_t$ included in $Y^{\text {DIS}}$. The full conditional distribution of $y_t$ corresponds to the smoothed distribution arising from forward (predicting) and backward (smoothing) recursion of the Kalman filter. The corresponding sample provides the basis for posterior predictive model assessment. Note that the involved predictive distribution (PR) is directly provided by the transition equation, whereas the full conditional distribution (SM) is implied via the backward smoothing recursion. Given the model setup, we have

$$\begin{aligned} f_{\text {VECM}}(y_t|y_1,\ldots ,y_{t-1},y_{t+1},\ldots ,y_T,Z_1,\ldots ,Z_T,\Theta )\propto \prod _{k=0}^K f(y_{t+k}|y_{t+k-1},\ldots ,y_1,Z_1,\ldots ,Z_T,\Theta ), \end{aligned}$$

where $f(y_{t+k}|y_{t+k-1},\ldots ,y_1,Z_1,\ldots ,Z_T,\Theta )$ for $k=0,\ldots ,K$ corresponds to the predictive distribution as implied by the transition equation corresponding to a normal distribution with expected value and covariance matrix given as

$$\begin{aligned} \mu _{y_t}^{\text {PR}}=(I_P+\alpha \beta '+\Phi _1)y_{t-1}+ \sum _{k=1}^K(\Phi _{k+1}-\Phi _k)y_{t-k}\quad \text {and}\quad \Omega _{y_t}^{\text {PR}}=\Sigma . \end{aligned}$$

Hence, the full conditional distribution corresponds to a normal distribution as implied by

$$\begin{aligned} f_{\text {VECM}}(y_t|y_1,\ldots ,y_{t-1},y_{t+1}, \ldots ,y_T,Z_1,\ldots ,Z_T,\Theta )\propto \prod _{k=0}^K \exp \left\{ -\frac{1}{2}(y_{t+k}-\mu _{y_{t+k}}^{\text {PR}})' \Sigma ^{-1}(y_{t+k}-\mu _{y_{t+k}}^{\text {PR}})\right\} . \end{aligned}$$

The corresponding full conditional expectation ($\mu _{y_t}^{\text {SM}}$) and covariance ($\Omega _{y_t}^{\text {SM}}$) are given as $\mu _{y_t}^{\text {SM}}=\Omega _{y_t}^{\text {SM}} \kappa _{y_t}^{\text {SM}}$, where

$$\begin{aligned} \Omega _{y_t}^{\text {SM}}=[\Sigma ^{-1}+(I_P+\alpha \beta '+ \Phi _1)'\Sigma ^{-1}(I_P+\alpha \beta '+\Phi _1)+\sum _{k=2}^{K} (\Phi _k-\Phi _{k-1})'\Sigma ^{-1}(\Phi _k-\Phi _{k-1})]^{-1} \end{aligned}$$

and

$$\begin{aligned} \kappa _{y_t}^{\text {SM}}&= \Sigma ^{-1}\left( (I_P+\alpha \beta '+\Phi _1+\sum _{k=1}^K (\Phi _{k+1}-\Phi _k)y_{t-k-1})\right)\\& \quad + \left( (I_p+\alpha \beta '+\Phi _1)'\Sigma ^{-1}(y_{t+1}-\sum _{k=1}^K (\Phi _{k+1}-\Phi _k)y_{t-k})\right)\\ & \quad + \sum _{k=1}^K \left( (\Phi _{k+1}-\Phi _k)'\Sigma ^{-1} \left( y_{t+k+1}-(I_P+\alpha \beta '+\Phi _1)y_{t+k}-\underset{k'\ne k}{\sum _{k'=1}^K} (\Phi _{k'+1}-\Phi _{k'})y_{t-k'+1}\right) \right) . \end{aligned}$$

Using the observed values as initializations of the discarded values, sampling of the set of discarded values $\{y_{t}^{\text {DIS}}\}_{t=1}^T$ is then possible via iteratively sampling from

$$\begin{aligned} f_{\text {VECM}}(y_t^{\text {DIS}}|y_1^{\text {COM}},\ldots , y_{t-1}^{\text {COM}},y_t^{\text {REM}},y_{t+1}^{\text {COM}}, \ldots ,y_T^{\text {COM}},Z_1,\ldots ,Z_T,\Theta ), \end{aligned}$$

as implied by multivariate normal theory and with $y_t^{\text {COM}}$ denoting, if applicable, the completed vector $y_t$, where the discarded values are replaced by their sampled counterparts.

Given a sample of the discarded values drawn from the posterior predictive distributions, model fit is measured as $SSE=\sum _{s=1}^S \frac{1}{O_{\text {DIS}}}\text {vec}(Y-Y_{\text {COM}}^{(s)})'\text {vec}(Y-Y_{\text {COM}}^{(s)})$, where $Y_{\text {COM}}^{(s)}$ denotes the matrix of completed observations with discarded values replaced by the draws from the posterior predictive distribution at each iteration $s=1,\ldots ,S$.¹² Model selection using posterior predictive assessment does not require a post-processed sample, as the quantities involved in the posterior predictive distribution, i.e., the full conditional distribution of the discarded values, are all invariant quantities.

To highlight the precision of the posterior predictive assessment approach, we vary the number of cross-sections P, the number of observations in time T, the signal-to-noise ratio, and the way the information from the incomplete data sets is used in a simulation study involving a static factor model setup. We set the fraction of discarded values to 1%, but the correspondingly implied partition is different for each incomplete data set.¹³ The SSE is then calculated for all of these data sets, conditional on the same specific choice of the number of factors R. The choices for the parameters are $P=\{10, 20, 40, 80\}$, $T=\{100, 200\}$, and $R=\{2,3\}$, and the signal-to-noise ratio is varied between 10 and 1. The simulation study hence covers the arising 32 scenarios. For each scenario, $G=50$ data sets are simulated. From each data set, $J=100$ incomplete versions are generated, removing 1% of the data at random. For each incomplete data set per scenario, the model is estimated for a set of candidate values given as $R^C=\{1,2,3,4,5\}$, thus providing five Gibbs sequences of length $S=$ 5,000 after discarding burn-in sequences of length 2,000. Now for each simulated data set, there are $J = 100$ five-dimensional vectors, containing the SSE values for the set of candidate values $R^C$. Hence $SSE_{g,j}(\tilde{R})$ with $g=1,\ldots ,G$ and $j=1,\ldots ,J$ denotes the sum of squared errors for the jth incomplete version of the gth simulated data set when the number of factors in the estimation is set to $\tilde{R}$.

Next, in a bootstrap step, we obtain samples of size $Q = 25$ and $Q = 100$, respectively, by drawing with replacement from the $J = 100$ vectors of SSE values obtained for the set of candidate values $R^C$. Proceeding accordingly, we create $L =$ 10,000 such bootstrap samples for each of the $G = 50$ simulated data sets per scenario. Each bootstrap sample can be referred to by the index set $\mathcal {B}_{l,g}$, which contains the indices of the bootstrapped elements in bootstrap sample l for the simulated data set g. These indices range from 1 to J, and the index set may contain duplicate entries. We then calculate the average SSE for each bootstrap sample for every candidate value in $R^C$, i.e., $C_{l,g}(\tilde{R}) = \frac{1}{Q}\sum _{q \in \mathcal {B}_{l,g}} SSE_{g,q}(\tilde{R})$ for all $\tilde{R} \in R^C$. Eventually, we estimate for each l and each g the number of factors as the $\tilde{R}$ from $R^C$ that yields the lowest average SSE, i.e., $\hat{R}_{l,g} = \arg \min _{\tilde{R}\in R^C} C_{l,g}(\tilde{R})$. With $l \in \{1,\ldots ,L\}$ and $g \in \{1,\ldots ,G\}$, this gives us 500,000 estimates for the number of factors per scenario and per value chosen for Q, denoted as $\hat{R}$.

Table 4 reports the corresponding shares for $\hat{R}$ from $R^C$ for each scenario. Overall, the obtained results indicate that the chance to underestimate R is virtually zero for all scenarios, except those with $P = 10$ and $R = 3$, where a signal-to-noise ratio of 1 results in frequent underestimations. The underestimation is more pronounced for the scenarios with $T=100$. In the following, the scenarios with$P=\{20,40,80\}$ are summarized. In these 24 scenarios the number of factors is sometimes overestimated, but it must be noted that in all of these scenarios, the correct model is identified in more than 90% of the cases. On average, models are correctly identified in about 97% of all cases for the signal-to-noise ratio of 1 and in about 96% of all cases for the signal-to-noise ratio of 10. If Q is reduced to 25, the correct model is identified in more than 88% of the cases. On average, models are correctly identified in about 94% of all cases for the signal-to-noise ratio of 1 and in about 92% of all cases for the signal-to-noise ratio of 10.¹⁴

Table 4 Results of the posterior predictive simulation study

6 Empirical illustration

In this section, we illustrate the suggested ex-post approach using a data set from financial economics. This empirical illustration closely follows Frühwirth-Schnatter and Lopes (2018). The data set consists of monthly log returns of 22 exchange rates against the Euro from February 1999 to September 2018, see Fig. 3.¹⁵ The data are demeaned and standardized. In the first step, the posterior predictive assessment is used to determine the appropriate number of factors. The method described in Sect. 5 is applied via generating $J = 100$ incomplete data sets from the available one, and then using the bootstrap procedure to produce $L = 10,000$ samples of size $Q = 100$ to determine $\hat{R}$. Discarding 1% of the data, $\hat{R} = 2$ is chosen in 96.9% of all cases, and $\hat{R} = 3$ is chosen in 3.1% of all cases. If we discard 5% of the data, $\hat{R} = 2$ is chosen in 100% of all cases. We therefore estimate the model with two factors. To allow for directed estimates and inference for $\beta$ in the FOC approach, we again augment the information contained in the sequence $D^{(s)}$, $s=1,\ldots ,S$.

Fig. 3

Demeaned and standardized monthly log returns based on the first trading day in a month for 22 currencies against the Euro from February 1999 until September 2018

After estimation, both the factors and factor loadings are orthogonally transformed to obtain an economically interpretable solution. The orthogonal transformation performed here turns the first factor into a US Dollar factor, maximizing the loading on the first factor for the exchange rate between the US Dollar and the Euro. The loading on the second factor for this pair of exchange rates is zero accordingly. The resulting loading matrix is hence a version of the positive lower triangular form of $\alpha$ mentioned in Sect. 3. The required orthogonal transformation matrix $D_{\text {PLT}}$ is obtained by reordering the rows of $\alpha ^*$ such that the USD/EUR exchange rate forms the first row, and all remaining rows of $\alpha ^*$ are shifted downwards. This yields the row-permuted matrix

$$\begin{aligned} \alpha _P^* = \begin{pmatrix} 0_{1 \times (R-1)} &{} 1 \\ I_{R-1} &{} 0_{(R-1) \times 1}\end{pmatrix}\alpha ^*. \end{aligned}$$

Next, the QR decomposition ${\alpha _P^*}' = E_DL'$ is used to obtain $D_{\text {PLT}} = E_{D} \cdot \text {diag}(\text {sgn}(l_{1,1}),\ldots ,\text {sgn}(l_{R,R}))$, as described in Sect. 2. The reported estimates then correspond to $\alpha ^*D_{\text {PLT}}.$ The estimates of rotated factor loadings and corresponding 95% HPDIs are shown in Table 5, whereas the estimated factors and corresponding 95% HPDIs are displayed in Fig. 4. Again, estimates resulting from both FOC and EOT loss functions are reported. The upper parts of Table 5 and Fig. 4 corresponds to FOC estimates, whereas the lower parts correspond to EOT estimates. Further, we like to stress that HPDIs can only be interpreted for a each loading on its own. Indeed, the rotated first factor is virtually perfectly correlated with the exchange rate between the US Dollar and the Euro, with a factor loading of 1.0026 as the FOC estimate and 1.0027 as the EOT estimate. The US Dollar factor also clearly shows the (flexible) peg between the US Dollar and the Hongkong Dollar, which has a factor loading of 1.0026 (FOC) and 1.0027 (EOT), respectively, and strong loadings with a number of south east Asian currencies, such as the Indonesian Rupiah, the Malaysian Ringgit, the Philippine Peso, the Singapore Dollar, and the Thai Baht. Less pronounced loadings are found for the Japanese Yen, the Canadian Dollar and the Korean Won. The factor is virtually orthogonal to the Czech Koruna, the Mexican Peso, the Norwegian Krone, the Swedish Krona and the Romanian Leu and affects the Polish Złoty slightly negatively. The second factor cannot be linked to any particular exchange rate, but shows the largest loadings for the Australian Dollar and the Korean Won. From the perspective of investors from the Euro area this gives rise for the opportunity to diversify exchange rate risks. Overall, the estimation uncertainty for the US Dollar factor is substantially lower than that for the second factor. With regard to differences between the FOC and EOT loss function, we find the point estimates to be virtually identical, whereas the empirical illustration shows slightly broader HPDIs for the EOT loss function approach. This reflects that for the EOT loss function orthogonal invariance is contributed by $\alpha$ and $\beta$.

Table 5 Estimated factor loadings for the exchange rate data, after rotation (95% HPDIs in parentheses)

Fig. 4

Estimated factors for the exchange rate data, after rotation. Blue denotes the US dollar factor, and red denotes the second factor. Shaded areas denote 95% HPDIs. Top two graphs show estimates with the FOC loss function, bottom two graphs show estimates with the EOT loss function

7 Conclusion

This paper discusses the handling of orthonormality restrictions constraining parts of the parameter space to the Stiefel manifold in the context of reduced rank regressions via a novel post-processing algorithm. The output of the rotation-invariant sampler of Koop et al. (2010) is the starting point for the ex-post algorithm. We consider appropriate formulations of loss functions and propose corresponding post-processing algorithms for the posterior sample that allow for identification and directed inference. Thereby, the possibilities to conduct valid inference for cointegration vectors or factors restricted to the Stiefel manifold are extended. We discuss the differences and similarities implied by defining as a loss function for the parameters defined on the Stiefel manifold either a Euclidean distance function involving an orthogonal transformation or the Frobenius norm involving orthogonal complements for handling the orthogonal invariance present in the output of the rotation-invariant sampler. We illustrate how the post-processing works for vector error correction models in a simulation study and show an application of the sampling procedure suggested by Koop et al. (2010) for factor models. Further, we propose to use posterior predictive assessment to obtain model evidence and to compare models. We do so, because obtaining the marginal likelihood is computationally extremely demanding when the Stiefel manifold is involved. Overall, the results suggest that the two alternative loss functions lead to virtually equivalent results. Finally, our approach to the analysis of reduced rank models is illustrated in an empirical example. Future research may focus on alternative possibilities to provide model comparison and assessment in a Bayesian framework.

Appendices

Appendix A: Prior distribution on $\alpha$ and $\beta$

The prior distribution for $\alpha$ and $\beta$ provided in Eq. (4) corresponds to a marginal matrix angular central Gaussian distribution with parameter $C_{\tau }$ for $\beta$, see Chikuse (1990, 2003), and a conditional multivariate normal prior for $\alpha$ conditional on $\beta$ with expected value zero and covariance matrix $\tau (\beta 'C_{\tau }^{-1}\beta )^{-1}\otimes \Sigma$, hence $\pi (\alpha ,\beta |\Sigma )\propto \pi (\alpha |\beta ,\Sigma )\pi (\beta )$, where

$$\begin{aligned} \pi (\beta )\propto |C_{\tau }|^{-\frac{R}{2}}|\beta 'C_{\tau }^{-1}\beta |^{-\frac{P}{2}}I(\beta '\beta =I_R) \end{aligned}$$

and

$$\begin{aligned} \pi (\alpha |\beta ,\Sigma )\propto |\nu (\beta 'C_{\tau }^{-1}\beta )^{-1}\otimes \Sigma |^{-\frac{1}{2}}\exp \left\{ -\frac{1}{2}\text {vec}(\alpha )'(\nu (\beta 'C_{\tau }^{-1}\beta )^{-1}\otimes \Sigma )^{-1}\text {vec}(\alpha )\right\} . \end{aligned}$$

This implies the form for $\pi (\alpha ,\beta |\Sigma )$ given in Eq. (4) since we have that

$$\begin{aligned} |\nu (\beta 'C_{\tau }^{-1}\beta )^{-1}\otimes \Sigma |^{-\frac{1}{2}}=\nu ^{-\frac{RP}{2}}| (\beta 'C_{\tau }^{-1}\beta )|^{\frac{P}{2}}|\Sigma |^{-\frac{R}{2}} \end{aligned}$$

and

$$\begin{aligned} -\frac{1}{2}\text {vec}(\alpha )'(\nu (\beta 'C_{\tau }^{-1}\beta )^{-1}\otimes \Sigma )^{-1}\text {vec}(\alpha )= & {} -\frac{1}{2}\text {vec}(\alpha )' \left( \nu ^{-1}(\beta 'C_{\tau }^{-1}\beta )\otimes \Sigma ^{-1}\right) \text {vec}(\alpha )\\= & {} -\frac{1}{2}\text {tr}\left[ \nu ^{-1}\beta 'C_{\tau }^{-1}\beta \alpha '\Sigma ^{-1}\alpha \right] . \end{aligned}$$

Note that with regard to $\pi (\beta )$ the choice $\tau =1$ implies a noninformative, i.e., uniform prior on the Stiefel manifold, see Chikuse (1990). Opting additionally for $\nu =1$ implies for $\pi (\alpha |\beta ,\Sigma )$ that scaling is proportial to $(\beta 'C_{\tau }^{-1}\beta )^{-1}\otimes \Sigma$ with no further shrinkage considered.

Appendix B: Invariance of the posterior when considering the reparametrization in terms of A and B

The posterior distribution is also invariant under the reparametrization of $\alpha$ and $\beta$ considered to facilitate efficient sampling, i.e.,

$$\begin{aligned} A=\alpha (\alpha '\alpha )^{-\frac{1}{2}},\quad B=\beta (\alpha '\alpha )^{\frac{1}{2}}, \end{aligned}$$

as $\text {vec}(\alpha D)$ and $\text {vec}(\beta D)$ imply $\text {vec}(A D)$ and $\text {vec}(B D)$, i.e.,

$$\begin{aligned} (\alpha D)((\alpha D)'(\alpha D))^{-\frac{1}{2}}=\alpha (\alpha '\alpha )^{-\frac{1}{2}} D=AD,\end{aligned}$$

(18)

and

$$\begin{aligned} (\beta D)( (\alpha D)' (\alpha D))^{\frac{1}{2}}=\beta (\alpha '\alpha )^{\frac{1}{2}}D=BD. \end{aligned}$$

(19)

This follows from the singular value decomposition of a real symmetric matrix as defined in Lütkepohl (1996), since

$$\begin{aligned} (\alpha '\alpha ) = \mathcal {S}_1 \Lambda ^{} \mathcal {S}_1' \quad \text {and}\quad ((\alpha D)' (\alpha D)) = \mathcal {S}_2 \Lambda ^{} \mathcal {S}_2', \end{aligned}$$

where $\mathcal {S}_1$ and $\mathcal {S}_2$ are orthogonal matrices and $\Lambda$ is the diagonal matrix of eigenvalues of both the matrix $\alpha '\alpha$ and the matrix $D'\alpha '\alpha D$, as multiplying $\alpha$ by an orthogonal matrix D does not change the eigenvalues. Then

$$\begin{aligned} \mathcal {S}_2\Lambda \mathcal {S}_2'=D'\alpha '\alpha D =D' \mathcal {S}_1 \Lambda \mathcal {S}_1' D, \end{aligned}$$

implying $\mathcal {S}_2 =D' \mathcal {S}_1$. Then from the definition of the square root matrix given, e.g., in Abadir and Magnus (2005), we have

$$\begin{aligned} (D'\alpha '\alpha D)^{-\frac{1}{2}} = \mathcal {S}_2\Lambda ^{-\frac{1}{2}}\mathcal {S}_2' = D'\mathcal {S}_1 \Lambda ^{-\frac{1}{2}} \mathcal {S}_1'D = D'(\alpha '\alpha )^{-\frac{1}{2}}D. \end{aligned}$$

Therefore, we obtain

$$\begin{aligned} \alpha D((\alpha D)'(\alpha D))^{-\frac{1}{2}}= & {} \alpha D D'(\alpha '\alpha )^{-\frac{1}{2}}D = \alpha (\alpha '\alpha )^{-\frac{1}{2}}D = AD. \end{aligned}$$

(20)

The result from Eq. (3) can be derived analogously, using the square root of the elements in $\Lambda$ instead of the inverse square root. Inserting AD and BD into the corresponding posterior distribution provided in Eq. (8) reveals invariance under the orthogonal transformation described in Eq. (5).