Multiple imputation of ordinal missing not at random data

Abstract

We introduce a selection model-based imputation approach to be used within the Fully Conditional Specification (FCS) framework for the Multiple Imputation (MI) of incomplete ordinal variables that are supposed to be Missing Not at Random (MNAR). Thereby, we generalise previous work on this topic which involved binary single-level and multilevel data to ordinal variables. We apply an ordered probit model with sample selection as base of our imputation algorithm. The applied model involves two equations that are modelled jointly where the first one describes the missing-data mechanism and the second one specifies the variable to be imputed. In addition, we develop a version for hierarchical data by incorporating random intercept terms in both equations. To fit this multilevel imputation model we use quadrature techniques. Two simulation studies validate the overall good performance of our single-level and multilevel imputation methods. In addition, we show its applicability to empirical data by applying it to a common research topic in educational science using data of the National Educational Panel Study (NEPS) and conducting a short sensitivity analysis. Our approach is designed to be used within the R software package mice which makes it easy to access and apply.

1 Introduction

Missing values are a typical occurence in statistical analyses of survey data. When dealing with missing data, it is usually assumed that the data are Missing at Random (MAR), i.e., the misssing data are only related to observed information in the data (Rubin 1976). However, in many situations it seems very realistic that the missing values depend on the incomplete variable Y itself, even after conditioning on all available information in the data, and thus follow a Missing Not at Random (MNAR) mechanism. A famous example for MNAR in social science applications are income-related questions where individuals with very low and very high-income values have a higher chance to not reporting it. If this is not considered, biased estimates and misleading inferences might result.

In social sciences, most currently existing MNAR approaches cannot be applied, since they usually only target continuous variables. However, social sciences data sets mostly involve binary or categorical data. In addition, hierarchical structured data are very common. Since survey data usually offer a lot of potential auxiliary information which may be helpful for predicting missing values, the method of multiple imputation (MI) (Rubin 1987) is very well suited for handling incomplete survey variables in social sciences. Especially the framework of Fully Conditional Specification (FCS) (Raghunathan et al. 2001; Van Buuren et al. 2006) mostly presents the ideal MI approach since it allows to specify an appropriate imputation model for each incomplete variable. This is very beneficial for survey data, since they usually involve various variable types on different scales that require distinct model specifications. In addition, FCS allows to incorporate straightforwardly multilevel structures during imputation.

For MAR data, there exists nowadays a great number of imputation methods for all kind of different data situations and also the field of multilevel imputation techniques has grown immensely in the last years [see e.g., Audigier et al. (2017); Lüdtke et al. (2017); Enders et al. (2017)]. However, for MNAR data the current available implementations are very sparse. In the context of FCS,  Galimard et al. (2016) use a two-stage selection model for imputing continuous MNAR data and Galimard et al. (2018) and Galimard et al. (2015) apply a bivariate probit model with sample selection as imputation model for binary MNAR data. Hammon and Zinn (2020) extend their idea by adding random intercepts to both equations to be able to deal with binary clustered data that are supposed to be MNAR. However, to the author’s knowledge, there is currently no appropriate method available to handle ordinal-scaled data under the MNAR assumption in the context of MI.

In this paper, we want to close this gap by extending the approach of Hammon and Zinn (2020) for imputing binary clustered data to ordinal single-level and multilevel variables. For this purpose, we apply an ordered probit model with sample selection and additionally incorporate random intercept terms in both equations to be able to consider multilevel structures in the data.

The remainder of this article is structured as follows. First, we describe the imputation method and how parameters of the impuation model are estimated. We show the feasibilty of our method by two meaningful simulation studies. Thereafter, we apply the method to empirical survey data by analyzing the impact of social background factors on the educational aspirations of ninth grade students in Germany. We conclude with a short summary of the results, a discussion of some critical issues, and tasks for future work.

2 Method

The basic idea of FCS is to specify separate imputation models for each incomplete variable and to impute the missing data on a variable-by-variable basis. That is, for an ordinal variable with missing values a model describing this variable appropriately is required. If data are additionally MNAR, then the mechanism that caused the missing values also has to be modelled. For this purpose, alike Galimard et al. (2015, 2016); Galimard et al. (2018) & Hammon and Zinn (2020) we use a selection model-based approach consisting of a two-equation system: one equation for the selection process and one equation describing Y. Since the focal variable is ordinal, we use an ordered probit model with sample selection (Greene 2012) to specify this two-equation system. Adding a random intercept term to the two equations of the purposed selection model allows accounting for hierarchical structures in the data, which expands the model to multilevel ordinal data.

Models for ordinal variables are computationally very intensive and can rapidly run into estimation difficulties in the presence of many categories or predictors. Thus, to impute ordinal variables with many categories it can be more beneficial to use nearest-neighbor approaches such as predictive mean matching to prevent potential issues such as unstable estimates, empty cells, and poor and unreasonably slow performance. For a more detailed discussion of these potential difficulties in practice refer to Van Buuren (2018).

Below, we describe the single and multilevel models in detail and present an efficient way to estimate them. This is followed by the presentation of the related imputation algorithms which can be incorporated into the FCS imputation scheme. R describes the missing-data indicator of Y that takes on the value 1 if Y is observed and 0 otherwise. Observations of Y and R are denoted by y and r.

2.1 Ordered probit model with sample selection

Using the standard probit specification based on latent variable formulation, an ordered probit model with sample selection can be specified as follows for $i=1,\ldots ,n$ individuals:

$$\begin{aligned} r^{*}_{i}&=\varvec{\beta _{R}}{^\top } \varvec{x_{R,i}} + \epsilon _{R,i} \nonumber \\ y^{*}_{i}&=\varvec{\beta _{Y}}{^\top } \varvec{x_{Y,i}} + \epsilon _{Y,i} \end{aligned}$$

(2.1)

with

$$\begin{aligned} r_{i}=&~{\mathbf {1}}(r^{*}_{i} > 0), \\ y_{i}=&{\left\{ \begin{array}{ll} ~h~~~~~\text {if}~~\kappa _{h-1} < y^{*}_{i} \le \kappa _{h} ~~ \& ~~ r_i=1 \\ \text {NA} ~~~ \text {if} ~~ r_{i}=0. \end{array}\right. } \end{aligned}$$

where $h=1,\ldots ,H$ denote the observed, ordered categories of the outcome variable Y. $\kappa _h$ are strictly increasing threshold parameters, with $\kappa _0=-\infty$ and $\kappa _H=+\infty$, that partition $y^{*}_{i}$ into H exhaustive and mutually exclusive intervals. The first equation describes the non-random selection process, that is, for the missing-data mechanism in our case. The second equation models the focal variable Y and defines the outcome equation. The asterisk marks the latent variables $r^{*}_{i}$ and $y^{*}_{i}$, whose observed equivalents are $r_{i}$ and $y_{i}$. The covariates of the two regression equations are given by the vectors $\varvec{x_{R}}$ and $\varvec{x_{Y}}$, and $\varvec{\beta _{R}}{^\top }$ and $\varvec{\beta _{Y}}{^\top }$ are the vectors of the related coefficients. Due to the utilized parametrization of the thresholdparameters $\kappa _h$, $\varvec{\beta _{Y}}{^\top}$ does not contain an intercept term. This is a standard identifiability restriction used for ordinal models since it is not possible to separately identify the intercept term from the threshold parameters (Greene 2012).

The function ${\mathbf {1}}$ denotes the indicator function and “NA” marks a missing value. To assure model identifiability, $\varvec{x_{Y}}$ has to be a subset of $\varvec{x_{R}}$ and $\varvec{x^e_{R}} = \varvec{x_{R}} \setminus \varvec{x_{Y}}$ to be highly correlated with r and hardly connected to y (Rendtel 1992). The set $\varvec{x^e_{R}}$ is called the exclusion restriction.

The selection and the outcome equation are linked through correlated error terms $\epsilon _{R,i}$ and $\epsilon _{Y,i}$:

$$\begin{aligned} \begin{pmatrix} \epsilon _{R} \\ \epsilon _{Y} \end{pmatrix}&\sim ~ N \left( \begin{pmatrix} 0 \\ 0 \end{pmatrix},\begin{pmatrix} 1 &{} \rho \\ \rho &{} 1 \end{pmatrix} \right) \end{aligned}$$

(2.2)

where $\rho$ describes the correlation of the bivariate distribution of $R^*$ and $Y^*$, and therefore models the relation between the selection and outcome equation. This two-equation system only specifies the dependence of the missing-data mechanism on the outcome variable appropriately if the normality assumptions hold.

The log likelihood function of the two-equation model (2.1) can be expressed as

$$\begin{aligned} \ln {L}=&\sum _{i=1}^n~ \! \Bigg [ (1-r_i) \ln \Big \{ \Phi \left( - \varvec{\beta _R}{^\top } \varvec{x_{R,i}} \right) \Big \}\nonumber \\&+ r_i \sum _{h=1}^{H} \! m_{ih} \ln \Big \{ \Phi _2 \left( \varvec{\beta _{R}}{^\top } \varvec{x_{R,i}},\kappa _h -\varvec{\beta _{Y}}{^\top } \varvec{x_{Y,i}},-\rho \right) \nonumber \\&- \Phi _2 \left( \varvec{\beta _{R}}{^\top } \varvec{x_{R,i}}, \kappa _{h-1} - \varvec{\beta _{Y}}{^\top } \varvec{x_{Y,i}}, -\rho \right) \Big \} \Bigg ] \end{aligned}$$

(2.3)

with $m_{ih}=1$ if $y_{i}=h$ and $m_{ih}=0$ otherwise. Here, $\Phi _2(\ldots )$ denotes the cumulative distribution function (cdf) of the bivariate standard normal distribution and $\Phi (\ldots )$ is the cdf of the univariate standard normal.

For fitting the parameters of the log-likelihood function (2.3) standard ML estimation can be used. For the numerical optimization required in this context, we suggest applying the Broyden–Fletcher–Goldfarb–Shanno (BFGS) method [e.g., Goldfarb (1970)]—a very powerful and efficient optimization algorithm that belongs to the group of Quasi-Newton methods. The BGFS algorithm does not require the computation of the Hessian matrix, but approximates it in each iteration using the gradients which makes it computationally very attractive [e.g., Nocedal and Wright (2006)]. The provision of the analytic gradients of the paramaters of Eq. (2.3) speed up the maximization process of parameter estimation. Their calculation is given in the supplementary material of this article.

2.2 Ordered probit model with sample selection and random intercept

Given the data at hand contain $j=1,\ldots ,J$ clusters each consisting of $i=1,\ldots ,n_j$ individuals, extending model (2.1) by random intercepts to account for this yields:

$$\begin{aligned} r^{*}_{ji}&=\varvec{\beta _{R}}{^\top } \varvec{x_{R,ji}} + \alpha _{R,j} + \epsilon _{R,ji} \nonumber \\ y^{*}_{ji}&=\varvec{\beta _{Y}}{^\top } \varvec{x_{Y,ji}} + \alpha _{Y,j} + \epsilon _{Y,ji} \end{aligned}$$

(2.4)

with

$$\begin{aligned} r_{ji}=&~{\mathbf {1}}(r^{*}_{ji} > 0), \\ y_{ji}=&{\left\{ \begin{array}{ll}~h~~~~~\text {if}~~\kappa _{h-1} < y^{*}_{ji} \le \kappa _{h} ~~ \& ~~ r_{ji}=1 \\ \text {NA} ~~~ \text {if} ~~ r_{ji}=0. \end{array}\right. } \end{aligned}$$

Here, $\alpha _{R,j}$ and $\alpha _{Y,j}$ are the random intercepts for describing cluster effects. Again, $\varvec{\beta _{Y}}{^\top }$ does not involve an overall fixed intercept term as identifiying constraint.

The selection and the outcome equation are linked through correlated error terms and random intercepts:

$$\begin{aligned} \begin{pmatrix} \epsilon _{R} \\ \epsilon _{Y} \end{pmatrix}&\sim ~ N \left( \begin{pmatrix} 0 \\ 0 \end{pmatrix},\begin{pmatrix} 1 &{} \rho \\ \rho &{} 1 \end{pmatrix} \right) , \nonumber \\ \begin{pmatrix} \alpha _{R} \\ \alpha _{Y} \end{pmatrix}&\sim ~ N \left( \begin{pmatrix} 0 \\ 0 \end{pmatrix},\begin{pmatrix} \sigma _R^2 &{} \tau \sigma _R \sigma _Y \\ \tau \sigma _R \sigma _Y &{} \sigma _Y^2 \end{pmatrix} \right) . \end{aligned}$$

(2.5)

where $\tau$ denotes the correlation parameter of the bivariate normal distribution of $\alpha _{R}$ and $\alpha _{Y}$, and $\varvec{\Sigma }$ their variance-covariance matrix. The additional consideration of $\tau$ allows to capture potential dependencies of the missing-data mechanism on the cluster structure of the data. This model describes a two-level hierarchy. However, an extension to further levels is straightforward.

The log likelihood function of the two-equation model (2.4) can be expressed as

$$\begin{aligned} \ln {L}=&\sum _{j=1}^J~ \ln \int _{-\infty }^{+\infty } \! \int _{-\infty }^{+\infty } \! \! ~~ \prod _{i=1}^{n_{j}} \Bigg [ (1-r_{ji}) \Phi \left( - (\varvec{\beta _R}{^\top } \varvec{x_{R,ji}} + \alpha _{R,j}) \right) \nonumber \\&+ r_{ji} \sum _{h=1}^{H} \! m_{jih} \bigg ( \Phi _2 \left( \varvec{\beta _{R}}{^\top } \varvec{x_{R,ji}} + \alpha _{R,j},\kappa _h -(\varvec{\beta _{Y}}{^\top } \varvec{x_{Y,ji}} + \alpha _{Y,j}),-\rho \right) \nonumber \\&- \Phi _2 \left( \varvec{\beta _{R}}{^\top } \varvec{x_{R,ji}} + \alpha _{R,j},\kappa _{h-1} -(\varvec{\beta _{Y}}{^\top } \varvec{x_{Y,ji}} + \alpha _{Y,j}),-\rho \right) \bigg ) \Bigg ] \nonumber \\&\cdot \phi _2(\alpha _{R,j},\alpha _{Y,j} \mid \varvec{0}, \varvec{\Sigma }) \,\mathrm {d} \alpha _{R,j} \, \mathrm {d} \alpha _{Y,j}. \end{aligned}$$

(2.6)

with $m_{jih}=1$ if $y_{ji}=h$ and $m_{jih}=0$ otherwise. The function $\phi _2(\ldots |\varvec{0},\varvec{\Sigma })$ is the probability density function (pdf) of a bivariate normal distribution with mean zero and variance-covariance matrix $\varvec{\Sigma }$. As usual in multilevel modelling, the two random intercepts $\alpha _{R}$ and $\alpha _{Y}$ are treated as nuisance parameters. Thus, they can be integrated out. The double integral of the log likelihood function (2.6) has no closed-form solution. One way to solve the integral nevertheless is to approximate the area under the integrand. There exist different approaches for achieving this. As in Hammon and Zinn (2020), we will use quadrature techniques for solving the double integral.

We apply Adaptive Gauss-Hermite quadrature (AGHQ) (Naylor and Smith 1982; Liu and Donald 1994) an improved version of the standard Gauss-Hermite quadrature (GHQ). Here, in contrast to the traditional GHQ, the quadrature points are set symmetrically around the maximum value of the integrand and not around 0. In other words, AGHQ shifts and scales the quadrature locations to place them under the peak of the integrand, so that the function is evaluated where the area is expected to be largest. Applying the AGHQ rule on the log likelihood Eq. (2.6) gives the following approximation:

$$\begin{aligned} \ln {L}^{AGHQ}\simeq&\sum _{j=1}^J~ \ln \Bigg \{ |\varvec{\Omega }_{\varvec{j}}|^{1/2} ~ 2 \sum _{p_{1}=1}^{P} \! ~ \sum _{p_{2}=1}^{P} \! \! ~ \omega _{p_{1}} \omega _{p_{2}} \prod _{i=1}^{n_{j}} \Bigg [ (1-r_{ji}) \Phi \left( - (\varvec{\beta _R}{^\top } \varvec{x_{R,ji}} + {\tilde{a}}_{jp_{1}}) \right) \nonumber \\&+ r_{ji} \sum _{h=1}^{H} \! m_{jih} \bigg ( \Phi _2 \left( \varvec{\beta _{R}}{^\top } \varvec{x_{R,ji}} + {\tilde{a}}_{jp_{1}},\kappa _h -(\varvec{\beta _{Y}}{^\top } \varvec{x_{Y,ji}} + {\tilde{a}}_{jp_{2}}),-\rho \right) \nonumber \\&- \Phi _2 \left( \varvec{\beta _{R}}{^\top } \varvec{x_{R,ji}} + {\tilde{a}}_{jp_{1}},\kappa _{h-1} -(\varvec{\beta _{Y}}{^\top } \varvec{x_{Y,ji}} + {\tilde{a}}_{jp_{2}}),-\rho \right) \bigg ) \Bigg ] \nonumber \\&\cdot \phi _2(\tilde{\varvec{a}}_{\varvec{jp}}|\varvec{0},\varvec{\Sigma }) ~ \exp (\varvec{a}_{\varvec{p}}{^\top}\varvec{a}_{\varvec{p}})\Bigg \}, \end{aligned}$$

(2.7)

The related bivariate quadrature nodes $\tilde{\varvec{a}}_{\varvec{jp}}=({\tilde{a}}_{jp_{1}} {\tilde{a}}_{jp_{2}}){^\top}$ with $\varvec{p}=(p_1,p_2){^\top }$, are defined as:

$$\begin{aligned} \tilde{\varvec{a}}_{\varvec{jp}}=\varvec{\mu }_{\varvec{j}}+\sqrt{2}\hat{\varvec{\Omega }}_{\varvec{j}}^{1/2} \varvec{a_p}{^\top }, \end{aligned}$$

where $p_1=1,\dots ,P$ and $p_2=1,\dots ,P$ are the quadrature points for the selection and outcome equation, respectively. $\varvec{a_p}=(a_{p_{1}},a_{p_{2}}){^\top }$ and $\varvec{\omega _{p}}=(\omega _{p_{1}} \omega _{p_{2}}){^\top }$ are the standard Gauss-Hermite nodes and weights which can be found in tables of Abramowitz and Stegun (1964) or can be computed using an algorithm proposed by Golub and Welsch (1969). Here, the matrix $\varvec{\Omega _j}$ scales $\varvec{a_p}$ and the vector $\varvec{\mu _j}$ centres them. The function $|\varvec{\Omega _j}|$ denotes the determinant of $\varvec{\Omega _j}$. The square root of $\varvec{\Omega _j}$, $\varvec{\Omega _j}^{1/2}$, can be properly described by the lower triangular matrix $\varvec{T}$ of the Cholesky decomposition of $\varvec{\Omega _j}=\textit{\textbf{T T}}{^\top }$. To specify $\varvec{\mu _j}$ we use the mode, i.e., the most likely value for the random effects given the observed data and the current estimates of all of the other model parameters. To estimate $\varvec{\Omega _j}$ the curvature matrix, the negative inverse Hessian matrix, at the modes is used (Liu and Donald 1994). For the exact calculation of mode $\hat{\varvec{\mu }}_{\varvec{j}}$ and curvature $\hat{\varvec{\Omega }}_{\varvec{j}}$ see Hammon and Zinn (2020). For more detailed information about the applied quadrature technique see also Hammon and Zinn (2020) and the respective supplementary material of the article.

As for the single-level model, we rely on standard ML estimation to fit the parameters of the approximated log-likelihood functions in Eq. (2.7) and use the BFGS method for numerical optimization. To speed up the maximization process of parameter estimation, we calculated the analytic gradients of Eq. (2.7) and use them during optimization. These gradients can be found in the supplementary material of this article.

2.3 Imputation algorithm

With the two introduced models, we can impute missing values in single-level or multilevel ordinal data. In FCS, plausible replacements are drawn variable-by-variable from the related conditional densities. FCS has the theoretical weakness that it is usually not possible to verify if the conditional distributions are compatible, why we never know if the theoretical joint distribution we want to approximate really exists. However, Van Buuren et al. (2006) could show that FCS performs very well, even under strong incompatible models. It seems that incompatibility is usually not a big issue in practice and has only minor influence on the quality of imputed values. For a comprehensive discussion about FCS, its general performance and theoretical limitations refer to Van Buuren et al. (2006); Zhu and Raghunathan (2015); Van Buuren (2018).

For single-level ordinal variables we use model (2.1) as univariate imputation model to reflect a possible MNAR mechanism during imputation. Let $\theta =(\beta _Y,\beta _R,r,\delta _l)$ with $l=1,\dots ,H-1$ be the unknown parameters of the ordered probit model with sample selection, where $r={{\,\mathrm{atanh}\,}}\rho$, $\delta _1=\kappa _1$, and $\delta _l=\ln (\kappa _l - \kappa _{l-1})$ for $l>1$ are common transformations to preserve range constraints of the parameters during maximization. At each iteration of the FCS procedure, the following four steps are conducted to impute the missing values of a single-level ordinal variable Y. We consider parameter uncertainty by drawing parameter candidates ${\dot{\theta }}$ using a normal approximation to the posterior distribution of ${\hat{\theta }}$ [e.g., Gelman et al. (2013), Ch. 4].

• 1. Estimate model parameters of (2.1) by ML using equation (2.3), which yields

  • (a) ${\hat{\theta }}=({\hat{\beta }}_Y,{\hat{\beta }}_{R},{\hat{r}},{\hat{\delta }}_l)$,

  • (b) ${\hat{\psi }}$, the variance-covariance matrix of ${\hat{\theta }}$.

• 2. Draw $\dot{\theta }=({\dot{\beta }}_Y,{\dot{\beta }}_{R},\dot{r},{\dot{\delta }}_l)$ from $N({\hat{\theta }},{\hat{\psi }})$, and re-transform ${\dot{\rho }}=\tanh \dot{r}$, ${\dot{\kappa }}_1={\dot{\delta }}_1$, and ${\dot{\kappa }}_l=\exp ({\dot{\delta }}_l) + {\dot{\kappa }}_{l-1}$ for $l>1$.

• 3. Calculate for each unit with missing Y the probability $\dot{p}_h$ that Y falls into category $h=1,\dots ,H$:

  $$\begin{aligned} \dot{p}_h=P(\dot{Y}=h|X_Y,X_{R},R=0)=&\frac{\Phi _2(-(X_{R}{\dot{\beta }}_{R},{\dot{\kappa }}_h - (X_Y {\dot{\beta }}_Y),{\dot{\rho }})}{{\Phi (-(X_{R}{\dot{\beta }}_{R}))}}~~-\\&\frac{\Phi _2(-(X_{R}{\dot{\beta }}_{R}),{\dot{\kappa }}_{h-1} - (X_Y {\dot{\beta }}_Y),{\dot{\rho }})}{\Phi (-(X_{R}{\dot{\beta }}_{R}))} \end{aligned}$$

• 4. Draw for each missing value $Y_{mis}$ a replacement from the Multinomial distribution $Multinom(\dot{p}_1,\dots ,\dot{p}_H)$.

To generate M imputed data sets, these steps are repeated M times.

In the multilevel case, the ordered probit model with sample selection and random intercepts (2.4) determines the conditional density of Y. Let $\theta =(\beta _Y,\beta _R,r,\xi ^2_Y,\xi ^2_{R},z,\delta _l)$ with $l=1,\dots ,H-1$ be the unknown parameters of the ordered probit model, where $\xi ^2_Y=\ln \sigma ^2_Y$, $\xi ^2_R=\ln \sigma ^2_R$ and $z={{\,\mathrm{atanh}\,}}\tau$ are additional transformations to preserve further range constraints of the parameters during maximization. At each iteration the following five steps are conducted to impute the missing values of a clustered ordinal variable Y. Note that at each FCS iteration step the approximated log-likelihood (2.7) has to be maximised to obtain updated estimates ${\hat{\theta }}$ for $\theta$. We again consider parameter uncertainty by drawing new parameter values ${\dot{\theta }}$ from their approximate normal posterior distribution.

• 1. Estimate model parameters of (2.4) by ML and AGHQ using Eq. (2.7), which yields

  • (a) ${\hat{\theta }}=({\hat{\beta }}_Y,{\hat{\beta }}_{R},{\hat{r}},{\hat{\xi }}^2_Y,{\hat{\xi }}^2_{R},{\hat{z}},{\hat{\delta }}_l)$,

  • (b) ${\hat{\psi }}$, the variance-covariance matrix of ${\hat{\theta }}$.

• 2. Draw $\dot{\theta }=({\dot{\beta }}_Y,{\dot{\beta }}_{R},\dot{r},{\dot{\xi }}^2_Y,{\dot{\xi }}^2_{R},\dot{z},{\dot{\delta }}_l)$ from $N({\hat{\theta }},{\hat{\psi }})$, and re-transform ${\dot{\rho }}=\tanh \dot{r}$, ${\dot{\tau }}=\tanh \dot{z}$, ${\dot{\sigma }}^2_Y= \exp {\dot{\xi }}^2_Y$, ${\dot{\sigma }}^2_{R}=\exp {\dot{\xi }}^2_{R}$, ${\dot{\kappa }}_1={\dot{\delta }}_1$, and ${\dot{\kappa }}_l=\exp ({\dot{\delta }}_l) + {\dot{\kappa }}_{l-1}$ for $l>1$.

• 3. Draw random intercept candidates $({\dot{\alpha }}_{R,j}, {\dot{\alpha }}_{Y,j}){^\top }$ for each cluster j from $N \left( \hat{\varvec{\mu }}_{\varvec{j}},\hat{\varvec{\Omega }}_{\varvec{j}}\right)$.¹

• 4. Calculate for each unit with missing Y the probability $\dot{p}_h$ that Y falls into category $h=1,\dots ,H$:

  $$\begin{aligned} \dot{p}_h=P(\dot{Y}=h|X_Y,X_{R},R=0)=&\frac{\Phi _2(-(X_{R}{\dot{\beta }}_{R} + {\dot{\alpha }}_R),{\dot{\kappa }}_h - (X_Y {\dot{\beta }}_Y + {\dot{\alpha }}_Y),{\dot{\rho }})}{{\Phi (-(X_{R}{\dot{\beta }}_{R} + {\dot{\alpha }}_R))}}~~-\\&\frac{\Phi _2(-(X_{R}{\dot{\beta }}_{R} + {\dot{\alpha }}_R),{\dot{\kappa }}_{h-1} - (X_Y {\dot{\beta }}_Y + {\dot{\alpha }}_Y),{\dot{\rho }})}{\Phi (-(X_{R}{\dot{\beta }}_{R} + {\dot{\alpha }}_R))} \end{aligned}$$

• 5. Draw for each missing value $Y_{mis}$ a replacement from the Multinomial distribution $Multinom(\dot{p}_1,\dots ,\dot{p}_H)$.

To generate M imputed data sets, these steps are repeated M times.

This imputation algorithm extends the work of Hammon and Zinn (2020) to ordinal data. For handling multivariate missing data, the two algorithms can simply be implemented in a FCS scheme (Raghunathan et al. 2001; Van Buuren 2007, 2018) and serve as univariate imputation model for an incomplete variable which is suspected to be MNAR. We have implemented both algortihms in a way that they can be used within the mice() function of the R software (R Core Team 2020)² package mice (version 3.13.0, see Van Buuren and Groothuis-Oudshoorn (2011)).³ In case of multivariate missing data, it is necessary to include R as predictor in the imputation models of all the other incomplete variables that are part of $X_Y$, otherwise biased imputations may arise; see also Galimard et al. (2016).

3 Simulation study

To evaluate the performance of the novel imputation procedures introduced in this paper, we conduct a set of Monte-Carlo simulation studies using different data generating processes to represent possible real-world scenarios. For reasons of clarity, we concentrate on the univariate imputation model of Y, and assume that all of the covariates considered are observed completely. An application of the algorithm to multivariate missing data is straightforward. The number of replications is set to 1000 for the simulation study with single-level data and for the one dealing with multilevel data we use 500 iterations due to high computational times.⁴ In sum, we consider ten different simulation scenarios, five scenarios for Y being ordinal, single-level data and five scenarios for Y being ordinal, two-level data. The complete code for data generation and analysis of our simulation studies is available at http://github.com/AngelinaHammon/PaperOrderedMNAR. In addition to the scenarios that are introduced below, we also considered more complex settings with further complexities in covariates and response categories which however did not influence the performance of our imputation methods and are therefore not presented here. However, the detailed results are available upon request from the corresponding author.

3.1 Single-level data

3.1.1 Data generation

In any simulation scenario, we initially create complete data sets with an ordinal outcome variable $y_{i}$, with $i=1,\ldots ,n$ and $h=1,\ldots ,H$ where $H=3$ is the number of ordered categories into which $y_{i}$ may fall. We set the total sample size to $n=2000$, and generate three different normally distributed covariates $x_{1,i}, x_{2,i}$, and $x_{3,i}$ according to

$$\begin{aligned} x_{1,i} \sim N(0,0.3^2),~~~x_{2,i} \sim N(0,0.8^2),~~~ x_{3,i} \sim N(0,4^2) \end{aligned}$$

and

$$\begin{aligned} y_{i}^{*}=x_{1,i}+0.5x_{2,i}+\epsilon _{Y,i}~~\text {with}~~y_{i}= ~h~~\text {if}~~\kappa _{h-1} < y^{*}_{i} \le \kappa _{h} \end{aligned}$$

with $\kappa _1=-0.75$ and $\kappa _2=0.5$. Missing values are imposed on $y_{i}$ by specifying a model for the response indicator $r_{i}$, where $r_{i}$ equals 1 if $y_{i}$ is observed and is 0 otherwise. To assess the performance of our imputation method under distinct (realistic) missing data situations, we implement models for five different missing-data mechanisms. We specify four models for MNAR and one model for MAR. Depending on the mechanism considered the parameters $\rho$ of Eq. (2.2) take on varying values expressing different relations between the response indicator r and the outcome variable y. We include different types of MNAR missing data, where we assume that the probability of observing $y_{i}$ increases with the value of $y_{i}^{*}$. Under the first three MNAR scenarios (MNAR sel.), missing data are produced using the following parametrisation of the selection equation:

$$\begin{aligned} r_{i}^{*}=0.5+1.5 x_{1,i}-0.25 x_{2,i}+0.1 x_{3,i}+\epsilon _{R,i}~~\text {with}~~ r_{i}=~{\mathbf {1}} (r_{i}^{*} > 0). \end{aligned}$$

(3.1)

To take into account different magnitudes of correlation between $y_{i}$ and $r_{i}$, we assume three different values for $\rho$, namely $\rho \in \{ 0.3,0.6,0.9 \}$, reflecting weak, medium, and strong correlation. The variable $x_3$ represents the exclusion criterion. To evaluate the performance of our method in an MNAR situation, where the missing-data mechanism does not strictly follow the selection model specification of the imputation model introduced (MNAR non-sel.), we consider

$$\begin{aligned} P(r_{i}=1)=~ \Phi \left( 1.25+1.75 y_{i}^{*}+1.5 x_{1,i}-2.5 x_{2,i} \right) ~~\text {with}~~ r_{i} \sim ~ Ber(P(r_{i}=1)) \end{aligned}$$

as a further MNAR scenario. Here, $Ber(\ldots )$ denotes the Bernoulli distribution and $\rho$ of Eq. (2.2) is set to zero.

Since there is no way testing MAR against MNAR, each MAR or MNAR analysis should be accompanied by a feasible sensitivity analysis (Molenberghs and Fitzmaurice 2008). To conduct effective sensitivity analyses with imputed data it is crucial that the alternative imputation models are not only able to handle MNAR data, but also yield valid inferences under MAR. Therefore, we additionally consider an MAR scenario where the missingness does not depend on $y_{i}$ to evaluate how our new method performs under MAR. For this purpose, we specify the latent response indicator $r_{i}^{*}$ by using Eq. (3.1) with $\rho =0$. All examined missing-data scenarios yield approximately 35% missing values in y.

3.1.2 Data analysis

To evaluate the performance of the new imputation method (referred to in the following as MNAR), we compare it to the currently available method in the R package mice for ordinal variables which uses an ordinal logit model for impuation, but assumes MAR missing data (MAR) (Van Buuren and Groothuis-Oudshoorn 2011). We also present the results of a complete case analysis (CCA), i.e., estimates based on an ordered probit model, which in the case considered, i.e. only missing values in y, is also valid under MAR (Von Hippel 2007). As benchmark we also include the Before deletion result to show that there is no issue with the data generation process. We used $M=10$ multiple imputations for each scenario and imputation procedure. Since we only focus on univariate missing data, which are a special case of monotone missingness, there is no need to iterate the MICE algorithm (Van Buuren 2018). Each completed data set is analysed by estimating an ordered probit regression on y with covariates $x_1$ and $x_2$. After estimation, all estimates are pooled using Rubin’s combining rules (Rubin 1987). Since the regression parameters of $x_1$ and $x_2$ constitute the quantities of interest, we do not further examine the estimates of the threshold values $\kappa$. We assess the performance of each imputation method using the empirical means of the parameter estimates, their relative bias and the coverage rates (CR) of the nominal 95% confidence intervals.

3.1.3 Results

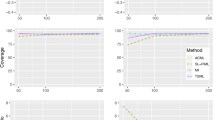
Table 1 shows the results for the regression parameter $\beta _1$ of the first covariate $x_1$ for the different imputation strategies and simulation scenarios including the MNAR scenario based on a selection model with medium correlation, i.e., for $\rho =0.6$. Table 2 gives the respective estimates for the slope parameter $\beta _2$ of variable $x_2$. The results for the selection model-based scenarios with low and high correlation, that is, $\rho \in \{0.3, 0.9\}$, are not reported here since they are similar in terms of relative bias and coverage rates.

In the considered MNAR scenarios, our MNAR imputation method clearly outperforms all competing approaches. For $\beta _1$, it yields, under both MNAR conditions, a relative absolute bias of lower than 0.5% and coverage rates near the nominal coverage probability of 95%. The two MAR methods underestimate $\beta _1$ up to 48.20% in both MNAR scenarios.

If the true missing-data mechanism is MAR, the CCA and the mice imputation model based on the ordered logit model (MAR), which are both designed for this type of missing data, perform—as expected—very well in terms of bias. The coverage of the MAR imputation method is slightly lower than the expected nominal coverage rate of 95%, which could indicate that not all sources of variances are considered properly during the imputation process. Our novel approach MNAR performs well under the MAR scenario, with an average relative downwards bias of 1.11% and a reasonable coverage rate of 94.6% for $\beta _1$. Of course, the bias is slightly higher than for CCA or MAR. Nevertheless, these results confirm that our novel approach also works well for missing data that are MAR - which is a crucial property for conducting adequate sensitivity analyses.

In principle, the results for parameter $\beta _2$ are very similar to those of parameter $\beta _1$. The MAR approaches show a high upward bias in all considered MNAR scenarios along with very low coverage rates, especially in the non-selection model scenario. The MAR methods overestimate $\beta _2$ up to 91.64% under MNAR. Our new approach MNAR again shows a good performance in terms of bias and coverage in all of the scenarios considered.

Table 1 Single-level simulation results for $\beta _1=1$ estimates (with $\rho =0.6$ for MNAR sel.) in 1000 simulation runs

Table 2 Single-level simulation results for $\beta _2=0.5$ estimates (with $\rho =0.6$ for MNAR sel.) in 1000 simulation runs

3.2 Multilevel data

3.2.1 Data generation

For all multilevel simulation scenarios, the total sample size is set to $n=2500$ and the number of clusters equals $m=20$ leading to a cluster size of $n_j=125$, $j=1,\ldots ,m$. For simplicity, we assume that all clusters comprise the same number of units. However, the method can also be applied without any problems in case of different cluster sizes. Varying the number of clusters and cluster sizes is beyond the scope of this paper and is left for future work. Imputation methods for multilevel data, in general, may have their limitations if the number of clusters or cluster sizes become too small. For a comprehensive overview about potential difficulties that can arise when imputing multilevel data in the FCS context, refer to e.g., Audigier et al. (2017); Enders et al. (2017); Lüdtke et al. (2017); Van Buuren (2018).

In any simulation scenario, we initially generate complete data sets with an ordinal outcome variable $y_{ji}$, with $i=1,\ldots ,n_j$ and $h=1,\ldots ,H$ where $H=3$ is the number of ordered categories into which $y_{ji}$ may fall. We introduce three different normally distributed covariates $x_{1,ji}, x_{2,ji}$, and $x_{3,ji}$ according to

$$\begin{aligned} x_{1,ji} \sim N(0,0.3^2),~~~x_{2,ji} \sim N(0,0.8^2),~~~ x_{3,ji} \sim N(0,4^2) \end{aligned}$$

and

$$\begin{aligned} y_{ji}^{*}=x_{1,ji}+0.5x_{2,ji}+\alpha _{Y,j}+\epsilon _{Y,ji}~~\text {with}~~y_{ji}= ~h~~\text {if}~~\kappa _{h-1} < y^{*}_{ji} \le \kappa _{h}. \end{aligned}$$

using $\kappa _1=-0.75$ and $\kappa _2=0.5$ as threshold values.

Here $\alpha _{Y,j}$ and $\epsilon _{Y,ji}$ are drawn according to the model assumptions (2.5) with $\sigma _R^2=0.5$ and $\sigma _Y^2=0.9$. This yields an intraclass correlation of about 0.3 for the selection indicator r and of approximately 0.45 for the outcome variable y. To take into account different magnitudes of correlation between $y_{ji}$ and $r_{ji}$, we use three different values for $\rho$, namely $\rho \in \{ 0.3,0.6,0.9 \}$, reflecting weak, medium, and strong correlation. We set $\tau =0.5$ to allow for a medium correlation between the random intercepts of both equations. Missing values are imposed on $y_{ji}$ by specifying a model for the response indicator $r_{ji}$, where $r_{ji}$ equals 1 if $y_{ji}$ is observed and is 0 otherwise. We again implement five different missing-data mechanisms to evaluate our imputation method under varying missing data scenarios. We specify four models for MNAR and one model for MAR. The different types of considered MNAR mechanisms assume that the probability of observing $y_{ji}$ increases with the value of $y_{ji}^{*}$. Under the first three MNAR scenarios (MNAR sel.), missing data are produced using the following parametrization of the selection equation:

$$\begin{aligned} r_{ji}^{*}=0.5+1.5 x_{1,ji}-0.25 x_{2,ji}+0.1 x_{3,ji}+\alpha _{R,j}+\epsilon _{R,ji}~~\text {with}~~ r_{ji}=~{\mathbf {1}} (r_{ji}^{*} > 0). \end{aligned}$$

(3.2)

The variable $x_3$ represents the exclusion criterion. To evaluate our method for imputing clustered, ordered data in an MNAR situation, where the missing-data mechanism does not strictly follow the selection model specification of the imputation procedure, we consider another MNAR scenario (MNAR non-sel.), where the missing data are imposed by

$$\begin{aligned} P(r_{ji}=1)=~ \Phi \left( 1.25+1.75 y_{ji}^{*}+1.5 x_{1,ji}-2.5 x_{2,ji} + \alpha _{R,j} \right) ~~\text {with}~~ r_{ji} \sim ~ Ber(P(r_{ji}=1)). \end{aligned}$$

Since this scenario is designed to not rely on the two-equation selection model (2.4), $\rho$ and $\tau$ of Eq. (2.5) are set to zero. To check whether our method is also suitable for sensitivity analyses, we additionally consider an MAR scenario where the missingness does not depend on $y_{ji}$ to evaluate how our new method performs under MAR. For this purpose, we specify the latent response indicator $r_{ji}^{*}$ by using Eq. (3.2) with $\rho =0$ and $\tau =0$. All examined missing-data scenarios yield again approximately 35% missing values in y.

3.2.2 Data analysis

To assess the adequacy of our imputation method (MNAR AGHQ), its performance will be compared to an already existing multilevel MAR approach for ordered, clustered data available for the mice package in R via the package miceadds [version 3.11-6, see Robitzsch and Grund (2020)]. We use a multilevel version of predictive mean matching (MAR 2l.pmm), since at the moment there does not exist an implementation of a special imputation model for ordinal multilevel data that is compatible with mice. We also present the results of a complete case analysis (CCA) by estimating an ordered probit model with random intercept which is again valid under MAR since we only generated missing values in y (Von Hippel 2007). We used $M=5$ multiple imputations for each scenario and imputation procedure. As for the single-level case we only focus on univariate missing data, why there is no need to iterate the MICE algorithm.

Each completed data set is analyzed by estimating a mixed effects ordered probit regression on y with covariates $x_1$ and $x_2$. For this purpose, we use the clmm() function of the R package ordinal (version 2019.12-10, see  Christensen (2019)). After estimation, all of the estimates are pooled using Rubin’s combining rules (Rubin 1987). The regression parameters of $x_1$ and $x_2$ constitute the quantities of interest and the estimates of the treshold values $\kappa$ are considered as incidental. To evaluate the performance of each procedure we use the empirical means of the parameter estimates, their relative bias, and the coverage rates (CR) of the nominal 95% confidence intervals.

3.2.3 Results

Table 3 shows the results for the regression parameter $\beta _1$ of the first covariate $x_1$ for the different imputation strategies and simulation scenarios including the MNAR scenario based on a selection model with medium correlation, i.e., for $\rho =0.6$. The respective estimates for the slope parameter $\beta _2$ of variable $x_2$ can be found in Table 4. The results for the selection model-based scenarios with low and high correlation, that is, $\rho \in \{0.3, 0.9\}$, are not reported here since they are similar to $\rho =0.6$ in terms of relative bias and coverage rates.

In the considered MNAR scenarios, the MNAR AGHQ method clearly outperforms all competing approaches. For $\beta _1$, it yield, under both MNAR conditions, relative biases lower than 1.2% and reasonable coverage rates. The two MAR methods (CCA and MAR 2l.pmm) underestimate $\beta _1$ up to 50.01% in both MNAR scenarios and result in very low coverage rates. If the true missing-data mechanism is MAR, the CCA and the two-level imputation model based on predictive mean matching (MAR 2l.pmm) show a very good performance in terms of bias. Nevertheless, MAR 2l.pmm shows a slightly too low coverage rate of 91.4% which might indicate that not all sources of variance are reflected properly. The novel approach MNAR AGHQ performs very well under the MAR scenario, with an average relative downwards bias of only 0.1% and an optimal coverage rate of 94.6% for $\beta _1$. These results confirm that our novel approach also works for missing data that are MAR.

In principle, the results for parameter $\beta _2$ are very similar to those of $\beta _1$. CCA and MAR 2l.pmm overestimate $\beta _2$ up to 94.8% under MNAR and even yield a coverage rate of 0% for the MNAR non-sel. scenario. Our new approach MNAR AGHQ shows again reasonable performance in terms of bias and coverage in all of the scenarios considered. However, in a data situation where missing data are created under a non-selection model, the estimate shows a higher bias than for the other scenarios. The bias is also higher than for the estimate of $\beta _1$ in the same missing-data situation. Nevertheless, the average relative bias of 2.52% still lies within an acceptable range. In summary, our novel method is cleary superior to the other investigated methods when the missing-data mechanism deviates from MAR.

Table 3 Mulitlevel simulation results for $\beta _1=1$ estimates (with $\tau =0.5$ and $\rho =0.6$ for MNAR sel.) in 500 simulation runs

Table 4 Multilevel simulation results for $\beta _2=0.5$ estimates (with $\tau =0.5$ and $\rho =0.6$ for MNAR sel.) in 500 simulation runs

4 Application to empirical data

To evaluate the applicability of our new approach to empirical data we use a classical research question from educational sciences and survey data from a large-scale panel study in Germany: Wave 1 of Starting Cohort “School and Vocational Training: Educational Pathways of Students in Grade 9 and Higher” of the NEPS.⁵ We investigate the impact of young people’s social background on their educational aspirations to graduate with a degree that is higher than the one offered by the school they are currently visiting. Our analysis focuses on ninth-grade students attending lower secondary school Hauptschule, the lowest track of secondary school in Germany, because they are particularly affected by social disadvantage (Wößmann 2007; Schneider 2018). For these students, a higher degree is either an intermediate secondary degree or a degree allowing for university admission. Our data set comprises observations on 3291 ninth graders in 142 schools who were surveyed in 2011. The average number of ninth graders in a school is 23.2 (with a minimum of 10 students and a maximum of 48 students). The intra-class correlation (ICC) concerning higher aspirations of students is 22.15%. Hence, the multilevel structure of our data is obvious.

The students’ social background is reflected by their mothers’ highest educational qualification. This variable can take on four ordered categories based on the CASMIN classification [see e.g., Brauns et al. (2003)]: “basic and intermediate general education”, “basic and intermediate vocational training”, “high secondary education” and “tertiary education”. The ICC of maternal education is 0.2882 which clearly indicates a multilevel structure in this variable. In addition, we consider personal attributes, namely the students’ grades in mathematics and German, their competencies in mathematics and reading, their sex, as well as their migration background (measured by generation status smaller than 3.5), as potential influencing factors for their educational aspirations. Competency scores are estimated as weighted maximum likelihood estimates (Warm 1989). Grades range from “1=very good” to “6=insufficient”. The variables on competencies and sex exhibit very few missing values (at maximum 4%), whereas the variables on migration background, aspirations, and grades show a few more missing values (from 13 to 17%). We find a high percentage of missing values (more than 50%) for maternal education. From non-response analyses with similar NEPS data, we know that persons with lower educational attainment are less likely to take part in the survey [see Zinn et al. (2020)], why we suppose that maternal education might follow an MNAR mechanism. Thus, to reduce the risk of erroneous analysis it is advisable to conduct a sensitivity analysis with different assumptions about the missing-data mechanism of maternal education and compare the robustness of the resulting inferences (Molenberghs and Fitzmaurice 2008). Sensitivity analyses are the only possibility to assess whether a potential plausible MNAR mechanism would make a difference in statistical inferences and conclusions.

FCS is used as imputation framework requiring an imputation method for each variable in the data set with missing values. The variables migration background, higher aspirations and maternal education are imputed using multilevel imputation approaches since they possess ICC values higher than 20% which speaks for a relevant multilevel structure in these data. All other variables are imputed using a single-level approach.

Maternal education is imputed under two assumptions: MAR and MNAR. For the latter our novel method is used and we apply 2l.pmm from the R package miceadds as multilevel MAR method. As exclusion criterion in the respective selection model, we use the information on whether students were ever surveyed individually at home, online, or by phone - that is, not at school - within nine waves (i.e., within five years). All other variables are imputed using an MAR approach. Grades are imputed using predictive mean matching, competence categories by a polytomous regression approach, sex is imputed using a single-level logistic regression model, whereas migration background and aspirations are imputed using a two-level logistic regression model. As a benchmark, we also conduct a complete case analysis (CCA) though Little’s MCAR test (Little 1988) rejects MCAR in the considered case.

Table 5 shows the results of our MNAR analysis, contrasted with the results of the CCA, and the MAR multiple imputation approach for maternal education. The number of imputed data sets is 10 with 15 iterations per imputed data set. For a general discussion about the optimal choice of the number of imputations refer to Van Buuren (2018).

Under all three missing-data schemes, we find stable significant effects (i.e., with a p-value<0.05) for higher grades in German, sex, and migration background. Students with better grades in German show higher aspirations than students with lower grades. Female students and those with migration background also have higher educational aspirations than the respective reference categories. The results under CCA are quite different to those of the other two approaches. The under CCA significant effect of competencies in reading disappears under MAR or MNAR. Furthermore, we do not find any significant effect of mathematics grades under CCA. However, the impact of the mathematics grades is significant at the 0.1 level under MAR or MNAR. Thus, there is slight evidence that grades in mathematics are important for students’ aspirations. Under MAR, competencies in mathematics do not show any significant influence, however, under MNAR their effect is significant again. In addition, “high secondary” maternal education yields a smaller p-value under MNAR compared to MAR. Under MNAR, the effect size of this variable category is also notably larger than under MAR. Thus, under MNAR “high secondary” maternal education has a positive significant impact on higher aspirations compared to the lowest level of maternal education at the 0.1 level.

Our sensitivity analysis shows that a CCA can provide very different and misleading results, if the respective underlying assumptions do not hold. Comparing the MAR and MNAR imputation, the picture is less obvious, but there are small differences in estimators and standard errors, which might indicate the plausibility of the MNAR assumption concerning maternal education. Even if the inferences are shown to be fairly robust at the end, we would not have been able to know that without conducting a sensitivity analysis.

Table 5 Effects on Higher Aspirations: Analyses Using Different Methods for Handling Missing Values for Maternal Education

5 Conclusion

In this paper, we introduced an extension of the work of Galimard et al. (2018); Galimard et al. (2015) and Hammon and Zinn (2020) on imputing binary MNAR data to ordered single-level and multilevel data. In doing so, we closed an important gap in the field of survey statistics. The two univariate imputation methods, we have developed, can easily be incorporated into the FCS framework to deal with multivariate missingness which makes them very versatile. Both methods are designed to directly be used in the R software package mice which makes them easy to access and apply.⁶ Our simulation studies show that the two methods outperform competing techniques in terms of bias and coverage when data are affected by distinct MNAR mechanisms. They were able to produce unbiased and accurate estimates of the quantities of interest in case of MNAR and they also demonstrated to yield valid estimates if the missing data were produced by an MAR mechanism. Thus, our two novel imputation methods are well suited for conducting sensible sensitivity analyses.

We proved our approach to be applicable to real data problems as well by studying the impact of maternal education on the educational aspirations of students in lower secondary education. However, we have to point out that analysing large data sets with many clusters and incomplete predictors may result in long computing times of possibly several hours. Therefore, we highly recommend executing the multiple imputations of mice in parallel on multiple cores to run our approach. In our application, the complete imputation of our empirical data set lasted around eight hours since it was computationally very intensive involving multivariate missing data and a high number of cases and clusters.

Of course, our research has not yet ended. For example, one limitation of the conducted multilevel simulation study is that we kept the number of clusters and cluster sizes constant. Thus, one of our future tasks will be to find out whether varying cluster conditions affect our method’s performance. A further future project is to extend the procedure to deal not only with ordinal variables, but with unordered categorical data, too, using a multinomial probit model with sample selection. Such an extension is very useful for practice, since survey data, especially in the social sciences, often include categorical variables.

Inferences on the missing-data mechanism heavily depend on the distributional model assumptions. De facto, there is not only one way of specifying MNAR models but many. Selection models are often criticised due to several reasons. They are completely identified by their distributional parametric assumptions and do not provide obvious sensitivity parameters. This makes the underlying untestable assumptions less clear and more difficult to communicate. For conducting a meaningful sensitivity analysis it is crucial to not only use one alternative MNAR model, but to compare inferences of various plausible MNAR models with different assumptions about the missing-data mechanism. For this purpose, an alternative modelling strategy based on pattern-mixture modelling could be used such as the the proxy pattern-mixture approach of Andridge and Little (2009, 2011, 2020) which includes one sensitivity parameter to assess the robustness of inferences and does not require the explicit specification of a parametric model for the missing-data mechanism. This will be a further aspect to look at in future work. Another frequently mentioned point of criticism of selection models is the identification of an appropriate exclusion criterion. It is true that the choice of the exclusion criterion plays a crucial role in the successful application of our method. However, when working with survey data, there usually exists meta-information such as the survey mode or access corridors, which is suspected to be strongly correlated with the respondents’ willingness to provide information, but not with the outcome variable to be imputed and therefore forms an optimal exclusion criterion. Nevertheless, it might be advisable to carry out sensitivity analyses with regard to the exclusion criterion as well.

If baring these points in mind and not missunderstanding the selection model-based MNAR imputation model as the one and only model to describe a potential MNAR mechanism, our presented approach is a good choice for providing a specification of an alternative MNAR model that can be used within a broader sensitvity analysis.