Abstract
The evaluation of the possible effects of a treatment on an outcome plays a central role in both theoretical and applied statistical and econometrical literature. This paper focuses on nonparametric tests for possible difference in the distribution of potential outcomes due to receiving or not receiving a treatment. The approach is based on weighting observed data on the basis on the estimated propensity score. Kolmogorov–Smirnov type and Wilcoxon–Mann–Whitney type tests are constructed, and their limiting distributions are studied. Rejection regions are obtained by inverting confidence intervals. This involves the study of appropriate estimators of the limiting variance of test statistics. Approximations of quantiles via subsampling are also considered. The merits of the different tests are studied by Monte Carlo simulation. An application to the construction of tests for stochastic dominance is provided.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 General aspects
The evaluation of the possible effects of a treatment on an outcome plays a central role in both theoretical and applied statistical and econometrical literature; cfr. the excellent review papers by Athey and Imbens (2017) and Imbens and Wooldridge (2009). The main source of difficulty is that data are usually observational, so that the estimation of the treatment effect by simply comparing outcomes for treated vs. control subjects is prone to a relevant source of bias: receiving a treatment is not a “purely random” event, and there could be relevant differences between treated and control subjects. This motivates the need to account for confounding covariates.
As it appears from Sect. 3 of Imbens and Wooldridge (2009), the literature is mainly concerned with estimation of the difference between the expected value of outcomes for treated and control (untreated) subjects, i.e. ATE (Average Treatment Effect). Another quantity of interest is the effect of treatment on outcome quantiles, which is summarized by QTE (Quantile Treatment Effect). Several different techniques have been proposed to estimate ATE, under various assumptions (see Athey and Imbens 2017, Imbens and Wooldridge 2009 and references therein). As far as QTE is concerned, cfr. the paper by Firpo (2007).
Much less effort is devoted to testing for hypotheses on treatment effect, as stressed in Imbens and Wooldridge (2009). Using the symbols of Sect. 1.2, One question of interest is whether there is any effect of the program, that is whether the distribution of Y(1) differs from that of Y(0). This is equivalent to the hypothesis that not just the mean, but all moments, are identical in the two treatment groups. (cfr. Imbens and Wooldridge (2009)). Noticeable exceptions are in Abadie (2002), where tests are studied in settings with randomized experiments, and possibly with instrumental variables, and Crump et al. (2008), where tests for the hypothesis \(ATE =0\), as well as tests for the null hypothesis that there is no effect on average outcome conditional on the covariates, are proposed. In the present paper, we propose new nonparametric tests for the presence of a treatment effect. Such tests are essentially based on nonparametric estimates of the distribution functions of potential outcomes. In particular, in the present paper, nonparametric Wilcoxon–Mann–Whitney type and Kolmogorov–Smirnov type tests for two-group comparison are considered. Their main merit is to go beyond the simple difference in expectations of potential outcomes, i.e. beyond testing for the treatment effect on the basis of ATE to capture the possible difference between treated and untreated subjects due to difference in the shape of their distributions.
Testing the hypotheses of treatment effect has received considerable attention mainly in the case of a complete randomization scheme for the assignment-to-treatment mechanism; cfr. Ding (2017) Li et al. (2018), where permutation tests are proposed. Similarities and differences with the present paper are stressed in Sect. 3.
1.2 Problem description
Let Y be an outcome of interest, observed on a sample of n independent subjects. Some of the sample units are treated with an appropriate treatment (treated group); the other sample units are untreated (control group). If T denotes the treatment indicator variable, then whenever \(T= 1\), \(Y_{(1)}\) is observed; otherwise, if \(T= 0\), \(Y_{(0)}\) is observed. Here, \(Y_{(1)}\) and \(Y_{(0)}\) are the potential outcomes due to receiving or not receiving the treatment, respectively. The observed outcome is then equal to \(Y= TY_{(1)} + (1 - T) Y_{(0)}\). In the sequel, \(F_1(y)=P(Y_{(1)} \le y)\) will denote the distribution function (d.f.) of \(Y_{(1)}\), and \(F_0(y)=P(Y_{(0)} \le y)\) the d.f. of \(Y_{(0)}\).
Since receiving a treatment is not a purely random event, as in experimental framework, there could be relevant differences between treated and untreated subjects, due to the presence of confounding covariates. In the sequel, we will denote by X the (random) vector of relevant covariates, that is assumed to be observed.
In order to get consistent estimates, identification restrictions are necessary. The relevant restriction assumed in the sequel is that selection of treatment is based on observable variables: given a set of observed covariates, assignment either to the treatment group or to the control group is random. Formally speaking, let \(p(x) = P(T = 1 \vert X = x)\) be the conditional probability of receiving the treatment given covariates X; it is the propensity score. The marginal probability of being treated, \(P(T = 1)\), is equal to E[p(X)].
In the sequel, the main assumption is strong ignorability (cfr. Rosenbaum and Rubin 1983). In more detail, consider the joint distribution of (\(Y_{(1)}, \, Y_{(0)}, \, T, \, X\)), and denote by \({\mathcal {X}}\) the support of X. The following assumptions are assumed to hold.
-
(i)
Unconfoundedness (cfr. Rubin 1977): given X, \((Y_{(1)}, \, Y_{(0)})\) are jointly independent of
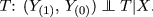
-
(ii)
The support of X, \({\mathcal {X}}\) is a compact subset of \({\mathbb {R}}^l\).
-
(iii)
Common support: there exists \(\delta >0\) for which \(\delta \le p(x) \le 1-\delta \; \forall \, x \in {\mathcal {X}}\), so that \(\underset{x}{\inf } \, p(x) \ge \delta \), \(\underset{x}{\sup } \, p(x) \le 1-\delta \).
Assumption (i) is also known as Conditional Independence Assumption (CIA).
For the sake of simplicity, we will use in the sequel the notation
From (i)-(iii), the basic relationships
are obtained.
The Average Treatment Effect (ATE) is \(\tau = E[ Y_{(1)} ] - E[ Y_{(0)} ]\). The estimation of ATE is a problem of primary importance in the literature, and several different approaches have been proposed ( Athey and Imbens 2017 and references therein). Another parameter of interest is the Quantile Treatment Effect (QTE), which is the difference between quantiles of \(F_1\) and \(F_0\): \(F_1^{-1} (p) - F_0^{-1} (p)\), with \(0<p<1\); cfr. Firpo (2007). In particular, when \(p=1/2\), it reduces to the Median Treatment Effect.
As already remarked, in the present paper, we focus on testing for treatment effect, where the null hypothesis is the equality of \(F_0\) and \(F_1\) (absence of treatment effect). Now, testing for a treatment effect has received considerable attention within the complete randomization scheme ( Ding 2017, Li et al. 2018). Let \(n_1 = T_1 + \cdots + T_n\), \(n_0 = n- n_1\). The basic assumption of the above mentioned papers is that the distribution of \((T_1 , \, \dots , \, T_n )\), given the covariates \(X_i\)s, is such that each value \((t_1 , \, \dots , \, t_n) \in \{ 0, \, 1 \}^n\) has probability \(n_1! n_0! / n!\) that does not depend on the values of any observed (or unobserved) covariates. On the contrary, in the present paper, the “selection on observable” assumption is made.
A second important difference is that, if \(Y_{i,(0)}\), \( Y_{i,(1)}\) are the potential outcomes for sample unit i, in Ding (2017), Li et al. (2018) \(Y_{i,(0)}\) and \( Y_{i,(1)}\) are considered as fixed, although unknown. The only involved probability distribution is that of \((T_1 , \, \dots , \, T_n )\). The main hypotheses of the treatment effect are essentially two: the sharp hypothesis \(Y_{i,(0)} = Y_{i,(1)}\) for all is, and the weak hypothesis \(\sum _i Y_{i,(0)} /n = \sum _i Y_{i,(1)} /n\).
In the present paper, an extra source of variability is considered, namely the probability distribution of \(Y_{i,(0)}\) and \(Y_{i,(1)}\), that can be viewed as a superpopulation model (cfr. Cassel et al. 1977). The hypothesis \(F_0 = F_1\) is in a sense in between the sharp and the weak hypotheses, because it is equivalent to test \(Y_{i,(0)} {\mathop {=}\limits ^{d}} Y_{i,(1)}\), where \({\mathop {=}\limits ^{d}}\) denotes equality in distribution.
1.3 Basic limiting results
The basic approach to the estimation of \(F_1\), \(F_0\) is in Donald and Hsu (2014). A crucial point consists in estimating the propensity score \(p(x) = P(T = 1 \vert X = x)\). A nonparametric estimator based on a logit series estimation is developed in Hirano et al. (2003). The essential idea consists in writing the propensity score p(x) in the form \(L( h_0 (x) )\), where \(L(z) = e^z / ( 1- e^z )\) is the logit function. In the second place, \(h_0 (x)\) is approximated through a (linear) sieve \(h_K (x) = {{\varvec{H}}}_K (x)^T {\varvec{\pi }} _K\) (with K depending on the sample size), \({{\varvec{H}}}_K (x)\) being a polynomial in xs. The K-dimensional vector \({\widehat{{\varvec{\pi }} }}_K\) is estimated by maximum likelihood method:
In Kim (2013, 2019), a generalization including the case of splines is considered.
For notational simplicity, and similarly to (1), define:
In order to estimate \(F_1\) and \(F_0\), in Donald and Hsu (2014), the following “Hájek - type” estimators are considered:
where
The large sample distribution of the above estimators is studied via the bivariate process:
that plays the same role as the empirical process in classical nonparametric statistics. The subsequent result is a minor generalization of Donald and Hsu (2014), based on Theorem 3.1 in Kim (2013). Its main interest is that it covers the case of propensity scores nonparametrically estimated through arbitrary link functions (for instance, Probit instead of Logit) and constructed through sieves not necessarily based on polynomials (for instance splines, as in Kim (2013)).
Proposition 1
Suppose that Assumptions 2.1–2.3 and 3.3 in Kim (2013) are satisfied, and suppose further that, for \(j=0\), 1, \(Y_{(j)}\) possesses finite second moment, that \(E[Y_{(j)} \vert x ]\) is continuously differentiable, and that \(F_j (y)\), \(F_j (y \vert x ) \) are continuous. Then, the sequence of stochastic processes (6) converges weakly, as n goes to infinity, to a Gaussian process \(W(y) = [ W_1 (y) , \, W_0 (y) ]^{T}\) with null mean function (\(E[ W_j (y) ] = 0\), \(j=1, \, 0\)) and covariance kernel:
where:
Weak convergence takes place in the set \(l_2^{\infty } ( {\mathbb {R}} )\) of bounded functions \({\mathbb {R}} \mapsto {\mathbb {R}}^2\) equipped with the sup-norm (if \(f = (f_1 , \, f_0 )\), \(\Vert f \Vert = \sup _y \vert f_1 (y ) \vert + \sup _y \vert f_0 (y ) \vert \)).
Proof
Cfr. “Appendix”.
Due to the continuity of \(F_1\), \(F_0\), the weak convergence of Proposition 1 also holds in the space \(D[-\infty , +\infty ]^2\) of \({\mathbb {R}}^2\)-valued càdlàg functions equipped with the Skorokhod topology.
The limiting process \(W( \cdot )\) in Proposition 1 is a Gaussian process, possessing trajectories that are a.s. continuous. This result will be used in the next Sections.\(\square \)
Proposition 2
If \(F_0\) and \(F_1\) are continuous, the limiting process \(W ( \cdot ) = [ W_1 ( \cdot ) , \, W_0 ( \cdot ) ] \) possesses trajectories that are continuous and bounded with probability 1.
If, in addition, the cross-covariance matrix \(C(y, \, t) = E\bigl [W(y) \otimes W(t) \bigr ]\) is such that \(C(y, \,y)\) is a positive-definite matrix, for every real y, then the functionals:
have absolutely continuous distribution on \((0, \, + \infty )\).
Proof
See “Appendix”.\(\square \)
The paper is organized as follows: In Sect. 1.2, the problem is described, and basic preliminary results in the literature are provided in Sect. 1.3. Section 2 is devoted to the construction of a Wilcoxon–Mann–Whitney type test for the treatment effect, and in Sect. 3, a Kolmogorov–Smirnov type test for the same problem is considered. In Sect. 4, a test for stochastic dominance of the treatment is introduced and studied. The finite sample performance of the proposed methodologies is studied via Monte Carlo simulation in Sect. 5, where comparisons are made with other commonly used tests. An empirical application is presented in Sect. 6. Finally, Sect. 7 is devoted to conclusions.
2 Testing for the presence of a treatment effect: two (sub)sample Wilcoxon test
2.1 Wilcoxon-type statistic
In nonparametric statistics, a problem of considerable relevance consists in testing for the possible difference between two samples. Among several proposals, the two-sample Wilcoxon (or Wilcoxon–Mann–Whitney) test plays a central role in applications, mainly because of its properties. The goal of the present section is to propose a Wilcoxon-type statistic to test for the possible difference between the (sub)sample of treated subjects and the (sub)sample of untreated subjects. In other terms, we aim at developing a Wilcoxon-type statistic to test for the possible presence of a treatment effect.
From now on, we will assume \(F_0\) and \(F_1\) are both continuous. As in the classical Wilcoxon two-sample test, in order to measure the difference between the distributions of \(Y_{(1)}\) and \(Y_{(0)}\), we consider:
The parameter \(\theta _{01}\) (12) possesses a natural interpretation, because it is equal to the probability that a treated subject possesses a y-value greater than the y-value for an independent, untreated subject. A few properties of \(\theta _{01}\) are listed as follows:
-
(1)
\(\theta _{01}\) depends only on the marginal d.f.s \(F_0\), \(F_1\) (not on the way \(Y_{(0)}\), \(Y_{(1)}\) are associated in the same subject).
-
(2)
If \(F_0 = F_1\) then \(\theta _{01}=\frac{1}{2}\).
-
(3)
Using \(\theta _{01}\) is equivalent to use \(\theta _{10}=\int F_1(y) \, \mathrm{d}F_0(y)\), as it is seen by an integration by parts.
-
(4)
If \(F_1(y) \le F_0(y)\) \(\forall \, y \in {\mathbb {R}}\), i.e. if \(Y_{(1)}\) is stochastically larger than \(Y_{(0)}\), then:
$$\begin{aligned} \theta _{01}=1- \int _{{\mathbb {R}}} F_1(y) \, \mathrm{d}F_0(y) \ge 1-\int _{{\mathbb {R}}} F_0(y) \, \mathrm{d}F_0(y) =\frac{1}{2} . \end{aligned}$$
The Wilcoxon-type statistic considered here is obtained in two steps, essentially by a plug-in approach.
-
Step 1.
Estimation of the marginal d.f.s \(F_1\), \(F_0\):
$$\begin{aligned} {\widehat{F}}_{j,n}(y)=\sum _{i=1}^{n} w^{(j)}_{i,n}I_{(Y_i \le y)}, \ w^{(j)}_{i,n}=\frac{I_{(T_i=1)}/{\widehat{p}}_{j,n}(x_i) }{\sum _{k=1}^{n} I_{(T_k=1)} / {\widehat{p}}_{j,n} (x_k) } , \;\; j=1, \, 0. \end{aligned}$$(13) -
Step 2.
Estimation of \(\theta _{01}\):
$$\begin{aligned} {\widehat{\theta }}_{01,n}&= \theta ( {\widehat{F}}_0 , \, {\widehat{F}}_1 ) \nonumber \\&= \int _{{\mathbb {R}}} {\widehat{F}}_{0,n}(y) \, \mathrm{d} {\widehat{F}}_{1,n}(y) \nonumber \\&= \sum _{i=1}^{n} \sum _{k=1}^{n} w^{(1)}_{i,n} w^{(0)}_{k,n} I_{(y_{k} \le y_{i})} . \end{aligned}$$(14)
Note that \(w^{(1)}_{i,n} w^{(0)}_{k,n} \ne 0 \) if and only if (iff) \((I_{(T_i=1)}=1) \wedge (I_{(T_k=0)}=1)\), i.e. iff i is treated and k is untreated. This shows that \({\widehat{\theta }}_{01}\) is based on the comparison treated/untreated.
The limiting distribution of the statistic (14) is obtained as a consequence of Proposition 1.
Proposition 3
Assume that the conditions of Proposition 1are fulfilled. Then,
where
and
Proof
See “Appendix”.
Before closing the present section, a few remarks.\(\square \)
Remark 1
We notice in passim that \(F_0 \equiv F_1\) implies \(\theta _{01} = 1/2\), but the converse is false. In other words, \(\theta _{01}\) could take the value 1/2 even when \(F_0\) and \(F_1\) do not coincide. As a consequence, and similarly to what happens in “usual” nonparametric statistics, the Wilcoxon-type test developed here is not consistent for all departures from \(F_0 \equiv F_1\).
Remark 2
From a practical point of view, rejecting the null hypothesis \(\theta _{01} =1/2\) in favor of \(\theta _{01} > 1/2\) means that the outcome for treated subjects tends to be larger than the outcome for untreated subjects. The higher \(\theta _{01}\), the larger the gap, in terms of outcomes, of untreated subjects when compared to treated subjects. The opposite occurs when the null hypothesis \(\theta _{01} =1/2\) is rejected in favor of \(\theta _{01} < 1/2\).
Remark 3
A referee asked whether it possible to extend the Wilcoxon-type test to the case when the treatment assignment is endogenous, but there is a binary Instrumental Variable available, as in Hsu et al. (2020). In principle, Theorem 3.1 in Hsu et al. (2020) could be used in place of Proposition 1 of the present paper, and the technique of Proposition 3 still applies provided that the trajectories of the limiting process are continuous. For the sake of brevity, we do not pursue this topic here.
2.2 Variance estimation
The asymptotic variance V appearing in (16) contains unknown terms, that can be consistently estimated on the basis of sample data. In particular, the estimation of \(\gamma _{01}(x) = E [ I_{(T=1)} p(x)^{-1} F_0(Y) \vert x ]\) can be simply developed by considering the regression of:
on \(x_i\), \(i = 1, \, \dots , \, n\), and by estimating the regression function via a method ensuring consistency (e.g. local polynomials, Nadaraya-Watson kernel regression, spline). The resulting estimator \({\widehat{\gamma }}_{01,n}(x)\) is uniformly consistent on compact sets of xs under few regularity conditions. In the same way, \(\gamma _{10}(x)\) can be consistently estimated by \({\widehat{\gamma }}_{10,n}(x)\), say. As a consequence the term \(V_x(\gamma _{10}(x)-\gamma _{01}(x))\) can be estimated by:
Note that as an alternative estimator, one could consider:
Next, we have to estimate:
The term \(E_x [ p(x)^{-1} \gamma _{01}(x)^2 ]\) can be estimated with:
The term:
can be estimated by means of a nonparametric regression of:
with respect to \(x_i\)s. The resulting estimator \({\widehat{M}}_{01,n}(x)\) is consistent under few conditions. In the same way, an estimator \({\widehat{M}}_{10,n}(x)\) of:
is obtained.
The asymptotic variance of \({\widehat{\theta }}_{10,n}\) can be finally estimated by:
2.3 Testing the equality of \(F_1\) and \(F_0\) via Wilcoxon-type statistic
A test for the equality of \(F_1\) and \(F_0\) can be constructed via the statistic \({\widehat{\theta }}_{01,n}\) (14). As already seen, when \(F_1\) and \(F_0\) coincide, \(\theta _{01}\) is equal to 1/2. Hence, the idea is to construct a test for the hypotheses problem
On the basis of Proposition 3, and the variance estimator (20), the region:
(where \(z_{\frac{\alpha }{2}}\) is the \((1-\frac{\alpha }{2})\) quantile of the standard Normal distribution) is an acceptance region of asymptotic significance level \(\alpha \).
2.4 Subsampling approach
As an alternative to variance estimation, one could approximate the quantiles of the distribution of \({\widehat{\theta }}_{01,n}\) using the subsampling technique. Generally speaking, subsampling possesses several important properties (cfr. Politis and Romano 1994). First of all, its computational burden is frequently less heavy than bootstrap, because replications are taken for subsamples of size \(m < n\). Secondly, and more importantly, it is asymptotically first-order correct (namely, it recovers the asymptotic distribution of the statistic under consideration) without imposing extra regularity conditions, such as bootstrap (cfr. van der Vaart (1998), p. 333). Define \(A_i=(X_i, T_i, Y_i)\), \(i=1, \, \dots , \, n\), and consider all the \({n}\atopwithdelims (){m}\) subsamples of size m of \((A_1, \, \dots , \, A_n)\). The subsampling procedure, in the present case, can be described as follows:
-
1.
Select M independent subsamples of size m from the sample of \((X_i,T_i,Y_i) \)s, \(i=1, \, \dots , \, n\).
-
2.
Denote by \({\widehat{F}}_{1,m;l}(y)\), \({\widehat{F}}_{0,m;l}(y)\) the estimates of \(F_1\), \(F_0\), respectively, from subsample l, and let \({\widehat{\theta }}_{01,m;l} (y)\) be equal to the Wilcoxon statistic (14) for the lth subsample.
-
3.
Compute the subsample statistics:
$$\begin{aligned} Z_{m,l}=\sqrt{m} \left( {\widehat{\theta }}_{01,m;l} - {\widehat{\theta }}_{01,n} \right) , \;\; l=1, \, \dots , \, M . \end{aligned}$$ -
4.
Compute the corresponding empirical d.f.:
$$\begin{aligned} {\widehat{R}}_{n,m}(z) = \frac{1}{M} \sum _{l=1}^{M} I_{( Z_{m,l} \le z)} . \end{aligned}$$ -
5.
Compute the corresponding quantile:
$$\begin{aligned} {\widehat{R}}_{n,m}^{-1}(p) = \inf \left\{ z: \; {\widehat{R}}_{n,m}(z) \ge p \right\} . \end{aligned}$$
Assuming that \(m/n \rightarrow 0\) as \(n \rightarrow \infty \), and using Th. 2.1 in Politis and Romano (1994), we have:
where \(\Phi \) denotes the Standard Normal d.f. The convergence in (22) is uniform in z. Moreover, from the continuity and strict monotonicity of \(\Phi \), it follows that the empirical quantile \({\widehat{R}}^{-1}_{n,m}(p)= \inf \{ z: \; {\widehat{R}}_{n,m}(z) \ge p \}\) converges in probability to the quantile of order p of the Standard Normal distribution:
From the above results, the asymptotically exact approximation:
is obtained. As a consequence, the interval:
is a confidence interval for \(\theta _{01}\) of asymptotic level \(1- \alpha \). Hence, the test consisting in rejecting \(H_0\) whenever the interval (24) does not contain 1/2, possesses asymptotic significance level \(\alpha \).
Before ending the present section, we remark that an alternative to subsampling is the multiplier method by Donald and Hsu (2014). From a theoretical point of view, subsampling does not require Assumption 3.1-1 and requires a weaker version of Assumption 3.3-2 in Donald and Hsu (2014).
3 Testing for the presence of a treatment effect: two (sub)sample Kolmogorov–Smirnov test
In this section, we deal with the construction of a Kolmogorov–Smirnov test of (asymptotic) size \(\alpha \) for the hypotheses problem:
where \(\Delta (y) = F_1 (y) - F_0 (y)\). The main merit of this test, as it will be clear in the sequel, is that it is consistent for all alternatives, i.e. for all departures from \(F_0 \equiv F_1\).
Similarly to what was done at the end of the above section, a simple idea to construct a test for the hypotheses problem (25) is to invert a confidence region for \(\Delta ( \cdot )\). The null hypothesis \(H_0\) is rejected whenever the confidence region has empty intersection with \(H_0\). More formally, the test procedure we consider here is defined as follows:
-
(i)
Compute a confidence region for \(\Delta (\cdot )\) of (at least asymptotic) level \(1-\alpha \).
-
(ii)
Reject \(H_0\) if the confidence region for \(\Delta (\cdot )\) and \(H_0\) are disjoint, i.e. if for at least a real y the region does not contain the value zero.
Define:
From Proposition 1, \(\sqrt{n} ( {\widehat{\Delta }}_n ( \cdot ) - \Delta ( \cdot ) )\) converges weakly to a Gaussian process that can be represented as \(W_1 ( \cdot ) - W_0 ( \cdot )\). Define next:
Assuming that both \(F_0\), \(F_1\) are continuous d.f.s., from Proposition 2, it follows that:
Moreover, again assuming the continuity of \(F_0\), \(F_1\), as a further consequence of Proposition 2, the r.v. D (26) is absolutely continuous with strictly positive density. Hence, for every \(0< \alpha < 1\), there exists a unique \(d_{1-\alpha }\) such that:
The quantile \(d_{1-\alpha }\) can be estimated by the subsampling technique (cfr. Politis and Romano 1994). Define again \(A_i=(X_i, T_i, Y_i)\), \(i=1, \, \dots , \, n\), and consider all the \({n}\atopwithdelims (){m}\) subsamples of size m of \((A_1, \, \dots , \, A_n)\). Similarly to Sect. 2.4, the subsampling procedure, in the present case, can be described as follows:
-
1.
Select M independent subsamples of size m from the sample of \((X_i,T_i,Y_i) \)s, \(i=1, \, \dots , \, n\).
-
2.
Denote by \({\widehat{F}}_{1,m;l}(y)\), \({\widehat{F}}_{0,m;l}(y)\) the estimates of \(F_1\), \(F_0\), respectively, from subsample l, and let \({\widehat{\Delta }}_{m;l} (y)\) be equal to \({\widehat{F}}_{1,m;l}(y) - {\widehat{F}}_{0,m;l}(y)\).
-
3.
Compute the subsample statistics:
$$\begin{aligned} {\widehat{D}}_{m,l}=\sqrt{m} \sup _y \left| {\widehat{\Delta }}_{m;l} (y) - {\widehat{\Delta }}_{n}(y) \right| , \;\; l=1, \, \dots , \, M . \end{aligned}$$ -
4.
Compute the corresponding empirical d.f.:
$$\begin{aligned} {\widehat{R}}_{n,m}(d) = \frac{1}{M} \sum _{l=1}^{M} I_{( {\widehat{D}}_{m,l} \le d)} . \end{aligned}$$ -
5.
Compute the corresponding quantile:
$$\begin{aligned} {\widehat{d}}_{1-\alpha } = {\widehat{R}}_{n,m}^{-1}(1- \alpha ) = \inf \left\{ d: \; {\widehat{R}}_{n,m}(d) \ge 1-\alpha \right\} . \end{aligned}$$
Under the same regularity conditions as in Sect. 2.4, it is easy to see that:
where the convergence in (29) is uniform in d. In addition, from the continuity and strict monotonicity of \(P ( D \le d )\), it follows that the empirical quantile \(R^{-1}_{n,m}(p)= \inf \{ d: \; R_{n,m}(d) \ge p \}\) converges in probability to the pth quantile of the distribution of D:
From the above results, the asymptotically exact approximation:
holds. Hence, the region:
is a confidence band of (asymptotic) level \(1- \alpha \) for \(\Delta ( \cdot )\). The null hypothesis \(H_0\) is rejected whenever the confidence band (31) does not intersect 0 for some real y. It is immediate to see that the constructed test has (asymptotic) size \(\alpha \).
4 Testing for stochastic dominance
4.1 The problem
In evaluating the effect of a treatment, it is sometimes of interest to test whether the treatment itself has an effect on the whole distribution function of Y, i.e. whether the treatment improves the behavior of the whole d.f. of Y. Various forms of stochastic dominance are discussed in McFadden (1989), Anderson (1996). In particular, in the present section, we will focus on testing for first-order stochastic dominance. The d.f. \(F_1\) first-order stochastically dominates \(F_0\) if \(F_1(y) \le F_0(y)\) \(\forall \, y \in {\mathbb {R}}\). Our main goal is to construct a test for the (unidirectional) hypotheses:
where \(\Delta (y)=F_1(y)-F_0(y)\).
In econometrics and statistics, there is an extensive amount of literature on testing for stochastic dominance, since the papers by Anderson (1996), Davidson and Duclos (2000). In Linton et al. (2005), a Kolmogorov–Smirnov type test is proposed, and a method to construct critical values based on subsampling is proposed. For further bibliographic reference, and a deep analysis of contributions to testing for stochastic dominance, cfr. the recent paper by Donald and Hsu (2016).
In the present paper, we confine ourselves to a simple, intuitive procedure to test for unidirectional dominance.
4.2 Approach based on Kolmogorov–Smirnov statistic
A simple idea to construct a test for the hypotheses problem of Sect. 4.1 is to invert a confidence region for \(\Delta ( \cdot )\). The null hypothesis \(H_0\) is rejected whenever the confidence region has empty intersection with \(H_0\). More formally, the test procedure we consider here is defined as follows:
-
(i)
Compute a confidence region for \(\Delta (\cdot )\) of (at least asymptotic) level \(1-\alpha \);
-
(ii)
Reject \(H_0\) if the confidence region for \(\Delta (\cdot )\) and \(H_0\) are disjoint, that is if for at least a real y the region has lower bound greater than zero.
From now on, we will assume that both \(F_0\), \(F_1\) are continuous d.f.s. Using the arguments in Sect. 3, it is possible to see that the r.v.:
has absolutely continuous distribution, with \(P \left( \sup _y \left( W_1(y)-W_0(y) \right) \ge 0 \right) =1\). Hence, there exists a single \(d_{1-\alpha }\) such that:
The quantile \(d_{1-\alpha }\) can be estimated by subsampling, as outlined in Sect. 3. Define:
A subsampling procedure to estimate \(d_{1-\alpha }\) is described as follows:
-
1.
Select M independent subsamples of size m from the sample of \((X_i,T_i,Y_i) \)s, \(i=1, \, \dots , \, n\).
-
2.
Compute the subsample statistics:
$$\begin{aligned} {\widehat{\theta }}_{m,l}=\sqrt{m} \sup _y \left( {\widehat{F}}_{1,m;l}(y) -{\widehat{F}}_{0,m;l}(y) - ( {\widehat{F}}_{1,n}(y) - {\widehat{F}}_{0,n}(y) \right) , \;\; l=1, \, \dots , \, M . \end{aligned}$$ -
3.
Compute the corresponding empirical d.f.:
$$\begin{aligned} {\widehat{R}}_{n,m}(u) = \frac{1}{M} \sum _{l=1}^{M} I_{( {\widehat{\theta }}_{m,l} \le u)} . \end{aligned}$$ -
4.
Compute the corresponding quantile:
$$\begin{aligned} {\widehat{d}}_{1-\alpha } = {\widehat{R}}_{n,m}^{-1}(u) = \inf \left\{ u: \; {\widehat{R}}_{n,m}(u) \ge 1-\alpha \right\} . \end{aligned}$$
The arguments in Sect. 3 show that:
Hence, the asymptotically exact approximation
holds. As a consequence, the region:
is a confidence region for \(\Delta (\cdot )\) with asymptotic level \(1-\alpha \). The null hypothesis \(H_0\) is rejected whenever:
The main feature of the test developed here is that it is computationally simpler than the test(s) proposed in Donald and Hsu (2014). Its relative merits will be evaluated by simulation in Sect. 5.
4.3 Approach based on Wilcoxon statistic
As remarked by a referee, the unidirectional Wilcoxon-type test proposed in Sect. 2 may be used to construct a simplified test for stochastic dominance, easier to implement if compared to that of Sect. 4.2. More precisely, if \(F_1(y) \le F_0(y)\) \(\forall \, y \in {\mathbb {R}}\), then \(\theta _{01} \ge 1/2\), so that the stochastic dominance problem may be transformed into:
Using the same reasoning of Sect. 2.4, a rejection region of asymptotic significance level \(\alpha \) is as follows:
\(z_{\alpha }\) being the \((1- \alpha )\) quantile of the standard Normal distribution.
Alternatively, we may resort to the subsampling approach of Sect. 2.4. In this case, the idea is to construct a unidirectional confidence region for \(\theta _{01}\), and in rejecting \(H_0\) whenever such a region is within the interval \([0, \, 1/2 )\). With the usual symbols, at an asymptotic significance level \(\alpha \), the stochastic dominance hypothesis is rejected whenever \({\widehat{\theta }}_{01,n} - \frac{1}{\sqrt{n}} R^{-1}_{n,m} \left( 1- \alpha \right) < 1/2\).
5 A simulation study
The goals of the present section are essentially two. First of all, (i) the performance (in terms of significance level and power) of the Wilcoxon-type and Kolmogorov–Smirnov type tests introduced so far are compared with “traditional” tests proposed in the literature. Secondly, (ii) the performance of the stochastic dominance test introduced in Sect. 4 is studied, again by Monte Carlo simulation.
As far as the comparison (i) is concerned, the tests considered are listed as follows:
-
Wilcoxon-type test with variance estimated as in Sect. 2.2;
-
Wilcoxon-type test with quantiles estimated by subsampling;
-
Kolmogorov–Smirnov type test, as introduced in Sect. 3;
-
test based on the estimator of ATE proposed in Hirano et al. (2003) (with variance estimated as in Hirano et al. (2003))
-
Mann-Whitney test;
-
Conditional randomization test in Branson et al. (2019);
-
Conditional permutation test under a logistic model for the propensity score Rosenbaum (1984).
The size and power of the above tests are compared in two different cases: (a) there is no treatment effect, i.e. \(F_{1} \) coincides with \(F_{0}\); (b) there is treatment effect, i.e. \(F_{1} \) is different from \( F_0\). The treatment effect may involve a shift alternative and/or a shape alternative. The simulation scenarios are described in Table 1.
\(N=1000\) replications with samples sizes \(n=50, 100, 200, 400\) have been obtained by Monte Carlo simulation. The propensity score has been estimated via the estimator considered in Sects. 1.3, (3); the term K has been chosen through least squares cross-validation. As far as subsample approximation is concerned, \(M=1000\) subsamples of size \(m=n^{0.8}\) have been drawn by simple random sampling from each of the \(N=1000\) original samples.
In simulation scenario I (absence of treatment effect), the potential outcome \(Y_{(j)}\) is specified as:
where X has a Bernoulli distribution with success probability 1/2 (\(X \sim Be (1/2))\) and \(U_j\) has a uniform distribution in the interval \([ - 10 , \, 10]\) (\(U_j \sim U (-10 , \, 10)\)). The r.v.s \(U_1\), \(U_0\) are mutually independent. Clearly, \(\theta _{01} = 1/2\), \(E[Y_{(0)}]=E[Y_{(1)}]=75\), and \(ATE=0\).
The exact distribution function of \(Y_{(j)}\) is as follows:
The d.f. \(F_j\) (35), and the corresponding density functions \(f_j\), are depicted in Fig. 1.
The propensity score, in this case, is as follows:
Furthermore, we have \(E[ Y \vert T=0]=72.5\) and \(E[Y \vert T=1 ]=77.5\), so that \(E[Y \vert T=1] - E[ Y \vert T=0]=5.0\) even if \(ATE =0\). This is clearly due to the confounding effect of X, and makes it difficult to detect the absence of treatment effect.
In scenario IV (presence of treatment effect), the potential outcome \(Y_{(0)}\) is specified as in (34) with \(j=0\). The potential outcome \(Y_{(1)}\) is specified as:
where X has a Bernoulli distribution \(X \sim Be(0.5)\) and \(U_{0}\), \(U_{1}\) have a Uniform distribution \(U_1 \sim U[-10;10]\). The r.v.s X, \(U_{0}\), \(U_{1}\) are mutually independent.
The exact distribution function of \(Y_{(1)}\) is reported as follows:
and depicted in Fig. 2.
In scenario IV, we have \(\theta _{01} = 0.67\), \(E[Y_{(0)}]=75\), \(E[Y_{(1)}]=80\), and then \(ATE=5\). Furthermore, \(F_{1}\) stochastically dominates \(F_0\).
The propensity score is as follows:
so that \(E[Y \vert T=0]=77.5\) and \(E[ Y \vert T=1 ]=77.5\) even if \(ATE \ne 0\). As in scenario I, this is due to the confounding effect of X that makes it difficult to detect a treatment effect through a naive analysis. Scenario III is similar to scenario IV, but with \(E[ Y_{(1)} ]=76\). Since the shift of \(F_1\) w.r.t. \(F_0\) in scenario IV is higher than in scenario III, detecting treatment effect in scenario III is more difficult than in scenario IV.
In Scenario II, the treatment effect is due to a shape difference of \(F_1\) w.r.t. \(F_0\), without shift. In more detail, \(E[Y_{(1)}] = E[Y_{(0)}]\), so that \(ATE =0\), but \(\theta _{01} \ne 1/2\). Again, this makes it difficult to detect a treatment effect through ATE.
Scenario V is generated as scenario IV with a shape effect in addition to the shift effect.
As an overall comment, in scenarios II-V (\(H_0\) false), the propensity score is chosen to compensate the effect of shape and shift giving rise to a confounding no treatment effect. In scenarios III and IV, the treatment effect is due to a shift of \(F_1\) w.r.t. \(F_0\), so that ATE is non-null. In scenario II, detecting treatment effect is difficult, because it is only due to a difference if shape of \(F_1\) w.r.t. \(F_0\), with \(ATE =0\). Finally, scenario V mixes together shift and shape in the treatment effect.
Table 2 summarizes the rejection probabilities of the null hypothesis for different scenarios and sample sizes.
The results show that the Wilcoxon-type test and the Kolmogorov–Smirnov test are better than the test based on estimated ATE, in terms of both actual significance level (scenario I) and power (scenarios II–V). Wilcoxon-type test with quantiles estimated by subsampling seems to offer the best performance in terms of power, although its actual significance level seems to be slightly worse than in the case of estimated variance. Among the others, the test based on the estimator of ATE proposed in Hirano et al. (2003) and the conditional randomization tests in Branson et al. (2019) and in Rosenbaum (1984) do not exhibit performances as good as Wilcoxon-type test with quantiles estimated via subsampling. As an overall remark, Wilcoxon test seems to offer good performance in terms of both simplicity and power.
As far as the test for stochastic dominance is concerned, the test procedures of Sects. 4.2, 4.3 have been studied under scenarios I - III, and for sample sizes 50, 100, 200, 400, together with the test of stochastic dominance proposed by Donald and Hsu (Donald and Hsu 2014). The corresponding rejection probabilities are shown in Table 3. Even if all tests do have an actual significance level larger than the nominal level \(5 \%\), Wilcoxon test exhibits rejection rates under \(H_0\) slightly better than other tests, especially for a sample size \(n \le 200\). When the null hypothesis \(H_0\) of stochastic dominance is false, all tests perform similarly for a sample size \(n \ge 200\). However, for sample sizes \(n= 50, \, 100\), the Wilcoxon has slightly better rejection rates.
6 Empirical study
In the present section, the test of stochastic dominance developed in Sect. 4 is applied to data from National Supported Work Demonstration (NSW) job training program described in LaLonde (1986) and analyzed by Dehejia and Wahba (1999), Wooldridge (2001). The data set we use corresponds to the subsample termed “RE74 subset” in Dehejia and Wahba (1999). The treatment variable T is equal to 1 if the individual participates in the job training. The outcome variable is “Earnings in 1978”. RE74 subset contains an experimental sample from a randomized evaluation of the NSW program, in which 185 individuals received the treatment and 260 did not.
As in Donald and Hsu (2014), our tests have been applied for the whole group to RE74 subset, because the treatment is randomly assigned in this subset, which implies the distribution functions of \(Y_{(0)}\), \(Y_{(1)} \) for the whole group are the same as the distribution functions for the treated group. As in Donald and Hsu (2014), the tests are evaluated for three different estimates of the propensity score: no covariates; constant, age and squared age; constant, age, squared age, real earnings in 1974 and 1975, a binary high school degree indicator, marital status, and dummy variables for Black and Hispanic ( Wooldridge (2002)). The estimated distribution functions are depicted in Fig. 3.
In the three cases, the hypothesis that the 1978 real earning under job training stochastically dominates the 1978 real earning without job training is accepted. The p values approximated by 1000 repetitions are equal to 1. The results are robust to different specifications of the propensity score. The results are coherent with Donald and Hsu (2014).
7 Conclusions
Detecting a treatment effect in the potential outcomes model is a problem of considerable importance in both theoretical and applied Statistics and Econometrics. In particular, in this paper, attention is focused on detecting treatment effect not necessarily consisting of a difference of expected outcome for treated and untreated subjects, namely in Average Treatment Effect (ATE). Nonparametric tests to detect a possible treatment effect on potential outcomes consisting of a change of their probability distributions are proposed. The basic approach is based on inverse probability weighting, consisting first of estimating propensity scores, and then in weighting observed outcomes through the reciprocal of the corresponding estimated propensity scores.
Wilcoxon-type tests and Kolmogorov–Smirnov test are constructed and compared to tests based on ATE, as well as to permutation tests proposed in the literature. The comparison is made via a simulation study, where the different scenarios listed below are considered.
-
1.
Absence of treatment effect (scenario I).
-
2.
Treatment effect consisting in a shift of the outcome distribution under treatment (scenario III, IV).
-
3.
Treatment effect consisting in a change of the shape of the outcome distribution under treatment (scenario II).
-
4.
Treatment effect consisting in both shift and change of shape of the outcome distribution under treatment (scenario V).
In all scenarios, the proposed tests perform better than the existing ones (permutation tests and test based on ATE) in terms of both power and approximation of significance level. In particular, due to its simplicity, the Wilcoxon-type test with quantiles estimated via subsampling can be considered slightly better than the other proposed tests.
A similar pattern holds in testing for stochastic dominance. A comparison through simulation shows that Wilcoxon test has rejection rates under \(H_0\) (i.e. under stochastic dominance) closer to the nominal level than other tests, especially for a sample size \(n \le 200\). Under the alternative (absence of stochastic dominance), the Wilcoxon test is comparable to other tests, and sometimes better, especially for moderate sample size. In view of these results, and of its simplicity, as well, the Wilcoxon test seems to be recommendable also for testing stochastic dominance.
References
Abadie, A.: Bootstrap tests for distributional treatment effects in instrumental variable models. J. Am. Stat. Assoc. 97, 284–292 (2002)
Anderson, G.: Nonparametric tests of stochastic dominance in income distribution. Econometrica 64, 1183–1193 (1996)
Athey, S., Imbens, G.W.: The state of applied econometrics: causality and policy evaluation. J. Econ. Persp. 31(2), 3–32 (2017)
Billingsley, P.: Convergence of Probability Measures, 2nd edn. Wiley, New York (1999)
Branson, Z. and Miratrix, L.: Randomization tests that condition on non-categorical covariate balance. J. Causal Inference 7 (2019)
Cassel, C., Särndal, C., Wretman, J.H.: Foundations of Inference in Survey Sampling. Wiley, New York (1977)
Crump, K., Hotz, V.J., Imbens, G.W., Mitnik, O.A.: Nonparametric tests for treatment effect heterpgeneity. Rev. Econ. Stat. XC(3), 389–405 (2008)
Davidson, R.S., Duclos, J.Y.: Statistical inference for stochastic dominance and for the measurement of poverty and inequality. Econometrica 68, 1435–1464 (2000)
Dehejia, R.H., Wahba, S.: Causal effects in nonexperimental studies: reevaluating the evaluation of training programs. J. Am. Stat. Assoc. 94(448), 1053–1062 (1999)
Ding, P.: A paradox from randomization-based causal inference. Stat. Sci. 32, 331–345 (2017)
Donald, S.G., Hsu, Y.C.: Estimation and inference for distribution functions and quantile functions in treatment effect models. J. Econom. 178, 383–397 (2014)
Donald, S.G., Hsu, Y.C.: Improving the power of tests of stochastic dominance. Economet. Rev. 35, 553–58 (2016)
Dudley, R.M.: Sample functions of the gaussian process. Ann. Probab. 1, 66–103 (1973)
Firpo, S.: Efficient semiparametric estimation of quantile treatment effects. Econometrica 75, 259–276 (2007)
Hirano, K., Imbens, G.W., Ridder, G.: Efficient estimation of average treatment effects using the estimated propensity score. Econometrica 71, 1161–1189 (2003)
Hsu, Y.C., Lai, T.C., Lieli, R.: Estimation and inference for distribution and quantile functions in endogenous treatment effect models. Econom. Rev. (2020). https://doi.org/10.1080/07474938.2020.1847479
Imbens, G.W., Wooldridge, J.M.: Recent developments in the econometrics of program evaluation. J. Econ. Lit. 47(1), 5–86 (2009)
Kim, K.I.: An alternative efficient estimation of average treatment effects. J. Market Econ. 42, 1–41 (2013)
Kim, K.I.: Efficiency of average treatment effect estimation when the true propensity is parametric. J. Market Econ. (2019). https://doi.org/10.3390/econometrics7020025
LaLonde, R.J.: Evaluating the econometric evaluations of training programs with experimental data. Am. Econ. Rev. 76(4), 604–620 (1986)
Leadbetter, M.R., Weissner, J.H.: On continuity and other analytic properties of stochastic process sample functions. Proc. Am. Math. Soc. 22, 291–294 (1969)
Li, X., Ding, P., Rubin, D.B.: Asymptotic theory of randomization in treatment-control experiments. PNAS 115, 2157–9162 (2018)
Lifshits, M.A.: On the absolute continuity of distributions of functionals of random processes. Theory Probab. Appl. 27, 600–607 (1982)
Linton, O., Maasoumi, E., Whang, Y.J.: Consistent testing for stochastic dominance under general sampling schemes. Rev. Econ. Stud. 72, 735–765 (2005)
McFadden, D.: Testing for stochastic dominance. In: Josef, H., Fombay, T.B., Seo, T.K. (eds.) Studies in Economics of Uncertainty. Springer, New York (1989)
Politis, D.N., Romano, J.P.: Large sample confidence regions based on subsamples under minimal assumptions. Ann. Stat. 22, 2031–2050 (1994)
Rosenbaum, P.R.: Conditional permutation tests and the propensity score in observational studies. J. Am. Stat. Assoc. 79(387), 565–574 (1984)
Rosenbaum, P.R., Rubin, D.B.: The central role of the propensity score in observational studies for causal effects. Biometrika 70, 41–55 (1983)
Rubin, D.B.: Assignment to treatment group on the basis of a covariate. J. Educ. Stat. 2, 1–26 (1977)
van der Vaart, A.: Asymptotic Statistics. Cambridge University Press, Cambridge (1998)
Wooldridge, J.M.: Econometric Analysis of Cross Section and Panel Data. The MIT Press (2001)
Wooldridge, J.M.: Econometric Analysis of Cross Section and Panel Data. MIT Press, Cambridge (2002)
Funding
Open access funding provided by Luiss University within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Proofs
Appendix: Proofs
Proof of Proposition 1
It is enough to use Theorem 3.1 in Kim (2013) and to repeat verbatim the arguments in Donald and Hsu (2014). \(\square \)
Proof of Proposition 2
Let \(Q_j(u)=F_j^{-1}(u) = \inf \{y : \; F_j(y) \ge u \}\), \(j=1, \, 0\). Then, \(W_j ( \cdot )\) possesses continuous trajectories almost surely if \(B_j (u)=W_1(Q(u))\) possesses continuous trajectories almost surely. From the proof of Proposition 1, it is not difficult to see that the inequality
holds, c being an appropriate constant. Hence, we may write
The continuity of the trajectories of \(B_j ( \cdot )\) follows from (38) and formula (6) in Leadbetter and Weissner (1969).
As far as boundedness is concerned, from the structure of the covariance kernel of \(W ( \cdot )\), t is now seen that
from which the almost sure boundedness of the trajectories of \(W_j( \cdot )\) follows.
Assume now that the cross-covariance matrix \(C(y, \, t) = E\bigl [W(y) \otimes W(t) \bigr ]\) is is positive-definite for every real y. Under this condition, it is possible to show ( Lifshits (1982)) that the functional
can only have an atom at the point
On the other hand, \(V( W_{j} (y) ) = 0\) only when \(y \rightarrow \pm \infty \), and, from Th. 8.1 in Dudley (1973) it follows that \(\sup _{\vert y \vert \le M} \vert W_j (y) \vert \) has absolutely continuous distribution in \((0, \, + \infty )\), for every positive M. Hence,
which proves that the distribution of \(\sup _{y} \left| W_j (y) \right| \) has no atom at 0. In other terms, \(\sup _{y} \left| W_j (y) \right| \) has absolutely continuous distribution on \((0, \, + \infty )\). \(\square \)
Proof of Proposition 3
First of all, using an integration by parts we have
and hence
where \(W_{j,n}(y)=\sqrt{n} ( {\widehat{F}}_{j,n}(y)- F_j (y))\), \(j=1\), 0.
Now, if \(F_0(y),F_1(y)\) are continuous, the limiting process \( W=[ W_1, \, W_0]^{\prime }\) possesses trajectories that are continuous (and bounded) with probability 1, so that it is concentrated on \(C( \overline{{\mathbb {R}}})^2\), that is separable and complete if equipped with the sup-norm. Using then the Skorokhod Representation Theorem (cfr. Billingsley 1999, p. 70), there exist processes \( {\widetilde{W}}_n = [ {\widetilde{W}}_{1,n} , \, {\widetilde{W}}_{0,n} ]^{\prime }\), \(n \ge 1\), and \( {\widetilde{W}} = [ {\widetilde{W}}_{1} , \, {\widetilde{W}}_{0} ]^{\prime }\), defined on a probability space \(({\widetilde{\Omega }}, \, \widetilde{{\mathcal {F}}} , \, {\widetilde{P}})\) such that
and
where the symbol \(\overset{d}{=}\) denotes equality in distribution.
From (40) and (39), the relationship
follows.
The terms appearing in the r.h.s. of (42) can be handled separately. First of all, we have
and since
we easily obtain
and similarly
Finally, for every integer n, \(n^{-1/2} {\tilde{W}}_{1,n}(y)\) is a bounded variation function, with total variation \(\le 2\), a.s.-\({\widetilde{P}}\), and since the trajectories of the process \({\widetilde{W}}_{1}\) are continuous and bounded, we may write
Relationship (45) the signed measure induced by \(n^{-1/2} {\widetilde{W}}_{1,n} \) converges weakly to a measure identically equal to zero. Hence:
where the term (a) goes to zero according to the Helly-Bray theorem (\({\widetilde{W}}_0 \) is continuous and bounded a.s. \(-{\widetilde{P}}\)), and the term (b) goes to zero according to the Skorokhod Representation Theorem.
From (43), (44), and (46) it follows that:
which is equivalent to:
The r.h.s. of (48) is a linear functional of a Gaussian process with continuous and bounded trajectories, so that it possesses Gaussian distribution with zero expectation and variance
where
The terms \(V_1\) - \(V_3\) in (50)–(52) can be written more compactly. Using the quantities \(\gamma _{10} (x)\), \(\gamma _{01} (x)\) defined in (17), it is not difficult to see that
In the same way, it is seen that:
and
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Conti, P.L., De Giovanni, L. Testing for the presence of treatment effect under selection on observables. AStA Adv Stat Anal 107, 641–669 (2023). https://doi.org/10.1007/s10182-022-00454-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10182-022-00454-8