Abstract
This article considers a modeling problem of integer-valued time series of bounded counts in which the binomial index of dispersion of the observations is greater than one, i.e., the observations inhere the characteristic of extra-binomial variation. Most methods analyzing such characteristic are based on the conditional mean process instead of the observed process itself. To fill this gap, we introduce a new class of beta-binomial integer-valued GARCH models, establish the geometric moment contracting property of its conditional mean process, discuss the stationarity and ergodicity of the observed process and its conditional mean process, and give some stochastic properties of them. We consider the conditional maximum likelihood estimates and establish the asymptotic properties of the estimators. The performances of these estimators are compared via simulation studies. Finally, we apply the proposed models to two real data sets.










Similar content being viewed by others
Notes
http://www.dwd.de.
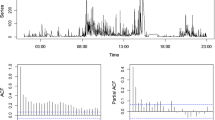
For an adequate model, its fitted standardized Pearson residuals are expected to be uncorrelated with a mean about 0 and a variance about 1, see Weiß (2018) for further details.
http://www.forecastingprinciples.com.
References
Agosto, A., Cavaliere, G., Kristensen, D., Rahbek, A.: Modeling corporate defaults: Poisson autoregressions with exogenous covariates (PARX). J. Empir. Fin. 38, 640–663 (2016)
Amemiya, T.: Advanced Econometrics. Harvard University Press, Cambridge (1985)
Bazzi, M., Blasques, F., Koopman, S.J., Lucas, A.: Time-varying transition probabilities for Markov regime switching models. J. Time Series Anal. 38, 458–478 (2017)
Billingsley, P.: Convergence of probability measures, 2nd edn. Wiley, New York (1999)
Blasques, F., Koopman, S.J., Lucas, A.: Information-theoretic optimality of observation-driven time series models for continuous responses. Biometrika 102, 325–343 (2015)
Blasques, F., Lucas, A., Silde, E.: A stochastic recurrence equations approach for score driven correlation models. Econ. Rev. 37, 166–181 (2018)
Chen, H., Li, Q., Zhu, F.: Two classes of dynamic binomial integer-valued ARCH models. Braz. J. Prob. Stat. 34, 685–711 (2020)
Chen, H., Li, Q., Zhu, F.: Binomial AR(1) processes with innovational outliers. Commun. Stat. Theory Methods 50, 446–472 (2021)
Davis, R.A., Holan, S.H., Lund, R., Ravishanker, N.: Handbook of discrete-valued time series. Chapman and Hall/CRC, Boca Raton (2016)
Davis, R.A., Liu, H.: Theory and inference for a class of observation-driven models with application to time series of counts. Stat. Sinica 26, 1673–1707 (2016)
Fokianos, K., Rahbek, A., Tjøstheim, D.: Poisson autoregression. J. Am. Stat. Assoc. 104, 1430–1439 (2009)
Gorgi, P.: Integer-valued autoregressive models with survival probability driven by a stochastic recurrence equation. J. Time Series Anal. 39, 150–171 (2018)
Han, H., Kristensen, D.: Asymptotic theory for the QMLE in GARCH-X models with stationary and nonstationary covariates. J. Bus. Econ. Stat. 32, 416–429 (2014)
Hu, T., Gallins, P., Zhou, Y.H.: A zero-inflated beta-binomial model for microbiome data analysis. Stat (2018). https://doi.org/10.1002/sta4.185
Jensen, S.T., Rahbek, A.: Asymptotic inference for nonstationary GARCH. Econ. Theory 20, 1203–1226 (2004)
Lee, Y., Lee, S.: CUSUM test for general nonlinear integer-valued GARCH models: comparison study. Ann. Inst. Stati. Math. 71, 1033–1057 (2019)
McKenzie, E.: Some simple models for discrete variate time series. Water Resour. Bull. 21, 645–650 (1985)
Möller, T.A., Weiß, C.H., Kim, H.Y., Sirchenko, A.: Modeling zero inflation in count data time series with bounded support. Methodol. Comput. Appl. Prob. 20, 589–609 (2018)
Ristić, M.M., Weiß, C.H., Janjić, A.D.: A binomial integer-valued ARCH model. Int. J. Biostat. 12, 20150051 (2016)
Skellam, J.: A probability distribution derived from the binomial distribution by regarding the probability of success as variable between the sets for trials. J. Royal Stat. Soc. 10, 257–261 (1948)
Steutel, F.W., van Harn, K.: Discrete analogues of self-decomposability and stability. Ann. Prob. 7, 893–899 (1979)
Straumann, D., Mikosch, T.: Quasi-maximum-likelihood estimation in conditionally heteroscedastic time series: a stochastic recurrence equations approach. Ann. Stat. 34, 2449–2495 (2006)
Wang, Z.: One mixed negative binomial distribution with application. J. Stat. Plan. Infer. 141, 1153–1160 (2011)
Weiß, C.H.: Thinning operations for modeling time series of counts-a survey. Adv. Stat. Anal. 92, 319–341 (2008)
Weiß, C.H.: An Introduction to Discrete-valued Time Series. Wiley, Chichester (2018)
Weiß, C.H., Kim, H.Y.: Diagnosing and modeling extra-binomial variation for time-dependent counts. Appl. Stoc. Model. Bus. Ind. 30, 588–608 (2014)
Weiß, C.H., Pollett, P.K.: Binomial autoregressive processes with density-dependent thinning. J. Time Series Anal. 35, 115–132 (2014)
Weiß, C.H., Testik, M.C.: On the Phase I analysis for monitoring time-dependent count processes. IIE Trans. 47, 294–306 (2015)
Williams, D.: The analysis of binary responses from toxicological experiments involving reproduction and teratogenicity. Biometrics 31, 949–952 (1975)
Wintenberger, O.: Continuous invertibility and stable QML estimation of the EGARCH(1,1) model. Scan. J. Stat. 40, 846–867 (2013)
Wu, W., Shao, X.: Limit theorems for iterated random functions. J. Appl. Prob. 41, 425–436 (2004)
Zhu, F., Shi, L., Liu, S.: Influence diagnostics in log-linear integer-valued GARCH models. Adv. Stat. Anal. 99, 311–335 (2015)
Zhu, F., Liu, S., Shi, L.: Local influence analysis for Poisson autoregression with an application to stock transaction data. Stat. Neerlandica 70, 4–25 (2016)
Acknowledgements
The authors thank the Editor-in-Chief and two anonymous referees for very valuable comments and suggestions that result in a substantial improvement of this paper. Li’s work is supported by Natural Science Found of Changchun Normal University, and Research Start-up Fund of Changchun Normal University. Zhu’s work is supported by National Natural Science Foundation of China (Nos. 11871027, 11731015).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Proof of Theorems
Theorem 1. (1). Let \(Z=E(Z_t)\) and \(f_u(Z)=g(Z,F_{Z}^{-1}(u)),\forall u \in (0,1)\), where \(F_Z(\cdot )\) is the cumulative distribution function of \(BB(n,\pi ,\phi )\) in Definition 1 with \(F_Z^{-1}(u):=\inf \{t\ge 0, F_Z(t)\ge u\}, \forall u \in [0,1]\). Then the BBGARCH(1,1) model can be rewritten as \(Z_t=F_{Z_t}^{-1}(u_t)\) with \(Y_t=g_{\varvec{\theta }}(Y_{t-1}, Z_{t-1}),\) Thus, \(\forall Z_0\) lies in the state space \(\chi \),
In the following, we first prove that \(\{Y_t, t \in \mathbb {Z}\}\) is geometric-moment contracting by induction. For all \(Y_0, Y_0^{'} \) and \(Y_0\) is independent of \(Y_0^{'}\), then
If \(E|Y_k(Y_0^{'})-Y_k(Y_0)|\le (a+b)^k|Y_0^{'}-Y_0|\), then
Note that \(Y_0 \sim \pi \) is independent of \(Y_0^{'} \sim \pi \). Hence, \(\{Y_t, t \in \mathbb {Z}\}\) is geometric-moment contracting with unique stationary distribution \(\pi \). Then, we prove \(E_{\pi }Y_0<\infty \). Note that
Note that \(Y_t(Y_0){{\mathop {\longrightarrow }\limits ^{L}}}Y_0\sim \pi \), as \(t\rightarrow \infty \). Hence, \(\displaystyle E_{\pi }Y_0<\liminf \limits _{t\rightarrow \infty }E(Y_t|Y_0) \le \dfrac{g(0,0)}{1-(a+b)}<\infty \) by Theorem 3.4 in Billingsley (1999).
(2). Define \(G_{k}(Y,Z_1,\ldots ,Z_k)=G_{k-1}(G(Y,Z_k),Z_1,\ldots ,Z_{k-1})\) and \(G_{1}=G\), \(\forall k=1,2,\ldots .\) Then \(Y_t=g_{\varvec{\theta }}(Y_{t-1}, Z_{t-1}):=G_{k}(Y_{t-k},Z_{t-1},\ldots , Z_{t-k}).\) Thus,
If \(E|Y_t-G_{k}(0,Z_{t-1},\ldots ,Z_{t-k})|\le a^k EY_{t-k},\) then
Hence, \(G_{k}(0,Z_{t-1},\ldots ,Z_{t-k}) ~{{\mathop {\rightarrow }\limits ^{L}}}~Y_t,\) i.e., there exists a measurable function \(G_{\infty }(Z_{t-1},\ldots ,Z_{t-k})\) such that \(Y_t~{{\mathop {=}\limits ^{a.s.}}}~G_{\infty }(Z_{t-1},\ldots ,Z_{t-k})\).
(3). The proof of the stationarity of \(\{Z_t\}\) and \(\{Z_t,Y_t\}\) is similar to that of Proposition 1 in Davis and Liu (2016). Similar to Proposition 2 in Davis and Liu (2016), we obtain \(\{Z_t\}\) is \(\beta \)-mixing with \(\beta (k)\le \dfrac{(a+b)^k}{1-a-b}\), where \(\beta (k)\) is the coefficient of absolute regularity. Thus, \(\{Z_t\}\) is an ergodic process. According to the results in (2), we obtain \(\{Y_t\}\) is also an ergodic process.
Theorem 2. Because \(Z_t\) is finite, any moment of \(Z_t\) or its conditional mean process \(Y_t\) exists. Then \(\forall t\), \(Y_t\in \mathbb {D}=(0,n]\), i.e., \(g_{\varvec{\theta }}(Y_{t-1},Z_{t-1}):=g_{\varvec{\theta }}^{t-1}=Y_{t}\in \mathbb {D}\). Denote
According to (2.4), \(\forall t \in \mathbb {Z}\), \(g_{\varvec{\theta }}^t(y,z)\) satisfies a contraction condition: \(\forall z_1,z_2\ge 0\) and \(\forall y_1, y_2 \in \mathbb {D}\), there exist two constants a and b such that \(\vert g_{\varvec{\theta }}^t(y_1,z_1)-g_{\varvec{\theta }}^t(y_2,z_2) \vert \le a|y_1-y_2|+b|z_1-z_2|\) with \(a,~b \in (0,1)\) and \(a+b<1\), i.e.,
Specially,
To prove \(Y_t\) satisfy the result of Theorem 2, we need to prove the following conditions hold:
-
(a)
There exists a \(y \in \mathbb {D}\) such that \(E\log ^+(\sup _{\varvec{\theta }\in \Theta }|g_{\varvec{\theta }}^0(y,z)|)< \infty \),
-
(b)
\(E\log ^+(\sup _{\varvec{\theta }\in \Theta }|\Lambda _0(\varvec{\theta })|)< \infty \),
-
(c)
\(E\log (\Lambda _0(\varvec{\theta }))< 0, \forall \theta \in \Theta \).
In the following, we first prove item (a). Using (3.2), we obtain that
Thus, (a) holds.
(b). Note that \(\forall z_1,z_2\), \(y_1\ne y_2\), \(\displaystyle \frac{g_{\varvec{\theta }}^0(y_1,z_1)-g_{\varvec{\theta }}^0(y_2,z_2)}{|y_1-y_2|} \le |a|+|b|\frac{|z_1-z_2|}{|y_1-y_2|}< 1+\frac{z_1+z_2}{\max \{y_1-y_2, y_2-y_1\}}<\infty ~ \text {by}\) (3.1). Hence, \(E\log ^+(\sup \limits _{\varvec{\theta }\in \Theta }|\Lambda _0(\varvec{\theta })|) =E\log ^+\sup \limits _{\varvec{\theta }\in \Theta } \sup \limits _ {{ \tiny \begin{array}{c} (y_1,y_2)\in \mathbb {D}^2\\ y_1\ne y_2 \end{array}}} \dfrac{|g_{\varvec{\theta }}^0(y_1,z_1)-g_{\varvec{\theta }}^0(y_2,z_2)|}{|y_1-y_2|} < \infty .\) Thus, (b) holds.
(c). \(E\log (\Lambda _0(\varvec{\theta })) \le E\log (|\partial {g_{\varvec{\theta }}^0(y,z)}/\partial {y}|) \le \log (|a|)<0\) by (3.3) and the strict monotonicity of \(g_{\varvec{\theta }}^t(y,z).\) Hence, (c) holds.
Thus, the conditions of Theorem 2 in Wintenberger (2013) hold, i.e., there exists a unique stationary and ergodic sequence \(\{\widetilde{Y}_t\}\) such that \(\{{Y}_t\}\) converges e.a.s. and uniformly to \(\{\widetilde{Y}_t\}\), \(t\rightarrow \infty \), which implies that the effect of the initialization \(Y_{0}\) asymptotically vanishes at an exponential rate. Thus, the results of Theorem 2 hold.
Corollary 1. Denote \((\mathrm{{I}}):=\vert Y_t(\hat{\varvec{\theta }}_l)- \widetilde{Y}_t(\varvec{\theta }_0))\vert \). Then \( (\mathrm{{I}})\le \underbrace{ \vert Y_t(\hat{\varvec{\theta }}_l)- \widetilde{Y}_t(\hat{\varvec{\theta }}_l)\vert }_\mathrm{{(II)}} + \underbrace{ \vert \widetilde{Y}_t(\hat{\varvec{\theta }}_l)- \widetilde{Y}_t({\varvec{\theta }}_0)\vert }_\mathrm{{(III)}}. \) According to Theorem 2, part \(\mathrm{{(II)}}~{{\mathop {\longrightarrow }\limits ^{a.s}}}~0\), as \(l\rightarrow \infty ,t\rightarrow \infty \).
In the following, we prove part \(\mathrm{{(III)}}~{{\mathop {\longrightarrow }\limits ^{a.s}}}~0\), as \(l\rightarrow \infty \) and \(t\rightarrow \infty \). Any positive and decreasing sequence \(\{\epsilon _i\}\) satisfies \(\lim \nolimits _{i \rightarrow \infty }\epsilon _i=0\), then there exists a monotonically increasing random-integer sequence \(\{l_i\}_{i \in \mathbb {Z}}\) such that \(\hat{\varvec{\theta }}_{l_i} \in \mathcal {B}_{\epsilon _i}(\varvec{\theta }_0)\) with probability one. Hence, for any \(\forall t' \in \mathbb {Z}\) and for all \(\delta >0\),
by the continuity of \(\widetilde{Y}_{t'} \) (in terms of each \(\theta _j, j=1,2,\ldots ,d\)) and the stationary of \(\{\widetilde{Y}_{t}\}\). Note that \(\lim \limits _{t\rightarrow \infty } P(\vert \widetilde{Y}_{t}(\hat{\varvec{\theta }}_{l})- \widetilde{Y}_{t}({\varvec{\theta }}_0)\vert \ge \delta ) \le \lim \limits _{t\rightarrow \infty }\sup \limits _{t' \in \mathbb {Z}} P(\vert \widetilde{Y}_{t'}(\hat{\varvec{\theta }}_{l_i})- \widetilde{Y}_{t'}({\varvec{\theta }}_0)\vert \ge \delta ) =0\). Hence, part (III) holds. In addition, \(\vert p_t(\hat{\varvec{\theta }}_l)- \widetilde{p}_t(\varvec{\theta }_0)) \vert ~{{\mathop {\longrightarrow }\limits ^{a.s.}}}~ 0\) by \(p_t=Y_t/n\). Thus, the results of Corollary 1 hold.
Theorem 3. To prove the consistency and asymptotic normality of \(\hat{{\varvec{\theta }}}_T^{cml}\), we first prove the consistency and asymptotic normality of \({\varvec{\widetilde{\theta }}}_T^{cml}\).
(1). Note that \(\overline{\widetilde{\ell }~}({\varvec{\theta }}) =E{\widetilde{l}}_t({\varvec{\theta }})~ \text {and}~ ~\widetilde{\ell }({\varvec{\theta }})=\sum \nolimits _{t=1}^{T} {\widetilde{l}}_t({\varvec{\theta }}) ~\text {with}~ {\widetilde{l}}_t({\varvec{\theta }}) =\log {P(Z_t|{\widetilde{Y}}_t)},\) where \(\{\widetilde{Y}_t\}\) is a stationary and ergodic random variable sequence. Denote
Note that Assumption 2 guarantees the existence of the average KL divergence, and then the maximizer of \(\overline{\widetilde{\ell }~}({\varvec{\theta }})\) corresponds to \(\varvec{\theta }_0\), which is the minimizer of the average KL divergence \(KL({\varvec{\theta }})\). According to Theorem 4.2.1 in Amemiya (1985), \(\frac{1}{T}\sum \nolimits _{t=1}^{T}{\widetilde{l}}_t(\varvec{\theta })~{{\mathop {\rightarrow }\limits ^{p}}}~E{\widetilde{l}}_t(\varvec{\theta }), ~T\rightarrow \infty .\) By Jensen’s inequality, Assumption 3 and \(\log (x)\le x-1, \forall x \in \mathbb {R}\), we obtain
Thus, \(E\widetilde{l}_t(\varvec{\theta })\) attains a strict local maximum at \(\varvec{\theta }_0\) by (3.4). Hence, the conditions of Theorem 4.1.2 of Amemiya (1985) are fulfilled. Thus, the consistence of \(\widetilde{{\varvec{\theta }}}_T^{cml}\) is obtained. Similar to Theorem 3.1 in Gorgi (2018), the consistence of \(\hat{{\varvec{\theta }}}_T^{cml}\) can be obtained by \(\text {(IV)}:=\Vert {\ell }_T({\varvec{\theta }}) - \overline{\widetilde{\ell }~}({\varvec{\theta }})\Vert _{\Theta } ~{{\mathop {\longrightarrow }\limits ^{a.s.}}} ~0,~T\rightarrow \infty .\) Note that
Using the ergodic Theorem, \({\text {(VI)}}~{{\mathop {\longrightarrow }\limits ^{a.s.}}} ~0, ~T\rightarrow \infty .\) By Lemma 2.1 in Straumann and Mikosch (2006) and Assumption 4, \(\forall t\ge N, N \in \mathbb {N}\), \(\sum _{t=N}^{\infty }\theta _t \Vert p_t({\varvec{\theta }}) - \widetilde{p}_t({\varvec{\theta }}) \Vert _{\Theta }\) converges a.s., hence \(\sum _{t=N}^{\infty }\Vert l_t({\varvec{\theta }}) - \widetilde{l}_t({\varvec{\theta }}) \Vert _{\Theta }<\infty .\) Thus, \(\text {(V)}~{{\mathop {\longrightarrow }\limits ^{a.s.}}} ~0, ~T\rightarrow \infty \). Therefore, we have \(\text {(IV)}~{{\mathop {\longrightarrow }\limits ^{a.s.}}} ~0, ~T\rightarrow \infty \). Then, the CML estimator \(\hat{{\varvec{\theta }}}_T^{cml}\) is strongly consistent with respect to \({\varvec{\theta }}_0.\)
(2). The proof of part 2 relies on the Taylor series expansion of the score vector around \({\varvec{\theta }}_0\), i.e.,
where \(\varvec{\theta }^{\star }\) lies in between \(\hat{\varvec{\theta }}_T^{cml}\) and \({\varvec{\theta }}_0\). Similar to Theorem 4 in Chen et al. (2020), \(\varvec{\widetilde{\theta }}_T^{cml}\) is asymptotically normal. To obtain the asymptotic distribution of \(\hat{\varvec{\theta }}_T^{cml}\), we need to prove the following two results: \(\text {(a)}.~~ T^{-1/2}\dfrac{\partial {\widetilde{\ell }{({{\varvec{\theta }}_0})}}}{\partial {\varvec{\theta }}} ~{{\mathop {\longrightarrow }\limits ^{d}}}~N(\varvec{0},\varvec{I}(\varvec{\theta }_0)) ~\text {with}~ \varvec{I}(\varvec{\theta }_0):=E\left[ \dfrac{\partial {l_t({\varvec{\theta }_0})}}{\partial {\varvec{\theta }}} \dfrac{\partial {l_t({\varvec{\theta }_0})}}{\partial {\varvec{\theta }^{\top }}} \right] . \text {(b)}.~~ \dfrac{1}{T} \dfrac{\partial ^2{\widetilde{\ell }({\varvec{\theta }^{\star })}}}{\partial {\varvec{\theta }}\partial {\varvec{\theta }^{\top }}}~ {\mathop {\longrightarrow }\limits ^{p}}~ -{\varvec{H}}({\varvec{\theta }}_0):= E\dfrac{\partial ^2{l_t({\varvec{\theta }_0)}}}{\partial {\varvec{\theta }}\partial {\varvec{\theta }^{\top }}},\) where \(\varvec{\theta }^{\star }\) lies in between \(\hat{\varvec{\theta }}_T^{cml}\) and \({\varvec{\theta }}_0\).
In the following, we first prove (a). Since \(\{\widetilde{Y}_t\}\) is a stationary and ergodic sequence, then \(E\left( {\partial {\widetilde{l}_t({\varvec{\theta }_0})}}/{\partial {\varvec{\theta }}}\right) =\varvec{0}\) and \(\mathrm{{Cov}}\left( {\partial {\widetilde{l}_t({\varvec{\theta }_0})}}/{\partial {\varvec{\theta }}}\right) =E\left( {\partial {\widetilde{l}_t({\varvec{\theta }_0})}}/{\partial {\varvec{\theta }}} {\partial {\widetilde{l}_t({\varvec{\theta }_0})}}/{\partial {\varvec{\theta }^{\top }}}\right) \). Using the ergodic theorem,
If \(\varvec{\widetilde{I}}(\varvec{\theta }_0) ~{{\mathop {=}\limits ^{a.s.}}}~ \varvec{ I}(\varvec{\theta }_0)\), then \(\dfrac{1}{\sqrt{T}}\dfrac{\partial {\widetilde{\ell }({\varvec{\theta }_0})}}{\partial {\varvec{\theta }}} ~{{\mathop {\longrightarrow }\limits ^{d}}}~N(\varvec{0},\varvec{I}(\varvec{\theta }_0))\), i.e., \(\dfrac{1}{\sqrt{T}}\sum \limits _{t=1}^T\dfrac{\partial {\widetilde{l}_t({\varvec{\theta }_0})}}{\partial {\varvec{\theta }}} {{\mathop {\longrightarrow }\limits ^{d}}}~N(\varvec{0},\varvec{I}(\varvec{\theta }_0))\) by martingale central limit theorem and the Cramér-Wold device. Hence, we need to prove
-
(a1)
\(\dfrac{1}{T}\dfrac{\partial {\widetilde{\ell }{({{\varvec{\theta }}_0})}}}{\partial {\varvec{\theta }}} ~{{\mathop {\longrightarrow }\limits ^{a.s.}}}~ \dfrac{1}{T} \dfrac{\partial { \ell {({{\varvec{\theta }}_0})}}}{\partial {\varvec{\theta }}}\), i.e., \(\Vert \dfrac{1}{T} \sum \limits _{t=1}^T \dfrac{\partial {\widetilde{l}_t{({{\varvec{\theta }}})}}}{\partial {\varvec{\theta }}} - \dfrac{1}{T} \sum \limits _{t=1}^T \dfrac{\partial { l_t{({{\varvec{\theta }}})}}}{\partial {\varvec{\theta }}} \Vert _{N(\varvec{\theta }_0)}~{{\mathop {\longrightarrow }\limits ^{a.s.}}}~0\);
-
(a2)
\(\varvec{\widetilde{I}}(\varvec{\theta }_0) ~{{\mathop {=}\limits ^{a.s.}}}~ \varvec{I}(\varvec{\theta }_0)\), i.e., \(\Vert \varvec{\widetilde{I}}(\varvec{\theta }) - \varvec{I}(\varvec{\theta }) \Vert _{N(\varvec{\theta }_0)} ~{{\mathop {\longrightarrow }\limits ^{a.s.}}}~0,\) where \(N(\varvec{\theta }_0)\) is an open and convex neighborhood of \(\varvec{\theta }_0\).
For convenience, we denote \(P_{n}(Z_t|\mathcal {F}_{t-1}):=P_{n}\) and \(P_{n}(Z_t|\widetilde{Y}_t):=\widetilde{P}_{n}\). According to Assumption 5(i), there exist positive constants \(c_1,~c_2,~c_3,~c_4\) such that \( \max \{\Vert P_{n}\Vert _{N(\varvec{\theta }_0)},~ \Vert \widetilde{P}_{n}\Vert _{N(\varvec{\theta }_0)}\}\ge ~1/{c_1},\) \(\max \{\Vert {\partial \widetilde{P}_{n}}/{\partial \varvec{\theta }} \Vert _{N(\varvec{\theta }_0)},~\) \( \Vert {\partial P_{n}}/{\partial \varvec{\theta }} \Vert _{N(\varvec{\theta }_0)} \}\le c_2,\) \(\max \left\{ \Vert {\partial { l_t({\varvec{\theta }})}}/{\partial {\varvec{\theta }^{\top }}}\Vert _{N(\varvec{\theta }_0)},~ \Vert {\partial { \widetilde{l}_t({\varvec{\theta }})}}/{\partial {\varvec{\theta }^{\top }}}\Vert _{N(\varvec{\theta }_0)} \right\} \le c_3\) and \(\max \{ \Vert {\partial ^2 \widetilde{P}_n}/ {\partial \varvec{\theta } \partial \varvec{\theta }^{\top }} \Vert _{N(\varvec{\theta }^\star )},\) \( ~\Vert {\partial ^2 P_n}/ {\partial \varvec{\theta } \partial \varvec{\theta }^{\top }} \Vert _{N(\varvec{\theta }^\star )} \}\le c_4. \) Then
Note that Assumption 4 implies that \(\Vert P_{n}-\widetilde{P}_{n} \Vert _{N(\varvec{\theta }_0)}~{{\mathop {\longrightarrow }\limits ^{a.s.}}}~0\). By Assumption 5(ii), we have \(\Vert {\partial P_{n}}/{\partial \varvec{\theta }} - {\partial \widetilde{P}_{n}}/{\partial \varvec{\theta }}\Vert _{N(\varvec{\theta }_0)}~{{\mathop {\longrightarrow }\limits ^{a.s.}}}~0.\) Hence, \(\text {(a1)}~{{\mathop {\longrightarrow }\limits ^{a.s.}}}~0\). Then we prove (a2). Denote \(\text {(VII)}=\varvec{\widetilde{I}}(\varvec{\theta }_0)-\varvec{I}(\varvec{\theta }_0)\).
Similar to (a1), we have \(\Vert \dfrac{\partial {\widetilde{l}_t({\varvec{\theta }})}}{\partial {\varvec{\theta }}}- \dfrac{\partial { l_t({\varvec{\theta }})}}{\partial {\varvec{\theta }}} \Vert _{N(\varvec{\theta }_0)}~{{\mathop {\longrightarrow }\limits ^{a.s.}}}~0\) and \(\Vert \dfrac{\partial {\widetilde{l}_t({\varvec{\theta }})}}{\partial {\varvec{\theta }^{\top }}}- \dfrac{\partial { l_t({\varvec{\theta }})}}{\partial {\varvec{\theta }^{\top }}} \Vert _{N(\varvec{\theta }_0)}{{\mathop {\longrightarrow }\limits ^{a.s.}}}~0\). Hence, (VII) \({{\mathop {\longrightarrow }\limits ^{a.s.}}}~0\), i.e., (a2) holds. Thus, \(\dfrac{1}{\sqrt{T}}\dfrac{\partial { \ell {({{\varvec{\theta }}_0})}}}{\partial {\varvec{\theta }}}~ {{\mathop {\longrightarrow }\limits ^{d}}}~ N(\varvec{0},\varvec{I}(\varvec{\theta }_0)) ~\text {with}~ \varvec{I}(\varvec{\theta }_0)=E\left[ \dfrac{\partial {l_t({\varvec{\theta }_0})}}{\partial {\varvec{\theta }}} \dfrac{\partial {l_t({\varvec{\theta }_0})}}{\partial {\varvec{\theta }^{\top }}} \right] \).
-
(b)
Similar to (a), we need to prove
-
(b1)
\(\dfrac{1}{T}\dfrac{\partial ^2\widetilde{\ell }(\varvec{\theta }^{\star })}{\partial \varvec{\theta }\partial \varvec{\theta }^{\top }} ~{{\mathop {\longrightarrow }\limits ^{a.s.}}}~ \dfrac{1}{T} \dfrac{\partial ^2\ell (\varvec{\theta }^{\star })}{\partial \varvec{\theta }\partial \varvec{\theta }^{\top }}\), i.e., \(\Vert \dfrac{1}{T}\dfrac{\partial ^2\widetilde{\ell }(\varvec{\theta })}{\partial \varvec{\theta }\partial \varvec{\theta }^{\top }} - \dfrac{1}{T} \dfrac{\partial ^2\ell (\varvec{\theta })}{\partial \varvec{\theta }\partial \varvec{\theta }^{\top }} \Vert _{N(\varvec{\theta }^\star )}~{{\mathop {\longrightarrow }\limits ^{a.s.}}}~0\);
-
(b2)
\(\varvec{\widetilde{H}}(\varvec{\theta }^\star ) ~{{\mathop {=}\limits ^{a.s.}}}~ \varvec{H}(\varvec{\theta }^\star )\), i.e., \(\Vert \varvec{\widetilde{H}}(\varvec{\theta }) - \varvec{H}(\varvec{\theta }) \Vert _{N(\varvec{\theta }^\star )} ~{{\mathop {\longrightarrow }\limits ^{a.s.}}}~0\), where \(N(\varvec{\theta }^\star )\) is an open and convex neighborhood of \(\varvec{\theta }^\star \) and \(N(\varvec{\theta }^\star )\) is a subset of \(N(\varvec{\theta }_0)\), \(\varvec{\theta }^{\star }\) lies in between \(\hat{\varvec{\theta }}_T^{cml}\) and \({\varvec{\theta }}_0\).
$$\begin{aligned}&\text {(b1).}~~\Vert \dfrac{1}{T}\dfrac{\partial ^2\widetilde{\ell }(\varvec{\theta })}{\partial \varvec{\theta }\partial \varvec{\theta }^{\top }} - \dfrac{1}{T} \dfrac{\partial ^2\ell (\varvec{\theta })}{\partial \varvec{\theta }\partial \varvec{\theta }^{\top }} \Vert _{N(\varvec{\theta }^\star )} \le \dfrac{1}{T}\sum \nolimits _{t=1}^{T} \Vert \dfrac{\partial ^2\widetilde{l}_t(\varvec{\theta })}{\partial \varvec{\theta }\partial \varvec{\theta }^{\top }} - \dfrac{\partial ^2 l_t (\varvec{\theta })}{\partial \varvec{\theta }\partial \varvec{\theta }^{\top }} \Vert _{N(\varvec{\theta }^\star )} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\&{}:=\dfrac{1}{T}\sum \nolimits _{t=1}^{T} \Vert \dfrac{1}{P_n} \dfrac{\partial ^2P_n}{\partial \varvec{\theta } \partial \varvec{\theta }^{\top }} - \dfrac{1}{\widetilde{P}_n} \dfrac{\partial ^2\widetilde{P}_n}{\partial \varvec{\theta } \partial \varvec{\theta }^{\top }} \Vert _{N(\varvec{\theta }^\star )} + \dfrac{1}{T}\sum \nolimits _{t=1}^{T} \Vert \dfrac{\partial P_n}{\partial \varvec{\theta }} \dfrac{\partial P_n}{\partial \varvec{\theta }^{\top }} - \dfrac{\partial \widetilde{P}_n}{\partial \varvec{\theta }} \dfrac{\partial \widetilde{P}_n}{\partial \varvec{\theta }^{\top }} \Vert _{N(\varvec{\theta }^\star )}\\&{}\le \dfrac{1}{T}\sum \nolimits _{t=1}^{T}\left( c_1 \Vert \dfrac{\partial ^2P_n}{\partial \varvec{\theta } \partial \varvec{\theta }^{\top }} - \dfrac{\partial ^2\widetilde{P}_n}{\partial \varvec{\theta } \partial \varvec{\theta }^{\top }} \Vert _{N(\varvec{\theta }^\star )} + c_1^2c_4 \Vert {P_n} - {\widetilde{P}_n} \Vert _{N(\varvec{\theta }^\star )} \right) \\&{}+ \dfrac{1}{T}\sum \nolimits _{t=1}^{T}\left( c_2 \Vert \dfrac{\partial P_n}{\partial \varvec{\theta }^{\top }} - \dfrac{\partial \widetilde{P}_n}{\partial \varvec{\theta }^{\top }} \Vert _{N(\varvec{\theta }^\star )} +c_2 \Vert \dfrac{\partial P_n}{\partial \varvec{\theta }} - \dfrac{\partial \widetilde{P}_n}{\partial \varvec{\theta }} \Vert _{N(\varvec{\theta }^\star )} \right) . \end{aligned}$$
Note that \(\Vert P_{n}-\widetilde{P}_{n} \Vert _{N(\varvec{\theta }_0)}~{{\mathop {\rightarrow }\limits ^{a.s.}}}~0\) by Assumption 4, \(\Vert {\partial P_{n}}/{\partial \varvec{\theta }} - {\partial \widetilde{P}_{n}}/{\partial \varvec{\theta }}\Vert _{N(\varvec{\theta }_0)}~{{\mathop {\rightarrow }\limits ^{a.s.}}}~0\) and \(\Vert {\partial P_{n}}/{\partial \varvec{\theta }^{\top }} - {\partial \widetilde{P}_{n}}/{\partial \varvec{\theta }^{\top }}\Vert _{N(\varvec{\theta }_0)} ~{{\mathop {\rightarrow }\limits ^{a.s.}}}~0\) by Assumption 5(ii), and Assumption 5(iii) implies \(\Vert {\partial ^2P_n}/{\partial \varvec{\theta } \partial \varvec{\theta }^{\top }} - {\partial ^2\widetilde{P}_n} / {\partial \varvec{\theta } \partial \varvec{\theta }^{\top }} \Vert _{N(\varvec{\theta }^\star )}\) \(~{{\mathop {\rightarrow }\limits ^{a.s.}}}~0\). Hence, \(\text {(b1)}\) holds.
(b2). Denote \(\text {(VIII)}:=\Vert \varvec{\widetilde{H}}(\varvec{\theta }) - \varvec{H}(\varvec{\theta }) \Vert _{N(\varvec{\theta }^\star )} \). Similar to the proof of (b1), we obtain
Hence, (b2) holds. Thus, \(\dfrac{1}{T} \dfrac{\partial ^2\ell (\varvec{\theta }^{\star })}{\partial \varvec{\theta }\partial \varvec{\theta }^{\top }} ~{{\mathop {\rightarrow }\limits ^{a.s.}}}~ \dfrac{1}{T}\dfrac{\partial ^2\widetilde{\ell }(\varvec{\theta }^{\star })}{\partial \varvec{\theta }\partial \varvec{\theta }^{\top }} \) and \(\dfrac{1}{T}\dfrac{\partial ^2\widetilde{\ell }(\varvec{\theta }^{\star })}{\partial \varvec{\theta }\partial \varvec{\theta }^{\top }} ~{{\mathop {\rightarrow }\limits ^{p}}}~-\varvec{H}(\varvec{\theta }_0)\), i.e.,
Hence, \(\sqrt{T}(\varvec{\hat{\theta }}^{cml}-\varvec{\theta }_0) ~{{\mathop {\longrightarrow }\limits ^{d}}}~ \mathcal {N}(\varvec{0}, {\varvec{H}}^{-1}(\varvec{\theta }_0) \varvec{I}(\varvec{\theta }_0){\varvec{H}}^{-1}(\varvec{\theta }_0)).\) Thus, the result in part (2) holds.
Appendix B: Auxiliary results
Lemma 1
Let \(\{Z_t,Y_t, t\in \mathbb {Z}\}\) satisfy Definition 1. Then \(Z_1\le _{lr} Z_2\), if \(Y_1\le _{lr} Y_2\).
Proof
The result of Lemma 1 can be obtained by \(Y_i=n\pi _i\) and Lemma 3, \(i=1,2.\) \(\square \)
Lemma 2
Let \(p(y,z)=\dfrac{\exp \big (w/(1-\alpha )+z\beta /(1-\alpha ) \big )}{1+\exp \big (w/(1-\alpha )+z\beta /(1-\alpha ) \big )}\). Then \(\forall z_1,z_2\ge 0\) and \(\forall y_1, y_2 \in \mathbb {D}\), if \(\alpha \in (0,1)\) and \(|\beta |\in (0,1)\), \( |p(y_1,z_1)-p(y_2,z_2)|\le \dfrac{|\beta |}{1-\alpha }|z_1-z_2| \) with \(0<\dfrac{|\beta |}{1-\alpha }<1\).
The proof of Lemma 2 can be obtained by Lemma 4 in Chen et al. (2020) and we omit it.
Lemma 3
If \(0<a_1\le a_2\) and \(b_1\ge b_2>0\), and random variable \(Z_i\) given \(\pi _i\) follows binomial distribution \(Bin(n,\pi _i)\) with \(\pi _i\) following beta distribution with parameters \(a_i\) and \(b_i\), then the following results hold and are equivalent:
-
(1)
\(\pi _1\le _{lr} \pi _2\)
-
(2)
\(Z_1\le _{lr} Z_2\).
Proof
-
(1)
Denote \(f_i(x)\) be the probability density function, i.e., \(f_i(x)=\dfrac{x^{a_i-1}(1-x)^{b_i-1}}{B(a_i,b_i)}, \forall x \in (0,1)\). Then \(\ell (x)=f_1(x)/f_2(x)=x^{a_1-a_2}(1-x)^{b_1-b_2}\) and \(\ell ^{'}(x)=(a_1-a_2)x^{a_1-a_2-1}(1-x)^{b_1-b_2}- (b_1-b_2)x^{a_1-a_2}(1-x)^{b_1-b_2-1}\le 0\) with equality only if \(a_1=a_2\) and \(b_1=b_2\). Thus, \(\pi _1\le _{lr} \pi _2\) by Theorem 4.2 in Wang (2011).
-
(2)
According to (2.1), we obtain that \( \ell (k):=\dfrac{B(k+a_1,n-k+b_1)}{B(k+a_2,n-k+b_2)} =\dfrac{(k+a_1-1)!(n-k+b_1-1)!}{(k+a_2-1)!(n-k+b_2-1)!}. \) Note that \(\ell (k+1)=\dfrac{k+a_1}{k+a_2} \dfrac{n-k+b_2-1}{n-k+b_1-1}\ell (k)\). If \(a_1\le a_2\) and \(b_1\ge b_2\), then \(k+a_1\le k+a_2\) and \(n-k+b_2-1\le n-k+b_1-1\). Thus, \(\forall k=0,1,2, \ldots \), \(\ell (k+1)\le \ell (k)\), i.e., \(Z_1\le _{lr} Z_2\) by the definition of likelihood ratio order. In fact, if \(\pi _1\le _{lr} \pi _2\), then \(a_1\le a_2\) and \(b_1\ge b_2\), hence, \(Z_1\le _{lr} Z_2\), and vice versa.
\(\square \)
Denote \(F_y\) be the cumulative distribution function of \(BB(n,\pi ,\phi )\) in (2.1) with \(y=n\pi =EZ\) and \(F_y^{-1}(u):=\inf \{t\ge 0, F_y(t)\ge u\}, \forall u \in [0,1]\).
Lemma 4
Let u be a uniform random variable in (0, 1) and \(Z_i=F_{Y_i}^{-1}(u), i=1,2\). Then \(E\vert Z_1-Z_2 \vert =\vert Y_1-Y_2 \vert \).
Proof
Note that \(E(Z_i)=Y_i\). Then if \(Y_1\le _{lr} Y_2\), we obtain \(Z_1\le _{lr} Z_2\) by Lemma 1, i.e., \(Z_1\le _{st} Z_2\) and \(F_{Y_1}^{-1}(t)\le F_{Y_2}^{-1}(t),\forall t\in (0,1)\). Hence \(E\vert Z_1-Z_2 \vert =E(Z_2-Z_1)=Y_2-Y_1=\vert Y_1-Y_2 \vert \). Similarly, \(E\vert Z_1-Z_2 \vert =E(Z_1-Z_2)=\vert Y_1-Y_2 \vert \), if \(Y_1\ge _{lr} Y_2\). Thus, \(E\vert Z_1-Z_2 \vert =\vert Y_1-Y_2 \vert \). \(\square \)
Rights and permissions
About this article
Cite this article
Chen, H., Li, Q. & Zhu, F. A new class of integer-valued GARCH models for time series of bounded counts with extra-binomial variation. AStA Adv Stat Anal 106, 243–270 (2022). https://doi.org/10.1007/s10182-021-00414-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10182-021-00414-8