Abstract
In a world that is increasingly connected on-line, cyber risks become critical. Cyber risk management is very difficult, as cyber loss data are typically not disclosed. To mitigate the reputational risks associated with their disclosure, loss data may be collected in terms of ordered severity levels. However, to date, there are no risk models for ordinal cyber data. We fill the gap, proposing a rank-based statistical model aimed at predicting the severity levels of cyber risks. The application of our approach to a real-world case shows that the proposed models are, while statistically sound, simple to implement and interpret.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Operational risk has been defined, by the Basel Committee on Banking Supervision, as “the risk of a monetary loss caused by human resources, IT systems, by organisation processes or by external events”. Within operational risks, those caused by IT systems are gaining increasing importance, due to technological advancements and to the globalisation of financial activities. Financial institutions are encouraged by regulators to use statistical approaches to measure operational risk, which include risks stemming from IT systems. This requires the presence of historical loss data, in a quantitative format. Within this framework, operational risks are usually classified in event types, according to the type of risk involved, and in business lines, according to area of the company that is mostly affected. To measure operational risks, the scientific literature suggests to collect past losses in each business line and event type and then calculate the corresponding severity and frequency distributions. Their convolution, by means of a Monte Carlo simulation, leads to the value at risk, which corresponds to the total economic capital required to protect an institution against possible operational losses (see, e.g., Cruz 2002; Alexander 2003; Giudici and Bilotta 2004).
Cyber risks can be defined as “any risk emerging from intentional attacks on information and communication technology (ICT) systems that compromises the confidentiality, availability, or the integrity of data or services” (see, e.g., Cebula and Young 2010; Edgar and Manz 2017; Kopp et al. 2017). Note that, according to this definition, cyber risk does not strictly coincide with IT operational risks, as it relates only to intentional attacks, on one hand, and it deals not only with monetary losses, but also with reputational losses, on the other.
In the last few years, the number of cyber attacks on information technology (IT) systems has surged: 1127 attacks occurred in 2017, against 1050 in 2016, 1012 in 2015 and 873 in 2014, with a growth of about 30% between 2014 and 2017. The trend in 2018 follows a similar behavior, with 730 cyber attacks observed only in the first half of the year (Clusit 2018). Thus, the need to measure cyber risks has increased considerably.
While the scientific literature on the measurement of operational risks (see, e.g., Cox 2012; MacKenzie 2014), based on loss data, constitutes a reasonably large body, that on cyber risk measurement is very limited. Some contributions can be found in Ruan (2017), Radanliev et al. (2018) and Shin et al. (2015), in which the focus is on the measurement of the value at risk, the maximum possible loss due to the occurrence of cyber attacks.
The lack of literature on cyber risk measurement may be due to the limited availability of cyber loss data, which are typically not disclosed, to avoid reputational losses. When disclosed, they are often expressed in terms of ordered levels of severity, such as “low”, “medium” or “high” severity. Unfortunately, the ordinal classification of risks prevents the calculation of the value at risk.
Although ordinal data cannot be used to calculate the value at risk, they can be used to rank risks by their “criticality”, so to prioritise interventions and, therefore, trigger mitigating actions. To our knowledge, there are very few papers that suggest how to deal with ordinal cyber data. Exceptions, that are however limited to specific issues, are Afful-Dadzie and Allen (2017), who focus on the problem of the scarcity of available data; Hubbard and Evans (2010), Sexton et al. (2015), Hubbard and Seiersen (2016) and Facchinetti et al. (2020), who introduce descriptive scoring methods.
Our paper fills this gap in the literature, providing a consistent statistical model aimed not only at describing, but also at predicting the ordinal severity levels of cyber risks. To increase the likelihood that our model can be actually implemented in daily risk management processes, we try to keep its complexity to a minimum, while maintaining its statistical consistency. To this aim, we propose a methodology that combines rank-based regression models with a rank-based predictive accuracy criterion. We test our model on a real data set of cyber events, ordered by severity levels. The application shows that the proposed methodology is, while statistically consistent, simple to implement and interpret.
The paper is organized as follows. The next section contains our methodology; Sect. 3 contains the empirical findings obtained applying our model to real cyber data; finally Sect. 4 contains some concluding remarks.
2 Methodology
Ordinal data for cyber risk measurement can be summarised by means of a pair of statistics for each event type: (1) the frequency of the event: how many times it has occurred, in a given period and (2) the severity of the event: the mean observed loss, in the same period. When quantitative loss data are available, the severity is a continuous random variable; in the context of ordinal data, the severity can be expressed on an ordinal scale with k distinct levels, ordered by an increasing magnitude.
To understand the causes that may determine cyber risks, the severity can be associated to a set of explanatory variables, such as the type of attacker, the technique of the attack, the victim type and the geographical area where the event has occurred. Then, based on the available data, a statistical model can learn which variables are significant to predict severity levels, and what are their estimated impacts and importance.
When the response variable is ordinal, and p explanatory variables of any type are available, typical statistical models that can be employed are generalised linear models, such as the ordered logit and the probit (see, for instance McCullagh 1980; Liddell and Kruschke 2018). Alternatively, to ease model interpretation and reproducibility by risk management professionals, the response variable can be expressed in terms of ranks, and the transformed rank variable can be explained by a linear regression model that explains the variability of the ranks with the available explanatory variables. This is the approach we follow here.
Formally, let Y be a random variable that indicates the severity of a cyber event, which can assume k possible levels. Y can be transformed assigning rank \(r_1=1\) to the smallest ordered category of Y and a rank \((r_{z-1}+n_{z-1})\) to the following categories, where \(n_{z-1}\) is the absolute frequency associated with the \((z-1)\)-th category with \(z=2,\ldots ,k\). For a general discussion on the construction of a rank response variable see, e.g., Ronald and Conover (1979).
Based on this transformation, the ordinal Y variable can be re-expressed into a rank response R variable, defined as:
with \(r_1=1\), \(r_2=r_1+n_1\) and \(r_k=r_{k-1}+n_{k-1}\).
Given p explanatory variables \((X_1, \ldots , X_p)\), a regression model for R can then be specified as:
where \(E(e)=0\), \(Var(e)=\sigma ^2\) and whose unknown parameters can be estimated by the standard ordinary least squares method.
To complete model specification, models should be compared in terms of their predictive accuracy, and the model with the highest accuracy will be selected. This task is usually accomplished by dividing the available data into a training sample, on which models learn from the data their parameter estimates, and a testing sample, in which the predictions obtained applying the models built on the training data are compared with the actual observed values. This approach, known as “cross-validation” procedure, mimics a real out-of-sample validation exercise, using data that are already available.
The best model is then selected minimising the root mean squared prediction error, defined as follows:
where for all the \(i=1,\ldots ,n\) observations in the test sample, \(y_i\) is the actually observed values of the severity measure Y, and \(\hat{y}_i\) is the predicted values.
In the case of an ordinal response variable, such as the cyber severity, the above measure may not be appropriate, as it would too strongly depend on the transformation used to map categories to real values. It would be desirable to have a predictive accuracy measure that, rather than using a Euclidean distance, as the RMSE does, can operate directly on the original ordinal levels.
To achieve this aim, and provide a statistical model that is fully consistent with the nature of the data, we propose a predictive accuracy measure based on the decomposition of the Gini measure of mutual variability, developing a suggestion contained in Giudici and Raffinetti (2011).
Let y be the vector of the observed values of the response variable Y in the test set and let \(\hat{y}\) be the vector of the corresponding predicted values. The y values can be used to build the \(L_Y\) Lorenz curve (Lorenz 1905), characterised by the following pairs: \((i/n,\sum _{j=1}^{i}y_{r_j}/\sum _{i=1}^{n} y_{r_i})\), for \(i=1,\ldots ,n\), where \(y_{r}\) is the vector of the response variable values reordered by the corresponding (non-decreasing) ranks r.
Analogously, the Y values can also be reordered in a non-increasing sense, providing the \(L^{'}_{Y}\) dual Lorenz curve.
Let \(\hat{r}\) indicate the (non-decreasing) ranks of \(\hat{Y}\). The set of pairs \((i/n,\sum _{j=1}^{i}y_{\hat{r}_j}/ \sum _{i=1}^{n}y_{r_i})\), where \(y_{\hat{r}}\) is the vector of the response variable values reordered by the ranks of the corresponding predicted values, provides the so-called C concordance curve, which measures the concordance between the response variable Y and the corresponding predicted variable \(\hat{Y}\) orderings.
Finally, let the set of pairs (i/n, i/n) provide the bisector 45° line, for \(i=1,\ldots ,n\), which corresponds to the case of a random model prediction.
Following Giudici and Raffinetti (2011), the four described curves can be represented in a joint graph, as in Fig. 1.
Figure 1 suggests that a new predictive accuracy measure may be based on the bisector 45° line and the underlying concordance curve. More precisely, it could use the measure, we called Rank Graduation Accuracy (RGA), which is defined as the ratio:
where \(y_{\hat{r}_j}\) is the response variable Y values, ordered according to the ranks \(\hat{r}\) of the corresponding predicted values, and \(\bar{y}\) is the mean value of Y (with \(j=1,\ldots ,i\) and \(i=1,\ldots ,n\)).
In the context of cyber risk management, the response variable Y can be replaced by the rank variable R, whose values are defined as in (1). We can then define a Rank Graduation Accuracy (RGA) measure, as follows:
where \(r_{ord(\hat{r})_j}\) is the rank transformed response variable values, reordered by the ranks predicted by the model (with \(j=1,\ldots ,i\) and \(i=1,\ldots ,n\)), and \(\bar{r}\) is the mean of all ranks.
Note that a more concise expression for RGA, denoted with \(RGA_{R_{cum}}\), can be derived as:
where \(C(r_{ord(\hat{r})_j})=\frac{\sum _{j=1}^{i}r_{ord (\hat{r})_j}}{\sum _{i=1}^{n}r_{ord(r)_i}}\) is the cumulative values of the (normalised) rank transformed response variable and \(r_{ord(r)_i}\) are the rank transformed response variable values ordered in non-decreasing sense.
We remark that the RGA measure in Eq. (5) is expressed in absolute terms. When comparing different models, a relative measure appears more appropriate. A relative RGA measure can be derived as the ratio between its value and its maximum value \(RGA_{max}\). The latter is achieved when the predicted values given by a model perfectly reflect the ordering of the response variable values. On the contrary, the RGA minimum value is reached when the predicted values provided by the model are the same, as for a random model.
To be proposed within a fully comprehensive statistical model, the RGA measure should be complemented with a statistical test, which can be employed to evaluate whether any given model is significantly better than a random model. We now show how to derive such test.
Let \(Y_{\hat{r}}^{e}\) be the expected concordance associated with a random model and let T be the test statistics:
Under the conditions of large n and small probability of success (rare events) (see, e.g., Cameron and Trivedi (1998)), it can be shown that, when Y is a binary response variable, the n variables \(Y_{\hat{r}_1},\ldots ,Y_{\hat{r}_i},\ldots ,Y_{\hat{r}_n}\) are Poisson counts and so \(T \sim \chi _{n}^{2}\).
In our context, the Y variable is ordinal. By transforming it into its ranks, the n variables \(R_{ord(\hat{r})_1},\ldots ,R_{ord (\hat{r})_i},\ldots ,R_{ord(\hat{r})_n}\) can also be shown to be distributed as Poisson counts and \(T\sim \chi _{n}^{2}\), where
where \(R_{ord(\hat{r})}^{e}\) is the expected concordance associated with a random model for a rank transformed response variable.
From a model comparison perspective, the test statistics should be extended to evaluate whether the difference in the RGA measures, between any two models, is significant. To achieve this goal assume, without loss of generality, that model comparison occurs between a full model (including all the covariates in the dataset) and a reduced model (including only some of the covariates in the dataset). Define with \(T_{full }\) the test statistics T computed under the full model, and with \(T_{reduced}\) the same statistics computed under the reduced model, and let \(T_{model}=T_{full}-T_{reduced}\) be the difference between the two test statistics. The following proposition can then be proved.
Proposition 1
\(T_{model}=T_{full}-T_{reduced}\) is distributed as a variance gamma distribution,Footnote 1with parameters \(\lambda =n/2\), \(\alpha =1/2\), \(\beta =0\) and \(\mu =0\), where \(\lambda >0\), \(\alpha \in {\mathbb {R}}\), \(\beta \in {\mathbb {R}}\) is the asymmetry parameter and \(\mu \in {\mathbb {R}}\) is the location parameter.
Proof
The proof of the proposition can be obtained using the moment generating function.
Let \(T_{model}=T_{full}-T_{reduced}\), where \(T_{full}\) and \(T_{reduced}\) are the test statistics defined in Eq. (7). It thus follows that \(T_{full}\) and \(T_{reduced}\) are both distributed according to a \(\chi ^2\) distribution with a number of degrees of freedom equivalent to the number of involved observations, n. The test statistics \(T_{model}\) is, therefore, the difference between two \(\chi ^2\) distributions with the same number of degrees of freedom. Consider now the \(\chi ^2\) moment generating functions \(M_{T_{full}}(t)\) and \(M_{T_{reduced}}(t)\), equal to \((1-2t)^{-\frac{n}{2}}\). As \(T_{full}\) and \(T_{reduced}\) are independent, the \(M_{T_{model}}\) moment generating function can be computed as:
Note that the moment generating function in (8) matches the moment generating function of the variance gamma distribution, defined as
where in our case \(\lambda =n/2\), \(\alpha =1/2\), \(\beta =0\) and \(\mu =0\).
Therefore, the density function of the test statistics \(T_{model}\) is
with \(\Gamma\) and \(K_{\lambda }\) denoting the Gamma function and the modified Bessel function of the second kind (see, e.g., Kotz et al. 2001; Seneta 2004). \(\square\)
The previous research design can be operationalised implementing a test statistics that can compare any two models.
To actually implement the proposed test statistics, we need further research work.
A first issue is that, if we resort to the variance gamma R package, recently proposed by Scott and Yang Dong (2018), the parameter \(\lambda\) must be equal to half of the number of observations included in the dataset. However, the computation of the p values of the variance gamma associated with the R package is not possible when \(\lambda\) takes large values. A possible solution is to draw subsamples of small size.
A second problem is that the variance gamma package in R uses a parameterisation different from that in Eq. (9). It employs that in Seneta (2004), where the parameters are the location parameter c, the spread parameter \(\sigma\), the asymmetry parameter \(\theta\) and the shape parameter \(\nu\). The parameterization we instead consider takes the form of a generalized hyperbolic distribution parameterization, for which the variance gamma distribution is a limiting case with \(\delta\) equal to 0 (see, e.g., Kotz et al. 2001). A possible solution is to convert our parameterization into that described in Scott and Yang Dong (2018), as the vgChangePars function in the variance gamma package was implemented to establish a map between the two different sets of parameterizations. To this aim, the parameter values can be fixed setting \(\alpha =1/2\), \(\beta =0\) and \(\mu =0\). The crucial point is choosing the \(\lambda\) parameter value: in the application section we select the representative value \(\lambda =5\), corresponding to a sample of size \(n=10\) (being \(\lambda =n/2\)). Then, exploiting the relations existing between the two sets of parameterization reported below:
the \(VG(c=0,\sigma =6.324555,\theta =0,\nu =0.2)\), corresponding to \(VG(\lambda =5,\alpha =0.5,\beta =0,\mu =0)\), was obtained.
Combining the two previous points, to implement the proposed model selection test, a sample of size \(n=10\) has to be drawn. To avoid issues concerned with small sample size and robustify the test, we follow the subsampling procedure introduced by Raffinetti and Romeo (2015). We consider a number h of different samples; for each sample, the value of \(T_{model}\) can be computed. As the variance gamma distribution with parameters \(c=0,\sigma =6.324555,\theta =0,\nu =0.2\) is symmetric around zero, we propose to employ a significance value (named s-value), defined as the relative percentage of significant tests, as follows:
where
For interpretation purposes, the s-value can be associated with a significance scale (s-scale), as summarised in Table 1 below:
3 Application
In this section we would like to check how our proposed method behaves on actual ordinal cyber risk data. From an applied viewpoint, we would like to understand, using the proposed statistical model, which are the main causal drivers of cyber risk severity levels, among the most common “suspects”: technique of attack, type of attacker, type of victim and location.
To this aim, we apply our proposal to real loss data, organised by severity levels, reported by Clusit (2018). Clusit, born in 2000 within the University of Milan, is the largest and most respected Italian association in the field of information security. The association includes, as member organisations, companies from different fields: banks, insurances, public administrations, health companies and telecommunication companies. The annual report of Clusit is the result of the work of a pool of experts and is based on an extensive collection of cyber data, carried out at the ordinal level to avoid reputational disclosure issues.
Specifically, the database consists of 6,865 worldwide observations on serious cyber attacks, in the period 2011-2017. An attack is classified as “serious” if it has led to a significant impact, in terms of economic losses and/or damages to reputation.
Here, we focus on a homogeneous set of data, observed in 2017 (the year in which most data was observed), consisting of 808 cyber attacks. Severity levels are reported according to the type of attacker, technique of attacks, victims and their country of origin. Moreover, it is worth noting that the considered data are the results of a data cleansing process which has allowed to remove outliers and other data anomalies.
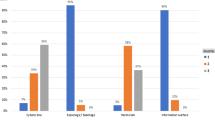
In Fig. 2, the relative frequency distribution of severity by attacker is graphically displayed, while in Tables 2 and 3, the absolute frequency distribution of the covariates and the severity variable are reported.
From Fig. 2, we note that espionage/sabotage and information warfare are concentrated on the most severe incidents.
We now proceed bulding a predictive model aimed at detecting the causal factors which may affect the severity levels. For this purpose, we consider two rank regression models which differ in terms of the variables taken into account. The first model (“full”) is built on all the explanatory variables appearing in our dataset: attacker, attack technique, victim type and location (continent). For the sake of clarity, location has to be intended as the geographic area in terms of continents (Africa, America, Asia, Europe, Oceania), where the victims reside. A second rank regression model (“reduced”) is specified removing from the full model the continent variable. This is to assess whether the geographical area where attacks occur impacts the severity levels.
In Table 4 we report the estimated coefficients obtained with a full and a reduced rank regression models, for the ordinal levels that correspond to: attacker type; victim type; attack technique; continent (from top to bottom). We break each of the four categorical variables into dummies, with the baseline cases being “Automotive” for victim, “Cybercrime” for type of attacker, “0-day” for attack technique and “Africa” for continent. We consider only the estimates that are significant at an \(\alpha =5\%\) level, together with the parameter estimates and p-values of continent variable of the full model. We preliminarily remark that, from a descriptive viewpoint, the adjusted-\(R^2\) is equal to 0.602 for the full model and to 0.603 for the reduced model.
From Table 4 note that the continent variable does not provide significant effects, indicating its limited importance to explain severity levels. Second, the two models provide similar signs for the effects of the other variables, indicating their stability. In more detail, in terms of attacker, the different cyber attack levels have the effect of decreasing the severity degree relative to the baseline case of “Cybercrime”. On the contrary, the levels related to the attack technique and to the victim type increase the severity level relative to the baselines of “0-day” and “Automative”, respectively.
We now move to model validation, with the purpose of selecting the rank-based causal model with the highest predictive accuracy, as measured by the rank-based RGA metric. For comparison, we also include the computation of the RMSE. The results are displayed in the first two rows of Table 5.
From Table 5 note that the difference between the RGA values computed in absolute terms on the two models is rather small. If on the one hand, the full model appears as the best one; on the other hand, it provides only a really small contribution in improving the overall predictive accuracy at the expense of a more parsimonious model, according to what stated by the Occam’s razor principle. These findings are consistent with the previously found the absence of significant effects for the continent variable.
We consider now the application of our proposed test statistics \(T_{model}\) that, differently from possible tests based on the RMSE, is consistent with the ordinal nature of the data. To implement the calculation, we follow the sampling procedure described in Sect. 2, randomly drawing k samples of size \(n=10\) from the dataset. The test statistics is computed in each sample and then the s-value is calculated to assess whether the difference between the two models is significant (fixing \(\alpha\) at 0.05). The sampling conditions are fixed varying the number of samples, so that \(h=\{100,500,1,000\}\).
It turns out that, when 100 and 500 samples are randomly selected, the full model is significant in less than the 15% of the samples, while if 1,000 samples are considered, the full model results as significant in about 18% of the samples. Thus, as suggested by the classification provided in Table 1, the s-scale is “Rarely significant” in all the three different sample scenarios. For the sake of completeness, also the cases of \(n=\{12,16\}\) were taken into account, leading to an s-scale which results as “Rarely significant” for \(n=12\) and “Sometimes significant” for \(n=16\). But, as specified by Raffinetti and Romeo (2015), the full model has to be evaluated as the best one only if the corresponding s-value belongs to the “Always significant” or at least “Almost always significant” s-scale class. This result is in line with the technical intuition and also with the descriptive result offered by the adjusted-\(R^2\) statistics. It allows us to conclude that the reduced rank regression model is preferred to the full rank regression model.
To further validate our model, we conducted a further comparison, between the full model and a reduced model without the attacker variable, which we expect to be a strong predictor, from the descriptive analysis in Fig. 2. We resort to the computation of the adjusted-\(R^2\) coefficients for both the models. For the reduced model, the adjusted-\(R^2\) (0.4606) is clearly smaller than the adjusted-\(R^2\) (0.6020) obtained on the full regression model.
The results obtained from the application of our RGA measure can be found in the last row of Table 5. Differently from what happens to the reduced rank regression model without the continent variable, which allows to explain almost the 74% of the actual severity rank ordering, the reduced rank regression model without the cyber attacker variable only explains about the 55.5% of the actual severity rank ordering. This finding shows that the role played by the type of attacker in explaining the severity rank ordering cannot be neglected. The application of our proposed test confirms this finding: when \(n=10\) and 100 and 500 samples are randomly selected, the full model is significant in more than the 75% of the samples, while if 1000 samples are considered, the full model results as significant in over the 80% of the samples. The same considerations can be drawn if referring to the cases of \(n=\{12,16\}\), for which the full model is significant in over the 88% and 96% of the 100, 500 and 1000 selected samples, respectively. This allows us to conclude that the full rank regression model has to be preferred to the reduced rank regression model, in this case.
To summarise, our approach selects cyber risk predictive models which are in line with what is expected, from a subject-matter perspective as well as from a statistically descriptive viewpoint. Moreover, from an applied viewpoint, our findings confirm that cyber severity levels are affected by the technique of attack, by the type of attacker, and by the type of victims; but not by the location of the attack.
4 Concluding remarks
In this paper, we have proposed a rank-based model, and a rank-based predictive accuracy measure aimed at predicting the severity levels of cyber risks.
Our proposal fills a gap in the literature, which does not contain, to our knowledge, risk management models based on ordinal cyber risk data.
Indeed, the advantage of our proposal is that it does not need actual loss data, typically not disclosed for reputational purposes. It can instead be applied to the ordinal severity levels of cyber attacks, easier to be disclosed and consequently, found by analysts.
The application of our model to a real cyber risk database, measured at the ordinal level, reveals that the proposed model is statistically consistent with the ordinal nature of the data. In addition, our approach is relatively simple to implement and interpret, providing a key advantage for the application of the model by risk professionals.
Further research work may involve the application of the proposed method to other cyber risk management problems. In particular, the model could be extended to investigate dependency patterns, that reveal forms of contagion, as deeply discussed by Duffie and Younger (2019) and Eisenbach et al. (2020), who address their research methodologies to the detection of common vulnerabilities which may increase the impact of a cyber shock. To this purpose and to assess how much the cyber risk estimate may change, the proposed rank-based model can be formalized in a multivariate setting by resorting to the use of copulas, as suggested by Brechmann et al. (2014) for modeling dependencies when dealing with ordinal-valued operational risks. Another extension could investigate the joint usage of ordinal data and text data, possibly within a Bayesian model as suggested by Cerchiello et al. (2017).
Notes
Note that the variance gamma distribution is also known as the generalized Laplace distribution. Given a variable Y distributed according to a variance gamma distribution, the associated probability density function is defined as: \(f_{Y}(y)=\frac{(\sqrt{\alpha ^2-\beta ^2})^{2\lambda }|y -\mu |^{\lambda -\frac{1}{2}}K_{\lambda -\frac{1}{2}}(\alpha |y-\mu |)}{\sqrt{\pi } \Gamma (\lambda )(2\alpha )^{\lambda -\frac{1}{2}}}e^{\beta (y-\mu )}\).
References
Afful-Dadzie, A., Allen, T.T.: Data-driven cyber-vulnerability maintenance policies. J. Qual. Technol. 46(3), 234–250 (2017)
Alexander, C.: Operational Risk: Regulation, Analysis and Management. Prentice Hall, New York (2003)
Brechmann, E., Czado, C., Paterlini, S.: Flexible dependence modeling of operational risk losses and its impact on total capital requirements. J. Bank. Finance 40, 271–285 (2014)
Cameron, A.C., Trivedi, P.K.: Regression Analysis of Count Data. Cambridge University Press, Cambridge (1998)
Cebula, J.J., Young, L.R.: A Taxonomy of Operational Cyber Security Risks. Technical Note, CMU/SEI-2010-TN-028, Software Engineering Institute, Carnegie Mellon University, pp. 1–34 (2010)
Cerchiello, P., Giudici, P., Nicola, G.: Twitter data models for bank risk contagion. Neurocomputing 264, 50–56 (2017)
Clusit: 2018 Report on ICT security in Italy (2018)
Cox Jr., L.A.: Evaluating and improving risk formulas for allocating limited budgets to expensive risk-reduction opportunities. Risk Anal. 32(7), 1244–1252 (2012)
Cruz, M.: Modeling, Measuring and Hedging Operational Risk. Wiley, New York (2002)
Duffie, D., Younger, J.: Cyber Runs. https://www.brookings.edu/wp-content/uploads/2019/06/WP51-Duffie-Younger-2.pdf (2019). Accessed 25 Sept 2020
Edgar, T.W., Manz, D.O.: Research Methods for Cyber Security. Elsevier, Amsterdam (2017)
Eisenbach, T.M., Kovner, A., Lee, M.: Cyber Risk and the U.S. Financial System: A Pre-Mortem Analysis. FRB of New York Staff Report No. 909, January 2020. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3522710 (2020). Accessed 25 Sept 2020
Facchinetti, S., Giudici, P., Osmetti, S.A.: Cyber risk measurement with ordinal data. Stat. Methods Appl. 29, 173–185 (2020)
Giudici, P., Bilotta, A.: Modelling operational losses: a Bayesian approach. Qual. Reliab. Eng. Int. 20(5), 407–417 (2004)
Giudici, P., Raffinetti, E.: On the Gini measure decomposition. Stat. Probab. Lett. 81(1), 133–139 (2011)
Hubbard, D.W., Evans, D.: Problems with scoring methods and ordinal scales in risk assessment. J. Res. Dev. 54(3), 2–10 (2010)
Hubbard, D.W., Seiersen, R.: How to Measure Anything in Cybersecurity Risk. Wiley, New York (2016)
Kopp, E., Kaffenberger, L., Wilson, C.: Cyber Risk, Market Failures, and Financial Stability. IMF Working Paper, WP/17/185, pp. 1–35 (2017)
Kotz, S., Kozubowski, T.J., Podgórski, K.: The Laplace Distribution and Generalizations. A Revisit with Applications to Communications, Economics, Engineering and Finance. Springer, Birkhauser (2001)
Liddell, T., Kruschke, J.: Analyzing ordinal data with metric models: What could possibly go wrong? J. Exp. Soc. Psychol. 79, 328–348 (2018)
Lorenz, M.O.: Methods of measuring the concentration of wealth. J. Am. Stat. Assoc. 9(70), 209–219 (1905)
MacKenzie, C.A.: Summarizing risk using risk measures and risk indices. Risk Anal. 34(12), 2143–2162 (2014)
McCullagh, P.: Regression models for ordinal data. J. R. Stat. Soc. Ser. B (Methodol.) 42(2), 109–142 (1980)
Radanliev, P., De Roure, D.C., Nicolescu, R., Huth, M., Montalvo, R.M., Cannady, S., Burnap, P.: Future developments in cyber risk assessment for the internet of things. Comput. Ind. 102, 14–22 (2018)
Raffinetti, E., Romeo, I.: Dealing with the biased effects issue when handling huge datasets: the case of INVALSI data. J. Appl. Stat. 42(12), 2554–2570 (2015)
Ronald, L.I., Conover, W.J.: The use of the rank transform in regression. Technometrics 21(4), 499–509 (1979)
Ruan, K.: Introducing cybernomics: a unifying economic framework for measuring cyber risk. Comput. Secur. 65, 77–89 (2017)
Scott, D., Yang Dong, C.: R package VarianceGamma. https://cran.r-project.org/web/packages/VarianceGamma/VarianceGamma.pdf (2018). Accessed 4 Feb 2019
Seneta, E.: Fitting the variance-gamma model to financial data. J. Appl. Probab. 41(A), 177–187 (2004)
Sexton, J., Storlie, C., Neil, J.: Attack chain detection, statistical analysis and data mining. Stat. Anal. Data Min. ASA Data Sci. J. 8, 353–363 (2015)
Shin, J., Son, H., Heo, G.: Development of a cyber security risk model using Bayesian networks. Reliab. Eng. Syst. Saf. 134, 208–217 (2015)
Acknowledgements
This research has received funding from the European Union’s Horizon 2020 research and innovation program “FIN-TECH: A Financial supervision and Technology compliance training programme” under the grant agreement No. 825215 (Topic: ICT-35-2018, Type of action: CSA). Acknowledgments go to the Associate Editor and the two anonymous reviewers, whose comments and suggestions helped to improve and clarify this manuscript. The paper is the result of the joint collaboration between the two authors.
Funding
Open access funding provided by Università degli Studi di Milano within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Giudici, P., Raffinetti, E. Cyber risk ordering with rank-based statistical models. AStA Adv Stat Anal 105, 469–484 (2021). https://doi.org/10.1007/s10182-020-00387-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10182-020-00387-0