Study of the bivariate survival data using frailty models based on Lévy processes

Abstract

Frailty models allow us to take into account the non-observable inhomogeneity of individual hazard functions. Although models with time-independent frailty have been intensively studied over the last decades and a wide range of applications in survival analysis have been found, the studies based on the models with time-dependent frailty are relatively rare. In this paper, we formulate and prove two propositions related to the identifiability of the bivariate survival models with frailty given by a nonnegative bivariate Lévy process. We discuss parametric and semiparametric procedures for estimating unknown parameters and baseline hazard functions. Numerical experiments with simulated and real data illustrate these procedures. The statements of the propositions can be easily extended to the multivariate case.

1 Introduction

In survival analysis, frailty is usually defined as a non-observable momentan risk of failure and is included in survival models in the form of an unknown nonnegative random variable or random process characterizing non-homogeneity of population with respect to hazard function. Usually, frailty enters the model multiplicatively to the hazard function and allows us to take into account the correlations between failure times. Observed covariates can also be included in the multivariate survival models in the form of Cox-like regression. Identifiability and other properties of the univariate and multivariate survival models with time-independent frailty have been studied in some depth, and these models now are popular and widely used in survival studies and in the search for genes influencing longevity. Several models with time-dependent frailty have also been suggested. Woodbury and Manton (1997) introduced a stochastic process model of human mortality and ageing. They considered hazard as a quadratic function of stochastically changing unobserved frailty. The model was further extended by Yashin and Manton (1997) to consider a partially observed frailty process. Modifications of this model were successfully applied to the analyses of longitudinal data with informative censoring. Ideas on further development and applications of these results to studying ageing and longevity are summarized by Yashin et al. (2012). Gjessing et al. (2003) considered an approach based on the proportional hazard model with time-dependent frailty given by the formula

$$\begin{aligned} Z(t)=\int _0^t a(u,t-u)\mathrm{d}X(R(u)). \end{aligned}$$

Here, X(t) is a nonnegative Lévy process (subordinator) with Laplace exponent $\Phi (c)$, $R(t)=\int _0^tr(u)\mathrm{d}u$ defines the time transformation of subordinator for a nonnegative rate function r(t), and the nonnegative weight function a(u, s) determines the extent to which the previous behavior of transformed subordinator influences the hazard function at time t. The authors derived the expressions for the population survival and hazard functions in a general case:

$$\begin{aligned} S(t)= & {} \exp \left( -\int _0^t \Phi (b(u,t))r(u)\mathrm{d}u\right) , \\ \mu (t)= & {} \lambda (t)\int _0^t \Phi ^{\prime }(b(u,t))a(u,t-u)r(u)\mathrm{d}u, \end{aligned}$$

where $\lambda (t)$ is the baseline hazard function and $b(u,t)=\int _u^t\lambda (s)a(u,s-u)\mathrm{d}s$. Gjessing et al. (2003) showed also that under some conditions, quasi-stationary distributions of survivors can arise. This implies the constant limiting population hazard rate, in spite of the increase of the baseline hazard function. Ata and Özel (2012) considered the proportional hazard model with time-dependent frailty given by the discrete compound Poisson process and applied this model to the earthquake data and to traffic accidents data from Turkey.

The aim of this paper is to study the problem of identifiability for bivariate survival models with/without observed covariates and with time-dependent frailty when this frailty is given by a Lévy process (or Lévy processes). In addition, we demonstrate how these models can be used for longevity datasets based on simulated data.

In Sect. 2, we give the definitions of the univariate survival model under mixed proportional hazard specification and the bivariate correlated frailty model. We then discuss the definitions of the uni- and bivariate survival model with time-dependent frailty given by the nonnegative Lévy processes. At the end of this section, we discuss known findings related to the identifiability of survival models with time-independent frailty, formulate two new propositions about the identifiability of the bivariate survival models with time-dependent frailties, and give the EM algorithm for estimating unknown baseline hazard functions and parameters for the correlated bivariate model with time-dependent frailty. In Sect. 3, we discuss the results of estimations of the baseline hazard functions and unknown parameters (including the Cox-regression coefficients and parameters characterizing the frailty process) in experiments with simulated and real data for parametric and semiparametric approaches. The real-world example was based on the data from the Danish Twin Registry. Conclusions and outlook are presented in Sect. 4.

2 Survival analysis under a frailty setting

Under mixed proportional hazard specification (Abbring and van den Berg 2003), the hazard rates of the failure times for two related individuals depend multiplicatively on the respective baseline hazards $\lambda _{j}(t)$, regressor functions $\chi _{j}({\mathbf {u}}_{j})$ with observed vector of covariates ${\mathbf {u}}_{j}$, and unobserved nonnegative random variable (frailty) $Z_{j}$, characterizing the heterogeneity in the population with respect to hazard $\lambda _j$

$$\begin{aligned} \mu _{j}(t_{j}|Z_{j},{\mathbf {u}}_{j})=Z_{j}\chi _{j}({\mathbf {u}}_{j})\lambda _j(t_{j}), \quad j=1,2. \end{aligned}$$

(1)

The function $\chi _{j}({\mathbf {u}}_{j})$ is frequently specified as $\chi _{j}({\mathbf {u}}_{j})=\exp (\beta _{j}^{*}{\mathbf {u}}_{j})$ (the Cox-regression term) for some transposed vector parameter $\beta _{j}^{*}$, $j=1,2$. The univariate population survivals $S_{j}(t|\chi _{j} ({\mathbf {u}}_{j}))=P(T_{j}>t_{j})$ for random times of death $T_{j}$ are

$$\begin{aligned} S_{j}(t|\chi _{j}({\mathbf {u}}_{j}))=&\mathbb {E}e^{-Z_{j}\chi _{j}({\mathbf {u}}_{j})\Lambda _{j}(t_{j} )}=L(\chi _{j}({\mathbf {u}}_{j})\Lambda _{j}(t_{j})),&j=1,2, \end{aligned}$$

(2)

with cumulative hazard function $\Lambda _{j}(t)=\int _{0}^{t}\lambda _{j}(\tau )\mathrm{d}\tau$ and Laplace transform $L(c)=\mathbb {E}e^{-cZ}$.

In the bivariate correlated frailty model proposed by Yashin et al. (1995), individual frailties $(Z_{1},Z_{2})$ were constructed under assumptions

$$\begin{aligned} Z_{1}= & {} \frac{m_{0}}{m_{1}}Y_{0}+Y_{1}, \nonumber \\ Z_{2}= & {} \frac{m_{0}}{m_{2}}Y_{0}+Y_{2} \end{aligned}$$

(3)

for independent nonnegative random variables $Y_{0}$, $Y_{1}$ and $Y_{2}$ and some nonnegative constants $m_{0}$, $m_{1}$ and $m_{2}$. Given frailties $(Z_{1},Z_{2})$, life spans for both individuals were assumed to be conditionally independent. Since the scale factor common to all subjects in the population can be absorbed into the baseline hazard functions $\lambda _{j}(.)$, $j=1,2$, we can put $\mathbb {E}Z_{1}=\mathbb {E}Z_{2}=1$. The heterogeneity in the population can be characterized by the variance of frailties $\text{ Var }Z_{1}=\sigma _{1} ^{2}$, $\text{ Var }Z_{2}=\sigma _{2}^{2}$. The correlation between frailties $\text{ Corr }(Z_{1},Z_{2})$ we will denote by $\rho$.

If $Y_{j}$ are gamma-distributed random variables, $Y_{j} \sim G(k_{j},m_{j})$, $j=0,1,2$, with $k_{0}=\rho /\sigma _{1}\sigma _{2}$, $k_{j}=1/\sigma _{j}^{2}-k_{0}$, $m_{j}=1/\sigma _{j}^{2}$, $j=1,2$; $0 \leqslant \rho \leqslant \min (\sigma _{1}/\sigma _{2},\sigma _{2}/\sigma _{1})$, then the non-conditional bivariate survival function is given by the formula

$$\begin{aligned} S(t_{1},t_{2}|\chi _{1}({\mathbf {u}}_{1}),\chi _{2}({\mathbf {u}}_{2}))= & {} \mathbb {E}e^{-Z_{1}\chi _{1}({\mathbf {u}}_{1})\Lambda _{1}(t_{1})}e^{-Z_{2}\chi _{2}({\mathbf {u}}_{2})\Lambda _{2} (t_{2})} \nonumber \\= & {} \frac{\left( 1+\sigma _{1}^{2}\chi _{1}({\mathbf {u}}_{1})\Lambda _{1}(t_{1})\right) ^{-k_{1}}\left( 1+\sigma _{2}^{2}\chi _{2} ({\mathbf {u}}_{2})\Lambda _{2} (t_{2})\right) ^{-k_{2}}}{\left( 1+\sigma _{1} ^{2}\chi _{1}({\mathbf {u}}_{1})\Lambda _{1}(t_{1})+\sigma _{2}^{2}\chi _{2} ({\mathbf {u}}_{2})\Lambda _{2}(t_{2})\right) ^{k_{0}}}\nonumber \\ \end{aligned}$$

(4)

(Wienke 2010). Note that without loss of generality, we can put $m_{0}=m_{1}$. If left truncation is present at ages $(t_{01},t_{02})$, we calculate the conditional survival function by dividing the bivariate survival function by $S(t_{01},t_{02}|\chi ({\mathbf {u}}_{1}),\chi ({\mathbf {u}}_{2}))$. To take into account information about censoring, we shall put $\delta _{j}=0,1$, where $\delta _{j}=0$ indicates right censoring, $j=0,1$.

The assumption that the individual frailty is determined at birth and does not change with age seems to be too strong and unrealistic. To make the approach more flexible, we can weaken this assumption and suppose that the frailty is a random process.

Similarly to Gjessing et al. (2003), we shall consider the frailty process $Z={Z(t):t\geqslant 0}$ defined by a nonnegative Lévy process. In accordance with Lévy-Khinchin formula, such a process can be characterized by its Laplace transform

$$\begin{aligned} L(c;t)=\mathbb {E}e^{-cZ(t)}=e^{-t\Phi (c)} \end{aligned}$$

with Laplace exponent $\Phi (c)$, while c is the argument of Laplace transform. Note that

$$\begin{aligned} \mathbb {E}Z(t)= & {} t\Phi ^{\prime }(0), \\ \text {Var}Z(t)= & {} -t\Phi ^{\prime \prime }(0). \end{aligned}$$

Examples of Lévy processes include the standard compound Poisson process, the compound Poisson process with general jump distribution, gamma processes, stable processes, and PVF (power variance function) processes (Gjessing et al. 2003). In this paper, we shall consider the nonnegative Lévy processes (subordinators) with the Laplace exponent given by

$$\begin{aligned} \Phi (c)= & {} dc+\int _{0}^{\infty }(1-\text{ e }^{-cx})\nu (\mathrm{d}x), \end{aligned}$$

(5)

nonnegative drift d and the jump measure $\nu$ with support $(0,\infty )$ satisfying $\int _{0}^{\infty }\min (1,x)\nu (\mathrm{d}x)<\infty$. The Laplace exponent is an increasing and concave function. The Laplace exponent and the jump measure for the gamma process are given by the formulas

$$\begin{aligned} \Phi _{G}(c)= & {} h[\ln (\gamma +c)-\ln \gamma ]=h\ln (1+\gamma ^{-1}c),\nonumber \\ \nu (\mathrm{d}x)= & {} h\text{ e }^{-\gamma x}x^{-1}\mathrm{d}x \end{aligned}$$

(6)

with the shape ht and the scale parameter $\gamma$ for the gamma-distributed random variable Z(t). This corresponds to the values of $ht\gamma ^{-1}$ and $ht\gamma ^{-2}$ for mean and variance of Z(t), respectively. To avoid non-identifiability of the model, we shall standardize the frailty distribution and put $h=\gamma$. In this case, $\mathbb {E}Z(t)=t$, $\text {Var} Z(t)=t\gamma ^{-1}$ for $t\geqslant 0$. In “Appendix 1,” we can find the formulas for calculating univariate population survivals in this case for a constant and an exponential (Gompertz) baseline hazard functions. We will denote the Laplace exponent for the univariate frailty processes $Z_{j}(t)$, $j=1,2$ by $\Phi _{j}(.)$.

Let $(Z_1(t),Z_2(t))$ be a bivariate Lévy process with nonnegative components and the Laplace exponent given by

$$\begin{aligned} \Phi _\mathrm{biv}(c)= & {} <d,c>+\int _{{R}_+^{2}}(1-\text{ e }^{-<c,x>})\nu (\mathrm{d}x), \end{aligned}$$

(7)

where $d,c\in \mathbb {R}_+^{2}$, $<x,y>$ denotes the dot product of vectors $x,y\in \mathbb {R}^{2}$, the Lévy measure $\nu (A)$ for any Borel set $A\in \mathbb {R}_+^{2}$ is the expected number of jumps on the time interval [0,1], whose sizes belong to A, and the following integrability conditions for Lévy measure are satisfied:

$$\begin{aligned}&\int _{{R}_+^{2}}\min (1,x)\nu (\mathrm{d}x)<\infty , \\&\quad \int _{{R}_+^{2}}\min (1,x^2)\nu (\mathrm{d}x) <\infty . \end{aligned}$$

Note that $\Phi _\mathrm{biv}(c_1,0)=\Phi _1(c_1)$ and $\Phi _\mathrm{biv}(0,c_2)=\Phi _2(c_2)$ for marginal Lévy processes.

The bivariate survival function under mixed proportional hazard specification with conditionally independent life spans and time-dependent frailties given by correlated Lévy processes is

$$\begin{aligned} S(t_{1},t_{2}|\chi _{1}({\mathbf {u}}_{1}),\chi _{2}({\mathbf {u}}_{2}))= & {} \mathbb {E}\text {e}^{-\chi _{1}({\mathbf {u}}_{1})\int _{0}^{t_{1}}Z_{1}(\tau )\lambda _{1}(\tau )\mathrm{d}\tau }\text {e}^{-\chi _{2}({\mathbf {u}}_{2})\int _{0}^{t_{2}}Z_{2}(\tau )\lambda _{2} (\tau )\mathrm{d}\tau }\\= & {} \exp \left( -\int _{0}^{t_{-}}\Phi _\mathrm{biv}(\chi _{1}({\mathbf {u}}_{1})\Lambda _{1}(\tau ,t_{1}),\chi _{2}({\mathbf {u}}_{2})\Lambda _{2}(\tau ,t_{2}))\mathrm{d}\tau \right) \\&\times \exp \left( -\int _{t_{-}}^{t_{+}}\Phi _\mathrm{uni}^{+}(\chi _{+}({\mathbf {u}}_{1},{\mathbf {u}}_{2})\Lambda _{+}(\tau ,t_{+}))\mathrm{d}\tau \right) , \end{aligned}$$

where $t_{-}=\min (t_{1},t_{2})$, $t_{+}=\max (t_{1},t_{2})$, $\Phi _\mathrm{biv}(.,.)$ is the Laplace exponent for the bivariate frailty process $(Z_{1},Z_{2})$,

$$\begin{aligned} \Phi _\mathrm{uni}^{+}(.)= & {} {\left\{ \begin{array}{ll} \Phi _{2}(.), \text{ if } t_{2}> t_{1},\\ \Phi _{1}(.), \text{ otherwise },\\ \end{array}\right. }\\ \Lambda _{j}(\tau ,t)= & {} \int _{\tau }^{t}\lambda _{j}(s)\mathrm{d}s,\qquad j=1,2, \\ \chi _{+}({\mathbf {u}}_{1},{\mathbf {u}}_{2})= & {} {\left\{ \begin{array}{ll} \chi _{2}({\mathbf {u}}_{2}),\quad \text{ if } \ t_{2}> t_{1},\\ \chi _{1}({\mathbf {u}}_{1}),\quad \text{ otherwise },\\ \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} \Lambda _{+}(\tau ,t)={\left\{ \begin{array}{ll} \int _{\tau }^{t}\lambda _{2}(s)\mathrm{d}s,\quad \text{ if } \ t_{2}> t_{1},\\ \int _{\tau }^{t}\lambda _{1}(s)\mathrm{d}s,\quad \text{ otherwise }.\\ \end{array}\right. } \end{aligned}$$

Similar to the model with time-independent frailties given by (3), we can construct the bivariate survival function for time-dependent frailties given by the correlated Lévy processes $Z_{1}(t)$ and $Z_{2}(t)$ with parameters $\mathbb {E}Z_{1}(1)=\mathbb {E}Z_{2}(1)=1$, $\text {Var} Z_{1}(1)=\gamma _{1}^{-1}$, $\text {Var} Z_{2}(1)=\gamma _{2}^{-1}$, and $\text {Corr} (Z_{1}(t),Z_{2}(t))=\varrho$, $t>0$. The formula for calculating bivariate population survival function for time-dependent frailties is given in “Appendix 2.”

2.1 Model identifiability

The identifiability of the univariate model with unspecified functional form of frailty distribution and baseline hazard has been studied by Elbers and Ridder (1982). This model is identifiable given information on T for finite $\mathbb {E}Z$ and is not identifiable when frailty has an infinite mean. Identifiability of the correlated frailty models using data on the pair $(T_{1},T_{2})$ was proved by Honoré (1993) under the assumption of finite means of $Z_{1}$ and $Z_{2}$. Yashin and Iachine (1999) proved the identifiability of the correlated frailty model without observed covariates assuming that $Z_{1}$ and $Z_{2}$ are gamma distributed. Abbring and van den Berg (2003) studied the identifiability of the mixed proportional hazards competing risks model. We adopt this method to investigate the identifiability of the mixed bivariate survival model for time-dependent correlated frailties.

Proposition 1

Let the following assumptions be satisfied.

• Assumption 1. Regressor functions $\chi _{i}:U _{i}\rightarrow \mathbb {R_{+}}$ are continuous with supports $U _{i}$, $U_{i}\subset \mathbb {R}^{n}$, $i=1,2$, and $\chi _{1}({\mathbf {u}}_{\mathbf{1}}^{*})=\chi _{2}(\mathbf {u}_{\mathbf{2}}^{*})=1$ for some $\mathbf {u}_{\mathbf{1}}^{*}\in U_{1}$, $\mathbf {u}_{\mathbf{2}}^{*}\in U_{2}$. Set $\Upsilon =\{(\chi _{1}({\mathbf {u}}_{1}),\chi _{2}({\mathbf {u}}_{2}))|\mathbf {u}_{\mathbf{1}}\in U_{1},\mathbf {u}_{\mathbf{2}}\in U_{2}\}$ contains a non-empty open set $\Upsilon _{0}\subset \mathbb {R}^{2}_{+}$.

• Assumption 2. Baseline hazard functions $\lambda _{j}(.)$ are integrable on [0, t] with $\Lambda _{j}(t)=\int _{0}^{t}\lambda _{j}(\tau ) d \tau <\infty$ for all $t\in \mathbb R_{+}$, and $\Lambda _{1}(t^{*})=\Lambda _{2}(t^{*})=1$ for some $t^{*}>0$, $j=1,2$.

• Assumption 3. Let $\mu$ be a probability measure corresponding to the bivariate frailty variable $(Z_{1}(1),Z_2(1))\in \mathbb {R}_{+}^{2}$. Then,

  $$\begin{aligned} \int _{0}^{\infty }\int _{0}^{\infty } e^{b(x_{1}+x_{2})}\mathrm{d}\mu <\infty \end{aligned}$$

  (8)

  for some real number $b>0$.

Then, the mixed bivariate survival model for time-dependent correlated frailties is identified from the bivariate distribution of the failure times $(T_{1},T_{2}|{\mathbf {u}}_{1},{\mathbf {u}}_{2})$.

Proof

Identification of the regressor functions.

From Assumption 3 and Theorem 2.1 in Brychkov et al. (1992), it follows that the Laplace exponent $\Phi _\mathrm{biv}(p_{1},p_{2})$ is an analytic function on $H_{b}=\{(p_{1},p_{2}|\text {Re}(p_{1})>-b,\text {Re}(p_{2})>-b)\}$ and therefore is a real analytic function on $\text {Re}H_{b}=\{(x_1,x_2)|x_{1}>-b,x_{2}>-b\}$. Note that $\Phi _{1}(p)=\Phi _\mathrm{biv}(p,0)$ and $\Phi _{2}(p)=\Phi _\mathrm{biv}(0,p)$. Since $\mathbb {E}Z(1)=\Phi _{1}^{\prime }(0)$, $\mathbb {E}Z(2)=\Phi _{2}^{\prime }(0)$ and the functions $\Phi _{1}(x)$ and $\Phi _{2}(x)$ are analytic in 0, it holds that $\mathbb {E}Z_{1}(1)<\infty$ and $\mathbb {E}Z_{2}(1)<\infty$. Gjessing et al. (2003) (Theorem 1) have shown that

$$\begin{aligned} S_{j}(t|\chi _{j}({\mathbf {u}}_{j}))=\mathbb {E} S_{j}(t|Z_{j},\chi _{j}({\mathbf {u}}_{j}))=\exp \left( -\int _{0}^{t}\Phi _{j}(\Lambda _{j}(\tau ,t;\chi _{j}({\mathbf {u}}_{j})))\mathrm{d}\tau \right) , \end{aligned}$$

where

$$\begin{aligned} \Lambda _{j}(\tau ,t;\chi _{j}({\mathbf {u}}_{j}))=\int _{\tau }^{t}\chi _{j}(\mathbf {u}_{\mathbf{j}})\lambda _{j}(s)\mathrm{d}s=\chi _{j}(\mathbf {u}_{\mathbf{j}})\Lambda _{j}(\tau ,t),\qquad j=1,2. \end{aligned}$$

As any subordinator frailty processes, $Z_{j}$ have increasing and concave Laplace exponents and their derivatives $\Phi _{j}^{\prime }(.)$ are decreasing. Moreover,

$$\begin{aligned} \mathrm{d}S_{j}(t|\chi _{j}({\mathbf {u}}_{j}))/\mathrm{d}t= & {} -\chi _{j}({\mathbf {u}}_{j})\lambda _{j}(t)\int _{0}^{t}\Phi _{j}^{\prime }(\Lambda _{j}(\tau ,t;\chi _{j}({\mathbf {u}}_{j})))\mathrm{d}\tau \\&\times \exp \left( -\int _{0}^{t}\Phi _{j}(\Lambda _{j}(\tau ,t;\chi _{j}({\mathbf {u}}_{j})))\mathrm{d}\tau \right) \end{aligned}$$

and

$$\begin{aligned} (t\lambda _{j}(t))^{-1}\mathrm{d}S_{j}(t|\chi _{j}({\mathbf {u}}_{j}))/\mathrm{d}t \rightarrow -\chi _{j}(\mathbf {u}_{\mathbf{j}})\mathbb {E}Z_{j}(1) \quad as \quad t\downarrow 0. \end{aligned}$$

From here and Assumption 1, it follows that

$$\begin{aligned} \frac{\mathrm{d}S_{j}(t|\chi _{j}({\mathbf {u}}_{j}))/\mathrm{d}t}{\mathrm{d}S_{j}(t|\chi _{j}({\mathbf {u}}_{j}^{*}))/\mathrm{d}t}&\rightarrow \chi _{j}(\mathbf {u}_{\mathbf{j}}) \quad as \quad t\downarrow 0, \quad j=1,2. \end{aligned}$$

This formula identifies $\chi _{j}(.)$ in $U_{j}$, since marginal survival functions $S_{j}(t|\chi _{j}({\mathbf {u}}_{j}))$ are observed for $t\geqslant 0$ and $\mathbf {u}_{\mathbf{j}}$ are arbitrary for $j=1,2$.

Identification of the hazard functions.

For $0\leqslant \tau \leqslant t\leqslant T<\infty$, it holds that $\Lambda _{j}(\tau , t)\leqslant C< \infty$, $j=1,2$. Therefore, there exists a real $b(T)>0$ such that the bivariate function $\Phi _\mathrm{biv}(\chi _{1}\Lambda _{1}(\tau ,t),\chi _{2}\Lambda _{2}(\tau ,t))$ and the univariate functions $\Phi _{j}(\chi _{j}\Lambda _{j}(\tau ,t))$ are real analytic functions on the set $\Upsilon _{T}=\{(\chi _{1},\chi _{2})|\chi _{1}>-b(T), \chi _{2}>-b(T)\}$ containing the point (0,0) for fixed $(\tau ,t)$, $0\leqslant \tau \leqslant t\leqslant T<\infty$ and $j=1,2$. Moreover, the univariate survival functions $S_{j}(t_{j}|\chi _{j})$, their derivatives $S_{j}^{\prime }(t_{j}|\chi _{j})$ in $t_{j}$, $j=1,2$, and the bivariate survival function $S(t_{1},t_{2}|{\chi }_{1},\mathbf \chi _{2})$ are real analytic functions uniquely defined on $\Upsilon _{T}$ for $\{(t_{1},t_{2})|0\leqslant t_{1},t_{2}\leqslant T<\infty \}$.

Differentiating $S_{j}(t|\chi _{j})$ in t, dividing then by $\chi _{j}$, and setting formally $\chi _{j}\rightarrow 0$, we get the following equations:

$$\begin{aligned} -\lim _{\chi _{j}(u_{j})\downarrow 0}\frac{S_{j}^{\prime }(t|\chi _{j})}{\chi _{j}S_{j}(t|\chi _{j})}= \Phi _{j}^{\prime }(0)\lambda _{j}(t)=\mathbb {E}Z_{j}(1)\lambda _{j}(t), \quad j=1,2. \end{aligned}$$

(9)

Since the expression on the right hand of (9) is observed, we find the hazard function in the form

$$\begin{aligned} \lambda _{j}(t)=-\Phi _{j}^{\prime }(0)^{-1}\lim _{\chi _{j}\downarrow 0}\frac{S_{j}^{\prime }(t|\chi _{j})}{\chi _{j}(u_{j})S_{j}(t|\chi _{j})}), \quad j=1,2. \end{aligned}$$

The constant $\Phi _{j}^{\prime }(0)$ can be found from the equation $\Lambda _{j}(t^{*})=1$, $j=1,2$ (Assumption 2).

Identification of the Laplace exponent.

Since $S(0,0|{\chi }_{1}, \chi _{2})=1$ and the bivariate Laplace exponent is regular in the point (0,0), the following formula holds in some neighborhood $O\subset \mathbb R_{+}^{1}$ of the point $t=0$

$$\begin{aligned} -\ln S(t^{**},t^{**}|\chi _{1},\chi _{2})= & {} \sum _{n_{1}=1}^{\infty }\sum _{n_{2}=1}^{\infty }\frac{\chi _{1}^{n_{1}}}{n_{1}!}\frac{\chi _{2}^{n_{2}}}{n_{2}!}\frac{\partial ^{n_{1}+n_{2}}\Phi _\mathrm{biv}(c_{1},c_{2})}{\partial c_{1}^{n_{1}}\partial c_{2}^{n_{2}}}|_{c_{1}=0,c_{2}=0} \nonumber \\&\times \int _{0}^{t^{**}}(\Lambda _{1}(t^{**})-\Lambda _{1}(\tau ))^{n_{1}}(\Lambda _{2}(t^{**})-\Lambda _{2}(\tau ))^{n_{2}}\mathrm{d}\tau .\nonumber \\ \end{aligned}$$

(10)

Mixed partial derivatives in (10) can be calculated using the finite difference method as the distance between spaced nodes tends to zero. Note that $\int _{0}^{t^{**}}(\Lambda _{1}(t^{**})-\Lambda _{1}(\tau ))^{n_{1}}(\Lambda _{2}(t^{**})-\Lambda _{2}(\tau ))^{n_{2}}\mathrm{d}\tau >0$ for all $n_{1}\in \mathbb {N}$ and $n_{2}\in \mathbb {N}$ if $t^{**}>t^{*}$. The mixed partial derivatives $\partial ^{n_{1}+n_{2}}\Phi _\mathrm{biv}(c_{1},c_{2})/\partial c_{1}^{n_{1}}\partial c_{2}^{n_{2}}$ at the point (0, 0) are uniquely defined from (10), and therefore, $\Phi _\mathrm{biv}(c_1,c_2)$ can be uniquely defined in some open neighborhood of the point (0,0). That is, the real analytic function $\Phi _\mathrm{biv}(.,.)$ is uniquely defined in some open set containing $\mathbb {R}^{2}_{+}$. Similarly, it can be shown that the real analytic functions $\Phi _{j}$, $j=1,2$, are uniquely defined in some open set containing $R^{1}_{+}$. $\square$

If individual frailties $(Z_{1},Z_{2})$ are constructed under assumptions given by

$$\begin{aligned} \begin{aligned} Z_{1}=&Y_{0}+Y_{1}, \\ Z_{2}=&\alpha Y_{0}+Y_{2} \end{aligned} \end{aligned}$$

(11)

for some positive $\alpha$, we can weaken the conditions of Proposition 1 and prove the identifiability of the model in the absence of observed covariates.

Proposition 2

Let the following assumptions be satisfied.

• 1. Assumption 1. Decomposition (11) holds for independent positive Lévy processes $Y_{0}$, $Y_{1}$, $Y_{2}$ with zero drift and some $\alpha >0$.

  Assumption 2. Baseline hazard functions $\lambda _{j}(.)$ are integrable on [0, t] with $\Lambda _{j}(t)=\int _{0}^{t}\lambda _{j}(\tau ) d \tau <\infty$ for all $t\in \mathbb R_{+}$, $\lim _{t\rightarrow \infty }\Lambda _{j}(t)=\infty$, and $\Lambda _{j}(t^{*})=1$ for some $t^{*}>0$, $j=1,2$.

  Assumption 3. Jump measures $\nu _{i}$ satisfy $\int _{0}^{\infty }x\nu _{i}(\mathrm{d}x)<\infty$, $i=0,1,2$.

  Assumption 4. Let $\mu _i$ is a probability measure corresponding to the frailty $Y_i(1)\in \mathbb {R}_{+}^{1}$, $i=0,1,2$. Then,

  $$\begin{aligned} \int _{0}^{\infty }\int _{0}^{\infty } e^{bx}\mathrm{d}\mu _i<\infty \end{aligned}$$

  (12)

  for some real number $b>0$ and $i=0,1,2$.

Then, the mixed bivariate survival model for time-dependent correlated frailties is identified from the bivariate distribution of the failure times $(T_{1},T_{2})$.

The proof of Proposition 2 is given in “Appendix 3.”

2.2 Model validation

In this section, we will assume that $\chi ({\mathbf {u}})=\exp (\beta ^{*}{\mathbf {u}})$. To validate the regression model, we need to estimate the vectors of Cox-regression parameters $\beta _{1}$ and $\beta _{2}$, vector parameter defining frailty $\zeta$ [in the case of correlated frailty model either $(\sigma _{1}^{2},\sigma _{2}^{2},\rho )$ for time-independent gamma-frailty or $(\gamma _{1}^{-1}, \gamma _{2}^{-1}, \varrho )$ for gamma-frailty process given by the Laplace exponent (6)], and the baseline hazard function $\lambda _{1}(t)$ and $\lambda _{2}(t)$. If the baseline hazard functions follow a parametric form such as the Gompertz or the Weibull function with vector parameter $\xi$, we can use the classic maximum likelihood method to estimate all unknown parameters. The log-likelihood in this case is given by

$$\begin{aligned} \begin{aligned} \ln L(Data;\theta )&= (1-\delta _{i1})(1-\delta _{i2})\sum _{i}\ln S(t_{i1},t_{i2}|{\mathbf {u}}_{i1},{\mathbf {u}}_{i2}) \\&\quad -\,\delta _{i1}(1-\delta _{i2})\sum _{i}\ln \left( \partial S(t_{i1},t_{i2}|{\mathbf {u}}_{i1},{\mathbf {u}}_{i2})/\partial t_{i1}\right) \\&\quad -\,(1-\delta _{i1})\delta _{i2}\sum _{i}\ln \left( \partial S(t_{i1},t_{i2}|{\mathbf {u}}_{i1},{\mathbf {u}}_{i2})/\partial t_{i2}\right) \\&\quad +\,\delta _{i1}\delta _{i2}\sum _{i}\ln \left( \partial ^{2}S(t_{i1},t_{i2}|{\mathbf {u}}_{i1},{\mathbf {u}}_{i2})/\partial t_{i1}\partial t_{i2}\right) \end{aligned} \end{aligned}$$

(13)

Here, $\theta =(\beta ,\zeta ,\xi )$ is the vector of unknown parameters, $\beta =(\beta _{1},\beta _{2})$ stands for Cox-regression coefficients, $\zeta$ for frailty parameters, and $\xi$ for parameters defining the baseline hazard functions $\lambda _{j}(t)$, $j=1,2$. The data include information about life spans $(t_{i1},t_{i2})$, observed covariates $({\mathbf {u}}_{i1},{\mathbf {u}}_{i2})$, and censoring $(\delta _{i1},\delta _{i2})$ for a twin pair i, $i=1,\ldots ,n$. The estimate of the vector parameter $\theta$ we can find by maximizing the log-likelihood function (13).

If the form of the baseline hazard functions is not specified, the estimates can be obtained by the EM algorithm. This algorithm combines the maximum partial likelihood estimator of the vector parameter $(\beta ,\zeta )$ with the Breslow estimator (Breslow 1972) of the cumulative baseline hazard function $\Lambda (t)=(\Lambda _{1}(t),\Lambda _{2}(t))$. The EM algorithm is an iterative procedure with two steps—E (expectation) and M (maximization) on each iteration. It works as follows: Let $f(z_{i1},z_{i2}|t_{i1},t_{i2},\zeta )$ be the density function of the random variable $(Z_{i1}(t_{i1}),Z_{i2}(t_{i2}))$ given parameter vector $\zeta$, $i=1,\ldots ,n$. Denote the estimates of $\Lambda (t)$, $\zeta$, and $\beta$ on the $l^{th}$ iteration by $\hat{\Lambda } _{l}(t)$, $\hat{\zeta } _{l}$, and $\hat{\beta }_{l}$, respectively. Similar to Gorfine and Hsu (2011), we define the failure counting process $N_{ij}=\delta _{ij}\text {Ind}(T_{ij}\leqslant t)$ and the at-risk process $X_{ij}=\text {Ind}(T_{ij}\geqslant t)$, where $T_{ij}$ is the random time to the failure of twin j in twin pair i, $i=1,\ldots ,n$, $j=1,2$. Define random processes

$$\begin{aligned} S_{j}^{(0)}(\beta ,t)= & {} \sum _{i=1}^{n}\sum _{j=1}^{2}X_{ij}(t)Z_{ij}(t)\exp (\beta _{j}^{*}{\mathbf {u}}_{ij}),\\ S_{j}^{(1)}(\beta ,t)= & {} \sum _{i=1}^{n}\sum _{j=1}^{2}X_{ij}(t)Z_{ij}(t)u_{ij}\exp (\beta _{j}^{*}{\mathbf {u}}_{ij}) \end{aligned}$$

and equations

$$\begin{aligned}&\int _{0}^{\infty }\sum _{i=1}^{n}\left( {\mathbf {u}}_{ij}-\frac{\hat{S}_{j}^{(1)}(\beta ,t)}{\hat{S}_{j}^{(0)}(\beta ,t)}\right) \mathrm{d}N_{ij}(t)=0, \end{aligned}$$

(14)

where the symbol $\hbox {''}\hat{\ }\hbox {''}$ means replacing the unknown frailty $Z_{ij}(t)$ with its conditional expectation given the observed data and the current estimates of $\Lambda (t)$, $\zeta$ and $\beta$.

To estimate the cumulative baseline hazard functions $\Lambda _{j}(t)$, we shall use the following estimator

$$\begin{aligned} \hat{\Lambda }_{j}(t)=\int _{0}^{t}\frac{\sum _{i=1}^{n}\mathrm{d}N_{ij}(\tau )}{\hat{S}_{j}^{(0)}(\beta ,t)}, \quad j=1,2. \end{aligned}$$

(15)

This estimator is a step function with jumps at the observed failure times of twins.

Using Bayes’ formula, we calculate in the E-step conditional expectation of the log-density function

$$\begin{aligned} \sum _{i=1}^{n}{\hat{\mathrm{E}}}\ln (f(Z_{i1}(.),Z_{i2}(.)|\zeta )) \end{aligned}$$

(16)

given observed data and the current estimates of $\Lambda (t)$, $\zeta$ and $\beta$. In the M-step, we update these estimates.

The EM algorithm proceeds as follows:

• 1. Initialization. Set $l=0$. Put $\hat{\zeta } _{0}=(0, \varrho _{0})$ for any $0\leqslant \varrho _{0}\leqslant 1$ in the case of time-dependent frailty and $\hat{\zeta } _{0}=(0, \rho _{0})$ for any $0\leqslant \rho _{0}\leqslant 1$, otherwise. This corresponds to $\hat{Z}_{ij}(t)=t$ and $\hat{Z}_{ij}=1$, respectively. Calculate $\hat{\beta } _{1}$ and $\hat{\Lambda } _{1}(t)$ from (14) and (15), respectively. Given the estimates $\hat{\beta } _{1}$ and $\hat{\Lambda } _{1}(t)$, calculate $\hat{\zeta } _{1}$ by maximizing (16). Set $l=1$.

• 2. Given $\hat{\Lambda } _{l}(t)$ and $\hat{\zeta } _{l}$, calculate $\hat{\beta } _{l+1}$ from (14).

• 3. Given the estimates $\hat{\zeta } _{l}$ and $\hat{\beta } _{l+1}$, calculate $\hat{\Lambda } _{l+1}(t)$ by using formula (15).

• 4. Given the estimates $\hat{\beta } _{l+1}$, $\hat{\Lambda } _{l+1}(t)$, calculate $\hat{\zeta } _{l+1}$ by maximizing (16).

• 5. Stop if convergence is reached with respect to estimates of $\beta$ and $\zeta$. Otherwise, $l\rightarrow l+1$ and repeat steps 2-5.

The convergence of the EM algorithm and the properties of parameter estimates have been discussed elsewhere (Zeng and Lin 2007). For the correlated frailty model with time-independent gamma-distributed frailty, the calculation of expression (16) has been discussed in detail by Iachine (1995). The calculation of this expression in the case of the gamma-frailty process for the same model can be found in “Appendix 4.”

In the parametric approach, the choice of the appropriate baseline hazard function plays an important role. The Gompertz function does not guarantee the good fit of the marginal survival function for real longevity data. The following gamma parameterization of the univariate survival function gives better results by fitting the real data in the model with time-independent frailty

$$\begin{aligned} S (t)= & {} (1+s^2\tilde{\Lambda }(t))^{-1/s^2}=(1+\sigma ^2\Lambda (t))^{-1/\sigma ^2}, \end{aligned}$$

(17)

where $\tilde{\Lambda }(t)=(\tilde{a}/\tilde{b})(\exp (\tilde{b}t)-1)$ is the pseudo-baseline cumulative hazard, $t\geqslant 30$, $s^2,\tilde{a},\tilde{b}>0$, and $\sigma ^2>0$ is the variance of the time-independent frailty. Given parameters $s^2,\sigma ^2,\tilde{a}$, and $\tilde{b}$, it is not difficult to find the true baseline cumulative hazard $\Lambda (t)$ in the form

$$\begin{aligned} \Lambda (t)= & {} ((1+s^2\tilde{\Lambda }(t))^{\sigma ^2/s^2}-1)/\sigma ^2. \end{aligned}$$

In the case of the time-dependent frailty given by a Lévy process with Laplace exponent $\Phi (c)$, we need to consider the following analog of Eq.  (17):

$$\begin{aligned} S (t)= & {} (1+s^2\tilde{\Lambda }(t))^{-1/s^2}=\exp \left( -\int _0^t\Phi (\Lambda (\tau ,t))\mathrm{d}\tau \right) . \end{aligned}$$

(18)

Unfortunately, Eq. (18) does not have a closed-form solution with respect to $\Lambda (t)$. In experiments with real data, we will find the approximative solution to (18) such that the function $\Lambda _\mathrm{appr}^\mathrm{dyn}(t)$ is a non-decreasing, nonnegative, piecewise-constant function satisfying the following conditions:

$$\begin{aligned} \begin{aligned} \Lambda _\mathrm{appr}^\mathrm{dyn}(0)&=0,\\ (1/s^2)\ln (1+s^2\tilde{\Lambda }(t_i))&=\gamma \int _0^{t_i}\ln \left( 1+\left( \Lambda _\mathrm{appr}^\mathrm{dyn}(t_i)-\Lambda _\mathrm{appr}^\mathrm{dyn}(\tau )\right) /\gamma \right) \mathrm{d}\tau \end{aligned} \end{aligned}$$

(19)

for times-to-event $t_i$, $i=1,\ldots ,2n$, sorted in non-decreasing order, $0\leqslant t_1\leqslant t_2\leqslant \cdots \leqslant t_{2n-1}\leqslant t_{2n}=\max \nolimits _{i=1}^{2n}t_i$ (here, n is the number of pairs). The values of $\Lambda _\mathrm{appr}^\mathrm{dyn}(t_i)$ can be calculated recurrently for $i=1,2,\ldots ,2n$ using a simple bisectional procedure. Note that the function $\Lambda _\mathrm{appr}^\mathrm{dyn}(t)$ converges pointwise to the solution of (19) as $n\rightarrow \infty$ and the distance between neighboring moments $t_i$ tends to zero.

To compare two approaches, we assume that in the case of the time-independent frailty, the cumulative hazard is also a non-decreasing, nonnegative, piecewise-constant function $\Lambda _\mathrm{appr}^\mathrm{stat}(t)$ satisfying the following conditions:

$$\begin{aligned} \begin{aligned} \Lambda _\mathrm{appr}^\mathrm{stat}(0)&=0,\\ \Lambda _\mathrm{appr}^\mathrm{stat}(t_i)&= ((1+s^2\tilde{\Lambda }(t_i))^{\sigma ^2/s^2}-1)/\sigma ^2. \end{aligned} \end{aligned}$$

(20)

3 Results

3.1 Experiments with simulated data

In this subsection, we will discuss the results of the consistency test for the correlated frailty models with time-dependent and time-independent frailties (11). It was assumed that $\alpha =1$, $\text{ Var }Z_1=\text{ Var }Z_2=\sigma ^2$, and $\text{ Corr }(Z_1,Z_2)=\rho$ in the case of the time-independent frailty or $\text{ Var }Z_1(1)=\text{ Var }Z_2(1)=\gamma ^{-1}$ and $\text{ Corr }(Z_1(1),Z_2(1))=\varrho$ in the case of the time-dependent frailty, baseline hazard functions $\lambda _j(t)$ followed Gompertz (exponential) form $\lambda _j(t)=a\exp (bt)$, and an observed covariate ${\mathbf {u}}$ influenced longevity so that the conditional hazard function was defined by $\mu _j(t_j|Z_j,{\mathbf {u}}_j)=Z_j\exp (\beta {\mathbf {u}}_j)\lambda _j(t)$, $j=1,2$. The covariates were randomly generated from the uniform distribution on the interval [0,1] and were independent for the individuals. The (true) values for data generating are given in Tables 1 and 2 and have been chosen so that the mean and the standard deviation of the generated times-to-event were equal to approximately 75 and 12 years, respectively. The bivariate times-to-event have been generated using formula (4) with $\sigma _1=\sigma _2=\sigma$ in the case of the time-independent frailty and using formula (25) given in “Appendix 2” in the case of time-dependent frailty. In both cases, it was assumed that $\Lambda _1(t)=\Lambda _2(t)=(a/b)(\exp (bt)-1)$ and $\chi _1({\mathbf {u}})=\chi _2({\mathbf {u}})=\exp (\beta {\mathbf {u}})$. We have not truncated or censored the generated data. We estimated unknown parameters and cumulative hazard functions using the classic maximum likelihood estimator (parametric method) and the EM algorithm (semiparametric method). In all cases, we simulated 100 datasets for 500 twin pairs.

Table 1 shows the results of simulation study for the time-independent gamma-frailty model without truncation and censoring. Empirical means and standard deviations of estimates were calculated using the classic maximum likelihood method and the EM algorithm, respectively.

Table 1 Estimates of unknown parameters for the time-independent frailty model

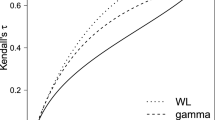
Table 2 shows the results of the simulation study for the time-dependent gamma-frailty model without truncation and censoring. Empirical means and standard deviations of estimates were also calculated using the classic maximum likelihood method and the EM algorithm, respectively. Analysis of estimates in both tables does not indicate the presence of any bias, and estimates calculated using the classic maximum likelihood estimator are generally more efficient. Furthermore, the estimates of the Cox-regression coefficients and parameters characterizing the frailty distribution are closer to true vales than those for the EM algorithm. One can see in Fig. 1 that in both cases (the time-dependent and the time-independent frailty), the empirical mean log baseline cumulative hazard trajectory calculated using the EM algorithm fits the true log baseline cumulative hazard trajectory very well.

Table 2 Estimates of unknown parameters for the time-dependent frailty model

Fig. 1

Dependency of $\ln (\Lambda )$ on age. True trajectory (solid line), the empirical mean trajectory, and its lower and upper 95% limit trajectories (dashed lines)

3.2 Experiments with real data

For experiments with real data, we used the datasets from the Danish Twin Registry (DTR). This registry was created in the 1950s. It is one of the oldest population-based registries in the world and contains information about twins born in Denmark since 1870 and who survived to age 6. Multiple births were manually ascertained in birth registers from all 2200 parishes in Denmark. As soon as a twin was traced, a questionnaire was mailed to the twin, to her/his partner or to their closest relatives if neither of the twin partners were alive. The zygosity of twins was assessed on the basis of questions about phenotypic similarities. The reliability of the zygosity diagnosis was validated by comparing laboratory methods based on the blood, serum, and enzyme group determination. In general, the misclassification rates were less than 5$\%$. Other information includes the data on sex, birth, cause of death, health, and lifestyle. An important feature of the Danish twin survival data is their right censoring and left truncation. In our study, we used the longevity data on the like-sex twins with known zygosity born between 1870 and 1900 and who survived until age 30. This non-censored data include 470 male monozygotic (MZ) twin pairs, 475 female MZ twin pairs, 780 male dizygotic (DZ) twin pairs, and 835 male DZ twin pairs. Further details on the Danish Twin Registry can be found in Hauge (1981).

Since the EM algorithm suffers from its slow convergence, we have estimated unknown parameters for the time-independent and the time-dependent frailty models using the classic maximum likelihood method. Table 3 shows these estimates, the logarithm of the maximum value of the likelihood function, and the value of the AKAIKE Information Criterion (AIC) for the data from the Danish Twin Registry described above. The estimates of parameter $s^2$ were very close to zero in all experiments with real data. We have put this parameter equal to zero to avoid the efficiency loss of estimates. The AIC values for the model with time-dependent frailty are slightly smaller than the ones for the model with time-independent frailty. That is, the model with time-dependent frailty is slightly more informative than the one with time-independent frailty. Figures 2 and 3 show estimated and empirical bivariate probability density functions for the time-independent and the time-dependent frailty models. Note that the shapes of the estimated bivariate probability density functions are very similar.

Table 3 Estimates of unknown parameters (standard errors) for the time-independent and $^{\dag }$the time-dependent frailty models

Fig. 2

Estimated and empirical bivariate probability density functions for the time-dependent (solid line) frailty and the time-independent (dashed line) frailty. Male twin pairs from the Danish Twin Registry

Fig. 3

Estimated and empirical bivariate probability density functions for the time-dependent (solid line) frailty and the time-independent (dashed line) frailty. Female twin pairs from the Danish Twin Registry

4 Discussion

Frailty models are a powerful tool for studying non-observable inhomogeneity in a population related to time-to-failure (e.g., death or disease). Models with time-independent frailty have been intensively studied over the last decades and have found a wide range of applications in survival analysis and in searching for genes influencing longevity. However, the studies based on the models with time-dependent frailty are scarce. In this paper, we have attempted to improve the knowledge in this area and to study some properties of multivariate survival models with time-dependent frailty components.

Proposition 1 we have formulated and proved for the bivariate case. It is not difficult to generalize this result and to prove the identifiability of the frailty model with observed covariates for any number J of related individuals equal or greater than 1 if the time-dependent frailty is a multivariate Lévy process. Similarly, we can generalize Proposition 2 for the case of $J\geqslant 2$. However, the number of frailty components in the multivariate analog of the decomposition (11) will be equal to $2^J-1$. The shared frailty model where all individuals in a family or cluster share the same non-observable risk of failure does not meet this problem.

In experiments with simulated data, we tested for consistency and used parametric and semiparametric approaches. In the parametric approach, we assumed that the parametric form of the baseline hazard functions is known and follows the Gompertz form. All unknown parameters characterizing frailty distribution, baseline hazard function, and Cox-regression parameters were estimated directly by maximizing the likelihood function. In the semiparametric approach, we used the EM algorithm and estimated the Cox-regression parameters and the parameters of frailty distribution by maximizing the partial likelihood function. The cumulative baseline hazard function was estimated using the Breslow estimator regarding this function as infinite-dimensional parameters. The EM algorithm suffers from its slow convergence. Moreover, in the semiparametric approach, the number of calculations increases with the number of individuals much more rapidly than in the parametric one. It leads to the drastic slowing of the convergence of the EM algorithm and increases substantially the time of estimation. It makes implementing the EM algorithm in the case of the time-dependent frailty for analysis of the real data problematic.

Experiments with real data show that the proposed method and the method with time-independent frailty produce similar shapes of the estimated bivariate probability density functions. The baseline cumulative hazard functions have been chosen so that the estimated marginal survival functions guarantee the best fit to the empirical ones according to Eqs. (19)–(20). A large degree of similarity of the estimated bivariate density functions for the models with time-dependent and time-independent frailties in the range of ages 30–100 years guarantees the similar bivariate fit. The difference between the two approaches can involve the shape of the baseline hazard functions and the asymptotic behavior of the bivariate probability density functions. The models with time-dependent and time-independent frailties are not nested. Therefore, we cannot compare them using the likelihood ratio test. For this purpose, the AKAIKE Information Criterion can be used. In accordance with this criterion, the model with time-dependent frailty is slightly more informative compared to the one with time-independent frailty for the data we considered.

Gorfine and Hsu (2011) studied the robustness of the multivariate survival models with frailty components against the violations of the model assumptions. It was found that unnecessary modeling of the dependency between the frailty variates can lead to some efficiency loss of parameter estimates. Misspecification of the frailty distribution can introduce a bias in estimates. Misspecification of the baseline hazard functions can lead to severe bias of all estimates if we use the parametric maximum likelihood estimator, where the baseline hazard functions follow the parametric form. The nonparametric maximum likelihood estimator does not suffer from this drawback. Note that in experiments with real data, we have used a flexible parametrization of the baseline cumulative hazard functions given by formulas (19)–(20). This parameterization does not presume any knowledge about the form of the baseline hazard function. It is sufficient to have a good approximation of the marginal survival function.

An extension of the present study can include the investigation of identifiability of the survival models with competing risks and time-dependent frailty components. The piecewise-constant approximation of the cumulative hazard function has been used in experiments with real data [formulas (19)–(20)]. Other approximative functions such as piecewise linear or piecewise exponential can be used to improve the bivariate goodness-of-fit. Further, numerical experiments with real data are needed to understand whether the proposed method improves the goodness-of fit on the method with time-independent frailty.

Appendices

Appendix 1: Univariate survival function for frailty model based on a gamma process

Let $Z=\{Z(t):t\geqslant 0\}$ is a gamma process with Laplace transform given by the Lévy-Khinchin formula

$$\begin{aligned} L(c;t)=\mathbb {E}e^{-cZ(t)}=e^{-t\Phi _{G}(c)}, \end{aligned}$$

where $\Phi _{G}(c)$ is the Laplace exponent of the Lévy process Z, the argument for Laplace transform $c\geqslant 0$ and

$$\begin{aligned} \Phi _{G}(c)=h[\ln (\gamma +c)-\ln \gamma ]=h\ln (1+\gamma ^{-1}c). \end{aligned}$$

Here, ht and $\gamma$ are the shape and the scale parameters, respectively, for gamma-distributed random variable Z(t). Since Z(t) is a.s. increasing in t, we can consider it as subordinator. It is easy to check that

$$\begin{aligned} \begin{aligned} \mathbb {E}Z(t)e^{-cZ(t)}&= t\Phi _{G}^{(1)}(c)e^{-t\Phi _{G}(c)}\\ \mathbb {E}Z(t)^{2}e^{-cZ(t)}&= \left( t^{2}\Phi _{G}^{(1)}(c)^{2}-t\Phi _{G}^{(2)}(c)\right) e^{-t\Phi _{G}(c)}\\ \mathbb {E}Z(t)^{3}e^{-cZ(t)}&= \left( t\Phi _{G}^{(3)}(c)+t^{3}\Phi _{G}^{(1)}(c)^{3}-3t^{2}\Phi _{G}^{(1)}(c)\Phi _{G}^{(2)}(c)\right) e^{-t\Phi _{G}(c)}, \end{aligned} \end{aligned}$$

(21)

where superscript $\hbox {''}(l)\hbox {''}$ stands for lth-order argument derivative.

In nonhomogeneous population, the process Z (individual for each member of population) can characterize the individual risk of mortality (frailty). In accordance with the definition of the frailty model under mixed proportional hazard specification, we have

$$\begin{aligned} \mu (t|(Z,{\mathbf {u}})=Z(t)\chi ({\mathbf {u}})\lambda (t) \end{aligned}$$

for covariate vector ${\mathbf {u}}$, parameter vector ${\beta }$, and baseline hazard $\lambda (t)$. In Gjessing et al. (2003) (Theorem 1), it was shown that the population survival in this case can be calculated

$$\begin{aligned} S(t|{\mathbf {u}})=\mathbb {E} S(t|Z,{\mathbf {u}})=\exp \left( -\int _{0}^{t}\Phi _{G}(\Lambda (\tau ,t;{\mathbf {u}}))\mathrm{d}\tau \right) , \end{aligned}$$

where

$$\begin{aligned} \Lambda (\tau ,t;{\mathbf {u}})=\int _{\tau }^{t}\chi ({\mathbf {u}})\lambda (s)\mathrm{d}s. \end{aligned}$$

For constant $\lambda (t)=\lambda _{0}$, it holds that $\Lambda (\tau ,t;{\mathbf {u}})=\lambda _{0}e^{{\beta ^{*}}{\mathbf {u}}}(t-\tau )$,

$$\begin{aligned} S(t|{\mathbf {u}})=\exp \left( h\left( t-\frac{\gamma }{\chi ({\mathbf {u}})\lambda _{0}}\left( 1+\frac{\chi ({\mathbf {u}})\lambda _{0}t}{\gamma }\right) \ln \left( 1+\frac{\chi ({\mathbf {u}})\lambda _{0}t}{\gamma }\right) \right) \right) , \end{aligned}$$

and

$$\begin{aligned} \mu (t|{\mathbf {u}})=-\frac{d\ln S(t|{\mathbf {u}})}{\mathrm{d}t}= h\ln \left( 1+\frac{\chi ({\mathbf {u}})\lambda _{0}t}{\gamma }\right) . \end{aligned}$$

Using the following formula for indefinite integral

$$\begin{aligned} \int \ln (1+\alpha (\exp (\kappa t)-\exp (\kappa \tau )))\mathrm{d}\tau= & {} -\kappa ^{-1}\text{ Li }_{2}\left( \frac{\alpha \exp (\kappa \tau )}{\alpha \exp (\kappa t)+1}\right) \nonumber \\&-\,\tau \ln \left( 1-\frac{\alpha \exp (\kappa t)}{1+\alpha \exp (\kappa t)}\right) \end{aligned}$$

we get for the baseline hazard given by the Gompertz function $\lambda (t)=a\exp (bt)$

$$\begin{aligned}&S(t|{\mathbf {u}})\nonumber \\&\quad =\exp \left( -h\int _{0}^{t} \ln \left( 1+\gamma ^{-1}\Lambda (\tau ,t;{\mathbf {u}})\right) \mathrm{d}\tau \right) \nonumber \\&\quad =\exp \left( -h\int _{0}^{t} \ln \left( 1+\frac{a\chi ({\mathbf {u}})}{\gamma b}(\exp (bt)-\exp (b\tau )\right) \mathrm{d}\tau \right) \nonumber \\&\quad =\exp \left( -h\left( -t\ln (1-f(t,{\mathbf {u}})e^{bt})-b^{-1}\text {Li}_{2}(f(t,{\mathbf {u}}) e^{bt})+b^{-1}\text {Li}_{2}(f(t,{\mathbf {u}}))\right) \right) .\nonumber \\ \end{aligned}$$

(22)

Here, $f(t,{\mathbf {u}})=(a\chi ({\mathbf {u}})/(b\gamma (1+a\chi ({\mathbf {u}})e^{bt}/(b\gamma ))$ and $\text {Li}_{2}(z)$ is the dilogarithm function defined by

$$\begin{aligned} \text {Li}_{2}(z)=-\int _{0}^{z}\frac{\ln (1-u)}{u}\mathrm{d}u, z\in \mathbb {C}\backslash [1,\infty ). \end{aligned}$$

This function is an analytical extension of the infinite series

$$\begin{aligned} \text {Li}_{2}=\sum \limits _{i=1}^{\infty }\frac{z^{k}}{k^{2}}, |z|<1. \end{aligned}$$

Appendix 2: Bivariate survival function for frailty model based on gamma processes

Analogously to the univariate case, we can write the bivariate survival function for the bivariate mixed proportional hazard model for the correlated time-dependent frailties given by Lévy processes $Z_{1}=\{Z_{1}(t):t\geqslant 0\}$ and $Z_{2}=\{Z_{2}(t):t\geqslant 0\}$ in the form

$$\begin{aligned} S(t_{1},t_{2}|{\mathbf {u}}_{1},{\mathbf {u}}_{2})= & {} \mathbb {E}\text {e}^{-\chi _{1}({\mathbf {u}}_{1})\int _{0}^{t_{1}}Z_{1}(\tau )\lambda _{1}(\tau )\mathrm{d}\tau }\text {e}^{-\chi _{2}({\mathbf {u}}_{2})\int _{0}^{t_{2}}Z_{2}(\tau )\lambda _{2} (\tau )\mathrm{d}\tau }\\= & {} \exp \left( -\int _{0}^{t_{-}}\Phi _\mathrm{biv}(\chi _{1}({\mathbf {u}}_{1})\Lambda _{1}(\tau ,t_{1}),\chi _{2}({\mathbf {u}}_{2})\Lambda _{2}(\tau ,t_{2}))\mathrm{d}\tau \right) \\&\times \exp \left( -\int _{t_{-}}^{t_{+}}\Phi _\mathrm{uni}^{+}(\chi _{+}({\mathbf {u}}_{1},{\mathbf {u}}_{2})\Lambda _{+}(\tau ,t_{+}))\mathrm{d}\tau \right) , \end{aligned}$$

where $t_{-}=\min (t_{1},t_{2})$, $t_{+}=\max (t_{1},t_{2})$, $\Phi _\mathrm{biv}(.,.)$ is the Laplace exponent for the bivariate frailty process $(Z_{1},Z_{2})$,

$$\begin{aligned} \Lambda _{j}(\tau ,t)= & {} \int _{\tau }^{t}\lambda _{j}(s)\mathrm{d}s,\qquad j=1,2, \\ \chi _{+}({\mathbf {u}}_{1},{\mathbf {u}}_{2})= & {} {\left\{ \begin{array}{ll} \chi _{2}({\mathbf {u}}_{2}), \text{ if } t_{2}> t_{1},\\ \chi _{1}({\mathbf {u}}_{1}), \text{ if } t_{1}> t_{2},\\ \end{array}\right. }\\ \Phi _\mathrm{uni}^{+}(.)= & {} {\left\{ \begin{array}{ll} \Phi _{2}(.), \text{ if } t_{2}> t_{1},\\ \Phi _{1}(.), \text{ otherwise },\\ \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} \Lambda _{+}(\tau ,t)={\left\{ \begin{array}{ll} \int _{\tau }^{t}\lambda _{2}(s)\mathrm{d}s, \text{ if } t_{2}> t_{1},\\ \int _{\tau }^{t}\lambda _{1}(s)\mathrm{d}s, \text{ if } t_{1}> t_{2}.\\ \end{array}\right. } \end{aligned}$$

Assume now that related individuals (e.g., twins) have individual frailty processes $Z_{1}=\{Z_{1}(t):t\geqslant 0\}$ and $Z_{2}=\{Z_{2}(t):t\geqslant 0\}$, respectively, so that

$$\begin{aligned} \begin{aligned} Z_{1}=&Y_{0}+Y_{1}, \\ Z_{2}=&Y_{0}+Y_{2}, \end{aligned} \end{aligned}$$

(23)

where $Y_{0}=\{Y_{0}(t):t\geqslant 0\}$, $Y_{1}=\{Y_{1}(t):t\geqslant 0\}$, and $Y_{2}=\{Y_{2}(t):t\geqslant 0\}$ are the gamma processes with Laplace exponents

$$\begin{aligned} \begin{aligned} \Phi _{G,j}(c)= h _{j}[\ln (\gamma +c)-\ln \gamma ], \qquad j=0,1,2. \end{aligned} \end{aligned}$$

(24)

with $h_{1}=h_{2}$. Denote $\varrho =h_{0}/(h_{0}+h_{1})$. To make the model identifiable, we standardize the gamma-frailty process putting $h=h_{0}+h_{1}=\gamma$ so that $\text{ E }Z_{j}(1)=1$, $j=1,2$. It is easy to check that $Z_{1}$ and $Z_{2}$ are also gamma processes with Laplace exponents

$$\begin{aligned} \Phi _{G,j}(c)= h_j \ln (1+\gamma ^{-1}c), \qquad j=1,2. \end{aligned}$$

Assume that conditional hazard functions for twins are given by the model with proportional hazard

$$\begin{aligned} \mu _{j}(t|(Z_{j},{\mathbf {u}}_{j})=Z_{j}(t)\chi _{j}({\mathbf {u}}_{j})\lambda _{j}(t), \qquad j=1,2. \end{aligned}$$

Then, the bivariate population survival function has the form

$$\begin{aligned} \begin{aligned} S(t_{1},t_{2}|{\mathbf {u}}_{1},{\mathbf {u}}_{2})&= \exp \left( -\int _{0}^{t_{1}}\Phi _{G,1}(\Lambda (\tau ,t_{1};{\mathbf {u}}_{1}))\mathrm{d}\tau \right) \\&\quad \times \exp \left( -\int _{0}^{t_{2}}\Phi _{G,2}(\Lambda (\tau ,t_{2};{\mathbf {u}}_{2}))\mathrm{d}\tau \right) \\&\quad \times \exp \left( -\int _{0}^{t_{-}}\Phi _{G,0}(\Lambda _{-}(\tau ,t_{1},t_2;{\mathbf {u}}_{1},{\mathbf {u}}_{2}))\mathrm{d}\tau \right) \\&\quad \times \exp \left( -\int _{t_{-}}^{t_{+}}\Phi _{G,0}(\Lambda _{+}(\tau ,t_{+};{\mathbf {u}}_{1},{\mathbf {u}}_{2}))\mathrm{d}\tau \right) \end{aligned} \end{aligned}$$

(25)

with

$$\begin{aligned} \Lambda _{-}(\tau ,t_{1},t_2;{\mathbf {u}}_{1},{\mathbf {u}}_{2})=&\chi _{1}({\mathbf {u}}_{1})\Lambda _{1}(\tau ,t_1)+\chi _{2}({\mathbf {u}}_{2})\Lambda _{2}(\tau ,t_2)). \end{aligned}$$

If the baseline hazard function is given by the Gompertz function, we can use formula (22) to calculate the bivariate population survival.

Appendix 3: The proof of Proposition 2

To prove Proposition 2, we need to check several auxiliary statements.

Lemma 1

Let $c_{1}$, $c_{2}\geqslant 0$. Then,

$$\begin{aligned} \left| \text{ e }^{-c_{2}}-\text{ e }^{-c_{1}}\right| \leqslant&\left| c_{2}-c_{1}\right| . \end{aligned}$$

(26)

Proof

Assume that $c_{1}\geqslant c_{2}\geqslant 0$ and set $\Delta c=c_{1}-c_{2}$. Then,

$$\begin{aligned} \left| \text{ e }^{-c_{2}}-\text{ e }^{-c_{1}}\right| = \text{ e }^{-c_{2}}-\text{ e }^{-c_{1}}\leqslant&\frac{\text {e}^{\Delta c}-1}{\text{ e }^{c_{2}+\Delta c}} \leqslant 1-\text {e}^{-\Delta c}. \end{aligned}$$

It is easy to check that

$$\begin{aligned} \max _{\Delta c\geqslant 0}(1-\text {e}^{-\Delta c}-\Delta c)=0. \end{aligned}$$

Therefore,

$$\begin{aligned} \left| \text{ e }^{-c_{2}}-\text{ e }^{-c_{1}}\right| \leqslant&\Delta c. \end{aligned}$$

Last result holds also in the case of $c_{2}> c_{1}\geqslant 0$. $\square$

Lemma 2

Let $\Phi (c)$ be a Laplace exponent given by (5), and $\Lambda (t)$ is an increasing continuous function defined in $\mathbb {R}_{+}$. Then,

$$\begin{aligned} \int _{0}^{\tau }\Phi ^{\prime }(\Lambda (\tau )-\Lambda (s))\mathrm{d}s \geqslant b\tau +\tau \int _{0}^{\infty }x\text {e}^{-\Lambda (\tau )x}\nu (\mathrm{d}x). \end{aligned}$$

(27)

Proof

The statement of lemma follows directly from formula (5) and monotone increase of the function $\Lambda (.)$. $\square$

The bivariate survival function for correlated frailty processes given by (11) is

$$\begin{aligned} S(t_{1},t_{2})= & {} \mathbb {E}\text {e}^{-\int _{0}^{t_{1}}Z_{1}(\tau )\lambda _{1}(\tau )\mathrm{d}\tau -\int _{0}^{t_{2}}Z_{2}(\tau )\lambda _{2} (\tau )\mathrm{d}\tau } \nonumber \\= & {} \text {e}^{ -\int _{0}^{t_{1}}\Phi _{1}(\Lambda _{1}(\tau ,t_{1}))\mathrm{d}\tau }\text {e}^{ -\int _{0}^{t_{2}}\Phi _{2}(\Lambda _{2}(\tau ,t_{2}))\mathrm{d}\tau } \nonumber \\&\times \,\text {e}^{ -\int _{0}^{t_{-}}\Phi _{0}(\Lambda _{1}(\tau ,t_{1})+\alpha \Lambda _{2}(\tau ,t_{2}))\mathrm{d}\tau }\text {e}^{ -\int _{t_{-}}^{t_{+}}\Phi _{0}(\Lambda _{0}(\tau ,t_{+}))\mathrm{d}\tau }, \end{aligned}$$

(28)

where $\Phi _{i}(.)$, $i=0,1,2$, is the Laplace exponent for the frailty process $Y_{i}(t)$ and

$$\begin{aligned} \Lambda _{0}(\tau ,t)={\left\{ \begin{array}{ll} \alpha \Lambda _{2}(\tau ,t),\quad \text{ if } t_{2}> t_{1},\\ \Lambda _{1}(\tau ,t),\quad \text{ otherwise }.\\ \end{array}\right. } \end{aligned}$$

Using formula (28) and Assumptions 2-3 of Proposition 2, it can be shown that

$$\begin{aligned}&\int _{0}^{t}\Phi _{1}(\Lambda _{1}(\tau ,t))\mathrm{d}\tau = -\ln \left( \lim _{t_{2}\uparrow \infty } \frac{S(t,t_{2})}{S(0,t_{2})}\right) = g_{1}(t) ,\nonumber \\&\quad \int _{0}^{t}\Phi _{2}(\alpha \Lambda _{2}(\tau ,t))\mathrm{d}\tau = -\ln \left( \lim _{t_{1}\uparrow \infty } \frac{S(t_{1},t)}{S(t_{1},0)}\right) = g_{2}(t) ,\nonumber \\&\quad \int _{0}^{t_{-}}\Phi _{0}(\Lambda _{1}(\tau ,t_{1})+\alpha \Lambda _{2}(\tau ,t_{2}))\mathrm{d}\tau +\int _{t_{-}}^{t_{+}}\Phi _{0}(\Lambda _{0}(\tau ,t_{+}))\mathrm{d}\tau \nonumber \\&\quad =-\ln \left( \frac{S(t_{1},t_{2})}{\lim _{t_{1}\uparrow \infty } \frac{S(t_{1},t_{2})}{S(t_{1},0)}\lim _{t_{2}\uparrow \infty } \frac{S(t_{1},t_{2})}{S(0,t_{2})}}\right) = g_{0}(t_{1},t_{2}). \end{aligned}$$

(29)

Note that expressions on the left hand of (29) are observable, $g_1(t)=g_0(t,0)$ and $g_2(t)=g_0(0,t)$.

Let $\mathcal L_1$ be a set of all continuous increasing functions $\Lambda (t)$ on $\mathbb R_{+}$ satisfying $\Lambda (0)=0$ and $\Lambda (t)\rightarrow \infty$ as $t\rightarrow \infty$. Given Laplace exponent $\Phi _0$, consider the map $A_1$ defined by

$$\begin{aligned} (A_1\Lambda )(t):=&\int _{0}^{t}\Phi _{0}(\Lambda (t)-\Lambda (\tau ))\mathrm{d}\tau . \end{aligned}$$

(30)

Lemma 3

$A_1$ is a bijective map from $\mathcal L_1$ to image $A_1(\mathcal L_1)$ of $\mathcal L_1$ under $A_1$.

Proof

It is easy to see that $(A_1\Lambda )(t)$ is a continuous monotone increasing function with $(A_1\Lambda )(0)=0$ and $(A_1\Lambda )(t)\rightarrow \infty$ as $t\rightarrow \infty$ for $\Lambda \in \mathcal L_1$. That is, $A_1(\mathcal L_1)\subset \mathcal L_1$. For any $0<T<\infty$, the set $\mathcal L_1^T$ of all continuous monotone increasing functions on [0, T] satisfying $\Lambda (0)=0$ is a complete metric space with usual supremum distance

$$\begin{aligned} d_{T}(\Lambda ^{a}(.),\Lambda ^{b}(.))=\sup \limits _{t\in [0.T]}|\Lambda ^{a}(t)-\Lambda ^{b}(t)|=||f(.)||_{T ,\infty }. \end{aligned}$$

Let $g(t)=\int _{0}^{t}\Phi _{0}(\Lambda (t)-\Lambda (\tau ))\mathrm{d}\tau$ for $\Lambda \in \mathcal L_1$. Taking into account that $\Lambda (t)$ is differentiable in t a.e. and $\Phi _{0}(0)=0$, we get that

$$\begin{aligned} g^{\prime }(t)= \Lambda ^{\prime }(t)\int _{0}^{t}\Phi _{0}^{ \prime }(\Lambda (t)-\Lambda (\tau ))\mathrm{d}\tau \end{aligned}$$

(31)

and, therefore,

$$\begin{aligned} \Lambda (t)= \int _{0}^{t}g^{\prime }(\tau )\left( \int _{0}^{\tau }\Phi _{0}^{ \prime }(\Lambda (\tau )-\Lambda (s))\mathrm{d}s\right) ^{-1}\mathrm{d}\tau . \end{aligned}$$

(32)

In accordance with the mean value theorem applied to the integral on the right hand of (31), there exists $\tau ^{\prime }\in [0,\tau ]$ such that

$$\begin{aligned} \tau ^{-1}g^{\prime }(\tau )=\Lambda ^{\prime }(\tau )\Phi _{0}^{\prime }(\Lambda (\tau )-\Lambda (\tau ^{\prime }))\leqslant \Lambda ^{\prime }(\tau )\int _{0}^{\infty }x\nu (\mathrm{d}x). \end{aligned}$$

(33)

Since $\int _0^{\infty }x\nu (\mathrm{d}x)$ is finite, the function on the left hand of (33) is integrable on [0, t], $t<\infty$. Assume that two solutions $\Lambda ^{a}, \Lambda ^{b}$ of (32) satisfy $\Lambda ^{a}(t)= \Lambda ^{b}(t)$ on the interval $[0,t_{0}]$, $t_{0}\geqslant 0$. We shall show now that these solutions satisfy this property on the interval $[t_{0},t_{0}+t_{\varepsilon }]$ for some $t_{\varepsilon }>0$ too. Let the map $B_1$ be given by

$$\begin{aligned} (B_1\Lambda )(t)= \Lambda (t_{0})+\int _{t_{0}}^{t}g^{\prime }(\tau )\left( \int _{0}^{\tau }\Phi _{0}^{ \prime }(\Lambda (\tau )-\Lambda (s))\mathrm{d}s\right) ^{-1}\mathrm{d}\tau . \end{aligned}$$

Taking into account $g^{\prime }(\tau )\geqslant 0$ and inequalities (26) and (27), we get that

$$\begin{aligned}&\left| \Lambda ^{a}(t)-\Lambda ^{b}(t)\right| = \left| (B_1\Lambda ^{a})(t)-(B_1\Lambda ^{b})(t)\right| \\&\quad = \left| \int _{t_{0}}^{t}\frac{g^{\prime }(\tau )\mathrm{d}\tau }{\int _{0}^{\tau }\Phi _{0}^{ \prime }(\Lambda ^{a}(\tau )-\Lambda ^{a}(s))\mathrm{d}s}-\int _{t_{0}}^{t}\frac{g^{\prime }(\tau )\mathrm{d}\tau }{\int _{0}^{\tau }\Phi _{0}^{ \prime }(\Lambda ^{b}(\tau )-\Lambda ^{b}(s))\mathrm{d}s}\right| \\&\quad = \left| \int _{t_{0}}^{t}\frac{g^{\prime }(\tau )\left( \int _{0}^{\tau }\Phi _{0}^{ \prime }(\Lambda ^{b}(\tau )-\Lambda ^{b}(s))\mathrm{d}s-\int _{0}^{\tau }\Phi _{0}^{ \prime }(\Lambda ^{a}(\tau )-\Lambda ^{a}(s))\mathrm{d}s\right) \mathrm{d}\tau }{\left( \int _{0}^{\tau }\Phi _{0}^{ \prime }(\Lambda ^{b}(\tau )-\Lambda ^{b}(s))\mathrm{d}s\right) \left( \int _{0}^{\tau }\Phi _{0}^{ \prime }(\Lambda ^{a}(\tau )-\Lambda ^{a}(s))\mathrm{d}s\right) }\right| \\&\quad \leqslant \int _{t_{0}}^{t}\frac{g^{\prime }(\tau )\left| \int _{0}^{\tau }\Phi _{0}^{ \prime }(\Lambda ^{b}(\tau )-\Lambda ^{b}(s))\mathrm{d}s-\int _{0}^{\tau }\Phi _{0}^{ \prime }(\Lambda ^{a}(\tau )-\Lambda ^{a}(s))\mathrm{d}s\right| \mathrm{d}\tau }{\left| \int _{0}^{\tau }\Phi _{0}^{ \prime }(\Lambda ^{b}(\tau )-\Lambda ^{b}(s))\mathrm{d}s\right| \left| \int _{0}^{\tau }\Phi _{0}^{ \prime }(\Lambda ^{a}(\tau )-\Lambda ^{a}(s))\mathrm{d}s\right| } \\&\quad \leqslant \int _{t_{0}}^{t}\frac{g^{\prime }(\tau )\left( \int _{0}^{\tau }\int _{0}^{\infty }x\left| \exp (-(\Lambda ^{b}(\tau )-\Lambda ^{b}(s))x)-\exp (-(\Lambda ^{a}(\tau )+\Lambda ^{a}(s))x)\right| \nu (\mathrm{d}x)\mathrm{d}s\right) \mathrm{d}\tau }{\left| \int _{0}^{\tau }\Phi _{0}^{ \prime }(\Lambda ^{b}(\tau )-\Lambda ^{b}(s))\mathrm{d}s\right| \left| \int _{0}^{\tau }\Phi _{0}^{ \prime }(\Lambda ^{a}(\tau )-\Lambda ^{a}(s))\mathrm{d}s\right| } \\&\quad \leqslant \int _{t_{0}}^{t}\frac{g^{\prime }(\tau )\left( \int _{0}^{\tau }\int _{0}^{\infty }x^{2}|| \Lambda ^{a}(.)- \Lambda ^{b}(.)||_{\tau ,\infty }\nu (\mathrm{d}x)\mathrm{d}s\right) \mathrm{d}\tau }{\left( \tau \int _{0}^{\infty }x\exp (-x\Lambda ^{a}(\tau ))\nu (\mathrm{d}x)\right) \left( \tau \int _{0}^{\infty }x\exp (-x\Lambda ^{b}(\tau ))\nu (\mathrm{d}x)\right) } \\&\quad \leqslant \frac{C_{0}\left( \int _{t_{0}}^{t}\tau ^{-1}g^{\prime }(\tau )\mathrm{d}\tau \right) }{C_{a}(t)C_{b}(t)}|| \Lambda ^{a}(.)- \Lambda ^{b}(.)||_{t,\infty }, \end{aligned}$$

where $0<C_{0}=\int _{0}^{\infty }x^{2}\nu (\mathrm{d}x)<\infty$, $0<C_{i}(t)=\int _{0}^{\infty }x\exp (-x\Lambda ^{i}(t))\nu (\mathrm{d}x)<\infty$, $i=a,b$.

Let $C(t_{0})=\Lambda ^{a}(t_{0})=\Lambda ^{b}(t_{0})$. Taking $t_{\varepsilon _{1}}>0$ small enough, we can guarantee that $\Lambda ^{i}(t)=(B_1\Lambda ^{i})(t)\leqslant 2C(t_{0})$, $i=a,b$, and, therefore, $C_{a}(t)C_{b}(t)\geqslant C_{3}>0$ for all $t\in [t_{0},t_{0}+t_{\varepsilon _{1}}]$. Now we can find $t_{\varepsilon }$, $0<t_{\varepsilon }\leqslant t_{\varepsilon _{1}}$, small enough so that

$$\begin{aligned} \left| (B_1\Lambda ^{a})(t)-(B_1\Lambda ^{b})(t)\right| \leqslant&q|| \Lambda ^{a}(.)- \Lambda ^{b}(.)||_{t_{0}+t_{\varepsilon },\infty } \end{aligned}$$

for all $t\in [0,t_{0}+t_{\varepsilon }]$ and some positive $q<1$. It means that

$$\begin{aligned}&||\Lambda ^{a}(t)-\Lambda ^{b}(t)||_{t_{0}+t_{\varepsilon },\infty } = || (B_1\Lambda ^{a})- (B_1\Lambda ^{b})||_{t_{0}+t_{\varepsilon },\infty }\\&\quad \leqslant q|| \Lambda ^{a}(.)- \Lambda ^{b}(.)||_{t_{0}+t_{\varepsilon },\infty }<||\Lambda ^{a}(t)-\Lambda ^{b}(t)||_{t_{0}+t_{\varepsilon },\infty .} \end{aligned}$$

From here, it follows that $||\Lambda ^{a}(t)-\Lambda ^{b}(t)||_{t_{0}+t_{\varepsilon },\infty } =0$. We continue this process until we get that $||\Lambda ^{a}(t)-\Lambda ^{b}(t)||_{\infty ,\infty } =0$. Hence, the map $A_1: \mathcal L_1 \rightarrow A_1(\mathcal L_1)$ is injective. Since this map is also surjective, it is bijective $\square$

Define the set $\mathcal L_2$ of all functions $\Lambda _{12}(t_1,t_2,\alpha )$ such that

$$\begin{aligned} \Lambda _{12}(t_1,t_2)= \Lambda _{1}(t_1)+\alpha \Lambda _{2}(t_2) \end{aligned}$$

for $\Lambda _{1},\Lambda _{2} \in \mathcal L_1$, and $\alpha >0$. Given Laplace exponent $\Phi _0$, consider the map $A_2$ defined by

$$\begin{aligned} (A_2\Lambda _{12})(t_1,t_2):= \int _{0}^{t_{-}}\Phi _{0}(\Lambda _{1}(\tau ,t_{1})+\alpha \Lambda _{2}(\tau ,t_{2}))\mathrm{d}\tau +\int _{t_{-}}^{t_{+}}\Phi _{0}(\Lambda _{0}(\tau ,t_{+}))\mathrm{d}\tau .\nonumber \\ \end{aligned}$$

(34)

Lemma 4

$A_2$ is a bijective map from $\mathcal L_2$ to image $A_2(\mathcal L_2)$ of $\mathcal L_2$ under $A_2$.

Proof

Since $\Lambda (t)=\Lambda _{12}(t,t)\in \mathcal L_1$, $\Lambda _1(t)=\Lambda _{12}(t,0)\in \mathcal L_1$, and $\alpha \Lambda _2(t)=\Lambda _{12}(0,t)\in \mathcal L_1$ for $t\in [0,\infty )$, in accordance with Lemma 3, these functions can be uniquely defined by their images $g_0(t,t)=(A_2\Lambda _{1,2})(t,t)=(A_1\Lambda )(t)$, $g_0(t,0)=(A_2\Lambda _{12})(t,0)=(A_1\Lambda _1)(t)$, and $g_0(0,t)=(A_2(\alpha \Lambda _{12}))(0,t)=(A_1(\alpha \Lambda _2))(t)$, respectively. Assume now that $t_2>t_1$ and the solution $\Lambda _{12}(t_1,t)$ to (34) is uniquely defined for $0\leqslant t \leqslant t_0$ with $t_0\geqslant t_1$. Define the map $B_2$ for $t>t_0$ by

$$\begin{aligned}&(B_2\Lambda _{12})(t_1,t)= \Lambda _{12}(t_1,t_0)\\&\quad +\int _{t_0}^{t}\frac{dg_0(t_1,\tau )}{\int _{0}^{t_1 }\Phi _{0}^{ \prime }(\Lambda _{12}(t_1,\tau )-\Lambda _{12}(s,s))\mathrm{d}s+\int _{t_1}^{\tau }\Phi _{0}^{ \prime }(\Lambda _{12}(0,\tau )-\Lambda _{12}(0,s))\mathrm{d}s}. \end{aligned}$$

Similarly to the proof of Lemma 3, it can be shown that the solution to

$$\begin{aligned} \Lambda _{12}(t_1,t)=(B_2\Lambda _{12})(t_1,t) \end{aligned}$$

is also uniquely defined on the interval $[t_0,t_0+t_\varepsilon ]$ for some $t_\varepsilon >0$ and, therefore, is uniquely defined for all $t\geqslant t_1$. The same result can be checked in the case of $t_1>t_2$. $\square$

For the sake of contradiction, assume now that there are functions $\Phi _{0}^{a}(.)$, $\Phi _{0}^{b}(.)$, $\Lambda _{1}^{a}(.)$, $\Lambda _{1}^{b}(.)$, $\Lambda _{2}^{a}(.)$, $\Lambda _{2}^{b}(.)$, and real positive numbers $\alpha ^{a}$ and $\alpha ^{b}$ such that

$$\begin{aligned} g_{0}(t_{1},t_{2})=(A_2^{a}\Lambda _{12}^{a})(t_1,t_2)=(A_2^{b}\Lambda _{12}^{b})(t_1,t_2) \end{aligned}$$

(35)

holds for all $t_1,t_2\geqslant 0$. In accordance with Lemmas 3–4, the maps $A_i^{a}$ and $A_i^{b}$ are invertible on their images of $\mathcal L_i$, $i=1,2$. Moreover, $g_0\in A_2^{a}\mathcal L_2$, $g_0\in A_2^{b}\mathcal L_2$, $g_i\in A_1^{a}\mathcal L_1$, and $g_i\in A_1^{b}\mathcal L_1$, $i=1,2$. Denote maps $(A_i^{b})^{-1}A_i^{a}$ and $(A_i^{a})^{-1}A_i^{b}$ by $T_i^{ba}$ and $T_i^{ab}$, $i=1,2$, respectively. It holds that

$$\begin{aligned} \Lambda _{12}^{b}(t_1,t_2)= & {} (T_2^{ba}\Lambda _{12}^{a})(t_1,t_2)= ((A_2^{b})^{-1}g_{0})(t_1,t_2),\nonumber \\ \Lambda _{12}^{a}(t_1,t_2)= & {} (T_2^{ab}\Lambda _{12}^{b})(t_1,t_2)= ((A_2^{a})^{-1}g_{0})(t_1,t_2),\nonumber \\ \Lambda _{i}^{a}(t_i)= & {} (T_1^{ab}\Lambda _{i}^{b})(t_i)= ((A_1^{a})^{-1}g_{i})(t_i), i=1,2. \end{aligned}$$

(36)

Note that $\Lambda _{1}^{i}(t_1)=\Lambda _{12}^{i}(t_1,0)$ and $\alpha ^i\Lambda _{2}^{i}(t_2)=\Lambda _{12}^{i}(0,t_2)$, $i\in \{a,b\}$. Taking into account that

$$\begin{aligned} \Lambda _1^{b}(t_1)= & {} (T_1^{ba}\Lambda _{1}^{a})(t_1),\quad \alpha ^{b}\Lambda _2^{b}(t_2)=(T_1^{ba}(\alpha ^{a}\Lambda _{2}^{a}))(t_2),\nonumber \\ \Lambda _1^{a}(t_1)= & {} (T_1^{ab}\Lambda _{1}^{b})(t_1),\quad \alpha ^{a}\Lambda _2^{a}(t_2)=(T_1^{ab}(\alpha ^{b}\Lambda _{2}^{b}))(t_2) \end{aligned}$$

(37)

we get from (36) that

$$\begin{aligned} \begin{aligned} \Lambda _{1}^{b}(t_1)+\alpha ^{b}\Lambda _{2}^{b}(t_2)&= (T_1^{ba}\Lambda _{1}^{a})(t_1)+(T_1^{ba}(\alpha ^{a}\Lambda _{2}^{a}))(t_2)\\&=(T_2^{ba}(\Lambda _{1}^{a}+\alpha ^{a}\Lambda _{2}^{a}))(t_1,t_2),\\ \Lambda _{1}^{a}(t_1)+\alpha ^{a}\Lambda _{2}^{a}(t_2)&= (T_1^{ab}\Lambda _{1}^{b})(t_1)+(T_1^{ab}(\alpha ^{b}\Lambda _{2}^{b}))(t_2),\\&=(T_2^{ab}(\Lambda _{1}^{b}+\alpha ^{b}\Lambda _{2}^{b}))(t_1,t_2). \end{aligned} \end{aligned}$$

(38)

Now we will prove that the action of the map $T_2^{ba}$ (resp. $T_2^{ab}$) on the function $\Lambda _{12}^{a}$ (resp. $\Lambda _{12}^{b}$) calculated in the point $(t_1,t_2)$ depends only on the value of $\Lambda _{12}^{b}(t_1,t_2)$ (resp. $\Lambda _{12}^{a}(t_1,t_2)$).

Lemma 5

Given the maps $\Phi _{0}^{a}(.)$, $\Phi _{0}^{b}(.)$, $\Lambda _{1}^{a}(.)$, $\Lambda _{1}^{b}(.)$, $\Lambda _{2}^{a}(.)$, $\Lambda _{2}^{b}(.)$, and real positive numbers $\alpha ^{a}$ and $\alpha ^{b}$, there exist uniquely defined, monotone increasing, continuous functions $f^{ab}:\mathbb {R}_+^{1}\rightarrow \mathbb {R}_+^{1}$ and $f^{ba}:\mathbb {R}_+^{1}\rightarrow \mathbb {R}_+^{1}$ such that

$$\begin{aligned} \begin{aligned} \Lambda _{1}^{a}(t_1)+\alpha ^{a}\Lambda _{2}^{a}(t_2)&=f^{ab}(\Lambda _{1}^{b}(t_1)+\alpha ^{b}\Lambda _{2}^{b}(t_2)),\\ \Lambda _{1}^{b}(t_1)+\alpha ^{b}\Lambda _{2}^{a}(t_2)&=f^{ba}(\Lambda _{1}^{a}(t_1)+\alpha ^{a}\Lambda _{2}^{a}(t_2)). \end{aligned} \end{aligned}$$

Proof

Put $\alpha _{1}^{a}=\alpha _{1}^{b}=1$. From (33) and Lemma 3, it follows that given the functions $g_i(t)$ the maps $(f _i^{a})^{-1}: g_i(t)\rightarrow \alpha _{i}^{a}\Lambda _i^{a}(t)$ and $(f_i^{b})^{-1}: g_i(t)\rightarrow \alpha _{i}^{b}\Lambda _i^{b}(t)$ are strictly monotone increasing, continuous, and uniquely defined. It holds that $g_i(t)=f_i^{a}(\alpha _i^{a}\Lambda _{1}^{a}(t))=f_i^{b}(\alpha _i^{b}\Lambda _{1}^{b}(t))$. Therefore, the maps $f_i^{ba}=(f_i^{b})^{-1}f_i^{a}: \mathbb {R}_+^{1}\rightarrow \mathbb {R}_+^{1}$ and $f_i^{ab}=(f_i^{a})^{-1}f_i^{b}: \mathbb {R}_+^{1}\rightarrow \mathbb {R}_+^{1}$, $i=1,2$, are also strictly monotone increasing and continuous. Since $(T_i^{ba}(\alpha _i^{a}\Lambda _{i}^{a}))(t_i)=f_i^{ba}(\alpha _i^{a}\Lambda _i^{a}(t_i))$ and $(T_i^{ab}(\alpha _i^{b}\Lambda _{i}^{b}))(t_i)=f_i^{ab}(\alpha _i^{b}\Lambda _i^{b}(t_i))$ for $i=1,2$, the middle terms of Eq. (38) depend only on the values of $\alpha _i^{b}\Lambda _i^{b}(t_i)$ and $\alpha _i^{a}\Lambda _i^{a}(t_i)$ and do not depend on the behavior of the functions $\Lambda _i^{a}(t_i)$ and $\Lambda _i^{b}(t_i)$ on the intervals $[0,t_i)$. Therefore, we can rewrite equations in (38) as follows:

$$\begin{aligned} \begin{aligned} \Lambda _{1}^{b}(t_1)+\alpha ^{b}\Lambda _{2}^{b}(t_2) =&f_1^{ba}(\Lambda _{1}^{a}(t_1))+f_2^{ba}(\alpha ^{a}\Lambda _{2}^{a}(t_2))\\ =&f^{ba}(\Lambda _{1}^{a}(t_1)+\alpha ^{a}\Lambda _{2}^{a}(t_2)),\\ \Lambda _{1}^{a}(t_1)+\alpha ^{a}\Lambda _{2}^{a}(t_2) =&f_1^{ab}(\Lambda _{1}^{b}(t_1)+f_2^{ab}(\alpha ^{b}\Lambda _{2}^{b}(t_2)),\\ =&f^{ab}(\Lambda _{1}^{b}(t_1)+\alpha ^{b}\Lambda _{2}^{b}(t_2)). \end{aligned} \end{aligned}$$

(39)

for some continuous monotone increasing functions $f^{ba}: \mathbb {R}_+^{1}\rightarrow \mathbb {R}_+^{1}$ and $f^{ab}: \mathbb {R}_+^{1}\rightarrow \mathbb {R}_+^{1}$. Substituting in (39) $t_2=0$ or $t_1=0$, we get that $f_1^{ab}=f_2^{ab}=f^{ab}$ and $f_1^{ba}=f_2^{ba}=f^{ba}$. $\square$

Proof of Proposition 2

Note firstly that in accordance with Assumption 4, the functions $\Phi _i(c)$, $i=0,1,2$, are analytic ones on $\text {Re} (c)>-b$. Since $f^{ba}(.)$ and $f^{ab}(.)$ are defined on $\mathbb {R}_+^{1}$, additive and continuous, they are linear and it holds that $f^{ab}(x)=C_1^{ab}x+C_2^{ab}$ and $f^{ba}(x)=C_1^{ba}x+C_2^{ba}$ for some constant $C_1^{ab}$, $C_2^{ab}$, $C_1^{ba}$, and $C_2^{ba}$. As $f^{ab}(0)=f^{ba}(0)=0$, we have that $C_2^{ab}=C_2^{ba}=0$. Moreover, $C_1^{ab}=C_1^{ba}=1$ and $\alpha ^{a}=\alpha ^{b}$ because $\Lambda _i^{a}(t^{*})=\Lambda _i^{b}(t^{*})=1$ for some $t^{*}>0$ and $i=1,2$. From here, it follows that $f^{ab}(.)$ and $f^{ba}(.)$ are identity transformations and $\Lambda _i^{a}(t)=\Lambda _i^{b}(t)=\Lambda _i(t)$ for all $t\geqslant 0$, $i=1,2$. It holds also that $(A_1^{a}\Lambda _i)(t)=(A_1^{b}\Lambda _i)(t)$ for all $t\geqslant 0$, $i=1,2$. To complete the proof of Proposition 2, we need to show that $\Phi _0^{a}(x)=\Phi _0^{b}(x)$ for any $x \in \mathbb {R}_+^{1}$. Indeed, the maps $\Phi _0^{a}$ and $\Phi _0^{b}$ are real analytic functions on $\mathbb {R}_+^{1}$ and, therefore,

$$\begin{aligned} \begin{aligned} (A_1^{a}\Lambda _1)(t)=&\int _0^{t}\Phi _0^{a}(\Lambda _1(t)-\Lambda _1(\tau ))\mathrm{d}\tau \\ =&\sum _{n=0}^{\infty }\frac{(\Phi _0^{a})^{(n)}(0)}{n!}\int _0^{t}(\Lambda _1 (t)-\Lambda _1 (\tau ))^{n}\mathrm{d}\tau \\ (A_1^{b}\Lambda _1)(t)=&\int _0^{t}\Phi _0^{b}(\Lambda _1(t)-\Lambda _1(\tau ))\mathrm{d}\tau \\ =&\sum _{n=0}^{\infty }\frac{(\Phi _0^{b})^{(n)}(0)}{n!}\int _0^{t}(\Lambda _1 (t)-\Lambda _1 (\tau ))^{n}\mathrm{d}\tau \end{aligned} \end{aligned}$$

for small values of $\Lambda _1 (t)$. This holds iff $(\Phi _0^{a})^{(n)}(0)=(\Phi _0^{b})^{(n)}(0)$ for all nonnegative integer n and means that $\Phi _0^{a}(x)=\Phi _0^{b}(x)=\Phi _0(x)$ in some neighborhood of 0. Since $\Phi _0(x)$ is a real analytic function on $\mathbb {R}_+^{1}$, this function is uniquely defined in this area. Similarly, it can be proved that the functions $\Phi _i(x)$, $i=1,2$, are also uniquely defined in $\mathbb {R}_+^{1}$. $\square$

Appendix 4: Calculation of the conditional expectation of the log-density function

Case$t_{2}\geqslant t_{1}$.

Let all failure and censoring times $t^{(k)}$, $0\leqslant t^{(k)}\leqslant t_{2}$, $k=1,\ldots ,N_{2}$, be arranged in ascending order so that $0=t^{(0)}\leqslant t^{(1)}\leqslant t^{(2)}\leqslant \cdots \leqslant t^{(N_{2})}=t_{2}$ and $t_{1}=t^{(N_{1})}$, $N_{1}\leqslant N_{2}$. The estimate of the cumulative hazard function $\hat{\Lambda } (t)$ is a step function with $\hat{\Lambda } (0_{-})=0$ and jumps (if non-censored) at times $t^{(k)}$, $k=1,\ldots ,N_{2}$. Since $Y_{j}(t)$, $j=0,1,2$, are gamma processes, it holds that

$$\begin{aligned} Y_{j}(t_{l})= \sum _{k=1}^{N_{l_{j}}}\left( Y_{j}(t^{(k)})-Y_{j}(t^{(k-1)})\right) , \quad j=0,1,2, \quad l_{0}=l_{2}=2,\quad l_{1}=1, \end{aligned}$$

(40)

where increments $\Delta Y_{j}^{(k-1)}=Y_{j}(t^{(k)})-Y_{j}(t^{(k-1)})$ are independent gamma-distributed random variables with means $h_{j}\gamma ^{-1}\Delta t^{(k-1)}$ and the variances $h_{j}\gamma ^{-2}\Delta t^{(k-1)}$ for $\Delta t^{(k-1)}=t^{(k)}-t^{(k-1)}$, $h_{1}=h_{2}=(1-\varrho )\gamma$ and $h_{0}=\varrho \gamma$, $j=0,1,2$, $k=1,\ldots ,N_{l_{j}}$.

Using decomposition (23) with independent gamma processes $Y_{j}(t)$, $j=0,1,2$, we calculate the log-density function as follows:

$$\begin{aligned} \begin{aligned}&\ln (f(Z_{1}(.),Z_{2}(.)|t_{1},t_{2},\zeta )) \\&\quad =-\gamma \left( \sum _{k=0}^{N_{1}-1}\Delta Y_{1}^{(k)}+\sum _{k=0}^{N_{2}-1}\Delta Y_{0}^{(k)}+\sum _{k=0}^{N_{2}-1}\Delta Y_{2}^{(k)}\right) \\&\quad -\sum _{k=0}^{N_{1}-1}\ln \left( \Gamma (\gamma (1-\varrho )\Delta t^{(k)})\right) -\sum _{k=0}^{N_{2}-1}\ln \left( \Gamma (\gamma \varrho \Delta t^{(k)})\Gamma (\gamma (1-\varrho )\Delta t^{(k)})\right) \\&\quad +\gamma (1-\varrho )\left( \sum _{k=0}^{N_{1}-1}\Delta t^{(k)}\ln (\Delta Y_{1}^{(k)})+\sum _{k=0}^{N_{2}-1}\Delta t^{(k)}\ln (\Delta Y_{2}^{(k)})\right) \\&\quad +\gamma \varrho \sum _{k=0}^{N_{2}-1}\Delta t^{(k)}\ln (\Delta Y_{0}^{(k)}) -\sum _{k=0}^{N_{1}-1}\ln (\Delta Y_{1}^{(k)})-\sum _{k=0}^{N_{2}-1}\ln (\Delta Y_{0}^{(k)})\\&\quad -\sum _{k=0}^{N_{2}-1}\ln (\Delta Y_{2}^{(k)}) \end{aligned} \end{aligned}$$

(41)

(index i denoting the twin pair is here omitted).

Given current estimates $\hat{\beta }$, $\hat{\Lambda } (t)$, $\hat{\zeta }$, and the observed data, the conditional expectation of the log-density function (41) (taking into account only summands depending on $\gamma$ and $\varrho$) is equal to

$$\begin{aligned} \begin{aligned}&{\mathbb {E}}\ln (f(Z_{1}(.),Z_{2}(.)|t_{1},t_{2},\hat{\beta } ,\hat{\Lambda } (t),\hat{\zeta }))\\&\quad =-\gamma \left( \sum _{k=0}^{N_{1}-1}\widehat{\Delta Y_{1}^{(k)}}+\sum _{k=0}^{N_{2}-1}\widehat{\Delta Y_{0}^{(k)}}+\sum _{k=0}^{N_{2}-1}\widehat{\Delta Y_{2}^{(k)}}\right) \\&\quad -\sum _{k=0}^{N_{1}-1}\ln \left( \Gamma (\gamma (1-\varrho )\Delta t^{(k)})\right) -\sum _{k=0}^{N_{2}-1}\ln \left( \Gamma (\gamma \varrho \Delta t^{(k)})\Gamma (\gamma (1-\varrho )\Delta t^{(k)})\right) \\&\quad +\gamma (1-\varrho )\left( \sum _{k=0}^{N_{1}-1}\Delta t^{(k)}\widehat{\ln (\Delta Y_{1}^{(k)})}+\sum _{k=0}^{N_{2}-1}\Delta t^{(k)}\widehat{\ln (\Delta Y_{2}^{(k)})}\right) \\&\quad +\gamma \varrho \sum _{k=0}^{N_{2}-1}\Delta t^{(k)}\widehat{\ln (\Delta Y_{0}^{(k)})}. \end{aligned} \end{aligned}$$

(42)

Here, $\widehat{\Delta Y_{i}^{k}}$ and $\widehat{\ln (\Delta Y_{i}^{k})}$ are conditional expectations of $\Delta Y_{i}^{k}$ and $\ln (\Delta Y_{i}^{k})$ given current estimates $\hat{\beta }$, $\hat{\Lambda } (t)$, $\hat{\zeta }$, and the observed data.

From formulas (21), (23), (24), and (40) after a number of transformations, we get for $\chi (u)=e^{\beta {\mathbf {u}}}$ that

$$\begin{aligned} \begin{aligned}&\mathbb {E}\exp \left( -\int _{0}^{t_{l_{j}}}Y_{j}(\tau )e^{\beta ^{*}{\mathbf {u}}}\lambda (\tau )\mathrm{d}\tau \right) =e^{-E_{j}^{0}} \\&\quad \mathbb {E}\Delta Y_{j}^{(k)}\exp \left( -\int _{0}^{t_{l_{j}}}Y_{j}(\tau )e^{\beta ^{*}{\mathbf {u}}}\lambda (\tau )\mathrm{d}\tau \right) = \Delta t^{(k)}E_{j}^{1,k}e^{-E_{j}^{0}} \\&\quad \mathbb {E} \left( \Delta Y_{j}^{(k)}\right) ^{2}\exp \left( -\int _{0}^{t_{l_{j}}}Y_j(\tau )e^{\beta ^{*}{\mathbf {u}}}\lambda (\tau )\mathrm{d}\tau \right) \\&\quad =\left( \left( \Delta t^{(k)}E_{j}^{1,k}\right) ^{2}-\Delta t^{(k)}E_{j}^{2,k}\right) e^{-E_{j}^{0}}\\&\quad \mathbb {E} \left( \Delta Y_{j}^{(k)}\right) ^{3}\exp \left( -\int _{0}^{t_{l_{j}}}Y_j(\tau )e^{\beta ^{*}{\mathbf {u}}}\lambda (\tau )\mathrm{d}\tau \right) \\&\quad =\left( \left( \Delta t^{(k)}E_{j}^{1,k}\right) ^{3}-3\left( \Delta t^{(k)}\right) ^{2}E_{j}^{1,k}E_{j}^{2,k}+\Delta t^{(k)}E_{j}^{3,k} \right) e^{-E_{j}^{0}}, \qquad j=0,1,2, \end{aligned} \end{aligned}$$

(43)

where

$$\begin{aligned} \begin{aligned}&E_{j}^{0}=\sum _{k=0}^{N_{l_{j}}-1}\Delta t^{(k)}\Phi _{G }^{(0)}(0,t_{l_{j}};\Lambda ,\beta , {\mathbf {u}})\\&\quad E_{j}^{m,k}=\Phi _{G }^{(m)}(t^{(k)},t_{l_{j}};\Lambda ,\beta , {\mathbf {u}}),\qquad k=0,\ldots ,N_{l_{j}}-1,\\&\quad \Phi _{G}^{(m)}(\tau ,t;\Lambda ,\beta , {\mathbf {u}})= \Phi _{G}^{(m)} \left( e^{\beta ^{*}{\mathbf {u}}}\Lambda (\tau ,t )\right) , \qquad m=1,2,3, \end{aligned} \end{aligned}$$

and incomplete cumulative hazard function $\Lambda (\tau ,t )=\int _{\tau }^{t}\lambda (s )\mathrm{d}s$ is a step function, and $\Phi _{G}^{(m)}(.)$ stands for mth-order argument derivative.

For a gamma-distributed random variable Y with shape parameter h and the scale parameter $\gamma$, it holds that

$$\begin{aligned} \begin{aligned} \mathbb {E}\ln (Y) e^{-cY}=&\left[ \psi (h)-\ln (\gamma +c)\right] e^{-\Phi _{G}^{(0)} (c)} \\ \mathbb {E}Y\ln (Y) e^{-cY}=&\left[ \psi (h+1)-\ln (\gamma +c)\right] \Phi _{G} ^{(1)}(c)e^{-\Phi _{G}^{(0)}(c)} \\ \mathbb {E}Y^{2}\ln (Y)e^{-cY}=&\left[ \psi (h+2)-\ln (\gamma +c)\right] \left[ \Phi _{G} ^{(1)}(c)^{2}-\Phi _{G} ^{(2)}(c)\right] e^{-\Phi _{G} ^{(0)}(c)}, \end{aligned} \end{aligned}$$

(44)

where $c\geqslant 0$ and $\psi (.)$ is the digamma function defined by $\psi (x)=d\ln (\Gamma (x))/\mathrm{d}x$. Last formulas can be obtained by differentiating the integral representation of the gamma function and not difficult transformations after that.

Using formulas (44), we get additionally to formulas (43)

$$\begin{aligned} \begin{aligned}&\mathbb {E}\ln (\Delta Y_{j}^{(k)})\exp \left( -\int _{0}^{t_{l_{j}}}Y_{j}(\tau )e^{\beta ^{*}{\mathbf {u}}}\lambda (\tau )\mathrm{d}\tau \right) =F_{j}^{0,k}e^{-E_{j}^{0}} \\&\quad \mathbb {E}\Delta Y_{j}^{(k)}\ln (\Delta Y_{j}^{(k)})\exp \left( -\int _{0}^{t_{l_{j}}}Y_{j}(\tau )e^{\beta ^{*}{\mathbf {u}}}\lambda (\tau )\mathrm{d}\tau \right) = \Delta t^{(k)}E_{j}^{1,k}F_{j}^{1,k}e^{-E_{j}^{0}} \\&\quad \mathbb {E}\left( \Delta Y_{j}^{(k)}\right) ^{2} \ln (\Delta Y_{j}^{(k)})\exp \left( -\int _{0}^{t_{l_{j}}}Y_j(\tau )e^{\beta ^{*}{\mathbf {u}}}\lambda (\tau )\mathrm{d}\tau \right) \\&\quad =\left( \left( \Delta t^{(k)}E_{j}^{1,k}\right) ^{2}-\Delta t^{(k)}E_{j}^{2,k}\right) F_{j}^{2,k}e^{-E_{j}^{0}}, \end{aligned} \end{aligned}$$

(45)

where

$$\begin{aligned} F_{j}^{m,k}=\psi \left( h_{j}\Delta t^{(k)}+m\right) -\ln \left( \gamma +e^{\beta ^{*}{\mathbf {u}}}\Lambda (t^{(k)},t^{l_{j}} ) \right) \end{aligned}$$

for $m=0,1,2$, $k=0,\ldots ,N_{l_{j}}$, and $j=0,1,2$.

In accordance with Bayes’ theorem, we get for the conditional density function that

$$\begin{aligned}&f\left( Z_{1}(.),Z_{2}(.)|\beta , {\mathbf {u}}_{1}, {\mathbf {u}}_{2}, \Lambda (.), \zeta , t_{1},t_{2},\delta _{1},\delta _{2}\right) \nonumber \\&\quad =\frac{g\left( Z_{1}(.),Z_{2}(.),t_{1},t_{2}|\beta , {\mathbf {u}}_{1}, {\mathbf {u}}_{2}, \Lambda (.), \zeta , \delta _{1},\delta _{2}\right) }{\text{ E }g\left( Z_{1}(.),Z_{2}(.),t_{1},t_{2}|\beta , {\mathbf {u}}_{1}, {\mathbf {u}}_{2}, \Lambda (.), \zeta , \delta _{1},\delta _{2}\right) } \end{aligned}$$

(46)

with

$$\begin{aligned}&g\left( Z_{1}(.).Z_{2}(.)t_{1},t_{2}|\beta , {\mathbf {u}}_{1}, {\mathbf {u}}_{2}, \Lambda (.), \zeta , \delta _{1},\delta _{2}\right) \\&\quad =\left( Z_{1}(t_{1})e^{\beta ^{*}{\mathbf {u}}_{1}}\lambda (t_{1})\right) ^{\delta _{1}}\left( Z_{2}(t_{2})e^{\beta ^{*}{\mathbf {u}}_{2}}\lambda (t_{2})\right) ^{\delta _{2}}f(Z_{1}(.),Z_{2}(.)|\zeta )\\&\qquad \times \exp \left( -\int _{0}^{t_{1}}Z_{1}(\tau )e^{\beta ^{*}{\mathbf {u}}_{1}}\lambda (\tau )\mathrm{d}\tau -\int _{0}^{t_{2}}Z_{2}(\tau )e^{\beta ^{*}{\mathbf {u}}_{2}}\lambda (\tau )\mathrm{d}\tau \right) . \end{aligned}$$

Expression (46) can be calculated using Eq. (43) and the formulas

$$\begin{aligned}&Z_{1}(t_{1})=\sum _{k=0}^{N_{1}-1}\left( Y_{0}^{(k)}+Y_{1}^{(k)}\right) ,\\&\quad Z_{2}(t_{1})=\sum _{k=0}^{N_{2}-1}\left( Y_{0}^{(k)}+Y_{2}^{(k)}\right) , \\&\quad \int _{0}^{t_{1}}Z_{1}(\tau )e^{\beta ^{*}{\mathbf {u}}_{1}}\lambda (\tau )\mathrm{d}\tau = \sum _{k=0}^{N_{1}-1}e^{\beta ^{*}{\mathbf {u}}_{1}}\Lambda (t^{(k)},t_{1})\left( \Delta Y_{0}^{(k)}+\Delta Y_{1}^{(k)}\right) ,\\&\quad \int _{0}^{t_{2}}Z_{2}(\tau )e^{\beta ^{*}{\mathbf {u}}_{2}}\lambda (\tau )\mathrm{d}\tau = \sum _{k=0}^{N_{2}-1}e^{\beta ^{*}{\mathbf {u}}_{2}}\Lambda (t^{(k)},t_{2})\left( \Delta Y_{0}^{(k)}+\Delta Y_{1}^{(k)}\right) , \\&\quad f(Z_{1}(.),Z_{2}(.)|\zeta )=\prod _{k=0}^{N_{1}-1}f(\Delta Y_{1}^{(k)}|\zeta )\prod _{k=0}^{N_{2}-1}f(\Delta Y_{0}^{(k)}|\zeta )\prod _{k=0}^{N_{2}-1}f(\Delta Y_{2}^{(k)}|\zeta ). \end{aligned}$$

Finally, we calculate the conditional log-density function (42) using formulas (43), (45), (46), and replacing $\beta$, $\zeta$, and $\Lambda$ with their current estimates $\hat{\beta }$, $\hat{\zeta }$, and $\hat{\Lambda }$.