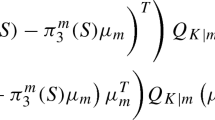Discriminant analysis with Gaussian graphical tree models

Abstract

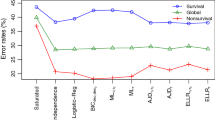
We consider Gaussian graphical tree models in discriminant analysis for two populations. Both the parameters and the structure of the graph are assumed to be unknown. For the estimation of the parameters maximum likelihood is used, and for the estimation of the structure of the tree graph we propose three methods; in these, the function to be optimized is the J-divergence for one and the empirical log-likelihood ratio for the two others. The main contribution of this paper is the introduction of these three computationally efficient methods. We show that the optimization problem of each proposed method is equivalent to one of finding a minimum weight spanning tree, which can be solved efficiently even if the number of variables is large. This property together with the existence of the maximum likelihood estimators for small group sample sizes is the main advantage of the proposed methods. A numerical comparison of the classification performance of discriminant analysis using these methods, as well as three other existing ones, is presented. This comparison is based on the estimated error rates of the corresponding plug-in allocation rules obtained from real and simulated data. Diagonal discriminant analysis is considered as a benchmark, as well as quadratic and linear discriminant analysis whenever the sample size is sufficient. The results show that discriminant analysis with Gaussian tree models, using these methods for selecting the graph structure, is competitive with diagonal discriminant analysis in high-dimensional settings.

Appendix

1.1 A.1 Proofs

The following properties for Gaussian graphical models with tree graph $\tau =(V,E_{\tau })$ and distribution $N(\varvec{\mu }, \varvec{{\Sigma }}_{\tau })$ are used in the proofs of Propositions 1, 2, and Corollary 1, some of which can be found in Lauritzen (2011). Let $\widehat{\varvec{{\Sigma }}}_{\tau }=\widehat{\mathbf {K}}_{\tau }^{-1}$, where $\widehat{\mathbf {K}}_{\tau }$ is the MLE of $\mathbf {K}_{\tau }$.

A.1 :

$f_{\tau }(x_1,\ldots ,x_{p})=\left. \prod _{i=1}^{p}f(x_i)\right. \left. \prod _{\begin{array}{c} i < j\\ (i,j)\in E_{\tau } \end{array}}\dfrac{f(x_i,x_j)}{f(x_i) \ f(x_j)}\right. .$

A.2 :

$\widehat{\varvec{{\Sigma }}}_{\tau }(\tau )=\mathbf {W}(\tau ),$ with $\mathbf {W}=\sum _{j=1}^{n}({ \mathbf {x}_j-\overline{\mathbf {x}}})({ \mathbf {x}_j-\overline{\mathbf {x}}})^t/n$ for a sample $\mathbf {x}_1, \ldots , \mathbf {x}_{n}$, and where for any square matrix $\mathbf {A}$, $\mathbf {A}(\tau )$ is the square matrix such that

$(\mathbf {A}(\tau ))_{ij}=\left\{ \begin{array}{l@{\quad }l} (\mathbf {A})_{ij} &{} \text{ if } i=j \; \text{ or } \; (i,j)\in E_{\tau }, \\ 0 &{} \text{ otherwise }. \end{array} \right.$

A.3 :

For any square matrix $\mathbf {A}$, $tr(\mathbf {K}_{\tau }\mathbf {A})=tr(\mathbf {K}_{\tau }\mathbf {A}(\tau )).$ Moreover, if $\widehat{\mathbf {K}}_{\tau }$ exists, then $tr(\widehat{\mathbf {K}}_{\tau }\mathbf {A})=tr(\widehat{\mathbf {K}}_{\tau }\mathbf {A}(\tau )).$

A.4 :

$$\begin{aligned} \widehat{\mathbf {K}}_{\tau }= & {} \sum _{\mathcal {C} \in \mathscr {C}}[\mathbf {W}^{-1}_\mathcal {C}]^{p}-\sum _{\mathcal {S} \in \mathscr {S}}v(\mathcal {S})[\mathbf {W}^{-1}_\mathcal {S}]^{p}\nonumber \\= & {} \sum _{\begin{array}{c} i < j \\ (i,j) \in E_{\tau } \end{array}}\left( [\mathbf {W}^{-1}_{(i,j)}]^{p}-[\mathbf {W}^{-1}_{(i)}]^{p}-[\mathbf {W}^{-1}_{(j)}]^{p}\right) +\sum _{j=1}^{p}\left( [\mathbf {W}^{-1}_{(j)}]^{p}\right) . \end{aligned}$$

A.5 :

$\widehat{f}_{{\tau }}(x_1,\ldots ,x_{p})=\left. \prod _{i=1}^{p}\widehat{f}(x_i)\right. \left. \prod _{\begin{array}{c} i < j \\ (i,j) \in E_{\tau } \end{array}}\dfrac{\widehat{f}(x_i,x_j)}{\widehat{f}(x_i) \ \widehat{f}(x_j)}\right. ,$ where $\widehat{f}_{{\tau }}$ is the density of $N(\widehat{\varvec{\mu }}, \widehat{\mathbf {K}}_{{\tau }}^{-1})$.

A.6 :

$$\begin{aligned} \ln \dfrac{\widehat{f}(x_i,x_j)}{\widehat{f}(x_i) \widehat{f}(x_j)}= & {} -\frac{1}{2}\ln (1-\widehat{\rho }_{ij}^2)-\dfrac{\widehat{\rho }_{ij}^2}{2(1-\widehat{\rho }_{ij}^2)}\left\{ \dfrac{(x_i-\overline{x}_i)^2}{w_{ii}}+\dfrac{(x_j-\overline{x}_j)^2}{w_{jj}}\right. \\&\left. -\,\dfrac{2(x_i-\overline{x}_i)(x_j-\overline{x}_j)}{w_{ij}}\right\} , \end{aligned}$$

where $\left. \widehat{\rho }_{ij}\right. =w_{ij}/\sqrt{w_{ii}w_{jj}}$.

Proof of Proposition 1

We note that for a given tree graph $\tau =(V,E_{\tau })$ with p nodes

$$\begin{aligned} J(\widehat{f}_{1_{\tau }},\widehat{f}_{2_{\tau }})= & {} \dfrac{1}{2}\left[ tr(\widehat{\varvec{{\Sigma }}}_{1_{\tau }}\widehat{\mathbf {K}}_{2_{\tau }})+tr(\widehat{\varvec{{\Sigma }}}_{2_{\tau }}\widehat{\mathbf {K}}_{1_{\tau }}) + tr(\widehat{\mathbf {K}}_{1_{\tau }}(\overline{\mathbf {x}}_1-\overline{\mathbf {x}}_2)(\overline{\mathbf {x}}_1-\overline{\mathbf {x}}_2)^t)\right. \\&\left. + \ tr(\widehat{\mathbf {K}}_{2_{\tau }}(\overline{\mathbf {x}}_1-\overline{\mathbf {x}}_2)(\overline{\mathbf {x}}_1-\overline{\mathbf {x}}_2)^t)\right] -p\qquad \qquad \, \text{ equation } \text{10 }\\= & {} \dfrac{1}{2}\left[ tr(\widehat{\mathbf {K}}_{2_{\tau }}\widehat{\varvec{{\Sigma }}}_{1_{\tau }}(\tau ))+tr(\widehat{\mathbf {K}}_{1_{\tau }}\widehat{\varvec{{\Sigma }}}_{2_{\tau }}(\tau ))+tr(\widehat{\mathbf {K}}_{1_{\tau }}\mathbf {D}+\widehat{\mathbf {K}}_{2_{\tau }}\mathbf {D}) \right] \\&\quad -p\quad \qquad \qquad \text{ prop. } \text{ A.3 }\\= & {} \dfrac{1}{2}\left[ tr(\widehat{\mathbf {K}}_{2_{\tau }}\mathbf {W}_1(\tau ))+tr(\widehat{\mathbf {K}}_{1_{\tau }}\mathbf {W}_2(\tau )) + tr(\widehat{\mathbf {K}}_{1_{\tau }}\mathbf {D}+\widehat{\mathbf {K}}_{2_{\tau }}\mathbf {D})\right] \\&\quad -p\quad \qquad \qquad \text{ prop. } \text{ A.2 }\\= & {} \frac{1}{2}\sum _{\begin{array}{c} i < j \\ (i,j)\in E_{\tau } \end{array}}\left[ tr([{\mathbf {W}_1}^{-1}_{(i,j)}]^{p}\mathbf {D})-tr([{\mathbf {W}_1}^{-1}_{(i)}]^{p}\mathbf {D})-tr([{\mathbf {W}_1}^{-1}_{(j)}]^{p}\mathbf {D})\right. \\&\left. + \ tr([{\mathbf {W}_2}^{-1}_{(i,j)}]^{p}\mathbf {D})-tr([{\mathbf {W}_2}^{-1}_{(i)}]^{p}\mathbf {D})-tr([{\mathbf {W}_2}^{-1}_{(j)}]^{p}\mathbf {D})\right. \\&\left. + \ tr([{\mathbf {W}_2}^{-1}_{(i,j)}]^{p}\mathbf {W}_1)-tr([{\mathbf {W}_2}^{-1}_{(i)}]^{p}\mathbf {W}_1)-tr([{\mathbf {W}_2}^{-1}_{(j)}]^{p}\mathbf {W}_1)\right. \\&\left. + \ tr([{\mathbf {W}_1}^{-1}_{(i,j)}]^{p}\mathbf {W}_2)-tr([{\mathbf {W}_1}^{-1}_{(i)}]^{p}\mathbf {W}_2)-tr([{\mathbf {W}_1}^{-1}_{(j)}]^{p}\mathbf {W}_2)\right] \\&+ \ \frac{1}{2}\sum _{j=1}^{p}tr\left( [{\mathbf {W}_2}^{-1}_{(j)}]^{p}\mathbf {W}_1\right) +\frac{1}{2}\sum _{j=1}^{p}tr\left( [{\mathbf {W}_1}^{-1}_{(j)}]^{p}\mathbf {W}_2\right) \\&+ \ \frac{1}{2}\sum _{j=1}^{p}tr\left( [{\mathbf {W}_1}^{-1}_{(j)}]^{p}\mathbf {D}\right) +\frac{1}{2}\sum _{j=1}^{p}tr\left( [{\mathbf {W}_2}^{-1}_{(j)}]^{p}\mathbf {D}\right) -p\quad \text{ prop. } \text{ A.4 }\\= & {} -\sum _{\begin{array}{c} i < j \\ (i,j)\in E_{\tau } \end{array}}\lambda (i,j) +C = -\lambda (\tau ) +C, \end{aligned}$$

where $\lambda (\tau )=\sum _{\begin{array}{c} i < j \\ (i,j)\in E_{\tau } \end{array}}\lambda (i,j)$ is the total weight of $\tau$, $\mathbf {D}=(\overline{\mathbf {x}}_1-\overline{\mathbf {x}}_2)(\overline{\mathbf {x}}_1-\overline{\mathbf {x}}_2)^t$, $\widehat{\varvec{{\Sigma }}}_{c_{\tau }}=\widehat{\mathbf {K}}_{c_{\tau }}^{-1}$, $c=1,2$, C is a constant, and

$$\begin{aligned}&\lambda (i,j)= -\frac{1}{2}\left[ tr\left( \left( \begin{array}{c@{\quad }c} w^{(2)}_{ii} &{} w^{(2)}_{ij} \\ w^{(2)}_{ij} &{} w^{(2)}_{jj} \end{array}\right) ^{-1}\left( \begin{array}{c@{\quad }c} w^{(1)}_{ii} &{} w^{(1)}_{ij} \\ w^{(1)}_{ij} &{} w^{(1)}_{jj} \end{array}\right) \right) \right. \nonumber \\&\qquad \qquad \quad +\,tr\left( \left( \begin{array}{c@{\quad }c} w^{(1)}_{ii} &{} w^{(1)}_{ij} \\ w^{(1)}_{ij} &{} w^{(1)}_{jj} \end{array}\right) ^{-1}\left( \begin{array}{c@{\quad }c} w^{(2)}_{ii} &{} w^{(2)}_{ij} \\ w^{(2)}_{ij} &{} w^{(2)}_{jj} \end{array}\right) \right) \nonumber \\&\qquad \left. \qquad \quad + \ tr\left( \left( \begin{array}{c@{\quad }c} w^{(1)}_{ii} &{} w^{(1)}_{ij} \\ w^{(1)}_{ij} &{} w^{(1)}_{jj} \end{array}\right) ^{-1}\left( \begin{array}{c@{\quad }c} (\overline{x}_i^{(1)}-\overline{x}_i^{(2)})^2 &{} (\overline{x}_i^{(1)}-\overline{x}_i^{(2)})(\overline{x}_j^{(1)}-\overline{x}_j^{(2)}) \\ (\overline{x}_i^{(1)}-\overline{x}_i^{(2)})(\overline{x}_j^{(1)}-\overline{x}_j^{(2)}) &{} (\overline{x}_j^{(1)}-\overline{x}_j^{(2)})^2 \end{array}\right) \right) \right. \nonumber \\&\qquad \left. \quad \qquad + \ tr\left( \left( \begin{array}{c@{\quad }c} w^{(2)}_{ii} &{} w^{(2)}_{ij} \\ w^{(2)}_{ij} &{} w^{(2)}_{jj} \end{array}\right) ^{-1}\left( \begin{array}{c@{\quad }c} (\overline{x}_i^{(1)}-\overline{x}_i^{(2)})^2 &{} (\overline{x}_i^{(1)}-\overline{x}_i^{(2)})(\overline{x}_j^{(1)}-\overline{x}_j^{(2)}) \\ (\overline{x}_i^{(1)}-\overline{x}_i^{(2)})(\overline{x}_j^{(1)}-\overline{x}_j^{(2)}) &{} (\overline{x}_j^{(1)}-\overline{x}_j^{(2)})^2 \end{array}\right) \right) \right. \nonumber \\&\qquad \qquad \quad \left. -\,\dfrac{w^{(1)}_{ii}}{w^{(2)}_{ii}}-\dfrac{w^{(1)}_{jj}}{w^{(2)}_{jj}}-\dfrac{w^{(2)}_{ii}}{w^{(1)}_{ii}}-\dfrac{w^{(2)}_{jj}}{w^{(1)}_{jj}}-\dfrac{(\overline{x}_i^{(1)}-\overline{x}_i^{(2)})^2}{w^{(1)}_{ii}}-\dfrac{(\overline{x}_j^{(1)}-\overline{x}_j^{(2)})^2}{w^{(1)}_{jj}}\right. \nonumber \\&\qquad \qquad \quad -\,\dfrac{(\overline{x}_i^{(1)}-\overline{x}_i^{(2)})^2}{w^{(2)}_{ii}}\left. -\dfrac{(\overline{x}_j^{(1)}-\overline{x}_j^{(2)})^2}{w^{(2)}_{jj}}\right] . \end{aligned}$$

(24)

Since $-\lambda (\tau )$ is the only term in $J(\widehat{f}_{1_{\tau }},\widehat{f}_{2_{\tau }})$ that varies depending on $\tau$, the problem of maximizing $J(\widehat{f}_{1_{\tau }},\widehat{f}_{2_{\tau }})$ over $T_p$ in (18) is equivalent to the problem of finding a MWST for the complete graph with p nodes and weights given in (24) for each edge (i, j). We note that weights in (24) are equal to those in (19). $\square$

Proof of Proposition 2

The problem in (20) can be expressed as finding $\tau _1^*$ and $\tau _2^*$ such that

$$\begin{aligned} \tau _1^*= & {} \underset{\tau _1 \in T_p}{\mathrm {argmax}\,} \left\{ \sum _{l=1}^{n_1}\ln {\widehat{f}_{1_{\tau _1}}(\mathbf {x}_l)}-\sum _{l=n_1+1}^{n_1+n_2}\ln {{\widehat{f}_{1_{\tau _1}}(\mathbf {x}_l)}}\right\} \end{aligned}$$

(25)

$$\begin{aligned} \tau _2^*= & {} \underset{\tau _2 \in T_p}{\mathrm {argmax}\,} \left\{ \sum _{l=n_1+1}^{n_1+n_2}\ln {\widehat{f}_{2_{\tau _2}}(\mathbf {x}_l)}-\sum _{l=1}^{n_1}\ln {{\widehat{f}_{2_{\tau _2}}(\mathbf {x}_l)}}\right\} . \end{aligned}$$

(26)

Considering the problem for $\tau _1^*$ in (25), we note that for a given tree $\tau =(V,E_{\tau })$ with p nodes

$$\begin{aligned}&\sum _{l=1}^{n_1}\ln {\widehat{f}_{1_{\tau }}(\mathbf {x}_l)}-\sum _{l=n_1+1}^{n_1+n_2}\ln {{\widehat{f}_{1_{\tau }}(\mathbf {x}_l)}}\\&\quad =\sum _{i=1}^{p} \; \sum _{l=1}^{n_1}\ln {\left. \widehat{f}_1(x_{i_l})\right. +\sum _{\begin{array}{c} i < j \\ (i,j)\in E_{\tau } \end{array}} \; \sum _{l=1}^{n_1} \left. \ln \dfrac{\widehat{f}_1(x_{i_l},x_{j_l})}{\widehat{f}_1(x_{i_l}) \ \widehat{f}_1(x_{j_l})}\right. }\\&\qquad -\sum _{i=1}^{p}\; \sum _{l=n_1+1}^{n_1+n_2}\ln {\left. \widehat{f}_1(x_{i_l})\right. -\sum _{\begin{array}{c} i < j \\ (i,j)\in E_{\tau } \end{array}} \; \sum _{l=n_1+1}^{n_1+n_2} \left. \ln \dfrac{\widehat{f}_1(x_{i_l},x_{j_l})}{\widehat{f}_1(x_{i_l}) \ \widehat{f}_1(x_{j_l})}\right. } \quad \text{ prop. } \text{ A.5 }\\&\quad =\sum _{i=1}^{p}\; \left( \sum _{l=1}^{n_1}\ln {\left. \widehat{f}_1(x_{i_l})\right. }-\sum _{l=n_1+1}^{n_1+n_2}\ln {\left. \widehat{f}_1(x_{i_l})\right. }\right) -\sum _{\begin{array}{c} i < j \\ (i,j)\in E_{\tau } \end{array}}\lambda (i,j), \end{aligned}$$

where

$$\begin{aligned} \lambda (i,j)=\sum _{l=n_1+1}^{n_1+n_2} \left. \ln \dfrac{\widehat{f}_1(x_{i_l},x_{j_l})}{\widehat{f}_1(x_{i_l}) \ \widehat{f}_1(x_{j_l})}\right. -\sum _{l=1}^{n_1} \left. \ln \dfrac{\widehat{f}_1(x_{i_l},x_{j_l})}{\widehat{f}_1(x_{i_l}) \ \widehat{f}_1(x_{j_l})}\right. . \end{aligned}$$

(27)

Since $-\sum _{\begin{array}{c} i < j \\ (i,j)\in E_{\tau } \end{array}}\lambda (i,j)$ is the only term that varies depending on $\tau$, the problem of maximizing ${\sum }_{l=1}^{n_1}\ln {\widehat{f}_{1_{\tau }}(\mathbf {x}_l)}- \sum _{l=n_1+1}^{n_1+n_2}\ln {{\widehat{f}_{1_{\tau }}(\mathbf {x}_l)}}$ over $T_p$ is equivalent to the problem of finding a MWST for the complete graph with p nodes and weights given in (27) for each edge (i, j). Using property A.6 in (27) we can obtain the weights given in (21) for $c=1$. A similar procedure can be done for the problem for $\tau _2^*$ in (26). $\square$

Proof of Corollary 1

We note that for a given tree $\tau =(V,E_{\tau })$ with p nodes

$$\begin{aligned}&\sum _{l=1}^{n_1}\ln \dfrac{\widehat{f}_{1_{\tau }}(\mathbf {x}_l)}{\widehat{f}_{2_{\tau }}(\mathbf {x}_l)}+\sum _{l=n_1+1}^{n_1+n_2}\ln \dfrac{{\widehat{f}_{2_{\tau }}(\mathbf {x}_l)}}{{\widehat{f}_{1_{\tau }}(\mathbf {x}_l)}}\\&\quad =\left\{ \sum _{l=1}^{n_1}\ln {\widehat{f}_{1_{\tau }}(\mathbf {x}_l)}-\sum _{l=n_1+1}^{n_1+n_2}\ln {{\widehat{f}_{1_{\tau }}(\mathbf {x}_l)}}\right\} \nonumber \\&\qquad +\left\{ \sum _{l=n_1+1}^{n_1+n_2}\ln {\widehat{f}_{2_{\tau }}(\mathbf {x}_l)}-\sum _{l=1}^{n_1}\ln {{\widehat{f}_{2_{\tau }}(\mathbf {x}_l)}}\right\} . \end{aligned}$$

The rest can be obtained using simultaneously the two procedures given in the proof of Proposition 2 for (25) and (26). $\square$

1.2 A.2 Random concentration matrix

Let $p_k$ be the fraction of vertices in the graph that have degree k. A power law network is a graph with $p_k\propto k^{-\alpha }$, where $\alpha$ is the power parameter. We consider $\alpha =2.3$ and simulate the two networks with graphs presented in Fig. 2. Given a specific network with graph $G=(V,E)$, we use the following procedure to specify the associated covariance matrix. Let $\mathbf {A}$ be a matrix with entries

$$\begin{aligned} a_{ij}=\left\{ \begin{array}{l@{\quad }l} u_{ij}&{} \text{ if } \;(i,j) \in E,\\ 0 &{} \text{ if } \;(i,j) \not \in E, \end{array}\right. \end{aligned}$$

where $u_{ij}$ is a random number from a uniform distribution U(D). Then the diagonal elements of $\mathbf {A}$ are defined such that the final matrix is a diagonally dominant matrix, i.e., $a_{ii}=R \times \sum _{j\ne i}|a_{ij}|, \; i= 1, \ldots , p,$ where $R>1$. The covariance matrix $\varvec{{\Sigma }}$ is then determined by $\sigma _{ij}=a^{ij}/\sqrt{a^{ii}a^{jj}},$ where $a^{ij}$ is the entry ij of the matrix $\mathbf {A}^{-1}$.

For the numerical study, the RAND models associated with a power law network use $R=1.01$ and graph given in Fig. 2a with $D= (-1,-0.5) \cup (0.5,1)$, and graph given in Fig. 2b with $D=(-0.5, 0.5)$.

1.3 A.3 Asymptotic error rates of LDA and DLDA

When a common concentration matrix is assumed for both populations, $N(\varvec{\mu }_1, \varvec{{\Sigma }})$ and $N(\varvec{\mu }_2, \varvec{{\Sigma }})$, the error rate of the optimal allocation rule given in (4) with $\pi _1=\pi _2$ is

$$\begin{aligned} P(e)=P(1|2)=P(2|1)={\varPhi } \left( -\frac{1}{2}\sqrt{({ \varvec{{\mu }}_{1}-\varvec{{\mu }}_{2}})^t \varvec{{\Sigma }}^{-1}({ \varvec{{\mu }}_{1}-\varvec{{\mu }}_{2}})} \right) . \end{aligned}$$

(28)

This corresponds to the asymptotic error rate of LDA. On the other hand, the asymptotic error rate of DLDA when $\pi _1=\pi _2=1/2$, that is, the error rate for the allocation rule: $\mathbf {x}$ is assigned to ${\varPi }_1$ when

$$\begin{aligned} \mathbf {x}^t\mathbf {D}^{-1}({ \varvec{\mu }_{1}-\varvec{\mu }_{2}})- \frac{1}{2}({ \varvec{\mu }_{1}+\varvec{\mu }_{2}})^t\mathbf {D}^{-1}({ \varvec{\mu }_{1}-\varvec{\mu }_{2}})>0, \end{aligned}$$

and otherwise to ${\varPi }_2$, is given by

$$\begin{aligned} P(e)={\varPhi } \left( \dfrac{-({ \varvec{\mu }_{1}-\varvec{\mu }_{2}})^t\mathbf {D}^{-1}({ \varvec{\mu }_{1}-\varvec{\mu }_{2}})/2}{\sqrt{({ \varvec{\mu }_{1}-\varvec{\mu }_{2}})^t\mathbf {D}^{-1}\varvec{{\Sigma }}\mathbf {D}^{-1}({ \varvec{\mu }_{1}-\varvec{\mu }_{2}})}}\right) , \end{aligned}$$

(29)

where $\mathbf {D}=\text{ diag }(\varvec{{\Sigma }})$.

Let $\{{\mathbf {v}}_1,\ldots ,\mathbf {v}_p\}$ and $\{l_1,\ldots ,l_p\}$ be the set of orthonormal eigenvectors and eigenvalues of $\varvec{{\Sigma }}$, respectively. The asymptotic error rates for LDA and DLDA are the same under the following conditions: (a) $\varvec{{\Sigma }}$ with its diagonal elements all equal to a constant value, (b) $\pi _1=\pi _2$, and (c) the pair of mean vectors is $\{{\varvec{\mu }}_1=a_1\mathbf {v}_j, \; \varvec{\mu }_2=a_2{\mathbf {v}}_j\}$; with $a_i \in \mathbb {R}$, $i=1,2$, and $\mathbf {v}_j \in \{{\mathbf {v}}_1,\ldots ,{\mathbf {v}}_p\}$. To verify this, we write $\varvec{{\Sigma }}$ and $\mathbf {K}$ as

$$\begin{aligned} \varvec{{\Sigma }}= \sum _{i=1}^{p} l_i\mathbf {v}_i\mathbf {v}_i^t \quad \text{ and } \quad \mathbf {K}= \sum _{i=1}^{p} {l_i^{-1}}{\mathbf {v}_i\mathbf {v}_i^t}. \end{aligned}$$

Then the probability of misclassification in (28) is given by

$$\begin{aligned} P(e)={\varPhi }\left( {-\frac{1}{2}\sqrt{ a\mathbf {v}^t_j\left( \sum _{i=1}^{p} {l_i^{-1}}{\mathbf {v}_i\mathbf {v}_i^t}\right) a\mathbf {v}_j}}\right) ={\varPhi }\left( \dfrac{-a/2}{\sqrt{l_j}}\right) , \end{aligned}$$

and (29) is

$$\begin{aligned} P(e)={\varPhi }\left( \dfrac{-a^2/2}{\sqrt{ a\mathbf {v}^t_j\left( \sum _{i=1}^{p} l_i\mathbf {v}_i\mathbf {v}_i^t\right) a\mathbf {v}_j}}\right) = {\varPhi }\left( \dfrac{-a/2}{\sqrt{l_j}}\right) , \end{aligned}$$

where $a=|a_1-a_2|$. In particular, this is true for $a_1=0$, $\mathbf {v}_j=\mathbf {v}_\mathrm{max}$ or $\mathbf {v}_j=\mathbf {v}_\mathrm{min}$.