INTRODUCTION

A primary cue to sound localization is the interaural time difference (ITD). Sounds arriving at the left ear before the right, for example, indicate a source positioned to the animal's left. The largest naturally occurring ITD depends on the animal's head size. For small animals, such as owls and cats, the maximum delay is about 200 (owl) to 500 (cat) µs, which occurs when a source is positioned approximately opposite to one ear (Roth et al. 1980; Moiseff and Konishi 1981; Calford et al. 1986). For humans, the maximum ITD is 650–800 µs (Feddersen et al. 1957; Kuhn 1977; Middlebrooks 1999).

Psychophysical research on humans has shown that when headphones are used to deliver steady-state noise waveforms with larger than the natural maximum delay, listeners can accurately discriminate ITDs as large as 3000–30,000 µs, depending on the stimulus spectrum (Blodgett et al. 1956; Durlach and Colburn 1978). Therefore, the human auditory system can process ITDs 35 times larger than that which it will ever encounter in nature. How is this achieved and what does it imply about the neural mechanisms of sound localization?

ITDs are initially encoded by a set of coincidence-detector brainstem neurons that receive inputs from left and right ears (Carr and Konishi 1988, 1990; Yin and Chan 1990). Axonal inputs to these neurons serve as delay lines that translate a time difference between the ears to a place code. Mathematically, delay lines and coincidence detectors have been modeled as a cross-correlator (Jeffress 1948; Sayers and Cherry 1957; Blauert and Cobben 1978). Models of cross-correlation often assume long delay lines that produce lags several times the maximum natural ITD (Stern et al. 1988). However, neurophysiological data from the owl (Carr and Konishi 1990) has shown that axonal delays for binaural coincidence are approximately equal to the maximum naturally occurring delay. The problem is even more complicated when one considers higher-order neurons, for example, neurons of the optic tectum or inferior colliculus. As shown in the right panels of Figure 1, the great majority of these neurons have characteristics delays that are smaller than half the maximum natural range (Mazer 1995, 1999).

Figure 1
figure 1

Results from neurophysiological experiments. Left panels show ITD-tuning curves for two tectal neurons. The gray regions have a width of 400 µs, equal to the total range of natural ITDs for owls (±200 µs). See text for details. Right panels show best ITDs for 324 lateral shell neurons and 98 optic tectum neurons.

Full size image

Here we report on behavioral sensitivity of owls to large ITDs in sounds presented through miniaturized headphones. We show that owls, as humans, can detect ITDs several times the maximum natural range. We report on sensitivity of higher-order neurons to sounds with large ITDs and compare these with behavioral responses. We also discuss limitations of current models and show that a cross-correlation model with short delay lines accurately predicts detection of large ITDs. Finally, we show how such a model predicts localization reversals for narrow bands of noise by owls and humans.

METHODS

Surgery and animal care

We describe here the surgical procedures used for both behavioral and neurophysiological experiments. The owls used in behavioral experiments were not the same as the physiology owls. All owls were used in other parallel behavioral and neurophysiological studies. All surgical instruments were sterilized. Owls were anesthetized with intramuscular injections of ketamine (10–20 mg/kg/h, Phoenix Pharmaceutical, St. Joeseph, MO, USA) and diazepam (0.25–0.5 mg/kg/h, Steris Laboratories, Phoenix, AZ, USA). A scalp area about 10 mm × 10 mm was incised after subcutaneous injection of the local anesthetic xylocaine (0.2 mL 2% lidocaine HCL; Astrazeneca Pharmaceuticals, Wilmington, DE, USA). The first layer of the skull was removed within this area by using a pair of rongeurs, and a stainless steel post for the behavioral owls, or an inverted T-shaped post for the physiology owls, was fixed to the underlying trabeculae with dental cement (Hygenic, Perm Reline & Repair Resin Type II Class I). The procedure lasted about an hour. After the surgery, owls were encased in a snugly fitting cylinder to prevent struggling and kicking as they recovered from anesthesia. Owls were observed in small cages in a separate recovery room until they came out of the cylinder. When owls recovered well enough to fly, they were returned to their living cages where the owls for neurophysiological experiments were fed two mice a day. The weights of the owls for behavioral experiments had to be maintained at about 90% of their free-feeding values to ensure well-motivated behavioral performance.

The surgery for neurophysiological experiments involved the removal of a scalp area and the underlying skull area about 7 mm × 7 mm in size to expose the brain surface. The surgery was performed under anesthesia as described above. After each experimental session, which lasted several hours, the craniotomy was cleaned with the antibacterial agent: Chlorhexiderm (0.05% chlorhexidine gluconate, DVM Pharmaceuticals, Miami, FL, USA) and resealed with a small plastic sheet and dental cement. The scalp wounds were sutured shut. Sutures and the plastic sheet were removed before each experiment and replaced afterward. The owls for behavioral experiments were not subjected to any additional surgery.

Neurophysiological methods

Owls were anesthetized with ketamine throughout the experiment and lidocaine was applied to the edges of the skin incision once per hour. Since ketamine caused a temporary reduction in neuronal discharge, we did not collect data for approximately 15 minutes after each booster injection of ketamine (20 mg/kg/h). Single units were isolated in the optic tectum with parylene-insulated tungsten microelectrodes (250 µm thick shaft, 5 MΩ impedance at 1 kHz), A-M Systems, Carlsborg, WA, USA.

Neural waveforms were amplified and filtered from 1 to 10 kHz (Microamp 200, Beckman Electronics, Fishers, IN, USA) and simultaneously monitored with an oscilloscope (5110, Tektronix, Beaverton, OR, USA), and an audio amplifier (AM8, Grass, West Warwick, RI, USA). A spike discriminator (SD1, Tucker–Davis Technologies, Gainesville, FL, USA) converted neural spikes to computer-compatible TTL pulses, the times of occurrence of which were stored in a computer file. The identity of optic-tectum neurons was also confirmed by their histological locations, some of which were marked with electrolytic lesions and visualized in cresyl-violet-stained sections.

The auditory stimuli were bursts of broadband Gaussian noise, 0.5–12 kHz, 100 ms in duration with left and right channels simultaneously gated with 5-ms rise/decay times. The noise bursts contained different values of ITD and interaural level differences (ILD) to which tectal neurons are tuned. All sound stimuli were digitally synthesized by a Dell Dimension XPS Pro200n computer and delivered by a digital signal processor equipped with a 16-bit, 48-kHz digital-to-analog converter (Tucker–Davis Technologies). ITDs were computed online, whereas ILDs were set by two digital attenuators (PA4, Tucker Davis Technologies) which were controlled by the computer. ILDs were varied in 5-dB steps from -40 to 40 dB. Once the neuron's best ILD was determined, all ITD measurements were made at that ILD. Best ILDs were within the range of ±15 dB. ITDs could be varied in 30-µs steps in either direction, i.e., leading or lagging to each ear.

Sound stimuli were delivered through an earphone assembly consisting of a Knowles (Itaska, IL) ED-1914 receiver as a sound source and a Knowles BF-1743 damped coupling assembly for smoothing the frequency response of the receiver. These components were encased in an aluminum cylinder 7 mm in diameter and 8.1 mm in length that fit into the external ear canal. In addition, a Knowles 1939 microphone for monitoring sound pressure levels in the ear canal was included in the earphone cylinder. The cylinder was inserted into the ear canal and the gaps between the cylinder and the canal were filled with a silicon compound (Earmold & Research Laboratories, Whichita, KS, USA). The microphone was initially calibrated against a 12-mm Brüel & Kjær (Norcross, GA, USA) microphone with a probe tube whose tip was placed close to the center of the eardrum. This procedure allowed translation of the voltage output of the Knowles microphone into dB SPL. A standard value of 20 dB above a neuron's threshold was chosen as the stimulus sound level in all cases.

Behavioral methods for owls

We used three tame adult owls for behavioral experiments. The head-turning response did not need any training, but it had to be reinforced by food for repeated trials. We trained the owls to feed from an apparatus which dispensed a small amount of mouse meat at a time, allowing 20–30 trials in an hour. Test sessions seldom continued more than 2 hours. We initially used a small freefield speaker ("hoop speaker") mounted on a semicircular track to encourage the owls to localize it at various azimuthal angles. The owls had to initially orient to another source ("zero speaker") placed straight ahead and wait for the signal from the hoop speaker.

When the owls became consistent in localizing both speakers, they were trained with earphones. We used earphone assemblies similar to the ones used for neurophysiological experiments. A metal bar was attached to the head post and held the left and right earphones in place. All sound stimuli were digitally synthesized in an IBM-compatible PC using Matlab and presented, after appropriate lowpass filtering, through 16-bit D/A converters at a rate of 40 kHz (Sound Blaster Live, -120 dB noise floor; Milpitas, CA). The sound pressure level for all stimuli used in the behavioral experiments was 20 dB above the owl's threshold, which is about 0 dB SPL between 3 and 8 kHz at the eardrum (Dyson et al. 1998). Interaural level differences (ILDs) were always kept zero so that the owls turned their heads only in the horizontal plane in response to an ITD (Moiseff 1989). The onset and offset of the sounds were not interaurally delayed and, therefore, the detection of ITD was based on the ongoing part of the waveforms. Sound stimuli were delivered by an earphone assembly consisting of Knowles components as described earlier.

The experiments consisted of two parts. The rationale for the first part was to determine the largest ITD that could be detected by owls. For this part, the acoustic stimulus was a single burst of broadband Gaussian noise, 100 ms in duration with a 10-ms rise/decay time. The value of ITD was varied on each presentation. The owls performed in complete darkness in an IAC anechoic chamber (5 × 3 × 3 m) and were monitored with an infrared video camera. On each trial, a broadband click was presented from a loudspeaker directly in front of the owl. The purpose of this click was to have the owl fixate at 0°. After the owl had fixated at 0°, the target stimulus was presented through headphones. For the target sound, the computer would randomly select one of 14 ITDs. The ITD had an equal a priori probability of leading to the left or the right ear. The 14 values were 150, 200, 300, 400, 500, 750, and 1000 µs leading to the left or the right ear. The owl's task was to orient to the side (hemifield) corresponding to the sign of the ITD, i.e., if the stimulus had an ITD leading to the left ear, the owl's task was to orient its head to the left and pause for a minimum of 0.5 s. If the head orientation was to the correct direction, the owl was immediately rewarded with a small amount of mouse meat.

To prevent experimenter bias, the computer did not display the value or the sign of the ITD until after the owl had responded and the trial had been scored. The experimenter observed the owl on a monitor outside the anechoic chamber and scored a left or a right head turn by watching the monitor. Once the experimenter recorded the head-orienting response, the computer displayed the sign and magnitude of ITD. If the direction of head-turning was consistent with the sign of ITD, the experimenter would dispense the food reward. Only the direction of the response (left vs. right) and not the absolute angular magnitude of the head orientation was used in analysis. When the owls were not motivated to localize the sound, response latencies were long and head-turning responses were slow. This occurred only on a small proportion of trials near the end of an experimental run. Since these responses were always correlated with decreased accuracy, all trials in which time to head fixation exceeded 1 s were excluded from further analysis.

The rationale for the second part of this study, as elaborated fully in "Psychophysical Predictions" subsection of the Discussion section, was to determine if the perceived position of noise bands may be predicted from a model of binaural interaction with short delay lines. Such a model predicts localization reversals at specific regions of the frequency spectrum, and therefore, we employed narrow bands of noise for this study. All conditions were the same as the first part of this study except for the following changes: The stimulus was a narrow band of noise with a large ITD. The ITD was either 400 or -400 µs, randomly selected on each trial. A calibration sound was used to determine the ITD that produced a 0° head-pointing response. This calibration ITD was +50 µs for one owl and was used to offset a small initial bias. For the other owl, the calibration ITD was 0 µs. The stimulus ITDs were -400 and 400 µs relative to calibration ITD. The bandwidth of the noise was also selected randomly on each trial from a set of seven predetermined values: 2–2.5 kHz, 2.2–2.5 kHz, 2.3–2.5 kHz, 2.5 kHz tone, 2.5–2.7 kHz, 2.5–2.8 kHz, and 2.5–3 kHz. Thus, one edge of the noise band was always at 2.5 kHz and the other edge was either above or below the first edge by 200, 300, or 500 Hz. The owl was trained to point its head to the perceived position of the sound. Head orientation was measured by a magnetic tracker (Polhemus 3Space Isotrack, Colchester, VT, USA) mounted on the owl's head. This system measured orientation to within 0.5°.

Behavioral methods for human subjects

Three normal-hearing individuals served as subjects. They were seated in a dimly lit double-walled steel chamber (IAC with interior dimensions of 1.8 × 1.9 × 2 m) and listened to the stimuli through headphones (Sony Model MDR-V1). Each run consisted of a presentation of 150 trials. Each trial began with the presentation of a 300-ms target stimulus (a Gaussian noise band) followed by a 300-ms acoustic "pointer" (white noise burst). The task of the subject was to adjust the ITD of the pointer such that its perceived location matched that of the test stimulus. This pointing paradigm is a standard method of estimating the perceived position of complex sounds by human subjects (Stern et al. 1988; Domnitz and Colburn 1977).

The design of this experiment was similar to the second part of the behavioral experiments for owls. The test stimulus was assigned one of two ITDs with an equal prior probability on each trial (-4000 or 4000 µs). The frequency band of the test stimulus was randomly selected on each trial from a set of 6 conditions: 200–250 Hz, 225–250 Hz, 240–250 Hz, 250–260 Hz, 250–275 Hz, and 250–300 Hz. Thus, one edge of the band was always at 250 Hz and the bandwidths were 10, 25, and 50 Hz. On each trial, one of two ITDs was paired with one of 6 noise bands. The noise bands were generated by summation of components in the frequency domain. Their amplitudes were selected from a Rayleigh distribution and their phases from a uniform distribution (0, 2π), thus producing a Gaussian band of noise (Rice 1954). The level of the stimulus was 65 dB SPL measured with a 6-cc coupler and sound level meter (Brüel & Kjær Model 2260, B&K 0.5-in. microphone model 4189). Sounds were presented through D/A converters (Sound Blaster Live, Milpitas, CA, USA) at a rate of 40 kHz.

The initial ITD of the pointer was randomly selected from a range of -600–600 µs. The pointer ITD could not exceed these limits. If the perceived position of the pointer did not match that of the target stimulus, the subject pressed either a left or right key to "move" the pointer closer to the target. A large step size (100 µs) was available to the subjects for rapid pointer adjustment, and a small step size (25 µs) was available for fine tuning. The subject could listen to the target–pointer pair and adjust the pointer ITD as many times as s/he required until satisfied that the perceived positions of the target and pointer were the same. At this time, the subject pressed a separate key to terminate the trial, record the final ITD of the pointer, and proceed to the next trial. Approximately 10 pointing estimates were obtained for each combination of ITD and bandwidth. No feedback was provided during the run.

RESULTS

Neurophysiological results

The left panels of Figure 1 show ITD-tuning curves for two optic-tectum neurons. ITDs were sampled from -1000 to +1000 µs in steps of 30 µs, with 10 stimulus presentations per ITD. The ordinate shows the average number of spikes per 100-ms duration of the stimulus. The right panels show histograms of the best ITDs of a large number of neurons in the lateral shell of the inferior colliculus (n = 324; data from Mazer 1995), and the optic tectum from the current study (n = 98). Of these 422 higher-order neurons, none has a best delay greater than 150 µs.

One feature of the tuning curves is that ITDs greater than the natural range produce significant response peaks. Secondary peaks beyond the natural range are observed in all such neurons. Considerably smaller but noticeable peaks are also identifiable at ITDs as large as 500–700 µs. The shaded areas in the left panels are related to a model of cross-correlation that is described in the Discussion section.

Detection of the sign of a large ITD by owls

Figure 2 shows averaged results from two owls. The ordinate represents an index of detectability, d′ (Green and Swets 1966), calculated from hit and false-alarm rates associated with the owls' head-turning responses. Hit rates were defined as the number of head-turning responses to the right when the stimulus ITD was positive (right-ear leading) divided by total number of trials with positive ITDs. False-alarm rates were defined as number of head-turning responses to the right when the stimulus ITD was negative (left-ear leading) divided by total number of trials with negative ITDs. The Tables of Elliot (Swets 1964) were used to obtain d′ from these hit and false-alarm rates.

Figure 2
figure 2

Result of behavioral experiment on detection of large ITDs by owls. Index of detectability, d′, as a function of ITD calculated from head-turning responses of two owls. Error bars are one standard error. The solid curve shows prediction from a model of binaural cross-correlation with a maximum delay line of 200 µs.

Full size image

By convention, a d′ = 1 is taken as threshold for detection. This value corresponds to a 0.76 correct-response probability in a two-interval forced-choice design. It is clear that owls can discriminate ITDs as large as 750–1000 µs. These large values of ITD are between 4 and 6 times the owl's maximum natural ITD (170–200 µs). We did not systematically collect data beyond 1000 µs, but informal sampling at ITDs of 2000 and 3000 µs indicated that owls could not detect these values. Additional data were collected on a third owl using noise that was high-pass filtered at 3 kHz to establish that discrimination is maintained at high frequencies. It has previously been shown that owls use ITDs in the fine structure of waveforms up to 9 kHz, with a dominant frequency region between 4 and 6 kHz (Knudsen and Konishi 1979). Data were collected at an ITD of 500 µs. The owl showed a detection index of d′ = 3.55.

Localization of narrow bands of noise by owls and humans

Figure 3 shows data from localization of narrow bands of noise by two owls (top panel) and three human subjects (bottom panel). The squares and circles represent data for positive and negative ITDs, respectively. The dashed and solid lines are linear regression fits. For the owl, the ITD was either 400 or -400 µs, and for the human subjects it was 4000 or -4000 µs. The abscissa shows the bandwidth of the stimulus, Δf. Negative bandwidths represent a band from f to -Δf, and positive bandwidths from f to +Δf, where f = 2500 Hz for the owl and 250 Hz for human subjects.

Figure 3
figure 3

Results from behavioral experiments using narrow bands of noise. Top panel shows averaged results from two owls and the bottom panel shows results from three human subjects. Squares and circles are results for positive and negative ITDs, respectively. For owls, the ITDs were -400 and 400 µs, and for humans they were -4000 and 4000 µs. The lines are least-squares fits. Error bars are one standard error of the mean. The abscissa shows the bandwidth of the stimulus, Δf. Negative bandwidths represent frequencies extending from f to f - Δf, and positive bandwidths represent a noise band from f to f = Δf. For the owl, f = 2500 Hz, and for human subjects, f = 250 Hz (see Fig. 4).

Full size image

Note that for a given ITD, both the owls and human subjects respond to the right or left depending on the spectral position of the band. For example, when the ITD is positive, the owls respond consistently to the right when the noise spectrum is 2500–3000 Hz and respond consistently to the left when the noise spectrum is 2000–2500 Hz. Another important aspect of the data is that response angles increase with the stimulus bandwidth, for both owls and humans. A repeated-measures ANOVA showed statistically significant interactions between bandwidth and ITD for owls (F (6,6) = 38.14, p < 0.001) and for human subjects (F (4,8) = 46.89, p < 0.001).

DISCUSSION

Detection of large delays with short delay lines

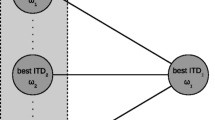
Figure 4 shows one possible mechanism for detection of large ITDs. The top diagram shows the pattern of activity that results from cross-correlation of a band of noise. The pattern is a frequently-by-delay surface in which axonal delay, or equivalently the cross-correlation lag, is represented along the abscissa and the frequency spectrum along the ordinate. This pattern contains a straight trajectory across frequencies at the stimulus' true (group) delay and curved trajectories at phase-equivalent delays (Sayers and Cherry 1957; Jeffress 1972; Stern and Colburn 1978; Stern et al. 1988). The light-gray region represents the range of physiologically available delay lines. If the stimulus contains a delay that is greater than the largest available delay line, then the straight trajectory lies outside the natural range. However, the least-curved trajectory within the natural range lies on the side of the true stimulus delay.

Figure 4
figure 4

Possible mechanism for detection of large ITDs. Top diagram shows the hypothetical activity resulting from cross-correlation of a band of noise. The pattern is a frequency-by-delay surface in which axonal delay, or equivalently the cross-correlation lag, is represented along the abscissa and the frequency spectrum along the ordinate. Light-gray area represents the range of physiologically available neural delay lines. Dark gray shows regions of frequency convergence at higher neural centers. The stimulus in this representation has an ITD that lies outside the physiological range (straight vertical line). The least-curved trajectory within the natural range may signal the correct sign of the ITD. The lower diagram shows two opposite predictions of this model for a narrow band of noise with an ITD that is outside the natural range. If the stimulus bandwidth is f to f + Δf, an image to the right is predicted. If the bandwidth is f - Δf, an image to the left is predicted.

Full size image

Each dark-gray region represents the receptive field of a higher-order neuron. These neurons receive information from a range of frequencies and a limited range of delays (Knudsen 1984). Convergence of information across frequency produces the largest peak of neural activity in neurons that receive information from the least-curved trajectory (Jeffress 1972; Shackleton et al. 1992; Saberi 1995, 1996, 1998; Saberi et al. 1998a, 1998b, 1999). A system that evaluates this pattern recognizes the correct direction of the sound source.

Such a pattern is observed in recordings from tectal neurons (Fig. 1). An ITD-tuning curve may represent, to a first approximation, a cross-correlation pattern after frequency convergence. The gray region in the left panels of Figure 1 has a width of 400 µs, approximating the range of natural delays for owls (±200 µs). If the midpoint of the gray region (dashed line) is the center of a putative cross-correlation surface, then a stimulus with an ITD of -500 µs (the distance between the main peak and the dashed line) is detectable because of the side peak that falls within the gray region. This side peak is predicted from Figure 4.

Simulations

To establish that large ITDs may be detected by small delay lines, we compared the owls' behavioral detection of large ITDs (>200 µs) with a cross-correlation model constrained by short delay lines <200 µs). Details of this model have been published elsewhere (Saberi et al. 1998b). Briefly, it consists of a filterbank, followed by half-wave rectification and cross-correlation within corresponding (left and right ear) filters. The output activity is then integrated across frequency. The integration bandwidth and internal noise were free parameters of the model.

On each simulation trial, the model produces a main peak in the pooled cross-correlation function at either a positive or a negative delay, similar to those observed in neural ITD-tuning curves in response to bands of noise. The sign of this delay, positive or negative, is used as a dichotomous decision statistic on the direction of the "source" (left or right). Predicted d′s are estimated from hit and false-alarm rates from 1000 simulation trials. The curve in Figure 2 shows the model's fit to the data. The optimum bandwidth that produced the best fit is 2.9 kHz. This value is consistent with bandwidths of optic-tectum neurons (Knudsen 1984). The model's response is robust to moderate changes in bandwidth as observed for tectal neurons. For example, an approximately 10% change in ITD threshold is observed as a result of a 30% change in bandwidth. d′s are relatively constant and large when the ITD is small. A gradual decline in performance is observed for ITDs greater than 300 µs, approaching chance for ITDs greater than 1000 µs. While these features are consistent with the data, the most pertinent outcome is that large ITDs beyond the natural range are detectable without having large delay lines.

Psychophysical predictions

If the detection of large ITDs is based in some measure on curved trajectories of the cross-correlation function (i.e., side peaks in neural terms), then one may make interesting predictions of how sounds may be localized based on the position of the side peaks. The bottom diagram of Figure 4 shows one such prediction. A low-frequency stimulus is selected such that only a single curved trajectory falls within the natural range. If a tone of frequency f has an ITD of + 1/f, then the first phase-equivalent delay will be at 0 µs and the tone will be perceived at 0°. Increasing the bandwidth of this sound will lead to two opposite predictions, depending on the direction of bandwidth increase. If the bandwidth is extended from f to f + Δf, an image on the positive side is predicted, with larger displacements for larger bandwidths. If the bandwidth is extended from f to f - Δf, it is predicted that the image will be displaced to the negative side (i.e., localization reversal). Thus, for the same nominal positive ITD and the same constant bandwidth, the percept is predicted to be to the left or right, depending solely on the spectral position of the band.

Figure 3 shows results of this experiment for two owls (top panel) and three human subjects (bottom panel). For a constant value of ITD, e.g., -400 µs (solid line), owls point to the left when the noise band ranges from 2000 to 2500 Hz and look to the right when the band ranges from 2500 to 3000 Hz. Responses for the positive ITD (dashed line) are mirror images of the negative ITD. Identical patterns are observed for human subjects. The pointing responses are exactly as would be predicted from the bottom diagram of Figure 4.

Comparison to findings from previous reports

Other explanations for detection of large ITDs have previously been considered. One such explanation is that by Mossop and Culling (1998) who showed that increasing the cutoff frequency of a noise band reduces the maximum detectable ITD in that noise band. They additionally showed that lateralization of very large ITDs (e.g., 10,000 µs) by humans requires the presence of low-frequency cues. High-pass noise, however, may be lateralized for ITDs up to only about 3000 µs. Mossop and Culling correctly rejected the idea that the largest detectable ITD is related to the period of the cutoff frequency, since the longest available period is considerably smaller than the maximum detectable ITD. A second explanation for their data is that a stimulus whose ITD is larger than the available range of physiological delay lines may be detected if the edge of the cross-correlation function's envelope in the lowest available frequency band overlaps with the range of available delay lines. They noted that because low-frequency channels have a narrower bandwidth, this envelope will be broader at low frequencies. For high-pass noise, this cue is diminished and the maximum detectable ITD is reduced.

Mossop and Culling (1998) used low-pass, binaurally uncorrelated masking noise to eliminate cues below the stimulus cutoff frequency. They showed that even in the presence of low-pass masking noise, some subjects could detect ITDs as large as 10,000 µs in a stimulus high-pass filtered at 500 Hz. We have, in informal observations, replicated this finding. For a channel centered near 500 Hz, the envelope at the output of this filter would be quasiperiodic, with the largest possible period equal to 2 ms (i.e., given an infinitely narrow channel). This period is significantly shorter than the maximum detectable ITD in such a stimulus (see Fig. 2 of Mossop and Culling) and, therefore, cannot be a cue for detection of very large ITDs.

Another explanation for detection of large ITDs is provided by Fitzpatrick et al. (2000) who recently reported on a type of auditory neuron, called trough type, that responds to large delays. However, they admit that such neurons respond only to binaurally uncorrelated sounds and, thus, are not relevant to localization by cross-correlation.

In view of the physiological and psychophysical findings on owls and humans, we suggest that the detection of a large ITD is likely based on several factors, each contributing to some extent depending on the stimulus spectrum. Owls can use carrier phase at very high frequencies since their space-tuned neurons can phase lock to tones as high as 10 kHz (Sullivan and Konishi 1984; Köppl 1997). For humans, however, carrier phase is useful up to only 1.2 kHz, above which lateralization is based on waveform envelope. From the current experiments, it is clear that at low frequencies, secondary trajectories of the cross-correlation function contribute to detection of large ITDs. Another cue, which possibly operates at primarily high frequencies for humans but which also may contribute at low-frequencies, is an envelope cue. As the stimulus spectrum is confined to high frequencies, the influence of carrier phase is diminished and a slowly modulating envelope is used for detection. Such a cue can be modeled by inclusion of an envelope extractor in the cross-correlation mechanism, for example, by a half-wave rectifier and low-pass filter. Since owls can use carrier phase at high frequencies, exclusion of carrier cues would be inaccurate and the envelope is probably not used to the same extent or in the same manner as it is for humans.

When ITD is very large and the stimulus spectrum contains low frequencies, a cue best described as a center-of-gravity measure may contribute to detection. Within each frequency channel, there is some effect of the carrier and some of the envelope; however, as the channels are pooled together the effects of the carrier are averaged out if they are not concordant, leaving only the envelope. Subtle envelope effects across frequency may provide a clear overall lateralization. Both envelope and carrier cues, therefore, probably play a role at low frequencies, but as ITD becomes larger, the trajectories within the cross-correlation range will become ever more curved so that an across-frequency pooling mechanism will average out ever more of the carrier cues. The very largest ITDs, therefore, may be discriminated by across-frequency pooling of envelope information.

In summary, it is highly likely that models of binaural interaction that incorporate long delay lines, e.g., as long as 30,000 µs (Stern et al. 1988), are placing the accuracy of their predictions on inexact assumptions. Alternative cues based on the pattern of cross-correlation activity in a network of short delay lines, including the curvature, positioning, and skirts of secondary and tertiary trajectories of the cross-correlation surface, as well as envelope cues, are physiologically more realistic. It would be useful for current binaural theory to recast psychophysical findings in terms of cross-correlation models constrained by short delay lines within the natural range.