Abstract
In heterogeneous landscapes individuals select among several habitat patches. The fitness rewards of these choices are assumed to play an important role in the distribution of individuals across landscapes. Individuals can either use environmental cues to directly assess the quality of breeding sites, or rely on social cues to guide the settlement decision. We estimated the density of adult birds and per capita reproductive success of willow ptarmigan over 5–15 years in 42 survey areas, nested within 5 spatially separated populations in south-central Norway. Our aims were to (1) examine spatial and temporal patterns of variation in densities of adult birds (i.e., the breeding densities) and reproductive success (juveniles/pair) measured in autumn and (2) evaluate which habitat distribution model best described the distribution of willow ptarmigan across heterogeneous mountain landscapes. Variation in density of adult birds was primarily attributable to variation between survey areas which could arise from spatial heterogeneity in adult survival or as a consequence of spacing behavior of juveniles during the settlement stage. In contrast, reproductive success was more variable between years and did not vary consistently between survey areas once year effects were accounted for. The lack of any relationship between the density of adult birds and reproductive success supported the predictions of an ideal free distribution (IFD), implying that within years, the mean reproductive success was approximately equal across survey areas. However, analysis based on Taylor’s power law (i.e., the relationship between logarithms of spatial variance and mean density of adult birds) suggested that aggregation was stronger than expected under IFD. This implies that the relative change in density of adult birds was larger in areas with high mean densities than in areas with low densities. The exact mechanisms causing this statistical pattern are unclear, but based on the breeding biology of willow ptarmigan we suggest that yearlings are attracted to areas of high densities during the settlement period in spring. Our study was conducted during a period of low overall density and we suggest that this pattern might be particular to such situations. This implies that the presence of conspecifics might represent a cue signaling high adult survival and thus high habitat quality.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Spatial heterogeneity in habitat quality is known to be a potent source of between-individual differences in fitness (Fretwell and Lucas 1969; Erikstad 1985; Andren 1990; Calsbeek and Sinervo 2002; Nilsen et al. 2004). The quality of a given habitat is shaped by the combined effects of resource availability (food and shelter) and environmental conditions (abiotic variables such as temperature and biotic variables such as competitors and predators) (Sinclair et al. 2006). Generally, when individuals settle in a given site at moderate to high densities, both competition for limited resources and predation rates may increase with density, resulting in reduced quality (Fretwell and Lucas 1969; Martin 1988; Sergio and Newton 2003). Consequently, as density of the focal species increases, density dependence may offset the individual benefits of inhabiting seemingly high quality habitats (Fretwell and Lucas 1969; Morris 2003). However, at low densities, positive interactions among settlers may occur (e.g., Allee effects after Allee 1938) resulting in positive fitness effects with increasing density (Greene and Stamps 2001).
In heterogeneous landscapes individuals select among habitat patches or units of land of varying quality. The fitness rewards of these patches are assumed to play an important role in the distribution of individuals across landscapes (Fretwell and Lucas 1969). To this end, several models have been suggested to explain the distribution of individuals under different conditions (Fretwell and Lucas 1969; Pulliam and Danielson 1991). When applied to breeding-habitat selection, the ideal free distribution model (IFD) predicts that individuals should be distributed in proportion to the amount and quality of the habitat, so that all individuals have equal access to resources causing reproduction to be equal at all sites (Fretwell and Lucas 1969; Milinski 1979). The ideal despotic distribution model (IDD) predicts a hierarchical distribution where the quality of each individual’s territory reflects their rank in the population (Fretwell and Lucas 1969). Lower-ranked individuals are excluded from the best habitats and reproduction is expected to vary among sites (Fretwell and Lucas 1969; Andren 1990; Calsbeek and Sinervo 2002). A third model, the ideal preemptive distribution model (IPD), predicts that individuals always select the best unoccupied site (Pulliam and Danielson 1991), causing differences in reproductive rates among sites. Some authors consider IDD and IPD to be similar models despite a major difference in the mechanism (despotism with and preemption without aggressive behavior) (Holmes et al. 1996; Pöysä 2001; Manning and Garton 2013). All three models assume that the individuals are “ideal” in the sense that they are omniscient and select the best option available. Consequently, the spatial arrangement of individuals across the landscape and the spatial distribution of vital rates should be related to the quality of habitat patches throughout the landscape, but the actual relationship is predicted to vary depending on the model that determines the settlement process.
When settling on their breeding grounds, many species use environmental cues to assess the quality of the physical environment (Muller et al. 1997; Campomizzi et al. 2008). If intrinsic habitat quality is important during settlement, then the density of adult individuals and habitat quality should be correlated across the landscape. However, in human-modified landscapes, the ability to recognize site quality or utilize high quality sites may be hampered if the cues used for selecting habitats are corrupted (McClaren et al. 2002; Battin 2004; Bock and Jones 2004). Furthermore, when individuals use environmental cues and the settlement patterns follow IDD or IPD, an ecological trap may occur if high numbers of individuals are forced to aggregate in low quality sites (Van Horne 1983). Many species also rely on social cues during settlement, with settlement patterns being positively affected by the presence or abundance of conspecifics, i.e., conspecific attraction (Stamps 1988; Danchin and Wagner 1997; Pöysä 2001; Ward and Schlossberg 2004; Farrell et al. 2012), or by conspecific reproductive success (Danchin and Wagner 1997; Doligez et al. 2003). The use of either environmental or social cues in settlement decisions can cause aggregated distributions (Stamps 1988; Danchin and Wagner 1997; Doligez et al. 2003) that may have significant impacts on species persistence and conservation (Reed and Dobson 1993; Reed 1999).
The willow ptarmigan (Lagopus lagopus Linnaeus, 1758) is a medium-sized tetraonid species distributed in alpine tundra habitats in the northern hemisphere. In Scandinavia, ptarmigan are hunted and bag size, as well as abundance, varies considerably in time and space (Solvang et al. 2007; Kvasnes et al. 2010; Statistics Norway 2013). Within their range, individual birds generally prefer habitats with a high density of food and cover from predators (Erikstad 1985; Bergerud and Gratson 1988; Schieck and Hannon 1993). Males are highly philopatric (Pedersen et al. 1983; Schieck and Hannon 1989; Brøseth et al. 2005) and in spring they defend breeding territories of 2–12 ha (Pedersen 1984). Females are less philopatric but are more likely to re-use a breeding area following a successful breeding attempt in the previous year (Schieck and Hannon 1989). Although some juveniles return to their natal area (Martin and Hannon 1987; Rørvik et al. 1998), most male and female juveniles disperse to other breeding grounds (Martin and Hannon 1987; Brøseth et al. 2005; Hörnell-Willebrand et al. 2014) in the period between brood break up in late September and the following spring (Bergerud and Gratson 1988). Thus birds newly establishing breeding territories in an area are most likely naïve juveniles dispersing from other breeding grounds within a radius of 2–20 km (Brøseth et al. 2005; Hörnell-Willebrand et al. 2014; but see Watson et al. 1994). Steen et al. (1985) were unable to find any vegetative features common to all territories at breeding grounds in Norway, with broods leaving their territories shortly after hatching. After hatching, brood movements are focused on habitats rich in food, but broods remain within the general area of the natal territory (Andersen et al. 1986). This suggests that breeding territories are not selected on the basis of securing food for chicks after hatching and it has been suggested that the main function of the territory is to signal social status of the males (Steen et al. 1985). As snow usually covers the ground during the settlement period in spring it might be difficult for birds to assess habitat quality, and young birds might use conspecific abundance as a guide when selecting breeding territories (Stamps 1988; Pöysä 2001; Ward and Schlossberg 2004). However, it is not completely clear at what time of the year the actual territory selection occurs in willow ptarmigan, as cocks in southern Norway also display in late autumn before the ground is covered by snow (Pedersen et al. 1983). Old cocks display in their former area (Pedersen et al. 1983), but the role of old females and juvenile birds in autumn displays is not known.
Aggressive behavior during settlement and density dependent territory sizes might suggest some dominance hierarchy among willow ptarmigan males, in accordance with the IDD (Fretwell and Lucas 1969) or IPD (Pulliam and Danielson 1991). However, the relaxation of aggressive behavior after hatching might indicate that individuals are “free” during brood rearing, thus following an IFD (Fretwell and Lucas 1969). If conspecific attraction influences spacing patterns in willow ptarmigan, the resulting distribution would be predicted to be more aggregated than any of the above models predict (Pöysä 2001).
In this paper we used autumn line transect survey data to assess the spatial and temporal variation in density of adult birds (i.e., breeding population) and reproductive success in 42 survey areas distributed across five different mountain regions in south-central and eastern Norway. In particular, we examined the extent to which willow ptarmigan were distributed in agreement with the predictions of the IFD, IDD or IPD. To this end, we used two different approaches. First, we examined the relationship between survey area-specific estimates of adult density and reproductive success. The surveys were conducted in August before autumn dispersal so juvenile birds were assumed to be locally recruited within the survey area (Andersen et al. 1986). If individuals follow an IFD it is predicted that there should be no correlation between density of adult birds and reproductive success (Fretwell and Lucas 1969; Danchin and Wagner 1997; Skagen and Adams 2011). Several studies suggest that when animals form an IDD or IPD, individuals aggregate at higher densities in high quality habitats and achieve higher success rates than individuals settling in low quality habitats at lower densities (Fretwell and Lucas 1969; Holmes et al. 1996; Calsbeek and Sinervo 2002). In these situations one would expect a positive relationship between density of adult birds and reproductive success. In contrast, Skagen and Adams (2011) suggested that an IDD would generally generate a negative relationship between density and per capita fecundity (i.e., reproductive success). This could occur if many individuals were forced to settle in lower quality habitats (Van Horne 1983) either through despotism or preemption (Fretwell and Lucas 1969; Pulliam and Danielson 1991). Most importantly, a critical premise of an IDD or IPD, but not an IFD, is that reproductive success is correlated with density (Fretwell and Lucas 1969; Pulliam and Danielson 1991), either negatively (Skagen and Adams 2011) or positively (Fretwell and Lucas 1969; Holmes et al. 1996; Calsbeek and Sinervo 2002). Second, we used Taylor’s power law (TPL: Taylor 1961) to assess the levels of aggregation within mountain region populations. TPL states that the spatial variance in density increases as a power function of mean density, and that the function reflects the spatial distribution of the population (Taylor 1961). On a logarithmic scale this function becomes linear with the slope (b) considered by several authors to be a useful index of aggregation (Taylor 1984; Tsai et al. 2000; Jimenez et al. 2001; Kendal 2004; Detsis 2009; Christel et al. 2013; Kristensen et al. 2013). In general, b → 0 implies a uniform distribution, b = 1 suggests a random distribution and b → ∞ indicates a higher degree of aggregation. In Taylor’s pioneering work the slope b ranged from 0.7 to 3.1, with most values ranging from 1.0 to 2.0 (Taylor 1961). Gillis et al. (1986) showed theoretically that a slope b ~ 2.0 is in agreement with the predictions of an IFD, while a steeper slope (b > 2.0) indicates a higher level of aggregation than predicted by the IFD (Taylor 1984; Tsai et al. 2000; Jimenez et al. 2001; Kendal 2004; Detsis 2009; Christel et al. 2013; Kristensen et al. 2013). Although b = 2.0 agrees with the predictions of an IFD, the TPL is not a conclusive test as other mechanisms might also cause b ~ 2.0. Following Gillis et al. (1986), b = 2.0 might imply that density changes proportionally among areas (i.e., resource matching). Further, b > 2.0 might indicate a disproportional change in density among samples, arising either from the attraction of juvenile birds to survey areas of high initial philopatric adult density or as a result of temporal changes in habitat quality.
Methods
Data collection
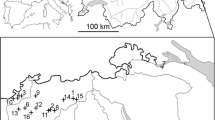
Line-transect surveys were conducted in August from 1996 to 2011 in up to 54 survey areas across south-central and eastern Norway (Fig. 1). Four areas were surveyed from 1996 onwards and new areas were subsequently added throughout the study period. Due to logistical constraints, not all areas were surveyed every year. Further, due to the sub-alpine distribution of willow ptarmigan, survey areas were geographically clustered within five mountain regions (Fig. 1). Each survey area was thus assigned to a mountain region based on its geographical location (n = 5, Fig. 1). Volunteer dog handlers with pointing dogs walked along predetermined transect lines and the free-ranging dogs searched the area on both sides of the line following the procedure of distance sampling (Pedersen et al. 1999, 2004; Buckland et al. 2001; Warren and Baines 2011). At each encounter, the number of birds (juveniles, adult males, adult females and birds of unknown age/sex) and the perpendicular distance from the line to the observed birds (m) were recorded. Pedersen et al. (2004) provide a detailed description of the sampling protocol, and previous experiments have shown that line transect distance sampling with pointing dogs is a robust method for estimating willow ptarmigan densities (Pedersen et al. 1999, 2004). The number of years in each survey area varied between 3 and 15 (median = 8), the number of areas surveyed each year varied between 4 and 51 (median = 30), the number of observations per year per survey area varied between 5 and 179 (median = 32) and the total transect length per survey area varied between 8 and 107 km (median = 33 km).
Statistical analysis
Density and recruitment assessment
Based on the survey data, we used multiple covariate distance sampling (MCDS) in the program Distance 6.0 (Thomas et al. 2010) to estimate half-normal detection functions and cluster densities (DS) in all survey areas and years (428 survey area–year combinations). Due to few observations in many survey area–year combinations, we opted to pool observations from all years for each survey area and use year as a covariate factor to account for possible variation in detection probability between years (Marques et al. 2007; Pedersen et al. 2012). The data were truncated at distances greater than the 95 % percentile in all analyses (Buckland et al. 2001). Following Buckland et al. (2001), we estimated cluster size (ES) separately for all survey areas and years as a function of distance from the line using regression. This is likely to result in unbiased estimates when larger clusters of birds are more likely to be detected at long distances (Pedersen et al. 1999). For the resulting 428 estimates of cluster density and cluster size, the unweighted geometric mean (min–max) coefficients of variation (CV %) were 27.4 % (16.2–49.6) and 16.4 % (9.7–27.8), respectively.
To obtain proper estimates of reproductive success (juveniles/pair) and density of adult birds (adults/km2) we estimated the proportion of juveniles and adults in each survey area and year. Due to missing information about the age and sex of birds in some encounters, we omitted 23 survey area–year combinations when estimating the proportion of juveniles. Then we used mixed effects models with a binomial link function for each mountain region separately (Crawley 2007) to estimate the proportion of juveniles in the samples. We fitted a variable linking survey areas to years (called survey area–year) as a random intercept. This allowed us to estimate the proportion of juveniles (PJ) from each encounter for each year in all survey areas separately. As large clusters of birds are more likely to be detected at long distances (Pedersen et al. 1999), and larger clusters usually have higher proportions of juveniles than smaller clusters, we fitted distance from the line as a fixed effect (Buckland et al. 2001). To estimate reproductive success (number of juveniles/pair) we first estimated PJ: the proportion of juveniles in the sample estimated at the intercept (i.e., the back-transformed logit-value at the intercept), which corresponded to the proportion of juveniles on the line where detection probability ≈1 (Buckland et al. 2001). The number of juveniles/pair was then estimated as \( PJ/\left[ {\frac{1 - PJ}{2}} \right] \). Finally, the density of adult birds was estimated as \( DS \times ES \times [1 - PJ] \), where \( DS \times ES \) is the total density.
Prior to further analysis, we excluded estimates from all survey area–year combinations that were lacking information about age and sex (23 survey area–year combinations) and that were based on <10 encounters (1 survey area–year combination). In addition we excluded survey areas with <5 years of data. Our final dataset consisted of 360 estimates of total density, density of adult birds and reproductive success (juveniles/pair) from 42 survey areas between 1996 and 2011. Density of adult birds in August was used as a proxy for the density of breeding birds in spring because mortality in adults is generally low from June to August (Sandercock et al. 2011). Juveniles/pair was used as a measure of per capita reproductive success. In the context of the analysis presented here, successful reproduction at time t in each survey area creates a pool of juvenile birds that will be distributed within the mountain region populations (Brøseth et al. 2005; Hörnell-Willebrand et al. 2014) in the period after our surveys until the next spring and will add into the populations at t + 1, i.e., next year’s recruits to the breeding population.
Spatial and temporal variation
To investigate the spatial and temporal sources of variation in adult density and reproductive success, we conducted a variance components analysis. This allowed us to quantify the proportion of variation in each that was attributable to differences among mountain regions, survey areas and years (Crawley 2007; Nilsen et al. 2008; Kvasnes et al. 2010). Analyses were performed using mixed effects models, with mountain region (five levels), survey area (42 levels) and year nested within mountain region (16 levels) fitted as random intercepts. By nesting year in mountain region, we assumed year effects to be correlated within mountain regions but not among them.
Evaluation of distribution models
To test the predictions of IFD, IDD and IPD (see “Introduction”), we used a linear mixed effect model to assess the relationship between reproductive success (dependent variable) and adult density (independent variable). We used the same random structure as described above.
Finally, we used Taylor’s power law (TPL: Taylor 1961) to assess the level of aggregation. Due to missing data (years) in some survey areas, we opted to create a new data set with no missing records to ensure that variances and means within each mountain region were calculated across the same set of survey areas in all years. Further, to ensure that variances and means were estimated across a sufficient number of survey areas we made a rule to maximize the number of survey areas having at least 5 areas in each mountain region and at least 5 years of data from each mountain region. This rule excluded one mountain region (Glomma south-east). Our final dataset for analyzing the TPL consisted of 4 mountain regions each including 5–10 survey areas covering 5 years (DF: 5 survey areas from 2007 to 2011, FH: 10 survey areas from 2005, 2007 to 2009 and 2011, GNE: 5 survey areas from 2005 to 2007 and 2009 to 2011, RS: 8 survey areas from 2006 to 2009 and 2011, for details see Electronic Supplementary Material). We calculated the spatial variation and the mean density of adult birds among survey areas within each mountain region. First we fitted linear mixed effect models with the log of spatial variance as the dependent variable, the log of mean density as a fixed effect and either mountain region as a random intercept or mountain region as both a random slope and a random intercept. The most parsimonious model describing the relationship was assessed with AICc, which is suitable when sample sizes are low as in our case (Burnham and Anderson 2002). Second, since the random effect term only consisted of four levels (i.e., four mountain regions) which is rather low for a random effect, we also fitted an ordinary linear regression model for the Taylor power law with mountain region as a fixed factor. The results from both models were compared and presented.
All statistical analysis were carried out in the program R (R Core Team 2012) using packages “lme4” for mixed models (Bates et al. 2011), and “AICcmodavg” for model selection (Mazerolle 2013).
Results
The unweighted geometric mean total density in the survey areas was 26.5 birds/km2, with the highest survey-area mean density being 91.8 birds/km2 and the lowest being 8.2 birds/km2. The unweighted geometric mean density of adult birds and reproductive success were 7.8 adults/km2 (highest mean: 25.3, lowest mean: 2.2) and 4.8 juveniles/pair (highest mean: 6.4, lowest mean: 3.0), respectively.
Survey areas differed in terms of the density of adult birds. The variance components analysis showed that survey area was the most important component explaining overall variance and accounted for more than three times the variation explained by year or mountain region (Table 1). This result is further supported by the area-specific boxplots in Fig. 2. In contrast, reproductive success varied more between years and less between survey areas and mountain regions (Table 1). This suggest that in a given year reproductive success does not differ much between survey areas or mountain regions but that some years are better than others across all survey areas and regions, i.e., reproductive success is spatially correlated. It is also worth noting that nearly half of the variance in reproductive success was attributable to factors not accounted for in the model (Table 1).
Boxplots of density of adult birds (top) and reproductive success (bottom) in the survey areas in south-central and eastern Norway. Survey areas are ranked within mountain regions by density of adult birds from left to right. Boxes represent the 95 % confidence intervals (±2SE) of the mean with upper and lower ends of the vertical lines representing maximum and minimum values, respectively. The horizontal broken lines represent the overall mean density and reproductive success, respectively. RS Rondane, DF Dovre and Folldal, FH Forollhogna, GNE Glomma north-east, GSE Glomma south-east
We found no clear relationship between adult density and reproductive success (slope ± SE: −0.011 ± 0.015, Fig. 3). When modelling reproductive success, the null model (i.e., with no fixed effects) was better supported, based on AICc, than a model with adult density fitted as a fixed effect (AICc with adult density: 1213.35 and AICc for null model: 1211.84). This is in contrast to the predictions of the IDD and IPD (negative or positive relationship), but supports the predictions of the IFD (no relationship).
Model selection based on AICc suggested that a mixed effect model with a random intercept was adequate to describe the relationship between the logs of spatial variance and mean density of adult birds (random intercept model; AICc = 46.99, random slope model; AICc = 54.49, respectively). As predicted by Taylor’s power law, the log of spatial variance in density of adult birds increased with log density of adult birds (slope ± SE: 2.83 ± 0.27). Similarly, the slope from the linear regression that included mountain region as a fixed factor was highly significant (slope ± SE: 3.07 ± 0.42, F 4,16 = 22.92, P < 0.001, Fig. 4). The aggregation index b (i.e., the linear slope coefficient) suggested strong aggregation in willow ptarmigan within mountain regions, with the lower 95 % confidence limit above 2 (95 % LCL: mixed effect model 2.3 and linear regression: 2.2).
Logarithm of spatial variance in density of adult birds plotted against logarithm of mean density of adult birds within mountain regions. The solid line is fitted from the linear regression model (for details see the “Methods” section) with slope (b)
Discussion
In this paper, we have investigated the spatial distribution of willow ptarmigan in south-central Norway during a period of varying adult densities, and compared the observed distribution to well known models characterizing the distribution of individuals across a landscape (Fretwell and Lucas 1969; Pulliam and Danielson 1991). We found that the density of adult birds (representing density of breeding birds in spring) varied more between survey areas than between years and mountain regions, with some survey areas supporting consistently higher densities of willow ptarmigan than others. In contrast, reproductive success varied more between years and less between survey areas and mountain regions. Moreover, the lack of a clear relationship between area-specific densities of breeding birds and reproductive success supported the IFD (Fretwell and Lucas 1969; Skagen and Adams 2011), whereas the steep scaling coefficient of Taylor’s power law suggested that the distribution of breeding birds was even more aggregated than expected under the IFD (Gillis et al. 1986).
Almost half of the variation in density of adult birds was attributable to variation between survey areas. If the local dynamics in the survey areas were mainly driven by local survival and reproductive success, then such patterns might arise because of spatial heterogeneity in survival or reproduction. However, the relatively limited spatial structuring of reproductive success indicates that local variation in reproductive success was not the key factor determining sustained variations in adult densities among survey areas. This is also supported by the fact that we did not find a positive relationship between local densities of adult birds and reproductive success. Survival rates may vary spatially as a consequence of local variation in the risk of harvest mortality (Smith and Willebrand 1999; Sandercock et al. 2011) or spatial variation in predation rates (Marcström et al. 1988). Previous studies have also indicated that human activities might facilitate medium sized generalist predators (e.g., Kurki et al. 1998; Støen et al. 2010) which may increase predation on game species and thus affect local demographic rates (Marcström et al. 1988) independently of intrinsic quality. Alternatively, spacing behavior during settlement may cause variation in densities of breeding birds either because young birds select to settle in high quality survey areas using environmental cues (i.e., selecting for intrinsic habitat characteristics) or using social indicators (i.e., conspecific attraction) (Stamps 1988; Pöysä 2001; Ward and Schlossberg 2004).
Although spatial variation in reproductive success was obviously present, it was much smaller than the temporal variation caused by differences between years. Temporal variation in reproductive success of willow ptarmigan is not surprising given that reproduction has previously been shown to be sensitive to environmental variability in factors such as climate and predation (Steen et al. 1988; Martin and Wiebe 2004). These factors might vary between years and are thus likely explanations for the temporal variation in reproductive success in our survey areas.
The lack of relationship between density of adult birds and reproductive success suggested that willow ptarmigan populations within mountain regions in south-central Norway are distributed in agreement with a resource matching distribution model. This would result in an equal per capita resource availability among survey areas of different quality, i.e., IFD (Skagen and Adams 2011), and an equal proportional increase or reduction in density of adult birds. A precise IFD would thus generate an exponent (b) of 2.0 in the relationship between the logs of spatial variance and mean density of adult birds (Gillis et al. 1986). However, with a scaling parameter above 2.0, our results suggest that willow ptarmigan within mountain region populations are more aggregated than would be expected under an IFD. The steep scaling parameter may imply that high density survey areas became increasingly crowded relative to low density areas, when the overall population density increased. Such breeding aggregations could arise by two different mechanisms. (1) Individuals are able to assess intrinsic habitat quality and aggregate in the best areas or (2) individuals settle in breeding areas using the abundance of philopatric adults as a guide. In the first case, breeding aggregations could occur if there were contemporary changes in intrinsic habitat quality causing high quality survey areas to be relatively more suitable compared to low quality survey areas. However, we have no reason to suspect that a disproportional change in habitat quality has occurred during our study. In an example of the second case, Pöysä (2001) found similar breeding aggregations in mallards (Anas platyrhynchos Linnaeus, 1758) where high quality areas became increasingly crowded when overall density increased. He suggested that the birds probably used presence of conspecifics as cues when selecting habitats.
Juvenile willow ptarmigan are accompanied by the adult male and female throughout the breeding season from hatching in June to the brood’s break up in late September. During the period between brood breakup and the next spring, juveniles disperse and most will settle in a breeding area within their natal mountain region (mountain region as defined in this study, cf. the scale of Fig. 1) (Brøseth et al. 2005; Hörnell-Willebrand et al. 2014). Stamps (1988) suggested that the presence of conspecifics could provide valuable information about habitat quality. If territory selection among juvenile birds occured in spring they would have few opportunities to assess intrinsic habitat quality since the vegetation at that time is usually covered by snow. The majority of new breeders are naïve (1 year old) and may therefore use the abundance of surviving philopatric adults as a cue to assess habitat quality. Due to high levels of philopatry in adults, the spring density of adults in a survey area may signal high survival probability or good reproductive prospects (Schieck and Hannon 1989). For naïve 1-year-old birds, conspecific cuing may be a cost-effective strategy as they have a short life expectancy and thus few opportunities to acquire personal information through trial and error tactics (Danchin et al. 2004).
The aggregated distribution we observed in this study, whether caused by conspecific attraction or not, could be related to the fact that our studies took place during a period of low population densities. Densities of adult birds in our study varied from about 2–25 adults/km2, which is much lower than previously reported densities in Norway. Myrberget (1988) reported densities of adult birds ranging from 19 to 172 pairs/km2 on an island in northern Norway (1960–1980) while Pedersen (1988) reported densities of territorial cocks of between 12 and 24 cocks/km2 in south-central Norway (1979–1986) (same area as DF in Fig. 1). This large difference in abundance also coincides with a significant long-term decline in Fennoscandian willow ptarmigan populations (Lehikoinen et al. 2014) and a marked reduction in national harvest bags in Norway (Statistics Norway 2013). This suggests that most populations in the present study are well below saturation. Greene and Stamps (2001) proposed that settling patterns may change with density, where individuals at low densities have fitness gains rather than reductions with increasing density (Fretwell and Lucas 1969), thus causing positive effects of conspecific interactions at low densities due to Allee effects. Using simulations, Greene and Stamps (2001) showed that Allee effects could generate aggregated distributions even if all habitat patches had the same intrinsic quality.
To our knowledge, social cues have not been considered before when studying willow ptarmigan habitat relationships to predict occurrence and habitat selection across landscapes (Erikstad 1985; Kastdalen et al. 2003; Henden et al. 2011; Ehrich et al. 2012). The role of social cues in habitat selection in general might be more important than previously recognized, and for many species it might be the most influential factor affecting habitat selection (Danchin et al. 2004; Campomizzi et al. 2008), especially for new settlers (Muller et al. 1997). Since little is known about the role of social cues in willow ptarmigan distribution, especially conspecific attraction, they should be considered in future habitat modeling attempts (Campomizzi et al. 2008). The use of conspecifics as cues in the settlement process could also have important implications for the management of harvested populations. If conspecific attraction is operating in willow ptarmigan through the abundance of philopatric adults, management areas with higher adult survival rates (possibly achieved through sustainable harvest rates) may benefit through increased attractiveness, independently of intrinsic habitat quality.
References
Allee WC (1938) The social life of animals. W.W. Norton and Company inc., New York
Andersen R, Pedersen HC, Steen JB (1986) Annual variation in movements of sub-alpine hatched willow ptarmigan Lagopus l. lagopus broods in central Norway. Ornis Scand 17:180–182
Andren H (1990) Despotic distribution, unequal reproductive success, and population regulation in the Jay Garrulus glandarius L. Ecology 71:1796–1803
Bates D, Maechler M, Bolker B (2011) lme4: linear mixed-effects models using S4 classes. R package version 0.999375-41. http://CRAN.R-project.org/package=lme4
Battin J (2004) When good animals love bad habitats: ecological traps and the conservation of animal populations. Conserv Biol 18:1482–1491
Bergerud AT, Gratson MW (1988) Survival and breeding strategies of grouse. In: Bergerud AT, Gratson MW (eds) Adaptive strategies and population ecology of northern grouse. University of Minnesota Press, Minneapolis, pp 473–577
Bock CE, Jones ZF (2004) Avian habitat evaluation: should counting birds count? Front Ecol Environ 2:403–410
Brøseth H, Tufto J, Pedersen HC, Steen H, Kastdalen L (2005) Dispersal patterns in a harvested willow ptarmigan population. J Appl Ecol 42:453–459
Buckland ST, Anderson DR, Burnham KP, Laake JL, Borchers DL, Thomas L (2001) Introduction to distance sampling: estimating abundance of biological populations. Oxford Univerity Press Inc., New York
Burnham KP, Anderson DR (2002) Model selection and multimodel inference: a practical information-theoretic approach. Springer, New York
Calsbeek R, Sinervo B (2002) An experimental test of the ideal despotic distribution. J Anim Ecol 71:513–523
Campomizzi AJ, Butcher JA, Farrell SL, Snelgrove AG, Collier BA, Gutzwiller KJ, Morrison ML, Wilkins RN (2008) Conspecific attraction is a missing component in wildlife habitat modeling. J Wildl Manag 72:331–336
Christel I, Certain G, Cama A, Vieites DR, Ferrer X (2013) Seabird aggregative patterns: a new tool for offshore wind energy risk assessment. Mar Pollut Bull 66:84–91
Crawley MJ (2007) The R book. Wiley, Chichester
Danchin E, Wagner RH (1997) The evolution of coloniality: the emergence of new perspectives. Trends Ecol Evol 12:342–347
Danchin E, Giraldeau LA, Valone TJ, Wagner RH (2004) Public information: from nosy neighbors to cultural evolution. Science 305:487–491
Detsis V (2009) Relationships of some environmental variables to the aggregation patterns of soil microarthropod populations in forests. Eur J Soil Biol 45:409–416
Doligez B, Cadet C, Danchin E, Boulinier T (2003) When to use public information for breeding habitat selection? The role of environmental predictability and density dependence. Anim Behav 66:973–988
Ehrich D, Henden JA, Ims RA, Doronina LO, Killengren ST, Lecomte N, Pokrovsky IG, Skogstad G, Sokolov AA, Sokolov VA, Yoccoz NG (2012) The importance of willow thickets for ptarmigan and hares in shrub tundra: the more the better? Oecologia 168:141–151
Erikstad KE (1985) Growth and survival of willow grouse chicks in relation to home range size, brood movements and habitat selection. Ornis Scand 16:181–190
Farrell SL, Morrison ML, Campomizzi A, Wilkins RN (2012) Conspecific cues and breeding habitat selection in an endangered woodland warbler. J Anim Ecol 81:1056–1064
Fretwell SD, Lucas HL (1969) On territorial behavior and other factors influencing habitat distribution in birds. Acta Biotheor 19:16–36
Gillis DM, Kramer DL, Bell G (1986) Taylor power law as a consequence of Fretwell ideal free distribution. J Theor Biol 123:281–287
Greene CM, Stamps JA (2001) Habitat selection at low population densities. Ecology 82:2091–2100
Henden JA, Ims RA, Yoccoz NG, Killengreen ST (2011) Declining willow ptarmigan populations: the role of habitat structure and community dynamics. Basic Appl Ecol 12:413–422
Holmes RT, Marra PP, Sherry TW (1996) Habitat-specific demography of breeding black throated blue warblers (Dendroica caerulescens): implications for population dynamics. J Anim Ecol 65:183–195
Hörnell-Willebrand M, Willebrand T, Smith AA (2014) Seasonal movements and dispersal patterns: implications for recruitment and management of willow ptarmigan (Lagopus lagopus). J Wildl Manag 78:194–201
Jimenez JJ, Rossi JP, Lavelle P (2001) Spatial distribution of earthworms in acid-soil savannas of the eastern plains of Colombia. Appl Soil Ecol 17:267–278
Kastdalen L, Pedersen HC, Fjone G, Andreassen HP (2003) Combining resource selection functions and distance sampling: an example with willow ptarmigan. In: Huzurbazar S (ed) Resource selection methods and application. Western EcoSystems Technology, Cheyenne, pp 52–59
Kendal WS (2004) Taylor’s ecological power law as a consequence of scale invariant exponential dispersion models. Ecol Complex 1:193–209
Kristensen E, Delefosse M, Quintana CO, Banta GT, Petersen HC, Jørgensen B (2013) Distribution pattern of benthic invertebrates in Danish estuaries: the use of Taylor’s power law as a species-specific indicator of dispersion and behavior. J Sea Res 77:70–78
Kurki S, Nikula A, Helle P, Linden H (1998) Abundances of red fox and pine marten in relation to the composition of boreal forest landscapes. J Anim Ecol 67:874–886
Kvasnes MAJ, Storaas T, Pedersen HC, Bjørk S, Nilsen EB (2010) Spatial dynamics of Norwegian tetraonid populations. Ecol Res 25:367–374
Lehikoinen A, Green M, Husby M, Kålås JA, Lindström A (2014) Common montane birds are declining in northern Europe. J Avian Biol 45:3–14
Manning JA, Garton EO (2013) A piecewise linear modeling approach for testing competing theories of habitat selection: an example with mule deer in northern winter ranges. Oecologia 172:725–735
Marcström V, Kenward RE, Engren E (1988) The impact of predation on boreal tetraonids during the vole cycles—an experimental study. J Anim Ecol 57:859–872
Marques TA, Thomas L, Fancy SG, Buckland ST (2007) Improving estimates of bird density using multiple-covariate distance sampling. Auk 124:1229–1243
Martin TE (1988) Processes organizing open-nesting bird assemblages: competition or nest predation? Evol Ecol 2:37–50
Martin K, Hannon SJ (1987) Natal philopatry and recruitment of willow ptarmigan in north central and northwestern Canada. Oecologia 71:518–524
Martin K, Wiebe KL (2004) Coping mechanisms of alpine and arctic breeding birds: extreme weather and limitations to reproductive resilience. Integr Comp Biol 44:177–185
Mazerolle MJ (2013) AICcmodavg: model selection and multimodel inference based on (Q)AIC(c). R package version 1.27. http://CRAN.R-project.org/package=AICcmodavg
McClaren EL, Kennedy PL, Dewey SR (2002) Do some northern goshawk nest areas consistently fledge more young than others? Condor 104:343–352
Milinski M (1979) Evolutionarily stable feeding strategy in Sticklebacks. J Comp Ethol 51:36–40
Morris DW (2003) Toward an ecological synthesis: a case for habitat selection. Oecologia 136:1–13
Muller KL, Stamps JA, Krishnan VV, Willits NH (1997) The effects of conspecific attraction and habitat quality on habitat selection in territorial birds (Troglodytes aedon). Am Nat 150:650–661
Myrberget S (1988) Demography of an island population of willow ptarmigan in northern Norway. In: Bergerud AT, Gratson MW (eds) Adaptive strategies and population ecology of northern grouse. University of Minnesota Press, Minneapolis, pp 379–419
Nilsen EB, Linnell JDC, Andersen R (2004) Individual access to preferred habitat affects fitness components in female roe deer Capreolus capreolus. J Anim Ecol 73:44–50
Nilsen EB, Pedersen S, Linnell JDC (2008) Can minimum convex polygon home ranges be used to draw biologically meaningful conclusions? Ecol Res 23:635–639
Pedersen HC (1984) Territory size, mating status, and individual survival of males in a fluctuating population of willow ptarmigan. Ornis Scand 15:197–203
Pedersen HC (1988) Territorial behavior and breeding numbers in Norwegian willow ptarmigan - a removal experiment. Ornis Scand 19:81–87
Pedersen HC, Steen JB, Andersen R (1983) Social organization and territorial behavior in a willow ptarmigan population. Ornis Scand 14:263–272
Pedersen HC, Steen H, Kastdalen L, Svendsen W, Brøseth H (1999) Betydningen av jakt på lirypebestander. Framdriftsrapport 1996–1998 [The impact of hunting on willow ptarmigan populations. Progress report 1996–1998]. NINA oppdragsmelding 578:1–43 (in Norwegian with English summary)
Pedersen HC, Steen H, Kastdalen L, Brøseth H, Ims RA, Svendsen W, Yoccoz NG (2004) Weak compensation of harvest despite strong density-dependent growth in willow ptarmigan. Proc R Soc B Biol Sci 271:381–385
Pedersen ÅØ, Bårdsen BJ, Yoccoz NG, Lecomte N, Fuglei E (2012) Monitoring Svalbard rock ptarmigan: distance sampling and occupancy modeling. J Wildl Manag 76:308–316
Pöysä H (2001) Dynamics of habitat distribution in breeding mallards: assessing the applicability of current habitat selection models. Oikos 94:365–373
Pulliam HR, Danielson BJ (1991) Sources, sinks, and habitat selection—a landscape perspective on population-dynamics. Am Nat 137:50–66
R Core Team (2012) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. http://www.R-project.org/. ISBN 3-900051-07-0
Reed JM (1999) The role of behavior in recent avian extinctions and endangerments. Conserv Biol 13:232–241
Reed JM, Dobson AP (1993) Behavioral constraints and conservation biology—conspecific attraction and recruitment. Trends Ecol Evol 8:253–256
Rørvik KA, Pedersen HC, Steen JB (1998) Dispersal in willow ptarmigan Lagopus lagopus—who is dispersing and why? Wildl Biol 4:91–96
Sandercock BK, Nilsen EB, Brøseth H, Pedersen HC (2011) Is hunting mortality additive or compensatory to natural mortality? Effects of experimental harvest on the survival and cause-specific mortality of willow ptarmigan. J Anim Ecol 80:244–258
Schieck JO, Hannon SJ (1989) Breeding site fidelity in willow ptarmigan—the influence of previous reproductive success and familiarity with partner and territory. Oecologia 81:465–472
Schieck JO, Hannon SJ (1993) Clutch predation, cover, and the overdispersion of nests of the willow ptarmigan. Ecology 74:743–750
Sergio F, Newton I (2003) Occupancy as a measure of territory quality. J Anim Ecol 72:857–865
Sinclair ARE, Fryxell JM, Caughley G (2006) Wildlife ecology, conservation, and management. Blackwell Pub, Malden
Skagen SK, Adams AAY (2011) Potential misuse of avian density as a conservation metric. Conserv Biol 25:48–55
Smith A, Willebrand T (1999) Mortality causes and survival rates of hunted and unhunted willow grouse. J Wildl Manag 63:722–730
Solvang H, Pedersen HC, Storaas T, Fossland Moa P, Breisjøberget JI (2007) Årsrapport for rypetaksering 2006. Rypeforvaltningsprosjektet 2006–2011 [Annual report of the willow ptarmigan survey 2006. Grouse management 2006–2011]. Oppdragsrapport nr. 2 2007 Hogskolen i Hedmark. (in Norwegian with English abstract)
Stamps JA (1988) Conspecific attraction and aggregation in territorial species. Am Nat 131:329–347
Statistics Norway (2013) Small game and roe deer hunting, 2012/2013. https://www.ssb.no/en/jordskog-jakt-og-fiskeri/statistikker/srjakt
Steen JB, Pedersen HC, Erikstad KE, Hansen KB, Høydal K, Størdal A (1985) The significance of cock territories in willow ptarmigan. Ornis Scand 16:277–282
Steen JB, Steen H, Stenseth NC, Myrberget S, Marcström V (1988) Microtine density and weather as predictors of chick production in willow ptarmigan, Lagopus l. lagopus. Oikos 51:367–373
Støen O-G, Wegge P, Heid S, Hjeljord O, Nellemann C (2010) The effect of recreational homes on willow ptarmigan (Lagopus lagopus) in a mountain area of Norway. Eur J Wildl Res 56:789–795
Taylor LR (1961) Aggregation, variance and the mean. Nature 189:732–735
Taylor LR (1984) Assessing and interpreting the spatial distributions of insect populations. Annu Rev Entomol 29:321–357
Thomas L, Buckland ST, Rexstad EA, Laake JL, Strindberg S, Hedley SL, Bishop JRB, Marques TA, Burnham KP (2010) Distance software: design and analysis of distance sampling surveys for estimating population size. J Appl Ecol 47:5–14
Tsai JH, Wang JJ, Liu YH (2000) Sampling of Diaphorina citri (Homoptera: Psyllidae) on orange jessamine in southern Florida. Fla Entomol 83:446–459
Van Horne B (1983) Density as a misleading indicator of habitat quality. J Wildl Manag 47:893–901
Ward MP, Schlossberg S (2004) Conspecific attraction and the conservation of territorial songbirds. Conserv Biol 18:519–525
Warren P, Baines D (2011) Evaluation of the distance sampling technique to survey red grouse Lagopus lagopus scoticus on moors in northern England. Wildl Biol 17:135–142
Watson A, Moss R, Parr R, Mountford MD, Rothery P (1994) Kin landownership, differential aggression between kin and nonkin, and population fluctuations in red grouse. J Anim Ecol 63:39–50
Acknowledgments
This work was carried as a part of the grouse management project 2006–2011 founded by Norwegian Research Council and Norwegian Directorate for Nature Management. Additional founding was received from Hedmark University College and Norwegian Institute for Nature Research (NINA). We are grateful to all the volunteer dog handlers who have collected all the field data and three anonymous reviewers who improved the manuscript immensely. We also wish to thank Jos M. Milner for valuable comments and help with the English.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Kvasnes, M.A.J., Pedersen, H.C., Solvang, H. et al. Spatial distribution and settlement strategies in willow ptarmigan. Popul Ecol 57, 151–161 (2015). https://doi.org/10.1007/s10144-014-0454-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10144-014-0454-1