Abstract
In most metapopulation models dispersal is assumed to be a fixed species-specific trait, but in reality dispersal abilities are highly sensitive to various selective pressures. Strict isolation of a metapopulation, which precludes any influx of immigrants (and their genes) from outside and makes it impossible for emigrants to reach other localities with suitable habitat, thus reducing fitness benefits of long-distance dispersal to zero, may be expected to impose strong selection against dispersal. We tested the above prediction by comparing dispersal parameters derived with the Virtual Migration model for isolated and non-isolated metapopulations of two species of large blue Maculinea (= Phengaris) butterflies, surveyed with intensive mark-recapture. Mortality during dispersal was found to be twice (in M. teleius) to five times higher (in M. arion) in isolated metapopulations. Isolation also resulted in significantly reduced dispersal distances in isolated metapopulations, with the effect being particularly strong in M. arion females. Apart from its evolutionary and ecological consequences, dispersal depression in isolated butterfly metapopulations implied by our results has serious conservation implications. It provides a clear argument against using parameter values obtained in a different environmental setting in modelling applications, e.g., Population Viability Analyses or environmental impact assessment. Furthermore, it underlines the importance of establishing well-connected networks of suitable habitats prior to species release in areas where reintroductions are planned.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Classic metapopulation theory as well as a great majority of metapopulation models assume that dispersal abilities of a given species are fixed traits (Travis and French 2000; Goodwin 2003; Bowler and Benton 2005). Consequently, the exchange of individuals between local populations is modelled as a function of these fixed dispersal traits on one hand and of highly variable spatial configurations of habitat patches on the other hand. However, recently there have been a growing number of empirical studies documenting considerable intra-specific variability in dispersal (Clobert et al. 2004; Bowler and Benton 2005; Stevens et al. 2010a). This is particularly true for butterflies, which constitute the most popular model organisms for dispersal studies (Stevens et al. 2010a, b).
Dispersal parameters of many butterfly species have been proven to vary strongly in both time and space. A manifestation of the former pattern is density-dependence of emigration, for which both positive and negative relationships have been well documented (Brown and Ehrlich 1980; Nowicki and Vrabec 2011). In turn, classic examples of spatial intra-specific variability in dispersal abilities are morphological changes in populations at the expanding edge of species distribution range, such as larger body mass, wider thorax, and longer and narrower wings (Hill et al. 1999; Simmons and Thomas 2004; Hughes et al. 2007), which are related to better flight performance (Berwaerts et al. 2002; Fric and Konvicka 2002; Stevens et al. 2012; but see Sekar 2012). There are also studies that explicitly demonstrated greater mobility of individuals living in recently established populations (Hanski et al. 2002, 2006). In the light of generally observed heritability of dispersal traits (Roff and Fairbairn 2001; Haag et al. 2005), better dispersal abilities in new populations are easy to explain since animals living there are descendants of more dispersive individuals.
Dispersal abilities may be also selected for or against as a result of landscape structure. Hanski et al. (2004) found that butterfly mobility was positively correlated with habitat patch isolation, but only among individuals living in newly established local populations. In contrast, among individuals from long-lasting populations mobility decreased with increasing isolation (Hanski et al. 2004). Similarly, Schtickzelle et al. (2006) proved that increasing habitat fragmentation negatively affects dispersal within metapopulations, reducing emigration rate and movement distances. Positive impact of isolation in newly established populations is quite intuitive, because the isolation of habitat patches allows only the most dispersive individuals to reach and colonise them, thus serving as a positive selection driver. In turn, within stable systems of long-lasting populations the effect of isolation is in the opposite direction, because greater inter-patch distances and smaller patch sizes lead to higher costs of dispersal and lower chances of successfully reaching non-natal patches by emigrants. Both factors impose strong selection against dispersers.
Dispersal depression may also be expected due to isolation at a larger scale, i.e., isolation of entire metapopulations. A complete isolation at the metapopulation scale not only precludes any influx of dispersers, and their genes, from outside, but it also makes it impossible to reach other metapopulations, thus reducing fitness benefits of long-distance dispersal to zero. Consequently, dispersal abilities should gradually decrease in such a situation.
Quite surprisingly, the above prediction has not been investigated empirically so far, although some indirect evidence provides support for its validity (Dempster 1991; Adamski and Witkowski 2007). Therefore, our aim was to test the prediction by comparing dispersal parameters derived for isolated and non-isolated metapopulations. We did so by applying the Virtual Migration (VM) model (Hanski et al. 2000) to the extensive mark-recapture data collected for two species of the large blue Maculinea (= Phengaris) butterflies.
Methods
Study species and sites
Maculinea are highly specialised myrmecophilous butterflies. To complete their life cycle they require two crucial resources, namely specific foodplants and specific host ants of the genus Myrmica (Thomas et al. 1998). While ants are typically scarce but widely distributed, the foodplants are highly abundant but occur in patches (Nowicki et al. 2005a, 2007; Anton et al. 2008). Consequently, foodplant distribution defines the spatial structure of local populations of Maculinea butterflies, which often form metapopulation systems (cf. Nowicki et al. 2007; Dierks and Fischer 2009).
We investigated dispersal in two Italian metapopulations of M. arion: Val Ferret and Cuneo, as well as in two M. teleius metapopulations from the Czech Republic: Přelouč and Podebrady, which were intensively surveyed with mark-recapture. In each case the sampling covered each local population within a system and it was conducted daily (with few gaps due to unfavourable weather) throughout the entire flight period, i.e., roughly from late June through late July for M. arion, and from early July to mid August for M. teleius. None of the data collected in the surveys have been published previously, apart from those coming from the Přelouč metapopulation, which were used in the analysis of density-dependence of dispersal (Nowicki and Vrabec 2011, see this reference for the details of the field sampling method).
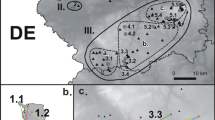
The summary of the information about the investigated metapopulations is given in Table 1. It is important to note that for each species one of the metapopulations is relatively well-connected with other conspecific metapopulations in its region, while the other experiences strong isolation. The ca. 2–3 km distance separating the Val Ferret and the Přelouč metapopulations from the nearest neighbouring metapopulations allows occasional exchange of individuals. At the same time such inter-metapopulation movements have been sporadic only (altogether only two cases recorded), and thus it is valid to restrict dispersal analyses to the investigated metapopulations. In contrast, the isolation of the two other metapopulation far exceeds 5 km, which is roughly the maximum movement distance recorded for Maculinea butterflies (see review in Nowicki et al. 2005b). The Cuneo metapopulation is ca. 30 km away from the nearest other metapopulations with M. arion located at the outskirts of the Alpi Marittime Regional Park, and this isolation persists for at least 50 years. Similarly, the distance between the Podebrady metapopulation and other known localities (in fact much smaller ones) with M. teleius reaches almost 20 km. While the past record of the species occurrence is not known in full details, considering the history of the landscape changes in the region, it can be expected that the present situation lasts since the early 1990s. Consequently, in the present study we regard the metapopulations of M. arion in Val Ferret and M. teleius in Přelouč as non-isolated ones, whereas those of the respective species in Cuneo and Podebrady as strongly isolated ones.
Admittedly, apart from the isolation level the investigated metapopulations differ also in their internal fragmentation (Fig. 1). As indicated by the shorter inter-patch distances, the isolated metapopulations are less fragmented, which is particularly the case for M. arion (Table 1). Consequently, the set of investigated metapopulation does not constitute the perfect experimental design for analysing the effect of isolation, which we take into account while interpreting the results (see “Discussion”). However, achieving such a design appears impossible in reality. We were not able to find any metapopulation of Maculinea butterflies that would be strongly isolated and highly fragmented, since in such conditions the species are unlikely to persist. On the other hand, while non-isolated and little fragmented metapopulation do exist in the regions where the species are relatively wide-spread, they are too large to be feasibly surveyed with mark-recapture (cf. Nowicki et al. 2007).
We have also focused on minimising the potential effects of differences in butterfly densities on the recorded patterns of their dispersal, as Maculinea butterflies are known to experience substantial annual fluctuations in their numbers (Thomas et al. 1998; Nowicki et al. 2009). Our earlier study has demonstrated a positive impact of butterfly density on their emigration propensity (but not on any other dispersal parameter), which however was considerable only at densities exceeding carrying capacity (Nowicki and Vrabec 2011). In 2009, when M. arion was intensively surveyed in Val Ferret and Cuneo, its densities in both metapopulations were comparable (Table 1). More importantly, in both cases they were similar to the densities recorded through preliminary sampling (restricted to few habitat patches and not relevant for dispersal analyses) in two earlier years, and thus apparently at their normal levels below carrying capacities. Maculinea teleius in Podebrady was studied for 4 years, but the sampling was comprehensive enough for dispersal analysis only in 2006, when the metapopulation was at its peak. Consequently, to facilitate comparisons with the Přelouč metapopulation, we used its results for 2008 when M. teleius numbers peaked there. In both cases the species densities were ca. 1.5 higher than the carrying capacities estimated on the basis of available time-series (cf. Nowicki and Vrabec 2011).
Dispersal analysis
We analysed the mark-recapture data with the Virtual Migration model, using the program VM2 (Hanski et al. 2000). Since the rationale and a detailed description of the model can be found elsewhere (Hanski et al. 2000; Wahlberg et al. 2002), in the present paper we only briefly outline its features.
The VM model is a well-established standard for dispersal analysis in metapopulations, based on mark-recapture data, and has been frequently used in butterfly studies (e.g., Wahlberg et al. 2002; Schtickzelle et al. 2006; Fric et al. 2010). Although it is preferable to apply the model to relatively large metapopulations comprising 10 or more local populations (Hanski et al. 2000), the model can also be successfully applied to slightly smaller systems provided that there is substantial variation in habitat patch areas and inter-patch distances (e.g., Petit et al. 2001; Schtickzelle and Baguette 2003; Schtickzelle et al. 2006).
Dispersal within a metapopulation is described with six parameters, including: (1) mortality in habitat patches (μp); (2) emigration propensity (η), defined as daily emigration rate scaled to 1 ha patch; (3) emigration scaling with natal patch area (ζem,); (4) immigration scaling with target patch area (ζim); (5) scaling of mortality during dispersal with natal patch connectivity (λ); (6) distance dependence of dispersal (α). Both emigration and immigration scaling parameters reflect the power relationship with patch area (A j ), assumed to be negative for emigration (\( E_{j} \sim A_{j}^{{\zeta {}_{\text{em}}}} , \, \zeta_{\text{em}} < \, 0 \)) and positive for immigration (\( I_{j} \sim A_{j}^{{\zeta {}_{\text{im}}}} , \, \zeta_{\text{im}} > \, 0 \)). The probability of successful dispersal (dispersal survival φmj ) is modelled to increase sigmoidally with the natal patch connectivity: \( \varphi_{{{\text{m}}j}} = {{S_{j}^{2} } \mathord{\left/ {\vphantom {{S_{j}^{2} } {(\lambda + S_{j}^{2} )}}} \right. \kern-0pt} {(\lambda + S_{j}^{2} )}} \), where S j is patch connectivity defined as in Hanski (1994). Hence, the square root of λ is the equivalent of patch connectivity, for which half of dispersers starting from the patch die during dispersal. The α parameter describes the dispersal kernel. We chose the negative exponential function (NEF) as the kernel (as in Hanski et al. 2000), in which mean dispersal distance (measured in km) corresponds to 1/α, rather than the inverse power function (IPF, used e.g., by Schtickzelle et al. 2006; Fric et al. 2010). The NEF was found to describe movements of Maculinea butterflies quite well in previous studies (Hovestadt and Nowicki 2008; Nowicki and Vrabec 2011), and in the present one it also fitted the empirical data better as revealed by the VM model goodness-of-fit tests. Nevertheless, it should be stressed that the estimates of all the VM model parameters (obviously apart from α) remained virtually unchanged when the IPF was attempted as the dispersal kernel.
The VM model allows the estimation of its parameters together with their 95 % confidence intervals. Since the parameter estimates are expressed in uniform units, they can be used for comparisons between metapopulations of different spatial structure; with non-overlapping 95 % confidence intervals indicating statistically significant differences between the estimates (Schtickzelle and Baguette 2003; Schtickzelle et al. 2006). The accuracy of the model estimates is not affected by sample size, though small sample size clearly reduces the estimate precision (Nowicki and Vrabec 2011).
Furthermore, the model estimates are not biased by the spatial extent of the study area, which is a frequent problem with descriptive statistics based on mark-recapture data, such as maximum or mean movement distance recorded (Schneider 2003). We derived parameter estimates separately for males and females as well as for all individuals pooled together. Obtaining sex-specific parameters was important, because inter-sexual differences in dispersal, although often neglected, are typically strong in butterflies (Ovaskainen et al. 2008; Schultz et al. 2012).
Results
In both investigated M. arion metapopulations altogether 530 individuals were captured 1147 times with 252 inter-patch movements recorded. The respective figures for M. teleius comprise 2033 individuals, 3587 captures, and 208 inter-patch movements. The sex ratio was well balanced in each metapopulation. Large sample sizes enabled us to achieve relatively precise estimates of the VM model parameters, except for M. arion metapopulation in Val Ferret, for which the estimate precision was slightly lower due to lower sampling effort, but still acceptable. All the parameter estimates are presented in Figs. 2 and 3. Maculinea arion showed better dispersal abilities than M. teleius, as indicated by consistently higher emigration propensity, longer dispersal distances, and lower mortality during dispersal. Similarly, females were typically more dispersive than males.
Mean dispersal distances (with 95 % confidence intervals) in the investigated metapopulations of Maculinea butterflies (M. arion Val Ferret and Cuneo; M. teleius Přelouč and Podebrady), estimated with the Virtual Migration model (1/α). circles females, triangles males, squares all individuals pooled together. Note the logarithmic scale applied. The differences in the pairs of estimates obtained for isolated and non-isolated metapopulations are statistically significant (P < 0.05) in all the cases
Parameters of the Virtual Migration model and their 95 % confidence intervals (a within-patch mortality; b emigration propensity; c emigration scaling; d dispersal mortality scaling; e immigration scaling), derived for the investigated metapopulations of Maculinea butterflies (M. arion Val Ferret and Cuneo; M. teleius Přelouč and Podebrady). The estimates of distance dependence (α) are not included as they are presented in Fig. 2, transformed into mean dispersal distances (1/α). circles females, triangles males, squares all individuals pooled together. Horizontal arrows indicate statistically significant differences (P < 0.05) in the pairs of estimates obtained for isolated and non-isolated metapopulations
Concerning the main topic of our study, i.e., the effects of isolation, the most evident one was significantly reduced dispersal distance in isolated metapopulations of both species (Fig. 2). The effect was the strongest in M. arion females, in which the mean dispersal distance in the isolated Cuneo metapopulation was about six times lower than in the non-isolated Val Ferret one (1/α = 162 and 928 m respectively). In all other cases, the reduction in dispersal distance with isolation was approximately two- to three-fold.
Apparently, isolation also led to increased dispersal mortality, although the difference was significant only in the case of the M. arion estimates for all individuals (Fig. 3d). While the confidence intervals of the dispersal mortality scaling parameter overlapped in all other cases (which is in fact a common problem with this parameter as it is the most difficult one to estimate with the VM model), the estimate values were consistently higher in isolated metapopulations. In absolute terms they corresponded to twice higher proportion of individuals that die during dispersal in M. teleius (52 % in Podebrady vs. 28 % in Přelouč) and five times higher one in M. arion (21 % in Cuneo vs. 4 % in Val Ferret).
The pattern in emigration was less consistent and not significant in any case (Fig. 3b). The highest emigration probability was recorded in M. arion males in Cuneo, approaching 0.30 per day per 1 ha patch. The relationships of emigration and immigration rate with patch area were apparently not affected by isolation of a metapopulation (Fig. 3c, e). The scaling values were close to 0, indicating that the processes were fairly independent of patch area, apart from immigration in Cuneo and Přelouč as well as emigration in the latter locality. Similarly, the variation in mortality within habitat patches did not reflect the difference in isolation (Fig. 3a). The mortality was significantly higher in the Podebrady metapopulation of M. teleius. The parameter values were almost identical for both sexes, except for Val Ferret, where resident females suffered higher resident mortality (μp = 0.31 vs. 0.21 in males). While the difference may seem slight, it translates into considerably shorter life span of non-dispersing individuals (2.73 vs. 4.26 days in males).
Discussion
Main results of our analyses revealed differences in average dispersal distances and dispersal mortality between the investigated metapopulations of Maculinea butterflies. Regretfully, as explained in the “Methods”, in both species the metapopulations differ not only in isolation level, but also in their internal fragmentation, with the isolated ones being less fragmented. Therefore, the results obtained can be interpreted in two alternative ways: either as a positive effect of internal fragmentation of metapopulations on butterfly dispersal or as a negative effects of their external isolation. The first explanation is in line with the findings of Hanski et al. (2004), who demonstrated that decreasing connectivity of local populations promotes individuals with better dispersal abilities, which are able to colonise vacant habitat patches and establish new populations. On the other hand, habitat fragmentation within stable metapopulations with long-lasting local populations can be assumed to negatively affect dispersal through increasing its costs, as predicted by theoretical models (Leimar and Norberg 1997; Travis and Dytham 1999; Heino and Hanski 2001) and confirmed empirically (Hanski et al. 2004; Schtickzelle et al. 2006). If it is the case also for the investigated metapopulations of Maculinea butterflies, then our results, namely dispersal depression in relatively little fragmented but strongly isolated metapopulations, would imply that the external isolation of metapopulations has a stronger negative impact on dispersal than their fragmentation.
While both aforementioned explanations, i.e., fragmentation promoting dispersal and isolation suppressing it, are equally supported by our results, we believe that latter one is more plausible for the metapopulations of Maculinea butterflies investigated in the present study. First of all, all these metapopulations are relatively stable, with hardly any local extinctions and recolonisations, and thus with well-established local populations. Apart from this, a positive effect of fragmentation on mobility, possible in newly-established populations, could only explain longer dispersal distances (Hanski et al. 2004), but not lower dispersal mortality, as the risk of unsuccessful dispersal is likely to rise with increasing fragmentation in any scenario.
Strong reduction in dispersal distance that we have found in strictly isolated metapopulations of both species is easy to understand. Selection against long-distance dispersers is inevitable in such conditions as any individual that moves far enough to leave its metapopulation is bound to die without a possibility to reach suitable habitat. It is worth noting that this selection provides a feedback effect, because shorter dispersal distance increases the effective isolation through reducing the chances of exchange of individuals with other metapopulations. Based on the VM model parameters obtained, the estimated metapopulation sizes, and the inter-metapopulation distances, it can be estimated that per single generation approximately 2.2 M. arion individuals from Val Ferret and 0.25 M. teleius individual from Přelouč are able to get to neighbouring metapopulations. In contrast, butterflies starting from the isolated metapopulations in Cuneo or Podebrady have no chance of reaching other localities with their species (the derived numbers of successful ‘external’ emigrants are less than one per billion generations).
The differences in dispersal mortality recorded for the investigated metapopulations may be less spectacular and confirmed as significant only for M. arion, but they possibly offer the most direct evidence for ongoing selection against dispersers. The increased mortality in isolated metapopulations stems from two separate phenomena. First, lower values of dispersal mortality scaling indicate that for a given connectivity of a natal patch the butterflies are more likely to die while dispersing, which e.g., may imply their decreased ability of finding other patches (cf. Merckx and Van Dyck 2007). Second, shorter dispersal distances mean that the connectivity of each patch becomes lower. The latter phenomenon is a good illustration of the discrepancy between structural connectivity defined by the spatial structure of habitat patches, and functional connectivity reflecting the actual potential for the exchange of individuals, which has been recently gaining a growing attention in ecology (Goodwin 2003; Baguette and Van Dyck 2007; Pe’er et al. 2011).
Relatively high levels of dispersal mortality in M. teleius as compared with those found M. arion should not be viewed as a genuine interspecific difference. Instead, they apparently reveal the typical increase in years when butterflies densities peak above carrying capacities and dispersal is undertaken also by individuals less adapted to it (Nowicki and Vrabec 2011). Although densities exceeding carrying capacities occur only once in a few years (Nowicki et al. 2009), thus rather infrequently, extremely high mortality of adult dispersers in such years (over 50 % in the isolated Podebrady metapopulation) becomes strong selection driver, especially because it coincides with high mortality of larvae due to severe intra-specific competition (Hochberg et al. 1994).
Schtickzelle et al. (2006) proved the decrease in emigration rate in a highly fragmented metapopulation, but our evidence for the negative impact of isolation on emigration is unconvincing; in the case of M. arion we even found the opposite trend. In other words, while isolation results in the shorter inter-patch movement distances and higher mortality associated with the movements, it does not necessarily reduce the number of movements undertaken. The explanation for this pattern may be the fact that although long-distance movements, constituting genuine dispersal, are suppressed, daily routine movements are not affected. It has been recently shown that many such routine movements are performed between separate habitat patches, if these are small and located close to one another (Hovestadt et al. 2011). The same argument may be used to explain particularly high emigration rate of M. arion in Cuneo. It may be expected that a great majority of their inter-patch movements were routine flights in search of females, since several patches in this metapopulation are very small and inhabited by few butterflies. To support the above hypothesis it is worth mentioning that many male movements in Cuneo were back and forth flights between pairs of small patches.
Other dispersal parameters considered in the present study do not seem affected by isolation. We suggest that the observed patterns in emigration and immigration scaling parameters stem from the fact that the negative effect of patch area on emigration and its positive effect on immigration were moderated by the existing strong variation in patch shape and quality (Casacci et al. 2011; P. Nowicki, unpublished data). Only in the Přelouč metapopulation the largest patches were also of the best quality, which discourages emigration and promotes immigration. In turn, adult mortality within patches is most likely shaped by weather as frequently found in butterflies (Schtickzelle et al. 2002; Casula and Nichols 2003; Nowicki et al. 2009; Matter et al. 2011). Similarly, while it is tempting to view lower within-patch mortality rate of M. arion females from Val Ferret (which were the most dispersive of all groups investigated in our study) as a manifestation of a trade-off between longevity and dispersal abilities (Hanski et al. 2006), this finding should also be attributed to weather conditions. Like most other butterflies Maculinea are characterised by protandry, i.e., most females eclose later in the season during the flight period (Pfeifer et al. 2000; Nowicki et al. 2005c), and indeed in the second half of the surveyed season the weather in Val Ferret was unfavourable for butterflies with many rainy days.
Apart from its evolutionary and ecological consequences discussed above, dispersal depression in isolated metapopulations has serious conservation implications. First of all, our findings, revealing strong spatial variability of dispersal parameters in both investigated species, provide a clear argument against using parameter values obtained in a different environmental setting in modelling applications, e.g., population viability analyses. This is, unfortunately, a common problem due to little availability of dispersal parameters even for well-studied species (Schtickzelle and Baguette 2009; Radchuk et al. 2012). In addition, one cannot rely on dispersal parameters to remain unchanged, if the isolation of a focal locality increases. To illustrate the point: even if at present butterflies of a given species easily cover the distance of a few kilometres separating two metapopulations, one should not expect that they will still be able to do so after a barrier, e.g., a highway, emerges between them. Admittedly, in present study we only documented the impact of isolation by distance, nevertheless any barrier reducing functional connectivity should also impose selection against dispersal. This needs to be taken into account, for instance in environmental impact assessment. Finally, similar selection against dispersal may happen in reintroduced populations. Despite the fact that reintroduced individuals typically originate from non-isolated localities, their descendants are bound to gradually loose their dispersal abilities if the reintroduction site is severely isolated. The above prediction is confirmed by the case of M. nausithous and M. teleius reintroduction in the Netherlands. The Moerputten site where both species have been released in 1990 was strictly isolated in early years after the reintroduction; only later suitable habitats were created in its vicinity, but their colonisation is going very slowly (Wynhoff 1998; van Langevelde and Wynhoff 2009). To avoid such a situation it is recommended to establish a well-connected network of suitable habitats before (rather than after) the reintroduction takes place.
References
Adamski P, Witkowski ZJ (2007) Effectiveness of population recovery projects based on captive breeding. Biol Conserv 140:1–7
Anton C, Musche M, Hula V, Settele J (2008) Myrmica host-ants limit the density of the ant-predatory large blue Maculinea nausithous. J Insect Conserv 12:511–517
Arnason AN, Schwarz CJ (1999) Using POPAN-5 to analyse banding data. Bird Study 46:157–168
Baguette M, Van Dyck H (2007) Landscape connectivity and animal behavior: functional grain as a key determinant for dispersal. Landsc Ecol 22:117–129
Berwaerts K, Van Dyck H, Aerts P (2002) Does flight morphology relate to flight performance? An experimental test with the butterfly Pararge aegeria. Funct Ecol 16:484–491
Bowler DE, Benton TG (2005) Causes and consequences of animal dispersal strategies: relating individual behaviour to spatial dynamics. Biol Rev 80:205–225
Brown IL, Ehrlich PR (1980) Population biology of the checkerspot butterfly, Euphydryas chalcedona. Structure of the Jasper Ridge colony. Oecologia 47:239–251
Casacci LP, Witek M, Barbero F, Patricelli D, Solazzo G, Balletto E, Bonelli S (2011) Habitat preferences of Maculinea arion and its Myrmica host ants: implications for habitat management in Italian Alps. J Insect Conserv 15:103–110
Casula P, Nichols JD (2003) Temporal variability of local abundance, sex ratio and activity in the Sardinian chalk hill blue butterfly. Oecologia 136:374–382
Clobert J, Ims RA, Rousset F (2004) Causes, mechanisms and consequences of dispersal. In: Hanski I, Gaggiotti OE (eds) Ecology, genetics and evolution of metapopulation. Elsevier Academic Press, San Diego, pp 307–335
Dempster JP (1991) Fragmentation, isolation and mobility of insect populations. In: Collins NM, Thomas JA (eds) The conservation of insects and their habitats. Academic Press, London, pp 143–154
Dierks A, Fischer K (2009) Habitat requirements and niche selection of Maculinea nausithous and M. teleius (Lepidoptera: Lycaenidae) within a large sympatric metapopulation. Biodivers Conserv 18:3663–3676
Fric Z, Konvicka M (2002) Generations of the polyphenic butterfly Araschnia levana differ in body design. Evol Ecol Res 4:1017–1032
Fric Z, Hula V, Klimova M, Zimmermann K, Konvicka M (2010) Dispersal of four fritillary butterflies within identical landscape. Ecol Res 25:543–552
Goodwin BJ (2003) Is landscape connectivity a dependent or independent variable? Landsc Ecol 18:687–699
Haag CR, Saastamoinen M, Marden JH, Hanski I (2005) A candidate locus for variation in dispersal rate in a butterfly metapopulation. Proc R Soc B 272:2449–2456
Hanski I (1994) A practical model of metapopulation dynamics. J Anim Ecol 63:151–162
Hanski I, Alho J, Moilanen A (2000) Estimating the parameters of survival and migration of individuals in metapopulations. Ecology 81:239–251
Hanski I, Breuker CJ, Schöps K, Setchfield R, Nieminen M (2002) Population history and life history influence the migration rate of female Glanville fritillary butterflies. Oikos 98:87–97
Hanski I, Erälahti C, Kankare M, Ovaskainen O, Siren H (2004) Variation in migration rate among individuals maintained by landscape structure. Ecol Lett 7:958–966
Hanski I, Saastamoinen M, Ovaskainen O (2006) Dispersal related life-history trade-offs in a butterfly metapopulation. J Anim Ecol 75:91–100
Heino M, Hanski I (2001) Evolution of migration rate in a spatially realistic metapopulation model. Am Nat 157:495–511
Hill JK, Thomas CD, Blakeley DS (1999) Evolution of flight morphology in a butterfly that has recently expanded its geographic range. Oecologia 121:165–170
Hochberg ME, Clarke RT, Elmes GW, Thomas JA (1994) Population dynamic consequences of direct and indirect interactions involving a large blue butterfly and its plant and red ant hosts. J Anim Ecol 63:375–391
Hovestadt T, Nowicki P (2008) Investigating movement within irregularly shaped patches: analysis of MRR data using randomisation procedures. Isr J Ecol Evol 54:137–154
Hovestadt T, Binzenhöfer B, Nowicki P, Settele J (2011) Do all inter-patch movements represent dispersal? A mixed kernel study of butterfly mobility in fragmented landscapes. J Anim Ecol 80:1070–1077
Hughes CL, Dytham C, Hill J (2007) Modelling and analysing evolution of dispersal in populations at expanding range boundaries. Ecol Entomol 32:437–445
Leimar O, Norberg U (1997) Metapopulation extinction and genetic variation in dispersal-related traits. Oikos 80:448–458
Matter SF, Doyle A, Illerbrun K, Wheeler J, Roland J (2011) An assessment of direct and indirect effects of climate change for populations of the Rocky Mountain Apollo butterfly (Parnassius smintheus Doubleday). Insect Sci 18:385–392
Merckx T, Van Dyck H (2007) Landscape of origin affects habitat-finding ability of the speckled wood butterfly (Pararge aegeria). Anim Behav 74:1029–1037
Nowicki P, Vrabec V (2011) Evidence for positive density-dependent emigration in butterfly metapopulations. Oecologia 167:657–665
Nowicki P, Witek M, Skórka P, Settele J, Woyciechowski M (2005a) Population ecology of the endangered butterflies Maculinea teleius and M. nausithous, and its implications for conservation. Popul Ecol 47:193–202
Nowicki P, Settele J, Thomas JA, Woyciechowski M (2005b) A review of population structure of Maculinea butterflies. In: Settele J, Kuhn E, Thomas JA (eds) Studies in the ecology and conservation of butterflies in Europe. Species ecology along a European gradient: Maculinea butterflies as a model, vol 2. Pensoft Publishers, Sofia–Moscow, pp 144–149
Nowicki P, Richter A, Glinka U, Holzschuh A, Toelke U, Henle K, Woyciechowski M, Settele J (2005c) Less input same output—simplified approach for population size assessment in Lepidoptera. Popul Ecol 47:203–212
Nowicki P, Pepkowska A, Kudlek J, Skórka P, Witek M, Settele J, Woyciechowski M (2007) From metapopulation theory to conservation recommendations: lessons from spatial occurrence and abundance patterns of Maculinea butterflies. Biol Conserv 140:119–129
Nowicki P, Bonelli S, Barbero F, Balletto E (2009) Relative importance of density-dependent regulation and environmental stochasticity for butterfly population dynamics. Oecologia 161:227–239
Ovaskainen O, Luoto M, Ikonen I, Rekola H, Meyke E, Kuussaari M (2008) An empirical test of a diffusion model: predicting clouded apollo movements in a novel environment. Am Nat 171:610–619
Pe’er G, Henle K, Dislich C, Frank K (2011) Breaking functional connectivity into components: a novel approach using an individual-based model, and first outcomes. PLoS One 6:e22355
Petit S, Moilanen A, Hanski I, Baguette M (2001) Metapopulation dynamics of the bog fritillary butterfly: movements between habitat patches. Oikos 92:491–500
Pfeifer MA, Andrick UR, Frey W, Settele J (2000) On the ethology and ecology of a small and isolated population of the Dusky Large Blue Butterfly Glaucopsyche (Maculinea) nausithous (Lycaenidae). Nota Lepid 23:147–172
Radchuk V, WallisDeVries MF, Schtickzelle N (2012) Spatially and financially explicit population viability analysis of Maculinea alcon in The Netherlands. PLoS One 7:e38684
Roff DA, Fairbairn DJ (2001) The genetic basis of dispersal and migration, and its consequences for the evolution of correlated traits. In: Clobert J, Danchin E, Dhondt AA, Nichols JD (eds) Dispersal. Oxford University Press, Oxford, pp 191–202
Schneider C (2003) The influence of spatial scale on quantifying insect dispersal: an analysis of butterfly data. Ecol Entomol 28:252–256
Schtickzelle N, Baguette M (2003) Behavioural responses to habitat patch boundaries restrict dispersal and generate emigration–patch area relationships in fragmented landscapes. J Anim Ecol 72:533–545
Schtickzelle N, Baguette M (2009) Metapopulation viability analysis: a crystal ball for the conservation of endangered butterflies? In: Settele J, Shreeve TG, Konvicka M, Van Dyck H (eds) Ecology of butterflies in Europe. Cambridge University Press, London, pp 339–352
Schtickzelle N, Le Boulenge E, Baguette M (2002) Metapopulation dynamics of the bog fritillary butterfly: demographic processes in a patchy population. Oikos 97:349–360
Schtickzelle N, Mennechez G, Baguette M (2006) Dispersal depression with habitat fragmentation in the bog fritillary butterfly. Ecology 87:1057–1065
Schultz CB, Franco AMA, Crone EE (2012) Response of butterflies to structural and resource boundaries. J Anim Ecol 81:724–734
Sekar S (2012) A meta-analysis of the traits affecting dispersal ability in butterflies: can wingspan be used as a proxy? J Anim Ecol 81:174–184
Simmons AD, Thomas CD (2004) Changes in dispersal during species’ range expansion. Am Nat 164:378–395
Stevens VM, Turlure C, Baguette M (2010a) Filling in the tapestry: a meta-analysis of dispersal in butterflies. Biol Rev 85:625–642
Stevens VM, Pavoine S, Baguette M (2010b) Variation within and between closely related species uncovers high intra-specific variability in dispersal. PLoS One 5:e11123
Stevens VM, Trochet A, Van Dyck H, Clobert J, Baguette M (2012) How is dispersal integrated in life histories: a quantitative analysis using butterflies. Ecol Lett 15:74–86
Thomas JA, Clarke RT, Elmes GW, Hochberg ME (1998) Population dynamics in the genus Maculinea (Lepidoptera: Lycaenidae). In: Dempster JP, McLean IFG (eds) Insect population dynamics in theory and practice. Symposia of the Royal Entomological Society 19, Chapman & Hall, London, pp 261–290
Travis JMJ, Dytham C (1999) Habitat persistence, habitat availability and the evolution of dispersal. P Roy Soc B 266:723–728
Travis JMJ, French DR (2000) Dispersal functions and spatial models: expanding our dispersal toolbox. Ecol Lett 3:163–165
van Langevelde F, Wynhoff I (2009) What limits the spread of two congeneric butterfly species after their reintroduction: quality or spatial arrangement of habitat? Anim Conserv 12:540–548
Wahlberg N, Klemetti T, Selonen V, Hanski I (2002) Metapopulation structure and movements in five species of checkerspot butterflies. Oecologia 130:33–43
Wynhoff I (1998) Lessons from the reintroduction of Maculinea teleius and M. nausithous in the Netherlands. J Insect Conserv 2:47–57
Acknowledgments
Butterfly surveys were conducted with proper permissions and supported by the FP6 BiodivERsA Eranet through its CLIMIT project, the Lagrange-CRT Foundation, and the Italian Ministry of University and Research (in Italy) as well as by the Research Project MSM 6046070901 of the Faculty of Agrobiology, Food and Natural Resources, Czech University of Life Sciences Prague (in the Czech Republic). Analyses were financed by the Polish National Science Centre Grant N N304 064139 and by the European Commission within its project SCALES (FP7 contract no. 226852). We are grateful to Gaetano Solazzo, Lorenzo Boggia, Jana Bouberlova-Gurna, Hana Hanouskova, Jana Hatlapatkova, Jiří Kosan, Helena Lalova, Kristyna Marušakova, Jana Pravdova, Milena Spalova, and Hana Vesela-Kosanova for their help in the fieldwork. Christine Richards improved the English of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Bonelli, S., Vrabec, V., Witek, M. et al. Selection on dispersal in isolated butterfly metapopulations. Popul Ecol 55, 469–478 (2013). https://doi.org/10.1007/s10144-013-0377-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10144-013-0377-2