Preventing active re-identification attacks on social graphs via sybil subgraph obfuscation

Abstract

Active re-identification attacks constitute a serious threat to privacy-preserving social graph publication, because of the ability of active adversaries to leverage fake accounts, a.k.a. sybil nodes, to enforce structural patterns that can be used to re-identify their victims on anonymised graphs. Several formal privacy properties have been enunciated with the purpose of characterising the resistance of a graph against active attacks. However, anonymisation methods devised on the basis of these properties have so far been able to address only restricted special cases, where the adversaries are assumed to leverage a very small number of sybil nodes. In this paper, we present a new probabilistic interpretation of active re-identification attacks on social graphs. Unlike the aforementioned privacy properties, which model the protection from active adversaries as the task of making victim nodes indistinguishable in terms of their fingerprints with respect to all potential attackers, our new formulation introduces a more complete view, where the attack is countered by jointly preventing the attacker from retrieving the set of sybil nodes, and from using these sybil nodes for re-identifying the victims. Under the new formulation, we show that k-symmetry, a privacy property introduced in the context of passive attacks, provides a sufficient condition for the protection against active re-identification attacks leveraging an arbitrary number of sybil nodes. Moreover, we show that the algorithm K-Match, originally devised for efficiently enforcing the related notion of k-automorphism, also guarantees k-symmetry. Empirical results on real-life and synthetic graphs demonstrate that our formulation allows, for the first time, to publish anonymised social graphs (with formal privacy guarantees) that effectively resist the strongest active re-identification attack reported in the literature, even when it leverages a large number of sybil nodes.

1 Introduction

The last decade has witnessed a formidable explosion in the use of social networking sites. Although the discipline of social network analysis has existed already for quite some time, today’s scientists potentially have access as never before to massive amounts of social network data. Social graphs are a particular example of this type of data, in which vertices typically represent users (e.g. Facebook or Twitter users, e-mail addresses) and edges represent relations between these users (e.g. becoming “friends”, following someone, exchanging e-mails). The analysis of social graphs can help scientists and other actors to discover important societal trends, study consumption habits, understand the spread of news or diseases, etc. For these goals to be achievable, it is necessary that the holders of this information, e.g. online social networks, messaging services, among others, release samples of their social graphs. However, ethical considerations, increased public awareness and reinforced legislation¹ place an increasingly strong emphasis on the need to protect individuals’ privacy via anonymisation.

Social graphs have proven themselves a challenging data type to anonymise. Even a simple undirected graph, with arbitrary node labels and no attributes on vertices or edges, is susceptible of leaking private information, due to the existence of unique structural patterns that characterise some individuals, e.g. the number of friends or the relations in the immediate vicinity [35]. Many privacy attacks that solely rely on the underlying graph topology of the social graph exist [1], and they are still effective [32], despite advances on social graph anonymisation. A particularly effective privacy attack is the so-called active attack, which uses a strategy consisting in inserting fake accounts, commonly referred to as sybils, into the real network. Once inserted, these fake users interact with legitimate users and among themselves, and create structures that allow the adversary to retrieve the sybil nodes from a sanitised social graph and use the connection patterns between sybils and legitimate nodes to re-identify the original users and infer sensitive information about them, such as the existence of relations.

The publication of social graphs that effectively resist active attacks was initially addressed by Trujillo-Rasua and Yero [46]. They introduced the notion of $(k,\ell )$-anonymity, the first privacy property to explicitly model the protection of published graphs against active adversaries. A graph satisfying $(k,\ell )$-anonymity ensures that an adversary leveraging up to $\ell$ sybil nodes and knowing the pairwise distances of all victims to all sybil nodes, is still unable to distinguish each victim from at least $k-1$ other vertices in the graph. This privacy property served as the basis for defining several anonymisation methods for a particular case, namely the one where either $k>1$ or $\ell >1$ [30, 33]. In other words, non-trivial anonymity ($k>1$) was only guaranteed against an adversary leveraging exactly one sybil node. Later, the introduction of the notion of $(k,\ell )$-adjacency anonymity [31] allowed to arbitrarily increase the values of k for which a formal privacy guarantee can be provided, but the proposed methods remained unable to address scenarios where the adversary can leverage more than two sybil nodes. In consequence, until now no anonymisation method with theoretically sound privacy guarantees against active attackers leveraging three or more sybil nodes has been made available to data publishers. This article solves such problem.

Our solution consists of identifying and formalising a more precise privacy model for active attacks, in terms of the capabilities the adversary is supposed to have, than those existing in the literature. We remove the assumption that the adversary is always capable of identifying the set of sybil nodes in the published graph, which appears in all privacy properties for active attacks [31, 46] that we are aware of. In this new model, instead, the analyst needs to calculate the actual probability of success of the attacker on re-identifying the sybil nodes and combines it with the attacker’s probability of re-identifying the victims.

By studying active attacks without the assumption that the attacker first needs to re-identify sybil nodes, we reached two main results: one of practical interest and another one theoretical. Of practical interest is our proof that the algorithm K-Match [54], originally devised for efficiently enforcing the notion of k-automorphism, makes it impossible for an active attacker to re-identify a victim with probability higher than 1/k, regardless of the adversary strength. Hence we show K-Match to be the first anonymisation method that protects against active attackers of arbitrary strength. Second, we prove our privacy model to be a proper extension of previous models [31, 46, 50], in the sense that it describes all graphs that have been previously considered private, and describes others that are not captured by existing models. This allowed us to establish the first connection between privacy models for passive attacks, such as k-symmetry [50], and privacy models for active attacks. For example, we prove that k-symmetry and $(k, \ell )$-anonymity are mutually exclusive, yet they are both proper instances of our privacy model. In other words, both models are sound, as far as resistance to active attack is concerned, but not complete. Whether there exists a k-anonymity model that captures all graphs resistant to active attacks, i.e. that is complete, is an open question.

Summary of contributions:

• We show that no privacy property in the literature characterises all anonymous graphs with respect to active attacks.

• We introduce a general definition of resistance to active attacks that can be used to analyse the actual resistance of a graph.

• We use the introduced privacy model to prove that k-symmetry, the strongest notion of anonymity against passive attacks, also protects against active attacks.

• Of independent interest is our proof that k-automorphism does not protect against active attacks. This is a surprising result, considering that k-automorphism and k-symmetry have traditionally been deemed as conceptually equivalent.

• We prove that the algorithm K-Match, devised to ensure a sufficient condition for k-automorphism, also guarantees k-symmetry.

• We provide empirical evidence on the effectiveness of K-Match as an anonymisation strategy against the strongest active attack reported in the literature, namely the robust active attack presented in [32], even when it leverages a large number of sybil nodes.

1.1 Structure of the paper

We discuss related work in Sect. 2 and describe our new probabilistic interpretation of the adversarial model for active re-identification attacks in Sect. 3. Then, we discuss the applicability of k-symmetry for modelling protection against active attackers in Sect. 4 and show in Sect. 5 that the algorithm K-Match efficiently provides a sufficient condition for k-symmetry. Finally, we empirically demonstrate the effectiveness of K-Match against the robust active attack from [32] in Sect. 6 and give our conclusions in Sect. 7.

2 Related work

In this paper, we focus on a particular family of properties for privacy-preserving publication of social graphs: those based on the notion of k-anonymity [43, 45]. These privacy properties depend on assumptions about the type of knowledge that a malicious agent, the adversary, possesses. According to this criterion, adversaries can be divided into two types. On the one hand, passive adversaries rely on information that can be collected from public sources, such as public profiles in online social networks, where a majority of users keep unmodified default privacy settings that pose no access restrictions on friend lists and other types of information. A passive adversary attempts to re-identify users in a published social graph by matching this information to the released data. On the other hand, active adversaries not only use publicly available information, but also attempt to interact with the real social network before the data is published, with the purpose of forcing the occurrence of unique structural patterns that can be retrieved after publication and used for learning sensitive information.

2.1 k-anonymity models against passive attacks

k-anonymity is based on a notion of indistinguishability between users in a dataset, which is used to create equivalence classes of users that are pairwise indistinguishable to the eyes of an attacker. Formally, given a symmetric, reflexive and transitive indistinguishability relation $\sim$ on the users of a graph G, G satisfies k-anonymity with respect to $\sim$ if and only if the equivalence class with respect to $\sim$ of each user in G has cardinality at least k.

Several graph-oriented notions of indistinguishably appear in the literature. For example, Liu and Terzi [25] consider two users indistinguishable if they have the same degree. Their model is known as k-degree anonymity and gives protection against attackers capable of accurately estimating the number of connections of a user. The notion of k-degree anonymity has been widely studied, and numerous anonymisation methods based on it have been proposed, e.g. [5, 6, 12, 26, 27, 39, 41, 48]. Zhou and Pei [53] assume a stronger attacker able to determine not only the connections of a user u, but also whether u’s friends (i.e. those users that u is connected to) are connected. This means that the adversary is assumed to know the induced subgraphs created by the users and their neighbours. It is simple to see that Zhou and Pei’s model, known as k-neighbourhood anonymity, is stronger than k-degree anonymity.

Another privacy notion that relies on the neighbourhood of a user is $(k, \ell )$-anonymity [16], introduced by Feder, Nabar and Terzi and later generalised by Stokes and Torra [44]. In $(k, \ell )$-anonymity, $\ell$ represents the number of neighbours two vertices ought to have to be considered indistinguishable. This indistinguishability relation is not transitive, though, making $(k, \ell )$-anonymity hard to compare with other privacy properties based on neighbourhood, such as k-degree anonymity and k-neighbourhood anonymity.

The notion of k-automorphism [54] was introduced with the goal of modelling the knowledge of any passive adversary. Two users u and v in a graph G are said to be automorphically equivalent, or indistinguishable, if $\varphi (u) = v$ for some automorphism $\varphi$ in G. The notion of k-automorphism ensures that every vertex in the graph is automorphically equivalent to $k-1$ other vertices. Although k-automorphism itself does not in general imply all other privacy properties (as we will show in Appendix A), the method proposed in [54] for enforcing the (stronger) k different matches principle does achieve this goal. Similar formulations of indistinguishability in terms of graph automorphisms were presented independently in the work on k-symmetry [50] and k-isomorphism [11]. While k-symmetry and k-automorphism have traditionally been viewed as equivalent, k-symmetry is actually stronger, and it does imply all other privacy properties for passive attacks. In this paper, we additionally show that, in the context of active attacks, k-symmetry always guarantees a 1/k upper bound on the re-identification probability for each vertex, which k-automorphism does not.

A natural trade-off between the strength of the privacy notions and the amount of structural disruption caused by the anonymisation methods based on them has been empirically demonstrated in [54]. The three privacy models described above form a hierarchy, which is displayed in the left branch of Fig. 1. Privacy models tailored to active attacks also form a hierarchy, displayed in the right branch of Fig. 1, which we describe next. Interrogation marks in Fig. 1 indicate that connections between properties tailored for passive attacks and those tailored for active attacks have not been established yet, neither directly nor via some additional property.

Fig. 1

A hierarchy of privacy properties. An arrow has the standard logical interpretation, i.e. $P \implies P'$ means that a graph satisfying P also satisfies $P'$. Left side: models for passive attacks. Right side: models for active attacks. Interrogation marks indicate connections that have not been established yet

2.2 k-anonymity models against active attacks

Backstrom et al. were the first to show the impact of active attacks in social networks back in 2007 [2]. Their attack has been optimised a number of times, see [32, 37, 38], and two privacy models particularly tailored to measure the resistance of social graphs to this type of attack have been recently proposed [31, 46]. The first of those models is $(k, \ell )$-anonymity, introduced in 2016 by Trujillo-Rasua and Yero [46]. They consider adversaries capable of re-identifying their own sets of sybil nodes in the anonymised graph. Adversaries are also assumed to know or able to estimate the distances of the victims to the set of sybil nodes. This last assumption was weakened later in [31] by restricting the adversary’s knowledge to distances between victims and sybil nodes of length one. That is, the adversary only knows whether the victim is connected to a sybil node. That restriction led to a weaker version of $(k, \ell )$-anonymity called $(k, \ell )$-adjacency anonymity, as displayed in Fig. 1.

It is worth pointing out the clash in terminology with the use of $(k, \ell )$-anonymity in [16] and [46]. Because this article focuses on active attacks, from now on whenever we write $(k, \ell )$-anonymity we are referring to the privacy model that captures the resistance of a graph to active attacks, i.e. to that introduced in [46].

There exist three anonymisation algorithms [30, 31, 33] that aim to create graphs satisfying $(k, \ell )$-(adjacency) anonymity. Their approach consists in determining a candidate set of sybil vertices in the original graph that breaks the desired anonymity property, and forcing via graph transformation that every vertex has a common pattern of connections with the sybil vertices shared by at least $k-1$ other vertices. A common shortcoming of these methods is that they only provide formal guarantees against attackers leveraging a very small number of sybil nodes (no more than two). This limitation seems to be an inherent shortcoming of the entire family of properties of which $(k,\ell )$-anonymity and $(k,\ell )$-adjacency anonymity are members. Indeed, for large values of $\ell$, which are required in order to account for reasonably capable adversaries, anonymisation methods based on this type of property face the problem that any change introduced in the original graph to render one vertex indistinguishable from others, in terms of its distances to a vertex subset, is likely to render this vertex unique in terms of its distances to other vertex subsets.

2.3 Other privacy models

For the sake of completeness, we finish this brief literature review by surveying probabilistic privacy models. A popular example is differential privacy (DP) [13], a semantic privacy notion which, instead of anonymising the dataset, focuses on the methods accessing the sensitive data and provides a quantifiable privacy guarantee against an adversary who knows all but one entry in the dataset. In the context of graph data, the notion of two datasets differing by exactly one entry can have multiple interpretations, the two most common being edge-differential privacy and vertex-differential privacy. While a number of queries, e.g. degree sequences [18, 22] and subgraph counts [21, 52], have been addressed under (edge-)differential privacy, the use of this notion for numerous very basic queries, e.g. graph diameter, remains a challenge. Recently, differentially private methods leveraging the randomised response strategy for publishing a graph’s adjacency matrix were proposed in [42]. While these methods do not necessarily view vertex ids as sensitive, data holders whose goal in preventing re-identification attacks is to prevent the adversary from learning the existence of relations may view this approach as an alternative to k-anonymity-based methods. Another DP-based alternative to k-anonymity-based methods consists in learning the parameters of a graph generative model under differential privacy and then using this model to publish synthetic graphs that resemble the original one in some structural properties [10, 20, 34, 40, 49, 51].

Random perturbation for graph privacy has been used prior the introduction of differential privacy [7]. For example, within the context of passive attacks, Bonchi et al. [4] introduced a method that randomly removes and adds edges to the original graph. The anonymity level offered by their approach is evaluated against an information-theoretic measure that considers the uncertainty added to the original graph. We observe that randomisation techniques have not been successfully adapted to counteract active attacks. While intuition suggests that the task of re-identification becomes harder for the adversary as the amount of random noise added to a graph grows, it has been shown in [32] that active attacks can be made robust against reasonably large amounts of random perturbation.

Other probabilistic privacy models rely on the notion of adversary’s prior belief, defined as a probability distribution on sensitive values. For example, t-closeness [24] measures attribute protection in terms of the distance between the distribution of sensitive values in the anonymised dataset with respect to the distribution of sensitive attribute values in the original table. Such definition of prior belief is different to other works, such as $(\rho _1, \rho _2)$-privacy [15] and $\epsilon$-privacy [28], where prior belief represents the adversary’s knowledge in the absence of knowledge about the dataset. In either case, estimating the prior belief of the adversary is challenging, as discussed in [13].

2.4 Concluding remarks

As illustrated in Fig. 1, the development of k-anonymity models against passive and active attacks has been traditionally split and had no apparent intersection. This article provides, to the best of our knowledge, the first connection between the two developments. This is achieved by introducing a probabilistic model for active attacks that characterises all graphs that resists active attacks, of which k-symmetry and $(k,\ell )$-anonymity are proven to be sufficient, yet not necessary, conditions.

3 Probabilistic adversarial model

Our adversarial model is a generalisation of the model introduced in [32], which captures the capabilities of an active attacker and allows one to analyse the resistance of anonymisation methods to active attacks. Such analysis is expressed as a three-step game between the attacker and the defender. In the first step, the attacker is allowed to interact with the network, insert sybil accounts and establish links with other users (called the victims). The defender uses the second step to anonymise and perturb the network, which was previously manipulated by the attacker. Lastly, the attacker receives the anonymised network and makes a guess on the pseudonyms used to anonymise the victims. Each of these steps is formalised in what follows.

3.1 Attacker subgraph creation

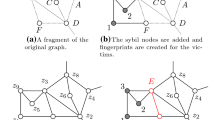
The attacker–defender game starts with a graph $G=(V,E)$ representing a snapshot of a social network, as in Fig. 2a. The attacker knows a subset of the users, called the victims and denoted I, but not the connections between them. The attacker is allowed to insert a set of sybil nodes S into G and establish connections with their victims.

This step of the attack transforms the original graph $G=(V,E)$ into a graph $G^{+}=(V', E')$ satisfying the following two properties: i) $V' = V \cup S$ and ii) $E' \setminus E \subseteq (S\times S) \cup (S\times I) \cup (I \times S)$. The second condition says that relations established by the adversary are constrained to the set of sybil and victim nodes. We call the resulting graph $G^{+}$ the sybil-extended graph of G. An example of a sybil-extended graph is depicted in Fig. 2b.

The attacker does not know the entire graph $G^{+}$, unless the original graph was empty. The adversary knows, however, the subgraph formed by the set of sybil nodes S, their connections to the victims, and the victim set I. This notion of adversary knowledge is formalised next.

Definition 1

(Adversary knowledge) Let $G = (V, E)$ be an original graph and $G^{+}=(V \cup S, E')$ the sybil-extended graph created by an adversary that targets a set of victims $I \subseteq V$. The adversary knowledge is defined as the subgraph $G_{S, I}$ of G defined by

$$\begin{aligned} G_{S, I} = (S \cup I, \{(u,v)\in E \mid \{u, v\} \subseteq S \cup I \wedge \{u, v\} \not \subseteq I\}) \end{aligned}$$

Fig. 2

An active re-identification attack viewed as an attacker–defender game

Note that connections between victims are not part of the adversary knowledge.

3.2 Pseudonymisation and perturbation

When the defender decides to publish the graph $G^{+}$, she pseudonymises it by replacing the real user identities with pseudonyms. That is to say, the defender obtains $G^{+}$ and constructs an isomorphism $\varphi$ from $G^{+}$ to $\varphi G^{+}$. An isomorphism between two graphs $G=(V,E)$ and $G'=(V',E')$ is a bijective function $\varphi :V \rightarrow V'$, such that $\forall v_1,v_2\in V :(v_1,v_2)\in E \iff (\varphi (v_1),\varphi (v_2))\in E'$. Two graphs are isomorphic, denoted by $G\simeq _{\varphi } G'$, or briefly $G\simeq _{} G'$, if there exists an isomorphism $\varphi$ between them. Given a subset of vertices $S \subseteq V$, we will often use $\varphi S$ to denote the set $\{\varphi (v) | v \in S\}$. In Fig. 2c, we illustrate a pseudonymisation of the graph in Fig. 2b.

We call $\varphi G^{+}$ the pseudonymised graph. Pseudonymisation serves the purpose of removing personally identifiable information from the graph. Because pseudonymisation is insufficient to protect a graph against re-identification, the defender is also allowed to perturb the graph. This is captured by a non-deterministic procedure $t$ that maps graphs to graphs. The procedure t modifies $\varphi G^{+}$, resulting in the transformed graph $t(\varphi G^{+})$. We assume that $t(\varphi G^{+})$ is ultimately made available to the public, hence it is known to the adversary.

3.3 Re-identification

The last step of the attacker–defender game is where the attacker analyses the published graph $t(\varphi G^{+})$ to re-identify her own sybil accounts and the victims (see Fig. 2d). This allows her to acquire new information, which was supposed to remain private, such as the fact that E and F are friends.

We define the output of the adversary re-identification attempt as a mapping $\rho$ from the set of vertices $S \cup I$ to the set of vertices in $t(\varphi G^{+})$. This represents the adversary’s belief on the pseudonyms used to anonymise the attacker and victim vertices in $t(\varphi G^{+})$. To account for uncertainty on the adversary’s belief, we consider that the adversary assigns a probability value $p(\rho )$ to each mapping, denoting the probability that the adversary chooses $\rho$ as the output of the re-identification attack. Let $\varPhi _{S,I}$ be the universe of mappings from the set of vertices in $S \cup I$ to the set $t(\varphi G^{+})$. The law of total probability allows us to quantify the adversary’s probability of success in re-identifying one victim as follows.

Proposition 1

Let $G = (V, E)$ be an original graph, $G^{+}=(V \cup S, E')$ the sybil-extended graph created by an adversary that targets a set of victims $I \subseteq V$, and $t(\varphi G^{+})$ the anonymised version of $G^{+}$ created by the defender. Then, the probability $A_{t(\varphi G^{+})}^{S,I}(u)$ that the adversary successfully re-identifies a victim $u \in I$ in $t(\varphi G^{+})$ is

$$\begin{aligned} A_{t(\varphi G^{+})}^{S,I}(u) = \sum _{\rho \in \varPhi _{S,I}, \rho (u) = \varphi (u)} p(\rho ). \end{aligned}$$

(1)

In our analyses, we restrict the function $p$ to be a probability distribution on the domain $\varPhi _{S,I}$, i.e. $\sum _{\rho \in \varPhi _{S,I}} p(\rho ) = 1$. We also assume that $p$ satisfies the standard random worlds assumption enunciated in [8, 29], which expresses that, in the absence of any information in addition to $t(\varphi G^{+})$, any two isomorphic subgraphs in $t(\varphi G^{+})$ are indistinguishable for the adversary. We enunciate the random worlds assumption next, adapting the terminology to the one used in this paper.

Assumption 1

(Random worlds assumption [8, 29]) Let $G = (V, E)$ be an original graph, $G^{+}=(V \cup S, E')$ the sybil-extended graph created by an adversary that targets a set of victims $I \subseteq V$, and $G' = t(\varphi G^{+})$ the anonymised version of $G^{+}$ created by the defender. Let $\rho _1$ and $\rho _2$ be two bijective functions from $S\cup I$ to the set of vertices $V_{G'}$ in $G'$. Let $G'_{\rho _1 S, \rho _1 I}$ and $G'_{\rho _2 S, \rho _2 I}$ be the two attacker subgraphs in $G'$ that correspond to the adversary’s guesses $\rho _1$ and $\rho _2$, respectively. If $G'_{\rho _1 S, \rho _1 I}$ and $G'_{\rho _2 S, \rho _2 I}$ are isomorphic, then $p(\rho _1) = p(\rho _2)$.

In the remainder of this article, we will analyse the effectiveness of various anonymisation procedures by calculating the success probability of the adversary based on Proposition 1, and we will often resort to Assumption 1 when reasoning about the adversary’s belief $\rho$.

4 Applicability of current privacy properties against active attacks

In this section, we make, to the best of our knowledge, the first connection between passive and active attacks by formally proving that k-symmetry provides protection against active attacks. We also prove that k-symmetry is incomplete, just like $(k, \ell )$-anonymity, in the sense that none of them characterises all anonymous graphs with respect to active attacks. Last, but not least, we show that neither k-symmetry implies $(k, \ell )$-anonymity, nor the other way around.

4.1 k-symmetry: an effective privacy model against active attacks

We use the introduced privacy model to prove that k-symmetry, the strongest notion of anonymity against passive attacks, also protects against active attacks.

Definition 2

(k-symmetry [50]) Let $\varGamma _G$ be the universe of automorphisms in G. Two vertices u and v in G are said to be automorphically equivalent, denoted $u \cong v$, if there exists an automorphism $\gamma \in \varGamma _G$ such that $\gamma (u) = v$. Because the relation $\cong _{}$ is an equivalence relation in the set of vertices of G, let $[u]_{\cong }$ be the equivalence class of u. G is said to satisfy k-symmetry if for every vertex u it holds that $|[u]_{\cong }| \ge k$.

Theorem 1

Let $G' = (V', E')$ be an original graph, $G^{+}=(V' \cup S, E')$ the sybil-extended graph created by an adversary that targets a set of victims $I \subseteq V'$, and $t(\varphi G^{+})= (V, E)$ the anonymised version of $G^{+}$ created by the defender. If $t(\varphi G^{+})$ satisfies k-symmetry, then for every vertex $u \in I$ the probability of the adversary guessing the output of $\varphi (u)$ is lower than or equal to 1/k.

Proof

Let G be a shorthand notation for $t(\varphi G^{+})$. Let $\varPhi _{S,I}$ be the universe of mappings from the set of vertices in $S \cup I$ to the set of vertices in G. We define a relation $\sim$ between adversary’s guesses in $\varPhi _{S,I}$ by

$$\begin{aligned}\rho \sim \rho ' \iff G_{\rho S, \rho I} \simeq _{} G_{\rho ' S, \rho ' I} \end{aligned}$$

Because $\simeq _{}$ is an equivalence relation, it follows that $\sim$ is also an equivalence relation. We use $\varPhi _{S,I}/{\sim }$ to denote the partition of $\varPhi _{S,I}$ into the set of equivalence classes with respect to $\sim$, and $[\rho ]_{\sim }$ to denote the equivalence class containing $\rho$. Consider, given a victim u, a successful adversary guess $\rho _0 \in \varPhi _{S,I}$, i.e. a mapping satisfying that $\rho _0(u) = \varphi (u)$. Our first proof step is about showing that there exist $k-1$ other mappings $\rho _1, \ldots , \rho _{k-1}$ in $[\rho ]_{\sim }$ satisfying that

$$\begin{aligned} \forall i, j \in \{0, \ldots , k-1\} :i \ne j \implies \rho _i(u) \ne \rho _j(u) \text {.} \end{aligned}$$

(2)

Let $\rho _0(u) = v$. Because G satisfies k-symmetry, it follows that there exist $k-1$ different vertices $\{v_1, \ldots , v_{k-1}\}$ that are automorphically equivalent to v. That is to say, there exist $k-1$ automorphisms $\gamma _1, \ldots , \gamma _{k-1}$ in $\varGamma _G$ such that $\forall i \in \{1, \ldots , k-1\} :\gamma _i(v) = v_i \ne v$. Now, consider the mappings $\rho _i:S \cup I \rightarrow S_i \cup I_i$ defined by $\rho _i = \gamma _i \circ \rho _0$, for every $i \in \{1, \ldots , k-1\}$. On the one hand, given that $\gamma _1, \cdots , \gamma _{k-1}$ are automorphisms, it follows that $G_{S_0, I_0} \simeq _{\gamma _i} G_{S_i, I_i}$, for every $i \in \{1, \ldots , k-1\}$, which implies that $\rho _0 \sim \rho _i$. On the other hand, $\rho _i(u) = u_i \ne u_j = \rho _j(u)$ for every $i \ne j \in \{0, \ldots , k-1\}$. This allows us to conclude that $\rho _0, \ldots , \rho _{k-1}$ are pairwise different and that $\{\rho _0, \ldots , \rho _{k-1}\} \subseteq [\rho ]_{\sim }$.

Our second proof step consists of showing that, given two mappings $\rho _0$ and $\rho _0'$ in $\varPhi _{S,I}$ such that $\rho _0(u) = \rho _0'(u) = v$, and the mappings $\{\rho _1, \ldots , \rho _{k-1}\}$ and $\{\rho _1', \ldots , \rho _{k-1}'\}$ constructed as previously, it holds that

$$\begin{aligned} \rho _0 \ne \rho _0' \implies \rho _i \ne \rho _j' \ \forall i, j \in \{1, \ldots , k-1\} \text {.} \end{aligned}$$

Let $x \in S \cup I$ such that $\rho _0(x) \ne \rho _0'(x)$. Take any two integers $i, j \in \{1, \ldots , k-1 \}$. We analyse two cases.

Case 1 $(i = j)$. Let $\rho _0(x) = y$ and $\rho _0'(x) = y'$. By construction, $\rho _i(x) = \gamma _i(\rho _0(x)) = \gamma _i(y)$ and $\rho _i'(x) = \gamma _i(\rho _0'(x)) = \gamma _i(y')$. The fact that $\gamma _i$ is a bijective function and that $y \ne y'$ gives that $\gamma _i(y) \ne \gamma _i(y')$, which implies that $\rho _i \ne \rho _i'$.

Case 2 $(i \ne j)$. Observe that $\rho _i(u) = \gamma _i(\rho _0(u)) = \gamma _i(v) = v_i$ and $\rho _j'(u) = \gamma _j(\rho _0'(u)) = \gamma _j(v) = v_j$. Because $v_i \ne v_j$ it follows that $\rho _i(u) \ne \rho _j'(u)$, hence $\rho _i \ne \rho _j'$.

The last proof step consists of using the formula to calculate adversary success to obtain a probability bound. The adversary’s probability of success in re-identifying a victim $u \in I$ is calculated by,

$$\begin{aligned} \sum _{\rho \in \varPhi _{S,I}, \rho (u) = \varphi (u)} p(\rho ). \end{aligned}$$

Let $\rho _1^0, \ldots , \rho _n^0$ be all functions in $\varPhi _{S,I}$ satisfying $\rho _1^0(u) = \rho _2^0(u) = \cdots = \rho _n^0(u) = \varphi (u)$. It follows that the probability of success of the adversary is equal to $p(\rho _1^0) + \cdots + p(\rho _n^0)$. Now, for each $\rho _i$, consider the mappings $\rho _i^1, \ldots , \rho _i^{k-1}$ defined by $\rho _i^j = \varphi _j \circ \rho _i^0$, for every $j \in \{1, \ldots , k-1\}$. Previously we proved the following two intermediate results.

• 1. For every $i \in \{1, \ldots , n\}$, the set $\{\rho _i^0, \rho _i^1, \ldots , \rho _i^{k-1}\} \subseteq \varPhi _{S,I}$ has cardinality k and its elements satisfy $\rho _i^0 \sim \rho _i^1 \sim \ldots \sim \rho _i^{k-1}$.

• 2. $\forall i, j \in \{1, \ldots , n\} \implies \{\rho _i^0, \rho _i^1, \ldots , \rho _i^{k-1}\}\cap \{\rho _j^0, \rho _j^1, \ldots , \rho _j^{k-1}\} = \emptyset$.

The second result and the fact that $p$ is a probability distribution give,

$$\begin{aligned} \sum _{i \in \{1, \ldots , n\}} \sum _{j \in \{0, \ldots , k-1\}} p(\rho _i^j) \le 1 \text {.} \end{aligned}$$

We use the first result and the random worlds assumption (Proposition 1) to conclude that $p(\rho _i^0) = p(\rho _i^1) = \cdots = p(\rho _i^{k-1})$, for every $i \in \{1, \ldots , n\}$, which gives,

$$\begin{aligned} \sum _{i \in \{1, \ldots , n\}} \sum _{j \in \{0, \ldots , k-1\}} p(\rho _i^j) = \sum _{i \in \{1, \ldots , n\}} k p(\rho _i^0) \le 1 \text {.} \end{aligned}$$

The last inequality states that $p(\rho _1^0) + \cdots + p(\rho _n^0) \le 1/k$. $\square$

4.2 k-symmetry versus $(k, \ell )$-anonymity

As proven in Theorem 1, k-symmetry provides protection against active attacks regardless of the number of sybil nodes inserted by the attacker, as opposed to $(k, \ell )$-anonymity which uses $\ell$ as a parameter on the maximum number of sybil nodes. In spite of that, $(k, \ell )$-anonymity is not weaker than k-symmetry. As we prove next, they are in fact incomparable.

Theorem 2

Let $\mathcal {G}_{k, \ell }$ be the universe of anonymised graphs such that no adversary with $\ell$ sybil nodes or less can re-identify a victim with probability lower or equal than 1/k. There exist $k > 1$ and graphs $G, G', G'' \in \mathcal {G}_{k, \ell }$ such that:

• G satisfies k-symmetry, but G does not satisfy $(k, \ell )$-anonymity for some $\ell \ge 1$.

• $G'$ satisfies $(k, \ell )$-anonymity for some $\ell \ge 1$, but $G'$ does not satisfy k-symmetry.

• $G''$ neither satisfy k-symmetry nor $(k, \ell )$-anonymity for some $\ell \ge 1$.

Proof

Figure 3a shows a 2-symmetric graph G which, for $2\le \ell \le 8$, does not satisfy $(k,\ell )$-anonymity for any $k>1$. Moreover, Fig. 3b shows a (2, 1)-anonymous graph $G'$ which can be verified not to satisfy k-symmetry for any $k>1$. In fact, this graph even fails to satisfy k-degree anonymity for any $k>1$. An example of a graph $G''$ proving the correctness of the last statement is displayed in Fig. 3c. That graph is neither 2-symmetric nor (2, 2)-anonymous. $\square$

Fig. 3

Example graphs. a A 2-symmetric graph not satisfying $(k,\ell )$-anonymity for $k>1$ and $2\le \ell \le 8$. b A (2, 1)-anonymous graph not satisfying k-symmetry for $k>1$. c A graph where the success probability of any active attack leveraging 2 sybil nodes is at most 1/2, despite the graph neither satisfying (2, 2)-anonymity nor 2-symmetry

Of independent interest is our proof that k-automorphism [54] does not protect against active attacks. This is a surprising result, given that k-automorphism and k-symmetry have traditionally been considered equivalent. We refer the interested reader to Appendix A.

5 Algorithm K-Match guarantees k-symmetry

In this section we prove that the algorithm K-Match, proposed in [54] as a sufficient condition to achieve k-automorphism, also guarantees k-symmetry. Given a graph G and a value of k, the K-Match algorithm obtains a supergraph $G'$ of G satisfying the following conditions:

• 1. $V_{G'}\supseteq V_G$ and $E_{G'}\supseteq E_G$.

• 2. There exist $k-1$ automorphisms $\gamma _1, \gamma _2, \ldots , \gamma _{k-1}$ of $G'$ such that:

  • (a) For every $v\in V_{G'}$ and every $i\in \{1,\ldots ,k-1\}$, $\gamma _i(v)\ne v$.

  • (b) For every $v\in V_{G'}$ and every $i,j\in \{1,\ldots ,k-1\}$, $i\ne j \Longleftrightarrow \gamma _i(v)\ne \gamma _j(v)$.

  • (c) For every $v\in V_{G'}$ and every i, j such that $1\le i<j\le k-1$, $\gamma _{i+j}(v)=\gamma _i(\gamma _j(v))=\gamma _j(\gamma _i(v))$, with addition taken modulo k.

To obtain $G'$, the algorithm first splits the vertices of $G'$ into k groups and arranges them in a k-column matrix M called the vertex alignment table (VAT for short). If $|V_G|$ is not a multiple of k, a number of dummy vertices are added to achieve this property. The VAT is organised in such a manner that the number of graph editions to perform in the second step of the process is close to the minimum. For convenience, in what follows we will denote by $v_{ij}$ the vertex of $G'$ placed in position $M_{ij}$ of the VAT. The second step of the method consists in adding edges to $E_{G'}$ in such a way that conditions 2.a to 2.c are enforced. To that end, for every edge $(v_{ij},v_{pq})$, all edges of the form $(v_{i,j+t},v_{p,q+t})$, additions modulo k, are added to $E_{G'}$ if they did not previously exist.

Figure 4 shows an example of a VAT allowing to enforce 3-automorphism on the graph of Fig. 2b². This VAT encodes two functions $f_1,f_2:V_{G'}\rightarrow V_{G'}$:

$$\begin{aligned} f_1=\{(1,F),(F,D),(D,1),(C,A),(A,B),(B,C),(2,3),(3,E),(E,2)\}, \end{aligned}$$

that is, a function such that the image of every element is the one located one column to its right (modulo 3) on the same row, and

$$\begin{aligned} f_2=\{(1,D),(F,1),(D,F),(C,B),(A,C),(B,A),(2,E),(3,2),(E,3)\}, \end{aligned}$$

that is, a function such that the image of every element is the one located two columns to its right (modulo 3) on the same row.

Fig. 4

An example of a VAT for the graph shown in Fig. 2b

In general, these functions are not automorphisms of $G'$ upon creation of the VAT. It is the second step of the method that will transform them into automorphisms by performing all necessary edge-copying operations. For example, the edge (C, A) needs to be added to $G'$ because $(A,B)\in E_G$ but $(f_2(A),f_2(B))=(C,A)\notin E_G$; and (A, 3) needs to be added because $(B,E)\in E_G$ but $(f_2(B),f_2(E))=(A,3)\notin E_G$. Once the method is executed, each automorphism $\gamma _t$, $t\in \{1,\ldots ,k-1\}$, defined in item 2 above is completely specified by the VAT, as $\gamma _t(v_{ij})=v_{i,j+t}$, with addition modulo k, for every $i\in \left\{ 1,\ldots ,\left\lceil \frac{|V_G|}{k}\right\rceil \right\}$ and every $j\in \{1,\ldots ,k\}$.

We now show the link between the K-Match method and k-symmetry.

Theorem 3

Let $G=(V,E)$ be a graph and let $G'=(V',E')$ the result of applying algorithm K-Match to G for some parameter k. Then, $G'$ satisfies k-symmetry.

Proof

Let $u\in V_{G'}$ be an arbitrary vertex of $G'$, and let $v_1=\gamma _1(u)$, $v_2=\gamma _2(u)$, ..., $v_{k-1}=\gamma _{k-1}(u)$ be the images of u by the automorphisms $\gamma _1, \gamma _2, \ldots , \gamma _{k-1}$ enforced on $G'$ by the execution of K-Match. By definition, we have that $u \cong v_1 \cong v_2 \cong \ldots \cong v_{k-1}$ and, by conditions 2.a and 2.b, they are pairwise different. Thus, $\left| [u]_{\cong }\right| =k$, hence $G'$ is k-symmetric. $\square$

The most relevant consequence of Theorem 3 is that algorithm K-Match can also be used for protecting graphs against active adversaries, as it will ensure that no victim is re-identified with probability greater than 1/k.

6 Experiments

The purpose of these experiments³ is to demonstrate the effectiveness and usability of k-symmetry, enforced using the K-Match algorithm, for protecting graphs against active adversaries leveraging a sufficiently large number of sybil nodes and the strongest attack strategy reported in the literature, namely the robust active attack introduced in [32]. Effectiveness is assessed in terms of the success rate measure used in previous works on active attacks [30,31,32], whereas usability is assessed in terms of several structural utility measures. In what follows, we describe the experimental setting, display the empirical results obtained and conclude the section with a discussion of these results.

6.1 Experimental setting

In order to make the results reported in this section comparable to previous works on active attacks and countermeasures against them [31, 32], we study the behaviour of our proposed method on two collections of randomly generated synthetic graphs and two real-life datasets. For the first collection of synthetic graphs, we used Erdős–Rényi (ER) random graphs [14]. We generated 200, 000 ER graphs, 10, 000 for each density value in the set $\{0.1, 0.15, \ldots , 0.95, 1.0\}$. The second group of synthetic graphs was generated according to the Barabási–Albert (BA) model [3], which generates scale-free graphs. We used seed graphs of order 50 and every graph was grown by adding 150 vertices and performing the corresponding edge additions. The BA model has a parameter m defining the number of new edges added for every new vertex. We generated 10, 000 graphs for every value of m in the set $\{5, 10, \ldots , 50\}$. In generating each graph, the type of the seed graph was randomly selected among the following choices: a complete graph, an m-regular ring lattice, or an ER random graph of density 0.5. The probability of selecting each choice was set to $\frac{1}{3}$. In both cases, the generated synthetic graphs have 200 nodes. Based on the discussion on the plausible number of sybil nodes in Sect. 3, we make the number of sybils $\ell =\lceil \log _2 200\rceil =8$.

The first real-life social graph used in the experiments is the so-called Panzarasa graph, named after one of its creators [36]. This graph was collected from an online community of students at the University of California, Irvine. In the Panzarasa graph, a directed edge (A, B) represents that student A sent at least one message to student B. In our experiments, we used a processed version of this graph, where edge orientation, loops and isolated vertices were removed. This graph has 1, 893 vertices and 20, 296 edges. The second real-life social graph that we used was constructed from a collection of e-mail messages exchanged between students, professors and staff at Universitat Rovira i Virgili (URV), Spain [17]. For the construction of the graph, the data collectors added an edge between every pair of users that messaged each other. In doing so, they ignored group messages with more than 50 recipients. Moreover, they removed isolated vertices and connected components of order 2. The URV graph has 1, 133 vertices and 5, 451 edges. For both real-life graphs, we set the number of sybil nodes to be $\ell =\lceil \log _2 \vert V\vert \rceil =11$.

We analyse three values for the privacy parameter k: a low value, $k=2$; a high value, $k=8$; and an intermediate value, $k=5$. For every value of k, we compare the behaviour of the K-Match algorithm, which ensures k-symmetry, and several other anonymisation methods. We consider Mauw et al.’s algorithm for enforcing $(k,\varGamma _{G,1})$-adjacency anonymity [31], which explicitly addresses active adversaries and has demonstrated effectiveness in some instances of the active attack scenario [31, 32]. Additionally, to enrich the comparison, we included perturbation methods devised in terms of other privacy notions, namely the edge-addition method proposed in [25] for enforcing k-degree anonymity (for $k\in \{2,5,8\}$) and the edge-set perturbation method proposed in [42] for enforcing $\varepsilon$-differential privacy (for $\varepsilon \in \{0.1, 0.5, 1.0\}$).

In order to build the vertex alignment table, algorithm K-Match requires the vertex set of the input graph to be partitioned into k subsets such that the number of edges linking vertices in different subsets is close to the minimum. We used the multilevel k-way partitioning method reported in [23], in specific its implementation included in the METIS library⁴, for efficiently obtaining such a partition. The effectiveness of the anonymisation methods is measured in terms of their resistance to the robust active attack described in [32]. Thus, following the attacker–defender game described in Sect. 3, for every graph we first run the attacker subgraph creation stage. Then, for every resulting graph, we obtain all variants of anonymised graphs. Finally, for each perturbed graph, we simulate the execution of the re-identification stage and compute its success rate as defined in [32], that is

$$\begin{aligned} SuccessRate=\left\{ \begin{array}{ll} \frac{\sum _{X\in \mathcal {X}} p_{X}}{|\mathcal {X}|} &{}\quad \text {if }\mathcal {X}\ne \emptyset \\ 0&{}\quad \text {otherwise} \end{array} \right. \end{aligned}$$

(3)

where $\mathcal {X}$ is the set of equally-most-likely sybil subgraphs retrieved in $t(\varphi G^{+})$ by the third phase of the attack, and

$$\begin{aligned} p_{X} =\left\{ \begin{array}{ll} \frac{1}{|\mathcal {Y}_{X}|} \quad &{} \quad \text {if} \quad Y \in \mathcal {Y}_{X}\\ 0 \quad &{} \quad \text {otherwise} \end{array} \right. \end{aligned}$$

with $\mathcal {Y}_{X}$ containing all equally-most-likely fingerprint matchings according to X. For the collections of synthetic graphs, in order to obtain the scores used for the comparisons, we computed for every method the average of the success rates over every group of 10, 000 graphs sharing the same set of parameter choices. In the case of real-life graphs, we executed, for each perturbation method, 20 runs on the Panzarasa graph and 400 runs on the URV graph. In each of these runs, a different set of victims was randomly chosen. The final scores used for comparisons were the averaged success probabilities over every group of runs.

The anonymisation methods are also compared in terms of utility. To that end, we measure the distortion caused by each method on a number of global graph statistics, namely the global clustering coefficient, the averaged local clustering coefficient and the similarity between the degree distributions, measured in terms of the cosine of the angle between the degree vectors, following the approach introduced in [19, 30].

Fig. 5

Success rates of the robust active attack on the collections of Erdős–Rényi (left) and Barabási–Albert (right) random graphs, with $\ell =8$ and $k\in \{2,5,8\}$

Fig. 6

Degree distribution similarities on the collections of Erdős–Rényi (left) and Barabási–Albert (right) random graphs, with $\ell =8$ and $k\in \{2,5,8\}$

6.2 Results and discussion

Figure 5 shows the success rates of the attack on both random graph collections, whereas Figs. 6, 7 and 8 show utility values in terms of degree distribution similarity, variation of global clustering coefficient and variation of averaged local clustering coefficient, respectively. Analogous results on the real-life datasets are presented in Tables 1 and 2.

Regarding the effectiveness of the anonymisation methods, the results in Fig. 5 and both tables clearly show that K-Match is considerably more effective against the robust active attack than $(k,\varGamma _{G,1})$-adjacency anonymity. These results are particularly relevant in the light of the fact that $(k,\varGamma _{G,1})$-adjacency anonymity was until now the sole formal privacy property to demonstrate non-negligible protection against the original active attack and some instances of the robust active attack [31, 32]. As expected, these results show that K-Match consistently outperforms the formally weaker k-degree anonymity, displaying in most cases a significant difference. Finally, we can see that, for sufficiently large values of k, algorithm K-Match and edge-set perturbation-based differential privacy are both effective against the robust active attack. It is worth highlighting that the experiments shown here are the first ones where the robust active attack leveraging $\lceil \log _2 n \rceil$ sybil nodes is shown to be consistently thwarted by anonymisation methods based on formal privacy properties. So far, this had only been achieved in [32] via the addition of random noise, with the limitation that this work used no principled approach in determining the amount of noise to use.

Regarding utility, there is a number of scenarios where the strong protection offered by K-Match is obtained at a smaller cost than that of DP, notably for low-density and scale-free synthetic graphs, as well as both real-life graphs. Both K-Match and $(k,\varGamma _{G,1})$-adjacency anonymity have a small impact on the overall similarities of the degree distributions. This does not mean that the degrees are not affected by the methods. In fact, both methods make most degrees increase, but in a manner that does not significantly affect the ordering of vertices in terms of their degrees. Regarding clustering coefficient-based utilities, we can observe in Figs. 7 and 8, and both tables, that the superior effectiveness of K-Match and DP does come at the price of a larger degradation of the values of local and global clustering coefficients, although the scenarios where each method is the best differ from one method to the other. It is worth highlighting that K-Match considerably outperforms DP in terms of most utility criteria on both real-life datasets.

In our opinion, the main takeaway from the experimental results presented in this section is that our refinement of the notion of re-identification probability for active adversaries has led to identifying, for the first time, an anonymisation method satisfying two key properties: (i) featuring a theoretically sound privacy guarantee against active attackers and (ii) having this privacy guarantee translate into effective resistance to the strongest active attack reported so far, even when the attacker leverages a large number of sybil nodes.

Fig. 7

Variations in global clustering coefficients on the collections of Erdős–Rényi (left) and Barabási–Albert (right) random graphs, with $\ell =8$ and $k\in \{2,5,8\}$

Fig. 8

Variations in averaged local clustering coefficients on the collections of Erdős–Rényi (left) and Barabási–Albert (right) random graphs, with $\ell =8$ and $k\in \{2,5,8\}$

7 Conclusions

We have introduced a new probabilistic interpretation of active re-identification attacks on social graphs. This enables the privacy-preserving publication of social graphs in the presence of active adversaries by jointly preventing the attacker from unambiguously retrieving the set of sybil nodes, and from using the sybil nodes for re-identifying the victims. Under the new formulation, we have shown that the privacy property k-symmetry provides a sufficient condition for the protection against active re-identification attacks. Moreover, we have shown that a previously existing efficient algorithm, K-Match, provides a sufficient condition for ensuring k-symmetry. Through a series of experiments, we have demonstrated that our approach allows, for the first time, to publish anonymised social graphs with formal privacy guarantees that effectively resist the robust active attack introduced in [32], which is the strongest active re-identification attack reported in the literature, even when it leverages a large number of sybil nodes.

Table 1 Results on the Panzarasa dataset

Table 2 Results on the URV dataset

The active adversary model addressed in this paper assumes that the (inherently dynamic) social graph is published only once. A more general scenario, where snapshots of a dynamic social network are periodically published in the presence of active adversaries, has recently been proposed in [9], and the robust active attack from [32] has been adapted to benefit from this scenario. Our main direction for future work consists in leveraging our methodology to propose anonymisation methods suited for this new publication scenario.

Appendix

It is claimed in [54] that every vertex v of a k-automorphic graph (see Definition 3) is structurally indistinguishable from $k-1$ other vertices $\varphi _1(v),\varphi _2(v),\ldots ,\varphi _{k-1}(v)$.

Definition 3

(k-automorphism [54]) An automorphism is an isomorphism from a graph to itself. Formally, an automorphism $\gamma$ within a graph $G=(V,E)$ is a bijective function $\gamma :V \rightarrow V$, such that $\forall v_1,v_2\in V :(v_1,v_2)\in E \iff (\gamma (v_1),\gamma (v_2))\in E$. A graph G is said to be k-automorphic if there exist $k-1$ non-trivial automorphisms $\varphi _1, \varphi _2, \ldots , \varphi _{k-1}$ of G such that $\varphi _i(v)\ne \varphi _j(v)$ for every $v\in V_G$ and every pair i, j satisfying $1\le i<j\le k-1$.

Fig. 9

A graph counterexample showing that k-automorphism does not achieve the intended privacy protection

However, a missing condition in Definition 3, namely requiring every $\varphi _i$ to satisfy $\varphi _i(v)\ne v$, invalidates this claim. Consider the graph shown in Fig. 9. This graph satisfies k-automorphism as defined in Definition 3, as can be verified by the existence of the non-trivial automorphism $\gamma =\{(v_1,v_5), (v_2, v_6), (v_3, v_4), (u,u)\}$, yet the graph is vulnerable even to the simplest structural attack, the degree-based attack, as vertex u is the sole vertex with degree 2. It is worth noting that this limitation of k-automorphism does not necessarily invalidate existing anonymisation methods. This is exemplified by the K-Match algorithm itself, which does provide the intended protection because the property it directly enforces is the so-called k different matches principle (see [54]), which in turn is not equivalent to k-automorphism, but stronger.