Abstract
Suppose we are given a discrete-valued time series \(X \) of observed events and an equally long binary sequence \(Y \) that indicates whether something of interest happened at that particular point in time. We consider the problem of mining serial episodes, sequential patterns allowing for gaps, from \(X \) that reliably predict those interesting events. With reliable we mean patterns that not only predict that an interesting event is likely to follow, but in particular that we can also accurately tell how how long until that event will happen. In other words, we are specifically interested in patterns with a highly skewed distribution of delays between pattern occurrences and predicted events. As it is unlikely that a single pattern can explain a complex real-world progress, we are after the smallest, least redundant set of such patterns that together explain the interesting events well. We formally define this problem in terms of the Minimum Description Length principle, by which we identify the best patterns as those that describe the occurrences of interesting events \(Y \) most succinctly given the data over \(X \). As neither discovering the optimal explanation of \(Y \) given a set of patterns, nor the discovery of optimal pattern set are problems that allow for straightforward optimization, we break the problem in two and propose effective heuristics for both. Through extensive empirical evaluation, we show that both our main method, Omen, and its fast approximation fOmen, work well in practice and both quantitatively and qualitatively beat the state of the art.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Suppose we are given a discrete-valued time series \(X \) of observed events, and an equally long binary sequence \(Y \) that indicates at which points in time something of interest happened that we would like to predict—earthquakes, for example. We consider the problem of mining a small set of interpretable and actionable patterns from \(X \) that reliably predict those interesting events. With reliable and actionable, we mean those patterns that not only highly accurately predict that an interesting event will follow, but which additionally can tell with high precision how long it will be until that event will happen. That is, we are after patterns that have a compact distribution of delays between pattern occurrences and predicted events. As real processes are rarely trivial, it is unlikely that a single patterns will suffice to explain all interesting events, and hence, we consider the problem of discovering a small and non-redundant set of patterns that together reliably predict the interesting events.
Event prediction is well studied in time series analysis. Most work considers on continuous-valued data and, if at all, focuses on tasks such as detecting abrupt distributional changes [18] and identifying events that precede such changes [31]. As we aim to discover patterns that explain the interesting time points, our work is closer to that of sequence classification [43] and similar to the task of learning patterns to reconstruct a labels of a sequence [40]. Existing solutions, however, focus purely on discovering all patterns that sufficiently accurately predict that an interesting event will follow some time after their occurrence [42], rather than our goal of discovering a small set of patterns for which we can reliably say how long it will take before that event occurs. As such, our work is related to information flow [32] and Granger causality [15], in the sense that patterns are only interesting if their occurrences provide significantly more information about Y than the history of Y does by itself.
We formalize the problem of finding a set of patterns predictive for \(Y \), in terms of the Minimum Description Length (MDL) principle [28], by which we identify the best patterns in X as those that describe Y most succinctly. We model the data such that for every occurrence of a pattern in X we encode the delay until the predicted associated interesting event: The more peaked this distribution, the cheaper it will be to encode the delays, and hence, we particularly favor patterns that accurately predict both the occurrence of and time until an interesting event. Discovering the optimal explanation of Y given a set of patterns, i.e., the alignment between the pattern occurrences and the interesting events, as well as discovering the optimal set of patterns, is both hard problems that do not permit straightforward optimization. We therefore split the problem in two and propose effective algorithms for each. To find a good explanation of \(Y \) given a single pattern, we propose both a general purpose solution and one that is particularly suited for long-range predictions. To discover good pattern sets, we present Omen, a greedy heuristic that iteratively optimizes the alignment of pattern occurrences to interesting events, and use this alignment to discover the best refinements of the patterns. We show a visualization of the Omen algorithm in Fig. 1 and will explain the details in Sect. 4. We additionally introduce fOmen, a faster alternative that is robust against high time delays. Neither Omen nor fOmen imposes restrictions on the delay distribution, both allow for overlap between predictions, and only have one hyperparameter that allows the user to specify to what extend gaps in patterns are allowed.
Visualization of the Omen algorithm: As input we are given an event sequence \(X \) and a target sequence \(Y \) and as output we obtain a set of patterns that together best explain \(Y \) given \(X \). The pattern search works by alternating between candidate generation and evaluation. We use the MDL principle to keep the pattern set small and non-redundant
We empirically evaluate Omen on both synthetic and real-world data. We show that our score reliably determines the predictiveness of patterns and compares favorably to state-of-the-art information flow scores [5, 32]. We show that Omen highly accurately reconstructs the ground truth, both in terms of discovering predictive patterns, as well as their delay distributions, outperforming four supervised and unsupervised sequential pattern miners [12, 35, 36, 43]. On real-world data, we confirm that Omen discovers meaningful and actionable patterns that give insight in the data generating process.
This paper builds upon and extends the work by Cüppers and Vreeken [9] that was published and presented at IEEE ICDM’20. Besides a thorough rewrite including a running example to explain the core concepts, the main additional contributions we make here are as follows. First, we extend our pattern language, score, and algorithms to allow for gaps in pattern occurrences—by which we can now discover patterns that we were previously unable to find. Second, we propose an alternative, highly efficient alignment algorithm that is particular adapt at discovering long-range time dependencies. Third, we propose a significantly faster pattern discovery algorithm that by focusing on patterns that likely belong together can effectively prune its search space.
Overall, our key contributions are that we
-
(a)
Introduce the problem of discovering patterns with precise predictions,
-
(b)
Formalize the minimal prediction problem using MDL,
-
(c)
Give an optimistic estimator to mine beyond surface level patterns,
-
(d)
Present two efficient alignment algorithms,
-
(e)
Propose the Omen algorithm for mining predictive pattern sets,
-
(f)
Give the more greedy yet significantly faster fOmen algorithm,
-
(g)
Provide extensive evaluation under wide range of different settings incl. data with very high noise to signal ratios,
-
(h)
Show the real-world applicability of Omen.
This paper is structured as usual. We start with notation and preliminaries in Sect. 2, after which we formally introduce the problem in Sect. 3. We present the Omen, as well as fOmen, in Sect. 4. We discuss related work in Sect. 5. We empirically evaluate in Sect. 6 and round up with discussion and conclusions in Sects. 7 and 8. We provide additional details in ‘Appendix’ and make all code and data publicly available.Footnote 1
2 Preliminaries
We start by introducing the notation and preliminaries we will use throughout this work.
2.1 Notation
Given an alphabet \(\varOmega \) of events \(e \in \varOmega \) we study finite sequences \(X \in \varOmega ^n\) of these events, where \(|X|=n\) is the length of the sequence. We denote \(X [{i}]\) to refer to the ith event in \(X \), and \(X [{i:j}]\) to denote the subsequence \(X [{i}],\ldots ,X [{j}]\). We write \(||X ||_a\) for the number of times we see event \(a \in \varOmega \) in X.
Our data consist of two sequences \(X\in \varOmega ^n\), and \(Y\in \{0,1\}^n\), both of length n. The former encodes an sequence of observed events, and the latter indicates the occurrence of something ‘interesting’ at every point i for which \(Y[{i}]=1\).
We consider sequential patterns \(s\in \varOmega ^m\) of length \(m = |s|<n\). We say that a pattern \(s\) occurs in a window \(w = X [{i:j}]\) when all events of s occur in w in the order specified by s. We call such a window minimal iff there does not exist any subwindow \(w' \prec w\) in which s occurs. By considering minimal windows, we avoid double counting of occurrences [34]. We say a pattern s matches sequence X at the jth event, \(X [{j}]\), iff there exists a minimal window \(X [{j-a:j}]\) of maximum window length \(a \le m \times g_f + g_a\)—where \(g_f\) and \(g_a\) are user defined parameters that allow to control the number of gaps we permit, respectively in terms relative to the pattern length, and absolute in number of gap events.
Given a pattern \(s\) and an event sequence \(X \), we can trivially construct a binary sequence \(Z_{s}\in \{0,1\}^n\) in which \(Z[j] = 1\) if pattern \(s\) matches \(X [{j}]\), and 0 otherwise. A predictive pattern \(s\) is a sequential pattern \(s\) with an associated discrete delay distribution that specifies the probability density \(P_{s}(\delta )\) that something interesting will happen \(\delta \) time steps after an occurrence of the pattern.
All logarithms are base 2, and we use the convention that \(0 \log 0 = 0\).
2.2 Minimum Description Length
The Minimum Description Length (MDL) principle [16] is a computable and statistically well-founded model selection criterion based on Kolmogorov Complexity [23]. For a given model class \(\mathcal {M}\), it identifies the best model \(M \in \mathcal {M}\) as the one that minimizes the number of bits needed to describe both model and data, \(L(M) + L(D\mid M)\) where L(M) is the length of model M in bits and \(L(D \mid M)\) the length of data D given M.
This is known as two-part, or crude MDL—in contrast to one-part, or refined MDL [16], which although preferred from a theoretical perspective, is not computable for arbitrary models. We use two-part MDL because we are particularly interested in the model: those patterns that given X allow us to describe Y most succinctly. Note that our goal here is to select the best model for the data at hand, and not to actually compress the data; we are hence not concerned with materialized codes, and only care about ideal code lengths.
To use MDL, we have to define a model class \(\mathcal {M}\), and encodings for data and model. We do so in the next section.
3 Theory
In this section, we introduce the problem at hand. We start with an informal definition of the problem, after which we define a model class, show how to encode a model and data given a model, and formally state the problem at hand.
3.1 The problem, informally
We are interested in discovering that set of predictive sequential patterns \(s\) that most reliably predict the interesting events in Y given observed events X. Our models consist of tuples \((s, P_{s})\) of sequential patterns s and their associated delay distributions \(P_{s}\), i.e., \(M= \{(s_1, P_{s_1}), (s_2, P_{s_2}), \ldots , (s_k, P_{s_k}) \}\).
Given X and a pattern \(s\), we have a binary sequence \(Z_{s}\) that marks those time points at which \(s\) matches \(X \). Every occurrence of a pattern predicts (in principle) that an interesting event is about to happen in Y. We call the mapping of occurrences of a pattern s to interesting events in Y its alignment \(A_{s}\). We allow for additive and destructive noise in X and Y, which is to say, we do not require that every occurrence of a true pattern s to be followed by an interesting event in Y, and neither require that all interesting events in Y are predictable by true patterns. To permit the former, we allow predictions to be ‘skipped.’ Formally, an alignment is hence a function \(a_s\) that maps each occurrence of pattern s to either an interesting event in \(Y \) or to an ‘skip’ token.
A delay distribution \(P_{s}\) provides the probabilities of an interesting event occurring \(\delta \) time steps after an occurrence of pattern \(s\). The higher the probability of \(\delta \), the fewer bits we will need to encode that particular value. Overall, the fewer predictions we have to ‘skip’ and the more peaked the delay distribution is, the more cost effective we can describe \(A_{s}\) in bits per interesting event, and hence, the more succinctly we will be able to describe Y.
Example 1
To illustrate, we consider a running example. We show in Fig. 2 an event sequence X of length 18, over an alphabet \(\varOmega = {a,\ldots ,f}\). There are four occurrences of pattern ab, which together define occurrence sequence \(Z_{ab}\). The best possible alignment of these occurrences to interesting events in Y is given as \(A_{ab}\), which maps the first, second, and fourth occurrence to actual interesting events, resp. with delays of \(+1\), \(+2\), and \(+1\) time steps, and as there is no interesting event corresponding to the third occurrences, it maps that one to a ‘skip.’ We show the corresponding delay distribution on the right of the figure, in which we see that in 50% of the cases an interesting event happens one time step after the occurrence of the pattern, in 25% two time steps later, as well as that it has a 25% probability of falsely predicting the occurrence of an interesting event (‘skip’).
Whereas in the toy example our model exists of only one pattern, \(M= \{ (ab, P_{ab})\}\), in general we allow Y to be complex, in the sense that multiple patterns may have generated and are hence needed to reliably predict all interesting events. In other words, we allow a single pattern \(s\in M\) to predict only some of the interesting events in Y. We denote by \({\hat{Y}}_{s}\) the binary sequence of interesting events in Y that are predicted by pattern \(s\). Loosely speaking \({\hat{Y}}_{s} = A_{s}(Z_{s})\).
Ideally, together the patterns in \(M\) predict each and every interesting event in Y, i.e., the combination of all predictions \({\hat{Y}} = \bigvee _{s \in M} {\hat{Y}}_s\) equals \(Y \). Some interesting events may, however, not have patterns that can explain their occurrence. To be able to fairly compare between models, we need to ensure losslessness and will therefore additionally need to transmit a residual sequence R that encoding all interesting events that are not predicted by any pattern. Formally, we define R as the bit-wise XOR between the predicted \({\hat{Y}}\) and the true Y, \(R ={\hat{Y}} \oplus Y\).
3.2 MDL for predictive sequential patterns
Based on the above intuition, we now proceed to define our score. We will first discuss how to encode sequence Y given a model \(M\) and observed events X and then detail how to encode such a model \(M\).
3.2.1 Encoding the data given a model
Given event sequence X and a pattern \(s\in M\), it is straightforward to construct the corresponding pattern occurrence sequences \(Z_{s}\). To determine \({\hat{Y}}_s\) from \(Z_{s}\), we need alignment \(A_{s}\) which gives us the delays and skips between pattern occurrences and predicted events.
To encode an alignment \(A_{s}\), we have to transmit each delay \(\delta \) corresponding to every pattern occurrence of \(s\) in X. We do so using optimal prefix codes over the time delay distribution \(P_{s}\) [8], which is to say, the lower the probability \(P_{s}(\delta )\) of a delay \(\delta \), the more bits we need. The encoded length of an alignment \(A_{s}\) for a pattern \(s\) is defined as
Once we know alignment \(A_{s}\), we can reconstruct \({\hat{Y}}_s\), and if we do so for all patterns \(s \in M\), we therewith have \({\hat{Y}}\).
To be able to reconstruct Y from \({\hat{Y}}\) without loss, we additionally need to encode the residual sequence R. We have
where we first encode the number of 1s in R using \(L_\mathbb {N}\), the MDL-optimal encoding for integers [29]. It is defined as
where \(\log ^*z \) is defined as \(\log z + \log \log z + \cdots \) , only including the positive terms in the sum. To obtain a valid encoding, i.e., to satisfy the Kraft inequality, we set \(c_0 = 2.865064\) [29].
As now we know the number of 1s in R, we can optimally encode the actual sequence R via an index over a canonically ordered set of all sequences of length n with \(||R||_1\) ones. Since we already know the location of predicted interesting events, we know these will be 0 in the residual and we can hence ignore \(||{\hat{Y}}||_1\) possible locations. As the binomial coefficient greatly increases with every additional interesting event in \(R\), we favor residuals that cover fewer interesting events.
Example 1
(continued) Consider again Fig. 2. Although data X are 18 events long, pattern ab predicts three interesting events, by which there are 15 out of 18 possible time steps at which the 2 unexplained events can occur. As such, we have \(L(R) = L_{\mathbb {N}}(2) + \log {15 \atopwithdelims ()2} \).
Putting these two parts together, we have
for the number of bits to encode Y given a model M and observed events X.
3.2.2 Encoding a model
Next, we formalize how we encode a model \(M \in \mathcal {M}\) in bits. At a high level, we have
where we first encode the number of patterns in the model, and then the patterns and their associated delay distributions.
Patterns are essentially just a sequence of k events from \(\varOmega \). We use \(L_\mathbb {N}\) to encode their length, and to avoid any bias toward events \(e \in \varOmega \), we encode the actual events in \(s\) using an index over \(\varOmega \). Thus, the cost of one pattern is
To encode a time delay distribution, it suffices to encode which time deltas have a probability greater zero, and then encoding how likely each of these deltas are. We write \(\varDelta _s = \{ \delta \mid P_s(\delta ) > 0 \}\) for the set of \(\delta \) values with nonzero probability, and \(\delta ^* = \max (\varDelta _s)\) for the highest value of delta with nonzero probability. Formally, we then have
where we first encode interval of possible deltas, \([0,\delta ^*]\), simply by encoding the value of \(\delta ^*\) using \(L_\mathbb {N}\). As we aim for actionable patterns, we are not interested in ‘instantaneous’ predictions. This allows us to repurpose \(\delta = 0\) to mean ‘skip,’ so avoiding unnecessary padding of the possible values that can be sent. Next we encode the number of \(\delta \)s with nonzero probability mass, \(k = |\varDelta _s|\), for which we need \(\log \delta ^*\) bits. We then encode those values \(\delta \in \varDelta _s\) through a strong number composition. The intuition is that the more deltas are left unused, i.e., \(P_s(\delta ) = 0\), the higher this cost. Finally, we have to specify the probability mass per \(\delta \), which reduces to encoding an index over a number composition, i.e., an index over every possible way to distribute the \(||Z_{s}||_1\) occurrences (balls) over k non-empty bins. Overall, the flatter the distribution, the more deltas we have to consider, the higher the cost will be, and hence we prefer peaked distributions.
Example 1
(continued) To illustrate this, we continue with our running example. Consider again Fig. 2. The delay distribution has a nonzero entries for ‘skip’, and values of delta of 1, 2. This means we first encode the maximum delta, \(\delta ^* = 2\), and then how many deltas out of the range [0, 2] have a probability greater zero. We then identify which, in this case three values, out of this range have nonzero probability. As there are only three possible values, this is trivial; the cost is 0 bits. Finally, we have to distribute the total probability mass of the four pattern occurrences of pattern ab over our three chosen delta, requiring 1.58 bits.
This concludes the description of how we encode a model \(M\) in bits.
3.3 The problem, formally
With the above, we can now formally state the problem.
The Minimal Event Prediction Problem Given event sequence X over alphabet \(\varOmega \) and binary sequence Y indicating time points of interest, find that set of predictive sequential patterns and associated time delay distributions \(M= \{(s_1, P_{s_1}), (s_2, P_{s_2}),\ldots ,(s_k, P_{s_k})\}\) and that alignment A of pattern occurrences to interesting events in Y, such that the total encoded length
is minimal.
To solve this problem exactly, we would have to consider a rather large, triply exponentially sized search space. As we do not wish to a priori limit the maximum length of any pattern beforehand, patterns can be up \(|X | -1\) long, resulting in \(\sum _{i=1}^{|X |-1} |\varOmega |^i \) possible patterns. Per pattern \(s\), there exist \((||Y ||_1 +1)^{||Z_{s}||_1}\) possible alignments. This leaves the final part, in which we have to select a set of patterns-alignment tuples. We can limit the number of tuples in our model to \(||Y||_1\). Combining this gives us
possible solutions, where S is the set of all patterns. Although we are not necessarily afraid of large search spaces, unfortunately this particular search space does not exhibit structure such as (weak) monotonicity, convexity, or submodularity that we could exploit to guide our search.
Hence, we resort to heuristics.
4 Algorithm
In this section we present the Omen algorithm for heuristically solving the Minimal Event Prediction Problem. Rather than solving it at once, we split the problem in two parts and propose effective solutions for both. First, given a pattern we aim to find its delay distribution by optimizing the alignment between pattern occurrences and interesting events. Second, we consider the problem of discovering good pattern sets.
We first introduce notation that will ease the exposition below. Whenever clear from context, we will write \(L_{s}(Y)\) rather than \(L(Y, \{(s,P_{s})\} \mid X)\) to denote the encoded length of Y under a model M that consists of a single pattern s. Analogue, we write \(L_0(Y)\) to denote the length of \(Y \) using the empty, or null model \(M_0\), which encodes all interesting events through the residual R. Finally, we overload the notation of an alignment \(A_{s}\), allowing ourselves to represent an alignment as a set of tuples (i, j) where i is the location of the pattern match in \(X \), and j the location of the aligned interesting event (or ‘skip’) in \(Y \).
4.1 Discovering alignments and delay distributions
Alignment optimization process. Given an initial time delay distribution, our goal is it to simplify the distribution to that version that minimizes the number of bits needed to describe \(Y \), essentially we trade of number of events explained by pattern s against the number of deltas in the delay distribution \(P_s\). To simplify the given distribution, we first drop all least frequent deltas from the distribution. Secondly, reassign the corresponding pattern occurrences to other IE or, if not possible, to ‘skip’. Thirdly, we update the delay distribution to match the new assignment. We repeat these steps until no deltas are left in our distribution, while keeping track of how many bits each alignment does need to encode \(Y \). Finally, we return that alignment with \(\min L_{s}(Y)\)
We start by discussing how to optimize an alignment \(A_s\) for a given pattern s. Solving \(L_{s}(Y)\) exactly would require us to consider all possible alignments, which is computationally unfeasible. We will therefore instead minimize \(L_{s}(Y)\) heuristically. The overall strategy is as follows. Given an initial alignment \(A_s\), and a corresponding delay distribution \(P_{s}\), we iteratively optimize \(L_{s}(Y)\) by taking all pattern occurrence with the lowest \(P_{s}(\delta )\) and either reassigning it to an interesting event such that we obtain a higher \(P_{s}(\delta ')\), or if no such interesting event exists, we map this pattern occurrence to ‘skip’ instead. We repeat this process for all \(\delta \ne \text {`skip'}\) and finally return that alignment \(A_s\) with the lowest \(L_{s}(Y)\). We show a visualization of this process in Fig. 3. In the worst case, we will have to consider all possible \(\delta \in P_{s}\) for each pattern occurrence that we reassign, by which we have a time complexity of \(\mathcal {O}(||Z_{s}||_1 |\varDelta _s|)\).
To optimize our alignment, we need an initial alignment that can be optimized. We will introduce two such methods. We give a general purpose approach below and discuss an approach particular adapt at long-range prediction in Sect. 4.4.
Our general purpose alignment initialization algorithm, AlignNext, consists of three main steps, each updating the alignment. First, based on the assumption that each pattern occurrence predicts the directly following interesting event, we simply align every occurrence \(X[i] = s\) of pattern s in X to that interesting event in Y that is closest in time but at least one time step into the future, i.e., \( A_s = \{(i,j) \mid X[i] = s\wedge \arg \min _{j > i} Y[j]=1\}\), and then determine the corresponding delay distribution \(P_s\) from this alignment. As by naively mapping occurrences to the earliest interesting event, multiple pattern occurrences may map to the same interesting event, while leaving other interesting events unexplained. We hence next realign all such pattern occurrences to ‘skip’, except for the one with maximal \(P_s(j-i)\), and re-infer the delay distribution. Last, we now use the new distribution to align every pattern occurrence mapped to ‘skip’ to that interesting event \(Y[j]=1\) that maximizes \(P_{s}(j - i)\). If there is no interesting event with nonzero probability under \(P_{s}\), we map it to ‘skip’. Reassigning a ‘skip’ requires us to consider all possible \(\delta \in P_{s}\) in the worst case, resulting in a complexity of \(\mathcal {O}((||Z_{s}||_1)^2)\). We can now, given a pattern, find an alignment between \(Z_{s}\) and \(Y \).
As we will see in the experiments, this approach works well in practice. However, it is easy to see that it has a bias toward alignments where interesting events are close in time to the pattern occurrences. Differently put, if we would increase the mean of the delay distribution, this approach will give a more and more undefined delay distribution. To obtain good initial alignments for such cases, we introduce an alternative initialization algorithm in Sect. 4.4.
With the above, we know how to find an alignment \(A_s\) for a given pattern s and can hence compute our score. Next, we discuss how to find good patterns.
4.2 Discovering a good set of patterns
There exist exponentially many patterns, and exponentially more sets of patterns. Evaluating these exhaustively is not feasible, and as there is also no structure that we can exploit, exact search for the best set of patterns is not an option. Instead, we propose a heuristic to find a good set of patterns. In particular, we take a greedy bottom-up approach, where we iteratively add and refine patterns in the model. Because of the complexity of X and sparsity of Y, it will often be the case, however, that only (large parts of) a true pattern s will lead to a gain in compression, while all small fragments of s do not improve over the null model. That is, we cannot directly use the score defined above to identify whether a pattern is ‘promising,’ and as only in trivial cases singleton events in X will help to compress \(Y \), we cannot start by adding ‘good’ singletons and then refine them.
Rather than resorting to exhaustively scoring every possible pattern s under some arbitrary constraints, we define an optimistic estimator \(\bar{L}_{s}(Y)\) by which we bound the length \(L_{s'}(Y)\) of the theoretically best possible extension \(s'\) of s. The key idea is that by extending s to \(s'\), the number of occurrences will monotonically decrease. We hence aim to estimate the score of the theoretically best possible extension (refinement) \(s'\) of s that exactly obtains the subset of occurrences of s that align best with Y. Interestingly, this is equivalent to only aligning the ‘best’ occurrences of s to interesting events in \(Y \), and treating the remaining pattern matches as if they do not exist—i.e., play-pretending that the (unknown) \(s'\) simply does not match those occurrences of s. We can straightforwardly achieve this by mapping the non-matching occurrences of s to ‘skip’, and treating the encoding cost for such skipped pattern occurrences as zero. Hence, \(\bar{L}_{s}(Y)\) gives the length of \(Y \) where we set \(P_{s}({skip}) = 1\) for the encoding of \(A_s\) and \(P_{s}({skip}) = 0\) for the encoding of \(P_s\), as if only the pattern occurrences aligned to interesting events exist.
Exactly optimizing the subset of occurrences of s, i.e., finding those that together compress Y best, is infeasible as it requires us to find the best alignment for every possible subset of occurrences. We therefore instead start by inferring an initial alignment using either the algorithm described above or the one in Sec. 4.4, optimize that alignment as described in Sect. 4.1, but setting the cost of ‘skip’ to zero, and so obtain \(\bar{L}_{s}(Y)\). With \(\bar{L}_{s}(Y)\) we know, if a gain is found, whether there exists a subset of occurrences of s that would improve our model and the next task is hence to find whether there indeed exists an extension \(s'\) of s that does improve our score.
With the optimistic estimator in place, we can now introduce the Omen algorithm for mining sets of predictive patterns. We give the pseudo-code as Algorithm 1. Omen starts with an empty model where all interesting events are unexplained by patterns, i.e., encoded via residual \(R\) (line 1). The main idea is to iteratively add patterns to the model \(M\) that predict interesting events in \(R\), by which we focus the search on those interesting events that are currently not yet predicted (explained).

Starting from the singletons as candidate set C, we take a breadth-first search approach where we extend all candidates that are promising with regard to our optimistic estimate (l. 4–6) and identify those that help to better compress Y (l. 7–8). As extensions of promising patterns, we consider all patterns \(s'\) where we add any single symbol from alphabet \(\varOmega \) at either the end or beginning of s (l. 6). Next, we iteratively consider adding those candidates \(s \in S\) that passed the compression-check into the model (l. 9–14). We do so in order of how much they help to compress (l. 9) and to avoid redundancy only consider those that indeed improve the score (l. 10)—for example, if abcd is the true pattern and \(ab \in S\) and \(cd \in S\), then both (probably) explain the same interesting events. Once we added one, the other does not offer any additional information. When adding a pattern to our model we search for the best possible refinement, that is we greedly extend our pattern to that version that gives us the highest gain in bits saved, we refer the reader to ‘Appendix A.1’ where we provide a more detailed explanation. After adding a pattern, we re-compute the residual (l. 13–14). We repeat these steps until we have no further candidates (l. 3) and then return the final model \(M\). In Fig. 1, we show a visualization of this algorithm.
In the worst case, Omen considers every possible sequential pattern over \(\varOmega \), which means a complexity of \(\mathcal {O}(|\varOmega |^{|X |-1})\).
4.3 Faster Omen
As we will see in the experiments, Omen works very well in practice. At the same time, it is a bit naive: It considers as candidates extended patterns es and se, without taking into account whether these extensions e predict any of the same interesting events as s. As this information is readily available, an alternate and more targeted search strategy presents itself. We call this, much faster, procedure fOmen. We give the pseudo-code of fOmen as Algorithm 2. We first describe the algorithm in general and then detail the special case of singletons.
The main idea is to greedily combine those patterns in our candidate set that have the largest intersection of predicted events (l. 4). When combining two such patterns, a and b, we choose that ordering ab or ba that results in the most pattern matches in \(X \) (l. 6). If the optimistic estimator indicates that the new pattern is potentially compressing, we mark the events in \(X \) for each used pattern occurrence as usedFootnote 2 (l. 12), for reasons that will become apparent when we study the singletons. We add all pairs between patterns already in our candidate set and the newly created pattern to our candidate set (l. 19). Unless the new pattern predicts previously unexplained events, i.e., those in the residual, then we greedily refine it to its best version (l. 14) and add the refined version to our model and compute a new partial prediction and update our residual accordingly (l. 15 to 17). We repeat this process until no candidates are left. To prune candidates that are very unlikely to lead to improvement, we permit the user to set a threshold on the minimum overlap in predicted events. Per default we set this threshold to \(0.01 \times ||Y ||_1\).
The refinement of an already compressing pattern works similar to the mining approach. We simply keep combining those patterns with the highest intersection of predicted interesting events, up until the optimistic estimator indicates no better extension exists. We then return the refined pattern with lowest \(L_{s}(R)\). We give the pseudo-code as Algorithm 4 in ‘Appendix A.2.’
We now consider the special case of candidates (a, b) where a and b are singletons. If we were to treat such candidates the same as we do above and, for example, find that ba is the most promising instantiation of (a, b), we would remove (a, b) and add any combination (ba, s) where s is a pattern in C to the candidate set. For non-singleton patterns this is fine, as long as we can re-build them from scratch if needs be, which is even desirable from a run-time perspective. However, to be able to re-build patterns we do need to ensure that the singletons, the most elementary building blocks, are always present as candidates. To make sure they are, we hence should not simply remove singleton pairs (a, b) after exploring (and possibly accepting into the model) their refinement. At the same time, we should not just put (a, b) back just like that, as the just-extended pattern will already explain some or even many of the interesting events. If we do not account for this, we would hence be too optimistic in our estimate \(\bar{L}_{s}(\cdot )\) of the potential gain of any new pattern that is based on the re-added (a, b). To this end, we mark those events that the just-extended candidate pattern uses and update the intersection counts of the singleton pair with un-used interesting events. If the optimistic estimate of (a, b), \(\bar{L}_{(a,b)}(R)\), indicates a gain, we add (a, b) back into the candidate set and otherwise discard it.

4.4 Alignment with overlapping predictions
Toy example for time-overlapping predictions. \(Z_{s}\) shows the pattern occurrences of pattern \(s\). The arrows show the ground truth alignment to the interesting events in \(Y \). The second (and third) pattern match occurs before the interesting event predicted by the first pattern. To find good alignments in settings like this, we give a specialized alignment approach in Sect. 4.4
As the final technical contribution, we propose a fast alignment strategy that is particularly suited for cases where there is long delay between patterns and interesting events, and hence a high chance of overlap of occurrence-prediction intervals. As an example of why such an algorithm is necessary in addition to the general purpose one described above, consider Fig. 4. It is easy to see that the vanilla strategy, where we initially map a pattern occurrence to the earliest interesting event, would fail to discover a sensible (let alone, the ground truth) initial alignment; because the third, fourth, and fifth occurrence would all be mapped to an interesting event at the next time step, they would amass as much probability density as the true delay of 6 time steps and so create a local minimum out of which the optimization cannot escape.
We therefore present an alternative alignment algorithm, AlignFar, which is unaffected by such overlapping predictions. At a glance, it first computes the mean of our delay distribution and then assigns to each pattern the interesting event that is closest to this mean. More specifically, we seek this delay \(\mu \) for which each pattern occurrence delayed by \(\mu \) lies as close as possible to an interesting event occurrence following the pattern occurrence. We propose an algorithm that computes this optimal delay within \(O(\Vert Z_s\Vert _{1}\Vert Y\Vert _{1}\log \Vert Z_s\Vert _{1})\) time.
For convenience, we define the set of occurrence indices for the patterns, \(I_s=\{i\mid Z_s[i]=1\}\), and the set of occurrences for the interesting events, \(I_Y= \{i\mid Y[i]=1\}\). Given a pattern occurrence \({i_s}\in I_s\), we can now express its candidate interesting event occurrences as the set \(I_Y^{{i_s}}= \{{i_Y}| {i_Y}\in I_Y\wedge {i_Y}> {i_s}\}\); this set consists of all event occurrences that follow the pattern occurrence. Intuitively, we seek to find the delay \(\mu \) that minimizes the total distance between every pattern \({i_s}\)—delayed by \(\mu \), and the event occurrence within \(I_Y^{{i_s}}\) that lies nearest to \({i_s}\). As a distance between these two occurrence indices, we adopt the quadratic one, after which we can formally express our problem as:
To demonstrate the intuition of this, we consider the toy setting of Fig. 5, in which the pattern matches \(I_s=\{3, 6, 8\}\) can each be aligned to any of the interesting events \(I_Y=\{4, 5, 11, 12\}\). Out of the latter, the candidate interesting event occurrences for the each pattern match are the sets \(I^{3}_{Y}=\{4, 5, 11, 12\}, I^{6}_{Y}=\{11,12\}, and I^{8}_{Y}=\{11,12\}\), respectively.
Toy example showing three pattern matches with all possible alignments (left) and the resulting midpoints (right) that define the intervals with local optimum to be tested in the AlignFar alignment algorithm. The global optimum lies between 3 and 4 as it has the smallest distance to all candidate pattern matches
We can optimize Equation 1 by the following procedure. We first create the union of all event candidate offsets \(I_Y^{\cup }= \bigcup _{{i_s}\in I_s}I_Y^{{i_s}}\), sorted in ascending order.
Lemma 1
Let \(I_Y^{\cup }\) be the sorted (multi-set) union of all possible interesting event candidates and denote \(U\) the midpoints between each 2 consecutive elements of \(I_Y^{\cup }\). Then, the candidate within \(I_Y^{\cup }\) that lies closest to a pattern occurrence changes only when \(\mu \) crosses a midpoint in \(U\). This change affects exactly those pattern occurrences that contributes an elements in \(I_Y^{\cup }\) adjacent to the crossed midpoint in \(U\).
Using Lemma 1, we can partition the real line in exactly \(|I_Y^{\cup }|+1\) segments,Footnote 3 within which the configuration of closest events remains constant, and therefore also the objective value of Eq. (1). For each segment, we can compute this value, as well as its optimizer, by carefully keeping track of the updates induced to the optimizer and optimal of the preceding segment, and in fact in constant time. By using appropriate data structures and a mutatis mutandis MergeSort algorithm, we can perform the search for the next midpoint in \(O\big (\log {\Vert Z_s\Vert _{1}}\big )\) time. Overall, this gives our algorithm a computational complexity of \(O(|I_Y^{\cup }|\log {\Vert Z_s\Vert _{1}})\).
Returning to the example of Fig. 5, the delay offsets \({i_s}-{i_Y}\) in Eq. (1) for each pattern match lie in the sequences (1, 2, 8, 9), (5, 6), and (3, 4), respectively, as shown in Fig. 5 (right). Importantly, the union of all midpoints between every two consecutive elements in each of the above sequences gives the set \(I_Y^{\cup }=\{1.5, 3.5, 5, 5.5, 8.5\}\). Due to Lemma 1, for each interval between consecutive midpoints the best offset \({i_s}-{i_Y}\) for each pattern remains constant and yields one single minimizer of \(\mu \) for the specific interval (which need not necessarily lie within the interval itself). Thus, the global optimizer can be retrieved as the minimum over all these per-interval minimizers, which here is \(\mu ^*=\min \{3, \frac{10}{3}, \frac{11}{3}, \frac{17}{3}, 6, \frac{19}{3}\}=\frac{10}{3}\).
Once we have computed our optimizer \(\mu ^*\) of Eq. (1), we can simply select for each pattern occurrence \({i_s}\) the interesting event closest to \({i_s}+ \mu \) from its candidate set \(I_Y^{{i_s}}\). If the candidate set is empty, we align that pattern occurrence to a ‘skip’. This gives us an alignment for all pattern occurrences without a bias toward closer interesting events.
5 Related work
Our work is related both to prediction and information flow in time series, as well as to pattern mining.
At its core, the Omen score aims to measure how the occurrences of a pattern s in X help to reliably predict the occurrences of interesting events in Y. As such, it is strongly related to Granger causality [15]. Granger causality is based on the idea that if the past of a time series Z does help to predict \(Y \), given the past of \(Y \), it ‘Granger-causes’ \(Y \). Linear [15] and nonlinear [6] scores have been proposed, whereas others studied the effects of events on time series [31]. Transfer entropy (Tent) [32] and Cute [5] are both information-theoretic instantiations of Granger causality for discrete data, where the one measures information flow in terms of entropy, and the other in terms of MDL. In the experiments, we will compare our score to both.
Prediction and forecasting in time series [7, 22, 30, 38, 39, 41, 42] are a classic research topic to which Omen is related. A prototypical example is failure prediction, where the goal is to predict upcoming failures with sufficient time to act on the prediction. By far most, work focuses on the case where X is continuous valued and the goal is to discover time points where the distribution of X changes [18, 37]. Another popular task is the prediction of upcoming events based on social media activities and text [14, 27]. Related to prediction which is the task studied by Yeh et al. [40], they considered the problem of reconstructing a Boolean annotation sequence given a real-valued time series.
Discovering interpretable sequential patterns has been extensively studied [1]. We can differentiate between two settings, based on the notion of support of a pattern. The first, where we have a database of sequences and support is defined by the number of instances containing a pattern [36], and the second where we have one or multiple sequences where support is defined as the number of occurrences within a sequence, measured using either a sliding window [25] or counting the number of minimal windows [21]. Both settings have been studied in detail, especially for the goal of mining all (closed) frequent patterns [36].
Recently, research in pattern mining focused instead on discovering small, non-redundant sets of patterns that together generalize the data, for which MDL based approaches, such as Sqs [35], Squish [4], and Ditto [3] have been shown to be highly effective. The general idea of these approaches is similar to ours, but inherently different as they are unsupervised. The goal is to find that set of patterns that together describe the given sequence database most concisely. All use greedy search algorithms, iteratively adding patterns to a model until convergence. Galbrun et al. [13] studied the problem of discovering sequential patterns with reliably periodically appear. Instead of taking a descriptive approach, Fowkes and Sutton [12] proposed a method to discover small sets of informative patterns based on a generative model. More precisely, they define a probabilistic generating model that given a set of sequences generates the input sequence database. The goal is to infer set of subsequences which is most likely to generate the input sequence database under the generating model. Although all related to Omen in the sense that they also discover small sets of patterns, these methods are all strictly unsupervised. In the experiments, we will compare to appropriately modified versions of both Sqs [35] and Ism [12].
Identifying patterns that predict the occurrence of events can be approached as a supervised sequence classification problem, where given a labeled sequence database the goal is to find those sequential patterns that allow a classification [2, 11, 43]. Scis [43], a recently proposed rule-based sequence classifier, is trained by mining rules above a set interesting threshold, where interestingness is the product of cohesion (average proximity of items that make up that rule) and frequency. A unseen sequence is classified by taking the top-k best fitting rules. We consider a different setting, where instead of a sequence database, we only have two sequences X and Y, where Y can be interpreted as our labels. We include a comparison to Scis in the experiments.
6 Experiments
In this section, we will empirically evaluate on synthetic and real-world data. To determine how well our score and methods can tell predictive from non-predictive patterns, we compare to Tent [32] and Cute [5], and to determine how well they discover predictive patterns from data we compare to Sqs [35], Bide+ [36], Ism [12], and Scis [43].
We implemented Omen in C++ and provide the source code for research purposes, along with all datasets, experiment specifications, and generators.Footnote 4 All experiments were executed single-threaded on machines with two Intel Xeon CPU E5-2643 processors and 256 GB of memory, running Linux. We report wall-clock running times.
6.1 Synthetic data
To assess performance against known ground truth, we consider synthetic data, which we generate as follows. We first generate event sequence X of length \(n = 300\,000\) by uniformly at random drawing n events from an alphabet \(\varOmega \) of length 50, i.e., \(X \in \varOmega ^n\), and initialize \(Y = \{0\}^n\). We add structure by planting 20 predictive and 10 non-predictive patterns. Every pattern is generated independently, where we first draw its length l from [3, 6], its events \(s=\{e_1,\ldots ,e_l\}\) from \(\varOmega \), and its frequency f from [5, 50], again all uniformly at random. We plant patterns into X by sampling u.a.r. f insertion positions \(i \in [0,n]\), where we simply overwrite the existing values in X, i.e., \(X[i:i+l] = s\). To ensure the ground truth holds, we do not overwrite previously planted patterns. For the predictive patterns s, we additionally generate interesting events in Y by, per insertion position i, sampling a delay \(\delta \) u.a.r. from [8, 12] and setting \(Y[i+l+\delta ] = 1\). Finally, we add noise to the data by flipping values in Y. We consider both destructive noise, where we flip 1s to 0, as well as additive noise, where we flip 0s to 1. Unless specified otherwise, all results on synthetic data are averaged over 10 independently generated datasets.
6.2 Evaluating the score
Higher is better. Omen reliably determines predictiveness of patterns, both for a destructive and b additive noise, meaning that in Y we flip 1s to 0s, resp. 0s to 1s. Stand-alone, neither Cute nor Tent differentiate at all between predictive and non-predictive patterns. When applied on the \({\hat{Y}}_{s}\) discovered by Omen and AlignNext, they do achieve reasonable performance (Cute+Omen, resp. Tent+Omen, dashed lines). Omen beats all methods by a large margin
We first evaluate how well Omen can tell predictive from non-predictive patterns. For Omen, we consider a pattern to be predictive if it helps to compress \(Y \). We compare Omen to Tent [32] and Cute [5], two state-of-the-art methods based on Granger causality that measure how much information \(Z_{s}\) provides toward \(Y \). For both, we say \(Z_{s}\) predicts Y if they conclude that \(Z_{s}\) Granger-causes Y. We optimize the lag-parameter of Tent over [1, 15] per experiment.
We generate data with varying amounts and type of noise as described above, and for every planted pattern in every dataset test whether the score considers it predictive or not. We give the average weighted accuracies, where weighted accuracy is defined as \(\frac{1}{2} (\frac{tn}{tn + fp} + \frac{tp}{tp + fn})\)Footnote 5 in Fig. 6. We see that Omen is able to identify predictive patterns with high accuracies even for large amounts of noise, whereas Tent and Cute applied on \(Z_{s}\) and Y reduce to a coin flip as they expect all (most) interesting events to be explained by \(Z_{s}\). When we apply Tent and Cute not on the raw data Y but rather on that \({\hat{Y}}_{s}\) that Omen discovers as the best explanation of Y given \(s\) (Cute+Omen and Tent+Omen), we see that their accuracies increase up to \(90\%\), yet remain much worse than those of Omen.
6.3 Evaluating the discovered patterns
Next, we evaluate how well Omen discovers predictive patterns from synthetic data. We compare Omen to Bide+ [36], Scis [43], Sqs [35], and Ism [12].
Scis discovers predictive patterns (rules) given a labeled sequence database as input. As positive samples, we consider the window of w events in X that lead up to each interesting event in Y. As negative samples, we then split the remaining data into non-overlapping windows of length w, which avoids skew (in positive and negative samples) as well as bias (non-intersecting with positive samples). We ensure Scis can discover all planted patterns by setting \(w=20\). From all reported rules, we consider those who predict the positive class.
Bide+, Sqs, and Ism are all unsupervised by nature, but we can use them to discover predictive patterns as follows. First, we split X at the location of the interesting events in Y—so creating a database of sequences leading up to the next interesting event. We then run the respective method on the created sequence database—and subsequently use the Omen alignment and score to identify, out of all reported patterns, those who are predictive. As in Sect. 6.2, we consider a pattern to be predictive if it does compress \(Y \). Bide+ tends to discover far too many patterns, i.e., millions more than planted, and hence, we only consider the top-200 of its results. Sqs and Ism discover reasonable number of results, and those we consider all.
As metric to evaluate success, we compute \(\text {recall} = \frac{tp}{|\{\text {planted patterns}\}|}\) and \(\text {precision} = \frac{tp}{|\{\text {received patterns}\}|}\) over a pair-wise mapping between planted and discovered patterns. We map each reported pattern to at most one planted pattern and to each planted pattern at most one reported pattern. We allow a mapping between two patterns if the found pattern is a subsequence of the planted one or vice versa. We choose that mapping that results in the maximum number of pairs. This also allows us to rewards partial discoveries. As the number of true positives, i.e., correctly received pattern, we consider the number of pairs in the mapping, consequently the false positives are \(|\{\text {received patterns}\}| - \text {true positives}\). We refer the reader to ‘Appendix B.1’ for more details on how we compute the mapping.
We first consider a setting which favors unsupervised pattern mining methods like Sqs, Ism and Bide+ by planting predictive patterns that are frequent in X, sampling the number of pattern occurrences from [25 : 500]. As we find that Ism reports only singletons and Bide+ does not return any predictive patterns, we omit them from further analysis. For the remaining methods we report the F1 scores, \(F1 = \frac{2* \text {precision} * \text {recall}}{\text {precision} + \text {recall}}\), in Fig. 7. We see that Omen and fOmen both outperform Scis and Sqs by a wide margin. Quantitatively, Sqs is a good second, but Scis returns very many patterns that do not match the planted ones and hence obtains very low precision and recall scores. fOmen, and especially Omen, has close to perfect F1 scores for nearly all noise levels.
For the next analysis, we hence consider a more challenging setting where we sample the frequency of the planted predictive patterns instead from the range [5 : 50]. We report the F1 scores on the left-hand side of Figs. 8, 9 and 10 and provide the precision and recall plots in ‘Appendix B.2.’ We see that in this more sparse setting, Sqs and Scis do no longer discover any predictive patterns; Omen and fOmen, on the other hand, still discover most up to all. We additionally see that Omen is especially robust against additive noise, while for destructive resp. combined noise it performs well up to 60% noise. fOmen performs slightly worse, but obtains these results in only a fraction of the time that Omen takes; on average over these experiments it needs only 8 instead of 81 seconds.
Higher is better. F1 score results for Omen, fOmen, Sqs, and Scis, on synthetic data with ‘frequently’ occurring patterns and a destructive resp. b additive noise in Y. Scis fails to report any meaningful patterns. Sqs, with our score to filter out non-predictive patterns, recovers a large fraction of the ground truth patterns. fOmen outperform both by a large margin, except for high levels of additive noise. Omen is the best method overall
F1 score results (a, higher is better), and number of bits needed to encode \(Y \) given different models (b, lower is better) on data with destructive noise. As models we consider the empty null model, the ground truth model, and the models discovered by Omen and fOmen, respectively. Omen and fOmen report most of the planted patterns up to 60% of noise. Sqs and Scis do not report any predictive patterns. We observe that the reported models match the ground truth closely
F1 score results (a higher is better) and number of bits needed to encode \(Y \) given the null model, the ground truth model and discovered model by Omen and fOmen respectively (b lower is better) on data with ‘unfrequent’ patterns and additive noise. Omen is especially robust against additive noise. We observe that the reported models match the ground truth near exactly, especially Omen
F1 score results (a higher is better) and number of bits needed to encode \(Y \) given the null model, the ground truth model and discovered model by Omen and fOmen respectively (b lower is better) on data with ‘unfrequent’ patterns, destructive and additive noise. Omen and fOmen report most of the planted patterns up to 50% of noise. Sqs and Scis do not report any predictive patterns. We observe that the reported models match the ground truth closely
6.4 Evaluating the discovered models
In addition to measuring performance in recall and precision, we evaluate how close the models that we discover get to the ground truth. We start with a sanity check, considering data where Y is independent from X. We do so by generating data without noise and then destroying any dependence between X and Y by randomly permuting Y. When we run either Omen or fOmen on this data, both correctly report no patterns.
Using the same data generating scheme as above, we now compare the number of bits that Omen resp. fOmen require to describe the data, to the encoded length using either the ground truth model, and the null model where Y is described without any patterns. We describe in Sect. 3 how the number of bits needed to encode \(Y \) and \(M\), under the respective models, is computed. We report the average over all experiment per noise level. We give the results on the right-hand side of Figs. 8, 9 and 10. In addition, we give the worst-case performance per noise level in ‘Appendix B.2.’
Overall, we see that both Omen and fOmen return high quality models and are both highly robust against noise. We see that the results of Omen in particular are always very close to the ground truth, and far from the null model—except for when the null model is the most succinct description of the data, after which it correctly returns the null model as the best (simplest) description of the data.
In some cases, we discover a shorter description then the ground truth, which can be explained by the fact that due to noise, the ground truth pattern set and alignment does not necessarily have to be the shortest description of the data at hand. If we consider, for example, the case of destructive noise where, with increasing noise, pattern will predict fewer and fewer interesting events. At some point, it requires less bits to describe these events using the residual than using patterns. This also explains the drop in F1 that we observed above for when there is destructive noise; above \(80\%\), the data simply do no longer exhibit any significant structure.
Last, we consider the robustness of Omen and fOmen against patterns with noisy delay distributions. To this end, we generate synthetic data as above, but, to keep the results interpretable, we now plant only a single pattern of length 6 that predicts \(2\,000\) events. As time delay distribution, we consider a Normal distribution with mean 50 and vary the standard deviation from 2 to 60 in steps of 2. We record the number of bits \(L(Y,M \mid X)\) needed by resp. the null model, the ground truth model, and the model discovered by our methods. We give the average results per standard deviation, out of 10 experiments, as shown in Fig. 11. We see that both Omen and fOmen are robust to patterns with wide delay distributions, discovering models that compress better than the null—and hence, discovering the true pattern—consistently up to a delay distribution with a standard deviation of 24. From a standard deviation of 44 onward, the null model beats the planted model.
6.5 Evaluating on data with gaps
Until now, we have only looked at synthetic data with strict subsequences as patterns. Next, we evaluate on synthetic data where the planted patterns do have gaps. We keep the data generating process the same except we plant a pattern by sampling u.a.r. f insertion points \(i\in [0,n]\) and for each sampled i we select a window \(X [i:i+lk]\) where l is the length of the pattern to be planted and k is a factor, specifying how large the window is. To plant the pattern, we sample l insertions points from the window and plant the pattern accordingly. For predictive patterns, we set \(Y [\max \text { sample} + \delta ] = 1\)
F1 score results on synthetic data where predictive patterns include gaps (higher is better). Omen (a) and fOmen (b) without allowing for gaps (i.e., by setting a maximum–minimum window length factor \(g=1\)) do unsurprisingly poorly on data with gaps (i.e., data generated with a window factor \(k > 1\)). Omen performs surprisingly well until we plant patterns with significantly larger windows than we allow it to model. fOmen is much faster, allowing us to consider mine at a much larger gap factor (\(g=5\)), but overall performs worse than Omen as it is more susceptible to randomly generated (not planted) pattern occurrences
To evaluate how well our methods recover patterns with gaps, we consider a setting where we increase k in the experiment generation from 1 (no gaps) to 5 (window 5 times longer than the actual pattern). We present the results in Fig. 12. Our base setup is to either not allow any gaps (\(g=1\)) and allowing for a minimal window lengths of up to twice the length of the discovered pattern (\(g=2\)). By its efficiency, we also consider fOmen with windows of up to 5 times the pattern length.Footnote 6
We observe that if do not allow for gaps, yet plant patterns with increasing window length, performance quickly converges to 0. When we do allow for gaps up to factor of twice the pattern length, we see that Omen recovers (close to) all patterns and does so up to a planted window length of \(k=3\), after which performance deteriorates. fOmen shows the same performance for \(g=1\), and somewhat worse results for \(g=2\). As it is much more efficient than Omen, we can also run it with a much higher gap factor of 5, which coincides with a much larger search space. We see that for this large gap factor the results are reasonable at best—by allowing for such large windows, it gets confused by random ‘patterns’ that are only due to chance.
6.6 Evaluating on data with large time delays
In our final experiment in synthetic data, we evaluate how well our methods deals with overlapping predictions, as shown in Fig. 4. In particular, we aim to compare our two alignment approaches. To this extend ,we generate data where we slowly increase the expected overlap. We start with our usual experimental setup of 20 predictive and 10 frequent patterns, except that we now set the median of our planted delay distribution to 350, and slowly increase the number of pattern occurrences. We start by sampling from the range [10, 50] and shift it up to [100, 500]. This slowly increases the number of pattern and therefore the likelihood that pattern predictions will overlap. We report the result in Fig. 13.
For low overlap, we observe that AlignFar does significantly worse than AlignNext, which is explained by the small number of pattern occurrences; given the small pattern occurrences relative to the sequence length it is very likely that there exists a better alignment for pattern generated by chance. The bias of AlignNext toward interesting events that happen closer to the pattern occurrences here helps it to discover the correct patterns. Once we increase the overlap, however, we see that AlignFar-based methods quickly start to perform on par with AlignNext, and for an expected frequency of 120 and up it overtakes it. We further see that for particularly high expected frequencies, fOmen with AlignFar consistently performs best.
6.7 Evaluating on real data
Last, we evaluate our methods on real-world data. We consider three datasets, electrocardiograms (ECG) of an exercise stress test, a daily activities log (Lifelog) and water levels combined with precipitation records (Saar). We give the basic statistics in Table 1. Since fOmen and AlignFar essential reported the same patterns, analog performance relative to Omen as for the synthetic data, we present the results reported by Omen with the AlignNext; we compare to Sqs and Scis. As Sqs allows for gaps, and real-world patterns might show these, we interpret its results as minimal windows for which we again use the Omen score and alignment to determine which ones are predictive.
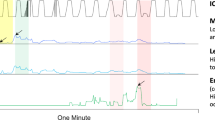
On the ECG dataset, the goal is to find patterns that predict the occurrence of a heartbeat. Our dataset is based on the first record (id 300.1) of the MIT-BIH ST Change Database.Footnote 7 We subsampled the record, replacing each 5 subsequent values with their average, transformed the result into a relative sequence by replacing each value with the difference to the previous value. Finally, using SAX [24] we discretize the sequence to 3 symbols. The heartbeats are annotated in the data. As we do not permit instantaneous predictions, we shift the annotation slightly forward such that they are strictly before the heartbeat.
When we run it on this data, Sqs discovers 12 patterns out of which only one is predictive: It corresponds to the previous heartbeat. Scis requires a window length, which we set to the approximate length of one cardiac cycle, excluding the heartbeat (\(w=40\)), for which it then returns \(41\,318\) patterns. Omen needs 1.9 seconds to discover two predictive patterns that together compress Y to only \(65\%\) of the number of bits needed by the null model. The first pattern corresponds to the previous heartbeat, the discovered time delay distribution exhibits structure of a bimodal normal distribution. We visualize this pattern in Fig. 14. Closer inspection of the data shows that the data are indeed composed of two different modes, high and low intensity exercises.
Next we consider Lifelog, which is based on the life of Sacha Chua who logs and publishes all her daily activities.Footnote 8 We considered the data over 2017, removing any activities with having the same start and stop timestamp. As this dataset provides many events that are potentially interesting, we consider every \(e \in \varOmega \) as target and have 40 target sequences with \(Y[i] = 1\) iff \(X[i] = e\). In addition, we consider a Y where we marked all business related activities as interesting.
Over all these targets, Scis discovers on average 695 patterns, many of which are redundant and not all make intuitive sense. While Sqs only discovers 3 predictive patterns, these do make sense: Cook, Dinner \(\rightarrow \) Clean the Kitchen and Subway, Social \(\rightarrow \) Subway. Omen takes between 0.005 and 5.9 seconds per dataset and overall discovers 32 patterns. Many of these, such as Sleep \(\rightarrow \) Childcare, Cook \(\rightarrow \) Dinner, and Dinner \(\rightarrow \) Clean the Kitchen, predict the next action, i.e., a time delay distribution with a peak at 1. A more interesting pattern is Subway \(\rightarrow \) Subway which has its peak at \(\delta =2\), and for which a natural interpretation is that Sacha takes the subway, logs on average one activity, and then takes the subway back.
Finally, we consider the Saar dataset [5], where the goal is to use daily precipitation recordsFootnote 9 to explain the rise (Saar-Rise) or fall (Saar-Fall) of the Saar riverFootnote 10 by 10cm or more over one day. We considered the timespan from 2007 to 2018. We discretize the values to 17 symbols using \(\lceil \log _{1.25} 1+x \rceil \) where we accumulate all values \(\ge 15\) into one symbol.
With Scis (\(w=10\)), we discover more than 400 patterns from either dataset. Most make little to no sense, such as that two successive days without rain predict a rise in water level. Sqs does not discover any descriptive nor predictive patterns. For both datasets, Omen terminates within 0.08 seconds and only reports singleton patterns. It finds, for example, that the more it rains, the more likely it is for the Saar to have risen by 10cm or more, either by the next day, or even two days later. For Saar-Fall, we find an interesting pattern that expresses that approximately three days after heavy rain the water levels quickly drop—which indeed is likely as the water levels first rose due to rain.
7 Discussion
The experiments showed that both Omen and fOmen work well in practice. We saw that the Omen score is very good at telling predictive from spurious patterns, and that the mining algorithms are able to reconstructs the ground truth without picking up spurious or redundant patterns. In experiments on synthetic data, we observed that it is highly robust against noise and can handle patterns with large gaps and high time delays, whereas the state of the art fails to report meaningful patterns. On real-world data, we showed that it discovers easily interpretable patterns that reliably explain our target events. The results of the ECG experiment demonstrate that Omen finds interesting patterns and time delay distribution that represent the real-world data well. In summary, on all considered settings it discovers small, easily interpretable, and non-redundant sets of reliable patterns that together predict the interesting events well.
We do observe that when we planting particularly long patterns with high occurrences, Omen tends to report partial rather than complete patterns. That is, if we plant pattern \( abcdef \), Omen is likely to report \( abcd \) whenever that is already sufficient to accurately predict all interesting events that \( abcdef \) matches. It is easy to see why this is the case, as our score is only concerned with describing Y as succinctly as possible and hence does not provide any incentive to extend patterns further than strictly necessary. As in certain cases it is important to retrieve the entire predictive pattern, we plan to extend Omen to report longer patterns when possible. One possible approach, to this end, is to additional encode \(X \) along with \(Y \) creating an incentive for longer patterns.
Although Omen is effective at discovering meaningful patterns, it currently considers a relatively simple pattern language. At the expense of additional computation, it is straightforward to extend our score and search to sequences with complex multivariate patterns [3]. In a similar line of thought, we currently model time delay distributions nonparametrically. While this comes with the advantage of not being restricted to any specific distribution, it does increase the sample complexity of our method—we may miss certain patterns or fail to predict certain events, simply because we have too little data to model the delay distribution well. It hence makes sense to contemplate an extension of Omen where we model the delay distributions parametrically, e.g., using domain knowledge to choose it as a Gaussian or Poisson distribution, as this will permit discovering more subtle patterns. A challenge with such an approach will be to find truly significant patterns.
We consider mining predictive rather than causal patterns. We do note, however, the close kinship between the two, in the sense that the discovered pattern could cause our interesting event. We share at least one common assumption: A cause needs to precede the effect in time [15, 26]. It will be interesting to explore under which additional conditions (assumptions) our patterns are indeed causal. By encoding Y using delay distributions that are independent of the actual pattern occurrences in X, our framework naturally fits the algorithmic model of causality [20], which could explain why our score performs so well in comparison with Cute [5] and Tent [32]. By explicitly maximizing this independence, we could possibly adapt Omen to discover sequential patterns that are causal under the additive noise model [19, 33], which is an interesting direction for future work.
8 Conclusion
We considered the problem of discovering small sets of sequential patterns that not only predict that something interesting will happen, but for which it is additionally easy to tell how long it will be until the predicted event. We formulated the problem in information-theoretic terms using the Minimum Description Length principle. As the resulting problem does not lend itself to efficient exact optimization, we propose the Omen and fOmen to heuristically discover good pattern sets. Both rely on a method to infer an initial alignment between pattern occurrences and interesting events, for which we propose two algorithms one general purpose one and an alternative approach which is particular adapt at long-range predictions. Extensive evaluation on synthetic and real-world data showed that Omen and fOmen compare favorably to the state of the art. In particular, our score performs very well in telling predictive from associative patterns, even under large quantities of noise. Omen efficiently discovers high-quality sets of predictive patterns which give clear insight into the data generating process. In future work, we will focus on generalizing the pattern language, as well as investigating under which conditions we can discover sequential patterns that are causal.
Notes
We say an event is used if it is part of pattern that is aligned to an interesting event.
Equal elements in the set are gracefully treated, but they still contribute to the complexity of the algorithm.
tp = true positives, fp = false positives, tn = true negatives, fn = false negatives.
Technically we allow for window of length \(g\times l+1\) where g is the gap factor and l the pattern length, except for no gaps case (\(g=1\)).
https://www.dwd.de/DE/leistungen/klimadatendeutschland/klarchivtagmonat.html (Ensheim weather station).
Measured at Sankt Arnual by the German Federal Institute of Hydrology (BfG).
References
Aggarwal CC, Han J (eds) (2004) Frequent pattern mining. Springer
Batal I, Cooper GF, Fradkin D, Harrison J, Moerchen F, Hauskrecht M (2016) An efficient pattern mining approach for event detection in multivariate temporal data. Knowl Inf Syst 46(1):115–150
Bertens R, Vreeken J, Siebes A (2016) Keeping it short and simple: summarising complex event sequences with multivariate patterns. In: Proceedings of the 22nd ACM international conference on knowledge discovery and data mining (SIGKDD), San Francisco, CA, pp 735–744
Bhattacharyya A, Vreeken J (2017) Efficiently summarising event sequences with rich interleaving patterns. In: Proceedings of the SIAM international conference on data mining (SDM), Houston, TX, SIAM, pp 795–803
Budhathoki K, Vreeken J (2018) Causal inference on event sequences. In: Proceedings of the SIAM international conference on data mining (SDM), San Diego, CA, SIAM, pp 55–63
Chen Y, Rangarajan G, Feng J, Ding M (2004) Analyzing multiple nonlinear time series with extended granger causality. Phys Lett A 324(1):26–35
Corbière C, Thome N, Bar-Hen A, Cord M, Pérez P (2019) Addressing failure prediction by learning model confidence. pp 2898–2909
Cover TM, Thomas JA (2006) Elements of information theory. Wiley, New York
Cüppers J, Vreeken J (2020) Just wait for it... mining sequential patterns with reliable prediction delays. In: Proceedings of the 20th IEEE international conference on data mining (ICDM), Virtual Event, Sorrento, Italy
Edmonds J, Karp RM (1972) Theoretical improvements in algorithmic efficiency for network flow problems. J ACM 19(2):248–264
Egho E, Gay D, Boullé M, Voisine N, Clérot F (2017) A user parameter-free approach for mining robust sequential classification rules. Knowl Inf Syst 52(1):53–81
Fowkes J, Sutton C (2016) A subsequence interleaving model for sequential pattern mining. In: Proceedings of the 22nd ACM international conference on knowledge discovery and data mining (SIGKDD), San Francisco, CA, pp 835–844
Galbrun E, Cellier P, Tatti N, Termier A, Crémilleux B (2018) Mining periodic patterns with a mdl criterion. In: Proceedings of the European conference on machine learning and principles and practice of knowledge discovery in databases (ECML PKDD), Dublin, Ireland, Springer, pp 535–551
Gerber MS (2014) Predicting crime using twitter and kernel density estimation. Decis Supp Syst 61:115–125
Granger CW (1969) Investigating causal relations by econometric models and cross-spectral methods. Econometrica: 424–438
Grünwald PD, Grunwald A (2007) The minimum description length principle. MIT press
Hagberg AA, Schult DA, Swart PJ (2008) Exploring network structure, dynamics, and function using networkx. In: Varoquaux G, Vaught T, Millman J (eds) Proceedings of the 7th Python in Science conference, Pasadena, CA USA, pp 11 – 15
Hooi B, Faloutsos C (2019) Branch and border: partition-based change detection in multivariate time series. In: Proceedings of the SIAM international conference on data mining (SDM), Alberta, Canada, SIAM, pp 504–512
Hoyer P, Janzing D, Mooij J, Peters J, Schölkopf B (2009) Nonlinear causal discovery with additive noise models. pp 689–696
Janzing D, Scholkopf B (2010) Causal inference using the algorithmic markov condition. IEEE Trans Inf Technol 56(10):5168–5194
Laxman S, Sastry PS, Unnikrishnan KP (2007) A fast algorithm for finding frequent episodes in event streams. In: Proceedings of the 13th ACM international conference on knowledge discovery and data mining (SIGKDD), San Jose, CA, ACM, pp 410–419
Laxman S, Tankasali V, White RW (2008) Stream prediction using a generative model based on frequent episodes in event sequences. In: Proceedings of the 14th ACM international conference on knowledge discovery and data mining (SIGKDD), Las Vegas, NV, pp 453–461
Li M, Vitányi P (1993) An introduction to kolmogorov complexity and its applications. Springer
Lin J, Keogh E, Wei L, Lonardi S (2007) Experiencing sax: a novel symbolic representation of time series. Data Min Knowl Discov 15(2):107–144
Mannila H, Toivonen H, Verkamo AI (1997) Discovery of frequent episodes in event sequences. Data Min Knowl Discov 1(3):259–289
Pearl J (2009) Causality: models, reasoning and inference, 2nd edn. Cambridge University Press
Radinsky K, Horvitz E (2013) Mining the web to predict future events. In: WSDM, pp 255–264
Rissanen J (1978) Modeling by shortest data description. Automatica 14(5):465–471
Rissanen J (1983) A universal prior for integers and estimation by minimum description length. Ann Stat 11(2):416–431
Saadallah A, Jakobs M, Morik K (2021) Explainable online deep neural network selection using adaptive saliency maps for time series forecasting. In: Proceedings of the European conference on machine learning and principles and practice of knowledge discovery in databases (ECML PKDD), Virtual
Scharwächter E, Müller E (2020) Two-sample testing for event impacts in time series. In: Proceedings of the SIAM international conference on data mining (SDM), SIAM, pp 10–18
Schreiber T (2000) Measuring information transfer. Phys Rev Lett 85(2):461
Shimizu S, Hoyer PO, Hyvärinen A, Kerminen A (2006) A linear non-gaussian acyclic model for causal discovery. J Mach Learn Res 7:2003–2030
Tatti N (2014) Discovering episodes with compact minimal windows. Data Min Knowl Discov 28(4):1046–1077
Tatti N, Vreeken J (2012) The long and the short of it: summarising event sequences with serial episodes. In: Proceedings of the 18th ACM international conference on knowledge discovery and data mining (SIGKDD), Beijing, China, pp 462–470
Wang J, Han J, Li C (2007) Frequent closed sequence mining without candidate maintenance. IEEE Trans Knowl Data Eng 19(8):1042–1056
Weiss GM, Hirsh H (1998) Learning to predict rare events in event sequences. Proc ACM Int Conf Knowl Discov Data Min (SIGKDD) 98:359–363
Wu Q, Gao Y, Gao X, Weng P, Chen G (2019) Dual sequential prediction models linking sequential recommendation and information dissemination. In: Proceedings of the ACM international conference on knowledge discovery and data mining (SIGKDD), pp 447–457
Wu Z, Pan S, Long G, Jiang J, Chang X, Zhang C (2020) Connecting the dots: multivariate time series forecasting with graph neural networks. In: Proceedings of the ACM international conference on knowledge discovery and data mining (SIGKDD), ACM, Virtual Event CA USA, pp 753–763
Yeh CCM, Kavantzas N, Keogh E (2017) Matrix profile IV: using weakly labeled time series to predict outcomes. Proc VLDB Endow 10(12):1802–1812
Zhao L, Ye J, Chen F, Lu CT, Ramakrishnan N (2016) Hierarchical incomplete multi-source feature learning for spatiotemporal event forecasting. In: Proceedings of the ACM international conference on knowledge discovery and data mining (SIGKDD), pp 2085–2094
Zhou C, Cule B, Goethals B (2015) A pattern based predictor for event streams. Expert Syst Appl 42(23):9294–9306
Zhou C, Cule B, Goethals B (2016) Pattern based sequence classification. IEEE Trans Knowl Data Eng 28(5):1285–1298
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Refinement algorithms
1.1 Omen refinement
When adding a pattern to our model we fist refine, i.e., extend it, to the best version we can find, we do so in a greedy fashion. We give the pseudo-code for refining a pattern as Algorithm 3. We start with a pattern s (l. 1) and consider the extensions es and se, where \(e \in \varOmega \), and choose the one with maximal frequency. To do so efficiently, we only consider events e that are adjacent to pattern occurrences that are currently aligned to an interesting event (l. 3–4). The key idea is that extending a pattern makes it more specific and hence reduce recall—while, by maintaining the current predictions, we maximize precision. We repeat this process until our optimistic estimator no longer gives a better estimation than the best seen pattern up to this point. We then return that pattern with lowest \(L_{s}(R)\).

1.2 fOmen refinement

When we find a compressing pattern, we greedily refine it to its most compressing form. We do this by combining our compressing pattern with the candidate pattern that has the highest intersection of predicted interesting events. We repeat this process until our optimistic estimator no longer estimates a better refinement. From the chain of created patterns, we return the most compressing version. As Algorithm 4, we give the pseudo-code of the refinement procedure.
Experiments
1.1 Evaluation metric
As metric to evaluate success, we consider a mapping between planted and discovered patterns. Where we map each reported pattern to at most one planted pattern and to each planted pattern at most one reported pattern, we allow a mapping between two patterns if the found pattern is a subsequence of the planted one or vice versa. We choose the mapping that results in the maximum number of pairs. To find the maximum number of pairs, we reformulate the problem as a flow network optimization problem. And compute the maximum flow. We connect each planed pattern to our source and each found pattern to the sink. We connect a planted to a found pattern if the found is a subsequence of the planted one or vice versa. The capacity of all links is set to one. We then compute the maximum flow of the created flow network which maximizes the number of planted, found pairs. This setup ensures that we match at most one found pattern to a planted pattern and vice versa. We maximize the flow using the Edmonds–Karp Algorithm [10] implemented by Hagberg et al. [17]. In Fig. 15, we give a toy example of such a flow network.
While there might exist multiple equivalent pairing solutions, this is not a problem for us, as we are not interested in the actual pairing. In the example shown in Fig. 15, we find pattern ab with just the pattern we do not know if it is a partial pattern of the planted pattern abcd or abe or both and hence count it as one correctly found pattern, which means we did not find, according to our evaluation metric, either pattern abcd or abe.
1.2 Additional experiment results
In Sect. 6, we show the F1 results for synthetic data. Here, we provide the recall and precision results for destructive noise in Fig. 16, additive noise in Fig. 17, and for both additive and destructive (combined) noise in Fig. 18. For all three settings, we see that Omen and fOmen have near perfect precision, whereas the recall scores reflect the F1 scores. From this, we can conclude as the signal-to-noise ratio increases, it becomes more difficult to find the planted patterns but our scores correctly filters non-predictive patterns even under high noise.
Lower is better. fOmen discovers models close to the ground truth for destructive (a), additive (b), and combined (c) noise. Plots show bits needed to encode \(Y \) given the null, planted, and discovered model. We show for each noise level the experiment with the worst performance, i.e., where the difference, in bits, between discovered and planted model is greatest
Lower is better. Omen discovers models close to the ground truth for destructive (a), additive (b), and combined (c) noise. Plots show bits needed to encode \(Y \) given the null, planted, and discovered model. We show for each noise level the experiment with the worst performance, i.e., where the difference, in bits, between discovered and planted model is greatest
In Figs. 19 and 20, we report the worst model discovered by Omen and fOmen, respectively. The worst model is the one that has the largest difference between the number of bits needed to encode \(Y \) compared to the ground truth model. We see that there are no big differences between the average and the worst case showing that Omen and fOmen return consistently good models.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cüppers, J., Kalofolias, J. & Vreeken, J. Omen: discovering sequential patterns with reliable prediction delays. Knowl Inf Syst 64, 1013–1045 (2022). https://doi.org/10.1007/s10115-022-01660-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10115-022-01660-1