Introduction

Participatory Integrated Assessment (PIA) refers to a transdisciplinary process for organizing and combining the constituent elements of a sustainability problem into a harmonious scheme to improve environmental planning and decision-making (Ridder and Pahl-Wostl 2005; de Ridder et al. 2007; Holman et al. 2008; Salter et al. 2010). A transdisciplinary process involves the integration of diverse perspectives, knowledge, and methods from different disciplines to address complex issues and entails ongoing communication and collaboration with stakeholders (Brandt et al. 2013; Scholz and Steiner 2015a, 2015b; Bojórquez-Tapia et al. 2021a). PIA has been used to engage governments, civil society, and investors in devising and implementing practical solutions to sustainability issues and concerns (Delmotte et al. 2016; Van Soest et al. 2019). Ideally, PIA involves forecasting futures and transcending disciplinary worldviews to address wicked problems that lack definitive solutions, i.e., multi-causal, technically complex, controversial, and contested problems (Rittel and Webber 1973). Thus, the outputs of PIA should help identify the pathways toward sustainable development (de Kraker et al. 2011; Wise et al. 2014).

The PIA process is not without its challenges. It involves dealing with large amounts of information and diverse sources of knowledge (Rotmans and van Asselt 2001). PIA entails a multi-scalar and multi-sectoral process, which requires the involvement of stakeholders from different sectors and at different levels of governance (van de Kerkhof 2001). Thus, achieving the PIA ideal concerns the systemic and enabling dimensions of sustainable development (Bojórquez-Tapia et al. 2022). The systemic dimension addresses the complex interdependencies of socio-ecological systems. The enabling dimension deals with socio-political processes underlying the decisions of public and private actors (Pereira et al. 2018; Small et al. 2019; Cotterman et al. 2021). This underscores the need for a more comprehensive and integrated approach to PIA that considers the technical and socio-political scopes of sustainability issues (van Asselt and Rotmans 2002; Siebenhüner and Barth 2005; Villamor et al. 2022). In practice, however, the multidimensional context of PIA presents substantial conceptual and methodological challenges, not the least of which is unveiling the different forms of uncertainty present within both the systemic and enabling dimensions (Bojórquez-Tapia et al. 2022). Typically, these challenges can be addressed through Decision Making under Deep Uncertainty (DMDU), an advanced decision analytics framework to portray alternative future states of the world (SOW) (Lempert et al. 2003; Marchau et al. 2019; Malekpour et al. 2020).

Nevertheless, the implementation of the PIA faces additional hurdles in countries of the Global South, like Mexico. In these cases, the chronic lack of knowledge and data hampers conventional PIA’s ability to comprehensively capture the intricacies of socio-ecological systems and empower stakeholders for effective decision-making. Therefore, these hurdles lead to the question: How can the effectiveness of PIA be enhanced in the context of the Global South? This question underscores the need for innovative approaches or methodologies that can overcome the limitations posed by inadequate data and knowledge.

In this paper, we introduce a PIA approach to efficiently integrate qualitative and quantitative data while addressing the systemic and enabling dimensions of sustainable development. Methodologically, one innovation of our approach is the integration of DMDU with qualitative simulation methods, unlike conventional DMDU approaches that rely on quantitative simulations. While we illustrate our approach through a case study—the Ecological Ordinance of the state of Yucatán, México—it can be applied to analyze any socio-ecological system at different scales. As the primary platform of PIA in Mexico, the Ecological Ordinance is a collaborative, multisectoral, environmental planning tool that seeks to identify the optimal zoning scheme of a territory, maximizing consensus on land suitability while minimizing intersectoral conflicts (Páez et al. 2020). As in PIA in general, a fundamental aspect of the Ecological Ordinance involves the step of forecasting the vulnerability of socio-ecological systems, impacted by sectoral activities and climate change. However, the forecasting step encounters significant limitations due to data scarcity and various forms of uncertainty encompassing complex drivers and adverse ecological effects, as well as subjective and contentious knowledge.

In the subsequent section, we provide a brief description of our study area and an overview of the theoretical and technical underpinnings of our PIA approach. Subsequently, we detail the methodological approaches we employed to address various forms of uncertainty. To maintain clarity, our “Results” section centers on examining the impact of urban and industrial sprawl on the decline of coastal wetlands within one of the seven administrative divisions of Yucatán. In the last two sections, we examine the advantages and limitations of employing qualitative DMDU to enhance PIA’s capacity in integrating diverse forms of knowledge into actionable information for environmental planning.

Background

Study area

Yucatán, covering 39,524 km2 in the northern part of the Yucatán Peninsula, is administratively divided into seven Regions: I West, II Northeast, III Central, IV Central Coast, V Northeast, VI East, and VII South (Fig. 1). The environmental sensitivity of Yucatán is significantly influenced not only by the high porosity and permeability of its underwater platform (Escolero et al. 2000; Bauer-Gottwein et al. 2011), which renders it highly prone to contamination (Marín and Perry 1994), but also by its expansive forest cover, accounting for 50% of the total area.

Fig. 1
figure 1

Administrative Regions (I–VII) of Yucatán, Mexico

Full size image

Participatory Integrated Assessment

Based on Salter et al. (2010), our PIA consists of three key components: structure, participatory mechanisms, and outcome. Structure pertains to the overarching analytical framework employing Ecological Risk Assessment (Norton et al. 1992; Eduljee 2000; Hope 2006). Participatory mechanisms involve engaging stakeholders through mediated modeling (van den Belt 2004) supported by simulation modeling techniques, such as K-Simulation (KSIM) (Kane 1972; Kane et al. 1973) and DMDU. Lastly, the outcome refers to the ultimate goal of developing early warning indicators of ecological risk (from now on “indicators”) (Rodríguez-Izquierdo et al. 2019; Bojórquez-Tapia et al. 2021b) based on the probability of effects caused by different drivers (Calow 1998; Eduljee 2000; Chapman et al. 2003; Hope 2006). The term adverse ecological effects (from now on “effects”) refers to a disturbance that results in an undesirable state of the environment. These effects may be expressed as deterministic, probabilistic, or qualitative estimates (Norton et al. 1992). Drivers are exogenous stressors of an ecosystem that can be of different nature (e.g., water pollution, habitat destruction, and fishing overexploitation).

We adopt a probabilistic approach and thus follow the three general phases of Ecological Risk Assessment (Eduljee 2000; Hope 2006): (1) problem formulation, (2) analysis, and (3) risk characterization. Problem formulation entails framing the problem and defining the system’s composition (elements) and structure (linkages between elements) (Bunge 2004). The analysis involves collecting and evaluating different types of information, assumptions, and uncertainties to establish a credible, legitimate, and salient scientific representation (Cash et al. 2003). Risk characterization involves the estimation, evaluation, and interpretation of ecological risks (Eduljee 2000). Following the Ecological Risk Assessment framework, our PIA addresses both the systemic and enabling dimensions of sustainable development, accounting for the various forms of uncertainty inherent in socio-ecological systems (Table 1).

Table 1 Forms of uncertainty (elaborated from Bojórquez-Tapia et al. 2022)
Full size table

Phase 1: problem formulation

Problem formulation (phase 1) entails the implementation of mediated modeling—an interactive participatory approach to develop a system dynamic model (van den Belt 2004). It aims to tackle the enabling dimension by involving stakeholders in framing the problem and defining the socio-ecological system. The complexity of dynamic behavior in socio-ecological systems often exceeds individual cognitive capacity, making it difficult to fully comprehend the long-term consequences of human actions at multiple scales (García 2006).

In mediated modeling, stakeholders work with a modeling team through five general steps (van den Belt 2004): (1) development of a preliminary model as an influence diagram that describes the system in terms of causalities between elements interconnected by arrows (Mendoza and Prabhu 2006; Meadows 2008); (2) collaborative translation of the preliminary model into a formal model; (3) calibration based on knowledge, observed past behavior, and information; (4) exploration of alternative scenarios; and (5) evaluation of the desirability of the potential outputs. In our PIA, this collaborative approach is supported by a system dynamics software to enable a rigorous and replicable representation of the socio-ecological system (Bryant and Lempert 2010; Bojórquez-Tapia et al. 2017; Rodríguez-Izquierdo et al. 2019).

Phase 2: analysis

Analysis (phase 2) involves forecasting scenarios related to effects. Considering the intricate context and specific challenges encountered in PIA within the Global South, our forecasting tools are based on a qualitative implementation of DMDU. As a framework, DMDU encompasses a set of computational approaches that incorporates advanced decision analytics and stakeholder engagement procedures, such as Dynamic Adaptive Policy Pathways, Robust Decision-Making, Decision Scaling, and Info-Gap Decision Theory (Lempert et al. 2003; Marchau et al. 2019). Conventionally, this framework employs exploratory modeling and scenario discovery to examine alternative model structures and system values (Hadjimichael et al. 2020a; Kwakkel et al. 2013; Lempert et al. 2006; Bankes 1993). Drawing from Herman et al.’s (2015) taxonomy, our approach employs the stochastic version of KSIM in exploratory modeling to generate alternative SOW that are later evaluated to identify thresholds associated with effects through scenario discovery.

Operationally, exploratory modeling entails the implementation of many computational experiments with specific structural and parameterization conditions (Moallemi et al. 2020), revealing how a synthetic world would behave under those given conditions (Kwakkel et al. 2013; Hadjimichael et al. 2020b). In our PIA, exploratory modeling is implemented using Monte Carlo simulation, which requires the differential equation of the KSIM (Kane 1972) to emphasize the significance of the socio-ecological system’s complex and dynamic interdependencies rather than numerical predictions.

$$\begin{array}{cc}\frac{dx_{it}}{dt}=-x_{it}\ln x_{it}\left(\sum\limits_j^J\alpha_{ij}x_{jt}\sum\limits_j^J\beta_{ij}{\dot x}_{jt}\right),\forall i=1,2,\dots,I;&j=1,2,\dots,J\end{array}$$
(1)

where \({\dot{x}}_{jt}\) is the derivative of xj with respect to time; t, αij and βij are the values of the two interaction matrices Q = |I × J|.

KSIM is a dynamic modeling technique that generates graphs showing a system’s behavior over time, based on its causal mechanisms (Burns and Marcy 1979; Mohapatra and Vizayakumar 1989). This technique has been used in environmental impact assessment (Bojórquez-Tapia 1989), forecasting (Wissema and Benes 1980), natural resource management (Kane et al. 1973), and electricity generation projects (Weimer-Jehle 2006). KSIM is founded on the following postulates (Kane 1972; Kane et al. 1973): (1) all variables are state variables and are bounded; therefore, they cannot increase nor decrease indefinitely; (2) a variable increases or decreases according to the net interaction of other variables; (3) a variable’s response to a given interaction decreases to zero as that variable approaches its upper or lower bound; therefore, the response of a variable is sigmoidal; (4) all other things being equal, a variable will produce greater interaction on the system as it grows larger; (5) complex interactions are described by a looped network of binary interactions; therefore, the relationships between variables can be described using interaction matrices.

Postulate (1) implies that the values of the state variables, xit, are restricted to [0,1]. Postulates (2) and (4) imply that interactions on a variable are additive. Postulate (3) implies the modulation function (−xit ln xit) to generate the sigmoidal growth or decay effect. Postulate (5) implies the specification of the set of state variables, N, the initial conditions or quantities of each state variable, xi, and the set of interactions, Q = |N × N|, between variable pairs, qij = {xi, xj}, where qij is the interaction of j over i.

The interaction between a pair of variables, qij, is represented by matrices, Qα and Qβ, where the magnitude and type of an interaction are indicated in the corresponding cells. The impact can be represented as long-term (α-interactions), instantaneous (β-interactions), or both, while the type can be either positive or negative (Mohapatra and Vizayakumar 1989). Following our qualitative implementation of DMDU, Monte Carlo simulation involves the selection of the corresponding probability functions for xi0, αij, and βij.

Phase 3: risk characterization

Risk characterization (phase 3) involves implementing DMDU scenario discovery to analyze the output of exploratory modeling. This phase aims to estimate, evaluate, and interpret the SOW concerning effects. Scenario discovery is a technique that uses machine learning (i.e., artificial intelligence approach to identify patterns through algorithms) to analyze massive simulation runs and identify the SOW that exceeds predefined thresholds (Hadjimichael et al. 2020a; Kwakkel et al. 2013; Lempert et al. 2006).

An essential aspect of this phase is defining indicators that serve as signal alerts when the system approaches a critical transition point—stage beyond which the system becomes vulnerable and transforms into an undesirable condition (Scheffer et al. 2012; Dakos and Bascompte 2014). Within our PIA approach, indicators are deployed to assess the vulnerability of the socio-ecological system to prevent ecological risks.

Methods

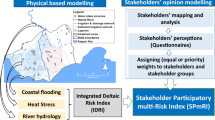
The forecasting step within Yucatán’s Ecological Ordinance aimed to evaluate the vulnerability of its socio-ecological system to different drivers. This step, aligned with the three-phased Ecological Risk Assessment framework, consisted of specific tasks and outputs designed to tackle various forms of uncertainty (Fig. 2).

Fig. 2
figure 2

Three-phased PIA of the forecasting step of the Ecological Ordinance in Yucatán

Full size image

Phase 1: problem formulation

Phase 1 of the PIA focused on the development of the socio-ecological system of Yucatán using mediated modeling. During problem formulation, we addressed three forms of uncertainty: (1) Knightian, concerning climate change, future technological demands across different sectors, and the synergistic relationships among population growth and urban sprawl; (2) ambiguity, concerning the different knowledge frames of the stakeholders regarding the definition of the socio-ecological system; and (3) linguistic, concerning the discursive interactions of stakeholders.

To address both Knightian uncertainty and ambiguity, we conducted interviews and surveys with stakeholders from various backgrounds, including governmental entities, businesses, industries, cooperatives, civil society organizations, academic and research institutions, and concerned citizens. Additionally, we identified the drivers by referencing specialized and gray literature. These drivers included (1) urban and industrial sprawl, (2) agriculture, (3) cattle ranching, (4) swine and poultry plants, (5) tourism, (6) power generation, and (7) climate change. To address linguistic uncertainty, we proceeded by developing preliminary models for each of the identified drivers, as mandated by mediated modeling practices. These models comprised influence diagrams intended to illustrate the causal mechanisms steering systemic change. Our objective was to establish a common language and comprehension of system dynamics, addressing challenges arising from stakeholders’ discursive interactions. These challenges encompassed inaccurate expressions and polysemous terms regarding the causal mechanisms.

Subsequently, a series of workshops was conducted to collectively translate the preliminary influence diagrams into KSIM models. Each workshop, dedicated to a specific driver of change, involved representatives from the private, governmental, and social sectors. The organization of these workshops adhered to established formalized procedures in Mexico for the Ecological Ordinance. A total of 391 stakeholders participated, with varying numbers of attendees from each sector and workshop (further information given in the Online Resource 1). Throughout each workshop, participants assessed and adjusted the preliminary influence diagrams using their expertise and experiences. Next, participants established both type and magnitude for xi0, αij, and βij employing the following linguistic scale:

$${\alpha}_{ij}={\beta}_{ij}=\left\{\textrm{VL}\ \left(\textrm{very}\ \textrm{low}\right),\textrm{L}\ \left(\textrm{low}\right),\textrm{M}\ \left(\textrm{moderate}\right),\textrm{H}\ \left(\textrm{high}\right),\textrm{VH}\ \left(\textrm{very}\ \textrm{high}\right)\right\}$$

The linguistic scale was converted into numerical category cuts within the range [1, 9] and was considered to be inputs for constructing Qα and Qβ.

$${\alpha}_{ij}={\beta}_{ij}=\left\{\textrm{VL}=1,\textrm{L}=3,\textrm{M}=5,\textrm{H}=7,\textrm{VH}=9\right\}$$

The workshops’ activities were designed to shape a salient, legitimate, and credible analytical framework—a foundation conducive to consensus-building, as highlighted by Pedroza et. al (2020). Facilitators of the modeling team oversaw the overall problem formulation process providing participants the opportunity to equally contribute and express their opinions or concerns. The facilitators synthesized the knowledge, information, and viewpoints shared by the participants to create a unified understanding of the multifaceted interdependencies of the socio-ecological system. At the end of phase 1, an influence diagram for each of the seven drivers and the corresponding Qα and Qβ matrices were obtained.

Phase 2: analysis

Phase 2 of the PIA focused on the analysis of the socio-ecological system using exploratory modeling to generate multiple representations of future SOW. An integrated socio-ecological system model was developed by consolidating the seven influence diagrams developed in the previous phase (a description of the model is given in the Online Resource 1). Exploratory modeling was implemented by means of KSIM and Monte Carlo simulation to address three forms of uncertainty: (1) ontological, concerning the necessary assumptions of the specific entities, properties, and causal mechanisms underlying the relationships between drivers and state variables; (2) epistemic, concerning the lack of data and information about the initial conditions and trends of both drivers and state variables; and (3) deep, concerning the lack of consensus among participants of alternative model formulations and the implications of ecological risk.

Regarding ontological uncertainty, adhered to the recommendation put forth Holling (1980: p.13), analysis entailed the consolidation, refinement, and testing of the socio-ecological system model by the modeling team. In this way, we were able to deal with the diversity of variables, objectives, time horizon, and spatial extent that are involved in the drivers affecting the socio-ecological system. Regarding epistemic uncertainty, the model was calibrated using information collected from stakeholders, distribution maps of sectoral activities, and statistical data on past behavior. The calibration process involved a comparison between the prognostic outputs generated by the KSIM and the observed behavior of the seven Regions of Yucatán, as inferred from the knowledge of the participants and the historical trends. The parameters αij and βij were iteratively adjusted to optimize the concordance between the simulated and empirical data. Regarding deep uncertainty, uniform probability functions were assigned to xi0, αij, and βij, with the lower and upper limits established using the values obtained during phase 1 and complemented with the stakeholders’ judgments during analysis. Exploratory modeling involved implementing KSIM and executing 1000 Monte Carlo simulations using the software Crystal Ball®. At the end of phase 2, the results of exploratory modeling included the integrated socio-ecological system model for each of the seven administrative Regions, along with their respective 1000 SOW.

Phase 3: risk characterization

Phase 3 of the PIA focused on the detection of the worst SOW as vulnerable states of the socio-ecological system. Vulnerability, which refers to the susceptibility of a system to damage or harm, was measured using the exposure-sensitivity-adaptive capacity scheme (Eakin and Luers 2006). Vulnerability, vm, was quantified with Eq. (2) as the change in a state variable, ∆xm, caused by a driver, ∆xl, relative to a predetermined threshold, ρm, and normalized by the closeness of the system variable, xm, to the threshold, κm (Luers et al. 2003; Luers 2005):

$${v}_m=\frac{\left|\frac{\Delta {x}_m}{\Delta {x}_l}\right|}{\kappa_m}$$
(2)
$${\kappa}_m=\left\{\begin{array}{c}\frac{x_m}{\rho_m},\textrm{if}\ {x}_m\to {x}_m^{-}\kern0.5em \\ {}\frac{\rho_m}{x_m},\textrm{if}\ {x}_m\to {x}_m^{+}\ \end{array}\right.$$

where \({x}_m^{+}\) is the maximum value, \({x}_m^{-}\) is the minimum value, and m and l are indices for variables.

During phase 3, we identified two forms of uncertainty: (1) normative, concerning the different value judgments about the evolution of potential consequences of the public policies in the territory; and (2) politically induced, concerning the intersectoral deliberations among government representatives pertaining to the national agenda of geographically targeted strategies aimed at achieving conservation objectives. Regarding normative uncertainty, we identified the cause-effect interactions that corresponded to the Ecological Ordinance procedural issues established by law (DOF 2003). Regarding politically induced uncertainty, we identified indicators for the different drivers in a way that minimized regret in the long term. To address these forms of uncertainty, the output of phase 2 was compiled in a database and submitted to scenario discovery analysis. We performed scenario discovery through Classification and Regression Trees (Breiman et al. 1984; Hartshorn 2016) to obtain orthogonal subsets, Bk, from the data base \(\textrm{L}={\left\{{x}_m,{y}_m\right\}}_{m=1}^N\), where xm is a system state variable, ym is a binary variable, 𝑚 is the variable index, and N is the total number of parameters. The partition (“above” or “beneath” vm) was based on ym, which determined the membership of the orthogonal subset of xm from its vulnerability condition, vm, and the partition parameter, Cm:

$${y}_m=\left\{\begin{array}{c}1,\textrm{if}\ {v}_m<{C}_m\\ {}0,\textrm{if}\ {v}_m\ge {C}_m\end{array}\right.$$

In this way, if ym = 1, then xm ∈ Bk, and if ym = 0, then xm ∉ Bk. Progressively, further delimitations of Bk resulted in increasingly homogeneous subsets based on the Gini coefficient (Lerman and Yitzhaki 1989).

We obtained the Classification and Regression Tree that described each causal mechanism of interest to the stakeholders. Subsequently, we selected the Bk representing the most severe effects at the end of the 25-year simulation period, considering a minimum probability of occurrence of 5%. To compare the system states at the initial (t = 0) and the final (t = 25) simulation times, we employed parallel coordinates, a multidimensional visualization technique (Johansson and Forsell 2016; Savoska and Loskovska 2009). To evaluate the risk associated with these effects, we considered three factors: (1) the probability of occurrence as obtained from Bk; (2) the initial average value of the state variable, \({\overline{x}}_{j0}\); and (3) the mean change in the state variable over time \(\left({\overline{x}}_{j25}-{\overline{x}}_{j0}\right)\times 100\). At the end of phase 3, regional indicators were obtained.

Results

During the participatory workshops, the major concerns that emerged were the degradation of coastal wetlands (HUMC), forest cover (CFOR), and aquifer (VACUI) caused by urban sprawl (URB), agriculture expansion (AGR), and cultural and ecological tourism development (TUNT), respectively. To measure the extent of effects, we used the integrated socio-ecological system model with xi0, Qα and Qβ calibrated for Region IV (given in the Online Resource 2-4). We identified three causal mechanisms closely linked to the drivers and the state variables of concern (Fig. 3): (1) the decline in the functional integrity of coastal wetlands (↓HUMC), caused by the reduction in aquifer levels resulting from increased water consumption due to urban and industrial sprawl (URB → CONH2O → CANH2O → HUMC); (2) the increase of aquifer vulnerability (↑VACUI), caused by the increase of solid and liquid waste from the rise in cultural and ecological tourism (TUNT → SW/WW → VACUI); and (3) the decrease in forest cover area (↓CFOR), caused by the expansion of agricultural land (AGR → CFOR).

Fig. 3
figure 3

Exploratory modeling results of three drivers a urban and industrial sprawl (URB), b cultural tourism and ecotourism (TUNT), and c agriculture (AGR); and three state variables d coastal wetlands (HUMC), e aquifer vulnerability (VACUI), and f forest cover (CFOR). The average behavior is shown in darker gray, and the initial condition interval is written between parentheses

Full size image

In scenario discovery, we analyzed each of these causal mechanisms by utilizing the vulnerability binary variable and developed their corresponding Classification and Regression Trees. Accordingly, the binary variable for ↑URB →  ↓ HUMC was determined using Eq. (2):

$${v}_{HUMC}=\frac{\left|\frac{\Delta {x}_{HUMC}}{\Delta {x}_{URB}}\right|}{\kappa_{HUMC}}$$

Because the worst undesirable state corresponded to \({x}_{HUMC}^{-}\), then:

$${\kappa}_{HUMC}=\frac{x_{HUMC}^{-}}{\rho_{HUMC}}$$

We assumed that the vulnerability threshold corresponded to the current average state of coastal wetlands (HUMC); consequently, \({\rho}_{HUMC}={\overline{x}}_{HUMC,0}\). Results showed that the worst SOW was Bk ∈ CANH2O < 0.36 ∧ URB ≥ 0.61 (Fig. 4a), with a probability of occurrence of 0.20 with respect to the total number of cases. A close inspection of parallel coordinates (Fig. 4b) revealed the justification for an indicator. The annual rate of urban and industrial sprawl was \(\left(\ln {\overline{x}}_{URB,25}-\ln {\overline{x}}_{URB,0}\right)/25\times 100=\left(\ln 0.50-\ln 0.40\right)/25\times 100=1\%\), whereas the effect on coastal wetlands was equivalent to \(\left({\overline{x}}_{HUMC,25}-{\overline{x}}_{HUMC,0}\right)\times 100=\left(0.70-0.25\right)\times 100=35\%\). Regarding ↑URB →  ↓ HUMC, results suggested a 0.20 probability of an effect on coastal wetlands with a 1% annual rate of urban and industrial sprawl over the next 25 years. These effects would manifest as a decline in functional integrity equivalent to 35% of the current area occupied by coastal wetlands. Thus, the indicator cautions against a 1% annual increase in urban and industrial sprawl to prevent the undesirable decline of coastal wetlands caused by decreasing aquifer levels resulting from increased water consumption. An analogous procedure was employed to derive indicators of ecological risk for each causal mechanism within each Region (Table 2).

Fig. 4
figure 4

Scenario discovery of the effect of urban and industrial sprawl (URB) over coastal wetlands (HUMC): a Classification and Regression Tree and b parallel coordinates of the worst SOW

Full size image
Table 2 Regional indicators expressed as the percentage of the annual growth rate of the drivers (URB, urban and industrial sprawl; TUNT, cultural tourism and ecotourism; AGR,agriculture) and the percentage of change in the state variables (HUMC, coastal wetlands; VACUI,aquifer vulnerability; CFOR, forest cover) over a 25-year period; p, probability
Full size table

Discussion

Our findings align with van Asselt and Rijkens-Klomp’s (2002) assertion on the necessity of constructing scenarios to address the complexity and uncertainty of sustainability issues. While scenarios are valuable depictions of potential futures, a notable challenge lies in uncovering inherent uncertainties within modeling processes. These hidden uncertainties can undermine credibility, hindering consensus-building in the enabling dimension. Consequently, our focus was on systematically accounting for different forms of uncertainty across the three phases of the forecasting step within the Ecological Ordinance of Yucatán (Fig. 2).

During phase 1, addressing the irreducible forms of uncertainty was crucial for defining the scope (i.e., what was included and what was excluded) and boundaries (i.e., the limits of its applicability and the constraints on the inputs and outputs) of the integrated socio-ecological system model. The consideration of Knightian uncertainty guided us to exclude highly speculative elements from the model, such as technological advancements and emerging societal needs, as well as temperature fluctuations, forest fires, plagues, and vegetation transformations related to climate change. Moreover, restricting the simulation time to 25 years allowed us to overlook the impacts of climate change, assuming a stationary probability of hydrometeorological risk events. We argue that these decisions are consistent with other studies that have shown the consequences of uncertain or speculative variables regarding the reliability of results (Walker et al. 2002; Dietz et al. 2008).

To manage ambiguity and linguistic uncertainty, furthermore, we ensured uniform definitions and meanings for variables with the same names across the seven influence diagrams. This was necessary given the presence of highly polysemous variables involved in the modeling process. In the KSIM, the use of a uniform linguistic scale allowed us to integrate qualitative and quantitative data into the model, in a manner congruent with knowledge and data availability. However, as highlighted by White (1981), the dynamics of the KSIM lean toward extremal equilibrium states, where variables reach either their minimum (0) or maximum (1) individually. Consequently, the KSIM is often unsuitable for portraying systems that maintain stability and self-regulation without necessarily tending to extreme conditions. In our PIA, this limitation was inconsequential since our focus was on identifying risks of critical transitions, rather than portraying the homeostasis of the socio-ecological system.

During phase 2, addressing ontological and epistemic uncertainties enabled us to formally recognize the underlying assumptions of the intricate multi-scalar and multi-temporal processes governing the evolutionary trajectories of the socio-ecological system. For instance, establishing a causal relationship between the growth of urban areas and the decline in the functional integrity of coastal wetlands in Region IV involved subsuming the complexity of the hydrological processes and the aquifer dynamics into the rudimentary simplification URB → CONH2O → CANH2O → HUMC. Our exploratory modeling results (Fig. 3) were consistent with Reed et al.’s (2022), emphasizing the importance of simulating a wide range of SOW to handle deep uncertainty within a multi-sector dynamics context.

During phase 3, employing Eq. (2) helped address normative and politically induced uncertainties. This facilitated a nuanced understanding of the enabling dimension, which allowed to produce usable knowledge and facilitated a collective definition of the desirable state of specific attributes of the socio-ecological system in relation to ecological risks. The use of Classification and Regression Trees and parallel coordinates (Fig. 4) provided transparency for the identification of complex relationships between drivers and variables, allowing for an objective ecological risk identification. We thus argue that our PIA served as an analytical platform to engage sociopolitical concerns, indirectly addressing power dynamics, justice, and equity issues noted by Fletcher et al. (2022) and Moss et al. (2021).

Malekpour et al. (2020) advocate for the usefulness of DMDU in policy-making, emphasizing transparency and desirability of outcomes. This echoes Ridder and Pahl-Wostl’s (2005) caution about selecting participatory mechanisms for legitimate PIA outcomes. We propose expanding the DMDU framework to integrate qualitative and quantitative data, engage stakeholders, and address power imbalances in PIA. Our PIA demonstrated qualitative DMDU’s value in developing indicators (Table 2), fostering deliberation and consensus-building despite limited resources. Analyzing state variables, HUMC, VACUI, and CFOR, revealed different strategies. First, to prevent a decline of over 30% in coastal wetlands (HUMC, p > 0.10), Regions IV and V should avoid doubling the urban and industrial area in less than 50 years (a growth rate of 1%). Second, to prevent a more than 10% increase in aquifer vulnerability (VACUI, p > 0.15), Regions II, IV, and V should refrain from doubling the cultural tourism and ecotourism area in under 20 years. Third, to prevent a decline of over 20% in forest cover (CFOR, p > 0.10), Regions III, IV, and VII should avoid doubling the agricultural area in less than 20 years. Our three-phased forecasting method responds to Villamor et al.’s (2022) call for adaptable and stakeholder-oriented PIA, significantly improving environmental planning by depicting scenarios across scales.

Conclusions

We have introduced an innovative forecasting approach designed to overcome the challenges of PIA, particularly in contexts of the Global South, where limited knowledge and data often hinder effective regional environmental planning. Our approach enhances the effectiveness of PIA in these contexts by (1) unveiling different forms of uncertainty, (2) allowing policymakers and stakeholders to explore the social and ecological implications of their activities (enabling dimension), and (3) fostering an understanding of the intricate interdependencies across scales, timeframes, and drivers shaping the socio-ecological system (systemic dimension). Through a case study, we have demonstrated how our three-phased approach improves the implementation of indicators of ecological risk during the forecasting step of the Ecological Ordinance in Yucatán. The main methodological contribution of our approach lies in its capacity for integrating qualitative and quantitative data alongside increased stakeholder engagement.

In the context of mediated modeling, the use of KSIM was effective for exploring both long-term and instantaneous effects in a collaborative way. Scenario discovery, for its part, enabled a multi-scalar systematic comparison of the severity of the vulnerability of state variables in relation to univariate thresholds as the probability of reaching a critical transition. The combination of these analytical tools, as a qualitative DMDU implementation, streamlined the measurement of the multiple vulnerabilities associated with the social and environmental heterogeneity of Yucatán. Results revealed distinct regional management strategies that aimed to preserve both forest cover and coastal wetlands while preventing aquifer vulnerability by restricting the territorial expansion of urban, industrial, tourism, and agricultural activities. Our approach, thus, provided a robust framework capable of capturing both the uncertainties and complexities across the systemic and enabling dimensions of sustainable development.