Induced earthquakes and house prices: the role of spatiotemporal and global effects

Abstract

This paper contributes to the existing literature on the explanation of housing prices. First, our proposed methodology accounts for cross-sectional dependence, both locally and globally, using individual data of more than 200,000 transactions in the three most northern provinces of the Netherlands over the period 1993–2014. Second, the selection of houses within each focal house’s sub-market is not only based on distance and time, but also on their degree of similarity. Third, global cross-sectional dependence is not modeled by time-fixed effects, as in previous studies, but by cross-sectional price averages. Fourth, we accumulate the strength and frequency with which earthquakes affect each focal house before it was sold into one single measure using a seismological model and then subdivide it into different bins to account for nonlinear effects and to determine a threshold below which earthquakes have no effect. This way we are able to investigate the propagation of the detrimental impact of earthquakes on housing prices over space and time without the need to select a reference area in advance, which potentially might also have been affected by earthquakes.

1 Introduction

The north of the Netherlands hosts Europe’s largest natural gas field, which has provided energy to most Dutch households since the 1960s. However, extracting gas from it induces mild earthquakes (Kamp 2013, p.443) that negatively impact house prices in the region. Although this impact has been clearly documented in the literature (Francke and Lee 2013, 2014; Koster and van Ommeren 2015; Bosker et al. 2016; Marlet et al. 2017), there is still uncertainty about the spatial and temporal extensions of the problem. Their determination is as policy relevant as it is difficult to achieve for at least two reasons. First, simultaneously measuring the magnitude of the impact, determining the extent of the area, and the length of the period in which the earthquakes affected house prices is challenging. Second, a fundamental, yet overlooked aspect in estimating the impact from externalities on house prices is that housing market transactions data typically present weak cross-sectional dependence (Chudik et al. 2011), i.e., house prices affect each other locally.¹

Real estate agents in the Netherlands apply the sales comparison approach (SCA) to advice their clients on a suitable list price when they try to sell their properties (Op’t Veld et al. 2008). To calculate it, they use transaction prices of recently sold, nearby dwellings with similar hedonic characteristics. List and transaction prices of the same house are usually highly correlated since both are increasing functions of the seller’s reservation price, implying that price data from house transactions are not independent from other similar, proximate, and previously settled house prices. Consequently, if the price of a specific house is affected by earthquakes, all prices for which this house has served as a reference will be indirectly impacted.

Much of the literature measuring housing market effects from earthquakes in the Netherlands have turned to the comparison between house prices in so-called affected and those in neighboring areas, assumed to be unaffected. In addition, many studies take the event of the strongest earthquake, the so-called Huizinge earthquake of August 2012, as the moment that earthquakes began to affect house prices in the region. However, the phenomenon of weak cross-sectional dependence may have led to an insufficiently accurate determination of the area and period in which earthquakes have affected house prices. The underlying spatiotemporal relationship between similar dwellings needs to be modeled to adequately measure the magnitude of the impact of earthquakes on house prices and determine the extent of the area and period over which earthquakes affected the housing market. Jansen et al. (2016) evaluate 13 models and methods that have been proposed to study the impact of earthquakes on housing prices in the north of the Netherlands. However, none of them has used spatial econometric methods, leading the authors of this report to recommend further exploring this method (p.96). This study fills this gap.

In addition to previous housing market studies using spatial econometric models, the spatiotemporal relationships are not only based on distance and time, but also on the pairwise degree of similarity between dwellings computed as an index described in Op’t Veld et al. (2008), extensively used by Dutch real estate agents associated to the NVM.² Moreover, we account for strong cross-sectional dependence. This concerns international perturbations and shocks, such as recessions, banking and currency crises, technological breakthroughs, changes in the supply of oil that affect confidence in the economy, as well as national policy changes in the tax, social security and pension systems, such as an increase of the retirement age, the interest deduction scheme in tax legislation, and the transfer tax on house transactions. Most studies control for cyclical patterns by adding time-period fixed effects to their price equations. However, several studies show that a fixed effects strategy is a special case of a much wider class of models that control for strong cross-sectional dependence (Pesaran 2006; Bailey et al. 2016a; Halleck Vega and Elhorst 2016; Shi and Lee 2017). Following Pesaran (2006), we include period-specific cross-sectional averages of the dependent variable and allow its coefficient to vary across space. Bailey et al. (2016a) are one of the first studies combining both weak (local) and strong (global) cross-sectional dependence in one framework. In contrast to this study, we use individual rather than aggregated data and a simultaneous rather than a two-stage approach, with the difference that the response to the cross-sectional average only differs between municipalities and not between individual observations.

We calculate each earthquakes’ peak ground velocity (PGV) at each house’s geographical coordinates using a seismological model presented in Dost et al. (2004). PGV gives the speed with which the ground moved at a given location because of the tremor of an earthquake, providing a proxy for the seismic intensity that a tremor exerted on a specific house. Although this measure has been used in the literature before, it has only been employed to identify the number of earthquakes that could be felt, i.e., PGV$>0.5$ cm/s (Koster and van Ommeren 2015). Alternatively, we construct a variable that accumulates the PGV of each earthquake that took place before each house was sold and subsequently break it into different bins to allow for potential nonlinear effects. We also compare the results with those that are obtained when using one overall PGV measure or when measuring PGV over the last year only.

We use detailed data on housing transactions taking place between 1993 and 2014 in the three most northern provinces of the Netherlands: Groningen, Drenthe, and Friesland. This research area is wider and this period is longer compared to that in Koster and van Ommeren (2015), which is the closest study to this one, since these authors used data on transactions restricted to the period 1996 to 2013 and to the province of Groningen. These extensions are important in determining the extent of the impact without any prior and arbitrarily set area of study. Similarly, a more extensive period will allow for a better identification of the effects stemming from earthquakes before the Huizinge earthquake in 2012. In the concluding section, we discuss additional problems that need to be accounted for when using data after 2014.

The paper proceeds as follows. Section 2 provides a brief literature overview on hedonic models for house prices and on spatiotemporal modeling of real estate markets. Section 3 describes the data employed and the applied empirical strategy. Section 4 reports and discusses the main empirical findings. Finally, Section 5 concludes.

2 Literature review

Hedonic models using house prices identify the marginal willingness to pay (MWTP) for improving the quality of each of the house’s characteristics and its non-marketed neighborhood amenities, indirectly retrieving households’ preferences for the provision of public goods.³ They have been widely employed in the literature to retrieve preferences on e.g. crime (Bishop and Murphy 2011), racial segregation after a terrorist attack (Gautier et al. 2009), noise exposure (Andersson et al. 2010), new low-income housing projects (Funderburg and MacDonald 2010), quality of schools (Bayer et al. 2016), housing renovations (Billings 2015), environmental quality (Hanna 2007), and proximity to industrial sites (De Vor and de Groot 2011). These estimates have been instrumental in informing a wide range of public policy interventions.

The literature on the effect of hazardous events on housing prices is also extensive. Muehlenbachs et al. (2015) estimate the impact of underground water contamination by shale gas developments on houses sold in the US state of Pennsylvania. Similarly, Gawande and Jenkins-Smith (2001) estimate the effects of perceived risks on residential property values in locations near a road transited by nuclear waste transporters in South Carolina. A couple of Dutch studies address the impact on housing prices, insurance premiums, and capital accumulation of being located in areas prone to be flooded since a large part of the Netherlands is located below sea level (Ermolieva et al. 2017; Bosker et al. 2019). Regarding the specific case of earthquakes, in addition to those on the impact of induced earthquakes, there are many studies on the impact of natural earthquakes, among which Brookshire et al. (1997), Beron et al. (1997), Nakagawa et al. (2007), and Naoi et al. (2009).

The spatial econometrics literature has consistently found empirical evidence in favor of local cross-sectional dependence in hedonic house price models. This puts at risk the findings of the hedonic literature, since failing to account for this dependence can bias their MWTP estimations (Kim et al. 2003; Brasington and Hite 2005; Anselin and Lozano-Gracia 2008; Cohen and Coughlin 2008; Leonard and Murdoch 2009; Mínguez et al. 2013; Baltagi and Li 2014; Baltagi et al. 2015). In addition, house prices might co-move due to external factors, known as global cross-sectional dependence that also needs to be accounted for to obtain accurate estimates. Bailey et al. (2016b) developed the exponent $\alpha$, a statistic used to measure the degree of cross-sectional dependence or the degree of distance decay over space. We present similar test results applied to our data set in Sect. 4 and use the outcomes to construct the connectivity matrix between houses.

The source of the local cross-sectional dependence observed in so many studies has recently been underpinned by an economic-theoretical model of Szumilo (2021). The spatial lag of the dependent variable measuring house prices captures the extent to which the price of a house is affected by the price of houses surrounding it. This lag is motivated by the fact that the asking price is often set with the knowledge of the transaction prices of similar houses in the neighborhood. Op’t Veld et al. (2008) document this behavior for NVM real estate agents in the Netherlands. They assist their clients by forecasting the price of every single house using a hedonic price regression that is estimated using data from a selection of similar nearby and previously sold houses. Spatial lags of the explanatory variables, the structural housing characteristics and local (dis-)amenities of houses surrounding the focal house, may also influence its price. If a house is surrounded by similar houses that are located closer to better schools and parks, or closer to busy roads and polluting industries, this might positively or negatively affect the price of the focal house, respectively.

A relevant strand of the literature for this paper are studies using spatiotemporal models looking at house prices. These studies combine the microapproach used by real estate agents to assist their clients with the macro approach used in so many non-spatial studies to study the effect of housing characteristics and neighborhood (dis-)amenities. This literature has persistently shown that spatiotemporal models significantly improve the predictive power of hedonic price equations. One of the first papers in this field is Pace et al. (1998). They compute a mix of spatial and temporal weight matrices to determine the effect from predated and nearby price transactions onto the focal house. These matrices are lower triangular and therefore the models are recursive, allowing them to use OLS in the estimation. The latter point has recently been made again by Bhattacharjee et al. (2016). In a similar type of study, Pace et al. (2000) find that a model with spatial, temporal, as well as both spatial–temporal and temporal–spatial interactions in the error terms outperforms a traditional hedonic model with 122 housing characteristics and including space and time indicator variables.

Similarly to these two studies, Smith and Wu (2009) allow for both spatiotemporal lag effects by assuming that there is some threshold time interval and some threshold distance beyond which other housing sales have no direct influence on the price of the focal house. In addition, they assume that the error terms follow a first-order autoregressive process with unequally spaced serially lagged terms depending on the time that previous sales occurred. Similarly, Füss and Koller (2016) develop a spatiotemporal approach to forecast housing prices using a classification and regression tree method to define which houses belong to the focal house’s sub-market. In addition, they partition the research area in several discrete sub-markets and the sample period in several discrete time intervals, so as to be able to control for sub-market and time-period fixed effects. Spatial fixed effects may control for local-specific time-invariant (dis-)amenities that affect the dependent variable, but that are unobserved. In this paper we will also use local fixed effects to account for discrete sub-market heterogeneity. As indicated in the introduction, although time-period effects may control for spatial-invariant variables, to control for these we incorporate time-specific cross-sectional averages of the dependent variable to the model, and allow this coefficient to vary across space.

In sum, there are two types of studies using spatiotemporal model approaches. One type focuses on analyzing the effect of one or a set of its attributes as accurately as possible and another type on predicting house prices as accurately as possible. Given the aim of this paper, this paper belongs to the first type.

3 Data and empirical setup

3.1 Data employed

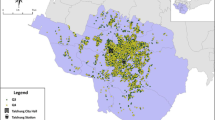
We employ data on 216,126 housing transactions over the period 1993–2014 for the three most northern provinces of the Netherlands (Groningen, Friesland, and Drenthe). The houses are sorted in the sample by the day of sale, starting with January 1, 1993. The data set was provided by the Dutch Association of Realtors (NVM), the largest association of real estate agents in the Netherlands, and contains data on 69 housing characteristics, among which the home address. Given this address, we geo-referenced each house to its longitude and latitude coordinates and subsequently used this information to gather neighborhood characteristics from the Central Bureau of Statistics (CBS) in the Netherlands. Data on earthquakes are publicly available at the Dutch meteorology institute (KNMI). They detail each earthquake taking place in the Netherlands since 1985. Between 1985 and 2014, the region was hit by 663 earthquakes with a magnitude greater than 1 on the Richter scale. Figure 1 gives an overview. In sect. 3.2 we explain the implementation of this information into our model setup.

Fig. 1

Relatively strong earthquakes induced by gas extraction between 1986 and 2014. Notes: The height of the bars indicate the number of earthquakes related to gas extraction activities with epicenters in the north region of the Netherlands and occurring each year between 1986 and 2014. The colors discriminate them according to their local magnitudes abbreviated by the term M_L

3.2 Measuring the effect of earthquakes

An earthquake’s PGV at any given location is a function of its magnitude, depth, and distance between the location and the earthquake’s epicenter, plus a random error term (Dost et al. 2004). Koster and van Ommeren (2015) employ the PGV variable to count the number of earthquakes that could be felt at a house location, i.e., when the ground moves at speeds greater than half a centimeter per second (PGV>0.5 cm/s). However, this count variable makes no distinction between the magnitudes of the earthquakes and consequently may fail to identify the cumulative dimension of their effects. Earthquakes are recurrent and have gotten more frequent and stronger with time. Furthermore, sustained shakes on a house from felt or non-felt earthquakes may inflict physical damages, ultimately impacting its price. Koster and van Ommeren (2015) argue that since there are compensations in place to pay for these physical damages and any damage from past earthquakes are sunk costs that rational sellers would be better off repairing before putting their houses for sale, damages are not relevant in the study of this effect. However, there are expectation issues over the compensating scheme and future damages that make them a mechanism worthy of consideration. The recurrence of earthquakes and their increasing frequency and strength may have fostered expectations about future damages being more severe, reducing incentives for homeowners to maintain their dwellings. Moreover, there was widespread uncertainty about whether or not home owners would really receive a compensation to repair the damages during the period of this study and, if so, whether it would be sufficient. Hence, a proxy for the accumulated seismic activity sustained by a house provides a better and more comprehensive assessment identification of the effect’s magnitude. We also come back to this in the concluding section.

To compute the PGV variable, consider a house i sold at day t, and an earthquake j occurring at day $\tau <t$, with magnitude $M_j$, at $s_j$ kilometers of depth from the surface and at a distance of $d_{ij}$ kilometers from the house. Then following Dost et al. (2004):

$$\begin{aligned} \log _{10}v_{ij} = -1.53+0.74M_{j}-1.33\log _{10}r_{ij}-0.00139r_{ij} \end{aligned}$$

(1)

where $v_{ij}$ is the PGV in cm/s of earthquake j on house i, and $r_{ij}=\sqrt{s_j^2+d_{ij}^2}$ is the hypo-central distance (km) between the epicenter and the house. After computing the PGV of every earthquake onto each house, a matrix of order $216,126 \times 663$ is obtained with typical element

$$\begin{aligned} v_{ji}=\left\{ \begin{aligned}&10^{-1.53+0.74M_{j}-1.33\log _{10}r_{ij}-0.00139r_{ij}}\ &\textrm{if}\ \tau <t\\&0\ &\textrm{otherwise}. \end{aligned} \right. \end{aligned}$$

(2)

The natural log of every row sum of this matrix is used to represent the total PGV (denoted by $e_i$) received by a particular house i from every earthquake prior to its transaction date. Since this measure increases slowly over time and also takes positive values outside the area formally labeled as being subject to earthquakes by the national government, we are able to simulate the propagation of the impact of earthquakes on housing prices over time and across space without the limitations that setting a-priory the affected area imposes. To flexibly estimate the effect, we not only measure the impact of $e_i$, but we also split $e_i$ into 0.1 log-points width bins ($e_{b_i}$) and determine the impact of each segment relative to houses at the lowest bin. A similar kind of approach is used by Cheung et al. (2018) based on the number of earthquakes in different categories of magnitude and by Marlet et al. (2017) based on the percentage of damages in different sub-areas recognized by the gas-extracting company NAM.

3.3 Spatiotemporal-similarity W matrices

Real estate agents who are member of the NVM determine asking prices by fitting a house-specific hedonic model using data on past transactions. Each transaction is weighted by its degree of similarity with the house about to be put up for sale; nearer and more similar houses are given larger weights than distant and less similar ones. Similarity between houses is assessed by computing an index that quantifies the “distance” for a set of characteristics. A detailed description of this methodology is given in Op’t Veld et al. (2008). Based on this study we have developed a comparable similarity index.

Let $N_F$ denote the number of houses in the full (F) sample, and $\varvec{S}$ a symmetric $N_F$ by $N_F$ matrix whose elements $s_{ij}$ measure the degree of similarity between each pair of houses i and j. Following Op’t Veld et al. (2008), three groups of housing characteristics are ranked according to their relevance in the determination of a house’s market value: (i) structural characteristics that cannot be changed, among which location, type of house, and lot size, (ii) secondary characteristics that can be changed, among which bathing facilities and state of maintenance, and (iii) subjective characteristics like the kitchen layout (open, living-kitchen integrated space, etc.). Let $k_{xig}$ denote the standardized score of characteristic $x_{ig}$ of house i within the group of characteristics g. The overall sub-score of house i within group g is obtained by summing its standardized score over all the characteristics in that group, getting $sc_{ig}=\sum _x k_{xig}$, and normalizing it to range within the interval [0, 1], yielding

$$\begin{aligned} sc_{ig}=\frac{\sum _xk_{xig}-sc^{min}_g}{sc^{max}_g}. \end{aligned}$$

(3)

We average these three sub-scores by their relevance, and compute each $s_{ij}$ element in matrix $\varvec{S}$, representing the similarity between houses i and j as follows:

$$\begin{aligned} s_{ij}=\exp \left\{ -\left| \sum _{g=1}^{3}r_g{sc_{ig}}-\sum _{g=1}^{3}r_g{sc_{jg}}\right| \right\} , \end{aligned}$$

(4)

where $r_g$ are weights given to each group, such that $\sum ^{g=3}_{g=1}r_g=1$.⁴ If a pair of houses is identical then $\exp (0)=1$ and as the degree of similarity diminishes this value decreases exponentially to zero.

Let $\varvec{W}^{*}$ denote an $N_F$ by $N_F$ spatial weight matrix whose elements $w_{ij}^{*}$ equal one if another house j has been sold in the neighborhood of house i before its asking price has been set, and zero otherwise. Then a spatiotemporal-similarity matrix is obtained by computing the Hadamard product of the two matrices $\varvec{W}^{*}$ and $\varvec{S}$, yielding

$$\begin{aligned} \varvec{W}^{*} \odot \varvec{S}=\left( \begin{array}{ccccccc} &0&0&\dots &0&0\\ &\vdots &\vdots &\ddots &\vdots &\vdots \\ &0&0&\dots &0&0\\ &w_{2,1}^{*} s_{2,1}&0&\dots &0&0\\ &\vdots &\vdots &\ddots &\vdots &\vdots \\ &w_{N-1,1}^{*} s_{N-1,1}&w_{N-1,2}^{*} s_{N-1,2}&\dots &0&0\\ &w_{N,1}^{*} s_{N,1}&w_{N,2}^{*} s_{N,2}&\dots &w_{N,N-1}^{*} s_{N,N-1}&0 \end{array} \right). \end{aligned}$$

(5)

The first $N_F - N$ rows of this matrix contain zeros only since the houses sold in 1993 do not have any similar houses sold previously, where N denotes the number of houses that remains when these houses would be removed. Since we need data of previously sold houses to be able to construct spatiotemporal-similarity matrices, the price of these houses will not be explained but still utilized to explain houses sold later, as a result of which the sample size and the number of rows of $\varvec{W}^{*} \odot \varvec{S}$ decreases to N. Due to removing the rows with zeros only, the resulting $N \times N_F$ matrix can also be normalized such that the elements in each row sum up to one, to get $\varvec{W}$. As thresholds we use a distance of 10 kilometers from the focal house and a time period of six months prior to the date at which it was put for sale or when it was sold. This period of six months is in line with a recent study of Dubé et al. (2018). In addition, we also investigate the sensitivity of the results when considering other threshold values (see Section 4).

3.4 Econometric specification

The hedonic equation adopted in this paper to determine the impact of earthquakes on housing prices reads as:

$$\begin{aligned} p_{i} & = \delta \sum\limits_{{j = N - N_{F} }}^{{i - 1}} {w_{{ij}} } p_{j} + \sum\limits_{{b = 1}}^{B} {\lambda _{b} } e_{{b_{i} }} + X_{i} \beta \\ & \quad + \left( {\sum\limits_{{j = N - N_{F} }}^{{i - 1}} {w_{{ij}} } X_{{j}} } \right)\theta + \gamma _{{0m_{i} }} + \gamma _{{1m_{i} }} \bar{p}_{{t_{i} }} + \epsilon_{i} \\ \end{aligned}$$

(6)

where $p_i$ denotes the log transaction price of house i per square meter of living space.⁵ The spatiotemporal lag $\sum _{j=N-N_F}^{i-1} w_{ij} p_j$ with coefficient $\delta$ captures the extent to which the price of a house is affected by its comparison set. The index j runs to $i-1$ since only previously sold houses can affect the price of house i, while the index starts with negative numbers due to $N-N_F$. These negative numbers represent houses in the first part of the sample whose prices are not explained but used to explain the price of houses sold later. $w_{ij}$ are elements of the spatiotemporal-similarity matrix $\varvec{W}$. The variable $e_{b_i}$ with coefficient $\lambda _b$ represents one of the B bins denoted by b in which total PGV is split up; it takes a value of one if total PGV for house i before it is sold reaches a value within that bin, and zero otherwise. The row-vector $X_i$ with coefficients $\beta$ covers the characteristics of the house and of the neighborhood. The set of variables $w_{ij} X_j$ captures the extent to which the price of a house is affected by the explanatory variables of houses in its comparison set, i.e., their housing and neighborhood characteristics. Their impacts are measured by the coefficients contained in the vector $\theta$. Due to the inclusion of spatiotemporal lags in both the dependent and the explanatory variables, the model may be labeled a spatiotemporal Durbin model, after the spatial Durbin model in the spatial econometric literature (LeSage and Pace 2009). Nevertheless, there are two differences between these two models that are specific to the data set we are analyzing. $\varvec{W}$ is lower triangular and we have a small set of initial observations whose prices are not explained but only used to explain later sales.

The variables described so far cover potential local spatial (cross-sectional) dependence among the observations. Cross-sectional averages of the dependent variable for each year are incorporated to control for global cross-sectional dependence and denoted by $\bar{p}_{t_i}$, where the index $t_i$ indicates that the transaction of house i took place in year t. This variable enters the equation with unit-specific coefficients for each municipality $\gamma _{1m_i}$, where the index $m_i$ indicates that house i is located in municipality m ($m=1,\ldots ,M$).

The original idea to control for global factors in a non-spatial model goes back to Pesaran (2006), while Bailey et al. (2016a) extend this idea to a spatial model by addressing strong and weak cross-sectional dependence in two separate stages. Halleck Vega and Elhorst (2016) and Shi and Lee (2017) demonstrate that both types of cross-sectional dependence can also be accounted for simultaneously: the former when using cross-sectional averages and the latter when using principal components to approach common factors. Both studies also demonstrate that time-period fixed effects are a special case of global factors, as it requires the restriction $\gamma _{11}=\ldots =\gamma _{1M}=\gamma _1$, i.e., the global factor with municipality-specific coefficients is replaced by a time dummy with a common coefficient $\gamma _1$ for all municipalities. In contrast to these cited studies, this paper is among the first to apply this approach to individual rather than macro or aggregated data.

The development of $\bar{p}$ over time closely follows the business cycle. The municipality-specific slope coefficients $\gamma _{1m_i}$ allow the impact of this variable to vary across space, as some municipalities might have been hit harder by or recovered faster from business cycle effects than others. In addition, they may capture the impact of population growth or decline in that the slopes for mainly rural municipalities are expected to be lower than those for mainly urban municipalities. Furthermore, they may control for other demographic variables at the neighborhood level, such as the number of addresses per square km, distance to the nearest restaurant, supermarket, and train station, the percentage of people aged between 15 and 24, 25 and 65, as well as over 65, for as far they have not been taken up in the model already. The set of parameters $\gamma _{0m_i}$ represent municipality fixed effects which control for unit-specific variables that are constant over time, while $\epsilon _i$ denotes a disturbance term with zero mean and finite variance $\sigma ^2$.

The parameters of Equ. (6) can be estimated by ordinary least squares (OLS).⁶ Importantly, the right-hand side variable $\sum _{j=N-N_F}^{i-1} w_{ij} p_j$ may be treated as exogenous due to the lower triangular structure of the spatial weight matrices $\varvec{W}$.⁷ This structure assures that the transaction price of houses that were sold before the focal house may affect its transaction price, but not vice versa. Note that also according to the sales comparison approach, $\varvec{W}$ should be lower triangular since a later sale cannot affect an earlier sale (Anselin and Lozano-Gracia 2009). Similarly, $\bar{p}_{t_i}$ may be treated as exogenous based on the assumption that the contribution of each single house to this cross-sectional average at a particular point in time goes to zero as the number of houses sold within each year tends to infinity (Pesaran 2006, assumption 5 and remark 3). Since the minimum number of houses that has been sold in a particular year amounts to 4228, this assumption is satisfied. Finally, since this number is relative small relative to the total number of observations (4228 with regard to 216,126 observations in total or one year of observations relative to 25 years), any Nickell type of bias due to also including municipality dummies will be negligible (Baltagi, 2008, Ch.8).

3.5 From short-term direct to long-term total effects

Direct interpretation of Equ. (6), after it has been estimated, is difficult because its coefficients do not represent marginal effects of the explanatory variables. The latter can be obtained by taking partial derivatives of the reduced form of the model in vector notation. Decomposing the observations that are both explained and used to explain later sales, and the observations that are only used to explain later sales, yields $\sum _{j=N-N_F}^{i-1} w_{ij} p_j=\sum _{j=1}^{i-1} w_{ij} p_j+\sum _{j=N-N_F}^{0} w_{ij} p_j$. The model when switching to vector notation can then be written as:

$$\begin{aligned} \varvec{P}_N=\delta \varvec{W}_N \varvec{P}_N+ \delta \varvec{W}_0 \varvec{P}_0+ \varvec{E} \lambda + \varvec{X} \beta +\varvec{W}_N\varvec{X}\theta + \varvec{\Gamma }_0+\varvec{\Gamma }_1 \varvec{\bar{P}}+\varvec{\epsilon }, \end{aligned}$$

(7)

where all small letters in Equ. (6) are changed into bold capitals and/or their index i have been removed to denote their vector or matrix counterparts. $\varvec{P}_N$ is an $N \times 1$ vector containing the prices we explain in our model and $\varvec{W}_N$ an $N \times N$ matrix with spatiotemporal-similarity weighing elements for each house’s comparison set. $\varvec{P}_0$ is an $(N_F-N) \times 1$ vector of prices of houses sold in 1993 which are not explained but used to explain house prices sold afterward and $\varvec{W}_0$ is the accompanying $N \times (N_F-N)$ matrix. Moving the right-hand side variable $\varvec{W}_N \varvec{P}_N$ to the left, and multiplying both sides of Equ. (7) by the spatiotemporal multiplier matrix $\left( \varvec{I}_N-\delta \varvec{W}_N\right) ^{-1}$, yields the reduced form of the model. The partial derivatives of the expectation of the dependent variable, $E\left[ \varvec{P}_N\right]$,⁸ with respect to each PGV bin, given by the vector columns $\varvec{E}_b$ ($b=1,\ldots ,B)$, which represents the impact of earthquakes, take the form

$$\begin{aligned} \left( \frac{\partial E\left[ \varvec{P}_N\right] }{\partial \varvec{E}_b}\right) = \left( \varvec{I}_N-\delta \varvec{W}_N\right) ^{-1}\lambda _b= \left( \varvec{I}_N+\delta \varvec{W}_N+\delta ^2 \varvec{W}_N^2+\ldots \right) \lambda _b. \end{aligned}$$

(8)

The diagonal elements of this N by N matrix of marginal effects represent direct effects of PGV bin b and its off-diagonal elements the indirect or spillover effects. Generally, these two types of effects are summarized by one summary indicator for the direct effect and one indicator for the spillover effect over all units in the sample; the average diagonal element, and the average row sum of the off-diagonal elements of the N by N matrix of marginal effects, respectively (LeSage and Pace 2009). However, the purpose of this study is to determine the impact of earthquakes for each individual house.

The total effect for each house can be subdivided into different components. First, the term $\varvec{I}_N\lambda _b$ represents the short-term direct effect of earthquakes on the log of house prices per square meter. For each individual house this reads as $\lambda _b$. To obtain the impact on the house price itself rather than its log, this parameter further needs to be transformed by $\text {exp}(\lambda _b)-1$. The same exponential transformation applies to the effects below. Second, the spillover effect $\delta \varvec{W}_N \lambda _b$ measures the extent to which the price of each focal house is dependent on the price of its comparison set. It concerns houses surrounding the focal house which have similar characteristics and have been sold within a distance of 10 kilometers in the preceding six months. The sum of the short-term direct and the first-order spillover effects reflects the intermediate effect of earthquakes. Third, second and higher-order terms, starting with $\delta ^2 \varvec{W}_N^2 \lambda _b$, need to be considered to obtain long-term direct and spillover effects. According to Bhattacharjee et al. (2016), these terms can be ignored when $\varvec{W}_N$ is triangular: $\left( \varvec{I}_N-\delta \varvec{W}_N\right) ^{-1} \approx \varvec{I}_N+\delta \varvec{W}_N$, which would imply that it is sufficient to limit the analysis to intermediate effects. However, on simulating these second and higher-order terms, which is computationally demanding due to the size of the $\varvec{W}_N$ (211,898 by 211,898), it appeared that this property is not true, as is also shown by Martellosio (2012).⁹ We do know, however, that the sum of all direct and spillover effects amounts to $\lambda _b/(1-\delta )$, provided that $\varvec{W}_N$ is row normalized. This sum reflects the long-term total effect of earthquakes on house prices.

4 Results

Table 1 reports the results of eleven initial models in which total PGV is taken up as one single measure to further explain the decision to adopt the econometric model set out in Equ. (6) from an empirical viewpoint. The first row reports the coefficient and its t statistic of the PGV measure in a standard hedonic regression model with time-fixed effects but without spatiotemporal lags. Contrary to expectations, the PGV measure turns out to have a positive rather than a negative effect when adopting this model specification. This positive effect remains when extending the model with spatiotemporal lags in the dependent and in the explanatory variables in the second row of Table 1. The explanation for this is that total PGV appears to be trend-stationary, as is already illustrated in Fig. 1. A regression explaining total PGV on a set of year dummies (21 in total) returns an R-squared of 0.327. This implies that if house prices are modeled as depending on both total PGV and a set of year dummies, the year dummies absorb part of the impact from earthquakes which might lead to biased estimates.¹⁰ To prevent this we control for business cycle effects through the cross-sectional average house price observed in each year. Regressing total PGV on this variable yields a negligible R-squared of 0.005. The third and fourth rows of Table 1 show that total PGV takes the expected negative sign when using yearly cross-sectional averages of the dependent variable. To compare the effect of PGV between these two models, the PGV coefficient of $-0.033$ should be divided by $1-0.577$ (see previous section), to get $-0.078$. The coefficient of $-0.033$ reflects the short-term direct effect of earthquakes and the coefficient $-0.078$ its long-term total effect. Generally, it is assumed that the impact of a variable in a model that contains no dynamic effects in space and time also reflects long-term effects. This implies that the coefficient of $-0.106$ of total PGV in the third row of Table 1 is overestimated when the spatiotemporal lag in the price variable is ignored. It also ignores that it takes time before this long-term effect occurs.

Table 1 Estimation results of several models explaining log price per square meter

The need to control for both the cross-sectional average house price observed in each year and spatiotemporal lags in the price variable and the explanatory variables can also be illustrated by the exponent $\alpha$ developed by Bailey et al. (2016b) based on the delineation of the research area into 66 municipalities and the research period into 21 years. This statistic measures the degree of cross-sectional dependence, the complement of the distance decay effect. The exponent $\alpha$ can take values on the interval (0,1]: $\alpha \le 0.5$ points to weak cross-sectional dependence; $\alpha =1$ points to the strongest form of cross-sectional dependence, while values in between indicate moderate $0.5<\alpha \le 0.75$ to strong $0.75<\alpha <1$ cross-sectional dependence. Elhorst et al. (2021) explain in more detail the relationship between this statistic and the specification of the connectivity matrix. If $\alpha <0.5$, the cross-sectional connectivity is one between local, mutually dominant units represented by a sparse matrix $\varvec{W}$ with at most a fixed or a rapidly declining number of neighbors. In case this happens, practitioners should proceed by directly modeling the data with a spatial model structure. For outcomes pointing to moderate dependence ($1/2 \le \alpha <3/4)$, the cross-unit connectivity becomes denser but correlations still decay sufficiently fast such that after a certain distance the impact of neighboring units becomes negligible. When $\alpha >3/4$, the average correlation between the units of observations tends to go to zero slowly, such that each unit affects all other units even if they are very far apart. Should $\alpha$ not be significantly different from 1, then the data should first be modeled via a standard common factor model and then the residuals of this model should be tested again for any remaining cross-sectional dependence. It is this situation that occurs when computing the exponent $\alpha$ for the house price variable in our study; $\alpha = 0.961$ and not significantly different from 1, pointing to the strongest form of cross-sectional dependence, i.e., no distance decay effect, and the existence of a common factor. To filter out this common factor, Bailey et al. (2016b) propose to regress the house price variable on both a constant and the cross-sectional average of the house price in each year, whose coefficients are different from one unit to another, in this data set from one municipality to another. When running this regression and computing the exponent $\alpha$ on its residuals the outcome is 0.665. This points to the existence of moderate remaining cross-sectional dependence that should be modeled by a denser than normal connectivity matrix and with correlations that still decay sufficiently fast, such that after a certain distance the impact of neighboring units becomes negligible. The results reported in the fourth row of Table 1 build on a spatial–temporal-similarity weight matrix based on this observation, i.e., consisting of similar houses compared to the focal house up to a distance of 10 km and sold in the preceding six months period. The R-squared of this equation amounts to 0.828 and the exponent $\alpha$ of the residuals of this model to 0.569. The latter value shows that the degree of cross-sectional dependence has been modeled adequately, since $\alpha$ can only be consistently estimated if it is greater than 1/2 (Bailey et al. 2016b); if $\alpha <1/2$, its estimate will hover around the lower bound of 1/2 in empirical applications. Rows 6 to 9 in Table 1 report the R-squared and the coefficients estimates of total PGV and the spatiotemporal lag in the price variable when considering a different threshold for time and distance (three and nine months, 2.5, 5, and 20 km). The results of these robustness checks have in common that the R-squared falls, which indicates that the spatial–temporal-similarity weight matrix based on 10 km and six months is the most likely candidate within the considered choice set.

Row 10 of Table 1 reports the estimation results when total PGV is measured only over the last year prior to the transaction date, since it might be that buyers and sellers only remember the earthquakes that occurred in the recent past. Again the R-squared decreases. Furthermore, the coefficient of PGV falls to −0.009, which initially seems to be smaller. However, since the PGV coefficient calculated over the past year represents an elasticity due to the chosen log–log specification, an additional earthquake causes a larger change in this PGV measure when expressed in percentages, making the difference from previous results smaller than this coefficient suggests.¹¹

The final model in the last row of Table 1 contains two spatial regimes in the spatially lagged dependent variable. These regimes capture the extent to which the price of a house is affected by the price of houses surrounding it, first before it was put for sale and then before it was sold but only during the time it was on the market.¹² However, the coefficient of this second regime appeared to be insignificant and so small that it can be ignored.

Table 2 Estimation results (mean, coefficient, and clustered t value) of model in Equ. (6)

Table 2 reports the counterpart of the model in the fourth row of Table 1 when the PGV measure is split up into different bins. In addition to this, we computed t values of the coefficient estimates using regular standard errors and when clustering the observations per municipality (in Table 1 we only reported clustered t values), based on a methodology developed by Cameron et al. (2011). The results show that the coefficients of the PGV bins show an upward trend. The price of houses that have been hit by more or stronger earthquakes experience a larger price fall. The threshold above which houses experience a significant price fall starts with the 1.4–1.5 bin when using regular t values or standard errors and with the 1.6–1.7 bin when using clustered t values or standard errors. This difference is important since the share of houses in these two bins of 1.4 to 1.5 and 1.5 to 1.6 amounts to 30% of all houses affected by earthquakes and for almost 5% of all houses in the sample. The short-term direct effect of the 1.4–1.5 bin amounts to $100*(\text {exp}(-0.0071)-1)=-0.7\%$, the intermediate effect (the sum of the direct and first-order spillover effects) to $100*(\text {exp}(-0.0071*(1+0.5543))-1)=-1.1\%$, and the long-term total effect to $100*(\text {exp}(-0.0071/(1-0.5543))-1)=-1.6\%$. Generally, the long-term total effect is a factor 1.4 times greater than the intermediate effect, which in turn is a factor 1.5 times greater than the short-term direct effect for the different bins.

In addition to the housing and neighborhood attributes, the hedonic price model also contains their spatiotemporal lags (except for the three variables measuring the percentage of people in different age categories at the neighborhood level and the dummy whether its population has declined, see the continuation of Table 2 in Appendix). Many studies ignore these so-called spatial Durbin terms. However, no less than 41 out of 77 of these terms are statistically significant at the 5% level. They account for the microapproach used by real estate agents to assist their clients in setting asking prices. Since asking and transaction prices are highly correlated, this practice generates local cross-sectional dependence between house prices.

Fig. 2

Extension, size, and period of the induced earthquakes impact on the housing market. Notes: These series of maps show the impact of earthquakes in the north of the Netherlands measured at the postal code level and for those postal codes with observations in the sample used for the estimation

To further illustrate the importance of the spatial Durbin terms, we decompose the R-squared value using the Shapley-based method set out in Israeli (2007) for five sets of variables: the housing and neighborhood characteristics of the house itself, their spatial Durbin counterparts, the municipality dummies, the cross-sectional averages of housing prices with municipality-specific parameters, and the PGV dummy variables. The absolute contribution $C^A_S$ of each set S is calculated as

$$\begin{aligned} C^A_S=0.5*(R^2_{F}-R^2_{F-S})+0.5*(R^2_{S}-R^2_{0}), \end{aligned}$$

(9)

where F represents the full model, $F-S$ the full model excluding the set S, S the model with both the set S and the intercept, and 0 the model only including the intercept. We compute the relative contribution of each set of variables to the full R-squared value. The results suggest that housing and neighborhood characteristics of the house contribute the most to the explained variation in housing prices (69.39%) followed by the global factor controlling for the business cycle (13.20%) and spatial Durbin terms (11.63%). Further behind are municipality dummies (5.55%), and lastly the PGV variables (0.23%). The relatively low contribution of the PGV variables indicates that the number of houses that is affected by earthquakes is small relative to the total number of observations in the sample. Nevertheless, this set appears to have a major impact on house prices as is shown in what follows.

Fig. 2 shows the intermediate (direct plus first-order spillover) effects of earthquakes in 2008, 2010, 2012 and 2014. In 2008 there were already houses significantly affected by earthquakes, but the price fall of around 4.65% was still limited. The black points represent houses that according to the clustered t values were not significantly affected. In the years that followed, both the area of houses that were severely affected expanded and the price fall increased. In 2012, some houses in the hardest hit areas reached price falls up to 14.6% and in 2014 up to 26.6%.

These price reductions are greater than those found in previous studies. There are several reasons for why this is the case. Over the period 2012Q3-2016Q4, CBS (2015) finds a nonsignificant price differential of 1.9% between houses in the highest risk segments and those in their reference area. Similarly, Francke and Lee (2014) find that house prices in their reference area increased less than in their defined risk area over the period 1993Q1-2013Q1, decreased more over the period 2009Q1-2013Q1, as well as decreased more over the period 2012Q4-2013Q1, the period after the strongest earthquake of 3.6 at the location of Huizinge on August 16, 2012. However, both studies’ reference areas contain many municipalities within the province of Groningen, which according to the results of this study were also affected by earthquakes, limiting their identification strategy. The problem of using a predefined risk area, i.e., houses that have been sold in the eight municipalities belonging to the area formally declared earthquakes prone, also applies to Bosker et al. (2016), even though their reference area also consist of houses located in the neighboring provinces of Friesland and Drenthe, in other provinces along the east border of the country, the provinces of Zeeland and Limburg in the south of the Netherlands, and the upper part of North-Holland. These authors find no price differential over the period January 1^st 2011 to August 15^th, 2012, and a 2.2% decrease after it (until 2015Q3). The point is that the determination of the risk area should be part of the analysis and not predetermined as not only its real extension was unclear, but also how the effect has evolved over time, i.e., also the moment at which earthquakes started to have effect on housing prices should be determined. Most policy studies mainly focus on price effects after the Huizinge earthquake of August 16, 2012, or the period shortly before, while we find that the first effects occurred around 2008. Another issue is that they did not account for any price-spillover effects.

5 Conclusion and discussion

In this paper, we developed a hedonic model for house prices accounting for spatiotemporal effects that stems from real estate agents assisting their clients to set asking prices. Using this model on more than 220,000 housing transactions over the period 1994–2014 in the three northern provinces of the Netherlands, we determine the impact of many small gas extraction induced earthquakes on house prices. We identify the cumulative effects of these increasingly frequent and stronger earthquakes using a seismological model specifically developed to measure the seismic activity in the region. This model gives the so-called peak ground velocity (PGV), an estimate of the velocity at which the ground moved underneath each house because of the earthquakes’ tremors. Unlike previous research that identified this effect looking only at earthquakes that could be felt (PGV > 0.5 cm/s), we compute a variable that accumulates the PGV from all earthquakes taking place before the house was sold, such that it indicates the total seismic activity reached at the house’s location. Other studies on this issue have also looked at these effects by means of comparing between the evolution of house prices within an affected and a reference area. However, their definition of an affected area, as well as the choice of the reference area, is problematic. This paper sheds light on the reasons why and shows that especially the extent of the area considered as affected in previous research has been underestimated.

Three discussion points are worth mentioning. First, the formulas that give the PGV estimation used in this paper and which are based on Dost et al. (2004) have recently been updated by Bommer et al. (2017). The former were estimated using data on earthquakes originated after extraction from mainly the smaller fields in the Groningen gas reservoir. The latter, in turn, were estimated using earthquakes that originated from the main Groningen field, which have affected the region the most. Second, Kruiver et al. (2017) have computed a variable that characterizes how the composition of the soil’s underground mediates the severity of ground motions caused by earthquakes. Future research could investigate how robust our findings are to using these newly developed PGV measures and to including this soil variable in the model described in this paper. Third, data observed after 2014 may be used to investigate further the evolution of house prices in the region. However, this is not straightforward due to some events that took place during the years after. In 2014, a court ruled that the NAM should compensate for the loss in value of their properties to an association of property owners. In 2015 the decision was upheld meaning that the NAM will have to compensate every claimant for value loss, not just damages. To account for this, data on the financial compensation that each individual house owner has received from the NAM for physical damages are also required. In addition, these data can be used to better investigate whether there is any relation between the market value depreciation of houses and physical damages. Extending the data set to houses sold after 2014, incorporating compensations data, providing answers to whether damages were an important mechanism for the decline in house prices, and whether compensations have restored house prices in the region are important though also challenging topics for further research.

Appendices

Appendix

A Additional hedonic regression results

See Tables 3 and 4.

Table 3 Continuation of Table 2 with the estimation results of the remaining variables (clustered t values)

Table 4 Municipality-specific coefficients (clustered t values)