Abstract
The COVID-19 epidemic has raised major issues with regard to modelling and forecasting outcomes such as cases, deaths and hospitalisations. In particular, the forecasting of area-specific counts of infectious disease poses problems when counts are changing rapidly and there are infection hotspots, as in epidemic situations. Such forecasts are of central importance for prioritizing interventions or making severity designations for different areas. In this paper, we consider different specifications of autoregressive dependence in incidence counts as these may considerably impact on adaptivity in epidemic situations. In particular, we introduce parameters to allow temporal adaptivity in autoregressive dependence. A case study considers COVID-19 data for 144 English local authorities during the UK epidemic second wave in late 2020 and early 2021, which demonstrate geographical clustering in new cases—linked to the then emergent alpha variant. The model allows for both spatial and time variation in autoregressive effects. We assess sensitivity in short-term predictions and fit to specification (spatial vs space-time autoregression, linear vs log-linear, and form of space decay), and show improved one-step ahead and in-sample prediction using space-time autoregression including temporal adaptivity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Forecasts of future infectious disease incidence have had major policy importance, for example in the COVID-19 epidemic of 2020-2021. However, even short-term forecasts may face difficulties in practice. These include limited data, quantifying forecast uncertainty, and specification issues (Petropoulos and Makridakis 2020; Roda et al. 2020; Stehlík et al. 2020). Where separate infection time series for a number of areas are available, this may assist forecasts through a borrowing strength mechanism (Haining et al. 2021), with Shand et al. (2018) noting the gain from taking “advantage of the spatial and temporal dependence structures so that the statistical inference at one location can borrow strength from neighbouring regions in both space and time”. However, modelling and predicting area trajectories in infectious disease poses particular problems when counts are changing rapidly in epidemic situations, and there may well be geographic infection hotspots.
Notions of borrowing strength through spatial random effects are a major feature of the Bayesian disease mapping approach for area disease counts (Kang et al. 2016), and adaptations of disease mapping to modelling longitudinal infectious disease data have been discussed in a number of papers (e.g. Clements et al. 2006; Coly et al. 2021). Consider, in particular, applications to epidemic time series for sets of administrative areas, which are available in several countries for the COVID-19 epidemic. A widely adopted strategy for such data, aiming at short term prediction, involves low order autoregression in infectious disease counts or rates, in both an area itself (the focus area), and in areas surrounding the focus area (Shand et al. 2018; Paul and Held 2011). Existing approaches have focussed on spatial variation in autoregressive dependence, so allowing for geographic heterogeneity (Dowdy et al. 2012).
The contribution and novelty of this paper is to show how different specifications of autoregressive dependence in incidence counts may considerably impact on adaptivity in epidemic situations. In particular, we introduce temporal as well as spatial variation in autoregressive dependence and show that this feature provides much improved predictive performance in situations where infection counts are rapidly changing.
Such rapid fluctuations in cases, associated with multiple epidemic waves, have been a feature of the COVID-19 epidemic. Sharp upward trends in cases have initially tended to be geographically concentrated, with subsequent diffusion away from initial hotspots (Dowdy et al. 2012). Effective policy responses in such situations depend on forecasting approaches that provide a perspective on short-term future implications of current trends (Shinde et al. 2020). In particular, geographically disaggregated forecasts are important for prioritizing interventions or severity designations, such as the “local tiers” in the UK COVID-19 policy response (Hunter et al. 2021).
The approach used here can potentially be generalized to model longitudinal count data in non-disease applications involving areas, or for longitudinal count data for units other than areas. An example of the former might be applications involving spatial forecasting and spatial diffusion of count data (e.g. Glaser 2017; Glaser et al. 2021). Examples of such diffusion include behavioural copycat effects (Schweikert et al. 2021).
In this paper, we assess predictive performance of an autoregressive model for infectious disease counts, applied to COVID-19 data for 144 English local authorities during the UK epidemic second wave—at the end of 2020 and into early 2021. These local authorities are in the South East of England, where a sharp (and geographically concentrated) upturn in cases in late 2020 was attributed to the emergence of a new COVID variant, the “Kent variant” or alpha variant (World Health Organization 2021). The model proposed here allows for both spatial and time variation in autoregression coefficients. We show clear gains in prediction over a less general specification. Impacts of alternative model features are considered, namely the choice between a linear (identity link) or log-linear model form, and the assumed form of weighting infections in neighbouring areas. We use Bayesian inference and estimation, via the BUGS (Bayesian inference Using Gibbs Sampling) package (Lunn et al. 2009).
2 Related Research
The typical form of data encountered in analysis of spatio-temporal infections data involves incidence counts \(y_{it}\) for areas \(i=1,...,N\) and times \(t=1,...,T\). However, some spatio-temporal models for such data have used normalizing transformations of originally count data. Thus, Shand et al. (2018) consider a logarithmic transformation of yearly HIV diagnosis rates (per 100,000 population) for US counties.
Alternatively for models applied specifically to counts, Poisson and negative binomial time series regression methods may be used. Other count distributions may be used (Jalilian and Mateu 2021; Yu 2020). Spatio-temporal adaptations of disease mapping have been applied to analysis of infections, including across and within area random walks (e.g. Zhang et al. 2019; Jalilian and Mateu 2021; Lowe et al. 2021). Both Shand et al. (2018) and Paul and Held (2011), use spatially varying auto-regression applied either to lagged infection counts in an area itself (the focus area), or to areas surrounding the focus area (the neighbourhood), or both. A geographically adaptive scheme is also used by Lawson and Song (2010) in analysis of foot and mouth disease data. Lawson and Song (2010) use a focus area and neighbourhood lag in flu infection counts as an offset (with known coefficient) in Poisson regression, with an application to COVID forecasts by area in Sartorius et al. (2021). Applications to COVID-19 forecasting, based on Paul and Held (2011), are provided by Giuliani et al. (2020) and Rui et al. (2021). Detection of space-time clusters in COVID-19 is exemplified by Martines et al. (2021).
For applications without spatial disaggregation, a wide range of methods have been used for COVID-19, and infectious diseases generally. These include autoregressive integrated moving average (ARIMA) models (e.g. Maleki et al. 2020; Chintalapudi et al. 2020; Petukhova et al. 2018), integer-valued autoregressive (INAR) models (Chattopadhyay et al. 2021), exponential smoothing (Petropoulos and Makridakis (2020); Gecili et al. (2021)), or bivariate forecasts. For example, the study by Johndrow et al. (2020) models COVID deaths as a lagged function of earlier new cases. For infectious diseases with an established seasonal pattern, SARIMA (seasonal ARIMA) forecasting has been used (Qiu et al. 2021). Applications of phenomenological models to COVID-19 incidence forecasts—based on mathematical representations of epidemic curves, such as the Richards model (Richards 1959)—include Roosa et al. (2020).
3 Methods
We focus here on infectious disease models using count data regression. We consider first models for count time series, without area disaggregation, as these can provide a basis for generalisation to area-time data. Relevant specifications may specify AR dependence on previous counts, or on previous latent means; models with autoregressive (AR) dependent errors (Hay and Pettitt 2001) may also be considered (Jalilian and Mateu 2021).
3.1 Time dependent autoregressive count data models
Consider Poisson distributed counts at times \(t=1,...,T,\) namely \(y_{t}\) \( \thicksim Poi(\mu _{t}),\) (with Poi for Poisson density, with means \(\mu _{t}),\) or negative binomial (NB) counts, \(y_{t}\) \(\thicksim Negbin(\mu _{t},\Omega )\) (with Negbin for negative binomial density, with means \( \mu _{t}\) and dispersion parameter \(\Omega )\). The parameterisation of the negative binomial is as in Zhou et al. (2012), namely
In a simple autoregressive representation (Fokianos 2011), one may adopt an identity link, and, subject to suitable parameter constraints, specify AR1 (AR with first-order lag) dependence in lagged counts \(y_{t-1}\) and in latent means \(\mu _{t-1}.\) The general form of this representation is termed the autoregressive conditional Poisson (ACP) model by Heinen (2003), or the linear model by Fokianos (2011). Thus
where \(\phi \), \(\alpha ,\) and \(\gamma \) are all positive. An alternative log-linear model (Fokianos and Tjøstheim 2011) has a log-link with
where \(\nu _{t}\) and \(\nu _{t-1}\) are the logarithms of \(\mu _{t}\) and \(\mu _{t-1}\) respectively, f is an intercept, and a and c are autoregressive coefficients.
In both Eqs. (1) and (2), the autoregressive coefficients could be taken as time varying, namely \(\{\alpha _{t},\gamma _{t}\}\) and \(\{a_{t},c_{t}\}.\) Varying intercepts to represent time dependent effects other than autoregressive, could also be added. For example in Eq. (1), one may take
where \(\eta _{t}\thicksim \mathcal {N}(\eta _{t-1},\sigma _{\eta }^{2})\) is a random walk with variance \(\sigma _{\eta }^{2}\). However, random coefficients research so far have concentrated on random coefficient AR models, without lags in latent means (e.g. Sáfadi and Morettin 2003).
3.2 Random coefficient autoregressive area-time models
To generalize these representations to area-time infection count data (areas \(i=1,...,N\)), one may add lags to infection counts in spatially close areas (Martines et al. 2021). These reflect geographic infection spillover—due, for example, to social interactions between residents in different areas, or to cross boundary commuting (Mitze and Kosfeld 2021). To allow for spatial lag effects, let \(w_{ij}\) be row standardised spatial weights expressing spatial interaction between areas i and j, with \(\underset{j}{\sum } w_{ij}=1\). They may be based on adjacency of areas, or distances between them. For example, let \(h_{ij}=1\) for adjacent areas (with \(h_{ii}=0\)), and \( h_{ij}=0\) otherwise. Then, \(w_{ij}=h_{ij}/\underset{j}{\sum }h_{ij}.\) Consider Poisson distributed counts \(y_{it}\) \(\thicksim Poi(\mu _{it}),\) or NB counts, \(y_{it}\) \(\thicksim Negbin(\mu _{it},\Psi ).\)
As in panel data analysis (Greene 2011), randomly varying autoregressive parameters can be used to allow for different epidemic trajectories in different areas. The most general representation would allow interactive autoregressive coefficients varying simultaneously by time and area. We also allow for area specific permanent effects \(\varepsilon _{i}\) (and \(e_{i}\)) and space-time varying intercepts \(\phi _{it}\) (and \(f_{it}\)).
The linear and log-linear representations, generalizing Eqs. (1) and (2) to area-time, become
and
In Eq. (3), the \(\{\varepsilon _{i},\phi _{it},\alpha _{it},\beta _{it},\gamma _{it},\delta _{it}\}\) are assumed positive under the identity link. Covariate effects can be included in the specifications for \( \varepsilon _{i}\) and or \(\phi _{it},\) and for \(e_{i}\) and \(f_{it},\) though arguably are more straightforwardly obtained under Eq. (4); see Fokianos and Tjøstheim (2011, page 564) regarding the time series case.
Assuming positive dependence on infection count lags is a reasonable prior assumption anyway, on subject grounds, as higher existing numbers of infected subjects typically generate more future infections. It is implausible that more infections in period t in area i generate less infections in period \(t+1\). In Eq. (4), assuming positivity of the autoregressive coefficients \((a_{it},b_{it},c_{it},d_{it})\) is also a reasonable assumption, for the same reason. In practice, one may use log, or logit, links to space or space-time random effects. For example, a log-link involving fully interactive space-time structured random effects, \(\psi _{it} \) (e.g. Lagazio et al. 2001, Eq. 4) on the lagged focus area infection counts is
with an intercept \(\alpha _{0}\), and assuming the \(\psi _{it}\) are constrained for identifiability (e.g. zero centred or corner constrained). Similar schemes can be applied to the other autoregressive coefficients.
However, including lags in latent means in Eqs. (3) and (4) will typically increase computational intensivity, and a more tractable model is based only on lags in observed infection counts or log transformed infection counts. Hence, the linear and log-linear specifications become
and
Also area-time fully interactive specifications for autoregressive coefficients may be subject to overparameterisation (Regis et al. 2021, page 6), and one may propose reduced coefficient schemes. For example, for the lag term on \(y_{i,t-1}\) in Eq. (6), one may take
The option (8.1) is used in Paul and Held (2011), who assume \(\psi _{i}\) are spatially structured random effects.
Here we investigate the gains—in the context of predicting future COVID-19 counts—of an autoregressive specification with separate area and time effects, for example in the linear model,
where \(\psi _{1i}\) is a spatially structured conditional autoregressive or CAR effect (Besag et al. 1991), and \(\psi _{2t}\) is a random walk in time. Both \(\psi _{1i}\) and \(\psi _{2t}\) are zero centred; for instance, such centering is automatically implemented in the BUGS car.normal function. This specification may provide greater adaptivity to rapidly changing infection counts in epidemic exponential and downturn phases, and avoids the heavy parameterisation of a fully interactive scheme.
3.3 Remaining effects
For the permanent terms \(\varepsilon _{i}\) and \(e_{i}\), one might use iid or spatially correlated random effects \(\kappa _{i}\) to represent enduring risk variations for infectious disease, in both endemic and epidemic phases. For example, taking iid effects, and with a positivity constraint,
where \(\kappa _{i}\sim \mathcal {N}(\theta _{0},\sigma _{\kappa }^{2})\) are permanent effects across times. These terms might also include constant effects of covariates \(X_{i}\). Thus for a single covariate
where \(\theta =(\theta _{0},\theta _{1})\) are regression parameters.
For the general time terms \(\phi _{it}\) and \(f_{it}\), various specifications are possible. These might include Fourier series representations for an infectious disease with clear seasonal fluctuations (Paul and Held 2011), or a second degree polynomial (in days) in a COVID-19 application (Giuliani et al. 2020). The latter scheme is proposed as adapting to the exponential growth in the upturn phase of the epidemic. There is no conclusive evidence so far that COVID-19 is seasonal. For example, the UK first COVID-19 wave peaked in the spring and early summer of 2020. Some studies argue that COVID will eventually become seasonal (e.g. Greene 2011). However, there will likely still be considerable variation between areas in timing of COVID infections.
Here, we use area-specific first-order random walks to (a) represent trends not fully captured by the autoregressive effects on infection lags and (b) be geographically adaptive. Thus in Eq (6), we have
where \(\eta _{it}\thicksim \mathcal {N}(\eta _{i,t-1},\sigma _{\eta }^{2}).\) A corner constraint—setting selected parameter(s) to known values—is used for identifiability (Stegmueller 2014) and was less computationally intensive than centering samples at each iteration in the BUGS software. Thus, \(\phi _{it}=\exp (\eta _{it}^{\prime }),\) where \(\eta _{it}^{\prime }=\eta _{it}-\eta _{i1},\) which is equivalent to setting \(\eta _{i1}=0\) (Lagazio et al. 2001, page 29).
The area specific effects \(\eta _{it}\) will increase adaptivity. However, we also expect autoregressive coefficients including time effects, as in Eq. (9), to be adaptive to epidemic growth (and decay) phases. For example, in the growth phase with \(y_{i,t+1}\) typically much exceeding \(y_{it}\), the \( \psi _{2t}\) in Eq. (9) will tend to be higher in order to better predict increasing counts \(y_{i,t+1}\) in the next period.
The time varying terms \(\phi _{it}\) and \(f_{it}\) might also include time varying regression effects \(\theta _{t}\), or impacts of time varying covariates, including lagged covariates (e.g. Lowe et al. 2021).
3.4 Full model
In the case study analysis described below, we assume negative binomial sampling, with the linear model as in Eq (1) namely
and the log-linear, as in Eq (7), namely
Initially, we take \(w_{ij}\) to be first-order adjacency indicators: \(h_{ij}=1\) for areas i and j adjacent, and \(h_{ij}=0\) otherwise, with \( w_{ij}=h_{ij}/\underset{}{\sum _{j}}h_{ij}.\) The autoregressive coefficients are taken as
under the linear model, and
under the log-linear model. The parameters \(\{\psi _{1i},\psi _{3i},\psi _{5i},\psi _{7i}\}\) are spatial CAR effects (Besag et al. 1991), and \(\{\psi _{2t},\psi _{4t},\psi _{6t},\psi _{8t}\}\) are first-order random walks in time. The remaining effects are specified as
in the linear model, and
in the log-linear model. The parameters \(\{\alpha _{0},\beta _{0},a_{0},b_{0},\mu _{\kappa 1},\mu _{\kappa 2}\}\) are fixed effects.
Out-of-sample forecasts \(\widetilde{y}_{i,T+s}\) for periods \(T+1,T+2,...,etc.\) , are based on extrapolating \(\psi _{2t},\psi _{4t},\) and \(\eta _{1it}\) (or analogous log-linear effects) to provide means \(\widetilde{\mu }_{i,T+s}\) (Sáfadi and Morettin 2003). Thus, one-step ahead predictions to \(T+1\) in the linear model are
and these are incorporated in Eq. (6) to provide \(\mu _{i,T+1}\) from which forecast cases at \(T+1\) can be sampled.
3.5 Spatial weighting
There has been discussion on how to weight the contribution of neighbouring areas in the spatial lags, with proposals including a power law that has declining weights for second, third, etc., nearest neighbours (Cheng et al. 2016; Meyer and Held 2014). Here, we allow for an infection overspill effect from both first- and second-order neighbours in a sensitivity analysis.
Thus, first-order neighbours are assigned weights \(h_{ij1}=1\) for adjacent areas, and \(h_{ij1}=0\) otherwise; while second-order neighbours are assigned weights \(0<\lambda <1,\) so that \(h_{ij2}=\lambda \) for areas i and j which are second-order neighbours, and \(h_{ij2}=0\) otherwise. Then,
3.6 Space-time clusters
A range of methods have been proposed to assess space-time clustering (e.g. Chen et al. 2016; Mclafferty 2015). Here, we consider the LISA (Local Indicators of Spatial Association) indicator of spatial clustering in infection risk at one time point (Anselin 1995) and extend it to assess extended spatial clustering over various temporal windows—multiple successive time units (here these are successive weeks). A particular aim is to detect spatial clustering during the exponential ascent phase of the epidemic wave. Hence, one can assess where the epidemic phase, and its associated health care burden, is geographically concentrated.
Define predicted COVID case rates \(r_{it}=\mu _{it}/P_{i}\), where \(P_{i}\) are area populations. Predicted rates could also be defined for out-of-sample periods, with \(\widetilde{r}_{it}=\widetilde{\mu }_{it}/P_{i},\) \(t=T+1,T+2,...etc.,\) to predict future space-time risk patterns.
For a particular week define cluster indicators \(J_{it}=1\) if own area rates \(r_{it}\), and average rates in the locality \(r_{it}^{L}=\underset{}{ \sum _{j\ne i}}w_{ij}r_{jt}/\underset{}{\sum _{j\ne i}}w_{ij},\) are both elevated. This is known as a high-high cluster in LISA terminology. If either or both of these conditions do not hold, then \(J_{it}=0\).
Here, we define elevated rates as those more than 50% above the region wide or national rate—here the rate for the Greater South East, namely \(R_{t}= \underset{}{\sum _{i}}\mu _{it}/\underset{i}{\sum }P_{i}.\) So \(J_{it}=1\) if \( J_{1it}=J_{2it}=1\) where
\(J_{2it}=I(r_{it}^{L}>1.5R_{t}),\)
and where \(I(C)=1\) if the comparison C is true, 0 otherwise.
Elevated rates through D successive weeks define a space-time cluster. So if \(D=5\), a space-time cluster of length D would require \( J_{it}=J_{i,t+1}=J_{i,t+2}=J_{i,t+3}=J_{i,t+4}=1\). Using MCMC sampling one can obtain the probability that area i at week t defines a space-time cluster of length D.
3.7 Estimation
Bayesian estimation uses the BUGS (Bayesian inference Using Gibbs Sampling) program (Lunn et al. 2009). Two chains of 20,000 iterations are taken, with inferences from the last 10,000, and convergence checks as in Brooks and Gelman (1998).
Gamma priors with shape one, and rate 0.001, are adopted on inverse variance parameters and on the negative binomial overdispersion parameter \( \Omega \), while normal \(\mathcal {N}(0,100)\) priors are assumed on fixed effects \(\{\alpha _{0},\beta _{0},a_{0},b_{0},\mu _{\kappa 1},\mu _{\kappa 2}\}.\) A beta(1,1) prior is assigned to \(\lambda \) in the analysis including second-order neighbours.
4 Case study
4.1 Dataset and geographical setting
The data for the study consist of weekly totals of new COVID cases in a subregion of the UK. The time span considered starts at the week 19-26 July 2020 (constituting week 1), with one analysis considering the subsequent 24 weeks, and another considering 29 weeks through to the week 31 January-6 February, 2021. In July 2020, new COVID cases across the entire UK averaged under 700 daily, whereas towards the end of 2020, there was a pronounced increase, with some days reaching over 75 thousand; however, in early 2021, there was a tailing off in new cases. See Fig. 1 for daily UK data, which includes a loess smooth. The epidemic ascent phase is irregular, with an early lesser peak in October and early November 2020, a slight tailing off in new cases in early December 2020, then a major increase in late December and January 2021.
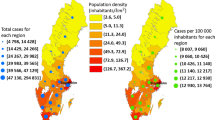
The analysis here considers part of England, namely three standard regions (London, South East, East) combined to give a broad region, here termed the Greater South East (GrSE for short), with a population of 24.4 million. Figure 2 shows weekly totals of new cases in this region. Starting at under 1,500 weekly, they rose to over 200,000 at the epidemic peak (on week 24) but then fell back sharply. As for the entire UK, there is a minor peak at week 17, preceding the main epidemic wave. There are \(N=144\) areas in the region, administrative areas called local authorities.
This part of England contains the epicentre of a localized cluster associated with a new variant (the Kent variant, or B.1.1.7 variant) (Challen et al. 2021). The surge in new cases associated with this cluster was the precursor to the larger national UK-wide escalation of cases. The outbreak of the new variant was concentrated in areas to the east of London (in Kent and Essex counties) and in the North East of London itself.
4.2 Model evaluations
As a first evaluation of alternative model forms, we make out-of-sample predictions for cases at weeks 24 and 29 across the Greater South East. The forecasts are based on training data for weeks 1-23, and weeks 1-28, respectively (so \(T=23\) and \(T=28\) respectively). Week 24 followed the ascent phase, when new cases of infection were sharply increasing, and in fact infections peaked in week 24. Week 29 was in a phase of sharp decline in new cases.
In a first analysis, a comparison between two different autoregressive formulations (M1 and M2) is made. Both specifications condition on the first week (\(t=1\)). Both specifications also assume a linear model, as in Eqs (6) and (12), namely
\(log(\varepsilon _{i})=\kappa _{1i},\)
\(log(\phi _{it})=\eta _{1it},\)
In the first specification (M1), the autoregressive coefficients \(\alpha _{it}\) and \(\beta _{it}\) are taken as spatially, but not temporally, varying:
\(log(\beta _{it})=\beta _{0}+\psi _{3i},\)
In the second (M2), the autoregressive coefficients are taken as both space and time varying
\(log(\beta _{it})=\beta _{0}+\psi _{3i}+\psi _{4t}.\)
The parameters \(\{\psi _{1i},\psi _{3i}\}\) are CAR effects (Besag et al. 1991), with \(h_{ij}=1\) for adjacent areas (\(h_{ij}=0\) otherwise), while \( \{\psi _{2t},\psi _{4t}\}\) are first-order random walks in time.
One-step ahead out-of-sample forecasts \(\widetilde{y}_{i,T+1}\) for week \(T+1\) (either week 24 or week 29) are based on extrapolating \(\psi _{2t},\psi _{4t},\) and \(\eta _{1it}\) to week \(T+1\).
Two subsequent analyses are made. In the first, we compare the best performing from M1 and M2 with its log-linear equivalent (M3). In the second analysis, we allow the spatial interaction weights \(w_{ij}\) to include both first- and second-order neighbours—this defines model M4. Both these analyses are for the case when \(T=23,\) and out-of-sample predictions are to week 24.
4.3 Assessing performance
Out-of-sample predictive performance is based on whether the 95% credible interval for predicted new cases \(\widetilde{y}_{\bullet ,T+1}\) (summing across 144 areas in the GrSE) in week \(T+1\) contains the actual number of new cases \(y_{\bullet ,T+1}\). An indicator of this is the posterior probability
that one-step ahead predicted cases exceed actual new cases. Tail probabilities (e.g. under 0.1 or over 0.9) represent under or over-prediction of actual cases. These probabilities can be obtained for individual areas, namely
Also considered is the ranked probability score, with abbreviation \( RPS_{T+1} \) Czado et al. (2009), which measures the accuracy of forecasts (in matching actual outcomes) when expressed as probability distributions. In a Bayesian context, the latter will be sampled values from posterior predictive densities for the outcome, \(p(\widetilde{y}|y).\) For area i, the ranked probability score is obtained by monitoring
where \(\overset{\thickapprox }{y}_{i,T+1}\) is an independent draw for the posterior predictive density. The second term is a penalty for uncertainty, which increases as does predictive variance. Lower \(RPS_{T+1}\) values represent better fit.
To assess fit for the observed (training) data, we obtain the widely applicable information criterion (WAIC) (Watanabe 2010), and also RPS scores for one-step ahead predictions, based on infections in the previous week. The RPS scores can be aggregated over areas for separate weeks, \( RPS_{t}\) \((t=2,...,T),\) to show where particular models are better or worse fitting.
5 Results
5.1 Predictive performance of space-time autoregression model
Table 1 compares the out-of-sample performance of models M1 and M2 for weeks 24 and 29, based, respectively, on training data for weeks 1-23 and 1-28. Table 2 compares model fit for the training data analysis, as well as predictive performance for one-step ahead predictions within the sample.
It can be seen from Table 1 that a model including time effects in the autoregressions on previous cases leads to improved out-of-sample predictions. The credible intervals under M2 for predicted new cases in weeks 24 and 29 comfortably include the actual total GrSE cases; though the M2 estimates of total cases are less precise and show some skew (posterior means exceeding medians). The mean RPS score under M2 also shows the effects of skewness, especially for the forecast to \(T+1=24\); the median values favour M2.
The probabilities \(\zeta \) in Eq. (21) indicate that model M1 underpredicts new cases at week 24; this week was in fact the peak of the epidemic, following weeks when actual cases were rapidly increasing. By contrast, in the downturn phase, at week 29, model M1 overpredicts new cases. Area specific probabilities \(\zeta _{i}\), as in Eq. (22), show higher totals of local authority areas with cases under or overpredicted under M1, especially in the downturn phase.
Table 2 shows that model M2 has a lower in-sample WAIC than model M1 in both training data analyses. One-step ahead predictions within the observed data periods also favour M2. For example, the total RPS for M1, accumulated over weeks 1-28, is around twice that for M2 (1.12 million vs 559 thousand). Some weeks show greater discrepancies between the models.
Table 3 compares the two models against information on changing infection totals (weekly totals across GrSE) for the analysis of weeks 1-28. Comparing \(RPS_{t}\) between models M1 and M2 (first three columns of Table 3) shows that model M1 has problematic fit in the irregular ascent phase (weeks 16-19 when cases rise then fall back again), and also, more markedly, in the epidemic descent phase (weeks 26 onwards), when the \(RPS_{t}\) under M1 is more than three times that of M2.
The last two columns of Table 3 and Fig. 3 show how the \(\psi _{2t}\) in model M2 adapt to the minor early peak at week 17, and then to sharply increasing cases in the exponential epidemic phase. They then decrease in line with the epidemic downturn.
5.2 Evaluating other model options
Table 4 compares linear and log-linear specifications (denoted M2 and M3) with space-time autoregressive effects, where the log-linear model M3 is defined by Eqs. (7), (13) and (15). This comparison is for weeks 1-23 as training data, and prediction ahead to week 24. For M3, we find a slight deterioration in fit to the training data and also a slight deterioration in out-of-sample prediction—though the latter is still satisfactory. However, skewness in the posterior density of \(\widetilde{y}_{\bullet ,T+1}\) is increased in M3 as against M2.
Another version of the linear model is also considered (as M4), with spatial weights \(w_{ij}\) including second-order as well as first-order neighbours—as per Eq. (16). For model M4, we find no gain in fit over model M2 using first-order neighbours only. The out-of-sample prediction is satisfactory though, with no evidence of under or overprediction of cases in week \(T+1\). The posterior median estimate of \(\widetilde{y}_{.,T+1},\) namely new cases in week \(T+1\) across the greater South East, is 211,272 compared to the actual total of 210,099. The \(\lambda \) parameter has mean 0.76 with 95% credible interval (0.40, 0.99).
5.3 Detecting significant space-time clusters
Space-time clustering in infectious disease outbreaks is important in identifying the epicentre(s) of an outbreak. Space-time cluster prediction, for example to assess continued excess spatial clustering in future periods, is important in prioritizing interventions.
The “Kent variant” of COVID-19 (code B117), also known as the “English variant”, emerged in late 2020 in specific parts of England, namely areas to the East and South East of London. The observed data suggest a localized surge of COVID-19 cases in November 2020 in these locations, which preceded the generalized national second wave epidemic peaking in late December of 2020 and early January of 2021. In terms of the weeks considered in the present study, we would expect significant space-time clustering in weeks 17-22, namely November 2020 and early December 2020.
We obtain—under model M2—area specific probabilities of D successive periods with excess incidence in both focus areas and their localities. Excess incidence is taken as more than 50% above the average (modelled) rate for the entire region, namely the Greater South East. Assuming \(D=5\), then for a single MCMC iteration (\(s=1,...,S\)), one requires for area i to be a space-time cluster of length 5 that \( J_{it}^{(s)}=J_{i,t+1}^{(s)}=J_{i,t+2}^{(s)}=J_{i,t+3}^{(s)}=J_{i,t+4}^{(s)}=1. \) One then obtains estimated posterior probabilities of such a sequence occurring, by accumulating over MCMC iterations.
Focussing on weeks 17-22, we find only one area with a posterior probability exceeding 0.9 of being centre of a persistent space-time cluster of length 5 weeks. However, considering persistent clusters of length \(D=4\) weeks, there are seven areas with probabilities over 0.9, and eight areas with probabilities over 0.8. Figure 4 shows the estimated probabilities for \(D=4\) across the Greater South East of England, with a sharp delineation apparent between the “Kent variant” epicentre, and other areas. Figure 5 shows in closer detail the areas in the epicentre. The Swale local authority, with a posterior probability of one, was among the Kent local authorities first affected by the new variant (Reuters 2021).
Of interest also are forecasts of clustering status. We consider training data for the first \(T=23\) weeks to make one-step ahead predictions of clustering in week 24. So cluster indicators \(J_{i,T+1}=1\) if own area rates \(\widetilde{r}_{i,T+1}=\widetilde{\mu }_{i,T+1}/P_{i}\), and average rates in the locality \(\widetilde{r}_{i,T+1}^{L}=\underset{}{\sum _{j\ne i}}w_{ij} \widetilde{r}_{j,T+1}/\underset{}{\sum _{j\ne i}}w_{ij},\) are both elevated as compared to the region wide rates, \(\widetilde{r}_{T+1}=\underset{}{ \sum _{i}}\widetilde{\mu }_{i,T+1}/\underset{}{\sum _{i}}P_{i}.\) Rates more than 50% above the region wide rate are considered elevated.
In such short-term forecasting, one may compare predicted future clustering with “actual” clustering defined by observed disease counts. Thus, actual rates for area i are \(y_{i,T+1}/P_{i}\), with corresponding locality averages and region-wide rates; these are reliable point estimators for large disease counts. In fact, seven of the 144 areas are identified as actual cluster centres at week 24, the epidemic peak. Predicted and actual cluster status are compared using a \(2\times 2\) table accumulating correct classifications along the diagonal (areas where both actual and predicted cluster status are the same). We can then assess sensitivity, the proportion of actual high-high cluster centres correctly identified, and specificity, the proportion of non-cluster areas correctly identified.
Under model M2, we obtain posterior mean sensitivity (with 95% credible interval) of 0.93 (0.43,1.0), and posterior mean specificity of 0.965 (0.95,0.985). The model prediction is for slightly higher numbers of cluster centres than is actually the case (false positives, with posterior mean 4.8), and this reduces specificity. False negatives are infrequent, with posterior mean 0.5. Using the relationship accuracy = (sensitivity)(prevalence) + (specificity)(1 - prevalence), where the prevalence of high-high clustering is 7/144, one obtains an accuracy of around 0.964.
5.4 Covariate effects
There have been many studies on socio-demographic and environmental risk factors for COVID outcomes. Both incidence and mortality have been linked to area deprivation, urbanicity, poor air quality, and nursing home location (as area risk factors), and non-white ethnicity, and existing medical conditions (as individual risk factors). Impacts of such risk factors were clearly observable in the UK first wave of the COVID pandemic, concentrated in March to May of 2020 (Public Health England 2020; O’Dowd 2020; Quinio 2021; Dutton 2020).
The second UK wave is distinct from the first, in being strongly linked to the emergence of a new virus strain, and by the form of geographic clustering associated with the new strain (see section 5.3), namely a concentration in non-metropolitan areas in the south east of England, areas with relatively low concentrations of ethnic groups and area deprivation. This may tend to attenuate or distort the effect of area predictors \(X_{i}\), so that although their inclusion may improve fit and predictions, the substantive rationale for including them—as disease risk factors per se—is in doubt.
To illustrate this potential for distortion, we estimate a time-varying effect of rurality on COVID infection rates. Rurality in each local authority (LA) is measured by the proportion of micro-areas (lower super output areas) within each LA that are classified as rural towns or villages (Office of National Statistics 2013, Table 1b). One would expect rural areas, with lower population densities, to have lower infection and mortality rates (Lai et al. 2020). Matheson et al. (2020) attribute excess urban mortality (in the UK first COVID wave) to higher population density and association, more people-facing occupations in cities, and greater home overcrowding.
To establish its role for the second wave data, a regression analysis (with \( T=28\) weeks) is carried out with a time varying effect of rurality (\(X_{i}\) ), using the log-linear model. Thus, Eq (6) is extended to include an additive term \(\theta _{t}X_{i},\) where \(\theta _{t}\) is a first-order random walk, with prior \(\theta _{t}\sim \mathcal {N}(\theta _{t-1},\sigma _{\theta }^{2}).\) We find an irregular effect on infection rates, with \( \theta _{t}\) significantly negative in the early weeks of the study period, significantly positive in some later weeks, and often non-significant, with 95% intervals including zero—see Figure 6.
6 Discussion and future research
Forecasts of future infectious disease incidence, especially with spatial disaggregation, are important for policy purposes in epidemic situations. There are benefits in a longitudinal model form which borrows strength over areas since incidence levels tend to be spatially clustered—an example being the geographically concentrated COVID-19 outbreak associated with the “Kent variant” in the UK. Subsequent epidemic diffusion will also be influenced by spatial proximity. Hence, several models in the literature allow spatially varying autoregressive effects, and spatially varying dependence on infection levels in nearby areas.
However, temporal adaptivity and forecasting performance may be improved by allowing for time variation in the epidemic path, for example through space-time autoregressive dependencies. An econometric perspective on autoregressive dependence allowing for both heterogeneity over units and over time is provided by Regis et al. (2021), though they suggest (Regis et al. 2021, p. 6)—from a classical estimation perspective—that a full unit-time random effect structure may be overparameterized.
A full spatio-temporal structure may be applied when longitudinal data cover a relatively short period and made identifiable subject to appropriate constraints. Thus, (Watson et al. 2017)—using a Bayesian perspective—consider area data on Lyme disease over \(T=5\) years. They use the first four years to predict the last, using a full spatio-temporal autoregressive scheme allowing both spatial and temporal correlation.
However, over a longer set of time points, there would be a heavy parameterisation in a fully interactive scheme. In the present application, fully interactive autoregressive effects as in Eq. (5), and other space-time parameters as in Eq. (11), would involve 3NT unknown random effects (i.e. three times the number of data points). By contrast, the newly proposed space-time model—for example, in Eq. (9)—involves considerably fewer, \(NT+2(N+T)\), random effects. A fully interactive specification would also limit the form of the time dependence in autoregression that can be considered; for example, a low order polynomial in time might be used for \( \{\psi _{2t},\psi _{4t}\}\) in Eq. (12), instead of a random walk in time. Finally, with the separate space and time effects, as in Eq. (9), their distinct contribution to improved fit and forecasts can be assessed, and interpretability is straightforward.
In the present study, over a longitudinal series of nearly 30 time points, the parsimonious space-time autoregressive representation provides improved one-step ahead forecasts as compared to a model allowing spatially varying autoregressive dependence only. The latter model is shown to underpredict new cases at in the ascent phase of the epidemic (in November and early December 2020 for the UK second COVID-19 wave), when actual cases were rapidly increasing. By contrast, in the downturn phase, the model with only spatial variation in autoregressive effects provides an overprediction of new cases.
Other substantive features of infectious epidemics have been be investigated, such as the location of prolonged space-time clusters. In the Greater South East of England, there is a clearly demarcated epicentre for the outbreak in the epidemic ascent phase (see Fig. 4).
Drawing on the time series literature on random coefficient autoregression, we have set out alternative linear and log-linear specifications applicable to the area-time situation. For the particular infectious disease data concerned, the linear model had a better fit, but further research on similar forms of data (including longitudinal area data on chronic as well as infectious disease, and indeed any form of longitudinal area count data) is indicated to establish the comparative strengths of the linear and log-linear forms. The above analysis has not considered the full scope of possible autoregressive dependence—including lags on latent means for both the focus area and its locality—as in Eqs. (3) and (4). Such a model was not tractable in the software used here. Extensions may also be envisaged to higher order lags, such as spatio-temporal AR1 (lag 1) and AR2 (lag 2) dependence for both the focus area and its surrounding locality in Eqs. (6) and (7).
Given that the COVID pandemic has typically involved multiple waves, one might also be interested in longitudinal modelling over two or more waves, for instance to compare area-specific infection rates at epidemic peaks. The method used here is more easily applied to multiwave data than one involving area specific phenomenological models (e.g. logistic, Richards) which would necessitate using latent switching parameters between waves.
Another generalisation is to related outcomes such as mortality and hospitalisations. This could involve generalisations of the linear and log-linear count regression specifications—such as Eqs. (6) and (7)—to include borrowing strength over space, time and outcomes. This would be combined with multiple outcome count regression (Poisson or negative binomial). Alternatively, conditioning on modelled infections, one could model case fatality and hospitalisation as binomial responses .
References
Anselin L (1995) Local indicators of spatial association–LISA. Geogr Anal 27(2):93–115
Besag J, York J, Mollié A (1991) Bayesian image restoration with two applications in spatial statistics. Ann Inst Statist Math 43(1):1–59
Brooks S, Gelman A (1998) General methods for monitoring convergence of iterative simulations. J Comput Gr Stat 7(4):434–455
Burra P, Soto-Díaz K, Chalen I, Gonzalez-Ricon R, Istanto D, Caetano-Anollés G (2021) Temperature and latitude correlate with SARS-CoV-2 epidemiological variables but not with genomic change worldwide. Evol Bioinf 17:1176934321989695
Challen R, Brooks-Pollock E, Read J, Dyson L, Tsaneva-Atanasova K, Danon L (2021) Risk of mortality in patients infected with SARS-CoV-2 variant of concern 202012/1: matched cohort study. British Medical Journal, 372. https://www.bmj.com/content/372/bmj.n579
Chattopadhyay S, Maiti R, Das S, Biswas A (2021) Change-point analysis through INAR process with application to some COVID-19 data. Statistica Neerlandica (in press)
Chen C, Teng Y, Lin B, Fan I, Chan T (2016) Online platform for applying space-time scan statistics for prospectively detecting emerging hot spots of dengue fever. Int J Health Geogr 15(1):1–9
Cheng Q, Lu X, Wu J, Liu Z, Huang J (2016) Analysis of heterogeneous dengue transmission in Guangdong in 2014 with multivariate time series model. Scientif Rep 6(1):1–9
Chintalapudi N, Battineni G, Amenta F (2020) COVID-19 disease outbreak forecasting of registered and recovered cases after sixty day lockdown in Italy: a data driven model approach. J Microbiol, Immunol Infect 53(3):396–403
Clements A, Lwambo N, Blair L, Nyandindi U, Kaatano G, Kinung’hi S, Webster J, Fenwick A, Brooker S (2006) Bayesian spatial analysis and disease mapping: tools to enhance planning and implementation of a schistosomiasis control programme in Tanzania. Trop Med Int Health 11(4):490–503
Coly S, Garrido M, Abrial D, Yao A (2021) Bayesian hierarchical models for disease mapping applied to contagious pathologies. PloS One 16(1):0222898
Czado C, Gneiting T, Held L (2009) Predictive model assessment for count data. Biometrics 65(4):1254–1261
Dowdy D, Golub J, Chaisson R, Saraceni V (2012) Heterogeneity in tuberculosis transmission and the role of geographic hotspots in propagating epidemics. Proc Nat Acad Sci 109(24):9557–9562
Dutton A (2020) Coronavirus (COVID-19) related mortality rates and the effects of air pollution in England. Office of National Statistics, London, UK
Fokianos K (2011) Some recent progress in count time series. Statistics 45(1):49–58
Fokianos K, Tjøstheim D (2011) Log-linear Poisson autoregression. J Multivar Anal 102(3):563–578
Gecili E, Ziady A, Szczesniak R (2021) Forecasting COVID-19 confirmed cases, deaths and recoveries: revisiting established time series modeling through novel applications for the USA and Italy. PloS One 16(1):e0244173
Giuliani D, Dickson M, Espa G, Santi F (2020) Modelling and predicting the spatio-temporal spread of COVID-19 in Italy. BMC Infect Dis 20(1):1–10
Glaser S. (2017) A review of spatial econometric models for count data. Hohenheim Discussion Papers in Business, Economics and Social Sciences, No. 19–2017
Glaser S, Jung R, Schweikert K (2021) Spatial Panel Count Data Models: Modeling and Forecasting of Urban Crimes. Available at SSRN 3701642
Greene W (2011) Econometric analysis, 7th edn. Prentice Hall, USA
Haining R, Li G (2021) Spatial Data and Spatial Statistics. In“Handbook of Regional Science”, pp 1961-1983, Springer, eds Fischer, M, Nijkamp, P
Hay J, Pettitt N (2001) Bayesian analysis of a time series of counts with covariates: an application to the control of an infectious disease. Biostatistics 2(4):433–44
Heinen A. (2003). Modelling time series count data: an autoregressive conditional Poisson model. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1117187
Hunter P, Brainard J, Grant A (2021) The impact of the November 2020 English national lockdown on COVID-19 case counts. https://www.medrxiv.org/content/10.1101/2021.01.03.21249169v1
Jalilian A, Mateu J (2021) A hierarchical spatio-temporal model to analyze relative risk variations of COVID-19: a focus on Spain, Italy and Germany. Stoch Environ Res Risk Assess 35:797–812
Johndrow J, Lum K, Gargiulo M, Ball P (2020) Estimating the number of SARS-CoV-2 infections and the impact of social distancing in the United States. https://arxiv.org/abs/2004.02605
Kang S, Cramb S, White N, Ball S, Mengersen K (2016) Making the most of spatial information in health: a tutorial in Bayesian disease mapping for areal data. Geosp Health 11(2):190–198
Lagazio C, Dreassi E, Biggeri A (2001) A hierarchical Bayesian model for space-time variation of disease risk. Stat Modell 1(1):17–29
Lai K, Webster C, Kumari S, Sarkar C (2020) The nature of cities and the Covid-19 pandemic. Curr Opin Environ Sustain 46:27–31
Lawson A, Song H (2010) Bayesian hierarchical modeling of the dynamics of spatio-temporal influenza season outbreaks. Spatial Spatio-temp Epidemiol 1(2–3):187–195
Lowe R, Lee S, O’Reilly K et al (2021) Combined effects of hydrometeorological hazards and urbanisation on dengue risk in Brazil: a spatiotemporal modelling study. Lancet Planet Health 5:e209-19
Lunn D, Spiegelhalter D, Thomas A, Best N (2009) The BUGS project: Evolution, critique and future directions. Stat Med 28(25):3049–67
Maleki M, Mahmoudi M, Wraith D, Pho K (2020) Time series modelling to forecast the confirmed and recovered cases of COVID-19. Travel Med Infect Dis 13:101742
Martines M, Ferreira R, Toppa R, Assunção L, Desjardins M, Delmelle E (2021) Detecting space-time clusters of COVID-19 in Brazil: mortality, inequality, socioeconomic vulnerability, and the relative risk of the disease in Brazilian municipalities. J Geogr Syst 23(1):7–36
Matheson J, Nathan M, Pickard H, Vanino E (2020) Why has coronavirus affected cities more than rural areas? Economics Observatory, https://www.coronavirusandtheeconomy.com/
Mclafferty S (2015) Disease cluster detection methods: recent developments and public health implications. Annal GIS 21(2):127–133
Meyer S, Held L (2014) Power-law models for infectious disease spread. Annal Appl Stat 8(3):1612–1639
Mitze T, Kosfeld R (2021) The propagation effect of commuting to work in the spatial transmission of COVID-19. J Geogr Syst. https://doi.org/10.1007/s10109-021-00349-3
O’Dowd A (2020) Covid-19: People in most deprived areas of England and Wales twice as likely to die. BMJ: British Med J. https://doi.org/10.1136/bmj.m2389
Office of National Statistics (2013) Urban and Rural Area Definitions for Policy Purposes in England and Wales: User Guide. Government Statistical Service, London
Paul M, Held L (2011) Predictive assessment of a non-linear random effects model for multivariate time series of infectious disease counts. Stat Med 30(10):1118–1136
Petropoulos F, Makridakis S (2020) Forecasting the novel coronavirus COVID-19. PLoS One. https://doi.org/10.1371/journal.pone.0231236
Petukhova T, Ojkic D, McEwen B, Deardon R, Poljak Z (2018) Assessment of autoregressive integrated moving average (ARIMA), generalized linear autoregressive moving average (GLARMA), and random forest (RF) time series regression models for predicting influenza A virus frequency in swine in Ontario Canada. PLoS One 13(6):0198313
Public Health England (2020) Disparities in the risk and outcomes of COVID-19. PHE, London, 2020
Qiu H, Zhao H, Xiang H, Ou R, Yi J, Hu L, Ye M (2021) Forecasting the incidence of mumps in Chongqing based on a SARIMA model. BMC Publ Health 21(1):1–12
Quinio V (2021) Have UK cities been hotbeds of the Covid-19 pandemic? Centre for Cities. https://www.centreforcities.org/blog/have-uk-cities-been-hotbeds-of-covid-19-pandemic
Regis M, Serra P, Heuvel E (2021) Random autoregressive models: a structured overview. Econ Rev 2021:1–24
Reuters (2021) A Reuters Special Report. The Fatal Shore. https://www.reuters.com/investigates/special-report/health-coronavirus-uk-variant/
Richards F (1959) A flexible growth function for empirical use. J Exper Bot 10(2):290–301
Roda W, Varughese M, Han D, Li M (2020) Why is it difficult to accurately predict the COVID-19 epidemic? Infect Dis Modell 5:271–281
Roosa K, Lee Y, Luo R, Kirpich A, Rothenberg R, Hyman J, Yan P, Chowell G (2020) Short-term forecasts of the COVID-19 epidemic in Guangdong and Zhejiang China. J Clin Med 9(2):596
Rui R, Tian M, Tang M, Ho G, Wu C (2021) Analysis of the spread of COVID-19 in the USA with a spatio-temporal multivariate time series model. Int J Environ Res Publ Health 18(2):774
Sáfadi T, Morettin P (2003) A Bayesian analysis of autoregressive models with random normal coefficients. J Stat Comput Simul 73(8):563–573
Sartorius B, Lawson A, Pullan R (2021) Modelling and predicting the spatio-temporal spread of COVID-19, associated deaths and impact of key risk factors in England. Scientif Rep 11(1):1–11
Schweikert K, Huth M, Gius M (2021) Detecting a copycat effect in school shootings using spatio-temporal panel count models. Contemp Econ Policy. https://doi.org/10.1111/.coep.12532
Shand L, Li B, Park T, Albarracín D (2018) Spatially varying auto-regressive models for prediction of new human immunodeficiency virus diagnoses. J Royal Stat Soc: Ser C (Appl Stat) 67(4):1003–1022
Shinde G, Kalamkar A, Mahalle P, Dey N, Chaki J, Hassanien A (2020) Forecasting models for coronavirus disease (COVID-19): a survey of the state-of-the-art. SN Computer Sci 1(4):1–15
Stegmueller D (2014) Bayesian hierarchical age-period-cohort models with time-structured effects: an application to religious voting in the US, 1972–2008. Elect Stud 33:52–62
Stehlík M, Kiseľák J, Dinamarca MA, Li Y, Ying Y (2020) On COVID-19 outbreaks predictions: issues on stability, parameter sensitivity, and precision. Stoch Anal Appl 39(3):383–4
Watanabe S (2010) Asymptotic equivalence of Bayes cross validation and Widely Applicable information Criterion in singular learning theory. J Mach Learn Res 11:3571–3594
Watson S, Liu Y, Lund R, Gettings J, Nordone S, McMahan C, Yabsley M (2017) A Bayesian spatio-temporal model for forecasting the prevalence of antibodies to Borrelia burgdorferi, causative agent of Lyme disease, in domestic dogs within the contiguous United States. PLoS One 12(5):e0174428
World Health Organization (WHO) (2021) Tracking SARS-CoV-2 Variants. WHO, Geneva. https://www.who.int/en/activities/tracking-SARS-CoV-2-variants/
Yu X (2020) Risk interactions of coronavirus infection across age groups after the peak of COVID-19 epidemic. Int J Environ Res Publ Health 17(14):5246
Zhang Y, Wang X, Li Y, Ma J (2019) Spatiotemporal analysis of influenza in China, 2005–2018. Scientif Rep 9:19650
Zhou M, Li L, Dunson D, Carin L (2012) Lognormal and gamma mixed negative binomial regression. Proc Int Conf Mach Learn 2012:1343–1350
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare no competing interests.
Code and Data availability
BUGS code and data for replication purposes are available at https://figshare.com/articles/software/SPATIOTEMP_REPLICATION_VERSION_txt/16628167
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Congdon, P. A spatio-temporal autoregressive model for monitoring and predicting COVID infection rates. J Geogr Syst 24, 583–610 (2022). https://doi.org/10.1007/s10109-021-00366-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10109-021-00366-2