The need for psychiatric care in England: a spatial factor methodology

Abstract

To ensure health resources are equitably distributed, composite indices of population morbidity or “health need” are often used. Measures of the dimensions of population morbidity (e.g. socioeconomic deprivation) relevant to health need are typically not directly available but indirectly measured through census or other sources. This paper considers measurement of latent population morbidity constructs using both health outcomes (e.g. hospital admissions, mortality) and observed area social and demographic indicators (e.g. census data). The constructs are allowed to be spatially correlated between areas, as well as correlated with one another within areas. The health outcomes may depend both on the latent constructs and on other relevant covariates (e.g. bed supply), with some covariates possibly measured only at higher (regional) scales. A case study considers variations in psychiatric admissions in 354 English local authority areas in relation to two latent constructs: area deprivation and social fragmentation.

1 Introduction

Summary indices of population morbidity or health need are frequently used to allocate health resources to different areas (Sundquist et al. 2003). One approach to deriving need indices involves what may be termed ecological outcome regression, whereby geographic contrasts in area health outcomes (such as health care usage or mortality) are explained by regression on a collection of socioeconomic indicators (e.g. Smith et al. 1996; Glover et al. 1998). The need index is based on regression coefficients obtained for significant indicators. However, this method has drawbacks. First, spatial patterning (i.e. spatial correlation) in population morbidity is typically neglected. Second, there is no obvious way in which multidimensional constructs are derivable under this approach. Third, the socioeconomic indicators used as predictors may be highly correlated, and multicollinearity may result in unexpected signs for effects and imprecise parameter estimates (Croudace et al. 2000, p. 179; Kidwell and Brown 1982). It is possible to select indicators with a significant effect, but the choice of significant variables and discarding of others as irrelevant to explaining outcome variation may run counter to epidemiological evidence. A related methodology, though with different outcomes (e.g. health expenditures) and more sophisticated regression techniques (e.g. seemingly unrelated regression) has recently developed in the health economics and mental health economics literature (e.g. Moscone et al. 2007). Some econometric work (e.g. by Moscone and Knapp 2005) does recognize spatial interdependencies in a geographic analysis of mental health expenditures, though they note that prior to their work “mental health economics appears to have been largely immune to these [methodological] developments [taking account of spatial correlation]”.

A somewhat contrasting approach for obtaining health need indices, termed here composite socioeconomic scoring, focuses on obtaining single indices of area deprivation to summarise socioeconomic hardship, or single needs measures to summarise morbidity, and does not analyse health outcomes that reflect such morbidity and hardship. Deprivation or health need has been measured in different ways (i.e. using different combinations of indices) in such studies. A recent UK example is the health deprivation and disability domain of the official 2007 Indices of Deprivation (Noble et al. 2004). Also widely used in health need applications are the Townsend index and the Carstairs index (Townsend et al. 1987; Carstairs and Morris 1991). These studies, like ecological outcome regression, have not included spatial correlation.

An alternative strategy, motivated both by high correlations between observed social indicators or health outcomes, and the fact that a spatial setting is involved, is to use latent variable methods that both explicitly model latent morbidity constructs and allow for correlation in such constructs over space. Early work on spatially configured factor models includes Wang and Wall (2003), Knorr-Held and Best (2001) and Congdon (2002a). In line with conventional factor and structural equation techniques, spatial factor models include both directly observed variables and latent variables or constructs that are postulated to exist but are not directly observable. The latent variables can, however, be proxied or “measured” by collections of observed area indicators. As to the form of factor model, there is often considerable existing evidence on how latent need constructs are related to observed indicators, and this can be expressed in a confirmatory model with certain loadings assumed to be zero.

Conventional structural equation and factor models have taken units of analysis to be independent. However, it is now recognised in several spatial health and econometric applications that unobservable area constructs are likely to be spatially correlated, so extending on foundational work by Anselin (1988) and others that focuses on spatial correlation in observed outcomes or in regression residuals. In health geography, the patterning of scores on latent factors, such as area deprivation, is likely to show spatial correlation, and this should be recognised in the derivation of the index (Hogan and Tchernis 2004). Thus Minozzo and Fruttini (2004) mention that “many diseases show similar patterns of geographical variation which may suggest the existence of common underlying risk factors”, while Moscone et al. (2007, p. 845) similarly note that local authority mental health expenditure choices are spatially correlated reflecting “either observable or unobservable common risk factors”.

The analysis here recognizes these developments in structural equation and factor analytic models for areas, but is distinctive in several ways from existing studies. First, the model developed below uses both outcomes and socioeconomic indicators to define need, relying on neither one source of information or another (in contrast to ecological outcome regression and composite socioeconomic scoring). In the terminology of factor models, there are two types of measurement model, one based on social indicators (Sect. 3), the other on health outcomes of various kinds (Sect. 4). Existing spatial factor models either just use health outcomes to measure need (e.g. Wang and Wall 2003), or use just socioeconomic indices (e.g. Hogan and Tchernis 2004). A second distinctive feature of the model developed below is that it recognises that latent need may be multidimensional, and so avoids conflating distinct dimensions of population morbidity; further, the latent constructs are allowed to be correlated within areas. Third, while allowing the latent morbidity construct to be spatially correlated, it also allows for some pure (white noise) random variation in the constructs, as determined by the data. This avoids a strong prior assumption that variation in latent constructs is solely spatially configured.

A fully Bayesian approach is adopted in the model specification, and in parameter estimation in the case study. A Bayesian strategy is advantageous for estimating models with several sets of random effects, including random effects which are spatially clustered (Tutz and Kauermann 2003). This involves specifying prior densities (or “priors” for short) for the parameters involved in defining the model, and updating of these densities (to provide “posterior” inferences) via the likelihoods of the observed health outcome and the social indicator data. Model estimation is based on iterative Monte Carlo Markov Chain techniques (Gelfand and Smith 1990), as implemented in the WINBUGS program (Spiegelhalter et al. 2003).

2 Latent constructs relevant to need for psychiatric care

A case study application (see Sects. 5, 6) considers the impact of two social constructs, namely area social deprivation and social fragmentation, on differences in hospital referrals for serious mental illness in 354 English local authorities. Both these constructs are unobservable and have been measured differently in various studies, where “measuring” refers to operationalising the constructs using a mix of observed indicators.

The deprivation concept is widely applied in analysis of inequalities in economics and health research (e.g. Yitzhaki 1979; Townsend et al. 1987). Area social deprivation, meaning material hardship represented by census (and increasingly intercensal) indicators such as unemployment and socially rented housing has been used widely in ecological studies of health variation, and in connection with many particular health conditions (e.g. Carr and Moffett 2005; Salmond et al. 1999). Of relevance to the case study below is the association between area deprivation and area mental health outcomes, including psychiatric hospital admissions (Koppel and McGuffin 1999; Harrison et al. 1995; Evans et al. 2004) and suicides (e.g. Boyle et al. 2005).

So also is social fragmentation, meaning low community cohesion associated with observed indices such as one person households, high population turnover and many adults outside married relationships. Similar latent constructs that are especially related to area mental health outcomes include social integration (Baller and Richardson 2002) and area social cohesion (Zubrick 2007). The fragmentation construct was proposed by Congdon (1996) in relation to area suicide contrasts, and has been used in several studies of mental health outcomes. For example, Allardyce et al. (2005) find fragmentation to be a significant risk factor for psychotic admissions after allowing for deprivation. Less commonly fragmentation is used to explain variation in other chronic disease, such as cirrhosis mortality (e.g. Davey Smith et al. 2001).

While both these factors may tend to be higher in more urbanised areas, and in inner cities rather than suburbs, they are conceptually distinct since fragmentation is primarily a feature of household composition and demographic structure, not intrinsically linked to socioeconomic status. For instance, Evans et al. (2004, p. 168) find relatively little overlap in the spatial distributions of deprivation and fragmentation. Nevertheless the spatial factor model below allows for within area correlation between the two constructs.

Figure 1 shows the major elements of the model developed in Sects. 3 and 4 schematically, including the loadings relating constructs to health outcomes and social indicators, and the within area correlation. Also shown schematically is the spatial interdependence in construct scores for areas i and k that are neighbours (contiguous to one another). More detailed features of the model—such as the effects used for modelling overdispersion in the health responses (Eqs. 5, 6 below)—are omitted from Fig. 1.

Fig. 1

Factors, relative risks and census (social) indices for neighbouring areas i and k

3 Social indicator measurement model for latent need constructs

The object of the methodology—with the case study application in mind but with a much wider possible relevance—is to derive multidimensional latent health need constructs $C_{i}=(C_{1i},\ldots,C_{Pi})$ for each area, with an additional feature that the constructs may be spatially correlated to some degree (Hogan and Tchernis 2004). It is preferable to avoid a strong priori assumption that need is necessarily spatially configured, and better to allow the data to determine the appropriate mix between spatial or exchangeable (white noise) dependence in the latent constructs. A multivariate version of the conditional autoregressive prior of Besag et al. (1991) is used for representing multiple latent constructs (see Appendix 1), with covariation between constructs within areas according to a P × P matrix Σ, and a parameter $\alpha \in \lbrack 0,1]$ with extremes α = 1 and α = 0 accordingly to pure spatial dependence or pure white noise. The parameter α is termed an index of spatial dependence by Sun et al. (2000, p. 2019). In practice the data is likely to choose an intermediate value for α between 0 and 1. The role of this parameter is demonstrated schematically in Fig. 1.

The latent constructs C _i are measured in part by a set of social indicators and in part by a relative risk model for health outcomes (see Sect. 4). To define the social indicator measurement model, consider indicators (e.g. from a census) in the form of rates $R_{hi}=T_{hi}/D_{hi} (h=1,\ldots,H)$ where T _hi are numerator totals (e.g. unmarried people, unemployed people, renting households), and D _hi are relevant denominators (total adult populations, working populations or total households). These are analyzed using a Gaussian approximation to the binomial, with a variance stabilizing transformation r _hi  = R ^0.5 _hi . Under this transformation ${\rm var}(r_{hi})=\phi _{h}/D_{hi}$ where ϕ _h is an overall scale parameter (Hogan and Tchernis 2004). The transformed rates r _hi are assumed conditionally independent given the constructs C _i  = (C _1i ,...,C _Pi ).

With loadings κ _h  = (κ _h1,..., κ _hP )′ for indicator h on construct p, and with intercepts η _h , one has

$$r_{hi}|C_{i}\backsim N(\eta _{h}+C_{i}\kappa _{h},\phi _{h}/D_{hi})\quad h=1,\ldots,H. $$

(1)

If (as is often the case) substantive knowledge regarding plausible links between indicators and constructs exists, a confirmatory factor analysis may be adopted, with particular loadings κ _hp set to zero (Lee 2007). For the mental illness case study the confirmatory assumptions are set out in Sect. 5.1. Furthermore for identification, fixed loading or fixed variance restrictions are needed (Skrondal and Rabe-Hesketh 2004). A fixed loading approach leaves all parameters in the within area covariance matrix Σ of the construct scores as unknowns, and involves setting one of the non-zero indicator-construct loadings κ _hp to a known value (usually 1) for a particular h. This amounts to setting the scale for construct p (Everitt and Dunn 1983). Alternatively all the loadings κ _hp are unknowns when the variances of the P construct scores are preset (usually to 1).

4 The relative risk measurement model; accounting for construct effects, direct influences and overdispersion

While need is obviously related to population social structure, the impact of health need is also apparent, albeit imperfectly measured (i.e. subject to measurement error), in varying health outcome and activity rates between areas. Hence an additional way of measuring latent need involves analysing area variation in relative risks of hospitalisation, community care referrals (e.g. Congdon 2002b), disease incidence, mortality or disease prevalence, depending on the application. The framework here extends with straightforward adaptations to analysing other outcomes, such as per-capita health expenditures (e.g. Moscone and Knapp 2005; Moscone et al. 2007) which may be continuous data.

However, here we let y _ji (i = 1,..., n;j = 1,..., J) be counts of health outcomes by area i and type j, such as hospital referrals or deaths. When events are infrequent in relation to the population at risk one may adopt Poisson sampling,

$$ y_{ji}\backsim Po(\mu _{ji}E_{ji})$$

(2)

where the counts have means μ _ji E _ji , with E _ji denoting expected referrals or deaths based on region wide age-sex standard rates applied to each area’s population. In the case of an internal standard one has $\sum\limits_{i} E_{ji}=\sum\limits_{i} y_{ji},$ and μ _ji is then a measure of relative risk of outcome j in area i, with average 1. High relative risk areas will be those with 95% intervals for μ _ji that are confined to values above 1.

Geographic variation in hospital referral or mortality rates is expected to be related to latent need constructs C _i which are also measured by the social indicator equation (1). Hence at a minimum, one has

$$log(\mu _{ji})=\alpha _{j}+C_{i}\lambda _{j} $$

(3)

with outcome to construct loadings λ _j  = (λ _j1,..., λ _jP )′. This equation system may also be confirmatory in the sense that some λ _jp loadings are set to zero (e.g. if a particular need construct C _p is judged not relevant to a particular y _j outcome). In the English case study below, we in fact assume that all pairings of outcomes and constructs are possible, and no λ _jp are set to zero a priori. The identifying strategy adopted in the social indicator measurement model (1) extends to the parameters in (3). Thus if a fixed loading approach has been used with the scale of construct p set in one of the equations in (1), it is not necessary also to have a fixed loading in (3).

Equation (3) represents links between health outcomes and unobservable constructs. However, some aspects of population morbidity X _i  = (X _1i ,...,X _Li ) that affect the health outcomes y _ji may be directly measured. For example, hospital admissions may be related to bed supply. Some directly measured predictors V _g  = (V _1g ,...,V _Kg ) may only be available for regional aggregates of areas, rather than for the original areas themselves. This raises the possibility of multilevel modelling in the health outcome equations. One might, for example, allow varying intercepts α _jg over outcomes j and regions g, with variation related to the region-level predictors V _kg . Defining a regional group index g _i  ∈ (1,...,G) for each area i, one would then have

$$ \begin{aligned} {\rm log}(\mu _{ji})&=\alpha _{jg_{i}}+C_{i}\lambda _{j}+X_{i}\beta _{j},\\ \alpha _{jg}&=V_{g}\delta _{j}+e_{jg},\\ \end{aligned} $$

(4)

where $\delta _{j}=(\delta _{j1},\ldots,\delta _{jK})^{\prime }, \beta _{j}=(\beta_{j1},\ldots,\beta _{jL})^{\prime },$ and region level errors e _g  = (e _1g ,...,e _Jg ) are multivariate over outcomes j, as in $e_{g}\sim N_{J}(0,\Sigma _{\alpha}).$

Although rare in relation to the population at risk, the number of health care events may be relatively large, and residual overdispersion may remain, as measured by the saturated deviance (McCullagh and Nelder 1989). Two options may be considered for modelling overdispersion. The first involves a common univariate random effect with value u _i in area i, and loading φ _j on u _i in the model for the relative risk of outcome j. These effects may represent institutional features of (mental) health care, such as hospitalisation thresholds or local need-care mismatches (Battersby et al. 2004; Thompson et al. 2004), that do not necessarily vary smoothly over space, and so u _i may be taken as spatially unstructured. In other applications, it may be more reasonable to take the u _i as spatially structured, mainly representing unknown population risk factors. The common factor u _i scores are similar to those of Wang and Wall (2003), in that they are “measured” only in the health outcome equations. With a log link, one has

$$ {\rm log}(\mu _{ji})=\alpha _{j}+C_{i}\lambda _{j}+X_{i}\beta _{j}+\varphi _{j}u_{i},$$

(5)

where $u_{i}\sim N(0,\tau ).$ If τ is an unknown, a constraint such as φ₁ = 1 may be applied to identify the scale of the u _i .

If the common residual factor option does not eliminate overdispersion, then a second, more heavily parameterised option may be considered. Thus the second option involves outcome specific unstructured residuals u _ji ,

$$ {\rm log}(\mu _{ji})=\alpha _{jg_{i}}+C_{i}\lambda _{j}+X_{i}\beta _{j}+u_{ji}.$$

(6)

The u _ji are analogous to unique errors in classical factor analysis, and so could be taken as spatially unstructured and independently distributed with outcome specific variances τ _j . However, remaining correlation between outcomes may justify a multivariate distribution, such as $u_{i}\sim N_{J}(0,\Sigma _{u}).$

5 Application: bivariate psychiatric need and hospitalisations for serious mental illness

The case study involves J = 2 health outcomes y _ji , and H = 7 census indicators which jointly act to measure a bivariate latent construct C _i  = (C _1i ,C _2i ). The health outcomes are total hospital referrals for schizophrenia and bipolar disorder combined for i = 1,..,354 English local authorities over three financial years, namely 2002–2003 to 2004–2005 (UHCE 2006). These two diagnostic categories account for most psychotic illness and form the majority of psychiatric hospitalisations in England. The counts are confined to ages 15–64 for males (giving y _1i ), and for females (giving y _2i ).

5.1 Social indicator measurement sub-model

The social indicator measurement sub-model (1) for deriving the need constructs is based on 2001 census indicators available for local authority districts in England. The social indicators {R _hi , h = 1, H} used are: proportions of (1) social class D and E (lower skill workers) among the economically active; of (2) unemployment among the economically active; of (3) social housing (renting from local authorities or housing associations) among total households; of (4) one person households among total households; of (5) private furnished rented households among total households; of (6) migrants into and within areas in the year 2000–2001 among the total population; and (7) unmarried adults (single, widowed, divorced) among adults.

The nature of the two constructs taken to represent population psychiatric morbidity is based on a number of previous studies (e.g. Allardyce et al. 2005) of variation in hospitalisations for psychotic illness, though these did not model the factor structure to take account of spatial correlation as the present paper does. Thus areas which have indicators of low social cohesion (i.e. of higher levels of social fragmentation)—such as a high proportion of single-person households, short stay private renting, divorced people and high population mobility—also have both high hospitalisation rates for psychotic illness (Evans et al. 2004). Many studies also show that populations in areas with greater material deprivation have higher rates of psychosis and high hospitalisation rates for serious mental illness (e.g. Boardman et al. 1997).

Drawing on such accumulated substantive knowledge regarding the two constructs, a confirmatory factor model is assumed. Thus {r _1i , r _2i , r _3i } have non-zero loadings only on the deprivation score C _1i , and {r _4i , r _5i , r _6i , r _7i } load only on the fragmentation score C _2i . Taking the loadings (κ _h1, h = 1, 3) as non-zero is based on evidence that area social deprivation is related to concentrations of social housing, low skill workers, and high unemployment (Carstairs and Morris 1991). Similarly, taking the loadings (κ _h2, h = 4, 7) as non-zero accords with studies into psychiatric and suicide outcomes that have used these indicators as positive measures of fragmentation, and negative measures of social cohesion (e.g. Allardyce et al. 2005; Evans et al. 2004). The constructs relate to different aspects of area structure: social cohesion may be relatively high in some residentially stable, albeit deprived, areas, while some affluent inner city areas (with transitory populations) may show high fragmentation. Hence loadings (κ _h1, h = 4, 7) and (κ _h2, h = 1, 3) are taken as zero. However, a correlation between the two constructs is allowed, in that Σ is not assumed to be diagonal.

The social indicator sub-model accordingly has the form,

$$ \begin{aligned} r_{hi}&=\eta _{h}+\kappa _{h1}C_{1i}+a_{hi}\quad h=1,3 \\ r_{hi}&=\eta _{h}+\kappa _{h2}C_{2i}+a_{hi}\quad h=4,7.\\ \end{aligned} $$

(7)

where errors a _hi are mutually uncorrelated with $a_{hi}\backsim N(0,\frac{\phi _{h}}{D_{hi}}).$ The precision parameters {ϕ ⁻¹ _h , h = 1,.,H} are assigned gamma priors with shape 1 and scale 0.001. For the bivariate spatial prior on (C _1i , C _2i ), as described in Appendix 1, area interactions are based on adjacency, namely w _ik  = 1 if local authorities i and k are neighbours, and w _ik  = 0 otherwise. A fixed loading constraint is adopted, namely κ₁₁ = κ₄₂ = 1, with the remaining κ _hp , {κ₂₁, κ₃₁, κ₅₂, κ₆₂, κ₇₂}, being unknowns. The η _h and unknown κ _hp are assigned N(0,100) priors. The within area construct covariance matrix Σ contains 3 unknowns under this fixed loadings constraint, and its inverse (known as a precision matrix) is assigned a Wishart prior with prior scale 2I and 2 degrees of freedom. This corresponds to assuming a prior variances of 1 for the factor scores.

5.2 Health risk models

While the social indicator sub-model has the same form across all models considered, models differ in terms of the relative risk health sub-model assumed. To define the relative risk health sub-model, we take account of the latent constructs, as discussed in Sect. 4, with none of the λ _jp loadings set to zero. However, there are additional directly measured influences. A directly measured area risk factor at local authority level, X _i , that has often been found relevant to psychiatric hospitalisation levels is the percent of nonwhite ethnicity (Dean et al. 1981).

Furthermore, there is a multilevel aspect to the data in that the local authorities are nested within 28 strategic health authorities (SHAs), for which K = 2 predictors {V _kg ,k = 1,...,K; g = 1,...,G} that may be relevant to hospital referral levels are observed (these are not available at the local authority level). These predictors relate to the supply of hospital beds and to levels of serious psychiatric illness registered in primary care. So V _1g  = the log of mental illness beds (2003–2004) per 100,000 SHA population aged 15–64; and V _2g  = the log of standard registration ratios for serious psychiatric conditions recorded under a primary care prevalence registration system (the Quality and Outcomes Framework) for 2004–2005, with a standard based on a national study of psychiatric morbidity (ONS 2002). The registration relates to patients receiving care, namely “treated” prevalence rather than population prevalence (Stuart et al. 1998); specifically the register includes “patients with severe long term mental health problems” (Department of Health 2003).

The first health sub-model is taken, as in (5), to involve a common residual factor (related especially to uncontrolled local service factors rather than smoothly varying risks) as in

$$ \begin{aligned} {\rm log}(\mu _{ji})&=\alpha _{jg_{i}}+C_{i}\lambda _{j}+X_{i}\beta _{j}+\varphi _{j}u_{i},\\ \alpha _{jg}&=V_{g}\delta _{j}+e_{jg},\\ \end{aligned} $$

(8)

where both region errors e _jg and common area residuals u _i are unstructured normal. So $e_{g}\sim N_{2}(0,\Sigma _{\alpha }),$ and $u_{i}\sim N(0,\tau ).$ A fixed loading constraint is used, namely φ₁ = 1, so that τ is an unknown; specifically, τ ⁻¹ is assigned a gamma prior with shape 1 and scale 0.001. The unknown fixed effects {δ _jk , λ _jp , β _jl , φ _j } are assigned N(0,100) priors, and the same prior is assumed for Σ ⁻¹_α as for the construct precision matrix Σ⁻¹.

Data analysis, as discussed in the next section, showed deficient fit for this model. A second model was therefore applied with the same social indicator model and higher level regional model as the first, but with outcome specific residual effects in the health risk model, as in (6). So Model 2 has a social indicator sub-model as in (7), but health response model

$$ {\rm log}(\mu _{ji})=\alpha _{jg_{i}}+C_{i}\lambda _{j}+X_{i}\beta _{j}+u_{ji}, $$

(9)

with $u_{i}\sim N_{J}(0,\Sigma _{u}),$ and with Wishart prior $\Sigma _{u}^{-1}\sim W(2I,2).$

6 Psychiatric need model: results and findings

Model estimates and inferences are based on two chain runs of 25,000 iterations with dispersed starting values. Convergence by Brooks-Gelman-Rubin criteria (Brooks and Gelman 1998; Gelman et al. 1995) is apparent from around 5000 iterations. Fit criteria (see Appendix 2 for definition) are summarised in Table 1. The last column of Table 1 shows that replicates from Model 1 are in line with the observations (Gelfand 1996). However, there is still deficiency in fit, with average deviances for male and female hospital counts both exceeding the number of observations, namely the 354 English local authorities districts (LADs). By contrast, Model 2 provides mean deviances close to the number of observations, and has better pseudo marginal likelihoods and posterior predictive loss criteria for both health responses y and transformed census data r.

Table 1 Model fit and checks

To see the relevance of the constructs to explaining service use, one may consider the unsmoothed relative risks of hospitalisation for psychotic diagnoses, sometimes called standard admission ratios (i.e. SAR_1i  = y _1i /E _1i and SAR_2i  = y _2i /E _2i ). These are imperfect measures of psychiatric morbidity due to procedural influences on admissions (Thompson et al. 2004). However, some impression of the explanatory power of the constructs is apparent in the correlations of the Model 2 posterior means of C ₁ and C ₂ with SAR₁ and SAR₂. The correlations of SAR₁ and SAR₂ with deprivation, C ₁, are 0.51 and 0.41, respectively, and the correlations of SAR₁ and SAR₂ with fragmentation are 0.55 and 0.48, respectively.

Table 2 presents the most relevant parameter estimates under the better fitting Model 2. The κ-coefficients from the social indicator measurement model (Sects. 3, 5.1) show how all the census indicators have positive loadings on the two latent constructs. The coefficient κ₁₁ (the loading of low skill workers on deprivation) is set at 1 for identification; the loading of unemployment on deprivation (κ₂₁) is a free parameter, estimated at 0.82 with 95% interval from 0.80 to 0.87, while the loading of social housing on deprivation is 1.24 with 95% interval from 1.12 to 1.36. Similarly the loading κ₄₂ of one person households on fragmentation is set at 1 for identification, while the unknown loading (κ₅₂) of private furnished renting on fragmentation is estimated as 1.35, the loading (κ₆₂) of the migration rate on fragmentation as 0.77, and the loading (κ₇₂) of unmarried adults on fragmentation as 1.23.

Table 2 Summary of model 2 parameter estimates

Table 2 shows that both constructs have positive effects on hospitalisation rates as reflected in the λ-coefficients from the health risk sub-model of Sects. 4 and 5.2. Hence the constructs are positive measures of different aspects of population morbidity that affect use of psychiatric services. The male coefficients are higher than the female coefficients for both constructs. By contrast, the impact of ethnicity after allowing for fragmentation and deprivation is stronger for females. There is a wide literature on ethnic differences in prevalence and/or hospitalisation for serious mental illness, and how far such differences can be explained away by ethnic differences in socioeconomic status (Breslau et al. 2005). While some studies find that higher ethnic prevalence for psychosis is explained largely by socio-economic factors (Jenkins et al. 1997), the fact that ethnicity remains significant here after controlling for deprivation supports research finding distinct ethnic and socioeconomic effects on hospitalisation for psychosis.

As argued in Sect. 4, service use levels may be subject to local variations due to particularities of service provision or resourcing (e.g. the relative balance between community and acute care for the seriously mentally ill). These particular features may mean hospital admission levels are considerably higher or lower than might be expected on the basis of population morbidity. To account for such factors separate unstructured effects have been introduced for males and females, as in equation (6), though Table 2 shows that the correlation between male and female unstructured effects (u ₁ and u _2i ), denoted as ρ _u , is in fact high. Some LADs have very low hospitalisation levels possibly due to well developed community alternatives (Wierdsma et al. 2007). An example is Tunbridge Wells with 30 male and 27 female admissions, compared to expected totals of 185 and 184; in consequence this LAD has highly negative u _ji . By contrast, the affluent market town of Harrogate in North Yorkshire has male and female SARs exceeding 150, despite its social structure (construct scores C ₁ = −1.21, C ₂ = 0.17); in consequence it has highly positive u _ji .

It is also apparent that the regional indicators, bed supply and registered serious psychiatric illness in primary care, have insignificant effects, namely effects with 95% intervals straddling zero. There is significant regional variation in intercepts (apparent from the significance of the σ_α1 and σ _α2 parameters), but these indicators do not explain it. There has been recent discussion about the spatial pattern of inpatient psychiatric beds in terms of possible mismatches with population need, and evidence of unacceptably high bed-occupancy levels (Griffiths 2002; Thompson et al. 2004). Harrison et al. (1995) found bed availability to have a greater relevance to explaining variation in admission for non-psychotic illness (including neurotic conditions), whereas socio-economic variables were most relevant to explaining variation in psychotic hospitalisations. As to the insignificant impact of treated prevalence, this may reflect issues of access to primary care for the seriously mentally ill (Lester et al. 2003).

Table 2 also shows parameters relevant to both sub-models. First of all, the high value of 0.94 for the index of spatial dependence (symbolically α) reflects the high level of spatial correlation in deprivation and fragmentation scores. By contrast, Table 2 shows only a moderate within-area correlation (symbolically ρ) of 0.30 between constructs. This is obtained by monitoring the quantity ρ = Σ₁₂/(Σ₂₂Σ₁₁)^0.5 through MCMC samples. The role of this parameter is demonstrated schematically in Fig. 1. It has been argued by some that deprivation and fragmentation are rather indistinct concepts (Stjärne et al. 2004), though Congdon (2004) provides evidence in support of their distinct nature. The evidence from the present analysis tends to confirm the Congdon (2004) study.

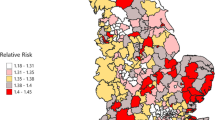
Figures 2 and 3 present the construct scores in standardised form - the model above uses unstandardised scores, but the corresponding standardised scores may be monitored and their posterior densities obtained. The standardised deprivation scores C _1i have a correlation of 0.89 with a recent UK government deprivation index, known as the Index of Multiple Deprivation (ODPM 2004). They are highest in urban areas of north west England and the coastal north east, as well as parts of Birmingham, and areas in inner east and south east London.

Fig. 2

Deprivation scores (Posterior Means, Model 2)

Fig. 3

Fragmentation scores (Posterior Means, Model 2)

The spatial pattern of the highest social fragmentation scores (Fig. 3) does show some overlap with that of high deprivation scores (Fig. 2). However, the finer detail shows contrasts. Within London, the highest ranking posterior means for fragmentation are in central and inner south London boroughs (Table 3). These are not the most deprived areas, but boroughs such as Camden, Kensington and Chelsea, Lambeth, and Westminster, with highly mobile populations, many one person households, but some highly affluent sub-areas. Fragmentation scores are also high in some university towns (especially Oxford and Cambridge) and resort coastal areas with transient sub-populations (such as Brighton and Bournemouth). As recognized in recent Parliamentary discussions, “..levels of social capital might also suffer in coastal towns as the transient population are less likely to involve themselves in social networks and associations, therefore contributing less to the well being of the community than the resident population” (House of Commons 2006).

Table 3 Highest posterior means on deprivation and fragmentation

Links with other area typologies are also of interest. For instance, the UK Office of National Statistics (ONS) has developed a classification of local authority districts (LADs) by cluster analysis, and Table 4 shows averages of deprivation and fragmentation scores by ONS cluster (ONS 2004). Deprivation is highest in manufacturing and industrial areas, as well as parts of London. Fragmentation is high in central London districts, and regional centres, which include many larger not necessarily deprived towns, such as Leeds,Bristol, Bournemouth, Eastbourne, and Norwich (see Table 4b).

Table 4 Deprivation and fragmentation by ONS cluster

A further feature is that fragmentation, and to a lesser extent, deprivation are higher in urbanised areas. A classification of the 354 LADs into six categories has been provided by the Department for Environment, Food and Rural Affairs (DEFRA 2005). These categories are “major urban” (76 LADs), “large urban” (45), “other urban” (55), “significant rural” (53), “rural 50” (52) and “Rural 80” (73). Table 5 shows fragmentation scores vary from 1.1 in major urban LADs to −0.3 in LADs with 50% or more of their population living in rural settlements.

Table 5 Local districts by urban–rural category and construct scores

7 Discussion

This paper has considered a health care application where measures of population morbidity are indirectly measured. The case study application involves hospitalisations for psychosis in England. Previous work to derive psychiatric health needs scores has typically used regression of service use on a mix of social indicators and derived the index using significant regression effects. Such approaches are not adapted to measuring multidimensional need, are subject to unexpected signs due to multicollinearity and with some recent exceptions have not included spatial dependence in need. By contrast the model of the paper allows for multidimensional constructs, for spatial correlation in construct scores, and for measurement of need taking account of both service use patterns and area social structure. The approach has involved need for psychiatric care but has wider applicability. In the case study application, the outcomes are hospitalisation counts, but they might equally be mortality or disease incidence totals. The health outcomes might also be per capita health expenditures (e.g. Moscone et al. 2007).

Existing spatial factor applications have simply included a social indicator measurement model (Hogan and Tchernis 2004); used common spatial factors that are not based on social indicators (i.e. common spatial residual factors) in a simple health response model (Wang and Wall 2003); or have confined themselves to a single indicator based construct (Liu et al. 2005). Existing spatial factor approaches also do not extend to multilevel nesting, apparent in the case study’s arrangement of English local authorities within Strategic Health Authorities.

Spatial factor models build on conventional factor and structural equation models but have distinct features (Oud and Folmer 2008). For example, the approach of the model in this paper does not fit neatly into the usual definition of a structural equation model, as there are no explicit structural equations interlinking the constructs. The constructs are correlated within areas, which amounts to a structural link between constructs, and one could say that the multivariate spatial prior on the constructs (e.g. see Appendix 1) is a type of structural model since it specifies both intercorrelation between variables and correlations between areas. Methodological extensions that are relatively straightforward to the method described are to allow nonlinear impacts of fragmentation or deprivation or interactions between them.

The analysis here has potential importance in the statistical methodology used in deriving health needs scores. Although a univariate need index has a straightforward appeal, population morbidity (and hence need for health care) may be multidimensional (Lloyd 2004). A data reduction approach which both recognises the potential multifactorial nature of population ill health and thereby need for care, and which also allows for spatial structuring of morbidity constructs therefore offers a way forward in modelling population health need.

Appendices

Appendix 1: Prior assumptions for multivariate latent construct scores

Define a spatial interaction matrix between areas {i,k = 1,...,n} by W = [w _ik ], and set D = Diag(d ₁,...,d _n ), where $d_{i}=\mathop{\Sigma} \limits_{k\neq i}w_{ik}.$ If w _ik  = 1 when areas i and k are contiguous, and zero otherwise, then d _i is the number of neighbors for area i. The multivariate spatial prior used follows Song et al. (2006) by taking

$$p(C|\Upphi ,\alpha ,\zeta )\sim |D-\alpha W|^{P/2}|\zeta |^{n/2}exp[-\frac{1}{2} C\Upphi ^{-1}C^{\prime }] $$

where C = (C ₁,...,C _n ) is the (1 × nP) latent construct vector defined over all areas, and the joint precision (inverse covariance) matrix is

$$\Upphi ^{-1}=(D-\alpha W)\otimes \zeta ,$$

where α ∈ (0,1) is an index of spatial dependence but also acts as a “propriety parameter”, ensuring invertibility of Φ. That is, C is multivariate normal with mean consisting of a vector of zeroes of length nP , and with nP × nP covariance matrix Φ. The P × P positive definite symmetric matrix Σ = ζ⁻¹ describes within area covariation between the P constructs, and D−αW is the precision matrix for the spatial effects. The latter matrix can also be written as D(I−αB) where B = D ⁻¹ W with B = [b _ik ]. Taking α = 1 provides purely spatial smoothing, while taking α = 0 leads to non-spatial exchangeable pooling of strength. Here α is estimated from the data, avoiding these extremes.

The conditional prior for C _i given the remaining effects C _[i] = (C ₁,...,C _i-1, C _i+1,...,C _n ) is multivariate normal with means E(C _i |C _[i]) and precisions Prec(C _i |C _[i]). Thus E(C _i |C _[i]) = (M _1i ,...,M _Pi ), where

$$E(C_{pi}|C_{[i]})=M_{pi}=\alpha \mathop{\Sigma} \limits_{k\neq i} w_{ik}C_{pk}/ \mathop{\Sigma} \limits_{k\neq i} w_{ik}=\alpha \mathop{\Sigma} \limits_{k\neq i} b_{ik} C_{pk}$$

and

$${\rm Prec}(C_{i}|C_{[i]})=d_{i}\zeta .$$

If the w _ik are set to 1 for neighbouring areas, and 0 otherwise, then

$$M_{pi}=\alpha \mathop{\Sigma}\limits_{k\in \partial _{i}}C_{pk}/d_{i}$$

are locality averages of the spatial effect for the pth construct, where ∂ _i is the locality for area i.

Appendix 2: Model fit and checks

Assessments of model fit are based on the pseudo marginal likelihood (psML) derived using Monte Carlo estimates of conditional predictive ordinates (CPOs) (Kuo and Cohen 1999), and the posterior predictive loss (PPL) criteria of Gelfand and Ghosh (1998). The CPO, p(y _i |y _[i]), defines the density for area i when the model is estimated using data for remaining areas y _[i] = (y ₁,...,y _i-1, y _i+1,...,y _n ) only (Geisser and Eddy 1979). If a particular observation has a higher CPO under a particular model, then that model provides a better fit to it; totalling log(CPO _i ) over observations provide the log(psML), and models with higher log(psML) values provide better fits (Sinha et al. 1999).

To derive the PPL criteria, samples of replicate data from the posterior predictive density P(y _rep,r _rep|y,r) are taken. With posterior means $\overline{r}_{\rm rep}$ and variances v _rep for r _rep, the social indicator model PPL for a specified k > 0 is

$$ \sum\limits_{i=1}^{n} \sum_{h=1}^{H} v_{\rm rep,hi}+ \frac{k}{k+1} \sum\limits_{i=1}^{n} \sum_{h=1}^{H} (r_{hi}-{\bar{r}}_{\rm rep,hi})^{2}.$$

(10)

For the health count outcome data y with replicates y _rep, the PPL is as in Eq. (18) of Gelfand and Ghosh (1998).

For model checking (assessing whether the models reproduce the data) a check is made whether observed {y, r} are within 95% intervals of {y _rep, r _rep}. In a satisfactory model predictive concordance is around 95% (Gelfand 1996, p. 158). Finally, to assess model fit for the health counts, the scaled deviance measure $\sum \sum [y_{ji}{\rm log}\left(\frac{y_{ji}}{E_{ji}\mu _{ji}}\right)-(y_{ji}-E_{ji}\mu _{ji})]$ is relevant (Knorr-Held and Rainer 2001; McCullagh and Nelder 1989).