Area-to-point Kriging with inequality-type data

Abstract

In practical applications of area-to-point spatial interpolation, inequality constraints, such as non-negativity or more general constraints on the maximum and/or minimum attribute value, should be taken into account. The geostatistical framework proposed in this paper deals with the spatial interpolation problem of downscaling areal data under such constraints, while: (1) explicitly accounting for support differences between sample data and unknown values, (2) guaranteeing coherent (mass-preserving) predictions, and (3) providing a measure of reliability (uncertainty) for the resulting predictions. The formal equivalence between Kriging and spline interpolation allows solving constrained area-to-point interpolation problems via quadratic programming (QP) algorithms, after accounting for the support differences between various constraints involved in the problem formulation. In addition, if inequality constraints are enforced on the entire set of points discretizing the study domain, the numerical algorithms for QP problems are applied only to selected locations where the corresponding predictions violate such constraints. The application of the proposed method of area-to-point spatial interpolation with inequality constraints in one and two dimension is demonstrated using realistically simulated data.

Appendices

Appendix

Derivation of bounded ordinary Kriging (BOK) variance

Let C be a ((K + 2) × (K + 2)) matrix that is partitioned as

$$ {\bf C} = \left[ \begin{array}{lll} {\bf C}_{ss} & {\bf 1} &\vline {\bf z}_s \\ {\bf 1}^{\rm T} & {0} &\vline {0} \\ \hline {\bf z}_s^{\rm T} & {0} &\vline {0} \end{array} \right] = \left[ \begin{array}{ll} {\bf C}_{11} & {\bf c}_{12} \\ {\bf c}_{21} & {\bf c}_{22} \end{array} \right]$$

(34)

where ${\bf C}_{11} = \left[\begin{array}{ll} {\bf C}_{ss} & {\bf 1} \\ {\bf 1}^{\rm T} & 0 \end{array}\right]$ ${\bf c}_{12} = \left[\begin{array}{l}{\bf z}_s \\ 0 \end{array}\right]$ c ₂₁ = [z ^T _s   0], and c ₂₂ = [0].

Consider now a ((K + 2) × 1) vector v containing a (K × 1) vector of covariances c ^s _p between areal data and unknowns, the sum of weights 1, and the lower bound value z _l . The vector v can also be partitioned into two vectors v ₀ = [[c ^s _p ]^T 1]^T and z _l , as

$$ {\bf v} = \left[\begin{array}{l}{\bf c}_p^s \\ 1 \\ \hline z_l \end{array} \right] = \left[\begin{array}{l} {\bf v}_0 \\ z_l \end{array}\right]$$

(35)

We assume that the inverse of C exists, and is denoted as ${\bf B} = {\bf C}^{-1} = \left[\begin{array}{ll} {\bf B}_{11} & {\bf b}_{12} \\ {\bf b}_{21} & {\bf b}_{22} \end{array}\right].$ Then, the BOK variance of Eq. 15a can be re-written as

$$ \begin{aligned} {\hat \sigma}_{\rm BOK}^2({\bf u}_p) = & C_Z({\bf 0}) - [{\bf v}_0^{\rm T} \quad z_l] {\bf C}^{-1} \left[\begin{array}{l}{\bf v}_0 \\ z_l\end{array}\right] = C_Z({\bf 0}) - [{\bf v}_0^{\rm T} \quad z_l] \left[\begin{array}{ll}{\bf B}_{11} & {\bf b}_{12} \\ {\bf b}_{21} & {\bf b}_{22} \end{array}\right] \left[\begin{array}{l}{\bf v}_0 \\ z_l \end{array}\right]\\ = & C_Z({\bf 0}) - ( {\bf v}_0^{\rm T}{\bf B}_{11}{\bf v}_0 + z_l {\bf b}_{21}{\bf v}_0 + {\bf v}_0^{\rm T}{\bf b}_{12}z_l + z_l {\bf b}_{22}z_l). \end{aligned} $$

(36)

According to the Partitioned Matrix Lemma (Meyer 2000), matrix B contains the following entries, provided that both C ₁₁ and b ₂₂ are nonsingular:

• b ₂₂ = [c ₂₂ − c ₂₁ C ⁻¹₁₁ c ₁₂]⁻¹ = [0 − c ₂₁ C ⁻¹₁₁ c ₁₂]⁻¹ = −[c ₂₁ C ⁻¹₁₁ c ₁₂]⁻¹

• b ₁₂ = −C ⁻¹₁₁ c ₁₂[c ₂₂ − c ₂₁ C ⁻¹₁₁ c ₁₂]⁻¹ = −C ⁻¹₁₁ c ₁₂ b ₂₂

• b ₂₁ = − b ₂₂ c ₂₁ C ⁻¹₁₁

• B ₁₁ = C ⁻¹₁₁  + C ⁻¹₁₁ c ₁₂ b ₂₂ c ₂₁ C ⁻¹₁₁

Let $\iota = {\bf c}_{21}{\bf C}_{11}^{-1}{\bf c}_{12}$ and recall that the predicted value at location u _p is expressed as $\hat z({\bf u}_p) = {\bf V}_0^{\rm T}{\bf C}_{11}^{-1}{\bf c}_{12}.$ The BOK variance of Eq. 36 then becomes:

$$ \begin{aligned} {\hat \sigma}_{\rm BOK}^2({\bf u}_p) = & C_Z({\bf 0}) - {\bf v}_0^{\rm T}{\bf B}_{11}^{-1}{\bf v}_0 + z_l{\bf c}_{21}{\bf C}_{11}^{-1}{\bf v}_0 \iota^{-1} + {\bf v}_0^{\rm T}{\bf C}_{11}^{-1}{\bf c}_{12}z_l\iota^{-1} - z_l^2 \iota^{-1} \\ = & C_Z({\bf 0}) - {\bf v}_0^{\rm T}{\bf B}_{11}^{-1}{\bf v}_0 + [2z_l\hat z({\bf u}_p) - z_l^2]\iota^{-1} \\ = & C_Z({\bf 0}) - {\bf v}_0^{\rm T}({\bf C}_{11}^{-1}){\bf v}_0 + [{\bf v}_0^{\rm T}\{{\bf C}_{11}^{-1}{\bf c}_{12}{\bf c}_{21}{\bf C}_{11}^{-1}\}{\bf v}_0 + 2z_l\hat z({\bf u}_p) - z_l^2]\iota^{-1} \\ = & {\hat \sigma}_{OK}^2({\bf u}_p) + [{\hat z}({\bf u}_p)^2 - 2z_l \hat z({\bf u}_p) + z_l^2 ]\iota^{-1} = {\hat \sigma}_{OK}^2({\bf u}_p) + \{{\hat z}({\bf u}_p) - z_l\}^2 \iota^{-1}, \end{aligned} $$

where ${\hat \sigma}_{OK}^2({\bf u}_p)$ denotes the unconstrained OK variance at location u _p .

Dual formalism of Kriging with a trend model

Universal Kriging (Matheron 1971) or Kriging with a trend (Goovaerts 1997; Deutsch and Journel 1998), is a general type of Kriging where the mean (trend component) of the random function varies in space. That trend component (or drift) is often modeled as a smoothly varying parametric function of the coordinates vector u:

$$ E\{ Z({\bf u})\} = \mu_Z({\bf u}) = \sum_{m = 0}^M{\beta_m f_m({\bf u})} $$

(37)

where f _m (·) is a deterministic function known at any point u, and β _m denotes its mth unknown parameter; there are (M + 1) such unknown parameters, which are determined by the data.

The other part of the Universal Kriging (UK) model is a second-order stationary residual, characterized by a zero mean and covariance function C _R (h). The dual UK prediction at location u _p using the K areal data can thus be written as

$$ \begin{aligned} \hat{z}({\bf u}_p) = & \sum_{k = 1}^K {w(s_k)C_Z(s_k, {\bf u}_p)} + \sum_{m = 0}^M \beta_m f_m({\bf u}_p) \\ = & [{\bf w}^{\rm T} \quad {\varvec{\upbeta}}^{\rm T}] \left [ \begin{array}{l} {\bf c}_p^s \\ {\bf f}_p \end{array}\right] = {\bf w}^{\rm T}{\bf c}_p^s + {\varvec{\upbeta}}^{\rm T}{\bf f}_p, \quad {\bf u}_p \in A \end{aligned} $$

(38)

with:

$$ \sum_{k = 1}^K w(s_k)f_m(s_k) = 0, \quad m = 0, \ldots, M$$

where w denotes a (K × 1) vector of coefficients of the stochastic interpolator, f _p  = [f _m (u _p ), m = 0, . . . , M]^T denotes a ((M + 1) × 1) vector of deterministic function values at location u _p , and ${\varvec{\upbeta}} = [\beta_m, m = 0,\ldots,M]^{\rm T}$ denotes a ((M + 1) × 1) vector of trend coefficients. Note that the covariance vector c ^s _p in the above equation is derived by regularization from the point residual covariance C _R (h).

In the context of interpolation, area-to-point Dual Kriging with a trend model can be viewed as the following problem: “find the coefficients w and ${\varvec{\upbeta}}$ in Eq. 38, satisfying the K areal data reproduction constraints and the (M + 1) unbiasedness constraints”:

$$ \begin{aligned} \sum_{k = 1}^K g_k({\bf u}_p)\hat {z}({\bf u}_p) |a| = & z(s_k), \quad k = 1, \ldots ,K, \\ \sum_{k = 1}^K w(s_k)f_m(s_k) = & 0, \quad m = 0, \ldots, M, \end{aligned} $$

where |a| denotes the elementary area represented by the pth prediction location, u _p ; this is used for numerical integration purposes. Term f _m (s _k ) denotes deterministic function values associated with the k-th areal support at location u _p .

The vector w of weights and the vector ${\varvec{\upbeta}}$ of trend coefficients in Eq. 38 are derived by solving the following system of normal equations:

$$ \left[\begin{array}{ll} {\bf C}_{ss} & \quad {\bf F} \\ {\bf F}^{\rm T} & \quad {\bf 0} \end{array}\right] \left[ \begin{array}{l} {\bf w} \\ {\varvec{\upbeta}} \end{array}\right] = \left[\begin{array}{l} {\bf z}_s \\ {\bf 0} \end{array}\right]$$

(39)

where F = [f ⁰   ... f ^m ...   f ^M] is a (K × (M + 1)) matrix of (M + 1) low-order drift functionals, with f ^m = [f _m (s _k ), k = 1, . . . , K]^T. Note that the covariance matrix C ^R _ss in the above equation is again derived by regularization from the point residual covariance C _R (h).

QP formalism of Kriging

4.1 A classical QP problem

QP problems involve the optimization of a quadratic objective function (maximization or minimization) subject to a number of constraints. More precisely, consider a quadratic minimization problem subject to the following linear inequality constraints:

$$ \begin{aligned} \hbox{Min} {\frac{1}{2}}{\bf x}^{\rm T}{\bf Cx} + {\bf f}^{\rm T}{\bf x} &\\ {\bf Ax} \geq {\bf b}, \end{aligned} $$

(40)

where x is a (K × 1) vector of decision variables whose respective values need to be determined, and C and f denote, respectively, a (K × K) matrix and a (K × 1) vector with the mathematical expression (function) of the variable considered. To obtain a unique solution of the QP problem, it is assumed that C is a symmetric and positive semi-definite matrix. The Q _l inequality constraints are imposed on the solution vector x by a (Q _l  × K) matrix A and the lower bound vector b; this forces the solution to be greater than the lower bound values.

The duality in QP problems often provides a convenient strategy for arriving at the same solution vector x. The dual form of Eq. 40 can be written as

$$ \begin{aligned} \hbox {Max} -{\frac{1}{2}}{\bf x}^{\rm T}{\bf Cx} + {\bf b}^{\rm T}{\bf t} &\\ {\bf A}^{\rm T}{\bf t} - {\bf Cx} = {\bf f} &\\ {\bf t} \geq {\bf 0}, \end{aligned} $$

(41)

where t is a (Q _l  × 1) vector of Lagrange multipliers associated with the Q _l inequality constraints.

The above dual QP problem in Eq. 41 can be simplified based on the fact that x is a linear combination of t, i.e.: x = C ⁻¹(A ^T t − f). By simply replacing x by the function of t, the dual form of the minimization QP problem in Eq. 40 can be represented as the maximization problem:

$$ \begin{aligned} \hbox {Max} -{\frac{1}{2}}({\bf A}^{\rm T}{\bf t} -{\bf f})^{\rm T}{\bf C}^{-1}({\bf A}^{\rm T}{\bf t} -{\bf f}) + {\bf b}^{\rm T}{\bf t} &\\ {\bf t \geq 0} \end{aligned} $$

which is again equivalent to the minimization problem:

$$ \begin{aligned} \hbox{Min} {\frac{1}{2}}({\bf A}^{\rm T}{\bf t} -{\bf f})^{\rm T}{\bf C}^{-1}({\bf A}^{\rm T}{\bf t} -{\bf f}) - {\bf b}^{\rm T}{\bf t}&\\ {\bf t \geq 0}. \end{aligned} $$

(42)

The dual form of QP problems with equality constraints alone also leads to the the same minimization problem as Eq. 42. The only difference between QP problems with equality and those with inequality constraints is that there are no positive constraints on the Lagrange multipliers in the former case.

4.2 QP problem formulation of CDOK

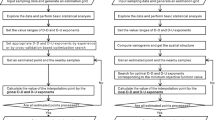
In Sect. 2.2.3, we showed that CDOK is equivalent to a constrained interpolator, which is determined by its coefficients; these coefficients are obtained by solving a quadratic minimization problem subject to linear constraints. In what follows, we will convert the dual form of area-to-point Kriging under constraints into a simplified quadratic programming problem. To keep the problem simple, and without loss of generality, we consider the task of predicting the unknown value at location u _p using the K areal data z _s  = [z(s ₁), . . . , z(s _K )]^T under lower bound inequality constraints only.

The primal QP problem is written in this case as

$$ \begin{aligned} \hbox{Min} {\frac{1}{2}} {\varvec{\upomega}}^{\rm T}{\varvec{\Upsigma}}{\varvec{\upomega}} & \\ {\bf A}_s {\varvec{\upomega}} + {\varvec{\upmu}}_s = {\bf z}_s, &\\ {\bf A}_l {\varvec{\upomega}} + {\varvec{\upmu}}_l \geq {\bf z}_{l}, \end{aligned} $$

(43)

where ${\varvec{\upomega}}$ is a ((K + Q _l ) × 1) vector of weights applied to the K areal data (associated with equality constraints) and the Q _l prediction points (associated with inequality constraints), and ${\varvec{\Upsigma}}$ is a ((K + Q _l ) × (K + Q _l )) matrix of covariances among all constraints. A _s denotes the (K × (K + Q _l )) matrix of equality constraints, and ${\varvec{\upmu}}_s = {\bf G}{\bf 1}_P \beta_0$ and ${\varvec{\upmu}}_l = {\bf 1}_{Q_l} \beta_0$ denote, respectively, a (K × 1) and and (Q _l  × 1) vector of mean values for the areal data RVs and the lower bound RVs. A _l denotes the (Q _l  × (K + Q _l )) matrix of inequality constraints, and z _l represents the lower bound values at Q _l point locations.

The dual form of the constrained DOK problem of Eq. 43 is then written as

$$ \hbox {Max} -{\frac{1}{2}}{\varvec{\upomega}}^{\rm T}{\varvec{\Upsigma}}{\varvec{\upomega}} + {\bf z}^{\rm T}{\varvec{\uppsi}} - {\varvec{\upmu}}^{\rm T}{\varvec{\uppsi}}$$

(44)

$$ {\bf A}^{\rm T}{\varvec{\uppsi}} - {\varvec{\Upsigma}}{\varvec{\upomega}} = {\bf 0}$$

(45)

$$ {\varvec{\uppsi}}_l \geq {\bf 0}$$

(46)

where the objective function is a maximization problem which involves a ((K + Q _l )  × 1) vector ${\varvec{\uppsi}} = [{\varvec{\uppsi}}_s^{\rm T} \quad {\varvec{\uppsi}}_l^{\rm T}]^{\rm T}$ of Lagrange multipliers, as well as data and bound values z = [z ^T _s   z ^T _l ]^T and their means ${\varvec{\upmu}} = [{\varvec{\upmu}}_s^{\rm T} \quad {\varvec{\upmu}}_l^{\rm T}]^{\rm T}.$ The new constraints in Eq. 45 for the dual form of the objective function combine both equality and inequality constraints in the primary form of Eq. 43. The constraints matrix A is written as A = [A ^T _s   A ^T _l ]^T, where A _s is a (K × (K + Q _l )) matrix of equality constraints and A _l is a (Q _l  × (K + Q _l )) matrix of inequality constraints. The corresponding Lagrange multipliers for each constraint are denoted by ${\varvec{\uppsi}}_s$ and ${\varvec{\uppsi}}_l$ respectively. Thus, Eq. 45 is a combination of the following two equations:

$$ \begin{aligned} {\bf A}_s^{\rm T}{\varvec{\uppsi}}_s - {\varvec{\Upsigma}}{\varvec{\upomega}} = {\bf 0},& \\ {\bf A}_l^{\rm T}{\varvec{\uppsi}}_l - {\varvec{\Upsigma}}{\varvec{\upomega}} = {\bf 0}. \end{aligned} $$

As shown in the case of the classical QP problem, the constrained DOK problem can be simplified by the following two steps. First, convert the minimization problem to a maximization problem, and note that ${\varvec{\upomega}}$ is a function of ${\varvec{\uppsi}}$ written as ${\varvec{\upomega}} = {\varvec{\Upsigma}}^{-1}{{\bf A}^{\rm T}{\varvec{\uppsi}}}$ from Eq. 45. Therefore, the simplified version of the dual form of QP problems for constrained DOK can be reformulated as

$$ \begin{aligned} \hbox {Max} -{\frac{1}{2}}[{\varvec{\uppsi}}^{\rm T}{\bf A}{\varvec{\Upsigma}}^{-1}]{\varvec{\Upsigma}}[{\varvec{\Upsigma}}^{-1}{\bf A}^{\rm T}{\varvec{\uppsi}}] + {\bf z}^{\rm T}{\varvec{\uppsi}} - {\varvec{\upmu}}^{\rm T}{\varvec{\uppsi}},& \\ {\varvec{\uppsi}}_l \geq {\bf 0}. \end{aligned} $$

(47)

By letting ${\bf Q}^* = ({\bf A}{\varvec{\Upsigma}}^{-1}{\bf A}^{\rm T})$ the simplified dual form of the CDOK maximization problem in Eq. 47 can be converted to the following minimization problem:

$$ \begin{aligned} \hbox{Min} {\frac{1}{2}} {\varvec{\uppsi}}^{\rm T}{\bf Q}^*{\varvec{\uppsi}} -{\bf z}^{\rm T}{\varvec{\uppsi}} + {\varvec{\upmu}}^{\rm T}{\varvec{\uppsi}}, \\ {\varvec{\uppsi}}_l \geq {\bf 0}. \end{aligned} $$

(48)

where Q ^* is a ((K + Q _l ) × (K + Q _l )) matrix of covariances involving K support-to-support covariances where equality constraints are assigned, and Q _l point covariances where inequality constraints are imposed.