Accelerated first-order methods for a class of semidefinite programs

Abstract

This paper introduces a new storage-optimal first-order method, CertSDP, for solving a special class of semidefinite programs (SDPs) to high accuracy. The class of SDPs that we consider, the exact QMP-like SDPs, is characterized by low-rank solutions, a priori knowledge of the restriction of the SDP solution to a small subspace, and standard regularity assumptions such as strict complementarity. Crucially, we show how to use a certificate of strict complementarity to construct a low-dimensional strongly convex minimax problem whose optimizer coincides with a factorization of the SDP optimizer. From an algorithmic standpoint, we show how to construct the necessary certificate and how to solve the minimax problem efficiently. Our algorithms for strongly convex minimax problems with inexact prox maps may be of independent interest. We accompany our theoretical results with preliminary numerical experiments suggesting that CertSDP significantly outperforms current state-of-the-art methods on large sparse exact QMP-like SDPs.

Appendices

Deferred proofs

Proof of Lemma 3

Let $\varDelta :={\tilde{X}} - X_L$. Then,

$$\begin{aligned} \frac{L}{2}\left\Vert X - X_L \right\Vert _F^2&= \frac{L}{2}\left\Vert X - {\tilde{X}} + \varDelta \right\Vert _F^2\\&= \frac{{\tilde{L}}}{2}\left\Vert X - {\tilde{X}} \right\Vert _F^2 + \frac{{\tilde{\mu }}}{2}\left\Vert X - {\tilde{X}} \right\Vert _F^2 + L\left\langle X - {\tilde{X}}, \varDelta \right\rangle + \frac{L}{2}\left\Vert \varDelta \right\Vert _F^2, \end{aligned}$$

where the second equality follows from expanding the square and the fact that $L = {\tilde{L}} + {\tilde{\mu }}$. Moreover,

$$\begin{aligned} 0\le \frac{L}{2}\left\Vert \sqrt{\frac{{\tilde{\mu }}}{L}} (X - {\tilde{X}}) + \sqrt{\frac{L}{{\tilde{\mu }}}}\varDelta \right\Vert _F^2 = \frac{{\tilde{\mu }}}{2}\left\Vert X - {\tilde{X}} \right\Vert _F^2 + L\left\langle X - {\tilde{X}}, \varDelta \right\rangle + L\kappa \left\Vert \varDelta \right\Vert _F^2. \end{aligned}$$

Combining these two inequalities gives

$$\begin{aligned} \frac{L}{2}\left\Vert X - X_L \right\Vert _F^2&\ge \frac{{\tilde{L}}}{2}\left\Vert X - {\tilde{X}} \right\Vert _F^2 - \frac{L\delta ^2}{2}\left( 2\kappa - 1\right) . \end{aligned}$$

$\square$

The following proof is adapted from [54].

Proof of Lemma 4

It is evident that $\phi _t(X)$ are quadratic matrix functions of the form (8) with $V_0=X_0$ and $\phi _0^*=Q(X_0)$. The remainder of the proof verifies the recurrences on $V_{t+1}$ and $\phi ^*_{t+1}$. We suppose that the stated form holds for some t, and we will show that it will hold for $t+1$ as well. We compute

$$\begin{aligned} \frac{1}{{\tilde{\mu }}}\nabla \phi _{t+1}(X)&= (1-\alpha )(X - V_t) + \alpha \left( X - \left( \varXi _t - \frac{1}{{\tilde{\mu }}}{\tilde{g}}_t\right) \right) . \end{aligned}$$

We deduce that $V_{t+1} = (1-\alpha )V_t + \alpha \left( \varXi _t - \frac{1}{{\tilde{\mu }}}{\tilde{g}}_t\right)$. Noting that $\phi _{t+1}^*=\phi _{t+1}(V_{t+1})$, and applying the recursive definition of $\phi _{t+1}(X)$ gives us

$$\begin{aligned} \phi _{t+1}^*&= (1-\alpha )\left( \phi _t^* + \frac{{\tilde{\mu }}}{2}\left\Vert V_{t+1} - V_t \right\Vert _F^2\right) \\&\quad + \alpha \left( Q(X_{t+1}) + \frac{1}{2{\tilde{L}}}\left\Vert {\tilde{g}}_t \right\Vert _F^2 + \left\langle {\tilde{g}}_t, V_{t+1} - \varXi _t \right\rangle + \frac{{\tilde{\mu }}}{2}\left\Vert V_{t+1} - \varXi _t \right\Vert _F^2 \right) \\&= (1-\alpha )\phi _t^* + \alpha \left( Q(X_{t+1}) + \frac{1}{2{\tilde{L}}}\left\Vert {\tilde{g}}_t \right\Vert _F^2\right) \\&\quad + (1-\alpha )\frac{{\tilde{\mu }}}{2}\left\Vert V_{t+1} - V_t \right\Vert _F^2 + \frac{\alpha {\tilde{\mu }}}{2}\left\Vert V_{t+1} - (\varXi _t - \tfrac{1}{{\tilde{\mu }}}{\tilde{g}}_t) \right\Vert _F^2 - \frac{\alpha }{2{\tilde{\mu }}}\left\Vert {\tilde{g}}_t \right\Vert _F^2\\&= (1-\alpha )\phi _t^* + \alpha \left( Q(X_{t+1}) + \frac{1}{2{\tilde{L}}}\left\Vert {\tilde{g}}_t \right\Vert _F^2\right) \\&\quad + \frac{{\tilde{\mu }}(1-\alpha )\alpha ^2}{2}\left\Vert V_{t} - (\varXi _t - \tfrac{1}{{\tilde{\mu }}}{\tilde{g}}_t) \right\Vert _F^2 + \frac{{\tilde{\mu }}\alpha (1-\alpha )^2}{2}\left\Vert V_{t} - (\varXi _t - \tfrac{1}{{\tilde{\mu }}}{\tilde{g}}_t) \right\Vert _F^2\\&\quad - \frac{\alpha }{2{\tilde{\mu }}}\left\Vert {\tilde{g}}_t \right\Vert _F^2\\&= (1-\alpha )\phi _t^* + \alpha \left( Q(X_{t+1}) + \frac{1}{2{\tilde{L}}}\left\Vert {\tilde{g}}_t \right\Vert _F^2\right) \\&\quad + \alpha (1-\alpha )\left( \frac{{\tilde{\mu }}}{2}\left\Vert \varXi _t - V_t \right\Vert _F^2 + \left\langle {\tilde{g}}_t, V_t - \varXi _t \right\rangle \right) -\frac{ \alpha ^2}{2{\tilde{\mu }}}\left\Vert {\tilde{g}}_t \right\Vert _F^2, \end{aligned}$$

where the third equation follows from substituting the expression for $V_{t+1}$, and the last one from regrouping the terms. $\square$

The following proof is adapted from [54, Page 92].

Proof of Lemma 5

Note that

$$\begin{aligned} \varXi _t&= \frac{X_t + \alpha V_t}{1+\alpha }\\ X_{t+1}&= \varXi _t - \frac{{\tilde{g}}_t}{{\tilde{L}}}\\ V_{t+1}&= (1-\alpha )V_t + \alpha \left( \varXi _t - \frac{1}{{\tilde{\mu }}}{\tilde{g}}_t\right) . \end{aligned}$$

Therefore,

$$\begin{aligned} V_{t+1}&= (1-\alpha )\frac{(1+\alpha )\varXi _t - X_t}{\alpha } + \alpha \left( \varXi _t - \frac{1}{{\tilde{\mu }}}{\tilde{g}}_t\right) \\&= X_t + \frac{1}{\alpha }\left( \varXi _t - X_t - \frac{1}{{\tilde{L}}}{\tilde{g}}_t\right) \\&= X_t + \frac{1}{\alpha }\left( X_{t+1} - X_t\right) . \end{aligned}$$

Then,

$$\begin{aligned} \varXi _{t+1}&= X_{t+1} + \frac{\alpha }{1+\alpha }\left( V_{t+1} - X_{t+1}\right) \\&= X_{t+1} + \frac{1-\alpha }{1+\alpha }\left( X_{t+1} - X_t\right) . \end{aligned}$$

$\square$

Proof of Lemma 6

It is clear that $Q(X_0)\le \phi _0^*$. Thus, consider $X_{t+1}$ with $t\ge 0$. By induction and Lemma 4,

$$\begin{aligned} \phi _{t+1}^*&\ge (1-\alpha )Q(X_t) + \alpha Q(X_{t+1}) + \left( \frac{\alpha }{2{\tilde{L}}} - \frac{\alpha ^2}{2{\tilde{\mu }}}\right) \left\Vert {\tilde{g}}_t \right\Vert _F^2\\&\quad + \alpha (1-\alpha )\left\langle {\tilde{g}}_t, V_t - \varXi _t \right\rangle - (1-\alpha )\left( 2\kappa E^{(1)}_t\right) . \end{aligned}$$

As $X_{t+1}$ satisfies $Q_L(\varXi _t; X_{t+1}) \le Q^*(\varXi _t) + \epsilon _t$, we deduce (see Theorem 2) that

$$\begin{aligned} Q(X_t)&\ge Q(X_{t+1}) + \frac{1}{2{\tilde{L}}}\left\Vert {\tilde{g}}_t \right\Vert _F^2 + \left\langle {\tilde{g}}_t, X_t - \varXi _t \right\rangle + \frac{{\tilde{\mu }}}{2}\left\Vert X_t - \varXi _t \right\Vert _F^2 - 2\kappa \epsilon _t. \end{aligned}$$

These two inequalities together lead to

$$\begin{aligned} \phi ^*_{t+1}&\ge Q(X_{t+1}) - 2\kappa (1-\alpha )(E^{(1)}_t + \epsilon _t)\\&\quad + \left( \frac{\alpha }{2{\tilde{L}}} - \frac{\alpha ^2}{2{\tilde{\mu }}} + \frac{1-\alpha }{2{\tilde{L}}}\right) \left\Vert {\tilde{g}}_t \right\Vert _F^2 + (1-\alpha )\left\langle {\tilde{g}}_t, \alpha (V_t-\varXi _t) + (X_t - \varXi _t) \right\rangle . \end{aligned}$$

It is straightforward to show that the two quantities on the final line are identically zero using the relations $\alpha ^2 = {\tilde{\mu }} / {\tilde{L}}$ and $\varXi _t = \tfrac{X_t + \alpha V_t}{1+\alpha }$ (see Lemma 5). $\square$

Proof of Lemma 7

The statement holds holds for $t = 0$. Thus, consider $\phi _{t+1}$ for $t\ge 0$. By definition

$$\begin{aligned} \phi _{t+1}(X)&= (1-\alpha )\phi _t(X) \\&\quad + \alpha \left( Q(X_{t+1}) + \frac{1}{2{\tilde{L}}}\left\Vert {\tilde{g}}_t \right\Vert _F^2 + \left\langle {\tilde{g}}_t, X - \varXi _t \right\rangle + \frac{{\tilde{\mu }}}{2}\left\Vert X - \varXi _t \right\Vert _F^2 \right) . \end{aligned}$$

As $X_{t+1}$ satisfies $Q_L(\varXi _t; X_{t+1}) \le Q^*(\varXi _t) + \epsilon _t$, we deduce (see Theorem 2) that

$$\begin{aligned} Q(X) \ge Q(X_{t+1}) + \frac{1}{2{\tilde{L}}} \left\Vert {\tilde{g}}_t \right\Vert _F^2 + \left\langle {\tilde{g}}_t, X - \varXi _t \right\rangle + \frac{{\tilde{\mu }}}{2}\left\Vert X - \varXi _t \right\Vert _F^2 - 2\kappa \epsilon . \end{aligned}$$

Then, these inequalities combined with the inductive hypothesis give

$$\begin{aligned} \phi _{t+1}(X)&\le (1-\alpha ) \phi _t(X) + \alpha Q(X) + 2\kappa \alpha \epsilon _t\\&= (1 - (1-\alpha )^{t+1}) Q(X) + (1-\alpha )(\phi _t(X) -(1- (1-\alpha )^{t})Q(X)) + 2\kappa \alpha \epsilon _t\\&\le (1 - (1-\alpha )^{t+1}) Q(X) + (1-\alpha )^{t+1}\phi _0(X) + 2\kappa \left( (1-\alpha )E^{(2)}_t+\alpha \epsilon _t\right) . \end{aligned}$$

$\square$

Proof of Corollary 1

Let $X^*_\mathcal{U}$ denote the optimizer of (QMMP) so that $Q(X^*_\mathcal{U}) = {{\,\textrm{Opt}\,}}_{\text {(QMMP)}}$. Then, Lemmas 6 and 7 give

$$\begin{aligned} Q(X_t)- {{\,\textrm{Opt}\,}}_{\text {(QMMP)}}&\le \phi _t^* + 2\kappa E_t^{(1)} - Q(X^*_\mathcal{U})\\&\le \phi _t(X^*_\mathcal{U}) +2\kappa E_t^{(1)} - Q(X^*_\mathcal{U})\\&\le (1 - (1-\alpha )^t)Q(X^*_\mathcal{U}) + (1-\alpha )^t \phi _0(X^*_\mathcal{U}) + 2\kappa E_t - Q(X^*_\mathcal{U})\\&= (1-\alpha )^t \left( \phi _0(X^*_\mathcal{U})- {{\,\textrm{Opt}\,}}_{\text {(QMMP)}}\right) + 2\kappa E_t. \end{aligned}$$

Note also that by the definition of $\phi _0(\cdot )$ and the $\mu$-strong convexity of Q, we have

$$\begin{aligned} \phi _0(X^*_\mathcal{U}) - {{\,\textrm{Opt}\,}}_{\text {(QMMP)}}&= Q(X_0) - {{\,\textrm{Opt}\,}}_{\text {(QMMP)}} + \frac{{\tilde{\mu }}}{2}\left\Vert X^*_\mathcal{U}- X_0 \right\Vert _F^2\\&\le 2\left( Q(X_0) - {{\,\textrm{Opt}\,}}_{\text {(QMMP)}}\right) . \end{aligned}$$

Combining the two inequalities completes the proof. $\square$

Proof of Lemma 8

Let ${\tilde{\gamma }}\in \mathop {\mathrm {arg\,max}}\limits _{\gamma \in \mathcal{U}}q(\gamma ,X_0)$. By $\mu$-strong convexity of Q(X), we have that

$$\begin{aligned} Q(X)&\ge q({\tilde{\gamma }}, X)\\&\ge q({\tilde{\gamma }}, X_0) + \left\langle \nabla _2\, q({\tilde{\gamma }}, X_0), X - X_0 \right\rangle + \frac{\mu }{2}\left\Vert X - X_0 \right\Vert _F^2\\&= Q(X_0) - \frac{1}{2\mu } \left\Vert \nabla _2\, q({\tilde{\gamma }}, X_0) \right\Vert _F^2 + \frac{\mu }{2}\left\Vert X - X_0 + \frac{\nabla _2\,q({\tilde{\gamma }}, X_0)}{\mu } \right\Vert _F^2. \end{aligned}$$

In particular, taking $X = \mathop {\mathrm {arg\,min}}\limits _{X\in {\mathbb {R}}^{(n-k)\times k}} Q(X)$ gives

$$\begin{aligned} Q(X_0) - {{\,\textrm{Opt}\,}}_{\text {(QMMP)}}\le \frac{\left\Vert \nabla _2\, q({\tilde{\gamma }}, X_0) \right\Vert _F^2}{2\mu }\le \frac{\mu \kappa ^2 R^2}{2}, \end{aligned}$$

where the last inequality follows from Assumption 4. This proves the first claim. Next, by Theorem 3, we have that for all $t\ge 0$, that $Q(X_t)-Q(X_0)\le Q(X_t)-{{\,\textrm{Opt}\,}}_{\text {(QMMP)}} \le 2\mu \kappa ^2 R^2$ and hence

$$\begin{aligned} \frac{\mu }{2}\left\Vert X_t - X_0 + \frac{\nabla _2\, q({\tilde{\gamma }}, X_0)}{\mu } \right\Vert _F^2 \le Q(X_t) - Q(X_0) + \frac{\left\Vert \nabla _2\, q({\tilde{\gamma }}, X_0) \right\Vert _F^2}{2\mu }\le \frac{5\mu \kappa ^2 R^2}{2}. \end{aligned}$$

Using the assumption $X_0 = 0_{(n-k)\times k}$ in Assumption 4 and applying triangle inequality together with the bound $\left\Vert \nabla _2\,q({\tilde{\gamma }}, X_0) \right\Vert _F^2\le \mu ^2\kappa ^2 R^2$ derived from Assumption 4, we deduce that for all $t\ge 0$,

$$\begin{aligned} \left\Vert X_t \right\Vert _F&\le \left( 1+\sqrt{5}\right) \kappa R. \end{aligned}$$

Then, as $\varXi _{t+1} = X_{t+1} + \frac{1-\alpha }{1+\alpha }\left( X_{t+1} - X_t\right)$, we have

$$\begin{aligned} \left\Vert \varXi _{t+1} \right\Vert _F&\le 3\left( 1+\sqrt{5}\right) \kappa R\le 10\kappa R. \end{aligned}$$

$\square$

Proof of Lemma 9

Recall that by definition, the linear operator $\mathcal{G}$ maps $\gamma$ to $\sum _{i=1}^m \gamma _i \left( A_i \varXi _t + B_i\right)$. Thus, for any $\gamma \in {\textbf{S}}^{m-1}$,

$$\begin{aligned} \left\Vert \mathcal{G}\gamma \right\Vert _F&= \left\Vert \sum _{i=1}^m \gamma _i \left( A_i \varXi _t + B_i\right) \right\Vert _F\\&\le \left\Vert \sum _{i=1}^m \gamma _i A_i \right\Vert _2\left\Vert \varXi _t \right\Vert _F+ \left\Vert \sum _{i=1}^m \gamma _i B_i \right\Vert _F\\&\le 11\frac{\mu \kappa H R}{D}. \end{aligned}$$

$\square$

Proof of Lemma 10

Let $r :=\left\Vert \gamma ^{(i)} - \gamma ^* \right\Vert _2$. Using Assumption 5, we may bound the individual terms within the definition of $r^{(i)}$ as

$$\begin{aligned}{} & {} 2{\hat{R}}_d - \left\Vert \gamma ^{(i)} \right\Vert _2 \ge {\hat{R}}_d - r \ge \frac{{\hat{\mu }}}{{\hat{\rho }}} - r,\\{} & {} \frac{\lambda _{\min }\left( A\left( \gamma ^{(i)}\right) \right) - {\hat{\mu }}/2}{{\hat{\rho }}} \ge \frac{{\hat{\mu }}/2 - {\hat{\rho }} r}{{\hat{\rho }}} = \frac{{\hat{\mu }}}{2{\hat{\rho }}} - r,\\{} & {} \frac{2{\hat{L}} - \lambda _{\max }\left( A\left( \gamma ^{(i)}\right) \right) }{{\hat{\rho }}} \ge \frac{{\hat{L}} - {\hat{\rho }} r}{{\hat{\rho }}} = \frac{{\hat{L}}}{{\hat{\rho }}} - r,\quad \text {and}\\{} & {} \frac{2{\hat{L}}{\hat{R}}_p - \left\Vert B\left( \gamma ^{(i)}\right) \right\Vert _F}{{\hat{\rho }}{\hat{R}}_p} \ge \frac{{\hat{L}} - {\hat{\rho }} r}{{\hat{\rho }}} = \frac{{\hat{L}}}{{\hat{\rho }}} - r. \end{aligned}$$

Thus, $r^{(i)} \ge \min \left( \frac{{\hat{\mu }}}{2{\hat{\rho }}},\,\frac{{\hat{\mu }}}{2{\hat{\rho }}} - r\right) = \frac{{\hat{\mu }}}{2{\hat{\rho }}} - r$. Then, when $r\le \frac{{\hat{\mu }}}{4{\hat{\rho }}}$, we have $r^{(i)}>0$ and furthermore, $r^{(i)}\ge r = \left\Vert \gamma ^{(i)} - \gamma ^* \right\Vert _2$. $\square$

Proof of Lemma 11

Begin by noting that for all $\gamma \in \mathcal{U}^{(i)}$,

$$\begin{aligned} \frac{{\hat{\mu }}}{2}I\preceq A\left( \gamma ^{(i)}\right) - r^{(i)}{\hat{\rho }} I \preceq A(\gamma ) \preceq A\left( \gamma ^{(i)}\right) + r^{(i)}{\hat{\rho }} I \preceq 2{\hat{L}} I. \end{aligned}$$

Let ${\tilde{\gamma }}\in \mathop {\mathrm {arg\,max}}\limits _{\gamma \in \mathcal{U}^{(i)}}q(\gamma ,0_{(n-k)\times k})$. Then,

$$\begin{aligned} \left\Vert B({\tilde{\gamma }}) \right\Vert _F \le \left\Vert B\left( \gamma ^{(i)}\right) \right\Vert _F + {\hat{\rho }} r^{(i)}{\hat{R}}_p \le 2{\hat{L}}{\hat{R}}_p = LR. \end{aligned}$$

Next, for $\gamma \in {\textbf{S}}^{m-1}$

$$\begin{aligned}{} & {} \frac{D\left\Vert \sum _{i=1}^m \gamma _i A_i \right\Vert _2}{\mu } \le \frac{4r^{(i)}{\hat{\rho }}}{{\hat{\mu }}} \le 2\\{} & {} \frac{D\left\Vert \sum _{i=1}^m \gamma _i B_i \right\Vert _F}{L R} \le \frac{r^{(i)}{\hat{\rho }}}{{\hat{L}}} \le 1/2. \end{aligned}$$

$\square$

Lemma 13

Consider an instance of (14) generated by the random procedure in Sect. 5.2. Then equality holds throughout (14).

Proof

It suffices to show that $\gamma ^*$ and $T^*$ are feasible and achieve value $\left\Vert X^* \right\Vert _F^2$ in the dual SDP (i.e., the third line of (14)).

Note that by Schur Complement Theorem,

$$\begin{aligned} \begin{pmatrix} A(\gamma ^*)/2 &{} B(\gamma ^*)/2\\ B(\gamma ^*)^\intercal /2 &{} \frac{c(\gamma ^*)}{k}I_k - T^* \end{pmatrix}&\sim \begin{pmatrix} I_{n-k} &{} \\ &{} \frac{c(\gamma ^*)}{k}I_k - T^* - \frac{B(\gamma ^*)^\intercal A(\gamma ^*)^{-1}B(\gamma ^*)}{2} \end{pmatrix} \\&= \begin{pmatrix} I_{n-k}&{}\\ {} &{}0_k \end{pmatrix}. \end{aligned}$$

Here, $\sim$ indicates matrix similarity. Thus, $\gamma ^*$ and $T^*$ are feasible in the dual SDP.

Next,

$$\begin{aligned} {{\,\textrm{tr}\,}}(T^*)&= {{\,\textrm{tr}\,}}\left( \frac{c(\gamma ^*)}{k}I_k - \frac{B(\gamma ^*)^\intercal A(\gamma ^*)^{-1}B(\gamma ^*)}{2}\right) \\&= \frac{{{\,\textrm{tr}\,}}\left( (X^*)^\intercal A(\gamma ^*) X^*\right) }{2}+ \left\langle B(\gamma ^*), X^* \right\rangle + c(\gamma ^*)\\&= \frac{\left\Vert X^* \right\Vert _F^2}{2} + \sum _{i=1}^m \gamma ^*_i\left( {{\,\textrm{tr}\,}}\left( \frac{(X^*)^\intercal A_i X^*}{2}\right) + \left\langle B_i, X^* \right\rangle + c_i\right) = \frac{\left\Vert X^* \right\Vert _F^2}{2}. \end{aligned}$$

$\square$

Strict complementarity in quadratic matrix programs

In this section, we show that a generic quadratic matrix program (QMP) in an $n\times k$ dimensional matrix variable with at most k constraints satisfies strict complementarity (assuming only existence of primal and dual solutions).

We will need the following lemma stating that a generic bilinear system has only the trivial solutions. This lemma follows from basic dimension-counting arguments in algebraic geometry. However, we will instead prove the lemma directly using only elementary tools.

Lemma 14

Let $n,p\in {\mathbb {N}}$ and consider the space $({\mathbb {R}}^{n\times p})^{n+p-1}$. Let the collection $(A_i) = (A_1,\ldots , A_{n+p-1})$ denote an element of this space. Here, each $A_i\in {\mathbb {R}}^{n\times p}$. Then, the collections $(A_i)$ for which the bilinear system

$$\begin{aligned} {\left\{ \begin{array}{ll} x^\intercal A_i y = 0 \qquad \forall i\in [n+p-1] \end{array}\right. } \end{aligned}$$

has a nontrivial solution (i.e., where $x\in {\mathbb {R}}^n$ and $y\in {\mathbb {R}}^p$ are both nonzero) forms a set of measure zero in $({\mathbb {R}}^{n\times p})^{n+p-1}$.

Proof

Let $\mathcal{S}$ be the exceptional set, i.e.,

$$\begin{aligned} \mathcal{S}:=\left\{ (A_i)\in ({\mathbb {R}}^{n\times p})^{n+p-1}:\, \begin{array}{l} \exists x\in {\mathbb {R}}^n\setminus \left\{ 0\right\} ,\, y\in {\mathbb {R}}^p\setminus \left\{ 0\right\} \\ x^\intercal A_i y = 0 ,\,\forall i\in [n+p-1] \end{array}\right\} . \end{aligned}$$

By homogeneity, we may require that $x\in {\mathbb {R}}^n$ has some coordinate equal to one. Similarly, we will require that $y\in {\mathbb {R}}^p$ has some coordinate equal to one. Thus, we may decompose $\mathcal{S}= \bigcup _{\ell =1}^n\bigcup _{r=1}^p \mathcal{S}_{\ell ,r}$, where

$$\begin{aligned} \mathcal{S}_{\ell ,r} = \left\{ (A_i)\in ({\mathbb {R}}^{n\times p})^{n+p-1}:\, \begin{array}{l} \exists x\in {\mathbb {R}}^n,\, y\in {\mathbb {R}}^p\\ x_\ell = 1\\ y_r = 1\\ x^\intercal A_i y = 0 ,\,\forall i\in [n+p-1] \end{array}\right\} . \end{aligned}$$

We will show that for each $\ell \in [n]$ and $r\in [p]$ that $\mathcal{S}_{\ell ,r}$ has measure zero. Without loss of generality, let $\ell = r= 1$.

Consider the affine space

$$\begin{aligned} \mathcal{M}:=\left\{ \begin{array}{l}(x,y,B_1,\ldots ,B_{n+p-1})\\ \quad \in {\mathbb {R}}^n\times {\mathbb {R}}^p\times ({\mathbb {R}}^{n\times p})^{n+p-1}\end{array}:\, \begin{array}{l} x_1 = 1\\ y_1 = 1\\ (B_i)_{1,1} = 0 ,\,\forall i\in [n+m-1] \end{array}\right\} . \end{aligned}$$

Let $\mathcal{F}_{1,1}: \mathcal{M}\rightarrow ({\mathbb {R}}^{n\times p})^{n+p-1}$ send the element $(x,y,B_1,\ldots ,B_{n+p-1})$ to $(A_1,\ldots ,A_{n+p-1})$ where

$$\begin{aligned} A_i = \begin{pmatrix} 1 &{} -x_2 &{} \dots &{} -x_n\\ x_2 &{} 1 &{} \\ \vdots &{} &{} \ddots \\ x_n &{} &{} &{} 1 \end{pmatrix}B_i \begin{pmatrix} 1 &{} y_2 &{} \dots &{} y_p\\ -y_2 &{} 1 &{} \\ \vdots &{} &{} \ddots \\ -y_p &{} &{} &{} 1 \end{pmatrix}. \end{aligned}$$

One may verify that $\mathcal{F}_{1,1}$ is a smooth map. Furthermore, its domain has dimension $(n-1) + (p-1) + (np - 1)(n+p-1) = np(n+p-1) - 1$. This is one less than the dimension of the space $\left( {\mathbb {R}}^{n\times p}\right) ^{n+p-1}$. It is known that the image of a Euclidean space under a smooth map into a Euclidean space of higher dimension must have Lebesgue measure zero (see Sard’s lemma [61]). Thus, $\mathcal{F}_{1,1}(\mathcal{M})$ has Lebesgue measure zero.

It remains to verify³ that $\mathcal{S}_{1,1}\subseteq \mathcal{F}_{1,1}(\mathcal{M})$. Suppose $(A_i)\in \mathcal{S}_{1,1}$ and let x, y with $x_1 = y_1 = 1$ satisfy $x^\intercal A_i y = 0$ for all $i\in [n+p-1]$. Let

$$\begin{aligned} B_i = \begin{pmatrix} 1 &{} -x_2 &{} \dots &{} -x_n\\ x_2 &{} 1 &{} \\ \vdots &{} &{} \ddots \\ x_n &{} &{} &{} 1 \end{pmatrix}^{-1} A_i \begin{pmatrix} 1 &{} y_2 &{} \dots &{} y_p\\ -y_2 &{} 1 &{} \\ \vdots &{} &{} \ddots \\ -y_p &{} &{} &{} 1 \end{pmatrix}^{-1}. \end{aligned}$$

Note that $(B_i)_{1,1} = \frac{1}{\left\Vert x \right\Vert ^2\left\Vert y \right\Vert ^2}x^\intercal A_i y = 0$ for all $i\in [n+p-1]$. The remaining sets $\mathcal{S}_{\ell ,r}$ can be shown to have measure zero using analogous maps $\mathcal{F}_{\ell ,r}$. This concludes the proof. $\square$

Lemma 15

Let $n,k\in {\mathbb {N}}$ and consider the SDP relaxation of a QMP with k constraints in a variable of size $n\times k$ and its dual:

$$\begin{aligned}&\inf _{Y\in {\mathbb {S}}^{n+k}}\left\{ \left\langle \begin{pmatrix} A_\text {obj}/2 &{} B_\text {obj}/2\\ B_\text {obj}^\intercal /2 &{} \tfrac{c_\text {obj}}{k}I_k \end{pmatrix}, Y \right\rangle :\, \begin{array}{l} \left\langle \begin{pmatrix} A_i/2 &{} B_i/2\\ B_i^\intercal /2 &{} \tfrac{c_i}{k}I_k \end{pmatrix}, Y \right\rangle = 0,\,\forall i\in [k]\\ Y = \begin{pmatrix} * &{} *\\ * &{} I_k \end{pmatrix}\succeq 0 \end{array}\right\} \\&\qquad \ge \sup _{\gamma \in {\mathbb {R}}^k,\, T\in {\mathbb {R}}^{k\times k}}\left\{ {{\,\textrm{tr}\,}}(T):\, \begin{pmatrix} A(\gamma )/2 &{} B(\gamma )/2\\ B(\gamma )^\intercal /2 &{} \frac{c(\gamma )}{k}I_k - T \end{pmatrix}\succeq 0\right\} . \end{aligned}$$

There exists a subset $\mathcal{E}\subseteq ({\mathbb {S}}^n)^{1+k} \times ({\mathbb {R}}^{n\times k})^{1+k}$ of measure zero such that if

$$\begin{aligned} (A_\text {obj}, A_1,\ldots ,A_k,B_\text {obj}, B_1,\ldots ,B_k)\notin \mathcal{E}\end{aligned}$$

and the primal and dual SDPs are both solvable, then strict complementarity holds and the primal and dual SDPs both have unique optimizers.

Proof

We will condition on the following bilinear system in the variables $(\gamma _\text {obj},\ldots ,\gamma _k)\in {\mathbb {R}}^{1+k}$ and $x\in {\mathbb {R}}^n$ having no nontrivial solutions:

$$\begin{aligned} {\left\{ \begin{array}{ll} \left( \gamma _\text {obj}A_\text {obj}+ \sum _{i=1}^k \gamma _i A_i \right) x = 0\\ \left( \gamma _\text {obj}B_\text {obj}+ \sum _{i=1}^k \gamma _i B_i\right) ^\intercal x = 0 \end{array}\right. }. \end{aligned}$$

This is a homogeneous bilinear system in $n + 1 + k$ variables with $n+k$ constraints. Thus, by Lemma 14, this system has no nontrivial solutions outside an exceptional set $\mathcal{E}$ of measure zero.

Let $(\gamma ^*,T^*)$ denote a dual optimum solution. We claim that $A(\gamma ^*)\succ 0$. For the sake of contradiction, assume that $x\in \ker (A(\gamma ^*))$ is nonzero. Then, by assumption, $x^*$ and $(1,\gamma ^*)$ are not a solution to the bilinear system above, i.e., $B(\gamma ^*)^\intercal x \ne 0$ and there exists a column of $B(\gamma ^*)$, say the first column, that has nonzero inner product with x. This contradicts the feasibility of $(\gamma ^*, T^*)$. Specifically for $\alpha \in {\mathbb {R}}$,

$$\begin{aligned} \begin{pmatrix} \alpha x\\ e_1 \end{pmatrix}^\intercal \begin{pmatrix} A(\gamma ^*)/2 &{} B(\gamma ^*)/2\\ B(\gamma ^*)^\intercal /2 &{} \frac{c(\gamma ^*)}{k}I_k - T^* \end{pmatrix} \begin{pmatrix} \alpha x\\ e_1 \end{pmatrix} = \alpha \left\langle x, B(\gamma ^*)e_1 \right\rangle + \left( c(\gamma ^*)/k + T^*_{1,1}\right) . \end{aligned}$$

Picking $\alpha$ large or small enough makes this quantity negative, contradicting that the matrix on the left is positive semidefinite.

We have shown that for every dual optimum solution $(\gamma ^*, T^*)$, the above slack matrix has rank at least n. Similarly, any primal optimum solution $Y^*$ must have rank at least k. We deduce that every primal optimum solution $Y^*$ has rank exactly k and that for every dual optimum solution $(\gamma ^*, T^*)$, the slack matrix has rank exactly n. Now, these optimizers must correspond to faces of slices of ${\mathbb {S}}^{n+k}_+$. As the only faces of slices of ${\mathbb {S}}^{n+k}_+$ with constant rank are singleton sets, we deduce that there is a unique primal optimizer and a unique dual optimizer. $\square$

Additional experiments on phase-retrieval inspired SDP instances

We perform additional experiments on SDP instances inspired by the phase retrieval problem.

The phase retrieval problem seeks to learn a vector $x^*$ given only the magnitudes of linear measurements of $x^*$, and finds applications in imaging. In the Gaussian model of phase retrieval [15], we assume $x^*\in {\mathbb {R}}^n$ is arbitrary and $G\in {\mathbb {R}}^{m \times n}$ is entrywise Gaussian with an appropriate normalization. We are given

$$\begin{aligned} \left|Gx^* \right|. \end{aligned}$$

Here, the absolute value is taken entrywise. Equivalently, we are given the entrywise square of $Gx^*$, or $b = {{\,\textrm{diag}\,}}(Gx^*(x^*)^\intercal G^\intercal )$. In this setting, it is known that the PhaseLift SDP,

$$\begin{aligned} \min _{Y\succeq 0}\left\{ {{\,\textrm{tr}\,}}(Y):\, \begin{array}{l} {{\,\textrm{diag}\,}}(GYG^\intercal ) = \beta \end{array}\right\} \end{aligned}$$

has $(x^*)(x^*)^\intercal$ as its unique solution with high probability once the number of observations m is roughly O(n). Recent work [25] shows that strict complementarity holds between this SDP and its dual with high probability in the same regime.

We note that the Gaussian model of phase retrieval requires storing the matrix G as part of the instance. This is a matrix of size $O(n^2)$ and thus limits the size of our current experiments. Nonetheless, we expect the behavior we observe with these experiments to hold in the real setting of phase retrieval where the matrix G is highly structured and can be stored implicitly. We leave this as important future work.

We compare CertSDP (Algorithm 2), CSSDP [26], SketchyCGAL [76], ProxSDP [65], SCS [56], and Burer–Monteiro [12].

Random instance generation. We generate instances as follows. Suppose n is given. We set $m = 5n$. We generate $G\in {\mathbb {R}}^{m\times n}$ where each entry is independent N(0, 1/m). We then preprocess G so that its mth observation vector, i.e., the mth row of G, is parallel to $e_n$. Next, we sample $x^*$ uniformly form

$$\begin{aligned} {\textbf{S}}^{n-1}\cap \left\{ x\in {\mathbb {R}}^n:\, x_n = 0.1\right\} . \end{aligned}$$

Thus, this is a random instance of phase retrieval where we are given one highly-correlated observation.

Implementation details. The algorithms we test are mostly as described in Sect. 5.1. The major differences in implementation are described below:

• In the instances tested in Sect. 5, the $A_i$ matrices encountered were sparse. In the phase retrieval problems we test in this appendix, the $A_i$ matrices are dense but rank-one. The implementations of CertSDP, CSSDP, and SketchyCGAL are modified to handle such instances.

• Phase retrieval instances are likely to contain many dual optimal solutions that may not satisfy strict complementarity. Within CertSDP and CSSDP, we employ the Accelegrad algorithm to approximately solve

  $$\begin{aligned}&\max _{\gamma \in {\mathbb {R}}^m} \beta ^\intercal \gamma + {\textrm{penalty}} \min \left( 0, \lambda _{\min }\left( I - G^\intercal {{\,\textrm{Diag}\,}}(\gamma )G\right) \right) \\&\quad + \min (0, \lambda _{1+2}(I - G^\intercal {{\,\textrm{Diag}\,}}(\gamma )G) - 0.1). \end{aligned}$$

  Here, $\lambda _{1+2}(\cdot )$ denotes the sum of the two smallest eigenvalues of a given matrix and is a concave expression in its input. This penalization/regularization encourages solutions $\gamma$ for which the second eigenvalue of $I - G^\intercal {{\,\textrm{Diag}\,}}(\gamma )G$ is positive, so that $A(\gamma )\succ 0$. We set ${{\textrm{penalty}}} = 10$.

• Recall that in Sect. 5, we replaced the random sketch in SketchyCGAL with a projection onto a submatrix to reflect the fact that for QMP instances, the goal is to recover the $(n-k)\times k$ top-right submatrix of the SDP optimizer. For the phase retrieval experiments, we employ the random sketch as originally described in [75].

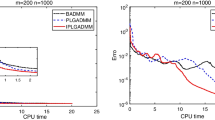
Numerical results. Due to memory constraints associated with storing $G\in {\mathbb {R}}^{m\times n}$, we test instances with size $n = 30,\, 100,\,300$. We set the time limit to 50, 500 and 5000 s respectively. The results are summarized in Tables 4, 5 and 6. The average memory usage of the algorithms is plotted in Fig. 4. We compare the convergence behavior of CertSDP with that of CSSDP and SketchyCGAL on a single instance of each size in Fig. 5.

Table 4 Experimental results for phase retrieval instances with $n = 30$ (10 instances) with time limit 50 s

Table 5 Experimental results for phase retrieval instances with $n = 100$ (10 instances) with time limit 500 s

Table 6 Experimental results for phase retrieval instances with $n = 300$ (10 instances) with time limit 5000 s

Fig. 4

Memory usage of different algorithms on our phase retrieval instances as a function of the size n. In this chart, we plot 0.0 MB at 1.0 MB (see Remark 8 for a discussion on measuring memory usage)

Fig. 5

Comparison of convergence behavior between CertSDP (Algorithm 2), CSSDP, and SketchyCGAL on our phase retrieval instances. The first, second, and third rows show experiments with $n=30$, 100, and 300 respectively

The results for these experiments are qualitatively similar to those of Appendix 5. We make a few additional observations:

• On these phase retrieval instances, the dual suboptimality decreases to $\approx 10^{-3}$ before CertSDP seems to find a certificate of strict complementarity (see Fig. 5). This suggests that the value of $\mu ^*$ in these instances is relatively small.

• CSSDP outperforms SketchyCGAL and also outperforms CertSDP initially. The “crossover” point where CertSDP outperforms CSSDP occurs only after CSSDP is able to produce a primal iterate with squared error $\approx 10^{-7}$.

• CertSDP seems to suffer from numerical issues for $n = 300$ and is unable to decrease the primal squared error beyond $10^{-10}$. Nonetheless, CertSDP outperforms CSSDP and SketchyCGAL on all instances tested.