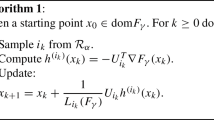Abstract
We propose and analyze a randomized zeroth-order optimization method based on approximating the exact gradient by finite differences computed in a set of orthogonal random directions that changes with each iteration. A number of previously proposed methods are recovered as special cases including spherical smoothing, coordinate descent, as well as discretized gradient descent. Our main contribution is proving convergence guarantees as well as convergence rates under different parameter choices and assumptions. In particular, we consider convex objectives, but also possibly non-convex objectives satisfying the Polyak-Łojasiewicz (PL) condition. Theoretical results are complemented and illustrated by numerical experiments.




Similar content being viewed by others
References
Agarwal, A., Dekel, O., Xiao, L.: Optimal algorithms for online convex optimization with multi-point bandit feedback. In: Proceedings of the Twenty Third Annual Conference on Computational Learning Theory, Citeseer, pp. 28–40 (2010)
Attouch, H., Bolte, J., Svaiter, B.F.: Convergence of descent methods for semi-algebraic and tame problems: proximal algorithms, forward-backward splitting, and regularized Gauss-Seidel methods. Math. Program. 137, 91–129 (2013)
Avron, H., Maymounkov, P., Toledo, S.: Blendenpik: supercharging Lapack’s least-squares solver. SIAM J. Sci. Comput. 32, 1217–1236 (2010)
Baillon, J.-B., Haddad, G.: Quelques propriétés des opérateurs angle-bornés et n-cycliquement monotones. Israel J. Math. 26, 137–150 (1977)
Beck, A., Tetruashvili, L.: On the convergence of block coordinate descent type methods. SIAM J. Optim. 23, 2037–2060 (2013)
Berahas, A.S., Byrd, R.H., Nocedal, J.: Derivative-free optimization of noisy functions via quasi-Newton methods. SIAM J. Optim. 29, 965–993 (2019)
Berahas, A.S., Cao, L., Choromanski, K., Scheinberg, K.: A theoretical and empirical comparison of gradient approximations in derivative-free optimization, arXiv preprint arXiv:1905.01332, (2019)
Berahas, A.S., Cao, L., Scheinberg, K.: Global convergence rate analysis of a generic line search algorithm with noise, arXiv preprint arXiv:1910.04055, (2019)
Bertsekas, D.P., Tsitsiklis, J.N.: Gradient convergence in gradient methods with errors. SIAM J. Optim. 10, 627–642 (2000)
Bollapragada R., Wild, S.M.: Adaptive sampling quasi-Newton methods for derivative-free stochastic optimization, arXiv preprint arXiv:1910.13516, (2019)
Cartis, C., Roberts, L.: Scalable subspace methods for derivative-free nonlinear least-squares optimization, arXiv preprint arXiv:2102.12016, (2021)
Cartis, C., Scheinberg, K.: Global convergence rate analysis of unconstrained optimization methods based on probabilistic models. Math. Program. 169, 337–375 (2018)
Cauchy, A.: Méthode générale pour la résolution des systemes d’équations simultanées. Comp. Rend. Sci. Paris 25, 536–538 (1847)
Choromanski, K., Rowland, M., Sindhwani, V., Turner, R., Weller, A.: Structured evolution with compact architectures for scalable policy optimization. In: Dy, J., Krause, A. (Eds.), Proceedings of the 35th International Conference on Machine Learning, vol. 80 of Proceedings of Machine Learning Research, Stockholmsmässan, Stockholm Sweden, PMLR, pp. 970–978, (10–15 Jul 2018)
Chung, K.L.: On a stochastic approximation method. Ann. Math. Stat. 25, 463–483 (1954)
Combettes, P.L., Pesquet, J.-C.: Stochastic quasi-Fejér block-coordinate fixed point iterations with random sweeping. SIAM J. Optim. 25, 1221–1248 (2015)
Conn, A.R., Scheinberg, K., Vicente, L.N.: Introduction to derivative-free optimization, vol. 8 of MPS/SIAM Series on Optimization, Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA; Mathematical Programming Society (MPS), Philadelphia, PA (2009)
Dodangeh, M., Vicente, L.N., Zhang, Z. a: On the optimal order of worst case complexity of direct search. Optim. Lett. 10, 699–708 (2016)
Drineas, P., Mahoney, M.W., Muthukrishnan, S., Sarlós, T.: Faster least squares approximation. Numer. Math. 117, 219–249 (2011)
Duchi, J.C., Jordan, M.I., Wainwright, M.J., Wibisono, A.: Optimal rates for zero-order convex optimization: The power of two function evaluations. IEEE Trans. Inf. Theory 61, 2788–2806 (2015)
Ehrhardt, M.J., Riis, E.S., Ringholm, T., Schönlieb, C.-B.: A geometric integration approach to smooth optimisation: Foundations of the discrete gradient method, arXiv preprint arXiv:1805.06444, (2018)
Finkel, D.E., Kelley, C.T.: Convergence analysis of sampling methods for perturbed Lipschitz functions. Pac. J. Optim. 5, 339–349 (2009)
Flaxman, A.D., Kalai, A.T., McMahan, H.B.: Online convex optimization in the bandit setting: gradient descent without a gradient. In: Proceedings of the Sixteenth Annual ACM-SIAM Symposium on Discrete Algorithms, ACM, New York, pp. 385–394 (2005)
Ghadimi, S., Lan, G.: Stochastic first-and zeroth-order methods for nonconvex stochastic programming. SIAM J. Optim. 23, 2341–2368 (2013)
Gilmore, P., Kelley, C.T.: An implicit filtering algorithm for optimization of functions with many local minima. SIAM J. Optim. 5, 269–285 (1995)
Gilmore, P., Kelley, C.T., Miller, C.T., Williams, G.A.: Implicit filtering and optimal design problems. In: Optimal design and control (Blacksburg, VA, 1994), vol. 19 of Progr. Systems Control Theory, Birkhäuser Boston, Boston, MA, pp. 159–176 (1995)
Gratton, S., Royer, C.W., Vicente, L.N., Zhang, Z.: Direct search based on probabilistic descent. SIAM J. Optim. 25, 1515–1541 (2015)
Grimm, V., McLachlan, R.I., McLaren, D.I., Quispel, G., Schönlieb, C.: Discrete gradient methods for solving variational image regularisation models. J. Phys. A: Math. Theor. 50, 295201 (2017)
Gupal, A.: A method for the minimization of almost-differentiable functions. Cybern. 13, 115–117 (1977)
Gupal, A., Norkin, V.: Algorithm for the minimization of discontinuous functions. Cybern. 13, 220–223 (1977)
Hanzely, F., Doikov, N., Nesterov, Y., Richtarik, P.: Stochastic subspace cubic Newton method. In: Proceedings of the 37th International Conference on Machine Learning, H. D. III and A. Singh, eds., vol. 119 of Proceedings of Machine Learning Research, PMLR, pp. 4027–4038 (13–18 Jul 2020)
Hanzely, F., Kovalev, D., Richtarik, P.: Variance reduced coordinate descent with acceleration: New method with a surprising application to finite-sum problems. In: Proceedings of the 37th International Conference on Machine Learning, H. D. III and A. Singh, eds., vol. 119 of Proceedings of Machine Learning Research, PMLR, pp. 4039–4048 (13–18 Jul 2020)
Karimi, H., Nutini, J., Schmidt, M.: Linear convergence of gradient and proximal-gradient methods under the Polyak-Łojasiewicz condition. In: Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Springer, pp. 795–811 (2016)
Kiefer, J., Wolfowitz, J.: Stochastic estimation of the maximum of a regression function. Ann. Math. Stat. 23, 462–466 (1952)
Bromwich, T.: Theory and application of infinite series. By Knopp K. Translated from the second German edition by Miss Young R.C. pp. xii 572. 30s. net. 1928. (Blackie) Math. Gaz. 14(199), 370–371. Cambridge University Press (1929). https://doi.org/:10.2307/3606730
Konecný, J., Richtárik, P.: Simple complexity analysis of simplified direct search, arXiv preprint arXiv:1411.5873, (2014)
Kozak, D., Becker, S., Doostan, A., Tenorio, L.: Stochastic subspace descent, arXiv preprint arXiv:1904.01145, (2019)
Kozak, D., Becker, S., Doostan, A., Tenorio, L.: A stochastic subspace approach to gradient-free optimization in high dimensions. Comput. Optim. Appl. 79, 339–368 (2021)
Kushner, H.J., Clark, D.S.: Stochastic approximation methods for constrained and unconstrained systems. Applied Mathematical Sciences, vol. 26. Springer-Verlag, New York-Berlin (1978)
Mania, H., Guy, A., Recht, B.: Simple random search of static linear policies is competitive for reinforcement learning. In: Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R. (eds.) Advances in Neural Information Processing Systems 31, pp. 1800–1809. Curran Associates, Inc., New York (2018)
Martinsson, P.-G., Tropp, J.A.: Randomized numerical linear algebra: foundations and algorithms. Acta Numer. 29, 403–572 (2020)
Matyas, J.: Random optimization. Autom. Remote. Control. 26, 246–253 (1965)
Mezzadri, F.: How to generate random matrices from the classical compact groups. Notices Amer. Math. Soc. 54, 592–604 (2007)
Nesterov, Y.: Random gradient-free minimization of convex functions. LIDAM Discussion Papers CORE 2011001, Université catholique de Louvain, Center for Operations Research and Econometrics (CORE), (Jan. 2011)
Nesterov, Y., Spokoiny, V.: Random gradient-free minimization of convex functions. Found. Comput. Math. 17, 527–566 (2017). (First appeard as CORE discussion paper 2011)
Opial, Z. a: Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bull. Amer. Math. Soc. 73, 591–597 (1967)
Paquette, C., Scheinberg, K.: A stochastic line search method with expected complexity analysis. SIAM J. Optim. 30, 349–376 (2020)
Polyak, B.T.: Introduction to optimization, vol. 1. Optimization Software Inc., New York (1987)
Rastrigin, L.A.: About convergence of random search method in extremal control of multi-parameter systems. Avtomat. i Telemekh 24, 1467–1473 (1963)
Riis, E.S., Ehrhardt, M.J., Quispel, G., Schönlieb, C.-B.: A geometric integration approach to nonsmooth, nonconvex optimisation, arXiv preprint arXiv:1807.07554, (2018)
Robbins, H., Monro, S.: A stochastic approximation method. Ann. Math. Stat. 22, 400–407 (1951)
Robbins, H., Siegmund, D.: A convergence theorem for non negative almost supermartingales and some applications. In: Optimizing methods in statistics (Proc. Sympos., Ohio State Univ., Columbus, Ohio, 1971), pp. 233–257 (1971)
Salimans, T., Ho, J., Chen, X., Sidor, S., Sutskever, I.: Evolution strategies as a scalable alternative to reinforcement learning, arXiv preprint arXiv:1703.03864, (2017)
Salzo, S., Villa, S.: Parallel random block-coordinate forward-backward algorithm: A unified convergence analysis, arXiv preprint arXiv:1906.07392, (2019)
Schmidt, M., Roux, N.L., Bach, F.: Convergence rates of inexact proximal-gradient methods for convex optimization, arXiv preprint arXiv:1109.2415, (2011)
Spall, J.C.: Multivariate stochastic approximation using a simultaneous perturbation gradient approximation. IEEE Trans. Automat. Control 37, 332–341 (1992)
Tappenden, R., Takáč, M., Richtárik, P.: On the complexity of parallel coordinate descent. Optim. Methods Softw. 33, 372–395 (2018)
Williams, R.J.: Simple statistical gradient-following algorithms for connectionist reinforcement learning. Mach. Learn. 8, 229–256 (1992)
Woodruff, D.P.: Sketching as a tool for numerical linear algebra. Found. Trends Theor. Comput. Sci. 10, iv+157 (2014)
Wright, S.J.: Coordinate descent algorithms. Math. Program. 151, 3–34 (2015)
Zavriev, S.K.: On the global optimization properties of finite-difference local descent algorithms. J. Global Optim. 3, 67–78 (1993)
Acknowledgements
L.R. acknowledges support from the Center for Brains, Minds and Machines (CBMM), funded by NSF STC award CCF-1231216, and the Italian Institute of Technology. L.R. also acknowledges the financial support of the European Research Council (grant SLING 819789), the AFOSR projects FA9550- 18-1-7009, FA9550-17-1-0390 and BAA-AFRL-AFOSR-2016-0007 (European Office of Aerospace Research and Development), and the EU H2020-MSCA-RISE project NoMADS - DLV-777826. This work has been supported by the ITN-ETN project TraDE-OPT funded by the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 861137. LT acknowledges funding by National Science Foundation grant DMS-1723005.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Auxiliary lemmas
Auxiliary lemmas
Here we collect the main auxiliary results used in the convergence analysis of Algorithm 1.
Proof of Lemma 1
Let \(k\in \mathbb {N}\), denoting by \(p^{(j)}\) the j-th column of \(P_k\), we want to estimate
To get an upper-bound for the term in parenthesis, we use H.1. As \(\nabla f\) is \(\lambda \)-Lipschitz, the Descent Lemma 7 holds: for every \(x\in \mathbb {R}^d\),
Then, rearranging,
Note that P.1 implies \(\Vert p^{(j)}\Vert ^2\overset{a.s.}{=}d/\ell \) and so (9.1) and (9.3) yield
\(\square \)
Lemma 5
Let \(\left( a_k\right) \) and \(\left( c_k\right) \) be non-negative sequences with \(\lim _k c_k =0\) and let \(\eta \in \left( 0,1\right) \). If for every \(k\in \mathbb {N}\)
then \(\lim _k a_k =0\). Moreover, if \(c_k=c/k^t\) for some \(c\ge 0\) and \(t>0\), then we have \(\limsup _k \ k^t a_k\le {c}/{\eta }.\)
Proof
Iterating the inequality in (9.4), we get
where we used the fact that \(\left( c_k\right) \) is convergent (and thus bounded) and that \(\eta \in \left( 0,1\right) \). In particular, the sequence \(\left( a_k\right) \) is bounded and so its \(\limsup \) is a real number. Then, again from the hypothesis that \(a_{k+1}\le (1-\eta ) a_k +c_k\) and the existence of \(\lim _k c_k\), we have \(\limsup _k a_{k} \le \limsup _k \left[ (1-\eta ) a_k + c_k \right] = (1-\eta ) \limsup _k a_k + \lim _k c_k.\) So, as \(\lim _k c_k =0\) and \(\limsup _k a_k \in \left[ 0,+\infty \right) \), \(\eta \limsup _k a_k\le 0\). Finally, as \(\eta \in \left( 0,1\right) \), \(\limsup _k a_k\le 0\), and so, as \(a_k\ge 0\), \(\lim _k a_k = 0\). Now assume that \(c_k=c/k^t\) for some \(c\ge 0\) and \(t>0\).
Let \(c'>c\). Then, following the proof of [15, Lemma 4], there exists \(k_0\in \mathbb {N}\) such that for every \(k\ge k_0\) it holds
Using the previous inequality in (9.4), we get
First suppose that there exists \({\bar{k}}\ge k_0\) such that \(a_{{\bar{k}}}\le \frac{c'}{\eta {\bar{k}}^{t}}\). Using (9.5), it is easy to see by recursion that, for every \(k\ge {\bar{k}}\),
Now suppose the opposite; namely, that for every \(k\ge k_0\)
Then, iterating (9.5), we get
In any of the two previous cases,
Finally, since the previous inequality holds for every \(c'>c\), we get the claim. \(\square \)
Remark 23
Consider a function \(f: {\mathbb {R}}^d \rightarrow {\mathbb {R}}\) with \(\lambda \)-Lipschitz gradient and at least one minimizer. Applying the recursion of Algorithm 1 to such a function with an arbitrary starting point \(x_0 \in {\mathbb {R}}^d\) we get that \(\left\Vert x_k-x_*\right\Vert ^2\), \(\langle P_kP_k^\top \nabla f_k, x_k-x_* \rangle \), and \(\left\Vert \nabla f_k\right\Vert ^2\) are bounded for all \(k>0\). In particular, \(\left\Vert \nabla f_k\right\Vert ^2\), \(\left\Vert x_k-x_*\right\Vert ^2\), and \(\langle P_kP_k^\top \nabla f_k, x_k-x_* \rangle \) are all integrable. To see this note first that \(\nabla f_k\) and \(x_k\) are both measurable. Recall that for finite \(x_k\), \(\lambda \)-Lipschitz gradient of f implies that \(\left\Vert \nabla f_k\right\Vert ^2 \le \lambda ^2 \left\Vert x_k-x_*\right\Vert ^2\). Choose an arbitrary finite \(x_0\) to begin the recursion. Then,
where \(C_1, C_2, C_3\) are fixed and finite, the values are unimportant but can be calculated. Repeated recursion reveals that \(\left\Vert x_k-x_*\right\Vert ^2\) is bounded for all \(k>0\). Further, by \(\lambda \)-Lipschitz gradient, \(\left\Vert \nabla f_k\right\Vert ^2 \le \lambda ^2 \left\Vert x_k-x_*\right\Vert ^2\). The claim on the inner product follows from Young’s inequality and the previous results. Finally, since \(\left\Vert \nabla f_k\right\Vert ^2\), \(\left\Vert x_k-x_*\right\Vert ^2\), and \(\langle P_kP_k^\top \nabla f_k, x_k-x_* \rangle \) are bounded, and measurable, they are integrable.
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Kozak, D., Molinari, C., Rosasco, L. et al. Zeroth-order optimization with orthogonal random directions. Math. Program. 199, 1179–1219 (2023). https://doi.org/10.1007/s10107-022-01866-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-022-01866-9
Keywords
- Zeroth-order optimization
- Derivative-free methods
- Stochastic algorithms
- Polyak-Łojasiewicz inequality
- Convex programming
- Finite differences approximation
- Random search