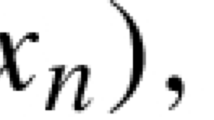Convergence of the forward-backward algorithm: beyond the worst-case with the help of geometry

Abstract

We provide a comprehensive study of the convergence of the forward-backward algorithm under suitable geometric conditions, such as conditioning or Łojasiewicz properties. These geometrical notions are usually local by nature, and may fail to describe the fine geometry of objective functions relevant in inverse problems and signal processing, that have a nice behaviour on manifolds, or sets open with respect to a weak topology. Motivated by this observation, we revisit those geometric notions over arbitrary sets. In turn, this allows us to present several new results as well as collect in a unified view a variety of results scattered in the literature. Our contributions include the analysis of infinite dimensional convex minimization problems, showing the first Łojasiewicz inequality for a quadratic function associated to a compact operator, and the derivation of new linear rates for problems arising from inverse problems with low-complexity priors. Our approach allows to establish unexpected connections between geometry and a priori conditions in inverse problems, such as source conditions, or restricted isometry properties.

A Appendix

1.1 A.1 Worst case analysis: proofs of Section 2

The following Lemma contains a detailed proof for the lower bound (7) in Remark 2.3, which can also be applied to (5) by using a symmetry argument.

Lemma A.1

(Lower bounds for the proximal algorithm). Let $p \in ]-\infty ,0[ \cup ]2,+\infty [$, and let $f_p \in \varGamma _0({\mathbb {R}})$ be the function defined by

$$\begin{aligned} \text { if } p<0, \, f_p(x) = {\left\{ \begin{array}{ll} \vert x \vert ^p &{} \text { if } x<0,\\ +\infty &{} \text { if } x \ge 0, \end{array}\right. } \quad \text { and if } p>2, \ f_p(x) = {\left\{ \begin{array}{ll} 0 &{} \text { if } x <0, \\ \vert x \vert ^p &{} \text { if } x \ge 0. \end{array}\right. } \end{aligned}$$

If $x_0 \in \mathop {\mathrm { dom}}f \setminus \mathrm{argmin\,}f$, and $x_{n+1} = \text{ prox}_{\lambda f}(x_n)$, then for all $n \ge 1$:

$$\begin{aligned} f_p(x_n) - \inf f_p \ge C_p^p n^{\frac{p}{2-p}} \quad \text { with } \quad C_p= \left( \vert x_0\vert ^{2-p} + p (p-2) \lambda \right) ^{\frac{1}{2-p}}. \end{aligned}$$

Proof

Note that $\mathop {\mathrm { dom}}f_p$ is an open interval, and that $f_p$ is infinitely differentiable there. We can then see that $f_p$, $f_p'$ and $f_p''$ are non-negative. In particular, we deduce that $f_p$ and $f'_p$ are non-decreasing on $\mathop {\mathrm { dom}}f$.

Let us now take some $x_0 \in \mathop {\mathrm { dom}}f\setminus \mathrm{argmin\,}f$, and consider the following continuous trajectory

$$\begin{aligned} (\forall t \ge 0) \quad x(t) := \mathrm{sgn}(p) \left( \vert x_0\vert ^{2-p} + p (p-2) t \right) ^{\frac{1}{2-p}}. \end{aligned}$$

It is a simple exercise to verify that $x(\cdot )$ is a solution of this differential equation:

$$\begin{aligned} x(0)=x_0, \quad {\dot{x}}(t) + f'(x(t)) = 0, \quad x(t) \in \mathop {\mathrm { dom}}f_p. \end{aligned}$$

The main step towards proving our lower bound is to show, by induction, that for every $n \in {\mathbb {N}}$, $x_n \ge x(n\lambda )$. This is clearly true for $n=0$, so, let us assume now that this is true for $n \in {\mathbb {N}}$, and show that this implies $x_{n+1} \ge x((n+1)\lambda )$. Start by writing

$$\begin{aligned} x((n+1)\lambda ) = x(n\lambda ) + \int _{n\lambda }^{(n+1)\lambda } \dot{x}(t) ~ dt = x(n\lambda ) + \int _{n\lambda }^{(n+1)\lambda } (-f_p' \circ x)(t) ~ dt. \end{aligned}$$

On the one hand, $f_p'$ is non-negative on $\mathop {\mathrm { dom}}f$, and $\dot{x}(t) = -f_p'(x(t))$, which means that $x(\cdot )$ is non-increasing. On the other hand, $-f_p'$ is non-increasing, which means that $(-f_p' \circ x)$ is non-decreasing. This fact, together with our induction assumption, allows us to write

$$\begin{aligned} x((n&+1)\lambda ) \le x_n + \int _{n\lambda }^{(n+1)\lambda } (-f_p' \circ x)((n+1)\lambda )) ~ dt = x_n - \lambda f_p'(x((n+1)\lambda )),\\&\quad \quad \quad \quad \Leftrightarrow \quad x((n+1)\lambda ) + \lambda f_p'(x((n+1)\lambda )) \le x_n. \end{aligned}$$

Consider now the function $\phi : \mathop {\mathrm { dom}}f_p \rightarrow ]0,+\infty [$ defined by $\phi (t) = t+ \lambda f_p'(t)$. It is clearly increasing and bijective on its image, so its inverse $\phi ^{-1}$ is also increasing. We observe moreover that, by definition, the proximal sequence satisfies $x_{n+1} = \phi ^{-1}(x_n)$. This allows us to write

$$\begin{aligned} \phi (x((n+1)\lambda )) \le x_n \quad \Leftrightarrow \quad x((n+1)\lambda ) \le \phi ^{-1}(x_n) = x_{n+1}. \end{aligned}$$

This ends the proof of the induction argument.

Observe that, given non-negative numbers $a,b>0$, the following inequality holds

$$\begin{aligned} (\forall n \ge 1) \quad \mathrm{sgn}(p)(a+bn)^{\frac{1}{2-p}} \ge \mathrm{sgn}(p)(a+b)^{\frac{1}{2-p}} n^{\frac{1}{2-p}}. \end{aligned}$$

This means that, for all $n \ge 1$,

$$\begin{aligned}&x_n \ge \mathrm{sgn}(p) \left( \vert x_0\vert ^{2-p} + p (p-2) \lambda n \right) ^{\frac{1}{2-p}} \\&\quad \ge \mathrm{sgn}(p) \left( \vert x_0\vert ^{2-p} + p (p-2) \lambda \right) ^{\frac{1}{2-p}} n^{\frac{1}{2-p}} = \mathrm{sgn}(p) C_p n^{\frac{1}{2-p}}. \end{aligned}$$

Passing this inequality through $f_p$ (which is non-decreasing) yields the desired result. $\square$

1.2 A.2 Proofs of Section 3

1.2.1 A.2.1. Invariant sets and proofs of Section 3.1

We provide here a result concerning the equivalence between all the notions in Definition 3.1, for a large class of sets $\varOmega \subset X$. The sets $\varOmega$ we will consider are directly related to the gradient flow induced by $\partial \!f$. Given $u_0 \in \mathop {\mathrm { dom}}f$, it is known⁵ that there exists a unique absolutely continuous trajectory noted $u(\cdot ;u_0) : [0,+\infty [ \longrightarrow X$, called the steepest descent trajectory, which satisfies:

$$\begin{aligned} (\text {for a.e. } t>0) \quad \frac{\mathrm{d}}{\mathrm{d}t} u(t;u_0) + \partial f(u(t;u_0)) \ni 0, \text { and } u(0;u_0) = u_0. \end{aligned}$$

(43)

Following [21], we introduce the notion of invariant sets for the flow of $\partial \!f$:

Definition A.2

A set $\varOmega \subset X$ is $\partial \!f$-invariant if for any $x \in \varOmega \cap \mathop {\mathrm { dom}}\partial \!f$ and a.e. $t>0$, $u(t;x) \in \varOmega$ holds.

In other words, $\varOmega$ is said to be $\partial f$-invariant if any steepest descent trajectory starting in $\varOmega$ remains therein. It is straightforward to see that the intersection of two $\partial \!f$-invariant sets is still $\partial \!f$-invariant.

Example A.3

An easy way to construct a $\partial \!f$-invariant set is to consider the sublevel set of a Lyapunov function $\psi : X \rightarrow {\mathbb {R}}\cup \{+\infty \}$ for the gradient flow induced by $\partial \!f$. A function is said to be Lyapunov if for any $x \in \mathop {\mathrm { dom}}f$, $\psi (u(\cdot ;x)) : [0, +\infty [ \rightarrow {\mathbb {R}}$ is decreasing. Classical examples of this kind are:

• $\varOmega =X$, which is $[\psi < 1]$ with $\psi = 0$.

• $\varOmega = [f<r]$ for $r >\inf f$, which is $[\psi <r]$ with $\psi =f$ (see [21, Theorem 3.2.17]).

• $\varOmega = {\mathbb {B}}({\bar{x}}, \delta )$ for ${\bar{x}} \in \mathrm{argmin\,}f$, $\delta >0$, which is $[\psi < \delta ]$ with $\psi (x)=\Vert x-{\bar{x}} \Vert$ (see [21, Theorem 3.1.7]).

• $\varOmega = \{x \in X \ | \ \Vert \partial \!f(x) \Vert _\_ < M \}$ for $M>0$, which is $[\psi < M]$ with $\psi (x)=\Vert \partial \!f(x) \Vert _\_$ (see [21, Theorem 3.1.6]).

See [21, Section IV.4] for more details on the subject, as well as [22, 63]. It is also a good exercise to verify that the source sets considered in Proposition 5.12 are $\partial \!f$-invariant.

We next prove Proposition 3.3, stating the equivalence between conditioning, metric subregularity and Łojasiewicz on $\partial \!f$-invariant sets. The proof is based on an argument used in [17, Theorem 5], which relies essentially on the following convergence rate property for the continuous steepest descent dynamic (43).

Proof of Proposition 3.3

Convexity of f and the Cauchy-Schwartz inequality imply

$$\begin{aligned} (\forall x \in \mathop {\mathrm { dom}}f) \quad f(x) - \inf f \le \Vert \partial \!f(x) \Vert _\_ \mathrm{dist\,}(x, \mathrm{argmin\,}f ), \end{aligned}$$

(44)

and so i) $\implies$ii) $\implies$ iii). Next, we just have to prove that the Łojasiewicz property implies the conditioning one. So let us assume that f is p-Łojasiewicz on $\varOmega$, which is $\partial f$-invariant, and fix $x \in \varOmega \cap \mathop {\mathrm { dom}}^* f$. Define, for all $t \ge 0$, $\varphi (t):=pc_{f,\varOmega }t^{1/p}$, which is differentiable on $]0,+\infty [$, and for all $u\in \mathop {\mathrm { dom}}f$, $r(u)=f(u)-\inf f$. Let us lighten the notations by noting $u(\cdot )$ instead of $u(\cdot ;x)$, so that $u(0)=x$. Because we will need to distinguish the case in which the trajectory converges in finite time, we introduce $T:= \inf \{t \ge 0 \ | \ u(t) \in \mathrm{{argmin}}~f \} \in [0, + \infty ]$. Since $x \in \mathop {\mathrm { dom}}^*\!\!f$ and $u(\cdot )$ is continuous, we see that $T >0$. For every $t \in [0,T[$, we have $u(t) \notin \mathrm{{argmin}}~f$, so $u(t) \in \varOmega \cap \mathop {\mathrm { dom}}^* f$ and $r(u(t)) \ne 0$. If $T < + \infty$, we also have for every $t > T$ that $u(t)=u(T)$ and $\dot{u}(t) =0$. Since $u(0)=x \in \mathop {\mathrm { dom}}f$, we know that $r \circ u$ is absolutely continuous on [0, t] for every $t \in ]0,T[$ [21, Theorem 3.6]. So $\varphi \circ r \circ u$ is also absolutely continuous on such intervals, and we can write:

$$\begin{aligned} (\forall t \in ]0,T[) \quad \varphi (r(x))\ge & {} \varphi (r(x)) - \varphi (r(u(t))) = \displaystyle \int _t^0 (\varphi \circ r \circ u)'(\tau ) \ \mathrm{d}\tau \\= & {} \int _t^0 \varphi ' (( r \circ u )(\tau ))\cdot (r \circ u)' (\tau ) \ \mathrm{d}\tau . \end{aligned}$$

But $\frac{\mathrm{d}}{\mathrm{d}\tau } (r \circ u) (\tau ) =- \Vert \dot{u}(\tau ) \Vert ^2 = - \Vert \partial \!f(u(\tau )) \Vert _\_^2$ for a.e. $t \in ]0,T[$ (see [21, Theorem 3.6 & Remark 3.9]), so the above inequality becomes

$$\begin{aligned} (\forall t \in ]0,T[) \quad \varphi (r(x)) \ge \int _0^t \varphi ' (( r \circ u )(\tau )) \Vert \partial \!f(u(\tau )) \Vert _\_^2 \ \mathrm{d}\tau . \end{aligned}$$

(45)

Since $\varOmega$ is $\partial \!f$-invariant, we can apply the Łojasiewicz inequality at $u(\tau ) \in \varOmega \cap \mathop {\mathrm { dom}}^* f$ for a.e. $\tau \in ]0,t[$, which can be rewritten in this case as $1 \le \varphi '(r(u(\tau ))) \Vert \partial \!f(u(\tau )) \Vert _\_.$ This applied to (45) gives us:

$$\begin{aligned} (\forall t \in ]0,T[) \quad \varphi (r(x)) \ge \int _0^t \Vert \dot{u}(\tau ) \Vert \ \mathrm{d}\tau . \end{aligned}$$

(46)

From (46) and the definition of T, we see that $\int _0^{+ \infty } \Vert \dot{u}(\tau ) \Vert \ \mathrm{d}\tau \le \varphi (r(x)) < +\infty$, meaning that the trajectory $u(\cdot )$ has finite length. As a consequence, it converges strongly to some ${\bar{u}}$ when t tends to T. Finally, we use on (46) the fact that $\Vert u(0) - u(t) \Vert \le \int _0^t \Vert \dot{u}(\tau ) \Vert \ \mathrm{d}\tau$, together with the fact that ${\bar{u}} \in \mathrm{argmin\,}f$ (see [21, Theorem 3.11]) to conclude that

$$\begin{aligned} \frac{1}{pc_{f,\varOmega }} \mathrm{dist\,}(x, \mathrm{argmin\,}f) \le \frac{1}{pc_{f,\varOmega }} \Vert x - {\bar{u}} \Vert \le (f(x) - \inf f)^{1/p}. \end{aligned}$$

$\square$

Proof of Proposition 3.4

i): let $S:= \mathrm{argmin\,}f \ne \emptyset$. Given $\delta >0$, there exists $M \in ]0, + \infty [$ such that

$$\begin{aligned} \sup \{ \mathrm{dist\,}(x,S) \ | \ {x \in \varOmega \cap \delta {\mathbb {B}}_X} \} \le M \end{aligned}$$

Since f is p-conditioned on $\varOmega$, we deduce that:

$$\begin{aligned} (\forall x \in \varOmega \cap \delta {\mathbb {B}}_X) \quad \mathrm{dist\,}(x,S)^{p'}= & {} \mathrm{dist\,}(x,S)^{p} \mathrm{dist\,}(x,S)^{p'-p} \\\le & {} (pM^{p'-p}/\gamma _{f,\varOmega }) (f(x) - \inf f), \end{aligned}$$

meaning that f is $p'$-conditioned on $\varOmega \cap \delta {\mathbb {B}}_X$. The proof relies on the same argument for the metric subregular case.

ii): Let $p,p',r$ be as in the statement. If $x \in \varOmega \cap [f<r] \cap \text{ dom}^* f$, we can use the fact that $\frac{1}{p} \ge \frac{1}{p'}$ to write

$$\begin{aligned} (f(x) - \inf f)^{1 - \frac{1}{p'}}= & {} (f(x) - \inf f)^{1 - \frac{1}{p}} \ (f(x) - \inf f)^{\frac{1}{p} - \frac{1}{p'}}\\\le & {} (f(x) - \inf f)^{1 - \frac{1}{p}} \ (r - \inf f)^{\frac{1}{p} - \frac{1}{p'}}. \end{aligned}$$

The conclusion follows immediately from the p-Łojasiewicz property of f on $\varOmega$. $\square$

Proof of Proposition 3.5

Assume by contradiction that there exists a sequence $(z^n)_{n\in {\mathbb {N}}} \subset \varOmega$ such that

$$\begin{aligned} n^{-1} \mathrm{dist\,}^p(z^n, \mathrm{argmin\,}f) > f(z^n) - \inf f. \end{aligned}$$

(47)

Since $\varOmega$ is weakly compact, we can assume without loss of generality that $z^n$ weakly converges to some $z^\infty \in \varOmega$ when $n \rightarrow + \infty$. Then, it follows from (47), the boundedness of $(z^n)_{n\in {\mathbb {N}}}\subset \varOmega$ and the weak lower semi-continuity of f that $f(z^\infty ) - \inf f \le 0$, meaning that $z^\infty \in \mathrm{argmin\,}f$, contradicting $\varOmega \cap \mathrm{argmin\,}f = \emptyset$. $\square$

Lemma A.4

Let $p\ge 1$, let $f \in \varGamma _0({\mathbb {R}}^N)$ with an open domain, and let $\varOmega \subset {\mathbb {R}}^N$ be a bounded open set such that $\varOmega \supset \mathrm{{argmin}}~f \ne \emptyset$. Then f is p-Łojasiewicz on $\varOmega$ if and only if f is “classically” p-Łojasiewicz on $\varOmega$, namely

Proof

$\Rightarrow$: Let ${\bar{x}} \in \varOmega$. Since $\varOmega$ is open, there exists $\delta >0$ such that ${\mathbb {B}}({\bar{x}}, \delta ) \subset \varOmega$. So f is p-Łojasiewicz on ${\mathbb {B}}({\bar{x}}, \delta ) \cap [f({\bar{x}})< f < f({\bar{x}}) +r] \subset \varOmega$, for any $r > 0$.

$\Leftarrow$: by assumption, $\mathrm{{argmin}}~f$ is compact, and f is “classically” Łojasiewicz on $\mathrm{{argmin}}~f$. The arguments in [18, Lemma 6] imply that there exist $\delta ,r >0$, such that f is p-Łojasiewicz on

$$\begin{aligned} {\hat{\varOmega }} := \{ x \in {\mathbb {R}}^N \ | \ \mathrm{dist\,}(x, \mathrm{{argmin}}~f)< \delta , f(x) < \inf f +r \}. \end{aligned}$$

Since $\mathop {\mathrm { dom}}f$ is open, f is continuous on $\mathop {\mathrm { dom}}f$ [11, Corollary 8.39], and we deduce that ${\hat{\varOmega }}$ is open. So $( \mathrm{cl\,}\varOmega \setminus {\hat{\varOmega }})$ is closed, it is bounded because $\varOmega$ is bounded, and it does not intersect $\mathrm{{argmin}}~f \subset {\hat{\varOmega }}$. Propositions 3.5 and 3.3 applied to $( \mathrm{cl\,}\varOmega \setminus {\hat{\varOmega }})$ imply that f is p-Łojasiewicz on $( \mathrm{cl\,}\varOmega \setminus {\hat{\varOmega }})$. We conclude that f is p-Łojasiewicz on $\varOmega$. $\square$

1.2.2 A.2.2 Proofs of Section 3.2

Lemma A.5

(The conditioning constant for uniformly convex functions). Let $f \in \varGamma _0(X)$, let $C \subset X$ be a closed convex set such that $C \cap \mathrm{{argmin}}~f \ne \emptyset$, and $p \ge 2$. Assume that f is p-uniformly convex on C, in the sense that (8) holds for all $x,y \in C \cap \mathop {\mathrm { dom}}f$. Then f is p-conditioned on C, with $\gamma _{f,C}$ being the constant $\gamma$ in (8). In particular, p-uniformly convex functions are globally p-conditioned.

Proof

Let $f_C := f + \delta _C \in \varGamma _0(X)$. Then $\mathop {\mathrm { dom}}f_C=\mathop {\mathrm { dom}}f \cap C$ and $f_C$ is uniformly convex on X. Let ${\bar{x}} \in \mathrm{{argmin}}~f \cap C$, and let $x \in \mathop {\mathrm { dom}}f \cap C$. Using [102, Corollary 3.5.11.ii] with (8), we obtain that

$$\begin{aligned} \frac{\gamma }{p}\Vert x - {\bar{x}} \Vert ^p +f_C'({\bar{x}} ; x- {\bar{x}} ) \le f_C(x) - f_C({\bar{x}}), \end{aligned}$$

(48)

where $f_C'({\bar{x}} ; x- {\bar{x}} )$ is the directional derivative of $f_C$ at ${\bar{x}}$ in the direction $x - {\bar{x}}$ (see its definition in [102, Theorem 2.1.13]). Given that ${\bar{x}} \in \mathrm{{argmin}}~f\cap C$, it is easy to see that $f_C'({\bar{x}} ; x- {\bar{x}} ) \ge 0$. Moreover, $f_C$ coincides with f on C, and $\mathrm{dist\,}(x,\mathrm{{argmin}}~f) \le \Vert x - {\bar{x}} \Vert$. We conclude then from (48) that f is p-conditioned on C with $\gamma _{f,C}=\gamma$. In the case that f is uniformly convex, we take $C=X$ and use the fact that $\mathrm{{argmin}}~f \ne \emptyset$ [102, Proposition 3.5.8]. $\square$

Lemma A.6

(The Łojasiewicz constant for uniformly convex functions). Let $p \ge 2$, and let $f \in \varGamma _0(X)$ be p-uniformly convex, with constant $\gamma$. Then f is p-Łojasiewicz on X, with $c_{f,X}=(1-1/p)^{1-1/p} \gamma ^{-1/p}$.

Proof

By [102, Corollary 3.5.11.iii], for all $x_1,x_2 \in \mathop {\mathrm { dom}}\partial \!f, x^*_1 \in \partial \!f(x_1)$:

$$\begin{aligned} f(x_2) - f(x_1)-\langle x_1^*,x_2 - x_1 \rangle \ge \frac{\gamma }{p}\Vert x_2 - x_1 \Vert ^p. \end{aligned}$$

Fix $x \in \mathop {\mathrm { dom}}\partial \!f$ and $x^* \in \partial \!f(x)$. The above inequality yields

$$\begin{aligned} f(x) - \inf f = \sup \limits _{u \in X} \ f(x) - f(u) \le - \inf \limits _{u \in X}\left( \langle x^* , u - x \rangle + (\gamma /p) \Vert u - x \Vert ^p \right) . \end{aligned}$$

(49)

The right hand side of the above inequality involves a strictly convex optimization problem, whose unique optimal value ${\bar{u}}$ can be determined by using Fermat’s rule:

$$\begin{aligned} 0= x^* + \gamma \Vert {\bar{u}} - x \Vert ^{p-2} ({\bar{u}}-x) \Leftrightarrow {\bar{u}} = x - \gamma ^{-1/(p-1)} \Vert x^* \Vert ^{(2-p)/(p-1)} x^*. \end{aligned}$$

Injecting this optimal value in (49) gives, after rearranging the terms,

$$\begin{aligned} f(x) - \inf f \le (1 - 1/p) \gamma ^{-1/(p-1)} \Vert x^* \Vert ^{p/(p-1)} , \end{aligned}$$

and, since $x^*$ is arbitrary in $\partial \!f (x)$, the result follows after passing this inequality to the power $1- 1/p$. $\square$

Proof of Example 3.10

ii). To prove the claim, it is enough to verify the three conditions of [40, Theorem 4.2]. The first condition (boundedness of $\mathrm{argmin\,}f$) is guaranteed by the fact that f is coercive. Indeed, h is strongly convex, therefore bounded from below, and g is itself coercive. The second condition (dual qualification conditions) follows immediately from the fact that both $h^*$ and $g^*$, and are continuously differentiable. To see this, observe that in this example $g^*$ is (up to a constant) $\Vert \cdot \Vert _q^q$, where q is the conjugate number of p: $(1/p) + (1/q) = 1$. Moreover, h being strongly convex means that $h^*$ is also continuously differentiable, with $\mathop {\mathrm { dom}}h^* = {\mathbb {R}}^M$. The third condition (firm convexity) is easy to check for h because it is strongly convex; for g the proof is left in the following Lemma. We can then apply [40, Theorem 4.2], which ensures that f is 2-conditioned on every compact set. Using again the fact that f is coercive, and therefore has bounded sublevel sets, we conclude that f is 2-conditioned on every sublevel set. $\square$

1.2.3 A.2.3 Proofs of Section 3.3

Lemma A.7

(p-powers are 2-tilt conditioned when $\mathbf{{p}}\varvec{\in }{} \mathbf{]}{} \mathbf{{1,2}])}$. Let $p \in ]1,2]$, $u \in {\mathbb {R}}^N$, and $f : {\mathbb {R}}^N \rightarrow {\mathbb {R}}$ be defined as $f(x)=\frac{1}{p}\Vert x \Vert _p^p - \langle u,x \rangle$. Then f is 2-conditioned on every bounded subset of ${\mathbb {R}}^N$.

Proof

This function is a separable sum, so, without loss of generality, we can assume from here that $N=1$ (see [40, Lemma 4.4]). Given a real $t \in {\mathbb {R}}$, we will note its sign with s(t), which is equal to $-1$ (resp. $+1$) if $t<0$ (resp. $t>0$), or 0 if $t=0$. Using the convexity, the differentiability of f, and the Fermat’s rule, we see that f admits a unique minimizer ${\bar{x}}$, defined by the relations

$$\begin{aligned} 0 = s({\bar{x}}) \vert {\bar{x}} \vert ^{p-1} - u \Leftrightarrow {\bar{x}} = s(u) \vert u \vert ^{\frac{1}{p-1}} \Leftrightarrow u = s({\bar{x}}) \vert {\bar{x}} \vert ^{p-1}. \end{aligned}$$

If $u=0$, it is immediate to see that f is 2-conditioned on $]-1,1[$, where the relation $\vert t \vert ^2 \le \vert t \vert ^p$ holds. We therefore assume from now that $u \ne 0$, which also means that ${\bar{x}} \ne 0$. We now compute (we note $q = p/(p-1)$)

$$\begin{aligned} \inf f = f({\bar{x}}) = \frac{1}{p}\vert {\bar{x}} \vert ^p - u {\bar{x}} = \frac{1}{p}\vert {\bar{x}} \vert ^p - s({\bar{x}}) \vert {\bar{x}} \vert ^{p-1} {\bar{x}} = \frac{1}{p}\vert {\bar{x}} \vert ^p - \vert {\bar{x}} \vert ^{p} = - \frac{1}{q} \vert {\bar{x}} \vert ^p, \end{aligned}$$

meaning that we are looking for an inequality like

$$\begin{aligned} \gamma \vert x - {\bar{x}} \vert ^2 \le \frac{1}{p}\vert x \vert ^p - ux - \inf f = \frac{1}{p}\vert x \vert ^p - s({\bar{x}}) \vert {\bar{x}} \vert ^{p-1} x + \frac{1}{q} \vert {\bar{x}} \vert ^p. \end{aligned}$$

Using the L’Hôpital rule twice allows us to study the following limit:

$$\begin{aligned} \lim \limits _{x \rightarrow {\bar{x}}} \ \frac{\frac{1}{p}\vert x \vert ^p - s({\bar{x}}) \vert {\bar{x}} \vert ^{p-1} x + \frac{1}{q} \vert {\bar{x}} \vert ^p}{\vert x - {\bar{x}} \vert ^2}= & {} \lim \limits _{x \rightarrow {\bar{x}}} \ \frac{s( x) \vert x \vert ^{p-1} - s({\bar{x}}) \vert {\bar{x}} \vert ^{p-1}}{2(x - {\bar{x}})} \\= & {} \lim \limits _{x \rightarrow {\bar{x}}} \ \frac{(p-1)\vert x \vert ^{p-2}}{2} = \frac{(p-1)}{2}\vert {\bar{x}} \vert ^{p-2}. \end{aligned}$$

Note that our assumption that ${\bar{x}} \ne 0$ ensures that we can take the derivative of the second numerator around ${\bar{x}}$. Since this limit is well-defined, and nonnegative, it means that f is 2-conditioned on a small enough neighbourhood of ${\bar{x}}$. To conclude the proof, it remains to verify that f is 2-conditioned on any bounded set. This follows immediately from Proposition 3.5 and the fact that $\mathrm{argmin\,}f = \{{\bar{x}} \}$. $\square$

Lemma A.8

If $f \in \varGamma _0(X)$ is p-uniformly convex on a bounded closed convex set $\varOmega \subset X$ with $p\ge 2$, then f is p-tilt-conditioned on $\varOmega$.

Proof

Let $u \in X$ and let ${\tilde{f}} := f + \langle u, \cdot \rangle$ which is also p-uniformly convex on $\varOmega$. We assume without loss of generality that $\mathrm{{argmin}}~{\tilde{f}} \ne \emptyset$. If $\varOmega \cap \mathrm{{argmin}}~{\tilde{f}} = \emptyset$, then ${\tilde{f}}$ is p-conditioned on $\varOmega$, according to Proposition 3.5. If instead $\varOmega \cap \mathrm{{argmin}}~{\tilde{f}} \ne \emptyset$, then we conclude the same with Lemma A.5. This proves the claim. $\square$

Lemma A.9

(Kullback-Leibler divergences are $\mathbf{2}$-tilt conditioned). Let ${\bar{x}} \in ]0,+\infty [^N$, and $f \in \varGamma _0({\mathbb {R}}^N)$ be the Kullback-Leibler divergence to ${\bar{x}}$:

$$\begin{aligned} f(x) = K\!L({\bar{x}} ; x) = \sum _{i=1}^N kl({\bar{x}}_i; x_i) \quad \text { where } \quad kl({\bar{t}}; t) = {\left\{ \begin{array}{ll} {\bar{t}} \log (\frac{{\bar{t}}}{t}) - {\bar{t}} + t &{} \text { if } t>0, \\ +\infty &{} \text { else.} \end{array}\right. } \end{aligned}$$

Then f is 2-tilt-conditioned on every bounded set of ${\mathbb {R}}^N$.

Proof

Let $d \in {\mathbb {R}}^N$, and define the tilted function ${\tilde{f}} = f + \langle d , \cdot \rangle$. Using Fermat’s rule, we see that $\mathrm{{argmin}}~{\tilde{f}} = \partial \!f^*(-d)$. It is a simple exercice to verify that $\mathop {\mathrm { dom}}\partial \!f^* = ]-\infty , 1[^N$, so $\mathrm{{argmin}}~{\tilde{f}} \ne \emptyset$ if and only if $d \in ]-1,+\infty [^N$. Let d be such vector, and write, for any $x_i>0$:

$$\begin{aligned} {\tilde{f}}_i(x_i)= & {} {\bar{x}}_i \log \left( \frac{{\bar{x}}_i}{x_i}\right) - {\bar{x}}_i + x_i + d_i x_i\\= & {} (1+d_i) \left( \frac{{\bar{x}}_i}{1+d_i} \log \left( \frac{{\bar{x}}_i}{x_i}\right) - \frac{{\bar{x}}_i}{1+d_i} + x_i \right) . \end{aligned}$$

Let $X_i := \frac{{\bar{x}}_i}{1+d_i}$, which is well defined under our assumption that $d_i > -1$. Then

$$\begin{aligned} {\tilde{f}}_i(x_i)&= (1+d_i) \left( X_i \log \left( \frac{X_i}{x_i}\right) - X_i + x_i + X_i \log (1+d_i) \right) \\&= (1+d_i) kl(X_i;x_i) + a_i , \end{aligned}$$

where $a_i = X_i (1+d_i) \log (1+d_i)$. We then observe that $\mathrm{{argmin}}~{\tilde{f}}_i = \{X_i\}$, from which we deduce that $\mathrm{{argmin}}~{\tilde{f}} = \{X\}$ with $X = (X_i)_{i=1}^N$.

Now, let $\delta >0$ be fixed, and let $x \in {\mathbb {B}}(X,\delta )$. Let ${\underline{d}} := \min _i d_i > -1$, $c := N \Vert X \Vert _\infty$, and

$$\begin{aligned}&C := \frac{1}{\delta ^2c} \left( \frac{\delta }{c} - \ln \left( 1+ \frac{\delta }{c} \right) \right) \end{aligned}$$

which is nonnegative since $t > \ln (1+t) \text { on} ]0,+\infty [.$ For each $i \in \{1,\dots ,N\}$, we have $\vert x_i - X_i \vert \le \delta$, so we can use [24, Lemma A.2] on ${\tilde{f}}_i$ to write

$$\begin{aligned} {\tilde{f}}(x) - \inf {\tilde{f}}= & {} \sum _{i=1}^N {\tilde{f}}_i(x) - {\tilde{f}}_i(X_i) = \sum _{i=1}^N (1+d_i) kl(X_i;x_i) \\\ge & {} \sum _{i=1}^N (1+d_i) C \vert X_i - x_i \vert ^2 \ge (1+{\underline{d}})C \Vert X-x \Vert ^2. \end{aligned}$$

This proves that ${\tilde{f}}$ is 2-conditioned on ${\mathbb {B}}(X,\delta )$, which conludes the proof. $\square$

1.3 A.3 The Forward-Backward algorithm and proofs of Section 4

Definition A.10

Given a positive real sequence $(r_n)_{{n\in {\mathbb {N}}}}$ converging to zero, we say that $r_n$ converges:

• sublinearly (of order $\alpha \in ]0,+\infty [$) if $\exists C \in ]0,+\infty [$ such that $\forall {n\in {\mathbb {N}}}$, $r_n \le C n^{-\alpha }$,

• Q-linearly if $\exists \varepsilon \in ]0,1[$ such that $\forall {n\in {\mathbb {N}}}$, $r_{n+1} \le \varepsilon r_n$,

• R-linearly if $\exists (s_n)_{n\in {\mathbb {N}}}$ Q-linearly converging such that $\forall {n\in {\mathbb {N}}}$, $r_n \le s_n$,

• Q-superlinearly (of order $\beta \in ]1,+\infty [$) if $\exists C \in ]0,+\infty [$ such that $\forall {n\in {\mathbb {N}}}$, $r_{n+1} \le C r_n^\beta$,

• R-superlinearly if $\exists (s_n)_{n\in {\mathbb {N}}}$ Q-superlinearly convergent such that $\forall {n\in {\mathbb {N}}}$, $r_n \le s_n$.

It is easy to verify that $r_n$ is R-superlinearly convergent of order $\beta > 1$ if and only if

$$\begin{aligned} (\forall \varepsilon \in ]0,1[)(\exists C>0)(\forall {n\in {\mathbb {N}}}) \quad r_n \le C \varepsilon ^{\beta ^n}. \end{aligned}$$

Note that R-linear and R-superlinear convergence ensures only the overall decrease of the sequence, while Q-linear and Q-superlinear convergence requires the sequence to decrease at a certain speed for each index. It is immediate from the definition that Q-convergence implies R-convergence.

Lemma A.11

(Estimate for sublinear real sequences). Let $(r_n)_{n\in {\mathbb {N}}}$ be a real sequence being strictly positive and satisfying, for some $\kappa > 0$, $\alpha > 1$ and all ${n\in {\mathbb {N}}}$: $r_n - r_{n+1} \ge \kappa r_{n+1}^\alpha .$ Define ${\tilde{\kappa }}:= \min \{\kappa ,\kappa ^\frac{\alpha -1}{\alpha } \}$, and $\delta := \max \limits _{s \ge 1} \min \left\{ \frac{ \alpha -1}{s} , \kappa ^{-\frac{\alpha - 1}{\alpha }} r_0^{1-\alpha } \left( 1 - s^{-\frac{\alpha - 1}{ \alpha }} \right) \right\} \in ]0, + \infty [.$ Then, for all ${n\in {\mathbb {N}}}$, $r_n \le ({\tilde{\kappa }} \delta n)^{-1/(\alpha -1)}.$

Proof

It can be found in [72, Lemma 7.1], see also the proofs of [3, Theorem 2] or [46, Theorem 3.4]. $\square$

Lemma A.12

If Assumption 2.1 holds, then for all $(x,u)\in X^2$ and all $\lambda >0$:

• i) $\Vert T_\lambda x - u \Vert ^2 - \Vert x - u \Vert ^2 \le \left( {\lambda L} - 1 \right) \Vert T_\lambda x - x \Vert ^2 + 2\lambda ( f(u) - f(T_\lambda x)).$

• ii) $\Vert \partial \!f(T_\lambda x) \Vert _\_ \le \lambda ^{-1} \Vert T_\lambda x - x \Vert \le \Vert \partial \!f(x) \Vert _\_.$

Proof of Lemma A.12

To prove item i), start by writing

$$\begin{aligned} \Vert T_\lambda x - u \Vert ^2 - \Vert x - u \Vert ^2 = - \Vert T_\lambda x - x \Vert ^2 + 2\left\langle {x - T_\lambda x} , u - T_\lambda x \right\rangle . \end{aligned}$$

The optimality condition in (2) gives ${x - T_\lambda x}\in \lambda \partial g(T_\lambda x) + \lambda \nabla h(x)$ so that, by using the convexity of g:

$$\begin{aligned} \Vert T_\lambda x - u \Vert ^2 - \Vert x - u \Vert ^2 \le - \Vert T_\lambda x - x \Vert ^2 + 2\lambda \left( g(u) - g(T_\lambda x) + \langle \nabla h(x),u - T_\lambda x \rangle \right) . \end{aligned}$$

Since we can write $\langle \nabla h(x),u -T_\lambda x \rangle = \langle \nabla h(x),u -x \rangle + \langle \nabla h(x),x - T_\lambda x\rangle$, we deduce from the convexity of h and the Descent Lemma ([11, Theorem 18.15]) that

$$\begin{aligned} \langle \nabla h(x),u -T_\lambda x \rangle\le & {} h(u) -h(x) + h(x) - h(T_\lambda x) + \frac{L}{2} \Vert T_\lambda x - x \Vert ^2 \\= & {} h(u) - h(T_\lambda x) + \frac{L}{2} \Vert T_\lambda x - x \Vert ^2. \end{aligned}$$

Item i) is then proved after combining the two previous inequalities. For item ii), the optimality condition in (2), together with a sum rule (see e.g. [88, Theorem 3.30]), allows to deduce that

$$\begin{aligned} \forall (u,v) \in X^2, \quad v = \mathrm{prox}_{\lambda g}(u) \Leftrightarrow \lambda ^{-1}(u-v) + \nabla h(v) \in \partial \!f(v). \end{aligned}$$

(50)

For the first inequality, use (50) with $(u,v)=(x-\lambda \nabla h(x),T_\lambda x)$, together with the contraction property of the gradient map $x \mapsto x - \lambda \nabla h(x)$ when $0<\lambda \le 2/L$ (see [11, Corollary 18.17 & Proposition 4.39 & Remark 4.34.i]) to obtain:

$$\begin{aligned} \Vert \partial \!f (T_\lambda x) \Vert _\_ \le \lambda ^{-1}\Vert (x - \lambda \nabla h(x) )-(T_\lambda x - \lambda \nabla h(T_\lambda x)) \Vert \le \lambda ^{-1} \Vert T_\lambda x - x \Vert . \end{aligned}$$

For the second inequality, consider $x^* := \mathrm{proj}(-\nabla h(x),\partial g(x))$, and use (50) with $(u,v)=(x + \lambda x^*,x)$, together with the nonexpansiveness of the proximal map (see [11, Proposition 12.28]):

$$\begin{aligned} \Vert T_\lambda x - x \Vert= & {} \Vert \mathrm{prox}_{\lambda g}(x - \lambda \nabla h(x)) - \mathrm{prox}_{\lambda g}(x + \lambda x^*)\Vert \\\le & {} \lambda \Vert \nabla h(x)+ x^*\Vert = \lambda \Vert \partial \!f(x) \Vert _\_. \end{aligned}$$

$\square$

Lemma A.13

(Descent Lemma for Hölder smooth functions). Let $f : X \longrightarrow {\mathbb {R}}$ and $C \subset X$ be convex. Assume that f is Gâteaux differentiable on C, and that there exists $(\alpha ,L) \in ]0,+\infty [^2$, such that for all $(x,y) \in C^2$, $\Vert \nabla f(x) - \nabla f(y) \Vert \le L \Vert x - y \Vert ^\alpha$ holds. Then:

$$\begin{aligned} (\forall (x,y) \in C^2) \quad f(y) - f(x) - \langle \nabla f(x) , y - x \rangle \le \frac{L}{\alpha + 1 } \Vert x - y \Vert ^{\alpha + 1 }. \end{aligned}$$

Proof

The argument used in [102, Remark 3.5.1, p.212] for $C=X$ extends directly to convex sets. $\square$

Now we can prove the convergence rate results of Sect. 4.1:

Proof of Theorem 4.1

We first show that $(x_n)_{{n\in {\mathbb {N}}}}$ has finite length. Since $\inf f > - \infty$, $r_n:=f(x_n) - \inf f \in [0, + \infty [$, and it follows from Lemma A.12 that

$$\begin{aligned} a \Vert x_{n+1} - x_n \Vert ^2\le & {} r_n - r_{n+1}, \text { with } a=\frac{1}{2\lambda }(2-\lambda L) > 0, \end{aligned}$$

(51)

$$\begin{aligned} \Vert \partial \!f (x_{n+1}) \Vert _\_\le & {} b \Vert x_n - x_{n+1} \Vert , \text { with } b= \lambda ^{-1}. \end{aligned}$$

(52)

If there exists ${n\in {\mathbb {N}}}$ such that $r_n=0$ then the algorithm would stop after a finite number of iterations (see (51)), therefore it is not restrictive to assume that $r_n>0$ for all ${n\in {\mathbb {N}}}$. We set $\varphi (t):=p t^{1/p}$ and $c:=c_{f,\varOmega }$, so that the Łojasiewicz inequality at $x_n \in \varOmega \cap \mathop {\mathrm { dom}}^* f$ can be rewritten as

$$\begin{aligned} (\forall {n\in {\mathbb {N}}}) \quad 1 \le c \varphi '(r_n) \Vert \partial \!f(x_n) \Vert _\_. \end{aligned}$$

(53)

Combining (51), (52), and (53), and using the concavity of $\varphi$, we obtain for all $n \ge 1$:

$$\begin{aligned} \Vert x_{n+1} - x_n \Vert ^2\le & {} \frac{bc}{a}\varphi '(r_n)(r_n - r_{n+1}) \Vert x_n - x_{n-1} \Vert \\\le & {} \frac{bc}{a} (\varphi (r_n) - \varphi (r_{n+1})) \Vert x_n - x_{n-1} \Vert . \end{aligned}$$

By taking the square root on both sides, and using Young’s inequality, we obtain

$$\begin{aligned} (\forall n \ge 1) \quad 2 \Vert x_{n+1} - x_n \Vert \le \frac{bc}{a}(\varphi (r_n) - \varphi (r_{n+1}))+ \Vert x_n - x_{n-1} \Vert . \end{aligned}$$

(54)

Sum this inequality, and reorder the terms to finally obtain

$$\begin{aligned} (\forall n \ge 1) \quad \sum \limits _{k=1}^{n} \Vert x_{k+1} - x_k \Vert \le \frac{bc}{a}\varphi (r_1) + \Vert x_1 - x_{0} \Vert . \end{aligned}$$

We deduce that $(x_n)_{n\in {\mathbb {N}}}$ has finite length and converges strongly to some $x_\infty$. Moreover, from (52) and the strong closedness of $\partial \!f : X \rightrightarrows X$, we conclude that $0 \in \partial \!f(x_\infty )$, meaning that $x_\infty \in \mathrm{{argmin}}~f$.

Now we prove the convergence rates. Let $c=c_{f,\varOmega }$ for short. We first derive rates for the sequence of values $r_n:=f(x_n) - \inf f$, from which we will derive the rates for the iterates. Equations (51) and (52) yield

$$\begin{aligned} r_n-r_{n+1} \ge a \Vert x_{n+1} - x_n \Vert ^2 \ge \frac{a}{b^2}\Vert \partial \!f(x_{n+1}) \Vert _\_^2. \end{aligned}$$

The Łojasiwecz inequality at $x_{n+1} \in \varOmega \cap \text{ dom}^* f$ implies $c^2 r_{n+1}^{2/p}(r_n - r_{n+1}) \ge ab^{-2} r_{n+1}^2,$ so we deduce that

$$\begin{aligned} (\forall {n\in {\mathbb {N}}}) \quad r_{n+1} \ne 0 \ \Rightarrow \ r_{n+1}^{2/p}(r_n - r_{n+1}) \ge \kappa r_{n+1}^2 , \quad \text { with } \kappa :={a}{(bc)^{-2}}. \end{aligned}$$

(55)

The rates for the values are derived from the analysis of the sequences satisfying the inequality in (55). Depending on the value of p, we obtain different rates.

$\bullet$ If $p=1$, then we deduce from (55) that for all ${n\in {\mathbb {N}}}, r_{n+1}\ne 0$ implies $r_{n+1} \le r_n - \kappa .$ Since the sequence $(r_n)_{n\in {\mathbb {N}}}$ is decreasing and positive, $r_{n+1}\ne 0$ implies $n\le r_0\kappa ^{-1}$.

For the other values of p, we will assume that $r_n >0$. In particular, we get from (55)

$$\begin{aligned} (\forall {n\in {\mathbb {N}}}) \quad r_n - r_{n+1} \ge \kappa r_{n+1}^\alpha , \quad \text { with }\ \alpha := {2(p-1)}{p^{-1}}\ \text { and }\ \kappa :={a}{b^{-2}c^{-2}}. \end{aligned}$$

(56)

$\bullet$ If $p\in ]1,2[$, then $\alpha \in ]0,1[$. The positivity of $r_{n+1}$ and (56) imply that for all ${n\in {\mathbb {N}}}$, $r_{n+1} \le \kappa ^{-1/\alpha } r_n^{1/\alpha }$, meaning that $r_n$ converges Q-superlinearly.

$\bullet$ If $p=2$, then $\alpha =1$ and we deduce from (56) that for all ${n\in {\mathbb {N}}}$, $r_{n+1} \le {(1+\kappa )^{-1}} r_n$, meaning that $r_n$ converges Q-linearly.

$\bullet$ If $p \in ]2,+\infty [$, then $\alpha \in ]1,2[$, and the analysis still relies on studying the asymptotic behaviour of a real sequence satisfying (56). Lemma A.11 shows that we have $r_{n+1} \le (C_p')^{p/(p-2)} n^{-p/(p-2)}$, by taking

$$\begin{aligned} (C_p')^{-1}:=\min \left\{ \kappa ,\kappa ^{\frac{p-2}{2p-2}} \right\} \max \limits _{s \ge 1} \min \left\{ \frac{ p-2}{ps} , \kappa ^{\frac{2-p}{2p-2}} r_0^{\frac{2-p}{p}} \left( 1 - s^{-{\frac{p-2}{2p-2}}} \right) \right\} . \end{aligned}$$

(57)

To end the proof, we will prove that the rates for $\Vert x_n - x_\infty \Vert$ are governed by the ones of $r_n$. Let $1\le n \le N < +\infty$, and sum the inequality in (54) between n and N to obtain (remind that $b=\lambda ^{-1}$):

$$\begin{aligned} \Vert x_N-x_n\Vert \le \sum \limits _{k=n}^{N} \Vert x_{k+1} - x_k \Vert \le \frac{pc}{a \lambda } r_{n}^{1/p} + \Vert x_n - x_{n-1} \Vert . \end{aligned}$$

Next, we pass to the limit for $N \rightarrow \infty$, we use (51), and the fact that $r_n$ is decreasing to obtain

$$\begin{aligned} (\forall n \ge 1) \quad \Vert x_\infty - x_n \Vert \le \frac{pc}{a\lambda } r_{n-1}^{1/p} + \frac{1}{\sqrt{a}} \sqrt{r_{n-1}}. \end{aligned}$$

(58)

Note that ${r_{n-1}^{1/2}} \le r_0^{\frac{1}{2}-\frac{1}{p}} r_{n-1}^{1/p}$ if $p\in [2,+\infty [$, and $r_{n-1}^{1/p} \le r_0^{\frac{1}{p}-\frac{1}{2}} {r_{n-1}^{1/2}}$ if $p\in [1,2]$. So, by defining

$$\begin{aligned} C_p:= {\left\{ \begin{array}{ll} 2pc(2-\lambda L)^{-1} + (2\lambda r_0)^{1/2} (2-\lambda L)^{-1/2} r_0^{-1/p} &{} \text { if } p \ge 2, \\ 2pcr_0^{1/p}(2-\lambda L)^{-1}r_0^{-1/2} + (2\lambda )^{1/2} (2-\lambda L)^{-1/2} &{} \text { if } p \le 2, \end{array}\right. } \end{aligned}$$

(59)

we finally conclude from (58) that $\Vert x_\infty - x_n \Vert \le C_p r_{n-1}^{1/\max \{2,p\}}$ when $n \ge 1$. $\square$

Proof of Proposition 4.7

Use the fact that $p<0$, the definition of $\varOmega$ in the claim and (44) to write that for all $x \in \varOmega \cap \text{ dom}^* f$, $\ (f(x) - \inf f)^{1 - \frac{1}{p}} \le (f(x) - \inf f) r^{- \frac{1}{p}} \le \delta r^{- \frac{1}{p}}\Vert \partial \!f(x) \Vert _\_ \ .$ $\square$

Proof of Proposition 4.8

It is the same as for Proposition 3.4, as the positivity of $p,p'$ is not needed. $\square$

Proof of Theorem 4.9

The proof is as for the case $p \in ]2,+\infty [$ of Theorem 4.1: the p-Łojasiewicz property implies (55), and the statement follows from Lemma A.11 with $\alpha =2(p-1)/p \in ]2,+\infty [$. $\square$

Proof of Theorem 4.11

The proofs of Theorems 4.1 and 4.9 rely on the combination of the Łojasiewicz inequality with the estimations (51) and (52), which can be replaced by (19) and (20). $\square$

1.4 A.4 Linear inverse problems and proofs of Section 5.1

Here we will make use of is the Moore-Penrose pseudo-inverse of A. It is a linear operator (not necessarily bounded), whose domain is $D(A^\dagger ):= R(A) + R(A)^\perp$, and satisfying

$$\begin{aligned} (\forall y \in D(A^\dagger )) \quad A^\dagger y := \mathrm{argmin\,}\{ \Vert x \Vert \ | \ A^*Ax = A^*y \}. \end{aligned}$$

It is easy to see that, whenever $y \in D(A^\dagger )$, the set of minimizers of the least squares (29) is $A^\dagger y + \ker A$.

Lemma A.14

Let A be a bounded linear operator from X to Y. Then $\mathrm{{spec}}^*(A^*A) = \mathrm{{spec}}^*(AA^*)$.

Proof

Let $\lambda \ne 0$ and denote by $I_X$ and $I_Y$ the identity operators of X and Y, respectively. It is enough to show that $\lambda I_Y - AA^*$ has a bounded linear inverse if and only if $\lambda I_X - A^*A$ has. Assume that $\lambda I_Y - AA^*$ has a bounded linear inverse, and consider $B = \frac{1}{\lambda }\left( I_X + A^*(\lambda I_Y-AA^*)^{-1} A \right)$. Clearly B is a bounded linear operator, and simple computations show that $(\lambda I_X - A^*A)B = I_X$. We see then that $\lambda I_X - A^*A$ has a bounded inverse. Repeating this argument by exchanging the roles of A and $A^*$ concludes the proof. $\square$

Lemma A.15

Let A be a bounded linear operator from X to Y. Then we have $A (A^*A)^\alpha = (AA^*)^\alpha A$ for every $\alpha >0$.

Proof

We remember from Sect. 5.1.1 that the power of a selfadjoint operator is defined in [56, Theorem VI.32.1]. A simple induction argument shows that, for every $k \in {\mathbb {N}}$, $A(A^*A)^k = (AA^*)^k A$. Taking linear combinations of this equality allows to see that, for every polynomial $P \in {\mathbb {R}}[X]$, $AP(A^*A) = P(AA^*)A$. Now, let $\phi : t \in [0,+\infty [ \mapsto t^\alpha$. Since $\phi$ is continuous on $[0,+\infty [$, it is in particular continuous on $[0, \Vert A \Vert ^2]$, which is an interval containing the spectrum of both $A^*A$ and $AA^*$. Thus, $\phi$ restricted to this interval can be written as the uniform limit of a certain sequence of polynomials $(P_n)_{n\in {\mathbb {N}}}$. This implies that

$$\begin{aligned} \lim \limits _{n \rightarrow +\infty } \sup \limits _{\lambda \in \mathrm{spec}(A^*A)} \vert \phi (\lambda ) - P_n(\lambda )\vert = 0. \end{aligned}$$

The conditions of [56, Theorem VI.32.1] are therefore met, and we obtain that $(A^*A)^\alpha$ is the limit of $P_n(A^*A)$ (the same reasoning applies to $AA^*$). Since $AP_n(A^*A) = P_n(AA^*)A$ as observed above, passing to the limit gives the desired result. $\square$

Lemma A.16

For all $b \in Y$, $r \in ]0,+\infty [$, the following two properties are equivalent:

• (1) $(\exists x \in \ker A^\perp ) \quad b=Ax, \quad \Vert x \Vert = r$

• (2) $(\exists y \in \mathrm{cl\,}R(A)) \quad b=\sqrt{AA^*} y, \quad \Vert y \Vert =r,$ where $\sqrt{AA^*}$ is a shorthand for $(AA^*)^{1/2}$.

Proof

It is shown in [42, Proposition 2.18] that $R(A) = R( \sqrt{AA^*})$, so it is enough to verify this implication:

$$\begin{aligned} (\forall (x,y)\in \ker A^\perp \times \mathrm{cl\,}R(A))\quad \ Ax = \sqrt{AA^*} y \ \Rightarrow \ \Vert x \Vert = \Vert y \Vert . \end{aligned}$$

Let (x, y) be such a pair. Since $Ax=\sqrt{AA^*}y$ and $y \in \mathrm{cl\,}R(A)=\ker \sqrt{AA^*}^\perp$, we deduce that $y=(\sqrt{AA^*})^\dagger Ax$. Therefore, since $(AA^*)^\dagger Ax = (A^*)^\dagger x$ (see [42, p.35]) and $A^*(A^*)^\dagger x= \mathrm{proj}(x;\ker A^\perp ) {=x}$, we get

$$\begin{aligned} \Vert y \Vert ^2 = \Vert (\sqrt{AA^*})^\dagger Ax \Vert ^2 = \langle ({AA^*})^\dagger Ax, Ax \rangle = \langle A^*(A^*)^\dagger x,x \rangle = \Vert x \Vert ^2. \end{aligned}$$

$\square$

Proof of Proposition 5.5

Recall that $y^\dagger =Ax^\dagger$ and let $\nu =\mu +1/2$. From Definition 5.4 we derive:

This equivalence proves the desired expression for $X_{\mu ,\delta }$. Since it holds for any $\delta >0$, it implies that $X_\mu =\{x^\dag \}+\ker A+R((A^*A)^\mu )$. $\square$

Lemma A.17

(Interpolation inequality[42, p. 47, eq. 2.49]). For all $x \in X$ and $0\le \alpha < \beta$, we have

$$\begin{aligned} \Vert (A^*A)^\alpha x \Vert \le \Vert (A^*A)^\beta x \Vert ^{\frac{\alpha }{\beta }} \ \Vert x \Vert ^{1- \frac{\alpha }{\beta }}. \end{aligned}$$

Lemma A.18

(Powers of self-adjoint operators). Let S be a bounded selfadjoint positive linear operator on a Hilbert space. Then, for all $\alpha >0$, $\ker S = \ker S^\alpha$, and $\mathrm{cl\,}R(S^\alpha ) = \mathrm{cl\,}R(S)$.

Proof

Given any $0<\alpha <\beta$, we can write $S^\beta = S^{\beta - \alpha } S^\alpha$, from which we deduce that $\ker S^\alpha \subset \ker S^\beta$. This means that $(\ker S^\alpha )_{\alpha >0}$ is a nondecreasing family. To prove that this family is constant, it remains to verify that $\ker S^2 \subset \ker S$: If $x \in \ker S^2$, then $\Vert Sx \Vert ^2 = \langle Sx,Sx \rangle = \langle S^2 x,x \rangle = 0$, therefore $x \in \text{ Ker }~S$. Since $S^{2\alpha }=(S^\alpha )^2$, what we proved shows that for all $\alpha >0$, $\mathrm{{Ker}}~S^{2\alpha } \subset \mathrm{{Ker}}~S^\alpha$. But we have seen that this family of null spaces is nondecreasing with respect to $\alpha$, so we can deduce that $\mathrm{{Ker}}~S^\alpha = \mathrm{{Ker}}~S^\beta$ for all $\beta \in [\alpha , 2\alpha ]$. This being true for any $\alpha >0$, we deduce that this family of null spaces is constant. The conclusion follows from the fact that $\ker S^\perp = \mathrm{cl\,}R(S)$. $\square$

Proof of Proposition 5.7

Given any $x \in X$, observe that $x \in X_0$ is, by definition, equivalent to $Ax \in Y_{1/2}$. Since $R(A)= R(({AA^*})^{1/2})$, the latter is equivalent to $Ax \in y^\dagger + R(A)$. We can then easily deduce that $X_0 = X \Leftrightarrow X_0 \ne \emptyset$. Indeed, $X_0$ is nonempty if and only if $y^\dagger \in R(A)$. But if $y^\dagger \in R(A)$ then every $x \in X$ verifies $Ax \in y^\dagger + R(A)$, since the latter is equivalent to $Ax \in R(A)$. Proposition 5.1 yields $X_0 = X \Leftrightarrow X_0 \ne \emptyset \Leftrightarrow y^\dagger \in R(A) \Leftrightarrow \mathrm{argmin\,}f \ne \emptyset .$ For items i) and ii), the claim follows directly from the nonincreasingness of $\{X_\mu \}_{-1/2< \mu < + \infty }$. For item iii), let $\mu ,\delta >0$. Start by assuming that R(A) is closed. Observe that for $\nu = \mu + 1/2 >0$, $\mathrm{spec}((AA^*)^\nu ) = \mathrm{spec}(AA^*)^\nu$ [56, §32 Theorem 3]. As a consequence of Proposition 5.2, we deduce that $R (AA^*)^\nu$ is closed, and therefore $R((AA^*)^\nu )=R(A)$ (see Lemma A.18). Moreover, R(A) being closed implies that $y^\dagger \in R(A)$. So $Y_\nu = y^\dagger + R((AA^*)^\nu ) = R(A)$, from which we deduce that $X_\mu = X$. Assume now that $X_\mu = X$, and let us show that $\mathrm{{int}}~X_{\mu ,\delta } \ne \emptyset$. Note that $X_\mu =X$ implies that $\mathrm{{argmin}}~f \ne \emptyset$ according to item i). Proposition 5.5 implies that $\{x^\dagger \} + {{\,\mathrm{Ker}\,}}A + P \subset X_{\mu ,\delta }$ where $P:=\{(A^*A)^\mu (w) \ | \ w \in \mathrm{{Ker}}~A^\bot , \Vert w \Vert < \delta \}$. To prove the claim, it is enough to show that $\ker A + P$ is open. We start by noting that P is the image by $(A^*A)^\mu$ of $\ker A^\bot \cap \delta {\mathbb {B}}_X$, which is a relatively open set in $\mathrm{{Ker}}~A^\bot$. Since $R((A^*A)^\mu ) \subset \mathrm{{Ker}}~A^\bot$ (see Lemma A.18) and $X_{\mu }=X$, we deduce from Proposition 5.5 that $R((A^*A)^\mu ) = \mathrm{{Ker}}~A^\bot$. Since $\mathrm{{Ker}}~(A^*A)^\mu = \mathrm{{Ker}}~A$ (Lemma A.18 again), we see that the restriction of $(A^*A)^\mu$ to $\mathrm{{Ker}}~A^\bot$ induces a surjective linear operator $\mathrm{{Ker}}~A^\bot \longrightarrow \mathrm{{Ker}}~A^\bot$, where $\mathrm{{Ker}}~A^\bot$ is a Hilbert space endowed with the induced metric of X. Therefore, the Banach-Schauder (open mapping) theorem tells us that P is relatively open in $\mathrm{{Ker}}~A^\bot$: there exists a set U open in X such that $P=\ker A^\bot \cap U$. Concluding that $\mathrm{{Ker}}~A + P$ is open is a simple exercise that we detail now. Given any $x \in \mathrm{{Ker}}~A +P$, we can decompose it as $x = k + p$, where $k \in \mathrm{{Ker}}~A$, $p \in P$. Since $P \subset U$, there exists $\varepsilon >0$ such that ${\mathbb {B}}(p,\varepsilon )\subset U$. Let us verify that ${\mathbb {B}}(x,\varepsilon ) \subset \mathrm{{Ker}}~A +P$. Every $x' \in {\mathbb {B}}(x,\varepsilon )$ can be decomposed as $x'=k' +p'$, where $k' \in \mathrm{{Ker}}~A$, $p'\in \mathrm{{Ker}}~ A^\bot$. Then we see that $p-p' = x-x' +k-k'$, where $p-p' \in \mathrm{{Ker}}~A^\bot$ and $k-k' \in \mathrm{{Ker}}~A$, which means that $p-p' = \mathrm{proj}(x-x'; \mathrm{{Ker}}~A^\bot )$. We conclude that $\Vert p-p'\Vert \le \Vert x-x'\Vert < \varepsilon$, which means that $p' \in U$, and proves that $x' \in \mathrm{{Ker}}~A + P$. We turn now to the last implication of this Proposition, by supposing that $\mathrm{{int}}~X_{\mu ,\delta } \ne \emptyset$. It implies in particular that $X_\mu$ has nonempty interior, and that $\mathrm{{argmin}}~f\ne \emptyset$ (see item i)). With Proposition 5.5, we see that $\mathrm{{Ker}}~A + R((A^*A)^\mu )$ has nonempty interior. Because it is a linear subspace, this means that $\mathrm{{Ker}}~A + R((A^*A)^\mu ) = X$. Reasoning as above, we obtain that $R((A^*A)^\mu ) = \ker A^\bot$, which is closed. Combining Proposition 5.2 with the fact that $\mathrm{spec}^*(A^*A)= \mathrm{spec}^*(AA^*)$ (see Lemma A.14), we conclude that R(A) is closed. $\square$

1.5 A.5 Regularized inverse problems and proofs of Section 5.2

Proposition A.19

A matrix $S\in {\mathcal {S}}_+({\mathbb {R}}^N)$ is coercive on a closed cone $K \subset {\mathbb {R}}^N$ if and only if $K \cap \ker S = \{0\}$.

Proof

The direct implication is immediate from Definition 5.15. For the reverse implication, let K be a closed cone such that $K \cap \ker S = \{0\}$. Since S is linear, we know that $d \mapsto \langle Sd,d \rangle$ is convex and continuous. So, using the compactness of $K \cap {\mathbb {S}}$ we deduce that:

$$\begin{aligned} (\exists {\bar{d}} \in K \cap {\mathbb {S}})\quad \inf \limits _{d \in K \cap {\mathbb {S}}} \langle S d,d \rangle = \langle S {\bar{d}}, {\bar{d}} \rangle . \end{aligned}$$

(60)

Because ${\bar{d}} \in K$ and ${\bar{d}} \ne 0$, we deduce from our assumption that ${\bar{d}} \notin \text{ Ker }~S$. Therefore, $\gamma :=\langle S {\bar{d}}, {\bar{d}} \rangle > 0$, from which we deduce that S is $\gamma$-coercive on K. $\square$

Definition A.20

(Cone enlargement). Let $K \subset {\mathbb {R}}^N$ be a cone, and $\theta \in [0, \frac{\pi }{2}]$. We define the $\theta$-enlargement of K as

$$\begin{aligned} K_\theta := {\mathbb {R}} \left\{ x \in {\mathbb {S}} \ | \ (\exists y \in K \cap {\mathbb {S}} \ \arccos \left( {\vert \langle x,y \rangle \vert }\right) \le \theta \right\} . \end{aligned}$$

Lemma A.21

If K is a closed cone, then $K_\theta$ is a closed cone containing K for all $\theta \in [0, \frac{\pi }{2}]$.

Proof

By definition, $K_\theta$ is a cone containing K and

$$\begin{aligned} \varDelta _\theta :=\Big \{ x \in {\mathbb {S}} \ | \ (\exists y \in K \cap {\mathbb {S}}) \arccos \left( {\vert \langle x,y \rangle \vert }\right) \le \theta \Big \} \end{aligned}$$

is compact, due to the compactness of $K\cap {\mathbb {S}}$. Since $0\not \in \varDelta _\theta$, by compactness of $\varDelta _\theta$, we deduce that $K_\theta ={\mathbb {R}}\varDelta _\theta$ is a closed cone (see e.g. [48, Proposition A.1.1]). $\square$

Proposition A.22

Let $S\in {\mathcal {S}}_+({\mathbb {R}}^N)$ which is $\gamma$-coercive on a closed cone K. Then, for every $\gamma ' \in ]0,\gamma ]$, S is $\gamma '$-coercive on $K_\theta$, with $\theta :=\arcsin \left( \frac{\gamma - \gamma '}{\Vert S \Vert } \right) \in [0, \frac{\pi }{2}[$.

Proof

Let $\theta$ and $\gamma$ be as in the statement. Since S is $\gamma$-coercive on K, we see that $\gamma \le \Vert S \Vert$, which guarantees that $\theta \in [0, \frac{\pi }{2}[$. Now, the fact that $K_\theta$ is closed (Lemma A.21) implies that $K_\theta \cap {\mathbb {S}}$ is compact in X, so we can use the same arguments as in (60) to deduce that there exists ${\bar{d}} \in K_\theta \cap {\mathbb {S}}$ such that $\langle S{\bar{d}}, {\bar{d}} \rangle = \inf \limits _{d \in K_\theta \cap {\mathbb {S}}} \langle Sd,d \rangle$. Since ${\bar{d}} \in K_\theta$, there exists by definition of $K_\theta$ some ${\bar{v}} \in K \cap {\mathbb {S}}$ such that $\arccos (\vert \langle {\bar{d}}, {\bar{v}} \rangle \vert ) \le \theta$. We can use [62, Theorem 1] to write

$$\begin{aligned} \vert \langle S {\bar{v}}, {\bar{v}} \rangle - \langle S {\bar{d}}, {\bar{d}} \rangle \vert \le \Vert S \Vert \sin \arccos (\vert \langle {\bar{v}}, {\bar{d}} \rangle \vert )\le \Vert S \Vert \sin \theta . \end{aligned}$$

(61)

Since ${\bar{v}} \in K \cap {\mathbb {S}} \subset K_\theta \cap {\mathbb {S}}$, we have $\langle S {\bar{v}}, {\bar{v}} \rangle \ge \langle S {\bar{d}}, {\bar{d}} \rangle$. Moreover, $\arccos (\vert \langle {\bar{v}}, {\bar{d}} \rangle \vert ) \le \theta$, so (61), implies

$$\begin{aligned} \langle S {\bar{d}} , {\bar{d}} \rangle \ge \langle S {\bar{v}} , {\bar{v}} \rangle - \Vert S \Vert \sin \theta \ge \gamma - \Vert S \Vert \sin \theta = \gamma '. \end{aligned}$$

We deduce from the definition of ${\bar{d}}$ that S is $\gamma '$-coercive on $K_\theta$. $\square$

Proposition A.23

Let $C \subset {\mathbb {R}}^N$ be locally closed at ${\bar{x}} \in C$.

• i) For $\rho >0$, C is $\rho$-reached at ${\bar{x}}$ if and only if :

  $$\begin{aligned} (\forall x \in C)(\forall \eta \in N_C({\bar{x}})) \quad \langle \eta , x - {\bar{x}} \rangle \le \frac{\rho }{2} \Vert \eta \Vert \Vert x - {\bar{x}} \Vert ^2. \end{aligned}$$

  (62)

• ii) Every $C^2$ manifold is prox-regular.

Proof

Item i) : Definition 5.20 can be rewritten as

$$\begin{aligned} (\forall \eta \in N_C({\bar{x}}) \cap {\mathbb {S}}) (\forall x \in C) \quad x \notin {\mathbb {B}}\left( {\bar{x}} + \frac{1}{\rho } \eta , \frac{1}{\rho }\right) , \end{aligned}$$

where the condition $x \notin {\mathbb {B}}({\bar{x}} + \frac{1}{\rho } \eta , \frac{1}{\rho })$ is equivalent to, after developing the square:

$$\begin{aligned} \frac{1}{\rho ^2}\le & {} \Vert x - {\bar{x}} - \frac{1}{\rho } \eta \Vert ^2 = \Vert x - {\bar{x}} \Vert ^2 + \frac{1}{\rho ^2} \Vert \eta \Vert ^2 - \frac{2}{\rho } \langle x - {\bar{x}} , \eta \rangle \\= & {} \Vert x - {\bar{x}} \Vert ^2 + \frac{1}{\rho ^2} - \frac{2}{\rho } \langle x - {\bar{x}} , \eta \rangle . \end{aligned}$$

The conclusion follows after cancelling and reorganizing the terms. Item ii) : By definition, every $C^2$-manifold C is strongly amenable in the sense of [94, Def. 10.23.b)]. Then [94, Proposition 13.32] tells us that C is prox-regular in the sense of [94, Exercice 13.31] : for every ${\bar{x}} \in C$, there exists $\delta , \rho >0$ such that for every $x \in C \cap \overline{{\mathbb {B}}}({\bar{x}},\delta )$, and for every $\eta \in N_C({\bar{x}}) \cap \overline{{\mathbb {B}}}(0, \delta )$, we have

$$\begin{aligned} (\forall x' \in C \cap {{\mathbb {B}}}({\bar{x}}, \delta )) \quad \langle \eta , x'-x \rangle \le \frac{\rho }{2} \Vert x'-x \Vert . \end{aligned}$$

Taking any nonzero ${\hat{\eta }} \in N_{C \cap {{\mathbb {B}}}({\bar{x}}, \delta )}(x) = N_C(x)$, we can define $\eta := {\hat{\eta }} \frac{\delta }{\Vert {\hat{\eta }} \Vert } \in N_C(x) \cap {\mathbb {B}}(0,\delta )$ and see that

$$\begin{aligned} (\forall x' \in C \cap {{\mathbb {B}}}({\bar{x}}, \delta )) \quad \langle {\hat{\eta }}, x'-x \rangle \le \frac{\rho }{2 \delta } \Vert {\hat{\eta }} \Vert \Vert x'-x \Vert . \end{aligned}$$

This being true independently of the choice of ${\hat{\eta }}$, we deduce from item i) that $C\cap {\mathbb {B}}({\bar{x}},\delta )$ is $\frac{\rho }{\delta }$-reached at x. We can then conclude that C is prox-regular in the sense of Definition 5.20. $\square$

Here is a needed result estimating locally the coercivity of a matrix on a reached set via its coercivity on the tangent cone.

Proposition A.24

Let $C \subset {\mathbb {R}}^N$ be $\rho$- reached at ${\bar{x}} \in C$. Let $S \in {\mathcal {S}}_+({\mathbb {R}}^N)$ be $\gamma$-coercive on $T_C({\bar{x}})$. Then, for all $\gamma ' \in ]0, \gamma [$, there exists a cone $K \subset {\mathbb {R}}^N$ such that S is $\gamma '$-coercive on K, and $C \cap {\mathbb {B}}({\bar{x}},\delta ) \subset {\bar{x}} + K$, with $\delta = \frac{2(\gamma - \gamma ')}{\rho \Vert S \Vert }$.

Proof

Let $\gamma ' \in ]0, \gamma [$ be fixed, and define $\theta :=\arcsin ((\gamma - \gamma ')\Vert S \Vert ^{-1}) \in ]0, \frac{\pi }{2}[$. Let $K_\theta$ be the $\theta$-enlargement of $T_{C}({\bar{x}})$, then Proposition A.22 guarantees that S is $\gamma '$-coercive on $K_\theta$. It remains to prove that there exists $\delta \in ]0,+\infty [$ such that $C \cap {\mathbb {B}}({\bar{x}} , \delta ) \subset {\bar{x}} + K_\theta$. Let $x \in C$. Because C is $\rho$-reached at ${\bar{x}}$, we know that $T_C({\bar{x}})$ is a convex cone (use [44, Theorem 4.8.(12)] and the fact that C is locally closed at ${\bar{x}}$), so we can define $y:= \mathrm{proj}(x - {\bar{x}}, T_C({\bar{x}}))$, and $\eta := \mathrm{proj}(x - {\bar{x}}, N_C({\bar{x}}))$. Using Moreau’s Theorem [11, Theorem 6.30], we deduce that $\eta =x - {\bar{x}} -y$ with $\langle \eta , y \rangle = 0$. We define $\delta := \Vert x- {\bar{x}}\Vert$, and look for a condition on it so that $x \in {\bar{x}} + K_\theta$. For this to happen, it is enough to verify that

$$\begin{aligned} \langle x - {\bar{x}}, y \rangle \ge \cos (\theta ) \Vert x - {\bar{x}} \Vert \Vert y \Vert . \end{aligned}$$

(63)

Now, use Proposition A.23.i) together with the Cauchy-Schwarz inequality, and the polynomial inequality $X^2 - cX \ge -c^2/4$, to write

$$\begin{aligned} \Vert y \Vert ^2 = \Vert x - {\bar{x}} - \eta \Vert ^2 \ge \Vert x-{\bar{x}} \Vert ^2 + \Vert \eta \Vert ^2 - \rho \Vert \eta \Vert \Vert x - {\bar{x}} \Vert ^2 \ge \delta ^2(1 - \rho ^2 \delta ^2 /4). \end{aligned}$$

This inequality, together with the facts that $x - {\bar{x}} = y + \eta$ and $\langle y,\eta \rangle =0$ (so $\langle x - {\bar{x}},y \rangle = \Vert y \Vert ^2$), imply that

$$\begin{aligned} \langle x - {\bar{x}},y \rangle ^2 = \Vert y \Vert ^4 \ge \Vert y \Vert ^2 \delta ^2(1 - \rho ^2 \delta ^2 /4). \end{aligned}$$

This allows us to conclude that (63) holds as long as:

$$\begin{aligned} 1 - \rho ^2 \delta ^2 /4 \ge \cos (\theta )^2&\ \Leftrightarrow \ \rho ^2 \delta ^2 /4 \le 1 -\cos (\theta )^2 \\&\ \Leftrightarrow \ \rho \delta /2 \le \sin (\theta ) = \frac{\gamma - \gamma '}{\Vert S \Vert }. \end{aligned}$$

$\square$

Proof of Proposition 5.18

Let $0<\gamma ' < \gamma$, and set $S:= \mathrm{argmin\,}f$. Since h is of class $C^2$ around ${\bar{x}} \in S$, there exists some $\delta >0$ such that for all $u \in \delta {\mathbb {B}}$, $\Vert \nabla ^2 h({\bar{x}} + u) - \nabla ^2 h({\bar{x}}) \Vert \le \gamma - \gamma '.$ Notice that when $\nabla ^2 h$ is Lipschitz continuous, we can take $\delta =(\gamma - \gamma ')/L$. Let us show that f is 2-conditioned on $\varOmega := {\bar{x}} + (K \cap \delta {\mathbb {B}})$ with the constant $\gamma _{f,\varOmega }=\gamma '$. Take $x \in \varOmega \cap \mathop {\mathrm { dom}}g$ and use the optimality condition at ${\bar{x}} \in S$ and the convexity of g to obtain

$$\begin{aligned} f(x) - \inf f= & {} g(x) - g({\bar{x}}) + \langle \nabla h({\bar{x}}), x - {\bar{x}} \rangle + h(x) - h({\bar{x}}) - \langle \nabla h ({\bar{x}}),x - {\bar{x}}) \rangle \\\ge & {} h(x) - h({\bar{x}}) - \langle \nabla h ({\bar{x}}), x - {\bar{x}} \rangle . \end{aligned}$$

By Taylor’s theorem applied to h, we deduce from the inequality above that there exists $y \in [x,{\bar{x}}]$ such that:

$$\begin{aligned} f(x)- \inf f\ge & {} (1/2) \langle \nabla ^2 h({\bar{x}}) (x-{\bar{x}}), x - {\bar{x}} \rangle \\&+ (1/2)\langle [ \nabla ^2 h(y) - \nabla ^2 h({\bar{x}})] (x- {\bar{x}}), x - {\bar{x}} \rangle . \end{aligned}$$

On the one hand, since $x\in \varOmega$, we have that $x - {\bar{x}} \in K$. Thus, from the coercivity of $\nabla ^2 h({\bar{x}})$ we have

$$\begin{aligned} \langle \nabla ^2 h({\bar{x}}) (x-{\bar{x}}), x - {\bar{x}} \rangle \ge \gamma \Vert x -{\bar{x}} \Vert ^2. \end{aligned}$$

On the other hand, we use the Cauchy-Schwarz inequality together with the definition of $\delta$ and the fact that $\Vert y - {\bar{x}} \Vert \le \Vert x - {\bar{x}} \Vert < \delta$ to obtain

$$\begin{aligned} \langle [ \nabla ^2 h(y) - \nabla ^2 h({\bar{x}})] (x- {\bar{x}}), x - {\bar{x}} \rangle \ge - (\gamma - \gamma ') \Vert x - {\bar{x}} \Vert ^2. \end{aligned}$$

By combining the three previous inequalities, we deduce that

$$\begin{aligned} f(x) - \inf f \ge (\gamma '/2) \Vert x - {\bar{x}} \Vert ^2. \end{aligned}$$

(64)

This implies that $\varOmega \cap \mathrm{argmin\,}f=\{\bar{x}\}$, and the statement follows from $\Vert x - {\bar{x}} \Vert \ge \mathrm{dist\,}(x;S)$. $\square$