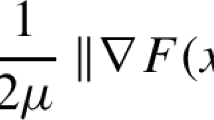Skip to main content
SpringerLink
Log in

Convergence rates of the Heavy-Ball method under the Łojasiewicz property

  • Full Length Paper
  • Series A
  • Published:
Mathematical Programming Submit manuscript

Abstract

In this paper, a joint study of the behavior of solutions of the Heavy Ball ODE and Heavy Ball type algorithms is given. Since the pioneering work of Polyak (USSR Comput Math Math Phys 4(5):1–17, 1964), it is well known that such a scheme is very efficient for \(C^2\) strongly convex functions with Lipschitz gradient. But much less is known when only growth conditions are considered. Depending on the geometry of the function to minimize, convergence rates for convex functions, with some additional regularity such as quasi-strong convexity, or strong convexity, were recently obtained in Aujol et al. (Convergence rates of the Heavy-Ball method for quasi-strongly convex optimization, 2020). Convergence results with much weaker assumptions are given in the present paper: namely, linear convergence rates when assuming a growth condition (which amounts to a Łojasiewicz property in the convex case). This analysis is firstly performed in continuous time for the ODE, and then transposed for discrete optimization schemes. In particular, a variant of the Heavy Ball algorithm is proposed, which converges geometrically whatever the parameters choice, and which has the best state of the art convergence rate for first order methods to minimize composite non smooth convex functions satisfying a Łojasiewicz property.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Alvarez, F.: On the minimizing property of a second order dissipative system in Hilbert spaces. SIAM J. Control Optim. 38(4), 1102–1119 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  2. Apidopoulos, V., Aujol, J.F., Dossal, C.: The differential inclusion modeling FISTA algorithm and optimality of convergence rate in the case \(b\leqslant 3\). SIAM J. Optim. 28(1), 551–574 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  3. Apidopoulos, V., Aujol, J.F., Dossal, C.: The differential inclusion modeling FISTA algorithm and optimality of convergence rate in the case \(b\le 3\). SIAM J. Optim. 28, 551–574 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  4. Attouch, H., Bolte, J.: On the convergence of the proximal algorithm for nonsmooth functions involving analytic features. Math. Program. 116(1), 5–16 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  5. Attouch, H., Cabot, A.: Asymptotic stabilization of inertial gradient dynamics with time-dependent viscosity. J. Differ. Equ. 263(9), 5412–5458 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  6. Attouch, H., Cabot, A.: Convergence rates of inertial forward-backward algorithms. SIAM J. Optim. 28(1), 849–874 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  7. Attouch, H., Cabot, A., Redont, P.: The dynamics of elastic shocks via epigraphical regularization of a differential inclusion. Barrier and penalty approximations. Adv. Math. Sci. Appl. 12(1), 273–306 (2002)

    MathSciNet  MATH  Google Scholar 

  8. Attouch, H., Chbani, Z., Peypouquet, J., Redont, P.: Fast convergence of inertial dynamics and algorithms with asymptotic vanishing viscosity. Math. Program. 168(1–2), 123–175 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  9. Aujol, J.F.: Some first-order algorithms for total variation based image restoration. J. Math. Imaging Vis. 34(3), 307–327 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  10. Aujol, J.F., Dossal, C.: Optimal rate of convergence of an ODE associated to the fast gradient descent schemes for \(b>0\). Hal Preprint hal-01547251 (2017)

  11. Aujol, J.F., Dossal, C., Rondepierre, A.: Optimal convergence rates for Nesterov acceleration. SIAM J. Optim. 29(4), 3131–3153 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  12. Aujol, J.F., Dossal, C., Rondepierre, A.: Convergence rates of the Heavy-Ball method for quasi-strongly convex optimization (2020). https://hal.archives-ouvertes.fr/hal-02545245. Preprint

  13. Balti, M., May, R.: Asymptotic for the perturbed heavy ball system with vanishing damping term. Evolut. Equ. Control Theory 6(2), 177–186 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  14. Beck, A., Teboulle, M.: A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Image Sci. 2(1), 183–202 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  15. Bégout, P., Bolte, J., Jendoubi, M.A.: On damped second order gradients systems. J. Differ. Equ. 259(9), 3115–3143 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  16. Bolte, J., Daniilidis, A., Lewis, A.: The Łojasiewicz inequality for nonsmooth subanalytic functions with applications to subgradient dynamical systems. SIAM J. Optim. 17(4), 1205–1223 (2007)

    Article  MATH  Google Scholar 

  17. Bolte, J., Daniilidis, A., Lewis, A., Shiota, M.: Clarke subgradients of stratifiable functions. SIAM J. Optim. 18(2), 556–572 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  18. Bolte, J., Nguyen, T., Peypouquet, J., Suter, B.: From error bounds to the complexity of first-order descent methods for convex functions. Math. Program. 165(2), 471–507 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  19. Brezis, H.: Opérateurs maximaux monotones et semi-groupes de contractions dans les espaces de Hilbert, vol. 5. Elsevier, New York (1973)

    MATH  Google Scholar 

  20. Cabot, A., Engler, H., Gadat, S.: On the long time behavior of second order differential equations with asymptotically small dissipation. Trans. Am. Math. Soc. 361(11), 5983–6017 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  21. Cabot, A., Paoli, L.: Asymptotics for some vibro-impact problems with a linear dissipation term. Journal de Mathématiques Pures et Appliquées 87(3), 291–323 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  22. Garrigos, G., Rosasco, L., Villa, S.: Convergence of the forward-backward algorithm: Beyond the worst case with the help of geometry. arXiv preprint arXiv:1703.09477 (2017)

  23. Ghadimi, E., Feyzmahdavian, H., Johansson, M.: Global convergence of the heavy-ball method for convex optimization. In: 2015 European Control Conference (ECC), pp. 310–315. IEEE (2015)

  24. Haraux, A., Jendoubi, M.: On a second order dissipative ODE in Hilbert space with an integrable source term. Acta Mathematica Scientia 32(1), 155–163 (2012), Mathematics Dedicated to professor Constantine M. Dafermos on the occasion of his 70th birthday

  25. Hiriart-Urruty, J.B., Lemaréchal, C.: Fundamentals of Convex Analysis. Springer, Berlin (2012)

    MATH  Google Scholar 

  26. Jendoubi, M.A., May, R.: Asymptotics for a second-order differential equation with nonautonomous damping and an integrable source term. Appl. Anal. 94(2), 435–443 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  27. Liang, J., Fadili, M., Peyré, G.: Activity identification and local linear convergence of forward–backward-type methods. SIAM J. Optim. 27(1) (2017)

  28. Łojasiewicz, S.: Une propriété topologique des sous-ensembles analytiques réels. In: Les Équations aux Dérivées Partielles (Paris, 1962), pp. 87–89. Éditions du Centre National de la Recherche Scientifique, Paris (1963)

  29. Łojasiewicz, S.: Sur la géométrie semi- et sous-analytique. Annales de l’Institut Fourier. Université de Grenoble 43(5), 1575–1595 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  30. Necoara, I., Nesterov, Y., Glineur, F.: Linear convergence of first order methods for non-strongly convex optimization. Math. Program. 175(1–2), 69–107 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  31. Nesterov, Y.: A method of solving a convex programming problem with convergence rate \(o(\frac{1}{k^2})\). Soviet Math. Doklady 27(2), 372–376 (1983)

    Google Scholar 

  32. Nesterov, Y.: Gradient methods for minimizing composite objective function. core discussion papers 2007076, université catholique de louvain. Center for Operations Research and Econometrics (CORE) 1, 4–4 (2007)

  33. Nesterov, Y.: Gradient methods for minimizing composite functions. Math. Program. 140(1), 125–161 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  34. Nesterov, Y.: Introductory Lectures on Convex Optimization: A Basic Course, vol. 87. Springer, Berlin (2013)

    MATH  Google Scholar 

  35. O’Donoghue, B., Candes, E.: Adaptive restart for accelerated gradient schemes. Found. Comput. Math. 15(3), 715–732 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  36. Paoli, L.: An existence result for vibrations with unilateral constraints: case of a nonsmooth set of constraints. Math. Models Methods Appl. Sci. 10(06), 815–831 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  37. Polyak, B.: Some methods of speeding up the convergence of iteration methods. USSR Comput. Math. Math. Phys. 4(5), 1–17 (1964)

    Article  Google Scholar 

  38. Polyak, B., Shcherbakov, P.: Lyapunov functions: an optimization theory perspective. IFAC-PapersOnLine 50(1), 7456–7461 (2017)

    Article  Google Scholar 

  39. Sebbouh, O., Dossal, C., Rondepierre, A.: Convergence rates of damped inertial dynamics under geometric conditions and perturbations. SIAM J. Optim. 30(3), 1850–1877 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  40. Siegel, J.: Accelerated first-order methods: Differential equations and Lyapunov functions. arXiv preprint arXiv:1903.05671 (2019)

  41. Su, W., Boyd, S., Candes, E.J.: A differential equation for modeling Nesterov’s accelerated gradient method: theory and insights. J. Mach. Learn. Res. 17(153), 1–43 (2016)

  42. Tibshirani, R.: The lasso problem and uniqueness. Electron. J. Stat. 7, 1456–1490 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  43. Van Scoy, B., Freeman, R., Lynch, K.: The fastest known globally convergent first-order method for minimizing strongly convex functions. IEEE Control Syst. Lett. 2(1), 49–54 (2017)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

J.-F. Aujol acknowledges the support of the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No777826. The authors acknowledge the support of the French Agence Nationale de la Recherche (ANR) under reference ANR-PRC-CE23 MaSDOL and the support of FMJH Program PGMO 2019-0024 and from the support to this program from EDF-Thales-Orange.

Author information

Authors and Affiliations

  1. Univ. Bordeaux, CNRS, Bordeaux INP, IMB, UMR 5251, 33400, Talence, France

    J.-F. Aujol

  2. IMT, Univ. Toulouse, INSA Toulouse, Toulouse, France

    Ch. Dossal & A. Rondepierre

  3. LAAS, Univ. Toulouse, CNRS, Toulouse, France

    A. Rondepierre

Authors
  1. J.-F. Aujol
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ch. Dossal
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. Rondepierre
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Rondepierre.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Aujol, JF., Dossal, C. & Rondepierre, A. Convergence rates of the Heavy-Ball method under the Łojasiewicz property. Math. Program. 198, 195–254 (2023). https://doi.org/10.1007/s10107-022-01770-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10107-022-01770-2

Keywords

Mathematics Subject Classification

Search

Navigation