A combinatorial cut-and-lift procedure with an application to 0–1 second-order conic programming

Abstract

Cut generation and lifting are key components for the performance of state-of-the-art mathematical programming solvers. This work proposes a new general cut-and-lift procedure that exploits the combinatorial structure of 0–1 problems via a binary decision diagram (BDD) encoding of their constraints. We present a general framework that can be applied to a wide range of binary optimization problems and show its applicability for second-order conic inequalities. We identify conditions for which our lifted inequalities are facet-defining and derive a new BDD-based cut generation linear program. Such a model serves as a basis for a max-flow combinatorial algorithm over the BDD that can be applied to derive valid cuts more efficiently. Our numerical results show encouraging performance when incorporated into a state-of-the-art mathematical programming solver, significantly reducing the root node gap, increasing the number of problems solved, and reducing the run-time by a factor of three on average.

Appendices

Relaxed BDD construction procedure for second-order cones

We now present the relaxed BDD construction procedure for SOC inequalities based on the RSOC model. The construction algorithm is analogous for the case of SOC knapsack constraints and the RSOC-K model.

The state information at the core of our BDD construction algorithm is based on recursive model RSOC. This information is stored in each node of the BDD and used to identify infeasible assignments and decide how to widen the BDD (i.e., split nodes). Our state information keeps track of each of the $l+1$ linear components in inequality (14), i.e., $\varvec{a}^\top \varvec{x}$ and $\varvec{d}_k^\top \varvec{x}- h_k$ for each $k \in \{1,\ldots ,l\}$. Thus, each node $u \in {\mathcal {N}}_i$ has two $l+1$ dimensional vectors for top-down information, $Q^{\downarrow \mathsf {min}}(u)$ and $Q^{\downarrow \mathsf {max}}(u)$, that approximate the linear components considering the partial assignments from ${\mathbf {r}}$ to u. We set the top-down state information at the root node as $Q^{\downarrow \mathsf {min}}_0({\mathbf {r}}):= Q^{\downarrow \mathsf {max}}_0({\mathbf {r}}):= 0$ and $Q^{\downarrow \mathsf {min}}_k({\mathbf {r}}):= Q^{\downarrow \mathsf {max}}_k({\mathbf {r}}):= -h_k$ for all $k \in \{1,\ldots ,l\}$. Then, for any $u \in {\mathcal {N}}_i$, $i \in \{2,\ldots ,n\}$, and $k \in \{1,\ldots , l\}$ we update the states as:

$$\begin{aligned} Q^{\downarrow \mathsf {min}}_0(u):=&\min _{a\in {\mathcal {A}}^{\mathsf {in} }(u)}\{ Q^{\downarrow \mathsf {min}}_0(s(a)) + a_{i-1}\cdot v_a \} , \\ Q^{\downarrow \mathsf {max}}_0(u):=&\max _{a\in {\mathcal {A}}^{\mathsf {in} }(u)}\{ Q^{\downarrow \mathsf {max}}_0(s(a)) + a_{i-1}\cdot v_a \}, \\ Q^{\downarrow \mathsf {min}}_k(u):=&\min _{a\in {\mathcal {A}}^{\mathsf {in} }(u)}\{ Q^{\downarrow \mathsf {min}}_k(s(a)) + d_{ki-1}\cdot v_a \}, \\ Q^{\downarrow \mathsf {max}}_k(u):=&\max _{a\in {\mathcal {A}}^{\mathsf {in} }(u)}\{ Q^{\downarrow \mathsf {max}}_k(s(a)) + d_{ki-1}\cdot v_a \}. \end{aligned}$$

Similarly, we use two $l+1$ dimensional vectors, $Q^{\uparrow \mathsf {min}} (u)$ and $Q^{\uparrow \mathsf {max}}(u)$, for our bottom-up state information for each node $u \in {\mathcal {N}}$. The information is initialized at the terminal node as $Q^{\uparrow \mathsf {min}} _0({\mathbf {t}} ):= Q^{\uparrow \mathsf {max}}_0({\mathbf {t}} ):= 0$ and $Q^{\uparrow \mathsf {min}} _k({\mathbf {t}} ):= Q^{\uparrow \mathsf {max}}_k({\mathbf {t}} ):= 0$ for all $k \in \{1,\ldots ,l\}$. Then, for any $u \in {\mathcal {N}}_i$, $i \in \{1,\ldots ,n-1\}$, and $k \in \{1,\ldots , l\}$, we have:

$$\begin{aligned} Q^{\uparrow \mathsf {min}} _0(u):=&\min _{a\in {\mathcal {A}}^{\mathsf {out}}(u)}\{ Q^{\uparrow \mathsf {min}} _0(t(a)) + a_k\cdot v_a \} , \\ Q^{\uparrow \mathsf {max}}_0(u):=&\max _{a\in {\mathcal {A}}^{\mathsf {out}}(u)}\{ Q^{\uparrow \mathsf {max}}_0(t(a)) + a_k\cdot v_a \}, \\ Q^{\uparrow \mathsf {min}} _k(u):=&\min _{a\in {\mathcal {A}}^{\mathsf {out}}(u)}\{ Q^{\uparrow \mathsf {min}} _k(t(a)) + d_{ki}\cdot v_a \}, \\ Q^{\uparrow \mathsf {max}}_k(u):=&\max _{a\in {\mathcal {A}}^{\mathsf {out}}(u)}\{ Q^{\uparrow \mathsf {max}}_k(t(a)) + d_{ki}\cdot v_a \}. \end{aligned}$$

For each node $u \in {\mathcal {N}}$, the state information under and over approximates the value of the linear components of (14) for all ${\mathbf {r}}-u$ paths (i.e., top-down information) and for all $u-{\mathbf {t}}$ paths (i.e., bottom-up information). We use the state information to identify if an arc corresponds to an infeasible assignment, i.e., all paths traversing it correspond to infeasible solutions of (14). In particular, we can remove an arc $a=(u,u')\in {\mathcal {A}}_i$ if the following condition holds:

$$\begin{aligned} Q^{\downarrow \mathsf {min}}_0(u) + a_i\cdot v_a + Q^{\uparrow \mathsf {min}} _0(u') + \varOmega \sqrt{ \sum _{k=1}^l g_k(a) } > b, \end{aligned}$$

(18)

where $g_k(a)$ for $k \in \{1,\ldots , l\}$ is given by:

$$\begin{aligned} g_k(a):= {\left\{ \begin{array}{ll} (Q^{\downarrow \mathsf {min}}_k(u) + d_{ki}\cdot v_a + Q^{\uparrow \mathsf {min}} _k(u')) ^2, &{} \!\!\text{ if } Q^{\downarrow \mathsf {min}}_k(u) + d_{ki}\cdot v_a + Q^{\uparrow \mathsf {min}} _k(u') >0, \\ (Q^{\downarrow \mathsf {max}}_k(u) + d_{ki}\cdot v_a + Q^{\uparrow \mathsf {max}}_k(u'))^2, &{} \!\!\text{ if } Q^{\downarrow \mathsf {max}}_k(u) + d_{ki}\cdot v_a + Q^{\uparrow \mathsf {max}}_k(u') <0, \\ 0, &{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$

Notice that $g_k(a)$ under approximates $(\varvec{d}_k^\top \varvec{x}-d_k)^2$ for all paths traversing arc $a\in {\mathcal {A}}$, and so the left-hand side (LHS) of (18) under approximates the LHS of (14) for all paths traversing arc $a\in {\mathcal {A}}_i$. Then, all paths traversing an arc a that satisfy (18) correspond to invalid assignments for (14).

If $Q^{\downarrow \mathsf {max}}_k(u) = Q^{\downarrow \mathsf {min}}_k(u)$ for all nodes $u \in {\mathcal {N}}$, we recover the exact BDD based on the recursive model RSOC and condition (18) is equivalent to (15d). Thus, our splitting procedure tries to achieve this property by selecting nodes u with $Q^{\downarrow \mathsf {max}}_k(u) - Q^{\downarrow \mathsf {min}}_k(u) \ge \delta$ ($\delta > 0$) for some $k \in \{0,\ldots ,l\}$ and then split it into two new nodes, $u'$ and $u''$, so $Q^{\downarrow \mathsf {max}}_k(u') - Q^{\downarrow \mathsf {min}}_k(u')<\delta$ and $Q^{\downarrow \mathsf {max}}_k(u'') - Q^{\downarrow \mathsf {min}}_k(u'')<\delta$. The splitting procedure then duplicates the outgoing arcs of u and assigns them to both $u'$ and $u''$ to keep the same set of paths in ${\mathcal {B}}$.

Our construction procedure creates a relaxed BDD ${\mathcal {B}}=({\mathcal {N}},{\mathcal {A}})$ by limiting its width $w({\mathcal {B}})$ by a positive value ${\mathcal {W}}$, where $w({\mathcal {B}}):=\max _{i\in I}\{|{\mathcal {N}}_i|\}$ represents the maximum number of nodes in each layer. The complete BDD construction procedure is shown in Algorithm 2. The algorithm starts creating a width-one BDD for the SOC constraint (line 2) and then updates the bottom-up information for all the nodes (line 4). During the top-down pass through the BDD (lines 5–9), the procedure updates the top-down information of layer ${\mathcal {N}}_i$, splits the nodes until we reach the width limit ${\mathcal {W}}$, and filters the emanating arcs of ${\mathcal {N}}_i$. The algorithm then checks if the BDD has been updated (line 3) and repeats the bottom-up and top-down iterations until the BDD cannot be updated any more. Lastly, we reduce the BDD (line 10) following the standard procedure in the literature [20].

The resulting BDD starts with all possible variable assignments (i.e., a width-one BDD) and removes arcs using condition (18). Thus, the procedure is guaranteed to construct a relaxed BDD for a SOC constraint. Notice that for a big enough ${\mathcal {W}}$, the procedure will return an exact BDD.

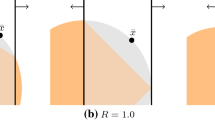
Example 5

Consider the following binary set defined by an SOC inequality $X= \{\varvec{x}\in \{0,1\}^3: 3x_1+x_2+x_3 + \sqrt{ (x_1+x_2+2x_3)^2 + (x_1+3x_2-x_3+3)^2 } \le 8 \}$. Figure 4 depicts some of the steps to construct an exact BDD for X. The left most diagram corresponds to a width-one BDD for this problem. The top-down state information in the root node is $( (Q^{\downarrow \mathsf {min}}_0({\mathbf {r}}), Q^{\downarrow \mathsf {max}}_0({\mathbf {r}})),\;(Q^{\downarrow \mathsf {min}}_1({\mathbf {r}}), Q^{\downarrow \mathsf {max}}_1({\mathbf {r}})),$ $(Q^{\downarrow \mathsf {min}}_2({\mathbf {r}}), Q^{\downarrow \mathsf {max}}_2({\mathbf {r}})) )= ( (0,0),\; (0,0),\; (3,3) )$, while for node $u_1$ is $( (0,3), \; (0,1),\; (3,4))$.

The middle BDD illustrates the resulting BDD after splitting node $u_1$. The resulting nodes, $u_1'$ and $u_1''$, have top-down state information $( (0,0),\; (0,0),\; (3,3) )$ and $( (3,3),\; (1,1),$ (4, 4) ), respectively. In addition, the gray arc from $u_1''$ to $u_2$ corresponds to an invalid assignment: the bottom-up information of $u_2$ is $( (0,1),\; (0,2),\; (-1,0) )$, thus, (18) evaluates to $10.3 > 8$.

Fig. 4

BDD construction procedure for set X defined in Example 5. The figure depicts a width-one BDD (left), a BDD after the splitting and filtering procedure over ${\mathcal {N}}_2$ (middle), and the resulting exact reduced BDD (right)

Experiments comparing different BDD widths

Table 4 presents the average performance for $\texttt {CPLEX}$ and our four alternatives (i.e., $\texttt {B-Flow}$, $\texttt {B-Flow+L}$, $\texttt {B-Gen}$, and $\texttt {B-Gen+L}$) with three different maximum width values, ${\mathcal {W}}\in \{2000,3000,4000\}$, over the SOC-CC instances. The table shows the number of instances solved, average root gap, and average final gap for all techniques. Our four alternatives with ${\mathcal {W}}\in \{2000,3000,4000\}$ each outperform $\texttt {CPLEX}$. ${\mathcal {W}}=4000$ achieves the best overall performance across the four combinatorial cut-and-lift alternatives. Similarly, ${\mathcal {W}}=4000$ achieves the best or comparable performance across the five BDD approaches over the SOC-K instances (right).

Table 4 Average performance of all techniques for different BDD widths for SOC-CC

Similarly, Table 5 presents the average performance over the SOC-K instances for $\texttt {CPLEX}$, our four alternatives (i.e., $\texttt {B-Flow}$, $\texttt {B-Flow+L}$, $\texttt {B-Gen}$, and $\texttt {B-Gen+L}$) with three different maximum width values, ${\mathcal {W}}\in \{2000,3000,4000\}$. Overall, ${\mathcal {W}}=4000$ achieves the best or comparable performance across the five BDD approaches. Bold numbers in Tables 4 and 5 correspond to the largest values in column “#Solve” and the smallest values in the other columns.

Table 5 Average performance of all techniques for different BDD widths for SOC-K

We note that these three BDD widths achieve competitive results with respect to $\texttt {CPLEX}$ in our dataset. However, problems with more variables (i.e., $n > 125$) would probably required a larger width to create a tight BDD relaxation and, thus, strong cuts.

Average performance comparison for Knapsack chance constraints

We now present additional results for the SOC-K dataset. As in Figs. 3, 5 illustrate the performance of each algorithm for the SOC-K dataset. We see a clear dominance of $\texttt {B-Gen+L}$, $\texttt {B-Target}$, and $\texttt {B-Ta+Fl+L}$ and also the positive impact of our combinatorial lifting in instances solved and gap reduction.

Fig. 5

Profile plot comparing the accumulated number of instances solved over time (left), and the accumulated number of instances over a final gap range (right) for SOC-K dataset

The following tables show average results for each parameter configuration over the SOC-CC benchmark. We present results for our four variants (i.e., $\texttt {B-Flow}$, $\texttt {B-Flow+L}$, $\texttt {B-Gen}$, and $\texttt {B-Gen+L}$), cover cut variants (i.e., $\texttt {Cover}$, $\texttt {CoverLift}$, and $\texttt {Cover+L}$), $\texttt {CPLEX}$, and best performing BDD-based cuts (i.e., $\texttt {B-Target}$ and $\texttt {B-Ta+Fl+L}$). All techniques add cuts only at the root node of the tree search. Tables 6, 7, and 8 show the number of instances solved, average root gap, and average final gap for each n, m, and $\varOmega$ combination with ${\mathcal {W}}=4000$, respectively. Similarly, Tables 9 and 10 show the average number of nodes in the branch-and-bound search and the average run time for the instances that all techniques solved to optimality. Bold numbers in Tables 6, 7, 8, 9, and 10 correspond to the largest values in column “#Solve” and the smallest values in the other columns.

Table 6 Instances solved to optimality comparison across all techniques for SOC-K benchmark

Table 7 Root Gap comparison across all techniques for SOC-K benchmark

Table 8 Final Gap comparison across all techniques for SOC-K benchmark

Table 9 Nodes explored comparison across all techniques for SOC-K benchmark

Table 10 Solving time comparison across all techniques for SOC-K benchmark

Average performance comparison for general chance constraints

We now present additional results for the SOC-CC dataset. Figure 6 shows two plots comparing the root gap of $\texttt {B-Gen+L}$ and $\texttt {CPLEX}$ for the SOC-CC instances and different values of $\varOmega$ and t. In each plot, an (x, y) point represents the root gap for an instance given by the x-axis and the y-axis technique, respectively. Overall, we can see that $\texttt {B-Gen+L}$ achieves a smaller or equal root gap to $\texttt {CPLEX}$, however, the difference is considerably larger when $\varOmega \ge 3$ and $t=0.1$.

The problems become more challenging with a larger $\varOmega$ (i.e., a predominant quadratic term) due to a weak SOC relaxation and linearization. Thus, our procedure can potentially generate stronger cuts than $\texttt {CPLEX}$. In fact, the left plot in Fig. 6 shows all instances with $\varOmega =1$ close to the diagonal, while problems with $\varOmega \in \{3,5\}$ have larger gap reductions. Lastly, the right plot of Fig. 6 shows that $\texttt {B-Gen+L}$ has significantly smaller gaps than $\texttt {CPLEX}$ over instances with a small t (i.e., small solution sets). Our relaxed BDDs are close to exact BDDs in these cases, thus, making our cuts more effective.

Fig. 6

Root node gap comparison with $\texttt {CPLEX}$ for the SOC-CC instances. The plot on the left considers different values of $\varOmega$, and the plot on the right different values of t

Table 11 Instances solved to Optimality comparison across all techniques for SOC-CC benchmark

Table 12 Root Gap comparison across all techniques for SOC-CC benchmark

Table 13 Final Gap comparison across all techniques for SOC-CC benchmark

Table 14 Nodes explored comparison across all techniques for SOC-CC benchmark

Table 15 Solving time comparison across all techniques for SOC-CC benchmark

The following tables show average results for each parameter configuration over the SOC-CC benchmark. We present results for our four variants (i.e., $\texttt {B-Flow}$, $\texttt {B-Flow+L}$, $\texttt {B-Gen}$, and $\texttt {B-Gen+L}$), $\texttt {CPLEX}$, and best performing BDD-based cuts (i.e., $\texttt {B-Target}$ and $\texttt {B-Ta+Fl+L}$). All techniques add cuts only at the root node of the tree search. Tables 11, 12, and 13 show the number of instances solved, average root gap, and average final gap for each n, m, $\varOmega$, and t combination, with ${\mathcal {W}}=4000$. Similarly, Tables 14 and 15 show the average number of nodes in the branch-and-bound search and the average run time for the instances that all techniques solved to optimality. Bold numbers in Tables 11, 12, 13, 14, and 15 correspond to the largest values in column “#Solve” and the smallest values in the other columns.

We note that in most instances the BDD cut algorithms have better performance than $\texttt {CPLEX}$. However, $\texttt {CPLEX}$ is competitive when $t=0.3$ and $\varOmega = 1$, as expected from the behavior observed in Fig. 6. We also note that $\texttt {CPLEX}$ has similar performance to the BDD techniques when $n=125$, which suggest that a tighter BDD relaxation (i.e., bigger BDD width) might be needed for larger problem instances.