Abstract
For two integers \(k>0\) and \(\ell \), a graph \(G=(V,E)\) is called \((k,\ell )\)-tight if \(|E|=k|V|-\ell \) and \(i_G(X)\le k|X|-\ell \) for each \(X\subseteq V\) for which \(i_G(X)\ge 1\), where \(i_G(X)\) denotes the number of induced edges by X. G is called \((k,\ell )\)-redundant if \(G-e\) has a spanning \((k,\ell )\)-tight subgraph for all \(e\in E\). We consider the following augmentation problem. Given a graph \(G=(V,E)\) that has a \((k,\ell )\)-tight spanning subgraph, find a graph \(H=(V,F)\) with the minimum number of edges, such that \(G\cup H\) is \((k,\ell )\)-redundant. We give a polynomial algorithm and a min-max theorem for this augmentation problem when the input is \((k,\ell )\)-tight. For general inputs, we give a polynomial algorithm when \(k\ge \ell \) and show the NP-hardness of the problem when \(k<\ell \). Since \((k,\ell )\)-tight graphs play an important role in rigidity theory, these algorithms can be used to make several types of rigid frameworks redundantly rigid by adding a smallest set of new bars.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let k be a positive integer and \(\ell \) be an integer such that \(\ell <2k\). A (multi)graph \(G=(V,E)\) is called \({\varvec{(k,\ell )}}\)-sparse if \(i_G(X)\le k|X|-\ell \) for all \(X\subseteq V\) for which \(i_G(X)>0\), where \({\varvec{i_G(X)}}\) denotes the number of edges of G induced by \(X\subseteq V\). A \((k,\ell )\)-sparse graph is called \({\varvec{(k,\ell )}}\)-tight if \(|E|=k|V|-\ell \). A graph G is called \({\varvec{{(k,\ell )}}}\)-rigid if G has a \((k,\ell )\)-tight spanning subgraph. We call an edge e of G a \({\varvec{(k,\ell )}}\)-redundant edge if \(G-e\) is \({(k,\ell )}\)-rigid. A graph G is a \({\varvec{(k,\ell )}}\)-redundant graph if each edge of G is \((k,\ell )\)-redundant. We consider the following problem that we call the general (augmentation) problem.
Problem
Let k and \(\ell \) be integers with \(k> 0\) and \(\ell <2k\) and let \(G=(V,E)\) be a \({(k,\ell )}\)-rigid graph. Find a graph \(H=(V,F)\) on the same vertex set with minimum number of edges, such that \(G\cup H=(V,E\cup F)\) is \((k,\ell )\)-redundant.
We call the special case of this problem, where the input graph G is \((k,\ell )\)-tight, the reduced (augmentation) problem. In this paper, we give a min-max theorem and an \(O(|V|^2)\) time algorithm for the reduced problem for each pair of k and \(\ell \). We also show how this algorithm can be extended to solve the general problem in the same running time when \(\ell \le k\). In contrast, we show that the general problem is NP-hard whenever \(\ell >k\).
Sparsity properties are important in rigidity theory as they can be used in the characterization of many rigidity classes. For example, the generically rigid graphs in \(\mathbb {R}^2\) are exactly the (2, 3)-rigid graphs by the fundamental theorems of Pollaczek-Geiringer [24] and Laman [18]. The ‘body-bar graph’ induced by a given graph G is generically rigid in \(\mathbb {R}^d\) if and only if G is \(\left( {{d+1}\atopwithdelims (){2}},{{d+1}\atopwithdelims (){2}}\right) \)-rigid by Tay’s theorem [26]. Note that G is (k, k)-rigid if and only if G contains k edge-disjoint spanning trees by the fundamental result of Nash-Williams [22].
Besides the effect of redundancy, redundant rigidity is an important concept in rigidity theory since variants of Hendrickson’s result [9] show that redundant rigidity is often a necessary condition for ‘global rigidity’ which plays a crucial role in many applications [1, 28, 29]. Furthermore, in some cases, for example for ‘body-bar graphs’ (see [3]), redundant rigidity is also a sufficient condition for global rigidity. It is thus natural to ask how many new edges are needed to make a rigid graph redundantly rigid.
There are special pairs of k and \(\ell \) for which these problems were already investigated. The general problem for (1, 1)-rigid graphs is a special case of the well-studied 2-edge-connectivity augmentation problem solved by Eswaran and Tarjan [4]. The general problem for \(k=\ell \) was solved by Frank and T. Király [7] who gave a polynomial algorithm to augment an arbitrary graph to an h-times (k, k)-redundant graph using polyhedral techniques (where h-times (k, k)-redundant means that it remains (k, k)-rigid after deleting any set of its edges of cardinality h). The algorithm, that will be presented here, is a more efficient solution for this problem, however, it does not deal with the case of \(h\ge 2\) and also the (k, k)-rigidity of the input is needed. García and Tejel [8] showed that the general problem is NP-hard for (2, 3)-rigid graphs but can be solved in polynomial time for (2, 3)-tight graphs. We use similar techniques to [8], however, our method is based on a new min-max theorem for the reduced problem, as follows.
For a \((k,\ell )\)-tight graph \(G=(V,E)\), we call a set of vertices \(\emptyset \ne C \subsetneq V\) \({\varvec{{(k,\ell )}}}\)-co-tight in G if the complement of C induces a \((k,\ell )\)-tight subgraph of G. We will see that it is possible that there is no \({(k,\ell )}\)-co-tight set in G in which case \(G+uv\) is \((k,\ell )\)-redundant for any \(u,v\in V\). Our main result is the following min-max theorem which is illustrated by Fig. 1.
Theorem 1.1
Let \(G=(V,E)\) be a \((k,\ell )\)-tight graph on at least \(k^2+3\) vertices. If there exists any \({(k,\ell )}\)-co-tight set in G, then
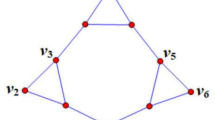
The solid edges form a (3, 4)-tight graph G. The three highlighted sets are pairwise disjoint (3, 4)-co-tight sets in G, hence no single edge augments G to a (3, 4)-redundant graph by Theorem 1.1. However, it is easy to check that the addition of the two edges uv and ux makes all edges of G (3, 4)-redundant, and hence this gives rise to an optimal solution of the reduced problem on G. For example, after the addition of the dashed edge ux we get a (3, 4)-rigid graph where ux and the bold edges are the only (3, 4)-redundant edges
To obtain the solution for the general problem by using the reduced problem when \(k\ge \ell \), we need more general concepts. The idea of our method comes from Jackson and Jordán [10] who proved that the (k, k)-redundant edges of a (k, k)-rigid graph \({\bar{G}}\) form induced subgraphs of \({\bar{G}}\) with disjoint vertex sets. If we contract these subgraphs into single vertices one can show that the resulting graph is (k, k)-tight for which we can use the algorithm of the reduced problem. In order to extend this idea for \(\ell <k\), we need the following generalization of sparsity. Let \(\ell \in \mathbb {Z}\) and \(m:V\rightarrow \mathbb {Z}_+\) be a map where \(\mathbb {Z}_+\) denotes the set of non-negative integers. A graph \(G=(V,E)\) is called \({\varvec{{({m},\ell )}}}\)-sparse if \(i_G(X)\le {m}(X)-\ell \) holds for every \(X\subseteq V\) for which \({m}(X)-\ell \ge 0\) and \(i_G(X)=0\) otherwise, where \({m}(X):=\sum _{v\in X}m(v)\). Observe that each subgraph of an \({({m},\ell )}\)-sparse graph is \({({m},\ell )}\)-sparse. To ensure that the condition \({m}(X)-\ell \ge 0\) holds (usually with strict inequality) for each set \(X\subseteq V\) with \(|X|\ge 2\), we take the following assumption throughout this paper.
-
(*)
(A0) \(\ell \in \mathbb {Z}\) and \(m:V\rightarrow \mathbb {Z}_+\) such that, for each pair \(u,v\in V\) with \(u\ne v\), either \(m(u)+m(v)> \ell \) or \(m(u)=m(v)=\ell =0\) holds.
Note that, when \(m\equiv k\), an \({({m},\ell )}\)-sparse graph is \((k,\ell )\)-sparse and (A0) holds by our assumption that \(\ell <2k\). \({\varvec{{({m},\ell )}}}\) -tight\(\varvec{/\mathrm{rigid} /\mathrm{redundant}}\) graphs and \({\varvec{({m},\ell )}}\)-co-tight sets can be defined by extending the definitions of \((k,\ell )\)-tight\(/\)rigid\(/\)redundant graphs and \({(k,\ell )}\)-co-tight sets similarly. For simplicity, we call a set \(X\subseteq V\) \({\varvec{{({m},\ell )}}}\)-tight (\({\varvec{(k,\ell )}}\)-tight, respectively) in \({\varvec{G}}\) if G[X] is \({({m},\ell )}\)-tight (\((k,\ell )\)-tight, respectively). Here \({\varvec{G[X]}}\) denotes the subgraph of G induced by X for \(X\subseteq V\). Note that (A0) implies that each \({({m},\ell )}\)-tight set X in G of cardinality at least two induces at least one edge in G, except when \(\ell =0\) and \(m(x)=0\) for each \(x\in X\). When the pair \({({m},\ell )}\) (\({(k,\ell )}\), respectively) is clear from the context we may omit the prefix \({({m},\ell )}\) (\({(k,\ell )}\), respectively) from the notions above.
We will see in Sect. 3 that, after using the above contraction idea for \({(k,\ell )}\)-rigid graphs with \(k>\ell \), the resulting graph \(G'=(V',E')\) on which we need to solve the reduced problem is \((m',\ell ')\)-tight for some \(m':V'\rightarrow \mathbb {Z}_+\) and \(\ell '\in \mathbb {Z}\) for which (A0) holds. Hence we will prove an extension of Theorem 1.1 for \({({m},\ell )}\)-tight graphs in Sect. 5 and we will give our algorithm for the reduced problem in Sect. 6 for \({({m},\ell )}\)-tight inputs.
1.1 Notation
All the graphs in this paper are multigraphs, that is, we allow parallel edges and loops. For simplicity, we do not distinguish graphs and their edge sets when it is clear from the context. Given a graph \(G=(V,E)\), \({\varvec{d_G(v)}}\) denotes the number of edges incident to a vertex \(v\in V\), \({\varvec{d_G(X,Y)}}\) denotes the number of edges between \(X-Y\) and \(Y-X\) for \(X,Y\subseteq V\), \({\varvec{d_G(X)}}\;\)\(:=d_G(X,V-X)\), and \({\varvec{e_G(X)}}\;\)\(:=i_G(X)+d_G(X)\). Note that our definition implies that \(d_G(v)\ne d_G(\{v\})\) if there is a loop incident with v. Also note that, in the usual definition of the degree, loop edges count twice for the degree of a vertex, however, we only count them once. We use \({\varvec{N_G(X)}}\) to denote the neighbor set of \(X\subseteq V\), that is, \(N_G(X)=\{v\in V-X:d_G(\{v\},X)\ge 1\}\), and \({\varvec{G/X}}\) to denote the graph arising from G by contracting X into a single vertex and deleting all the edges spanned by X. We can similarly define \({\varvec{D/X}}\) for a directed graph D. If \(G_1\) and \(G_2\) are graphs, then \(G_1\subseteq G_2\) denote that \(G_1\) is a subgraph of \(G_2\). When it is clear from the context, we omit the subscript G from the notation.
2 Preliminaries
In this section, we list some basic properties of \({({m},\ell )}\)-sparse graphs. We sketch their proofs for completeness. It follows from the definition that an \({({m},\ell )}\)-tight subgraph of an \({({m},\ell )}\)-sparse graph is always an induced subgraph. Therefore, if \(T_1=(V_1,E_1)\) and \(T_2=(V_2,E_2)\) both are \({({m},\ell )}\)-tight subgraphs of an \({({m},\ell )}\)-sparse graph G, then \(T_1\cap T_2=(V_1\cap V_2,E_1\cap E_2)\) is also an induced subgraph of G. Moreover, with standard submodular techniques we can prove the following.
Lemma 2.1
Let \(G=(V,E)\) be an \({({m},\ell )}\)-sparse graph, and let \(T_1=(V_1,E_1)\) and \(T_2=(V_2,E_2)\) be \({({m},\ell )}\)-tight subgraphs of G. If \({m}(V_1\cap V_2)\ge \ell \), then \(T_1\cup T_2\) is an \({({m},\ell )}\)-tight graph and \(d(V_1,V_2)=0\). Furthermore, if \(|V_1 \cap V_2|\ge 1\), then \(T_1 \cap T_2\) is \({({m},\ell )}\)-tight as well.
Note that the assumption on \({m}(V_1\cap V_2)\) always holds when \(|V_1\cap V_2|\ge 2\) by (A0), and also when \(\ell \le 0\) (since \(m\ge 0\)).
Proof
As \(T_1\) and \(T_2\) are \({({m},\ell )}\)-tight, \(i(V_1\cup V_2)+i(V_1\cap V_2)= i(V_1)+i(V_2)+d(V_1, V_2) \ge i(V_1)+i(V_2) ={m}(V_1)-\ell +{m}(V_2)-\ell ={m}(V_1\cup V_2)-\ell +{m}(V_1\cap V_2)-\ell . \) Note that \({m}(V_1\cap V_2)\ge \ell \). Hence, as G is an \({({m},\ell )}\)-sparse graph, \( i(V_1\cup V_2)+i(V_1\cap V_2) \le {m}(V_1\cup V_2)-\ell +{m}(V_1\cap V_2)-\ell \) holds thus equality stands in all the above inequalities. This proves the statement. \(\square \)
The \({({m},\ell )}\)-tight graphs have the following connectivity property.
Lemma 2.2
Let \(G=(V,E)\) be an \({({m},\ell )}\)-tight graph with \(|V|\ge 3\) and let \(v\in V\) with \(0<m(v)<\ell \). Then no loop is incident with v and \(d(v)\ge m(v)\).
Proof
Note that v cannot induce any loop by the \({({m},\ell )}\)-sparsity condition. Hence the \({({m},\ell )}\)-tightness of G, the \({({m},\ell )}\)-sparsity of \(V-v\) and (A0) imply that \({m}(V)-\ell =i(V)=d(v)+i(V-v)\le d(v)+{m}(V-v)-\ell ={m}(V)-\ell -m(v)+d(v)\) thus \(d(v)\ge m(v)\). Notice that this also means that v is connected to \(V-v\). \(\square \)
It is known that the edge sets of the \({({m},\ell )}\)-sparse subgraphs of a given graph form a matroid, called the \({\varvec{({m},\ell )}}\)-sparsity matroid or count matroid, which is a straightforward generalization of the well-known 2-dimensional rigidity matroid (see Frank [6, Sect. 13.5], Lorea [20], and Whiteley [27, Appendix A]). A circuit of this matroid is called an \({\varvec{{({m},\ell )}}}\)-circuit. By other words, a graph C is an \({({m},\ell )}\)-circuit if it is not \({({m},\ell )}\)-sparse and \(C-e\) is \({({m},\ell )}\)-sparse for every single edge e of C. It follows from matroid theory (see details in [6, Chapt. 5]) that for an \({({m},\ell )}\)-sparse graph \(G=(V,E)\) and \(i,j\in V\) for which \(G+ij\) is not \({({m},\ell )}\)-sparse, \(G+ij\) contains a unique \({({m},\ell )}\)-circuit \(C^G_{({m},\ell )}(ij)\). In this case, \({\varvec{T^G_{({m},\ell )}(ij)}}\,\)\(:=C^G_{({m},\ell )}(ij)-ij\) is \({({m},\ell )}\)-tight. (Note that \(C^G_{({m},\ell )}(ij)\) consists of the single edge ij when \(m(i)=m(j)=\ell =0\), and hence \(T^G_{({m},\ell )}(ij)\) consists of only two isolated vertices i and j in this case, however, this subgraph of G is \({({m},\ell )}\)-tight.) Let \({\varvec{V^G_{({m},\ell )}(ij)}}\,\) denote the vertex set of \(T^G_{({m},\ell )}(ij)\). (Recall that we do not distinguish graphs and their edge sets, hence \(T^G_{({m},\ell )}(ij)\) may be used to denote both a subgraph and its edge set.) For every edge \(e'\) of \(C^G_{({m},\ell )}(ij)\), \(G'=G+ij-e'\) is also \({({m},\ell )}\)-sparse and the unique \({({m},\ell )}\)-circuit of \(G'+e'\) is again \(C^G_{({m},\ell )}(ij)\). Moreover, if \(e''\not \in C^G_{({m},\ell )}(ij)\), then, \(G'+ij-e''\) is not \({({m},\ell )}\)-sparse. The main property of \(T^G_{({m},\ell )}(ij)\) is the following. It will be used several times in this paper.
Lemma 2.3
Let \(G=(V,E)\) be an \({({m},\ell )}\)-sparse graph and let \(i,j\in V\). Assume that \(G+ij\) is not \({({m},\ell )}\)-sparse. If \(G'=(V',E')\) is an \({({m},\ell )}\)-tight subgraph of G with \(i,j\in V'\), then \(T^G_{({m},\ell )}(ij)\subseteq G'\). Hence \(T^G_{({m},\ell )}(ij)=\bigcap \{T_h:T_h\) is an \({({m},\ell )}\)-tight subgraph of G including i and \(j\}\). \(\square \)
Let \({\varvec{R^G_{({m},\ell )}(i_1j_1,\dots , i_rj_r)}}\) denote the subgraph of \(G=(V,E)\) induced by the edges of E which are \({({m},\ell )}\)-redundant in \(G\cup \{i_1j_1, \dots ,i_rj_r\}\) where \(i_1,\dots ,i_r\), \(j_1,\dots ,j_r\in V\). For the sake of simplicity, when the graph G or \({({m},\ell )}\) is clear from the context, we will omit the superscript G or subscript \({({m},\ell )}\), respectively, from all of the above notation. Note that \(R(ij)=T(ij)\) for any \(i,j\in V\). (See Fig. 1 for an example, where the bold edges form \(R^G_{(3,4)}(ux)=T^G_{(3,4)}(ux)\).) The following lemma extends this simple fact by generalizing [8, Lemma 4] .
Lemma 2.4
If G is an \({({m},\ell )}\)-tight graph, then
Proof
Since \(R(ij)=T(ij)\), \(T(i_1j_1)\cup \dots \cup T(i_rj_r)\subseteq R(i_1j_1,\dots , i_rj_r)\). For the other direction, let \(e\in R(i_1j_1,\dots , i_rj_r)\) be an arbitrary edge. Now, \(G-e\) is \({({m},\ell )}\)-sparse and \(|E-e|={m}(V)-\ell -1\). \(G\cup \{i_1j_1,\dots , i_rj_r\}-e\) is \({({m},\ell )}\)-rigid, hence \(E\cup \{i_1j_1,\dots , i_rj_r\}-e\) has a rank of \({m}(V)-\ell \) in the \({({m},\ell )}\)-sparsity matroid. Thus there is an edge f in \(\{i_1j_1,\dots , i_rj_r\}\) for which \(E-e+f\) is a basis of the \({({m},\ell )}\)-sparsity matroid. Since \(E-e+f\) is independent in the \({({m},\ell )}\)-sparsity matroid, we must have \(e\in T(f)\). \(\square \)
As mentioned in the introduction, the main advantage of \({({m},\ell )}\)-tight graphs over \((k,\ell )\)-tight graphs is that an \({({m},\ell )}\)-tight graph remains \({({m}',{\ell }')}\)-tight after contracting an \({({m},\ell )}\)-tight subgraph for some pair \({({m}',{\ell }')}\), as follows.
Lemma 2.5
Let \(G=(V,E)\) be an \({({m},\ell )}\)-tight graph. Suppose that \(T \subsetneq V\) is an \({({m},\ell )}\)-tight set in G. Let \(t'\) be the new vertex that arises after contracting T in G. Let \(\ell ':= \max (\ell , 0)\) and let \(m':V(G/T)\rightarrow \mathbb {Z}_+\) be a map such that \(m'(v)=m(v)\) when \(v\in V(G/T)\cap V\) and \(m'(t')=\ell '\).
(a) A set \(S\subseteq V(G/T)\) containing \(t'\) induces an \({({m}',{\ell }')}\)-tight subgraph of G/T if and only if \((S-t') \cup T\) is \({({m},\ell )}\)-tight in G. In particular, G/T is \({({m}',{\ell }')}\)-tight.
(b) A set \(S\subseteq V(G/T)-t'\) is \({({m}',{\ell }')}\)-tight in G/T if and only if either \(\ell \ge 0\) and S is \({({m},\ell )}\)-tight in G, or \(\ell < 0\) and \(S\cup T\) is \({({m},\ell )}\)-tight in G such that \(d(S,T)=0\).
Proof
First, it is easy to see that, if the pair \({({m},\ell )}\) satisfies (A0), then so does \({({m}',{\ell }')}\), as the values of \(m'\) cannot decrease compared to the values of m.
(a) Let us show that G/T is \({({m}',{\ell }')}\)-sparse. Let \(X\subseteq V(G/T)\). Assume first that \(t'\in X\). Then \(i_{G/T}(X)=i_G((X-t')\cup T)-i_G(T)\le {m}((X-t')\cup T)-\ell -({m}(T)-\ell )={m}(X-t')={m}'(X)-m'(t')={m}'(X)-\ell '\) as T is \({({m},\ell )}\)-tight. If \(t'\notin X\) and \(\ell \ge 0\), then \(i_{G/T}(X)=i_G(X)\le \max ({m}(X)-\ell ,0)=\max ({m}'(X)-\ell ',0)\). If \(t'\notin X\) and \(\ell < 0\), then \(i_{G/T}(X)=i_G(X)\le i_G(X\cup T)-i_G(T)\le {m}(X\cup T)-\ell -({m}(T)-\ell )={m}(X)={m}'(X)-\ell '\). Hence G/T is \({({m}',{\ell }')}\)-sparse.
Assume now \(t'\in S\subseteq V(G/T)\). By the \({({m}',{\ell }')}\)-sparsity of G/T, the tightness of S means that \(i_{G/T}(S)={m}'(S)-\ell '={m}(S-t')\). Since \(i_G(T)={m}(T)-\ell \), replacing \(t'\) with T results \(i_G((S-t') \cup T)={m}((S-t') \cup T)-\ell \). The proof of the other direction is similar.
(b) First assume that \(\ell \ge 0\) and \(t'\notin S\subseteq V(G/T)\). Suppose S is \({({m}',{\ell }')}\)-tight. Then the \({({m}',{\ell }')}\)-sparsity of G/T means that \(i_{G/T}(S)={m}'(S)-\ell '={m}(S)-\ell \). On the other hand, the \({({m},\ell )}\)-tightness of S means that \(i_{G}(S)={m}(S)-\ell \). Since \(i_{G}(S)=i_{G/T}(S)\), these two are equivalent.
Now if \(\ell < 0\) and \(t'\notin S\subseteq V(G/T)\). Suppose S is \({({m}',{\ell }')}\)-tight. Then the \({({m}',{\ell }')}\)-sparsity of G/T means that \(i_{G/T}(S)={m}'(S)-\ell '={m}(S)-0\). Since T is \({({m},\ell )}\)-tight and \(i_{G}(S)=i_{G/T}(S)\), \({m}(S)+{m}(T)-\ell \ge i_G(S\cup T)=i_G(S)+i_G(T)+d_G(S,T)\ge ({m}(S)-0)+({m}(T)-\ell )+0\) follows, and hence equality must hold throughout, that is, \(i_G(S\cup T)\) is \({({m},\ell )}\)-tight and \(d_G(S,T)=0\). The proof of the other direction is similar. \(\square \)
2.1 Algorithmic preliminaries
To give a polynomial algorithm for our (general or reduced) augmentation problem, one first needs a polynomial algorithm for testing the \({({m},\ell )}\)-sparsity of a graph. Such an algorithm already exists for each pair of m and \(\ell \) (see the works of Hendrickson, Jacobs and Thorpe [12, 13] and Berg and Jordán [2] for the case where \(k=2\) and \(\ell =3\), the paper of Lee and Streinu [19] for general k and \(\ell \ge 0\), the book of Frank [6, Sect. 13.5.4] for the \({({m},\ell )}\) case, and the note of the first author [17] for the case of \(\ell <0\)). All the above mentioned algorithms are based on in-degree constrained orientations (see [6, Lemma 13.5.9]).
We note that in the main applications of \((k,\ell )\)-sparse graphs k and \(\ell \) are fixed constants thus we may assume the following condition.
- \({\varvec{(^*)}}\):
-
There exists a (universal) constant \(c>0\) such that \(m(v)\le c\) for every \(v\in V\) for every graph \(G=(V,E)\). We may also suppose that \(|\ell |\le c\).
We give the running time of our algorithms by assuming this condition. Observe that (*) implies that an \({({m},\ell )}\)-sparse graph on V has O(|V|) edges. For a directed graph D, let \({\varvec{ \varrho _D(v)}}\) denote the in-degree of a vertex v. We shall use the algorithm provided by the following theorem (which can be constructed based on the algorithms in [6, 17, 19]) as a subroutine in our algorithms.
Theorem 2.6
(Based on [6, 17, 19]) (a) There exists an algorithm which decides in \(O(|V|^2)\) time whether its input graph \(G=(V,E)\) is \({({m},\ell )}\)-sparse. It has the following outputs:
If G is \({({m},\ell )}\)-sparse, then it outputs this fact along with an orientation D of the edges in G minus a set \(F'\subseteq E\) of at most \(\max (-\ell ,0)\) edges, such that \(\varrho _D(v)\le m(v)\) holds for each \(v\in V\). If G is also \({({m},\ell )}\)-tight, then it also outputs this fact.
If G is not \({({m},\ell )}\)-sparse, then it outputs a maximal \({({m},\ell )}\)-sparse subgraph \(H=(V,F)\) of G along with an orientation D of the edges in H minus a set \(F'\) of \(\max (-\ell ,0)\) edges, such that \(\varrho _D(v)\le m(v)\) holds for each \(v\in V\). It also outputs the set R of edges in H which are \({({m},\ell )}\)-redundant in G.
(b) Furthermore, if G is \({({m},\ell )}\)-sparse (including the case when G is \({({m},\ell )}\)-tight), then by only using the in-degree constrained orientation D, one can decide in O(|V|) extra time whether \(G+e\) is \({({m},\ell )}\)-sparse for any new edge e, and if the answer is no, then output the \({({m},\ell )}\)-tight subgraph T(e) of G. \(\square \)
3 The reduction of the general problem
García and Tejel [8] showed that the general augmentation problem is NP-hard for (2, 3)-rigid graphs by reducing it to the set cover problem. Based on their method we will prove in Sect. 7 the NP-hardness of the general problem whenever \(k<\ell \). In this section we show that, in any other case (that is, if \(\ell \le k\)), there exists an \(O(|V|^2)\) time reduction from the general problem to the reduced problem that we shall solve in Sects. 5 and 6. Moreover, we give our reduction for all \({({m},\ell )}\)-rigid graphs for which \(m(v)\ge \ell \) for all \(v \in V\) (or \(m\ge \ell \) for the sake of brevity).
Throughout this section, let \({\varvec{{\bar{G}}=(V,{\bar{E}})}}\) denote an \({({m},\ell )}\)-rigid graph with \(m\ge \ell \) and \({\varvec{G=(V,E)}}\) denote an \({({m},\ell )}\)-tight spanning subgraph of \({\bar{G}}\). Obviously, every edge in \({\bar{E}}-E\) is \({({m},\ell )}\)-redundant in \({\bar{G}}\). By Lemma 2.4, the \({({m},\ell )}\)-redundant edges of G in \({\bar{G}}\) are the edges of \(R^G({\bar{E}}-E)=\bigcup _{e\in {\bar{E}}-E}T^G(e)\). Since \(m\ge \ell \), these edges induce vertex disjoint \({({m},\ell )}\)-tight subgraphs in G by Lemmas 2.1 and 2.4. (Note that we have only one such subgraph which may be disconnected when \(\ell \le 0\), and these subgraphs are exactly the connected components of \(R^G({\bar{E}}-E)\) when \(\ell >0\).) By contracting each of these subgraphs to a single vertex and by defining \({\varvec{\ell '}}\) as \(\max (\ell ,0)\) and \({\varvec{m'}}\) to be \(\ell '\) on each of the contracted vertices and to be m(v) on each non-contracted vertex v, we get the contracted graph \(G'=(V',E')\) along with the map \(m':V'\rightarrow \mathbb {Z}_+\). Notice, that this contraction yields a natural surjective map, \({\varvec{s}}\,\)\(: V \rightarrow V'\). By using Lemma 2.5(a) for each contracted tight subgraph of G sequentially it is easy to see that \(G'\) is \({({m}',{\ell }')}\)-tight. We can state even more.
Proposition 3.1
If \(X'\subseteq V'\) induces an \({({m}',{\ell }')}\)-tight subgraph of \(G'\), then \(s^{-1}(X')\) induces an \({({m},\ell )}\)-tight subgraph in V, or, when \(\ell <0\), it becomes \({({m},\ell )}\)-tight if we take its union with the vertices of the sole contracted \({({m},\ell )}\)-tight subgraph of G (that is, to \(V-V'\)).
Conversely, if \(X\subseteq V\) induces an \({({m},\ell )}\)-tight subgraph of G, then s(X) induces an \({({m}',{\ell }')}\)-tight subgraph in \(V'\), and, when \(\ell <0\), it contains the only contracted vertex (that is, the single element of \(V'-V\)).
Proof
The first statement follows directly by using Lemma 2.5 (b) for each contracted tight subgraph of G sequentially. For the second statement, let \(X^*\) be the union of X and all the contracted components \(V_i\)’s for which \(X \cap V_i \ne \emptyset \). Then \(X^*\) induces an \({({m},\ell )}\)-tight subgraph of G by Lemma 2.1 and \(s(X^*)=s(X)\) is \({({m}',\ell )}\)-tight by Lemma 2.5. (Note that if \(\ell <0\), then X must intersect the single contracted component \(V_1\) since otherwise \(X\cup V_1\) violates the \({({m},\ell )}\)-sparsity condition as \(i_G(X\cup V_1)\ge i_G(X)+i_G(V_1)={m}(X)-\ell +{m}(V_1)-\ell >{m}(X\cup V_1)-\ell \).) \(\square \)
If the union of some \({({m},\ell )}\)-tight subgraphs of G contains every edge of \({\bar{G}}\) which is not \((m,\ell )\)-redundant, then by Proposition 3.1 the union of corresponding \({({m}',{\ell }')}\)-tight subgraphs of \(G'\) is \(G'\) itself. Hence the minimum number of edges that we need to make \({\bar{G}}\) \({({m},\ell )}\)-redundant is at least the minimum number of edges that we need to make \(G'\) \({({m}',{\ell }')}\)-redundant. The following statement shows that these two values are equal.
Proposition 3.2
Let \(F'\) denote an edge set of minimum cardinality on \(V'\) for which \(G'+ F'\) is \({({m}',{\ell }')}\)-redundant. Let F be an arbitrary edge set on V for which \(\{s(u)s(v):uv\in F\}=F'\). Then \({\bar{G}}+ F\) is \({({m},\ell )}\)-redundant.
Proof
Given \(u,v \in V\), \(s(T^G_{{({m},\ell )}}(uv))\) is an \({({m}',\ell )}\)-tight subgraph of \(G'\) that contains both s(u) and s(v) by Proposition 3.1. Thus it is a supergraph of \(T^{G'}_{{({m}',{\ell }')}}(s(u)s(v))\) by Lemma 2.3. Since the image of each non-\({({m},\ell )}\)-redundant edge of \({\bar{G}}\) is in \(G'\) and the subgraphs \(\{T^{G'}_{{({m}',\ell )}}(s(u)s(v)):s(u)s(v)\in F'\}\) cover the edge set of \(G'\), the subgraphs \(\{T^G_{{({m},\ell )}}(uv):uv\in F\}\) cover every non-\({({m},\ell )}\)-redundant edge of \({\bar{G}}\). Hence \({\bar{G}}+ F\) is \({({m},\ell )}\)-redundant by Lemma 2.4. \(\square \)
With Proposition 3.2, we have reduced the problem of augmenting an \({({m},\ell )}\)-rigid graph to an \({({m},\ell )}\)-redundant graph to the problem of augmenting an \({({m}',{\ell }')}\)-tight graph to an \({({m}',{\ell }')}\)-redundant graph. It is easy to check that (A0) still holds after the reduction. Based on Theorem 2.6 the reduction can be done in \(O(|V|^2)\) time. Note that when we get a solution for the arisen reduced problem, we can get back a solution to the original problem in linear time. This implies the following.
Theorem 3.3
Let \(m:V\rightarrow \mathbb {Z}_+\) and \(\ell \in \mathbb {Z}\) for which \(m\ge \ell \) and (*) hold, and let \({\bar{G}}=(V,{\bar{E}})\) be an \({({m},\ell )}\)-rigid graph. In \(O(|V|^2)\) time, we can reduce the solution of the general augmentation problem on \({\bar{G}}\) to the solution of the reduced problem on an \({({m}',{\ell }')}\)-tight graph on a vertex set of cardinality at most |V|. \(\square \)
4 Preprocessing
Our goal is to provide a solution for the reduced problem for all \({({m},\ell )}\)-tight graphs, however, it is easier to formulate our results by assuming the following conditions when \(\ell >0\). Recall, that V(ij) denotes the vertex set of T(ij).
- (A):
-
Assuming (A0) and (*) for m and \(\ell \), \(G=(V,E)\) is an \({({m},\ell )}\)-tight graph on at least four vertices such that either \(\ell \le 0\) or all of the following three conditions hold.
- (A1):
-
There exists no \(v\in V\) such that \(m(v)=0\) and v is an isolated vertex.
- (A2):
-
There exist \(u,v \in V\) such that \(V(uv)\ne \{u,v\}\).
- (A3):
-
There exists no \(v \in V\) such that \(V(uv)=\{u,v\}\) for all \(u \in V-v\) and \(V-v\) induces an \({({m},\ell )}\)-tight graph.
We note that these conditions automatically hold for \((k,\ell )\)-tight graphs with sufficiently many vertices, as in this case there is at least one vertex-pair \(u,v \in V\) that does not induce any edge.
When we consider \({({m},\ell )}\)-tight graphs, it is not hard to see by using our conditions (A0) and (*) that (A2) and (A3) hold for every \({({m},\ell )}\)-tight graph on at least \(c^2+2\) vertices, where c is the constant in (*). Indeed, (A0) and \(\ell >0\) (which holds when we need assumption (A2) and (A3)) imply that, if \(\{u,v\}\) is an \({({m},\ell )}\)-tight set in G, then it induces at least one edge, and hence the denial of (A2) (or (A3), respectively) contradicts the \({({m},\ell )}\)-sparsity of G (or the \({({m},\ell )}\)-tightness of \(G[V-v]\) and G, respectively). Note that since c is considered as a constant in our algorithms, the solution of the reduced problem on less than \(c^2+2\) vertices can be provided in constant time. When G violates (A1), we may delete its isolated vertices with \(m(v)=0\) and solve the reduced problem for the arising graph. It is easy to check that the solution of our augmentation problem on this reduced input is a solution of our original problem. As reduction can be done in \(O(|V|^2)\) running time, the assumption of (A) does not restrict the usability of our results for all \({({m},\ell )}\)-tight graphs.
5 The min-max theorem for the reduced problem
In this section we prove Theorem 1.1 and its extension for \({({m},\ell )}\)-tight graphs for which, throughout this whole section, we assume (A), including that \(G=(V,E)\) is an \({({m},\ell )}\)-tight graph on at least 4 vertices. The generalization of Theorem 1.1 for \({({m},\ell )}\)-tight graphs is the following.
Theorem 5.1
If there exists any \({({m},\ell )}\)-co-tight set in G, then
Otherwise, \(G+uv\) is \({({m},\ell )}\)-redundant for every pair \(u,v \in V\).
Recall that we call a set of vertices \(\emptyset \ne C \subsetneq V\) \({({m},\ell )}\)-co-tight in G if \(i_G(V-C)={m}(V-C)-\ell \), that is, if the complement of C is an \({({m},\ell )}\)-tight set in G. Equivalently (by \(m(V)-\ell =|E|=e_G(C)+i_G(V-C)\)), C is \({({m},\ell )}\)-co-tight if \(e_G(C)={m}(C)\). Note that for every \(X \subset V\) for which \({m}(V-X)\ge \ell \), \(e_G(X)\ge m(X)\) holds by the sparsity of \(V-X\). Inclusion-wise minimal \({({m},\ell )}\)-co-tight sets will be called \({\varvec{({m},\ell )}}\)-MCT sets. (See Fig. 1 where the three highlighted sets \(\{u\},\{v\},\) and X are the (3, 4)-MCT sets of the graph G formed by the solid edges.)
Lemma 5.2
Assume that \(\ell >0\). Let C be an \({({m},\ell )}\)-MCT set and let \(v\in C\). Then \(m(v)\ne 0\).
Proof
Suppose that \(m(v)=0\). When \(|C|=1\), the co-tightness of C implies that \(d(v)=0\), contradicting (A1). When \(|C|\ge 2\), then \(i(V-(C-v))\ge i(V-C)={m}(V-C)-\ell ={m}(V-(C-v))-\ell \) follows by the co-tightness of C, hence \(V-(C-v)\) is also tight in G, contradicting the minimality of C. \(\square \)
Observation 5.3
Let \(G=(V,E)\) be an \({({m},\ell )}\)-tight graph and let \(C \subset V\) be an \({({m},\ell )}\)-co-tight set. If \(G\cup H\) is \({({m},\ell )}\)-redundant for \(H=(V,F)\), then there exists an edge \(uv\in F\) such that \(u \in C\) or \(v \in C\).
Proof
If an edge e is not incident with at least one vertex in a co-tight set C, then \(V(e)\subseteq V-C\) by Lemma 2.3. Thus no edge set that avoids C can augment G to \({({m},\ell )}\)-redundant by Lemma 2.4. \(\square \)
This observation immediately implies that \(\min \ge \max \) in Theorem 5.1 since each co-tight set in \(\mathcal {C}\) must contain an end-vertex of an edge of H.
We say that a set U covers a set family \({\mathcal {C}}\), if \(|U \cap C|\ge 1\) for every \(C \in {\mathcal {C}}\). Let us denote the family of all \({({m},\ell )}\)-MCT sets of G by \({\varvec{\mathcal {C}^*}}\) from now on.
Lemma 5.4
Suppose that \(U\subseteq V\) is a set that covers \(\mathcal {C}^*\). If \(V'\subseteq V\) is a set of vertices such that \(U\subseteq V'\) and \(V'\) induces an \({({m},\ell )}\)-tight subgraph in G, then \(V'=V\). In particular, for two vertices \(u,v\in V\), the set \(\{u,v\}\) covers \(\mathcal {C}^*\) if and only if \(G+uv\) is \({({m},\ell )}\)-redundant.
Proof
Let us suppose that there exists a tight set \(V' \subsetneq V\) in G for which \(U \subseteq V'\). Then \(V - V'\) is co-tight by definition, and hence there exists an MCT set \(C\in \mathcal {C}^*\) such that \(C\subseteq V-V'\). However, as \(U \subset V'\), this contradicts the assumption that \(|U \cap C|\ge 1\) for every \(C \in \mathcal {C}^*\). The ‘only if’ part of the second statement follows by the first one and the tightness of \(V(uv)\ni u,v\). The converse direction follows by Observation 5.3. \(\square \)
Note that it is possible that there are no co-tight sets in a graph G. For example, \(K_6-e\) is (3, 4)-tight and there are no (3, 4)-co-tight sets in it. By Lemma 5.4, if there are no MCT sets in G then \(G+uv\) is \({({m},\ell )}\)-redundant for any pair \(u,v \in V\) which proves the last part of Theorem 5.1. Thus we may suppose that G contains at least one MCT set. We shall show that in this case \(\min \le \max \) also holds. This statement is obvious when the minimum is one since we assumed the existence of an MCT set in G. Hence we may assume that the minimum is at least two. We will show that, in this case, the maximum in Theorem 5.1 is obtained by \(\mathcal {C}^*\). The following statement on the structure of MCT sets shows that the members of \(\mathcal {C}^*\) are pairwise disjoint. It is an extension of a result of Jordán [14, Theorem 3.9.13] that states the same for (2, 3)-MCT sets.
Theorem 5.5
The members of \(\mathcal {C}^*\) are either pairwise disjoint and \(|\mathcal {C}^*|\ge 3\) or there exists a pair \(u,v\in V\) such that \(T(uv)=G\), that is, \(G+uv\) is \({({m},\ell )}\)-redundant.
The proof of Theorem 5.5 requires more involved thoughts, hence we prove it separately in Sect. 5.1. Now, to finish the proof of Theorem 5.1, we need to show that G can be augmented to an \({({m},\ell )}\)-redundant graph by using a set of \(\left\lceil \frac{|\mathcal {C}^*|}{2}\right\rceil \) edges when at least two edges are needed for the augmentation. Our plan is to add these new edges between the members of \(\mathcal {C}^*\). By Theorem 5.5, we may suppose from now on that all the MCT sets of G are pairwise disjoint and \(|\mathcal {C}^*|\ge 3\). In this case the following stronger result also holds.
Lemma 5.6
Suppose that the members of \(\mathcal {C}^*\) are pairwise disjoint and \(|\mathcal {C}^*|\ge 3\). Let \(C,C'\in \mathcal {C}^*\). Then \(N(C)\cap C'=\emptyset \).
Proof
Suppose first that \({m}(V - (C \cup C')) < \ell \) (and \(\ell >0\)). In this case \(|V - (C \cup C')|\le 1\) holds by (A0). \(V \ne C \cup C'\) since there exist at least three MCT sets. Therefore, \(V - (C \cup C') = v\) for some \(v\in V\) and v is a co-tight set on its own with \(m(v)<\ell \). (A1) implies that \(m(v)>0\) also holds. By Lemma 2.2, there is no loop in G incident with v. Furthermore, since \(\{v\}\) is co-tight in G, \(d_G(v)=m(v)\). Note that \(C\cup \{v\}=V-C'\) and \(C'\cup \{v\}=V-C\) are tight sets in G each of which must induce at least one edge incident with v by Lemma 2.2. Since \(V=C\cup C'\cup \{v\}\) and \(|V|\ge 4\), at least one of C and \(C'\), say C, must contain at least 2 vertices. Hence \(d_{G[C\cup \{v\}]}(v)\ge m(v)\) also follows by Lemma 2.2. But now the disjointness of C and \(C'\) implies that \(d_G(v)>m(v)\), a contradiction.
On the other hand, if \({m}(V - (C \cup C')) \ge \ell \) (e.g. \(\ell \le 0\)), then the statement follows by using Lemma 2.1 for \(T_1=G[V-C]\) and \(T_2=G[V-C']\). \(\square \)
As we have noted before, we plan to connect the members of \(\mathcal {C}^*\) by the new edges. Based on the above result, the following statement provides a useful property of the arising redundant subgraphs. (It can be illustrated again by Fig. 1, where the highlighted sets are (3, 4)-MCT sets in G and T(ux) is the subgraph formed by the bold edges.)
Lemma 5.7
Let C be an \({({m},\ell )}\)-MCT set in G and let \(u\in C\) and \(v\in V-(C\cup N(C))\) such that \(m(v)\ne 0\). Then \(C\cup N(C)\subset V(uv)\).
Proof
As \(v \not \in N(u)\) and \(m(v)\ne 0\), condition (A0) implies that \(\{u,v\}\) is not tight in G.
First we show that \(C\subset V(uv)\). Note that \(V-C\) is maximal amongst all the proper tight subsets of V, which implies that either \(V(uv)\cup (V-C)=V\), and hence \(C\subset V(uv)\) or \(V(uv)\cup (V-C)\) is not tight in G. In the latter case, \(V(uv)\cap (V-C)=v\) and \(m(v)<\ell \) both follow by Lemma 2.1. Thus, since v is not connected to C, the tightness of T(uv) and the sparsity of G imply that \({m}(V(uv))-\ell =i(V(uv))=i(v)+i(V(uv)-v)\le 0+{m}(V(uv)-v)-\ell ={m}(V(uv))-\ell -m(v)\) contradicting \(m(v)>0\). Here \(i(v)=0\) because \(m(v) -\ell <0\).
Now the \({({m},\ell )}\)-tightness of V(uv), the \({({m},\ell )}\)-sparsity of G, and the co-tightness of C imply that \({m}(V(uv))-\ell =i_G(V(uv))=i_G(V(uv)-C)+e_{T(uv)}(C)\le i_G(V(uv)-C)+e_{G}(C)\le {m}(V(uv)-C)-\ell +{m}(C)\). Hence equality must hold throughout, in particular, \(e_{T(uv)}(C)=e_{G}(C)\) implying \(N(C)\subset V(uv)\). \(\square \)
A set X is called a transversal of a family \({\mathcal {S}}\) if \(|X\cap S|=1\) for each \(S \in {{\mathcal {S}}}\). Note that a transversal of \(\mathcal {C}^*\) can be easily constructed by taking one arbitrary element of each member of \(\mathcal {C}^*\) when the members of \(\mathcal {C}^*\) are pairwise disjoint. Next we show that any connected graph on a transversal of \(\mathcal {C}^*\) augments G to an \({({m},\ell )}\)-redundant graph, that is, \(|\mathcal {C}^*|-1\) edges are enough for the augmentation.
Lemma 5.8
Suppose that the members of \(\mathcal {C}^*\) are pairwise disjoint and \(|\mathcal {C}^*|\ge 3\). Let X be a transversal of \(\mathcal {C}^*\) and let F be an edge set which induces a connected graph on \(Y\subseteq X\). Then R(F) is the minimal \({({m},\ell )}\)-tight subgraph inducing all elements of Y. In particular, if F is the edge set of a star \(K_{1,|X|-1}\) on the vertex set X, then \(G+F\) is \({({m},\ell )}\)-redundant.
Proof
Recall that, R(F) denotes the set of \({({m},\ell )}\)-redundant edges of G in \(G+F\), and Lemma 2.4 claims that \(R(F)=\bigcup _{f\in F}T(f)\). Let us use induction on |F|. If \(F=\{yy'\}\), then \(R(F)=T(yy')\) which is the minimal \({({m},\ell )}\)-tight subgraph of G containing both of y and \(y'\) by Lemma 2.3.
Let \(yy'\in F\) such that \(F-yy'\) is connected. If \(y,y' \in V(R(F-yy'))\), then by Lemma 2.3, \(T(yy^{\prime })\subseteq R(F-yy')\).
We may assume now that \(\{y,y'\} \not \subseteq V(R(F-yy'))\) and, by switching the role of y and \(y'\) we may suppose that \(y\in V(F-yy')\). Let \(y^{\prime \prime }\in V(F-yy')-y\). By induction, \(R(F-yy')\) is a tight subgraph of G which induces each element of \(V(F-yy')\), in particular, it induces y and \(y^{\prime \prime }\). Thus by Lemma 2.3, \(T(yy^{\prime \prime })\) is a subgraph of \(R(F-yy')\).
Assume that the vertices \(y,y',y^{\prime \prime }\in Y\) are elements of the sets \(C, C',C^{\prime \prime }\in \mathcal {C}^*\), respectively. Lemmas 5.6 and 5.7 imply that \(C\cup N(C)\subseteq V(yy')\) and \(C\cup N(C)\subseteq V(yy^{\prime \prime } )\subseteq V(R(F-yy'))\). Note that \(i_G(C)\le {m}(C)-\ell \) by \({({m},\ell )}\)-sparsity and \(e_G(C)= {m}(C)\) by the co-tightness of C in G. Hence \(N(C)\ne \emptyset \) and \(|C\cup N(C)|\ge 2\) holds when \(\ell >0\). Therefore, \({m}(V(yy')\cap V(R(F-yy')))\ge {m}(C\cup N(C))\ge \ell \) always holds, and Lemma 2.1 implies that \(R(F-yy')\cup T(yy')\) is tight. This implies that R(F) is tight since \(R(F)= R(F-yy')\cup T(yy')\) follows by Lemma 2.4. Note that \(Y\subseteq R(F)\) is obvious by \(Y=V(F)\).
Let now T be the minimal tight subgraph of G which induces all elements of Y. Lemma 2.3 implies that \(T(f)\subseteq T\) for each \(f\in F\). Hence it follows by Lemma 2.4 that \(R(F)=\bigcup _{f\in F}T(f)\subseteq T\), that is, \(R(F)=T\).
Finally, observe that Lemma 5.4 and the tightness of R(F) imply that, if F induces the whole set X (in particular, when it is a star on X), then \(R(F)=G\). \(\square \)
The cardinality of the edge set provided by Lemma 5.8 can be decreased by iteratively using the following statement.
Lemma 5.9
Suppose that the members of \(\mathcal {C}^*\) are pairwise disjoint and \(|\mathcal {C}^*|\ge 4\). Let \( y, x_{1}, x_{2}, x_{3}\) be elements of distinct members of \(\mathcal {C}^*\). Let \(T^*=T(y x_{1}) \cup T(y x_{2}) \cup T(y x_{3})\). Then \(T^*=T(y x_{1}) \cup T( x_{2} x_{3})\) or \(T^*=T(y x_{3}) \cup T(x_{1}x_{3})\) holds.
Proof
Let us suppose that \(T^*\ne T(y x_{1}) \cup T( x_{2} x_{3})\). Thus there exists an edge e for which \(e \in T^*\) and \(e\notin T(y x_{1}) \cup T( x_{2} x_{3})\).
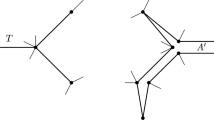
Lemmas 2.4 and 5.8 imply that \(T^*\) is the minimal tight subgraph of G inducing all of \(y,~ x_1,~x_2,\) and \(x_3\). However, they similarly imply that this statement also holds for \(T(y x_{1}) \cup T(x_{2}x_3) \cup T(y x_{3})\) and \(T(y x_{1}) \cup T(x_{2}x_3) \cup T(x_1 x_{2})\), that is, these two graphs both are equal to \(T^*\). Since \(e\in T^*\) and \(e\notin T(y x_{1}) \cup T( x_{2} x_{3})\), we get \(e\in T(y x_{3})\) and \(e\in T(x_1 x_{2}).\) (See Fig. 2.)
Illustrations of Lemma 5.9
Lemma 2.1 implies now that \( T(y x_{3})\cup T(x_1 x_{2})\) is a tight subgraph of G inducing all of \(y,~ x_1,~x_2,\) and \(x_3\), hence it must be equal to \(T^*\). (We note that if \(T^*\ne T(y x_{1}) \cup T( x_{2} x_{3})\), then \(T^*=T(yx_{2}) \cup T(x_{1}x_{3})\) also follows by a similar proof.)\(\square \)
This finally allows us to finish the proof of Theorem 5.1.
Proof
(Proof of Theorem 5.1) As mentioned before, we only need to prove that \(\max \ge \min \) holds. This is obvious when \(\min =1\). Hence we may assume that at least 2 edges are needed for the augmentation. In this case, the members of \(\mathcal {C}^*\) are pairwise disjoint by Theorem 5.5 and we need to show that the augmentation can be done by using \(\left\lceil \frac{|\mathcal {C}^*|}{2}\right\rceil \) edges. Let us denote a transversal of \(\mathcal {C}^*\) by X. For an arbitrary \(y \in X\), let the edge set \(F_0:=\{yx: x\in X-y\}\), and let \(H_0=(V,F_0)\). By Lemma 5.8\(G\cup H_0\) is redundant. Let us decrease the number of edges in \(H_i\) (that is \(H_0\) at the beginning). While there are at least three edges in \(H_i\) that are incident with y, we can decrease the number of edges in \(H_i\) and also the edges incident with y by Lemma 5.9 so that the arising graph \(H_{i+1}=(V,F_i)\) still augments G to an \({({m},\ell )}\)-redundant graph. We can repeat this until the degree of y is at most two and the degree of every other vertex is at most one in the final graph \(H=(V,F)\). Thus \(|F|=\left\lceil \frac{|X|}{2} \right\rceil =\left\lceil \frac{|\mathcal {C}^*|}{2}\right\rceil \) and \(G\cup H\) is \({({m},\ell )}\)-redundant. \(\square \)
Before we prove Theorem 5.5, we show the connection between the results of this paper and the paper of García and Tejel [8]. We also use this result in the proof of the NP-hardness result in Sect. 7. Let us call an \({({m},\ell )}\)-tight subgraph \(G'\) of G generated if there are \(u,v\in V\) such that \(T(uv)=G'\).
Lemma 5.10
Assume that there is no edge uv that augments G to an \({({m},\ell )}\)-redundant graph. Then T(uv) is inclusion-wise maximal amongst all the generated subgraphs of G if and only if \(u,v \in V\) are elements of two distinct \({({m},\ell )}\)-MCT sets. Moreover, two inclusion-wise maximal generated subgraphs \(T(uv_1)\) and \(T(uv_2)\) are equal if and only if \(v_1,v_2\) are in the same \({({m},\ell )}\)-MCT set.
Note that this result implies that ‘classes of extreme vertices’ defined in [8] are exactly the (2, 3)-MCT sets when no edge uv augments G to a (2, 3)-redundant graph.
Proof
By Theorem 5.5, all the MCT sets of G are pairwise disjoint. Assume that T(uv) is an inclusion-wise maximal generated subgraph of G for some \(u,v\in V\). Let \(\{x_1,\dots ,x_t\}\) be a transversal of \(\mathcal {C}^*\). By Lemma 5.8, \(G=T(x_1x_2)\cup \dots \cup T(x_1x_t)\), hence we can assume that \(u \in V(x_1x_2)\) and \(v \in V(x_1x_2)\cup V(x_1x_3)\). On the other hand, \(T(x_1x_2) \cup T(x_1x_3)=T(x_1x_2) \cup T(x_2x_3) =T(x_1x_3) \cup T(x_2x_3)\) by Lemmas 2.4 and 5.8. This means that one of the above three generated tight subgraphs, say \(T(x_1x_2)\), contains both u and v thus \(V(uv) \subseteq V(x_1x_2) \) by Lemma 2.3. Since T(uv) is inclusion-wise maximal equality must hold.
Let \(C_1,C_2\in \mathcal {C}^*\) such that \(x_1\in C_1\) and \(x_2\in C_2\). Suppose that \(\{u,v\}\cap C_1=\emptyset \). Note that \(V-C_1\) is a tight set in G, and hence V(uv) is disjoint from \(C_1\), in particular \(x_1 \not \in V(uv)\), contradicting \(V(uv)=V(x_1x_2)\). Therefore, with the same argument for \(C_2\), either \(u\in C_1\) and \(v\in C_2\), or \(u\in C_2\) and \(v\in C_1\).
It is clear that taking any element x of \(C_1\) and any element y of \(C_2\) the generated tight set T(xy) is the same by Lemmas 5.7, 5.6 and 2.3. On the other hand, if there are \(a,b \in V\) such that \(T(xy) \subseteq T(ab)\), then \(a\in C_1\) and \(b \in C_2\) or vice-versa by Observation 5.3. This proves that T(xy) is an inclusion-wise maximal generated subgraph of G. \(\square \)
5.1 Proof of Theorem 5.5
Recall that we assume (A) for our \({({m},\ell )}\)-tight graph G and \(\mathcal {C}^*\) denotes the family of all \({({m},\ell )}\)-MCT sets of G.
Lemma 5.11
If X and Y are two \({({m},\ell )}\)-MCT sets in G, such that \(X \cap Y \ne \emptyset \), then \({m}(V-(X \cup Y)) <\ell \). In particular, \(|X \cup Y| \ge |V|-1\).
Proof
For the sake of contradiction, let us suppose that \({m}(V-(X \cup Y)) \ge \ell \). \(V-X\) and \(V-Y\) are tight sets in G by the co-tightness of X and Y. \((V-X)\cap (V-Y)=V-(X \cup Y)\), hence \(V-(X\cap Y)\) is also tight by Lemma 2.1. Thus \(X\cap Y\) is co-tight, contradicting the minimality of X and Y. Finally, \(|X \cup Y| \ge |V|-1\) follows by (A0) and \({m}(V-(X \cup Y)) <\ell \). \(\square \)
Note that Lemma 5.11 implies that all the MCT sets of G are pairwise disjoint when \(\ell \le 0\). Hence we only need to prove Theorem 5.5 for the case where \(\ell >0\). In this case, we have two possibilities for intersecting MCT sets: their union may be equal to V or be of cardinality \(|V|-1\). As we will see, the latter possibility (which does not arise if \(m(v)\le \ell \) holds for all \(v\in V\)) is more difficult.
For a vertex \(v\in V\), let \({\varvec{\mathcal {C}^*(v)}}\) \(:=\{C\in \mathcal {C}^*:v\notin C\}\). Given a ground set S, a family of its subsets is called a co-partition of S, if their complements form a partition of S.
Lemma 5.12
Suppose that \(\ell >0\). Assume that there exist two \({({m},\ell )}\)-MCT sets \(X,Y\in \mathcal {C}^*\) such that \(X\cap Y\ne \emptyset \) and \(X\cup Y=V-v\) for some \(v\in V\). Then \(\mathcal {C}^*(v)\) is a co-partition of \(V-v\) with \(|\mathcal {C}^*(v)|\ge 3\) or there exists a vertex \(u\in V-v\) such that \(T(uv)=G\).
Proof
Assume that there exists no vertex \(u\in V-v\) such that \(T(uv)=G\). Then \(\mathcal {C}^*(v)\ne \{X,Y\}\) since otherwise the set formed by a vertex \(u\in X \cap Y\) and v would cover \({\mathcal {C}}^*\) contradicting Lemma 5.4 and \(T(uv)\ne G\). Hence \(|\mathcal {C}^*(v)|\ge 3\) as \(X,Y\in \mathcal {C}^*(v)\). Let \(Z \in \mathcal {C}^*(v)-\{X,Y\}\). As Z must intersect X or Y, \(X\cup Z\) or \(Y \cup Z\) is equal to \(V -v =X \cup Y\) according to Lemma 5.11. However, then both \(X\cup Z\) and \(Y \cup Z\) are equal to \(V -v\) by the same reasoning. Thus \(Z \supseteq (X - Y) \cup (Y-X)\). This implies also that every two members of \({{\mathcal {C}}}^*(v)\) are intersecting, and hence for every three members \(W_1\), \(W_2,\) and \(W_3\) of \(\mathcal {C}^*(v)\), \(W_3 \supseteq (W_1 - W_2) \cup (W_2-W_1)\) holds. Therefore, every vertex in \(V-v\) is avoided by at most one member of \(\mathcal {C}^*(v)\). If there exists a vertex u that is contained in every member of \(\mathcal {C}^*(v)\), then \(\{u,v\}\) covers \({\mathcal {C}}^*\) contradicting Lemma 5.4 and \(T(uv)\ne G\). Therefore, every vertex in \(V-v\) is avoided by exactly one member of \(\mathcal {C}^*(v)\), that is, \(\mathcal {C}^*(v)\) is a co-partition of \(V-v\). \(\square \)
For a vertex \(v\in V\) and a set \(W\subseteq V-v\), let \({\varvec{{\widetilde{W}}^v}}\,\)\(:=V-v-W\). This is the point where our proof gets more involved than that of [14, Theorem 3.9.13]. This is because the following lemma is quite complicated in the case of \(\ell > \frac{3}{2}k\). Otherwise we could state it in an even stronger form and the proof would come by a slightly different version of Lemma 2.1 easily.
Lemma 5.13
Suppose that \(\ell >0\). Let \(v\in V\) be a vertex for which the family \(\mathcal {C}^*(v)\) is a co-partition of \(V-v\) with \(|\mathcal {C}^*(v)|\ge 3\). Suppose that there exists a vertex \(u\in V-v\) with \(m(u)\le m(v)\). Let \(W_1,W_2\in \mathcal {C}^*(v)\) and let \(w_1\in {\widetilde{W}}^v_1\) and \(w_2 \in {\widetilde{W}}^v_2\). Suppose that \(V'\) is an \({({m},\ell )}\)-tight set in G with \(w_1,w_2 \in V'\). Then either \(V'=V\) or \(V'=\{w_1,w_2\}\). In particular, either \(V(w_1w_2)=V\) (and \(T(w_1w_2)=G\)) or \(V(w_1w_2)=\{w_1,w_2\}\).
Proof
Assume that \(V'\subsetneq V\) is a tight set in G such that \(w_1,w_2\in V'\) (for example, \(V(w_1w_2)\) is such a set if \(V(w_1w_2)\ne V\)). Note that \(\{v,w_1,w_2\}\) covers \(\mathcal {C}^*\), hence \(V' \ne V\) implies that \(v\notin V'\) by Lemma 5.4.
Suppose first that \(|V' \cap {\widetilde{Z}}^v|\ge 2\) for some \(Z\in {{\mathcal {C}}}^*(v)\). In this case \(V' \cup (V- Z)=V' \cup ({\widetilde{Z}}^v \cup v)\) is a tight set in G by Lemma 2.1. (See Fig. 3.) Hence \(V' \cup (V- Z)=V\) by Lemma 5.4, again. Lemma 2.1 also states that \(d(v,Z)=0\). This implies that \(d(v,{\widetilde{W}}^v)=0\) for each \(W\in {{\mathcal {C}}}^*(v)-\{Z\}\). Note that \(m(v)<\ell \) by Lemma 5.11 (since any two members of \(\mathcal {C}^*(v)\) are intersecting and their union avoids v). If \(m(v)>0\) then Lemma 2.2 on the tight graph \(G[V-W]\) implies that \(d(v,{\widetilde{W}}^v)>0\) for each \(W\in {{\mathcal {C}}}^*(v)-\{Z\}\), contradicting \(d(v,Z)=0\) as \(V-W-v={\widetilde{W}}^v\subset Z\). However, if \(m(v)= 0\), then by Lemma 5.2v is not in any MCT sets. Thus \(\{w_1,w_2\}\) covers all MCT sets, meaning that \(V(w_1w_2)=V\) by Lemma 5.4.
We may now suppose that \(|V' \cap {\widetilde{Z}}^v|\le 1\) for every \(Z \in \mathcal {C}^*(v)\). Let us consider the complement sets of the members of \(\mathcal {C}^*(v)\). \(V'\) intersects at least two of them: \({\widetilde{W}}^v_1\cup v\) and \({\widetilde{W}}^v_2 \cup v\). (See again Fig. 3 for an illustration.)
Claim 5.14
\(V'\) intersects exactly two maximal tight sets containing v, namely, \({\widetilde{W}}^v_1\cup v\) and \({\widetilde{W}}^v_2 \cup v\).
Proof
Let us denote the family of maximal tight sets containing v by \({{\mathcal {F}}}=\{{\widetilde{Z}}^v \cup v\) where \(Z \in \mathcal {C}^*(v)\}\). Suppose that \(V'\) intersects t members of \({{\mathcal {F}}}\), say \(V_1,\dots ,V_t\). Since \(|V' \cap {\widetilde{Z}}^v|\le 1\) for every \(Z \in \mathcal {C}^*(v)\) and \(v\notin V'\), \(|V'|=t\). Suppose that \(t\ge 3\). Let \(E'\) denote the set of edges induced by \(V'\).
As \(V'\) is \({({m},\ell )}\)-tight, \({m}(V')-\ell =|E'|\). Since every pair of vertices in \(V'\) induces an \({({m},\ell )}\)-sparse subgraph in G, \(|E'|\le (t-1){m}(V')-{{t}\atopwithdelims (){2}}\ell \). This results \({m}(V')-\ell \le (t-1){m}(V')-\frac{t(t-1)}{2}\ell \). Hence \(\frac{t(t-1)-2}{2}\frac{1}{t-2}\ell \le {m}(V')\), and thus \(\frac{t+1}{2}\ell \le {m}(V')\).
Let \(E^*\) denote the union of \(E'\) and the set of edges induced by \(V_1,\dots ,V_t\). Clearly, \( m(V')-\ell +{m}(V_1)-\ell +\dots +{m}(V_t)-\ell = |E^*|\). By the sparsity condition, \(|E^*|\le {m}(V_1\cup \dots \cup V_t)-\ell \). As \({m}(V_1\cup \dots \cup V_t)={m}(V_1)+\dots +{m}(V_t)-(t-1)m(v)\), we get \(t\ell \ge {m}(V')+(t-1)m(v)\ge \frac{t+1}{2}\ell + (t-1)m(v)\). Thus \(m(v)\le \ell \frac{2t-t-1}{2(t-1)}= \frac{\ell }{2}\). By our condition in the lemma, there exists a vertex \( u\in V-v\), for which \(m(u)\le m(v) \le \frac{\ell }{2}\). Since \(m(v)<\ell \) (by Lemma 5.11), \(m(u)=m(v)=\ell =0\) cannot hold. Hence \(m(u)+m(v)>\ell \) must hold by (A0), contradicting \(m(u)\le m(v) \le \frac{\ell }{2}\). Therefore, \(t=2\). \(\square \)
This finishes the proof of the Lemma 5.13. \(\square \)
Based on Lemma 5.13, using assumption (A2) one can prove the following.
Lemma 5.15
Suppose that \(\ell >0\). Let \(v\in V\) be a vertex for which the family \(\mathcal {C}^*(v)\) is a co-partition of \(V-v\) with \(|\mathcal {C}^*(v)|\ge 3\). Then \(m(v)< m(u)\) holds for every \(u\in V-v\) or there exist two vertices \(x,y\in V-v\) such that \(T(xy)=G\).
Proof
Suppose that there exists a vertex \(u\in V-v\) with \(m(u)\le m(v)\).
Suppose first that there is an MCT set \(Z \in \mathcal {C}^*(v)\) for which \(|{\widetilde{Z}}^v|\ge 2\). Let \(z_1,z_2 \in {\widetilde{Z}}^v\) and let us take a vertex \(x \in Z\) such that m(x) is not the unique minimum of m. (Note that such x must exist as \(|{{\mathcal {C}}}^*(v)|\ge 3\) and \(\mathcal {C}^*(v)\) is a co-partition of \(V-v\) so \(|Z|\ge 2\).)
By Lemma 5.13, a tight set containing both of x and \(z_i\) is \(\{x,z_i\}\) or V for \(i=1,2\). Hence, for \(i=1,2\), \(\{x,z_i\}\) is a maximal proper (that is, \(\ne V\)) tight set in G or \(T(xy)=G\) holds for \(y=z_i\). Hence we may assume that \(\{z_1,x\}\) and \(\{z_2,x\}\) are maximal proper tight sets in G and their complements are MCT sets. Therefore, there exist at least two MCT sets avoiding x which are intersecting. Hence \({{\mathcal {C}}}^*(x)\) is a co-partition of \(V-x\) or there exists a vertex \(y\in V-x\) such that \(T(xy)=G\) by Lemma 5.12. Note that in the latter case \(y\ne v\) since there exists an MCT set in the co-partition \(\mathcal {C}^*(v)\) of \(V-v\) avoiding x and v, hence in this case we are done. In the first case, note that \(z_1\) and \(z_2\) are avoided by different members of \({{\mathcal {C}}}^*(x)\) since \(V-\{z_1,x\},V-\{z_2,x\}\in {{\mathcal {C}}}^*(x)\). Thus Lemma 5.13 for x assures that any tight set in G containing \(z_1\) and \(z_2\) is \(\{z_1,z_2\}\) or V, however, this contradicts the tightness of \({\widetilde{Z}}^v \cup v\).
Finally, suppose that, \(|{\widetilde{Z}}^v|= 1\) for each co-tight set \(Z \in \mathcal {C}^*(v)\). This implies that \(V(uv)=\{u,v\}\) for every \(u \in V-v\). By (A2), there must exist a pair \(x,y \in V-v\) for which \(V(xy)\ne \{x,y\}\). Lemma 5.13 implies now that \(V(xy)=V\) and \(T(xy)=G\). \(\square \)
Note that, when \(m\equiv k\) (that is, when G is \((k,\ell )\)-tight), \(m(v)<m(u)\) cannot hold for any pair of \(u,v \in V\), and hence the following statement is an easy corollary of Lemma 5.15. However, for general m, the proof is less obvious.
Lemma 5.16
Suppose that \(\ell >0\). Let \(v\in V\) be a vertex for which the family \(\mathcal {C}^*(v)\) is a co-partition of \(V-v\) with \(|\mathcal {C}^*(v)|\ge 3\). Then there exists a pair of vertices \(x,y\in V-v\) such that \(T(xy)=G\).
Proof
By Lemma 5.15, we only need to prove the case where \(m(v)< m(u)\) holds for every \(u\in V-v\). Furthermore, in this case the following claim also follows by Lemma 5.12 and 5.15. (Note that there exists no vertex \(w\in V-v\) for which \(T(vw)=G\) since \(\mathcal {C}^*(v)\) is a co-partition.)
Claim 5.17
Assume that there exist two intersecting MCT sets X and Y for which \(X\cup Y=V-u\) for some \(u\in V-v\). Then there exists a pair of vertices \(x,y\in V-v\) for which \(T(xy)=G\).\(\square \)
We may suppose that there exists an MCT set Z containing v since otherwise the family \(\mathcal {C}^*\) is equal to \(\mathcal {C}^*(v)\) which is a co-partition; hence it could be covered by a set \(\{x,y\}\subseteq V-v\) implying \(T(xy)=G\) by Lemma 5.4. Then, for every \(X \in \mathcal {C}^*(v)\) intersecting Z, \(X \cup Z=V\) holds by Claim 5.17. Since \(\mathcal {C}^*(v)\) is a co-partition of \(V-v\) and \(Z\ne V\), Z cannot intersect any member of \(\mathcal {C}^*(v)\). Hence Z must be the singleton v. Therefore, \(V-v\) is tight and \(d_G(v)=m(v)\).
As \(V-v\) is tight, (A3) implies that there exists a vertex \(u\in V-v\) such that \(V(uv)\ne \{u,v\}\), that is, \(\{u,v\}\) is not tight. Let \(W_1\) be the member of the co-partition \(\mathcal {C}^*(v)\) of \(V-v\) which does not contain this u. Since \(\{u,v\}\) is not tight and \(W_1\) is a minimal co-tight set in G with \(u,v\notin W_1\), \(|V-W_1|\ge 3\). Note that Lemma 5.11 implies that \(m(v)< \ell \) and Lemma 5.2 implies that \(m(v)>0\). Hence Lemma 2.2 implies that \(d_G(v,\widetilde{W_1}^v)=d_{G[V-W_1]}(v)\ge m(v).\) Let \(W_2\) be another member of \(\mathcal {C}^*(v)\). Now the tightness of \(V-W_2\) in G and Lemma 2.2 implies that \(d_G(v,\widetilde{W_2}^v)=d_{G[V-W_2]}(v)>0\). However, since \(\mathcal {C}^*(v)\) is a co-partition of \(V-v\), \(\widetilde{W_1}^v\) and \(\widetilde{W_2}^v\) are disjoint, hence \(m(v)=d_G(v)\ge d_G(v,\widetilde{W_1}^v)+ d_G(v,\widetilde{W_2}^v)>m(v)\), a contradiction. \(\square \)
Now we are ready to finish the proof of Theorem 5.5.
Proof of Theorem 5.5
We have already seen that Lemma 5.11 implies the disjointness of the \({({m},\ell )}\)-MCT sets of G when \(\ell \le 0\). Hence it is enough to prove the statement when \(\ell >0\).
Let us suppose that there exists \(X,Y\in \mathcal {C}^*\) such that \(X\cap Y\ne \emptyset \). By Lemma 5.11, \(|X\cup Y| \ge |V|-1\) holds. According to Lemmas 5.12 and 5.16, either \(X \cup Y=V\) holds or there exists a pair \(u,v\in V\) such that \(T(uv)=G\). By the minimality of MCT sets, every member of \(\mathcal {C}^*-\{X,Y\}\) must contain at least one element of both of \(V-Y=X-Y\) and \(V-X=Y-X\). Hence each member \(W\in \mathcal {C}-\{X\}\) intersects X. Again by Lemmas 5.11, 5.12, and 5.16, \(X \cup W=V\) for every \(W\in \mathcal {C}-\{X\}\), that is, \(V-X\subset W\). Let us take \(u\in X\) and \(v \in V - X\). Then \(\{u,v\}\) covers \(\mathcal {C}\), and hence \(T(uv)=G\) by Lemma 5.4. \(\square \)
Note that it can be checked in polynomial time whether \(G+uv\) is \({({m},\ell )}\)-redundant for some pair \(u,v\in V\). The naïve algorithm (which can be constructed from the algorithm of Theorem 2.6) has \(O(|V|^3)\) running time. In Sect. 6, we give a rather complex algorithm for this problem based on the above proof that has \(O(|V|^2)\) running time.
6 Algorithmic aspects
Our goal in this section is to show that the reduced augmentation problem can be solved in \(O(|V|^2)\) time (under the assumption (*)).
By Sect. 5, the MCT sets of G play an important role in the solution of the reduced problem. To give an algorithm that finds an MCT set, we need to use the following observation.
Observation 6.1
For a \((k,\ell )\)-tight graph G, let D be the in-degree constrained orientation in the output of the algorithm of Theorem 2.6. Assume that T is an \({({m},\ell )}\)-tight set in G. And let us define \(m':V(G/T)\rightarrow \mathbb {Z}_+\) and \(\ell '\in \mathbb {Z}\) like in Lemma 2.5. Then D/T can be an output of that algorithm of Theorem 2.6 when we check the \({({m}',{\ell }')}\)-sparsity of G/T, that is, the in-degree of each vertex x in D/T is at most \(m'(x)\).
Proof
Since T is \({({m},\ell )}\)-tight, T induces \({m}(T)-\ell \) edges in G, that is, T induces \({m}(T)-\ell '\) arcs in D. (More precisely, when \(\ell <0\), it induces \({m}(T)\) arcs and all the \(\ell \) edges in the set \(F'\) of G which are not oriented by D, since D[T] may induce at most \(\sum _{v\in V}\varrho _D(v)\le {m}(T)\) arcs in this case.) Hence the in-degree of T is at most \(\ell '\) in D which implies that \(\varrho _{D/T}(v)\le m'(v)\) holds for each vertex of V(G/T) (and now all edges of G/T are oriented in D/T). \(\square \)
Algorithm 6.2
Input: A graph \(G=(V,E)\) along with \(m:V\rightarrow \mathbb {Z}_+\) and \(\ell \in \mathbb {Z}\) such that (A) and (*) hold, and two vertices \(u,v \in V\).
Output: An \({({m},\ell )}\)-MCT set in G that does not contain u, v or the edge uv when \(T(uv)=G\).
-
0.
Run the algorithm of Theorem 2.6(a) on G, let D be the output orientation.
-
1.
Calculate \(T:=V^G_{({m},\ell )}(uv)\) by using D and Theorem 2.6(b).
-
2.
If \(T=V\) then Output: the edge uv, STOP.
-
3.
Contract T to \(t'\) according to Lemma 2.5, that is, \(G':= G/T,\) \(D':=D/T\), \(\ell ':=\max (\ell ,0)\), \(m'(u):=m(u)\) for each \(u\in V(G')\cap V\), \(m'(t'):=\ell '\).
-
4.
\(v:=t'\) (hence \(m'(v)=\ell '\)), \(V^*:=V(G')-v\).
-
5.
While \(V^*\ne \emptyset \), do:
-
6.
Calculate \(T':=V^{G'}_{({m}',\ell ')}(uv)\) by using \(D'\) and Theorem 2.6(b).
-
7.
If \(V'=V(G')\), then \(V^*:=V^*-u\).
-
8.
Else, Contract \(T'\) to \(t'\), so \(G':= G'/T', D':=D'/T'\).
-
9.
\(v:=t'\), \(V^*:=V^*\cap V(G')-v\).
-
10.
Output: \(V(G')-v\).
Lemma 6.3
The output of Algorithm 6.2 is either the edge uv when \(T(uv)=G\) or an \({({m},\ell )}\)-MCT set of G not containing u and v. The running time of Algorithm 6.2 is \(O(|V|^2)\).
Proof
If the output is the edge uv, then the algorithm returns this in Step 2 because \(T^G_{({m},\ell )}(uv)=G\). Otherwise, the output of Algorithm 6.2 is a vertex set. Applying Lemma 2.5 repeatedly, we conclude that the original vertex set \(U \subset V\) which is contracted during the algorithm (that is, for which \(G'=G/U\)), is an \({({m},\ell )}\)-tight set in G. Thus the output of Algorithm 6.2 is an \({({m},\ell )}\)-co-tight set.
Suppose that U is not an inclusion-wise maximal proper \({({m},\ell )}\)-tight set in G, that is, there exists a proper \({({m},\ell )}\)-tight set \(T^* \supsetneq U\) in G. Take the image of \(T^*\) in the final \(G'\), denote it with \(T^*_{G'}\). By Lemma 2.5, \(T^*_{G'}\) is tight in \(G'\), and clearly \(v \in T^*_{G'}\). Let \(u\in T^*_{G'}-v\). Since \(V^*=\emptyset \), \(u \in V(G')-V^*-v\) also holds. It now follows that \(T^{G'}_{({m}',\ell ')}(uv)=G'\), which is a contradiction, because \(T^*_{G'}\supseteq V(T^{G'}_{({m}',\ell ')}(uv))\) holds by Lemma 2.3.
Step 0 runs in \(O(|V|^2)\) time by Theorem 2.6(a). After this, Step 1 needs O(|V|) running time and every execution of the loop takes at most O(|V|) time by Theorem 2.6(b) and Observation 6.1. Thus the total running time of the algorithm is \(O(|V|^2)\). \(\square \)
We need to decide now whether there is any pair of vertices \(u,v\in V\) for which \(G+uv\) is \({({m},\ell )}\)-redundant. The motivation for this lays in Theorem 5.5, as we saw in Sect. 5 how the structure of the MCT sets are completely different if there exists such an edge, or not. We noted in the end of Sect. 5.1 how this can be decided in \(O(|V|^3)\) time. Now we answer this question in \(O(|V|^2)\) time. We start with the case when we have an MCT set consisting of a single vertex.
Lemma 6.4
Assume (A) and (*). If \(C=\{v\}\) is an \({({m},\ell )}\)-MCT singleton set, then we can check whether there exists an edge xy such that \(T(xy)=G\) and return it in \(O(|V|^2)\) time.
Proof
By Observation 5.3, if there exists a pair \(x,y\in V\) such that \(T(xy)=G\), then x or y must be v. Hence we need to check for each \(x\in V-v\) whether \(T(xv)=G\). This can be done in \(O(|V|^2)\) total time by Theorem 2.6. \(\square \)
Now we give the algorithm that decides whether G can be augmented to an \({({m},\ell )}\)-redundant graph by using one edge.
Algorithm 6.5
Input: A graph \(G=(V,E)\) along with \(m:V\rightarrow \mathbb {Z}_+\) and \(\ell \in \mathbb {Z}\) such that (A) and (*) hold.
Output: If there exists an edge e such that \(T(e)=G\), then e, otherwise a vertex v of an \({({m},\ell )}\)-MCT set.
-
1.
Choose two vertices \(u,v\in V\) with \(m(v)\ge m(u)\), such that \(\{u,v\}\) induces less than \(m(u)+m(v)-\ell \) edges. Also suppose that \(m(v)\ge m(u)\).
-
2.
Run Algorithm 6.2 with u and v. Result: edge e or MCT set \(C_{uv}\). If the result is an edge e, then Output e, STOP.
-
3.
If \(|C_{uv}|=1\), then run the algorithm of Lemma 6.4 with \(C_{uv}\). If this outputs an edge e, then Output e, STOP. Else, Output the single element \(c_1\) of \(C_{uv}\), STOP.
-
4.
Let \(c_1 \in C_{uv}\) be such that \(m(c_1)\) is not the unique minimum of m.
-
5.
Run Algorithm 6.2 with v, and \(c_1\). Result: edge e or MCT set \(C_{vc_1}\). If the result is an edge e, then Output e, STOP.
-
7.
If \(|C_{vc_1}|=1\), then run the algorithm of Lemma 6.4 with \(C_{vc_1}\). If this outputs an edge e, then Output e, STOP. Else, Output the single element \(c_2\) of \(C_{vc_1}\), STOP.
-
8.
Let \(c_2 \in C_{vc_1}-C_{uv}\).
-
9.
Run Algorithm 6.2 with \(c_1\) and \(c_2\). Result: edge e or MCT set \(C_{c_1c_2}\). If the result is an edge e, then Output e, STOP.
-
10.
If \(C_{uv} \cap C_{vc_1} = \emptyset \), \(C_{vc_1} \cap C_{c_1c_2} = \emptyset \), and \(C_{c_1c_2} \cap C_{uv} = \emptyset \), then Output: \(c_1\).
-
11.
Else, check each possible edge from v and \(c_1\), it gives a suitable edge e. Output e.
Lemma 6.6
Algorithm 6.5 decides whether there exists one edge e such that \(T(e)=G\) and returns it. If there is no such edge, then it returns an element of an \({({m},\ell )}\)-MCT set. The algorithm runs in \(O(|V|^2)\) time.
For the proof of this lemma we shall use some notation from Sect. 5.
Proof
Observe that, whenever the algorithm returns a vertex, the output is a vertex \(c_1\in C_{uv}\) or \(c_2\in C_{vc_1}\) where \(C_{uv}\) and \(C_{vc_1}\) are MCT sets by Lemma 6.3.
Also by Lemma 6.3, if Algorithm 6.5 returns an edge e after any execution of Algorithm 6.2, then \(T(e)=G\) holds thus we can stop. By Lemma 6.4, if it outputs an edge e in Step 3 or 7, then \(T(e)=G\) holds thus we can stop. If the Algorithm returns \(c_1\) after Step 10, then it is easy to see that G cannot be augmented to a redundant graph with only one edge by Observation 5.3. Also if its output is given in Step 3 or 7, then this is correct due to Lemma 6.4 and Observation 5.3. Thus we only need to prove that if Algorithm 6.5 reaches Step 11, then one edge from v or \(c_1\) augments G to an \({({m},\ell )}\)-redundant graph.
Assume that we reached Step 11. Then neither m(v) nor \(m(c_1)\) is the unique minimum of m and \( |C_{uv}|,|C_{vc_1}| \ge 2\). Also notice that in this case \(\ell >0\) according to Lemma 5.11.
Suppose first that \(C_{c_1c_2}\) and \(C_{vc_1}\) are intersecting. \(C_{c_1c_2}, C_{vc_1} \in \mathcal {C}^*(c_1)\) holds by their construction. By Lemma 5.12, there exists a vertex \(w \in V-c_1\) such that \(T(wc_1)=G\), or \(\mathcal {C}^*(c_1)\) forms a co-partition. Note that \(V-C_{uv}\) is a tight set containing u, v and \(c_2\) (which is in \(C_{vc_1}-C_{uv}\)). Moreover, \(|V-C_{uv}|>2\) must hold since \(\{u,v\}\) is not tight in G as \(i(\{u,v\})<m(u)+m(v)-\ell \). Hence, if \(\mathcal {C}^*(c_1)\) forms a co-partition, then the tightness of \(V-C_{uv}\) contradicts Lemma 5.13. Therefore, in this case there exists a vertex \(w \in V-c_1\) such that \(T(wc_1)=G\).
Suppose now that \(C_{c_1c_2}\cap C_{vc_1}=\emptyset \). If \(C_{uv}\) and \(C_{vc_1}\) are intersecting, then \(C_{uv}, C_{vc_1} \in \mathcal {C}^*(v)\). Now Lemma 5.12 implies that there exists a vertex \(w \in V-v\) such that \(T(wv)=G\), or \(\mathcal {C}^*(v)\) forms a co-partition. However, if \(\mathcal {C}^*(v)\) forms a co-partition, then, by Lemma 5.13, either \(T(c_1c_2)= G\) or \(V-C_{c_1c_2}=\{c_1,c_2\}\), contradicting the assumptions that \(|C_{vc_1}|\ne 1\) and \(C_{c_1c_2}\cap C_{vc_1}=\emptyset \). Therefore, in this case there exists a vertex \(w \in V-v\) such that \(T(wv)=G\).
If neither \(C_{c_1c_2}\) and \(C_{vc_1}\) nor \(C_{uv}\) and \(C_{vc_1}\) are intersecting, then \(C_{c_1c_2}\) intersects \(C_{uv}\), and hence \(C_{c_1c_2}\) contains every vertex in \(C_{vc_1}-c_2\) by Lemma 5.11 since \(C_{uv}\cap C_{vc_1}=\emptyset \) and \(c_2\notin C_{c_1c_2}\). Thus \(C_{c_1c_2}\) intersects \(C_{vc_1}\) by \(|C_{vc_1}|>1\), a contradiction. This proves the correctness of Algorithm 6.5.
We can find appropriate vertices u and v for Step 1 by checking each 2-element vertex set in \(O(|V|^2)\) total time. As Algorithm 6.2 and checking the size of the generated tight set for each possible new edge from a vertex runs in \(O(|V|^2)\) time by Lemma 6.3 and Theorem 2.6 like in the proof of Lemma 6.4, and we need to run the \(O(|V|^2)\) time algorithm of Lemma 6.4 at most twice, the total running time of Algorithm 6.5 is \(O(|V|^2)\). \(\square \)
Now, we focus our attention to the case where there is no edge e that augments G to a redundant graph. From this point on, the idea of our algorithm is a generalization of that of García and Tejel [8] because of Lemma 5.10. Hence from this point on, our description will be more sketchy. By Lemma 5.10, it is easy to see that the following greedy algorithm finds a transversal of the MCT sets of G starting from a vertex v which is taken from an MCT set. The running time of this algorithm is again \(O(|V|^2)\) by Theorem 2.6.
Algorithm 6.7
Input: A graph \(G=(V,E)\) along with \(m:V\rightarrow \mathbb {Z}_+\) and \(\ell \in \mathbb {Z}\) such that (A) and (*) hold and there exists no edge e that augments G to an \({({m},\ell )}\)-redundant graph, and a vertex \(v\in V\) from an \({({m},\ell )}\)-MCT set of G.
Output: A transversal of the MCT sets of G.
-
0.
Run the algorithm of Theorem 2.6(a) on G.
-
1.
Initialize \(X=\emptyset \). All vertices are unmarked. Mark v.
-
2.
Explore all vertices \(j\in V\): If j is unmarked, then calculate T(vj) (by using the output of Step 0 and Theorem 2.6(b)) and Mark all unmarked vertices in V(vj). Let \(X:=(X-V(vj))+j\).
-
3.
Output: \(X+v\).
Finally, by using the reduction steps provided by Lemma 5.9 and the above algorithms, we can easily find an optimal solution of the reduced problem. Observe that, by Theorem 2.6(b), every reduction step can be executed in O(|V|) time thus the total running time of the reduction is again \(O(|V|^2)\).
Note that it follows by Sect. 4 that assumption (A) can be omitted in our algorithms. This implies the following.
Theorem 6.8
Assume (*). Let \(G=(V,E)\) be an \({({m},\ell )}\)-tight graph. Then there exists an algorithm that gives an optimal solution for the reduced augmentation problem in \(O(|V|^2)\) time. \(\square \)
Theorem 3.3 implies now the following.
Theorem 6.9
Assume (*). Let \({\bar{G}}\) be an \({({m},\ell )}\)-rigid graph for which \(m\ge \ell \). Then there exists an \(O(|V|^2)\) time algorithm to obtain a set of edges F of minimum cardinality, such that \({\bar{G}}+ F\) is \({({m},\ell )}\)-redundant. \(\square \)
7 Complexity results
In this section we prove that the general augmentation problem is NP-hard when \(\ell >k\). Moreover, our method also implies that there exists no polynomial time constant factor approximation algorithm for this problem if P\(\ne \)NP. García and Tejel showed in [8] that the general augmentation problem is NP-hard when \(k=2\) and \(\ell =3\). Our construction is based on their idea.
First we show the NP-hardness of the following problem, called the Colored Tight Augmentation problem or CTA problem.
Problem
Let \(G=(V,E)\) be a \({(k,\ell )}\)-tight graph such that the edges in E are colored to red or black. Find a graph H on the same vertex set with the minimum number of edges, such that each black edge of G is \((k,\ell )\)-redundant in \(G\cup H\).
The CTA problem is an extension of the general problem: given an instance \({\bar{G}}=(V,{\bar{E}})\) of the general problem, one can get an instance of the CTA problem by taking a spanning \((k,\ell )\)-tight subgraph of \({\bar{G}}\) and coloring each already redundant edge to red and each not redundant edge to black. Now, for a graph \(H=(V,F)\), \({\bar{G}}\cup H\) is \((k,\ell )\)-redundant if and only if all the black edges of G are \((k,\ell )\)-redundant in \(G\cup H\) by Lemma 2.4.
By extending the work of García and Tejel [8], we shall prove that the CTA problem is NP-hard for every \((k,\ell )\) where \(k>1\), that is, also for \(\ell \le k\) in which case the general augmentation problem is solvable in polynomial time by Theorem 6.9. On the other hand, for the \((k,\ell )=(2,3)\) case the CTA problem is equivalent to the general augmentation problem: adding parallel edges to the red ones reduces the solution of the CTA problem to the solution of the general problem. (We note that the same construction works whenever \(\ell =2k-1\). Also our general construction results in the very same graph for \(\ell =2k-1\).)
Our NP-hardness proofs for both the CTA problem and the general problem are based on the following statement which extends the well-known fact that an addition of a vertex of degree k maintains the \((k,\ell )\)-tightness (or the \((k,\ell )\)-rigidity of a graph).
Lemma 7.1
Let \(G=(V,E)\) be a \((k,\ell )\)-tight graph, let \(G'=(V'\cup S,E')\) be a connected \((k,\ell )\)-sparse graph where \( V \cap V'=\emptyset \) and \(S\subseteq V\). Let \(G^*=(V\cup V', E\cup E')\). Suppose that \(e_{G'}(X)>k|X|\) holds for each \(X\subsetneq V'\), and \(e_{G'}(V')=|E'|=k|V'|\). Then
(a) \(G^*\) is \((k,\ell )\)-tight and \(V'\) is a \({(k,\ell )}\)-MCT set in \(G^*\).
(b) Assume that there are at least two disjoint \((k,\ell )\)-MCT sets \(C_1\) and \(C_2\) in G which do not intersect S. Then the \((k,\ell )\)-MCT sets of \(G^*\) are exactly \(V'\) and those \((k,\ell )\)-MCT sets of G that do not intersect S.
(c) Moreover, with the assumption of (b), if X, Y are \({(k,\ell )}\)-MCT sets of G with \(X\cap S\ne \emptyset \) while \(Y \cap S = \emptyset \), then for each \(v'\in V'\), \(x\in X\) and \(y\in Y\), \(T^{G}(xy)\subset T^{G^*}(v'y)\) holds.
Lemma 7.1 is illustrated by Fig. 1 where the graph G, formed by the solid edges, arises by \(G-X\) this way. Observe that the MCT sets in \(G-X\) are the singletons \(\{u\}\), \(\{v\}\) and \(\{z\}\) and the MCT sets in G are \(\{u\}\), \(\{v\}\) and X, that is, z is removed from the family of (3, 4)-MCT sets as claimed by Lemma 7.1(b). \(T^G(ux)\) is the graph formed by the bold edges, thus \(z\in V^G(ux)\). This implies that \(T^{G-X}(uz)\subset T^{G}(ux)\) holds by Lemma 2.3, as claimed by Lemma 7.1(c).
Proof
(a) It follows by definition that \(G^*\) induces \(k|V\cup V'|-\ell \) edges. Hence we need to prove the \({(k,\ell )}\)-sparsity of \(G^*\). Let \(X\subseteq V'\cup V\). Now, \(i_{G^*}(X)= i_{G}(X\cap V)+|E'|-e_{G'}(V'-X)\le k|X\cap V|-\ell +k|V'|-k|V'-X|=k|X\cap V|-\ell +k|X \cap V'| = k|X|-\ell \) by the \({(k,\ell )}\)-sparsity of G and our assumption on \(e_{G'}\). It follows also by our assumption on \(e_{G'}\) that \(V'\) is MCT in \(G^*\).
(b) \(V'\) is MCT in \(G^*\) by part (a). Observe that \(e_{G^*}(Z)= e_G(Z)\) holds for each \(Z\subseteq V-S\). This implies that, beside \(V'\), every MCT set of G which does not intersect \(V'\) is also an MCT set in \(G^*\). Now the disjointness of the sets \(C_1\), \(C_2\) and \(V'\) implies that the MCT sets in \(G^*\) are pairwise disjoint by Theorem 5.5. However, then, by Lemma 5.6, there is no MCT set \(Z\ne V'\) in \(G^*\) which intersects \(S\cup V'\).
(c) By Lemmas 5.7 and 5.6, \(V'\cup N_{G^*}(V')=V'\cup S\subset V^{G^*}(v'y)\). Hence \(T^{G^*}(x'y)\subset T^{G^*}(v'y)\) holds for each \(x'\in X\cap S\) by Lemma 2.3. On the other hand, \(T^{G^*}(x'y)=T^G(x'y)\) since \(x',y\in V\) and \(V'\) is co-tight in \(G^*\). Furthermore, \(T^G(x'y)=T^G(xy)\) follows by Lemma 5.10, completing our proof. \(\square \)
We shall use the set cover problem to show the NP-hardness of the CTA problem. Given a ground set X and a family \(\mathcal {S}=\{S_1,\dots ,S_m\}\) of subsets of X, an optimal solution of the set cover problem is a subfamily \(\mathcal {S'} \subseteq \mathcal {S}\) of sets with minimal cardinality such that their union is X.
Theorem 7.2
Let \(k>1\) and \(\ell <2k\) be two integers. The CTA problem is NP-hard on \((k,\ell )\)-tight graphs, moreover, there exists no polynomial time constant factor approximation algorithm for it if P\(\ne \)NP.
Proof
Given an instance of the set cover problem, a family \(\mathcal {S}\) on ground set X such that \(|X|\ge 2k+1\) and no two members of \(\mathcal {S}\) cover X, let us construct a graph. (We note here that these assumptions do not change the complexity of the set cover problem.) First take a \((k,\ell )\)-tight graph \(G_0\) on a copy \(X'\) of X such that there are at least two disjoint MCT sets in \(G_0\). (It is easy to check that such a graph exists when \(|X|\ge 2k+1\).) Let us take another copy \(X^{\prime \prime } \) of X and connect the copies \(x'\) and \(x^{\prime \prime }\) of each \(x\in X\) by an edge \(e_x\). These |X| edges will be the only black edges in our final graph; every other edge will be red. Add new edges (not parallel to the previous ones) between \(X'\) and \(X^{\prime \prime }\) until \(d(x^{\prime \prime })=k\) holds for every \(x^{\prime \prime }\in X^{\prime \prime }\). Let us denote the graph we got with these steps by \(G_1\). Now, Lemma 7.1 and Lemma 5.7 imply the following.
Claim 7.3
\(G_1\) is \((k,\ell )\)-tight and the family of MCT sets in \(G_1\) equals to the family formed by all one element subsets of \(X^{\prime \prime }\). Furthermore, \(T^{G_1}( x^{\prime \prime }y^{\prime \prime })\) induces exactly two black edges \(e_x\) and \(e_y\) for each pair \(x,y\in X\).\(\square \)
Now for every \(S \in \mathcal {S}\) we make the following extension on \(G_1\). Let \(S^{\prime \prime }\) denote the copy of S in \(X^{\prime \prime }\). Start with \(V_S=\emptyset \). First choose one vertex from \(S^{\prime \prime }\) and \(k-1\) vertices from \(X^{\prime }\) and add a new vertex v with (red) edges to these k vertices. Add v to \(V_S\). Later, when \(V_S\) is not empty, take the last vertex that is added to \(V_S\), say v, one new vertex from \(S^{\prime \prime }\), and \(k-2\) vertices from \(X^{\prime }\) and add a new vertex w of degree k connecting to these k vertices. Add also w to \(V_S\). Repeat the above addition until there are no more vertices in \(S^{\prime \prime }\) that were not used in such a step. (See Fig. 4)
Let us denote the graph that we get from \(G_1\) after running the above procedure for each \(S\in \mathcal {S}\) by \(G^*=(V^*,E^*)\). For an arbitrary \(S\in \mathcal {S}\), \(d(v)=k\) holds for every \(v\in V_S\) in the moment when it is added to \(V_S\), however, in the subsequent step this is increased to \(k+1\), except for the last vertex added to \(V_S\) that we call \(m_S\). By Lemma 7.1(b), this shows that the only MCT sets in \(G^*\) are the singletons \( M_S:=\{m_S\}\) for all \(S\in \mathcal {S}\). By the construction, it is also easy to see that \(V_S\) is co-tight in \(G^*\) for every \(S\in \mathcal {S}\). By Lemma 5.10, we may assume that the optimal solution of the CTA problem consists of edges between MCT sets, that is between the vertices \(m_S\) (\(S\in \mathcal {S}\)).
Claim 7.4
Let \(S_1,S_2\in \mathcal {S}\) and let \(e=m_{S_1}m_{S_2}\) be an edge connecting the two \({(k,\ell )}\)-MCT sets \(M_{S_1}\) and \(M_{S_2}\) of \(G^*\). Then a black edge \(e_x\) is contained in \(T^{G^*}(e)\) if and only if \(x\in S_i\cup S_j\).
Proof
Since \(V_S\) is co-tight for each \(S\in \mathcal {S}\), \(T^{G^*}(e)\subseteq G^{*}[X'\cup X^{\prime \prime }\cup V_{S_i}\cup V_{S_j}]=:G_{ij} \) by Lemma 2.3, and hence \(T^{G^*}(e)=T^{G_{ij}}(e)\). Now, by using Lemma 7.1(c) several times following the construction of \(V_{S_i}\) and \(V_{S_j}\), we get that \(T^{G_0}(x^{\prime \prime }y^{\prime \prime })\subset T^{G_{ij}}(e)\) for each pair \(x,y\in S_i\cup S_j\). Hence \(T^{G^*}(e)=T^{G_{ij}}(e)\) induces the black edge \(e_x\) for each \(x\in S_i\cup S_j\) by Claim 7.3. On the other hand, \(z^{\prime \prime }\notin V^{G_{ij}}(e)\) for \(z\in X-(S_i\cup S_j)\) since \(\{z^{\prime \prime }\}\) is co-tight in \(G_{ij}\) by Lemma 7.1(b). Hence the black edge \(e_z\) is not induced by \(T^{G^*}(e)=T^{G_{ij}}(e)\). \(\square \)
Remember, that we only need to add edges so that all the black edges become redundant. Thus from Claim 7.4 one can see that any (not necessarily optimal) solution of the CTA problem on \({G^*}\) of cardinality q gives a (not necessarily optimal) solution of the set cover problem that uses at most 2q sets and every (not necessarily optimal) solution of the set cover problem with cardinality q gives a (not necessarily optimal) solution of the CTA problem with cardinality \(\lceil \frac{q}{2}\rceil \). However, there is no constant factor approximation of the set cover problem unless P=NP by [21]. Therefore, there is no constant factor approximation of the CTA problem unless P=NP. This finishes the proof of Theorem 7.2. \(\square \)
To show the NP hardness of the general problem for \(k<\ell \), we shall modify the above NP-hardness proof in such a way that we add now \(2k-\ell \) parallel copies of each edge during the construction. To this end, we shall attach MCT sets – other than the singletons used in the above proof – by using Lemma 7.1.
Theorem 7.5
Let k and \(\ell \) be two positive integers such that \(k<\ell <2k\). Then the general augmentation problem is NP-hard on \((k,\ell )\)-rigid graphs, moreover, there exists no polynomial time constant factor approximation algorithm for it if P\(\ne \)NP.
Proof
Let a denote the greatest common divisor of \(2k-\ell \) and \(\ell -k\), and let \(b=\frac{2k-\ell }{a}\) and \(c=\frac{\ell -k}{a}\). Let us define a tree \(H_{{(k,\ell )}}=(V_{{(k,\ell )}}\cup S,E_{{(k,\ell )}})\) on \(b+c+1\) vertices, called a \({(k,\ell )}\)-caterpillar, as follows. Let \(V_{{(k,\ell )}}=\{v_1,\dots ,v_b\}\), and \(E_{{(k,\ell )}}=P_{{(k,\ell )}}\cup L_{{(k,\ell )}}\) where \(P_{{(k,\ell )}}=\{v_iv_{i+1}:i=1,\dots ,b-1\}\) is path on \(V_{{(k,\ell )}}\) and the edges of \(L_{{(k,\ell )}}\) are edges between \(V_{{(k,\ell )}}\) and S in such a way that \(d_{H_{{(k,\ell )}}}(s)=1\) for each \(s\in S\), \(d_{H_{{(k,\ell )}}}(v_1)= \lceil \frac{\ell -k}{2k-\ell } \rceil +1\), and \(d_{H_{{(k,\ell )}}}(v_i)= \lceil \frac{\ell -k}{2k-\ell }i \rceil -\lceil \frac{\ell -k}{2k-\ell }(i-1) \rceil +2\) for each \(i \in \{2,\dots ,b\}\). For a set E and \(c\in \mathbb {Z}_+\) let \({\varvec{cE}}\) denote the multiset that arises by taking c copies of each element of E. For a graph \(G=(V,E)\), \({\varvec{cG}}\) denotes the graph (V, cE). It is easy to check that \(H'_{{(k,\ell )}}=(2k-\ell )H_{{(k,\ell )}}\) is \((k,\ell )\)-sparse and has \(k|V_{{(k,\ell )}}|\) edges. Moreover, is follows by a short calculation that \(e_{H'_{{(k,\ell )}}}(X)>k|X|\) for each \(X\subsetneq V_{{(k,\ell )}}\). (It is enough to check this for subpaths of \(P_{{(k,\ell )}}\) for which the calculation is simple.) Therefore, \(H'_{{(k,\ell )}}\) fulfills the conditions of Lemma 7.1. (Observe that in Fig. 1 the (3,4)-tight graph G is obtained from \(G-X\) by gluing \(2H_{(3,4)}\) to \(G-X\).)
We can now use \(H'_{{(k,\ell )}}\) in the proof of Theorem 7.2 instead of vertices of degree k since \(|S|=c+1\ge 2\). The only difference is that we do not naturally have the second copy \(X^{\prime \prime }\) in the construction of \(G_1\). Instead we perform |X| extensions on \(G_0\) with the \(H'_{{(k,\ell )}}\) in such a way that, in the step where we add \(V^x_{{(k,\ell )}}\) for \(x\in X\), we connect \(V^x_{{(k,\ell )}}\) only to \(X'\) and one of the edges, say, \(e_{x}\) connecting \(V^x_{{(k,\ell )}}\) and \(X'\) connects an element \(x^{\prime \prime }\in V^i_{{(k,\ell )}}\) to the copy \(x'\) of x. The second copy \(X^{\prime \prime }\) of X (in which we take the copy \(S^{\prime \prime }\) of each set \(S\in \mathcal {S}\) in the final phase of the construction) is the set of these vertices \(x^{\prime \prime }\). The \((2k-\ell )\) parallel copies of the edges \(e_{x}\) for all \(x\in X\) will be the only black edges in our final graph; every other edge will be red.
This way, for each input \(\mathcal {S}\) on ground set X of the set cover problem, we obtain an instance \(G^*_{{(k,\ell )}}\) of the CTA problem on which a solution of any (not necessarily optimal) solution of the CTA problem of cardinality q gives a (not necessarily optimal) solution of the set cover problem that uses at most 2q sets and every (not necessarily optimal) solution of the set cover problem with cardinality q gives a (not necessarily optimal) solution of the CTA problem on \(G^*_{{(k,\ell )}}\) with cardinality \(\lceil \frac{q}{2}\rceil \). Observe that each edge of \(G^*_{{(k,\ell )}}\) is present \(2k-\ell \) times except the edges of \(G_0\).
Now, given the instance \(G^*_{{{(k,\ell )}}}\), defined above, we construct an instance \({\bar{G}}^*_{{(k,\ell )}}\) of the general problem by adding a new parallel copy to each red edge of \(G^*_{{{(k,\ell )}}}\). It may mean more parallel new edges added between two vertices. It is clear that all red edges of \(G^*_{{(k,\ell )}}\) are \((k,\ell )\)-redundant in \({\bar{G}}\). On the other hand, for an edge e of \(G_0\), \(T^{G^*_{{(k,\ell )}}}(e)\) is a subgraph of the \((k,\ell )\)-tight subgraph \(G_0\) of \(G^*_{{(k,\ell )}}\) by Lemma 2.3; and, for an edge \(e=uv\) that we added later in the construction of \(G^*_{{(k,\ell )}}\), \(T^{G^*_{{(k,\ell )}}}(e)=G^*[\{u,v\}]\) since the set \(\{u,v\}\) induces \(2k-\ell \) parallel edges in \(G^*_{{(k,\ell )}}\), and hence it is \((k,\ell )\)-tight in \(G^*_{{(k,\ell )}}\). Therefore, no black edge of \(G^*_{{(k,\ell )}}\) is \((k,\ell )\)-redundant in \({\bar{G}}_{{(k,\ell )}}\), and hence a (not necessarily optimal) solution of the general problem on \({\bar{G}}^*_{{(k,\ell )}}\) is a (not necessarily optimal) solution of the CTA problem on \(G^*\) and vice versa. This finishes the proof of Theorem 7.5. \(\square \)
8 Concluding remarks
8.1 Hypergraphs
We can generalize the results if the input is a hypergraph instead of a graph. Most definitions (like \({({m},\ell )}\)-tight/rigid/redundant) are straightforward to generalize. The problem we seek to solve is the following. Given an \({({m},\ell )}\)-rigid hypergraph \(\mathcal {H}=(V,\mathcal {E})\), find an edge set F (and not hyperedge set) of minimum cardinality, such that \((V,\mathcal {E}\cup F)\) is an \({({m},\ell )}\)-redundant hypergraph. The generalization of the ideas and even the proofs is straightforward, however, some notation needs to be changed. Given a hypergraph \(\mathcal {H}=(V,\mathcal {E})\), \({\varvec{d_{\mathcal {H}}(v)}}\) denotes the number of hyperedges that contain \(v\in V\) and, for \(X,Y\subseteq V\), \({\varvec{d_{\mathcal {H}}(X,Y)}}\) denotes the number of hyperedges that are induced by \(X\cup Y\) but not induced by neither X nor Y. The neighbor set of \(X \subset V\) in this case is \(N_{\mathcal {H}}(X)=\{v\in V-X: \text { there is } x\in X \text { and } e \in \mathcal {E} \text { such that } \{v,x\} \subseteq e\}\).
We shall note here that, for hypergraphs, there also exists a polynomial algorithm that satisfies all requirements of Theorem 2.6 except for the running time, see the paper by Streinu and Theran [25]. Its running time is \(O(h|V|^2)\) where h is an upper bound on the size of the hyperedges. Thus the running time of all the algorithms gets a bit worse in this case, which particularly affects every result in Sect. 6. However, other than these changes the literatim copy of all the claims and the proofs of this paper remain correct for hypergraphs.
8.2 Simple graphs
In several applications in rigidity theory (see [11, 23]), it must be assumed that all considered graphs are simple, that is, have no loops nor parallel edges. Hence only those redundant augmentations are appropriate that maintain this property, that is, the input as well as the output graph is simple. (Notice that an optimal augmenting edge set never contains two parallel edges by Lemma 2.4.) We consider here a slight generalization of this problem that we call the \(E'\)-free general problem: Given an \({({m},\ell )}\)-rigid graph \(G=(V,E)\) and \(E'\subseteq E\), find a graph \(H=(V,F)\) on the same vertex set with minimum number of edges, such that \(G\cup H\) is \({({m},\ell )}\)-redundant and the edges in F are not parallel to the edges in \(E'\). We call the version where the input is \({({m},\ell )}\)-tight the \(E'\)-free reduced problem. By using the same reduction as in Sect. 3, we can reduce the solution of the \(E'\)-free general problem to the solution of the \(E'\)-free reduced problem in \(O(n^2)\) time when \(m\ge \ell \). Hence we only need to solve the \(E'\)-free reduced problem.
Run the algorithm of Theorem 6.8. First assume that the output is a single edge uv, that is, \(T(uv)=G\) for a pair \(u,v\in V\). If \(uv\notin E'\), then uv is an optimal solution of the \(E'\)-free reduced problem. Hence we may assume that \(uv\in E'\subseteq E\). Let \(E^*\) denote the edges not in \(E'\), that we may use. If \(G+E^*\) is not \({({m},\ell )}\)-redundant, then the \(E'\)-free reduced problem is not solvable. Thus suppose that \(G+E^*\) is \({({m},\ell )}\)-redundant, that is, \(T(uv)=G=R(E^*)=\bigcup _{e\in E^*}T(e)\). Then, as \(uv\in E\), \(uv\in T(e)\) for an edge \(e \in E^*\). Hence \(G=T(uv)\subseteq T(e)= G\) by Lemma 2.3. Therefore, in this case we may calculate T(e) for each edge \(e\in E^*\) that takes \(O(|V|^3)\) time by Theorem 2.6.
Next assume that the output consists of a set F of at least two edges and (A) holds for G. Then no edge in F is parallel to any edge \(e\in E\) by Lemma 5.6 since the algorithm outputs edges connecting members of \(\mathcal {C}^*\) in this case.
Finally assume that the output consists of a set F of at least two edges and (A) does not hold for G. If (A2) or (A3) does nor hold for G, then G has less than \(c^2+2\) vertices by Sect. 4, and hence the solution of the \(E'\)-free problem is straightforward by checking all possibilities. When G violates (A1), we may delete its isolated vertices with \(m(v)=0\) like in Sect. 4. If (A) holds for the resulting graph then the output of our algorithm does not use any edge parallel to any edge \(e\in E\) by Lemma 5.6 and we are done. Otherwise, the resulting graph again has less than \(c^2+2\) vertices. Here we need to be careful since it is possible that the \(E'\)-free augmentation is not solvable for the arising graph while it is solvable for G (for example by using some edges uv from a deleted vertex with \(m(u)=0\)). However, observe that the sets of edges in \(T(u_1v)\) and \(T(u_2v)\) are the same for \(u_1,u_2,v\in V\) with \(m(u_1)=m(u_2)=d(u_1)=d(u_2)=0\), moreover, the edge set of \(T(u_1u_2)\) is a subset of both. Hence, in this case, we may add back a single vertex u with \(m(u)=d(u)=0\) and solve the \(E'\)-free reduced problem on the arising graph on less than \(c^2+3\) vertices by checking all possibilities.
8.3 Adding multiple edges
In some other applications, instead of adding non parallel edges, in contrast, we need to add several parallel copies of each edge in the augmentation, that is, we want to minimize |F| such that \(G+cF\) is \({({m},\ell )}\)-redundant. (For example, such a problem arises for \(m\equiv k=\ell \) when one wants to augment a ‘rigid generic body-hinge framework’ to ‘globally rigid’ by adding some hinges (see [15]).) Note that, if G is an \({({m},\ell )}\)-tight graph and F is a set of edges on the same vertex set, then \(R(cF)=\bigcup _{f\in cF}T(f)=\bigcup _{f\in F}T(f)=R(F)\) by Lemma 2.4. Hence, for any \({({m},\ell )}\)-rigid graph G, \(G+cF\) is \({({m},\ell )}\)-redundant if and only if \(G+F\) is \({({m},\ell )}\)-redundant. Therefore, the above version of the augmentation problem is equivalent to the original one.
8.4 Further directions
We considered our augmentation problem only for \((k,\ell )\)-rigid inputs, that is, when the input graph has a spanning \((k,\ell )\)-tight subgraph. It would be natural to consider the problem for general input graphs. This problem was solved for the case where \(k=\ell \) by [4, 7], however, we leave it open for other values of k and \(\ell \). A specific instance of this open problem is the case where the input is \((k,\ell )\)-sparse or even more specifically contains no edges. Since there always exists a \({(k,\ell )}\)-circuit on a sufficiently large vertex set and such a graph is \((k,\ell )\)-redundant and has \(k|V|-\ell +1\) edges, this augmentation problem for edgeless graphs can be solved easily. However, if the edges are weighted, then even with a metric weight function the question becomes rather interesting. For example, the case of \(k=\ell =1\) is the well-known Minimum Cost 2-Edge Connected Spanning Subgraph problem. Recently, Jordán and the second author of this paper [16] considered the \((k,\ell )=(2,3)\) case of this problem and gave a 2-approximation algorithm to the metric weight case. By generalizing their method and using the results of this paper, it seems to be possible to obtain similar approximation algorithms for other values of k and \(\ell \).
Another problem, which is also closely related to our augmentation problem, is a version of the pinning problem from rigidity theory. In the pinning problem, our goal is to anchor a minimum set of joints in a bar-joint framework such that the resulting framework is rigid\(/\)globally rigid\(/\)redundantly rigid. In the generic case, pinning can be modeled by adding a complete graph on the anchored vertices to our graph (see [14]). Fekete and Jordán [5] investigated the (2-dimensional) global rigidity version of this problem and gave a 3-approximation algorithm. Jordán [14] obtained the optimal (2, 3)-redundant pinning of a (2, 3)-tight graph by using [14, Theorem 3.9.13] (that is, the special case of Theorem 5.5 for (2,3)-tight graphs). The main idea behind Jordán’s work is similar to Observation 5.3: it can be seen easily that each co-tight set must contain a pinned vertex. By using this idea, our results can be applied for the generalizations of this problem (with \((k,\ell )\)-tight or \((k,\ell )\)-rigid inputs) and one can obtain the similar positive and negative results to the ones what we obtained for our augmentation problem.
References
Aspnes, J., Eren, T., Goldenberg, D.K., Morse, A.S., Whiteley, W., Yang, Y.R., Anderson, B.D.O., Belhumeur, P.N.: A theory of network localization. IEEE Trans. Mob. Comput. 5(12), 1663–1678 (2006)
Berg, A.R., Jordán, T.: Algorithms for graph rigidity and scene analysis. In G. Di Battisa and U. Zwick (eds.), Algorithms: ESA, vol. 2832, pp. 78–89, Springer (2003)
Connelly, R., Jordán, T., Whiteley, W.: Generic global rigidity of body-bar frameworks. J. Comb. Theory Ser. B 103(6), 689–705 (2013)
Eswaran, K.P., Tarjan, R.E.: Augmentation problems. SIAM J. Comput. 5(4), 653–665 (1976)
Fekete, Zs., Jordán, T.: Uniquely localizable networks with few anchors. In: Nikoletseas, S.E., Rolim, J.D.P. (eds.) Algorithmic Aspects of Wireless Sensor Networks, pp. 176–183. Springer, Berlin (2006)
Frank, A.: Connections in Combinatorial Optimization. Oxford University Press, Oxford (2011)
Frank, A., Király, T.: Combined connectivity augmentation and orientation problems. Discrete Appl. Math. 131(2), 401–419 (2003)
García, A., Tejel, J.: Augmenting the rigidity of a graph in \({{{\mathbb{R}}}}^{{2}}\). Algorithmica 59(2), 145–168 (2011)
Hendrickson, B.: Conditions for unique graph realizations. SIAM J. Comput. 21(1), 65–84 (1992)
Jackson, B., Jordán, T.: Brick partitions of graphs. Discrete Math. 310(2), 270–275 (2010)
Jackson, B., Nixon, A.: Global rigidity of generic frameworks on the cylinder. J. Comb. Theory Ser. B 139, 193–229 (2019)
Jacobs, D.J., Hendrickson, B.: An algorithm for two dimensional rigidity percolation: the pebble game. J. Comput. Phys. 137, 346–365 (1997)
Jacobs, D.J., Thorpe, M.F.: Generic rigidity percolation: the pebble game. Phys. Rev. Lett. 75, 4051–4054 (1995)
Jordán, T.: Combinatorial rigidity: graphs and matroids in the theory of rigid frameworks. In: Discrete Geometric Analysis. volume 34 of MSJ Memoirs, pp. 33–112. Mathematical Society of Japan, Japan (2016)
Jordán, T., Király, Cs, Tanigawa, S.: Generic global rigidity of body-hinge frameworks. J. Comb. Theory Ser. B 117, 59–76 (2016)
Jordán, T., Mihálykó, A.: Minimum cost globally rigid subgraphs. In: Bárány, I., Katona, G.O.H., Sali, A. (eds.) Building Bridges II: Bolyai Society Mathematical Studies, vol. 28, pp. 257–278. Springer, Berlin, Heidelberg (2019)
Király, Cs.: An efficient algorithm for testing \((k,\ell )\)-sparsity when \(\ell <0\). Technical report (Quick Proof) QP-2019-04, Egerváry Research Group, Budapest, (2019). www.cs.elte.hu/egres
Laman, G.: On graphs and rigidity of plane skeletal structures. J. Eng. Math. 4, 331–340 (1970)
Lee, A., Streinu, I.: Pebble game algorithms and sparse graphs. Discrete Math. 308(8), 1425–1437 (2008)
Lorea, M.: On matroidal families. Discrete Math. 28(1), 103–106 (1979)
Lund, C., Yannakakis, M.: On the hardness of approximating minimization problems. J. ACM 41(5), 960–981 (1994)
Nash-Williams, C.S.J.A.: Decomposition of finite graphs into forests. J. London Math. Soc. 39, 12 (1961)
Nixon, A., Owen, J.C., Power, S.C.: Rigidity of frameworks supported on surfaces. SIAM J. Discrete Math. 26(4), 1733–1757 (2012)
Pollaczek-Geiringer, H.: Über die Gliederung ebener Fachwerke. ZAMM - J. Appl. Math. Mech. 7(1), 58–72 (1927)
Streinu, I., Theran, L.: Sparse hypergraphs and pebble game algorithms. Eur. J. Combinatorics 30(8), 1944–1964 (2009)
Tay, T.-S.: Henneberg’s method for bar and body frameworks. Struct. Topol. 17, 53–58 (1991)
Whiteley, W.: Some matroids from discrete applied geometry. In J.E. Bonin, J.G. Oxley, and B. Servatius (ed.), Matroid theory. volume 197 of Contemporary Mathematics. pages 171–311. AMS, (1996)
Whiteley, W.: Rigidity of molecular structures: generic and geometric analysis. In: Thorpe, M.F., Duxbury, P.M. (eds.) Rigidity Theory and Applications, pp. 21–46. Springer, US, Boston, MA (2002)
Yu, C., Anderson, B.D.O.: Development of redundant rigidity theory for formation control. Int. J. Robust Nonlinear Control 19(13), 1427–1446 (2009)
Acknowledgements
Projects Nos. NKFI-128673 and K-135421 have been implemented with the support provided from the National Research, Development and Innovation Fund of Hungary, financed under the Hungarian Scientific Research Fund FK_18 and K_20 funding schemes. The first author was supported by the János Bolyai Research Scholarship of the Hungarian Academy of Sciences and by the ÚNKP-19-4 and ÚNKP-20-5. New National Excellence Program of the Ministry for Innovation and Technology. The second author was supported by the ÚNKP-18-3 New National Excellence Program of the Ministry of Human Capacities, Hungary. The authors are grateful to Tibor Jordán for the inspiring discussions and his comments.
Funding
Open access funding provided by Eötvös Loránd University.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This paper is a full version of Cs. Király, A. Mihálykó: Sparse graphs and an augmentation problem. D. Bienstock and G. Zambelli (Eds.): IPCO 2020, LNCS 12125, pp. 238–251, 2020.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Király, C., Mihálykó, A. Sparse graphs and an augmentation problem. Math. Program. 192, 119–148 (2022). https://doi.org/10.1007/s10107-021-01689-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-021-01689-0