Penalty alternating direction methods for mixed-integer optimal control with combinatorial constraints

Abstract

We consider mixed-integer optimal control problems with combinatorial constraints that couple over time such as minimum dwell times. We analyze a lifting and decomposition approach into a mixed-integer optimal control problem without combinatorial constraints and a mixed-integer problem for the combinatorial constraints in the control space. Both problems can be solved very efficiently with existing methods such as outer convexification with sum-up-rounding strategies and mixed-integer linear programming techniques. The coupling is handled using a penalty-approach. We provide an exactness result for the penalty which yields a solution approach that convergences to partial minima. We compare the quality of these dedicated points with those of other heuristics amongst an academic example and also for the optimization of electric transmission lines with switching of the network topology for flow reallocation in order to satisfy demands.

1 Introduction

Optimal control problems subject to integer restrictions on some part of the controls have recently received a lot of attention in the literature. This problem class is a convenient way to model, for instance, autonomous driving in case of vehicles with gear shift power units [25], contact problems such as robotic multi-arm transport [5], or the operation of networked infrastructure systems such as gas pipelines [19], water canals [20], traffic roads [14], and power transmission lines [13] with switching of valves, gates, traffic lights and interconnectors, respectively. Often, the integer controls are additionally constrained in order to prevent certain switching configurations, to limit the number of switches or to enforce certain dwell or dead times after a switch. In this paper, we consider such combinatorial constraints with a focus on conditions which cannot be imposed pointwise and hence couple over time.

A discretization of such problems naturally leads to mixed-integer non-linear programs that often become computationally intractable when the discretization stepsizes tend to zero. Moreover, when passing to the limit, one may face convergence issues [22]. A computationally much more efficient alternative solution approach is based on decomposition techniques, splitting the problem into a continuous subproblem by partial outer convexification with relaxation of binary multipliers (POC) combined with a combinatorial integral approximation problem (CIAP) [21, 23, 24, 28, 34, 36, 37]. However, in the presence of combinatorial constraints that couple over time, this approach only yields feasible solutions with a priori lower bounds, but yet without any characterization of optimality in some reasonable sense on the mixed-integer level.

We consider here another approach based on the idea of alternating direction methods (ADM). This will provide feasible solutions which can be characterized as partially optimal in a lifted sense. The approach uses POC and CIAP in one direction and a mixed-integer linear problem (differing from the combinatorial integral approximation problem) in another direction. Both directions are weakly coupled using a penalty term with adapting an idea outlined in [11]. Based on exactness of this penalty, we provide a convergence result of this method. Our analysis applies to problems in the setting of abstract semilinear evolutions subject to control constraints. However, the methods can be extended to state constraints. In particular, the techniques apply to optimal control problems with ordinary differential equations. The method can be also seen as an adaptation of classical feasibility pump algorithms (for an overview, see [3]) with heavy structure exploitation for mixed-integer optimal control problems.

One feature of our approach is a clear separation of the combinatorial aspects from the continuous control aspects of the problem. This is in contrast to, e.g., the approach proposed in [38, 39]. There, the full problem is discretized and then a variant of an Alternating Direction Method of Multipliers (ADMM) is used to obtain heuristic solutions. Further recent applications of ADM type methods are related to electricity networks, see e.g. [4, 9, 27].

In a numerical study, we consider two problems from the mintOC.de library [35], which we augment by minimum dwell-time constraints. We compare the proposed approach with direct discretization and mixed-integer programming techniques in order to address local vs. global optimality and to the decomposition with POC and CIAP as a heuristic.

We note that continuous reformulations of such problems with switching time and mode insertion optimization or combinatorial constraints can also be seen as an alternating direction method [8, 29, 32, 33], but that the approach proposed here is different.

The article is organized as follows. In Sect. 2, we present the problem formulation. In Sect. 3, we extend the framework of alternating direction methods to partial $\varepsilon$-optimality. In Sect. 4, we apply the $\varepsilon$-ADM framework together with penalty techniques to mixed-integer optimal control problems as the main algorithm and develop the convergence theory. In Sect. 5, we provide our numerical results. In Sect. 6, we give concluding remarks.

2 Problem formulation

We consider a mixed-integer optimal control problem of the form

$$\begin{aligned} \min _{y,u,v}\quad&\Phi (y(T)) \end{aligned}$$

(1a)

$$\begin{aligned} \text {s.t.} ~&{\dot{y}}(t)=Ay(t)+f(y(t),u(t),v(t))\quad&\text {on}~Y,~t \in (0,T),~y(0)=y_0, \end{aligned}$$

(1b)

$$\begin{aligned}&u \in \Sigma \subset U_t, \end{aligned}$$

(1c)

$$\begin{aligned}&v \in \Gamma \subset V_t, \end{aligned}$$

(1d)

$$\begin{aligned}&y \in Y_t, \end{aligned}$$

(1e)

where for some $M\in \mathbb {N}$ and $p \in (0,\infty ]$, Y and U are Banach spaces, $Y_t=C([0,T];Y)$, $U_t=L^p(0,T;U)$, $V_t=L^\infty (0,T;\{0,1\}^M)$, A is a (densely defined) linear operator on Y, f is a nonlinear mapping $f: Y \times U \times \{0,1\}^M \rightarrow Y$, $\Phi$ is a nonlinear function $\Phi : Y \rightarrow \mathbb {R}\cup \{\infty \}$ representing state costs, $\Sigma$ is a subset of $U_t$ representing constraints on the continuous control u, and $\Gamma$ is a subset of $V_t$ representing combinatorial constraints (e. g., dwell-time constraints and switching order constraints).

We say that the set of combinatorial constraints $\Gamma$ has a uniform finiteness property, if there exists a constant $n_s \in \mathbb {N}$ such that $v \in \Gamma$ implies that v is piecewise constant with at most $n_s$ switching points.

Example 1

(Combinatorial constraints) With $v=(v_1,\ldots ,v_M)$ being the componentwise respresentation of $v \in V_t$ and the total variation of the ith component on the interval $(t_1,t_2) \subset (0,T)$ being denoted by

$$\begin{aligned} |v_i|_{(t_1,t_2)} = \sup \left\{ \int \limits _{t_1}^{t_2} v_i(t) \phi '(t)\,dt : \phi \in C^1_c(t_1,t_2), \Vert \phi \Vert _\infty \le 1 \right\} , \end{aligned}$$

where $C^1_c(t_1,t_2)$ denotes continuously differentiable vector functions of compact support on $(t_1,t_2)$, we can for example enforce a minimal dwell-time $\tau _{\min }$ with the constraint

$$\begin{aligned} v_i(t+\tau _{\min })-v_i(t)+|v_i|_{(t,t+\tau _{\min })} \le 2 ~\text {for all}~t \in (0,T-\tau _{\min }),~i=1,\ldots ,M \end{aligned}$$

(2)

or directly limit the total number of switches for the ith component to $n_s^{\max }$ by

$$\begin{aligned} |v_i|_{(0,T)} \le n_s^{\max },~i=1,\ldots ,M. \end{aligned}$$

(3)

In both cases it is easy to see that any set $\Gamma \subset V_t$ containing one of these constraints has the uniform finiteness property. Further additional constraints are of course possible, for instance, a maximum dwell-time $\tau _{\max }$ for a subset of components $I \subset \{1,\ldots ,M\}$

$$\begin{aligned} v_i(t)-v_i(t-\tau _{\max })+|v_i|_{(t-\tau _{\max },t)} \ge 2 ~\text {for all}~t \in (\tau _{\max },T),~i \in I. \end{aligned}$$

(4)

Constraints of the form (2)–(4) or variants of it are significant in many applications that involve switching control, but they are typically extremely difficult to be treated in the context of mixed-integer optimal control because they are not defined pointwise in time.

Concerning the wellposedness of the problem, we make the following assumptions.

Assumption 1

Suppose that A generates a strongly continuous semigroup $e^{tA}$ on Y, and that there exists a constant $K>0$ such that, for all $v \in \{0,1\}^M$,

• (i) the map $(y,u) \mapsto f(y,u,v)$ is continuous on $Y \times U$,

• (ii) $\Vert f(y,u,v)\Vert _Y \le K(1+\Vert y\Vert )$ for all $y \in Y$, $u \in U$,

• (iii) $\Vert f(y,u,v)-f(z,u,v)\Vert _Y \le K\Vert y-z\Vert _Y$ for all $y,z \in Y$, $u \in U$.

Moreover, assume that $\Phi :Y \rightarrow {\mathbb {R}}$ is Lipschitz continuous on bounded subsets of Y.

We note that the conditions of Assumption 1 are sufficient for the state equation (1b) to admit a unique solution $y(\cdot ;u,v)$ in C([0, T]; Y) given by

$$\begin{aligned} y(t)=e^{tA}y_0 + \int \limits _0^t e^{(t-\tau )A}f(y(\tau ),u(\tau ),v(\tau ))\,d\tau . \end{aligned}$$

(5)

Of course, other conditions are also possible, see e.g., [30]. Moreover, the uniform finiteness property is crucial for the existence of optimal solutions for the problem (1). For additional problem specific assumptions, appropriate wellposedness results can for example be obtained via parametric programming. The next theorem illustrates this for the case of generators of immediately compact semigroups.

Theorem 1

Suppose that Assumption 1 holds. Moreover, assume that X is separable and reflexive, $\Sigma =U_t$ and that $f(y,U,v_i)$ is closed and convex in Y, $e^{tA}$ is compact for $t>0$ and that $\Gamma$ has the uniform finiteness property. Then the problem (1) has an optimal solution $(y^*,u^*,v^*)$.

Proof

Under the uniform finiteness property, the problem (1) can be considered as a parametric two stage problem, where the inner problem consists of minimizing with respect to u and the outer problem is a minimization with respect to finitely many switching times $\tau _k$. Under the given assumptions, the inner problem has an optimal solution and the optimal value depends continuously on the initial data [6], and hence via (5) on the switching times $\tau _k \in [0,T]$. The claim then follows from the extreme value theorem of Weierstrass.$\square$

For the solution approach considered below, we note that under the Assumption 1, we can consider the reduced problem

$$\begin{aligned} \min _{u,v}\quad&\varPsi (u,v):=\Phi (y(T;u,v)) \end{aligned}$$

(6a)

$$\begin{aligned} \text {s.t.} ~&u \in \Sigma \subset U_t, v \in \Gamma \subset V_t\end{aligned}$$

(6b)

and results for (6) can be carried over to the original problem (1) via (5).

3 ADM with $\varepsilon$-optimality

As a solution approach we extend here the idea of ADM. Suppose we were to minimize a nonlinear function $\varPsi (u,v)$ over $u \in U$ and $v \in V$ subject to constraints $(u,v) \in \Omega$ for some given feasible set $\Omega$. Further suppose that we can compute $\varepsilon$-optimal solutions for each of the partials u (with v fixed) and v (with u fixed). Then, given some $\varepsilon \ge 0$ and some guess $(u^0,v^0)$, we can consider the following sequential approach to compute a solution candidate $(u^*,v^*)$:

• (i) Find $u^{l+1}$ such that $\varPsi (u^{l+1},v^l) \le \varPsi (u,v^l) + \frac{\varepsilon }{2}$ for all $(u,v^l) \in \Omega$.

• (ii) If $\varPsi (u^{l+1},v^l) \ge \varPsi (u^l,v^l)-\frac{\varepsilon }{2}$, set $(u^*,v^*)=(u^l,v^l)$.

• (iii) Find $v^{l+1}$ such that $\varPsi (u^{l+1},v^{l+1}) \le \varPsi (u^{l+1},v) + \frac{\varepsilon }{2}$ for all $(u^{l+1},v) \in \Omega$.

• (iv) If $\varPsi (u^{l+1},v^{l+1}) \ge \varPsi (u^{l+1},v^l)-\frac{\varepsilon }{2}$, set $(u^*,v^*)=(u^{l+1},v^l)$.

• (v) Set $l=l+1$ and continue with step (i).

This algorithm may not terminate. For classical ADM, there are well-known conditions under which we can ensure that the algorithm does not cycle, i.e. that the algorithm does not get stuck in a loop of different solutions; for a discussion, see [11]. However, if it terminates, we can conclude that $(u^*,v^*)$ satisfies

$$\begin{aligned} \varPsi (u^*,v^*)&\le \varPsi (u,v^*)+\varepsilon ,\quad \text {for all}~(u,v^*) \in \Omega \end{aligned}$$

(7a)

$$\begin{aligned} \varPsi (u^*,v^*)&\le \varPsi (u^*,v)+\varepsilon ,\quad \text {for all}~(u^*,v) \in \Omega . \end{aligned}$$

(7b)

This can be seen as follows: If the algorithms terminates in step (ii), we have for some ${\hat{l}}$ from (ii)

$$\begin{aligned} \varPsi (u^*,v^*)= \varPsi (u^{{\hat{l}}},v^{{\hat{l}}}) \le \varPsi (u^{{\hat{l}}+1},v^{{\hat{l}}}) + \frac{\varepsilon }{2} \end{aligned}$$

and from (i)

$$\begin{aligned} \varPsi (u^{{\hat{l}}+1},v^{{\hat{l}}}) \le \varPsi (u,v^{{\hat{l}}}) + \frac{\varepsilon }{2},\quad \text {for all}~(u,v^{{\hat{l}}}) \in \Omega , \end{aligned}$$

hence, with $v^{{\hat{l}}}=v^*$, we get

$$\begin{aligned} \varPsi (u^*,v^*) \le \varPsi (u,v^*) + \varepsilon ,\quad \text {for all}~(u,v^*) \in \Omega . \end{aligned}$$

Moreover, from step (iii) with $l={\hat{l}}-1$, we have

$$\begin{aligned} \varPsi (u^*,v^*)=\varPsi (u^{{\hat{l}}},v^{{\hat{l}}}) \le \varPsi (u^{{\hat{l}}},v)+\frac{\varepsilon }{2},\quad \text {for all}~(u^{{\hat{l}}},v) \in \Omega , \end{aligned}$$

hence, again with $u^{{\hat{l}}}=u^*$, we have

$$\begin{aligned} \varPsi (u^*,v^*) \le \varPsi (u^*,v)+\varepsilon ,\quad \text {for all}~(u^*,v)\in \Omega . \end{aligned}$$

If the algorithm terminates in step iv), we have for some ${\hat{l}}$ from iv)

$$\begin{aligned} \varPsi (u^*,v^*)=\varPsi (u^{{\hat{l}}+1},v^{{\hat{l}}})\le \varPsi (u^{{\hat{l}}+1},v^{{\hat{l}}+1})+\frac{\varepsilon }{2} \end{aligned}$$

and from (iii)

$$\begin{aligned} \varPsi (u^{{\hat{l}}+1},v^{{\hat{l}}+1}) \le \varPsi (u^{{\hat{l}}+1},v)+\frac{\varepsilon }{2},\quad \text {for all}~(u^{{\hat{l}}},v) \in \Omega . \end{aligned}$$

Hence, with $u^{{\hat{l}}+1}=u^*$, we get

$$\begin{aligned} \varPsi (u^*,v^*) \le \varPsi (u^*,v)+\varepsilon ,\quad \text {for all}~(u^*,v) \in \Omega . \end{aligned}$$

Moreover, from (i), we have

$$\begin{aligned} \varPsi (u^*,v^*)=\varPsi (u^{{\hat{l}}+1},v^{{\hat{l}}}) \le \varPsi (u,v^{{\hat{l}}})+\frac{\varepsilon }{2},\quad \text {for all}~(u,v^{{\hat{l}}}) \in \Omega . \end{aligned}$$

Hence with $v^{{\hat{l}}}=v^*$, we get

$$\begin{aligned} \varPsi (u^*,v^*) \le \varPsi (u,v^*) + \varepsilon ,\quad \text {for all}~(u,v^*) \in \Omega . \end{aligned}$$

We shall call points $(u^*,v^*)$ satisfying (7a) and (7b) p-$\varepsilon$-optimal as a shorthand for partially $\varepsilon$-optimal.

4 ADM and p-minima for mixed-integer optimal control problems

Concerning the mixed-integer optimal control problem (1) or equivalently for the reduced form (6), a natural ADM splitting is using the directions $u \in U$ and $v \in V$. However, in the direction of v, this still results in a mixed-integer nonlinear optimization problem subject to a differential equation. To avoid this, we will instead use that (1) is equivalent to

$$\begin{aligned} \min _{u,v,{\tilde{v}}}\quad&\varPsi (u,v) \end{aligned}$$

(8a)

$$\begin{aligned} \text {s.t.} ~&u \in \Sigma \subset U_t, \end{aligned}$$

(8b)

$$\begin{aligned}&v = {\tilde{v}} \end{aligned}$$

(8c)

$$\begin{aligned}&{\tilde{v}} \in \Gamma \subset V_t, v \in V_t, \end{aligned}$$

(8d)

and consider a splitting with respect to the directions (u, v) and $\tilde{v}$. This particular splitting is chosen deliberately in view of the fact that the two subproblems can be efficiently solved to $\varepsilon$-optimallity with existing techniques. Motivated by (7a) and (7b), we say that a point $(u^*,v^*)$ is p-$\varepsilon$-minimal for (6) if $([u^*,v^*],v^*)$ is p-$\varepsilon$-optimal for (8). Consistently, we say that a point $(y^*,u^*,v^*)$ is p-$\varepsilon$-minimal for the original problem (1) if $(u^*,v^*)$ is a p-$\varepsilon$-minimum of (6) and $y^*$ is a solution of the state equation (1b) with $u=u^*$ and $v=v^*$. We note that p-$\varepsilon$-minima are not necessarily global $\varepsilon$-minima. But any global minimum of (1) is p-$\varepsilon$-minimal with $\varepsilon =0$. For brevity, we call p-$\varepsilon$-minima with $\varepsilon =0$ just p-minima.

The above discussion motivates to compute p-minima of good quality. To this end, we enforce the coupling of v and ${\tilde{v}}$ in (8c) weakly with a suitable penalty term. The penalty parameter can then eventually be used to avoid getting stuck in p-$\varepsilon$-minima with too high objective. This idea was introduced recently in [11] for classical ADM in the context of feasibility pumps for MINLPs. Suitably adapted to our setting here, we are going to show an exactness result for the penalty problem.

We may consider the optimal value function of the reduced problem (6) partially with respect to u

$$\begin{aligned} \eta (v):=\inf _{u \in \Sigma \subset U_t} \varPsi (u,v) \end{aligned}$$

(9)

as a function $\eta :V_t\rightarrow \mathbb {R}\cup \{-\infty ,+\infty \}$. We will impose the following technical assumption on $\eta$ using the 1-norm $\mathchoice{\left|v \right|}{|v|}{|v\Vert }{|v|}_{l_1}=\sum _{i=1}^M |v_i|$ on $\{0,1\}^M$.

Assumption 2

Given an optimal solution $(y^*,u^*,v^*)$ of (1), or equivalently an optimal solution $(u^*,v^*)$ of problem (6) the value function $\eta$ defined in (9) is locally Lipschitz continuous in the sense that for all $\delta >0$ there exists a constant L such that

$$\begin{aligned} |\eta (v^*)-\eta (v)| \le L \int \limits _0^T \mathchoice{\left|v^*(t)-v(t) \right|}{|v^*(t)-v(t)|}{|v^*(t)-v(t)\Vert }{|v^*(t)-v(t)|}_{l_1}\,dt \end{aligned}$$

(10)

for all $v \in V_t$ with $\int _0^T \mathchoice{\left|v^*(t)-v(t) \right|}{|v^*(t)-v(t)|}{|v^*(t)-v(t)\Vert }{|v^*(t)-v(t)|}_{l_1}\,dt \le \delta$.

Assumption 2 is typically satisfied if the optimal solution $(y^*,u^*,v^*)$ satisfies a constraint qualification. For instance for mixed-integer linear quadratic optimal control problems the Lipschitz continuity of the optimal value function under a constraint qualification of a Slater-type is discussed in [16]. For mixed-integer finite-dimensional problems, conditions are provided in [15] and [22].

Now we consider the following auxiliary problem

$$\begin{aligned} \min _{y,u,v,{\tilde{v}}}\quad&\Phi (y(T))+ \rho \int \limits _0^T\mathchoice{\left|v(t)-{\tilde{v}}(t) \right|}{|v(t)-{\tilde{v}}(t)|}{|v(t)-{\tilde{v}}(t)\Vert }{|v(t)-{\tilde{v}}(t)|}_{l_1}\,dt \end{aligned}$$

(11a)

$$\begin{aligned} \text {s.t.} ~&{\dot{y}}(t)=Ay(t)+f(y(t),u(t),v(t))\quad \text {on}~Y,~t \in (0,T),~y(0)=y_0 \end{aligned}$$

(11b)

$$\begin{aligned}&u \in \Sigma \subset U_t, ~v \in V_t, ~{\tilde{v}} \in \Gamma \subset V_t, ~y \in Y_t, \end{aligned}$$

(11c)

with a penalty parameter $\rho \ge 0$. With (5) and (6a) we can reduce (11) to

$$\begin{aligned} \min _{u,v,{\tilde{v}}}\quad&\varPsi _\rho (u,v,{\tilde{v}}):=\varPsi (u,v)+ \rho \int \limits _0^T\mathchoice{\left|v(t)-{\tilde{v}}(t) \right|}{|v(t)-{\tilde{v}}(t)|}{|v(t)-{\tilde{v}}(t)\Vert }{|v(t)-{\tilde{v}}(t)|}_{l_1}\,dt \end{aligned}$$

(12a)

$$\begin{aligned} \text {s.t.} ~&u \in \Sigma \subset U_t, ~v \in V_t, ~{\tilde{v}} \in \Gamma \subset V_t. \end{aligned}$$

(12b)

The following result shows the exactness of the penalty term in (11) and relates global minima of (6) to p-minima of (12).

Theorem 2

Let $(u^*,v^*)$ be a global minimum of problem (6) satisfying Assumption 2. Then, there exists a penalty parameter $\bar{\rho }$ such that $([u^*,v^*], v^*)$ is a p-minimum of (12) for all $\rho \ge {\bar{\rho }}$.

Proof

Let $(u^{*}, v^{*})$ be an optimal solution of (6). We note that by construction $u = u^{*}$, $v = v^{*}$, $\tilde{v} = v^{*}$ is a global minimum of (8).

We have to show that $([u^*,v^*],{\tilde{v}}^*)$ satisfies

$$\begin{aligned} \varPsi _\rho (u^*,v^*,{\tilde{v}})&\ge \varPsi _\rho (u^*,v^*,{\tilde{v}}^*)-\varepsilon \quad \text {for all}~(u^*,v^*,{\tilde{v}})~\text {feasible for (12)} \end{aligned}$$

(13a)

$$\begin{aligned} \varPsi _\rho (u,v,{\tilde{v}}^*)&\ge \varPsi _\rho (u^*,v^*,\tilde{v}^*)-\varepsilon \quad \text {for all}~(u,v,\tilde{v}^*)~\text {feasible for (12)} \end{aligned}$$

(13b)

with $\varepsilon =0$.

It can be seen that condition (13a) holds with $\varepsilon =0$ for all $\rho \ge 0$. This follows directly from the definition of $\varPsi _{\rho }$.

To show condition (13b) with $\varepsilon =0$, we assume we are given (u, v) and consider the triple $(u, v, {v}^{*})$. Without loss of generality, we may assume that u is chosen optimally in the sense of (9). By the definition of $\varPsi _{\rho }$, condition (13b) with $\varepsilon =0$ is equivalent to

$$\begin{aligned} \varPsi (u,v) + \rho \int \limits _0^T\mathchoice{\left|v - {v}^{*} \right|}{|v - {v}^{*}|}{|v - {v}^{*}\Vert }{|v - {v}^{*}|}_{l_1}\,dt \ge \varPsi (u^*,v^*). \end{aligned}$$

(14)

We directly observe that if $\varPsi (u,v) \ge \varPsi (u^*,v^*)$ holds, then claim (14) is true for all $\rho \ge 0$. This is, for instance, the case if $v = {v}^{*}$ holds, i.e. if $(u,v,{v}^{*})$ is feasible for (8), because $(u^{*}, v^{*})$ is a global minimum of (8). Hence, we only need to consider the case in which $\varPsi (u,v) \le \varPsi (u^*,v^*)$ and $v \ne {v}^{*}$ hold.

As we have chosen u optimally and because $u^{*}$ is also an optimal choice for $v^{*}$ in the sense of (9), we can rewrite (14) further to obtain

$$\begin{aligned} \rho \int \limits _0^T\mathchoice{\left|v - {v}^{*} \right|}{|v - {v}^{*}|}{|v - {v}^{*}\Vert }{|v - {v}^{*}|}_{l_1}\,dt \ge \eta (v^{*}) - \eta (v). \end{aligned}$$

(15)

Now, we may use Assumption 2 to obtain

$$\begin{aligned} \eta (v^{*}) - \eta (v) = \mathchoice{\left|\eta (v^{*}) - \eta (v) \right|}{|\eta (v^{*}) - \eta (v)|}{|\eta (v^{*}) - \eta (v)|}{|\eta (v^{*}) - \eta (v)|} \le L \int \limits _0^T\mathchoice{\left|v - {v}^{*} \right|}{|v - {v}^{*}|}{|v - {v}^{*}\Vert }{|v - {v}^{*}|}_{l_1}\,dt. \end{aligned}$$

This shows that condition (15) is fulfilled for all $\rho \ge L$. Hence, we have shown that condition (13b) holds with $\varepsilon =0$ if we set ${\bar{\rho }} = L$. $\square$

The essential idea of the proposed method now is to solve (12) using the method discussed at the beginning of Sect. 3. So, in each iteration of the outer loop (index k) the penalty parameter $\rho$ is increased. In the inner loop (index l), we apply an alternating direction method to (12) with this parameter $\rho$ until we find a partial $\varepsilon$-optimum. For this, we need to be able to solve two subproblems to accuracy $\varepsilon$: (12) with fixed $\tilde{v}$ and (12) with fixed (u, v). For fixed $\tilde{v}$ (12) reduces to an optimal control problem and for fixed (u, v) (12) reduces to a mixed-integer linear problem (assuming the constraints describing $\Gamma$ are linear). Both of these problem types can be solved to $\varepsilon$ accuracy with standard techniques.

The algorithm is summarized in Algorithm 1.

Concerning the convergence of Algorithm 1, we can now make the following statements.

Theorem 3

Let $\rho ^k \nearrow \infty$ and let $(u^k,v^k,{\tilde{v}}^k)_k$ be a sequence generated by Algorithm 1 with $(u^k,v^k,{\tilde{v}}^k) \rightarrow (u^*,v^*,{\tilde{v}}^*)$. Then $(u^*,v^*,{\tilde{v}}^*)$ is a p-minimum of the feasibility measure $\chi (v,{\tilde{v}})=\int \limits _0^T |v(t)-{\tilde{v}}(t)|_{l_1}\,dt$.

Proof

Let $(u,v,{\tilde{v}}^k)$ be feasible for (12). Then

$$\begin{aligned} \varPsi (u,v)+ \rho ^k \int \limits _0^T\mathchoice{\left|v(t)-{\tilde{v}}^k(t) \right|}{|v(t)-{\tilde{v}}^k(t)|}{|v(t)-{\tilde{v}}^k(t)\Vert }{|v(t)-{\tilde{v}}^k(t)|}_{l_1}\,dt \ge \varPsi (u^k,v^k)+ \rho ^k \int \limits _0^T\mathchoice{\left|v^k(t)-{\tilde{v}}^k(t) \right|}{|v^k(t)-{\tilde{v}}^k(t)|}{|v^k(t)-{\tilde{v}}^k(t)\Vert }{|v^k(t)-{\tilde{v}}^k(t)|}_{l_1}\,dt - \epsilon . \end{aligned}$$

(16)

Let $\bar{\rho }$ be a cluster point of the sequence $\left( \frac{\rho ^k}{|\rho ^k|}\right) _k$ and $(\rho ^l)_l$ be a subsequence for which $\left( \frac{\rho ^l}{|\rho ^l|}\right) _l$ converges to $\bar{\rho }$. Then, dividing the inequality (16) by $|\rho ^l|$ yields

$$\begin{aligned} \frac{\varPsi (u,v)}{|\rho ^l|} + \frac{\rho ^l}{|\rho ^l|} \int \limits _0^T\mathchoice{\left|v(t)-{\tilde{v}}^k(t) \right|}{|v(t)-{\tilde{v}}^k(t)|}{|v(t)-{\tilde{v}}^k(t)\Vert }{|v(t)-{\tilde{v}}^k(t)|}_{l_1}\,dt \ge \frac{\varPsi (u^k,v^k)}{|\rho ^l|} + \frac{\rho ^l}{|\rho ^l|} \int \limits _0^T\mathchoice{\left|v^k(t)-{\tilde{v}}^k(t) \right|}{|v^k(t)-{\tilde{v}}^k(t)|}{|v^k(t)-{\tilde{v}}^k(t)\Vert }{|v^k(t)-{\tilde{v}}^k(t)|}_{l_1}\,dt - \frac{\epsilon }{|\rho ^l|}. \end{aligned}$$

Taking the limit $l \rightarrow \infty$ yields

$$\begin{aligned} \bar{\rho }\int \limits _0^T \mathchoice{\left|v-{\tilde{v}}^* \right|}{|v-{\tilde{v}}^*|}{|v-{\tilde{v}}^*\Vert }{|v-{\tilde{v}}^*|}_{l_1}\,dt \ge \bar{\rho }\int \limits _0^T\mathchoice{\left|v^*-{\tilde{v}}^* \right|}{|v^*-{\tilde{v}}^*|}{|v^*-{\tilde{v}}^*\Vert }{|v^*-{\tilde{v}}^*|}_{l_1}\,dt. \end{aligned}$$

An analogous inequality holds for any feasible $(u^k,v^k,{\tilde{v}})$. $\square$

Corollary 1

  Let $\rho ^k \nearrow \infty$ and let $(u^k,v^k,{\tilde{v}}^k)_k$ be a sequence generated by Algorithm 1 with $(u^k,v^k,{\tilde{v}}^k) \rightarrow (u^*,v^*,{\tilde{v}}^*)$ and let $(u^*,v^*,{\tilde{v}}^*)$ be feasible for (8). Then $(u^*,v^*)$ is p-minimal for (6).

Proof

This follows from Theorem 3 and using that feasibility of $(u^*,v^*,{\tilde{v}}^*)$ for (8) implies $v^*={\tilde{v}}^*$. $\square$

Note that in the inner loop of Algorithm 1, we compute p-$\varepsilon$-minima, but that Corollary 1 says that a feasible limit of a converging sequence generated by ADM-SUR is a p-$\varepsilon$-minimum with $\varepsilon =0$. Moreover, note that the two subproblems for (12) in Algorithm 1 can be solved efficiently. Finally, we note that $\rho ^k \nearrow \infty$ is needed in Theorem 3 and Corollary 1, because Theorem 2 guarantees exactness of the penalty only in a global minimum. It must be observed that even in the finite-dimensional case, there are only slightly stronger results known (see [11], Theorems 8 and 11). It is instructive to note that in the finite-dimensional case the assumption of convexity immediately yields convergence to global optima and the assumption of differentiabilty convergence to local optima. To us, this indicates that the mixed-integer part of the problem makes it difficult to prove anything about convergence to local (or even global) optima for these types of methods.

For any fixed $\tilde{v}$ the problem (12) is equivalent to the problem

$$\begin{aligned} \min _{y,z,u,w}\quad&\Phi (y(T)) + z(T) \end{aligned}$$

(17a)

$$\begin{aligned}&{\dot{y}}(t)=Ay(t)+\sum _{i=1}^{{\tilde{M}}} w_i(t) f(y(t),u(t),r^i),\quad&~t \in (0,T),~y(0)=y_0 \end{aligned}$$

(17b)

$$\begin{aligned}&{\dot{z}}(t)=\sum _{i=1}^{\tilde{M}} w_i(t) \rho |r^i-{\tilde{v}}|_{l_1},\quad&t \in (0,T),~z(0)=0 \end{aligned}$$

(17c)

$$\begin{aligned}&u \in \Sigma \subset U_t, \end{aligned}$$

(17d)

$$\begin{aligned}&\sum _{i=1}^{{\tilde{M}}} w_i(t)=1,~t\in (0,T)~\text {a.e.} \end{aligned}$$

(17e)

$$\begin{aligned}&y \in Y_t,~z \in Z_t,~w \in V_t, \end{aligned}$$

(17f)

with $r_i$, $i=1,\ldots ,\tilde{M}=2^M$, enumerating the configurations $\{0,1\}^M$, $Z_t=L^1(0,T)$ and $V_t=L^\infty (0,T;\{0,1\}^{{\tilde{M}}})$. Letting $({\bar{y}},\bar{z},{\bar{u}}, {\bar{w}})$ be a solution of (17) with the relaxation $w \in L^\infty (0,T;[0,1]^{{\tilde{M}}})$ and $w^n\in V_t$ be a sequence generated by the sum-up rounding algorithm of [34, 36] and $y_n$, $z_n$ be the corresponding solutions of (17b) and (17c) with $w=w^n$, then under Assumption 1

$$\begin{aligned} \Vert {\bar{y}}-y_n\Vert _{C([0,T];Y)}+\Vert {\bar{z}}-z_n\Vert _{C([0,T])} \rightarrow 0,\quad \text {for}~n\rightarrow \infty , \end{aligned}$$

(18)

see [28] for details. Under additional assumptions on A and f, even error estimates are available [18, 21, 36]. In particular, (18) shows that this solution approach yields an $\frac{\epsilon }{2}$-optimal solution for a sufficiently fine control grid. We refer to this solution approach for subproblem (17) as the (POC)-step.

Further, for any fixed (u, v) the problem (12) reduces to

$$\begin{aligned} \min _{\tilde{v} \in \Gamma }\quad&\int \limits _0^T |v-\tilde{v}|_{l_1}\,dt. \end{aligned}$$

(19)

Here, standard quadrature rules and mixed-integer linear programming techniques can be used to compute an $\frac{\varepsilon }{2}$-optimal solution again for a sufficiently fine control grid. We refer to this solution approach for the subproblem (19) as the (MIP) step.

The sum-up rounding algorithm in the (POC)-step can be interpreted as the solution of the following combinatorial integral approximation problem (CIAP)

$$\begin{aligned} \min _{w^n} \max _{t \in (0,T)} \quad&\left\Vert \int \limits _0^t w(s) - w^n(s) ds \right\Vert _{\infty } , \end{aligned}$$

(20)

for a piecewise constant function $w^n$ on a fixed grid, see [37]. We therefore refer to the penalty-$\varepsilon$ method in Algorithm 1 as ADM-SUR. An interesting variant of this Algorithm is to skip SUR in the POC-step, i.e., doing the step in the relaxed direction of w and using the MIP-step to recover integer feasibility. We refer to this variant as ADM (without SUR). For comparison, we also consider the heuristic to apply POC to the original problem formulation without combinatorial constraints and to recover a feasible solution via the following mixed-integer problem

$$\begin{aligned} \min _{w^n} \max _{t \in (0,T)} \quad&\left\Vert \int \limits _0^t w(s) - w^n(s) ds \right\Vert _{\infty } \end{aligned}$$

(21a)

$$\begin{aligned}&w^n \in \Gamma , \end{aligned}$$

(21b)

again on a fixed grid for $w^n$, see [21, 37]. We refer to this approach as CIAP. Note that in contrast to (19), the cost function in (21) is not a norm on $V_t$. A convergence result for this subproblem in an ADM framework such as for the ADM-SUR algorithm is therefore an open problem.

5 Numerical study

We test the proposed methods on two benchmark examples from the mintOC.de library [35], which we augment by minimum dwell-time constraints in order to prohibit infinitely many switching events. To model the dwell time condition we used the basic MIP constraints. These do not, however, form a complete description of the so-called min up/down polyhedron. One can either use a complete description in the original variable space [26], where additional constraints are separated with cutting planes or use an extended formulation [31] instead. As the main focus of this article is the solution quality, we stick to the basic formulation above.

Our computations are based on CasADi [1] for the model equations and their derivatives and the solvers Ipopt [40] for nonlinear programming problems and Gurobi [17] for quadratic and linear mixed-integer programs.

The ADM method was used with $\rho = 10^{-3}, 10^{-2}, \dotsc , 10^6$ and $\varepsilon = 10^{-3}$. We terminated the method when the value of the penalty term dropped below a tolerance of $10^{-4}$, because increasing $\rho$ beyond that point will not change the iterates much on a fixed discretization. At the end of this section, we study the dependency of the penalty parameter adaptation for smaller choices of the multiplicative increment. Our study confirms the experience from the finite-dimensional case (the version described in [11]) that the effect of the penalty adaptation strategy does not change the qualitiative behavior of the method. In our point of view, several different strategies can be used to identify p-minima with low objectives for example within a global search strategy like branch-and-bound. An interesting direction for further research seems to be the use of weighted 1-norm-penalties with adaption strategies for the weights as used in the finite-dimensional case (see, for instance, [10, 12]). This is not straight-forward in the infinite-dimensional case, because that would make the strategy discretization-dependent.

5.1 Fuller’s problem

For our numerical study, we consider a variant of Fuller’s problem augmented with minimum dwell-time constraints

$$\begin{aligned} \min _{y,v}&\int \limits _{0}^{1} y_1(t)^2 dt + \left( y_1(1) - \tfrac{1}{100}\right) ^2 + y_2(1)^2 \end{aligned}$$

(22a)

$$\begin{aligned} \text {s.t.~}&{\dot{y}}_1(t) = y_2(t),\quad t \in (0,1) \end{aligned}$$

(22b)

$$\begin{aligned}&{\dot{y}}_2(t) = 1 - 2 v(t),\quad t \in (0,1) \end{aligned}$$

(22c)

$$\begin{aligned}&y(0) = \left( \tfrac{1}{100}, 0\right) ^\top , \end{aligned}$$

(22d)

$$\begin{aligned}&v(t) \in \{0, 1\},\quad t \in (0,1) \end{aligned}$$

(22e)

$$\begin{aligned}&v(t+\tau _{\min })-v(t)+|v|_{(t,t+\tau _{\min })} \le 2,\quad t \in (0,1-\tau _{\min }). \end{aligned}$$

(22f)

The problem is notoriously difficult, because the solution of the problem without dwell-time constraints (i.e., for $\tau _{\min }=0$) exhibits chattering [41].

We compare our proposed ADM-based method (with and without SUR) with a direct global Mixed-Integer Quadratic Programming (MIQP) method and CIAP. We discretize Equations (22b) and (22c) using a Gauss–Legendre collocation of degree 4 on an equidistant partition of [0, 1] with 200 collocation intervals. The same collocation nodes are also used for approximating the integral term in (22a) via Gauss–Legendre quadrature. The control discretization is piecewise constant, with jumps allowed only at the boundary of the collocation intervals but not at the collocation nodes. Because the objective (22a) is quadratic in y and the constraints (22b) and (22c) are linear in y, the same holds for their discretized counterparts. Hence, we obtain a discretized MIQP, which we solve, where possible, to global optimality using Gurobi. The resulting objective values and corresponding single CPU runtimes are depicted in Tables 1 and 2. It appears that the ADM-based methods have some advantage both in quality and runtime over CIAP for the instances with larger $\tau _\mathrm {min}$, which are harder for POC-based heuristics (but appear to be simpler for the MIQP approach). Exemplary for two selected values dwell-times $\tau _{\min }$, the resulting state $y_1$ in problem (22) is shown in Fig. 1.

Table 1 Comparison of the objective function values for the four approaches on a Gauss–Legendre collocation discretization of degree 4 on an equidistant grid with 200 intervals for Fuller’s problem (22) with respect to varying values of the minimum dwell time $\tau _\mathrm {min}$

Table 2 Single CPU runtimes in seconds on an Intel(R) Core(TM) i7-5820K CPU @ 3.30GHz for the corresponding results in Table 1

Fig. 1

Results for Fuller’s problem with minimum dwell-times $\tau _\mathrm {min} = 0.04$ (left) and $\tau _\mathrm {min} = 0.05$ (right). The heuristic results based on ADM and CIAP can in a qualitative sense get close to the global solution computed with an MIQP solve

Fig. 2

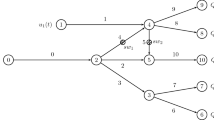
Network topology for the subgrid scenario of the transmission lines example. The objective is to continuously control the power generation at the producers via $u_1(t)$ and $u_2(t)$ and to switch on or off the dashed connections (via $v_1(t)$) and the dotted connection (via $v_2(t)$) in order to minimize the quadratic deviation of the power supply from the power demand at the five consumer nodes

Table 3 Scaled objective values for different approaches to the transmission lines example

Fig. 3

The resulting binary-valued controls in the transmission lines subgrid scenario for different solution approaches: The partially outer convexified relaxed solution (POC) delivers a lower bound, but is not binary feasible. The application of Sum-Up Rounding (SUR) yields binary feasible controls, which oscillate heavily and do not satisfy the minimum dwell-time constraint, however. The ADM-based heuristics result in fewer switches than the heuristic based on solving a Combinatorial Integral Approximation Problem with minimum dwell-time constraints (CIAP)

Fig. 4

The continuous-valued controls oscillate on a similar scale as the binary-valued controls in Fig. 3. The ADM-based results exhibit much smaller jumps

Fig. 5

Resulting power supply for the controls from Fig. 3 and Fig. 4. Due to the additional minimum dwell-time constraints, the deviation of power delivery from the demand at consumer nodes is raised in comparison to the lower bound given by POC. The ADM-based heuristical results are superior to both SUR (which does not satisfy the minimum dwell-time constraint) and CIAP

5.2 Network of transmission lines

This problem was described in [13]. The telegraph equations are based on a $2\times 2$ hyperbolic system of partial differential equations and describe the voltage and current on electrical transmission lines in time $t\in [0,T]$ and space $x\in [0,l]$. The state variable $\varvec{\xi }(x,t)=(\xi ^+(x,t),\xi ^-(x,t))$ represents right or left-traveling components on each line of the network and is governed by

$$\begin{aligned} \partial _t \varvec{\xi } + \varvec{\Lambda } \partial _x \varvec{\xi } + \mathbf {B} \varvec{\xi } = 0,\end{aligned}$$

(23)

where $\varvec{\Lambda }$ is a diagonal matrix including the speed of propagation in each direction and $\mathbf {B}$ denotes a symmetric matrix with non-negative entries. The dynamics on the lines are coupled at nodes via the boundary condition

$$\begin{aligned} \begin{pmatrix} \varvec{\Lambda }^+ &{} 0\\ 0 &{} \mathbf {D}^-(\varvec{v(t)}) \end{pmatrix} \varvec{\xi }(0,t) = \begin{pmatrix} \mathbf {D}^+(\varvec{v(t)}) &{} 0\\ 0 &{} \varvec{\Lambda }^- \end{pmatrix} \varvec{\xi }(l,t) + \begin{pmatrix} \varvec{\Lambda }^+ &{} 0\\ 0 &{} 0 \end{pmatrix} {\varvec{u}}(t). \end{aligned}$$

(24)

The distribution matrices $\mathbf {D}^{\pm }({\varvec{v}})$ depend on binary-valued controls ${\varvec{v}}(t)\in \{0,1\}$, which are used to switch off specified connections in the network while the continuous-valued controls ${\varvec{u}}(t)$ denote the power generation at the producer nodes in the network, cf. Fig. 2. The goal is to minimize the quadratic deviation of the accumulated power delivery $C_s(t,\varvec{\xi })=\sum _{r \in \delta _S} \xi ^+_r(l_r,t)$ (with $\delta _S$ being the set of all lines adjacent to node s) from the demand $Q_s(t)$ at the consumer nodes $V_S$, i.e.,

$$\begin{aligned} {\left\{ \begin{array}{ll} \quad \min \limits _{\varvec{v,u}} \frac{1}{2}\sum \limits _{s \in V_S} \int \limits _0^{T} \left( Q_s(t) - C_s(t,\varvec{\xi }) \right) ^2 dt\\ \quad \text {s.t. } (23) \text { and } (24). \end{array}\right. } \end{aligned}$$

(25)

This problem can be written in abstract form as

$$\begin{aligned} {\dot{y}}=Ay+B(v)u, \end{aligned}$$

(26)

with A and $B(v_i)$, $i=1,\ldots ,M$ being unbounded linear operators on Hilbert spaces using abstract semigroup theory [2]. Though (26) is not of the form (1), the solution is still given by the variation of constants formula (5) with $f(y,u,v)=B(v)u$, see e.g., [7].

For the computational experiments, we use the publicly available¹ Python implementation, which uses a classical upwinding Finite Volume discretization with 4 equidistant volumes per line with forward Euler timestepping with 104 equidistant time steps as in [13]. The minimum dwell-time constraints are set to $\tau _\mathrm {min} = 1$.

The Figs. 3, 4 and 5 illustrate the results for a scenario, in which a small subgrid of the network can be islanded, see Fig. 2. We observe that the binary decisions can be partly equalized by reactions in the power generation at the producer nodes.

Finally, we present a numerical study of the influence of the penalty parameter adaptation on the resulting objective function in Table 4. To this end, we use a coarser discretization of the subgrid scenario (2 equidistant finite volumes per transmission line, 52 equidistant time steps) and increase the penalty parameter in multiplicative steps of $\root i \of {10}$ for varying $i \in \{ 1, 2, 4, 8 \},$ starting from $\rho = 10^{-3}$. The outer loop is terminated when the value of the penalty term drops below $10^{-4}$. We observe that the ADM without CIAP is largely unaffected by the penalty adaptation choice, while the ADM with CIAP shows a more pronounced dependence.

Table 4 The final value $\rho ^*$ and the resulting objective value $\Phi ^*$ for the ADM without CIAP are only marginally influenced by the choice of increment factor in the adaptation of the penalty parameter $\rho$

6 Conclusion

We conclude that the proposed penalty-ADM method performs notably well for our benchmark problems within the class of mixed-integer optimal control problems with dwell-time constraints. The quality of the computed solutions outperforms the other considered heuristic solutions for large dwell-times. We think that it is worthwhile to use this heuristic inside of exact methods to ensure that good feasible solutions are found early on in the solution process. Moreover, the convergence theory shows that the proposed method computes partial minima in a lifted sense. The comparison with a global solution for a full discretization shows that these partial minima are in general not global minima. However, we note that this is not surprising because we used a local solver for the POC-step. The proposed methods can be extended in various directions such as considerations of state constraints, mixed-integer corrector steps from linearizations and of course more general problem classes.