Abstract
In this paper we reconsider a known technique for constructing strong MIP formulations for disjunctive constraints of the form \(x \in \bigcup _{i=1}^m P_i\), where the \(P_i\) are polytopes. The formulation is based on the Cayley Embedding of the union of polytopes, namely, \(Q := \mathrm {conv}(\bigcup _{i=1}^m P_i\times \{\epsilon ^i\})\), where \(\epsilon ^i\) is the ith unit vector in \({\mathbb {R}}^m\). Our main contribution is a full characterization of the facets of Q, provided it has a certain network representation. In the second half of the paper, we work-out a number of applications from the literature, e.g., special ordered sets of type 2, logical constraints, the cardinality indicating polytope, union of simplicies, etc., along with a more complex recent example. Furthermore, we describe a new formulation for piecewise linear functions defined on a grid triangulation of a rectangular region \(D \subset {\mathbb {R}}^d\) using a logarithmic number of auxilirary variables in the number of gridpoints in D for any fixed d. The series of applications demonstrates the richness of the class of disjunctive constraints for which our method can be applied.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Disjunctive programming was introduced by Egon Balas [2, 3] in the 1970s as an extension of linear programming with disjunctive constraints. Disjunctive constraints can express logical conditions that the feasible solutions must satisfy. A disjunctive constraint can be represented as
where each \(P_i\) is a polyhedron. Suppose \(P_i=\{x \in {\mathbb {R}}^n\ :\ A^{(i)} x \le b^{(i)}\}\), where \(A^{(i)}\) is a rational matrix and \(b^{(i)}\) is a rational vector of matching dimension. Balas [4], and Jeroslow and Lowe [32] proved that if the \(P_i\) are bounded and nonempty, then \({\bar{x}}\) satisfies (1) if and only if the following set of constraints admits a solution:
More generally, a MIP formulation for (1) is a set of constraints
such that \({\bar{x}}\) satisfies (1) if and only if (3) admits a feasible solution when \(x = {\bar{x}}\) (see e.g. [26, 32, 44,45,46]). The Linear Programming (LP) relaxation of (3) is the polyhedron Q determined by \(Ax + By + Cz \le b\). For simplicity we assume that Q has at least one extreme point. The formulation is ideal , if z is integral in all extreme points of Q, and non-extended if it contains no y variables, and extended otherwise. Balas’ formulation (2) is extended and ideal [32, 45]. A lot of work has been done for devising (ideal) formulations for disjunctive constraints that do only involve the original x variables (in particular, no copies of them) as well as some additional integral z-variables, see Sect. 2 for a brief overview, and it is the main topic of this paper.
For illustrating the benefits of such formulations in terms of the size of the formulation, consider the n-dimensional cross-polytope
In fact, P equals the convex hull of the union of polytopes \( P_i = \{ x\in {\mathbb {R}}\ :\ -1 \le x_i \le 1,\ x_j = 0\ \forall j \ne i\},\ i=1,\ldots ,n\). A minimal linear representation of P consists of \(2^n\) linear inequalities (see e.g. Balas [9], page 146), that is,
Now, an ideal, non-extended formulation for \(x\in \bigcup _{i=1}^n P_i\) is
This system has 2n continuous variables, and \(3n+1\) linear inequalities (including the nonnegativity of the variables).
A further advantage of ideal, non-extended formulations for (1) is that they may be more efficient computationally than (2), since they do not contain copies of the original problem variables and constraints. This claim is supported by a recent study of Anderson et al. [1], who compared ideal non-extended, and extended formulations for expressing the maximum of affine functions on polyhedral domains, and showed that the former formulations result much shorter computation times.
To derive ideal, non-extended formulations for (1), we focus on a particular technique, pioneered by Vielma [45], which is based on the Cayley Embedding of a finite union of polyhedra. The Cayley Embedding of polyhedra was proposed by Huber et al. [25] for studying the Minkowski sum of point configurations in \({\mathbb {R}}^n\), see also [34, 49], and for the union of polyhedra in (1) it would be of the form \(\bigcup _{i=1}^m P_i \times \{\epsilon ^i\}\), where \(\epsilon ^i\) is the ith unit vector in \({\mathbb {R}}^m\). Vielma generalized the Cayley Embedding by replacing the unit vectors with distinct binary vectors \(h^i \in \{0,1\}^d\) for some \(d \ge \lceil \log _2 m \rceil \). Under the conditions that all the \(P_i\) are non-empty, and pointed, Vielma proved that a non-extended, ideal MIP formulation for (1) is given by
where \({{{\mathcal {P}}}} = (P_i)_{i=1}^m\), and \({{{\mathcal {H}}}} = (h^i)_{i=1}^m\) is a family of distinct binary vectors in \(\{0,1\}^d\). This formulation is implicit in the sense that it does not provide a description of \(Q({{{\mathcal {P}}}}, {{{\mathcal {H}}}})\) in terms of linear inequalities. Neverthless, Vielma determined the non-trivial facetsFootnote 1 of the convex hull \(Q({{{\mathcal {P}}}}, {{{\mathcal {H}}}})\) for the SOS2 constraints of [13], and also for piecewise linear functions of two variables on grid triangulations of a square. In both cases, the number of binary variables and also that of the non-trivial facets were bounded by \(O( \log _2 n)\).
These ideas were generalized to combinatorial disjunctive constraints by Huchette and Vielma [27], which take the form
where the \(S_i\) are subsets of \(V:=\{1,\ldots ,n\}\) such that \(\bigcup _{i=1}^m S_i = V\), \(P(S) := \{x \in \varDelta ^V\ :\ x_j = 0\ \forall j \in V{\setminus } S\}\), and \(\varDelta ^V := \{ x \in {\mathbb {R}}^n_{\ge 0}\ :\ \sum _{j=1}^n x_j = 1 \}\) is the n–dimensional standard simplex. Huchette and Vielma gave an explicit description of \(Q({\mathcal {P}},{\mathcal {H}})\) by linear inequalities, where \({\mathcal {P}} := (P(S_i))_{i=1}^m\), and \({\mathcal {H}}\) is a set of m distinct binary vectors, under some mild technical assumptions. However, the construction of the inequalities may be computationally heavy in general, and the authors left open the characterization of those inequalities which induce facets of \(Q({\mathcal {P}},{\mathcal {H}})\).
In this paper we propose a new systematic way of constructing ideal, non-extended formulations for disjunctive constraints (1), when the \(P_i\) are polytopes, and a certain network representation exists. We will use the MIP formulation
of Vielma [45] restricted to the unit vectors \(\epsilon ^i\). Nevertheless, if \(P^{emb}\) admits a network representation of a given structure, to be defined next, then we can characterize the facets of \(P^{emb}\). Our method works not only for combinatorial disjunctions, but for a much wider class of polytopes, which will be illustrated in Sect. 5.
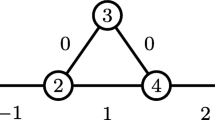
A network representation for \(P^{emb}\) consists of a network \(N = (V,A, c)\) from the following family. The set of nodes V comprises a source node s, and a sink node t, the nodes \(V_s := \{v_1,\ldots ,v_m\}\) representing m alternatives, the nodes \(V_t := \{1,\ldots ,n\}\) corresponding to the variables \(x_1,\ldots ,x_n\) in (6), and possibly some other nodes. We assume that \(V_s \cap V_t = \emptyset \). The set of arcs A contains, among others, the arcs \((s,v_i)\) for \(i \in \{1,\ldots ,m\}\), and also the arcs (j, t) for \(j\in \{1,\ldots ,n\}\), and neither s, nor t has other nodes adjacent to them. It is required that \(N{\setminus } \{t\}\) decomposes into m directed trees rooted at s, \(G^1,\ldots ,G^m\), where \(v_i\) is a node of \(G^i\), the leafs of each \(G^i\) lie in \(V_t\), and \(V(G^i) \cap V(G^k) \subseteq V_t \cup \{s\}\) for \(1\le i< k\le m\) (see Fig. 1). For each i and arc a of \(G^i\), the capacity of a is \(c(a):= k_a \lambda _i\) for some rational number \(k_a > 0\). Moreover, \(c(j,t) = x_j\) for each \(j\in V_t\).
We say that N represents \(P^{emb}\), if for each i, when setting \(\lambda _i =1\), and the other coordinates of \(\lambda \) to 0, and for any \(x\ge 0\), \((x,\lambda ) \in P^{emb}\) if and only if the network N parametrized by x and \(\lambda \) as above, admits a feasible \(s-t\) flow of value \(\sum _{j=1}^n x_j\), and \((x,\lambda )\) satisfies the valid equations for \(P^{emb}\). Deciding whether a particular \(P^{emb}\) admits a network representation from the above family is out of scope of this paper. However, in several practical applications, the construction of N is easy, see Sect. 5.
In the sequel we concentrate on two special cases only. Either the only valid equation for \(P^{emb}\) is \(\sum _{i=1}^m \lambda _i = 1\), or all \((x,\lambda ) \in P^{emb}\) also satisfy \(\sum _{i=1}^m \alpha _i \lambda _i = \sum _{j=1}^n x_j\), where \(\alpha _i \lambda _i = c(s,v_i)\). We distinguish these two cases by writing \(P^{emb}_\le \), and \(P^{emb}_=\), respectively, for \(P^{emb}\). To simplify the presentation, let \(P^{emb}_*\) denote any of \(P^{emb}_\le \) and \(P^{emb}_=\). We assume that each \(j \in V_t\) is reachable from s by a directed path. This implies that \(x_j = 0\) is not a valid equation for \(P^{emb}_*\). The following assumption is without loss of generality.
Assumption 1
For each \(i \in \{1,\ldots ,m\}\), \(P^{emb}_*\) contains a point \((x^i,\epsilon ^i)\).
Main results of the paper. In the first part of the paper, we fully characterize the non-trivial facets of \(P^{emb}_*\) for any choice of the \(P_i\), provided it has a network representation N. At first, we prove that any \(s-t\) cut of the network N yields a valid inequality for \(P^{emb}\), and moreover, along with the non-negativity of the variables, and the valid equation(s), they describe \(P^{emb}\). Then, we fully characterize those \(s-t\) cuts of N, that induce facets of \(P^{emb}\). Briefly, some \(s-t\) cut \((S,{\bar{S}})\) of N induces a facet of \(P^{emb}_\le \) if and only if the subgraphs of N spanned by \({\bar{S}}{\setminus } \{t\}\), and by S, respectively, admit some connectivity properties. In case of \(P^{emb}_=\), slightly stronger conditions must hold. These results, along with (6) provide an explicit, ideal, non-extended MIP formulation for (1).
In the second part of the paper, we demonstrate the richness of the class of problems for which our machinery can be applied by deriving well-known formulations for problems in the literature, and working out some new ones. The list of examples include reformulation of SOS2 and SOSk sets, the Cardinality Indicating Polytope, the \(EVEN^n\) polytope, the polytope of small cliques, the union of simplices, and some more complicated ones. In addition, based on the ideas of [28], we obtain a new formulation for piecewise linear functions defined on a grid-triangulation of a rectangular domain in \({\mathbb {R}}^d\) using \(O(d \log _2 n +2^d d!)\) auxiliary variables.
Our results complement those of Vielma [45] and Huchette and Vielma [26,27,28]. On the one hand, Vielma [45] was able to derive the facets of the generalized Cayley embedding of SOS2 sets for any choice of the (distinct) binary vectors \(h^i\), but our method works for a much wider class of disjunctive sets than SOS2, and we have a full characterization of the non-trivial facets. On the other hand, in [26] a linear representation is obtained for the convex hull \(Q({\mathcal {P}},{\mathcal {H}})\) of the MIP formulation for combinatorial disjunctive constraints (5) and any choice of distinct binary vectors \({\mathcal {H}} = (h^i)_{i=1}^m\), while our characterization of facets is valid for any choice of the \(P_i\) provided that \(P^{emb}\) in (6) admits a network representation.
In Sect. 2 we review some previous work. After some preliminaries in Sect. 3, we state and prove our main results in Sect. 4. In Sect. 5 we describe a series of applications, and conclude the paper in Sect. 6.
1.1 Terminology
Let \(P=\{x \in {\mathbb {R}}^n\ |\ Bx \le b\}\) be any convex polyhedron. A face F of P is a subset of P obtained by setting some inequalities to equations in the system of inequalities \(Bx \le b\) defining P. In particular, P is a face of itself, and also the empty set is a face of P. A facet F is a face of P such that \(F\ne P\), and there exists no face \(F'\) of P such that \(F \subset F'\subset P\) (the containments are proper). A vertex of P is a face which consists of exactly one point of P.
The dimension of P, \(\dim (P)\), is the maximum number of affinely independent points in P minus one. Equivalently, \(\dim (P) = n - m_=\), where \(m_=\) is the maximum number of linearly independent equations which are satisfied by all the points of P.
Let \(\epsilon ^i \in {\mathbb {R}}^m\) be the i-th unit vector in \({\mathbb {R}}^m\), i.e., \(\epsilon ^i_i = 1\) and \(\epsilon ^i_k = 0\) for all \(k \in \{1,\ldots ,m\}{\setminus } \{i\}\).
A network \(N=(V,A,c)\) is a directed graph with vertex set V, arc set A, and arc capacities c. Let \(V_1, V_2\) be disjoint subsets of the set of vertices V of the network N. Then \([V_1, V_2] \subseteq A\) is the set of those arcs \((u,v) \in A\) such that \(u \in V_1\) and \(v \in V_2\). Let s and t be distinct vertices of N. An \(s-t\) cut \((S,{\bar{S}})\) is a partitioning of V into subsets S and \({\bar{S}} = V{\setminus } S\) such that \(s \in S\) and \(t \in {\bar{S}}\). The associated cut-set is \([S,{\bar{S}}]\). For any node u, let \(\delta ^{out}_u := [\{u\}, V{\setminus } \{u\}]\), and \(\varGamma ^{out}_u = \{v \in V\ :\ (u,v) \in \delta ^{out}_u\}\).
Recall the general network N defined above. For fixed x and \(\lambda \), let \(N_{x,\lambda }\) denote the network with arc capacities determined by x and \(\lambda \).
2 Previous work
The ultimate reference on disjuntive programming is the recent book of Balas [9]. The first results were summarized in a research report which got published only some 24 years later [6], but the first papers appeared in print already in the 1970’s, see [2] and [3]. In these early works, extended formulations were obtained for general disjunctive programs, the concept of duality was developed and a sequential convexification procedure was devised. Questions related to facets of general disjunctive programs were raised and partially answered in [11].
Balas [2, 3, 6] investigated the convex hull of feasible points of a disjunctive program by giving two distinct linear programming formulations: one involving only the original problem variables, and another using additional continuous variables. We focus on the latter one. Let
where \(P_i := \{ x \in {\mathbb {R}}^n \ |\ A^{(i)} x\le b^{(i)}\}\) for some matrix \(A^{(i)}\) and vector \(b^{(i)}\) of matching dimensions, for \(i=1,\ldots ,m\), and \(\mathrm {cl\ conv}(\cdot )\) is the closed convex hull operator. Balas has shown that \({\bar{x}} \in P\) if and only if the LP-relaxation of (2) admits a feasible solution when \(x = {\bar{x}}\), provided that the \(P_i\) are nonempty and bounded, or some additional technical assumptions hold.
Jeroslow and Lowe [32] introduced the concept of MIP–representable sets, namely, \(S \subseteq {\mathbb {Q}}^n\) is MIP–representable if there are rational matrices A, B, C, and a vector b with the property that: \(x \in S\) if and only if, for some \(y,z \ge 0\) with z integer, \( A x + B y + C z \le b \). They also pointed out the connection to disjunctive programming, and in particular they showed that (2) is ideal. Basu et al. [12] gave an alternative definition, and the concept was generalized to convex sets by Lubin et al. [37]. Vielma [44] provided a broad overview of MIP formulations in mixed-integer programming, including MIP representability of sets and functions.
Conforti and Wolsey [19] generalized the idea of Balas [6] for expressing the union of polyhedra in a higher dimensional space by first lifting each polyhedron in some space where it admits an easy extended formulation. They applied this results to mixed integer sets, like the continuous mixing set with upper bound, a mixing set with two divisible capacities, and a divisible capacity single node flow model.
In the formulation (2), the original x variables are copied m times, which is computationally unattractive. However, Conforti et al. [18] has recently shown that Balas’ extended formulation for \(\mathrm {conv}(P_1 \cup P_2)\) is optimal in the following sense. For any polynomial \(\sigma \), there exist polytopes \(P_1\) and \(P_2\) of sizeFootnote 2\(f_1\) and \(f_2\), respectively, such that any formulation of \(\mathrm {conv}(P_1\cup P_2)\) of size bounded by \(\sigma (f_1+f_2)\) must have \(\varOmega (n)\) additional variables.
In the best case, neither variable copies, nor new \(\lambda _i\) variables are needed to get an explicit linear description of the convex hull of the union of some polyhedra. For instance, Balas et al. [10] considered upper monotone polytopes in \([0,1]^n\). A polytope \(P = \{ x \in [0,1]^n\ |\ Ax \ge 1\}\) is upper monotone if A is a non-negative matrix. Among other results, Balas and his co-authors derived the convex hull of the union of two upper monotone polytopes \(P_1\subseteq [0,1]^{n_1} \times \{0_{n_2}\}\) and \(P_2\subseteq \{0_{n_1}\}\times [0,1]^{n_2}\) in disjoint spaces, and in partially overlapping spaces as well without using any extra variables. They also obtained the facets of \(\mathrm {conv}(P_1 \cup P_2)\), and applied their characterizations to the union of matroid polytopes, and to logical inference. The latter result extends that of [50], see also [7]. These results were generalized to nonlinear and possibly unbounded orthogonal disjunctive sets in [42].
The second best option is that no variable copies are used in a formulation, only some new (binary) variables. Jeroslow [31] studied a special class of disjunctive constraints, where \(P_i := \{ x \in {\mathbb {R}}^n \ |\ A x\le b^{(i)}\}\) for \(i\in \{1,\ldots ,m\}\), that is, only the right-hand-sides change in the definitions of the \(P_i\). Let \(P:= \mathrm {cl\ conv}(\bigcup _{i=1}^m P_i)\) and Q the set of those \(x \in {\mathbb {R}}^n\) that have an extension \((x,\lambda )\in {\mathbb {R}}^{n+m}\) satisfying
While \(P \subseteq Q\) always holds, the converse inclusion is not true in general. Jeroslow gave two sufficient conditions for \(Q= P\). Blair [14] devised new necessary and sufficient conditions for \(Q= P\), and proved that deciding whether equality holds is an NP-hard decision problem. Blair’s condition was later generalized by Vielma [46] (Corollary 2). Balas [5] gave yet another sufficient condition for \(Q=P\), and applied it to multiple network polyhedra.
Vielma [45] developed ideal, non-extended MIP formulations for modeling disjunctive constraints based on the concept of Cayley Embedding, and applied it to SOS2 constraints, and to piecewise linear functions on the grid. In [27], Huchette and Vielma provided a very general ideal formulation for combinatorial disjunctive constraints based on the generalized Cayley Embedding of [45], and applied it to univariate and bivariate piecewise linear functions. Lee and Wilson [36] studied the modeling of piecewise linear functions on arbitrary triangulations of their domains. Their model can be reinterpreted as the Cayley Embeddig of a union of polyhedra (one polytope for each triangle) using the vectors \(\epsilon ^i\). Vielma [46] generalized the Cayley Trick for polyhedra to the union of convex sets. He obtained ideal, non-extended formulations for \(\bigcup _{i=1}^m C_i\) using the corresponding gauge functions, and applied them to a wide range of disjunctive constraints. Vielma also characterized the boundary structure of the Cayley Embedding of the union of convex sets, which in the polyhedral case is as follows. Each face of \(P^{emb}\) is of the form \(\mathrm {conv}(\cup _{i=1}^m (F_i \times \{\epsilon ^i\}))\), where the \(F_i\) are faces of the \(P_i\) with intersecting normal vectors, see also [51].
Branching schemes constitute another approach for deriving ideal, non-extended formulations for (combinatorial) disjunctive constraints. Tomlin [43] proposed a new modeling of SOS2 sets with binary variables, while Martin et al. [38] introduced SOSk constraints and a branching scheme for modeling two-variable piecewise linear functions. Vielma and Nemhauser introduced the concept of independent branching schemes for modeling a constraint very similar to the combinatorial disjunctive constraint (5) of [26], the only difference being that \(\varDelta ^V = \{x \in {\mathbb {R}}^V_{\ge 0}\ :\ \sum _{j \in V} x_j \le 1\}\) is the |V|–dimensional simplex in the definition of the \(Q(S_i)\), \(i=1,\ldots ,m\). An independent branching scheme of depth d for (5) is given by pairs of disjoint sets \(L_k, R_k \subset V\) for \(k =1,\ldots ,d\), such that \(\bigcup _{i=1}^m Q(S_i) = \bigcap _{k=1}^d (Q(L_k) \cup Q(R_k))\). This yields the formulation
This formulation is ideal. Of course, the existence of a branching scheme of depth d depends on the sets \(S_i\). For SOS1 and SOS2 constraints, the authors obtained formulations with \(\lceil \log _2 n \rceil \) binary variables and twice as many additional constraints. They also devised MIP formulations for 2-variable piecewise linear functions on a grid triangulation of a square using a logarithmic number of new variables and constraints in the number of triangles, see also [47]. When \(\varDelta ^V\) is replaced by \([0,1]^V\) in the above definitions, they obtained an independent branching scheme of depth \(d = m\). In [26], Huchette and Vielma gave a necessary and sufficient condition for the existence of an independent branching scheme of depth d for a combinatorial disjunctive constraint. The authors described a number of techniques for constructing independent branching schemes of depth \(\lceil \log _2 m\rceil \), and applied them to several well-known disjunctive constraints, including SOS2, SOSk, and Grid Triangulations. In [28], new methods are described for constructing independent branching schemes for univariate and bivariate piecewise linear functions (on grid triangulations), and the computational merits of the various approaches are evaluated.
Ceria and Soares [16] generalized the formulation (2) to closed convex sets \(C_i\) using the perspective mappings of the convex functions defining the \(C_i\). The authors also described a primal procedure which converges to the optimum under mild conditions. On/off constraints can be used to model disjunctive constraints and the description of the set of feasible solutions in linear and nonlinear mathematical programs is the topic of e.g., [15, 22,23,24, 42, 46]. In particular, Hijazi et al. [24] considered a linear program with a disjunctive constraint \(x \in P_0 \cup P_1\), where \(P_0\) is given by lower and upper bounds for the variables, while \(P_1\) is specified by one linear inequality and another set of lower and upper bounds on the variables. The authors provided a complete description of \(\mathrm {conv}(P_0\cup P_1)\) using one new binary variable only. Note that their description needs exponentially many new constraints in the number of the variables, but the authors left open which inequalities induce facets.
For more results on extended formulations in combinatorial optimization see the review paper [17], and also [35, 40].
3 Preliminaries
In this section we derive a (not necessarily minimal) linear representation of \(P^{emb}_*\). Here and below, we always assume that \(P^{emb}_*\) admits a network representation \(N=(V,A,c)\). As we will see, the linear representation is closely related to the \(s-t\) cuts of N. We will define a dominance relation between \(s-t\) cuts, and prove that dominated \(s-t\) cuts are redundant in the linear representation.
To start with, we describe some reduction rules for the arc capacities of N without affecting any \(s-t\) flow of value \(\sum _{j=1}^n x_j\). Recall that for any i the arc capacities of the subnetwork \(G^i\) of N are specified by \(c(a) = k_a \lambda _i\), for \(a \in E(G^i)\). Let us define \(k^{out}_v := \sum _{a \in \delta ^{out}_v} k_a\) for any node \(v \in V(G^i){\setminus } V_t\). Let \(v \in V(G^i){\setminus } \{s\}\). The capacity \(c(a) = k_a\lambda _i\) of the unique arc \(a = (u,v) \in E(G^i)\) can be reduced without affecting the set of feasible \(s-t\) flows of value \(\sum _{j=1}^n x_j\) in \(N_{x,\lambda }\) for any \((x,\lambda ) \in P^{emb}_*\) if one of the following two transformations can be applied to it:
-
If \(v \not \in V_t\) and \(k_a > k^{out}_v\), then \(k_a\) can be reduced to \(k^{out}_v\), thus c(a) becomes \(k^{out}_v \lambda _i\).
-
If \(v\ne v_i\), and \(k_a > k_{a'}\) for the unique arc \(a' := (u', u) \in E(G^i)\), then \(k_a\) can be reduced to \(k_{a'}\), thus c(a) becomes \(k_{a'} \lambda _i\).
Throughout the paper we assume that N is reduced , i.e., the above transformations cannot be applied to it. Now, we express the capacity of the \(s-t\) cuts of \(N_{x,\lambda }\) in terms of x and \(\lambda \).
Observation 1
Let \((S,{\bar{S}})\) be an \(s-t\) cut of \(N_{x,\lambda }\). Then \(c_{x,\lambda }([S,{\overline{S}}]) = \sum _{j \in V_t \cap S} x_j + \sum _{i=1}^m k_i \lambda _i\) for some rational numbers \(k_i\ge 0\).
In order to describe \(P^{emb}_{\le }\) by linear inequalities, we define the polytope
while for \(P^{emb}_=\) consider
Let \(Q_*\) denote one of \(Q_\le \) and \(Q_=\).
Proposition 1
\(P^{emb}_* \subseteq Q_*\).
Proof
By definition, for any \(i \in \llbracket m \rrbracket \), \((x,\epsilon ^i) \in P^{emb}_*\) if and only if \(N_{(x,\epsilon ^i)}\) admits an \(s-t\) flow of value \(\sum _{j=1}^n x_j\), \(x \ge 0\), and \((x,\epsilon ^i)\) satisfies the valid equations for \(P^{emb}_*\). By the MAX-FLOW MIN-CUT Theorem of Ford and Fulkerson [20], \(N_{(x,\epsilon ^i)}\) admits an \(s-t\) flow of value \(\sum _{j=1}^n x_j\) if and only if all the \(s-t\) cuts have a capacity of at least \(\sum _{j=1}^n x_j\). Now, observe that these are precisely the inequalities defining \(Q_*\), whence \((x,\epsilon ^i) \in Q_*\). To finish the proof, take any point \((x,\lambda )\in P^{emb}_*\), and notice that it is a convex combination of some points with \(\lambda \) integral. Since \(Q^*\) is a convex polytope, the statement follows. \(\square \)
Our next goal is to prove the converse inclusion.
Proposition 2
\(Q_*\) has vertices, and in each vertex \((x,\lambda )\) of \(Q_*\), the \(\lambda \) is a 0/1 vector.
Proof
By Assumption 1, and since \(P^{emb}_* \subseteq Q_*\), \(Q_*\) is not empty. Since all variables are non-negative in the definition of \(Q_*\), it resides in the non-negative orthant of the \((n+m)\)-dimensional real vector space, and thus it has vertices.
Let \(H_i := \{(x,\lambda ) \in Q_*\ :\ \lambda _i =1\}\) for each \(i \in \{1,\ldots ,m\}\). By Assumption 1, \(H_i \ne \emptyset \) for each i. Clearly, \(H_i\) is a face of \(Q_*\). We claim that \(Q_* = \mathrm {conv} (\cup _{i=1}^m H_i)\). On the one hand, \(\mathrm {conv} (\cup _{i=1}^m H_i) \subseteq Q_*\), since \(H_i \subseteq Q_*\) for each i, and \(Q_*\) is convex. Conversely, consider any point \((x, \lambda )\in Q_*\), and consider any \(s-t\) flow of \(N_{x,\lambda }\) of value \(\sum _{j=1}^n x_j\). Clearly, such a flow must exist, since the minimum capacity of an \(s-t\) cut of \(N_{x,\lambda }\) is \(\sum _{j=1}^n x_j\) by the definition of \(Q_*\). Let \(f^i_e\) be the flow on arc e of \(G^i\). Then we have \(x_j = \sum _{i=1}^m \sum _{e \in \delta ^{in}(j)} f^i_e\), since a flow of value \(\sum _{j=1}^n x_j\) must saturate all the (j, t) arcs of N. If \(\lambda _i = 0\), then we pick the vector \(x^i\) provided by Assumption 1, and we have \((x^i, \epsilon ^i) \in H_i\). Otherwise, we rescale the \(f^i_e\) for each arc e of \(G^i\), i.e., let \(g^i_e = f^i_e /\lambda _i\). Let \(x^i_j = \sum _{e \in \delta ^{in}_{G^i}(j)} g^i_e\) for each \(j \in V_t\cap V(G^i)\), and 0 otherwise. Then \((x^i, \epsilon ^i) \in H_i\), since \((g^i, x^i)\) is a feasible flow of value \(\sum _{j=1}^n x^ i_j\) in \(N_{x^i, \epsilon ^i}\), where the arc \((s, v_i)\) and all the arcs (j, t) are saturated. Hence, \((x,\lambda ) = \sum _{i=1}^m \lambda _i(x^i,\epsilon ^i) \in \mathrm {conv} (\cup _{i=1}^m H_i)\). \(\square \)
Corollary 1
\(P^{emb}_= = Q_=\) and \(P^{emb}_\le = Q_\le \).
Definition 1
For any \(s-t\) cut \((S,{\bar{S}})\) of N, the induced face of \(P^{emb}_*\) is \(F_S := \{ (x,\lambda ) \in P^{emb}_*\ |\ c_{x,\lambda }([S,{\bar{S}}]) = \sum _{j=1}^n x_j\}\).
Observation 2
The vertices of \(F_S\) are those vertices of \(P^{emb}_*\) that are in \(F_S\).
Consequently, in all the vertices \(({\hat{x}},{\hat{\lambda }})\) of \(F_S\), \({\hat{\lambda }} = \epsilon ^i\) for some i.
Proposition 3
No facet \(F_S\) of \(P^{emb}_*\) induced by an \(s-t\) cut \((S,{\bar{S}})\) of N equals the face induced by \(x_j = 0\) for any j.
Proof
We distinguish two cases. First suppose \(j \in V_t\cap S\). Since \(F_S = \{ (x,\lambda ) \in P^{emb}_*\ :\ \sum _{i=1}^m k_i\lambda _i = \sum _{j' \in V_t {\setminus } S} x_{j'} \}\), the equation defining \(F_S\) is linearly independent from \(x_j = 0\), so \(F_S\) cannot be induced by \(x_j = 0\).
Now suppose \(j \in V_t {\setminus } S\). Then \(x_j = 0\) is satisfied by all points \((x,\lambda ) \in F_S\) if and only if the source s is not connected to \(j\in V_t\) by a directed path, which we excluded. \(\square \)
In order to characterize those \(s-t\) cuts \((S,{\bar{S}})\) of N that induce facets of \(P^{emb}_*\), as we will see, the single most important parameter is the intersection of S with \(V_t\).
Definition 2
Let \(U \subseteq V_t\) be fixed. \({\mathcal {C}}(U)\) consists of all the \(s-t\) cuts of N such that \(S\cap V_t = U\).
A cut \((S,{\bar{S}})\in {\mathcal {C}}(U)\) induces an inequality of the following general form (cf. Observation 1):
We are only interested in the minimum capacity \(s-t\) cuts in \({\mathcal {C}}(U)\). We can identify these cuts without fixing \(\lambda \) and x as follows. Since \(N{\setminus } \{t\}\) is the union of the directed graphs \(G^i\), where the \(G^i\) share only the nodes \(\{s\}\cup V_t\), we can determine separately for each \(G^i\) which of its nodes belong to S in order to minimize the coefficients \(k_i\).
Observation 3
Let \(U \subseteq V_t\) be fixed. There exists an \((S,{\bar{S}})\in {\mathcal {C}}(U)\) which minimizes simultaneously all the coefficients \(k_i\) in \(c_{x,\lambda }([S,{\overline{S}}]) = \sum _{j \in U} x_j + \sum _{i=1}^m k_i \lambda _i\).
This observation motivates the following definition.
Definition 3
Let \(U \subseteq V_t\) be fixed. Let \({\mathcal {C}}_{\min }(U)\) consist of all the \(s-t\) cuts \((S,{\bar{S}}) \in {\mathcal {C}}(U)\) which minimize simultaneously all the coefficients \(k_i\) in \(c_{x,\lambda }([S,{\overline{S}}]) = \sum _{j \in U} x_j + \sum _{i=1}^m k_i \lambda _i\). The members of \({\mathcal {C}}_{\min }(U)\) are the minimum capacity \(s-t\) cuts of N with respect to U .
Remark 1
For any \((S,{\bar{S}}), (Z,{\bar{Z}}) \in {\mathcal {C}}_{\min }(U)\), \(c_{x,\lambda }([S,{\overline{S}}]) = c_{x,\lambda }([Z,{\overline{Z}}])\).
Proposition 4
Let \(U \subseteq V_t\) be fixed. There exists a unique \((S,{\bar{S}}) \in {\mathcal {C}}_{\min }(U)\) such that \(Z \subseteq S\) for all the \((Z,{\bar{Z}}) \in {\mathcal {C}}_{\min }(U)\).
Proof
We claim that if both of \((Z_1, {\bar{Z}}_1), (Z_2,{\bar{Z}}_2)\in {\mathcal {C}}_{\min }(U)\), then \((Z_1\cup Z_2, \overline{Z_1\cup Z_2}) \in {\mathcal {C}}_{\min }(U)\), which proves the statement. Recall that the set function which assigns to S the capacity of the \(s-t\) cut \((S,{\bar{S}})\) is submodular, see e.g., Frank [21]. Using this, we can derive
where the first inequality follows from the submodularity of the cut capacity function, and the second from the assumption that both of \((Z_1, {\bar{Z}}_1), (Z_2,{\bar{Z}}_2)\in {\mathcal {C}}_{\min }(U)\), which implies that \((Z_1\cap Z_2 , \overline{Z_1 \cap Z_2}), (Z_1\cup Z_2, \overline{Z_1\cup Z_2})\in {\mathcal {C}}(U)\). Consequently, equality holds throughout, and \((Z_1\cup Z_2, \overline{Z_1\cup Z_2})\in {\mathcal {C}}_{\min }(U)\). \(\square \)
Definition 4
Let \(U \subseteq V_t\). We call \((S,{\bar{S}}) \in {\mathcal {C}}_{\min }(U)\) dominating if \(Z \subseteq S\) for all \((Z,{\bar{Z}})\in {\mathcal {C}}_{\min }(U)\). If \((S,{\bar{S}})\in {\mathcal {C}}(U){\setminus } {\mathcal {C}}_{\min }(U)\), then we say that \((S,{\bar{S}})\) is a dominated \(s-t\) cut of N w.r.t. U, and any member of \({\mathcal {C}}_{\min }(U)\) is a non-dominated \(s-t\) cut of N w.r.t. U.
Remark 1 implies that in the following definition, the face \(F_S\) does not depend on which non-dominated \(s-t\) cut in \({\mathcal {C}}_{\min }(U)\) is chosen.
Definition 5
The face induced by \(U\subseteq V_t\) is \(F_S\), where \((S,{\overline{S}})\) is any non-dominated \(s-t\) cut in \({\mathcal {C}}_{\min }(U)\).
Observation 4
If \(F_S\) is a facet of \(P^{emb}_*\) induced by the \(s-t\) cut \((S,{\bar{S}})\), then \(V_t {\setminus } S\) is not empty.
Proposition 5
Consider any \(U \subseteq V_t\). For any non-dominated \(s-t\) cut \((S,{\overline{S}})\in {\mathcal {C}}_{\min }(U)\), the face \(F_{S}\) of \(P^{emb}_*\) contains a point \((x',\epsilon ^i)\) for any \(i \in \{1,\ldots ,m\}\).
Proof
Fix S and i, and we set \(\lambda = \epsilon ^i\). Thus, the arcs of \(G^i\) have some positive capacities, while all the arcs in the other \(G^k\), \(k\ne i\), subgraphs of N have zero capacity. We construct a vector \(x'\) such that \((x',\epsilon ^i) \in P^{emb}_*\), and \((x',\epsilon ^i)\) satisfies (11) at equality.
First we consider \(P^{emb}_\le \). We determine \(x'\) by constructing an \(s-t\) flow \(f^i\) saturating all the arcs in \(E(G^i)\cap [S,{\bar{S}}]\), and which has zero flow on any arc \((u,v) \in E(G^i)\) such that \(u \in V(G^i) {\setminus } S\), and \(v \in V(G^i) \cap S\). The total capacity of the arcs in \(E(G^i)\cap [S,{\bar{S}}]\) is \(k_i\), when \(\lambda = \epsilon ^i\). Since \((S,{\bar{S}}) \in {\mathcal {C}}_{\min }(U)\), we can send \(k_i\) amount of flow in \(G^i\) from s to the nodes \(V_t {\setminus } U\). If \(k_i >0\), then this flow necessarily saturates the arcs \(E(G^i)\cap [S,{\bar{S}}]\). Then, we just set \(x'_j = f^i_{(j,t)}\) for all j, and it is easy to verify that (11) is satisfied by \((x',\epsilon ^i)\) at equality.
As for \(P^{emb}_=\), if the flow \(f^i\) constructed above saturates the arc \((s,v_i)\) (which is of capacity \(\alpha _i\)), then we are done, since then \(\sum _{j=1}^n x'_j = f^i_{(s,v_i)} = \alpha _i\), by flow conservation at the nodes. Otherwise, we have to augment \(f^i\) with additional flow restricted to the subgraph \(G^i(S)\) of \(G^i\) spanned by the nodes \(S\cap V(G^i)\). Consider any \(s-j\) path in \(G^i(S)\) for some \(j \in U\) which consist of non-saturated arcs only. We increase the flow along this path until some arc becomes saturated. We repeat this until no more flow can be sent from s to some node in U in \(G^i(S)\). Let \({\hat{f}}^i\) be the resulting flow. If the arc \((s,v_i)\) is saturated by \({\hat{f}}^i\), then we are done, since we can set \(x'_j = {\hat{f}}^i_{(j,t)}\) for all j, and \((x',\epsilon ^i) \in F_S\). Otherwise, a subset of the arcs saturated by \({\hat{f}}^i\) constitutes a cut-set separating \(v_i\) from all the nodes in \(V_t\) having capacity smaller than \(\alpha _i\). But this contradicts Assumption 1. \(\square \)
Proposition 6
For any \(U\subseteq V_t\), dominated \(s-t\) cuts in \({\mathcal {C}}(U)\) cannot induce facets of \(P^{emb}_*\).
Proof
Let \((S, {\overline{S}})\) and \((Z,{\overline{Z}})\) be a dominating and a dominated \(s-t\) cut in \({\mathcal {C}}(U)\), respectively. We claim that \(F_Z \subset F_S\), and \(F_Z \ne F_S\). Let \(c_{x,\lambda }([S,{\overline{S}}]) = \sum _{j \in U} x_j + \sum _{i=1}^m k_i \lambda _i\), and \(c_{x,\lambda }([Z,{\overline{Z}}]) = \sum _{j \in U} x_j + \sum _{i=1}^m k'_i \lambda _i\). Since \((Z,{\overline{Z}}) \in {\mathcal {C}}(U)\) is dominated, \(k_i \le k'_i\) for all i, and at least one of these inequalities is strict. Hence, any point \((x,\lambda )\in P^{emb}_*\) satisfies
Consequently, if \(\sum _{j \in U} x_j + \sum _{i=1}^m k'_i \lambda _i = \sum _{j=1}^n x_j\), then also \(\sum _{j \in U} x_j + \sum _{i=1}^m k_i \lambda _i = \sum _{j=1}^n x_j\), i.e., \(F_Z \subseteq F_S\). Now let \(i^*\) be an index such that \(k'_{i^*}> k_{i^*}\). Then by Proposition 5, there is an x such that \((x,\epsilon ^{i^*}) \in F_S\). Substituting \((x,\epsilon ^{i^*})\) into the cut capacity functions we obtain
Hence \((x, \epsilon ^{i^*}) \in F_S{\setminus } F_Z\). \(\square \)
4 Main results
Theorem 1
The set \(U \subset V_t\) induces a facet of \(P^{emb}_\le \) if and only if
-
(i)
for the dominating \(s-t\) cut \((S, {\overline{S}}) \in {\mathcal {C}}_{\min }(U)\), the subgraph \(N{\setminus }(S\cup \{t\})\) is connected, and
-
(ii)
for each \(j \in U\), there exists some \(v_i \in S\) such that there is a directed path from \(v_i\) to j with all nodes in S, and \(\alpha _i > k_i\), where \(c(s,v_i) = \alpha _i \lambda _i\), and \(k_i\lambda _i\) is the total capacity of those arcs of \(G^i\) in \([S,{\bar{S}}]\).
Proof
Necessity : suppose that U induces a facet F of \(P^{emb}_\le \), but the dominating \(s-t\) cut \((S,{\overline{S}})\in {\mathcal {C}}_{\min }(U)\) is such that \(N{\setminus }(S\cup \{t\})\) is not connected. Let \(C_1,\ldots , C_q\) (\(q \ge 2\)) be the connected components of \(N{\setminus }(\{t\} \cup S)\). Consider the face \(F_Z\) induced by the \(s-t\) cut \((Z,{\bar{Z}})\) of N, where \(Z := S \cup \left( \bigcup _{g=2}^q V(C_g)\right) \). We claim that \(F \subset F_Z\) and \(F\ne F_Z\), and thus F cannot be a facet, which contradicts our initial assumption.
Let \((x,\lambda ) \in F\), and suppose that the capacity of \((S,{\overline{S}})\) is \(\sum _{j \in U} x_j + \sum _{i=1}^m k_i \lambda _i\). We can decompose the second term of this sum along the components of \(N{\setminus }(S\cup \{t\})\) as follows:
where \(\sum _{i=1}^m k^g_i \lambda _i\) is the capacity of those arcs of \([S,{\overline{S}}]\) that lead from S to the component \(C_g\) of \(N {\setminus } (S\cup \{t\})\). But then \((x,\lambda )\) satisfies the equation
However, this equation is equivalent to
which is the capacity of the \(s-t\) cut \((Z,{\bar{Z}})\) of N. This shows that \(F \subseteq F_Z\). It remains to construct a point in \(F_Z {\setminus } F\). Since F is a facet, for each \(j \in V_t \cap (\bigcup _{g=2}^q V(C_g))\), there exist some x and i such that \((x,\epsilon ^i) \in F\), and \(x_j > 0\), otherwise all points in F satisfy \(x_j = 0\), and thus F cannot be a facet by Proposition 3. For each such j, we define a vector \({\tilde{x}}\) as follows: \({\tilde{x}}_j := 0\), and \({\tilde{x}}_\ell := x_\ell \) for all \(\ell \ne j\). Then \(({\tilde{x}},\epsilon ^i) \in F_Z {\setminus } F\).
As for (ii), suppose the condition does not hold for some \(j \in U\). Then \(x_j = 0\) holds for all \((x,\lambda ) \in F\), which leads to a contradiction by Proposition 3.
Sufficiency : Assume that conditions (i) and (ii) of the Theorem hold. Let \(F := F_{S}\) be the face of \(P^{emb}_\le \) induced by the dominating \(s-t\) cut \((S, {\overline{S}}) \in {\mathcal {C}}_{\min }(U)\). It suffices to prove that \(P^{emb}_\le \) does not admit any facet \(F'\) such that F is a proper face of \(F'\). By condition (ii), for each j there exists i and x such that \((x,\epsilon ^i) \in F\) and \(x_j > 0\), and therefore, F cannot be a proper face of a facet induced by \(x_j = 0\). Furthermore, by Proposition 5, F cannot be a proper face of a facet induced by \(\lambda _i = 0\) for any i.
Consider any \(s-t\) cut \((Z,{\bar{Z}})\) of N which induces a facet \(F_Z \ne F\) of \(P^{emb}_\le \). By Proposition 6, we may also assume that \((Z,{\overline{Z}})\) is a dominating member of \({\mathcal {C}}_{\min }(Z\cap V_t)\). We distinguish two cases: \(U {\setminus } Z \ne \emptyset \), and \(U \subset Z\).
First suppose \(U {\setminus } Z \ne \emptyset \), and we construct a point in \(F {\setminus } F_Z\) to show that \(F \not \subseteq F_Z\). Let \(\sum _{i=1}^m k^Z_i \lambda _i\) be the total capacity of those arcs directed from Z to some nodes of \(N{\setminus }(Z \cup \{t\})\). Clearly, all points \((x,\lambda ) \in F_Z\) satisfy \(\sum _{{j'}\in V_t{\setminus } Z} x_{j'} = \sum _{i=1}^m k^Z_i \lambda _i\). Let \(R_i\) be the set of those nodes in \(V_t {\setminus } Z\) that are reachable from \(v_i\) along a directed path in N. Then choose index \(i^*\) such that \(R_{i^*}\cap U \ne \emptyset \), \(v_{i^*} \in S\), \(\alpha _i > k_i\), and there is a directed path with all nodes in S from \(v_{i^*}\) to some \(j \in R_{i^*} \cap U\). If none of the sets \(R_i\) satisfies these conditions, then S violates condition (ii) of the theorem.
Consider some \(j \in R_{i^*} \cap U\) such that there is a directed path from s to \(j\in V_t\) in the subnetwork \(G^i(S)\) of \(G^i\) (such a node exists by the choice of \(R_{i^*}\)). Then there exists a point \(({\bar{x}}, \epsilon ^{i^*}) \in F\) such that \({\bar{x}}_j > 0\), since \(\alpha _i > k_i\). Consider the set of points \(X_j = \{x \ |\ 0\le x_j \le {\bar{x}}_j,\ x_{j'} = {\bar{x}}_{j'} \text { for all } j' \ne j\}\). On the one hand, \((x,\epsilon ^{i^*}) \in F\) for all \(x \in X_j\). On the other hand, \(\sum _{{j'} \in R_{i^*}\cap V_t} x_{j'}\) is not a constant on \(X_j\). Hence, there exists \(x \in X_j\) such that \((x,\epsilon ^{i^*}) \not \in F_Z\).
Finally, assume \(U \subset Z\).
Claim \(S \subset Z\).
Proof
Suppose \(S{\setminus } Z\) is not empty. We define the quantities \(A_{\lambda }\), \(B_{\lambda }\), \(C_{\lambda }\), and \(D_{\lambda }\) as follows. Let \(A_{\lambda }\) be the total capacity of those arcs (u, v) such that \(u \in S\cap Z\) and \(v \in S{\setminus } Z\). We have \(A_{\lambda }:=c_{x,\lambda }([S\cap Z, S{\setminus } Z]) = \sum _{i=1}^m k_i^A \lambda _i\) for some non-negative rationals \(k^A_i\). Likewise, \(B_{\lambda }:= c_{x,\lambda }([Z{\setminus } S, S{\setminus } Z])\), \(C_{\lambda }:= c_{x,\lambda }([S{\setminus } Z, Z{\setminus } S])\), and \(D_{\lambda }:= c_{x,\lambda }([S{\setminus } Z, \overline{Z\cup S}{\setminus }\{t\}])\), see Fig. 2. Since \(S \cap Z \subseteq S\), and \(S\cap Z \cap V_t = U\) by assumption, \((S\cap Z, \overline{S\cap Z}) \in {\mathcal {C}}(U)\), and therefore its capacity is at least that of \((S,{\bar{S}})\). Consequently, \(A_{\lambda }\ge C_{\lambda }+D_{\lambda }\) for all \((x,\lambda ) \in P\) (where we compare the coefficients of the \(\lambda _i\)). On the other hand, \((Z,{\bar{Z}})\) is a dominating member of \({\mathcal {C}}_{\min }(Z\cap V_t)\), whence \(A_{\lambda }+B_{\lambda }< D_{\lambda }\) for some \((x,\lambda ) \in P\). Combining the two inequalities, we obtain \(B_{\lambda }+C_{\lambda }+ D_{\lambda }< D_{\lambda }\) for some \((x,\lambda ) \in P\), which is impossible, since \(B_{\lambda },C_{\lambda }\ge 0\) always hold. \(\square \)
Indirectly, suppose \(F \subseteq F_Z\), and let \(c_{x,\lambda }([S,{\bar{S}}]) = \sum _{j \in U} x_j + \sum _{i=1}^m k_i \lambda _i\) for some rationals \(k_i\ge 0\), and \(c_{x,\lambda }([Z,{\bar{Z}}]) = \sum _{j \in V_t \cap Z} x_j + \sum _{i=1}^m k^Z_i \lambda _i\) for some rationals \( k^Z_i\ge 0\). Then, for all \((x,\lambda ) \in F\), \(\sum _{i=1}^m k_i \lambda _i = \sum _{j \in V_t {\setminus } U} x_j\), and \(\sum _{i=1}^m k_i^Z \lambda _i = \sum _{j \in V_t {\setminus } Z} x_j\). By condition (i), there is some i, and x such that \((x,\epsilon ^i) \in F\), \(\sum _{j \in V_t\cap Z{\setminus } U} x_j > 0\), \(\sum _{j \in V_t {\setminus } Z} x_j > 0\), and \(G^i{\setminus } S\) has a connected component with non-empty intersection with \(V_t\cap Z{\setminus } U\) and also with \(V_t {\setminus } Z\). However, \(\sum _{j \in V_t {\setminus } Z} x_j = k^Z_i\) (\(\lambda \) is fixed to \(\epsilon ^i\)). Hence, \(k_i> k^Z_i > 0\). Therefore, for any x such that \((x,\epsilon ^i) \in F\), we cannot send less flow than \(k^Z_i\) through the edges of \([Z,{\bar{Z}}{\setminus } \{t\}]\) in a feasible \(s-t\) flow of value \(\sum _{j=1}^n x_j\) in \(N_{x,\epsilon ^i}\). But this is only possible, if the maximum amount of flow that can be sent in \(G^i\) from S to \(Z\cap V_t {\setminus } U\) is at most \((k_i - k^Z_i)\lambda _i\).
Claim There exists \(S' \subset Z\) such that \(S \subseteq S'\), \(S'{\setminus } S \subset V(G^i){\setminus } V_t\), and (a) \(c_{x,\lambda }([S'\cap V(G^i),Z\cap V(G^i){\setminus } S' ]) = (k_i - k^Z_i)\lambda _i\), and (b) there is no arc (u, v) of \(G^i\) such that \(u\in Z\cap V(G^i){\setminus } S'\) and \(v \in {\bar{Z}}\).
Proof
Suppose indirectly that any \(S'\subset Z\) such that \(S\subseteq S'\) and \(S'{\setminus }S \subset V(G^i){\setminus } V_t\), violates condition (a), see Fig. 3. If \(c_{x,\lambda }([S'\cap V(G^i),Z\cap V(G^i){\setminus } S']) > (k_i - k^Z_i)\lambda _i\) for all \(S'\) such that \(S \subseteq S' \subset Z\), then the total flow that can be sent from S to those nodes \(j \in V_t \cap V(G^i) \cap Z{\setminus } U\) can be more than \((k_i - k^i_Z)\). Therefore, there exists \((x,\epsilon ^i)\in F\) such \(\sum _{j \in V_t\cap Z{\setminus } U} x_j > (k_i - k^Z_i)\), while \(\sum _{j \in V_t {\setminus } Z} x_j < k_i^Z\), which implies \((x,\epsilon ^i)\not \in F_Z\), a contradiction.
Let \(S'\) be a subset of nodes that satisfies condition (a). Indirectly, suppose it violates (b). Then the cut-set \([V(G^i) \cap Z, V(G^i) \cap {\bar{Z}}]\) contains those edges (u, v) of \(G^i\) such that \(u\in Z\cap V(G^i){\setminus } S'\) and \(v \in {\bar{Z}}\). Then, in order to saturate all arcs of \([V(G^i) \cap Z, V(G^i) \cap {\bar{Z}}]\), the flow through the arcs of \([S'\cap V(G^i),Z\cap V(G^i){\setminus } S' ]\) must be split, and less than \((k_i -k^Z_i)\) of it reaches the nodes \(j \in Z \cap V_t{\setminus } U\) for any \((x,\epsilon ^i) \in F\). But then \(\sum _{j \in V_t\cap Z{\setminus } U} x_j < k_i-k^Z_i\), again a contradiction. \(\square \)
Using this claim, we can replace S by \(S_2 := S' \cup (Z\cap V(G^i) {\setminus } S')\). Then \(F_{S_2} = F\). Therefore, if \(S_2 \ne S\), then S is not dominating, a contradiction. Otherwise, \(G^i{\setminus } S\) has no connected component which contains some nodes \(j \in V(G^i) \cap V_t \cap Z {\setminus } U\) and \({j'} \in V(G^i) \cap V_t {\setminus } Z\) simultaneously, again a contradiction. \(\square \)
Now we turn to \(P^{emb}_=\). By definition, \(\sum _{i=1}^m \lambda _i = 1\), and \(\sum _{i=1}^m \alpha _i \lambda _i = \sum _{j=1}^n x_j\) are valid for \(P^{emb}_=\). However, adding the latter equation to \(Q_\le \) may render some of the inequalities induced by \(s-t\) cuts to implicit equations for \(P^{emb}_=\) (for the same problem data).
Example 1
Suppose \(P_1 = \{ x \in {\mathbb {R}}^3_{\ge 0}\ : \ x_1 \le \frac{1}{3},\ x_2 \le \frac{2}{3},\ x_3 = 0 \}\), and \(P_2 = \{ x \in {\mathbb {R}}^3_{\ge 0}\ :\ x_1 = 0,\ x_2 \le 1,\ x_3 \le 1 \}\). Then
Now we add \(x_1 + x_2 + x_3 = 1\) to \(Q_{\le }\) to obtain \(Q_=\). But then \(x_1 = \frac{1}{3}\lambda _1\) is a valid equation for \(Q_=\) and it is linearly independent of \(x_1 + x_2 + x_3 = 1\) and \(\lambda _1 + \lambda _2 = 1\). Thus, a minimal linear representation of \(Q_=\) is
After these preliminaries, we determine the maximum number of linearly independent valid equations for \(P^{emb}_=\).
Proposition 7
Let \(E_1,\ldots ,E_\kappa \) be a maximum number of disjoint subsets of \(V_t\) such that \(\bigcup _{\ell =1}^\kappa E_\ell = V_t\), and for arbitrary \((S_\ell ,{\bar{S}}_\ell ) \in {\mathcal {C}}_{\min }(E_\ell )\), \(\ell =1,\ldots ,\kappa \),
are all valid equations for \(P^{emb}_=\), where \(c_{x,\lambda }([S_\ell ,{\bar{S}}_\ell ]) = \sum _{i=1}^m k_{i\ell } \lambda _i + \sum _{j\in E_\ell } x_j\), and \(\beta _{i\ell } = \alpha _i - k_{i \ell }\). Then \(\sum _{i=1}^m \lambda _i = 1\), and (12) are linearly independent, and imply all valid equations for \(P^{emb}_=\). Moreover, \(\sum _{\ell =1}^\kappa \beta _{i\ell } = \alpha _i\) for all \(i\in \llbracket m \rrbracket \), and the partitioning is unique.
Proof
First notice that (12) is obtained from \(c_{x,\lambda }([S_\ell ,{\bar{S}}_\ell ]) = \sum _{j=1}^n x_j\) by subtracting it from the equation \(\sum _{i=1}^m \alpha _i \lambda _i = \sum _{j=1}^n x_j\) valid for \(P^{emb}_=\). Since \(\sum _{i=1}^m \alpha _i \lambda _i = \sum _{j=1}^n x_j\) is a defining equation for \(P^{emb}_=\), the claimed partitioning exists and \(\kappa \ge 1\). The linear independence of the given equations is straightforward. Now we turn to the second part of the statement. Since a complete linear description of \(P^{emb}_=\) is known, any valid equation must correspond to some \(s-t\) cut \((S,{\bar{S}})\) of N. Using the submodularity of the cut capacity function \(c_{x,\lambda }\), we derive
Hence, equality holds throughout, and in particular \((S_\ell \cap S, \overline{S_\ell \cap S})\) induces a valid equation for \(P^{emb}_=\). Now, if \(V_t\cap S_\ell \cap S \ne \emptyset \), and \(V_t \cap S_\ell {\setminus } (V_t \cap S) \ne \emptyset \), then \(E_\ell \) can be further split, whence \(\kappa \) is not maximal, a contradiction. On the other hand, if \(S\cap V_t\) is the union of some of the \(E_\ell \), then the equation induced by \((S,{\bar{S}})\) is implied by (12). The same argument shows that the above partitioning is unique. Finally, by substituting \(\epsilon _i\) to \(\lambda _i\), we immediately derive \(\sum _{\ell =1}^\kappa \beta _{i\ell } = \alpha _i\). \(\square \)
Corollary 2
Let \(\kappa \) be defined as in Proposition 7. Then \(\dim (P^{emb}_=) = n+m-1-\kappa \).
To facilitate the presentation, we assume that the rooted trees \(G^i\) that constitute the network N have the following additional structure. For each \(i \in \llbracket m \rrbracket \), let \(A_i \subseteq \llbracket \kappa \rrbracket \) be the subset of those indices such that \(\beta _{i\ell } > 0\). If \(|A_i| \ge 2\), then \(G^i\) has exactly \(|A_i|\) outgoing arcs at node \(v_i\), i.e., \(\delta ^{out}_{v_i} = \{(v_i,w_{i\ell })\ :\ \ell \in A_i\}\), and the capacity of \((v_i,w_{i\ell })\) is \(\beta _{i\ell } \lambda _i\). Moreover, the subtree of \(G^i\) rooted at \(w_{i\ell }\) has all leafs in \(E_\ell \). If \(A_i = \{\ell \}\) for some \(\ell \in \llbracket \kappa \rrbracket \), then all leafs of \(G^i\) are in \(E_\ell \), and no further assumptions are needed. Let \(N^\ell \) be the subnetwork of N spanned by the nodes \(\{s,t\}\cup E_\ell \) along with those nodes of \(G^i\), \(i\in \llbracket \kappa \rrbracket \), which are on a directed path from \(v_i\) to \(E_\ell \).
Due to the valid equations, the facets of \(P^{emb}_=\) may have several equivalent forms. We argue that there is a normal form, which is easy to construct.
Proposition 8
Any facet \(F_S\) of \(P^{emb}_=\) is induced by the dominating \(s-t\) cut \((S,{\bar{S}}) \in {\mathcal {C}}_{\min }(U)\) for some \(U \subset V_t\) such that \(U \subset E_\ell \) for some \(\ell \in \llbracket \kappa \rrbracket \).
Proof
The facet inducing inequality induced by \((S,{\bar{S}})\) is \(\sum _{i=1}^m k_i \lambda _i \ge \sum _{j \in V_t {\setminus } U} x_j\). If U is the union of some of the \(E_\ell \), then \(F_S\) is not a proper face of \(P^{emb}_=\), a contradiction. Hence, there exists some \(E_\ell \) such that \(E_\ell {\setminus } U \ne \emptyset \) and \(U\cap E_\ell \ne \emptyset \). If \(U \cap E_\mu = \emptyset \) for all \(\mu \ne \ell \), then \(U \subset E_\ell \) and we are done. Otherwise, there are two cases. First suppose there exists \(E_\mu \subset U\). If we add the valid equation (12) for \(E_\ell \) to the inequality induced by \((S,{\bar{S}})\) we obtain
This inequality corresponds to the dominating \(s-t\) cut \((S_1,{\bar{S}}_1) \in {\mathcal {C}}_{\min }(U {\setminus } E_\ell )\), and \(F_S = F_{S_1}\). Finally, suppose \(U\cap E_\mu \ne \emptyset \) for some \(E_\mu \ne E_\ell \). Since \(E_\ell \cap E_\mu = \emptyset \) by definition, it means that a proper subset of \(E_\mu \) is contained in U. We will show that then \(F_S\) is not a facet of \(P^{emb}_=\), a contradiction. For any \((x,\lambda ) \in F_S\), consider a feasible flow of value \(\sum _{j=1}^n x_j\). This flow saturates the arcs of \(G^i\) in the cut-set \([S,{\bar{S}}]\) for any \(i \in \llbracket m \rrbracket \), and it is split between the nodes \(E_\mu {\setminus } U\) and \(V_t {\setminus } (U\cup E_\mu )\). Hence, there exists \(\beta ^1_{i\mu } \in [0,\beta _{i\mu }]\), independent of \((x,\lambda )\), such that the amount of flow toward \(E_\mu {\setminus } U\) is \(\beta ^1_{i\mu }\lambda _i\), since the total flow toward the nodes of \(E_\mu \) is \(\beta _{i\mu }\) for any \((x,\lambda ) \in P^{emb}_=\). Therefore, the dominating \(s-t\) cut \((Z,{\bar{Z}}) \in {\mathcal {C}}_{\min }(U\cup E_\mu )\) is such that \(F_S \subseteq F_Z\). Moreover, \(F_S \ne F_Z\), otherwise \(E_\mu \) could be further split, and \(F_Z \ne P^{emb}_=\), since \(Z \cap E_\ell = S\cap E_\ell \ne \emptyset \), and \(V_t \cap Z {\setminus } E_\ell = V_t \cap S{\setminus } E_\ell \ne \emptyset \). Then, \(F_S\) is not a facet of \(P^{emb}_=\). \(\square \)
Theorem 2
For any \(\ell \in \llbracket \kappa \rrbracket \), the set \(U \subset E_\ell \) induces a facet of \(P^{emb}_=\) if and only if
-
(i)
for the dominating \(s-t\) cut \((S, {\overline{S}}) \in {\mathcal {C}}_{\min }(U)\), the subgraph \(N^\ell {\setminus } (S\cup \{t\})\) is connected, and
-
(ii)
if \(|U|\ge 2\), then for any partitioning of U into non-empty subsets \(U_1\) and \(U_2\), there exist \(i\in \llbracket m \rrbracket \), and a connected component C of \((V(G^i)\cap S, E(V(G^i)\cap S))\) which contains \(v_i\), and at least one point from each of \(U_1\) and \(U_2\), such that for \(\lambda = \epsilon ^i\), the minimum capacity of a cut in C separating \(v_i\) from \(V(G^i)\cap U\) is larger than \(\alpha _i - k_i\), where \(k_i\) is the total capacity of those arcs of \(G^i\) which are in \([S,{\bar{S}}]\), and \(\alpha _i - k_i > 0\).
Proof
Necessity : Suppose that the dominating \(s-t\) cut \((S,{\bar{S}}) \in {\mathcal {C}}_{\min }(U)\) induces a facet of \(P^{emb}_=\). Observe that condition (i) coincides with Theorem 1(i). Since \(P^{emb}_= \subset P^{emb}_\le \) (for the same data), it is enough to verify that U satisfies condition (ii). Indirectly, suppose this is not the case, and there exists a partitioning \(U_1\cup U_2\) of U into nonempty subsets along with non-negative numbers \(\beta ^i_1, \beta ^i_2\) for all \(i \in \{1,\ldots ,m\}\) such that \(\sum _{i=1}^m \beta ^i_k \lambda _i = \sum _{j \in U_k} x_j\) is satisfied by all \((x,\epsilon ^{i'}) \in F_S\) for \(k =1,2\). Therefore, \(F_S\) cannot be a facet of \(P^{emb}_=\).
Sufficiency: Suppose conditions (i) and (ii) are satisfied by U, and we have to prove that \(F := F_S\) is a facet of \(P^{emb}_=\) for the dominating \(s-t\) cut \((S,{\bar{S}}) \in {\mathcal {C}}_{\min }(U)\). As in the proof of Theorem 1, we may assume that F is not contained in the faces of \(P^{emb}_=\) induced by \(x_j = 0\) for any j, or by \(\lambda _i = 0\) for any i. So, suppose \((Z,{\bar{Z}})\) induces a facet \(F_Z\) of \(P^{emb}_=\) and \(F \subset F_Z\). Since \(F_Z\) is a facet, by Proposition 6, \((Z,{\bar{Z}})\) is a dominating \(s-t\) cut in \({\mathcal {C}}_{\min }(Z\cap V_t)\). We distinguish two cases: \(U {\setminus } Z \ne \emptyset \), and \(U \subset Z\).
First suppose \(U {\setminus } Z \ne \emptyset \), and \(U\cap Z \ne \emptyset \). We construct a point \((x,\lambda )\) in \(F {\setminus } F_Z\) to show that \(F \not \subseteq F_Z\). By condition (ii), there exist i and a connected component C of \((V(G^i)\cap S, A(V(G^i)\cap S))\) such that \(v_i \in C\), C has non-empty intersection with \(U{\setminus } Z\) and also with \(U\cap Z\), and for \(\lambda = \epsilon ^i\), the minimum capacity of a cut separating \(v_i\) from \(V(G^i)\cap U\) is larger than \(\alpha _i - k_i\), where \(\alpha _i - k_i\) is the remaining quantity to be covered by a flow from \(v_i\). Since this minimum capacity is larger than the amount of flow to be sent from \(v_i\) to the nodes \(V(G^i) \cap U\), the flows on the arcs of component C are not fixed. Therefore, there exist points \((x^1,\epsilon ^i), (x^2,\epsilon ^i) \in F\) such that \(\sum _{j \in U{\setminus } Z} x^1_j \ne \sum _{j \in U{\setminus } Z} x^2_j\), while \(\sum _{j \in V_t {\setminus } (U\cup Z)} x^1_j = \sum _{j \in V_t {\setminus } (U\cup Z)} x^2_j\). But then \(\sum _{j \in V_t {\setminus } Z} x^1_j \ne \sum _{j \in V_t {\setminus } Z} x^2_j\), whence it is impossible that both of \((x^1,\epsilon ^i)\) and \((x^2,\epsilon ^i)\) are in \(F_Z\).
Now suppose \(U \cap Z = \emptyset \). Let \(k^Z_i\) be the coefficient of \(\lambda _i\) in the linear expression for the capacity of \((Z,{\bar{Z}})\) as in Observation 1. Consider the partitioning \(V_t = U \cup (V_t \cap Z) \cup (V_t {\setminus } (U\cup Z))\). We argue that for any i, and any \((x,\epsilon ^i) \in F\), the sum of the \(x_j\) in the three subsets equals \(\alpha _i - k_i\), \(\alpha _i-k^Z_i\), and \(k_i + k_i^Z - \alpha _i\), respectively. For any \((x,\epsilon ^i) \in F\), \(\sum _{j \in V_t {\setminus } U} x_j = k_i\) by definition, and thus \(\sum _{j \in U} x_j = \alpha _i - k_i\). Since \(F\subset F_Z\), x also satisfies \(\sum _{j \in V_t\cap Z} x_j = \alpha _i-k_i^Z\). Since \(\sum _{j=1}^n x_j = \alpha _i\), we get that \(\sum _{j \in (V_t {\setminus } (U\cup Z)} x_j = \alpha _i - (\alpha _i-k_i) - (\alpha _i - k^Z_i) = k_i + k_i^Z - \alpha _i\). Therefore, if \(U \cup (V_t \cap Z) = V_t\), then \(k_i + k_i^Z = \alpha _i\), and thus \(F_Z\subseteq F\), a contradiction. Now suppose \(U \cup (V_t \cap Z) \subset V_t\). Then, by condition (i), there exists \(v_i \in V_s {\setminus } S\), such that \(v_i\) is connected to some \(j_1 \in V_t \cap Z\), and also to some node \(j_2 \in V_t{\setminus } (U\cup Z)\). Moreover, the capacity of the cut (in \(G^i\)) separating \(v_i\) from these two sets must be greater than \(k_i\), since \((S,{\bar{S}})\) is a dominating \(s-t\) cut. Clearly, there must exist \((x,\epsilon ^i)\in F\) such that \(x_{j_2} > 0\), say. Let \(\delta > 0\) be small enough such that increasing \(x_{j_1}\) by \(\delta \), while decreasing \(x_{j_2}\) by \(\delta \) yields a vector \(x'\) such that \((x',\epsilon ^i)\in F\). But \(x'\) does not satisfy the equation \(\sum _{j \in V_t\cap Z} x'_j = \alpha _i-k_i^Z\), hence \((x',\epsilon ^i) \notin F_Z\), a contradiction.
Finally, if \(U \subset Z\), then we can proceed as in the proof of Theorem 1. \(\square \)
5 Applications
In this section we present a number of applications where we apply Theorem 1 or Theorem 2 in order to derive the non-trivial facets (different to the non-negativity of the variables) of the corresponding formulations. For each application we will present a MIP formulation, then a network representation, and finally derive the dominating and facet defining inequalities, but we abandon straightforward technical details such as the network correctly represents the feasible solutions of the MIP formulation in a higher dimensional space. If not stated otherwise, the formulations contain no implicit equations.
5.1 Special ordered sets of type 2
A special ordered set of type 2 (SOS2) consists of vectors \(x \in {\mathbb {R}}^n_{\ge 0}\) such that \(\sum _{j=1}^n x_j = 1\), and x has either one nonzero coordinate, or two consecutive nonzero coordinates, see [13].
Let \(2\le n\in {\mathbb {Z}}\) and consider the polytope \((P^{SOS2}_n)^{emb}\subseteq {\mathbb {R}}^{2n-1}_{\ge 0}\) defined as the convex hull of points
Observe that in this formulation, if \(\lambda _j = 1\), then \(x_j\) and \(x_{j+1}\) may be positive, but all other coordinates of x must be 0. Hence, if \(\lambda \) is integral, then \(\mathrm {proj}_x (P^{SOS2}_n)^{emb}\) is indeed a SOS2. However, relaxing the integrality of the \(\lambda _i\) variables in (13), we obtain a polytope \({\tilde{P}}_n^{SOS2}\) which has a number of vertices with fractional \(\lambda _i\) variables. For instance, for \(n=5\), \(x = (1/2, 1/2, 0,0,0)\), and \(\lambda = (1/2, 0, 1/2, 0)\), \((x,\lambda )\) is a vertex of \({\tilde{P}}_5^{SOS2}\).
We create a network \(N^{SOS2}_n=(V,A,c)\) with \(V=\{s\}\cup V_s\cup V_t\cup \{t\}\), where \(V_s=\{v_1,\ldots ,v_{n-1}\}\) and \(V_t=\{1,\ldots ,n\}\). For all \(i=1,\ldots ,n-1\) we add arcs \((s,v_i)\), \((v_i,{i})\) and \((v_i,{i+1})\) to the network of capacity \(\lambda _i\) each, and the arcs (j, t) of capacity \(x_j\) for \(j \in V_t\), see Fig. 4.
By construction, we have
Proposition 9
The non-trivial facets of \((P^{SOS2}_n)^{emb}\) are
Proof
Consider a nonempty set \(U\subset V_t\) and the corresponding unique dominating \(s-t\) cut \((S,{\bar{S}})\) w.r.t. U. By definition, \(v_k\in S\) if and only if \(S\cap \{k,{k+1}\}\ne \emptyset \). Clearly, if \(i, k\notin U\) and \(j\in U\) for some \(1\le i<j<k \le n\), then \(N^{SOS2}_n{\setminus }(S\cup \{t\})\) is disconnected, and thus the set U does not induce a facet of \((P^{SOS2}_n)^{emb}\). We distinguish three cases.
First, suppose \(U=\{1,\ldots ,{\ell }\}\) for some \(1\le \ell \le n-1\), then \(S=\{s\}\cup \{v_1,\ldots ,v_{\ell }\}\cup U\) which clearly satisfies the conditions of Theorem 2, and thus yields the inequality (14).
Second, suppose \(U=\{{\ell },\ldots ,n\}\) for some \(2\le \ell \le n\), then \(S=\{s\}\cup \{v_{\ell -1},\ldots ,v_{n-1}\}\cup U\) which clearly satisfies the conditions of Theorem 2, and thus yields the inequality
which can be reformulated as (15).
Third, suppose \(V_t {\setminus } U=\{k,\ldots , \ell \}\) for some \(2\le k\le \ell \le n-1\). Then \(S = \{s\}\cup \{v_i \in V_s\ |\ 1\le i\le k-1 \text { or } \ell \le i\le n-1\} \cup U\). However, \((S,{\bar{S}})\) violates condition (ii) of Theorem 2, since \((S{\setminus } \{s\}, A(S{\setminus } \{s\}))\) is not connected. \(\square \)
Observe that (14) and (15) along with the non-negativity of the variables and the two valid equations, is precisely the reformulation of Padberg [39] for SOS2 (obtained by complety different means), see also [26, 28, 45].
5.2 Special ordered sets of type k
A special ordered set of type k (SOSk) consists of vectors \(x \in {\mathbb {R}}^n_{\ge 0}\) such that \(\sum _{j=1}^n x_j = 1\), and x has at most k consecutive non-zero components, see [26, 38]. Clearly, it generalizes SOS2 discussed in the previous section. Let \((P^{\mathrm {SOS}k}_n)^{emb}\) be the convex hull of those \((x,\lambda )\) that satisfy the constraints
The corresponding network \(N=(V,A, c)\) has a set of nodes V comprising a source s, a sink t, the nodes \(V_s = \{v_1,\ldots ,v_{n-k+1}\}\), and also \(V_t := \{1,\ldots ,n\}\). s is connected to each of the \(v_i\) by a directed arc of capacity \(\lambda _i\), and each \(j \in V_t\) to t by a directed arc of capacity \(x_j\). Finally, \(v_i\) is connected to the nodes \(i,\ldots , i+k-1\) in \(V_t\) by directed arcs of capacity \(\lambda _i\) each. By applying Theorem 2 to the network N, one can prove analogously to the SOS2 special case the following:
Proposition 10
The non-trivial facets of \((P^{\mathrm {SOS}k}_n)^{emb}\) are
5.3 Logical constraints
Consider a set of binary variables \(x_j\) indexed by \(j \in J=\{1,\ldots ,n\}\). For each \(i=1,\ldots ,m\), let \({\mathcal {E}}_i \subseteq \{ H\subseteq J: H \ne \emptyset \}\) be a set of pairwise disjoint subsets of \(J\), that is, \( E_{ik} \cap E_{ik'} = \emptyset \) for distinct sets \(E_{ik}, E_{ik'} \in {\mathcal {E}}_i \). Note however, that for distinct i and \(i'\), there may exist \(E \in {\mathcal {E}}_i\) and \(E' \in {\mathcal {E}}_{i'}\) such that \(E\cap E' \ne \emptyset \). We also assume that \(V = \bigcup _{i=1}^m \bigcup _{k=1}^{|{\mathcal {E}}_i|} E_{ik}\). Let \(P^{LOG}_\le \) be the convext hull of those binary vectors \(x \in \{0,1\}^J\) that satisfy the following disjunctive constraints:
In order to obtain a MIP formulation for \(P^{LOG}_\le \), we introduce a binary variable \(\lambda _i\) for \(i=1,\ldots ,m\). Let \((P_{\le }^{LOG})^{emb}\) be the convex hull of points \((x,\lambda ) \in \{0,1\}^{n} \times \{0,1\}^m\) that satisfy the constraints
Define the network \(N = (V,A,c)\), where \(V = \{s,t\} \cup V_s \cup W \cup V_t\), where \(V_s :=\{v_1,\ldots ,v_m\}\), \(V_t = J\), and \(W = \{w_{ik}\ |\ i=1,\ldots ,m,\ k = 1,\ldots ,|{\mathcal {E}}_i|\}\). The set of arcs A comprises the \((s,v_i)\) of capacity \((n-\sum _{k=1}^{|{\mathcal {E}}_i|} (|E_{ik}|-p_{ik}))\lambda _i\) for each \(i=1,\ldots ,m\); the \((v_i,w_{ik})\) of capacity \(p_{ik}\lambda _i\) for \(i=1,\ldots ,m\), \(k = 1,\ldots ,|{\mathcal {E}}_i|\); the arcs \((v_i, j)\) of capacity \(\lambda _i\) for \(i=1,\ldots ,m\), and \(j \in V_t {\setminus } \cup (E_{ik}\ |\ k=1,\ldots ,|{\mathcal {E}}_i|)\); and the \((w_{ik},j)\) of capacity \(\lambda _i\) for \(i=1,\ldots ,m\), \(k=1,\ldots ,|{\mathcal {E}}_i|\), \(j \in E_{ik}\).
Firstly, we identify the dominating \(s-t\) cut \((S,{\bar{S}})\) w.r.t. some \(U \subset V_t\). Clearly, \(S = \{s\} \cup V_s \cup U \cup \{ w_{ik}\in W \ :\ |E_{ik}{\setminus }U|\le p_{ik} \}\), because the capacity of the arc \((v_i, w_{ik})\) is \(p_{ik}\lambda _i\), while the total capacity of those arcs from \(w_{ik}\) to \(V_t{\setminus }U\) is \(|E_{ik}{\setminus } U|\lambda _i\).
We can apply Theorem 1 to determine those dominating \(s-t\) cuts of N with respect to some \(U \subset V_t\) that induce facets of \((P^{LOG}_\le )^{emb}\), however, the condition we get is not much more specific than that of the theorem. All we can say is that the dominating \(s-t\) cut w.r.t. any \(U\subset V_t\) satisfies condition (ii) of Theorem 1.
As a special case we reconsider the logical constraints of [7], which we summarized in Sect. 2. By splitting J into two subsets \(J_1\) and \(J_2\), and after complementing all the variables, i.e., \({\bar{x}}_j = 1-x_j\) for all j, we can express \(P_1\) and \(P_2\) as
and
Since \(P_1\) and \(P_2\) are in disjoint subspaces, the characterization of Theorem 1 becomes more apparent. Let \(E_{1i} = M_i\), and \(E_{2j} = N_j\).
Proposition 11
The subset \(U \subset V_t\) induces a facet of \(\mathrm {conv}(P_1\cup P_2)\) if \(|V_t {\setminus } U|= 1\), or there exists \(w_{1i}\) or \(w_{2j}\) such that for the dominating \(s-t\) cut \((S,{\bar{S}}) \in {\mathcal {C}}_{\min }(U)\), \(w_{1i} \in {\bar{S}}\) and \(M_i{\setminus } U = V_t {\setminus } U\), or \(w_{2j} \in {\bar{S}}\) and \(N_j{\setminus } U = V_t {\setminus } U\).
Proof
By Theorem 1, \(N{\setminus }(S\cup \{t\})\) must be connected. However, the \(M_i\) and the \(N_j\) are disjoint by assumption, so, condition (i) holds only if the conditions of this statement are satisfied. On the other hand, \(V_s \subset S\), and thus condition (ii) of the same theorem is met as well. \(\square \)
5.4 Cardinality indicating polytope
The cardinality indicating polytope \(P^{CARD}_n\subseteq {\mathbb {R}}^{2n+1}_{\ge 0}\) is defined as the convex hull of the points
Clearly, \(\sum _{k=0}^n \lambda _k = 1\) holds for each \((x,\lambda )\in P^{CARD}_n\).
First, we create a network \(N^{CARD}_n=(V,A,c)\) with \(V=\{s\}\cup \{t\}\cup V_s \cup V_t\), where \(V_s = \{v_0,v_1,\ldots ,v_n\}\), and \(V_t = \{1,\ldots ,n\}\), and A comprising the following arcs. For \(k=0,\ldots ,n\), the arcs \((s,v_k) \in A\) of capacity \(k\lambda _k\). For \(k=0,\ldots ,n\) and \(j=1,\ldots ,n\), the arcs \((v_k,j) \in A\) of capacity \(\lambda _k\). For \(j=1,\ldots ,n\), the arcs \((j,t)\in A\) of capacity \(x_j\) (Fig. 5).
By construction, we have
Proposition 12
The non-trivial facets of \(P^{CARD}_n\) are
Proof
By Proposition 6 it suffices to consider dominating \(s-t\) cuts to identify the facets of \(P^{CARD}_n\). For any nonempty subset \(I \subseteq \{1,\ldots ,n\}\), let \(U :=V_t{\setminus } I\), and \((S,{\bar{S}})\) the unique dominating \(s-t\) cut w.r.t. U. Since \((S,{\bar{S}})\) is of minimum capacity w.r.t. U, \(v_k\in S\) for all \(k>|I|\), and \(v_k\in {\bar{S}}\) for all \(k<|I|\). Since, \((S,{\bar{S}})\) is dominating w.r.t. U, \(v_{|I|}\in S\). Clearly, \((S,{\bar{S}})\) satisfies the conditions of Theorem 2, thus the corresponding face \(F_S\) is a facet of \(P^{CARD}_n\), and takes the form (19). \(\square \)
Notice that Theorem 10 of [35] gives precisely the same description of \(P^{CARD}_n\).
5.5 All even subsets
The parity polytope \(P^{EVEN}_n\) is defined as the convex hull of points
The minimal description of \(P^{EVEN}_n\) in terms of linear inequalities in the space of original variables is attributed to Jeroslow [30]. We apply our technique to get one in a higher dimensional space. Let \((P^{EVEN}_n)^{emb}\) be the convex hull of the set of points
Similarly to Sect. 5.4, we create a network \(N^{EVEN}_n=(V,A,c)\) with \(V=\{s\}\cup V_s\cup V_t\cup \{t\}\), where \(V_s:=\{ v_0,\ldots ,v_{\lfloor n/2\rfloor }\}\) and \(V_t := \{1,\ldots ,n\}\), and the set of arcs is defined analogously to that of \(N^{card}_n\). The arc capacities are \(c(s,v_k)=2k\lambda _k\), for \(k=0,\ldots , \lfloor n/2 \rfloor \), \(c(v_k,j) = \lambda _k\) for all \(j \in V_t)\), and \(c(j,t) = x_j\) for \(j \in V_t\). By construction we have
Proposition 13
The non-trivial facets of \((P^{EVEN}_n)^{emb}\) are
where \({\mathcal {I}}_n := \{ I\subseteq \{1,\ldots ,n\}\ :\ |I| \ne 2, \exists \ k\in {\mathbb {Z}} \text { such that } n> 2k > |I|\}\).
Proof
By Proposition 6 only dominating \(s-t\) cuts of \(N^{EVEN}_n\) can define facets. For any nonempty subset \(I \subseteq \{1,\ldots ,n\}\), let \(U := V_t {\setminus } I\), and \((S,{\bar{S}})\) the unique dominating \(s-t\) cut w.r.t. U. Since \((S,{\bar{S}})\) is of minimum capacity w.r.t. U, \(v_k\in S\) for all \(2k\ge |I|\), and \(v_k\in {\bar{S}}\) for all \(2k< |I|\). In contrast to the cardinality indicating polytope, not all I determine facets of \((P^{EVEN}_n)^{emb}\), namely, |I| induces a facet if and only if \(|I| \ne 2\), and there exists an integer k such that \(n > 2k\) and \(2k > |I|\). If this condition fails, then the \(s-t\) cut \((S,{\bar{S}})\) corresponding to I does not satisfy condition (i) or (ii) of Theorem 2. The statement follows. \(\square \)
5.6 Polytopes of small cliques
Given a simple graph \(G = ({\mathcal {V}}, {\mathcal {E}})\), and a constant c, let
be the polytope whose vertices correspond to cliques of G of size at most c, and
Let \(C_1,\ldots , C_m\) be the node sets of the cliques of size c of G, and \(n = |{\mathcal {V}}|\). Clearly, \(m\le \left( \begin{array}{c}n\\ c\end{array}\right) \). The corresponding MIP formulations can be derived using a network \(N=(V,A,c)\), where \(V = \{s,t\}\cup V_s \cup V_t\) such that \(V_s\) comprises a distinct node \(v_i\) for each \(C_i\), and \(V_t = {\mathcal {V}}\) (the set of nodes of G). The source s is connected to each \(v_i\), each j is connected to the sink t, and each node \(v_i\) is connected to every \(j \in C_i\). \(c(s,v_i) = c\lambda _i\), \(c(v_i,j) = \lambda _i\) for \(j \in C_i\), and \(c(j,t) = x_j\) for all \(j \in V_t\). First we consider \((P^{CLQ}_{=c})^{emb}\). It is easy to see that
In fact, this polytope has a very simple structure.
Proposition 14
Proof
The validity of the equations is easy to verify. They correspond to the dominating \(s-t\) cuts for \(U\subset V_t\) such that \(|U| = n-1\), but they hold at equality for all \((x,\lambda ) \in (P^{CLQ}_{=c})^{emb}\) and together imply \(\sum _{j \in {\mathcal {V}}} x_j = c\). Moreover, the polyhedron on the right is integral, which can be verified by ad-hoc methods. \(\square \)
When \(c = 2\), we can easily project out the \(\lambda _i\) variables, by considering the stables sets of G. That is, using a result of [8], we apply the extreme rays of the polyhedron \(y B \ge 0\), where \(B\lambda = x\) is the subsystem defining the connection between the x and \(\lambda \) in the definition of \((P^{CLQ}_{=c})^{emb}\). For any stable set I of G, let \(y_j = -1\) for \(j \in I\), and \(y_j = 1\) for \(j\in \varGamma (I)\), the neighbors of I in G. These extreme rays y yield the valid inequalities
These inequalities were derived in [33] by starting out from a different extended formulation, and Kaibel and Loos also show that along with \(x_j \ge 0\), \(j \in {\mathcal {V}}\), and \(\sum _{j\in {\mathcal {V}}} x_j = 2\), they suffice to describe \(P^{CLQ}_{=c}\), and they give conditions for these inequalities to define facets.
Now let us turn to \((P^{CLQ}_{\le c})^{emb}\). Clearly,
Proposition 15
The non-trivial facets of \((P^{CLQ}_{\le c})^{emb}\) are
Proof
By Theorem 1, the only sets \(U\subset V_t\) that induce facets of \((P^{CLQ}_{\le c})^{emb}\) are those, where U contains all but one of the nodes \(j\in V_t\), and the statement follows. \(\square \)
The special case with \(c=2\) is extensively studied in [29] and [33], where all facets of \(P^{CLQ}_{\le c}\) are determined in the space of the original problem variables.
5.7 Union of simplicies
This application is from Jeroslow [31]. Let \(P^\varDelta := \mathrm {conv}(\cup _{i=1}^m P^\varDelta _i)\), where
We assume that \(\sum _{j=1}^n LB^i_j \le UB^i\) for all i, and all bounds are finite. Let \((P^\varDelta )^{emb} = \mathrm {conv}(\cup _{i=1}^m (P^\varDelta _i\times \epsilon ^i) )\). Clearly, \((P^\varDelta )^{emb}\) is the convex hull of those \((x,\lambda )\) that satisfy the constraints
In order to describe \((P^\varDelta )^{emb}\), we form a network \(N = (V,A,c,lb)\), where V comprises a source s, sink t, the nodes \(V_s = \{v_1,\ldots ,v_m\}\) as well as \(V_t = \{1,\ldots ,n\}\). The set of arcs A comprises \((s,v_i)\) for all \(v_i \in V_s\), \((v_i,j)\) for all \(v_i \in V_s\), and \(j \in V_t\), and (j, t) for all \(j \in V_t\). There are both capacities c, and lower bounds lb on the arcs. Let \(c(s,v_i) = UB^i\lambda _i\), \(lb(s,v_i) = \lambda _i \sum _{j=1}^n LB^i_j\), \(c(v_i,j) = (UB^i-\sum _{k\ne j} LB^i_k) \lambda _i\), \(lb(v_i,j) = LB^i_j\lambda _i\), and \(c(j,t) = x_j\), and \(lb(j,t) = 0\) for all i and j. The lower bounds on the arcs \((s, v_i)\), and \((v_i,j)\) can be eliminated by the following transformation. We derive a new network \(N' = (V,A,c')\) from N by modifying the upper bounds as follows. \(c'(s,v_i) := (UB^i - \sum _{k=1}^n LB^i_k) \lambda _i\), \(c'(v_i,j) := (UB^i - \sum _{k=1}^n LB^i_k)\lambda _i\), and \(c'(j,t) := x'_j\), where \(x_j' = x_j - \sum _{i=1}^m LB^i_j \lambda _i\). We have the following relation between the feasible flows of N and \(N'\).
Proposition 16
Let \(x \in {\mathbb {R}}^n\), \(y \in {\mathbb {R}}^m\) be vectors such that \(\lambda \ge 0\), and \(\sum _{i=1}^n \lambda _i = 1\). We have the equivalences
-
i)
\((x,\lambda ) \in (P^\varDelta )^{emb}\) if and only if \(N_{x,\lambda }\) admits a feasible \(s-t\) flow of value \(\sum _{j=1}^n x_j\).
-
ii)
\(N_{x,\lambda }\) admits a feasible \(s-t\) flow of value \(\sum _{j=1}^n x_j\) if and only if \(N'_{x',\lambda }\) admits a feasible \(s-t\) flow of value \(\sum _{j=1}^n x'_j\), where \(x'_j = x_j - \sum _{i=1}^m LB^i_j \lambda _i\).
Proof
Part i) is obvious. As for ii), first suppose \(N_{x,\lambda }\) admits a feasible flow f of value \(\sum _{j=1}^ n x_j\). Let \(f'_{(s,v_i)} = f_{(s,v_i)} - \lambda _i \sum _{j=1}^n LB^i_j\), \(f'_{(v_j,j)} = f_{(v_i,j)} - \lambda _i LB^i_j\), and \(f'_{(j,t)} = f_{(j,t)} - \sum _{i=1}^m \lambda _i LB^i_j\). Clearly, \(f'\) is a feasible \(s-t\) flow in \(N'_{x',\lambda }\) of value \(\sum _{j=1}^n x'_j\), as claimed. The opposite direction can be proved similarly. \(\square \)
Let \(Q'\) be convex hull of those \((x',\lambda )\) such that \(x',\lambda \ge 0\), and \(N'_{x',\lambda }\) admits a feasible \(s-t\) flow of value \(\sum _{j=1}^n x'_j\). Now we use Theorem 1 to identify those facets of \(Q'\) that corresponds to some \(s-t\) cuts of \(N'\) and then we lift the description of \(Q'\) to that of \((P^\varDelta )^{emb}\).
Observation 5
\(Q'\) is of dimension \(n+m-1\) if there exists \(i \in \{1,\ldots ,m\}\) such that \(\sum _{j=1}^n LB^i_j < UB^i\), otherwise it has dimension \(m-1\).
Proposition 17
Any proper subset \(U \subset V_t\) does not induce a facet of \(Q'\). If \(\dim Q' = n+m-1\), then the set \(U = V_t\) induces the facet
Proof
Let \(U \subseteq V_t\). If \(|U| \le n-2\), then any \(s-t\) cut \((S,{\bar{S}})\) in \({\mathcal {C}}_{\min }(U)\) has the following structure: \(S = \{s\} \cup U\). But then condition (ii) of Theorem 1 is not satisfied by \((S,{\bar{S}})\). Now suppose \(|U| = n-1\). Then the dominating \(s-t\) cut \((S,{\bar{S}})\) in \({\mathcal {C}}_{\min }(U)\) has the following structure: \(S = \{s\} \cup V_t \cup U\). But then condition (i) of Theorem 1 is not satisfied by \((S,{\bar{S}})\), since for each \(v_i\), a single arc of capacity \(\lambda _i(UB^i- \sum _{k=1}^n LB^i_k)\) leaves S, but this matches the capacity of \((s,v_i)\). Finally, if \(U= V_t\), then the conditions of Theorem 1 are satisfied (the first one is void), and thus we get the inequality in the statement. \(\square \)
So, we have the following description for \(Q'\):
Notice that this description is valid even if \(UB^i = \sum _{j=1}^n LB^i_j\) for all i. Now we transform this description to one for \((P^\varDelta )^{emb}\). But this is easy. By Proposition 16 we know that \((x,\lambda ) \in (P^\varDelta )^{emb}\) if and only if \(x_j \ge \sum _{i=1}^m LB^i_j\lambda _i\) for each j, and \((x',\lambda ) \in Q'\), where \(x'_j = x_j -\sum _{i=1}^m LB^i_j\lambda _i\) for all j. Consequently, we have the following:
Proposition 18
A minimal linear description of \((P^\varDelta )^{emb}\) is
This is precisely the description of Jeroslow obtained by completely different means.
5.8 Multi-variate piecewise linear functions
This application is from [26], see also [28]. The objective is to model the graph of a continuous piecewise linear function \(f\ :\ D\rightarrow {\mathbb {R}}\) on a bounded domain \(D\subseteq {\mathbb {R}}^d\), where D admits a polyhedral partition \(\bigcup _{i=1}^m C_i = D\) (\(\mathrm {relint}(C_i) \cap \mathrm {relint}(C_j) = \emptyset \) for \(i\ne j\)) such that \(x \in C_i\) implies \(f(x) = a_i \cdot x + b_i\), for some \(a_i \in {\mathbb {R}}^d\) and \(b_i\in {\mathbb {R}}\). The graph of f is \(\mathrm {gr}(f):= \{ (x, f(x))\ :\ x \in D\}\). Let \(W := \bigcup _{i=1}^m \mathrm {vert}(C_i)\). In fact, we have
where \(P_i := \{ x \in {\mathbb {R}}^W_{\ge 0}\ :\ \sum _{w \in W} x_w = 1,\ x_w = 0\ \forall w \in W{\setminus } \mathrm {vert}(C_i)\}\). Here, \(x \in \bigcup _{i=1}^m P_i\) is the combinatorial disjunctive constraint (5).
Let \(P^{pwl} = \mathrm {conv}(\bigcup _{i=1}^m P_i)\). Suppose \(W = \{w_1,\ldots ,w_n\}\). Then \((P^{pwl})^{emb}\) is the convex hull of those \((x,\lambda )\) which satisfy
It is easy to see that \((P^{pwl})^{emb}\) admits a network representation \(N=(V,A,c)\), where \(V = \{s,t\}\cup V_s \cup V_t\) such that \(V_s = \{v_1,\ldots ,v_m\}\), \(V_t=\{1,\ldots ,n\}\), and \((v_i,j) \in A\) if and only if \(w_j \in C_i\). Furthermore, A contains all the arcs \((s,v_i)\) for \(i=1,\ldots ,m\), and (j, t) for \(j=1,\ldots ,n\). As usual, \(c(j,t) = x_j\) for \(j \in V_t\), while \(c(s,v_i) = \lambda _i\), and \(c(v_i,j) = \lambda _i\) for all \((v_i,j) \in A\). The facets of \((P^{pwl})^{emb}\) have a particularly nice geometrical characterization. Let \(\kappa (T)\) denote the number of connected componentsFootnote 3 of some \(T \subset {\mathbb {R}}^d\). Clearly, the dimension of \((P^{pwl})^{emb}\) is \(n+m-1-\kappa (D)\).
Proposition 19
The non-trivial facets of \((P^{pwl})^{emb}\) take the form
where \(M \subset \{1,\ldots ,m\}\) is such that \(\kappa (D{\setminus } (\bigcup _{i \in M} C_i))+\kappa (\bigcup _{i \in M} C_i) = \kappa (D)+1\).
Proof
We construct a dominating \(s-t\) cut \((S,{\bar{S}})\) from M and show that it determines an inequality equivalent to (24). Let \(U := \cup _{i \in M} \varGamma ^{out}_{v_i}\), and \(S := \{s\}\cup \{v_i \in V_s\ :\ |\varGamma ^{out}_{v_i} {\setminus } U| \le 1 \} \cup U\). Observe that \(v_i \notin S\) if and only if \(|\varGamma ^{out}_{v_i} {\setminus } U|\ge 2\) and \(i\in M\) if and only if \(\varGamma ^{out}_{v_i} \subseteq U\). Therefore, the corresponding inequality for \((S,{\bar{S}})\) is
Since \(\sum _{i=1}^m \lambda _i = \sum _{j=1}^n x_j=1\) by assumption, we can rewrite this as
Rearranging terms yields (24).
We still have to verify that S meets the conditions of Theorem 2. In fact, if either of the conditions does not hold, then either the nodes in U are disconnected in the subnetwork spanned by \(S{\setminus } \{s\}\), or those in \(V_t {\setminus } U\) are disconnected in \(N{\setminus } (S\cup \{t\})\), which implies \(\kappa (D{\setminus } (\bigcup _{i \in M} C_i))+\kappa (\bigcup _{i \in M} C_i) > \kappa (D)+1\).\(\square \)
In fact, this characterization is the same as that of Lee and Wilson [36].
The 2-dimensional special case, where \(D = [0,S_1]\times [0,S_2]\), and the \(\{C_i\}_{i=1}^m\) constitute a grid triangulation of D with \(m = 2S_1 S_2\) triangles, is extensively studied in [26,27,28, 45, 48], and ideal formulations with \(O(\log _2 m)\) new (binary) variables and constraints are provided. Different triangulation of the grid may define different piecewise linear functions, even if they agree on the grid points, for an example we refer the reader to [28].
The naive modelling (23) of the grid triangulations leads to m auxiliray \(\lambda _i\) variables, which is far more than \(O(\log _2 m)\) needed by the methods of [26,27,28, 45, 48]. On the other hand, the techniques of the above papers are difficult to generalize for 3 or more dimensions. Nevertheless, Huchette and Vielma [28] proved that intersecting ideal formulations for combinatorial disjunctions yields an ideal formulation:
Theorem 3
[28] Fix \(s \in {\mathbb {Z}}_{\ge 1}\), and consider s distinct combinatorial disjunctive constraints \(B^t = \bigcup _{i=1}^{m_t} Q(T^{i,t})\) on the same set V, where \(\bigcup _{i=1}^{m_t} T^{i,t} = V\), for \(t \in \llbracket s \rrbracket \). Let \(\varPi ^t \subseteq {\mathbb {R}}^V \times {\mathbb {R}}^{r_t}\) be such that \(\{ (x,\lambda ^t)\in \varPi ^t\ :\ \lambda ^t \in {\mathbb {Z}}^{r_t}\}\) is an ideal formulation for \(B^t\), for each \(t \in \llbracket s \rrbracket \). Then, an ideal formulation for \(\bigcap _{t=1}^s B^t\) is
Huchette and Vielma suggested that this result permits to go beyond the 2-variable special case. Below we describe a possible realization of their idea. In d dimensions, the unit grid for \(D := \times _{t=1}^d [0,S_k]\) consists of \(\prod _{t=1}^d S_t\) unit cubes. Let \(n = \prod _{t=1}^d (S_t+1)\) be the number of grid points in \(W := D\cap {\mathbb {Z}}^d\). For each unit cube in the grid, a partitioning into d! simplices of \([0,1]^d\) is specified. Let \({\mathcal {C}}\) be the set of all the simplices given in all the unit cubes of the grid W. We can use d distinct combinatorial disjunctions for selecting a cube, and then some additional combinatorial disjunction(s) to select a single simplex in the selected cube (this is how the compact formulation of [28] works in 2 dimensions). So, for \(t \in \llbracket d \rrbracket \), let \(m_t = S_t\), and \(T^{i,t} = \{ w \in W\ :\ w_t \in \{i-1,i\} \}\) for \(i\in \llbracket m_t \rrbracket \), namely, in \(T^{i,t}\) we select all the grid points \(w \in D\) such that \(w_t \in \{i-1,i\}\). Let \(B^t = \bigcup _{i=1}^{m_t} Q(T^{i,t})\), and observe that this is the SOS2 constraint along the \(t^{th}\) axis. Let \(\varPi ^t \subset {\mathbb {R}}^n \times {\mathbb {R}}^{r_t}\) be any ideal formulation for \(B^t\) with \(r_t = O(\log S_t)\) variables and \(O(\log S_t)\) constraints, see e.g., [28], and Sect. 2. By Theorem 3, joining the \(\varPi ^t\), \(t \in \llbracket d \rrbracket \), yields an ideal formulation for \(\bigcap _{t=1}^d B^t\), and in fact it selects a single cube from the grid (by setting the \(\lambda ^t\) to unit vectors). However, we still have to select a simplex. All we need is one more combinatorial disjunction, which covers the vertices of all the \(d! \prod _{t=1}^d S_t\) simplices such that each term in this disjunction covers simplices of node disjoint cubes. In fact, \(2^d d!\) terms suffice, as the following statement shows.
Proposition 20
There is a combinatorial disjunction \(B^{d+1} = \bigcup _{i=1}^{2^d d!} Q(T^{i,d+1})\) such that
-
\(\bigcup _{i=1}^{2^d d!} T^{i,d+1} = D \cap {\mathbb {Z}}^d\),
-
for any unit cube in the grid \(D \cap {\mathbb {Z}}^d\), and any simplex \(C \in {\mathcal {C}}\) from the cube, there is a unique \(T^{i,d+1}\) containing \(\mathrm {vert}(C)\), and
-
Any \(T^{i,d+1}\) consists of the vertices of simplices from vertex disjoint unit cubes of the grid.
Proof
To cover a grid in \({\mathbb {Z}}^d\) by sets of node disjoint unit cubes, we can partition the grid into \(2^d\) subsets, see Fig. 6. Each of the \(2^d\) sets of cubes yields d! disjunctive terms, namely, we identify each simplex in each unit cube uniquely by a number from \(1,\ldots ,d!\), and then we collect all vertices of those simplices having the same id. in a term of the disjunction. More formally, let \(R^k\) for \(k\in \llbracket 2^d \rrbracket \) be the sets of node disjoint unit cubes from the grid which together cover D. Each \(R^k\) gives rise to d! sets \(T^{i,d+1}\) for \(i\in \{d! (k-1)+1,\ldots , d!k\}\), where \(T^{i,d+1}\) contains \(\mathrm {vert}(C)\) for those simplices C from the cubes of \(R^k\) having id (\(i - d! (k-1)\)). It is easy to see that the sets \(T^{i,d+1}\) satisfy the conditions of the statement. \(\square \)
Corollary 3
Let \(\varDelta ^W_C = \{ x \in {\mathbb {R}}^W_{\ge 0}\ :\ \sum _{w \in W} x_w = 1,\ x_w = 0\ \forall w \notin \mathrm {vert}(C)\}\). Then \(\mathrm {conv}(\bigcap _{t=1}^{d+1} B^t) = \mathrm {conv}\{ \varDelta ^W_C\ :\ C \in {\mathcal {C}} \}\). Moreover, joining any ideal formulations \(\varPi ^t\) for \(B^t\), \(t \in \llbracket d+1 \rrbracket \), as in Theorem 3, yields an ideal formulation for \(\bigcap _{t=1}^{d+1} B^t\).
Finally, using our techniques, it is straightforward to obtain an ideal formulation for \(P^{d+1}_= := \mathrm {conv}(B^{d+1})\). Let \(m = 2^d d!\), and \(n = |W|\). The underlying network \(N=(V,A,c)\) has nodes \(\{s,t\} \cup V_s \cup V_t\), where \(V_s = \{v_1,\ldots ,v_m\}\), and \(V_t = \{1,\ldots ,n\}\). Node s is connected to each \(v_i \in V_s\) by an arc of capacity \(\lambda _i\), node \(v_i\) is connected to each node \(j \in V_t\) such that \(w_j \in T^{i,d+1}\) by an arc of capacity \(\lambda _i\), and finally, each \(j \in V_t\) is connected to t by an arc of capacity \(x_j\). We also have the equations \(\sum _{i=1}^m \lambda _i = \sum _{j=1}^n x_j = 1\). However, there are no implicit equations for \((P^{d+1}_=)^{emb}\), because if a partitioning \(E_1,\ldots ,E_\kappa \) of W, for some \(\kappa \ge 2\), induces linearly independent valid equations for \((P^{d+1}_=)^{emb}\), then each \(T^{i,d+1}\) must be a subset of some \(E_\ell \). It is easy to verify that this is impossible.
Observation 6
\(\dim ((P^{d+1}_=)^{emb}) = n+m-2\).
We can apply Theorem 2 to obtain the non-trivial facets of \((P^{d+1}_=)^{emb} := \mathrm {conv}\{\bigcup _{i=1}^{2^d d!} Q(T^{i,d+1}) \times \{ \epsilon ^i \})\). Note that there are only \(2^d d!\) auxiliary variables in the resulting formulation, which is just 8 for \(d=2\), 48 for \(d=3\), and 384 for \(d=4\), and it is independent of the size of n. As for the number of facets of \((P^{d+1}_=)^{emb}\), it can be exponential in n even if \(d=2\). However, to our best knowledge, for \(d\ge 3\), no ideal formulation is known with a logarithmic number of auxiliary variables and linear inequalities in n.
Proposition 21
Let \(U \subset V_t\), and \((S,{\bar{S}}) \in {\mathcal {C}}_{\min }(U)\). Then \(F_S\) is a facet of \((P^{d+1}_=)^{emb}\) if and only if (a) \(N{\setminus } (S\cup \{t\})\) is connected, and (b) for any partitioning of U into nonempty subsets \(U_1\) and \(U_2\), there is some i such that \(T^{i,d+1} \cap U_\ell \ne \emptyset \) for \(\ell =1,2\), and \(T^{i,d+1} \subseteq U\).
5.9 Modeling of variable intensity activities in a resource loading problem
This application stems from the paper [41], where a resource loading problem is studied. Here we give a new derivation of the polyhedral description of feasible intensity assignments to an activity.
Suppose there is a time horizon of n consecutive time periods of unit length each, and an activity which has to be scheduled in an interval of time periods uninterruptedly. In those time periods when it is processed, a fraction between given lower and upper bounds, LB and UB, must be assigned such that the sum of fractions is 1, where \(0 < LB \le UB \le 1\). Let \({\mathcal {E}}\) consist of all the possible execution intervals for the activity, i.e., \([k,\ell ] \in {\mathcal {E}}\) if and only if \(1\le k\le \ell \le n\), and \((\ell -k+1)LB \le 1 \le (\ell -k+1)UB\). For ease of notation, \([k,\ell ]\) also represents the set of integers \(\{t \in {\mathbb {Z}}\ :\ k\le t \le \ell \}\). If we select \([k,\ell ] \in {\mathcal {E}}\), then the intensity assignment \(x \in {\mathbb {R}}^n\) of the activity must satisfy the conditions \(\sum _{j=k}^{\ell } x_j = 1\), \(LB \le x_j \le UB\) for \(j \in [k,\ell ]\), and \(x_j = 0\) otherwise.
For each interval \([k,\ell ]\in {\mathcal {E}}\), we can strengthen the lower and upper bounds as follows: \(LB_{k\ell } = \max \{LB, 1-(\ell -k)UB\}\) and \(UB_{k\ell } = \min \{UB, 1-(\ell -k)LB\}\). To avoid implicit equations, we assume that for each pair of consecutive time periods j, and \(j+1\), there exists some execution interval \([k,\ell ] \in {\mathcal {E}}\) such that \(j, j+1\in [k,\ell ]\), and \((\ell -k+1)LB_{k\ell }< 1 < (\ell -k+1)UB_{k\ell }\).
We can model the feasible intensity assignments by means of the following integer program:
Let \(P^{RLP}\) be the convex hull of those \((x,\lambda )\) vectors that satisfy these constraint. In order to get the (non-trivial) facets of \(P^{RLP}\), we model the above integer program by a network \(N = (V,A,c,lb)\), where V comprises a source node s, a sink node t, the nodes \(V_s := \{ v_{k\ell }\ |\ [k,\ell ] \in {\mathcal {E}}\}\), and the nodes \(V_t := \{1,\ldots ,n\}\). We have one arc from s to each \(v_{k\ell }\) with lower bound \(lb(s,v_{k\ell }) = (\ell -k+1)LB_{k\ell }\lambda _{k\ell }\), and capacity \(c(s,v_{k\ell }) = \lambda _{k\ell }\). Further on, for each \(v_{k\ell } \in V_s\) and \(j \in V_t\), we have one arc \((v_{k\ell }, j)\) of lower bound \(\lambda _{k\ell } LB_{k\ell }\), and capacity \(\lambda _{k\ell } U_{k\ell }\). Finally, we have one arc from each \(j\in V_t\) to t of lower bound 0, and capacity \(x_j\). Observe that the positive lower bounds stem from the left hand side of (26). Let \(x'_j = x_j - \sum _{[k,\ell ]\in {\mathcal {E}}: j \in [k,\ell ]} \lambda _{k\ell } LB_{k\ell }\), and we derive network \(N' = (V,A,c')\) from N as follows. The capacity of the arcs \((s,v_{k\ell })\) reduces to \((1-(\ell -k+1)LB_{k\ell }) \lambda _{k\ell }\), that of \((v_{k\ell }, j)\) becomes \((UB_{k\ell } - LB_{k\ell })\lambda _{k\ell }\), while on the arcs (j, t) the new capacity is \(x'_j\). Let \(m = |{\mathcal {E}}|\). The following statement is analogous to Proposition 16.
Proposition 22
Suppose \(\sum _{[k,\ell ] \in {\mathcal {E}}} \lambda _{k\ell } = 1\), \(x\ge 0\), and \(\lambda \ge 0\). \((x,\lambda ) \in P^{RLP}\) if and only if \(N_{x,\lambda }\) admits a feasible \(s-t\) flow of value 1 if and only if \(N'_{x',\lambda }\) admits a feasible \(s-t\) flow of value \(\sum _{[k,\ell ] \in {\mathcal {E}}} (1-(\ell -k+1)LB_{k\ell })\lambda _{k\ell }\).
Let \(P^{RLP'}\) be the convex hull of those \((x',\lambda )\) such that \(x,\lambda \ge 0\), \(\sum _{[k,\ell ] \in {\mathcal {E}}} \lambda _{k\ell } = 1\), and \(N'_{x',\lambda }\) admits a feasible \(s-t\) flow of value \(\sum _{[k,\ell ]\in {\mathcal {E}}} (1-(\ell -k+1)LB_{k\ell })\lambda _{k\ell }\). We apply the MAX FLOW-MIN CUT theorem to \(N'\) to obtain a linear representation of \(P^{RLP'}\):
Let \((S,{\bar{S}})\) be any \(s-t\) cut of \(N'\), the corresponding inequality is
If we increase both sides by \(\sum _{[k,\ell ]\in {\mathcal {E}}} |[k,\ell ]{\setminus } U| \cdot LB_{k\ell } \lambda _{k\ell }\), we obtain
where we used \(x_j = x'_j + \sum _{[k,\ell ]\in {\mathcal {E}}: j \in [k,\ell ]} LB_{k\ell } \lambda _{k\ell }\). These are precisely the inequalities (27) obtained in [41] by a different argument. The following statement is analogous to Proposition 18.
Proposition 23
A minimal linear description of \(P^{RLP}\) consists \(\lambda \ge 0\), the inequalities \(x_j \ge \sum _{[k,\ell ] \in {\mathcal {E}}} LB_{k\ell } \lambda _{k\ell }\), (27)–(29), and those inequalities from (31) for which the corresponding inequality from (30) induces a facet of \(P^{RLP'}\).
It remains to characterize those \(U \subset V_t\) that induce facets of \(P^{RLP'}\). First, for a fixed \(U \subset V_t\), we determine the non-dominated \(s-t\) cuts of \(N'\) w.r.t. U. So we build a set S containing \(\{s\}\cup U\), and some of the nodes \(v_{k\ell }\). We can decide for each \(v_{k\ell }\) whether to include in S or not in order to minimize the capacity of \((S,{\bar{S}})\).
-
If \(v_{k\ell } \in S\), then the arcs \((v_{k\ell },j)\) for \(j \in [k,\ell ]{\setminus } U\) are adjacent to \(v_{k\ell }\) and leave S. The total capacity of these arcs is
$$\begin{aligned} \lambda _{k\ell }|[k,\ell ]{\setminus } U|\cdot \left( U_{k\ell } - LB_{k\ell }\right) = \lambda _{k\ell }|[k,\ell ]{\setminus } U|\cdot U_{k\ell } - \lambda _{k\ell }|[k,\ell ] {\setminus } U|\cdot LB_{k\ell }.\nonumber \\ \end{aligned}$$(32) -
If \(v_{k\ell } \not \in S\), then the arc \((s,v_{k\ell })\) leaves S and its capacity is
$$\begin{aligned} \lambda _{k\ell }(1 - (\ell -k+1)\cdot LB_{k\ell }) = \lambda _{k\ell }\left( 1 - |[k,\ell ]\cap U|\right) \cdot LB_{k\ell }) - \lambda _{k\ell }|[k,\ell ] {\setminus } U|\cdot LB_{k\ell }.\nonumber \\ \end{aligned}$$(33)
Comparing (32) and (33), we can derive the following.
Observation 7
\((S,{\bar{S}}) \in {\mathcal {C}}_{\min }(U)\) if and only if \(v_{k\ell } \in S\) when \(|[k,\ell ]{\setminus } U|\cdot UB_{k\ell } < 1 - |[k,\ell ]\cap U|\cdot LB_{k\ell }\), and \(v_{k\ell } \not \in S\) when \(|[k,\ell ]{\setminus } U|\cdot UB_{k\ell } > 1 - |[k,\ell ]\cap U|\cdot LB_{k\ell }\).
Now we apply Theorem 2 to single out those subsets \(U \subset V_t\) that induce facets of \(P^{RLP'}\). Let \({\mathcal {E}}^+\) consist of those \([k,\ell ]\in {\mathcal {E}}\) for which \((\ell -k+1) UB_{k\ell }> 1 > (\ell -k+1) LB_{k\ell }\).
Theorem 4
Fix \(U \subset V_t\), and let \((S,{\bar{S}})\) the dominating \(s-t\) cut of \(N'\) w.r.t. U. It induces a facet of \(P^{RLP'}\) if and only if both of the following conditions hold.
-
i)
If \(|V_t {\setminus } U| \ge 2\), then for each \(j \in V_t {\setminus } U\) except the last one, there exists \([k,\ell ] \in {\mathcal {E}}^+\) such that \(v_{k\ell } \in {\bar{S}}\), \([k,\ell ]\cap [1,j] \cap (V_t {\setminus } U) \ne \emptyset \) and \([k,\ell ]\cap [j+1,n] \cap (V_t {\setminus } U) \ne \emptyset \).
-
ii)
If \(|U| \ge 2\), then for each \(j \in U\) except the last one, there exists \([k,\ell ] \in {\mathcal {E}}^+\) such that \(v_{k\ell } \in S\), \([k,\ell ]\cap [1,j] \cap U \ne \emptyset \) and \([k,\ell ]\cap [j+1,n] \cap U \ne \emptyset \).
Proof
We derive the two conditions of the theorem from those of Theorem 2. First note that if \(v_{k\ell } \not \in {\mathcal {E}}^+\), then \(v_{k\ell } \in S\), as \((S,{\bar{S}})\) is the dominating \(s-t\) cut of \(N'\) w.r.t. U. Consider the first condition of Theorem 2. \(N{\setminus } (S\cup \{t\})\) is not connected if and only if there exists a partitioning of \(V_t{\setminus } U\) into two subsets \({\bar{U}}_1 \ne \emptyset \) and \({\bar{U}}_2 \ne \emptyset \), such that each \(v_{k\ell } \in {\bar{S}}\cap V_s\) is adjacent to some nodes of \({\bar{U}}_1\) only, or to some nodes of \({\bar{U}}_2\) only, that is, \([k,\ell ] {\setminus } U \subseteq {\bar{U}}_1\) or \([k,\ell ] {\setminus } U \subseteq {\bar{U}}_2\). Since \([k,\ell ]\) is an interval, \([k,\ell ]{\setminus } U\) consists of consecutive members of \(V_t {\setminus } U\), and thus the latter condition is equivalent to the existence of some \(j \in V_t {\setminus } U\) (but not the last one) such that \([k,\ell ] {\setminus } U \subseteq [1,j]\) or \([k,\ell ] {\setminus } U \subseteq [j+1,n]\) for each \(v_{k\ell } \in {\bar{S}}\). But this is precisely the negation of the first condition of this theorem.
The equivalence of the second condition of Theorem 2 to that of the present theorem can be shown analogously. \(\square \)
The above characterization of the facets of \(P^{RLP'}\) is equivalent to that obtained in [41] for the non-trivial facets of \(P^{RLP}\). However, in that paper a more problem specific approach is used.
6 Final remarks
In this paper we have proposed a new systematic way of constructing ideal, non-extended MIP formulations for disjunctive constraints of the form \(x \in \bigcup _{i=1}^m P_i\), where the \(P_i\) are polytopes. Our method works if the Cayley Embedding of this union of polytopes admits a certain network representation. Then we can characterize the facets of the LP-relaxation of the MIP formulation. We have illustrated the richness of the class of problems that fits this framework by several examples from the literature, and we have also worked out a new one. We emphasize that our characterization of facets is valid for any union of polytopes such that the corresponding Cayley Embedding admits a network representation.
These results may also pave the way for modeling problems using building blocks representing the convex hull of polytopes with the above properties. Then, the solver could generate cuts for such building blocks as needed in the course of solving the problem by branch-and-cut.
Notes
Those beyond the non-negativity of the variables.
Size of a (linear) formulation is measured by the number of inequalities.
Path-connected in topological sense.
References
Anderson, R., Huchette, J., Ma, W., Tjandraatmadja, C., Vielma, J.P.: Strong mixed-integer programming formulations for trained neural networks. Math. Program. 193, 3–39 (2020)
Balas, E.: Disjunctive programming: cutting planes from logical conditions. In: Nonlinear Programming 2, pp. 279–312. Elsevier (1975)
Balas, E.: Disjunctive programming. In: Annals of Discrete Mathematics, vol. 5, pp. 3–51. Elsevier (1979)
Balas, E.: Disjunctive programming and a hierarchy of relaxations for discrete optimization problems. SIAM J. Algebraic Discrete Methods 6(3), 466–486 (1985)
Balas, E.: On the convex hull of the union of certain polyhedra. Oper. Res. Lett. 7(6), 279–283 (1988)
Balas, E.: Disjunctive programming: properties of the convex hull of feasible points. Discrete Appl. Math. 89(1–3), 3–44 (1998)
Balas, E.: Logical constraints as cardinality rules: tight representation. J. Comb. Optim. 8(2), 115–128 (2004)
Balas, E.: Projection, lifting and extended formulation in integer and combinatorial optimization. Ann. Oper. Res. 140(1), 125–161 (2005)
Balas, E.: Disjunctive Programming. Springer, Berlin (2018)
Balas, E., Bockmayr, A., Pisaruk, N., Wolsey, L.: On unions and dominants of polytopes. Math. Program. 99(2), 223–239 (2004)
Balas, E., Oosten, M.: On the dimension of projected polyhedra. Discrete Appl. Math. 87(1–3), 1–9 (1998)
Basu, A., Martin, K., Ryan, C.T., Wang, G.: Mixed-integer linear representability, disjunctions, and variable elimination. In: International Conference on Integer Programming and Combinatorial Optimization, Springer, Berlin, pp. 75–85 (2017)
Beale, E.M.L., Tomlin, J.A.: Special facilities in a general mathematical programming system for non-convex problems using ordered sets of variables. In: Lawrence, J., (ed.) OR 69: Proceedings of the Fifth International Conference on Operational Research, pp. 447–454 (1970)
Blair, C.: Representation for multiple right-hand sides. Math. Program. 49(1–3), 1–5 (1990)
Bonami, P., Lodi, A., Tramontani, A., Wiese, S.: On mathematical programming with indicator constraints. Math. Program. 151(1), 191–223 (2015)
Ceria, S., Soares, J.: Convex programming for disjunctive convex optimization. Math. Program. 86(3), 595–614 (1999)
Conforti, M., Cornuéjols, G., Zambelli, G.: Extended formulations in combinatorial optimization. 4OR 8(1), 1–48 (2010)
Conforti, M., Di Summa, M., Faenza, Y.: Balas formulation for the union of polytopes is optimal. Math. Program. 180(1), 311–326 (2020)
Conforti, M., Wolsey, L.A.: Compact formulations as a union of polyhedra. Math. Program. 114(2), 277–289 (2008)
Ford Jr., L.R., Fulkerson, D.R.: Maximal flow through a network. Can. J. Math. 8, 399–404 (1956)
Frank, A.: Submodular functions in graph theory. Discrete Math. 111(1–3), 231–243 (1993)
Günlük, O., Linderoth, J.: Perspective reformulations of mixed integer nonlinear programs with indicator variables. Math. Program. 124(1–2), 183–205 (2010)
Hijazi, H., Bonami, P., Cornuéjols, G., Ouorou, A.: Mixed-integer nonlinear programs featuring “on/off” constraints. Comput. Optim. Appl. 52(2), 537–558 (2012)
Hijazi, H.L., Bonami, P., Ouorou, A.: A note on linear on/off constraints. http://www.optimization-online.org/DB_FILE/2014/04/4309.pdf (2014)
Huber, B., Rambau, J., Santos, F.: The cayley trick, lifting subdivisions and the bohne-dress theorem on zonotopal tilings. J. Eur. Math. Soc. 2(2), 179–198 (2000)
Huchette, J., Vielma, J.P.: A combinatorial approach for small and strong formulations of disjunctive constraints. Math. Oper. Res. 44(3), 793–820 (2019)
Huchette, J., Vielma, J.P.: A geometric way to build strong mixed-integer programming formulations. Oper. Res. Lett. 47(6), 601–606 (2019)
Huchette, J., Vielma, J.P.: Nonconvex piecewise linear functions: advanced formulations and simple modeling tools. to appear in Oprations Research, arXiv:1708.00050 (2019)
Janssen, J., Kilakos, K.: Bounded stable sets: polytopes and colorings. SIAM J. Discrete Math. 12(2), 262–275 (1999)
Jeroslow, R.G.: On defining sets of vertices of the hypercube by linear inequalities. Discrete Math. 11(2), 119–124 (1975)
Jeroslow, R.G.: A simplification for some disjunctive formulations. Eur. J. Oper. Res. 36(1), 116–121 (1988)
Jeroslow, R.G., Lowe, J.K.: Modelling with integer variables. 22, 167–184 (1984)
Kaibel, V., Loos, A.: Finding descriptions of polytopes via extended formulations and liftings. arXiv preprint arXiv:1109.0815 (2011)
Karavelas, M.I., Konaxis, C., Tzanaki, E.: The maximum number of faces of the minkowski sum of three convex polytopes. In: Proceedings of the Twenty-Ninth Annual Symposium on Computational Geometry, pp. 187–196 (2013)
Köppe, M., Louveaux, Q., Weismantel, R.: Intermediate integer programming representations using value disjunctions. Discrete Optim. 5(2), 293–313 (2008)
Lee, J., Wilson, D.: Polyhedral methods for piecewise-linear functions I: the lambda method. Discrete Appl. Math. 108(3), 269–285 (2001)
Lubin, M., Zadik, I., Vielma, J.P.: Mixed-integer convex representability. In: International Conference on Integer Programming and Combinatorial Optimization. Springer, Berlin, pp. 392–404 (2017)
Martin, A., Möller, M., Moritz, S.: Mixed integer models for the stationary case of gas network optimization. Math. Program. 105(2–3), 563–582 (2006)
Padberg, M.: Approximating separable nonlinear functions via mixed zero-one programs. Oper. Res. Lett. 27(1), 1–5 (2000)
Pashkovich, K.: Extended formulations for combinatorial polytopes. Ph.D. thesis, Fakultät fürr Mathematik der Otto-von-Guericke-Universität Magdeburg (2012)
Song, G., Kis, T., Leus, R.: Polyhedral results and branch-and-cut for the resource loading problem. INFORMS J. Comput., accepted (2020)
Tawarmalani, M., Richard, J.-P.P., Chung, K.: Strong valid inequalities for orthogonal disjunctions and bilinear covering sets. Math. Program. 124(1–2), 481–512 (2010)
Tomlin, J.A.: Special ordered sets and an application to gas supply operations planning. Math. Program. 42(1–3), 69–84 (1988)
Vielma, J.P.: Mixed integer linear programming formulation techniques. SIAM Rev. 57(1), 3–57 (2015)
Vielma, J.P.: Embedding formulations and complexity for unions of polyhedra. Manag. Sci. 64(10), 4721–4734 (2018)
Vielma, J.P.: Small and strong formulations for unions of convex sets from the cayley embedding. Math. Program. 177(1–2), 21–53 (2019)
Vielma, J.P., Ahmed, S., Nemhauser, G.: Mixed-integer models for nonseparable piecewise-linear optimization: unifying framework and extensions. Oper. Res. 58(2), 303–315 (2010)
Vielma, J.P., Nemhauser, G.L.: Modeling disjunctive constraints with a logarithmic number of binary variables and constraints. Math. Program. 128(1–2), 49–72 (2011)
Weibel, C.: Minkowski sums of polytopes: combinatorics and computation. PhD thesis, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland (2007)
Yan, H., Hooker, J.N.: Tight representation of logical constraints as cardinality rules. Math. Program. 85(2), (1999)
Ziegler, G.M: Lectures on polytopes. Springer, Berlin, 152 (2012)
Acknowledgements
The authors are grateful to an anonymous referee for many constructive comments that helped to improve the paper significantly, and to the editor and another anonymous referee for comments that led to better positioning our results.
Funding
Open access funding provided by ELKH Institute for Computer Science and Control.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
There are no conflicts of interest.
Additional information
To the memory of Egon Balas.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work has been supported by the National Research, Development and Innovation Office—NKFIH, Grant No. SNN 129178, and ED_18-2-2018-0006.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kis, T., Horváth, M. Ideal, non-extended formulations for disjunctive constraints admitting a network representation. Math. Program. 194, 831–869 (2022). https://doi.org/10.1007/s10107-021-01652-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-021-01652-z