Abstract
We consider randomized QMC methods for approximating the expected recourse in two-stage stochastic optimization problems containing mixed-integer decisions in the second stage. It is known that the second-stage optimal value function is piecewise linear-quadratic with possible kinks and discontinuities at the boundaries of certain convex polyhedral sets. This structure is exploited to provide conditions implying that first and higher order terms of the integrand’s ANOVA decomposition (Math. Comp. 79 (2010), 953–966) have mixed weak first order partial derivatives. This leads to a good smooth approximation of the integrand and, hence, to good convergence rates of randomized QMC methods if the effective (superposition) dimension is low.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Two-stage stochastic mixed-integer programs belong to the most complicated optimization problems due to multivariate integrals and discontinuous integrands (see [32, 46]). Most approaches for their computational solution require first a numerical integration scheme for the multivariate integral and second an efficient solution method for the resulting specifically structured large scale mixed-integer program. For some time Monte Carlo methods appeared as the only convergent numerical integration technique for such optimization models [21] while several numerical techniques are available for solving the discrete stochastic program efficiently. For the latter we refer to approaches based on combinations of decomposition, branch-and-bound and branch-and-cut (see [1, 48] and the survey [47]).
The aim of the present paper is to contribute to the first computational step. Although Monte Carlo sampling methods are well established in theory and practice (see, for example, [5, 12] and [49, Chapter 5]), they suffer from slow convergence rate \(O(n^{-\frac{1}{2}})\). In recent years much progress has been achieved in the construction and analysis of Quasi-Monte Carlo (QMC) methods for computing integrals in high dimension d. We refer to the monograph [9], the survey [8] and the state-of-the-art [24] for presenting recent developments. For example, it is known that certain randomized QMC methods can achieve almost the optimal convergence rate \(O(n^{-1})\) if the integrands admit mixed weak first partial derivatives and, hence, belong to certain weighted tensor product Sobolev spaces on the unit cube \([0,1]^{d}\) or on \(\mathbb {R}^{d}\). We refer to the origins of randomized QMC methods in [39, 40], a survey [28] and a short introduction [29, Section 2].
In the present paper we study the applicability of randomized QMC methods to two-stage stochastic mixed-integer programs. Integrands arising in such models are piecewise linear-quadratic and contain kinks and discontinuties along faces of convex polyhedral sets (see Sect. 2). Hence, they do not have mixed first derivatives in the classical or weak sense. However, many such integrands allow an approximate representation by a function which can be much smoother than the original integrand under certain conditions and by a nonsmooth remainder. The key here consists in a specific decomposition of the multivariate integrand with d variables into a sum of \(2^{d}\) terms each depending on a group of variables indexed by a subset of \(\{1,\ldots ,d\}\). Such decompositions depend on the choice of d commuting projections \(P_{k}\), \(k\in \{1,\ldots ,d\}\). An important example is the analysis-of-variance (ANOVA) decomposition in which the projection \(P_{k}\) integrates with respect to the kth variable (see Sect. 3). As first observed in [14,15,16] such ANOVA decompositions may gain smoothness due to the specific projections. Our results in Sect. 4 show that such smoothness properties hold indeed for low order ANOVA terms of the integrands in two-stage stochastic mixed-integer programming if a geometric condition is imposed on the faces of the convex polyhedral sets. Our main result in Sect. 4 (Theorem 1) states that truncated ANOVA decompositions of the integrands have mixed weak first derivatives and represent good approximations of the integrands if the marginal densities of the underlying probability distribution are sufficiently smooth and the effective (superposition) dimension (23) is low.
Thereby we extend our earlier work [29] for two-stage models without integer decisions substantially. In particular, we show that the ANOVA terms of linear two-stage integrands satisfy the relevant smoothness properties not only until order 2 (as asserted in the main result of [29]) but until any order less than \(\frac{d}{2}\). In addition, we extend the convergence analysis for randomly shifted lattice rules to such discontinuous integrands (in Sect. 5). Compared to [29] the proofs of our main results in Sects. 4 and 6 require new tools like a characterization of faces of projected polyhedra and the theory of Haar measures on the topological group of real orthogonal matrices. The latter is needed to show that for multivariate normal distributions the geometric condition is satisfied almost everywhere with respect to the Haar measure defined on the group of orthogonal matrices needed for transforming the covariance matrix to diagonal form.
In general the performance of randomized QMC methods may be significantly deteriorated for discontinuous integrands. In [17], for example, the authors derive convergence rates for functions of the form \(g(x)\mathbb {1}_{B}(x)\), \(x\in [0,1]^{d}\), where g is smooth and B is convex polyhedral. They show that the convergence rate is much lower than optimal, but it improves if some of the discontinuity faces of B are parallel to some coordinate axes (best case being all faces parallel to some coordinate axes). As noted earlier the integrands of two-stage stochastic mixed-integer programs have also discontinuities at the boundaries of convex polyhedral sets but their structure is unknown and hidden in the problem data.
Numerical experience on comparing Monte Carlo sampling, randomly scrambled Sobol’ point sets and randomly shifted lattice rules for a two-stage stochastic mixed-integer electricity portfolio optimization problem is reported in detail in the accompanying paper [30]. In Sect. 7 we recall and discuss the computational results and add some conclusions.
2 Two-stage stochastic mixed-integer programs
Let us consider the two-stage stochastic mixed-integer program
where \(\Phi \) is the infimum function of the second-stage mixed-integer linear program
for all pairs \((u,t)\in \mathbb {R}^{m_{1}+m_{2}}\times \mathbb {R}^{r}\), where \(c\in \mathbb {R}^{m}\), X is a closed subset of \(\mathbb {R}^{m}\), \(W_{1}\) and \(W_{2}\) are \((r,m_{1})\) and \((r,m_{2})\)-matrices, respectively, \(q(\xi )\in \mathbb {R}^{m_{1}+m_{2}}\), \(h(\xi )\in \mathbb {R}^{r}\), and the (r, m)-matrix \(T(\xi )\) are affine functions of \(\xi \in \mathbb {R}^{d}\), and \(\rho \) is the probability density of a Borel probability measure \(\mathbb {P}\) on \(\mathbb {R}^{d}\).
The primal and dual feasible right-hand side sets for the second-stage program are
Clearly, \(\Phi (u,t)\) is finite for all \((u,t)\in \mathcal {U}\times \mathcal {T}\), it holds \((0,0)\in \mathcal {U}\times \mathcal {T}\) and \(\Phi (0,t)=0\) for any \(t\in \mathcal {T}\). While \(\mathcal {U}\) is a convex polyhedral cone in \(\mathbb {R}^{m_{1}+m_{2}}\), the structure of \(\mathcal {T}\) is more complicated. The latter has the representation
where \(\mathcal {K}\) is the convex polyhedral cone
Specific cases are (i) \(W_{2}=0\) (pure continuous recourse) implying \(\mathcal {T}=\mathcal {K}\) and (ii) \(W_{1}=0\) (pure integer recourse) leading to \(\mathcal {K}=\mathbb {R}_{+}^{r}\).
Next we introduce two assumptions:
- (A1):
-
The matrices \(W_{1}\) and \(W_{2}\) have only rational elements.
- (A2):
-
The cardinality of the set
$$\begin{aligned} Z=\bigcup _{t\in \mathcal {T}}Z(t), \text{ where } Z(t)=\left\{ y_{2} \in \mathbb {Z}^{m_{2}}:\exists y_{1}\in \mathbb {R}^{m_{1}} \text{ such } \text{ that } W_{1}y_{1}+W_{2}y_{2}\le t\right\} , \end{aligned}$$is finite, i.e., the number of integer decisions in (1) is finite. It is known that the set \(\mathcal {T}\) is always connected (i.e., there exists a polygon connecting two arbitrary points of \(\mathcal {T}\)) and closed if (A1) is satisfied (see [4, Theorems 5.6.1 and 5.6.2]). The representation (3) implies that \(\mathcal {T}\) can be decomposed into subsets of the form
$$\begin{aligned} \mathcal {T}(t_{0}):=\{t\in \mathcal {T}:Z(t)=Z(t_{0})\}=\bigcap _{z\in Z(t_{0})} (W_{2}z+\mathcal {K}){\setminus }\bigcup _{z\in Z{\setminus } Z(t_{0})} (W_{2}z+\mathcal {K}) \end{aligned}$$(5)for each fixed \(t_{0}\in \mathcal {T}\). Condition (A1) implies that the intersection in (5) may be replaced by \(\bar{t}+\mathcal {K}\) for some \(\bar{t}\in \mathcal {T}\) (see [4, Lemma 5.6.1]).
Hence, if (A1) is satisfied, there exist a finite subset N of \(\mathbb {N}\) and elements \(t_{i}\in \mathcal {T}\) and \(z_{ij}\in \mathbb {Z}^{m_{2}}\) for \(i\in N\) and j belonging to a finite subset \(N_{i}\) of N, such that \(\mathcal {T}\) admits the representation
The sets \(\mathcal {T}(t_{i})\), \(i\in N\), are nonempty and connected (even star-shaped cf. [4, Theorem 5.6.3]), but nonconvex in general. If for some \(i\in N\) the set \(\mathcal {T}(t_{i})\) is nonconvex, it can be decomposed into a finite number of disjoint subsets whose closures are convex polyhedra with facets parallel to suitable facets of \(\mathcal {K}\). By renumbering all such subsets (for every \(i\in N\)) one obtains a finite index set which is again denoted by N and subsets \(B_{i}\), \(i\in N\), forming a partition of \(\mathcal {T}\).
We will need the following result on optimal value functions of linear programs. For a given \((r,\overline{m})\)-matrix W we consider the function
from \(\mathbb {R}^{\overline{m}}\times \mathbb {R}^r\) to \(\overline{\mathbb {R}}\). We define the primal and dual feasibility sets
and recall some well-known properties of \(\Phi _{L}\) (see [37, 55]).
Lemma 1
The function \(\Phi _{L}\) is finite and continuous on the convex polyhedral cone \(\mathcal {D}\times \mathcal {P}\) in \(\mathbb {R}^{\overline{m}} \times \mathbb {R}^{r}\) and there exist \((\overline{m},r)\)-matrices \(C_{j}\) and convex polyhedral cones \(K_{j}\), \(j=1,\ldots ,\ell \), such that
The function \(\Phi _{L}(u,\cdot )\) is convex on \(\mathcal {P}\) for each \(u\in \mathcal {D}\), and \(\Phi _{L}(\cdot ,t)\) is concave on \(\mathcal {D}\) for each \(t\in \mathcal {P}\). Furthermore, the intersection \(K_{j}\cap K_{j'}\), \(j\ne j'\), is either equal to \(\{0\}\) or contained in a \((\overline{m}+r-1)\)-dimensional subspace of \(\mathbb {R}^{\overline{m}+r}\) if the two cones are adjacent.
Now we are in the position to prove the following result on the representation and properties of the infimum function \(\Phi \) (see also [32, (2.10)] for the case of fixed u).
Lemma 2
Assume (A1) and (A2). Then there exists a finite set N and Borel sets \(B_{i}\), \(i\in N\), such that \(\mathcal {T}=\bigcup _{i\in N}B_{i}\), and the closures of \(B_{i}\) are convex polyhedral with facets parallel to suitable facets of \(\mathcal {K}=W_{1}(\mathbb {R}^{m_{1}})+\mathbb {R}_{+}^{r}\).
The function \(\Phi \) is lower semicontinuous on \(\mathcal {U}\times \mathcal {T}\) and there exist \((r,m_{1})\) matrices \(C_{j}\), \(j=1,\ldots ,\ell \), \(\ell \in \mathbb {N}\), such that
where \(Z_{i}(t)=Z(t)\) is fixed for \(t\in B_{i}\), \(i\in N\). \(\Phi \) is continuous on \(\mathcal {U}\times B_{i}\) for each \(i\in N\) and there exists a constant \(C>0\) such that
holds for all pairs \((u,t)\in \mathcal {U}\times \mathcal {T}\).
Proof
The existence of the sets \(B_{i}\) and their properties are discussed after Eq. (6). The lower semicontinuity of \(\Phi \) follows from general results in parametric optimization, for example, [4, Theorem 4.2.1]. Next we prove the representation (8) of \(\Phi \). Due to the above construction the set Z(t) remains constant for all \(t\in B_{i}\). Hence, \(Z_{i}(t)\) is well defined and
holds for every \((u,t)\in \mathcal {U}\times B_{i}\) and \(i\in N\). Due to Lemma 1 there exist \((r,m_{1})\) matrices \(C_{j}\), \(j=1,\ldots ,\ell \), such that
The first infimum in (10) is lower bounded and, thus, attained. Hence, one obtains
for every pair \((u,t)\in \mathcal {U}\times B_{i}\). For the remaining statements we refer to [43]. \(\square \)
For more information on the continuity properties of \(\Phi \) on \(\mathcal {U}\times B_{i}\) for any \(i\in N\), we refer to [43]. Next we state our main representation result of the function \(\Phi \).
Proposition 1
Assume (A1) and (A2). The function \(\Phi \) is finite and lower semicontinuous on \(\mathcal {U}\times \mathcal {T}\). There exists a finite decomposition of \(\mathcal {U}\times \mathcal {T}\) consisting of Borel sets \(U_{\nu }\times B_{\nu }\), \(\nu \in \mathcal {N}\), such that their closures are convex polyhedral and \(\Phi \) is bilinear on each \(U_{\nu }\times B_{\nu }\). More precisely, there exist \((r,m_{1})\) matrices \(C_{\nu }\) and elements \(z_{\nu }\in \mathbb {Z}^{m_{2}}\) such that \(\Phi \) is of the form
for each \((u,t)\in U_{\nu }\times B_{\nu }\). The function \(\Phi \) may have kinks or discontinuities at the boundaries of \(U_{\nu }\times B_{\nu }\), \(\nu \in \mathcal {N}\).
Proof
We start from the representation (8) of \(\Phi \) on \(\mathcal {U}\times B_{i}\) for some \(i\in N\) and derive a further partition of \(\mathcal {U}\times B_{i}\). To this end we consider the sets \(N_{i}(t)=\{k:z_{k}\in Z_{i}(t)\}\) and \(V_{il}(t)=\{v\in \mathbb {R}^{m_{2}}:\langle v,z_{l}\rangle \le \langle v,z_{k}\rangle \), \(k\in N_{i}(t)\}\), for \(t\in B_{i}\), \(l\in N_{i}(t)\). In addition, we consider the \((r,m_{1})\) matrices \(C_{j}\) and the polyhedral cones \(K_{j}\), \(j=1,\ldots ,\ell \), appearing in Lemma 2. More precisely, we need the projections \(\mathrm{pr}_{1}\) and \(\mathrm{pr}_{2}\) from \(\mathbb {R}^{m_{1}+r}\) to \(\mathbb {R}^{m_{1}}\) and \(\mathbb {R}^{r}\), respectively, and the fact that \(\mathrm{pr}_{1}(K_{j})\) and \(\mathrm{pr}_{2}(K_{j})\) are also polyhedral cones for each \(j=1,\ldots ,\ell \). For each \(i\in N\) we define the following subsets of \(\mathcal {U}\) and of \(B_{i}\):
for all \(i\in N\), \(j=1,\ldots ,\ell \) and \(l\in N_{i}\). For any \((u,t)\in U_{ijl}\times B_{ijl}\) we obtain
starting from (8) in Lemma 2, using Lemma 1 and the definition of \(V_{il}\). Finally, we introduce a new index \(\nu \) varying in a new (finite) index set \(\mathcal {N}\) and a bijective mapping \(\nu \leftrightarrow (i,j,l)\). By writing \(U_{\nu }\) instead of \(U_{ijl}\) and \(B_{\nu }\) instead of \(B_{ijl}\) we arrive at (11) by noting that \(C_{\nu }=C_{j}\) and \(z_{\nu }=z_{l}\) if \(\nu \leftrightarrow (i,j,l)\). We also note that the sets \(U_{\nu }\) and the closures of \(B_{\nu }\) are convex polyhedral. \(\square \)
When defining the two-stage mixed-integer integrand \(f:\mathbb {R}^m\times \mathbb {R}^{d}\rightarrow \overline{\mathbb {R}}\) by
problem (1) may be rewritten as
We introduce the additional assumption
- (A3):
-
For each pair \((x,\xi )\in X\times \mathbb {R}^{d}\) it holds \((q(\xi ),h(\xi )-T(\xi )x)\in \mathcal {U}\times \mathcal {T}\).
Condition (A3) refers to the standard requirements relatively complete recourse and dual feasibility (see [49, Section 2.1]). The structural result for \(\Phi \) in Proposition 1 leads to the following representation of the integrand f.
Proposition 2
Assume (A1)–(A3) and let \(x\in X\). Then the integrand f is lower semicontinuous on \(X\times \mathbb {R}^{d}\) and \(f(x,\cdot )\) is finite and linear-quadratic on the sets
for each \(\nu \in \mathcal {N}\), where \(\mathcal {N}\), \(U_{\nu }\) and \(B_{\nu }\) are defined in Proposition 1.
The function \(f(x,\cdot )\) is of the form
on the sets \(\Xi _{\nu }(x)\), where the \((r,m_{1})\) matrix \(C_{\nu }\) and \(z_{\nu }\in \mathbb {Z}^{m_{2}}\) are explained in Proposition 1. The functions \(f(x,\cdot )\) may have points of discontinuity or nondifferentiability at the boundaries of \(\Xi _{\nu }(x)\). The union of all \(\Xi _{\nu }(x)\) equals \(\mathbb {R}^{d}\) and their closures are convex polyhedral. Moreover, the estimate
is valid for every pair \((x,\xi )\in X\times \mathbb {R}^{d}\) and some constant \(\hat{C}>0\).
Proof
The sets \(\Xi _{\nu }(x)\), \(\nu \in \mathcal {N}\), form a partition of \(\mathbb {R}^{d}\) into Borel sets whose closures, denoted by \(\mathrm{cl}\,\Xi _{\nu }(x)\), are of the form
and, thus, are convex polyhedral, since \(h(\cdot )\), \(T(\cdot )\) and \(q(\cdot )\) are affine functions, \(\mathrm{cl}\,B_{\nu }\), the closure of \(B_{\nu }\), is convex polyhedral and \(U_{\nu }\) is convex polyhedral, too. The lower semicontinuity of f follows from Lemma 2.
The representation (15) of \(f(x,\xi )\) for every pair \((x,\xi )\in X\times \Xi _{\nu }(x)\) and \(\nu \in \mathcal {N}\) follows immediately from (11). Since \(q_{1}(\cdot )\), \(q_{2}(\cdot )\), \(h(\cdot )\) and \(T(\cdot )\) are affine functions of \(\xi \), the second summand of (15) is an affine function of \(\xi \) while the third represents a quadratic function. The final statement follows from (9) and the estimate
after a few calculations for all pairs \((x,\xi )\in X\times \mathbb {R}^{d}\) and some constant \(\hat{C}>0\). \(\square \)
3 ANOVA decomposition and effective dimension
The analysis of variance (ANOVA) decomposition of a function was first proposed as a tool in statistical analysis (see [18] and the survey [53]). Later it was often used for the analysis of quadrature methods mainly on \([0,1]^{d}\). Here, we make use of it on \(\mathbb {R}^{d}\) equipped with a probability density function \(\rho \) given in product form
As in [15] we consider the weighted \(\mathcal {L}_{p}\) space over \(\mathbb {R}^{d}\), i.e., \(\mathcal {L}_{p,\rho }(\mathbb {R}^{d})\), with the norm
Let \(f\in \mathcal {L}_{1,\rho }(\mathbb {R}^{d})\). The ANOVA projection \(P_{k}\), \(k\in \mathfrak {D}=\{1,\ldots ,d\}\), is defined by
Clearly, the function \(P_{k}f\) is constant with respect to \(\xi _{k}\). For \(u\subseteq \mathfrak {D}\) we use |u| for its cardinality, \(-u\) for \(\mathfrak {D}{\setminus } u\) and define the higher order ANOVA projection by
where the product sign means composition. Due to Fubini’s theorem the ordering within the product is not important and \(P_{u}f\) is constant with respect to all \(\xi _{k}\), \(k\in u\). The ANOVA decomposition of \(f\in \mathcal {L}_{1,\rho }(\mathbb {R}^{d})\) is of the form [26, 56]
where each ANOVA term \(f_{u}\) depends only on \(\xi ^{u}\), i.e., on the variables \(\xi _{j}\) with indices \(j\in u\), and satisfies the property \(P_{j}f_{u}=0\) for all \(j\in u\). It admits the recurrence relation
It is known from [26] that the ANOVA terms are given explicitly in terms of the ANOVA projections by
where \(P_{-u}\) and \(P_{u-v}\) mean integration with respect to \(\xi _{j}\), \(j\in \mathfrak {D}{\setminus } u\) and \(j\in u{\setminus } v\), respectively. The first representation shows that lower order ANOVA terms \(f_{u}\) with small |u| are given by higher order projections. The second representation reveals that the ANOVA term \(f_{u}\) is essentially as smooth as the ANOVA Projection \(P_{-u}(f)\) due to the Inheritance theorem [15, Theorem 2].
If f belongs to \(\mathcal {L}_{2,\rho }(\mathbb {R}^{d})\), the projections \(P_{u}f\) and the ANOVA terms \(f_{u}\) also belong to \(\mathcal {L}_{2,\rho }(\mathbb {R}^{d})\), and the system \(\{f_{u}\}_{u\subseteq \mathfrak {D}}\) is orthogonal in \(\mathcal {L}_{2,\rho }(\mathbb {R}^{d})\) (see e.g. [56]).
Let the variance of f be given by
To avoid trivial cases we assume \(\sigma (f)>0\) in the following. The normalized ratios \(\sigma _{u}^{2}(f)/\sigma ^{2}(f)\), where \(\sigma _{u}(f)=\Vert f_{u}\Vert _{2,\rho }\), serve as indicators for the importance of the variable \(\xi ^{u}\) in f. They are used to define sensitivity indices of a set \(u\subseteq \mathfrak {D}\) for f in [52] and the dimension distribution of f in [31, 41].
For small \(\varepsilon \in (0,1)\) (\(\varepsilon =0.01\) is suggested in a number of papers), the effective superposition (truncation) dimension \(d_{S}(\varepsilon )\in \mathfrak {D}\) (\(d_{T}(\varepsilon )\in \mathfrak {D}\)) of f is defined by
We note that the effective superposition dimension \(d_{S}(\varepsilon )\) is important for the error analysis of Quasi-Monte Carlo methods, but its computation is complicated. The effective truncation dimension is computationally accessible (see [52, 56]). Note also that \(d_{S}(\varepsilon )\le d_{T}(\varepsilon )\) holds and the estimate
is valid (see [13, 56]). The estimate (25) means that the truncated ANOVA decomposition of f containing all ANOVA terms \(f_{u}\) until \(|u|\le d_{S}(\varepsilon )\) (or \(|u|\le d_{T}(\varepsilon )\)) represents an approximation of f. The importance of (25) is due to the fact that lower order ANOVA terms of f may have smoothness properties even if f is known to be nondifferentiable or discontinuous (see [14, 15]). In that case (25) may be used in error estimates by exploiting the eventual smoothness of the lower order ANOVA terms.
To formulate smoothness conditions we follow [15] and use the notation \(D_{i}f\), \(i\in \mathfrak {D}\), to denote the classical partial derivative \(\frac{\partial f}{\partial \xi _{i}}\). For a multi-index \(\alpha =(\alpha _{1},\ldots ,\alpha _{d})\) with \(\alpha _{i}\in \mathbb {N}_{0}\) we set
and call \(D^{\alpha }f\) the partial derivative of order \(|\alpha |=\sum _{i=1}^{d}\alpha _{i}\). A real-valued function g on \(\mathbb {R}^{d}\) is called weak derivative of order \(|\alpha |\) if it is measurable on \(\mathbb {R}^{d}\) and satisfies
where \(C_{0}^{\infty }(\mathbb {R}^{d})\) denotes the space of infinitely differentiable functions with compact support in \(\mathbb {R}^{d}\) and \(D^{\alpha }v\) the classical derivative of v. We will use the same symbol for the weak derivative as for the classical one, i.e., we set \(D^{\alpha }f=g\) if (26) is satisfied, since classical derivatives are also weak derivatives. The latter holds because classical derivatives satisfy (26) which is just the multivariate integration by parts formula in the classical sense. We consider in the next sections the mixed Sobolev space
of functions on \(\mathbb {R}^{d}\) having mixed weak first order derivatives that are quadratically integrable. In [54] such spaces are called Sobolev spaces with dominating mixed smoothness.
4 ANOVA decomposition of two-stage mixed-integer integrands
According to Proposition 2 two-stage mixed-integer integrands are discontinuous and piecewise linear-quadratic, hence, may be written in the form
for all \((x,\xi )\in X\times \Xi _{\nu }(x)\) and some symmetric (d, d)-matrices \(A_{\nu }(\cdot )\), d-dimensional vectors \(b_{\nu }(\cdot )\) and real numbers \(c_{\nu }(\cdot )\), which are all affine functions of x. The Borel sets \(\Xi _{\nu }(x)\), \(\nu \in \mathcal {N}\) are defined by (14) and have convex polyhedral closures.
In addition to the conditions (A1)–(A3) we need to impose:
- (A4):
-
The probability distribution \(\mathbb {P}\) has finite fourth order absolute moments. Due to (16) the two-stage stochastic mixed-integer program (1) is already well defined if \(\mathbb {P}\) has finite second order moments. However, the stronger condition (A4) together with the next one enable the use of the concepts from Sect. 3.
- (A5):
-
\(\mathbb {P}\) has a density \(\rho \) with respect to the Lebesgue measure on \(\mathbb {R}^{d}\) and \(\rho \) admits product form
$$\begin{aligned} \rho (\xi )=\prod _{i=1}^{d}\rho _{i}(\xi _{i})\quad (\xi =(\xi _{1},\ldots ,\xi _{d}) \in \mathbb {R}^{d}), \end{aligned}$$where the densities \(\rho _{i}\) are positive and continuously differentiable, and \(\rho _{i}\) and its derivative are bounded on \(\mathbb {R}\). To apply the results in this section to general probability distributions \(\mathbb {P}\), one has to decompose the dependence structure of \(\mathbb {P}\). The latter is always possible using the multivariate distributional transform, which was first established in [44] in case that the conditional distribution functions of \(\mathbb {P}\) are absolutely continuous. Later the distributional transform was extended to the general case (see [45]).
- (A6):
-
For each face F of dimension greater than zero of the convex polyhedral sets \(\mathrm{cl}\,\Xi _{\nu }(x)\), \(\nu \in \mathcal {N}\), the affine hull \(\mathrm{aff}(F)\) of F does not parallel any coordinate axis in \(\mathbb {R}^{d}\) for each \(x\in X\) (geometric condition). Recall that a face F of a polyhedron P in \(\mathbb {R}^{d}\) is defined by \(F=\{\xi \in P:\langle a,\xi \rangle =b\}\) for some \(a\in \mathbb {R}^{d}\) and \(b\in \mathbb {R}\) such that P is contained in the halfspace \(\{\xi \in \mathbb {R}^{d}:\langle a,\xi \rangle \le b\}\). The face F is said to be defined by the inequality \(\langle a,\xi \rangle \le b\). Clearly, each face is itself a polyhedron. The dimension \(\mathrm{dim}(P)\) of a polyhedron P is the dimension of its affine hull \(\mathrm{aff}(P)\). A facet F of a polyhedron P with \(P\ne F\) is a face of dimension \(\mathrm{dim}(P)-1\). Vertices of polyhedra are faces of dimension zero. For a short review of basic polyhedral theory we refer the reader to [20]. If F is any face of a polyhedron \(\mathrm{cl}\,\Xi _{\nu }(x)\) for some \(\nu \in \mathcal {N}\) defined by the inequality \(\langle g,\xi \rangle \le a\) for some \(g\in \mathbb {R}^{d}\) and \(a\in \mathbb {R}\), then (A6) means that all components of g do not vanish. Condition (A6) is stronger than the geometric condition imposed in [29] and important for deriving the results in this section. It will be illustrated in Example 1 and further discussed in Sect. 6. Since the polyhedra \(\mathrm{cl}\,\Xi _{\nu }(x)\) are not explicitly given, condition (A6) has implicit character.
In the following we consider the ANOVA decomposition of \(f=f_{x}\) (see (20)) for any fixed \(x\in X\) and show that lower order ANOVA terms of f are smoother than the function f itself. Since the ANOVA terms are given in terms of (ANOVA) projections \(P_{u}\) (see (21)), we study first properties of projections.
For \(u\subset \mathfrak {D}=\{1,\ldots ,d\}\) we define the mapping \(\Pi _{u}:\mathbb {R}^{d}\rightarrow \mathbb {R}^{d-|u|}\) by
If \(u=\{k\}\) for some \(k\in \mathfrak {D}\) we write \(\xi ^{-k}\) and \(\xi _{s}^{-k}\) with \(s\in \mathbb {R}\).
First we derive bounds for \(P_{u}f\) where f is given by (28).
Proposition 3
Let (A1)–(A5) be satisfied, \(x\in X\) be fixed, \(u\subset \mathfrak {D}\) and we consider an integrand \(f=f_{x}\) of the form (28). Then there exists a constant \(\hat{C}>0\) such that
holds for all \(\xi ^{-u}\in \Pi _{u}(\mathbb {R}^{d})\).
Proof
Using the representation \(u=\{i_{1},\ldots ,i_{|u|})\) and the definition (19) of \(P_{u}f\), we obtain from (16)
for some positive constant \(\hat{C}\) and all \(\xi ^{-u}\in \Pi _{u}(\mathbb {R}^{d})\). \(\square \)
Next we study continuity and differentiability properties of projections and we start with first order projections \(P_{k}f\) of \(f=f_{x}\) for some \(k\in \mathfrak {D}\). We know that
holds for fixed \(\xi ^{-k}\) and every \(s\in \mathbb {R}\). According to (18) we have
Due to (30) there exists a finite subset \(\hat{\mathcal {N}}=\hat{\mathcal {N}}(\xi ^{-k})\) of \(\mathcal {N}\) such that the one-dimensional affine subspace \(\{\xi _{s}^{-k}:s\in \mathbb {R}\}\) intersects the sets \(\Xi _{\nu }(x)\) for \(\nu \in \hat{\mathcal {N}}\), where \(\mathrm{cl}\,\Xi _{\nu }(x)\) and its adjacent sets have a common facet for every \(\nu \in \hat{\mathcal {N}}\). Hence, there exists a partition of \(\mathbb {R}\) into subintervals \(I_{\nu }=I_{\nu }(\xi ^{-k})\), \(\nu \in \hat{\mathcal {N}}\), such that \(\xi _{s}^{-k}\in \Xi _{\nu }(x)\) for all \(s\in I_{\nu }\) and \(\nu \in \hat{\mathcal {N}}\). We obtain the following representation of \(P_{k}f\) by setting \(f^{\nu }(x,\xi ^{-k}_{s}):=\langle A_{\nu }(x)\xi _{s}^{-k}, \xi _{s}^{-k}\rangle +\langle b_{\nu }(x),\xi _{s}^{-k}\rangle + c_{\nu }(x)\) and using the identity \(\xi ^{-k}_{s}=\xi ^{-k}_{0}+s\,e_{k}\) with \(e_{k}\) denoting the element of \(\mathbb {R}^{d}\) having components \(\delta _{ik}\), \(i=1,\ldots ,d\):
where we define \(s_{\nu }=s_{\nu }(\xi ^{-k})=\inf \,I_{\nu } (\xi ^{-k})\) and \(s_{\nu +1}=s_{\nu +1}(\xi ^{-k})=\sup \,I_{\nu } (\xi ^{-k})\). The functions \(p_{j,\nu }(\cdot ;x)\) are \((d-1)\)-variate polynomials in \(\xi ^{-k}\) of degree \(2-j\) with coefficients being affine functions of x. If \(s_{\nu }\) is finite, the point \(\xi _{s_{\nu }}^{-k}\) belongs to the common facet of \(\mathrm{cl}\,\Xi _{\nu }(x)\) and \(\mathrm{cl}\,\Xi _{\nu -1}(x)\). Let \(g_{\nu }=(g_{\nu ,1},\ldots ,g_{\nu ,d})\in \mathbb {R}^{d}\) and \(a_{\nu }\in \mathbb {R}\) be selected such that the facet is defined by the inequality
Hence, for finite \(s_{\nu }\) we obtain
Since \(g_{\nu ,k}\ne 0\) due to condition (A6), we arrive at the representation
Since the points \(s_{\nu }=s_{\nu }(\xi ^{-k})\) are affine functions of \(\xi ^{-k}\) and the integrands \(f^{\nu }(\cdot ,\xi ^{-k})\) are linear-quadratic in \(I_{\nu }(\xi ^{-k})\), classical results on integrals depending on parameters may be used to derive continuity and continuous differentiability of the projections \(P_{k}f\) at any \(\bar{\xi }^{-k}\in \Pi _{k}(\mathbb {R}^{d})\) as functions of \(\xi ^{-k}\) if the index set \(\hat{\mathcal {N}}(\xi ^{k})\) does not change in some neighborhood of \(\bar{\xi }^{-k}\). In order to study the continuity of \(P_{k}f\) also at points \(\bar{\xi }^{-k}\) where the index sets \(\hat{\mathcal {N}}(\xi ^{-k})\) do change in any neighborhood of \(\bar{\xi }^{-k}\), we introduce some additional notation. Let \(\mathbb {B}_{\epsilon }(\bar{\xi }^{-k})\) denote the open ball around \(\bar{\xi }^{-k}\) with radius \(\epsilon >0\) and let
denote sets of convex polyhedra \(\mathrm{cl}\,\Xi _{\nu }(x)\) that are met by the one-dimensional affine subspace \(\{\xi _{s}^{-k}:s\in \mathbb {R}\}\). Because any such subspace \(\{\xi _{s}^{-k}:s\in \mathbb {R}\}\) for some \(\xi ^{-k}\in \mathbb {B}_{\epsilon }(\bar{\xi }^{-k})\) is a parallel translation of \(\{\bar{\xi }_{s}^{-k}:s\in \mathbb {R}\}\), \(\epsilon _{0}\) can be chosen small enough such that \(\mathcal {P}(\xi ^{-k})\subseteq \mathcal {P}(\bar{\xi }^{-k})\) holds for every \(\xi ^{-k}\in \mathbb {B}_{\epsilon _{0}}(\bar{\xi }^{-k})\). Therefore we have
Since the polyhedra \(\mathrm{cl}\,\Xi _{\nu }(x)\) are convex, the sets \(\{\xi _{s}^{-k}\in \mathrm{cl}\,\Xi _{\nu }(x):s\in \mathbb {R}\}\) are convex, too, and, hence, represent either an interval or a single point if \(\mathrm{cl}\,\Xi _{\nu }(x)\) belongs to \(\mathcal {P}(\xi ^{-k})\). The latter is only possible if the one-dimensional affine space meets a vertex or an edge (i.e., faces of dimension zero or one) of \(\mathrm{cl}\,\Xi _{\nu }(x)\). The subset of \(\mathbb {R}^{d}\) that contains all vertices and edges of all such polyhedra \(\mathrm{cl}\,\Xi _{\nu }(x)\) has Lebesgue measure zero in \(\mathbb {R}^{d}\). If the set \(\{\xi _{s}^{-k}\in \mathrm{cl}\,\Xi _{\nu }(x): s\in \mathbb {R}\}\) is an interval \(I_{\nu }\), the set \(\{\xi _{s}^{-k}:s\in \mathrm{int}\, I_{\nu }\}\) belongs to the interior of \(\mathrm{cl}\,\Xi _{\nu }(x)\). Otherwise, the interval \(I_{\nu }\) belongs to a facet of \(\mathrm{cl}\,\Xi _{\nu }(x)\) which in turn is parallel to the canonical basis element \(e_{k}\) contradicting the geometric condition (A6).
Proposition 4
Let (A1)–(A6) be satisfied, \(x\in X\) be fixed, \(k\in \mathfrak {D}\) and we consider an integrand \(f=f_{x}\) of the form (28). Then its kth projection \(P_{k}f\) is continuous on \(\Pi _{k}(\mathbb {R}^{d})\) and first order continuously differentiable on \(\Pi _{k}(\mathbb {R}^{d}){\setminus } M\), where M is a closed set that is contained in the union of finitely many hyperplanes of dimension at most \(d-2\) and, thus, has Lebesgue measure zero in \(\mathbb {R}^{d-1}\). Moreover, the estimate
holds for almost every \(\xi ^{-k}\in \Pi _{k}(\mathbb {R}^{d})\), for all \(r\in \mathfrak {D}\), \(r\ne k\), and some constant \(\hat{C}>0\).
Proof
Let \(x\in X\), \(k\in \mathfrak {D}\) and \(\bar{\xi }^{-k}\in \Pi _{k}(\mathbb {R}^{d})\). First we prove continuity of \(P_{k}f\) at \(\bar{\xi }^{-k}\) and distinguish the following two cases:
-
(i)
There exists \(\epsilon _0>0\) such that \(\mathcal {P}(\xi ^{-k})=\mathcal {P}(\bar{\xi }^{-k})\) for all \(\xi ^{-k}\in \mathbb {B}_{\epsilon _0} (\bar{\xi }^{-k})\).
-
(ii)
For each \(\epsilon >0\) there exists \(\xi ^{-k}\in \mathbb {B}_{\epsilon }(\bar{\xi }^{-k})\) such that \(\mathcal {P}(\xi ^{-k}) \subsetneq \mathcal {P}(\bar{\xi }^{-k})\).
In case (i) we know that the function \(\xi ^{-k}\mapsto f(\xi _{s}^{-k})=f(\xi _{1},\ldots ,\xi _{k-1},s,\xi _{k+1}, \ldots ,\xi _{d})\) is continuous in \(\mathbb {B}_{\epsilon _0} (\bar{\xi }^{-k})\) for all \(s\in \mathbb {R}\) except at the points \(s_{\nu }\), \(\nu \in \hat{\mathcal {N}}(\bar{\xi }^{-k})\).
Due to Proposition 2 the estimate
holds for all \((s,\xi ^{-k})\in \mathbb {R}\times \mathbb {B}_{\epsilon _0} (\bar{\xi }^{-k})\) and some constant \(C>0\). The latter right-hand side represents an integrable majorant for \(f(\xi _{s}^{-k})\) and, hence, Lebesgue’s dominated convergence theorem implies that \(P_{k}f\) is continuous at \(\bar{\xi }^{-k}\).
In case (ii) we choose \(\epsilon _{0}>0\) small enough such that the identity (36) is valid. We consider the index set \(\hat{\mathcal {N}}(\bar{\xi }^{-k})\) of all intervals \(I_{\nu }(\bar{\xi }^{-k})\) with left end points \(s_{\nu }(\bar{\xi }^{-k})\) and allow explicitly that \(s_{\nu }(\bar{\xi }^{-k})=s_{\nu +1}(\bar{\xi }^{-k})\) holds for some \(\nu \in \hat{\mathcal {N}}(\bar{\xi }^{-k})\). Then the representation
is valid, where \(s_{\nu }(\bar{\xi }^{-k})\) is given by (33). Now, let \(\xi ^{-k}\in \mathbb {B}_{\epsilon _0} (\bar{\xi }^{-k})\). Then \(P_{k}f(\xi ^{-k})\) may be represented by a subset of the set \(\hat{\mathcal {N}}(\bar{\xi }^{-k})\). Of course, all intervals \(I_{\nu }(\bar{\xi }^{-k})\) with \(s_{\nu }(\bar{\xi }^{-k})< s_{\nu +1}(\bar{\xi }^{-k})\) appear also in the representation of \(P_{k}f(\xi ^{-k})\) if \(\epsilon _{0}\) is small enough. Here, we used that \(\mathcal {N}\) and, hence, \(\hat{\mathcal {N}}(\bar{\xi }^{-k})\) are finite. Those intervals with \(s_{\nu }(\bar{\xi }^{-k})=s_{\nu +1}(\bar{\xi }^{-k})\) may either disappear or appear with \(s_{\nu }(\xi ^{-k})< s_{\nu +1}(\xi ^{-k})\). If they disappear we set \(s_{\nu }(\xi ^{-k})=s_{\nu +1}(\xi ^{-k})\) and include them formally into the representation of \(P_{k}f(\xi ^{-k})\) which is of the form
Letting \(\xi ^{-k}\) in (39) tend to \(\bar{\xi }^{-k}\) and using the continuity of \(s_{\nu }(\cdot )\) and of \(p_{j,\nu }(\cdot ;x)\) for \(\nu \) belonging to the finite index set \(\hat{\mathcal {N}}(\bar{\xi }^{-k})\), a comparison with (38) proves the continuity of \(P_{k}f\) at \(\bar{\xi }^{-k}\) in case (ii), too.
Finally, we return to case (i) and study differentiability properties of \(P_{k}f\) at such points \(\xi ^{-k}\in \Pi _{k}(\mathbb {R}^{d})\). From (32) we obtain for \(r\in \mathfrak {D}\), \(r\ne k\), that
holds, where the corresponding term in (41) vanishes if \(s_{\nu }\) and \(s_{\nu +1}\), respectively, are not finite. Hence, \(P_{k}f\) is first order continuously differentiable at points \(\xi ^{-k}\) satisfying (i) and, thus, on \(\Pi _{k}(\mathbb {R}^{d})\) except at all boundary points of the polyhedra \(\Pi _{k}\Xi _{\nu }(x)\), \(\nu \in \mathcal {N}\). All boundaries are contained in a finite union of hyperplanes of dimension at most \(d-2\) which has Lebesgue measure 0 in \(\mathbb {R}^{d-1}\).
To prove the estimate (37) we fix \(n\in \hat{N}\). To bound the first summand in (40) we note that \(\frac{\partial }{\partial \xi _{r}}p_{j,\nu }(\xi ^{-k};x)\) is linear in \(\xi ^{-k}\) for \(j=0\) and constant for \(j=1\). The integral \(\int _{s_{\nu }(\xi ^{-k})}^{s_{\nu +1}(\xi ^{-k})}s^{j} \rho _{k}(s)ds\) is bounded by 1 for \(j=0\) and by a constant for \(j=1\). To bound the second summand in (40) and (41) we observe that the first factor \(p_{j,\nu }(\xi ^{-k};x)\) of each summand is bounded by a constant for \(j=2\), by a constant times \(\Vert \xi ^{-k}\Vert \) for \(j=1\), and by a constant times \(\Vert \xi ^{-k}\Vert ^{2}\) for \(j=0\). The second factor is bounded by a constant for \(j=0\), by a constant times \(\Vert \xi ^{-k}\Vert \) for \(j=1\), and by a constant times \(\Vert \xi ^{-k}\Vert ^{2}\) for \(j=2\). Furthermore, the coefficients of the polynoms \(p_{j,\nu }\) are affine functions of x, thus, can be bounded by a constant times \(\max \{1,\Vert x\Vert \}\). Altogether, both summands can be estimated from above by a constant times \(\max \{1,\Vert x\Vert \}\max \{1,\Vert \xi ^{-k}\Vert ^{2}\}\), where the constant depends on \(\nu \) and r. Finally, we note that \(\nu \) and r vary in finite sets and arrive at the desired estimate (37). \(\square \)
Remark 1
When looking at the formula for the first order partial derivative of \(P_{k}f\) in the proof of Proposition 4 given in (40), (41), it becomes evident that the first order differentiability result on \(\Pi _{k}(\mathbb {R}^{d}){\setminus } M\) can be extended to twice partial differentiability if the conditions (A1)–(A6) are satisfied. Moreover, we state without recording the elementary proof and analogous arguments as in the last part of the preceding proof that the estimate
holds for all \(\xi ^{-k}\in \Pi _{k}(\mathbb {R}^{d}){\setminus } M\), all \(q,r\in \mathfrak {D}{\setminus }\{k\}\) and some constant \(\bar{C}>0\).
The following example shows that the geometric condition (A6) is indispensable for Proposition 4 to hold true.
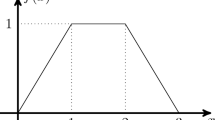
Example 1
Let \(d=2\) and P denote a two-dimensional probability distribution with independent continuous marginal densities \(\rho _{k}\), \(k=1,2\). We consider the two convex polyhedral cones (see the picture below)

and the infimal functions
which are piecewise constant lower semicontinuous functions. Both are simple (but typical) infimal value functions for pure integer optimization models.
Let the integrands \(f_{i}\) be defined by
where we let for simplicity \(x=0\).
Then its kth first order ANOVA projections \(P_{k}f_{i}\) are
where \(\xi ^{-k}\in \mathbb {R}\), \(k\in \{1,2\}\). We obtain for \(i=1\)
Hence, in general \(P_{1}f_{1}\) isn’t continuous, but \(P_{2}f_{1}\) is continuous on \(\mathbb {R}\). The reason is that a facet of \(\mathcal {K}_{1}\) is parallel to the \(t_{1}\)-axis. For \(i=2\) we have
and, thus, \(P_{1}f_{2}\) and \(P_{2}f_{2}\) are continuous and piecewise continuously differentiable. For a discussion of the geometric condition (A6) we refer the reader to Sect. 6.
Using Proposition 4 we show now that second order projections \(P_{u}f\), of f with \(u\subsetneq \mathfrak {D}\), \(|u|=2\), are even continuously differentiable on the entire space \(\Pi _{u}\mathbb {R}^{d}\).
For \(k,l\in \mathfrak {D}\), \(k\ne l\), we consider \(P_{k}f\) and its projection \(P_{l}P_{k}f\), i.e., the second order projection \(P_{u}f\) of f with \(u=\{k,l\}\). The function \(P_{k}f\) is given on the space \(\Pi _{k}\mathbb {R}^{d}\) which is subdivided into the sets \(\Pi _{k}(\Xi _{\nu })\), i.e., the kth projections of the original sets \(\Xi _{\nu }\), \(\nu \in \hat{\mathcal {N}}\), in \(\mathbb {R}^{d}\). The closures \(\Pi _{k}(\mathrm{cl}\,\Xi _{\nu })\) of the sets \(\Pi _{k}(\Xi _{\nu })\) are convex polyhedral and have dimension \(d-1\) [3, Proposition 2.1]. We obtain
where \(\xi ^{-u}=\Pi _{u}\xi \) and \(\xi _{s}^{-u}= \Pi _{k}\xi _{s}^{-l}\), \(s\in \mathbb {R}\), and know that
holds for each \(s\in \mathbb {R}\). Hence, similar as before Proposition 4 for \(\xi ^{-k}\), for given \(\xi ^{-u}\) there exist a finite index set \(\mathcal {N}_{1}=\mathcal {N}_{1}(\xi ^{-u})\) and intervals \(I_{1,\nu }\) with \(s_{1,\nu }=\inf I_{1,\nu }\) and \(s_{1,\nu +1}=\sup I_{1,\nu }\) for \(\nu \in \mathcal {N}_{1}\) such that
where the first and the last interval are unbounded and the finite points \(s_{1,\nu }\) belong to common facets \(G_{\nu }\) of two adjacent convex polyhedra of the form \(\Pi _{k}(\mathrm{cl}\,\Xi _{\nu })\). All such facets are kth projections of certain faces \(F_{\nu }\) of the polyhedra \(\mathrm{cl}\,\Xi _{\nu }\), i.e., \(\Pi _{k}(F_{\nu })=G_{\nu }\) (see [20, Theorem 16] or [59, Lemma 7.10]). If the faces \(F_{\nu }\) are defined by the inequalities \(\langle g_{1,\nu },\xi \rangle \le a_{1,\nu }\), the points \(s_{1,\nu }\) may be represented in the form
as in (33). Note that \(g_{1,\nu ,l}\ne 0\) holds due to condition (A6).
To state our next result, we need the following notion. A real function g on \(\mathbb {R}^{d}\) is called locally Lipschitz continuous on lines if for each \(k\in \mathfrak {D}\) the function \(t\mapsto g(\xi ^{-k}_{t})\) is Lipschitz continuous in t on compact subsets of \(\mathbb {R}\) for almost every \(\xi ^{-k}\in \Pi _{k}\mathbb {R}^{d}\).
Proposition 5
Let (A1)–(A6) be satisfied, \(x\in X\) be fixed and consider the integrand \(f=f_{x}\) in (28). For any \(k,l\in \mathfrak {D}\), \(k\ne l\), \(u=\{k,l\}\), the (ANOVA) projection \(P_{u}f\) is continuously differentiable on \(\Pi _{u}(\mathbb {R}^{d})\). In addition, the partial derivatives \(\frac{\partial P_{u}f}{\partial \xi _{r}}(\xi ^{-u})\) are locally Lipschitz continuous on lines and there exists \(C>0\) such that
holds for every \(\xi ^{-u}\in \Pi _{u}(\mathbb {R}^{d})\) and \(r\in -u\).
Proof
Let M be the closed set in Proposition 4. We consider \(k,l\in \mathfrak {D}\) with \(k\ne l\) and set \(u=\{k,l\}\). From Proposition 4 we know that \(P_{k}f\) is continuously differentiable at any \(\bar{\xi }^{-k} \in \Pi _{k}(\mathbb {R}^{d}){\setminus } M\). Hence, for any such \(\bar{\xi }^{-k}\) and \(\bar{\xi }^{-u}=\Pi _{l}\bar{\xi }^{-k}\) we know that \(P_{k}f\) is continuously differentiable at \(\bar{\xi }^{-u}_{s}\in \Pi _{k}(\mathbb {R}^{d})\) if \(\bar{\xi }^{-u}_{s}\not \in M\). Since \(\bar{\xi }^{-u}_{s}\in M\) happens only at the finitely many points \(s=s_{1,\nu }(\bar{\xi }^{-u})\) due to (A6) and the bound (37) is valid, we can use Lebesgue’s theorem on dominated convergence. We conclude that \(P_{u}f\) is continuously differentiable at \(\bar{\xi }^{-u}\) and the identity
holds for any \(r\in -u\). To prove that \(P_{u}f\) is continuously differentiable at any \(\bar{\xi }^{-u}\in \Pi _{u}(\mathbb {R}^{d})\) we proceed as in the proof of Proposition 4 and consider the set \(\mathcal {P}_{1}(\bar{\xi }^{-u})\) of all convex polyhedra \(\Pi _{k}(\Xi _{\nu })\) such that \(\bar{\xi }^{-u}_{s}\in \Pi _{k}(\Xi _{\nu })\) for some \(s\in \mathbb {R}\). The first case in the proof of Proposition 4 corresponds to the result (45). In the second case we know that for each \(\epsilon >0\) there exists \(\xi ^{-u}\in \mathbb {B}_{\epsilon }(\bar{\xi }^{-u})\) such that
and the representation
holds according to (43). We choose \(\epsilon >0\) small enough such that the relation \(s_{1,\nu }(\bar{\xi }^{-u})<s_{1,\nu +1}(\bar{\xi }^{-u})\) in the representation (47) leads to \(s_{1,\nu }(\xi ^{-u})< s_{1,\nu +1}(\xi ^{-u})\), too. Those \(\nu \in \mathcal {N}_{1}(\bar{\xi }^{-u})\) with \(s_{1,\nu }(\bar{\xi }^{-u})=s_{1,\nu +1}(\bar{\xi }^{-u})\) may either disappear or appear with \(s_{1,\nu }(\xi ^{-u})<s_{1,\nu +1}(\xi ^{-u})\). If they disappear we set \(s_{1,\nu }(\xi ^{-u})=s_{1,\nu +1}(\xi ^{-u})\) and include them formally into the representation of \(P_{u}f(\xi ^{-u})\) which is of the form
In a small ball around \(\xi ^{-u}\) this representation doesn’t change. Hence, \(P_{u}f\) is differentiable at \(\xi ^{u}\) and we obtain for any \(r\in -u\)
where the summands in (48) cancel successively, and the first and the last term in (48) vanish by definition. Letting \(\xi ^{-u}\) converge to \(\bar{\xi }^{-u}\) in the right-hand side of (49) proves the continuous differentiability of \(P_{u}f\) at \(\bar{\xi }^{u}\), where the partial derivative with respect to \(\xi _{r}\) is given by (45).
To show that the partial derivatives \(\frac{\partial P_{u}f}{\partial \xi _{r}}\) are locally Lipschitz continuous on lines, we consider first the partial derivative of the first order projection \(\frac{\partial P_{k}f}{\partial \xi _{r}}(\xi ^{-k})\) given by the Eqs. (40) and (41). Let \(p\in -u\). We fix all components of \(\xi ^{-k}\) except the pth component \(\xi _{p}\). The representation (40) and (41) of \(\frac{\partial P_{k}f}{\partial \xi _{r}}(\xi ^{-k})\) is valid for all \(\xi _{p}\in \mathbb {R}\) except at finitely many points \(\bar{\xi }_{p,\nu }\), \(\nu =1,\ldots ,N_{p}=N_{p}(\xi ^{-\{k,p\}})\). We assume that the points are ordered with respect to the natural order and observe that in each of the open intervals \(I_{p,0}=(-\infty ,\bar{\xi }_{p,1})\), \(I_{p,\nu }=(\bar{\xi }_{p,\nu },\bar{\xi }_{p,\nu +1})\) and \(I_{p,N_{p}}=(\bar{\xi }_{p,N_{p}},+\infty )\) the partial derivative \(\frac{\partial P_{k}f}{\partial \xi _{r}}(\xi ^{-k})\) is equal to a sum of products of functions that are locally Lipschitz continuous with respect to \(\xi _{p}\). Hence, \(\frac{\partial P_{k}f}{\partial \xi _{r}}(\xi ^{-k})\) is Lipschitz continuous on each bounded part of \(I_{p,0}\) and \(I_{p,N_{p}}\), and on each interval \(I_{p,\nu }\), \(\nu =1,\ldots ,N_{p}-1\), respectively. Now, let \(I_{B}\) denote a bounded interval and let \(\xi _{p},\tilde{\xi }_{p}\in I_{B}\), \(\xi _{p}<\tilde{\xi }_{p}\). We choose \(\varepsilon >0\) and \(\kappa \le \mu \) such that \(\bar{\xi }_{p,\kappa -1}<\xi _{p}+\varepsilon<\bar{\xi }_{p,\kappa }-\varepsilon<\bar{\xi }_{p,\mu }+\varepsilon<\tilde{\xi }_{p}-\varepsilon <\tilde{\xi }_{p}\le \bar{\xi }_{p,\mu +1}\) and denote by \(\xi ^{-u}_{\varepsilon }\) and \(\tilde{\xi }^{-u}_{-\varepsilon }\) the elements in \(\mathbb {R}^{d-2}\) in which the pth components are \(\xi _{p}+\varepsilon \) and \(\tilde{\xi }_{p}-\varepsilon \), respectively, and all other components be fixed. Similarly, we introduce the notations \(\xi ^{-u}_{s,\pm \varepsilon }\) and \(\bar{\xi }^{-u}_{s,\nu ,\pm \varepsilon }\). Then we obtain
Using the local Lipschitz continuity property of \(\frac{\partial P_{k}f}{\partial \xi _{r}}\) on the intervals \(I_{p,\nu }\) with (maximal) Lipschitz modulus \(L>0\), we may continue the estimate
Next we let \(\varepsilon \) tend to zero and make use of the continuity of \(\frac{\partial P_{u}f}{\partial \xi _{r}}\). This leads to
and, hence, to the desired Lipschitz continuity property on lines.
For \(r\in -u\) and \(\xi ^{-u}\in \Pi _{u}(\mathbb {R}^{d})\) we conclude finally from (49) and (37) that
and, thus, (44) holds for some sufficiently large constant \(C>0\). \(\square \)
The following is our main result in this section. It states that the first and second order ANOVA terms of f have mixed weak first order partial derivatives.
Theorem 1
Let (A1)–(A6) be satisfied, \(x\in X\) be fixed and we consider an integrand \(f=f_{x}\) of the form (28). Then all first and second order ANOVA terms \(f_{u}\), \(0\ne |u|\le 2\), \(u\subseteq \mathfrak {D}\), are first order continuously differentiable and have second order mixed weak first order derivatives that belong to \(\mathcal {L}_{2,\rho }(\mathbb {R}^{d})\). Hence, they belong to the mixed Sobolev space \(\mathcal {W}^{(1,\ldots ,1)}_{2,\rho ,\mathrm{mix}}(\mathbb {R}^{d})\).
Proof
Due to Proposition 5 all second order projections \(P_{u}f\) of f with \(|u|=2\) are continuously differentiable and their partial derivatives are locally Lipschitz continuous on lines on \(\Pi _{u}(\mathbb {R}^{d})\). These properties carry over to higher order projections \(P_{v}f\) with \(2<|v|<d\). While the continuous differentiability follows from the dominated convergence theorem using the bound (44), the local Lipschitz continuity on lines of the partial derivatives is a consequence of Proposition 5 and of the following estimate for subsets u, v of \(\mathfrak {D}\) with \(u\subset v\) and \(2=|u|<|v|\):
According to (21) the ANOVA terms of f are given by
for all nonempty subsets u of \(\mathfrak {D}\). Hence, all ANOVA terms \(f_{u}\) of f for \(|u|< d-1\) are continuously differentiable on \(\Pi _{u}(\mathbb {R}^{d})\). The non-vanishing first order partial derivatives of the first and second order ANOVA terms are of the form
for any \(l,k\in \mathfrak {D}\). Hence, the functions \(D_{l}f_{\{l,k\}}\) and \(D_{k}f_{\{l,k\}}\) are locally Lipschitz continuous with respect to each of the two variables \(\xi _{l}\) and \(\xi _{r}\) independently when the other variable is fixed almost everywhere. Hence, \(D_{l}f_{\{l,k\}}\) and \(D_{k}f_{\{l,k\}}\) are partially differentiable with respect to \(\xi _{k}\) and \(\xi _{l}\), respectively, in the sense of Sobolev (see, for example, [10, Section 4.2.3]). Furthermore, the mixed weak first derivatives coincide with the mixed first classical derivatives at some point if the latter exist at this point. We know from Remark 1 that second order classical mixed first derivatives of \(P_{k}f\) and, thus, of all projections \(P_{v}f\) with \(|v|\le d-1\) exist almost everywhere due to the dominated convergence theorem. Hence, the classical mixed first derivatives \(D_{lk}f_{\{l,k\}}= \frac{\partial ^{2}f_{\{l,k\}}}{\partial \xi _{k}\partial \xi _{l}}\) exist almost everywhere and coincide there with the mixed weak first derivatives. The bound (42) then implies that the estimate
is valid for almost every pair \((\xi _{l},\xi _{k})\in \Pi _{-\{l,k\}}\mathbb {R}^{d}\), any \(l,k\in \mathfrak {D}\), any \(x\in X\) and some constant \(C>0\). We conclude that \(D_{lk}f_{\{l,k\}}\) belongs to \(\mathcal {L}_{2,\rho }(\mathbb {R}^{d})\) for all \(l,k\in \mathfrak {D}\) due to (A4). \(\square \)
Remark 2
Let \(f^{(k)}\) denote the kth order ANOVA approximation
of the two-stage mixed-integer integrand f (see (28)) for some \(1\le k< d\). Theorem 1 furnishes conditions implying that \(f^{(2)}\) has all mixed weak first order partial derivatives and our next Remark discusses its extension to \(f^{(k)}\) for \(k>2\). According to (20) and to the orthogonality of the ANOVA terms \(f_{u}\) in \(\mathcal {L}_{2,\rho }\) one has
If the effective superposition dimension \(d_{S}(\varepsilon )\) of f (see (23)) is at most k, the mean square error of the integrands f and \(f^{(k)}\) satisfies
due to (25). For a discussion of techniques for determining and reducing the effective superposition dimension in case of (log)normal probability distributions we refer to [31, 41, 56,57,58].
Remark 3
If in addition to (A1)–(A6) the densities \(\rho _{i}\), \(i\in \mathfrak {D}\), have also continuous derivatives of order \(k\ge 1\) and all derivatives are bounded on \(\mathbb {R}\), the result in Remark 1 extends to mixed first derivatives of order \(k+1\) for \(P_{j}f\) on \(\Pi _{j}(\mathbb {R}^{d}){\setminus } M\), \(j\in \mathfrak {D}\). With the techniques used in Proposition 5 this allows to prove that \(P_{u}f\) has second order mixed first derivatives if \(|u|=3\) and, more general, that \(P_{u}f\) has kth order mixed first derivatives which are locally Lipschitz continuous on lines if \(|u|=k+1\). The corresponding bounds for the mixed derivatives can be proved, too. Finally, Theorem 1 extends to the existence of kth order mixed weak first derivatives for \(P_{u}f\) if \(|u|=k\), \(k\le \frac{d}{2}\). The representation (21) of ANOVA terms then implies that \(f_{u}\) with \(|u|=k\) belongs to \(\mathcal {W}^{(1,\ldots ,1)}_{2,\rho ,\mathrm{mix}}(\mathbb {R}^{d})\) for \(1\le k\le \frac{d}{2}-1\).
An important consequence is that Theorem 2 in Sect. 5 remains valid for two-stage mixed-integer integrands with effective superposition dimension \(2\ge d_{S}(\varepsilon )=k\le \frac{d}{2}-1\) for some \(\varepsilon >0\) by arguing with kth order ANOVA approximations.
Remark 4
For the special case of linear two-stage integrands f it is shown in [29] that \(P_{k}f\) is continuously differentiable on \(\mathbb {R}^{d}\) and has mixed weak first derivatives of order 2. Under the assumptions imposed in [29] we obtain in this case from Remark 3 that the projection \(P_{u}f\) with \(|u|=k\) has mixed weak first derivatives of order \(k+1\) for \(1\le k\le \frac{d}{2}\) and the ANOVA term \(f_{u}\) with \(|u|=k\) belongs to \(\mathcal {W}^{(1,\ldots ,1)}_{2,\rho ,\mathrm{mix}}(\mathbb {R}^{d})\) for \(1\le k\le \frac{d}{2}\).
5 Error analysis for randomly shifted lattice rules
In this section we provide an error analysis for randomly shifted lattice rules. Convergence results for this method are known for integrands from weighted tensor product Sobolev spaces on \([0,1]^{d}\) (see [8, 23]). Since typical integrands in stochastic programming are defined on \(\mathbb {R}^{d}\), we introduce first appropriate Sobolev spaces.
Following [26, 36] we start with the weighted Sobolev spaces \(W_{2,\gamma _{i},\rho _{i},\psi _{i}}^{1}(\mathbb {R})\) of functions \(h\in L_{2,\rho _i}(\mathbb {R})\) that are absolutely continuous with derivatives \(h'\in L_{2,\psi _{i}}(\mathbb {R})\) and positive continuous weight functions \(\psi _{i}\), \(i\in \mathfrak {D}=\{1,\ldots ,d\}\). They are endowed with the weighted inner product
where for each \(i\in \mathfrak {D}\) the weight \(\gamma _{i}\) is positive. We know that for any \(x,\tilde{x}\in \mathbb {R}\)
The latter condition implies that the weighted Sobolev space is complete [22] and, thus, a Hilbert space. Furthermore, it is known that there exists a reproducing kernel, i.e., a function \(K_{i}(x,\tilde{x})=1+\gamma _{i}\eta _{i}(x,\tilde{x})\) for \(x,\tilde{x}\in \mathbb {R}\), where
and \(\phi _{i}\) is the distribution function of the density \(\rho _{i}\) (see [36, Lemma 1]). This means that \(K_{i}:\mathbb {R}\times \mathbb {R}\rightarrow \mathbb {R}\) satisfies \(K_{i}(\cdot ,x)\in W_{2,\gamma _{i},\rho _{i},\psi _{i}}^{1}(\mathbb {R})\) and \(\langle h,K_{i}(\cdot ,x)\rangle _{\gamma _{i},\psi _{i}}=h(x)\) for all \(x\in \mathbb {R}\) and \(h\in W_{2,\gamma _{i},\rho _{i},\psi _{i}}^{1}(\mathbb {R})\). For more information on reproducing kernel Hilbert spaces we refer to the seminal paper [2] and to the monograph [6]. It is known from [2] that the weighted tensor product Sobolev space
is also a kernel reproducing Hilbert space with the reproducing kernel
The inner product of \(\mathbb {F}_{d}\) is given by
where the integrands \(I_{u,\rho }(f)(\xi ^{u})\) and the weights \(\gamma _{u}\) are defined by
In the QMC literature, this is called the unanchored setting with product weights.
In order to apply QMC methods to the computation of integrals
with \(f\in \mathbb {F}_{d}\) the Hilbert space \(\mathbb {F}_{d}\) has to be transformed to a Hilbert space \(\mathbb {G}_{d}\) of functions g on \([0,1]^{d}\) by the isometry
where \(\Phi ^{-1}(t)=(\phi _{1}^{-1}(t_{1}),\ldots , \phi _{d}^{-1}(t_{d}))\), \(t\in [0,1]^{d}\). The reproducing kernel and inner product of \(\mathbb {G}_{d}\) are
The choice of the weight functions \(\psi _{i}\) depends on the marginal densities \(\rho _{i}\), \(i\in \mathfrak {D}\). We refer to [25, 36] for a discussion of this aspect and for a list of marginal densities and the corresponding weight functions.
Now, we consider randomly shifted lattice rules for numerical integration in \(\mathbb {G}_{d}\) (see [23, 50]). Let \(Z_{n}=\{z\in \mathbb {N}:1\le z\le n,\,\mathrm{gcd}\,(z,n)=1\}\) denote the set of natural numbers between 1 and n that are relatively prime to n. Given a generating vector \(\mathbf{g}\in Z_{n}^{d}\) and a random shift vector \(\triangle \) which is uniformly distributed in \([0,1]^{d}\), the shifted lattice rule points are \(t^{j}=\{\frac{j \mathbf{g}}{n}+\triangle \}\), \(j=1,\ldots ,n\), where the braces indicate taking componentwise the fractional part. The corresponding randomized QMC method on \(\mathbb {G}_{d}\) is of the form
and its shift-averaged worst-case error can be computed using the reproducing kernel. Let \(\varphi (n)\) denote the cardinality of \(Z_{n}\), thus, \(\varphi (n)=n\) if n is prime, and \(\xi ^{j}=\Phi ^{-1}(t^{j})\) for \(j=1,\ldots ,n\). Then we obtain from [36, Theorem 8] that a generating vector \(\mathbf{g}\in Z_{n}^{d}\) can be constructed by a component-by-component algorithm such that for each \(\delta \in (0,\frac{1}{2}]\) there exists \(C(\delta )>0\) (not depending on d) with
if the following condition
on the weights is satisfied and f belongs to \(\mathbb {F}_{d}\). To state our next result we denote by v(P) the infimal value of (1) and by \(v(Q_{n,d})\) the infimum if the integral in (1) is replaced by the randomly shifted lattice rule (51) with sample size n.
Theorem 2
Let (A1)–(A6) be satisfied, the densities \(\rho _{i}\), \(i\in \mathfrak {D}\), be \(k\ge 2\) times differentiable and all derivatives be bounded on \(\mathbb {R}\) and X be compact. Assume that all integrands \(f=f_{x}\), \(x\in X\), of the form (28) have effective superposition dimension \(d_{S}(\varepsilon )=k\le \frac{d}{2}-1\) for some \(\varepsilon >0\) and that the kth order ANOVA approximation \(f^{(k)}\) of f (see (50)) belongs to \(\mathbb {F}_{d}\). Furthermore, we assume that \(Q_{n,d}\) is a randomly shifted lattice rule (51) satisfying (52). For each \(\delta \in (0,\frac{1}{2}]\) there exists \(\hat{C}(\delta )>0\) such that
where the sequence \((a_{n})\) converges to zero and allows the estimate
with \(\sigma (f)\) denoting the standard deviation of f (22).
The result means that the sequence of random infima \(v(Q_{n,d})\) converges in quadratic mean to the true infimum with the optimal convergence rate \(O(\varphi (n)^{-1+\delta })\) at least until the error becomes very small. Theorem 2 can be proved by following the lines of the proof of [30, Theorem 3] for \(k=2\) with obvious modifications by using [27, Proposition 4] and [42, Theorem 5]. We note that the differentiability properties of the kth order ANOVA approximation \(f^{(k)}\) of f discussed in Remark 3 motivate the imposed condition for \(f^{(k)}\).
6 Generic smoothness in the normal case
Let \(\xi \) be a d-dimensional normal random vector with mean \(\mu \) and nonsingular covariance matrix \(\Sigma \). Then there exists an orthogonal matrix Q such that \(Q\,\Sigma \,Q^{\top }\) is a diagonal matrix. Then the d-dimensional random vector \(\eta \) given by the transformation
is normal with zero mean and diagonal covariance matrix, i.e., \(\eta \) has independent components. For fixed \(x\in X\), let \(\Xi _{\nu }(x)\), \(\nu \in \mathcal {N}\), denote the decomposition (14) of \(\mathbb {R}^{d}\) into Borel sets whose closures are convex polyhedral. The transformed function \(\hat{f}(x,\eta )=f(x,Q\eta +\mu )\) is linear-quadratic on the sets \(Q^{\top }\Xi _{\nu }(x)-Q^{\top }\mu \), \(\nu \in \mathcal {N}\), whose closures are again convex polyhedral.
The intersections of two adjacent convex polyhedral sets \(\mathrm{cl}\,\Xi _{\nu }(x)\) are facets, which are contained in \((d-1)\)-dimensional affine subspaces \(H_{\nu }(x)\), \(\nu \in \mathcal {N}\). The space \(H_{\nu }(x)\) can be described by an equation \(v_{H_{\nu }(x)}^{\top }\xi =b_{H_{\nu }(x)}\) with a d-dimensional nonzero vector \(v_{H_{\nu }(x)}\) and a constant \(b_{H_{\nu }(x)}\in \mathbb {R}\). Since the number of facets of each polyhedral set \(\mathrm{cl}\,\Xi _{\nu }(x)\) is finite, there are finitely many equations
that describe all \((d-1)\)-dimensional affine subspaces each containing at least one facet of some polyhedron \(\mathrm{cl}\,\Xi _{\nu }(x)\). A \(d-k\) dimensional face of a given polyhedral set \(\mathrm{cl}\,\Xi _{\nu }(x)\) is then a subset of an affine subspace described by a system of k linear independent equations (intersection of k hyperplanes)
or shortly \(V_k\xi =b\), where \(V_{k}\) is a (k, d)-matrix and \(b\in \mathbb {R}^{k}\). Under the linear transformation (56), the corresponding face of the transformed polyhedron \(\mathrm{cl}\,(Q^{\top }\Xi _{\nu }(x)-Q^{\top }\mu )\) is a subset of an affine space described by the system
In order to make sure that the face of the transformed polyhedron does not parallel any coordinate axis, it is sufficient to show that the system \(V_kQ\eta =b'\) must be solvable for each subset of k variables \(\eta _{i_{1}},\ldots ,\eta _{i_{k}}\) in terms of the remaining components of \(\eta \). The latter condition is satisfied if each square submatrix of the (k, d)-matrix \(A=V_{k}Q\) is nonsingular or, equivalently, each minor of order r for \(1\le r\le k\) of the matrix A is nonzero. Now, let \(1\le r\le k\) and \(A_{r}\) be any (r, r)-submatrix of A. Then \(A_{r}\) is given as product of r rows of the matrix \(V_{k}=(v_{il})\) and r columns of the matrix \(Q=(q_{lj})\), i.e.,
According to the Cauchy–Binet formula the minor \(|A_r|=\mathrm{det}(A_{r})\) is of the form

In particular, the minor \(|A_r|=\mathrm{det}(A_{r})\) can be interpreted as a multivariate polynomial function where the variables are the entries of the r columns of Q, and the coefficients are given in terms of the entries of the r selected rows of \(V_k\). Hence, zeros of the multivariate polynomial correspond to an orthogonal matrix Q for which condition (A6) after the transformation is violated.
Next we argue that the multivariate polynomial \(|A_{r}|\) is non-constant. Assuming the contrary means that all r-minors that can be obtained from the selected r rows of the matrix \(V_k\) must be zero. This implies that those r rows are not linearly independent which contradicts the construction of \(V_{k}\). We also note that for any \(d-k\) dimensional face with \(1\le k< d\) which defines a system \(V_{k}\xi =b\), a multivariate polynomial \(|A_{r}|\) as considered above cannot contain all entries of a column of Q in its variables. It follows that the equations on the entries of Q defining the matrix Q as orthogonal cannot imply that \(|A_r|\) is a constant polynomial (as it is for the polynomial |Q| over \(O(d,\mathbb {R})\)). For the following part we refer to [7] for an introductory presentation of the Haar measure on topological groups. It is known that \(O(d,\mathbb {R})\) is a compact topological group and a smooth manifold of dimension
where the first term on the right-hand side corresponds to the number of elements of a matrix \(Q\in O(d,\mathbb {R})\) and the second term is the number of equations \(\langle Q_{i},Q_{j}\rangle =\delta _{i,j}\), \(i,j\in \mathfrak {D}\), \(i\le j\), describing the orthonormality of the columns of Q. One important fact of \(O(d,\mathbb {R})\) is that this group has two connected components, one for matrices having determinant equal to 1 including the identity matrix, and the other one for matrices having determinant equal to \(-1\). The set of real orthogonal matrices having determinant equal to 1 build a subgroup, called the special orthogonal group, and is denoted by \(SO(d,\mathbb {R})\).
If a matrix Q belongs to \(SO(d,\mathbb {R})\), then by multiplying Q by the \(d\times d\) matrix \(I_{-}=\mathrm{diag}(1,\ldots ,1,-1)\), we obtain \(\mathrm{det}(I_{-}Q)=-1\) and, hence, \(I_{-}Q\) belongs to the connected component of \(O(d,\mathbb {R})\) having determinant equal to \(-1\). The matrix \(I_{-}\) just creates a mirroring of the last coordinate without affecting the others. Therefore if \(Q \in O(d,\mathbb {R})\) and \(Q=I_{-}Q_{+}\), with \(Q_{+} \in SO(d,\mathbb {R})\), then Q transforms a polyhedron such that a face of the transformed polyhedron parallels a coordinate axis if and only if \(Q_{+}\) parallels the same axis. Therefore, the set of orthogonal matrices transforming a polyhedron such that a resulting face parallels some axis can be described as a set \(S_{Q_{+}} \subset SO(d,\mathbb {R})\) having this property, or a set \(S_{Q_{-}} \subset (O(d,\mathbb {R}) {\setminus } SO(d,\mathbb {R}))\) having this property, where \(S_{Q_{-}}\) can be described as \(S_{Q_{-}}= I_{-} S_{Q_{+}}\) (that is, every matrix in \(S_{Q_{-}}\) is given as a matrix in \(S_{Q_{+}}\) multiplied by \(I_{-}\)). By the invariance property of the Haar measure \(\lambda \) over \(O(d,\mathbb {R})\), we have that \(\lambda (S_{Q_{-}}) =\lambda (I_{-} S_{Q_{+}})=\lambda (S_{Q_{+}})\).
The restriction of the Haar measure over \(O(d,\mathbb {R})\) to its subgroup \(SO(d,\mathbb {R})\) coincides with the Haar measure on \(SO(d,\mathbb {R})\) up to a normalization constant. Considering now especially \(S_{Q_{+}}\), our aim is to show that the zero-set of the multivariate polynomial \(|A_{r}|\) is a set of Haar measure zero over the group \(SO(d,\mathbb {R})\). The special orthogonal group \(SO(d,\mathbb {R})\) allows a parametrization via hyperspherical coordinates. We follow the presentation in [11, Chapter 1] and obtain that each \(Q\in SO(d,\mathbb {R})\) allows a representation in the form
where the orthogonal matrices \(T_{ij}(\varphi _{ij})\) define a rotation in the coordinate plane \(\xi '_{i}=\cos {\varphi _{ij}}\xi _{i}+\sin {\varphi _{ij}}\xi _{j}\), \(\xi '_{j}=-\sin {\varphi _{ij}}\xi _{i}+\cos {\varphi _{ij}}\xi _{j}\), \(\xi '_{l}=\xi _{l}\), \(l\not \in \{i,j\}\), \(i<j\), \(i,j=1,\ldots ,d\). The representation of Q in this form is unique for almost all values of the angles \(\varphi _{ij}\). The angles vary in \(0\le \varphi _{id}<2\pi \), \(0\le \varphi _{ij}<\pi \), \(j=i+1,\ldots ,d-1\), \(i=1,\ldots ,d\). Moreover, the Haar measure on \(SO(d,\mathbb {R})\) is absolutely continuous with respect to the Lebesgue measure with the density [11, Theorem 1.2.1]
where \(c_{d}\) denotes some normalizing constant. By applying this parametrization to the multivariate polynomial \(|A_r|\), one obtains a non-constant analytic function. We recall that the zero-set of a non-constant multivariate analytic function has Lebesgue measure zero [35]. Therefore the restriction of the zero-set of the parametrized multivariate polynomial \(|A_r|\) to the parametrization domain box of the special orthogonal group has zero Lebesgue measure. Hence, the zero-set of the multivariate polynomial \(|A_r|\) has measure zero with respect to the Haar measure over \(SO(d,\mathbb {R})\). By taking finite unions of the corresponding sets of zero Haar measure over \(SO(d,\mathbb {R})\) with respect to all r-minors of A and all transformed polyhedra \(\mathrm{cl}\,(Q^{\top }\Xi _{\nu }(x)-Q^{\top }\mu )\) having a face parallel to some coordinate axis, the set of the corresponding special orthogonal matrices has Haar measure zero. Since the latter set transformed by \(I_{-}\) also has zero Haar measure, we arrive at the following statement as a consequence of Theorem 1.
Theorem 3
Let (A1)–(A5) be satisfied, \(x\in X\) be fixed, \(f=f(x,\cdot )\) be given by (28) and \(\xi \) be normally distributed with nonsingular covariance matrix \(\Sigma \). After the orthogonal transformation (56) of \(\xi \) the second order ANOVA approximation \(f^{(2)}\) of f (see Remark 2) belongs to \(\mathcal {W}_{2,\rho ,\mathrm{mix}}^{(1,\ldots ,1)}(\mathbb {R}^{d})\) for all orthogonal matrices in \(O(d,\mathbb {R})\) except for those belonging to a subset of \(O(d,\mathbb {R})\) having Haar measure zero.
According to Remarks 3 and 4 Theorem 3 remains valid for kth order ANOVA approximations (50) of the integrand f for \(k\le \frac{d}{2}-1\) in the two-stage mixed-integer case and for \(k\le \frac{d}{2}\) in the two-stage linear case.
7 Discussion of numerical experience and conclusions
In our numerical experiments reported in the companion paper [30] we compare two randomized QMC methods, namely, randomly shifted lattice rules [38, 50] and randomly scrambled Sobol’ point sets (based on [19, 51] and random linear scrambling [33]) with Monte Carlo methods [34] by applying them to a two-stage stochastic mixed-integer electricity portfolio optimization model. Its aim consists in minimizing the expected costs over a time horizon with T time intervals in the presence of stochastic load and prices. The latter are modelled as multivariate ARMA(1,1) process. The resulting multivariate probability distribution is normal with covariance matrix \(\Sigma \) of dimension \(d=2T\) which is factorized in the form \(\Sigma =B B^{\top }\). Two types of factorizations B are used, namely, (i) standard Cholesky (CH) and (ii) principal component analysis (PCA). Under PCA we obtained in our test runs with \(T=100\) that the effective truncation dimension \(d_{T}(\varepsilon )\) is equal to 2 for \(\varepsilon =0.01\) and the two-stage mixed-integer integrand f. We also observed that under PCA the first variable accumulates more than \(90\%\) of the total variance \(\sigma ^{2}(f)\). This means \(d_{S}(0.01)=2\) and indeed PCA is an excellent dimension reduction technique in this case. The average of the estimated rates of convergence \(O(n^{-\alpha })\) for the root mean square error of the optimal values under PCA in our computational tests were approximately \(\alpha =0.91\) for randomly shifted lattice rules, and \(\alpha =1.05\) for the randomly scrambled Sobol’ points. This is clearly superior to the MC convergence rate \(\alpha =0.5\). The same test runs were performed by using CH instead of PCA for factorizing \(\Sigma \). The average of the estimated rates of convergence were \(O(n^{-0.5})\) for all three methods under CH although the error constants of the randomized QMC methods seemed to be smaller. An explanation for the worse rates is that the approximate smoothing effect due to the eventual smoothness of lower order ANOVA terms does not occur since the effective truncation dimension under CH always remained \(d_{T}(0.01)=200\).
Compared to our earlier work in [29] we showed for linear two-stage integrands f in the present paper that even ANOVA terms \(f_{u}\) of order \(2\le |u|<\frac{d}{2}\) have mixed weak first partial derivatives (Remark 4) and that this property extends to two-stage mixed-integer integrands for \(2\le |u|\le \frac{d}{2}-1\) (Remark 3).
However, several questions still remain open. For example, a sufficient condition is desirable implying that lower order ANOVA terms belong to the tensor product Sobolev space \(\mathbb {F}_{d}\) (see Theorem 2 in Sect. 5). Furthermore, a discussion of the geometric condition (A6) in Sect. 6 beyond the case of normal probability distributions is important.
References
Ahmed, S., Tawarmalami, M., Sahinidis, N.V.: A finite branch-and-bound algorithm for two-stage stochastic integer programs. Math. Program. 100, 355–377 (2004)
Aronszajn, N.: Theory of reproducing kernels. Trans. Am. Math. Soc. 68, 307–404 (1950)
Balas, E., Oosten, M.: On the dimension of projected polyhedra. Discr. Appl. Math. 87, 1–9 (1998)
Bank, B., Guddat, J., Klatte, D., Kummer, B., Tammer, K.: Nonlinear Parametric Optimization. Akademie-Verlag, Berlin (1982)
Bayraksan, G., Morton, D.P.: A sequential sampling procedure for stochastic programming. Oper. Res. 59, 898–913 (2011)
Berlinet, A., Thomas-Agnan, C.: Reproducing Kernel Hilbert Spaces in Probability and Statistics. Springer, New York (2004)
Cohn, D.L.: Measure Theory, 2nd edn. Springer, New York (2013)
Dick, J., Kuo, F.Y., Sloan, I.H.: High-dimensional integration—The Quasi-Monte Carlo way. Acta Numer. 22, 133–288 (2013)
Dick, J., Pillichshammer, F.: Digital Nets and Sequences. Cambridge University Press, Cambridge (2010)
Evans, L.C., Gariepy, R.F.: Measure Theory and Fine Properties of Functions. CRC Press, Boca Raton (1992)
Girko, V.L.: Theory of Random Determinants. Kluwer, Dordrecht (1990)
Glasserman, P.: Monte-Carlo Methods in Financial Engineering. Springer, New York (2003)
Griebel, M., Holtz, M.: Dimension-wise integration of high-dimensional functions with applications to finance. J. Complex. 26, 455–489 (2010)
Griebel, M., Kuo, F.Y., Sloan, I.H.: The smoothing effect of the ANOVA decomposition. J. Complex. 26, 523–551 (2010)
Griebel, M., Kuo, F.Y., Sloan, I.H.: The smoothing effect of integration in \(\mathbb{R}^{d}\) and the ANOVA decomposition. Math. Comput. 82, 383–400 (2013)
Griewank, A., Kuo, F.Y., Leövey, H., Sloan, I.H.: High dimensional integration of kinks and jumps—smoothing by preintegration. J. Comput. Appl. Math. 344, 259–274 (2018)
He, Z., Wang, X.: On the convergence rate of randomized Quasi-Monte Carlo for discontinuous functions. SIAM J. Numer. Anal. 53, 2488–2503 (2015)
Hoeffding, W.: A class of statistics with asymptotically normal distribution. Ann. Math. Stat. 19, 293–325 (1948)
Joe, S., Kuo, F.Y.: Remark on Algorithm 659: implementing Sobol’s quasirandom sequence generator. ACM Trans. Math. Softw. 29, 49–57 (2003)
Kaibel, V.: Basic polyhedral theory. In: Cochran, J. (ed.) Encyclopedia of Operations Research and Management Science. Wiley, Hoboken (2010)
Kleywegt, A.J., Shapiro, A., Homem-de-Mello, T.: The sample average approximation method for stochastic discrete optimization. SIAM J. Optim. 12, 479–502 (2001)
Kufner, A., Opic, B.: How to define reasonably weighted Sobolev spaces. Comment. Math. Univ. Carol. 25, 537–554 (1984)
Kuo, F.Y.: Component-by-component constructions achieve the optimal rate of convergence in weighted Korobov and Sobolev spaces. J. Complex. 19, 301–320 (2003)
Kuo, F.Y., Nuyens, D.: Hot new directions for Quasi-Monte Carlo research in step with applications. In: Owen, B., Glynn, P.W. (eds.) Monte Carlo and Quasi-Monte Carlo Methods 2016, pp. 123–144. Springer, Cham (2018)
Kuo, F.Y., Sloan, I.H., Wasilkowski, G.W., Waterhouse, B.J.: Randomly shifted lattice rules with the optimal rate of convergence for unbounded integrands. J. Complex. 26, 135–160 (2010)
Kuo, F.Y., Sloan, I.H., Wasilkowski, G.W., Woźniakowski, H.: On decomposition of multivariate functions. Math. Comput. 79, 953–966 (2010)
L’Ecuyer, P., Lemieux, Ch.: Variance reduction via lattice rules. Manag. Sci. 46, 1214–1235 (2000)
L’Ecuyer, P., Lemieux, Ch.: Recent advances in randomized quasi-Monte Carlo methods. In: Dror, M., L’Ecuyer, P., Szidarovski, F. (eds.) Modeling Uncertainty, pp. 419–474. Kluwer, Boston (2002)
Leövey, H., Römisch, W.: Quasi-Monte Carlo methods for linear two-stage stochastic programming problems. Math. Program. 151, 315–345 (2015)
Leövey, H., Römisch, W.: Randomized QMC methods for mixed-integer two-stage stochastic programs with application to electricity optimization. In: Tuffin, B., L’Ecuyer, P. (eds.) Monte Carlo and Quasi-Monte Carlo Methods 2018, pp. 345–362. Springer, Cham (2020)
Liu, R., Owen, A.B.: Estimating mean dimensionality of analysis of variance decompositions. J. Am. Stat. Assoc. 101, 712–721 (2006)
Louveaux, F., Schultz, R.: Stochastic integer programming. In: Ruszczyński, A., Shapiro, A. (eds.) Stochastic Programming, Handbooks in Operations Research and Management Science, vol. 10, pp. 213–266. Elsevier, Amsterdam (2003)
Matoušek, J.: On the \(L_{2}\)-discrepancy for anchored boxes. J. Complex. 14, 527–556 (1998)
Matsumoto, M., Nishimura, T.: Mersenne Twister: a 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Trans. Model. Comput. Simul. 8, 3–30 (1998)
Mityagin, B.S.: The zero set of a real analytic function. Math. Notes 107(3), 473–475 (2020)
Nichols, J.A., Kuo, F.Y.: Fast CBC construction of randomly shifted lattice rules achieving \(O(n^{-1+\delta })\) convergence for unbounded integrands over \({\mathbb{R}}^{s}\) in weighted spaces with POD weights. J. Complex. 30, 444–468 (2014)
Nožička, F., Guddat, J., Hollatz, H., Bank, B.: Theory of Linear Parametric Programming. Akademie-Verlag, Berlin (1974). (in German)
Nuyens, D., Cools, R.: Fast algorithms for component-by-component constructions of rank-1 lattice rules in shift-invariant reproducing kernel Hilbert spaces. Math. Comput. 75, 903–922 (2006)
Owen, A.B.: Randomly permuted \((t,m,s)\)-nets and \((t,s)\)-sequences. In: Niederreiter, H., Shiue, P.J.-S. (eds.) Monte Carlo and Quasi-Monte Carlo Methods in Scientific Computing, Lecture Notes in Statistics, vol. 106, pp. 299–317. Springer, New York (1995)
Owen, A.B.: Scrambled net variance for integrals of smooth functions. Ann. Stat. 25, 1541–1562 (1997)
Owen, A.B.: The dimension distribution and quadrature test functions. Stat. Sin. 13, 1–17 (2003)
Römisch, W.: Stability of stochastic programming problems. In: Ruszczyński, A., Shapiro, A. (eds.) Stochastic Programming, Handbooks in Operations Research and Management Science, vol. 10, pp. 483–554. Elsevier, Amsterdam (2003)
Römisch, W., Vigerske, S.: Quantitative stability of fully random mixed-integer two-stage stochastic programs. Optim. Lett. 2, 377–388 (2008)
Rosenblatt, M.: Remarks on a multivariate transformation. Ann. Math. Stat. 23, 470–472 (1952)
Rüschendorf, L.: On the distributional transform, Sklar’s theorem, and the empirical copula process. J. Stat. Plan. Inference 139, 3921–3927 (2009)
Schultz, R.: Stochastic programming with integer variables. Math. Program. 97, 285–309 (2003)
Sen, S.: Algorithms for stochastic mixed-integer programming models. In: Aardal, K., Nemhauser, G.L., Weismantel, R. (eds.) Discrete Optimization, Handbooks in Operations Research and Management Science, vol. 12, pp. 515–558. Elsevier, Amsterdam (2005)
Sen, S., Sherali, H.D.: Decomposition with branch-and-cut approaches for two-stage stochastic mixed-integer programming. Math. Program. 106, 203–223 (2006)
Shapiro, A., Dentcheva, D., Ruszczyński, A.: Lectures on Stochastic Programming. MPS-SIAM Series on Optimization, 2nd edn. SIAM, Philadelphia (2014)
Sloan, I.H., Kuo, F.Y., Joe, S.: Constructing randomly shifted lattice rules in weighted Sobolev spaces. SIAM J. Numer. Anal. 40, 1650–1665 (2002)
Sobol’, I.M.: The distribution of points in a cube and the approximate evaluation of integrals. U.S.S.R. Comput. Math. Math. Phys. 7, 86–112 (1967)
Sobol’, I.M.: Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 55, 271–280 (2001)
Takemura, A.: Tensor analysis of ANOVA decomposition. J. Am. Stat. Assoc. 78, 894–900 (1983)
Triebel, H.: Bases in Function Spaces, Sampling, Discrepancy, Numerical Integration. European Mathematical Society, Zürich (2010)
Walkup, D., Wets, R.J.-B.: Lifting projections of convex polyhedra. Pac. J. Math. 28, 465–475 (1969)
Wang, X., Fang, K.-T.: The effective dimension and Quasi-Monte Carlo integration. J. Complex. 19, 101–124 (2003)
Wang, X., Sloan, I.H.: Quasi-Monte Carlo methods in financial engineering: an equivalence principle and dimension reduction. Oper. Res. 59, 80–95 (2011)
Wang, X., Tan, K.S.: Pricing and hedging with discontinuous functions: Quasi-Monte Carlo methods and dimension reduction. Manag. Sci. 59, 376–389 (2013)
Ziegler, G.M.: Lectures on Polytopes. Springer, New York (1995)
Acknowledgements
Open Access funding provided by Projekt DEAL. The second author wishes to thank Volker Kaibel (Otto-von-Guericke Universität Magdeburg) for helpful conversations on polyhedral theory.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Leövey, H., Römisch, W. Quasi-Monte Carlo methods for two-stage stochastic mixed-integer programs. Math. Program. 190, 361–392 (2021). https://doi.org/10.1007/s10107-020-01538-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-020-01538-6