Abstract
The Steiner forest problem asks for a minimum weight forest that spans a given number of terminal sets. We propose new cut- and flow-based integer linear programming formulations for the problem which yield stronger linear programming bounds than the two previous strongest formulations: The directed cut formulation (Balakrishnan et al. in Oper Res 37(5):716–740, 1989; Chopra and Rao in Math Prog 64(1):209–229, 1994) and the advanced flow formulation by Magnanti and Raghavan (Networks 45:61–79, 2005). We further introduce strengthening constraints and provide an example where the integrality gap of our models is 1.5. In an experimental evaluation, we show that the linear programming bounds of the new formulations are indeed strong on practical instances and that the related branch-and-cut algorithm outperforms algorithms based on the previous formulations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Steiner forest problem (SFP) is one of the fundamental network design problems. Given an edge-weighted undirected graph \(G=(V,E)\) and K terminal sets \(T^1,\ldots ,T^K \subseteq V\), it asks for a minimum weight forest in G such that the nodes inside each terminal set are connected. Its decision version is \(\mathsf {NP}\)-complete and it is inapproximable within 96/95 unless \(\mathsf {NP}= \mathsf {P}\) [7]. In the literature, the SFP was mostly studied in the context of approximation algorithms [1, 3, 16, 18,19,20]. Surprisingly, only few publications deal with integer linear programming (ILP) formulations, even though the known formulations either yield weak linear programming bounds or are too large to be practically viable.
For the primal-dual 2-approximation algorithms by Agrawal et al. [1] and Goemans and Williamson [16] the classical undirected cut-based formulation is considered. However, this formulation has an integrality gap of 2 even on simple instances. The same is true for the lifted cut relaxation introduced by Könemann et al. [23].
Moreover, the directed cut formulation for the Steiner tree problem [2, 8, 9, 22] can be easily extended to the Steiner forest case. This model cuts off fractional solutions by imposing a direction on each edge, looking for a rooted directed tree that connects all terminals. In the Steiner tree case, where only one terminal set exists, this process is straight-forward and the formulation has an integrality gap between \(36/31 \approx 1.161\) and 2, as was shown in [4]; It is widely believed that the true gap of the formulation lies close to 1.161. When multiple sets are present, however, one directed tree per set is needed and these, in general, can impose conflicting orientations to the edges. This is a major additional difficulty in solving the Steiner forest problem. Consequently, there are Steiner forest instances where the directed cut formulation has an integrality gap of 2. Magnanti and Raghavan [25] show how to consolidate the conflicts with an improved flow formulation. This formulation yields strong bounds in computational experiments on small instances, but is too large to be solved on a larger scale.
Lastly, the issues with conflicting orientations can be avoided altogether by using strong undirected formulations. Goemans [14], Lucena [24], as well as Margot et al. [26] independently propose an ILP formulation for the Steiner tree problem that builds on Edmond’s complete description of the tree polytope [12]. This tree-based formulation has a straight-forward extension to the Steiner forest problem and its LP-relaxation can be solved efficiently. However, its linear programming bounds are identical to the ones from the directed cut formulation.
A more extensive literature can be found for the Steiner tree problem as a special case of the SFP with \(K=1\): Several surveys compare ILP formulations and their polyhedral properties [9, 10, 15, 27, 28]. They are the basis for successful branch-and-cut (B&C) algorithms [8, 22].
Our contribution We propose two new formulations for the Steiner forest problem that combine the strong bounds of the improved flow formulation with the practical usefulness of the simpler cut models. Their corresponding LP relaxations are stronger than the improved flow relaxation by [25] and the directed cut relaxation, and therefore, as the undirected cut relaxation as well. In contrast to the improved flow formulation it can be solved in polynomial time. This answers an open problem in [25] which asks for a cut-based ILP formulation that is at least as strong as the improved flow formulation.
We introduce additional valid constraints that further strengthen our new models. Moreover, we are able to construct an instance with an integrality gap of 1.5; this is in particular interesting since the integrality gap of the directed model for the Steiner tree problem is a long-standing open problem and its best known lower bound is 1.161 [4].
Finally, we present the results of an experimental study in which all discussed models are compared against each other—both the LP relaxations as well as the related B&C or branch-and-bound (B&B) algorithms. We show that the LP bounds of our models are stronger than what can be achieved from any of the previous relaxations and that they can also be computed quickly and reliably; Fig. 1 shows a comparison of the formulations on widely-used small example instances. The resulting B&C algorithm of our models outperform B&B algorithms based on the previous formulations.
Overview In the remainder of this section we introduce the notations used in this article and give the formal definition of the Steiner forest problem. Section 2 recalls important ILP formulations from the literature along with main results concerning the strength. The main part is Sect. 3. Here, our new cut-based models along with their flow-based analogons are described. We prove the strength of the new models with respect to the improved flow formulation [25] and the directed formulation. Moreover, additional strengthening constraints are introduced and an example with integrality gap 1.5 is shown. Section 4 contains the computational study.
Notation Throughout, let \(G=(V,E)\) be an undirected, simple graph and let \(A=\{(i,j), (j,i) \mid \{i,j\} \in E\}\) be the arcs of the bidirection of G. A cut-set in G is a subset \(S \subseteq V\). Any cut-set \(S\subseteq V\) induces a cut \(\delta (S) := \{\{i,j\}\in E \mid {|}[1]{|} = 1\}\). We abbreviate \(\delta (i) := \delta (\{i\})\) if \(S=\{i\}\). If \(D=(V,A)\) is a directed graph, we distinguish the outgoing cut \(\delta ^+(S) = \{(i,j) \in A \mid i \in S\ \text {and}\ j \not \in S\}\) and the incoming cut \(\delta ^-(S) = \{(i,j) \in A \mid i \not \in S\ \text {and}\ j \in S\}\). Given a vector \(x \in X^d\), \(d \in \mathbb {Z}_{\ge 0}\), and an index set \(I \subseteq \{1,\ldots ,d\}\) we write x(I) to abbreviate \(\sum _{i \in I} x_i\). Moreover, for \(k \in \mathbb {Z}_{\ge 1}\) let \([k] := \{1,\ldots ,k\}\). Finally, if \(P := \{(x,y) \in \mathbb {R}^{n_1+n_2} \mid Ax + By = d\}\) is a polyhedron let \({{\,\mathrm{Proj}\,}}_x(P) := \{x \in \mathbb {R}^{n_1} \mid \exists \ y \in \mathbb {R}^{n_2} : (x,y) \in P\}\) be the projection of P onto the x variables.
The Steiner forest problem Consider the undirected graph \(G=(V,E)\) and let \(T^1,\ldots ,T^K \subseteq V\) be \(K \in \mathbb {N}\) terminal sets. A feasible Steiner forest of \((G, T^1,\ldots ,T^K)\) is a forest \((V_F \subseteq V, E_F \subseteq E)\) in G that, for all \(k \in [K]\), contains an s-t-path for all \(s,t \in T^k\). A feasible forest \((V_F, E_F)\) is optimum with respect to edge weights \(c \in \mathbb {R}_{\ge 0}^{|E|}\) if it minimizes the total cost \(\sum _{e \in E_F} c_e\). Assume without loss of generality that the terminal sets are pairwise disjoint: If \(T^k\) and \(T^\ell \) share at least one node, then any forest is feasible for \(T^1,\ldots ,T^K\) if and only if it is feasible for the instance where \(T^k\) and \(T^\ell \) are replaced by \(T^k\cup T^\ell \). We denote the set of all terminal nodes by \(\mathfrak {T}:= T^1 \cup \cdots \cup T^K\) and write \(\tau (t) := k\) if \(t \in T^k\). Furthermore, we say that the non-terminal nodes \(\mathfrak {N}:= V{\setminus } \mathfrak {T}\) are Steiner nodes. For each terminal set \(T^k\), \(k \in [K]\), we select an arbitrary node \(r^k\in T^k\) as a fixed root node and define \(T_r^k := T^k {\setminus }\{r^k\}\) and \(\mathfrak {R}:= \{r^1,\ldots ,r^K\}\). To make it easier to state the formulations, we define \(\mathfrak {T}^{i\ldots j}\) as \(T^i \cup \cdots \cup T^j\) and let \(\mathfrak {T}_r^{i\ldots j} := \mathfrak {T}^{i\ldots j}{\setminus }\{r^i\}\) be the same set without the ith root node (all other root nodes are still included).
A cut-set \(S \subseteq V\) is relevant for the terminal set \(T^k\) if it separates \(r^k\) from some terminal \(t \in T_r^k\), i.e., if \(r^k \in S\) but \(t \not \in S\). We write \(\mathfrak {S}^k\) for the set of all cut-sets that are relevant for \(T^k\) and \(\mathfrak {S}:= \mathfrak {S}^1 \cup \cdots \cup \mathfrak {S}^K\) for the set of all relevant cut-sets.
2 Eliminating cycles from the linear programming relaxation
Let us briefly review the existing ILP formulations for the Steiner forest problem. A forest F in \(G=(V,E)\) is feasible if and only if any relevant cut-set \(S \subset V\) contains at least one edge of F, i.e., if \(|\delta _F(S)| \ge 1\) for all \(S \in \mathfrak {S}\). Thus, since \(c \ge 0\), the undirected cut formulation

where
is a valid ILP formulation. While it can be solved efficiently, it yields weak bounds even on trivial instances (see Fig. 1). The reason for the weak bounds becomes apparent when we see formulation (\(\mathrm {IP}^{\mathrm {uc}}\)) as a set cover problem: We look for a choice of edges such that each cut \(\delta (S)\) in G is covered by at least one edge. Consider any cycle C of length s in G. Any set cover needs \(s-1\) edges to cover C. On the other hand, we obtain a fractional solution of value \(\frac{s}{2}\) by setting \(x_e = 0.5\) for all edges \(e \in C\). Figure 2 shows an example.
As for the Steiner tree problem there exists a model based on flows which is equivalent to the undirected cut-based model.

where
Thereby, x models the solution edges and f constitutes a flow of value one from the root nodes to each terminal in the same set, cf. (2b).
Observation 1
\(\mathrm {LP}^{\mathrm {uc}} = {{\,\mathrm{Proj}\,}}_x(\mathrm {LP}^{\mathrm {uf}})\).
The undirected formulations can be improved with a standard construction [2, 9]. Recall that we choose \(r^k \in T^k\) as an arbitrary root node of set \(T^k\) and consider the bi-directed graph underlying G. For all \(k \in [K]\), we now look for an arborescence (a directed tree) rooted at \(r^k\). If any cut-set S is relevant for \(T^k\), then at least one arc must leave S:

where
Since any solution (x, y) of (\(\mathrm {IP}^{\mathrm {dc}}\)) can be turned into a feasible Steiner forest \(F:=\{ \{i,j\} \in E \mid \exists \ k:y^k_{ij} + y^k_{ji} \ge 1\}\) and any feasible Steiner forest can be turned into a solution to (\(\mathrm {IP}^{\mathrm {dc}}\)), this strengthened formulation indeed captures the Steiner forest problem. Again, there exists an equivalent flow-based model:

where
Hence, we have the following well-known observation (see e.g., [15]).
Observation 2
\({{\,\mathrm{Proj}\,}}_x(\mathrm {LP}^{\mathrm {dc}}) = {{\,\mathrm{Proj}\,}}_x(\mathrm {LP}^{\mathrm {df}})\) and \(\mathrm {LP}^{\mathrm {uc}} \supsetneq {{\,\mathrm{Proj}\,}}_x(\mathrm {LP}^{\mathrm {dc}})\).
The directed formulations eliminate directed cycles from the basic optima of its LP relaxation and indeed the bound of the relaxation coincides with the integer optimum on instance A from Fig. 1. However, a slightly modified instance makes the problem reappear, see instance B in Figs. 1, or 2: While the support of any \(y^k\) is free of directed cycles, the union of the supports is not. This is the reason why the formulation works exceptionally well for the Steiner tree problem where \(K=1\). If \(K>1\), however, the LP relaxation of (\(\mathrm {IP}^{\mathrm {dc}}\)) is again weak. Still, for practical purposes no better formulation was known prior to this work.
a Example A from Fig. 1 where \(\mathrm {LP}^{\mathrm {dc}}\) yields a stronger LP bound than \(\mathrm {LP}^{\mathrm {uc}}\). The instance has unit costs and a single terminal set that contains all four nodes of the graph. Node a has been chosen as the root. a Shows a feasible fractional solution for \(\mathrm {LP}^{\mathrm {uc}}\) with cost 2. It is impossible to orient this solution such that it is feasible for \(\mathrm {LP}^{\mathrm {dc}}\) which implies an optimum integer solution of cost 3. b Slightly modified instance (B from Fig. 1) with two terminal sets ( 1,
1,  2, root nodes a and b). The
2, root nodes a and b). The  and
and  arcs form a solution for relaxation \(\mathrm {LP}^{\mathrm {dc}}\) for the
arcs form a solution for relaxation \(\mathrm {LP}^{\mathrm {dc}}\) for the  (
( ) and
) and  (
( ) terminal set. The
) terminal set. The  edges show the values of the x variables. Looking for a Steiner arborescence for each terminal set does not cut off a fractional optimum of cost 2. c A solution that roots both terminal sets at the root node a of the
edges show the values of the x variables. Looking for a Steiner arborescence for each terminal set does not cut off a fractional optimum of cost 2. c A solution that roots both terminal sets at the root node a of the  (
( ) terminal set. The fractional optimum is cut off
) terminal set. The fractional optimum is cut off
These directed cycles potentially appear whenever two terminal sets \(T^k\) and \(T^{\ell }\)—and thus their roots \(r^k\) and \(r^{\ell }\)—end up in the same connected component of the solution, i.e., of the support of x. If we knew beforehand that \(T^k\) and \(T^{\ell }\) lie in the same connected component of an optimum solution, we could simplify the instance, replacing \(T^k\) and \(T^{\ell }\) by their union \(T^k \cup T^{\ell }\). Iterating this idea would yield a solution where all the arborescences are disjoint, eliminating the directed cycles. Unfortunately, we cannot know the connected components of a Steiner forest a priori. Magnanti and Raghavan [25] instead propose to compute the connected components of a solution on-the-fly in the ILP formulation. Then, whenever \(T^k\) and \(T^\ell \), \(k \le \ell \), lie in the same connected component, they look for a common arborescence that is rooted at \(r^k\) and connects all terminals in \(T^k \cup T^\ell \). We recall their model \(\mathrm {IP}^{\mathrm {mr}}\)–translated to our notation—in the following.
For each \(k \in [K]\) let \( \mathcal {O}(r^k) := \bigl \{(r^k,t)\mathrel {}\bigm |\mathrel {} t \in \mathfrak {T}^{k\dots K}_r\bigr \},\) i.e., the set \(\mathcal {O}(r^k)\) contains a “commodity” (or a terminal pair) for each terminal node that can be connected to \(r^k\). We define \(\mathcal {D} := \mathcal {O}(r^1) \cup \cdots \cup \mathcal {O}(r^K)\) as the union of the \(\mathcal {O}(r^k)\), i.e., the set of all commodities. Let \(\mathcal {H} := \mathfrak {T}^{1\ldots K}_r \times \cdots \times \mathfrak {T}^{K\ldots K}_r\); any choice \(h \in \mathcal {H}\) assigns exactly one suitable terminal to each root node \(r^1,\ldots ,r^K\).

where
The constraints (5b) ensure that for each \(\ell \in [K]\) and each terminal \(t \in T_r^\ell \), there is a unique \(k \le \ell \) for which the solution contains a directed \(r^k\)-t-path. In other words, each terminal receives at least one unit of flow from one root node \(r^k\). If in the above condition we have \(k < \ell \), then the constraints (5c) ensure that there is a directed \(r^k\)-\(r^\ell \)-path, too.
The constraints (5d)–(5f) establish the property that for all edges \(\{i,j\} \in E\), the solution contains at most one of (i, j) and (j, i). Finally, (5g) limits each ingoing flow to one and (5h), (5i) remove some redundant flows, cf. [25].
Magnanti and Raghavan show that the improved formulation (\(\mathrm {IP}^{\mathrm {mr}}\)) is stronger than the undirected cut formulation (\(\mathrm {IP}^{\mathrm {uc}}\)). Unfortunately, their formulation has a size of \(\varOmega (\prod _{k=1}^K \sum _{\ell =k}^K |T^\ell |)\), i.e., it is exponential in the number of terminal sets K. We shall see in the next section how we achieve the same effect with a much smaller ILP formulation.
3 A new ILP formulation for the Steiner forest problem
Our new formulation contains three kinds of variables. As before, we use a variable \(x_{ij}\) for each edge \(\{i,j\} \in E\) to determine if \(\{i,j\}\) is included in the forest F and two corresponding directed variables \(y_{ij}, y_{ji}\). Likewise, the variables \(y^k_{ij}\) and \(y^k_{ji}\) for each \(k \in [K]\) and each \(\{i,j\} \in E\) determine if the arcs (i, j) and (j, i), respectively, are included in the arborescence rooted at \(r^k\). Finally, we introduce an additional variable \(z_{k\ell }\) for each \(k \in [K]\) and each \(\ell \ge k\), with the interpretation that \(z_{k\ell }=1\) iff \(T^k\) and \(T^\ell \) both lie in the arborescence spanned by \(y^k\). In the latter case, we say that \(r^k\) is responsible for the terminals in \(T^\ell \). Recall the definition of \(\mathfrak {T}^{i\ldots j}\) as \(T^i \cup \cdots \cup T^j\) and \(\mathfrak {T}_r^{i\ldots j} := \mathfrak {T}^{i\ldots j}{\setminus }\{r^i\}\); In particular, the set \(\mathfrak {T}^{\ell \cdots K}_r\) contains all the terminal nodes that can potentially be connected to \(r^\ell \). We extend our previous notion and say that a cut-set \(S \subseteq V\) is relevant for \(r^k\) and \(T^\ell \) if \(r^k \in S\) and some terminal \(t \in T^\ell \) is not in S. The set of all cut-sets that are relevant for \(r^k\) and \(T^\ell \) is written by \(\mathfrak {S}^k_\ell \) in the sequel. Then, our cut-based formulation reads as follows.

where
For any \(k, \ell \), the left hand side of the directed cut-set constraint (6a) is non-negative and the constraint is trivially satisfied if \(z_{k\ell } = 0\). If otherwise \(z_{k\ell }=1\), we need to connect all terminals from \(T^\ell \) to the k-th root \(r^k\). Then, any cut-set S separating \(r^k\) from some terminal in \(T^\ell \) must have at least one outgoing edge. This is exactly the condition modeled by (6a). For each \(k \in [K]\), the constraints (6b) ensure that exactly one root \(r^\ell \) is responsible for \(T^k\) (and \(r^1\) is always responsible for \(T^1\), i.e., \(z_{11} = 1\)). We use constraints (6c) to enforce that each edge \(\{i,j\}\) is part of at most one arborescence. We also want to make sure that no transitive responsibilities exist: If \(r^k\) is responsible for \(T^\ell \), then \(r^\ell \) cannot be responsible for some \(T^m\), \(m \not = \ell \). This is modeled by the symmetry breaking constraints (6d). They make sure that if root \(r^k\) is responsible for some terminal set \(T^\ell \), then \(r^k\) must be responsible for \(T^k\) as well. The capacity constraints (6e) say that if an edge \(\{i,j\}\) is used in any arborescence, then it must be included in the tree. Moreover, no node in any arborescence should have more than one incoming arc, as modeled by the indegree constraints (6f). Finally, the terminals in \(\mathfrak {T}^{1\cdots k-1}\) cannot be attached to root \(r^k\) and thus, no arc of the corresponding arborescence should enter such a terminal, see constraint (6g). The constraints (6f) and (6g) are not needed for integer feasibility.
Lemma 3
Formulation (\(\mathrm {IP}^{\mathrm {sedc}}\)) models the Steiner forest problem correctly. Its relaxation \(\mathrm {LP}^{\mathrm {sedc}}\) can be solved in time polynomial in the size of G and K.
Proof
Let \({\tilde{E}} \subseteq E\) be an optimal solution to the SFP. Start with \({\tilde{z}} := \mathbf {0}\). Now, for each connected component \(\mathcal {C}\) in \(G[{\tilde{E}}]\) set \({\tilde{z}}_{ii} = 1\) if \(r^i\) is the root node with lowest index contained in \(\mathcal {C}\) and for all other root nodes \(r^j\in \mathcal {C}, j\not = i\), set \(\tilde{z}_{ij} = 1\). The variables \({\tilde{z}}\) satisfy (6b) and (6d). Moreover, each terminal is assigned exactly one responsible root node. After fixing the z variables the remaining part of the model describes a union of disjoint Steiner trees, one for each connected component. Thereby, \({\tilde{E}}\) can be oriented such that each connected component is an arborescence rooted at its responsible root node giving values to variables \(y^1, \ldots , y^K\), y, and x. Since the arborescences are disjoint it follows that constraints (6e), (6c) are satisfied. Hence, we obtain a feasible solution to (\(\mathrm {IP}^{\mathrm {sedc}}\)) with the same objective value.
On the other hand, an optimum solution \(({\tilde{x}}, {\tilde{y}}, \tilde{z})\) to (\(\mathrm {IP}^{\mathrm {sedc}}\)) implies a valid hierarchy of the terminal sets. Moreover, constraints (6a) ensure that each terminal set is connected to its responsible root node. Hence, \({\tilde{E}} := \{e\in E \mid {\tilde{x}}_e = 1\}\) is a feasible solution to the SFP with the same cost.
The separation problem for the cut-set inequalities (6a) is polynomial time solveable with standard techniques (see Sect. 4 for details). \(\square \)
3.1 Strength of the new formulation
Instead of comparing the models directly we compare their equivalent flow-based variants. To obtain model (\(\mathrm {IP}^{\mathrm {sedf}}\)) with its relaxation \(\mathrm {LP}^{\mathrm {sedf}}\) from (\(\mathrm {IP}^{\mathrm {sedc}}\)) we replace the cut-conditions by flow-balance constraints and we also introduce additional flow variables f. Then, any feasible solution to \(\mathrm {LP}^{\mathrm {sedf}}\) defines a flow \(f^{kt}\) from \(r^k\) to any terminal \(t \in \mathfrak {T}^{k\cdots K}_r\) and ensures that the flow value of \(f^{kt}\) is exactly \(z_{k\ell }\), if \(t\in T^\ell \).
The constraints (7c) prohibit \(f^{kt}\) from leaving t and facilitate the comparison to \(\mathrm {LP}^{\mathrm {mr}}\).
Lemma 4
\({{\,\mathrm{Proj}\,}}_x(\mathrm {LP}^{\mathrm {sedf}}) = {{\,\mathrm{Proj}\,}}_x(\mathrm {LP}^{\mathrm {sedc}})\).
Proof
The constraints concerning the z variables are identical in both models, as are (6c) and (6e)–(6g). When considering one particular terminal set \(k\in [K]\) constraints (7b) model a flow of value \(z_{k\ell }\) from \(r^k\) to each terminal \(t\in T^\ell \), for each \(\ell \in \{k,\ldots , K\}\) (except \(r^k\) itself); and we can assume without loss of generality that this flow satisfies (7c). On the other hand, the directed cuts (6a) ensure that each directed cut separating \(r^k\) and t has a value of at least \(z_{k\ell }\). This is equivalent. \(\square \)
Theorem 1
\({{\,\mathrm{Proj}\,}}_x(\mathrm {LP}^{\mathrm {sedc}}) \subsetneq {{\,\mathrm{Proj}\,}}_x(\mathrm {LP}^{\mathrm {dc}})\)
Proof
We equivalently show that \({{\,\mathrm{Proj}\,}}_x(\mathrm {LP}^{\mathrm {sedf}}) \subsetneq {{\,\mathrm{Proj}\,}}_x(\mathrm {LP}^{\mathrm {df}})\). Let \(({\tilde{x}}, {\tilde{y}}, {\tilde{f}}, {\tilde{z}}) \in \mathrm {LP}^{\mathrm {sedf}}\). Moreover, let \({\tilde{x}}^k_{ij} := {\tilde{y}}^k_{ij} + {\tilde{y}}_{ji}^k, \forall \ k\in [K], \forall \ \{i,j\}\in E\). Due to (6c) and (6e) it holds \(x^k\in [0,1]^{|E|}, \forall \ k\in [K]\), \(\sum _{k\in [K]} {\tilde{x}}_{ij}^k = {\tilde{x}}_{ij}\), and

analogously to the Steiner tree problem, cf. [15].
For better overview we divide the proof into several parts. Parts (A)–(D) show that \({{\,\mathrm{Proj}\,}}_x(\mathrm {LP}^{\mathrm {sedf}}) \subseteq {{\,\mathrm{Proj}\,}}_x(\mathrm {LP}^{\mathrm {df}})\) and (E) gives an example where the strict inequality holds. In particular, in part (D) we construct a solution \(({\hat{x}}, {\hat{f}}) \in \mathrm {LP}^{\mathrm {df}}\) with \({\hat{x}} = {\tilde{x}}\).
A. Flows are 2-acyclic W.l.o.g. we assume that any flow \({\tilde{f}}^{kt}, \forall \ k\in [K], \forall \ t \in \mathfrak {T}_r^{k\ldots K}\), is free of 2-cycles, i.e., it satisfies \({\tilde{f}}_{ij}^{kt}=0 \vee {\tilde{f}}_{ji}^{kt} = 0, \forall \ \{i,j\}\in E\). Otherwise, one can modify the flow \({\tilde{f}}\) as follows such that the assumption is satisfied. Consider an edge \(\{i,j\}\in E\), let \(a_1\in \{(i,j), (j,i)\}\) and let \(a_2\) be the reverse arc, and w.l.o.g. let \({\tilde{f}}_{a_1}^{kt}\ge \tilde{f}_{a_2}^{kt} > 0\). Then, set \({\tilde{f}}_{a_1}^{kt} := \tilde{f}_{a_1}^{kt} - {\tilde{f}}_{a_2}^{kt}\) and \({\tilde{f}}_{a_2}^{kt} := 0\). Afterwards, \({\tilde{f}}\) is still a valid flow (both \(\tilde{f}(\delta ^-(\cdot ))\) and \({\tilde{f}}(\delta ^+(\cdot ))\) decrease by \({\tilde{f}}_{a_2}^{kt}\) for i and j) with the same value and all constraints in \(\mathrm {LP}^{\mathrm {sedf}}\) are still satisfied.
B. Reverse flow We first introduce additional flow variables \({\check{f}}^{k r^\ell }\), \(\forall \ \ell \in [K-1], \forall \ k\in \{\ell + 1, \ldots , K\}\), i.e., \(k > \ell \). Notice that these flow variables do not exist since we have only flow variables \(f^{kt}\) for a set k and terminal \(t\in \mathfrak {T}_r^{k\ldots K} \), i.e., \(\tau (t)\) \(\ge k\). The values of the new variables are set such that the flow from \(r^\ell \) to \(r^k\) is simply reversed: \(\forall \ (i,j)\in A:{\check{f}}_{ij}^{k r^\ell } := \tilde{f}_{ji}^{\ell r^k}\).
C. Flow from \(r^k\) to t over \(r^\ell \). Now, we construct a flow \({\bar{f}}^{k\ell t}\) for a set \(k\in [K]{\setminus }\{1\}\), a set \(\ell \in [k-1]\), and a terminal \(t\in T_r^k\). This flow will send \({\tilde{z}}_{\ell k}\) from \(r^k\) to t (over \(r^\ell \)) by using the reverse flow from \(r^\ell \) to \(r^k\), i.e., \({\bar{f}}^{k\ell t} := {\tilde{f}}^{\ell t} + {\check{f}}^{k r^\ell }\).
C.1. Feasibility and value We show that \(\bar{f}^{k\ell t}\) is a feasible flow from \(r^k\) to t with value \(\tilde{z}_{\ell k}\), \(\forall \ k\in [K]{\setminus }\{1\}, \forall \ t\in T_r^k, \forall \ \ell \in [k-1]\). Let \(i\in V\). We have:
-
Case “\(i=r^k\)”: \({\tilde{f}}^{\ell t}(\delta ^+(r^k)) - \tilde{f}^{\ell t}(\delta ^-(r^k)) = 0\) since \(r^k\) is an internal node under flow \({\tilde{f}}^{\ell t}\). Moreover, \({\check{f}}^{k r^\ell }(\delta ^+(r^k)) - {\check{f}}^{k r^\ell }(\delta ^-(r^k)) = \tilde{z}_{\ell k}\) (the reverse flow).
-
Case “\(i=t\)”: Similar arguments: \({\check{f}}^{k r^\ell }(\delta ^+(t)) - {\check{f}}^{k r^\ell }(\delta ^-(t)) = 0\) since t is an internal node under \({\check{f}}^{k r^\ell }\) and \(\tilde{f}^{\ell t}(\delta ^+(t)) - {\tilde{f}}^{\ell t}(\delta ^-(t)) = - \tilde{z}_{\ell k}\).
-
Case “\(i=r^\ell \)”: \({\tilde{f}}^{\ell t}(\delta ^+(r^\ell )) - {\tilde{f}}^{\ell t}(\delta ^-(r^\ell )) = {\tilde{z}}_{\ell k}\) and \(\check{f}^{k r^\ell }(\delta ^+(r^\ell )) - {\check{f}}^{k r^\ell }(\delta ^-(r^\ell )) = -{\tilde{z}}_{\ell k}\). Hence, the sum is 0.
-
Otherwise : Since \({\tilde{f}}^{\ell t}\) and \({\check{f}}^{k r^\ell }\) are flows the sum is 0.
Hence, \({\bar{f}}^{k\ell t}\) is a feasible flow from \(r^k\) to t with value \({\tilde{z}}_{\ell k}\).
C.2. 2-Acyclic \({\bar{f}}^{k\ell t}\). Again, we assume w.l.o.g. that \({\bar{f}}^{k\ell t}\) is 2-acyclic, i.e, \(\bar{f}_{ij}^{k\ell t}=0 \vee {\bar{f}}_{ji}^{k\ell t} = 0, \forall \ \{i,j\}\in E\). Otherwise, we modify the flow similar to before. Consider an edge \(\{i,j\}\in E\). Again, let \(a_1\in \{(i,j), (j,i)\}\) with reverse arc \(a_2\) and with \({\bar{f}}^{k\ell t}_{a_1} \ge \bar{f}^{k\ell t}_{a_2} > 0\). Then, set \({\bar{f}}^{k\ell t}_{a_1} := \bar{f}^{k\ell t}_{a_1} - {\bar{f}}^{k\ell t}_{a_2} ={\tilde{f}}_{a_1}^{\ell t} + {\check{f}}_{a_1}^{k r^\ell } - {\tilde{f}}_{a_2}^{\ell t} - \check{f}_{a_2}^{k r^\ell }\) and \({\bar{f}}^{k\ell t}_{a_2} := 0\). Notice that for any arc \(a_1\) with reverse arc \(a_2\) it holds \({\bar{f}}^{k\ell t}_{a_1} = \max \{0, {\tilde{f}}_{a_1}^{\ell t} + {\check{f}}_{a_1}^{k r^\ell } - {\tilde{f}}_{a_2}^{\ell t} - {\check{f}}_{a_2}^{k r^\ell }\}\).
Schematic view on the involved flows in the proof of Theorem 1. \(r^k\) and \(r^\ell \) are root nodes for sets \(T^k\) and \(T^\ell \), with \(\ell < k\) and \(t\in T_r^k\). a The original flows. b The reverse flow \({\check{f}}^{k r^\ell }\) from \(r^k\) to \(r^\ell \), cf. part B in the proof, and the combined flow \({\bar{f}}^{k \ell t}\) from \(r^k\) to t over \(r^\ell \), cf. part C
C.3. Capacity \({\bar{f}}^{k\ell s}_{ij} + \bar{f}^{k\ell t}_{ji} \le {\tilde{x}}_{ij}^\ell \). Now, for any \(k \in [K]{\setminus }\{1\}\) and any \(\ell \in [k-1]\), consider two terminals \(s, t\in T_r^k\) from the same terminal set, and an edge \(\{i,j\}\in E\) with the two related arcs \(a_1\in \{(i,j), (j,i)\}\) and the reverse arc \(a_2\). We argue that \({\bar{f}}^{k\ell s}_{a_1} + \bar{f}^{k\ell t}_{a_2} \le {\tilde{x}}_{ij}^\ell \).
If one flow is zero the inequality holds: E.g., if \({\bar{f}}^{k\ell t}_{a_2} = 0 \) we have: \( {\bar{f}}^{k\ell s}_{a_1} + {\bar{f}}^{k\ell t}_{a_2} = {\bar{f}}_{a_1}^{k \ell s} = {\tilde{f}}_{a_1}^{\ell s} + {\check{f}}_{a_2}^{\ell r^k} \le {\tilde{x}}_{ij}^\ell \). The last inequality is true due to constraint (7a\(^*\)). The part with \({\bar{f}}^{k\ell s}_{a_1} = 0\) works analogously.
Otherwise, if both parts are \(> 0\) we have: \({\bar{f}}^{k\ell s}_{a_1} + {\bar{f}}^{k\ell t}_{a_2} = {\tilde{f}}_{a_1}^{\ell s} + \check{f}_{a_1}^{k r^\ell } - {\tilde{f}}_{a_2}^{\ell s} - {\check{f}}_{a_2}^{k r^\ell } + {\tilde{f}}_{a_2}^{\ell t} + {\check{f}}_{a_2}^{k r^\ell } - {\tilde{f}}_{a_1}^{\ell t} - {\check{f}}_{a_1}^{k r^\ell } = \tilde{f}_{a_1}^{\ell s} - {\tilde{f}}_{a_2}^{\ell s} + {\tilde{f}}_{a_2}^{\ell t} - {\tilde{f}}_{a_1}^{\ell t} \le {\tilde{x}}_{ij}^\ell \), again by constraint (7a\(^*\)).
D. Solution to \(\mathrm {LP}^{\mathrm {df}}\) Due to the previous discussion we are now able to construct a solution \(({\hat{x}}, {\hat{f}}) \in \mathrm {LP}^{\mathrm {df}}\) with the same objective value. See Fig. 3 for an sketch of the construction.
D.1. Variable assignment We use the same values for the undirected edges by assigning \({\hat{x}} := {\tilde{x}}\). Trivially, \({\hat{x}}\in [0,1]^{|E|}\).
The flow variables \({\bar{f}}^{t}, \forall \ t\in \mathfrak {T}{\setminus }\mathfrak {R}\), with \(k=\tau (t)\), are assigned the following values: \({\hat{f}}^{t} := {\tilde{f}}^{kt} + \sum _{\ell \in [k-1]} {\bar{f}}^{k\ell t}\). Obviously, it holds \({\hat{f}}^{t} \ge 0\); the upper bound of 1 follows from part D.3.
D.2. Flow conservation and flow value 1 Consider a terminal \(t\in \mathfrak {T}{\setminus }\mathfrak {R}\) with \(k=\tau (t)\) and a vertex \(i\in V\). By inserting the definition we have:
-
Case “\(i=r^k\)”: \({\tilde{f}}^{kt}(\delta ^+(i)) - \tilde{f}^{kt}(\delta ^-(i)) = {\tilde{z}}_{kk}\) and for each \(\ell < k\) it holds \({\bar{f}}^{k\ell t}(\delta ^+(i)) - {\bar{f}}^{k\ell t}(\delta ^-(i)) = {\tilde{z}}_{\ell k}\) (due to C.1). Overall we get \(\tilde{z}_{kk} + \sum _{\ell < k} {\tilde{z}}_{\ell k} = 1\) (due to constraint (6b)).
-
Case “\(i=t\)”: Analogously, \(\tilde{f}^{kt}(\delta ^+(i)) - {\tilde{f}}^{kt}(\delta ^-(i)) = -{\tilde{z}}_{kk}\) and for each \(\ell < k\) it holds \({\bar{f}}^{k\ell t}(\delta ^+(i)) - {\bar{f}}^{k\ell t}(\delta ^-(i)) = -{\tilde{z}}_{\ell k}\) (due to C.1), and overall we have \(-{\tilde{z}}_{kk} + \sum _{\ell < k} - \tilde{z}_{\ell k} = -1\) (due to constraint (6b)).
-
Otherwise: Since \({\tilde{f}}^{kt}\) and \({\bar{f}}^{k\ell t}(\delta ^-(i)), \forall \ \ell < k\), are flows (cf. C.1) the sum is 0.
We conclude that \({\hat{f}}^{t}\) is a flow from \(r^k\) to t with value 1, \(\forall \ k\in [K], \forall \ t\in T_r^k\).
D.3. \({\hat{x}}_{ij} \ge {\hat{f}}_{ij}^{s} + {\hat{f}}_{ji}^{t}\) Last but not least, we need to show that constraints (4a) are satisfied. Let \(\{i,j\}\in E\), \(k\in [K]\), and \(s, t\in T_r^k\).
An instance where the LP relaxation of the extended directed flow formulation gives a better bound than the one of the directed flow formulation, cf. part (E) in the proof of Theorem 1. a Depicts the input graph and b, c give valid flows for sets 1 and 2 for \(\mathrm {LP}^{\mathrm {df}}\)
E. Example for strict inequality Figure 4 gives an example with \(x\in {{\,\mathrm{Proj}\,}}_x(\mathrm {LP}^{\mathrm {df}})\) but \(x\not \in {{\,\mathrm{Proj}\,}}_x(\mathrm {LP}^{\mathrm {sedf}})\). The instance has unit edge costs and the two terminal sets \(T^1 = \{a, d\}\) and \(T^2 = \{b, c\}\) with \(r^1 = a, r^2 = b\). The optimum solution to \(\mathrm {LP}^{\mathrm {df}}\) sets \(x_{ij} := 0.5, \forall \ \{i,j\}\in E\), and the flows are given by Figure (b) and (c) with the depicted arcs routing a flow of value 0.5. Hence, the optimum solution value of \(\mathrm {LP}^{\mathrm {df}}\) is 2.
On the other hand, this solution is not valid for model \(\mathrm {LP}^{\mathrm {sedf}}\). A value of 0.5 for each edge implies a flow for the first terminal set as depicted in Figure (b). Then, it is not possible to route any flow for the second set (from node b to c) without increasing the x variables. Hence, it has to hold \(z_{12} = 1\). However, sending a flow with value 1 from a to nodes b and c while using the same arcs as in (b) is not possible. It is easy to see that the optimum solution to the LP relaxation of \(\mathrm {LP}^{\mathrm {sedf}}\) has a value of 3 by picking any three edges. \(\square \)
Our next theoretical result is that the new relaxation \(\mathrm {LP}^{\mathrm {sedc}}\) is strictly stronger than the relaxation of Magnanti and Raghavan [25]. The major difference between \(\mathrm {LP}^{\mathrm {sedf}}\) and \(\mathrm {LP}^{\mathrm {mr}}\) is this: While in \(\mathrm {LP}^{\mathrm {sedf}}\), any two flows \(f^{kt}\) and \(f^{kt'}\) for \(t,t' \in T^\ell \) must have the same flow value \(z_{k\ell }\), the same flows can have different values in \(\mathrm {LP}^{\mathrm {mr}}\). In that sense, \(\mathrm {LP}^{\mathrm {sedf}}\) is more restricted and it makes sense that any flow that is feasible in \(\mathrm {LP}^{\mathrm {sedf}}\) is feasible in \(\mathrm {LP}^{\mathrm {mr}}\), too, whereas the converse is not necessarily true (see Fig. 5).
Theorem 2
\({{\,\mathrm{Proj}\,}}_x(\mathrm {LP}^{\mathrm {sedc}}) \subsetneq {{\,\mathrm{Proj}\,}}_x(\mathrm {LP}^{\mathrm {mr}})\)
Proof
As before, we compare \(\mathrm {LP}^{\mathrm {sedf}}\) instead of \(\mathrm {LP}^{\mathrm {sedc}}\). Let \((\bar{x},\bar{y},\bar{z},\bar{f}) \in \mathrm {LP}^{\mathrm {sedf}}\). We show that \((\bar{x},\bar{y},\bar{f}) \in \mathrm {LP}^{\mathrm {mr}}\), too. To see why (5a) is satisfied, fix some \(\bar{i}\in V\), \(\bar{k}\in [K]\), and \(\bar{t}\in \mathfrak {T}^{k\ldots K}_r\). Then,
where \(\bar{\ell }= \tau (\bar{t})\). For (5b), fix \(\bar{\ell }\in [K]\) and \(t \in T^{\bar{\ell }}_r\). We have
Next, fix \(\bar{\ell }\in [K]\), \(\bar{k}< \bar{\ell }\), and let \(\bar{t}\in T^{\bar{\ell }}_r\). We show that (5c) is satisfied. As before, we have
where the second invocation of (7b) is for \(t = r^{\bar{\ell }}\). To show that (5d), fix a choice \((\bar{t}_1,\ldots ,\bar{t}_K) \in \mathcal {C}\) and \(\{\bar{i}, \bar{j}\} \in E\). It follows that
It follows analogously that (5e) is satisfied by using (6c). Constraint (5f) is equivalent to (6e). Now, fix \(\bar{i}\in V\) and \((\bar{t}_1,\ldots ,\bar{t}_K)\in \mathcal {C}\). We have
and thus (5g) is satisfied. Finally, the constraint (5h) is implied by (6g) and (5i) is equivalent to (7c). Figure 5 shows an example where strict inequality holds. \(\square \)
Example instance where \(\mathrm {LP}^{\mathrm {sedf}}\) gives a stronger bound than \(\mathrm {LP}^{\mathrm {mr}}\). a Instance with three terminal sets ( 1,
1,  2,
2,  3) and unitary edge costs 1. b Optimum solution of \(\mathrm {LP}^{\mathrm {mr}}\) with overall cost 4.5. This solution is infeasible for \(\mathrm {LP}^{\mathrm {sedf}}\) since here we would have \(z_{22}=0.5\) and \(z_{23} = 1.0\), conflicting (6d). c Optimum solution of \(\mathrm {LP}^{\mathrm {sedf}}\) which is integer and has cost 5. Here, non-0 z-variables are \(z_{11}=z_{22}= z_{23} = 1.0\)
3) and unitary edge costs 1. b Optimum solution of \(\mathrm {LP}^{\mathrm {mr}}\) with overall cost 4.5. This solution is infeasible for \(\mathrm {LP}^{\mathrm {sedf}}\) since here we would have \(z_{22}=0.5\) and \(z_{23} = 1.0\), conflicting (6d). c Optimum solution of \(\mathrm {LP}^{\mathrm {sedf}}\) which is integer and has cost 5. Here, non-0 z-variables are \(z_{11}=z_{22}= z_{23} = 1.0\)
3.2 A smaller cut-based formulation
We remark that a directed cut-based model can be written in the slightly different form below. While this formulation is smaller and less involved, it turns out that its linear programming bounds are potentially weaker than the ones from (\(\mathrm {IP}^{\mathrm {sedc}}\)). Here, we only need two variables \(y_{ij}, y_{ji}\), and a variable \(x_{ij}\) for each edge \(\{i,j\} \in E\). As before, for all \(k \in [K]\) and all \(\ell \ge k\), we have a decision variable \(z_{k\ell }\) that tells us whether the terminals in \(T^\ell \) should be connected to the root \(r^k\).

where
To see why the formulation is correct, consider a cut-set \(S \subseteq V\) with \(t \not \in S\) for some terminal \(t \in T^\ell \). If S contains a root node \(r^k\) with \(z_{k\ell } = 1\), then S must have at least one outgoing arc and the right-hand side of (8a) evaluates to 1 (because of (8b) the right-hand side never exceeds 1). Otherwise, the right-hand side of (8a) evaluates to 0 and the constraint is trivially satisfied. The LP relaxation of (\(\mathrm {IP}^{\mathrm {edc}}\)) can be solved in polynomial time using standard methods to separate the inequalities of type (8a). We sketch the separation algorithm in Sect. 4.
Lemma 5
\({{\,\mathrm{Proj}\,}}_x(\mathrm {LP}^{\mathrm {sedc}}) \subsetneq {{\,\mathrm{Proj}\,}}_x(\mathrm {LP}^{\mathrm {edc}})\).
Proof
Let \(({\tilde{x}},{\tilde{y}}, {\tilde{y}}^1, \ldots , {\tilde{y}}^K, {\tilde{z}}) \in \mathrm {LP}^{\mathrm {sedc}}\). We argue that \(({\tilde{x}},{\tilde{y}},{\tilde{z}}) \in \mathrm {LP}^{\mathrm {edc}}\). The constraints (8b)–(8d) are trivially satisfied. Now, consider a directed cut \(S \subseteq V:S\cap T^\ell \not =\emptyset \), for some set \(\ell \in [K]\). Any cut S is relevant to the sum in the right-hand side of constraint (8a) if and only if it is a valid cut for constraint (6a), hence
and thus (8a) is satisfied. Strictness follows from instance (B) in Fig. 1. \(\square \)
On the other hand, the model is stronger than the directed model without the z variables. The following arguments and the used flow construction are similar to the proof of Theorem 1.
Lemma 6
\({{\,\mathrm{Proj}\,}}_x(\mathrm {LP}^{\mathrm {edc}}) \subsetneq {{\,\mathrm{Proj}\,}}_x(\mathrm {LP}^{\mathrm {dc}})\).
Proof
Let \(({\tilde{x}}, {\tilde{y}}, {\tilde{z}})\in \mathrm {LP}^{\mathrm {edc}}\). Set \({\hat{x}} := {\tilde{x}}\). Consider a terminal set \(k\in [K]\). Then, for each terminal \(t\in T^k\), and each root \(r^\ell \) with \(\ell \le k\) construct a flow \({\tilde{f}}^{\ell t}\) from \(r^\ell \) to t of value \({\tilde{z}}_{\ell k}\) (except for \(t=r^\ell \)). Notice that if \(k > 1\) we also have a flow from \(r^\ell \) to \(r^k\). Similar to the proof of Theorem 1 we also consider the reversed flow \({\check{f}}^{k r^\ell }\) (\(k > \ell \)) and combine the flows to \({\hat{f}}^{k t} := {\tilde{f}}^{k t} + \sum _{\ell < k} ({\check{f}}^{k r^\ell } + {\tilde{f}}^{\ell t})\).
Due to the directed cuts (8a) and capacity constraints (8d) it is valid to assume that \({\hat{f}}\) exists satisfying the following properties: (i) \({\hat{f}}_{ij}^{k t} \le {\tilde{y}}_{ij}\) and \({\hat{f}}_{ji}^{k t} \le \tilde{y}_{ji}, \forall \ \{i,j\}\in E\), (ii) \({\hat{f}}^{k t}\) is 2-acyclic (as discussed in Theorem 1), (iii) \({\hat{f}}^{k t}\) is a feasible flow, and (iv) the flow value of \({\hat{f}}^{k t}\) is 1. Using this flow we set \({\hat{y}}_{ij}^k := \max _{t\in T^k}\{{\hat{f}}^{k t}_{ij}\}, \forall \ (i,j)\in A, \forall k\in [K]\). Due to properties (i)+(ii) it holds \({\hat{y}}_{ij}^k + {\hat{y}}_{ji}^k \le {\hat{x}}_{ij}, \forall \ \{i,j\}\in E\), and due to (iii)+(iv) \({\hat{y}}\) satisfies the directed cuts (3a). Hence, \(({\hat{x}}, {\hat{y}})\) is a feasible solution to \(\mathrm {LP}^{\mathrm {dc}}\) with the same solution value.
An instance showing the strict inequality is given by Fig. 1. \(\square \)
We summarize the results of the discussion in Fig. 6 and remark that the relationship of \(\mathrm {LP}^{\mathrm {mr}}\) to the models \(\mathrm {LP}^{\mathrm {dc}}\) and \(\mathrm {LP}^{\mathrm {edc}}\) is an open problem. Our conjecture is that it holds \({{\,\mathrm{Proj}\,}}_x(\mathrm {LP}^{\mathrm {mr}}) \subsetneq {{\,\mathrm{Proj}\,}}_x(\mathrm {LP}^{\mathrm {edc}}) \subsetneq {{\,\mathrm{Proj}\,}}_x(\mathrm {LP}^{\mathrm {dc}})\).
3.3 Redundancy in the models and additional valid constraints
Interestingly, the constraints



are all binding in the formulations \(\mathrm {LP}^{\mathrm {sedc}}\) and \(\mathrm {LP}^{\mathrm {sedf}}\). Examples are given by Figs. 7, 8, and 5. In particular, this may be surprising for the first inequality since every terminal requires only one path (or a flow of value 1) and moreover, this constraint is non-binding for the Steiner tree problem.
Example instance where \(\mathrm {LP}^{\mathrm {sedf}}\) and \(\mathrm {LP}^{\mathrm {sedc}}\) are strengthened by \(y(\delta ^-(v)) \le 1\). a Instance with three terminal sets ( 1,
1,  2,
2,  3) and unitary edge costs 1; the integer optimum is 15. b Optimum solution of \(\mathrm {LP}^{\mathrm {sedf}}\), \(\mathrm {LP}^{\mathrm {sedc}}\) without indegree constraints (6f) with cost 13.5; the dashed arcs are set to 0.5 and the indegree at the central vertex is violated. c Optimum solution of \(\mathrm {LP}^{\mathrm {sedf}}\), \(\mathrm {LP}^{\mathrm {sedc}}\) with indegree constraints (6f) and with cost 14; dashed arcs are assigned value 0.5 and solid arcs value 1
3) and unitary edge costs 1; the integer optimum is 15. b Optimum solution of \(\mathrm {LP}^{\mathrm {sedf}}\), \(\mathrm {LP}^{\mathrm {sedc}}\) without indegree constraints (6f) with cost 13.5; the dashed arcs are set to 0.5 and the indegree at the central vertex is violated. c Optimum solution of \(\mathrm {LP}^{\mathrm {sedf}}\), \(\mathrm {LP}^{\mathrm {sedc}}\) with indegree constraints (6f) and with cost 14; dashed arcs are assigned value 0.5 and solid arcs value 1
Example instance where \(\mathrm {LP}^{\mathrm {sedf}}\) and \(\mathrm {LP}^{\mathrm {sedc}}\) are strengthened by \(y^k(\delta ^-(t)) = 0, \forall \ k \in [K]{\setminus }\{1\}, \forall \ t \in \mathfrak {T}^{1\cdots k-1}\). a Instance with two terminal sets ( 1,
1,  2) and unitary edge costs 1; the integer optimum is 10. b Optimum solution of \(\mathrm {LP}^{\mathrm {sedf}}\), \(\mathrm {LP}^{\mathrm {sedc}}\) without indegree constraints \(y^k(\delta ^-(t)) = 0\) with cost 9; again, dashed arcs are set to 0.5 and the indegree is violated at the root node of the red set. c Optimum solution of \(\mathrm {LP}^{\mathrm {sedf}}\), \(\mathrm {LP}^{\mathrm {sedc}}\) with indegree constraints which has cost 9.5; dashed arcs are set to 0.5 and solid arcs to 1
2) and unitary edge costs 1; the integer optimum is 10. b Optimum solution of \(\mathrm {LP}^{\mathrm {sedf}}\), \(\mathrm {LP}^{\mathrm {sedc}}\) without indegree constraints \(y^k(\delta ^-(t)) = 0\) with cost 9; again, dashed arcs are set to 0.5 and the indegree is violated at the root node of the red set. c Optimum solution of \(\mathrm {LP}^{\mathrm {sedf}}\), \(\mathrm {LP}^{\mathrm {sedc}}\) with indegree constraints which has cost 9.5; dashed arcs are set to 0.5 and solid arcs to 1
In the following, we discuss additional constraints for the two models (\(\mathrm {IP}^{\mathrm {sedc}}\)) and (\(\mathrm {IP}^{\mathrm {sedf}}\)), respectively. These constraints strengthen the models further and we denote the expanded models by (\(\mathrm {IP}^{\mathrm {sedc^*}}\)) and (\(\mathrm {IP}^{\mathrm {sedf^*}}\)), respectively. Again, we focus on the cut-based model.

where
The constraints (9a) and (9b) are the well-known flow-balance constraints from the Steiner tree problem: (9a) affects the overall solution and (9b) each subtree independently. They state that the indegree of a non-terminal vertex is not larger than its outdegree. Since the flow-balance constraints are strengthening for the Steiner tree problem, see e.g., [28], both constraints are strengthening for the SFP, too. We can also incorporate (9a) into \(\mathrm {LP}^{\mathrm {mr}}\) and \(\mathrm {LP}^{\mathrm {edc}}\), strengthening these models, too. However, this does not hold for constraints (9b).
The latter fact is interesting since it is possible to construct instances where (9b) is violated, but (9a) is not. Such an instance can be constructed by joining two Steiner tree instances—while each instance implies one terminal set—at a non-terminal v. Thereby, the constraint for \(y^1\) and v is violated whereas \(y^2\) has a larger outdegree such that the aggregated constraint is not violated. The first instance is described in [11, 27] and is due to Goemans; with \(k=4\) and \(r^1 = a_0\) the optimum solution sets all arcs to 0.25, and with \(v=c_{34}\) we have \(y^1(\delta ^-(v)) = 0.5\) and \(y^1(\delta ^+(v)) = 0.25\). The second instance is the classical instance with integrality gap 10/9 which can be found in, e.g., [10] Fig. 8.1. With \(r^2\) being the topmost terminal \(u_1\) and v the left non-terminal \(v_3\) the optimum solution sets all arcs to 0.5, and \(y^2(\delta ^-(v)) = 0.5\) and \(y^2(\delta ^+(v)) = 1\). The whole example is depicted in Fig. 9.
Example instance where (9b) is violated, but (9a) is not. All edge costs are one and there are two terminal sets ( 1,
1,  2). Due to the size of the graph we already show the optimum solution to \(\mathrm {LP}^{\mathrm {sedc}}\): thin solid arcs are assigned 0.25, dashed arcs are set to 0.5, and \(z_{11} = z_{22} = 1\). (9b) is violated at v for \(y^1\) but not for y
2). Due to the size of the graph we already show the optimum solution to \(\mathrm {LP}^{\mathrm {sedc}}\): thin solid arcs are assigned 0.25, dashed arcs are set to 0.5, and \(z_{11} = z_{22} = 1\). (9b) is violated at v for \(y^1\) but not for y
Last but not least, consider constraints (9c) which state that the subtree rooted at \(r^k\) can only use another root node \(r^\ell , \ell > k\), when \(z_{k\ell } = 1\). Notice that the constraint is feasible for a terminal t in \(T^\ell \), too, i.e., \(y^k(\delta ^-(t)) \le z_{k\ell }\). However, any solution with \(y^k(\delta ^-(t)) > z_{k\ell }\) is already infeasible due to (6a), (6b), and (6f).
Observation 7
The constraints (9c) are valid.
Proof
Consider an optimum solution \(({\hat{x}}, {\hat{y}}, {\hat{z}})\) to (\(\mathrm {IP}^{\mathrm {sedc}}\)) such that (9c) is violated, i.e., \({\hat{y}}^k(\delta ^-(r^\ell )) = 1 > {\hat{z}}_{k\ell } = 0\), for some \(k < \ell \). Since \({\hat{z}}_{k\ell } = 0\) there exists \(j\not =k\) with \({\hat{z}}_{j\ell } = 1\) (possibly \(j=\ell \)). If \(j\not =\ell \) then \(y(\delta ^-(r^\ell )) \ge y^k(\delta ^-(r^\ell )) + y^j(\delta ^-(r^\ell )) \ge 2\) which violates (6f). Hence, \(z_{\ell \ell } = 1\) and \(r^\ell \) is the root node of a subtree containing \(T^\ell \) (possibly more sets). This subtree can be attached to the kth tree and variables \({\hat{y}}^\ell , {\hat{y}}^k\), and \({\hat{z}}\) can be set accordingly while \({\hat{x}}\) and \({\hat{y}}\) remain unchanged. \(\square \)
An example for the strength of (9c) is given by Fig. 8 if the two sets are interchanged, i.e., if the blue terminal set (diamonds) is the first set and the red set (rectangles) the second set. Without these constraints the optimum LP solution has cost 9 and is depicted in Fig. 8b. Adding the constraints increases the optimum solution to 9.5 as, e.g., in Fig. 8c.
3.4 Integrality gap
For the Steiner tree problem the integrality gap of the undirected models is 2 and for the directed models the gap is still unknown. Byrka, Grandoni, Rothvoß, and Sanità [4] were able to show that the gap is at least \(36/31 \approx 1.161\), but the upper bound is still 2 through the undirected model. Although our Steiner forest models \(\mathrm {LP}^{\mathrm {sedc^*}}\), \(\mathrm {LP}^{\mathrm {sedf^*}}\) coincide with the directed models for the case \(K=1\) we give a series of instances where the gap approaches 3/2 = 1.5 for larger K.
Such an instance depends on an integer \(M > 0\) and consists of \(M+1\) terminal sets; an example with \(M=3\) is depicted in Fig. 10. Thereby, the graph consists of M identical subgraphs, one for each set \(T^1, \ldots , T^M\). Here, the two terminals of each set are connected by M paths. Each path has a length of 2 with one internal non-terminal vertex. Finally, set \(T^{M+1}\) contains M terminals which are connected to the corresponding non-terminals of each subgraph by zero-cost edges, cf. Fig. 10a.
a Example instance where the integrality gap of \(\mathrm {LP}^{\mathrm {sedf^*}}\) and \(\mathrm {LP}^{\mathrm {sedc^*}}\) is 4/3. We have four terminal sets ( 1,
1,  2,
2,  3,
3,  4) and the edge cost for the thick edges is 1 and for the thin edges 0. Since \(T^4\) can only be connected via the other sets the optimum solution constructs three trees, e.g., \(T^1\) and \(T^4\) are connected in one tree and \(T^2\) and \(T^3\) get stand-alone trees. Hence, the cost is \(4 + 2 + 2 = 8\). b Shows the optimum solution to the LP relaxation which sets \(z_{11} = z_{22} = z_{33} = 1\) and \(z_{14} = z_{24} = z_{34} = 1/3\) and all dashed arcs are set to 1/3. The overall cost is 6
4) and the edge cost for the thick edges is 1 and for the thin edges 0. Since \(T^4\) can only be connected via the other sets the optimum solution constructs three trees, e.g., \(T^1\) and \(T^4\) are connected in one tree and \(T^2\) and \(T^3\) get stand-alone trees. Hence, the cost is \(4 + 2 + 2 = 8\). b Shows the optimum solution to the LP relaxation which sets \(z_{11} = z_{22} = z_{33} = 1\) and \(z_{14} = z_{24} = z_{34} = 1/3\) and all dashed arcs are set to 1/3. The overall cost is 6
In the optimum integer solution \(T^{M+1}\) needs to be connected to another set, say \(T^1\); hence, the tree containing \(T^1\cup T^{M+1}\) induces cost \(M+1\). All other sets \(T^2, \ldots , T^M\) can be connected independently by choosing one of the paths. Hence, the overall cost is \(M+1 + (M-1)\cdot 2 = 3M - 1\). On the other hand, the LP relaxation sets \(z_{kk} = 1\) and \(z_{k(M+1)} = 1/M\), \(\forall k\in \{1,\ldots , M\}\). Then, each root node \(r^1, \ldots , r^M\) sends 1/M over each path to its terminal and also 1/M to each terminal in \(T^{M+1}\). This LP solution has cost \(1/M \cdot 2M \cdot M = 2M\). Hence, with arbitrarily large M the integrality gap approaches 1.5.
4 Experimental results
Settings. All experiments were performed on a Debian 10.1 machine with an Intel(R) Xeon(R) CPU E5-2643 running at 3.30GHz. Our code is written in C++ using ILOG CPLEX 12.6.3 and the 2012.07 release of the Open Graph Drawing Framework [6]. We compiled with g++-8.3 and -O2 flags. Automatic symmetry breaking and presolving was disabled in CPLEX, as well as all general integer cuts.
Instances For the JMP instance set, we generated 580 random graphs with a frequently used method by Johnson et al. [21]: First, distribute n nodes uniformly at random in a unit square. Then, insert an edge \(\{i,j\}\) if the Euclidean distance between i and j is less than \(\alpha / \sqrt{n}\), where \(\alpha \) is a parameter for the random generator. The cost of the edge \(\{i,j\}\) is proportional to the Euclidean distance. Finally, connect all nodes with a minimum Euclidean spanning tree to ensure that the instance is connected.
To determine K random terminal sets, we first select \(t \cdot |V|\) nodes uniformly at random (the number \(K\in [n/2]\) of terminal sets and the terminal percentage \(t \in [0,1]\) are again parameters). We then bring the selected nodes into a random order and draw \(K-1\) distinct split points from \(\{2,\ldots ,t\cdot |V|-1\}\), thus splitting the random node order into K distinct terminal sets. For each \(n \in \{25, 50, 150, 200, 500\}\), we choose a small, a medium, and a large number of terminal sets K.
|V| | 25 | 50 | 100 | 200 | 500 |
|---|---|---|---|---|---|
\(K \in \) | \(\{2,3,4\}\) | \(\{3,4,5\}\) | \(\{5, 10, 15\}\) | \(\{10, 15, 20\}\) | \(\{20,35,50\}\) |
The percentage t of terminal nodes is picked from \(\{0.25, 0.5, 0.75, 1.0\}\) unless a combination of n, K, and t results in a terminal set size of less than two. For each choice of n, K, and t, we generate five instances with \(\alpha =1.6\) and five instances with \(\alpha =2.0\); leading to 580 JMP instances. The MR instance set is generated based on [25] and contains 85 instances.
4.1 Solving the LP-relaxations
Separating cut-set inequalities No separation procedures are known for the inequalities of (\(\mathrm {IP}^{\mathrm {mr}}\)). The cut-set inequalities in the three other formulations can be separated with standard techniques, however:
-
We separate a point \((x,y^1,\ldots ,y^k)\) from (\(\mathrm {IP}^{\mathrm {dc}}\)) with inequalities of type (3a) in the following way. We compute a maximum \(r^k\)-t-flow f in the support graph of \(y^k\), for each \(k \in [K]\) and each \(t \in T^k{\setminus }\{r^k\}\). If the value of f is strictly less than one, we derive a violated inequality of type (3a) from the \(r^k\)-t-cut \(S:=\{{v \in V}\mid \text { there is a }v-t\text {-path in the residual network of }f\}\).
-
For (\(\mathrm {IP}^{\mathrm {edc}}\)) we want to separate a point (x, y, z) from the feasible region with inequalities of type (8a). For a fixed \(\ell \in [K]\) we augment the support graph of y with a super source s and insert an arc \((s,r^k)\) with capacity \(z_{k\ell }\) for all \(k\le \ell \). We then look for a maximum s-t-flow f for all \(t \in T^\ell {\setminus }\{r^\ell \}\). Analogously to the previous case, the corresponding minimum s-t-cut induces a violated inequality of type (8a) if f has a value of strictly less than \(\sum _{k=1}^\ell z_{k\ell }\). To check that \(r^\ell \) is connected to \(r^1,\ldots ,r^{\ell -1}\) as well, we remove \((s, r^\ell )\) from the augmented support graph in a second step and look for a maximum s-\(r^\ell \)-flow f of value at most \(\sum _{k=1}^{\ell -1} z_{k\ell }\).
-
For (\(\mathrm {IP}^{\mathrm {sedc}}\)), we want to separate a point \((x,y^1,\ldots ,y^K, z)\) with inequalities of type (6a). For each \(\ell \in [K]\) and each \(k \le \ell \), we compute a maximum \(r^\ell \)-t-flow f in the support graph of \(y^\ell \) for each \(t \in T^k\). If the value of f is strictly less than \(z_{k\ell }\) the corresponding minimum \(r^\ell \)-t-cut induces an inequality of type (6a) that separates \((x,y^1,\ldots ,y^K,z)\).
Some algorithmic techniques have the potential to improve this on-the-fly generation [22]:
-
Back cuts
Additionally add the cut-set inequality corresponding to \(\bar{S}\) where \(v \in V\) is included in \(\bar{S}\) if and only if there is a directed s-v-path in the residual network of f.
-
Nested cuts
Assign an infinite capacity to all saturated edges in the residual network of f and iterate. Nested cuts can be combined with back cuts: We first compute S and \(\bar{S}\) and then compute nested cuts on both sets.
-
Creep flows
Add a small \(\varepsilon =10^{-8}\) to all capacities. This lets us find a minimum weight cut that cuts few edges. The creep flow variant works together with both nested cuts and back cuts.
-
Cut purging
Finally, it can be beneficial to remove cut-set inequalities from the relaxation if they have not been binding for a number of iterations.
It is not clear a priori which combination of these variants leads to the best performance of the algorithm. In a preliminary experiment, we evaluated all 16 combinations for all the formulations under consideration (the results are shown in Fig. 15 in the Appendix. To avoid overfitting, we tested on a random subset of the instances only. Back cuts were beneficial in all cases. The \(\mathrm {LP}^{\mathrm {sedc}}\) relaxation benefited from additional creep flows, while \(\mathrm {LP}^{\mathrm {dc}}\) worked best with additional nested cuts and purging. In all cases, we compute the maximum s-t-flows with a custom implementation of the push-relabel algorithm with the highest-label strategy and the gap heuristic [5, 17].
Additional valid inequalities Our analysis in Sect. 3.3 shows that \(\mathrm {LP}^{\mathrm {sedc}}\) can be strengthened with additional flow-balance and indegree constraints. Similar improvements can be made for the other LP-relaxations. To allow for a fair comparison, we incorporate these improvements and compare the (theoretically) strongest known versions of the LP-relaxations in the sequel: We obtain \(\mathrm {LP}^{\mathrm {mr^*}}\) by adding the flow-balance constraints
to \(\mathrm {LP}^{\mathrm {mr}}\). Likewise, we obtain a strengthened version \(\mathrm {LP}^{\mathrm {dc^*}}\) of \(\mathrm {LP}^{\mathrm {dc}}\) by adding the flow-balance constraints
Analogously, we strengthen \(\mathrm {LP}^{\mathrm {edc}}\) with
and obtain \(\mathrm {LP}^{\mathrm {edc^*}}\). Finally, we compare against \(\mathrm {LP}^{\mathrm {sedc^*}}\) as defined in Sect. 3.3.
Order of the terminal sets. The size of (\(\mathrm {IP}^{\mathrm {mr}}\)) depends on the order of the terminal sets and is minimized if—without loss of generality—the sets are sorted by decreasing size, i.e., such that \(|T^1| \ge \cdots \ge |T^K|\). The same holds for the running time of the separation procedures for the cut-set inequalities (6a) of (\(\mathrm {IP}^{\mathrm {sedc}}\)) and (8a) of (\(\mathrm {IP}^{\mathrm {edc}}\)), respectively. Therefore, in our experiments we index the terminal sets satisfying this decreasing order. A preliminary comparison to a version with the default terminal set order shows that this initial optimization makes solving the LP-relaxation of (\(\mathrm {IP}^{\mathrm {mr}}\)) more consistent and yields small improvements over the number of instances that could be solved to optimality; e.g., about 7% more instances could be solved. We remark that the order of the terminal sets might have an impact on the LP-bound as well, even though we did not observe significant changes in our experiments.
Improvement of the linear programming bound over the bound obtained from \(\mathrm {LP}^{\mathrm {uc}}\). The plots show the ratio of the best bound after 3600 seconds over the optimum bound from \(\mathrm {LP}^{\mathrm {uc}}\). The theoretical maximum improvement is 2. For the JMP instances and \(|V| \in \{25, 50\}\) all bounds are optimum; for \(|V|\in \{100, 200\}\) only the \(\mathrm {LP}^{\mathrm {edc^*}}\) and \(\mathrm {LP}^{\mathrm {sedc^*}}\) bounds are optimum. For \(|V| = 500\), about 75% of the \(\mathrm {LP}^{\mathrm {edc^*}}\) and \(\mathrm {LP}^{\mathrm {sedc^*}}\) and none of the \(\mathrm {LP}^{\mathrm {dc}}\) bounds are optimum
Time to solve the LP-relaxations One important factor for the practical usefulness of an IP formulation is the speed at which its LP-relaxation can be solved to optimality. We evaluate this speed in a computational experiment, comparing the state-of-the-art to our new formulations on the 580 JMP instances. Figure 11 shows how many LP-relaxations were solved to optimality after \(x\in [0,3600]\) seconds. After 3600 seconds, the relaxations \(\mathrm {LP}^{\mathrm {edc^*}}\), \(\mathrm {LP}^{\mathrm {sedc^*}}\), \(\mathrm {LP}^{\mathrm {dc^*}}\), and \(\mathrm {LP}^{\mathrm {mr^*}}\) were solved to optimality on 567, 554, 292, and 140 instances, respectively; moreover, the bulk of these instances is solved in the first 300 seconds. As observed before, \(\mathrm {LP}^{\mathrm {mr^*}}\) has exponential size and has to be solved as a static model, so that its poor performance is not surprising (in fact, it is in line with what Magnanti and Raghavan predict [25]). On the other hand, we would have expected a better performance of the \(\mathrm {LP}^{\mathrm {dc^*}}\) model. The \(\mathrm {LP}^{\mathrm {edc^*}}\) relaxation solves slightly more instances than the \(\mathrm {LP}^{\mathrm {sedc^*}}\) relaxation. This was to be expected, given the smaller size of \(\mathrm {LP}^{\mathrm {edc^*}}\).
Although not shown here, solving the non-starred variants of the formulations has had no significant impact on the solution times in our experiments. Furthermore, the relaxations \(\mathrm {LP}^{\mathrm {dc^*}}\), \(\mathrm {LP}^{\mathrm {edc^*}}\), and \(\mathrm {LP}^{\mathrm {sedc*}}\) can all be solved in less than a second on the 85 instances of the MR set whereas the optimum of \(\mathrm {LP}^{\mathrm {mr^*}}\) was reached on 46 MR instances in less than a second of time. We conclude that reliably solving the LP-relaxation is a major hurdle in some cases.
Quality of the LP-bounds Solving the LP-relaxation to optimality is not necessary as long as a “good-enough” bound is obtained. For instance, it is conceivable that a suboptimum bound from \(\mathrm {LP}^{\mathrm {mr^*}}\) is better than an optimum bound from \(\mathrm {LP}^{\mathrm {dc^*}}\) and further investigation is needed. To that aim, we solve the LP-relaxations with a time limit of 3600 seconds and take the best bound L found up to that point. We then compare L to the optimum LP bound of \(\mathrm {LP}^{\mathrm {uc}}\), i.e., \(L^{uc}\). Figure 12 shows the improvement \(L/L^{uc}\) in a box plot diagram (maximum, minimum, and quantiles). As the integrality gap of \(\mathrm {LP}^{\mathrm {uc}}\) is two, the maximum improvement is bounded by two as well. Our experiments complement the theoretical analysis from the previous section by quantifying how much stronger the new formulations are.
For the MR instance set, we observe that the bound from \(\mathrm {LP}^{\mathrm {sedc^*}}\) is comparable to the one from \(\mathrm {LP}^{\mathrm {mr^*}}\) on the smallest instances. For the largest instances, fewer optimum bounds are obtained from \(\mathrm {LP}^{\mathrm {mr^*}}\) so that \(\mathrm {LP}^{\mathrm {sedc^*}}\) has a smaller spread. The bounds from \(\mathrm {LP}^{\mathrm {dc^*}}\) are inferior to the ones from the other relaxations.
Being a large static model, \(\mathrm {LP}^{\mathrm {mr^*}}\) did not fit into the memory limit of 3 GB for the majority of the JMP instances. No bound could be obtained in these cases and we thus had to remove \(\mathrm {LP}^{\mathrm {mr^*}}\) from the comparison. On this instance set, the new relaxations \(\mathrm {LP}^{\mathrm {edc^*}}\) and \(\mathrm {LP}^{\mathrm {sedc^*}}\) provide comparable bounds (with \(\mathrm {LP}^{\mathrm {sedc^*}}\) seeming slightly stronger) and dominate the bounds from \(\mathrm {LP}^{\mathrm {dc^*}}\). A decrease in quality of the \(\mathrm {LP}^{\mathrm {dc^*}}\) bound can be observed for the larger instances. This is in part because fewer and fewer \(\mathrm {LP}^{\mathrm {dc^*}}\)-relaxations are solved to optimality. Here, the plotted bound is suboptimum. In an additional experiment, we evaluated the bounds from the lifted-cut relaxation [23] and found them to be identical to the bounds from \(\mathrm {LP}^{\mathrm {uc}}\) on both the JMP and the MR instance set.
Overall, we find that LP-bounds from \(\mathrm {LP}^{\mathrm {sedc^*}}\) are at least as good as the ones from the previously strongest relaxation \(\mathrm {LP}^{\mathrm {mr^*}}\). Yet, they can be computed more reliably.
4.2 Integrality gaps
We evaluate the integrality gap \((OPT_I - LP) / OPT_I\) (where \(OPT_I\) is the integer optimum and LP is the optimum of the LP-relaxation) of the formulations computationally in Fig. 13. The figure is coherent with Fig. 12: The integrality gap of the relaxations \(\mathrm {LP}^{\mathrm {mr^*}}\) and \(\mathrm {LP}^{\mathrm {sedc^*}}\) disappears on almost all instances. We also see that the bounds obtained from \(\mathrm {LP}^{\mathrm {edc^*}}\) indeed are weaker than the ones from \(\mathrm {LP}^{\mathrm {sedc^*}}\). The relaxation \(\mathrm {LP}^{\mathrm {dc^*}}\) has significantly larger integrality gaps than the other three relaxations, even for smaller instances where it can be solved to optimality.
4.3 Branch-and-bound
As a proof of concept, we implemented a branch-and-bound (B&B) scheme by letting CPLEX solve \(\mathrm {IP}^{\mathrm {mr^*}}\), \(\mathrm {IP}^{\mathrm {dc^*}}\), \(\mathrm {IP}^{\mathrm {edc^*}}\), and \(\mathrm {IP}^{\mathrm {sedc^*}}\) on the MR and the JMP instance set. We set a time and memory limit of 3600 seconds and 3 GB, respectively. In each B&B node, we solve the LP-relaxations as discussed previously, in particular, we separate cut-set-inequalities for the cut based formulations \(\mathrm {IP}^{\mathrm {dc^*}}\), \(\mathrm {IP}^{\mathrm {edc^*}}\), and \(\mathrm {IP}^{\mathrm {sedc^*}}\) in a branch-and-cut manner using CPLEX callbacks.
Solution progress Figure 14 gives an overview over the computational results. It shows how many of the 580 JMP instances were solved to optimality after x seconds. We observe that using \(\mathrm {IP}^{\mathrm {sedc^*}}\) leads to the largest number of instances solved. This is surprising when we compare to the results from the LP-experiment where the bounds of \(\mathrm {LP}^{\mathrm {edc^*}}\) and \(\mathrm {LP}^{\mathrm {sedc^*}}\) seemed on par while \(\mathrm {LP}^{\mathrm {edc^*}}\) was solved more reliably. Yet, \(\mathrm {IP}^{\mathrm {sedc^*}}\) seems better suited for a B&B scheme. The formulations \(\mathrm {IP}^{\mathrm {mr^*}}\) and \(\mathrm {IP}^{\mathrm {dc^*}}\) struggle to solve the instances to optimality. This observation agrees with the LP-experiment where already the LP-relaxations \(\mathrm {LP}^{\mathrm {mr^*}}\) and \(\mathrm {LP}^{\mathrm {dc^*}}\) were difficult to solve.
Layout of the detailed tables More detailed results are given in Tables 1 and 2. Each row of the tables is grouped in three parts and corresponds to a combination of an IP formulation and an instance class in which each instance has \(\mathbf {|V|}\) nodes and \(\mathbf {K}\) terminal sets, as shown in the first group of the row. The last column (#) in the first group contains the size of the instance class. The second group shows average values over those instances in each class that were solved to optimality. We show in the first column (#) of the second group how many instances were solved to optimality. The CPU column shows the average CPU time required for optimality to be proven while CPUR gives the cpu time required to solve the root node. The RG column provides the average root gap \((OPT - LP_r) / OPT\) where OPT is the optimum integer solution of an instance and \(LP_r\) is the dual bound at the end of the root node. As usual, the dual bound \(LP_r\) may be different from the optimum value of the LP-relaxation if CPLEX decides to branch early in view of the time limit or tailing off effects. Finally, BN shows the average number of processed branch-and-bound nodes. Again, all averages are over solved instances only. The third column group gives averages for those instances that could not be solved to optimality. Its first column (#) shows how many instances could not be solved, but still provided a non-trivial dual bound (for this reason, the number of solved/unsolved instances does not add up to the total number of instances in some cases). The second column GAP provides the average gap \((OPT-LP) / OPT\) where LP is the global dual bound after 3600 seconds. The CPUR and BN columns again show the root gap and number of B&B nodes processed. We do not know the optima for 13 of the largest instances and removed those instances from the comparison.
Details on the MR instances We see in Table 1 that the cut-based IP formulations solve all MR instances with ease. For \(\mathrm {IP}^{\mathrm {sedc^*}}\), the root relaxation is integral in all cases. For \(\mathrm {IP}^{\mathrm {edc^*}}\), we need to process a small B&B tree, whereas \(\mathrm {IP}^{\mathrm {dc^*}}\) needs to close a much larger gap and considerably more branching is needed. We fail to solve all the instances to optimality with \(\mathrm {IP}^{\mathrm {mr^*}}\): The memory limit is not always sufficient to build the IP model. However, wherever \(\mathrm {IP}^{\mathrm {mr^*}}\) is successful, little branching is needed and the root gap is small. Similar observations where made in [25].
Details on the JMP instances Table 2 provides detailed B&B results on the JMP instances. As before, the B&B based on \(\mathrm {IP}^{\mathrm {mr^*}}\) struggles with the larger instances but seems to profit from tight bounds and small B&B trees wherever it is successful. The \(\mathrm {IP}^{\mathrm {dc^*}}\)-based B&B shows the opposite behaviour: In comparison, it needs to close larger gaps and processes larger B&B trees. However, it is more successful than \(\mathrm {IP}^{\mathrm {mr^*}}\). In part, this is due to the high throughput of the algorithm: It processes more B&B nodes per second than any other algorithm in the comparison—at least on the small and medium sized instances. On the larger instances, \(\mathrm {IP}^{\mathrm {dc^*}}\) struggles to solve the root relaxations and consequently has little opportunity to close the significant gaps.
The B&B based on \(\mathrm {IP}^{\mathrm {edc^*}}\) solves instances with up to 200 nodes and up to 10 terminal sets reliably. Despite the relatively small root gap, many of the larger instances pose a challenge for the algorithm. We observe that even though \(\mathrm {IP}^{\mathrm {edc^*}}\) spends little time at the root node, it processes few B&B nodes. This seems to prohibit closing the gap entirely on the large instances, even though the algorithm gets close (within 5%) to the optimum solution—as opposed to \(\mathrm {IP}^{\mathrm {dc^*}}\) with a final gap of 20–40%.
Finally, the \(\mathrm {IP}^{\mathrm {sedc^*}}\) based B&B solves all instances with up to 200 nodes in less than a minute. We confirm that the root relaxation on these instances is tight, as the algorithm requires little branching (less than 3 nodes on average). However, we observe some failures on the larger instances; in particular, the algorithm fails to solve the root relaxation on some of the instances with 500 nodes and 35/50 terminal sets. On the unsolved instances with 500 nodes, a large part of the computation time is spent at the root node, leaving little time for branching. Comparing the root gaps to the integrality gaps in Fig. 13 it becomes appearent that CPLEX branches prematurly.
5 Conclusion and outlook
We answer a long-standing open problem by Magnanti and Raghavan [25] and give a cut-based ILP formulation for the Steiner forest problem which is stronger than the classical undirected and directed models. Actually, our new model is even stronger than the improved flow model by [25] and hence, it is the strongest known model for the SFP. The computational study shows that our new branch-and-bound algorithm works very well and its performance seems to be due to the strong bounds obtained from the new formulation \(\mathrm {IP}^{\mathrm {sedc^*}}\). While its relaxation \(\mathrm {LP}^{\mathrm {sedc^*}}\) is solved less quickly than the simplified relaxation \(\mathrm {LP}^{\mathrm {edc^*}}\), its stronger bounds seem to pay off overall.
On the theoretical side, we would like to obtain an LP relaxation with an integrality gap of less than 2. This problem is not solved by \(\mathrm {LP}^{\mathrm {sedc^*}}\): We observe that it coincides with \(\mathrm {LP}^{\mathrm {dc}}\) if \(K=1\). On the other hand, we are able to give a stronger lower bound of 1.5 for the integrality gap. This is a clear improvement over the Steiner tree problem where the gap of the directed models is somewhere between 1.161 and 2.
The relationship to the Steiner tree problem raises some further questions and directions for future research. Since both the Steiner tree problem [30] and the Steiner forest problem [3] are solvable in polynomial time on series-parallel graphs (graphs of treewidth at most 2, partial 2-trees) and there exists a full description of the Steiner tree polytope for this type of graphs [13, 26], the existence of such a model for the SFP is an open problem. Notice that \(\mathrm {LP}^{\mathrm {sedc^*}}\) does not have the property: inserting an edge between the terminals of the second set in instance B of Fig. 1 gives an example where \(\mathrm {LP}^{\mathrm {sedc^*}}\) selects all edges at 0.5. We remark that this instance was already given by [25].
Finally, the polyhedra of our new models and the constraints should be investigated. For example, are the directed cuts facet-defining and are there further strengthening and facet-defining constraints?
Change history
04 May 2021
A Correction to this paper has been published: https://doi.org/10.1007/s10107-021-01648-9
References
Agrawal, A., Klein, P., Ravi, R.: When trees collide: an approximation algorithm for the generalized Steiner problem on networks. SIAM J. Comput. 24(3), 440–456 (1995)
Balakrishnan, A., Magnanti, T.L., Wong, R.T.: A dual-ascent procedure for large-scale uncapacitated network design. Oper. Res. 37(5), 716–740 (1989)
Bateni, M., Hajiaghayi, M.T., Marx, D.: Approximation schemes for Steiner forest on planar graphs and graphs of bounded treewidth. J. ACM 58(5), 21:1–21:37 (2011)
Byrka, J., Grandoni, F., Rothvoß, T., Sanità, L.: Steiner tree approximation via iterative randomized rounding. J. ACM 60(1), 1–33 (2013)
Cherkassky, B.V., Goldberg, A.V.: On implementing the push-relabel method for the maximum flow problem. Algorithmica 19(4), 390–410 (1997)
Chimani, M., Gutwenger, C., Jünger, M., Klau, G.W., Mutzel, P.: The Open Graph Drawing Framework (OGDF). In: Tamassia, R. (ed.) Handbook of Graph Drawing and Visualization, Discrete Mathematics and Its Applications, pp. 543–569. Chapman and Hall, London (2016)
Chlebík, M., Chlebíková, J.: The Steiner tree problem on graphs: inapproximability results. Theor. Comput. Sci. 406(3), 207–214 (2008)
Chopra, S., Gorres, E.R., Rao, M.R.: Solving the Steiner tree problem on a graph using branch and cut. ORSA J. Comput. 4(3), 320–335 (1992)
Chopra, S., Rao, M.R.: The Steiner tree problem I: formulations, compositions and extension of facets. Math. Prog. 64(1), 209–229 (1994)
Chopra, S., Rao, M.R.: The Steiner tree problem II: properties and classes of facets. Math. Prog. 64(1–3), 231–246 (1994)
Daneshmand, S.: Algorithmic approaches to the Steiner problem in networks. Ph.D. thesis, Universität Mannheim (2003)
Edmonds, J.: Submodular functions, matroids, and certain polyhedra. In: Jünger, M., Reinelt, G., Rinaldi, G. (eds.) Combinatorial Optimization-Eureka, You Shrink!, no. 2570 in LNCS, pp. 11–26. Springer, Berlin (2003)
Goemans, M.X.: Arborescence polytopes for series-parallel graphs. Discrete Appl. Math. 51(3), 277–289 (1994)
Goemans, M.X.: The Steiner tree polytope and related polyhedra. Math. Prog. 63(1–3), 157–182 (1994)
Goemans, M.X., Myung, Y.S.: A catalog of Steiner tree formulations. Networks 23(1), 19–28 (1993)
Goemans, M.X., Williamson, D.: A general approximation technique for constrained forest problems. SIAM J. Comput. 24(2), 296–317 (1995)
Goldberg, A.V., Tarjan, R.E.: A new approach to the maximum-flow problem. J. ACM 35(4), 921–940 (1988)
Groß, M., Gupta, A., Kumar, A., Matuschke, J., Schmidt, D.R., Schmidt, M., Verschae, J.: A local-search algorithm for Steiner forest. In: A.R. Karlin (ed.) 9th Innovations in Theoretical Computer Science Conference (ITCS 2018), Leibniz International Proceedings in Informatics (LIPIcs), vol. 94, pp. 31:1–31:17. Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik (2018)
Gupta, A., Kumar, A.: Greedy algorithms for steiner forest. In: Proceedings of the Forty-Seventh Annual ACM on Symposium on Theory of Computing, STOC ’15, pp. 871–878. ACM (2015)
Jain, K.: A factor 2 approximation algorithm for the generalized Steiner network problem. Combinatorica 21(1), 39–60 (2001)
Johnson, D.S., Minkoff, M., Phillips, S.: The prize collecting Steiner tree problem: theory and practice. In: Proceedings of the Symposium on Discrete Algorithms, SODA ’00, pp. 760–769. SIAM (2000)
Koch, T., Martin, A.: Solving Steiner tree problems in graphs to optimality. Networks 32(3), 207–232 (1998)
Könemann, J., Leonardi, S., Schäfer, G., van Zwam, S.: A group-strategyproof cost sharing mechanism for the Steiner forest game. SIAM J. Comput. 37(5), 1319–1341 (2008)
Lucena, A.: Tight bounds for the Steiner problem in graphs. Technical report, RC for Process Systems Engineering, Imperial College, London (1993)
Magnanti, T.L., Raghavan, S.: Strong formulations for network design problems with connectivity requirements. Networks 45, 61–79 (2005)
Margot, F., Prodon, A., Liebling, T.M.: Tree polytope on 2-trees. Math. Prog. 63(1–3), 183–191 (1994)
Polzin, T.: Algorithms for the Steiner problem in networks. Ph.D. thesis, Universität des Saarlandes (2004)
Polzin, T., Daneshmand, S.: A comparison of Steiner tree relaxations. Discrete Appl. Math. 112(1–3), 241–261 (2001)
Schmidt, D.R., Zey, B., Margot, F.: An exact algorithm for the Steiner forest problem. In: Azar, Y., Bast, H., Herman, G. (eds.) 26th Annual European Symposium on Algorithms (ESA), LIPIcs, vol. 112, pp. 70:1–70:14. Schloss Dagstuhl, Helsinki (2018). https://doi.org/10.4230/LIPIcs.ESA.2018.70
Wald, J.A., Colbourn, C.J.: Steiner trees, partial 2-trees and minimum IFI networks. Networks 13, 159–167 (1983)
Acknowledgements
We thank the anonymous referees for their helpful comments and suggestions that helped to improve the article. The first author was supported by a fellowship within the Postdoc-Program of the German Academic Exchange Service (DAAD).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original version of this article was revised due to a retrospective Open Access order.
A preliminary version of this work has appeared in [29].
Appendix
Appendix
See Fig. 15.
Preliminary experiment on a random subset of the instances. The plots show all possible parameter combinations of back cuts (B), creep flows (C), nested cuts (N) and cut purging (P). Each row corresponds to one LP relaxation. The last picture plots the 6 best variants from each previous plot against each other
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schmidt, D., Zey, B. & Margot, F. Stronger MIP formulations for the Steiner forest problem. Math. Program. 186, 373–407 (2021). https://doi.org/10.1007/s10107-019-01460-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-019-01460-6


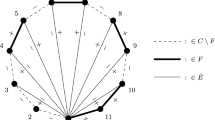

 ,
,  ,
,  , and
, and  ). All edges have unit cost
). All edges have unit cost












