Exploiting partial correlations in distributionally robust optimization

Abstract

In this paper, we identify partial correlation information structures that allow for simpler reformulations in evaluating the maximum expected value of mixed integer linear programs with random objective coefficients. To this end, assuming only the knowledge of the mean and the covariance matrix entries restricted to block-diagonal patterns, we develop a reduced semidefinite programming formulation, the complexity of solving which is related to characterizing a suitable projection of the convex hull of the set $\{(\mathbf x , \mathbf x {} \mathbf x '): \mathbf x \in \mathcal {X}\}$ where $\mathcal {X}$ is the feasible region. In some cases, this lends itself to efficient representations that result in polynomial-time solvable instances, most notably for the distributionally robust appointment scheduling problem with random job durations as well as for computing tight bounds in the newsvendor problem, project evaluation and review technique networks and linear assignment problems. To the best of our knowledge, this is the first example of a distributionally robust optimization formulation for appointment scheduling that permits a tight polynomial-time solvable semidefinite programming reformulation which explicitly captures partially known correlation information between uncertain processing times of the jobs to be scheduled. We also discuss extensions where the random coefficients are assumed to be non-negative and additional overlapping correlation information is available.

Appendices

Appendix A: On the structure of a worst-case distribution

In this section, we exhibit a probability distribution for $\tilde{\mathbf{c }}$ that attains the optimal value $Z^*$ of (7). The construction is along the lines of the worst case distribution proposed in proof of Theorem 1—step 2 of [43]. The worst-case distribution we identify in particular is a mixture of normal distributions. Each of these normal distributions is in turn constructed by first constructing suitable marginal distributions and then applying conditional independence.

We begin with a result on psd matrix factorization in [43]. The following definition of Moore–Penrose pseudoinverse (see [48, 50]) is useful in stating the psd matrix factorization in Lemma 6. Let $\mathbf X$ be a matrix of dimension $k_1 \times k_2$. Then the Moore–Penrose pseudoinverse of $\mathbf X$ is a matrix $\mathbf X ^\dagger$ of dimension $k_2 \times k_1$ and is defined as a unique solution to the set of four equations:

$$\begin{aligned} \mathbf X {} \mathbf X ^\dagger \mathbf X = \mathbf X , \quad \mathbf X ^\dagger \mathbf X \mathbf X ^\dagger = \mathbf X ^\dagger , \quad \mathbf X {} \mathbf X ^\dagger = (\mathbf X {} \mathbf X ^\dagger )', \quad \text { and } \quad \mathbf X ^\dagger \mathbf X = (\mathbf X ^\dagger \mathbf X )'. \end{aligned}$$

Theorem 6

 [43, Theorem 1] Suppose that $\mathbf L$ is a $(k_1 + k_2) \times (k_1+k_2)$ positive semidefinite block matrix of the form,

$$\begin{aligned} \mathbf L =\begin{bmatrix} \mathbf A&\quad \mathbf B ' \\ \mathbf B&\quad \mathbf C \end{bmatrix} \succeq 0, \end{aligned}$$

(52)

where the matrices $\mathbf A \in \mathbb {R}^{k_1 \times k_1}, \mathbf C \in \mathbb {R}^{k_2 \times k_2}$ are symmetric and the matrix $\mathbf C$ admits an explicit factorization given by $\mathbf C = \mathbf V {} \mathbf V '$. Then $\mathbf L$ admits the following factorization:

$$\begin{aligned} \mathbf L = \begin{bmatrix} \mathbf B '(\mathbf V ^{\dagger })' \\ \mathbf V \end{bmatrix} \begin{bmatrix} \mathbf B '(\mathbf V ^{\dagger })' \\ \mathbf V \end{bmatrix}' + \begin{bmatrix} \mathbf U \\ 0 \end{bmatrix}\begin{bmatrix} \mathbf U \\ 0 \end{bmatrix}', \end{aligned}$$

(53)

where the matrix $\mathbf U$ is defined such that $\mathbf A - \mathbf B '{} \mathbf C ^{\dagger }{} \mathbf B = \mathbf U U ' \succeq 0$.

For a given partition $\{\mathcal {N}_r: r \in [R\,]\}$ and projected covariance matrices $\{{\varvec{\Pi }}^r: r \in [R\,]\}$, suppose that $\{\mathbf{p}_*, \mathbf{X}_*^r, \mathbf{Y}^r_*: r \in [R]\}$ maximizes (7). As in the proof of Theorem 1, it follows from Carathéodory’s theorem and the convex hull constraint in (7) that there exists $\hat{\mathcal {X}}$, a subset of $\mathcal {X}$, containing at most $1+\sum _r (n_r^2 + 3n_r)/2$ elements such that,

$$\begin{aligned} \left( \mathbf p _*,\mathbf X ^1_*, \ldots , \mathbf X ^R_* \right) = \sum _\mathbf{x \in \hat{\mathcal {X}}}\alpha _\mathbf x \left( \mathbf x ,\ \mathbf x ^1\mathbf{x ^1}', \ldots ,\mathbf x ^R \mathbf{x ^R}' \right) , \end{aligned}$$

for some $\{\alpha _\mathbf{x }: \mathbf x \in \hat{\mathcal {X}}\}$ satisfying $\alpha _\mathbf x \ge 0$, $\sum _\mathbf{x \in \hat{\mathcal {X}}} \alpha _\mathbf{x } = 1$. Consequently, for any $r \in [R\,]$, we have from Lemma 6 that,

$$\begin{aligned} \begin{bmatrix} {\varvec{\Pi }}^r&\quad {\varvec{\mu }^r}&\quad \mathbf{Y _*^r}' \\ {\varvec{\mu }^r}'&\quad 1&\quad \mathbf{p _*^r}'\\ \mathbf Y _*^r&\quad \mathbf p _*^r&\quad \mathbf X _*^r \end{bmatrix}&= \sum \limits _\mathbf{x \in \hat{\mathcal {X}}} \alpha _\mathbf{x } \begin{bmatrix} {\varvec{\Pi }}^r&\quad {\varvec{\mu }^r}&\quad \mathbf{Y _*^r}' \\ {\varvec{\mu }^r}'&\quad 1&\quad \mathbf{x ^r}'\\ \mathbf Y _*^r&\quad \mathbf x ^r&\quad \mathbf x ^r \mathbf{x ^r}' \end{bmatrix} \nonumber \\&= \sum \limits _\mathbf{x \in \hat{\mathcal {X}}} \alpha _\mathbf{x } \begin{bmatrix} \mathbf d _r(\mathbf x ^r)\\1\\ \mathbf x ^r \end{bmatrix} \begin{bmatrix} \mathbf d _r(\mathbf x ^r)\\1\\ \mathbf x ^r \end{bmatrix}' + \begin{bmatrix} {\varvec{\Phi }}_{r}&\quad \mathbf 0 _{n_r,1}&\quad \mathbf 0 _{n_r,n_r} \\ \mathbf 0 _{1,n_r}&\quad 0&\quad \mathbf 0 _{1,n_r} \\ \mathbf 0 _{n_r,n_r}&\quad 0&\quad \mathbf 0 _{n_r,n_r} \\ \end{bmatrix}, \end{aligned}$$

(54)

where $\mathbf d _r(\mathbf x ^r)\in \mathbb {R}^{n_r}$ and ${\varvec{\Phi }}_r \in \mathcal {S}_{n_r}^+$ for every $r \in [R\,]$. From the above factorization, observe that,

$$\begin{aligned} trace(\mathbf Y ^r_*) = trace\left( \sum _{x \in \hat{\mathcal {X}}} \alpha _\mathbf{x }{} \mathbf x ^r\mathbf d _r(\mathbf x ^r)'\right) = \sum _{x \in \hat{\mathcal {X}}} \alpha _\mathbf{x } \sum _{r = 1}^R \mathbf d _r(\mathbf x ^r)' \mathbf{x ^r}. \end{aligned}$$

(55)

For completeness, we will now list explicitly the expressions for the means $\mathbf d _r(\mathbf x ^r)$ and ${\varvec{\Phi }}_{\mathbf{r}}$. These expressions are obtained by making appropriate substitutions as per Theorem 6. For every $r \in [R]$, define the matrix $\mathbf V _r$ of size $(n_r + 1) \times m_r$ where $m_r$ is the number of points in the projected space $\mathcal {X}^r$ as follows.

$$\begin{aligned} \mathbf V _r = \begin{bmatrix} \ldots&\quad \sqrt{\alpha _r(\mathbf x ^r)}&\quad \ldots \\ \vdots&\quad \sqrt{\alpha _r(\mathbf x ^r) }{} \mathbf x ^r&\quad \vdots \end{bmatrix} \end{aligned}$$

Each column of $\mathbf V _r$ corresponds to an element $\mathbf x ^r$ of $\mathcal {X}^r$ and is of the form $\begin{bmatrix}\sqrt{\alpha _r(\mathbf x ^r)} \\ \sqrt{\alpha _r(\mathbf x ^r) }{} \mathbf x ^r \end{bmatrix}$. Define ${\varvec{\Phi }}_r$ of size $n_r \times n_r$ as:

$$\begin{aligned} {\varvec{\Phi }}_r = {\varvec{\Pi }}^r - [\varvec{\mu }^r \quad \hat{\mathbf{Y }}_*^r]\begin{bmatrix} 1&\quad \sum _\mathbf{x ^r} \alpha _r(\mathbf x ^r) (\mathbf x ^{r})'\\ \sum _\mathbf{x ^r}\alpha _r(\mathbf x ^r) \mathbf x ^{r}&\quad \sum _\mathbf{x ^r}\alpha _r(\mathbf x ^r) \mathbf x ^{r} (\mathbf x ^{r})' \end{bmatrix}^{\dagger } \begin{bmatrix} \varvec{\mu }^r \\ \hat{\mathbf{Y }}_*^r \end{bmatrix} \end{aligned}$$

The mean vector $\mathbf d _{r}(\mathbf x _r)$ is set to be the column vector of the matrix $\begin{bmatrix} \varvec{\mu }^r&\quad \hat{\mathbf{Y }}_*^r \end{bmatrix}(\mathbf V _r^{\dagger })'\times 1/\sqrt{\alpha _{r}(\mathbf x ^r})$ corresponding to where $\mathbf x _r$ occurs in $\mathbf V _r$.

Proposition 2

Suppose that $\{\mathbf{p}_*, \mathbf{X}_*^r, \mathbf{Y}^r_*: r \in [R]\}$ maximizes (7). Let $\hat{\mathcal {X}} \subseteq \mathcal {X}$ be a finite subset and $\{\alpha _\mathbf{x }: \mathbf x \in \hat{\mathcal {X}}\}$ satisfy (54). Let $\theta ^*$ be the distribution of $\tilde{\mathbf{c }}$ generated as follows:

• Step 1: Generate a random vector $\tilde{\mathbf{x }} \in \hat{\mathcal {X}} \subseteq \mathcal {X}$ such that $P(\tilde{\mathbf{x }} = \mathbf x ) = \alpha _\mathbf{x }$.

• Step 2: For every $r \in [R\,]$, independently generate a normally distributed random vector $\tilde{\mathbf{z }}_r \in \mathbb {R}^{n_r}$, conditionally on $\mathbf{x }$, with mean $\mathbf d _r(\mathbf x ^r)$ and covariance ${\varvec{\Phi }}_{\mathbf{r}}$. Set $\tilde{\mathbf{c }}^r = \tilde{\mathbf{z }}_r$.

Then $\theta ^*$ attains the maximum in (2).

Proof

Consider $(\tilde{\mathbf{x }} ,\tilde{\mathbf{c }})$ generated jointly according to the described steps. Then it follows from the law of iterated expectations that, $\mathbb {E}[f(\tilde{\mathbf{c }})] = \mathbb {E}[ \mathbb {E}[f(\tilde{\mathbf{c }}) \vert \tilde{\mathbf{x }} ] = \sum _\mathbf{x \in \hat{\mathcal {X}}}\alpha _\mathbf{x }\mathbb {E}[f(\tilde{\mathbf{c }}) \vert \tilde{\mathbf{x }} = \mathbf x ]$, for any function f. As a result, we have from (54) that for any $r \in [R\,]$,

$$\begin{aligned} \mathbb {E} \begin{bmatrix} \tilde{\mathbf{c }}^r \\ 1 \end{bmatrix}\begin{bmatrix} \tilde{\mathbf{c }}^r \\ 1 \end{bmatrix}'&= \sum _\mathbf{x \in \hat{\mathcal {X}}} \alpha _ \mathbf{x } \begin{bmatrix} \mathbf d _r(\mathbf x ^r)\mathbf d _r(\mathbf x ^r)' + {\varvec{\Phi }}_r&\quad \mathbf d _r(\mathbf{x ^r})\\ \mathbf{d _r(\mathbf x ^r)}'&\quad 1 \end{bmatrix} = \begin{bmatrix} {\varvec{\Pi }}^r&\quad \varvec{\mu }^r\\ {\varvec{\mu }^r}'&\quad 1 \end{bmatrix}. \end{aligned}$$

(56)

Moreover, as $\tilde{\mathbf{x }}\in \mathcal {X}$, the objective $\mathbb {E}[\max _\mathbf{x \in \mathcal {X}}\tilde{\mathbf{c }}'{} \mathbf x ]$ satisfies,

$$\begin{aligned} Z^*&\ge \mathbb {E}\left[ \max _\mathbf{x \in \mathcal {X}}\tilde{\mathbf{c }}'{} \mathbf x \right] \ge \mathbb {E}[\tilde{\mathbf{c }}'\tilde{\mathbf{x }}] = \mathbb {E}\left[ \mathbb {E}\left[ \tilde{\mathbf{c }} \, \vert \, \tilde{\mathbf{x }} \right] ' \tilde{\mathbf{x }}\right] = \mathbb {E}\left[ \sum _{r=1}^R \mathbb {E}\left[ \tilde{\mathbf{c }}^r \, \vert \, \tilde{\mathbf{x }} \right] ' \tilde{\mathbf{x }}^r \right] \\&= \mathbb {E}\left[ \sum _{r=1}^R \mathbf d _r(\tilde{\mathbf{x }}^r)' \tilde{\mathbf{x }}^r \right] = \sum _\mathbf{x \in \mathcal {X}} \alpha _\mathbf{x } \sum _{r=1}^{R} \mathbf d _{r}(\mathbf x ^r)'{} \mathbf x ^r = \sum _{r=1}^{R} trace(\hat{\mathbf{Y }}^r_*) = \hat{Z}^*= Z^*, \end{aligned}$$

where the last three equalities follow, respectively, from (55), the optimality of $\{\mathbf{p}_*, \mathbf{X}_*^r, \mathbf{Y}_*^r: r \in [R\,]\}$ for (7), and Theorem 1. Combining this observation with (56), we have that the distribution of $\tilde{\mathbf{c }}$, denoted by $\theta ^*$, is feasible and it attains the maximum in (2). $\square$

The generation of the normal distributions for each of $\tilde{\mathbf{c }}^r$ and the mixture proportions $\alpha _\mathbf{x }$ are both identical to [43]. The difference is that in step 2 above, the joint distributions over the whole vector $\tilde{\mathbf{c }}$ is the independent distribution on $\tilde{\mathbf{c }}^r, \, r \in [R\,]$ conditional on $\mathbf x$. Note that in [43], this additional step of constructing a joint distribution was not required as the whole vector $\tilde{\mathbf{c }}$ was entirely generated at once.

Appendix B: Reasoning for gap in bounds produced by formulation (48)

In this section we investigate why the formulation (48) does not necessarily provide tight bounds for $Z^*_{\mathrm{series}}$.

Using a similar reasoning in proof of Theorem 1, Step 1, we can show that $Z^*_{\mathrm{series}} \le \hat{Z}^{*}_{\mathrm{series}}$. However a similar adoption of Step 2, proof of Theorem 1 to check $Z^*_{\mathrm{series}} \ge \hat{Z}_{\mathrm{series}}$ does not go through, unfortunately. To see this, let $\mathbf p ^*, \mathbf X ^{*}, \mathbf Y ^{*}$ be an optimal solution to formulation (48) and let us attempt to construct a solution $\bar{\mathbf{p }}, \bar{\mathbf{X }}, \bar{\mathbf{Y }}, \bar{{\varvec{\Delta }}}$ feasible to (47) such that $trace(\bar{\mathbf{Y }}) = \hat{Z}^*_{\mathrm{series}} = \sum _{i=1}^n trace(\mathbf Y ^{*}_{ii})$.

Construction of $\bar{\mathbf{p }}$ and $\bar{\mathbf{X }}$: Analogous to proof of Theorem 1, step 2.

Construction of $\bar{\mathbf{Y }}$ and $\bar{{\varvec{\Delta }}}$:

Set $\bar{Y}_{ii} = Y_{ii}, \bar{Y}_{i,i+1} = Y_{i,i+1}, \bar{Y}_{i+1,i} =Y_{i+1,i}$ and $\bar{\varDelta }_{ii} = \varPi _{ii}$, $\bar{\varDelta }_{i,i+1} =\varPi _{i,i+1}$.

As before, consider a $(2n+1) \times (2n+1)$ partial symmetric matrix $\mathbf L _p$ constructed using the analogous partial matrices $\bar{\mathbf{Y }}_p$ (with entries $\bar{Y}_{ii}$ and $\bar{Y}_{i,i+1}$ described above), $\bar{{\varvec{\Delta }}}_p$(with entries $\bar{\varDelta }_{ii}$ and $\bar{\varDelta }_{i,i+1}$ described above) and the fully specified matrix $\bar{\mathbf{X }}$ as follows:

$$\begin{aligned} \bar{\mathbf{L }}_p&= \begin{bmatrix} 1&\quad \varvec{\mu }'&\quad \bar{\mathbf{p }}' \\ \varvec{\mu }&\quad \bar{{\varvec{\Delta }}}_p&\quad \bar{\mathbf{Y }}_p\\ \bar{\mathbf{p }}&\quad {\bar{\mathbf{Y }}_p}'&\quad \bar{\mathbf{X }}\\ \end{bmatrix}\\&= \left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} 1 &{} \mu _1 &{} \mu _2 &{} \mu _3 &{} \mu _4 &{} \mu _5 &{} \ldots &{} p^*_1 &{} p^*_2 &{} p^*_3 &{} p^*_4 &{} \ldots \\ \mu _1 &{} \varPi _{11} &{} \varPi _{12} &{} ? &{} ? &{} ?&{} \ldots &{} Y^*_{11} &{} Y^*_{12} &{} ? &{} ? &{} \ldots \\ \mu _2 &{} \varPi _{21} &{} \varPi _{22} &{} \varPi _{23} &{} ? &{} ? &{} \ldots &{} Y^*_{21} &{} Y^*_{12} &{} Y^*_{23}&{} ?\\ \mu _3 &{} ? &{} \varPi _{32} &{} \varPi _{33} &{} \varPi _{34} &{} ? &{} \ldots &{} ? &{} Y^*_{32} &{} Y^*_{33}&{} Y^*_{34} &{} ?\ldots \\ \mu _4 &{} ? &{} ? &{} \varPi _{43} &{} \varPi _{44} &{} \varPi _{45} &{} ?\ldots &{} ? &{} ? &{} Y^*_{43} &{} Y^*_{44} &{} \ldots \\ &{}\vdots &{} &{} \vdots &{}&{}&{} \vdots &{} &{}&{} \vdots \\ p^*_1&{} Y^*_{11} &{} Y^*_{21} &{} ? &{} ? &{} ? \ldots &{} &{} &{} &{}\\ p^*_2 &{} Y^*_{12} &{} Y^*_{22} &{} Y^*_{32} &{} ? &{} ? \ldots &{} &{} &{}&{}&{} &{} \\ p^*_3&{}? &{} Y^*_{23} &{} Y^*_{33} &{}Y^*_{43} &{} ? \ldots &{} &{} &{} \bar{\mathbf{X }}&{}\\ p^*_4&{}? &{} ? &{} Y^*_{34} &{}Y^*_{44} &{} Y^*_{54} \ldots &{} &{} &{} &{} \\ &{}\vdots &{} &{} \vdots &{}&{}&{} \vdots &{} &{}&{} \\ \end{array}\right] \end{aligned}$$

We note that the fully specified principal submatrices of $\bar{\mathbf{L }}_p$ are exactly the matrices that appear in the positive semidefinite constraints in formulation (48) and are therefore guaranteed to be positive-semidefinite. Similar to proof of Theorem 1, if the partial matrix $\bar{\mathbf{L }}_p$ can be shown to admit a completion $\bar{\mathbf{L }}_{\mathrm{comp}}$ such that $\bar{\mathbf{L }}_{\mathrm{comp}} \succeq 0$ then the rest of the entries in $\bar{\mathbf{Y }}$ and $\bar{{\varvec{\Delta }}}$ can be computed. However in this stage, the analogous graph constructed as in Lemma 3 is not chordal (refer to Fig. 10). Since the graph constructed is not chordal, the construction of a positive semidefinite completion cannot be guaranteed. Therefore the bound $\hat{Z}^*_{\mathrm{series}}$ is not necessarily tight. However it may be used as a polynomial time computable upper bound for $Z^*_{\mathrm{series}}$. Whether $Z^*_{\mathrm{series}}$ can be solved in polynomial time or not, is an interesting open question.

Fig. 10

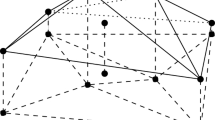
Illustration of a graph G for the case where $n=4$ and the moments corresponding to $\{\{1,2\},\{2,3\},\{3,4\}\}$ are known. The whole graph additionally includes a vertex s connected to all the nodes in the graph and is omitted here for clarity. Consider a subgraph formed by the vertices $\{c_2, x_1, x_4, c_3\}$. The edges induced by this subset of vertices are shown in red. These edges form a chordless cycle and therefore the graph is not chordal (color figure online)