Abstract
Beck and Teboulle’s FISTA method for finding a minimizer of the sum of two convex functions, one of which has a Lipschitz continuous gradient whereas the other may be nonsmooth, is arguably the most important optimization algorithm of the past decade. While research activity on FISTA has exploded ever since, the mathematically challenging case when the original optimization problem has no minimizer has found only limited attention. In this work, we systematically study FISTA and its variants. We present general results that are applicable, regardless of the existence of minimizers.
Similar content being viewed by others
References
Attouch, H., Cabot, A.: Convergence rates of inertial forward-backward algorithms. SIAM J. Optim. 28, 849–874 (2018)
Attouch, H., Cabot, A., Chbani, Z., Riahi, H.: Inertial forward-backward algorithms with perturbations: application to Tikhonov regularization. J. Optim. Theory Appl. 179, 1–36 (2018)
Attouch, H., Chbani, Z., Peypouquet, J., Redont, P.: Fast convergence of inertial dynamics and algorithms with asymptotic vanishing viscosity. Math. Program. Ser. B 168, 123–175 (2018)
Attouch, H., Chbani, Z., Riahi, H.: Rate of convergence of the Nesterov accelerated gradient method in the subcritical case \(\alpha \le 3\). ESAIM Control Optim. Calc. Var. (2019). https://doi.org/10.1051/cocv/2017083
Attouch, H., Peypouquet, J.: The rate of convergence of Nesterov’s accelerated forward-backward method is actually faster than \(1/k^2\). SIAM J. Optim. 26, 1824–1834 (2016)
Attouch, H., Peypouquet, J., Redont, P.: Fast convergence of an inertial gradient-like system with vanishing viscosity. (2015) arXiv:1507.04782
Aujol, J.-F., Dossal, C.: Stability of over-relaxations for the forward-backward algorithm, application to FISTA. SIAM J. Optim. 25, 2408–2433 (2015)
Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces, second edn. Springer, New York (2017)
Beck, A.: First-Order Methods in Optimization. SIAM, Philadelphia (2017)
Beck, A., Teboulle, M.: Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans. Image Process. 18, 2419–2434 (2009)
Beck, A., Teboulle, M.: A fast iterative shrinkage-thresholding algorithm for linear inverse problem. SIAM J. Imaging Sci. 2, 183–202 (2009)
Bello Cruz, J.Y., Nghia, T.T.A.: On the convergence of the forward-backward splitting method with linesearches. Optim. Methods Softw. 31, 1209–1238 (2016)
Bredies, K.: A forward-backward splitting algorithm for the minimization of non-smooth convex functionals in Banach space. Inverse Probl. 25, 015005 (2009)
Bruck, R.E., Reich, S.: Nonexpansive projections and resolvents of accretive operators in Banach spaces. Houst. J. Math. 3, 459–470 (1977)
Chambolle, A., Dossal, C.: On the convergence of the iterates of the “fast iterative shrinkage/thresholding algorithm”. J. Optim. Theory Appl. 166, 968–982 (2015)
Chambolle, A., Pock, T.: An introduction to continuous optimization for imaging. Acta Numer. 25, 161–319 (2016)
Combettes, P.L.: Quasi-Fejérian analysis of some optimization algorithms. In: Butnariu, D., Censor, Y., Reich, S. (eds.) Inherently Parallel Algorithms in Feasibility and Optimization and Their Applications, vol. 8, pp. 115–152. North-Holland, Amsterdam (2001)
Combettes, P.L., Glaudin, L.E.: Quasinonexpansive iterations on the affine hull of orbits: from Mann’s mean value algorithm to inertial methods. SIAM J. Optim. 27, 2356–2380 (2017)
Combettes, P.L., Salzo, S., Villa, S.: Consistent learning by composite proximal thresholding. Math. Program. Ser. B 167, 99–127 (2018)
Kaczor, W.J., Nowak, M.T.: Problems in Mathematical Analysis. I. Real Numbers, Sequences and Series. American Mathematical Society, Providence, RI (2000)
Moursi, W.M.: The forward-backward algorithm and the normal problem. J. Optim. Theory Appl. 176, 605–624 (2018)
Nesterov, Y.E.: A method for solving the convex programming problem with convergence rate \(O(1/k^{2})\). Dokl. Akad. Nauk 269, 543–547 (1983)
Opial, Z.: Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bull. Am. Math. Soc. 73, 591–597 (1967)
Pazy, A.: Asymptotic behavior of contractions in Hilbert space. Israel J. Math. 9, 235–240 (1971)
Rǎdulescu, T.-L., Rǎdulescu, V.D., Andreescu, T.: Problems in Real Analysis: Advanced Calculus on the Real Axis. Springer, New York (2009)
Schmidt, M., Roux, N.L., Bach, F.: Convergence rates of inexact proximal-gradient methods for convex optimization. In: Shawe-Taylor, J., Zemel, R.S., Bartlett, P.L., Pereira, F., Weinberger, K.Q. (eds.) Advances in Neural Information Processing Systems 24, pp. 1458–1466. Curran Associates Inc., Red Hook (2011)
Su, W., Boyd, S., Candès, E.J.: A differential equation for modeling Nesterov’s accelerated gradient method: theory and insights. J. Mach. Learn. Res. 17, 1–43 (2016)
Villa, S., Salzo, S., Baldassarre, L., Verri, A.: Accelerated and inexact forward-backward algorithms. SIAM J. Optim. 23, 1607–1633 (2013)
Acknowledgements
We thank two referees for their very careful reading and constructive comments. HHB and XW were partially supported by NSERC Discovery Grants while MNB was partially supported by a Mitacs Globalink Graduate Fellowship Award.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendices
1.1 Appendix A
For the sake of completeness, we provide the following proof of Lemma 2.1 based on [20, Problem 3.2.43].
Proof of Lemma 2.1
Because  due to the assumption that
due to the assumption that  , it is sufficient to establish that
, it is sufficient to establish that

Indeed, since \(\tau _{n}\rightarrow {+}\infty \), there exists \(N \in \mathbb {N}^{*}\) such that

Now, set  , and
, and  . Then, on the one hand, since
. Then, on the one hand, since  is increasing and positive, we have
is increasing and positive, we have  , and
, and  is therefore an increasing sequence in \(\mathbb {R}_{+}\); moreover, due to (127),
is therefore an increasing sequence in \(\mathbb {R}_{+}\); moreover, due to (127),  . On the other hand, because \(\tau _{n}\rightarrow {+}\infty \), we have \(\sigma _{n} =\tau _{n+1}^{2}-\tau _{1}^{2} \rightarrow {+}\infty \). Altogether, since
. On the other hand, because \(\tau _{n}\rightarrow {+}\infty \), we have \(\sigma _{n} =\tau _{n+1}^{2}-\tau _{1}^{2} \rightarrow {+}\infty \). Altogether, since

by the fact that  is increasing, we see that
is increasing, we see that  . It follows that the partial sums of
. It follows that the partial sums of  do not satisfy the Cauchy property. Hence, since
do not satisfy the Cauchy property. Hence, since  , we obtain
, we obtain
Consequently, in the light of (127),

and (126) follows. \(\square \)
1.2 Appendix B
Proof of Lemma 2.2
Let us argue by contradiction. Towards this goal, assume that \(\varliminf \beta _{n} \in ] 0, {+}\infty ]\) and fix \( \beta \in ] 0 , \varliminf \beta _{n} [\). Then, there exists \(N \in \mathbb {N}^{*}\) such that  , and hence, because
, and hence, because  , we have
, we have  , it follows that \(\sum _{n \geqslant N}\alpha _{n}\beta _{n} \geqslant \sum _{n \geqslant N} \beta \alpha _{n} = {+}\infty \), which violates our assumption. To sum up, \(\varliminf \beta _{n} = 0\). \(\square \)
, it follows that \(\sum _{n \geqslant N}\alpha _{n}\beta _{n} \geqslant \sum _{n \geqslant N} \beta \alpha _{n} = {+}\infty \), which violates our assumption. To sum up, \(\varliminf \beta _{n} = 0\). \(\square \)
1.3 Appendix C
The following self-contained proof of Lemma 2.3 follows [17, Lemma 3.1] in the case \(\chi =1\); however, we do not require the error sequence  to be positive.
to be positive.
Proof of Lemma 2.3
-
(i):
Set \(\alpha :=\varliminf _{n}\alpha _{n} \in \left[ \inf _{n \in \mathbb {N}^{*}}\alpha _{n}, {+}\infty \right] \) and let
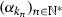 be a subsequence of
be a subsequence of  that converges to \(\alpha \). We first show that \(\alpha < {+}\infty \). Since
that converges to \(\alpha \). We first show that \(\alpha < {+}\infty \). Since 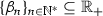 , it follows from (9) that
, it follows from (9) that  . Thus,
. Thus, 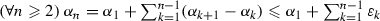 ; in particular,
; in particular, 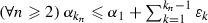 . Hence, since \(\alpha _{k_{n}}\rightarrow \alpha \) and \(\sum _{n \in \mathbb {N}^{*}}\varepsilon _{n}\) converges, it follows that \(\alpha \leqslant \alpha _{1} + \sum _{k \in \mathbb {N}}\varepsilon _{k } < {+}\infty \), as claimed. In turn, to establish the convergence of
. Hence, since \(\alpha _{k_{n}}\rightarrow \alpha \) and \(\sum _{n \in \mathbb {N}^{*}}\varepsilon _{n}\) converges, it follows that \(\alpha \leqslant \alpha _{1} + \sum _{k \in \mathbb {N}}\varepsilon _{k } < {+}\infty \), as claimed. In turn, to establish the convergence of  , it suffices to verify that \(\varlimsup _{n}\alpha _{n} \leqslant \varliminf _{n} \alpha _{n}\). Towards this goal, let \(\delta \) be in \(]0, {+}\infty [\). Then, on the one hand, Cauchy’s criterion ensures the existence of \(k_{n_{0}} \in \mathbb {N}^{*}\) such that \(\alpha _{k_{n_{0} } } - \alpha \leqslant \delta /2 \) and that
, it suffices to verify that \(\varlimsup _{n}\alpha _{n} \leqslant \varliminf _{n} \alpha _{n}\). Towards this goal, let \(\delta \) be in \(]0, {+}\infty [\). Then, on the one hand, Cauchy’s criterion ensures the existence of \(k_{n_{0}} \in \mathbb {N}^{*}\) such that \(\alpha _{k_{n_{0} } } - \alpha \leqslant \delta /2 \) and that 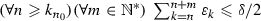 . On the other hand, because
. On the other hand, because 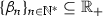 , (9) implies that
, (9) implies that 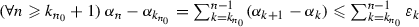 . Altogether,
. Altogether, 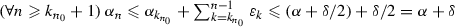 , from which we deduce that \(\varlimsup _{n} \alpha _{n} \leqslant \alpha + \delta \). Consequently, since \(\delta \) is arbitrarily chosen in \(]0, {+}\infty [\), it follows that \(\varlimsup _{n}\alpha _{n} \leqslant \alpha = \varliminf _{n}\alpha _{n}\), and therefore,
, from which we deduce that \(\varlimsup _{n} \alpha _{n} \leqslant \alpha + \delta \). Consequently, since \(\delta \) is arbitrarily chosen in \(]0, {+}\infty [\), it follows that \(\varlimsup _{n}\alpha _{n} \leqslant \alpha = \varliminf _{n}\alpha _{n}\), and therefore,  converges to \(\alpha \).
converges to \(\alpha \). -
(ii):
We derive from (9) that
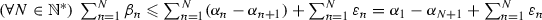 . Hence, since \(\sum _{n \in \mathbb {N}^{*}}\varepsilon _{n}\) is convergent and, by (i), \(\lim _{n}\alpha _{n} =\alpha \), letting \(N \rightarrow {+}\infty \) yields \(\sum _{n \in \mathbb {N}} \beta _{n} \leqslant \alpha _{1} - \alpha + \sum _{n \in \mathbb {N}}\varepsilon _{n } < {+}\infty \), and so \(\sum _{n \in \mathbb {N}^{*}}\beta _{n} < {+}\infty \), as required.
. Hence, since \(\sum _{n \in \mathbb {N}^{*}}\varepsilon _{n}\) is convergent and, by (i), \(\lim _{n}\alpha _{n} =\alpha \), letting \(N \rightarrow {+}\infty \) yields \(\sum _{n \in \mathbb {N}} \beta _{n} \leqslant \alpha _{1} - \alpha + \sum _{n \in \mathbb {N}}\varepsilon _{n } < {+}\infty \), and so \(\sum _{n \in \mathbb {N}^{*}}\beta _{n} < {+}\infty \), as required.
\(\square \)
1.4 Appendix D
Proof of Lemma 2.4
Indeed, since 


we readily obtain the conclusion. \(\square \)
1.5 Appendix E
Proof of Lemma 2.5
“\(\Rightarrow \)”: Since  is a decreasing sequence in \(\mathbb {R}_{+}\) and \(\sum _{n \in \mathbb {N}^{*}}\alpha _{n} < {+}\infty \), it follows that \(n\alpha _{n}\rightarrow 0\) (see, e.g., [20, Problem 3.2.35]). Invoking the assumption that \(\sum _{n \in \mathbb {N}^{*}}\alpha _{n} < {+}\infty \) once more, we infer from Lemma 2.4 that
is a decreasing sequence in \(\mathbb {R}_{+}\) and \(\sum _{n \in \mathbb {N}^{*}}\alpha _{n} < {+}\infty \), it follows that \(n\alpha _{n}\rightarrow 0\) (see, e.g., [20, Problem 3.2.35]). Invoking the assumption that \(\sum _{n \in \mathbb {N}^{*}}\alpha _{n} < {+}\infty \) once more, we infer from Lemma 2.4 that  , as desired.
, as desired.
“\(\Leftarrow \)”: A consequence of Lemma 2.4. \(\square \)
1.6 Appendix F
Proof of Lemma 3.1
This is similar to the one found in [11, Lemma 2.3] and included for completeness; see also [15, Lemma 3.1]. Fix  . On the one hand, by (A1) and (A3) in Assumption 1.1, \({\nabla {f} } \) is Lipschitz continuous with constant \(\gamma ^{-1}\), from which, the Descent Lemma (see, e.g., [8, Lemma 2.64]), and the convexity of f we infer that
. On the one hand, by (A1) and (A3) in Assumption 1.1, \({\nabla {f} } \) is Lipschitz continuous with constant \(\gamma ^{-1}\), from which, the Descent Lemma (see, e.g., [8, Lemma 2.64]), and the convexity of f we infer that



On the other hand, because  , [8, Proposition 12.26] asserts that
, [8, Proposition 12.26] asserts that


Altogether, upon adding (132) and (133), it follows that



which yields (18). \(\square \)
1.7 Appendix G
Proof of (50)
Recall that \(\lim (\tau _n/n)=1/2\). In turn, because \((\forall n\in \mathbb {N}^{*})\) \(\tau _n^2=\tau _{n+1}^2-\tau _{n+1}\), it follows that
and therefore that
Hence, (50) holds. \(\square \)
Rights and permissions
About this article
Cite this article
Bauschke, H.H., Bui, M.N. & Wang, X. Applying FISTA to optimization problems (with or) without minimizers. Math. Program. 184, 349–381 (2020). https://doi.org/10.1007/s10107-019-01415-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-019-01415-x





 is closed and convex by [
is closed and convex by [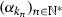 be a subsequence of
be a subsequence of  that converges to
that converges to 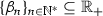 , it follows from (
, it follows from ( . Thus,
. Thus, 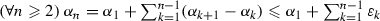 ; in particular,
; in particular, 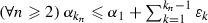 . Hence, since
. Hence, since  , it suffices to verify that
, it suffices to verify that 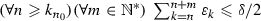 . On the other hand, because
. On the other hand, because 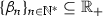 , (
, (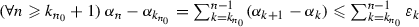 . Altogether,
. Altogether, 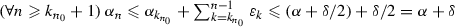 , from which we deduce that
, from which we deduce that  converges to
converges to 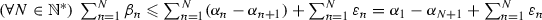 . Hence, since
. Hence, since