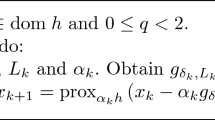Abstract
Second-order methods, which utilize gradients as well as Hessians to optimize a given function, are of major importance in mathematical optimization. In this work, we prove tight bounds on the oracle complexity of such methods for smooth convex functions, or equivalently, the worst-case number of iterations required to optimize such functions to a given accuracy. In particular, these bounds indicate when such methods can or cannot improve on gradient-based methods, whose oracle complexity is much better understood. We also provide generalizations of our results to higher-order methods.
Similar content being viewed by others
Notes
Assuming f is twice-differentiable, this corresponds to \(\nabla ^2 f(\mathbf {w})\succeq \lambda I\) for all \(\mathbf {w}\).
That is, for any vectors \(\mathbf {v},\mathbf {w}\), the function \(g(t)=f(\mathbf {w}+t\mathbf {v})\) satisfies \(|g'''(t)|\le 2g''(t)^{3/2}\).
Ultimately, we will choose \(\gamma =\min \left\{ \left( \frac{3(\mu _1-\lambda )}{2\mu _2}\right) ^2, \root 7 \of {\frac{D^8(12\lambda )^6}{2^4\mu _2^6}}\right\} \) and \(\Delta =\sqrt{\gamma }\), see Subsection 4.3.
This is trivially true for \(i<j_0\). For \(i=j_0\), we have \(|w_{j_0}-w_{j_0+1}|^3=0< |\tilde{w}^*_{j_0}-\tilde{w}^*_{j_0+1}|^3\) and \(w_{j_0}^2=(\tilde{w}^*_{j_0})^2\). For \(i>j_0\), we have \(|w_i-w_{i+1}|^3= |\max \{0,\tilde{w}^*_i-\Delta \}-\max \{0,\tilde{w}^*_{i+1}-\Delta \}|^3\le |(\tilde{w}^*_i-\Delta )-(\tilde{w}^*_{i+1}-\Delta )|^3 = |\tilde{w}^*_i-\tilde{w}^*_{i+1}|^3\), and moreover, \(w_i^2 = \max \{0,\tilde{w}^*_i-\Delta \}^2\), which is 0 (hence \(\le (\tilde{w}^*_i)^2\)) if \(\tilde{w}^*_i\le \Delta \) and less than \((\tilde{w}^*_i)^2\) if \(\tilde{w}^*_i>\Delta \).
Such an index must exist: By assumption, \({\tilde{T}}\ge 2\gamma \left( \frac{\mu _2}{6\lambda }\right) ^2=\frac{2\gamma }{{\tilde{\lambda }}^2}\), so by Lemma 1, \(\frac{\gamma }{{\tilde{\lambda }}} =\sum _{t=1}^{{\tilde{T}}}\tilde{w}^*_t \ge {\tilde{T}}\tilde{w}^*_{{\tilde{T}}} \ge \frac{2\gamma }{{\tilde{\lambda }}^2}\tilde{w}^*_{{\tilde{T}}}\), hence \(\tilde{w}_{{\tilde{T}}}\le {\tilde{\lambda }}/2\).
Since \(\tilde{w}^*_t\) monotonically decrease in t, such an index must exist: On the one hand, \(\tilde{w}^*_1\) can be verified to be at least \({\tilde{\lambda }}>{\tilde{\lambda }}/2\) (by Lemma 2 and the assumption \(\gamma \ge 10^4(\lambda /\mu _2)^2\), hence \(\gamma \ge 277{\tilde{\lambda }}^2\)). On the other hand, if we let \(t_1\) be the largest index \(\le {\tilde{T}}\) satisfying \(\tilde{w}^*_{t_1}>{\tilde{\lambda }}/2\), we have by Lemma 1 that \(\frac{\gamma }{{\tilde{\lambda }}} \ge \sum _{t=1}^{t_1}\tilde{w}^*_t \ge t_1\tilde{w}_{t_1}^*> \frac{t_1 {\tilde{\lambda }}}{2}\), which implies that \(t_1 \le \frac{2\gamma }{{\tilde{\lambda }}^2}\), which is less than \({\tilde{T}}/2\) by the assumption on \({\tilde{T}}\) being large enough. Therefore, \(t_0\) is at most \({\tilde{T}}/2\) as well.
We note that the reverse direction, of adapting strongly convex optimization algorithms to the convex case, is more common in the literature, and can be achieved using regularization or more sophisticated approaches [2].
Specifically, since in our framework we do not limit computational resources, we assume that the minimization problem in Eq. (6.1) of [10] can be solved exactly.
References
Agarwal, N., Hazan, E.: Lower bounds for higher-order optimization. Working draft (2017)
Allen-Zhu, Z., Hazan, E.: Optimal black-box reductions between optimization objectives. In: Advances in Neural Information Processing Systems, pp. 1614–1622 (2016)
Arjevani, Y., Shamir, O.: On the iteration complexity of oblivious first-order optimization algorithms. In: International Conference on Machine Learning, pp. 908–916 (2016)
Arjevani, Y., Shamir, O.: Oracle complexity of second-order methods for finite-sum problems. arXiv preprint arXiv:1611.04982 (2016)
Baes, M.: Estimate Sequence Methods: Extensions and Approximations. Institute for Operations Research, ETH, Zürich (2009)
Boyd, S., Vandenberghe, L.: Convex Optimization. Cambridge University Press, Cambridge (2004)
Cartis, C., Gould, N.I., Toint, P.L.: On the complexity of steepest descent, newton’s and regularized newton’s methods for nonconvex unconstrained optimization problems. SIAM J. Optim. 20(6), 2833–2852 (2010)
Cartis, C., Gould, N.I., Toint, P.L.: Evaluation complexity of adaptive cubic regularization methods for convex unconstrained optimization. Optim Methods Softw. 27(2), 197–219 (2012)
Kantorovich, L.V.: Functional analysis and applied mathematics. Uspekhi Matematicheskikh Nauk 3(6), 89–185 (1948)
Monteiro, R.D., Svaiter, B.F.: An accelerated hybrid proximal extragradient method for convex optimization and its implications to second-order methods. SIAM J. Optim. 23(2), 1092–1125 (2013)
Mu, C., Hsu, D., Goldfarb, D.: Successive rank-one approximations for nearly orthogonally decomposable symmetric tensors. SIAM J. Matrix Anal. Appl. 36(4), 1638–1659 (2015)
Nemirovski, A.: Efficient methods in convex programming—lecture notes (2005)
Nemirovsky, A., Yudin, D.: Problem Complexity and Method Efficiency in Optimization. Wiley, New York (1983)
Nesterov, Y.: A method of solving a convex programming problem with convergence rate \(O(1/k^2)\). Sov. Math. Dokl. 27(2), 372–376 (1983)
Nesterov, Y.: Introductory Lectures on Convex Optimization: A Basic Course, vol. 87. Springer, Berlin (2004)
Nesterov, Y.: Accelerating the cubic regularization of newton method on convex problems. Math. Program. 112(1), 159–181 (2008)
Nesterov, Y., Nemirovskii, A.: Interior-Point Polynomial Algorithms in Convex Programming. SIAM, Philadelphia (1994)
Nesterov, Y., Polyak, B.T.: Cubic regularization of newton method and its global performance. Math. Program. 108(1), 177–205 (2006)
Vladimirov, A., Nesterov, Y.E., Chekanov, Y.N.: On uniformly convex functionals. Vestnik Moskov. Univ. Ser. XV Vychisl. Mat. Kibernet 3, 12–23 (1978)
Woodworth, B., Srebro, N.: Lower bound for randomized first order convex optimization. arXiv preprint arXiv:1709.03594 (2017)
Acknowledgements
We thank Yurii Nesterov for several helpful comments on a preliminary version of this paper, as well as Naman Agarwal, Elad Hazan and Zeyuan Allen-Zhu for informing us about the A-NPE algorithm of [10].
Author information
Authors and Affiliations
Corresponding author
Appendix A: An improved second-order oracle complexity bound for strongly convex functions
Appendix A: An improved second-order oracle complexity bound for strongly convex functions
In this section, we show how the A-NPE algorithm of [10], which is a second-order method analyzed for smooth convex functions, can be used to yield near-optimal performance if the function is also strongly convex. Rather than directly adapting their analysis, which is non-trivial, we use a simple restarting scheme, which allows one to convert an algorithm for the convex setting, to an algorithm in the strongly convex settingFootnote 7.
Our algorithm is described as follows: In the first phase, we apply a generic restarting scheme (based on [3, Subsction 4.2]), where we repeatedly run A-NPE for a bounded number of steps, followed by restarting the algorithm, running it from the last iterate obtained. By strong convexity, we show that each such epoch reduces the suboptimality by a constant factor. Once we reach a point sufficiently close to the global optimum, we switch to the second phase, where we use the cubic-regularized Newton method to get a quadratic convergence rate.
To formalize this, let us first analyze the convergence rate of the first phase. We assume that we use the algorithm described in [10, Subsection 7.4]Footnote 8. By [10, Theorem 6.4 and Theorem 3.10], we have that the t’th iterate satisfies
where \(\mu _2\) is the Lipschitz constant of \(\nabla ^2 f\), \(\mathbf {w}_1\) is the initialization point, \(\mathbf {w}^*\) is the unique minimizer (due to strong convexity) of f, D bounds \(\Vert \mathbf {w}_1-\mathbf {w}^*\Vert \) from above, and \(c>0\) is some universal constant. Since f is also assumed to be \(\lambda \)-strongly convex, we have \( \frac{\lambda }{2}\Vert \mathbf {w}_1 - \mathbf {w}^*\Vert ^2 \le f(\mathbf {w}_1) - f(\mathbf {w}^*) \), hence \(f(\mathbf {w}_t)-f(\mathbf {w}^*)\) is at most
Thus, running the algorithm for \(\tau = \left( \frac{4c\mu _2 D}{\lambda }\right) ^{2/7} \) iterations, we see that \(f(\mathbf {w}_t) - f(\mathbf {w}^*) \le {(f(\mathbf {w}_1)-f(\mathbf {w}^*))}/{2}\). Now, since the distance from \(\mathbf {w}_t\) to \(\mathbf {w}^*\) is also smaller than D, we may initialize the algorithm at the last iterate returned by the previous run and run it for \(\tau \) iterations to reduce \(f(\mathbf {w}_t) - f(\mathbf {w}^*)\) in, yet again, a factor of 2. Applying the algorithm for T iterations (and restarting the algorithmic parameters after every \(\tau \) iterations) yields \(f(\mathbf {w}_T)-f(\mathbf {w}^*) \le \frac{f(\mathbf {w}_1)-f(\mathbf {w}^*) }{2^{T/\tau }}\). Equivalently, to obtain an \(\epsilon \)-optimal solution, we need at most \( \left( \frac{4c\mu _2 D}{\lambda }\right) ^{2/7}\log _2\left( \frac{f(\mathbf {w}_1)-f(\mathbf {w}^*) }{\epsilon }\right) \) oracle calls (note that this restarting scheme can be applied also on uniform convex functions of any order, as defined in, e.g., [19]).
Next, after performing a number of iterations sufficiently large to obtain high accuracy solutions, we proceed to the second phase of the algorithm where cubic-regularized Newton steps are applied (see [16]). According to that analysis, after reducing the optimization error to below \(\lambda ^3/4\mu _2^2\), the number of cubic-regularized Newton steps required to achieve an \(\epsilon \)-suboptimal solution is \( \mathcal {O}\left( \log \log _2\left( \frac{\lambda ^3}{\mu _2^2\epsilon }\right) \right) \). Thus, using the \(\mu _1\)-Lipschitzness of the gradient to bound \(f(\mathbf {w}_1)-f(\mathbf {w}^*)\) from above by \(\mu _1 D^2/2\), we get that the overall number of iterations is at most \( \mathcal {O}\left( \left( \frac{\mu _2 D}{\lambda }\right) ^{2/7}\log _2\left( \frac{\mu _1 \mu _2^2D^2 }{\lambda ^3}\right) + \log \log _2\left( \frac{\lambda ^3}{\mu _2^2\epsilon }\right) \right) \).
Rights and permissions
About this article
Cite this article
Arjevani, Y., Shamir, O. & Shiff, R. Oracle complexity of second-order methods for smooth convex optimization. Math. Program. 178, 327–360 (2019). https://doi.org/10.1007/s10107-018-1293-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-018-1293-1