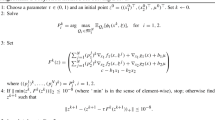Identifying effective scenarios in distributionally robust stochastic programs with total variation distance

Abstract

Traditional stochastic programs assume that the probability distribution of uncertainty is known. However, in practice, the probability distribution oftentimes is not known or cannot be accurately approximated. One way to address such distributional ambiguity is to work with distributionally robust convex stochastic programs (DRSPs), which minimize the worst-case expected cost with respect to a set of probability distributions. In this paper we analyze the case where there is a finite number of possible scenarios and study the question of how to identify the critical scenarios resulting from solving a DRSP. We illustrate that not all, but only some scenarios might have “effect” on the optimal value, and we formally define this notion for our general class of problems. In particular, we examine problems where the distributional ambiguity is modeled by the so-called total variation distance. We propose easy-to-check conditions to identify effective and ineffective scenarios for that class of problems. Computational results show that identifying effective scenarios provides useful insight on the underlying uncertainties of the problem.

Appendix

In Sect. A.1, we provide the results and proofs that were relegated to the Appendix. Then, in Sect. A.2, we propose a decomposition method to solve (DRSP-V).

1.1 A-1 Proofs

In this section, we first provide the proof of Proposition 4. Then, in Sect. A.1.2, we present Proposition A-1. In Sect. A.1.3, we state Lemma A-1, used in the proof of Proposition 5. In Sect. A.1.4, we provide Lemma A-2, used in the proof of Proposition 7. Finally, in Sect. A.1.5, we preset Lemmas A-3 and A-4, which are used in the proof of Theorem 5.

1.1.1 A-1.1 Proof of Proposition 4

Proof of Proposition 4

For a fixed $x \in \mathbb {X}$, the worst-case expected problem can be written as follows

$$\begin{aligned} \max _{\mathbf {p}, \mathbf {e}} \;&\sum _{\omega \in \varOmega } p_\omega h_\omega (x) \end{aligned}$$

(A-1a)

$$\begin{aligned} \text {s.t.}\quad&p_\omega -e_\omega \le q_\omega , \; \forall \omega , \; : [u^{\prime }_{\omega } ] \end{aligned}$$

(A-1b)

$$\begin{aligned}&-p_\omega -e_\omega \le -q_\omega , \; \forall \omega , \; : [u^{\prime \prime }_{\omega }] \end{aligned}$$

(A-1c)

$$\begin{aligned}&\frac{1}{2}\sum _{\omega \in \varOmega } e_\omega \le \gamma , \; :[\lambda (x)] \end{aligned}$$

(A-1d)

$$\begin{aligned}&\sum _{\omega \in \varOmega } p_\omega =1, \; :[\mu (x)] \end{aligned}$$

(A-1e)

$$\begin{aligned}&p_\omega , e_\omega \ge 0, \; \forall \omega . \end{aligned}$$

(A-1f)

where $u^{\prime }_{\omega }$, $u^{\prime \prime }_{\omega }$, $\lambda (x)$, and $\mu (x)$ are the associated dual variables for the constraints. Define now

$$\begin{aligned} \lambda (x)= \sup _{\omega \in \varOmega } h_{\omega }(x) - \mathrm {VaR}_{\gamma } \left[ \mathbf {h}(x) \right] , \; \mu (x)= \frac{1}{2}\left( \sup _{\omega \in \varOmega } h_{\omega }(x) + \mathrm {VaR}_{\gamma } \left[ \mathbf {h}(x) \right] \right) . \end{aligned}$$

We consider two cases (i) $\mathrm {VaR}_{\gamma } \left[ \mathbf {h}(x) \right] <\sup _{\omega \in \varOmega } h_{\omega }(x)$ and (ii) $\mathrm {VaR}_{\gamma } \left[ \mathbf {h}(x) \right] =\sup _{\omega \in \varOmega } h_{\omega }(x)$. In case (i), we have $\lambda (x)>0$. Then,

$$\begin{aligned} {\left\{ \begin{array}{ll} p_\omega =0, \; u^{\prime }_{\omega }=0, \; u^{\prime \prime }_{\omega }=\frac{\lambda (x)}{2}, \; e_\omega =q_\omega ,&{} \omega \in \varOmega _{1}(x),\\ p_\omega \le q_\omega , \; u^{\prime }_{\omega }=0, \; u^{\prime \prime }_{\omega }=\frac{\lambda (x)}{2}, \; e_\omega =q_\omega -p_\omega ,&{} \omega \in \varOmega _{2}(x),\\ p_\omega = q_\omega , \; u^{\prime }_{\omega }=\frac{h_{\omega }(x)-\mu (x)+\frac{\lambda (x)}{2}}{2}, \; u^{\prime \prime }_{\omega }=\frac{\lambda (x)}{2}-\frac{h_{\omega }(x)-\mu (x)+\frac{\lambda (x)}{2}}{2}, \; e_\omega =0,&{} \omega \in \varOmega _{3}(x),\\ p_\omega \ge q_\omega , \; u^{\prime }_{\omega }=\frac{\lambda (x)}{2}, \; u^{\prime \prime }_{\omega }=0, \; e_\omega =p_\omega -q_\omega , &{} \omega \in \varOmega _{4}(x), \end{array}\right. } \end{aligned}$$

together with $\sum _{\omega \in \varOmega } p_\omega =1$, is primal-dual feasible. For the complementary slackness condition to hold, (A-1d) must hold with equality at an optimal $(\mathbf {p}, \mathbf {e}, \mu (x), \lambda (x), \mathbf {u}^{\prime }, \mathbf {u}^{\prime \prime })$ when $\lambda (x)>0$. Indeed, we have

$$\begin{aligned} \sum _{\omega \in \varOmega }e_{\omega }&=\sum _{\omega \in \varOmega _{1}(x)} q_{\omega } + \sum _{\omega \in \varOmega _{2}(x)} (q_{\omega }-p_{\omega })+ \sum _{\omega \in \varOmega _{4}(x)}(p_{\omega }-q_{\omega }) \nonumber \\&=\sum _{\omega \in \varOmega _{1}(x) \cup \varOmega _{2}(x)} q_{\omega } - \sum _{\omega \in \varOmega _{4}(x)} q_{\omega }- \sum _{\omega \in \varOmega _{2}(x)} p_{\omega }+ \sum _{\omega \in \varOmega _{4}(x)} p_{\omega } \nonumber \\&= 1-2\sum _{\omega \in \varOmega _{4}(x)} q_{\omega }-\sum _{\omega \in \varOmega _{3}(x)} q_{\omega } - \sum _{\omega \in \varOmega _{2}(x)} p_{\omega }+ \sum _{\omega \in \varOmega _{4}(x)} p_{\omega } \quad \nonumber \\&\qquad \left[ \text {because} \ \sum _{\omega \in \varOmega }q_{\omega }=1\right] \nonumber \\&= 1-2\sum _{\omega \in \varOmega _{4}(x)} q_{\omega }-\sum _{\omega \in \varOmega _{3}(x)} p_{\omega } - \sum _{\omega \in \varOmega _{2}(x)} p_{\omega }+ \sum _{\omega \in \varOmega _{4}(x)} p_{\omega } \, \nonumber \\&\qquad [\text {because} \ p_{\omega }=q_{\omega } \ \text {on} \ \varOmega _{3}(x)] \nonumber \\&= 2\sum _{\omega \in \varOmega _{4}(x)} (p_{\omega }-q_{\omega }) \; \left[ \text {because} \ \sum _{\omega \in \varOmega }p_{\omega }=1\right] \nonumber \\&= 2\gamma , \end{aligned}$$

(A-2)

where the last equality follows from (8). Now, by substituting (8) in (A-2) we obtain (7).

On the other hand, in case (ii), we have $\lambda (x)=0$, $\varOmega _{3}(x)=\emptyset$ and $\varOmega _{2}(x)=\varOmega _{4}(x)$. Then, all $u^{\prime }_{\omega }$s and $u^{\prime \prime }_{\omega }$s are zero, and we have $\mu (x)=\sup _{\omega \in \varOmega } h_{\omega }(x)$. In this case, if $h_\omega (x) = \sup _{\omega \in \varOmega } h_{\omega }(x)$, we have $e_\omega =|p_\omega -q_\omega |$ and $p_\omega \ge 0$ is chosen so that it satisfies $\sum _{\omega \in \varOmega } p_{\omega }=1$ and $\frac{1}{2}\sum _{\omega \in \varOmega } e_{\omega } \le \gamma$. Otherwise, $p_\omega = 0$. $\square$

1.1.2 A-1.2 Proposition A-1

Proposition A-1 shows the equivalence of the ambiguity sets induced by the right- and left-sided variation distances.

Proposition A-1

The ambiguity sets induced by the right- and left-sided variation distances are the same.

Proof of Proposition A-1

Let $\mathcal {P}^{\text {V}^{\text {R}}}_{\gamma }$ and $\mathcal {P}^{\text {V}^{\text {L}}}_{\gamma }$ denote the ambiguity set induced by the right- and left-sided variation distances, respectively. Recall $\text {V}^{\text {R}}(\mathbf {p},\mathbf {q})= \frac{1}{2}\sum _{\omega \in \varOmega } (p_{\omega }-q_{\omega })_{+}$ and $\text {V}^{\text {L}}(\mathbf {p},\mathbf {q})= \frac{1}{2}\sum _{\omega \in \varOmega } (q_{\omega }-p_{\omega })_{+}$. Now, if we show $\text {V}^{\text {R}}(\mathbf {p},\mathbf {q})$ and $\text {V}^{\text {L}}(\mathbf {p},\mathbf {q})$ are equal, it would show the equivalence of $\mathcal {P}^{\text {V}^{\text {R}}}_{\gamma }$ and $\mathcal {P}^{\text {V}^{\text {L}}}_{\gamma }$. Let $M:=\{\omega \in \varOmega \,:\, p_{\omega } \ge q_{\omega } \}$. So, we can write $\text {V}^{\text {R}}(\mathbf {p},\mathbf {q})=\frac{1}{2}\sum _{\omega \in M} (p_{\omega }-q_{\omega })=\frac{1}{2}\sum _{\omega \in {M}^{\mathsf {c}}} (q_{\omega }-p_{\omega })= \text {V}^{\text {L}}(\mathbf {p},\mathbf {q})$ by using the facts that $\sum _{\omega \in \varOmega } p_{\omega }=1$ and $\sum _{\omega \in \varOmega } q_{\omega }=1$. $\square$

1.1.3 A-1.3 Lemma A-1

In this section, we state Lemma A-1, which is used in the proof of Proposition 5. The proof of this lemma is presented in the Online Supplement.

Lemma A-1

Consider a fixed $x \in \mathbb {X}$ and level $\beta \in [0,1)$. Then, $\mathrm {CVaR}_{\beta } \left[ \mathbf {h}(x) \right] =\max _{\mathbf {z}\in \mathfrak {A}_{\beta }} \sum _{\omega \in \varOmega } z_{\omega }h_{\omega }(x)$, where

$$\begin{aligned} \mathfrak {A}_{\beta }:=\left\{ \mathbf {z}\,:\, \sum _{\omega \in \varOmega } z_\omega =1, \; 0 \le z_{\omega } \le \frac{q_{\omega }}{1-\beta }, \ \forall \omega \in \varOmega \right\} . \end{aligned}$$

(A-3)

Moreover, the set of all optimal solutions $\mathbf {z}$ is given by

$$\begin{aligned} \mathfrak {D}_{\beta }(x):=\left\{ \begin{array}{lll} &{} z_{\omega }=0, &{} \text {if} \;\; \omega \in \left[ \mathbf {h}(x)<\mathrm {VaR}_{\beta } \left[ \mathbf {h}(x) \right] \right] ,\\ \mathbf {z}\,:\, &{} z_{\omega }=\frac{q_{\omega }}{1-\beta }, &{} \text {if} \;\; \omega \in \left[ \mathbf {h}(x)>\mathrm {VaR}_{\beta } \left[ \mathbf {h}(x) \right] \right] ,\\ &{} z_{\omega } \in [0, \frac{q_{\omega }}{1-\beta }], &{} \text {if} \;\; \omega \in \left[ \mathbf {h}(x) = \mathrm {VaR}_{\beta } \left[ \mathbf {h}(x) \right] \right] ,\\ &{} \sum _{\omega \in \left[ \mathbf {h}(x)=\mathrm {VaR}_{\beta } \left[ \mathbf {h}(x) \right] \right] } z_{\omega }&{}=\frac{1}{1-\beta }\left[ \varPsi \Big (x, \mathrm {VaR}_{\beta } \left[ \mathbf {h}(x) \right] \Big )-\beta \right] . \end{array} \right. \end{aligned}$$

(A-4)

1.1.4 A-1.4 Lemma A-2

In this section, we present Lemma A-2, which is used in the proof of Proposition 7.

Lemma A-2

Consider a scenario $\omega ^{\prime }$ with $q_{\omega ^{\prime }}>0$. If $h_{\omega ^{\prime }}(x^{*}) > \mathrm {VaR}_{\gamma } \left[ \mathbf {h}(x^{*}) \right]$, then scenario $\omega ^{\prime }$ is effective for (DRSP-V).

Proof of Lemma A-2

Suppose $\bar{x}$ solves the assessment problem of $\mathcal {F}=\{\omega ^{\prime }\}$ with $q_{\omega ^{\prime }}>0$. By (3), we have $f^\text {A}_{\gamma }(\bar{x};\mathcal {F}) \le f^\text {A}_{\gamma }(x^{*};\mathcal {F}) \le f_{\gamma }(x^{*})$. Consequently, $f_{\gamma }(x^{*})-f^\text {A}_{\gamma }(x^{*};\mathcal {F})$ gives a lower bound on $f_{\gamma }(x^{*})- f^\text {A}_{\gamma }(\bar{x};\mathcal {F})$. If this lower bound is positive, then scenario $\omega ^{\prime }$ is effective. To check this lower bound, let us consider the objective function of the dual problem of (A-1a) (presented in the proof of Proposition 3 in the Online Supplement) and (13), both evaluated at $x^{*}$. Note that $(\mu ^{*}, \lambda ^{*})$ belongs to the feasible region of (13) because $\mu ^{*}+\frac{\lambda ^{*}}{2}= \sup _{\omega \in \varOmega } h_{\omega }(x^{*}) \ge \sup _{\omega \in {\mathcal {F}}^{\mathsf {c}}} h_{\omega }(x^{*})$ and $\lambda ^{*} \ge 0$. Thus, we have

$$\begin{aligned} \begin{aligned} f_{\gamma }(x^{*})-f^\text {A}_{\gamma }(x^{*};\mathcal {F})&\ge \mu ^{*}-\frac{\lambda ^{*}}{2}(1-2\gamma )+\sum _{\omega \in \varOmega } q_{\omega } \left( h_{\omega }(x^{*})-\mu ^{*}+\frac{\lambda ^{*}}{2}\right) _{+} \\&\quad -\,\left[ \mu ^{*}-\frac{\lambda ^{*}}{2}(1-2\gamma )+\sum _{\omega \in {\mathcal {F}}^{\mathsf {c}}} q_{\omega }\left( h_{\omega }(x^{*})-\mu ^{*}+\frac{\lambda ^{*}}{2}\right) _{+} \right] \\&=q_{\omega ^{\prime }}\left( h_{\omega ^{\prime }}(x^{*})-\mu ^{*}+\frac{\lambda ^{*}}{2}\right) _{+}\\&= q_{\omega ^{\prime }}\Big (h_{\omega ^{\prime }}(x^{*})-\mathrm {VaR}_{\gamma } \left[ \mathbf {h}(x^{*}) \right] \Big )_{+}, \end{aligned} \end{aligned}$$

where the last equality follows from the fact $\mu ^{*}-\frac{\lambda ^{*}}{2}=\mathrm {VaR}_{\gamma } \left[ \mathbf {h}(x^{*}) \right]$ by (5). Now, dividing by $q_{\omega ^{\prime }}$ shows that the lower bound is positive if $h_{\omega ^{\prime }}(x^{*}) > \mathrm {VaR}_{\gamma } \left[ \mathbf {h}(x^{*}) \right]$. $\square$

1.1.5 A-1.5 Lemmas used in the Proof of Theorem 5

For the following two lemmas, we consider a fixed $x \in X$. Also, we suppose $\mathbf {p}$ solves the worst-case expected problem in (DRSP-V) at x, and $(\mu , \lambda )$ are the optimal dual variables at x, given by (5).

Lemma A-3

For a fixed $x \in \mathbb {X}$, suppose $\lambda =0$ and there is a scenario $\omega ^{\prime } \in \varOmega _{4}(x)$ with $p_{\omega ^{\prime }}=0$. Then, $\varOmega _{4}(x)$ is not a singleton set, and for a scenario $\omega ^{\prime \prime } \in \varOmega _{4}(x)$ with $p_{\omega ^{\prime \prime }}>0$, there is always $\epsilon >0$ such that $\mathbf {p}^{\prime }$, with $p^{\prime }_{\omega ^{\prime }}=p_{\omega ^{\prime }}+\epsilon$, $p^{\prime }_{\omega ^{\prime \prime }}=p_{\omega ^{\prime \prime }}-\epsilon$, and $p^{\prime }_{\omega }=p_{\omega }$, $\omega \notin \{ \omega ^{\prime }, \omega ^{\prime \prime }\}$, is feasible to the worst-case expected problem at x.

Proof of Lemma A-3

Note that $\varOmega _{4}(x)$ is not a singleton set by Corollary 3. To show the existence of another feasible solution $\mathbf {p}^{\prime }$, we first examine the left-hand side of the distance constraint $\frac{1}{2} \sum _{\omega \in \varOmega } |p_{\omega }-q_{\omega }|\le \gamma$ in (4). Then, we find $\epsilon >0$ such that the change in the left-hand side of the distance constraint in (4) is smaller than or equal to zero; hence, $\mathbf {p}^{\prime }$ is feasible to the worst-case expected problem at x. We consider two cases.

• Case 1. $q_{\omega ^{\prime }}=0$. Let us consider two further cases.

  • Case 1.1. There is a scenario $\omega ^{\prime \prime } \in \varOmega _{4}(x)$ with $p_{\omega ^{\prime \prime }}>q_{\omega ^{\prime \prime }}$. By choosing $\epsilon \le p_{\omega ^{\prime \prime }}-q_{\omega ^{\prime \prime }}$ for $\mathbf {p}^{\prime }$, the change in the left-hand side of the distance constraint is zero.

  • Case 1.2. For all $\omega ^{\prime \prime } \in \varOmega _{4}(x)$, we have $p_{\omega ^{\prime \prime }} \le q_{\omega ^{\prime \prime }}$. Then, set ${\varOmega }^{\mathsf {c}}_{4}(x)$ is either empty or there is no scenario $\omega \in {\varOmega }^{\mathsf {c}}_{4}(x)$ with $q_{\omega }>0$. Otherwise, $\sum _{\omega \in \varOmega } p_\omega \le \sum _{\omega \in \varOmega _{4}(x)} q_\omega <1$. Moreover, we must have $p_{\omega ^{\prime \prime }} = q_{\omega ^{\prime \prime }}$ for all $\omega ^{\prime \prime } \in \varOmega _{4}(x)$. Otherwise, $\sum _{\omega \in \varOmega } p_\omega < \sum _{\omega \in \varOmega _{4}(x)} q_\omega =1$. Consequently, the left-hand side of the distance constraint for $\mathbf {p}$ is zero. Because for $\mathbf {p}^{\prime }$ the change in the left-hand side of the distance constraint is $\epsilon$, we choose $\epsilon \le \gamma$.

• Case 2. $q_{\omega ^{\prime }}>0$. Then, there is a scenario $\omega ^{\prime \prime } \in \varOmega _{4}(x)$ with $p_{\omega ^{\prime \prime }}>q_{\omega ^{\prime \prime }}$. Otherwise, $\sum _{\omega \in \varOmega } p_\omega \le \sum _{\begin{array}{c} \omega \in \varOmega _{4}(x) \\ \omega \ne \omega ^{\prime } \end{array}} q_{\omega } <1$. By choosing $\epsilon \le \min \{q_{\omega ^{\prime }}, p_{\omega ^{\prime \prime }}-q_{\omega ^{\prime \prime }}\}$ for $\mathbf {p}^{\prime }$, the change in the left-hand side of the distance constraint is $-\epsilon$. $\square$

Lemma A-4

For a fixed $x \in \mathbb {X}$, suppose $\lambda =0$ and there is a scenario $\omega ^{\prime } \in \varOmega _{4}(x)$ with $p_{\omega ^{\prime }}>0$. Moreover, suppose there is a scenario $\omega ^{\prime } \ne \omega ^{\prime \prime } \in \varOmega _{4}(x)$. Then, there is always $\epsilon >0$ such that either $\mathbf {p}^{\prime }$ or $\mathbf {p}^{\prime \prime }$ is feasible to the worst-case expected problem at x, where $\mathbf {p}^{\prime }$ is defined as $p^{\prime }_{\omega ^{\prime }}=p_{\omega ^{\prime }}+\epsilon$, $p^{\prime }_{\omega ^{\prime \prime }}=p_{\omega ^{\prime \prime }}-\epsilon$, and $p^{\prime }_{\omega }=p_{\omega }$, $\omega \notin \{ \omega ^{\prime }, \omega ^{\prime \prime }\}$, and $\mathbf {p}^{\prime \prime }$ is defined as $p^{\prime \prime }_{\omega ^{\prime }}=p_{\omega ^{\prime }}-\epsilon$, $p^{\prime \prime }_{\omega ^{\prime \prime }}=p_{\omega ^{\prime \prime }}+\epsilon$, and $p^{\prime \prime }_{\omega }=p_{\omega }$, $\omega \notin \{ \omega ^{\prime }, \omega ^{\prime \prime }\}$.

Proof of Lemma A-4

Similar to Lemma A-3, we examine the left-hand side of the distance constraint and find $\epsilon >0$ such that $\mathbf {p}^{\prime }$ or $\mathbf {p}^{\prime \prime }$ is feasible to the worst-case expected problem at x. We consider two cases.

• Case 1. $p_{\omega ^{\prime }} \ge q_{\omega ^{\prime }}$. Let us consider two further cases.

  • Case 1.1. There is a scenario $\omega ^{\prime \prime } \in \varOmega _{4}(x)$ with $p_{\omega ^{\prime \prime }} \ge q_{\omega ^{\prime \prime }}$. By choosing $\epsilon \le p_{\omega ^{\prime \prime }}-q_{\omega ^{\prime \prime }}$ for $\mathbf {p}^{\prime }$ or $\epsilon \le p_{\omega ^{\prime }}-q_{\omega ^{\prime }}$ for $\mathbf {p}^{\prime \prime }$, the change in the left-hand side of the distance constraint is zero.

  • Case 1.2. For all $\omega ^{\prime } \ne \omega ^{\prime \prime } \in \varOmega _{4}(x)$, we have $p_{\omega ^{\prime \prime }} < q_{\omega ^{\prime \prime }}$. By choosing $\epsilon \le \min \{p_{\omega ^{\prime }}-q_{\omega ^{\prime }}, q_{\omega ^{\prime \prime }}-p_{\omega ^{\prime \prime }}\}$ for $\mathbf {p}^{\prime \prime }$, the change in the left-hand side of the distance constraint is $-\epsilon$.

• Case 2. $p_{\omega ^{\prime }}<q_{\omega ^{\prime }}$. Then, there is a scenario $\omega ^{\prime \prime } \in \varOmega _{4}(x)$ with $p_{\omega ^{\prime \prime }}>q_{\omega ^{\prime \prime }}$. Otherwise, $\sum _{\omega \in \varOmega } p_\omega < \sum _{\omega \in \varOmega _{4}(x)} q_{\omega } \le 1$. By choosing $\epsilon \le \min \{p_{\omega ^{\prime \prime }}-q_{\omega ^{\prime \prime }}, q_{\omega ^{\prime }}-p_{\omega ^{\prime }}\}$ for $\mathbf {p}^{\prime }$, the change in the left-hand side of the distance constraint is $-\epsilon$. $\square$

1.2 A-2 Primal decomposition

As the number of scenarios increases, solving (DRSP-V) becomes computationally expensive. Decomposition-based methods could significantly reduce the solution time and allow larger problems to be solved efficiently. In the following, we propose a cutting-plane approach, referred to as Primal Decomposition, to solve (DRSP-V) and obtain an optimal solution $x^{*}$ and an optimal worst-case probability distribution $\mathbf {p}^{*}$.

Let us consider, $\mathcal {P}_{\gamma }$, the ambiguity set induced by the total variation distance. Let $\{\mathbf {p}^k\}_{k \in K}$ denote the set of extreme points of the polytope $\mathcal {P}_{\gamma }$. Then, (DRSP-V) can be written equivalently as

$$\begin{aligned}&\min _{x \in \mathbb {X}} \, \theta \nonumber \\&\quad \text {s.t.}\, \theta \ge \sum _{\omega \in \varOmega } p^k_\omega h_{\omega } (x), \; k \in K . \end{aligned}$$

(A-5)

One can solve this problem using a cut generation approach. That is, the restricted master problem is solved with a smaller subset of constraints (A-5) in order to get $(\hat{x}, \hat{\theta })$. Then, the worst-case expected problem is solved at $\hat{x}$ to obtain optimal value $f_{\gamma }(\hat{x})$. If $\hat{\theta } < f_{\gamma }(\hat{x})$, then the optimality cut (A-5)—corresponding to the extreme point $\mathbf {p}^k$, $k \in K$, that solves the worst-case expected problem at $\hat{x}$—is added to the restricted master problem. The Primal Decomposition approach to obtain $x^{*}$ and $\mathbf {p}^{*}$ is presented in Algorithm A-1.

Since the restricted master problem is a relaxation of (DRSP-V), $\hat{\theta }$ provides a lower bound on the optimal value of (DRSP-V). Moreover, since $\hat{x} \in \mathbb {X}$, $f_{\gamma }(\hat{x})$ gives an upper bound on the optimal value of (DRSP-V). The algorithm continues until $\hat{\theta }=f_{\gamma }(\hat{x})$, where $\hat{x}$ and the extreme point that solves the worst-case expected problem at $\hat{x}$ are an optimal $x^{*}$ and $\mathbf {p}^{*}$, respectively. Because the polytope $\mathcal {P}_{\gamma }$ has finitely many extreme points, finitely many optimality cuts (A-5) are added before $x^{*}$ and $\mathbf {p}^{*}$ are obtained. In other words, the Primal Decomposition algorithm converges in a finite number of iterations. However, at each iteration a convex optimization problem is solved. For algorithms to solve these problems, we refer interested readers to [7] and references therein. In the particular case of SLP-2, one can apply a decomposition-based method to obtain an outer approximation to $h_\omega (x)$. In fact, this is what we use in our numerical illustration in Sect. 5.

Algorithm A-1 decomposes primal formulation of (DRSP-V) and obtain $x^{*}$ and $\mathbf {p}^{*}$ concurrently and directly. Because the Primal Decomposition exploits the polyhedral structure of the ambiguity set formed using the total variation distance, it might have computational benefits over those decomposition methods that solve the dual formulation. A comprehensive computational study will provide more insight on the performance of these algorithms; however, such a study is out of the scope of this paper.