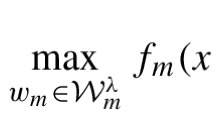Data-driven robust optimization

Abstract

The last decade witnessed an explosion in the availability of data for operations research applications. Motivated by this growing availability, we propose a novel schema for utilizing data to design uncertainty sets for robust optimization using statistical hypothesis tests. The approach is flexible and widely applicable, and robust optimization problems built from our new sets are computationally tractable, both theoretically and practically. Furthermore, optimal solutions to these problems enjoy a strong, finite-sample probabilistic guarantee whenever the constraints and objective function are concave in the uncertainty. We describe concrete procedures for choosing an appropriate set for a given application and applying our approach to multiple uncertain constraints. Computational evidence in portfolio management and queueing confirm that our data-driven sets significantly outperform traditional robust optimization techniques whenever data are available.

Appendices

Appendix 1: Omitted Proofs

1.1 Proof of Theorem 1

Proof

For the first part, let ${\mathbf {x}}^*$ be such that $f\left( {\mathbf {u}}, {\mathbf {x}}^*\right) \le 0$ for all ${\mathbf {u}}\in {\mathcal {U}}_\epsilon$, and consider the closed, convex set $\{ {\mathbf {u}}\in {{\mathbb {R}}}^d : f\left( {\mathbf {u}}, {\mathbf {x}}^*\right) \ge t \}$ where $t > 0$. That ${\mathbf {x}}^*$ is robust feasible implies $\max _{{\mathbf {u}}\in {\mathcal {U}}} f\left( {\mathbf {u}}, {\mathbf {x}}^*\right) \le 0$ which implies that ${\mathcal {U}}$ and $\{ {\mathbf {u}}\in {{\mathbb {R}}}^d : f\left( {\mathbf {u}}, {\mathbf {x}}^*\right) \ge t \}$ are disjoint. From the separating hyperplane theorem, there exists a strict separating hyperplane ${\mathbf {v}}^T{\mathbf {u}}= v_0$ such that $v_0 > {\mathbf {v}}^T {\mathbf {u}}$ for all ${\mathbf {u}}\in {\mathcal {U}}$ and ${\mathbf {v}}^T{\mathbf {u}}> v_0$ for all ${\mathbf {u}}\in \{ {\mathbf {u}}\in {{\mathbb {R}}}^d: f\left( {\mathbf {u}}, {\mathbf {x}}^*\right) \ge t \}$. Observe

$$\begin{aligned} v_0 > \max _{{\mathbf {u}}\in {\mathcal {U}}} {\mathbf {v}}^T{\mathbf {u}}= \delta ^*({\mathbf {v}}| \ {\mathcal {U}}) \ge \text {VaR}_{\epsilon }^{{\mathbb {P}}}\left( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}\right) , \end{aligned}$$

and

$$\begin{aligned} {\mathbb {P}}\left( f\left( {\tilde{{\mathbf {u}}}}, {\mathbf {x}}^*\right) \ge t \right) \le {\mathbb {P}}\left( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}> v_0 \right) \le {\mathbb {P}}\left( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}> \text {VaR}_{\epsilon }^{{\mathbb {P}}}\left( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}\right) \right) \le \epsilon . \end{aligned}$$

Taking the limit as $t \downarrow 0$ and using the continuity of probability proves ${\mathbb {P}}( f({\tilde{{\mathbf {u}}}}, {\mathbf {x}}^*) > 0 ) \le \epsilon$ and that (2) is satisfied.

For the second part of the theorem, let $t > 0$ be such that $\delta ^*( {\mathbf {v}}| \ {\mathcal {U}}) \le \text {VaR}_{\epsilon }^{{\mathbb {P}}}\left( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}\right) - t$. Define $f({\mathbf {u}}, x) \equiv {\mathbf {v}}^T{\mathbf {u}}- x$. Then $x^* = {\delta ^*}({\mathbf {v}}| \ {\mathcal {U}})$ satisfies $f\left( {\mathbf {u}}, {\mathbf {x}}^*\right) \le 0$ for all ${\mathbf {u}}\in {\mathcal {U}}$, but

$$\begin{aligned} {\mathbb {P}}\left( f({\tilde{{\mathbf {u}}}}, {\mathbf {x}})> 0 \right) = {\mathbb {P}}\left( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}> {\delta ^*}\left( {\mathbf {v}}| \ {\mathcal {U}}\right) \right) \ge {\mathbb {P}}\left( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}\ge \text {VaR}_{\epsilon }^{{\mathbb {P}}}\left( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}\right) - t\right) > \epsilon \end{aligned}$$

by (7). Thus, (2) does not hold. $\square$

1.2 Proofs of Theorems 2–4

Proof of Theorem 2

$$\begin{aligned}&{\mathbb {P}}^*_{\mathcal {S}}\biggr ( {\mathcal {U}}({\mathcal {S}}, \epsilon , \alpha ) \text { implies a probabilistic guarantee at level} \epsilon \text { for }{\mathbb {P}}^*\biggr )\\&\quad = {\mathbb {P}}^*_{\mathcal {S}}\left( \delta ^*\left( {\mathbf {v}}| \ {\mathcal {U}}({\mathcal {S}}, \epsilon , \alpha ) \right) \ge \text {VaR}_{\epsilon }^{{\mathbb {P}}^*}\left( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}\right) \ \forall {\mathbf {v}}\in {{\mathbb {R}}}^d\right)&\hbox { Theorem }1\\&\quad \ge {\mathbb {P}}^*_{\mathcal {S}}\left( {\mathbb {P}}^* \in {\mathcal {P}}({\mathcal {S}}, \epsilon , \alpha ) \right)&\text {(Step 2 of schema)}\\&\quad \ge 1-\alpha&\text {(Confidence region).} \end{aligned}$$

$\square$

Proof

For the first part,

$$\begin{aligned}&{\mathbb {P}}^*_{\mathcal {S}}( \{ {\mathcal {U}}({\mathcal {S}}, \epsilon , \alpha ): \ 0< \epsilon< 1 \} \text { simultaneously implies a probabilistic guarantee})\\&\quad \begin{aligned}&= {\mathbb {P}}^*_{\mathcal {S}}(\delta ^*({\mathbf {v}}| \ {\mathcal {U}}({\mathcal {S}}, \epsilon , \alpha ) ) \ge \text {VaR}_{\epsilon }^{{\mathbb {P}}^*}\left( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}\right) \ \forall {\mathbf {v}}\in {{\mathbb {R}}}^d, \ 0< \epsilon< 1 )&\hbox { Theorem} 1\\&\ge {\mathbb {P}}^*_{\mathcal {S}}( {\mathbb {P}}^* \in \bigcap _{\epsilon : 0< \epsilon < 1} {\mathcal {P}}({\mathcal {S}}, \epsilon , \alpha ) )&\text {(Step 2 of schema)}\\&= {\mathbb {P}}^*_{\mathcal {S}}( {\mathbb {P}}^* \in {\mathcal {P}}({\mathcal {S}}, \alpha ) )&(({\mathcal {P}}({\mathcal {S}}, \alpha ))\text { is independent of }\epsilon )\\&\ge 1-\alpha&\text {(Confidence region).} \end{aligned} \end{aligned}$$

For the second part, let $\epsilon _1, \ldots , \epsilon _m$ denote any feasible $\epsilon _j$’s in (10).

$$\begin{aligned} 1-\alpha&\le {\mathbb {P}}^*_{\mathcal {S}}\left( \{ {\mathcal {U}}\left( {\mathcal {S}}, \epsilon , \alpha \right) : \ 0< \epsilon < 1 \} \text { simultaneously implies a probabilistic guarantee}\right) \\&\le {\mathbb {P}}^*_{\mathcal {S}}\left( {\mathcal {U}}\left( {\mathcal {S}}, \epsilon _j, \alpha \right) \text { implies a probabilistic guarantee at level } \epsilon _j, \ j=1, \ldots , m\right) . \end{aligned}$$

Applying the union-bound and Theorem 2 yields the result. $\square$

Proof of Theorem 4

Consider the first statement. By Theorem 1, $\text {VaR}_{\epsilon }^{{\mathbb {P}}}\left( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}\right) \le \delta ^*({\mathbf {v}}| {\mathcal {U}}_\epsilon )$. Moreover, since ${{\mathrm{\text {supp}}}}({\mathbb {P}}^*) \subseteq {\mathcal {U}}_0$, $0 = {\mathbb {P}}( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}> \max _{{\mathbf {u}}\in {{\mathrm{\text {supp}}}}({\mathbb {P}}^*)} {\mathbf {v}}^T{\mathbf {u}}) \ge {\mathbb {P}}( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}> \max _{{\mathbf {u}}\in {\mathcal {U}}_0} {\mathbf {v}}^T{\mathbf {u}}) = {\mathbb {P}}( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}> \delta ^*({\mathbf {v}}| \ {\mathcal {U}}_0) )$ This, in turn, implies $\text {VaR}_{\epsilon }^{{\mathbb {P}}}\left( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}\right) \le \delta ^*({\mathbf {v}}| {\mathcal {U}}_0)$. Combining, we have $\text {VaR}_{\epsilon }^{{\mathbb {P}}}\left( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}\right) \le \min \left( \delta ^*({\mathbf {v}}| {\mathcal {U}}_\epsilon ), \delta ^*({\mathbf {v}}| {\mathcal {U}}_0) \right) = \delta ^*({\mathbf {v}}| \ {\mathcal {U}}_\epsilon \cap {\mathcal {U}}_0 )$ where the last equality follows because both ${\mathcal {U}}_0$ and ${\mathcal {U}}_\epsilon$ are convex. Thus, ${\mathcal {U}}_\epsilon \cap {\mathcal {U}}_0$ implies a probabilistic guarantee by Theorem 1. The second statement is entirely similar. $\square$

1.3 Proof of Theorem 5 and Proposition 1

We require the following well-known result.

Theorem 14

(Rockafellar and Ursayev [43]) Suppose ${{\mathrm{\text {supp}}}}({\mathbb {P}}) \subseteq \{{\mathbf {a}}_0, \ldots , {\mathbf {a}}_{n-1} \}$ and let ${\mathbb {P}}({\tilde{{\mathbf {u}}}}= {\mathbf {a}}_j) = p_j$. Let

$$\begin{aligned} {\mathcal {U}}^{{{\mathrm{\text {CVaR}}}}_\epsilon ^{\mathbb {P}}} = \left\{ {\mathbf {u}}\in {{\mathbb {R}}}^d : {\mathbf {u}}= \sum _{j=0}^{n-1} q_j {\mathbf {a}}_j, \ {\mathbf {q}}\in {\varDelta }_n, \ {\mathbf {q}}\le \frac{1}{\epsilon } {\mathbf {p}}\right\} . \end{aligned}$$

(44)

Then, $\delta ^*({\mathbf {v}}| \ {\mathcal {U}}^{{{\mathrm{\text {CVaR}}}}_\epsilon ^{{\mathbb {P}}}}) = {{\mathrm{\text {CVaR}}}}^{{\mathbb {P}}}\left( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}\right)$.

We now prove the theorem.

Proof of Theorem 5

We prove the theorem for ${\mathcal {U}}^{\chi ^2}_\epsilon$. The proof for ${\mathcal {U}}^G_\epsilon$ is similar. From Theorem 2, it suffices to show that $\delta ^*( {\mathbf {v}}| \ {\mathcal {U}}^{\chi ^2}_\epsilon )$ is an upper bound to $\sup _{{\mathbb {P}}\in {\mathcal {P}}^{\chi ^2}} \text {VaR}_{\epsilon }^{{\mathbb {P}}}\left( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}\right)$:

$$\begin{aligned} \sup _{{\mathbb {P}}\in {\mathcal {P}}^{\chi ^2}} \text {VaR}_{\epsilon }^{{\mathbb {P}}}\left( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}\right)&\le \sup _{{\mathbb {P}}\in {\mathcal {P}}^{\chi ^2}} {{\mathrm{\text {CVaR}}}}_\epsilon ^{\mathbb {P}}\left( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}\right)&\left( {{\mathrm{\text {CVaR}}}}_\epsilon ^{\mathbb {P}}\text { is an upper bound to } \text {VaR}_{\epsilon }^{{\mathbb {P}}} \right) \\&= \sup _{{\mathbb {P}}\in {\mathcal {P}}^{\chi ^2}} \max _{{\mathbf {u}}\in {\mathcal {U}}^{{{\mathrm{\text {CVaR}}}}_\epsilon ^{\mathbb {P}}}} {{\mathbf {v}}^T{\mathbf {u}}}&({\hbox {Thm}. 14})\\&= \max _{{\mathbf {u}}\in {\mathcal {U}}^{\chi ^2}_\epsilon } {{\mathbf {v}}^T{\mathbf {u}}}&({\hbox {Combining Eqs}. 15\hbox { and }13}). \end{aligned}$$

To obtain the expression for $\delta ^*({\mathbf {v}}| \ {\mathcal {U}}^{\chi ^2}_\epsilon )$ observe,

$$\begin{aligned} \delta ^*\left( {\mathbf {v}}| \ {\mathcal {U}}^{\chi ^2}_\epsilon \right)&= \inf _{{\mathbf {w}}\ge 0} \left\{ \max _{ {\mathbf {q}}\in {\varDelta }_n} \sum _{i=0}^{n-1} q_i \left( {\mathbf {a}}_i^T{\mathbf {v}}- w_i\right) + \frac{1}{\epsilon } \max _{ {\mathbf {p}}\in {\mathcal {P}}^{\chi ^2} } {\mathbf {w}}^T {\mathbf {p}}\right\} , \end{aligned}$$

from Lagrangian duality. The optimal value of the first maximization is $\beta = \max _i {\mathbf {a}}_i^T{\mathbf {v}}- w_i$. The second maximization is of the form studied in [9, Corollary 1] and has optimal value

$$\begin{aligned} {\inf _{\lambda \ge 0, \left( \lambda + \eta \right) {\mathbf {e}}\ge {\mathbf {w}}, \eta }} \eta + \frac{\lambda \chi ^2_{n-1, 1-\alpha }}{N} + 2\lambda - 2 \sum _{i=0}^{n-1} {\hat{p}}_i \sqrt{\lambda }\sqrt{\lambda + \eta - w_i}. \end{aligned}$$

Introduce the auxiliary variables $s_i$, such that $s_i^2 \le \lambda \cdot (\lambda + \eta - w_i)$. This last constraint is of hyperbolic type. Using [37], we can rewrite

$$\begin{aligned} \begin{aligned} s_i^2&\le \lambda \cdot \left( \lambda + \eta - w_i\right) , \quad i =0, \ldots , n-1, \\ \lambda + \eta&\ge w_i, \quad i = 0, \ldots , n-1, \\ \lambda&\ge 0 \end{aligned} \Leftrightarrow \quad \left\| \begin{matrix} 2 s_i \\ \eta - w_i \end{matrix} \right\| \le 2 \lambda + \eta - w_i, \quad i = 0, \ldots , n-1. \end{aligned}$$

Substituting these constraints (and the auxiliary variable) above yields the given formulation. $\square$

Proof of Proposition 1

Let ${\varDelta }_j \equiv \frac{{\hat{p}}_j - p_j}{p_j}$. Then, $D( {\hat{ {\mathbf {p}}}}, {\mathbf {p}}) = \sum _{j=0}^{n-1} {\hat{p}}_j \log ( {\hat{p}}_j / p_j ) = \sum _{j=0}^{n-1} p_j ({\varDelta }_j + 1) \log ( {\varDelta }_j + 1)$. Using a Taylor expansion of $x \log x$ around $x=1$ yields,

$$\begin{aligned} D\left( {\hat{ {\mathbf {p}}}}, {\mathbf {p}}\right) = \sum _{j=0}^{n-1} p_j \left( {\varDelta }_j + \frac{{\varDelta }_j^2}{2} + O\left( {\varDelta }_j^3\right) \right) = \sum _{j=0}^{n-1} \frac{\left( {\hat{p}}_j - p_j\right) ^2}{2p_j} + \sum _{j=0}^{n-1} O\left( {\varDelta }_j^3\right) ,\nonumber \\ \end{aligned}$$

(45)

where the last equality follows by expanding out terms and observing that $\sum _{j=0}^{n-1} {\hat{p}}_j = \sum _{j=0}^{n-1} p_j = 1$. Next, note ${\mathbf {p}}\in {\mathcal {P}}^G \implies {\hat{p}}_j / p_j \le \exp ( \frac{\chi ^2_{n-1, 1-\alpha }}{2N{\hat{p}}_j} ).$ From the Strong Law of Large Numbers, for any $0< \alpha ^\prime < 1$, there exists M such that for all $N> M$, ${\hat{p}}_j \ge p^*_j / 2$ with probability at least $1 - \alpha ^\prime$ for all $j = 0, \ldots , n-1$, simultaneously. It follows that for N sufficiently large, with probability $1-\alpha ^\prime$, ${\mathbf {p}}\in {\mathcal {P}}^G \implies {\hat{p}}_j / p_j \le \exp ( \frac{\chi ^2_{n-1, 1-\alpha }}{Np^*_j} )$ which implies that $| {\varDelta }_j | \le \exp ( \frac{\chi ^2_{n-1, 1-\alpha }}{Np^*_j} ) -1 = O(N^{-1})$. Substituting into (45) completes the proof. $\square$

1.4 Proof of Theorems 6 and 7

We first prove the following auxiliary result that will allow us to evaluate the inner supremum in (19).

Theorem 15

Suppose g(u) is monotonic. Then,

$$\begin{aligned} \sup _{{\mathbb {P}}_i \in {\mathcal {P}}^{KS}_i} {{\mathbb {E}}}^{{\mathbb {P}}_i}\left[ g\left( {{\tilde{u}}}_i\right) \right] = \max \left( \sum _{j=0}^{N+1} q^L_j\left( {\varGamma }^{KS}\right) g\left( {\hat{u}}_i^{\left( j\right) }\right) , \sum _{j=0}^{N+1} q^R_j\left( {\varGamma }^{KS}\right) g\left( {\hat{u}}_i^{\left( j\right) }\right) \right) \nonumber \\ \end{aligned}$$

(46)

Proof

Observe that the discrete distribution which assigns mass $q^L_j\left( {\varGamma }^{KS}\right)$ (resp. $q^R_j\left( {\varGamma }^{KS}\right)$) to the point ${\hat{u}}^{(j)}$ for $j=0, \ldots , N+1$ is an element of ${\mathcal {P}}^{KS}_i$. Thus, Eq. (46) holds with “$=$” replaced by “$\ge$”.

For the reverse inequality, we have two cases. Suppose first that $g(u_i)$ is non-decreasing. Given ${\mathbb {P}}_i \in {\mathcal {P}}_i^{KS}$, consider the measure ${\mathbb {Q}}$ defined by

$$\begin{aligned}&{\mathbb {Q}}\left( {{\tilde{u}}}_i = {\hat{u}}_i^{\left( 0\right) }\right) \equiv 0, \ \ {\mathbb {Q}}\left( {{\tilde{u}}}_i = {\hat{u}}_i^{\left( 1\right) }\right) \equiv {\mathbb {P}}_i\left( {\hat{u}}_i^{\left( 0\right) } \le {{\tilde{u}}}_i \le {\hat{u}}_i^{\left( 1\right) }\right) , \nonumber \\&{\mathbb {Q}}\left( {{\tilde{u}}}_i = {\hat{u}}_i^{\left( j\right) }\right) \equiv {\mathbb {P}}_i\left( {\hat{u}}_i^{\left( j-1\right) } < {{\tilde{u}}}_i \le {\hat{u}}_i^{\left( j\right) }\right) , \ \ j = 2, \ldots , N+1. \end{aligned}$$

(47)

Then, ${\mathbb {Q}}\in {\mathcal {P}}^{KS}$, and since $g(u_i)$ is non-decreasing, ${{\mathbb {E}}}^{{\mathbb {P}}_i}[g({{\tilde{u}}}_i)] \le {{\mathbb {E}}}^{\mathbb {Q}}[g({{\tilde{u}}}_i)]$. Thus, the measure attaining the supremum on the left-hand side of Eq. (46) has discrete support $\{{\hat{u}}_i^{(0)}, \ldots , {\hat{u}}_i^{(N+1)} \}$, and the supremum is equivalent to the linear optimization problem:

$$\begin{aligned} \max _ {\mathbf {p}}\quad&\sum _{j=0}^{N+1} p_j g\left( {\hat{u}}^{(j)}\right) \nonumber \\ \text {s.t.} \quad&{\mathbf {p}}\ge {\mathbf {0}}, \ \ {\mathbf {e}}^T {\mathbf {p}}= 1, \nonumber \\&\sum _{k=0}^j p_k \ge \frac{j}{N} - {\varGamma }^{KS}, \quad \sum _{k=j}^{N+1} p_k \ge \frac{N-j +1}{N} - {\varGamma }^{KS}, \quad j=1, \ldots , N, \end{aligned}$$

(48)

(We have used the fact that ${\mathbb {P}}_i({{\tilde{u}}}_i < {\hat{u}}_i^{(j)}) = 1 - {\mathbb {P}}_i({{\tilde{u}}}\ge {\hat{u}}_i^{(j)})$.) Its dual is:

$$\begin{aligned} \min _{{\mathbf {x}}, {\mathbf {y}}, t} \quad&\sum _{j=1}^N x_j \left( {\varGamma }^{KS}- \frac{j}{N}\right) + \sum _{j=1}^N y_j\left( {\varGamma }^{KS} - \frac{N-j+1}{N}\right) + t \\ \text {s.t.} \quad&t -\sum _{k \le j \le N} x_j -\sum _{1 \le j \le k} y_j \ge g\left( {\hat{u}}^{(k)}\right) , \ \ k = 0, \ldots , N + 1, \\&{\mathbf {x}}, {\mathbf {y}}\ge {\mathbf {0}}. \end{aligned}$$

Observe that the primal solution ${\mathbf {q}}^R\left( {\varGamma }^{KS}\right)$ and dual solution ${\mathbf {y}}= {\mathbf {0}}$, $t = g({\hat{u}}_i^{(N+1)})$ and

$$\begin{aligned} x_j = {\left\{ \begin{array}{ll} g\left( {\hat{u}}_i^{(j+1)}\right) - g \left( {\hat{u}}_i^{(j)}\right) &{}\text { for } N-j^* \le j \le N, \\ 0 &{}\text { otherwise}, \end{array}\right. } \end{aligned}$$

constitute a primal-dual optimal pair. This proves (46) when g is non-decreasing. The case of $g(u_i)$ non-increasing is similar. $\square$

Proof of of Theorem 6

Notice by Theorem 15, Eq. (19) is equivalent to the given expression for $\delta ^*({\mathbf {v}}| \ {\mathcal {U}}^I_\epsilon )$. By our schema, it suffices to show then that this expression is truly the support function of ${\mathcal {U}}^I_\epsilon$. By Lagrangian duality,

$$\begin{aligned} \delta ^*\left( {\mathbf {v}}| \ {\mathcal {U}}^I_\epsilon \right) = \inf _{\lambda \ge 0} \left( \begin{aligned} \lambda \log (1/\epsilon ) + \max _{ {\mathbf {q}}, \varvec{\theta }} \quad&\sum _{i=1}^d v_i \sum _{j=0}^{N+1} {\hat{u}}_i^{(j)} q^i_j - \lambda \sum _{i=1}^d D\left( {\mathbf {q}}^i, \theta _i {\mathbf {q}}^L + (1-\theta _i) {\mathbf {q}}^R \right) \\ \text {s.t.} \quad&{\mathbf {q}}^i \in {\varDelta }_{N+2}, 0\le \theta _i \le 1, \ \ i = 1, \ldots , d. \end{aligned} \right) \end{aligned}$$

The inner maximization decouples in the variables indexed by i. The $i^{\text {th}}$ subproblem is

$$\begin{aligned} \max _{\theta _i \in [0, 1]} \lambda \left\{ \max _{ {\mathbf {q}}_i \in {\varDelta }_{N+2}} \left\{ \sum _{j=0}^{N+1} \frac{v_i{\hat{u}}_i^{(j)}}{\lambda } q_{ij} - D\left( {\mathbf {q}}^i, \theta _i {\mathbf {q}}^L + (1-\theta _i) {\mathbf {q}}^R \right) \right\} \right\} . \end{aligned}$$

The inner maximization can be solved analytically [17, p. 93], yielding:

$$\begin{aligned} q_j^i = \frac{p_j^i e^{v_i {\hat{u}}_{i}^{(j)} /\lambda }}{\sum _{j=0}^{N+1} p_j^i e^{v_i {\hat{u}}_{i}^{(j)} /\lambda } }, \quad p_j^i = \theta _i q^L_j\left( {\varGamma }^{KS}\right) + \left( 1-\theta _i\right) q^R_j\left( {\varGamma }^{KS}\right) . \end{aligned}$$

(49)

Substituting in this solution and recombining subproblems yields

$$\begin{aligned} \lambda \log \left( 1/\epsilon \right) + \lambda \sum _{i=1}^d \log \left( \max _{\theta _i \in [0, 1] }\sum _{j=0}^{N+1} \left( \theta _i q^L_j({\varGamma }^{KS}) + (1-\theta _i)q^R_j({\varGamma }^{KS})\right) e^{v_i {\hat{u}}_{i}^{\left( j\right) } /\lambda }. \right) \nonumber \\ \end{aligned}$$

(50)

The inner optimizations over $\theta _i$ are all linear, and hence achieve an optimal solution at one of the end points, i.e., either $\theta _i = 0$ or $\theta _i =1$. This yields the given expression for $\delta ^*({\mathbf {v}}| \ {\mathcal {U}})$.

Following this proof backwards to identify the optimal ${\mathbf {q}}^i$, and, thus, ${\mathbf {u}}\in {\mathcal {U}}^I$ also proves the validity of the procedure given in Remark 8 $\square$

Proof of Theorem 7

By inspection, (28) is the worst-case value of (26) over ${\mathcal {P}}^{FB}$. By Theorem 3, it suffices to show that this expression truly is the support function of ${\mathcal {U}}^{FB}_\epsilon$. First observe

$$\begin{aligned} \max _{{\mathbf {u}}\in {\mathcal {U}}^{FB}_\epsilon } {\mathbf {u}}^T{\mathbf {v}}= & {} \min _{\lambda \ge 0} \left\{ \lambda \log (1/\epsilon ) + \max _{\begin{array}{c} {\mathbf {m}}_b \le {\mathbf {y}}_1 \le {\mathbf {m}}_b, {\mathbf {y}}_2 \ge , {\mathbf {y}}_3 \ge {\mathbf {0}} \end{array}} \sum _{i=1}^d v_i \left( y_{1i} {+} y_{2i} {-} y_{3i} \right) \right. \\&\quad \quad \quad \quad \left. - \lambda \sum _{i=1}^d \frac{y_{2i}^2 }{2 {\overline{\sigma }}_{fi}^2} + \frac{y_{3i}^2 }{2 {\overline{\sigma }}_{bi}^2}\right\} \end{aligned}$$

by Lagrangian strong duality. The inner maximization decouples by i. The $i^{\text {th}}$ subproblem further decouples into three sub-subproblems. The first is $\max _{m_{bi} \le y_{i1} \le m_{fi} } v_i y_{1i}$ with optimal solution

$$\begin{aligned} y_{1i} = {\left\{ \begin{array}{ll} m_{fi} &{}\text { if } v_i \ge 0, \\ m_{bi} &{} \text { if } v_i < 0. \end{array}\right. } \end{aligned}$$

The second sub-subproblem is $\max _{y_{2i} \ge 0} v_i y_{2i} - \lambda \frac{y_{2i}^2}{2 {\overline{\sigma }}_{fi}^2}$. This is maximizing a concave quadratic function of one variable. Neglecting the non-negativity constraint, the optimum occurs at $y_{2i}^* = \frac{ v_i\sigma ^2_{fi}}{\lambda }$. If this value is negative, the optimum occurs at $y_{2i}^* = 0$. Consequently,

$$\begin{aligned} \max _{y_{2i} \ge 0} \ \ v_i y_{2i} - \lambda \frac{y_{2i}^2}{2 {\overline{\sigma }}_{fi}^2} = {\left\{ \begin{array}{ll} \frac{ v_i \sigma ^2_{fi}}{2\lambda } &{}\text { if } v_i \ge 0,\\ 0 &{}\text { if } v_i < 0. \end{array}\right. } \end{aligned}$$

Similarly, we can show that the third subproblem has the following optimum value

$$\begin{aligned} \max _{y_{3i} \ge 0} \ \ -v_i y_{3i} - \lambda \frac{y_{3i}^2}{2 {\overline{\sigma }}_{bi}^2} ={\left\{ \begin{array}{ll} \frac{ v_i \sigma ^2_{bi}}{2\lambda } &{}\text { if } v_i \le 0,\\ 0 &{}\text { if } v_i > 0. \end{array}\right. } \end{aligned}$$

Combining the three sub-subproblems yields

$$\begin{aligned} \delta ^*\left( {\mathbf {v}}| {\mathcal {U}}^{FB}_\epsilon \right)= & {} \sum _{i : v_i> 0 } v_i m_{fi} + \sum _{i: v_i< 0 } v_i m_{bi} + \min _{\lambda \ge 0} \lambda \log \left( 1/\epsilon \right) \\&+ \frac{1}{2\lambda } \left( \sum _{i: v_i > 0 } v_i^2 {\overline{\sigma }}_{fi}^2 + \sum _{i: v_i < 0 } v_i^2 {\overline{\sigma }}_{bi}^2 \right) . \end{aligned}$$

This optimization can be solved closed-form, yielding

$$\begin{aligned} \lambda ^* = \sqrt{\frac{\sum _{i: v_i > 0 } v_i^2 {\overline{\sigma }}_{fi}^2 + \sum _{i: v_i \le 0 } v_i^2 {\overline{\sigma }}_{bi}^2}{2 \log (1/\epsilon )} }. \end{aligned}$$

Simplifying yields the right hand side of (28). Moreover, following the proof backwards to identify the maximizing ${\mathbf {u}}\in {\mathcal {U}}^{FB}_\epsilon$ proves the validity of the procedure given in Remark 11. $\square$

1.5 Proof of Theorem 8

Proof

Observe,

$$\begin{aligned} \sup _{{\mathbb {P}}\in {\mathcal {P}}^M} \text {VaR}_{\epsilon }^{{\mathbb {P}}}\left( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}\right)&\le \sup _{{\mathbb {P}}\in {\mathcal {P}}^M} \sum _{i=1}^d \text {VaR}_{\epsilon /d}^{{\mathbb {P}}}\left( v_i {{\tilde{u}}}_i\right) = \sum _{i : v_i > 0 } v_i {\hat{u}}_i^{\left( s\right) } + \sum _{i : v_i \le 0 } v_i {\hat{u}}_i^{\left( N-s+1\right) }, \end{aligned}$$

(51)

where the equality follows from the positive homogeneity of $\text {VaR}_{\epsilon }^{{\mathbb {P}}}$, and this last expression is equivalent to (32) because ${\hat{u}}_i^{(N-s+1)} \le {\hat{u}}_i^{(s)}$. By Theorem 2, it suffices to show that $\delta ^*({\mathbf {v}}| \ {\mathcal {U}}^M)$ is the support function of ${\mathcal {U}}^M_\epsilon$, and this is immediate. $\square$

1.6 Proof of Theorem 9

Proof

We first compute $\sup _{{\mathbb {P}}\in {\mathcal {P}}^{LCX}} {\mathbb {P}}({\mathbf {v}}^T{\tilde{{\mathbf {u}}}}> t)$ for fixed ${\mathbf {v}}, t$. In this spirit of Bertsimas et al. [45] and Shapiro [15] this optimization admits the following strong dual:

$$\begin{aligned} \inf _{\theta , w_\sigma , \lambda ({\mathbf {a}}, b)} \quad&\theta - \left( \frac{1}{N}\sum _{j=1}^N \Vert \hat{{\mathbf {u}}}_j \Vert ^2 - {\varGamma }_\sigma \right) w_\sigma + \int _{{\mathcal {B}}} {\varGamma }({\mathbf {a}}, b) d\lambda ({\mathbf {a}}, b) \nonumber \\ \text {s.t.} \quad&\theta - w_\sigma \Vert {\mathbf {u}}\Vert ^2 + \int _{{\mathcal {B}}} \left( {\mathbf {a}}^T {\mathbf {u}}- b\right) ^+ d \lambda \left( {\mathbf {a}}, b\right) \ge {\mathbb {I}}\left( {\mathbf {u}}^T{\mathbf {v}}> t \right) \ \ \forall {\mathbf {u}}\in {{\mathbb {R}}}^d, \nonumber \\&w_\sigma \ge 0, \ \ d\lambda \left( {\mathbf {a}}, b\right) \ge 0, \end{aligned}$$

(52)

where ${\varGamma }({\mathbf {a}}, b) \equiv \frac{1}{N} \sum _{j=1}^N ({\mathbf {a}}^T\hat{{\mathbf {u}}}_j - b)^+ + {\varGamma }_{LCX}$. We claim that $w_\sigma = 0$ in any feasible solution. Indeed, suppose $w_\sigma > 0$ in some feasible solution. Note $({\mathbf {a}}, b) \in {\mathcal {B}}$ implies that $({\mathbf {a}}^T {\mathbf {u}}- b)^+ = O(\Vert {\mathbf {u}}\Vert )$ as $\Vert {\mathbf {u}}\Vert \rightarrow \infty$. Thus, the left-hand side of Eq. (52) tends to $-\infty$ as $\Vert {\mathbf {u}}\Vert \rightarrow \infty$ while the right-hand side is bounded below by zero. This contradicts the feasibility of the solution.

Since $w_\sigma = 0$ in any feasible solution, rewrite the above as

$$\begin{aligned} \inf _{\theta , \lambda \left( {\mathbf {a}}, b\right) } \quad&\theta + \int _{{\mathcal {B}}} {\varGamma }\left( {\mathbf {a}}, b\right) d\lambda \left( {\mathbf {a}}, b\right) \nonumber \\ \text {s.t.} \quad&\theta + \int _{{\mathcal {B}}} \left( {\mathbf {a}}^T {\mathbf {u}}- b\right) ^+ d \lambda \left( {\mathbf {a}}, b\right) \ge 0 \ \ \forall {\mathbf {u}}\in {{\mathbb {R}}}^d, \end{aligned}$$

(53a)

$$\begin{aligned}&\theta + \int _{{\mathcal {B}}} \left( {\mathbf {a}}^T {\mathbf {u}}- b\right) ^+ d \lambda \left( {\mathbf {a}}, b\right) \ge 1 \ \ \forall {\mathbf {u}}\in \{{\mathbf {u}}\in {{\mathbb {R}}}^d : {\mathbf {u}}^T{\mathbf {v}}> t \}, \nonumber \\&d\lambda \left( {\mathbf {a}}, b\right) \ge 0. \end{aligned}$$

(53b)

The two infinite constraints can be rewritten using duality. Specifically, Eq. (53a) is

$$\begin{aligned}&-\theta \le \quad \min _{s\left( {\mathbf {a}}, b\right) \ge 0, {\tilde{{\mathbf {u}}}}\in {{\mathbb {R}}}^d} \quad \int _{{\mathcal {B}}} s\left( {\mathbf {a}}, b\right) d\lambda \left( {\mathbf {a}}, b\right) \\&\qquad \text {s.t.} \quad s\left( {\mathbf {a}}, b\right) \ge \left( {\mathbf {a}}^T{\tilde{{\mathbf {u}}}}- b\right) \quad \forall \left( {\mathbf {a}}, b\right) \in {\mathcal {B}}, \end{aligned}$$

which admits the dual:

$$\begin{aligned}&-\theta \le \max _{y_1\left( {\mathbf {a}}, b\right) } \quad -\int _{{\mathcal {B}}} b \ dy_1\left( {\mathbf {a}}, b\right) \\&\qquad \text {s.t.} \quad 0 \le dy_1\left( {\mathbf {a}}, b\right) \le d\lambda \left( {\mathbf {a}}, b\right) \quad \forall \left( {\mathbf {a}}, b\right) \in {\mathcal {B}},\\&\qquad \int _{{\mathcal {B}}} {\mathbf {a}}\ dy_1\left( {\mathbf {a}}, b\right) = 0. \end{aligned}$$

Equation (53b) can be treated similarly using continuity to take the closure of $\{{\mathbf {u}}\in {{\mathbb {R}}}^d : {\mathbf {u}}^T{\mathbf {v}}> t\}$. Combining both constraints yields the equivalent representation of (53)

$$\begin{aligned} \inf _{\begin{array}{c} \theta , \tau , \lambda \left( {\mathbf {a}}, b\right) , \\ y_1\left( {\mathbf {a}}, b\right) , y_2\left( {\mathbf {a}}, b\right) \end{array}} \quad&\theta + \int _{{\mathcal {B}}} {\varGamma }\left( {\mathbf {a}}, b\right) d\lambda \left( {\mathbf {a}}, b\right) \nonumber \\ \text {s.t.} \quad&\theta -\int _{{\mathcal {B}}} b \ dy_1\left( {\mathbf {a}}, b\right) \ge 0 , \ \ \theta + t \tau - \int _{{\mathcal {B}}} b \ dy_2\left( {\mathbf {a}}, b\right) \ge 1, \nonumber \\&0 \le dy_1\left( {\mathbf {a}}, b\right) \le d\lambda \left( {\mathbf {a}}, b\right) \quad \forall \left( {\mathbf {a}}, b\right) \in {\mathcal {B}}, \nonumber \\&0 \le dy_2\left( {\mathbf {a}}, b\right) \le d\lambda \left( {\mathbf {a}}, b\right) \quad \forall \left( {\mathbf {a}}, b\right) \in {\mathcal {B}}, \nonumber \\&\int _{{\mathcal {B}}} {\mathbf {a}}\ dy_1\left( {\mathbf {a}}, b\right) = 0, \nonumber \\&\tau {\mathbf {v}}= \int _{{\mathcal {B}}} {\mathbf {a}}\ d y_2\left( {\mathbf {a}}, b\right) ,\nonumber \\&\tau \ge 0. \end{aligned}$$

(54)

Now the worst-case Value at Risk can be written as

$$\begin{aligned} \sup _{{\mathbb {P}}\in {\mathcal {P}}^{LCX}} \text {VaR}_{\epsilon }^{{\mathbb {P}}}\left( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}\right) =&\inf _{\begin{array}{c} \theta , \tau , t, \lambda ({\mathbf {a}}, b), \\ y_1({\mathbf {a}}, b), y_2({\mathbf {a}}, b) \end{array}} t\\ \text {s.t.} \quad&\theta + \int _{{\mathcal {B}}} {\varGamma }({\mathbf {a}}, b) d\lambda ({\mathbf {a}}, b) \le \epsilon ,\\&(\theta , \tau , \lambda ({\mathbf {a}}, b), y_1({\mathbf {a}}, b), y_2({\mathbf {a}}, b), t) (54) . \end{aligned}$$

We claim that $\tau > 0$ in an optimal solution. Suppose to the contrary that $\tau =0$ in a candidate solution to this optimization problem. As $t \rightarrow -\infty$, this candidate solution remains feasible, which implies that for all t arbitrarily small ${\mathbb {P}}({\tilde{{\mathbf {u}}}}^T{\mathbf {v}}> t) \le \epsilon$ for all ${\mathbb {P}}\in {\mathcal {P}}^{LCX}$. However, the empirical distribution ${\hat{{\mathbb {P}}}} \in {\mathcal {P}}^{LCX}$, and for this distribution, we can find a finite $t^\prime$ such that ${{\hat{{\mathbb {P}}}}}({\tilde{{\mathbf {u}}}}^T{\mathbf {v}}> t^\prime ) > \epsilon$. This is a contradiction.

Since $\tau > 0$, apply the transformation $(\theta /\tau , 1/\tau , \lambda ({\mathbf {a}}, b)/\tau , {\mathbf {y}}({\mathbf {a}}, b)/\tau ) \rightarrow (\theta , \tau , \lambda ({\mathbf {a}}, b), {\mathbf {y}}({\mathbf {a}}, b))$ yielding

$$\begin{aligned} \inf _{\begin{array}{c} \theta , \tau , t, \lambda ({\mathbf {a}}, b), \\ y_1({\mathbf {a}}, b), y_2({\mathbf {a}}, b) \end{array}} t\\ \text {s.t.} \quad&\theta + \int _{{\mathcal {B}}} {\varGamma }({\mathbf {a}}, b) d\lambda ({\mathbf {a}}, b) \le \epsilon \tau \\ \quad&\theta -\int _{{\mathcal {B}}} b \ dy_1({\mathbf {a}}, b) \ge 0 , \ \ \theta + t - \int _{{\mathcal {B}}} b \ dy_2({\mathbf {a}}, b) \ge \tau ,\\&0 \le dy_1({\mathbf {a}}, b) \le d\lambda ({\mathbf {a}}, b) \quad \forall ({\mathbf {a}}, b) \in {\mathcal {B}},\\&0 \le dy_2({\mathbf {a}}, b) \le d\lambda ({\mathbf {a}}, b) \quad \forall ({\mathbf {a}}, b) \in {\mathcal {B}}, \\&\int _{{\mathcal {B}}} {\mathbf {a}}\ dy_1({\mathbf {a}}, b) = 0, \ \ {\mathbf {v}}= \int _{{\mathcal {B}}} {\mathbf {a}}\ d y_2({\mathbf {a}}, b), \\&\tau \ge 0. \end{aligned}$$

Eliminate the variable t, and make the transformation $(\tau \epsilon , \theta - \int _{{\mathcal {B}}} b dy_1({\mathbf {a}}, b)) \rightarrow (\tau , \theta )$ to yield

$$\begin{aligned} \sup _{{\mathbb {P}}\in {\mathcal {P}}^{LCX}} \text {VaR}_{\epsilon }^{{\mathbb {P}}}\left( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}\right) = \min _{\tau , \theta , y_1, y_2, \lambda } \quad&\frac{1}{\epsilon } \tau - \theta - \int _{{\mathcal {B}}} b dy_1\left( {\mathbf {a}}, b\right) + \int _{{\mathcal {B}} } b dy_2\left( {\mathbf {a}}, b\right) \nonumber \\ \text {s.t.} \quad&\theta + \int _{{\mathcal {B}}} b dy_1\left( {\mathbf {a}}, b\right) + \int _{{\mathcal {B}}} {\varGamma }\left( {\mathbf {a}}, b\right) d\lambda \left( {\mathbf {a}}, b\right) \le \tau \nonumber \\&0 \le dy_1\left( {\mathbf {a}}, b\right) \le d\lambda \left( {\mathbf {a}}, b\right) \quad \forall \left( {\mathbf {a}}, b\right) \in {\mathcal {B}}, \nonumber \\&0 \le dy_2\left( {\mathbf {a}}, b\right) \le d\lambda \left( {\mathbf {a}}, b\right) \quad \forall \left( {\mathbf {a}}, b\right) \in {\mathcal {B}}, \nonumber \\&\int _{{\mathcal {B}}} {\mathbf {a}}\ dy_1\left( {\mathbf {a}}, b\right) = 0, \ \ {\mathbf {v}}= \int _{{\mathcal {B}}} {\mathbf {a}}\ d y_2\left( {\mathbf {a}}, b\right) , \nonumber \\&\theta , \tau \ge 0. \end{aligned}$$

(55)

Taking the dual of this last optimization problem and simplifying yields $\sup _{{\mathbb {P}}\in {\mathcal {P}}^{LCX}} \text {VaR}_{\epsilon }^{{\mathbb {P}}}\left( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}\right) = \max _{{\mathbf {u}}\in {\mathcal {U}}^{LCX}} {\mathbf {v}}^T{\mathbf {u}}$ where

$$\begin{aligned} {\mathcal {U}}^{LCX}_\epsilon = \Biggr \{&{\mathbf {u}}\in {{\mathbb {R}}}^d: \ \exists {\mathbf {r}}\in {{\mathbb {R}}}^d, \ 1 \le z \le 1/\epsilon , \ \text { s.t. } \nonumber \\&\left( {\mathbf {a}}^T {\mathbf {r}}- b \left( z-1\right) \right) ^+ + \left( {\mathbf {a}}^T {\mathbf {u}}-b\right) ^+ \le \frac{z}{N} \sum _{j=1}^N \left( {\mathbf {a}}^T\hat{{\mathbf {u}}}_j - b\right) ^+\nonumber \\&+ {\varGamma }_{LCX}, \ \forall \left( {\mathbf {a}}, b\right) \in {\mathcal {B}} \Biggr \}. \end{aligned}$$

(56)

We next seek to remove the semi-infinite constraint in the definition of ${\mathcal {U}}^{LCX}$. Note that by considering the four possible signs of the two left hand side terms,

$$\begin{aligned}&\left( {\mathbf {a}}^T {\mathbf {r}}- b \left( z-1\right) \right) ^+ + \left( {\mathbf {a}}^T {\mathbf {u}}-b\right) ^+ \\&\quad = \max \left( {\mathbf {a}}^T\left( {\mathbf {r}}+{\mathbf {u}}\right) - bz, {\mathbf {a}}^T{\mathbf {r}}- b \left( z-1\right) , {\mathbf {a}}^T {\mathbf {u}}- b, 0 \right) \end{aligned}$$

Thus, we can replace the original semi-infinite constraint with the following three semi-infinite constraints

$$\begin{aligned}&{\mathbf {a}}^T\left( {\mathbf {r}}+ {\mathbf {u}}\right) - b z - \frac{z}{N} \sum _{j=1}^N \left( {\mathbf {a}}^T\hat{{\mathbf {u}}}_j - b\right) ^+ \le {\varGamma }_{LCX} \ \forall \left( {\mathbf {a}}, b\right) \in {\mathcal {B}} \\&{\mathbf {a}}^T{\mathbf {r}}- b \left( z-1\right) - \frac{z}{N} \sum _{j=1}^N \left( {\mathbf {a}}^T\hat{{\mathbf {u}}}_j - b\right) ^+ \le {\varGamma }_{LCX} \ \forall \left( {\mathbf {a}}, b\right) \in {\mathcal {B}}\\&{\mathbf {a}}^T {\mathbf {u}}- b - \frac{z}{N} \sum _{j=1}^N \left( {\mathbf {a}}^T\hat{{\mathbf {u}}}_j - b\right) ^+ \le {\varGamma }_{LCX} \ \forall \left( {\mathbf {a}}, b\right) \in {\mathcal {B}}, \end{aligned}$$

where the last case (corresponding to the fourth assignment of signs) is trivial since ${\varGamma }_{LCX} + \frac{z}{N} \sum _{j=1}^N ({\mathbf {a}}^T\hat{{\mathbf {u}}}_j - b)^+ \ge 0$. In contrast to the constraint (56), each of these constraints is concave in $({\mathbf {a}}, b)$. We can find the robust counterpart of each constraint using [5] by computing the concave conjugate of the term functions on the left. The resulting representation is given in (34). Finally, to complete the theorem, we use linear programming duality to rewrite $\max _{{\mathbf {u}}\in {\mathcal {U}}^{LCX} }{\mathbf {v}}^T{\mathbf {u}}$ as a minimization, obtaining the representation of the support function and worst-case VaR. Some rearrangement yields the representation (35). $\square$

1.7 Proofs of Theorems 11 and 13

Proof of Theorem 11

By Theorem 3, it suffices to show that $\delta ^*({\mathbf {v}}| \ {\mathcal {U}}^{CS}_\epsilon )$ is given by (38), which follows immediately from two applications of the Cauchy-Schwartz inequality. $\square$

To prove Theorem 13 we require the following proposition:

Proposition 2

$$\begin{aligned} \sup _{{\mathbb {P}}\in {\mathcal {P}}^{DY}\left( \gamma _1^B, \gamma _2^B\right) } {\mathbb {P}}\left( {\tilde{{\mathbf {u}}}}^T{\mathbf {v}}> t \right)&= \min _{r, s, \theta , {\mathbf {y}}_1, {\mathbf {y}}_2, {\mathbf {Z}}} \quad r + s \nonumber \\ \text {s.t.} \quad&\begin{pmatrix} r + {\mathbf {y}}_1^{+T} \hat{{\mathbf {u}}}^{\left( 0\right) } - {\mathbf {y}}_1^{-T} \hat{{\mathbf {u}}}^{\left( N+1\right) } &{} \frac{1}{2} \left( {\mathbf {q}}- {\mathbf {y}}_1\right) ^T \nonumber \\ \frac{1}{2} \left( {\mathbf {q}}- {\mathbf {y}}_1\right) &{} {\mathbf {Z}}\end{pmatrix} \succeq {\mathbf {0}}, \nonumber \\&\begin{pmatrix} r + {\mathbf {y}}_2^{+T} \hat{{\mathbf {u}}}^{\left( 0\right) } - {\mathbf {y}}_2^{-T} \hat{{\mathbf {u}}}^{\left( N+1\right) } + \theta t - 1 &{} \frac{1}{2} \left( {\mathbf {q}}- {\mathbf {y}}_2 - \theta {\mathbf {v}}\right) ^T \nonumber \\ \frac{1}{2} \left( {\mathbf {q}}- {\mathbf {y}}_2 - \theta {\mathbf {v}}\right) &{} {\mathbf {Z}}\end{pmatrix} \succeq {\mathbf {0}}, \nonumber \\&s \ge \left( \gamma ^B_2 {\hat{\varvec{{\varSigma }}}} + {\hat{\varvec{\mu }}} {\hat{\varvec{\mu }}}^T\right) \circ {\mathbf {Z}}+ {\hat{\varvec{\mu }}}^T {\mathbf {q}}+ \sqrt{\gamma ^B_1} \Vert {\mathbf {q}}+ 2 {\mathbf {Z}}{\hat{\varvec{\mu }}} \Vert _{{\hat{\varvec{{\varSigma }}}}^{-1}}, \nonumber \\&{\mathbf {y}}_1 = {\mathbf {y}}_1^+ - {\mathbf {y}}_1^-, \ \ {\mathbf {y}}_2 = {\mathbf {y}}_2^+ - {\mathbf {y}}_2^-, \ \ {\mathbf {y}}_1^+, {\mathbf {y}}_1^-, {\mathbf {y}}_2^+,{\mathbf {y}}_2^- \theta \ge {\mathbf {0}}. \end{aligned}$$

(57)

Proof

We suppress the dependence on $\gamma _1^B, \gamma _2^B$ in the notation. We claim that $\sup _{{\mathbb {P}}\in {\mathcal {P}}^{DY}} {\mathbb {P}}({\tilde{{\mathbf {u}}}}^T{\mathbf {v}}> t)$ has the following dual representation:

$$\begin{aligned} \min _{r, s, {\mathbf {q}}, {\mathbf {Z}}, {\mathbf {y}}_1, {\mathbf {y}}_2, \theta } \quad r + s \nonumber \\ \text {s.t.} \quad&r + {\mathbf {u}}^T{\mathbf {Z}}{\mathbf {u}}+ {\mathbf {u}}^T {\mathbf {q}}\ge 0 \quad \forall {\mathbf {u}}\in \left[ \hat{{\mathbf {u}}}^{\left( 0\right) }, \hat{{\mathbf {u}}}^{\left( N+1\right) }\right] , \nonumber \\&r + {\mathbf {u}}^T{\mathbf {Z}}{\mathbf {u}}+ {\mathbf {u}}^T {\mathbf {q}}\ge 1 \quad \forall {\mathbf {u}}\in \left[ \hat{{\mathbf {u}}}^{\left( 0\right) }, \hat{{\mathbf {u}}}^{\left( N+1\right) }\right] \cap \left\{ {\mathbf {u}}: {\mathbf {u}}^T{\mathbf {v}}> t \right\} , \nonumber \\&s \ge \left( \gamma ^B_2 {\hat{\varvec{{\varSigma }}}} + {\hat{\varvec{\mu }}} {\hat{\varvec{\mu }}}^T\right) \circ {\mathbf {Z}}+ {\hat{\varvec{\mu }}}^T {\mathbf {q}}+ \sqrt{\gamma ^B_1} \Vert {\mathbf {q}}+ 2 {\mathbf {Z}}{\hat{\varvec{\mu }}} \Vert _{{\hat{\varvec{{\varSigma }}}}^{-1}}, \nonumber \\&{\mathbf {Z}}\succeq {\mathbf {0}}. \end{aligned}$$

(58)

See the proof of Lemma 1 in [25] for details. Since ${\mathbf {Z}}$ is positive semidefinite, we can use strong duality to rewrite the two semi-infinite constraints:

$$\begin{aligned} \begin{aligned} \min _{{\mathbf {u}}} \quad&{\mathbf {u}}^T {\mathbf {Z}}{\mathbf {u}}+ {\mathbf {u}}^T {\mathbf {q}}\\ \text {s.t.} \quad&\hat{{\mathbf {u}}}^{(0)} \le {\mathbf {u}}\le \hat{{\mathbf {u}}}^{(N+1)}, \end{aligned}&\iff \begin{aligned} \max _{{\mathbf {y}}_1, {\mathbf {y}}_1^+, {\mathbf {y}}_1^-} \quad&-\frac{1}{4} \left( {\mathbf {q}}- {\mathbf {y}}_1\right) ^T {\mathbf {Z}}^{-1} \left( {\mathbf {q}}- {\mathbf {y}}_1\right) + {\mathbf {y}}_1^+\hat{{\mathbf {u}}}^{(0)} - {\mathbf {y}}_1^{-}\hat{{\mathbf {u}}}^{(N+1)}\\ \text {s.t.} \quad&{\mathbf {y}}_1 = {\mathbf {y}}_1^+ - {\mathbf {y}}_1^-, \ \ {\mathbf {y}}_1^+, {\mathbf {y}}_1^- \ge {\mathbf {0}}, \end{aligned}\\ \\ \begin{aligned} \min _{{\mathbf {u}}} \quad&{\mathbf {u}}^T {\mathbf {Z}}{\mathbf {u}}+ {\mathbf {u}}^T {\mathbf {q}}\\ \text {s.t.} \quad&\hat{{\mathbf {u}}}^{(0)} \le {\mathbf {u}}\le \hat{{\mathbf {u}}}^{(N+1)}, \\&{\mathbf {u}}^T{\mathbf {v}}\ge t, \end{aligned}&\iff \begin{aligned} \max _{{\mathbf {y}}_2, {\mathbf {y}}_2^+, {\mathbf {y}}_2^-} \quad&-\frac{1}{4} \left( {\mathbf {q}}- {\mathbf {y}}_2 - \theta {\mathbf {v}}\right) ^T {\mathbf {Z}}^{-1} \left( {\mathbf {q}}- {\mathbf {y}}_2 - \theta {\mathbf {v}}\right) + {\mathbf {y}}_2^+ \hat{{\mathbf {u}}}^{(0)} - {\mathbf {y}}_2^{-} \hat{{\mathbf {u}}}^{(N+1)} + \theta t \\ \text {s.t.} \quad&{\mathbf {y}}_2 = {\mathbf {y}}_2^+ - {\mathbf {y}}_2^-, \ \ {\mathbf {y}}_2^+, {\mathbf {y}}_2^- \ge {\mathbf {0}}, \ \theta \ge 0. \end{aligned} \end{aligned}$$

Then, by using Schur-Complements, we can rewrite Problem (58) as in the proposition. $\square$

We can now prove the theorem.

Proof of Theorem 13

Using Proposition 2, we can characterize the worst-case VaR by

$$\begin{aligned}&\sup _{{\mathbb {P}}\in {\mathcal {P}}^{DY}} \text {VaR}_{\epsilon }^{{\mathbb {P}}}\left( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}\right) \nonumber \\&\quad = \inf \left\{ t: r + s \le \epsilon , \left( r, s, t, \theta , {\mathbf {y}}_1, {\mathbf {y}}_2, {\mathbf {Z}}\right) (\hbox { are feasible in problem } 57) \right\} .\nonumber \\ \end{aligned}$$

(59)

We claim that $\theta > 0$ in any feasible solution to the infimum in Eq. (59). Suppose to the contrary that $\theta = 0$. Then this solution is also feasible as $t \downarrow \infty$, which implies that ${\mathbb {P}}({\tilde{{\mathbf {u}}}}^T{\mathbf {v}}> -\infty ) \le \epsilon$ for all ${\mathbb {P}}\in {\mathcal {P}}^{DY}$. On the other hand, the empirical distribution ${\hat{{\mathbb {P}}}} \in {\mathcal {P}}^{DY}$, a contradiction.

Since $\theta > 0$, we can rescale all of the above optimization variables in problem (57) by $\theta$. Substituting this into Eq. (59) yields the given expression for $\sup _{{\mathbb {P}}\in {\mathcal {P}}^{DY}} \text {VaR}_{\epsilon }^{{\mathbb {P}}}\left( {\mathbf {v}}^T{\tilde{{\mathbf {u}}}}\right)$. Rewriting this optimization problem as a semidefinite optimization problem and taking its dual yields ${\mathcal {U}}^{DY}_\epsilon$ in the theorem. By Theorem 3, this set simultaneously implies a probabilistic guarantee. $\square$

1.8 Proof of Theorem 16

Proof

For each part, the convexity in $({\mathbf {v}}, t)$ is immediate since $\delta ^*({\mathbf {v}}| \ {\mathcal {U}}_\epsilon )$ is a support function of a convex set. For the first part, note that from the second part of Theorem 11, $\delta ^*({\mathbf {v}}| \ {\mathcal {U}}^{CS}_\epsilon ) \le t$ will be convex in $\epsilon$ for a fixed $({\mathbf {v}}, t)$ whenever $\sqrt{1/\epsilon -1}$ is convex. Examining the second derivative of this function, this occurs on the interval $0< \epsilon < .75$. Similarly, for the second part, note that from the second part of Theorem 7, $\delta ^*({\mathbf {v}}| \ {\mathcal {U}}^{FB}_\epsilon ) \le t$ will be convex in $\epsilon$ for a fixed $({\mathbf {v}}, t)$ whenever $\sqrt{2\log (1/\epsilon )}$ is convex. Examining the second derivative of this function, this occurs on the interval $0< \epsilon < 1\sqrt{e}$.

From the representations of $\delta ^*({\mathbf {v}}| {\mathcal {U}}^{\chi ^2}_\epsilon )$ and $\delta ^*({\mathbf {v}}| {\mathcal {U}}^{G}_\epsilon )$ in Theorem 5, we can see they will be convex in $\epsilon$ whenever $1/\epsilon$ is convex, i.e., $0< \epsilon < 1$. From the representation of $\delta ^*({\mathbf {v}}| {\mathcal {U}}^I_\epsilon )$ in Theorem 6 and since $\lambda \ge 0$, we see this function will be convex in $\epsilon$ whenever $\log (1/\epsilon )$ is convex, i.e., $0< \epsilon < 1$.

Finally, examining the support functions of ${\mathcal {U}}^{LCX}_\epsilon$ and ${\mathcal {U}}^{DY}_\epsilon$ shows that $\epsilon$ occurs linearly in each of these functions. $\square$

Appendix 2: Omitted Figures

This section contains additional figures omitted from the main text.

1.1 Additional Bootstrapping Results

Figure 5 illustrates the set ${\mathcal {U}}^{CS}_\epsilon$ for the example considered in Fig. 2 with thresholds computed with and without the bootstrap. Notice that for $N=1000$, the non-bootstrapped set is almost as big as the full support and shrinks slowly to its infinite limit. Furthermore, the bootstrapped set with $N=100$ points is smaller than the non-bootstrapped version with 50 times as many points.

Fig. 5

${\mathcal {U}}^{CS}_\epsilon$ with and without bootstrapping for the example from Fig. 2. $N_B=10{,}000$, $\alpha =10\%$, $\epsilon = 10\%$

1.2 Additional Portfolio Results

Figure 6 summarizes the case $N=2000$ for the experiment outlined in Sect. 9.3.

Fig. 6

The case $N=2000$ for the experiment outlined in Sect. 9.3. The left panel shows the cross-validation results. The right panel shows the average holdings by method. $\alpha = \epsilon = 10\%$

Appendix 3: Optimizing $\epsilon _j$’s for Multiple Constraints

In this section, we propose an approach for solving (10). We say that a constraint $f( {\mathbf {x}}, {\mathbf {y}}) \le 0$ is bi-convex in ${\mathbf {x}}$ and ${\mathbf {y}}$ if for every ${\mathbf {y}}$, the set $\{ {\mathbf {x}}: f({\mathbf {x}}, {\mathbf {y}}) \le 0\}$ is convex and for every ${\mathbf {x}}$, the set $\{ {\mathbf {y}}: f({\mathbf {x}}, {\mathbf {y}}) \le 0 \}$ is convex. The key observation is then

Theorem 16

• a) The constraint $\delta ^*({\mathbf {v}}|\ {\mathcal {U}}^{CS}_\epsilon ) \le t$ is bi-convex in $({\mathbf {v}}, t)$ and $\epsilon$, for $0< \epsilon < .75$.

• b) The constraint $\delta ^*({\mathbf {v}}|\ {\mathcal {U}}^{FB}_\epsilon ) \le t$ is bi-convex in $({\mathbf {v}}, t)$ and $\epsilon$, for $0< \epsilon < 1/\sqrt{e}$.

• c) The constraint $\delta ^*({\mathbf {v}}| \ {\mathcal {U}}_\epsilon ) \le t$ is bi-convex in $({\mathbf {v}}, t)$ and $\epsilon$, for $0< \epsilon < 1$, and ${\mathcal {U}}_\epsilon \in \{ {\mathcal {U}}^{\chi ^2}_\epsilon , {\mathcal {U}}^{G}_\epsilon , {\mathcal {U}}^I_\epsilon , {\mathcal {U}}^{LCX}_\epsilon , {\mathcal {U}}^{DY}_\epsilon \}$.

This observations suggests a heuristic: Fix the values of $\epsilon _j$, and solve the robust optimization problem in the original decision variables. Then fix this solution and optimize over the $\epsilon _j$. Repeat until some stopping criteria is met or no further improvement occurs. Chen et al. [22] suggested a similar heuristic for multiple chance-constraints in a different context. We propose a refinement of this approach that solves a linear optimization problem to obtain the next iterates for $\epsilon _j$, incorporating dual information from the overall optimization and other constraints. Our proposal ensures the optimization value is non-increasing between iterations and that the procedure is finitely convergent.

For simplicity, we present our approach using m constraints of the form $\delta ^*({\mathbf {v}}| \ {\mathcal {U}}_\epsilon ^{CS} ) \le t$. Without loss of generality, assume the overall optimization problem is a minimization. Consider the $j\text {th}$ constraint, and let $({\mathbf {v}}^\prime , t^\prime )$ denote the subset of the solution to the original optimization problem at the current iterate pertaining to the $j\text {th}$ constraint. Let $\epsilon ^\prime _j$, $j=1, \ldots , m$ denote the current iterate in $\epsilon$. Finally, let $\lambda _j$ denote the shadow price of the $j\text {th}$ constraint in the overall optimization problem.

Notice from the second part of Theorem 11 that $\delta ^*({\mathbf {v}}| \ {\mathcal {U}}^{CS}_{\epsilon })$ is decreasing in $\epsilon$. Thus, for all $\epsilon _j \ge {\underline{\epsilon }}_j$, $\delta ^*({\mathbf {v}}^\prime | \ {\mathcal {U}}^{CS}_{{\epsilon }_j}) \le t^\prime$, where,

$$\begin{aligned} {\underline{\epsilon }}_j \equiv \left[ \frac{\left( t^\prime - {\hat{\varvec{\mu }}}^T{\mathbf {v}}^\prime - {\varGamma }_1 \Vert {\mathbf {v}}^\prime \Vert _2\right) ^2}{{{\mathbf {v}}^\prime }^T \left( \varvec{{\varSigma }}+ {\varGamma }_2 {\mathbf {I}}\right) {\mathbf {v}}^\prime } + 1 \right] ^{-1}. \end{aligned}$$

Motivated by the shadow-price $\lambda _j$, we define the next iterates of $\epsilon _j$, $j=1, \ldots , m$ to be the solution of the linear optimization problem

$$\begin{aligned} \min _{\varvec{\epsilon }} \quad&- \sum _{j=1}^d \left( \frac{ \sqrt{{{\mathbf {v}}^ \prime }^T (\varvec{{\varSigma }}+ {\varGamma }_2 {\mathbf {I}}){\mathbf {v}}^\prime } }{ 2 {\epsilon ^\prime }^2 \sqrt{\frac{1}{\epsilon ^\prime }-1} } \right) \lambda _j \cdot \epsilon _j \nonumber \\ \text {s.t.} \quad&{\underline{\epsilon }}_j \le \epsilon _j \le .75, \ \ j=1, \ldots , m, \nonumber \\&\sum _{j=1}^m \epsilon _j \le {\overline{\epsilon }}, \ \ \Vert \varvec{\epsilon }^\prime - \varvec{\epsilon }\Vert _1 \le \kappa . \end{aligned}$$

(60)

The coefficient of $\epsilon _j$ in the objective function is $\lambda _j \cdot \partial _{\epsilon _j} \delta ^*({\mathbf {v}}^\prime | \ {\mathcal {U}}^{CS}_{\epsilon _j} )$ which is intuitively a first-order approximation to the improvement in the overall optimization problem for a small change in $\epsilon _j$. The norm constraint on $\varvec{\epsilon }$ ensures that the next iterate is not too far away from the current iterate, so that the shadow-price $\lambda _j$ remains a good approximation. (We use $\kappa = .05$ in our experiments.) The upper bound ensures that we remain in a region where $\delta ^*({\mathbf {v}}| \ {\mathcal {U}}^{CS}_{\epsilon _j})$ is convex in $\epsilon _j$. Finally, the lower bounds on $\epsilon _j$ ensure that the previous iterate of the original optimization problem $({\mathbf {v}}^\prime , t^\prime )$ will still be feasible for the new values of $\epsilon _j$. Consequently, the objective value of the original optimization problem is non-increasing. We terminate the procedure when the objective value no longer makes significant progress.

We can follow an entirely analogous procedure for each of our other sets, simply adjusting the formulas for ${\underline{\epsilon }}_j$, the upper bounds, and the objective coefficient appropriately. We omit the details.

Appendix 4: Queueing Analysis

One of the strengths of our approach is the ability to retrofit existing robust optimization models by replacing their uncertainty sets with our proposed sets, thereby creating new data-driven models that satisfy strong guarantees. In this section, we illustrate this idea with a robust queueing model as in [4, 14]. Bandi and Bertsimas [4] use robust optimization to generate approximations to a performance metric of a queueing network. We will combine their method with our new sets to generate probabilistic upper bounds to these metrics. For concreteness, we focus on the waiting time in a G/G/1 queue. Extending our analysis to more complex queueing networks can likely be accomplished similarly. We stress that we do not claim that our new bounds are the best possible – indeed there exist extremely accurate, specialized techniques for the G/G/1 queue – but, rather, that the retrofitting procedure is general purpose and yields reasonably good results. These features suggest that a host of other robust optimization applications in information theory [3], supply-chain management [7] and revenue management [44] might benefit from this retrofitting.

Let ${\tilde{{\mathbf {u}}}}_i = ({\tilde{x}}_i, {\tilde{t}}_i)$ for $i = 1, \ldots , n$ denote the uncertain service times and interarrival times of the first n customers in a queue. We assume that ${\tilde{{\mathbf {u}}}}_i$ is i.i.d. for all i and has independent components, and that there exists $\hat{{\mathbf {u}}}^{(N+1)} \equiv ({\overline{x}}, {\overline{t}})$ such that $0 \le {\tilde{x}}_i \le {\overline{x}}$ and $0 \le {\tilde{t}}_i \le {\overline{t}}$ almost surely.

From Lindley’s recursion [36], the waiting time of the $n\text {th}$ customer is

$$\begin{aligned} {\tilde{W}}_n = \max _{1 \le j \le n} \left( \max \left( \sum _{l=j}^{n-1} {\tilde{x}}_l - \sum _{l=j+1}^n {\tilde{t}}_l, 0\right) \right) = \max \left( 0, \max _{1 \le j \le n} \left( \sum _{l=j}^{n-1} {\tilde{x}}_l - \sum _{l=j+1}^n {\tilde{t}}_l\right) \right) .\nonumber \\ \end{aligned}$$

(61)

Motivated by Bandi and Bertsimas [4], we consider a worst-case realization of a Lindley recursion

$$\begin{aligned} \max \left( 0, \max _{1 \le j \le n} \max _{({\mathbf {x}}, {\mathbf {t}} ) \in {\mathcal {U}}} \left( \sum _{l=j}^{n-1} {\tilde{x}}_l - \sum _{l=j+1}^{n} {\tilde{t}}_l \right) \right) . \end{aligned}$$

(62)

Taking ${\mathcal {U}}= {\mathcal {U}}^{FB}_{{\overline{\epsilon }}/n}$ and applying Theorem 7 to the inner-most optimization yields

$$\begin{aligned} \max _{1 \le j \le n} \left( m_{f1} - m_{b2}\right) \left( n-j\right) + \sqrt{ 2 \log \left( n/{\overline{\epsilon }}\right) \left( \sigma _{f1}^2 + \sigma _{b2}^2 \right) } \sqrt{n-j} \end{aligned}$$

(63)

Relaxing the integrality on j, this optimization can be solved closed-form yielding

$$\begin{aligned} W_n^{1, FB}&\equiv {\left\{ \begin{array}{ll} \left( m_{f1} - m_{b2}\right) n + \sqrt{ 2 \log \left( \frac{n}{{\overline{\epsilon }}}\right) \left( \sigma _{f1}^2 + \sigma _{b2}^2 \right) } \sqrt{n} &{} \text { if } n < \frac{\log \left( \frac{n}{{\overline{\epsilon }}}\right) \left( \sigma _{f1}^2 + \sigma _{b2}^2 \right) }{2 \left( m_{b2} - m_{f1}\right) ^2} \text { or } m_{f1} > m_{b2},\\ \frac{\log \left( \frac{n}{{\overline{\epsilon }}}\right) \left( \sigma _{f1}^2 + \sigma _{b2}^2\right) }{ 2\left( m_{b2} - m_{f1}\right) } &{} \text { otherwise. } \end{array}\right. } \end{aligned}$$

(64)

From (62), with probability at least $1-\alpha$ with respect to ${\mathbb {P}}_{\mathcal {S}}$, each of the inner-most optimizations upper bound their corresponding random quantity with probability $1-{\overline{\epsilon }}/n$ with respect to ${\mathbb {P}}^*$. Thus, by union bound, ${\mathbb {P}}^*({\tilde{W}}_n \le W_n^{1, FB} ) \ge 1-{\overline{\epsilon }}$.

On the other hand, since $\{ {\mathcal {U}}^{FB}_\epsilon : 0< \epsilon < 1 \}$ simultaneously implies a probabilistic guarantee, we can also optimize the choice of $\epsilon _j$ in (63), yielding

$$\begin{aligned} W^{2, FB}_n&\equiv \min _{w, \varvec{\epsilon }} \quad w \nonumber \\ \text {s.t.} \quad&w \ge \left( m_{f1} - m_{b2}\right) \left( n-j\right) \nonumber \\&\qquad \quad + \sqrt{ 2 \log \left( 1/\epsilon _j\right) \left( \sigma _{f1}^2 + \sigma _{b2}^2 \right) } \sqrt{n-j}, \ \ j=1, \ldots , n-1, \nonumber \\&w \ge 0, \ \ \varvec{\epsilon }\ge {\mathbf {0}}, \ \ \sum _{j=1}^{n-1} \epsilon _j \le {\overline{\epsilon }}. \end{aligned}$$

(65)

From the KKT conditions, the constraint (65) will be tight for all j, so that $W^{2, FB}_n$ satisfies

$$\begin{aligned} \sum _{j=1}^{n-1} \exp \left( - \frac{\left( W_n^{2, FB} - \left( m_{f1} - m_{b2}\right) \right) ^2 }{2 (n-j) \left( \sigma _{f1}^2 + \sigma _{b2}^2 \right) ^2} \right) = {\overline{\epsilon }}, \end{aligned}$$

(66)

which can be solved by line search. Again, with probability $1-\alpha$ with respect to ${\mathbb {P}}_{\mathcal {S}}$, ${\mathbb {P}}^*({\tilde{W}}_n \le W_n^{2, FB}) \ge 1-{\overline{\epsilon }}$, and $W_n^{2, FB} \le W_n^{1, FB}$ by construction.

We can further refine our bound by truncating the recursion (61) at customer $\min (n, n^{(k)} )$ where, with high probability, ${\tilde{n}} \le n^{(k)}$. We next provide a formal derivation of this bound, which we denote $W_n^{3, FB}$. Notice that in (61), the optimizing index j represents the most recent customer to arrive when the queue was empty. Let ${\tilde{n}}$ denote the number of customers served in a typical busy period. Intuitively, it suffices to truncate the recursion (61) at customer $\min (n, n^{(k)} )$ where, with high probability, ${\tilde{n}} \le n^{(k)}$. More formally, considering only the first half of the data ${\hat{x}}^1, \ldots , {\hat{x}}^{\lceil N/2 \rceil }$ and ${\hat{t}}^1, \ldots , {\hat{t}}^{\lceil N/2 \rceil }$, we compute the number of customers served in each busy period of the queue, denoted ${\hat{n}}^1, \ldots , {\hat{n}}^K$, which are i.i.d. realizations of ${\tilde{n}}$. Using the KS test at level $\alpha _1$, we observe that with probability at least $1-\alpha$ with respect to ${\mathbb {P}}_{\mathcal {S}}$,

$$\begin{aligned} {\mathbb {P}}\left( {\tilde{n}} > {\hat{n}}^{(k)}\right) \le 1 - \frac{k}{K} + {\varGamma }^{KS}(\alpha ), \quad \forall k =1, \ldots , K. \end{aligned}$$

(67)

In other words, the queue empties every ${\hat{n}}^{(k)}$ customers with at least this probability.

Next, calculate the constants ${\mathbf {m}}_f, {\mathbf {m}}_b, \varvec{\sigma }_f, \varvec{\sigma }_b$ using only the second half of the data. Then, truncate the sum in (66) at $\min (n, n^{(k)})$ and replace the righthand side by ${\overline{\epsilon }} - 1 + \frac{k}{K} - {\varGamma }^{KS}(\alpha /2 )$. Denote the solution of this equation by $W_n^{2, FB}(k)$. Finally, let $W^{3, FB}_n \equiv \min _{1 \le k < K} W_n^{2, FB}(k)$, obtained by grid-search.

We claim that with probability at least $1-2\alpha$ with respect to ${\mathbb {P}}_{\mathcal {S}}$, ${\mathbb {P}}({\tilde{W}}_n > W^{3, FB}_n) \le {\overline{\epsilon }}$. Namely, from our choice of parameters, Eqs. (66) and (67) hold simultaneously with probability at least $1-2\alpha$. Restrict attention to a sample path where these equations hold. Since (67) holds for the optimal index $k^*$, recursion (61) truncated at $n^{(k^*)}$ is valid with probability at least $1 - \frac{k^*}{K} + {\varGamma }^{KS}(\alpha )$. Finally, ${\mathbb {P}}({\tilde{W}}_n> W^{3, FB}_n) \le {\mathbb {P}}((61) is invalid ) + {\mathbb {P}}(({\tilde{W}}_n > W^{2, FB}_n(k^*) \text { and }(61)\text { is valid} ) \le {\overline{\epsilon }}$. This proves the claim.

We observe in passing that since the constants ${\mathbf {m}}_f, {\mathbf {m}}_b, \varvec{\sigma }_f, \varvec{\sigma }_b$ are computed using only half the data, it may not be the case that $W^{3, FB}_n < W^{2, FB}_n$, particularly for small N, but that typically $W^{3, FB}_n$ is a much stronger bound than $W^{2, FB}_n$ (see also Fig. 7).

Finally, our choice of ${\mathcal {U}}^{FB}_\epsilon$ was somewhat arbitrary. Similar analysis can be performed for many of our sets. To illustrate, we next derive corresponding bounds for the set ${\mathcal {U}}^{CS}$. Following essentially the same argument yields:

$$\begin{aligned} W_n^{1, CS} \le {\left\{ \begin{array}{ll} \left( {\hat{\mu }}_1 - {\hat{\mu }}_2\right) n + \left( {\varGamma }_1 + \sqrt{(\frac{n}{{\overline{\epsilon }}} - 1)\left( \sigma _1^2 + \sigma _2^2 + 2{\varGamma }_2 \right) } \right) \sqrt{n} &{} \text { if } n < \frac{\left( {\varGamma }_1 + \sqrt{\left( \frac{n}{{\overline{\epsilon }}} - 1\right) \left( \sigma _1^2 + \sigma _2^2 + 2{\varGamma }_2 \right) } \right) ^2}{4 \left( {\hat{\mu }}_1 - {\hat{\mu }}_2\right) ^2} \\ &{}\quad \text { or } {\hat{\mu }}_1 > {\hat{\mu }}_2, \\ \frac{\left( {\varGamma }_1 + \sqrt{\left( \frac{n}{{\overline{\epsilon }}} - 1\right) \left( \sigma _1^2 + \sigma _2^2 + 2{\varGamma }_2 \right) } \right) ^2}{4 \left( {\hat{\mu }}_2 - {\hat{\mu }}_1\right) } &{} \text { otherwise } \end{array}\right. } \end{aligned}$$

$W_n^{2, CS}$ is the solution to

$$\begin{aligned} \sum _{j=1}^{n-1} \left[ \left( \frac{W_n^{2, CS}- \left( {\hat{\mu }}_1 - {\hat{\mu }}_2\right) (n-j)}{\sqrt{n-j}\sqrt{\sigma _1^2 + \sigma _2^2 + 2{\varGamma }_2 } } - \frac{{\varGamma }_1}{\sqrt{\sigma _1^2 + \sigma _2^2 + 2{\varGamma }_2}} \right) ^2 + 1 \right] ^{-1} = {\overline{\epsilon }}, \end{aligned}$$

(68)

and $W_n^{3, CS}$ defined analogously to $W_n^{3, FB}$ but using (68) in lieu of (66).

Fig. 7

The left panel shows various bounds on the median waiting time ($\epsilon =.5$) for $n=10$ and various values of N. The right panel bounds the entire cumulative distribution of the waiting time for $n=10$ and $N=1000$. using $W_n^{FB, 3}$. In both cases, $\alpha = 20\%$

We illustrate these ideas numerically. Let service times follow a Pareto distribution with parameter 1.1 truncated at 15, and the interarrival times follow an exponential distribution with rate 3.05 truncated at 15.25. The resulting truncated distributions have means of approximately 3.029 and 3.372, respectively, yielding an approximate 90% utilization.

As a first experiment, we bound the median waiting time ($\epsilon = 50\%$) for the $n=10$ customer, using each of our bounds with differing amounts of data. We repeat this procedure 100 times to study the variability of our bounds with respect to the data. The left panel of Fig. 7 shows the average value of the bound and error bars for the 10% and 90% quantiles. As can be seen, all of the bounds improve as we add more data. Moreover, optimizing the $\epsilon _j$’s (the difference between $W_n^{FB, 1}$ and $W_n^{FB, 2}$) is significant.

For comparison purposes, we include a sample analogue of Kingman’s bound [33] on the $1-\epsilon$ quantile of the waiting time, namely,

$$\begin{aligned} W^{King} \equiv \frac{ {\hat{\mu }}_x \left( {\hat{\sigma }}_a^2 {\hat{\mu }}_x^2 + {\hat{\sigma }}_x^2 {\hat{\mu }}_t^2\right) }{2{\overline{\epsilon }} {\hat{\mu }}_t^2 \left( {\hat{\mu }}_t - {\hat{\mu }}_x\right) }, \end{aligned}$$

where ${\hat{\mu }}_t, {\hat{\sigma }}^2_t$ are the sample mean and sample variance of the arrivals, ${\hat{\mu }}_x, {\hat{\sigma }}^2_x$ are the sample mean and sample variance of the service times, and we have applied Markov’s inequality. Unfortunately, this bound is extremely unstable, even for large N. The dotted line in the left-panel of Fig. 7 is the average value over the 100 runs of this bound for $N=10{,}000$ data points (the error-bars do not fit on graph.) Sample statistics for this bound and our bounds can also be seen in Table 4. As shown, our bounds are both significantly better (with less data), and exhibit less variability.

Table 4 Summary statistics for various bounds on median waiting time

As a second experiment, we use our bounds to calculate a probabilistic upper bound on the entire CDF of ${\tilde{W}}_n$ for $n=10$ with $N=1000$, $\alpha =20\%$. Results can be seen in the right panel of Fig. 7. We have included the empirical CDF of the waiting time and the sampled version of the Kingman bound comparison. As seen, our bounds significantly improve upon the sampled Kingman bound, and the benefit of optimizing the $\epsilon _j$’s is again, significant. We remark that the ability to simultaneously bound the entire CDF for any n, whether transient or steady-state, is an important strength of this type of analysis.

Appendix 5: Constructing ${\mathcal {U}}^I_\epsilon$ from Other EDF Tests

In this section we show how to extend our constructions for ${\mathcal {U}}^I_\epsilon$ to other EDF tests. We consider several of the most popular, univariate goodness-of-fit, empirical distribution function test. Each test below considers the null-hypothesis $H_0: {\mathbb {P}}^*_i = {\mathbb {P}}_{0,i}$.

• Kuiper (K) Test: The K test rejects the null hypothesis at level $\alpha$ if

  $$\begin{aligned} \max _{j=1, \ldots , N} \left( \frac{j}{N} - {\mathbb {P}}_{0,i}\left( {{\tilde{u}}}_i \le {\hat{u}}_i^{(j)}\right) \right) + \max _{j=1, \ldots , N} \left( {\mathbb {P}}_{0,i}\left( {{\tilde{u}}}_i < {\hat{u}}_i^{(j)}\right) - \frac{j-1}{N} \right) > V_{1-\alpha }. \end{aligned}$$

• Cramer von-Mises (CvM) Test: The CvM test rejects the null hypothesis at level $\alpha$ if

  $$\begin{aligned} \frac{1}{12N^2} + \frac{1}{N}\sum _{j=1}^N \left( \frac{ 2j-1}{2N} - {\mathbb {P}}_{0,i}\left( {{\tilde{u}}}_i \le {\hat{u}}_i^{(j)}\right) \right) ^2 > \left( T_{1-\alpha }\right) ^2. \end{aligned}$$

• Watson (W) Test: The W test rejects the null hypothesis at level $\alpha$ if

  $$\begin{aligned}&\frac{1}{12N^2} + \frac{1}{N} \sum _{j=1}^N \left( \frac{ 2j-1}{2N} - {\mathbb {P}}_{0, i}\left( {{\tilde{u}}}_i \le {\hat{u}}_i^{(j)}\right) \right) ^2 - \left( \frac{1}{N} \sum _{j=1}^N {\mathbb {P}}_{0, i}\left( {{\tilde{u}}}_i \le {\hat{u}}_i^{(j)}\right) - \frac{1}{2} \right) ^2\\&\quad > (U_{1-\alpha })^2. \end{aligned}$$

• Anderson-Darling (AD) Test: The AD test rejects the null hypothesis at level $\alpha$ if

  $$\begin{aligned}&-1 - \sum _{j=1}^N \frac{2j-1}{N^2} \left( \log \left( {\mathbb {P}}_{0,i}({{\tilde{u}}}_i \le {\hat{u}}_i^{(j)}) \right) + \log \left( 1- {\mathbb {P}}_{0, i}\left( {{\tilde{u}}}_i \le {\hat{u}}_i^{(N+1-j)}\right) \right) \right) \\&\quad > (A_{1-\alpha })^2 \end{aligned}$$

Tables of the thresholds above are readily available (e.g., [47, and references therein]).

As described in [15], the confidence regions of these tests can be expressed in the form

$$\begin{aligned} {\mathcal {P}}^{EDF}_i = \left\{ {\mathbb {P}}_i \in \theta \left[ {\hat{u}}_i^{(0)}, {\hat{u}}_i^{(N+1)}\right] : \exists \zeta \in {{\mathbb {R}}}^{N}, \ {\mathbb {P}}_i\left( {{\tilde{u}}}_i \le {\hat{u}}_i^{(j)} \right) = \zeta _i, \ {\mathbf {A}}_S \varvec{\zeta }- {\mathbf {b}}_ S \in {\mathcal {K}}_S \right\} , \end{aligned}$$

where the the matrix ${\mathbf {A}}_S$, vector ${\mathbf {b}}_S$ and cone ${\mathcal {K}}_S$ depend on the choice of test. Namely,

(69)

(70)

(71)

where ${\mathbf {I}}_N$ is the $N\times N$ identity matrix, ${{\tilde{{\mathbf {I}}}}}_N$ is the skew identity matrix $([{{\tilde{{\mathbf {I}}}}}_N]_{ij}={\mathbb {I}}[i=N-j])$, and ${\mathbf {E}}_N$ is the $N\times N$ matrix of all ones.

Let ${\mathcal {K}}^*$ denote the dual cone to ${\mathcal {K}}$. By specializing Theorem 10 of Bertsimas et al. [15], we obtain the following theorem, paralleling Theorem 15.

Theorem 17

Suppose g(u) is monotonic and right-continuous, and let ${\mathcal {P}}^S$ denote the confidence region of any of the above EDF tests.

$$\begin{aligned} \sup _{{\mathbb {P}}_i \in {\mathcal {P}}^{EDF}_i} {{\mathbb {E}}}^{{\mathbb {P}}_i}[ g\left( {{\tilde{u}}}_i\right) ] = \min _{{\mathbf {r}}, {\mathbf {c}}} \quad&{\mathbf {b}}_S^T {\mathbf {r}}+ c_{N+1} \nonumber \\ \text {s.t.} \quad&-{\mathbf {r}}\in {\mathcal {K}}_S^*, \ \ {\mathbf {c}}\in {{\mathbb {R}}}^{N+1}, \nonumber \\&\left( {\mathbf {A}}_S^T {\mathbf {r}}\right) _j = c_j - c_{j+1} \quad \forall j=1, \ldots , N, \nonumber \\&c_j \ge g\left( {\hat{u}}_i^{\left( j-1\right) }\right) , \ \ c_j \ge g\left( {\hat{u}}_i^{\left( j\right) }\right) , \quad j=1, \ldots , N+1. \end{aligned}$$

(72)

$$\begin{aligned} =\max _{{\mathbf {z}}, {\mathbf {q}}^L, {\mathbf {q}}^R, {\mathbf {p}}} \quad&\sum _{j=0}^{N+1} p_j g\left( {\hat{u}}_i^{\left( j\right) }\right) \nonumber \\ \text {s.t.} \quad&{\mathbf {A}}_S {\mathbf {z}}- {\mathbf {b}}_S \in {\mathcal {K}}_S, \ \ {\mathbf {q}}^L, {\mathbf {q}}^R, {\mathbf {p}}\in {{\mathbb {R}}}_+^{N+1} \nonumber \\&q^L_j + q^R_j = z_j - z_{j-1}, \ \ j=1, \ldots , N, \nonumber \\&q^L_{N+1} + q^R_{N+1} = 1 - z_{N} \nonumber \\&p_0 = q^L_1, \ \ p_{N+1} = q^R_{N+1}, \ \ p_j = q^L_{j+1} + q^R_j, \ \ j = 1, \ldots , N, \end{aligned}$$

(73)

where ${\mathbf {A}}_S, {\mathbf {b}}_S, {\mathcal {K}}_S$ are the appropriate matrix, vector and cone to the test. Moreover, when g(u) is non-decreasing (resp. non-increasing), there exists an optimal solution where ${\mathbf {q}}^L = {\mathbf {0}}$ (resp. ${\mathbf {q}}^R = {\mathbf {0}}$) in (73).

Proof

Apply Theorem 10 of Bertsimas et al. [15] and observe that since g(u) is monotonic and right continuous,

$$\begin{aligned} c_j \ge \sup _{u \in \left( {\hat{u}}_i^{\left( j-1\right) },\right. \left. {\hat{u}}_i^{\left( j\right) }\right] } g\left( u\right) \iff c_j \ge g\left( {\hat{u}}_i^{\left( j-1\right) }\right) , \ c_j \ge g\left( {\hat{u}}_i^{\left( j\right) }\right) . \end{aligned}$$

Take the dual of this (finite) conic optimization problem to obtain the given maximization formulation.

To prove the last statement, suppose first that g(u) is non-decreasing and fix some j. If $g({\hat{u}}_i^{(j)}) > g({\hat{u}}_i^{(j-1)})$, then by complementary slackness, ${\mathbf {q}}^L = 0$. If $g({\hat{u}}_i^{(j)}) = g({\hat{u}}_i^{(j-1)})$, then given any feasible $(q^L_j, q^R_j)$, the pair $(0, q^L_j+ q^R_j)$ is also feasible with the same objective value. Thus, without loss of generality, ${\mathbf {q}}^L= 0$. The case where g(u) is non-increasing is similar. $\square$

Remark 22

At optimality of (73), ${\mathbf {p}}$ can be considered a probability distribution, supported on the points ${\hat{u}}_i^{(j)}$ $j=0, \ldots , N+1$. This distribution is analogous to ${\mathbf {q}}^L({\varGamma }), {\mathbf {q}}^R({\varGamma })$ for the KS test.

In the special case of the K test, we can solve (73) explicitly to find this worst-case distribution.

Corollary 1

When ${\mathcal {P}}^{EDF}_i$ refers specifically to the K test in Theorem 17 and if g is monotonic, we have

$$\begin{aligned} \sup _{{\mathbb {P}}_i \in {\mathcal {P}}^{EDF}_i} {{\mathbb {E}}}^{{\mathbb {P}}_i}\left[ g({{\tilde{u}}}_i) \right] = \max \left( \sum _{j=0}^{N+1} q^L_j\left( {\varGamma }^{K}\right) g\left( {\hat{u}}_i^{(j)}\right) , \sum _{j=0}^{N+1} q^R_j\left( {\varGamma }^{K}\right) g\left( {\hat{u}}_i^{(j)}\right) \right) .\nonumber \\ \end{aligned}$$

(74)

Proof

One can check that in the case of the K test, the maximization formulation given is equivalent to (48) with ${\varGamma }^{KS}$ replaced by ${\varGamma }^{K}$. Following the proof of Theorem 15 yields the result. $\square$

Remark 23

One an prove that ${\varGamma }^K \ge {\varGamma }^{KS}$ for all N, $\alpha$. Consequently, ${\mathcal {P}}_i^{KS} \subseteq {\mathcal {P}}_i^K$. For practical purposes, one should thus prefer the KS test to the K test, as it will yield smaller sets.

We can now generalize Theorem 6. For each of K, CvM, W and AD tests, define the (finite dimensional) set

$$\begin{aligned} {\mathcal {P}}_i^{EDF} {=} \{ {\mathbf {p}}\in {{\mathbb {R}}}^{N+2}_+ : \exists {\mathbf {q}}^L, {\mathbf {q}}^R \in {{\mathbb {R}}}^{N+2}_+, {\mathbf {z}}\in {{\mathbb {R}}}^N \text { s.t. } {\mathbf {p}}, {\mathbf {q}}^L, {\mathbf {q}}^R, {\mathbf {z}}\text { are feasible in}\;(73) \},\nonumber \\ \end{aligned}$$

(75)

using the appropriate ${\mathbf {A}}_S, {\mathbf {b}}_S, {\mathcal {K}}_S$.

Theorem 18

Suppose ${\mathbb {P}}^*$ is known to have independent components, with ${{\mathrm{\text {supp}}}}({\mathbb {P}}^*) \subseteq [\hat{{\mathbf {u}}}^{(0)}, \hat{{\mathbf {u}}}^{(N+1)}]$.

• i) With probability at least $1-\alpha$ over the sample, the family $\{{\mathcal {U}}^I_\epsilon : 0< \epsilon < 1 \}$ simultaneously implies a probabilistic guarantee, where

  $$\begin{aligned} \begin{aligned} {\mathcal {U}}^I_\epsilon&= \,\Biggr \{ {\mathbf {u}}\in {{\mathbb {R}}}^d : \ \exists {\mathbf {p}}^i \in {\mathcal {P}}_i^{EDF}, \ {\mathbf {q}}^i \in {\varDelta }_{N+2}, \ i = 1\ldots , d,\\&\quad \sum _{j=0}^{N+1} {\hat{u}}_i^{(j)} q_j^i = u_i \ i = 1, \ldots , d, \ \ \sum _{i=1}^d D\left( {\mathbf {q}}^i, {\mathbf {p}}^i \right) \le \log ( 1/\epsilon ) \Biggr \}. \end{aligned} \end{aligned}$$

  (76)

• ii) In the special case of the K test, the above formulation simplifies to (21) with ${\varGamma }^{KS}$ replaced by ${\varGamma }^K$.

The proof of the first part is entirely analogous to Theorem 6, but uses Theorem 17 to evaluate the worst-case expectations. The proof of the second part follows by applying Corollary 1. We omit the details.

Remark 24

In contrast to our definition of ${\mathcal {U}}^I_\epsilon$ using the KS test, we know of no simple algorithm for evaluating $\delta ^*({\mathbf {v}}| \ {\mathcal {U}}^I_\epsilon )$ when using the CvM, W, or AD tests. (For the K test, the same algorithm applies but with ${\varGamma }^K$ replacing ${\varGamma }^{KS}$.) Although it still polynomial time to optimize over constraints $\delta ^*({\mathbf {v}}| \ {\mathcal {U}}^I_\epsilon ) \le t$ for these tests using interior-point solvers for conic optimization, it is more challenging numerically.