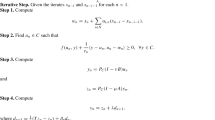Abstract
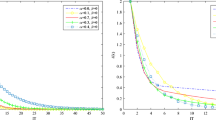
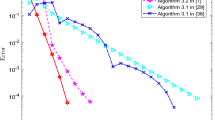
Affine variational inequalities (AVI) are an important problem class that subsumes systems of linear equations, linear complementarity problems and optimality conditions for quadratic programs. This paper describes PathAVI, a structure-preserving pivotal approach, that can efficiently process (solve or determine infeasible) large-scale sparse instances of the problem with theoretical guarantees and at high accuracy. PathAVI implements a strategy known to process models with good theoretical properties without reducing the problem to specialized forms, since such reductions may destroy sparsity in the models and can lead to very long computational times. We demonstrate formally that PathAVI implicitly follows the theoretically sound iteration paths, and can be implemented in a large scale setting using existing sparse linear algebra and linear programming techniques without employing a reduction. We also extend the class of problems that PathAVI can process. The paper illustrates the effectiveness of our approach by comparison to the Path solver used on a complementarity reformulation of the AVI in the context of applications in friction contact and Nash Equilibria. PathAVI is a general purpose solver, and freely available under the same conditions as Path.



Similar content being viewed by others
Notes
These index sets can be obtained using CPXgetbase() for CPLEX, for example.
The collection of problem can be freely downloaded by visiting http://fclib.gforge.inria.fr.
References
Acary, V., Brémond, M., Koziara, T., Pérignon, F.: FCLIB: a collection of discrete 3D Frictional Contact problems. Technical Report RT-0444, INRIA. https://hal.inria.fr/hal-00945820 (2014)
Acary, V., Brogliato, B.: Numerical Methods for Nonsmooth Dynamical Systems: Applications in Mechanics and Electronics. Lecture Notes in Applied and Computational Mechanics. Springer, Berlin (2008)
Acary V., Brémond M., Huber O., Pérignon F., Sinclair, S.: An introduction to SICONOS, Rapport Technique, INRIA (2017)
Bixby, R.E.: Implementing the simplex method: the initial basis. ORSA J. Comput. 4(3), 267–284 (1992)
Cao, M., Ferris, M.C.: Lineality removal for copositive-plus normal maps. Commun. Appl. Nonlinear Anal. 2, 1–10 (1995)
Cao, M., Ferris, M.C.: A pivotal method for affine variational inequalities. Math. Oper. Res. 21(1), 44–64 (1996)
Cottle, R., Pang, J.S., Stone, R.: The Linear Complementarity Problem. No. 60 in Classics in Applied Mathematics. Society for Industrial and Applied Mathematics, Philadelphia (2009)
Davis, T.A.: UMFPACK. http://faculty.cse.tamu.edu/davis/suitesparse.html (2007)
Dirkse, S.P., Ferris, M.C.: The PATH solver: a non-monotone stabilization scheme for mixed complementarity problems. Optim. Methods Softw. 5(2), 123–156 (1995)
Dirkse, S.P., Ferris, M.C.: A pathsearch damped newton method for computing general equilibria. Ann. Oper. Res. 68(2), 211–232 (1996)
Dirkse, S.P., Ferris, M.C.: Crash techniques for large-scale complementarity problems. In: Ferris, M.C., Pang J.S. (eds.) Complementarity and Variational Problems: State of the Art. SIAM, Philadelphia (1997)
Dubois, F., Jean, M., Renouf, M., Mozul, R., Martin, A., Bagneris, M.: LMGC90. In: 10e colloque national en calcul des structures. Giens. https://hal.archives-ouvertes.fr/hal-00596875 (2011)
Eaves, B.C.: A short course in solving equations with PL homotopies. Nonlinear Programming. In: SIAM-AMS Proceedings, vol. 9, pp. 73–143 (1976)
Eldersveld, S.K., Saunders, M.A.: A block-lu update for large-scale linear programming. SIAM J. Matrix Anal. Appl. 13(1), 191–201 (1992)
Facchinei, F., Pang, J.S.: Finite-Dimensional Variational Inequalities and Complementarity Problems, vol. I. Springer, New York (2003)
Ferris, M.C., Dirkse, S.P., Jagla, J.H., Meeraus, A.: An extended mathematical programming framework. Comput. Chem. Eng. 33(12), 1973–1982 (2009)
Ferris, M.C., Munson, T.S.: PATH 4.7. http://www.gams.com/dd/docs/solvers/path (2013)
Huber, O., Ferris, M.C.: Friction contact problems from a variational inequality perspective (2016) (in preparation)
Klarbring, A., Pang, J.S.: Existence of solutions to discrete semicoercive frictional contact problems. SIAM J. Optim. 8(2), 414–442 (1998)
Lemke, C.E.: Bimatrix equilibrium points and mathematical programming. Manag. Sci. 11(7), 681–689 (1965)
Liu, J.: Strong stability in variational inequalities. SIAM J. Control Optim. 33(3), 725–749 (1995)
Maros, I.: QP examples. http://www.doc.ic.ac.uk/~im/00README.QP (1998)
Murty, K.G.: Linear and Combinatorial Programming. Wiley, New York (1976)
Robinson, S.M.: Generalized equations and their solutions, part I: basic theory. Math. Program. Study 10, 128–141 (1979)
Robinson, S.M.: Normal maps induced by linear transformations. Math. Oper. Res. 17(3), 691–714 (1992)
Robinson, S.M.: Convexity in Finite-Dimensional Spaces (2015) (unpublished manuscript)
Rockafellar, R.T.: Convex Analysis. Princeton University Press, Princeton (1970)
Acknowledgements
This work is supported in part by the Air Force Office of Scientific Research and the Department of Energy. The authors are grateful to Steven Dirkse and Todd Munson for comments and suggestions leading to improved computational performance.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Lemma 5
(Theorem 4.4 [6]) Consider an \(\textit{AVI}(C,q,M)\) with \({\text {lin}}\,C = \{0\}\) and let M be semimonotone with respect to \({\text {rec}}\,C\). Suppose that an unbounded ray occurs. Then the value of the auxiliary variable t is constant on that ray and \(\varDelta z\), the variation in z, is nonzero and satisfies
Proof
The fact that t is constant and that \(\varDelta z\) is a solution to (14) follows from the first part of the proof of Theorem 4.4 in [6]. To see that the direction \(\varDelta z\) is nonzero, we proceed by contradiction: at the current iterate \((x^{k}, t^{k})\) we have
Let \(x^{k+1}\) belong to the unbounded ray and suppose that \(\varDelta z = 0\):
It immediately follows that \(x^{k+1} = x^{k}\). \(\square \)


Rights and permissions
About this article
Cite this article
Kim, Y., Huber, O. & Ferris, M.C. A structure-preserving pivotal method for affine variational inequalities. Math. Program. 168, 93–121 (2018). https://doi.org/10.1007/s10107-017-1124-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-017-1124-9