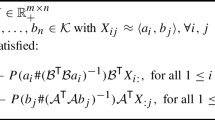Skip to main content
SpringerLink
Log in

Approximate cone factorizations and lifts of polytopes

  • Full Length Paper
  • Series B
  • Published:
Mathematical Programming Submit manuscript

Abstract

In this paper we show how to construct inner and outer convex approximations of a polytope from an approximate cone factorization of its slack matrix. This provides a robust generalization of the famous result of Yannakakis that polyhedral lifts of a polytope are controlled by (exact) nonnegative factorizations of its slack matrix. Our approximations behave well under polarity and have efficient representations using second order cones. We establish a direct relationship between the quality of the factorization and the quality of the approximations, and our results extend to generalized slack matrices that arise from a polytope contained in a polyhedron.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Alizadeh, F., Goldfarb, D.: Second-order cone programming. Math. Program. 95(1), 3–51 (2003)

  2. Borwein, J., Wolkowicz, H.: Regularizing the abstract convex program. J. Math. Anal. Appl. 83(2), 495–530 (1981)

    Article  MATH  MathSciNet  Google Scholar 

  3. Boyd, S., Vandenberghe, L.: Convex Optimization. Cambridge University Press, Cambridge (2004)

    Book  MATH  Google Scholar 

  4. Braun, G., Fiorini, S., Pokutta, S., Steurer, D.: Approximation limits of linear programs (beyond hierarchies). In: 2012 IEEE 53rd Annual Symposium on Foundations of Computer Science (FOCS), pp. 480–489. IEEE (2012)

  5. Braverman, M., Moitra, A.: An information complexity approach to extended formulations. In: Electronic Colloquium on Computational Complexity (ECCC), vol. 19, (2012)

  6. Gillis, N., Glineur, F.: On the geometric interpretation of the nonnegative rank. Linear Algebra Its Appl. 437, 2685–2712 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  7. Gouveia, J., Parrilo, P.A., Thomas, R.R.: Lifts of convex sets and cone factorizations. Math. Oper. Res. 38(2), 248–264 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  8. Gouveia, J., Robinson, R. Z., Thomas, R. R.: Worst-Case Results for Positive Semidefinite Rank. arXiv:1305.4600 (2013)

  9. Lobo, M., Vandenberghe, L., Boyd, S., Lebret, H.: Applications of second-order cone programming. Linear Algebra Its Appl. 284, 193–228 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  10. Nesterov, Y.E., Nemirovski, A.: Interior Point Polynomial Methods in Convex Programming, volume 13 of Studies in Applied Mathematics. Siam, Philadelphia (1994)

    Book  Google Scholar 

  11. Pashkovich, K.: Extended Formulations for Combinatorial Polytopes. PhD thesis, Magdeburg Universität (2012)

  12. Pataki, G.: On the closedness of the linear image of a closed convex cone. Math. Oper. Res. 32(2), 395–412 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  13. Pataki, G.: On the connection of facially exposed and nice cones. J. Math. Anal. Appl. 400(1), 211–221 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  14. Renegar, J.: Hyperbolic programs, and their derivative relaxations. Found. Comput. Math. 6(1), 59–79 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  15. Rockafellar, R.T.: Convex Analysis. Princeton Mathematical, vol. 28. Princeton University Press, Princeton (1970)

    Google Scholar 

  16. Saunderson, J., Parrilo, P.A.: Polynomial-sized semidefinite representations of derivative relaxations of spectrahedral cones. Math. Program. Ser. A. (2014). doi:10.1007/s10107-014-0804-y

  17. Sonnevend, Gy.: An “analytical centre” for polyhedrons and new classes of global algorithms for linear (smooth, convex) programming. In: System Modelling and Optimization, pp. 866–875. Springer, Berlin (1986)

  18. Sturm, J.F., Zhang, S.: An \({O(\sqrt{n L})}\) iteration bound primal-dual cone affine scaling algorithm for linear programming. Math. Program. 72(2), 177–194 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  19. Yannakakis, M.: Expressing combinatorial optimization problems by linear programs. J. Comput. Syst. Sci. 43(3), 441–466 (1991)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgments

We thank Anirudha Majumdar for the reference to [18], and Cynthia Vinzant for helpful discussions about cone closures.

Author information

Authors and Affiliations

  1. CMUC, Department of Mathematics, University of Coimbra, 3001-454, Coimbra, Portugal

    João Gouveia

  2. Laboratory for Information and Decision Systems, Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA, 02139, USA

    Pablo A. Parrilo

  3. Department of Mathematics, University of Washington, Box 354350, Seattle, WA, 98195, USA

    Rekha R. Thomas

Authors
  1. João Gouveia
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pablo A. Parrilo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Rekha R. Thomas
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rekha R. Thomas.

Additional information

Gouveia was supported by the Centre for Mathematics at the University of Coimbra and Fundação para a Ciência e a Tecnologia, through the European program COMPETE/FEDER. Parrilo was supported by AFOSR FA9550-11-1-0305, and Thomas by the US National Science Foundation Grant DMS-1115293.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gouveia, J., Parrilo, P.A. & Thomas, R.R. Approximate cone factorizations and lifts of polytopes. Math. Program. 151, 613–637 (2015). https://doi.org/10.1007/s10107-014-0848-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10107-014-0848-z

Keywords

Mathematics Subject Classification

Search

Navigation