Abstract
Corruption is an endemic societal problem with profound implications in the development of nations. In combating this issue, cross-national evidence supporting the effectiveness of the rule of law seems at odds with poorly realized outcomes from reforms inspired in the academic literature. This paper provides an explanation for such contradiction. By building a computational approach, we develop three methodological novelties into the empirical study of corruption: (1) modeling government expenditure as a more adequate intervention variable than traditional indicators, (2) generating large within-country variation by means of bottom-up simulations (instead of cross-national data pooling), and (2) accounting for all possible interactions between covariates through a spillover network. Our estimates suggest that, the least developed a country is, the more difficult it is to find the right combination of policies that lead to reductions in corruption. We characterize this difficulty through a rugged landscape that governments navigate when changing the total budget size and the relative expenditure towards the rule of law. Importantly our method helps identifying the—country-specific—policy issues that complement the rule of law in the fight against corruption.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent years, public governance has become one of the main topics in the international development agenda.Footnote 1 However, in spite of significant efforts to procure public governance through the rule of law,Footnote 2 there seems to be a mismatch between the expectations from policy prescriptions and real-world outcomes.Footnote 3 In this regard, the World Bank asserts—in its 2017 World Development Report: Governance and the Law—that legal improvements to the rule of law have rarely succeed in achieving drastic reductions of corruption.Footnote 4 Baez-Camargo and Passas (2017) offer a reasonable explanation: the ineffectiveness of reforms to the rule of law may originates from inconsistencies between the de jure governance and the social norms that guide citizens and bureaucrats; that is to say, from the disregard of systemic effects.
This paper studies, theoretically and empirically, the causal linkage between government expenditure, the rule of law, and corruption. We find that improvements to the rule of law do not necessarily generate lower levels of corruption in all countries because, in the real world, (1) the ceteris paribus condition for other policy issues does not hold (partly because of the trade-offs that emerge when prioritizing policy issues) and (2) co-movements in other topics introduce effects that may oppose the traditional conduits of anti-corruption policies (i.e., inverting the net benefit of misbehaving and curtailing the discretionary use of resources). Moreover, while overall increments in public expenditure tend to generate improvements in the rule of law and a fall in corruption, this relationship can easily become fuzzy if the relative levels of expenditure across multiple policy issues is altered.
We argue that the disappointing performance commonly observed in policies attempting to improve public governance is a consequence of dealing with a complex world, in which unexpected outcomes are the result of systemic considerations that produce non-linearities and a rugged landscape; blurring the mapping between policy packages and outcomes. In particular, the existence of spillover effects between socioeconomic indicators, and the associated policy issues, produce externalities that might distort the incentive structure of public officials in charge of implementing such policies. This, in turn, can create non-anticipated opportunities to divert funds under a setting of imperfect supervision. Accordingly, we introduce a systemic perspective that allows us to move beyond the principal-agent framework and consider the implicit trade-offs in any budgeting exercise that supports a multidimensional policy space.
Through simulations with an agent-based model, we produce country-level estimates for 140 nations during a period of 21 years, while taking into account interactions between numerous indicators. Our computational approach has three key advantages over traditional econometric analyses: (1) it does not require pooling cross-national data, so the model is calibrated for each country individually (i.e., it is consistent with the ‘context matters’ premise by incorporating country-specific characteristics); (2) it provides micro-foundations of a causal process that links expenditure, the rule of law, and corruption (i.e., it is more suitable to deal with problems of endogeneity and revere causation), and (3) it can control for the interactions that take place among a relatively high number of indicators (i.e., it is scalable with respect to the dimensions of the policy space).
The rest of the paper is structured in the following way. Section 2 provides a review of the literature on corruption with an emphasis in econometric studies, and presents some stylized facts that are key to understand why another approach is needed. Section 3 introduces the theoretical model, based on tools of agent-computing, network science, behavioral economics, and political economy games. Section 4 indicates the nature of the data employed for the analysis, how the spillover network is estimated, and how the computational model is calibrated. Section 5 presents empirical findings of the model that are consistent with the stylized facts and the hypothesis outlined in this introduction. Finally, Sect. 6 summarizes the arguments and results of this paper, and provides some additional reflections.
2 On the study of corruption and the rule of law
2.1 The principal-agent view versus a systemic analysis
Broadly speaking, the empirical literature on the determinants of corruption tends to agree on the statistical significance of the rule of law (hereby called the RoL), when tested in a cross-sectional setting. At the same time, however, there is disappointment among international organizations and NGOs with regards to the poor performance of institutional reforms inspired in such literature (World Bank 2017, pp. 77–79). We argue that such discrepancy originates from a view that focuses exclusively on the principal-agent problem (Rose-Ackerman 1975; Klitgaard 1988),Footnote 5 and that assumes a ceteris paribus condition. From such perspective, corruption arises from the presence of asymmetric information between the agents (i.e., public servants or elected officials) and a principal (i.e., government or voters) whose monitoring efforts are imperfect. Consequently, improvements to the RoL should reduce the agents’ expected net benefits from embezzling funds and curtail opportunities for the discretionary use of public resources.Footnote 6 One of the problems with the principal-agent view is that systemic properties of corruption are considered irrelevant. Thus, the co-evolution of other policy issues is assumed irrelevant in the incentive structure of the agents.
2.2 Econometric studies
The econometric literature on the determinants of corruption is extensive and shows consensus with respect to the statistical significance of the RoL. The theory proposed in this paper aligns with this consensus in several ways, but differs in others. In particular, considering the interactions between different policy issues is not standard in these studies. Furthermore, due to data limitations, country-specific policy prescriptions are difficult to infer through traditional econometric frameworks. In this section, we review some studies and elaborate on ways in which a computational approach could complement them.
Early studies on the determinants of corruption exploit the cross-national variation of different development indicators through pooled-regressions (Ades and Tella 1997; Leite and Weidmann 2002; La Porta et al. 1999; Treisman 2000; Broadman and Recanatini 2001; Dollar et al. 2001; Paldam 2002; Fisman and Gatti 2002; Herzfeld and Weiss 2003; Brunetti and Weder 2003; Knack and Azfar 2003). Overall, these studies have been consistent with the idea that public governance instruments are effective tools that can be used in the fight against corruption. As the econometric literature has progressed, more sophisticated approaches have been deployed in order to overcome some of the limitations in these works and to provide a fine-grained picture of the relevant policy tools.
In studies using Bayesian Model Averaging (BMA),Footnote 7 Gnimassoun and Massil (2016) and Jetter and Parmeter (2018) find that some policy variables are robust predictors and, thus, they can be utilized by governments for abating corruption in relatively short periods. Some of these predictors include quality of education, female participation in parliament, willingness to delegate authority, freedom of the press, burden of regulation, absence of political rights, property rights and rule of law (at least in one of the statistical analyses presented in those studies). It is important to emphasize that institutional covariates have a prominent role in this set of explanatory variables.
Jetter and Parmeter (2018) apply a variant of the BMA to consider endogeneity in a large set of independent variables, instrumented through their one-decade lagged values. They find that, out of 32 potential determinants of corruption across 123 countries, 10 are robust. Furthermore, they identify five determinants with direct policy instruments: years of primary education, trade freedom, rule of law, federal system, absence of political rights. Note that the last three are associated to the country’s governance framework. Consistent with most cross-sectional studies, the level of economic development (GDP per capita) is also significant.Footnote 8
Using quantile regression in order to deal with parameter heterogeneity, Billger and Goel (2009) identify that improvements in democracy have a negative effect on corruption only among the 50% most-corrupt nations. On the other hand, increments in the government size have negligible effects among the most corrupt countries. In an alternative strategy, Gnimassoun and Massil (2016) and Jetter and Parmeter (2018) split the sample by geographical region and development status, respectively. The latter authors, for example, find that the RoL is prominent among developing countries (i.e., non-members of the OECD), implying that the effectiveness of legal accountability diminishes once the quality of the RoL has reached certain level.Footnote 9 In this sub-sample, only two of the 11 robust predictors relate to governance (the RoL and absence of political rights) while two more are associated to some policy instrument (foreign direct investment and government size).
In spite of these commendable efforts, there are still empirical challenges that need to be addressed; some related to the course-grained nature of development-indicator data, and others to methodological issues that are inherent to the econometric study of aggregate relationships. Generally speaking, development indicators do not allow exploiting within-country variation (unless an extremely narrow set of covariates is used). While cross-national variation is, then, the dominant factor, its results have limited policy interpretations since the estimated coefficients correspond to a hypothetical country with the average characteristics of the sample. Another problematic issue comes from the Rodrik critique (Rodrik 2012) which points out that policy indicators are not proper exogenous random variables, but conscious and strategic decisions made by governments in an attempt to obtain specific goals. Thus, the choice of development indicators as explanatory variables might not be appropriate.
Furthermore, an additional methodological limitation comes from the Lucas critique, rejecting the assumption that, under regression analysis, the estimated effects during the sampling period will still be valid in an out-of-sample evaluation.Footnote 10 For example, given previous evidence on parameter heterogeneity across income groups, a country’s estimates are likely to shift as its economy develops. Hence, in order to try to overcome some of these challenges, we propose a bottom-up computational approach.
2.3 Stylized facts
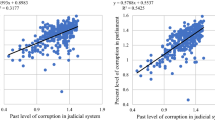
Using an indicator for the RoL—from the 2020 Worldwide Governance Indicators—and the Perception of Corruption Index—from Transparency International—, we corroborate in panels (a) and (b) of Fig. 1 the existence of a paradoxical empirical finding: a high cross-country and a low within-country correlation between corruption and the RoL.Footnote 11 The first correlation result is consistent with more sophisticated analyses using cross-section regressions,Footnote 12 while the second correlation highlights a missing link between theoretical and empirical studies. Because the vertical axis in panel (b) measures the degree of correlation between corruption (Perception index) and the RoL, this scatter plot indicates that, when analyzing within country variations in the RoL (horizontal axis), there are many countries with a negative relationship between these variables; this stands in contradiction with the policy prescriptions motivated from studies aligned with panel (a).Footnote 13 Likewise, in many more cases the positive correlation is relatively low (below 0.33) and, presumably, not statistically significant. Accordingly, all countries (colored dots) with a correlation below the 0.33 threshold are paradoxical cases for the econometric literature supporting improvements in the RoL with the aim of abating corruption.
Correlations between corruption and intervention variables. Note: Countries are colored by the geographic groups shown in Fig. 2 (color figure online).
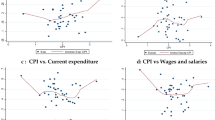
In order to propose a potential explanation of these paradoxical results, we also test whether a similar correlation structure exists between the level of per capita government expenditure and each of these two indicators. Panels (c) and (d) present the case for corruption, while panels (e) and (f) do the same but using the indicator for RoL. Because expenditure is a proper instrument of government intervention—as opposed to endogenous development indicators—this paper studies a causal mechanism that goes from expenditure to the RoL and from the RoL to the aggregate diversion of public funds.
Both development indicators are positively correlated with government expenditure per capita in cross-section comparisons. Hence, we hypothesize that, for establishing a conduit between the RoL and corruption, the expenditure channel needs to be studied further. Once more, when within country variations are analyzed, in this case for government expenditure, we find that the correlation between the RoL (or corruption) and per capita expenditure can be either positive or negative. This could be the result of violations to the ceteris paribus assumption and, therefore, it is convenient to analyze such relationships with a framework that incorporates systemic features and the causal mechanisms behind an economy’s emergent properties.
2.4 Proposed methodological framework
In this paper, we take a computational approach and argue that agent-computing can help overcome the problems of reverse causation, non-linearity, parameter homogeneity, and endogenous indicators. To show this, we model an economy’s policymaking process that allows producing country-specific relationships between the RoL and the diversion of public funds. In this model, a government intervention can be established at the level of the overall public expenditure or in the propensity to spend in a specific policy issue.
Micro-founded computational models have the ability of addressing generative causation (Epstein 2006); something that we exploit to produce macroscopic statistical relationships via controlled experiments. Generative causation means that the micro-level social mechanisms from our theory of corruption are formally specified in an algorithm, acting as the data-generating process. Through these experiments, we study the incidence that exogenous government decisions have on the aggregate level of corruption and on the evolution of the RoL. In addition, this approach allows considering the endogenous variation of other policy issues that affect or are affected by the RoL; circumventing the limitations of ceteris paribus assumptions.Footnote 14 More specifically, our model highlights three systemic features behind the emergence of corruption that are present in most nations: (1) an adaptive government that establishes budgetary priorities (resource allocations) across several policymaking offices; (2) public servants that make decisions on how to use those resources, and (3) a network of spillovers (externalities) among policy issues (e.g. health, education, infrastructure, public governance, etc.).
2.5 Public expenditure as an exogenous variable
Our empirical strategy consists in generating within-country variation in the level of corruption by exogenously increasing the expenditure dedicated to government programs with the mandate of improving the RoL. By discarding the possibility of intervening the indicator directly, we model a more realistic setting and allow for the endogenous evolution of the RoL, which is not entirely under the control of the central authority (e.g., for example, if the government programs are inherently ineffective).
There are several reasons why expenditure is closer to an exogenous variable in comparison to development indicators, at least in relation to the problem at hand. First, government budgets often come from various processes that are not necessarily related to policy implementation (at least not as strongly as indicators); for example, campaign promises, international agreements, political consensus, societal pressures, political negotiations, or even discretionary decisions. In contrast, empirical development indicators do originate from the policymaking process (which involves inefficiencies such as corruption), thus they are conflated with a wide variety of issues supported by different government programs. Second, when a policy prescription is justified through econometric studies, it is assumed that a change in an indicator equates to a similar change in policy priorities. This is unlikely to be the case since spillover effects and long-term structural factors are partially responsible for the indicators’ dynamics. Thus, changes in expenditure may not necessarily translate into similar changes in the indicators. Third, the opaque mapping between spending and indicators means that more resources to improve the RoL do not necessarily imply less corruption (a common assumption in linear models that use indicators). Thus, using the budget as the exogenous variable allows us to account for potential non-linearities and bottlenecks coming from the data-generating mechanism.
It is important to distinguish between two ways in which an exogenous change in the spending towards the RoL can be implemented. The first type of intervention consists in increasing the total budget available. By doing this, one induces higher success rates in the growth of all indicators because the associated programs are well funded. However, these improvements may be non-linear because the central authority decides how to allocate resources, partially, as a response to observed outcomes (e.g., disparities in the efficient use of resources). Overall, one would expect a negative relation between the size of the budget and the level of corruption if not other policy variable is affected simultaneously. This logic is consistent with cross-national regression studies, since per capita expenditure correlates with how developed is an economy.
The second type of intervention consists of inducing a higher propensity to spend in the RoL while keeping the same budget size. The theoretical implication here is that increments in expenditure towards the RoL take place at the cost of other policy issues. Thus, the relationship between more resources and less corruption is less clear than with the first type of intervention. Naturally, a combination of both types of budgetary changes takes place in the real world. As we argue, below, this may be an important factor to explain the poor experiences of some countries in curbing corruption through reforms to the rule of law.
3 Model
We develop an agent-computing model along the lines of Guerrero and Castañeda (2021), Guerrero and Castañeda (2020), Castañeda et al. (2018). The model consists of a political economy game where the central authority (the government) sets policy priorities in terms of resource allocations, while public servants (the agents) are in charge of implementing such policies. The agents may use the allocated resources towards the policies that will transform their corresponding development indicators, or they may divert part of these resources for personal gain. These decisions are shaped by the spillovers, the monitoring mechanism of the principal, the quality of the RoL, and the expected profitability of corruption. While aggregate corruption is an endogenous variable, the model has a unique way of dealing with the endogeneity issues that are common in econometric studies:
-
1.
All development indicators, including the one corresponding to the RoL are endogenous.
-
2.
Like in the real world, indicators cannot be directly intervened but, instead, the government can allocate more resources to existing programs in hopes of improving their respective indicators.
-
3.
The size of the government’s budget is exogenous; it is the result of longer-term processes such as political negotiations and societal agreements.
-
4.
In order to deal with the reverse-causation problem between expenditure and indicators, the distribution of the budget is endogenous; it emerges from the government’s behavioral model.
-
5.
While the government allocates resources endogenously, we can induce specific expenditure patterns through a set of exogenous ‘modulation’ parameters, which we use for counterfactual analysis.
In a typical simulation, the model begins with a vector of initial values for N different development indicators of a given country. Importantly, there is a subset \({\mathbf {I}}\) with \(n \le N\) indicators, that we call instrumental, for which there exist government programs. Policy issues without government programs are called collateral, and they respond to spillovers and other factors captured in their associated parameters. The government tries to improve the instrumental indicators by distributing its total budget \({\mathbf {B}}\) across its existing government programs. Following Guerrero and Castañeda (2021), we assume a homogeneous disbursement schedule so, every period \(t \in \{ 1, \dots , T\}\), the government establishes an allocation profile \(P_{1,t}, \dots P_{n,t}\) such that \(\sum _{i}^n P_{i,t} = B\) and that \(T \times B = {\mathbf {B}}\). Each allocation \(P_i\) is handed to a bureaucrat or agency with the mandate of improving indicator Ii . It is here, during the implementation of the relevant government program, where corruption in the form of embezzled public funds takes place. This leads to the first ingredient of the model, the public servant’s benefit function
where \(F_{i,t+1}\) represents the benefit or utility obtained in the next period. The first addend captures proficiency benefits. \(\Delta I^*_{i,t}\) corresponds the change in indicator i with respect to the previous period, relative to the changes of all other indicators, as expressed by
Going back to Eq. 1, \(C_{i,t} \le P_{i,t}\) are the resources that are effectively used towards the policy. We call it the contribution of agent i. Thus, the second addend corresponds to the utility from corruption. This summand is weighted by \(1 - \theta _{i,t} \tau\), which models the outcome of the government’s monitoring mechanisms. Variable \(\theta _{i,t}\) is a random binary variable representing the outcome of monitoring, so \(\theta _{i,t}=1\) when the government spots agent i embezzling public funds. The stochasticity of the monitoring outcomes means that the supervision mechanisms are imperfect. If an embezzlement is found, the responsible agent is penalized by a factor \(\tau _t \in [0,1]\), such that the benefit from these private gains are reduced. Parameter \(\tau _t\) corresponds to the indicator of the RoL, so it is an endogenous variable (with exogenous initial conditions). An improvement in the RoL would directly affect the benefits from corruption by introducing larger punishments.
Equation 1 captures the ‘incentive effect’ associated to an enhancement in the quality of the RoL. On the one hand, agents may receive political status from showing good performance in their indicators. On the other, they also benefit from extracting private rents by diverting funds through a lower contribution \(C_{i,t}\). However, their benefits are dampened if they get caught embezzling funds.
Next, let us explain how the monitoring outcomes are generated. \(\theta _{i,t}\) is a Bernoulli random variable with probability of success
where \(P^*_{t}\) is the largest allocation in period t. This probability is determined in relation to the maximum allocation in order to capture the standing-out-of-the-social-norm feature that makes the problem of corruption so deceptive (when there is a high-tolerance norm). Parameter \(\varphi _t\) is the value of the indicator of control of corruption.
The governance parameters \(\tau _t\) and \(\varphi _t\) are endogenously determined by the evolution of the corresponding indicators of rule of law and control of corruption.Footnote 15 While the contributions \(C_{i,t}\) are determined by each agent through reinforcement learning. If an agent becomes more inefficient and their benefits increase, then they become more inefficient the next period. If, in contrast, the government is able to penalize, they become more proficient the next period. Guerrero and Castañeda (2021, 2020) provide evidence of internal and external validity for this learning modeling choice. The level of proficiency/corruption is determined through an action
where \(\text {sgn}(\cdot )\) is the sign function. Actions are abstractions of any activity that the agent may undertake to increase/decrease its contribution. In order to map action \(X_{i,t}\) into the units of the budget, we use the link function
Now that we have modeled the contributions, we explain how the government determines the allocations \(P_{i,t}\). In the real world, identifying the precise mechanisms through which governments establish their allocations is extremely challenging. In the political science literature, allocations are modeled as a stochastic process that produces skewed distributions of budgetary changes: Jones et al. (2009). We combine this approach with the economic intuition that governments seek to increase the efficiency of public spending, so they ‘praise’ the most efficient agencies and ‘punish’ the most inefficient ones. These praises and punishments are modeled as propensities to spend in the most efficient policy issues (given the historical data provided by the imperfect monitoring mechanisms). Thus, we model the evolution of propensity \(q_{i}\) as
where U(0, 1) is a random draw from a uniform distribution in (0,1).Footnote 16
Next, we produce the normalized propensities
from which we then construct the modulated propensities
The modulated propensities reflect the fact that the allocation of a budget is often the result of factors that lie beyond economic considerations, for example, historical practices and political agreements. Therefore, \(b_i\) reflects an exogenous modulating exponent that helps explaining why a given country exhibits a specific expenditure pattern. Unfortunately, expenditure data disaggregated at the level of each indicator does not exist for any country in the world, so we assume \(b_i=1\) for every indicator in our benchmark estimations. Nevertheless, we use these parameters to explore counterfactuals of alternative allocation profiles in Sect. 5.3.
Finally, the allocation profile for a given period is determined by
The evolution of the indicators takes place through the dynamic equation
where \(\xi (\cdot )\) is the binary outcome (0 or 1) of a random growth process with a probability of success \(\gamma _{i,t}\). Parameter \(\alpha _i\) captures long-term structural factors that are partly responsible for the improvement of the indicators, but different from the existing government programs. Modifying these parameters would require creating new expenditure programs and micro-policies. This is why the model emphasizes government expenditure on existing programs, which has a short/mid-term nature.
The probability of success \(\gamma _{i,t}\) of an existing government program depends on the agents' contributions and on spillover effects. We model this probability as
where \(\beta\) is a normalizing parameter and \(S_{i,t}\) is the net amount of spillovers received by indicator i in period t (this could be positive or negative). The piece-wise structure of this functions indicates that instrumental indicators respond to the contributions made to their expenditure programs, while collateral ones respond to the overall level of effective expenditure in the economy; a sign of the financial health of the system. This implies that, should there be no resources or contributions, the indicators would not progress, even the collateral ones. Thus, all indicators are sensitive to the overall size of the budget, but only the instrumental ones respond (directly) to a reallocation of resources (assuming no spillovers).
The spillovers are computed every period according to \(S_{i,t}=\sum _j {\mathbf {1}}_{j,t} {\mathbb {A}}_{j,i}\), where \({\mathbf {1}}\) is the indicator function taking value 1 if indicator j grew in the previous period and 0 otherwise. Matrix \({\mathbb {A}}_{j,i}\) is exogenous, so the user of the model can assume any interdependency structure. Section 4.2 explains our method of choice to estimate country-specific networks. We consider this network to be exogenous because the specific topologies capture long-term features of the economy, while the particular realizations of the spillovers are short-term phenomena because they are the result of the previous performance of other indicators.
4 Data and calibration
4.1 Development indicators
Given the importance of interdependencies across numerous policy dimensions, we frame our study in the context of the Sustainable Development Goals (SDGs), and use a dataset prepared by Lafortune et al. (2018) for the 2020 Sustainable Development Report. These data contain time series on 77 indicators across 140 countries between 2000 and 2020. The indicators are classified into the 17 SDGs, so they provide a comprehensive view of the multidimensionality of development. The dataset, however, lacks indicators in SDG 12: ‘Responsible Consumption and Corruption’. The coverage over the 77 indicators may vary from one country to another, which would be problematic under a panel regression framework. However, since our model is calibrated for each country individually, this is not an issue. Appendix A provides further details on the indicators.
We complement the SDG data with two indicators from the Worldwide Governance Indicators (WGI): control of corruption and rule of law. These indicators reflect the perception of citizens, entrepreneurs, and experts in the public, private, and NGO sectors. Although perception-based indices have well-known limitations, they are still one of the best metrics used in corruption studies. Control of corruption reflects the quality of the monitoring efforts by the central authority, which is an important element in the model. The indicator of rule of law, on the other hand, captures the quality of institutions designed to develop or maintain a law-abiding society. The values of the simulated counterparts of these two indicators correspond to the model’s parameters \(\tau _{t}\) and \(\varphi _{t}\).
To facilitate the visual communication of the simulation outcomes, we color-code some of them according to six country clusters: Sub-Saharan Africa (Africa), Eastern Europe and Central Asia (E. Europe & C. Asia), East and South Asia (East & South Asia), Latin-America and the Caribbean (LAC), Middle-East and North Africa (MENA), and Western Countries (West). Figure 2 provides the geographical distribution of these groups. However, it is important to emphasize that the paper’s results are generated at the country level.
4.2 Spillover networks
The adjacency matrix \({\mathbb {A}}\) encodes conditional dependencies between the indicators (and has a zero-diagonal). This network is assumed to be exogenous, so it can be constructed through various alternative statistical methods or via expert opinion. Ospina-Forero et al. (2020) provide a comprehensive survey of statistical methods to estimate networks in the context of the SDGs. It is important to point out that, regardless of the estimation procedure, these spillover networks should not be interpreted as causal, but just as conditional dependencies; as a stylized fact that should be taken into account by the model. This is so because development indicators are too aggregate to disentangle all the confounders in a causal graph, and to assume that governments can directly intervene them through exogenous policies. Instead, by assuming conditional dependencies, the network provides structural information about the conditional co-movement of the indicators observed in the real world. The proper causal mechanisms are, instead, provided by the specification of the computational model.
The model formulates a data-generating process with explicit connections between the micro- and macro-levels. The network plays a ‘connecting’ role between these two. For instance, while policy interventions often take place at the micro-level (e.g., in the political arena), their measurement is captured in observational variables at the macro-level (e.g., population-level rates).Footnote 17 Because the network channels the agents’ contributions to the aggregate behavior of the indicators, it functions as a meso-level device that makes the bottom-up causal channel explicit.
In terms of the estimation of the networks, we take a Bayesian approach. Each network consists of a directed acyclic graph estimated through the Sparse Bayesian Networks package sparsebn (Aragam et al. 2019), which specializes in high-dimensional data. The estimation method assumes no temporal dependence. We transform the individual series into their first differences to remove the effect of temporal trends. In this manner, a unique dataset for each indicator is produced for each country, so the estimated networks are context-specific. Appendix B provides further details on the estimation of the networks.
4.3 Calibration
Once the input data are ready (the indicators, the budgets, and the network), we need to calibrate the model’s free parameters. Guerrero and Castañeda (2021) develop a multi-output gradient-descent algorithm to perform this calibration for each country individually; we provide its full detains in appendix C. For the structural factors \(\alpha _1, \dots , \alpha _{N}\), the idea is to find a vector that minimizes the average difference between the final simulated value and last empirical observation of each indicator. At the same time, for parameters \(\beta _1, \dots , \beta _n\), the criterion is to minimize the difference between the average probability of success \(\gamma _{i,t}\) and the empirical success rate of the corresponding indicator. Goodness-of-fit scores are constructed for each parameter by measuring the normalized parameter-specific error. A country-specific goodness-of-fit score is constructed by taking the average of all parameter-specific goodness-of-fit scores. A score with value 1 means no error; a score of 0 or less means an error of equal or larger magnitude than the observed target value. These metrics follow Guerrero and Castañeda (2021) and all the details are provided in appendix C.1.
We run each simulation for \(T=50\) periods (or disbursement events), equivalent to 21 years.Footnote 18 Then, we perform 10000 simulations for each country and report country-level goodness-of-fit scores, as well as a validation test in Fig. 3. The validation consists of obtaining the endogenous level of corruption for each country and compare it with its empirical counterpart, as reported by the perception of corruption index. Recall that we do not calibrate the model using cross-national data, but each country is independently calibrated. Our test yields an almost 90% cross-national linear correlation between the data and our model, which provides strong a empirical validation. With this evidence at hand, we continue to dig deeper into within-country variation in order to analyze the determinants of ineffective expenditure on the RoL.
Goodness of fit country-scores. Note: The goodness of fit scores are calculated for each country and presented in a histogram. A score of 1 represents no error between the target observation and the one produced by the model. The goodness-of-fit metric is detailed in appendix C.1. We report \(1-{\bar{D}}\) (see Eq. 13) as the model’s endogenous corruption in order to be consistent with the directionality of Transparency International’s perception of corruption index.
5 Results
We divide the analysis in three parts. First, we demonstrate that the expenditure-corruption relation—through the channel of the RoL—is not necessarily negative, and neither linear. For this, we perform counterfactual simulations in which we alter the government’s propensity to spend in the RoL during the sampling period. Second, we analyze the joint effects from total and relative budgetary increments to explain why within country variations in the RoL (or in government expenditure) can produce unexpected outcomes in the correlation between corruption and the RoL as those presented in Fig. 2. Third, we explore, through counterfactual simulations, what indicators could act as complements or bottlenecks to the RoL in curbing corruption.
Our measure of corruption consists of the total amount of embezzled resources, as a fraction of the total budget. That is, for a single simulation m, we quantify corruption as
We perform M independent Monte Carlo simulations to obtain the expected level of aggregate corruption across multiple realizations of the model according to
While \({\bar{D}}\) offers a measure of corruption produced by the model in terms of an empirical budget, it should not be interpreted as a precise quantitative estimate of the actual amount of embezzled resources in a country. Instead, it should be interpreted in a qualitative fashion in so far as it describes non-linear relationships between expenditure and corruption. We cannot provide point estimates of corruption because the factual probability of spotting an embezzlement is not necessarily equal to the one described in Eq. 3, while expression 6 does not necessarily describe the true cost of a penalty when public servants misbehave. Instead, \({\bar{D}}\) provides a relative metric that is consistent with an empirical index on the perception of corruption, as shown by Fig. 3b.
5.1 Non-linear responses to expenditure in the rule of law
One of the advantages of using computational models is that we can study the consequences of certain policy interventions without assuming that key endogenous variables do not change (i.e., that the ceteris paribus assumption holds). Accordingly, the whole set of development indicators keeps evolving in the model, as in the real world, despite that a certain intervention was designed to affect only a reduced subset of indicators. Thus, we perform two types of simulation counterfactuals: (i) one where we increase the total budget \({\mathbf {B}}\), and (ii) one in which we maintain the original budget, but induce a higher expenditure proportion towards the RoL.
The implementation of experiments type (i) is straightforward since we only need to increase \({\mathbf {B}}\) by a certain rate. Here, we simulate 1% increments along the [0,1] interval. Experiments type (ii) require a more subtle instrumentation because the allocation profile is endogenous. In order to induce more expenditure towards the RoL, we intervene the modulation parameter \(b_i\), where i corresponds to the indicator of the RoL. Recall that the modulating parameters can ‘nudge’ the government agent to establish certain allocation profiles, and that \(b_i=1\) by default across all indicators. By decreasing \(b_i\), we can induce a higher level of expenditure in the RoL, while still preserving the endogeneity of the rest of the allocation profile (and maintain the same budget level). Hence, the interventions consist of simulating values of \(b_i\) in (0,1) that yield an allocation \(P_i\) towards the RoL no greater than 10% of the overall budget. Of course, 10% is still an unrealistically large amount. However, since no disaggregate data of public expenditure on development indicators exist (which would replace the endogenous determination of the allocation profile), it is neither clear what should be a realistic bound. Hence, the outcomes of experiments type (ii) should be appreciated for their qualitative nature.
Figure 4, presents the results from these simulation exercises for specific countries that are illustrative of each geographical cluster. Each marker represents the average corruption level for a given set of simulations. In the case of the round markers (bottom x-axis), each one is the result of 1000 Monte Carlo simulations with the same budget level. The triangular markers (the top x-axis) are the average of Monte Carlo simulations with a similar expenditure allocation \(P_i\) towards the rule of law, which is the result of nudging the government agent through parameter \(b_i\) (but without having full control over \(P_i\)). Thus, the triangular markers bin the corruption variable according to \(P_i\). This is why both types of markers show different levels of corruption in the left-most part of the plots. For both types of markers, we implement a cubic-spline interpolation in order to visualize the general trend of the simulated responses.
The first thing to notice is that, for all country cases, the relationship between proportional expenditure and corruption is non-linear. This result is missing in traditional econometric studies because they cannot fully exploit within country variations. In contrast, the relationship between overall expenditure and corruption is apparently linear and negative.Footnote 19 The second thing to notice is that, in four of these countries, the relationship is not only negative but considerable (as expected by supporters of public governance) when the proportion of spending on the RoL is relatively low. However, for Mexico and Malawi, the negative relationship is weak and limited to a smaller proportion of expenditure, after which the two variables increase along a steep slope.
Correlations between corruption and intervention variables. Note: The colors correspond to the geographic groups shown in Fig. 2 (color figure online).
For a better understanding of these results a caveat is in order. The magnitude of proportional expenditure in the RoL should not be interpreted factually for two reasons. We do not have data on public expenditure disaggregated at the government program level. If that were the case, we would be able to produce analyses with realistic proportions. Lacking granular data, the modeling of endogenous budgetary allocations has to be done by perturbing a parameter describing modulated propensities. Therefore, our model is suitable for capturing country-specific statistical relationships on a qualitative basis, but not for producing point estimates. Nevertheless, let us insist in a major (unexploited) virtue of the model: if expenditure-indicator linked data exists, it can be an input of the model to produce country-indicator point estimates.
5.2 The rugged landscape of budgetary interventions
In this section we perform combined budgetary interventions of both types (overall size and proportion spend on the RoL), and display the resulting corruption landscape (or surface) in Fig. 5. The shapes of these landscapes are consistent with Fig. 4 when slicing any of the horizontal axis. On the one hand, these plots show the distinctive non-linearities observed when moving across relative expenditure for any budget size. In one extreme, China presents a U-shaped surface in which there is ample room for abating corruption through increments in the proportion of public expenses destined to the RoL. In the other extreme, Mexico exhibits a J-shaped surface indicating that, in a long range of relative expenditure, corruption increases in spite of budgetary advances in this issue.
On the other hand, these plots highlight the various degrees of roughness that these surfaces present. For example, Denmark shows a smooth landscape (brown color), while Russia’s corruption surface (orange color) is highly intricate. In general, a rugged landscape describes a scenario where it is very difficult for a policymaker to know with precision what the effects of a policy mix would be. We argue that this is an important reason for the unexpected outcomes that frequently appear in developing and emerging market economies—either in Latin America, Africa, or Asia—when implementing packages of policy reforms that include fostering programs related to the RoL. The model makes clear that the existence of intricate corruption landscapes is a consequence of moving beyond the principal-agent view to incorporate a systemic perspective.
Joint effects from total and relative budgetary increments. Note: Colors correspond to the geographic groups shown in Fig. 2 (color figure online).
Next, we test whether more advanced economies face smoother corruption landscapes. If this is the case, then the design of policies for curbing corruption would be more demanding where it is more needed, a very unfortunate result. In these countries, the implementation of allocation profiles may even backfire and produce a raise in corruption. In Fig. 6, we present the relationship between the roughness of the corruption landscape and the level of development of the countries. While the metric for calculating roughness is explained below, countries’ development is measured in terms of the average level of their indicators in panel (a), and in terms of their per capita government expenditure in panel (b). Clearly, there exists a negative (non-linear) relationship between the level of development of a country and how difficult is to avoid counterproductive policy mixes in the fight against corruption. According to panel (a), most African countries (blue dots) experience highly rugged corruption landscapes. In contrast, most countries clustered in the West grouping (brown dots) presents relatively smooth surfaces.
Roughness of the corruption landscape. Note: Colors correspond to the geographic groups shown in Fig. 2. We report Spearman correlations (color figure online).
The surfaces presented in Fig. 5 are obtained through a cubic bi-variate spline, which is the result of minimizing
where \({\hat{D}}_j\) is the corruption ratio (i.e., as a fraction of the budget) calculated for each combined budgetary intervention, f is a cubic polynomial function and X is a vector with tuples \(({\mathbf {B}}_j, b_{i_j})\) of each policy mix. This particular formulation is know as smoothing spline because parameter p is a penalty imposed over the roughness of the estimated surface (as a way to deal with overfitting). In the minimization procedure used here, we intentionally set \(p=0\) because we want to emphasize the roughness of the corruption landscapes. Then, we employ the expression \(\int f''(X)^2 dX\) to calculate the metric of roughness of each spline described in the vertical axis of Fig. 6.
5.3 Complementary issues to the rule of law
The roughness of anti-corruption funding interventions points to the complexity of choosing an adequate policy mix and, in particular, a proper allocation profile. Such complexity arises from the complementarities between the RoL and other policy issues when fighting corruption. Complementarities could originate from either spillover effects or indirect channels such as changes in the incentive structure across the entire system (given that ceteris paribus conditions do not hold). This makes the empirical identification of complementarities quite challenging and, evidently, beyond the possibility of traditional approaches.
For exploring potential complementarities, we analyze different allocation profiles under the same budget \({\mathbf {B}}\). First, we generate random vectors \(b_1, \dots , b_n\) to induce different allocation profiles. For each of these, we compute \({\bar{D}}\) and evaluate if it is lower than the one obtained from the calibrated model (the benchmark). If aggregate corruption decreases, then we store the difference \(\Delta P_i = ({\bar{P}}_{i}' - {\bar{P}}_{i})/{\bar{P}}_{i}\), where \({\bar{P}}_{i}\) is the average allocation that indicator i receives under the benchmark, and \({\bar{P}}_{i}'\) is the allocation under the counterfactual created through the random modulation parameters. After evaluating 10000 random vectors, we compute the average \(\Delta P_i\) of each indicator across those allocation profiles that generate less corruption than the benchmark. If \(\Delta P_i > 0\) it means that policy issue i receives, on average, a budgetary increment in allocation profiles that reduce corruption, i.e. it is a complement. In case \(\Delta P_i < 0\), we can say that i acts as a bottleneck.
The most important result that stands out in Fig. 7 is that there are several country cases in which the RoL (black stars) does not receive the largest increment in funding when compared to the other policy issues in the same country. In many cases, the increment is close to zero and in few of them it is negative (i.e., spending in these government programs is wasteful even for the purpose of diminishing corruption). Sometimes, a small increase in the RoL funding is the result of this indicator already performing well (e.g., Finland), hence fostering complementary policy issues provides higher returns in terms of boosting efficiency. In other cases, this outcome is a consequence of government programs related to the RoL being highly ineffective (e.g., Mexico) and thus a better option is to look for alternative policies to promote. Another interesting result is that policies across different SDGs, and not only those related to ‘peace, justice and strong institution’ (SDG 16) can be, for practical purposes, good complements to the RoL. Finally, the diverse coloring observed in the dots of each country (column) indicates that ‘context matters’ and, thus, no simple rule exists to formulate an efficient allocation profile.
6 Conclusions and reflections
Corruption is an endemic problem of societies and, in many cases, it persists for decades or even centuries. Since it is a multidimensional phenomenon, its origin and potential solutions have been studied from the perspective of different disciplines. For instance, from an anthropological and sociological point of view, it can be argued that corruption norms emerge in a decentralized manner and, hence, become entrenched; making it extremely difficult to suppress them. Economists, for example, emphasize the existence of material incentives and information asymmetries as the main culprits for the illegal diversion of funds. These two arguments and others are not contradictory but complement each other.
In this paper, we take an economic perspective and conceive corruption as a hurdle that inhibits countries’ economic, social, inclusive, and sustainable development. However, even with this narrow focus, we pose that, when moving from a principal-agent view to a systemic perspective, the problem becomes more complex. A systemic approach has to deal with issues of collective action, agents responding to social constructs, and spillover effects between policy issues and their associated development indicators. The formal modeling of these features requires the use of innovative analytical techniques such as those coming from network science, behavioral games, and agent-computing.
In this paper we propose a computational model of this nature to explain why policy reforms on public governance, and on the rule of law in particular, do not always produce the desired outcomes. The simulation results show that the combination of budgetary policies, in terms of the overall budget size and the allocation profile produce a rugged corruption landscape. This makes difficult to select the policy package capable of curbing corruption, and it is an especially troublesome result for the countries that need such packages the most. Moreover, we advocate for avoiding the search of ‘best practices’ since countries structural features require specific policy mixes.
Therefore, for some countries, the abatement of corruption is not as much in fostering the public expenditure devoted to strengthening rule of law institutions. Instead, a better use of resources can be to promote complementary issues that, for not being conceptually related to public governance, are usually discarded form policy packages. This paradoxical result is explained by the existence of indicators’ interdependencies and the possibility of changing the incentive structure through budgetary reallocation for those in charge of implementing government programs.
Notes
For example, the website http://www.oecd.org/governance provides a brochure on OECD’s work on public governance.
The Oxford English Dictionary defines rule of law as “the restriction of the arbitrary exercise of power by subordinating it to well-defined and established laws”.
These expectations are formed, to certain extent, by results from cross-national regression studies where the rule of law appears, persistently, as one of the policy instruments exhibiting a significant negative relationship with aggregate corruption.
Corruption is defined by the Oxford English Dictionary as the “dishonest or fraudulent conduct by those in power, typically involving bribery”. Another popular definition used by organizations such as Transparency International, the World Bank and the United Nations Development Program is “the misuse of public office for private gain”.
Although a study by Kwon (2014) shows a principal-agent model where reducing discretionary behavior has ambiguous effects in mitigating corruption.
This scenario occurs when the enforcement of the law increases the probability of catching offenders and when reforms to the RoL—and other public governance mechanisms—reduce the space for an unaccountable management of public funds. Broadly speaking, incentives for proper behavior are elicited through political competition, while rent-seeking opportunities are diminished by fostering economic competition (Ades and Tella 1997).
BMA is employed to deal with model uncertainty. A different approach, however, has been proposed by Serra (2006) via Extreme Bound Analysis. Here, a predictor is considered robust when it remains statistically significant and preserves the same sign in all models that include such variable. A less restrictive criterion for a predictor to be defined as robust is that the zero value is not included in the averaged 90% confidence interval of the estimated coefficients (Seldadyo and de Haan 2006). The reader should be aware that this method is prone to multicollinearity problems due to potential interdependencies among the determinants. Hence, auxiliary techniques are required to cope with this issue.
When causality is considered, years of primary education and GDP per capita become the two most relevant factors, while the RoL is still robust but less prominent. An alternative methodology that deals with reverse causality and heterskedasticity is three-stage least squares, as done by Croix and Delavallade (2011).
On one hand, several cross-country studies find a significant RoL coefficient (Ades and Tella 1997; Leite and Weidmann 2002; Broadman and Recanatini 2001; Brunetti and Weder 2003; Herzfeld and Weiss 2003; Ali and Isse 2002; Park 2003; Damania et al. 2004; Croix and Delavallade 2011; Iwasaki and Suzuki 2012; de Mendonça and da Fonseca 2012; Elbahnasawy and Revier 2012). On the other, several papers find significant coefficients among alternative governance indicators; some related to current policies (e.g., government effectiveness, decentralization, freedom of the press, federal system, women in parliament, etc.) and others associated to the origins of the legal system. For extensive reviews on corruption and their economic, institutional, and historical determinants see Jain (2001); Lambsdorff (2016); Pellegrini (2011); (Seldadyo 2008, Ch. 5); and Dimant and Tosato (2018).
In the neoclassical view, it is commonly argued that only ‘deep’ parameters (i.e., associated to technology or preferences) can be invariant. Hence, the associated prescription has to be estimated though micro-founded functional relationships. However, several authors have pointed out that such prescriptions are built on a flawed diagnostic on how complex societies operate (see Colander and Kupers (2014) for more on this criticism).
The reader should be aware that the Transparency International’s index indicates a lower level of corruption when its value increases, hence a positive relationship in panel (a) indicates a negative correlation between corruption and the RoL.
Notice that, in panel (a), the advanced market economies of the West (brown dots) tend to be in the upper-right quadrant.
Both, positive or negative, correlations can be observed either as a result of an improvement or a deterioration in the data for the RoL.
Recently, general equilibrium models have been developed to deal with interdependencies between endogenous (e.g., economic development and corruption) and exogenous variables (e.g., quality of governance). Here, inference comes from theorems (e.g., Blackburn et al. (2006, 2011)), regression estimates testing theoretical propositions (e.g., Croix and Delavallade (2011); Haque and Kneller (2009); Aidt et al. (2008)) or simulations (e.g., Dzhumashev (2014); Barreto (2000)). Although, this approach is explicit about the causal channels between governance structure and corruption, it also has several drawbacks. First, the outcomes and mechanisms from equilibrium models are not properly validated with empirical evidence. Second, in the associated regressions, governance factors such as the RoL are assumed to be exogenous instead of endogenous variables; neglecting important processes such as learning and collective action. Third, many equilibrium models that produce solutions through simulations have too many parameters, often calibrated through questionable criteria (e.g., by adopting parameter values used by another author in a study of a different country).
This allows estimating the effectiveness of the RoL while accounting for potential parameter shifts, interdependencies with other indicators, and inefficiencies arising from the policymaking process.
In the absence of priors about the propensities, a random vector of propensities is established at the beginning of every simulation.
For example, when analyzing the impact of financial development on economic growth, both the causal variable and the outcome are measured at the country level, but the policy interventions (e.g., rules of supervision and competition) are implemented at a lower level of aggregation (e.g., banks and other financial institutions).
Guerrero and Castañeda (2021) show that the calibration is robust to different T, as long as T is at least as large as the number of years in the data.
This outcome does not contradict the stylized facts presented in panel (d) of Fig. 2 since the latter does not control for other interventions such as a modification in policy priorities.
References
Ades A, Tella RD (1997) The new economics of corruption: a survey and some new results. Polit Stud 45(3):496–515
Aidt T, Dutta J, Sena V (2008) Governance regimes, corruption and growth: theory and evidence. J Comp Econ 36(2):195–220
Ali AM, Isse HS (2002) Determinants of economic corruption: a cross-country comparison. Cato J 22:449
Aragam B, Gu J, Zhou Q (2019) Learning large-scale Bayesian networks with the sparsebn package. J Stat Softw 91(1):1–38
Baez-Camargo C, Passas N (2017) Hidden agendas, social norms and why we need to re-think anti-corruption. Working Paper, Basel Institute on Governance
Barreto RA (2000) Endogenous corruption in a neoclassical growth model. Eur Econ Rev 44(1):35–60
Billger SM, Goel RK (2009) Do existing corruption levels matter in controlling corruption?: Cross-country quantile regression estimates. J Dev Econ 90(2):299–305
Blackburn K, Bose N, Emranul Haque M (2006) The incidence and persistence of corruption in economic development. J Econ Dyn Control 30(12):2447–2467
Blackburn K, Bose N, Haque ME (2011) Public expenditures, bureaucratic corruption and economic development. Manch Sch 79(3):405–428
Broadman HG, Recanatini F (2001) Seeds of corruption: Do market institutions matter? MOST Econ Pol Trans Econ 11(4):359–392
Brunetti A, Weder B (2003) A free press is bad news for corruption. J Publ Econ 87(7):1801–1824
Castañeda G, Chávez-Juárez F, Guerrero OA (2018) How do governments determine policy priorities? Studying development strategies through networked spillovers. J Econ Behav Organ 154:335–361
Colander D, Kupers R (2014) Complexity and the art of public policy: solving society’s problems from the bottom up. Princeton University Press
Croix DDL, Delavallade C (2011) Democracy, rule of law, corruption incentives, and growth. J Publ Econ Theory 13(2):155–187
Damania R, Fredriksson PG, Mani M (2004) The persistence of corruption and regulatory compliance failures: theory and evidence. Publ Choice 121(3):363–390
de Mendonça HF, da Fonseca AO (2012) Corruption, income, and rule of law: empirical evidence from developing and developed economies. Braz J Polit Econ 32(2):305–314
Dimant E, Tosato G (2018) Causes and effects of corruption: What has past decade’s empirical research taught us?: a survey. J Econ Surv 32(2):335–356
Dollar D, Fisman R, Gatti R (2001) Are women really the fairer sex? Corruption and women in government. J Econ Behav Organ 46(4):423–429
Dzhumashev R (2014) Corruption and growth: the role of governance, public spending, and economic development. Econ Model 37:202–215
Elbahnasawy NG, Revier CF (2012) The determinants of corruption: cross-country-panel-data analysis. Dev Econ 50(4):311–333
Epstein JM (2006) Chapter 34 remarks on the foundations of agent-based generative social science. In: Tesfatsion L, Judd KL (eds) Handbook of computational economics, Elsevier, vol 2, pp 1585–1604
Fisman R, Gatti R (2002) Decentralization and corruption: evidence across countries. J Publ Econ 83(3):325–345
Gnimassoun B, Massil JK (2016) Determinants of corruption: Can we put all countries in the same basket? Technical Report 2016–12. University of Paris Nanterre, EconomiX
Guerrero O, Castañeda G (2020) Policy priority inference: a computational framework to analyze the allocation of resources for the sustainable development goals. Data Pol 2
Guerrero O, Castañeda G (2021) How does government expenditure impact sustainable development? A bottom-up model of the link between budgets and development gaps. SSRN Working Paper
Haque ME, Kneller R (2009) Corruption clubs: endogenous thresholds in corruption and development. Econ Gov 10(4):345–373
Herzfeld T, Weiss C (2003) Corruption and legal (in)effectiveness: an empirical investigation. Eur J Polit Econ 19(3):621–632
Iwasaki I, Suzuki T (2012) The determinants of corruption in transition economies. Econ Lett 114(1):54–60
Jain AK (2001) Corruption: a review. J Econ Surv 15(1):71–121
Jetter M, Parmeter CF (2018) Sorting through global corruption determinants: institutions and education matter—not culture. World Dev 109:279–294
Jones B, Baumgartner F, Breunig C, Wlezien C, Soroka S, Foucault M, François A, Green-Pedersen C, Koski C, John P, Mortensen P, Varone F, Walgrave S (2009) A general empirical law of public budgets: a comparative analysis. Am J Polit Sci 53(4):855–873
Klitgaard R (1988) Controlling corruption. University of California Press
Knack S, Azfar O (2003) Trade intensity, country size and corruption. Econ Gov 4(1):1–18
Kwon I (2014) Motivation, discretion, and corruption. J Publ Adm Res Theory 24(3):765–794
La Porta R, Lopez-de-Silanes F, Shleifer A, Vishny RW (1999) The quality of government. J Law Econ Organ 15(1):222–279
Lafortune G, Fuller G, Moreno J, Schmidt-Traub G, Kroll C (2018) SDG index and dashboard: detailed methodological paper, volume 1. bertelsmann stiftung and sustainable development solutions network (SDSN), New York
Lambsdorff JG (2016) Measuring corruption: the validity and precision of subjective indicators. In: Shacklock A, Galtung F (eds) Measuring corruption, Routledge, pp 81–100
Leite C, Weidmann J (2002) Does mother nature corrupt? natural resources, corruption, and economic growth. In: Abed G, Gupta S (eds) Governance corruption & economic performance, vol 99. International Monetary Fund, Washington DC, pp 159–196
Ospina-Forero L, Castañeda G, Guerrero O (2020) Estimating networks of sustainable development goals. Inf Manag 103342
Paldam M (2002) The cross-country pattern of corruption: economics, culture and the seesaw dynamics. Eur J Polit Econ 18(2):215–240
Park H (2003) Determinants of corruption: a cross-national analysis. Multinatl Bus Rev 11(2):29–48
Pellegrini L (2011) Causes of corruption: a survey of cross-country analyses and extended results. In: Pellegrini L (ed) Corruption, development and the environment. Springer, Dordrecht, pp 29–51
Rodrik D (2012) Why we learn nothing from regressing economic growth on policies. Seoul J Econ 25(2):137–151
Rose-Ackerman S (1975) The economics of corruption. J Publ Econ 4(2):187–203
Seldadyo H (2008) Corruption and governance around the world: an empirical investigation. PhD thesis, University of Groningen
Seldadyo H, de Haan J (2006) The determinants of corruption: a literature survey and new evidence. In: EPCS Conference, Turku, Finland
Serra D (2006) Empirical determinants of corruption: a sensitivity analysis. Publ Choice 126(1):225–256
Treisman D (2000) The causes of corruption: a cross-national study. J Publ Econ 76(3):399–457
World Bank (2017) World Development Report 2017: Governance and the Law. International Bank for Reconstruction and Development/The World Bank, Washington, D.C
Funding
The funding was provided by the Engineering and Physical Sciences Research Council (Grant No. EP/N510129/1) and the Economic and Social Research Council (Grant No. ES/T005319/1).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Guerrero, O.A., Castañeda, G. Does expenditure in public governance guarantee less corruption? Non-linearities and complementarities of the rule of law. Econ Gov 22, 139–164 (2021). https://doi.org/10.1007/s10101-021-00252-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10101-021-00252-z