Abstract
Age is a crucial variable in social sciences and particularly in population dynamics. In this paper, we link methods from formal demography and Operations Research to investigate age-structured models to study the greying of academia. As scientific productivity is usually found to decrease at advanced ages, there was a vivid discussion on the ageing among tenured professors and faculty staff of universities. We investigate population ageing in academia from two perspectives. First, we propose a two-state optimal control model to explain the substantial variations of scientific production over the life cycle of researchers. We identify conditions under which typical hump-shaped age-specific patterns of scientific production turn out to be optimal for individual researchers. The second part of the paper deals with the dynamics of the age structure of scientific institutions. Similar to the university professors, many European learned societies experienced a rapid ageing of their member population, where they face the dilemma that keeping young, i.e. electing young entrants, has the drawback of reducing the replacement rate of members. It turns out that electing a mix of young and old members delivers the optimal solution of the problem, i.e. guaranteeing a young age structure, while ensuring a high recruitment rate.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Age is one of the most important variables in social sciences, psychology, biology and other disciplines. By definition, age is the synchronous lapse of calendar time and individual time. Not only that most physical and cognitive abilities are crucially dependent on age (e.g. Skirbekk 2004), age also underlies the organisation of family, education, work and leisure. Hence, whether through physiological capabilities, explicit age-related rules or informal expectations, age structures individual life courses (Settersten 2003). Accordingly, the rate of occurrence of any demographic event varies strongly with age. Therefore, age—besides gender—is the core variable in demography. With some exaggeration one could say that demography is the science dealing with ‘age’.
Age is not only important for individual life courses, but the composition by age is also crucial for the future development of aggregated entities such as nation states or the world population. Changes in a population’s age structure will have implications on almost all sectors of a society. The United Nations write in their World Population Ageing report that “[p]opulation ageing—the increasing share of older persons in the population—is poised to become one of the most significant social transformations of the twenty-first century, with implications for nearly all sectors of society, including labour and financial markets, the demand for goods and services, such as housing, transportation and social protection, as well as family structures and inter-generational ties” (United Nations 2017, p. 1).
The discussion on the consequences of population ageing has also reached scientific institutions and a growing concern on the greying of academia has been expressed (Stroebe 2010). In fact, the age distribution of faculty has gradually shifted to the right (Ashenfelter and Card 2002) and the percentage of faculty members and tenured professors aged 70 and older in American universities has substantially increased over the past decades (Bombardieri 2006). While the ageing among college and university faculty was commonly attributed to the abolishment of mandatory retirement in American universities, others also emphasised the role of a hiring boom in the 1960s and early 1970s and a slowdown in faculty inflow afterwards (Ashenfelter and Card 2002).
As a consequence, measures to rejuvenate the university faculty population were proposed in order to create opportunities for promising young academics. The discussion on the consequences of the ageing of academia was further spurred by the concern that older researchers are less likely to produce innovative research (Becker 2008). However, many of the arguments were rather of anecdotic nature, such as the early age of path-breaking discoveries by later Nobel laureates.Footnote 1
Several studies have investigated the relationship between scientific productivity and age (for a review see e.g. Stroebe 2010). The most usual pattern found is an initial increase with a peak around 40 to 45 years followed by a gradual decrease (Stroebe 2016). However, more recent studies showed that the usual hump-shaped pattern does not always occur. For instance, Way et al. (2017) analysed the publication history of tenure-track faculty members in computer science departments of the U.S. and Canada and they found that only one-fifth of the studied faculty exhibited the usual pattern of an “initial rise and gradual decline” publication trajectory, while the remaining faculty showed a large variety of other publication patterns over their working life course.
Nonetheless, many U.S. universities were concerned by a potential decreasing scientific productivity due to the ageing of their faculty and introduced early retirement incentive programmes. These programmes were partly motivated by the aim to create opportunities for promising young scholars once the older faculty staff retires (Stroebe 2010; Kim 2003). However, do such retirement programmes indeed constitute an appropriate measure to rejuvenate the faculty staff? Parallel experiences from European learned societies may provide informative insights into this question.
Around the turn of the millennium, several European learned societies got concerned about the gradually increasing ageing of their membership population, which has also been documented in a series of studies on European academies of sciences.Footnote 2 Although membership is usually lifelong, the bye-laws of many learned societies state a maximum size of members (under a certain statutory age), which allows elections only when places fall vacant (i.e. when members surpass that statutory age threshold). The bye-laws thus specify a similar mechanism as the early retirement programmes in the universities—allowing recruitment of young scholars when older members retire or surpass the age threshold, while holding the total population size fixed. These restrictions, though, create a dilemma for the learned societies in the context of population ageing, as Leridon (2004, p. 109) described it: “To counteract the spontaneous trends in ag[e]ing in the institution, [...] new members would have to be elected at increasingly younger ages year after year, which would have the drawback of reducing the rate of population replacement.” However, the latter strategy is in conflict with the academies’ desire of being representative for all research fields and thus being able to elect a sufficient number of young scientists from emerging research disciplines.
The dilemma of the learned societies illustrates the basic principles of constant-sized age-structured populations. In formal demography, it is stable population theory (including stationary populations as special case) where the basic principles of the study of age-structured populations have been formalised.Footnote 3 In particular, mathematical interrelationships between fertility and mortality rates with population age structure have been derived within the stable population theory. The most crucial result of the theory is strong ergodicity: it roughly says that in the long run, a population ‘forgets’ its past age structure if it is subject to constant age-dependent mortality and fertility rates over time. That means, stable population theory states what age distribution is implied by a given set of fixed age-specific birth and death rates (see e.g. Preston et al. 2000; Feichtinger 1979; Keyfitz 1985).
Formal demography and Operations Research—two seemingly unrelated fields—share several methodological links. Conceptionally, a population can be considered as a renewable aggregate of individuals, the investigation of which is part of renewal theory that also plays a key role in Operations Research. The methodological analogies become most apparent in parallel formulas in both fields (see e.g. the stationary population identity and Little’s formula below).
The purpose of this paper is to show how methods from formal demography and Operations Research—or more specifically, intertemporal optimisation—can be linked to study the greying of academia.Footnote 4 We investigate the topic from two perspectives. The first is located at the individual level and deals with the age pattern of scientific productivity. In particular, we present an optimal control model, which is able to explain the hump-shaped pattern of scientific production over age and we identify conditions at which other patterns may occur.
Secondly, we address the ageing of academia at a more aggregate level from a population dynamics perspective. In particular, we focus on the impact of the measures taken to counteract the ageing of the faculty staff, namely the early retirement programmes, on the age structure of the faculty. As mentioned above, the mechanisms introduced by early retirement programmes link recruitment and exits from faculty while holding total faculty size constant. Hence, in more general terms, we investigate the increasing ageing in age-structured populations with fixed size. In doing so, we draw on related research on European learned societies, more specifically on the Austrian Academy of Sciences (in German “Österreichische Akademie der Wissenschaften, OEAW”). We examine the population dynamics as well as the impact of various kinds of recruitment strategies and characteristics of the exit rates of OEAW members on their age structure. In a next step, we present an optimal control model designed to rejuvenate the age structure under the restriction of keeping the fixed size of the organisation. Finally, we discuss how the approach can be extended to firms and other hierarchical organisations as well. Note that models of this kind belong to manpower (personnel) planning, another important field of Operations Research.
2 Optimal scientific production over the life cycle
Scientific creativity usually tends to vary with age. Typical life cycle patterns are not only observed in academia, but also in artistic production (Simonton 2014). Not strikingly, there are many studies of career paths of creative people since the famous statistician Quetelet (1835) started researching this question almost 200 years ago.
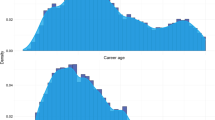
The overwhelming majority of studies on the scientific career paths of creative people illustrate a hump-shaped pattern with age (Stroebe 2010, 2016; Simonton 2014). However, most of these studies were conducted in the 1960s and 1970s. Recently, Way et al. (2017) identified several other distributions of research productivity over the life cycle. Using a large dataset originating in computer science departments of the U.S. and Canada, they showed that an age-specific hump-shaped productions trajectory does not always occur. Figure 1 illustrates four productivity patterns found by Way et al. (2017). In what follows, we try to provide a theoretical underpinning of the four different research patterns detected by Way et al. (2017).
Distribution of individuals’ productivity trajectory parameters. Diverse trends in the individual productivity fall into four quadrants based on their slopes. Plots show example publication trajectories to illustrate general characteristics of each quadrant. The shaded triangular region (bottom center) corresponds to the conventional narrative of early increase followed by gradual decline (Source: Way et al. 2017). The permission to reproduce this figure by the first author of the cited paper is gratefully acknowledged
Previous models to explain the age pattern of scientific productivity were mainly based on the human capital framework (see e.g. Diamond 1984; Levin and Stephan 1991; Stephan 1996), where the human capital stands for the professional prestige, which is reflected by the number of citations. The prestige creates income and it can be maintained by publishing papers, otherwise it depreciates. The main assumption in Diamond (1984) is that the individual maximises lifetime income. The latter decreases as individuals approach retirement and thus they invest less time in publishing papers and building up prestige.
However, the model of Diamond (1984) was criticised that it overestimates the importance of monetary income as motivation for scientists. Indeed, a main component in the reward structure of science is the importance of priority of discovery (Merton 1957, 1968). Recognition for priority includes, besides eponymy, prizes—of these the Nobel prize is best known—and election into prestigious institutions such as learned societies (Stephan 1996; Stroebe 2010). Publications can be regarded as a smaller form of recognition but are nonetheless a required step to establish priority. While prestigious awards and memberships are perceived by most beyond their reach and they usually occur, if at all, at an advanced career age, it is the reward of publishing one’s work which is attainable for all scientists at any time in the career (Stephan 1996). In addition, scientists derive satisfaction by the enjoyment of writing papers, conducting research, gaining new knowledge, and solving a puzzle (Levin and Stephan 1991; Stephan 1996; Stroebe 2010). Thus, later life cycle models (e.g. Levin and Stephan 1991) maximise a utility function that also includes research output.
Our model extends the previous literature by differentiating between human capital as the stock of knowledge and the reputation of a scientist and by modelling their evolution over the life cycle separately. The scientist can invest both in knowledge accumulation but also in reputation by networking. Both knowledge and reputation are inputs to the research output, which the scientist aims to maximise. Another distinct feature of our model is that the scientist values his reputation at the end of his career.
2.1 The model
The following deterministic continuous time-optimal control model has two state variables. The first is the stock of knowledge (human capital), K(t) an individual has accumulated at age t, while the second is the reputation R(t) of a scientist. The output of a scientist is publishing papers, P. A necessary condition to do so is having built up a stock of knowledge being strictly positive. Building up reputation can work as a leverage with respect to productivity. To model this we introduce the scientific production function
with \(\alpha \) and \(\beta \) denoting positive constants smaller than one. The functional form reflects that one can be productive without working on reputation. Investing in knowledge at a rate I(t) can be seen as a scientist’s major activity. Omitting the time arguments, the dynamics of the human capital of an individual satisfies
where g(K) reflects that investment in knowledge is more fruitful if one has already built up some knowledge, being an increasing function, and \(\delta _K\) is the obsolescence rate of the human capital.
Beside the major activity of knowledge production, the scientist is also embedded in a network of colleagues. Thus, there is a mutual influence in course of their common work. The second state variable we include in our model is the reputation R(t), measuring a scientist’s position within the scientific community. Denoting by N(t) the second control variable, i.e. networking as collaboration with colleagues, conference presentations etc., the reputation develops according to
where h(K) measures the efficiency of networking depending on the personal human capital and \(\delta _R\) is the obsolence rate of the reputation. Note the asymmetry of the right-hand sides of (2) and (3), as both \(g(\cdot )\) and \(h(\cdot )\) depend on K. Investing in knowledge is more effective if the researcher is already knowledgeable. Therefore g(K) is increasing in K. In addition, investing in networking pays off if the scientist is knowledgeable. Then the scientist makes a good impression when presenting his research, talking to other researchers, writing emails and so on. Therefore, h(K) is increasing in K.
It makes sense to assume both g(K) and h(K) as being S-shaped, i.e. as convex-concave (the latter referring to saturation effects). In particular, we use the following S-shaped functions
where \(\theta \), \(\sigma \), a, b, \(l_1\), and \(l_2\) are positive parameters.
The goal of the scientist is to maximise the, with rate r discounted, stream of his or her scientific publication, net of the costs for investing both in knowledge and networking
s.t. to the system dynamics (2) and (3), the initial conditions
and
An important feature of our model is the fact that doing research and networking usually create utility for a scientist as long as it is done ’to a reasonable extent’. Only if I and N exceed certain thresholds are these activities connected with disutilities, i.e. they must be seen as costly.
For simplicity we assume linear-quadratic functions \(C_i(\cdot ) \quad (i=1,2)\)
with \(c_1\), \(c_2\), \(d_1\) and \(d_2\) all positive.Footnote 5
Note that the reputation R(t) influences current utility only indirectly via the research output, P(K(t), R(t)), but it is the reputation at the end of their career which matters for scientists. The latter is reflected by the salvage value in (6) and the associated parameter \(\kappa >0\). However, the case of \(\kappa =0\) can be interpreted with the proverb shrouds have no pockets. Usually, the phrase refers to material goods, but in this case, there is of course the aspect of intellectual wealth.
2.2 Results
The application of Pontryagin’s maximum principle (see e.g. Grass et al. 2008) delivers some interesting insights into the optimal investment patterns resulting in various patterns of scientific output. In particular, it can be established that the four patterns identified by Way et al. (2017) can be generated as optimal paths for appropriate parameter values. If not otherwise noted, we set the parameter values according to Table 1.
We show that typical and fading patterns usually arise in scenarios where scientists themselves do not assign a too high positive value to being regarded as knowledgeable or having a high reputation at the end of their career (see Fig. 1, pattern Q4 and Q3, respectively). In such a case the scientist will opt for a typical pattern if the disutility for hard working is not too high. Here it could help that scientists during their studies obtain a lot of knowledge. This implies that when scientists start their career already being quite knowledgeable, any investments in knowledge and networking become more efficient.
If a scientist does assign a substantial positive value to being regarded as knowledgeable with a high reputation at the end of his or her career, the patterns slump and busy come into the picture (see Fig. 1, pattern Q2 and Q1, respectively). We show that a slump pattern, where the scientist is not very productive halfway through her career, can be avoided by high quality education. Again, starting the career with a lot of knowledge makes further investments in knowledge and networking more efficient. This raises productivity along the lifetime, resulting in the busy pattern. For details see Feichtinger et al. (2018).
In the following, we discuss the possibility of multiple equilibria whose basins of attraction are separated by Skiba thresholds. Starting at the threshold, the so-called Skiba point, the scientist is indifferent what career to choose.
The solid line shows the bifurcation diagram in \(d_1\) for the equilibria of the canonical system. For the parameter values between the dashed lines there exist Skiba solutions in finite time \(T=50\) with initial condition \(R(0)=0\). Note that in an interval on the right side of the Skiba region only one equilibrium exists. Thus, the existence of three equilibria is not necessary for the occurrence of a finite time Skiba solution
In Fig. 2 the bifurcation parameter is \(d_1\), which reflects the cost of investment in knowledge. This means that \(d_1\) specifies how fast the marginal utility of the scientist declines. For a large value of \(d_1\) it is therefore costly to increase knowledge and only convergence to the small steady state takes place.
In the following we consider three typical examples for solutions lying in the different regions given by the bifurcation diagram Fig. 2. Each of these figures shows the solution paths in the state space with initial values satisfying \(R(0)=0\) and \(K(0)\in [0,4]\). Additionally the manifold of the endpoints, i.e.
is depicted as a grey curve in Figs. 3, 4, 5. This manifold can be seen as the counterpart to a steady state of the infinite time horizon problem. Figure 3a shows optimal solution paths for a relatively small value of \(d_1\). This means that it is easy for the scientist to create knowledge and the positive value of \(\kappa =10\) indicates that the horizon date reputation is positively valued. Therefore the solutions end up with large values of reputation and values of knowledge above 1.5.
For the second scenario with \(d_1=3\) there is a Skiba solution with \(\tilde{K}=0.475\). The dashed lines represent the two different solution paths starting in the Skiba point at \(R = 0\). Left to the Skiba point \(\tilde{K}\) the solution paths end at a manifold very near the origin and is therefore hardly visibly in panel (a). Therefore the K axis is logarithmically scaled in panel (b). This reveals that the manifold of the endpoints is separated into two distinct arcs, which is the counterpart to two different equilibria for a usual Skiba solution
For the intermediate case (see Fig. 4) with values of \(d_1\) between 1.53 and 3.09 the solutions are history-dependent in the following sense: For small initial values of knowledge, i.e. \(K(0)<\tilde{K}=0.4754\), the solutions end up with very low reputation and knowledge (see Fig. 4b). In such a case, it might not be advisable to start an academic career. On the other hand, for larger values than \(\tilde{K}\) the researcher starts a scientific career and ends up with a high value of reputation and knowledge.
For the last scenario \(d_1=3.1\) is chosen to lie in region III of Fig. 2, and therefore yields again unique solutions. In the logarithmically scaled figure panel (b) it becomes apparent that the two previously disconnected manifolds of endpoints are now combined to a single continuous manifold
Finally for values of \(d_1>3.09\) the spectrum of research careers is continuous (cf. Fig. 5a, b). This means that with increasing initial knowledge the attractivity to start a scientific career increases continuously. Thus, other than in the previous Skiba case, researchers with some intermediate knowledge at the beginning also end up with average values of knowledge and reputation. There is no abrupt change in knowledge and reputation at the end like it was at \(\tilde{K}\). This is due to the relatively high costs of knowledge increase.
In Fig. 6 the time paths of productivity for the three previously explained scenarios are plotted. To make the results comparable, the initial states are chosen equally, namely \(R(0)=0\) and \(K(0)=\tilde{K}\), the Skiba value from \(d_1=3\). In the first case, for the low value of \(d_1=1.4\) productivity is steadily increasing until it reaches its maximum \(P(R,K)=4.84\) at \(t=44\). Finally it drops down to a rather high value of \(P(R,K)=4\) (cf. Fig. 6a).
For comparable high costs \(d_1=3.2\) the situation is quite different. The low maximum of productivity \(P(R,K)=0.24\) is already reached at \(t=5.27\) and drops down to the vanishing value of \(P(R,K)=0.004\) (cf. Fig. 6c).
For the Skiba case we find both patterns qualitatively repeated: a) the productive researcher, reaches his or her maximum at \(t=38.75\) and finally only loses around \(30\%\) of its productivity, whereas b) the less productive researcher reaches maximum productivity already at \(t=7.6\) and loses \(94\%\) of his or her highest productivity (cf. Fig. 6b).
The absolute value of the productive researcher in the Skiba cases is low compared to the researcher in Scenario I. This is due to the fact that we have chosen a high value \(d_1=3\) for the Skiba case, a choice we made for pragmatic reasons, since in this way the manifold of low end points in Fig. 4 was better visible.
Considering a lower value of \(d_1=2.75\) in region II we find a qualitatively different solution pattern for less productive researchers. In that case we find the so-called fading career, where researchers gradually reduce their research activities over time (cf. Fig. 6d). For an explanation of the different behaviour for both Skiba cases, we have to note that for lower \(d_1\) the Skiba point \(\bar{K}=0.107\) is smaller than the Skiba point for \(d_1=3\) with \(\tilde{K}=0.475\). Therefore, the starting situation for both cases differs substantially.
Summing up, in this section we tried to provide a theoretical underpinning of the four different research patterns detected by Way et al. (2017). In particular, we showed that the age-specific distribution Q4 of scientific work occurs if two conditions are fulfilled. A sufficiently high education level at the beginning of scientists’ careers usually leads to an increase of sufficient productivity. If they do not bother much about their reputation at the end of their career, the number of publications then gradually decreases until retirement.
3 The dilemma of learned societies
The following section uses methods from formal demography and Operations Research in conjunction to study the greying of academia at a more aggregate level. We use cohort component projection to illustrate the impact of the age at recruitment on the age structure of scientific institutions, where we distinguish between effects from past recruitment and long-term effects of various kinds of potential future recruitment policies. Next, we formalise the relationship between age at recruitment and retirement within the framework of stable (stationary) population theory and use intertemporal optimisation techniques to derive the optimal trade-off between recruitment of young academics and the mean age of the scientific institution. For this purpose, we draw on earlier work conducted for the Austrian Academy of Sciences (OEAW),Footnote 6 which was facing a significant ageing of its member population.Footnote 7 In the following paragraphs, we present, discuss and update selected results from related previous research articles (Dawid et al. 2009; Feichtinger and Veliov 2007; Feichtinger et al. 2007, 2012; Riosmena et al. 2012; Winkler-Dworak 2008).
In principle, the population dynamics of the Academy can be studied using the same methods as those employed when studying any other population. However, the Academy’s vital events differ from those of a conventional population. There, the current generation of individuals will spawn the following one, and current academy members will also elect the next generation of academicians, but different from fertility, where the intake occurs in the lowest age groups, an Academy’s intake may take place in all age groups, similar to immigration (see e.g. Espenshade et al. 1982; Feichtinger and Steinmann 1992). In addition, the total number of members is limited by the bye-laws. Hence, the number of elections is strictly determined by the number of exits from the Academy, i.e. mortality,Footnote 8 out-migration or leaving the Academy for other reasons, and retirement (i.e. surpassing the statutory age threshold of 70 years).
3.1 Projecting the impact of the age at election of Academy members
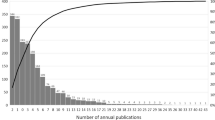
The population dynamics in hierarchical bodies in which the total membership size remains constant is determined by the rate of intake, the age distribution at entry into a given status, the number of exits (deaths or dismissals), the statutory retirement age and the population size. The intake itself is solely determined by the number of deaths and retirements. The only scope for modifying the age structure lies in the age distribution of entries, e.g. at election. Figure 7 shows the histogram of the age distribution of election into the OEAW for the years 2000–2015.
In the period 2000–2015, ages at election ranged over nearly 30 years of age, where the youngest member was elected at age 37 years, while it was age 65 years for the oldest member at election. The mean age of the age distribution at election was around 53.6 years with a standard deviation of 6.6 years. A Gaussian kernel estimate of the density function (see e.g. Hartung et al. 2002) yields a bimodal curve with the first mode around age 50 and the second mode around age 58 years (dark blue curve in Fig. 7). In principle, a bimodal function at election may arise because of a conjunction of two motives: on the one hand, electing young members may signify rewarding excellence, while on the other, electing older ones means a recognition of lifetime achievement.Footnote 9
In order to study the impact of the age distribution at election on the structure of the Academy population, we use demographic projection methods. First, we project the number of members per section for each single-year age group alive in the next year. The survivorship rates are based on forecasted age-specific life table death rates from Statistik Austria (2015), which were adjusted for the lower mortality of the academicians (see Appendix A; for more details on the adjustment see Feichtinger et al. 2007). The difference between the number of survivors and the maximum size of each section yields the number of vacant places in each section. We assume that vacant seats are immediately filled in the following year by electing new Academy members.
For the age distribution at election of new members, we consider two alternative scenarios. The first scenario represents the continuation of the status quo (dark blue curve in Fig. 7) and is captured by the estimated density of the observed age distribution at election from the years 2000–2015 for both sections combined. Second, we model the two motives of rewarding excellence vs lifetime recognition in a strongly polarised pattern by assuming a bimodal age distribution (green curve in Fig. 7), where members are uniformly elected only at very young ages (i.e. 37–47 years) and at older ages (i.e. 59–69 years). Note that such an election strategy is quite the opposite of current practice, as the vast majority of the members were elected at medium ages between 2000–2015 (cf. Fig. 7). Nonetheless, the mean ages of both election scenarios are very close to each other, whereas the standard deviation of the bimodal scenario is almost the double of the status quo one.
Figure 8 (top panel) depicts the projected number of vacancies from 2015–2075 for the two alternative scenarios and both sections combined.Footnote 10 Over the transitionary period ranging into the 2040s, the number of vacancies sharply fluctuates due to the initial age structure of members in 2015 and then stabilises for the status quo scenario around five elections per year. In contrast, the number of vacancies under the bimodal scenario seems to be characterised by longer-period waves in the later part of the projection horizon. Evidently, the number of vacancies in the first five years is almost solely determined by the age structure of members in 2015 and only afterwards small differences become visible between the alternative scenarios. In particular, the higher number of members elected close to the statutory age limit under the bimodal scenario results in a slightly higher projected number of vacancies than for the status quo scenario in the 2020s, while it is the opposite from mid-2030s onwards. The trough in the number of vacancies for the bimodal scenario in the early 2040s results from the fact that medium-aged scientists are not considered for election under the latter scenario. Only when the first very young elected members reach the statutory age threshold does the number of vacancies start rising again, reaching the projected number of vacancies for the status quo scenario in the early 2060s. As we assumed that vacancies are immediately filled, the longer tenure associated with the very young new members implies a decrease in the projected number of vacancies towards the end of the projection horizon. The latter result clearly demonstrates the trade-off of the academies between a young age structure of the members and high number of vacancies.
The bottom panel of Fig. 8 finally plots the projected mean age of members for the two scenarios, again for both sections combined (solid lines). In addition, the dashed lines represent the mean age of members only for those aged less than the statutory age threshold. Apart from around 2030 to 2040, the projected mean age of all members continuously increases over the projection period and eventually amounts to about 73.7 years for the status quo scenario. In contrast, the projected mean age under the bimodal scenario fluctuates around 71 years. Considering only members aged less than the statutory age threshold, the differences between the scenarios are more pronounced. While the projected mean age for the status quo stabilises around 60.6 years, the corresponding value for the bimodal scenario fluctuates between 55.2 and 57.6 years.
Summing up, the bimodal scenario would yield a substantially lower mean age for Academy members than a continuation of the current election practice, although both election policies exhibit a similar mean age. Intuitively, a lower/higher mean age at election should decrease/increase the mean age of the member population. However, the results of the projections suggest that other characteristics such as the spread of the age distribution at election substantially affect the mean age of the member population as well. In the next sections, we will formalise the trade-off between a young age structure and a high number of recruitment in constant-sized populations and we derive a relationship between the mean age of members and the characteristics of the age distribution of members. Later we will develop an age-structured optimal control model to counteract the ageing of the Academy population while ensuring a sufficient number of vacancies.
3.2 Formalising the dilemma of the academies
Intuitively, to counteract the trend of ageing, new members have to be elected at increasingly young ages. As mentioned earlier, this would have the drawback of reducing the inflow of new members. Thus, there is a fundamental dilemma in a constant-sized, age-structured population, such as in an academy of sciences: the desire to maintain a young age structure, while ensuring a high recruitment rate.
The following thought experiment by OEAW member Gerhart Bruckmann (cited in Feichtinger et al. 2007) illustrates this trade-off: “If the Academy elects only 47.5 year old members, they stay—neglecting mortality and other possibilities for exit—22.5 years in the membership population decisive for the maximum size. The OEAW comprises 90 full members (45 in each section) below the statutory age, which yields \(90{:}22.5 = 4\) entrants each year. If, on the other hand, only 55 year old members are elected, the same calculation results \(90{:}15 = 6\) entrants per year.” Carrying the argument to extremes, if all members are elected at age 69, then there will be maximum recruitment every year.
These simple calculations of a constant-sized population are based on a fundamental identity in demography. Denoting by M the total size of the population, by R the number of annual new entrants and by T the mean duration in the population, the stationary state is characterised by the relation
For conventional populations, the stationary state arises for a constant flow of births and unchanging age-specific death rates over time. Then, R denotes the annual constant number of births and the average duration T equals life expectancy at birth of the stationary population. Hence, the identity connects the three most important indicators of a stationary population, namely population size (stock), the births (entrants) and life expectancy (average duration).Footnote 11 Note that in queuing theory, which is based on birth-death processes, the identity (10) is known as Little’s formula (see Hillier and Lieberman 1974, p. 384)
For the sake of simplicity, we consider in what follows only the Academy members below the statutory age threshold as it is the total size of that group which is limited by the bye-laws. They correspond to a fixed-sized organisation (i.e. Eq. 10 holds) with a prescribed retirement age \(\omega \).
In this case, Dawid et al. (2009) derive an interesting relation between the mean age of the academicians, the mean age of entrants and the variance of the recruitment distribution:
where \(\bar{A}\) denotes the mean age of the fixed-sized organisation, m the mean age of recruitment distribution, \(\sigma ^2\) its variance, and \(\omega \) the statutory age.
On this formula, two issues are remarkable: (1) intuitively, the average age of the stock \(\bar{A}\) increases with the mean age of entrants, m. However, it can be shown that the latter holds if and only if \(\omega - m >\sigma \), which is numerically fulfilled for the age distributions at elections, which we considered. The latter case also implies that the mean age of the population \(\bar{A}\) and the mean duration in the system (i.e. the average tenure) \(T = \omega - m\) are inversely related. (2) The variance of the recruitment distribution, \(\sigma ^2\), influences \(\bar{A}\) negatively as suggested by the difference in the mean age of members between the two projection scenarios above.
Note again the parallels between population dynamics and Operations Research: The remarkable property that the arithmetic mean \(\bar{A}\) depends only on the first two moments of the recruitment distribution, m and \(\sigma ^2\) has an interesting analogue in queueing theory. For the single-channel queueing system M/G/1, i.e. exponentially distributed independent interarrival times and independent and identically distributed general service time distributions, the so-called Pollaczek-Khinchin formula is valid (Gross and Harris 1974). It says that the expected number of customers in the system depend exclusively on the first two moments of the service time distribution. More precisely, the length of an M/G/1 queue increases both with the mean duration of service as well as its variance. Note that the latter dependency is just opposite to the formula (11), where a concentrated entrance distribution yields the highest mean age.
As pointed out in the beginning of the subsection, academies are faced with two conflicting goals: to obtain a young age structure (or, mathematically equivalent, a high average duration), while ensuring a high recruitment rate. However, since the product of the right-hand side of identity (10) is constant, it is not possible to increase both R and T simultaneously. Hence, we define an objective function as a weighted mean of R and T, which we aim to maximise, i.e.
where \(\alpha \) and \(\beta \) are non-negative weights with \(\alpha + \beta =1\).
The maximisation of the objective function (12) subject to the condition (10) is depicted in Fig. 9. While the side condition (10) is represented by a hyperbola in the state space, the parallel lines with slope \(\alpha /\beta \) indicate the objective function with equal values. The higher the intercept of the lines, the higher the value of the objective function.
Figure 9 illustrates that corner solutions are optimal. If \(\alpha \) dominates, then it is optimal to elect a maximum number of entrants, who stay for only one year (point B in Fig. 9, left panel), while for large values of the weight \(\beta \) all entrants stay in the system for the maximal possible tenure (point A in Fig. 9, right panel). Note that the tangent to the hyperbola (point C in Fig. 9) refers to the smallest feasible value of the objective (12).
Illustration of maximising weighted sum of number of recruitments and mean length of tenure T subject to trade-off between recruitment R and average tenure T (blue curve) with alternative optimal corner solutions. The parallel grey lines represent indifference curves of equal objective value (color figure online)
3.3 An optimal age-structured control model
Let M(a, t) denote the number of members of a learned society at time t and age a. The dynamics of the age-structured population M(a, t) can be expressed in form of the McKendrick equation used in formal demography (McKendrick 1926; Keyfitz and Keyfitz 1997).
The population gains new members, not through birth or immigration, but by way of elections (recruitment of new members) indicated by the term R(t)u(t, a).
with the side conditions
where we used the following notation: \(\mu (a)\) the time-invariant mortality rate of members at age a, R(t) the intensity of recruitment at time t, \(u(t,\cdot )\) is the age densityFootnote 12 of recruitment at time t, \(M_0(\cdot )\) is the initial age-density of members, \(\omega \) is a fixed exit (retirement) age of members, \(M_t+M_a\) is the sum of the partial derivatives of M (strictly speaking, this is the derivative of M in the direction (1,1) in the (t, a)-plane, i.e. the change along a diagonal in the Lexis diagram).
The dynamics of the age structure of the learned society is given by the classical McKendrick equation (13), while (14) indicates that the size of the organisation is fixed and equals \(\bar{M}=\int _{0}^{\omega }M_0(a) \mathop {}\!\mathrm {d}a\) (this can be easily seen by integrating (13) over a and utilizing the assumption for fixed size). Alternatively (14) can be understood as follows: At any time t the recruitment R(t) is determined by the number of people reaching the threshold age \(\omega \) (first term on the r.h.s.) and the number of deaths, where the latter is determined by the sum of age-specific deaths (second term on the r.h.s.).
The following constraints are posed for the recruitment density, \(u(t,\cdot )\), which is considered as the control (decision) variable:
where \(\bar{u}(a)\) is an upper bound for the control.
As mentioned above, we focus our analysis on two objectives:
the recruitment intensity, R(t), which is to be maximised;
the average age \(\frac{1}{M}\int _{0}^{\omega } a M(t,a) \mathop {}\!\mathrm {d}a\), which is to be minimised.
Since two (conflicting) objectives are involved, we employ the Pareto optimisation framework, considering the aggregated objective function
where \(r>0\) is a time-preference rate, \(\alpha > 0\) and \(\beta \ge 0\) are weights attributed to the two objectives. The first objective is to maximise the recruitment intensity R(t), while the second objective is to minimize the average age \( \int _{0}^{\omega } a M(t,a) \mathop {}\!\mathrm {d}a\) of the members.
An important step to solve the optimal control problem Eqs. (13)–(17) is the fact that under a certain regularity assumption for stationary mortality patterns \(\mu (a)\), the time-invariant optimal control problem shows a remarkable property, which is crucial in population dynamics, namely strong ergodicity. This means that the age density of the population tends to a steady state, which is independent of the initial density (for a proof see Feichtinger and Veliov 2007). Moreover, it can be shown that the optimal control (i.e. recruitment density) is time-invariant and can be characterised by an ordinary differential equation.
In Dawid et al. (2009), it is shown that applying the Lagrange principle for the stationary version of the control problem Eqs. (13)–(17) with the Lagrange multipliers for \(\int _{0}^{\omega }M_0(a) \mathop {}\!\mathrm {d}a =\bar{M}\) and Eq. (16), we obtain a simple ordinary differential equation for the adjoint variable \(\xi (a)\). This shadow price \(\xi (a)\) measures the marginal value of a newly elected person at age a.
Assuming the mortality rate \(\mu (a)\) is a non-negative continuously differentiable convex function and increasing with age (which is satisfied for adult persons), the optimal recruitment policy, u(a), has the following structure: there are (possibly degenerate) intervals \([0,\theta ]\) and \([\tau ,\omega ]\) such that
Thus, the optimal strategy is to balance recruitment between as many candidates as possible of both young and old ages, but to recruit as few as possible who are middle-aged. This principle of bimodal recruitment has been established and has been proven within a somewhat different framework in Feichtinger and Veliov (2007) (also for non-stationary societies). It says essentially: that if the average age matters for the organization, then this has a polarising effect on the optimal recruitment policy: it shifts recruitment away from candidates of middle ages, while causing the organisation to concentrate its recruitment efforts partly on candidates of younger ages and partly on candidates of older ages.
To summarise our main result: the intertemporal optimisation procedure reveals that it is optimal to elect a mix of young and old entrants to guarantee a young Academy while avoiding a freeze of recruitment altogether. It should be noted that the election of medium-aged persons is the worst solution in terms of the proposed target (compare also Fig. 10).
4 Conclusions
Population ageing has become one of the major challenges in the 21st century, affecting all sectors in society. The purpose of the paper is to show how mathematical methods of demography can be used to investigate population ageing problems on the example of the greying of academia.
Several universities and colleges got alarmed by the gradual ageing of their faculty staff over the past decades and these concerns were at least partly fueled by the belief that science is a young man’s game. In fact, many studies on age and scientific achievement asserted that productivity rapidly increases to a peak around age 40 to 45 years and then declines. However, Stroebe (2010) ascertained that age only accounted for eight percent of the variance in productivity in these studies whereas Over (1982, p. 519) found that “a person’s previous research productivity was a far better predictor of subsequent research output than age was.”
Indeed, productivity patterns vary substantially across individuals and over the life cycle. Lotka (1926) stressed the highly skewed nature of scientific publications. In physics, for instance, he observed that six per cent of publishing scientists produced half of all papers. The inherent inequality of scientists has been formulated by Goodwin and Sauer (1995) as follows: “While some authors publish papers like a well-oiled machine, others produce at an erratic rate, and some others show early promise but become deadwood after a certain time.”
Several factors have been suggested to contribute to the inequality in productivity between scientists. While Symonds et al. (2006) refer to discrepancies between women and men appearing early in their scientific careers, the ‘Matthew Effect’ in science (Merton 1968) states that past success in research usually acts as leverage for future productivity (‘the winner takes it all’).
Despite the observed utmost inequality of scientific productivity (compare e.g. Stephan 1996), the predominant pattern was a rapid rise followed by a gradual decline over the life course. Such hump-shaped life cycle patterns are not only observed in academia, but also in other fields as in artistic production, consumption of illegal drugs as well as other criminal behaviour. Demographers will note the similarity to the age-specific first marriage and fertility curves.
In ‘The Wiley Handbook of Genius’, Simonton (2014) provides a rich collection of various forms of creativity. While almost all models dealing with the dynamics of scientific productivity are descriptive (for an interesting example see Rinaldi et al. 2000), there are a few normative approaches using the human capital approach proposed by Becker (1962), see Diamond (1984), Levin and Stephan (1991) and Stephan (1996) for such examples.
The approach we have chosen in part 1 of the present paper may be seen in this line. Assuming that the scientific output depends not only on knowledge, i.e. the human capital accumulated by a researcher but also on the network of colleagues he or she is embedded in, we are able to explain various productivity patterns over the life cycle identified empirically by Way et al. (2017). The present paper can be seen as a theoretical foundation of these empirical facts.
In the intertemporal optimisation model we assumed that the scientists derive utility from publishing papers and from performing research and networking. However, working too hard causes disutility, i.e. too large investments in knowledge and networking are costly.
If scientists do not bother about their reputation at the end of their career, we show that a sufficient education level is needed for scientists to develop a typical research pattern where productivity increases in the beginning of their career while declining towards retirement. If the education level is not sufficient, a fading research pattern will result where productivity declines over time. On the other hand, when a scientist is eager to have a good reputation at the end of his or her career, sufficient education will result in increasing productivity over the career lifetime, preventing a midlife slump.
Let us briefly mention a few possible extensions of the proposed model. While we did capture that the efficiency of research depends on the stock of knowledge already accumulated, the functions g and h in (2) and (3), respectively, might also depend on the quality of the colleagues in one’s network, i.e. on the reputation of the scientists. Another extension would be that the efficiency of accumulating knowledge and reputation explicitly depends on age, i.e. on time t. Thus, in a more realistic scenario, the effects of ageing and/or learning should be included. Moreover, in our model the scientist derives utility from reputation either indirectly by levering research output or directly at the end of the career as the prestigious rewards usually occur in an advanced career stage. A further extension may also incorporate reputation into the instantaneous utility. Lastly, a potential further extension of our model might be the introduction of leisure time, which adds utility but curtails time spent on investment into knowledge and reputation.
Scientists reaching a notably high level of reputation in their career are likely to be elected into an academy of sciences. The second part of the paper deals with the ageing of such learned societies. Similar to the U.S. faculty staff, European learned societies has experienced a pronounced ageing of its member population with marked shifts in the age distribution towards older ages. Taking the example of the Austrian Academy of Sciences (OEAW), we investigated the ageing of learned societies with special focus on the statutory restrictions on size and election policies. In particular, the statutory requirement of a maximum number of members below a certain statutory age threshold defines that election into the Academy is only possible if places fall vacant. As the inflow in such hierarchical organisations is predetermined by the current age structure of members, it is the age distribution at election which will govern the future age dynamics of the academies.
By employing demographic projection, we investigated how the age structure of the Academy might evolve if the current election policy were to be continued and contrasted the latter to alternative election scenarios. Our results highlighted that it is not only the mean age at election but also other characteristics such as the spread of the age distribution at election which affect the future age dynamics of the Academy.
In a second step, we developed an age-structured optimal control model in order to derive an optimal trade-off between the two conflicting goals of minimising the average age of the learned society and maximising the number of recruitments per year. Our results indicate that it is best to elect new members who are either young or old, with as few middle-aged new entrants as possible. Although the current election policy displays a somewhat bimodal pattern, the modes are still more concentrated around the mean than in the derived optimal recruitment policy.
Which lessons can be learned from the analysis of the European academies of sciences for the U.S. faculty? The purpose of the early retirement programmes was to rejuvenate the faculty by opening positions for young academics once the older faculty staff retires. Such a policy might be tempting in times of an ageing faculty, particularly if many of the staff are close to retirement. If the then vacant positions will be immediately filled with young promising academics, the mean age of the faculty will drop substantially as many young scholars will replace their older colleagues. However, the effect will only be temporary. As the newly appointed faculty will age with time, the mean age will rise again. But—unless additional positions will be created—the inflow of young scholars will be limited as long as the formerly young faculty will reach retirement age, and thus not be able to counteract the rising mean age of the established colleagues.
In the case of the European learned societies, a bimodal election policy turned out to be optimal. For the universities, this would imply to divide open positions to recruit on the one hand young academics and on the other hand scholars in an advanced career stage.
However, the assumption of being strictly increasing between entry age and statutory retirement age made on the mortality rate, or more general on the exit rate, is essential for the validity of the bimodal recruitment principle. It is usually satisfied for human populations at older adult ages and if membership is tenured. However, if the exit rate happens to reach a maximum at some intermediate age due to resignations or dismissals, then the bimodal recruitment pattern may not be optimal.
Another important factor contributing to the ageing of populations in general, but also particularly for academic and scientific institutions, are the continuing declines in mortality. Members of learned societies exhibit an outstanding longevity and are vanguards in the development of life expectancy. Indeed, the academicians’ life expectancy at age 50 of around twenty years ago has still not been reached by the Austrian total population of today. It has been suggested that the exceptional longevity is not only the result of selectivity into election to membership of academicians (for an extensive discussion see Andreev et al. 2011; Winkler-Dworak and Kaden 2013). According to the literature on the social gradient in mortality (e.g. Mackenbach et al. 1999), factors beneficial to health, such as a high educational level, upper professional status associated with high income accumulate for academicians and also for faculty staff.
However, Academy members may even enjoy a further longevity advantage compared to average scientists by the social circumstances that the status confers (Link et al. 2013): election into an Academy not only indicates (and rewards) scientific excellence and an outstanding contribution to science, but it certainly entails an enlargement of one’s personal academic network, providing further research opportunities and thus facilitating to stay scientifically active beyond retirement. Continued demanding mental activities to very high ages are clearly associated with less cognitive decline (Schooler and Mulatu 2001; Kliegel et al. 2004) and higher longevity (Ghisletta et al. 2006; Gondo and Poon 2007). On the other hand, it are the improvements in longevity which allows the faculty and academicians to stay active and productive into advanced ages (Weingart and Winterhager 2011).
Despite the large gains in life expectancy, the role of the latter has largely been ignored in the discussion on population ageing. However, a person aged 60 is nowadays considered middle-aged, while a century ago a person of the same age would have been considered elderly. In fact, a 60-year old Austrian male nowadays enjoys the same period life expectancy as a 50-year old peer in 1970 (Statistik Austria 2019), and the Austrian academicians have experienced even faster increases in life expectancy than the Austrian general population since the 1950s (Winkler-Dworak 2008).
Recently, new demographic indicators have been derived in order to allow comparison on population ageing over periods where life expectancy has varied considerably (Sanderson and Scherbov 2007, 2008, 2010, 2015; Scherbov and Sanderson 2016). These new indicators are prospective, i.e. they are based on the expected number of remaining years of life rather than on chronological age. Using these prospective age indicators, faster increases in life expectancy result in slower population ageing (Sanderson and Scherbov 2015). If the 60s are the new 50s, one may wonder how the assessment of population ageing of the academia would change if prospective rather than chronological age indicators were to be used. For sure, the ageing of the academicians would be decelerated, but might they even have become younger over time?
Notes
Albert Einstein published his famous articles on the theory of relativity at the age of 26 and Werner Heisenberg derived his matrix mechanics at age 23 and the uncertainty principle at age 25, though as Jones and Weinberg (2011) report, these very early ages of great achievements are special to physics at the time and coincide with the development of quantum mechanics in the early 20th century.
The studies examined the historic, present and future demographic developments of these learned societies with a special focus on the statutory restrictions governing size and election procedures of the academies and their impact on the age structure of the member population. See for the Académie des Sciences (Institut de France) (Leridon 2004), the Royal Danish Academy of Sciences and Letters (Matthiessen 1998), the Royal Netherlands Academy of Arts and Sciences (van de Kaa and de Roo 2008), the National Academy of Sciences [of the U.S.] (Cohen 2003), the Austrian Academy of Sciences (Feichtinger et al. 2007) and in an international comparison, the British Royal Society, the Russian Academy of Sciences, the Berlin-Brandenburg Academy of Sciences and Humanities, and the Norwegian Academy of Sciences and Letters (Riosmena et al. 2012).
Alfred J. Lotka, born in 1880 in Lemberg (at the time in Austria, now Lviv in Ukraine), can be considered as founder of formal demography, in particular of the stable population theory (Lotka 1907, 1922, 1939; see also Keyfitz 1968), the core concept of population dynamics. Although it was formalised by Lotka in the early 20th century, some features of the stable population theory had been known already much earlier. In fact, it was Nathan Keyfitz, the second most influential formal demographer of the past century, who discovered that already Leonhard Euler, the most productive mathematician of the 18th century, had been aware of the concept of asymptotic stable populations (Euler 1760).
For simplicity, we do not consider a time constraint in this model. For optimal time allocation models between research and teaching see e.g. El Ouardighi et al. (2013).
In 2005, the presidency of the OEAW got concerned on the ageing membership and they asked the first author of the present paper on possible measures to be taken to counter the increasing ageing of its member population given the statutory conditions. In a subsequent research project funded by the Austrian Science Fund (FWF, “Age Structured Populations with Fixed Size”, contract no. P20408-G14), we thoroughly analysed the age dynamics of the Austrian Academy of Sciences, projected the future age distribution of the Academy members based on several alternative scenarios, and developed an age-structured optimal control model to determine the optimal trade-off between the rate of elections and the mean age of the academicians (Dawid et al. 2009; Feichtinger and Veliov 2007; Feichtinger et al. 2007, 2012; Riosmena et al. 2012).
In Feichtinger et al. (2007) the population of the OEAW has been studied in detail. Appendix A briefly depicts the structure and data from the OEAW and shows the accelerated ageing of the member population.
The OEAW members have shown to exhibit a substantially lower mortality than the general Austrian population and Austrian tertiary-educated population. For more details see Appendix A.
We are grateful to Warren Sanderson for this interpretation.
The Kolmogorov–Smirnov test did not yield any statistically significant differences in the age distribution at election between the sections \((p = 0.9)\).
The stationary model is applicable to any kind of population. An example widely used in textbooks and lecture notes refers to student cohorts at university (see e.g. Preston et al. 2000): a graduate program enrols \(R=10\) students per year and has a student body of \(M=40\); it can be assumed to have a mean duration in graduate school of \(T=4\) years. If due to financial restrictions, the student body M must shrink, there are essentially two possibilities to reach this target: either the admissions R have to decrease or the mean length of the studies T must be reduced.
To avoid misunderstanding we stress that \(M(t,\cdot )\) need not be a probability density, while \(u(t,\cdot )\) is assumed to be a probability (normalised) density, in the sense given by the equality in (16) below.
References
Andreev EM, Jdanov D, Shkolnikov VM, Leon DA (2011) Long-term trends in the longevity of scientific elites: evidence from the British and the Russian academies of science. Popul Stud 65(3):319–334
Ashenfelter O, Card D (2002) Did the elimination of mandatory retirement affect faculty retirement? Am Econ Rev 92(4):957–980
Becker GS (1962) Investment in human capital: a theoretical analysis. J Polit Econ 70(5):9–49. https://doi.org/10.2307/1829103
Becker G (2008) The graying of college faculties. Retrieved from http://www.becker-posner-blog.com/2008/07/index.html
Bombardieri M (2006) Graying of US academia stirs debate. Retrieved from http://archive.boston.com/news/education/higher/articles/2006/12/27/graying_of_us_academia_stirs_debate/
Cohen JE (2003) How many members will the National Academy of Sciences. Unpublished manuscript (last revision: 2003-10-15)
Dawid H, Feichtinger G, Goldstein JR, Veliov VM (2009) Keeping a learned society young. Demogr Res 20:541–558
Diamond A (1984) An economic model of the life-cycle research productivity of scientists. Scientometrics 6(3):189–196
Doblhammer G, Rau R, Kytir J (2005) Trends in educational and occupational differentials in all-cause mortality in Austria between 1981/82 and 1991/92. Wien Klin Wochenschr 117(13–14):468–479
Doblhammer-Reiter G (1996) Soziale Ungleichheit vor dem Tod: Zum Ausmaß sozioökonomischer Unterschiede der Sterblichkeit in Österreich. Demogr Inf 1995(96):71–81
El Ouardighi F, Kogan K, Vranceanu R (2013) Publish or teach? Analysis of the professor’s optimal career path. J Econ Dyn Control 37(10):1995–2009
Espenshade TJ, Bouvier LF, Arthur WB (1982) Immigration and the stable population model. Demography 19(1):125–133
Euler L (1760) Recherches générales sur la mortalité et la multiplication du genre humain. Mémoires de l’Académie Royale des Sciences et Belles-Lettres de Berlin (1767, année 1760) 144–164. Theoretical Population Biology 1:307–314, English translation by N. and B. Keyfitz
Feichtinger G (1979) Demographische Analyse und populationsdynamische Modelle: Grundzüge der Bevölkerungsmathematik. Springer, Wien
Feichtinger G, Steinmann G (1992) Immigration into a population with fertility below replacement level—the case of Germany. Popul Stud 46(2):275–284
Feichtinger G, Veliov VM (2007) On a distributed control problem arising in dynamic optimization of a fixed-size population. SIAM J Optim 18(3):980–1003
Feichtinger G, Hartl RF, Kort PM, Veliov VM (2006a) Anticipation effects of technological progress on capital accumulation: a vintage capital approach. J Econ Theory 126(1):143–164
Feichtinger G, Winkler-Dworak M, Freund I, Fürnkranz-Prskawetz A (2006b) Zur Altersdynamik gelehrter Gesellschaften—dargestellt am Beispiel der ÖAW. Anzeiger der phil-hist Klasse 141(2):43–74
Feichtinger G, Winkler-Dworak M, Freund I, Prskawetz A, Riosmena F (2007) On the age dynamics of learned societies–taking the example of the Austrian Academy of Sciences. Vienna Yearb Popul Res 2007:107–131
Feichtinger G, Krasovskii AA, Prskawetz A, Veliov VM (2012) Optimal age-specific election policies in two-level organizations with fixed size. CEJOR 20(4):649–677
Feichtinger G, Grass D, Kort PM (2018) Optimal scientific production over the life cycle, Research Reports 2018–09. Vienna University of Technology, Institute of Statistics and Mathematical Methods in Economics, Operations Research and Control Systems
Ghisletta P, McArdle JJ, Lindenberger U (2006) Longitudinal cognition-survival relations in old and very old age: 13-year data from the Berlin aging study. Eur Psychol 11(3):204
Gondo Y, Poon LW (2007) Cognitive function of centenarians and its influence on longevity. Annu Rev Gerontol Geriatr 27(1):129–149
Goodwin TH, Sauer RD (1995) Life cycle productivity in academic research: evidence from cumulative publication histories of academic economists. South Econ J 61(3):728–743
Grass D, Caulkins JP, Feichtinger G, Tragler G, Behrens DA (2008) Optimal control of nonlinear processes. Springer, Berlin
Gross D, Harris C (1974) Fundamentals of queueing theory. Wiley, New York
Hartung J, Elpelt B, Klösener KH (2002) Statistik: Lehr- und Handbuch der angewandten Statistik, 13th edn. Oldenbourg, München, Wien
Hillier FS, Lieberman GJ (1974) Operation research. Holden-Day, San Francisco
Hittmair O, Hunger H (1997) Akademie der Wissenschaften. Entwicklung einer österreichischen Forschungsinstitution, Denkschriften der Gesamtakademie, vol 15. Verlag Der Österreichischen Akademie der Wissenchaften
Human Mortality Database (2019) University of California, Berkeley (USA) and Max Planck Institute for Demographic Research (Germany). http://www.mortality.org or http://www.humanmortality.de. Accessed 9th Jan 2019
Jones BF, Weinberg BA (2011) Age dynamics in scientific creativity. Proc Natl Acad Sci 108(47):18910–18914
Keyfitz N (1968) Introduction to the mathematics of population. Addison-Wesley, Reading
Keyfitz N (1985) Applied mathematical demography, 2nd edn. Springer, Berlin
Kim S (2003) The impact of research productivity on early retirement of university professors. Ind Relat J Econ Soc 42(1):106–125
Keyfitz BL, Keyfitz N (1997) The McKendrick partial differential equation and its uses in epidemiology and population study. Math Comput Model 26(6):1–9
Kliegel M, Zimprich D, Rott C (2004) Life-long intellectual activities mediate the predictive effect of early education on cognitive impairment in centenarians: a retrospective study. Aging Ment Health 8(5):430–437
Klotz J (2007) Soziale Unterschiede in der Sterblichkeit: Bildungsspezifische Sterbetafeln 2001/2002. Stat Nachr 62(4):296–311
Klotz J, Asamer EM (2014) Bildungsspezifische Sterbetafeln 2006/2007 sowie 2011/2012. Stat Nachr 3:209–214
Leridon H (2004) The demography of a learned society. The Académie des Sciences (Institut de France), 1666–2030. Population-E 59(1):81–114
Leridon H (2005) The demography of a learned society. The Académie de Sciences (Institut de France), 1666–2030, presentation given at the Workshop on “The Demography of Learned Societies”, Vienna, November 30th, 2005
Levin SG, Stephan PE (1991) Research productivity over the life cycle: evidence for academic scientists. Am Econ Rev 81(1):114–132
Link BG, Carpiano RM, Weden MM (2013) Can honorific awards give us clues about the connection between socioeconomic status and mortality? Am Sociol Rev 78(2):192–212
Lotka AJ (1907) Relation between birth rates and death rates. Science 26(653):21–22
Lotka AJ (1922) The stability of the normal age distribution. Proc Natl Acad Sci USA 8(11):339–345
Lotka AJ (1926) The frequency distribution of scientific productivity. J Wash Acad Sci 16(12):317–323
Lotka AJ (1939) Théorie Analytique des Associations Biologiques: Analyse Démographique avec Application Particulière à l’Espèce Humaine. Hermann, Paris
Mackenbach JP, Kunst AE, Groenhof F, Borgan JK, Costa G, Faggiano F, Jozan P, Leinsalu M, Martikainen P, Rychtarikova J et al (1999) Socioeconomic inequalities in mortality among women and among men: an international study. Am J Public Health 89(12):1800–1806
Matthiessen PC (1998) A demographic analysis of RDASL membership. In: Kuijsten A, de Gans H, de Feijter H (eds) The joy of demography ... and other disciplines. Liber amicorum presented to Dirk van de Kaa on the occasion at this retirement as Professor at the University of Amsterdam, Thela Thesis, Amsterdam
McKendrick A (1926) Applications of mathematics to medical problems. Proc Edinb Math Soc 44:98–130
Merton RK (1957) Priorities in scientific discovery: a chapter in the sociology of science. Am Sociol Rev 22(6):635–659
Merton RK (1968) The Matthew effect in science: the reward and communication systems of science are considered. Science 159(3810):56–63
Österreichische Akademie der Wissenschaften (1996–2005) Almanach. Verlag der Österreichischen Akademie der Wissenschaften, Vienna, pp 146–155 Jahrgang
Over R (1982) Does research productivity decline with age? High Educ 11(5):511–520
Preston S, Heuveline P, Guillot M (2000) Demography: measuring and modeling population processes. Wiley-Blackwell, Oxford
Quetelet LAJ (1835) Sur l’Homme et le Développement de ses Facultés, ou Essai de Physique Sociale. Bachelier imprimeur-libraire, Paris
Rinaldi S, Cordone R, Casagrandi R (2000) Instabilities in creative professions: a minimal model. Nonlinear Dyn Psychol Life Sci 4(3):255–273
Riosmena F, Winkler-Dworak M, Prskawetz A, Feichtinger G (2012) The impact of policies influencing the demography of age-structured populations: lessons from academies of sciences. Genus 68(2):29
Sanderson WC, Scherbov S (2007) A new perspective on population aging. Demogr Res 16(2):27–58
Sanderson W, Scherbov S (2008) Rethinking age and aging. Population Reference Bureau, Washington, D.C
Sanderson W, Scherbov S (2010) Remeasuring aging. Science 329(5997):1287–1288
Sanderson W, Scherbov S (2015) Faster increases in human life expectancy could lead to slower population aging. PLoS ONE 10(4):e0121922
Scherbov S, Sanderson W (2016) New approaches to the conceptualization and measurement of age and aging. J Aging Health 28(7):1159–1177
Schooler C, Mulatu MS (2001) The reciprocal effects of leisure time activities and intellectual functioning in older people: a longitudinal analysis. Psychol Aging 16(3):466
Settersten RA (2003) Age structuring and the rhythm of the life course. In: Mortimer JT, Shanahan MJ (eds) Handbook of the life course. Springer, New York, pp 81–98
Simonton DK (2014) The Wiley handbook of genius. Wiley, Hoboken
Skirbekk V (2004) Age and individual productivity: a literature survey. Vienna Yearb Popul Res 2004:133–153
Statistik Austria (2015) Alters- und geschlechtsspezifische Mortalitätsraten gemäß Hauptvariante der Bevölkerungsprognose 2015. für Österreich, Wien
Statistik Austria (2019) Jährliche Sterbetafeln 1947–2018 füur Österreich. http://www.statistik.at
Stephan PE (1996) The economics of science. J Econ Lit 34(3):1199–1235
Stroebe W (2010) The graying of academia: Will it reduce scientific productivity? Am Psychol 65(7):660
Stroebe W (2016) Age and scientific creativity. In: Whitbourne SK (ed) The encyclopedia of adulthood and aging. Wiley, Hoboken, pp 1–4. https://doi.org/10.1002/9781118521373.wbeaa026
Symonds MR, Gemmell NJ, Braisher TL, Gorringe KL, Elgar MA (2006) Gender differences in publication output: towards an unbiased metric of research performance. PLoS ONE 1(1):e127
United Nations (2017) World population ageing 2017. Department of Economic and Social Affairs, Population Division (ST/ESA/SER.A/408)
van de Kaa DJ, de Roo Y (2008) De leden van de Koninklijke Nederlandse Akademie van Wetenschappen: een demografisch perspectief: 1808 tot 2008, vol 8. Amsterdam University Press, Amsterdam
Way SF, Morgan AC, Clauset A, Larremore DB (2017) The misleading narrative of the canonical faculty productivity trajectory. Proc Natl Acad Sci 114(44):E9216–E9223
Weingart P, Winterhager M (2011) Altern in und altern der wissenschaft. Gegenworte: Hefte für den Disput über Wissen 25
Winkler-Dworak M (2008) The low mortality of a learned society. Eur J Popul/Revue européenne de Démographie 24(4):405–424
Winkler-Dworak M, Kaden H (2013) The longevity of academicians: evidence from the Saxonian Academy of Sciences and Humanities in Leipzig. Vienna Yearb Popul Res 2013:185–204
Acknowledgements
Open access funding provided by TU Wien (TUW). We are grateful to (in alphabetical order) Gerhart Bruckmann, Herbert Dawid, Fouad El Ouardighi, Inga Freund, Alexia Fürnkranz-Prskawetz, Richard Gisser, Josh Goldstein, Alexander Hanika, Peter Kort, Bernhard Rengs, Werner Richter, Fernando Riosmena, Warren Sanderson, Andrea Seidl, Vladimir Veliov, and Stefan Wrzaczek and two anonymous referees for helpful advice, comments and assistance.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: The rapid ageing of the Austrian Academy of Sciences
Appendix A: The rapid ageing of the Austrian Academy of Sciences
In Feichtinger et al. (2007) the population of the OEAW has been studied in detail, using data from the biographic records of the members of the Austrian Academy of Sciences (Hittmair and Hunger 1997; Österreichische Akademie der Wissenschaften 1996) from its foundation in 1847 to 2005. In December 2015, the presidency of the Academy asked for a re-evaluation of the ageing of the Academy and kindly provided updated records.
The Austrian Academy of Sciences was funded in 1847 as “Kaiserliche Akademie der Wissenschaften in Wien” (Imperial Academy of Sciences in Vienna) under the auspices of Emperor Ferdinand I. The Academy is structured around two sections: the section for mathematics and natural sciences and the section for humanities and social sciences. Membership distinguishes between honorary members, full members and corresponding members. Full membership requires residence in Austria. If a full member moves abroad, his or her status changes to that of a corresponding member abroad. In a similar vein, corresponding membership distinguishes between residence in Austria and abroad. For an illustrative example of multiple changes in membership status see that of the famous physicist Ludwig Boltzmann in Feichtinger et al. (2006b).
The bye-laws of the OEAW specify that the Academy comprises (at most) 90 full members, evenly divided between the two sections. Although membership is lifelong, members aged 70 years and above are, while fully retaining their rights, not considered for the maximum number of members. Finally, it is the full members who elect new Academy members.
The accelerated ageing of the Austrian Academy of Sciences becomes visible in Fig. 11, where the shares of members at older ages have been strongly rising across years. These shifts in the age distribution to higher ages have been attributed to a secular increasing trend in age at election but also to a remarkable longevity of the academicians.
Indeed, academies of sciences age more rapidly than national populations as members of learned societies have shown to exhibit a substantially lower mortality than the corresponding national populations. This finding has been documented for various European academies including the Austrian Academy of Sciences, see Andreev et al. (2011) for the Royal Society and the Russian Academy of Sciences; Matthiessen (1998) for the Royal Danish Academy of Sciences and Letters, van de Kaa and de Roo (2008) for the Royal Netherlands Academy of Arts and Sciences, Leridon (2005) for the French Academy of Sciences, and Winkler-Dworak and Kaden (2013) for the Saxon Academy of Sciences and Humanities in Leipzig, and Winkler-Dworak (2008) for the Austrian Academy of Sciences. The latter author investigated the mortality of the members of the Austrian Academy of Sciences since its foundation in 1847 to 2005 and contrasted it to life table death rates for the Austrian population. The analysis concerned only members residing in Austria and, due to the historically low number of women among Academy members, was limited only to male members. Winkler-Dworak (2008) found that during the first hundred years of the Academy’s existence, the members did not exhibit a significantly lower mortality than the general Austrian population, but after World War II a clear survival advantage of the academicians emerged (Winkler-Dworak 2008).
Figure 12 replicates the analysis presented in Winkler-Dworak (2008) for the life expectancy at age 50 in the second half of the 20th century and complements it with corresponding recent life expectancy values for the entire Austrian population and for those with tertiary education. Over the second half of the past century, academicians showed an increasingly higher life expectancy at age 50 than the Austrian male population, which is even more remarkable given the fact that also life expectancy for the latter has been steeply increasing since the 1970s. At the turn of the past century, Austrian academicians had a remaining life expectancy of about 35.1 years (95% confidence interval [32.9, 37.3]), about seven years more than the Austrian male population at the time. The survival advantage even persists, though at a smaller extent of about 3 years, compared to the population with tertiary education.

Source: Authors’ own computations (academicians); Human Mortality Database (2019) (total population); Doblhammer-Reiter (1996), Doblhammer et al. (2005), Klotz (2007), Klotz and Asamer (2014) (tertiary-educated population)
Life expectancy at age 50 for members of the Austrian Academy of Sciences (with 95% CI), Austrian general population and Austrian tertiary educated population (all only male populations).
From a time perspective, the latest available value for the life expectancy at age 50 of the Austrian tertiary educated population in 2011 is still slightly lower than the corresponding value for the Academy members a decade earlier. What is even more striking is that only very recently average Austrian men have reached a life expectancy value at age 50 similar to that which academicians already enjoyed around 1980. Therefore, several authors concluded that academicians indeed represent a vanguard group in the achievement of longevity (Andreev et al. 2011; Winkler-Dworak and Kaden 2013), and thus, academies age more rapidly than other population groups or general populations. However, in addition to the exceptionally high and increasing longevity, many European academies have experienced an upward secular trend in the mean age at election contributing to the ageing of academies via the inflow (Riosmena et al. 2012).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Feichtinger, G., Grass, D. & Winkler-Dworak, M. The mathematics of ageing:. Cent Eur J Oper Res 28, 371–399 (2020). https://doi.org/10.1007/s10100-019-00661-w
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10100-019-00661-w