Abstract
One of the UN Sustainable Development Goals is the supply of sustainable energy even where no electrical grid is available. The photovoltaic rural electrification programs are the most common systems implemented in remote areas, especially in developing countries. These programs include the systems installation and their maintenance for a given period. Installation costs and even spare parts costs over time are usually well estimated. However, design and cost estimation of the maintenance systems is a difficult task, whose wrong management has often resulted in the failure of these electrification programs. In this work, a methodology for designing maintenance systems and estimating costs is presented. The methodology includes a mixed integer linear programming model and a rule based expert system. The mathematical programming model allows obtaining the optimal size and accurate cost estimation of a maintenance system, based on precise information about the installed systems. This model is calibrated and validated with real running programs and will be used to get an enlarged data set of simulated cases if needed. The rule based expert system is obtained from the data set applying classification and regression methods with general information about the region and program to be run. It can be used for designing programs or for companies making decisions about being involved in a program to be developed. The methodology has been applied to real Morocco programs.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Human development is a concept that has evolved over time, increasingly incorporating concepts beyond the purely economic. On the UN General Assembly of 2015, a set of Sustainable Development Goals (SDGs) was debated and accepted by the participating countries for the period 2015–2030 (Division for Sustainable Development 2015). The 7th of the 17 established goals, “ensure access to affordable, reliable, sustainable and modern energy for all”, contains the targets proposed related to energy:
-
7.1
by 2030 ensure universal access to affordable, reliable, and modern energy services
-
7.2
increase substantially the share of renewable energy in the global energy mix by 2030
-
7.3
double the global rate of improvement in energy efficiency by 2030
-
7.a
by 2030 enhance international cooperation to facilitate access to clean energy research and technologies, including renewable energy, energy efficiency, and advanced and cleaner fossil fuel technologies, and promote investment in energy infrastructure and clean energy technologies
-
7.b
by 2030 expand infrastructure and upgrade technology for supplying modern and sustainable energy services for all in developing countries, particularly LDCs (least developing countries) and SIDS (Small Island Developing States).
Therefore, energy is currently considered one of the basic services, and governments are facing the challenge of providing it, even in remote and sparse areas, in a sustainable way. In rural areas off-grid, where weather conditions are suitable, photovoltaic electrification is a good option to reach these objectives.
Kanagawa and Nakata (2008) analyze quantitatively the access to electricity in rural areas of developing countries showing the importance of providing lighting to vulnerable people living in developing countries. Gómez-Hernández et al. (2019) propose a set of indicators to evaluate different rural electrification plans and apply them to a case study in Mexico.
For some years, the so-called photovoltaic rural electrification (PVRE) programs are being implemented in developing countries as an alternative to the grid, whose installation is too expensive, and to fossil fuels, which are nonrenewable, dirty, expensive, and difficult to be stored in safe conditions.
To achieve the objective of ensuring access to energy, these PVRE programs should include not only the installation of the systems but also support maintenance and access to spare parts when needed. In this way, these programs involve a service over time to beneficiaries.
This kind of programs is frequently developed in the Asian and African continents. Ellegård et al. (2004), Wamukonya (2007), Lemaire (2009) and Lemaire (2011), among others, review the effectiveness in the African continent by analyzing different countries such as Zimbabwe, Uganda, Ghana, etc., where solar home system based rural electrification programs were implemented. On the other hand, Sharif and Mithila (2013) and Borah et al. (2014) analyze the rural electrification using Solar Home Systems (SHSs) in Bangladesh and India, respectively. Reports from some institutions, as the World Bank (see Cabraal et al. 1996) and International Finance Corporation (International Finance Corporation 2012) present different case studies where the photovoltaic technologies have been applied in developing countries and their corresponding impact.
Governments or Development Agencies try to facilitate these programs, but usually, economic issues or lack of resources make it impossible to guarantee the success of such projects and then, public-private-partnerships (ppp) turn into a possible alternative. The project investments are normally taken from the two parts, where the private energy service company (ESCO) is in charge of managing the planning operations involved, and the Government, besides providing the corresponding public investments, is responsible for designing the PVRE program in a fee-for-service model. In this model, customers do not become owners of the systems, instead, the company continues to charge them a fee for keeping the systems in operation.
Fees are usually calculated according to what users pay for traditional lighting (candles, kerosene, etc.) to ensure access as well as the change to the new system. However, this quantity in most of the cases is not enough to cover the ESCO operations and maintenance costs (see Carrasco et al. 2013) having to be subsidized by the Government or by Development Agencies. The cause of high maintenance costs in PVRE is the decentralization of the service (remote and sparse areas). As a result of these over costs, many PVRE programs have failed because ESCOs have abandoned the programs due to financial imbalances, thus not achieving the goal of ensuring access to affordable, reliable, sustainable and modern energy for all (see Chaurey and Kandpal 2010 and van der Vleuten et al. 2007 for reviews). Garcia-Bernabeu et al. (2016) propose a multicriteria approach to obtain a fair price to investors constructing photovoltaic power plants, via government support. Domenech et al. (2019) use a multicriteria approach as well, assisting the promoters of wind-photovoltaic electrification projects.
For this reason, designing a PVRE program requires good models to estimate accurately these costs and to support decisions of sizing the maintenance systems for the ESCO at the time of bidding, and especially for the Government for designing the fee-for-service scheme. Maintenance and operation costs are unknown and uncertain depending on different aspects such as the geographical density of the systems, their reliability, road accesses, local costs, etc.
Although there are many studies on the cost estimation for the reliability of system parts, operational costs are not frequently studied in the literature. Carrasco et al. (2016), which serves as a starting point for this paper develops a mathematical programming model to obtain the key decisions that would lead to the minimum overall cost of the maintenance structure. An important drawback of that model is that it needs very precise data of the installed systems which are not usually available before operating and that it requires long runtimes as well. The review Hernández-Callejo et al. (2019) highlights Carrasco et al. (2016) as one of the few studying the design of a photovoltaic system.
The main objective of this paper is obtaining an expert system to estimate the maintenance system cost, to be used for designing the PVRE conditions or for suggesting under which conditions the participation on an electrification program is profitable before the program is implemented. A statistical approach can be an option to obtain such a procedure, but usually, there are not enough historical cases into the program to estimate costs from. The mathematical programming model introduced in Carrasco et al. (2016) can be used for obtaining a larger data set formed by synthetic cases based on simulated provinces.
The next methodology, whose aim is obtaining an easy-to-use model for maintenance cost estimation from a limited number of real cases, is presented:
-
1.
A mixed-integer linear programming model is calibrated with the real data available, in order to be useful to estimate costs and size the maintenance systems for new cases with similar conditions to the initial ones.
-
2.
Several simulated cases are created based on the original ones (keeping similar conditions) whose costs and maintenance system sizes are obtained from the mathematical programming model.
-
3.
A rule based expert system is obtained from the enlarged data set which will be useful for cost estimation before the program being run.
The paper is organised as follows. Sections 2 and 3 describe the problem in detail as well as the methodology proposed for parameter estimation and validation. Section 4 shows the proposed mathematical model and its application. In Sect. 5 the rule based expert system is developed and an illustrative example of application is represented. Finally, in Sect. 6 some conclusions and future work are summarized.
2 Problem description
In this section, general aspects of PVRE programs are discussed, being particularized for a Moroccan PVRE whose data are known in detail (provided by the ESCO Isofotón). It is described how its characteristics are taken into account in the models developed later.
2.1 PVRE programs
PVRE (photovoltaic rural electrification) programs are based on the installation and maintenance of SHSs. These systems include several components to transform and store energy and provide home services. There are different schemes depending on the services required. If home appliances are considered necessarily an inverter must be included in the basic requirements as well as bigger batteries, whereas if only lighting services are considered inverter will not be included (see Fig. 1). PVRE programs in developing countries are usually focused on the most basic service that is lighting. In this case, SHSs are composed of solar panels, a solar charge controller, a battery and lamps.
Once the SHS has been installed, operations carried out by ESCOs can be classified into three groups:
-
Collecting fees: Since a fee-for-service scheme is designed, the customers must pay monthly fees. These fees can be paid at home, if a visit is carried out during the month, at the ESCO agencies which are usually located in main villages, or in some meeting points that can attract the population of the area (markets/souks).
-
Preventive maintenance: To avoid blackouts due to failures of some parts of the SHS, preventive maintenance operations must be carried out. The component to be revised more frequently is the battery, which should be filled with distilled water once every 6 months. This determines the period between preventive maintenance operations.
-
Corrective maintenance: Despite preventive maintenance, some parts may fail. These events are subject to uncertainty, as it can never be known in advance when they are going to occur. Solar panels failures are extremely rare. Charge controllers and lamps exhibit a constant failure rate over time, but batteries usually exhibit an increasing failure rate caused by wearing out. Figure 2 shows the evolution along 10 years of spare parts consumed in a PRVE program in Morocco implemented in several provinces with 13,600 SHSs (Carrasco et al. 2013). These SHSs were formed by battery, charge controller, one 11w lamp and three 7w lamps.
Governments when designing the PRVE program must include precise conditions about the maintenance service to ensure a quality level. At least it should be included:
-
A maximum time to respond for corrective maintenance by the ESCO.
-
A minimum number of preventive maintenance operations per year.
-
The fees to be paid by customers.
-
A maximum time to pay fees (if it is exceeded, the ESCO is allowed to dismount the SHS).
-
Require the ESCO to maintain a minimum local structure to carry out the operation and maintenance service.
Number of spare parts replaced in a PVRE program of 13,600 SHSs along 10 years (Carrasco et al. 2013)
2.2 The Moroccan program
The models proposed in this article are based on the assumptions and data available of a real PVRE program in Morocco, the so-called Programme d’Electrification Rurale Global (PERG). This program was launched in 1995 when the rural electrification rate (TER) in Morocco was only 18%. The PERG implementation was based on two modes of electrification: connection to the interconnected network for the majority of villages, and decentralized rural electrification (mainly photovoltaic equipment) to remote areas of the network or sparsely populated. At the end of 2013, 37,099 villages corresponding to 2,027,120 households were electrified through networks; 51,559 homes in 3663 villages equipped with photovoltaic kits; and the TER reached 98.51%.
The models have been developed in general terms in order to be easily adapted to other programs, but the authors are aware that some differences can arise in other countries. The basic assumptions are as follows (a more exhaustive discussion can be found in Carrasco et al. 2016).
-
The maximum time to respond for corrective maintenance by the ESCO is 48 h.
-
The minimum number of preventive maintenance operations by year in a SHS is 2.
-
The PVRE program is subdivided by provinces, which are managed separately.
-
The SHSs are scattered in some minor villages, with the number of SHSs in each village known.
-
Villages are scattered in a rural community, with a main center. The average distance from the main center to the villages is known, but the precise location of each village is not provided. It will be assumed that always go from the main center to the villages and back, with length the average distance to a village.
-
Location of main centers of rural communities is known with exactitude.
-
Meeting points of the population at local markets, which in Morocco are known as souks, are weekly programmed.
-
Each province will always have a main agency, with a head of the agency, administrative staff and technicians. The head of the agency will have a car available for his own use that can operate as a reserve car if the operative vehicles are on maintenance.
-
Each car in operation will work with 2 technicians to carry out the maintenance operations.
2.3 Models assumptions
The following considerations will be incorporated into the models to approximate the cost and system sizing:
-
The expected number of corrective maintenance operations is set at the maximum observed value of operations required during a year (in our case, according to Fig. 2, it is the sixth year).
-
The number of SHSs of a rural community that will be visited annually is estimated as the total number of SHSs multiplied by 2 (since 2 visits per year are required for preventive maintenance) plus the expected number of corrective maintenance operations in a year.
-
The optimization model does not consider the cost of spare parts since that cost is included as a fixed number, estimated in advance.
As it can be observed, uncertainty related to corrective maintenance (and in some way to collecting unpaid fees), is not considered explicitly. Since a scenario representation that considers each day and each malfunction of an SHS is not viable, some additional conditions on preventive maintenance are included to approximate the solution and the cost. One of these conditions is to set a maximum time between two visits to a rural community assuming that it will be necessary to visit the community in that period either for preventive or corrective maintenance. Note that this period will be less than the already 6 months required for preventive maintenance. This period will be introduced in the optimization model as the planning period.
Another assumption will be that visits to rural communities for preventive maintenance will depart always from the local agency, preventing connections between communities. This assumption is made to capture the effect that corrective maintenance has to be provided within 48 h, often forcing communities to be visited directly from the agencies. For this reason, this model cannot be considered as a Travelling Salesman Problem or Vehicle Routing Problem.
3 Methodology
The main objective of this paper is obtaining an expert system to estimate the maintenance system cost, to be used for designing the PVRE conditions or for suggesting under which conditions the participation on an electrification program is profitable before the program is implemented. If many provinces were already participating in the program it could be possible to obtain simple rules to forecast the cost based on statistical methods. However, the program is generally defined without sufficient information, at most based on some pilot programs with few years in operation.
The methodology developed to obtain the expert system is as follows:
-
1.
Calibrate a mathematical programming model able to size the maintenance system and estimate its cost, based on the information provided by the available data.
-
2.
Create synthetic realistic cases modifying the provinces features and obtaining the estimated cost for the new cases using the mathematical programming model.
-
3.
Obtain the rule based expert system based on the information of this enlarged data set using statistical methods.
The optimization model and the expert system will be used later in the opposite sense, i.e., the expert system will be used initially to design the PVRE program or to make the decision to participate in an already designed program. Afterward, the optimization model will be used for designing the maintenance system once more detailed information about the number of SHS, location, etc., is available.
A summary of the steps of the methodology followed to obtain the models is described below, developed in depth in the following sections illustrated on the application to the Moroccan program.
3.1 Mathematical programming model
The methodology followed to calibrate the model is:
-
1.
Collecting data of representative PVRE programs in operation, in terms of number of SHSs, the extension of the province, etc. This includes real (or approximate) costs and structure to be functioning: number of agencies, location, number of cars and technicians.
-
2.
Calibration: Running the model with this data and comparing the obtained costs with the original ones. Some of the model parameters will be fixed. The model is also run with these data but without including anything about the structure currently functioning to know if a better configuration is possible.
-
3.
Validation: Running the model with data from a set of new validation provinces.
3.2 Enlarged data set and rule based expert system
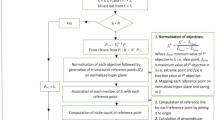
After developing the mathematical programming model, simpler rules are sought. The steps taken are schematized on Fig. 3.
-
1.
A set of simulated realistic cases are created based on the original real data. They are deemed realistic because they share some characteristics with the real ones, instead of generating completely random ones.
-
2.
The mathematical programming (MP) model is used to obtain the optimal infrastructure and cost for each of the new realistic provinces, obtaining an enlarged set of synthetic cases.
-
3.
A model is trained with the enlarged data set for predicting costs without having such detailed information about the provinces as the mathematical programming model requires.
4 Mathematical programming model
This section presents the mathematical model, whose aim is to determine the necessary local structure and to estimate the costs involved in the operations of a given province. The model was already introduced in Carrasco et al. (2016), here the study is extended including the validation phase. Given the relevance of this model for the development of the rule based expert system, it is shown below.
4.1 Notation and parameters
4.1.1 Indices sets
- \({\mathbf {R}} = \{1,\dots ,R\}\) :
-
Rural communities in the province
- \({\mathbf {V}} = \{1,\dots ,V\}\) :
-
Villages in the province
- \({\mathbf {D}} = \{1,\dots ,D\}\) :
-
Days in the planning period (maximum time between 2 visits to a rural community)
4.1.2 Parameters
- tp :
-
Estimated time between two consecutive visits to a village
- \(nvil_r\) :
-
Number of villages in each rural community \(r \in {\mathbf {R}}\)
- \(nv_r\) :
-
Number of villages of rural community \(r \in {\mathbf {R}}\) to be visited in the planning period. \(nv_r = nvil_r \frac{D}{tp}\)
- \(a_{v,r}\) :
-
0–1 parameter, 1 if village \(v \in {\mathbf {V}}\) belongs to rural community \(r \in {\mathbf {R}}\), 0 otherwise
- \(nshs_v\) :
-
Total number of SHSs in each village \(v \in {\mathbf {V}}\)
- fshs :
-
Expected percentage of SHS to fail in 1 year
- \(nsys_v\) :
-
Proportional part of the total SHSs to be visited during the planning horizon. \(nsys_v = \left\lceil (2 + fshs) \cdot nshs_v \frac{D}{365}\right\rceil \)
- tas :
-
Expected time needed to assist a SHS
- tw :
-
Technicians’ workday’s length
- nc :
-
Upper bound of the number of vehicles to be distributed among the local agencies
- \(b_{r,d}\) :
-
0–1 parameter, 1 if there is a souk in rural community \(r \in {\mathbf {R}}\) on day \(d \in {\mathbf {D}}\), 0 otherwise
- \(tb_{r,d}\) :
-
Time to be spent in a souk in rural community \(r \in {\mathbf {R}}\) on day \(d \in {\mathbf {D}}\)
- \(dist_{r,r'}\) :
-
Distance between the main rural centers \(r, r' \in {\mathbf {R}}\)
- \(td_{r,r'}\) :
-
Expected time needed for the displacements between the main rural centers \(r, r' \in {\mathbf {R}}\)
- \(dist'_r\) :
-
Average of distances from the main rural center \(r \in {\mathbf {R}}\) to each of its villages
- \(dist''_r\) :
-
Average of distance allocated to each SHS in rural community \(r \in {\mathbf {R}}\) (go and return). Introduction of this parameter avoids using an index for villages, \(dist''_r = \frac{2dist'_r nv_r}{\sum _{v \in {\mathbf {V}}} a_{v,r}\, nsys_v}\)
- \(td'_r\) :
-
Average time for displacements inside rural community \(r \in {\mathbf {R}}\)
- \(td''_r\) :
-
Average time needed to assist a SHS in rural community \(r \in {\mathbf {R}}\) (including displacement time into the rural community). \(td''_r = tas + \frac{td'_r nv_r}{\sum _{v \in {\mathbf {V}}} a_{v,r} \, nsys_v} \)
- cfp :
-
Provincial cost including head of the province (salary, telephone and fixed cost of his car) and administrative staff
- \(cmc_r\) :
-
Cost for locating a local agency on a rural community \(r \in {\mathbf {R}}\). It includes the rent and maintenance cost of the agency
- \(cnc_r\) :
-
Cost related to vehicles assigned to an agency located in rural community \(r \in {\mathbf {R}}\). It includes the fixed cost for vehicles, two technicians’ salary and telephone cost (estimated)
- ctr :
-
Cost of travelling per unit of distance (basically fuel)
4.2 Variables
- \(BL_r\) :
-
0–1 variable, 1 if a local agency is located on rural community \(r \in {\mathbf {R}}\), 0 otherwise
- \(BA_{r,r'}\) :
-
0–1 variable, 1 if an agency located on \(r \in {\mathbf {R}}\) assists rural community \(r' \in {\mathbf {R}}\), 0 otherwise
- \(BR_{r,r',d}\) :
-
0–1 variable, 1 if rural community \(r' \in {\mathbf {R}}\) is visited from the agency located on rural community \(r \in {\mathbf {R}}\) on day \(d \in {\mathbf {D}}\), 0 otherwise
- \(NS_{r',d}\) :
-
Number of assisted SHSs in rural community \(r' \in {\mathbf {R}}\) on day \(d \in {\mathbf {D}}\)
- \(NR_r\) :
-
Number of vehicles assigned to the local agency located on rural community \(r \in {\mathbf {R}}\)
- \(NT_{r,r',d}\) :
-
Number of vehicles travelling to rural community \(r' \in {\mathbf {R}}\) from the agency located on rural community \(r \in {\mathbf {R}}\) on day \(d \in {\mathbf {D}}\)
- \(TM_{r,r',d}\) :
-
Time spent in rural community \(r' \in {\mathbf {R}}\) coming from the agency located on rural community \(r \in {\mathbf {R}}\) on day \(d \in {\mathbf {D}}\)
4.3 Objective function and constraints
The objective function is composed by province fixed costs, agencies location costs, cars fixed costs (including costs related to the two technicians) and travelling costs.
Equations (1)–(6) relate to the location of agencies and the rural communities assisted by those. Equation (1) forces to open at least one agency. Equation (2) ensures each community is served by one agency. Equation (3) limits the visits that can be done to a community on a single day, and Eq. (4) makes sure communities are visited on souk days. Equations (5) and (6) relate the variables BA, BL and BR.
Equations (7)–(10) model the assignment of vehicles to agencies. Equation (7) limits the number of vehicles on a community. As markets are held at the same time of the day, a vehicle can only attend one at a time, and so Eq. (8) forces the number of vehicles to be at least the maximum number of markets held on communities without agencies on any single day. Equation (9) limits the number of vehicles travelling to any rural community from r to the number of vehicles assigned to r. Equation (10) links the trips of the vehicles with the binary variable BR.
Equations (11)–(12) track the number of visited systems. Equation (11) enforces the total number of SHSs are visited throughout the planning period and Eq. (12) forces a community to be assisted on day d in order to be able to visit any systems that day.
Equations (13)–(16) keep track of time and connect the previous groups. Equations (13) and (14) set the time spent in a rural community to be the maximum between the time spent in the souk and the time spent carrying out maintenances. Notice that if a local agency is located in a rural community where a souk is being held, it is not necessary to spend time there since the customers can go directly to the agency. Equations (15) and (16) ensure the workday of technicians is not be exceeded by the daily work (whole or by community). Equations (17)–(19) set the domain of the variables.
4.4 Calibration and validation
4.4.1 Collecting data
The methodology has been applied to the real PVRE program in Morocco described in Sect. 2.2. Into this program, the ESCO Isofoton is operating since 2005 in 9 provinces with more than 13,000 SHSs grouped on them at the time of the data collection. Such provinces are shown on Fig. 4. After discarding 3 provinces in which the system was not working properly (PRG requirements were not being met, such as providing corrective maintenance in less than 48 h), the other 6 provinces were divided into two groups:
-
Training provinces: Al Kalaa des Sraghnas (ALK), Azilal (AZI) and Ben Slimane (BSL) were used before on Carrasco et al. (2016) for fixing parameters of the model.
-
Validation provinces: Al Haouz (ALH), Beni Mellal (BME) and Errachidia (ERR) are used to confirm the validity of the model, once all the parameters are fixed.
The main characteristics of the provinces that will be used hereafter are shown in Table 1. Note that the province with more rural communities is Al Kalaa des Sraghnas (55), resulting in an integer programming model with roughly 700,000 constraints and 250,000 variables, one-third of them continuous, another third binary and another third integer.
Table 2 reports the system structure and related costs in the provinces under study. Operation costs have been aggregated into three main groups to compare them with the model results:
-
Province fixed costs: fixed costs in each province related to salaries of the head of the agency and administrative staff, fixed cost of the head of the agency’s car and communication cost of the main agency.
-
Cost related to system sizing: cost of renting buildings for agencies and their functioning (electricity, water, etc.), and cost of vehicles including salaries of the corresponding two technicians working with each vehicle
-
Cost related to operation: costs related to the fuel cost of the journeys performed.
It is worth noting that the cost of traveling (fuel and type of vehicles) is province-dependent, as some areas are more mountainous than others and so different vehicles are used.
4.4.2 Calibration: training provinces
The second step is to run the model fixing the current system structure, i.e. location of agency and number of technicians hired.
The model has been written in GAMS 23.5.1. and solved using CPLEX 12.2. Table 3 reports the obtained results of the training provinces, firstly imposing the implemented structure in the reality in order to assess the accuracy of the model; and then without any conditions in order to identify a possible better structure. Last row measures how accurately the mathematical programming model predicts the real costs, which were reported on Table 1. Variation is calculated as obtained cost minus real cost, divided by real cost.
The results obtained by the model identify a better structure on the Al Kalaa des Sraghnas province, in which opening a second agency leads to reducing the number of vehicles obtaining a cost reduction of around 20%. On the provinces of Azilal and Ben Slimane the results do not change when infrastructural decisions are not imposed.
These results have been considered good enough by the experts, and valuable since they did not have any tool able to approximate the costs in advance.
4.4.3 Validation: validation provinces
ESCO Isofoton provided data of three new provinces after having fitted the parameters: Errachidia (ERR), Beni Mellal (BME) and Al Haouz (ALH). The main characteristics of these provinces, which are referred as validation provinces, were shown on Table 1, and the costs arising with the current implemented structure were shown on Table 2.
As with the training provinces, the first step is running the developed model mimicking the current structure for each of these provinces, to validate the model. Then, it is run without predefining any structure, in order to look for a better configuration if possible. Results for both of these experiments are shown in Table 4.
It can be seen that cost estimation with the real implemented structure results in a maximum of 13.95% of deviation in Beni Mellal. It should be noticed that on the current structure of the provinces Beni Mellal and Errachicia there is one vehicle on each province with only one technician assigned to it, resulting in 3 and 5 technicians hired respectively. An assumption of our model (given by the ESCO) is that two technicians are hired for each vehicle, resulting in an overestimation of one technician for each of these provinces. If the cost of one technician is taken away (4,455.05 €/year) the variation with the original data would be much smaller (6.76% and − 1.54%, respectively). Therefore, the model can be considered able to estimate the costs with high accuracy.
Regarding the option of improving costs, the results of Al Haouz are the same in both cases. The agency is moved in Beni Mellal and a new one is opened on Errachidia, showing that the model can provide a better configuration for the maintenance systems.
4.4.4 Validation/application: economic viability
ESCO Isofoton also reported data about fees and real costs. The fees paid by users in the PERG are 59€/year/SHS, with an initial fee of 70€ (without taxes). The program was planned for 10 years, time for investment amortization and to support the operation and maintenance program. The company claimed that costs are not covered by those fees.
According to the costs provided by the company, the initial cost of this installation minus the initial fee would be 347€, which must be reimbursed in the next 10 years of the program. It will give 34.7€/year/SHS for recovering.
According to raw data of Fig. 2, multiplying the number of spare parts by their costs and adding up the costs over the 10 years, the global cost by spare parts replaced is obtained. Dividing by the number of SHSs and the 10 years, it is obtained 23.5€/year/SHS.
Adding installation and spare parts cost the result is 58.2€/year/SHS, which is almost the fee that customers are currently paying for the service, even when other costs are not considered. Maintenance costs must be computed to know the uncovered expenses, which will be different for each province. Three data sets will be used: those from the ESCO, those obtained with the model when fixing the structure beforehand and those from the model free.
These results are shown on Table 5, where three different costs are calculated:
-
Maintenance cost: fixed, system sizing and journey costs, per system.
-
Total cost: the sum of the maintenance cost, spare parts, and installation, per system.
-
Uncovered expenses: total cost minus income per system, multiplied by the number of systems.
There are important differences between provinces. Figure 5 shows that the sparser a province, the higher the maintenance cost. But, anyway, there is a lack of funds in every province enough to produce the undesired effect arising in the PERG companies closing and failing to provide the required service. These results confirm that the model results are in accordance with the reality observed.
5 Rule based expert system
The previous validation of the mathematical programming model shows that the model can be used for accurately predicting the cost and size of the infrastructure needed to perform the maintenance operations. Unfortunately for using the developed mathematical programming a lot of information is needed, such as, the number of rural communities and times needed to go from one another; the number of villages in each rural community and number of installed systems on each of them; or the time needed to visit a village within each rural community.
All that information will not be available when the program is designed or an ESCO must decide whether to participate in the program. For that reason, it is necessary to obtain simpler rules based on available information that can help with the estimation of size and cost.
Statistics and/or machine learning provide methods for obtaining such simple rules, but, to apply them, a larger number of cases is required. Hence a simulation procedure has been implemented, which is shown below.
5.1 Data gathering
For obtaining the aforementioned enlarged data set the next procedure has been followed:
-
1.
A larger data set of simulated realistic provinces is created. To maintain the feasibility of a province, rather than randomly creating new ones, each of the new provinces will be an original one with three of its original characteristics multiplied by a factor. A collection of values for these factors has been defined to obtain different infrastructure sizes than the existing ones, aiming to halve and double the number of systems and areas. For that purpose the number of systems was multiplied by 0.5 and 2, and since the areas are not an input of the mathematical programming model, a proxy based on the distances was used instead. If provinces and communities are simplified as circles, their radii should be multiplied by \(1/\sqrt{2} \approx 0.7\) and \(\sqrt{2} \approx 1.4\) for halving and doubling areas, respectively. Therefore these factors were used for the distances.
-
Number of systems on each village (factors: 0.5, 1, 2)
-
Mean distance from the center of a rural community to its villages (factors: 0.7, 1, 1.4)
-
Distances between rural communities (factors: 0.7, 1, 1.4)
In other words, a full factorial experiment was designed varying 3 characteristics, each with 3 possible factors, of 6 different provinces. This experiment provides 162 simulated provinces (\(6 \cdot 3^3\)).
-
-
2.
The mathematical programming model is run with each of the simulated provinces, limiting the runtime to 2 h. Only those results with less than 5% of integrality gap are kept, leading to a set of synthetic cases formed by the simulated provinces, coupled with their optimal configurations.
-
3.
A second set of simulated provinces is created, motivated by the results of the first round of synthetic cases. As it can be seen in Fig. 6, costs exhibit a clear jump. Trying to reduce such a gap and describe better the area around this jump, provinces with lower costs were multiplied by bigger factors and provinces with higher costs by smaller factors.
After solving these provinces with the mathematical programming model and runtime limits, a final data set of 177 synthetic cases was obtained. Each of the new provinces has its information as detailed as the original ones.
Execution for all the provinces accounted for 477.5 h, or almost 20 days, on a computer with an Intel Core i7 processor and 8gb RAM.
From this data set, a rule based expert system will be obtained based on characteristics general enough to be used before the program is run (real or estimated values). A small set of characteristics (explicative variables) will be considered. Such characteristics, which are shown in Table 6, are computed from some parameters that also were used in the mathematical programming model (Sect. 4.1).
The most direct method to obtain a simple rule is to develop a regression model. Nevertheless, as can be seen in Fig. 6, costs show an important shift. That shift might suggest that, before a regression model being fitted, a classification should be performed. Later, a different regression model for each class can be developed, or a dummy variable related to the class can be added.
5.2 Classification model
The objective of the classification model is to obtain a simple procedure to determine if a new province should be included in the branch with lower costs or in that one after the jump.
Initially, it was assumed that the most impact variable would be the number of centers to be opened. However, when inspecting the results it can be seen that the number of vehicles to allocate plays a crucial role in the total cost (Fig. 7). This was already observed in the Al Kalaa province: the maintenance cost was cut out by reducing the number of vehicles, even if a new maintenance center was opened. Moreover, regarding Fig. 7, a continuity in cost is observed using 2 or 3 vehicles, appearing only discontinuity when changing from one vehicle to multiple vehicles. This number of vehicles does not include the head of the agency’s car.
Therefore, the first step for building the expert system is to develop a classification model based on the characteristics previously described to predict if one or multiple vehicles will be needed within the province.
Classification tree has been chosen by its easy interpretation. The obtained tree, trained using all observations, is shown in Fig. 8 joined to its confusion matrix. The features on the tree are:
-
Mean distance between rural communities, in kilometers (dist)
-
Number of installed systems (NS)
-
Maximum number of systems on a village (MSV)
The split of the variables MSV is related to the density on a province: for the same number of systems installed, the smaller the maximum number of systems in a village, the greater the dispersion, so it will be more difficult to maintain all the systems with a single vehicle.
The obtained tree, albeit extremely simple and easy to interpret, has great performance: only 3 out of the 177 observations are misclassified (1.69%). Cross-validation was performed to validate the methodology, training 177 different trees leaving each observation out once, and obtaining a mean cross-validation error of 8%.
5.3 Regression model
Once the classification model is obtained to predict if a single vehicle will be enough, a linear regression model is sought to predict the maintenance costs including the dummy variable, multVeh. Its value will be 1 if more than one vehicle is needed, and 0 otherwise. The rest of the explanatory variables are the same as for the classification tree plus some products of variables included by the possible interaction between them. The cost is obtained for a 4 weeks period (length considered in the mathematical programming model).
The coefficients of the obtained linear regression model are shown in Table 7, and the description of the variables in Table 8. The adjusted R2 is 0.9953 when the true class for the number of vehicles is known, and 0.9616 when the number of vehicles class is predicted by the classification tree.
Rounding coefficients and grouping terms, the following rule for estimating cost is obtained:
The cost predicted by this formula is compared with the true cost on Fig. 9.
5.4 Application: economic analysis
One of the applications of the developed models is the assessment of a fair user fee. Let T€/year/SHS be the yearly fee users pay. Let C be the maintenance cost for 4 weeks provided by the regression model (20). Considering a year with 52 weeks, the cost per system and year is 13\(\frac{C}{NS}\), where NS is the number of installed systems. Adding to this value the installation costs and spare parts given in Sect. 4.4.4, the annual fee to cover expenses should be at least
As an example, for Azilal case, whose variables values are shown in Table 9, the classification tree predicts needing multiple vehicles. Once it has been classified, the linear regression model (20) gives an annual cost C of 4475.34€. And finally, from Eq. (21), the yearly fee T should be at least 92.91€. It can be compared with data included in Table 5 of Sect. 4.4.4, where this value was 89.54€ and 90.33€ using ESCO data and mathematical programming model results, respectively.
The expert system can also be used to estimate the effects in case of a variation in the number of systems. Let assume the number of clients from Table 9 is doubled:
-
1.
The classification tree still yields multiple vehicles in this case.
-
2.
The regression model does not explicitly include the variable NS, but there are two parameters subject to change:
-
If the number of systems doubles because in every village there are twice as many clients, the parameter MSV should double as well. In this case, the new monthly cost C is 4567.18€, and the lower bound of the fee becomes \(T=75.91\)€.
-
If the number of system doubles because the program reaches twice as many places, the parameter NV should double as well. In this case, the new monthly cost C is 4627.94€, and the lower bound on the fee becomes \(T=76.15\)€.
-
Both cases result in a similar decrease in cost per installed system.
6 Conclusions and future work
“Ensure access to affordable, reliable, sustainable and modern energy for all” is one of the Sustainable Development Goals of United Nations, which makes providing energy for all one of the basic challenges facing governments and international organizations nowadays.
Remote areas, especially in developing countries, must be serviced by off-grid technologies in a decentralized and sustainable way. Photovoltaic technology is the most widespread alternative through photovoltaic rural electrification programs based on solar home systems. These programs are launched by authorities, being carried out usually by private companies in a fee-for-service scheme. These fees can be satisfied by the end-users or subsidized by governments or Development Agencies. The access to the service must be ensured over time, establishing a maintenance program for medium to long term. Fees established must be enough to cover these costs, but they are difficult of being estimated. Both authorities and ESCOs need a method to estimate these costs when defining the program or at the bidding time.
A methodology for estimating costs and sizing maintenance systems has been presented in this paper. The methodology is based on a mathematical programming model and a rule based expert system. The mixed integer linear programming model allows to obtain accurate costs and design of the system for a well-described program, or for simulated cases to obtain a larger data set. The rule based expert system, comprised of a classification tree and a linear regression model, estimates the maintenance cost with little information from a data set of real or realistic cases. It can be used for designing the program, i.e. knowing the fees to be established in a program, or for an ESCO to decide about participating in the program or not. If the ESCO chooses to participate in the program, already with extended information, the mathematical programming model can obtain the optimal structure of the maintenance system to minimize costs.
An important limitation of the obtained ruled based expert system is that it cannot be directly applied to other countries. The reason for this is that the system is missing information on the economy of the region: how does the cost of opening a new agency relate to salaries or displacement costs? In this case, a suggested approach is generating new provinces with the mathematical programming model and then retrain the necessary models.
The methodology has been applied to and validated with a program in Morocco. The mathematical programming model is parameterized being suitable to be applied in other PVRE programs, and the rule based model is based on general parameters. Therefore, the full methodology is useful for PVRE programs supporting design decisions and providing realistic cost estimations, in order to achieve the desired Development Goal.
References
Borah RR, Palit D, Mahapatra S (2014) Comparative analysis of solar photovoltaic lighting systems in India. Energy Proc 54:680–689
Cabraal A, Cosgrove-Davies M, Schaeffer L (1996) Best practices for photovoltaic household electrification programs: lessons from experiences in selected countries. In: Technical report, World Bank technical paper
Carrasco L, Martín-Campo F, Narvarte L, Ortuño M, Vitoriano B (2016) Design of maintenance structures for rural electrification with solar home systems. The case of the Moroccan program. Energy 117(Part 1):47–57
Carrasco L, Narvarte L, Lorenzo E (2013) Operational costs of A 13,000 solar home systems rural electrification programme. Renew Sustain Energy Rev 20:1–7
Carrasco L, Narvarte L, Peral A, Vázquez M (2013) Reliability of a 13 000-SHS photovoltaic rural electrification programme. Prog Photovolt Res Appl 21(5):1136–1145
Chaurey A, Kandpal TC (2010) Assessment and evaluation of PV based decentralized rural electrification: an overview. Renew Sustain Energy Rev 14(8):2266–2278
Division for Sustainable Development, U. N. (2015) Sustainable development goals. https://sustainabledevelopment.un.org/topics/sustainabledevelopmentgoals
Domenech B, Ferrer-Martí L, Pastor R (2019) Multicriteria analysis of renewable-based electrification projects in developing countries. Ann Oper Res. https://doi.org/10.1007/s10479-019-03195-1
Ellegård A, Arvidson A, Nordström M, Kalumiana OS, Mwanza C (2004) Rural people pay for solar: experiences from the Zambia PV-ESCO project. Renew Energy 29(8):1251–1263
Garcia-Bernabeu A, Benito A, Bravo M, Pla-Santamaria D (2016) Photovoltaic power plants: a multicriteria approach to investment decisions and a case study in western Spain. Ann Oper Res 245(1):163–175
Gómez-Hernández D, Domenech B, Moreira J, Farrera N, López-González A, Ferrer-Martí L (2019) Comparative evaluation of rural electrification project plans: a case study in Mexico. Energy Policy 129:23–33
Hernández-Callejo L, Gallardo-Saavedra S, Alonso-Gómez V (2019) A review of photovoltaic systems: design, operation and maintenance. Sol Energy 188:426–440
International Finance Corporation (2012) Lighting Asia: solar off-grid lighting, market analysis of: India. Nepal, Pakistan, Indonesia, Cambodia and Philippines, Technical report, Bangladesh
Kanagawa M, Nakata T (2008) Assessment of access to electricity and the socio-economic impacts in rural areas of developing countries. Energy Policy 36(6):2016–2029
Lemaire X (2009) Fee-for-service companies for rural electrification with photovoltaic systems: the case of Zambia. Energy Sustain Dev 13(1):18–23
Lemaire X (2011) Off-grid electrification with solar home systems: the experience of a fee-for-service concession in South Africa. Energy Sustain Dev 15(3):277–283
Sharif I, Mithila M (2013) Rural electrification using PV: the success story of Bangladesh. In: Energy procedia, vol 33. Elsevier, Amsterdam, pp 343–354
van der Vleuten F, Stam N, van der Plas R (2007) Putting solar home system programmes into perspective: what lessons are relevant? Energy Policy 35(3):1439–1451
Wamukonya N (2007) Solar home system electrification as a viable technology option for Africa’s development. Energy Policy 35(1):6–14
Acknowledgements
The authors would like to thank Marta Artalejo Álvarez, MSc, and Isofoton, for their valuable collaboration. This work has been supported by the UCM-Santander grant (CT27/16-CT28/16), Santander grant PR26/16-15B-3, Government of Madrid grant P2018/EMT-4308 (MADRID-PV2-CM), Government of Spain grant MTM2015-65803-R and grant H2020 MSCA-RISE 691161 (GEO-SAFE).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
León, J., Martín-Campo, F.J., Ortuño, M.T. et al. A methodology for designing electrification programs for remote areas. Cent Eur J Oper Res 28, 1265–1290 (2020). https://doi.org/10.1007/s10100-019-00649-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10100-019-00649-6