Rotation of the age pattern of mortality improvements in the European Union

Abstract

Human mortality tends to decline in the long run, which is fortunate for humans, but less so for pension and health insurance schemes and annuity providers. Empirical studies have shown that rates of mortality improvement depend heavily on the age, gender and country in question, and additionally, they also tend to change in time. More specifically, the historical acceleration of mortality decreases among the elderly and a simultaneous slowdown of improvement at younger ages, which are sometimes jointly referred to as the rotation of the age pattern of mortality decline, have been observed in several populations. After a concise summary of the most relevant literature, this paper suggests a simple, largely data-driven methodology with few assumptions for the empirical examination of the rotation phenomenon in historical mortality datasets. These techniques are then applied on United Nations data from the period between 1950 and 2015 for both genders and all 28 countries of the European Union. The results indicate that rotation has indeed taken place in numerous member states, but its presence is far from universal, and it appears to have been notably more prevalent in populations of women than among men. Life expectancies seem to predict degrees of rotation only in the former Eastern bloc despite prominent literature that suggests otherwise, while increments of life expectancies over the observed period are better predictors of the degrees of rotation in the case of Western European women.

1 Introduction

Human mortality has decreased significantly since at least the beginning of the past century (Tuljapurkar 2000), which has resulted in an unprecedented increase of human life expectancies. Despite its nearly univeral occurence, the speed of mortality decline varies heavily by age, gender and country (Lee 2000), and to make things more complicated, mortality improvement rates themselves may very well change in time, even for the same triad of the aforementoned variables (Kannisto et al. 1994; Horiuchi and Wilmoth 1995; Lee and Miller 2001; Carter and Prskawetz 2001; Rau et al. 2008).

1.1 Rotation of the age pattern of mortality decline

More specifically, several authors have noted a historical pattern of diminishing mortality decline at relatively younger ages, accompanied by accelerating improvements at more advanced ages (Christensen et al. 2009). Li et al. (2013) call this phenomenon the “rotation” of the age pattern of mortality decline, which is captured by a counterclockwise rotation in Fig. 1.

A somewhat simplistic explanation of the rotation is that longevity increases used to be driven by rapidly declining infant and childhood mortality rates (e.g., due to widespread vaccination programs and improved child nutrition)—and to some extent, by improvements in middle-aged mortality—, where spectacular advances are less and less possible, but on the other hand, better medications, nutrition and lifestyle choices for the elderly and costly medical procedures to extend life at higher ages are increasingly available.¹ It should be noted that the investigation of the causes of the rotation falls outside the scope this paper.

The practical significance of the topic lies in the fact that ignoring rotation in long-term mortality forecasts leads to the systematic underestimation of the old-aged population, which exacerbates longevity risk. This may lead to serious financial consequences for life and health insurers as well as pension schemes.

1.2 Literature overview

Mortality forecasting techniques play a key role in demography, life insurance and pensions. Due to the immense and ever-growing literature on these methods (see e.g. (Booth and Tickle 2008) and (Pitacco et al. 2009) for comprehensive reviews), an exhaustive overview is not attempted here, but instead, this paper will only focus on sources related to the rotation phenomenon.

1.2.1 The Lee–Carter model

The famous paper of Lee and Carter (1992) has probably been the most important breakthrough in the history of mortality forecasting. The authors model the logarithm of the central mortality rate at age x and calendar year t as

$$\begin{aligned} \log m_{xt}=a_x+b_x k_t +\varepsilon _{xt}, \end{aligned}$$

(1)

where $a_x$ represents the mean of the observed logarithmic central mortality rates for a given age, the time series $k_t$ captures the evolution of the overall level of mortality across time, and $b_x$ denotes the speed of mortality decline for every age.

Fig. 1

Rotation of the age pattern of mortality decline (stylized illustration)

As the parameters $b_x$ do not depend on time, and the time series $k_t$ is overwhelmingly assumed to follow a linear pattern (Tuljapurkar 2000), age-specific mortality declines at a constant speed in the Lee–Carter model, and the rate of improvement only depends on the age of the individual in question. The latter implicit assumption of the model has attracted intense scrutiny by the scientific community.

1.2.2 Empirical evidence against constant age-specific improvements

Kannisto et al. (1994) find accelerating mortality improvements between 1950 and 1989 among those aged 80–99 years in 27 countries. Horiuchi and Wilmoth (1995) use Swedish data to demonstrate a shift in mortality improvements from younger towards older ages. Lee and Miller (2001) compare the average rates of mortality improvement by age across the first and second halves of the twentieth century, and observe the shift in mortality improvement from younger to older ages in several countries. Based on this observation, they propose using data from the years after 1950 for the estimation of the Lee–Carter model in order to reduce violations of the time-invariance assumption. Carter and Prskawetz (2001) estimate several Lee–Carter models on Austrian data using different time windows to illustrate the evolution of age-specific mortality decline.² Rau et al. (2008) and Christensen et al. (2009) note that mortality among the oldest old (aged 80 years or more) has overwhelmingly decreased in the second half of the twentieth century in the majority of more than 30 countries, and in some cases, the pace of this decline has accelerated.

1.2.3 The rotated Lee–Carter model

Several approaches have been developed to address the inflexibility of the classic Lee–Carter framework with respect to the age pattern of mortality decline. Notably, Li et al. (2013) have managed to incorporate the rotation into the original procedure.³ Instead of Eq. (1), they model the logarithms of central mortality rates as

$$\begin{aligned} \log m_{xt}=a_x+B(x,t) k_t +\varepsilon _{xt}. \end{aligned}$$

(2)

The parameters B(x, t) in Eq. (2) capture the rotation phenomenon by converging smoothly across time from their initial levels corresponding to $b_x$ in Eq. (1) to their assumed ultimate levels, as life expectancy at birth advances from an initial threshold to an upper ceiling (the authors propose 80 and 102 years, respectively) in the original model described by Eq. (1). It is important to note that the authors recommend their model for low-mortality countries and very long forecasting horizons, and knowledge of the estimated parameters of the original Lee–Carter model is sufficient to fit the rotated model to data. Ševčíková et al. (2016) and Dion et al. (2015) recently incorporated this technique into population projections for the United Nations Population Division and Statistics Canada, respectively.

1.2.4 Other modeling approaches

Another solution is to capture the rotation by modeling the evolution of age-specific mortality improvement rates instead of mortality rates, as proposed by Haberman and Renshaw (2012) and Mitchell et al. (2013), among others. Bohk-Ewald and Rau (2017) follow this line in a Bayesian framework capable of combining mortality trends of different countries. They demonstrate on British and Danish data that assuming constant age-specific mortality improvement rates may lead to the underestimation of life expectancies at birth, and also apply their framework on U.S. data in Bohk-Ewald and Rau (2016). These approaches are data-driven, as opposed to Li et al. (2013), who impose a somewhat arbitrary process on age-specific mortality improvement rates, as they are of the opinion that empirical evidence for the rotation is too subtle to govern forecasts.

Yet another alternative is the approach of Booth et al. (2002) and Hyndman and Ullah (2007), who recommend using more than one interaction of age- and time-dependent parameters in Eq. (1) in order to capture the non-constant evolution of age-specific mortality improvement rates, which produces so-called multi-factor mortality forecasting models. Bongaarts (2005) proposes a shifting logistic model to describe the transition in the age pattern of mortality decline. Li and Lee (2005), Cairns et al. (2011), Russolillo et al. (2011) and Hyndman et al. (2013) model mortality rates of several populations in a coherent framework. In a multi-population setting, age-specific rates of mortality improvement are not necessarily constant due to interactions among different populations.

Further recent developments in this field include De Beer and Janssen (2016), who aim to model the distribution of the age at death by calendar year, and Li and Li (2017), who propose a sequential statistical testing procedure to determine the starting point of the longest plausible estimation base period where the two conditions of the linearity of the time series $k_t$ and the time-invariance of the parameters $b_x$ jointly hold, and find that for the majority of the 34 countries examined, this period starts somewhere between 1960 and 1990.

2 Data and methods

2.1 Demographic data

The statistical analysis presented in this paper was performed in R (R Development Core Team 2008) using mortality rates, life expectancies at birth and population counts of the 28 members of the European Union.⁴ These indicators are available for both genders, all 28 EU member states, 22 age groups (0, 1–4, 5–9, 10–14, ..., 95–99 and 100 years and older) and 13 calendar periods (1950–1955, 1955–1960, ...2010–2015).⁵ The grouping of ages and calendar years smooths the data (akin to moving averages) so that they contain less undesirable random fluctuations. All data are the courtesy of the UN World Population Prospects 2017 (United Nations Population Division 2018).

Mortality improvement rates pertaining to age group $x \in \{x_1, x_2, \ldots , x_{22}\}$, calendar period $t \in \{1,2,\ldots ,12\}$, country $c \in \{c_1,c_2,\ldots ,c_{28}\}$ and gender $g \in \{M,W\}$, denoted by $r^{cg}_{xt}$ and computed as

$$\begin{aligned} r^{cg}_{xt}=-\log \Big (\frac{m^{cg}_{x,t+1}}{m^{cg}_{xt}}\Big ) \end{aligned}$$

(3)

will be used throughout this paper instead of the corresponding mortality rates $m^{cg}_{xt}$.

2.2 Measuring rotation

Based on the quantities defined by Eq. (3), acceleration rates $\beta ^{cg}_{x}$ may be computed for every age group $x \in \{x_1, x_2, \ldots , x_{22}\}$ and country $c \in \{c_1,c_2,\ldots ,c_{28}\}$ as well as both genders $g \in \{M,W\}$. Long-term mean acceleration is measured by the slope of the linear trend of mortality improvement rates⁶:

$$\begin{aligned} \beta ^{cg}_{x}=\frac{\sum _{t=1}^{12}{(r^{cg}_{xt}}-\bar{r}^{cg}_{x}) (t-\bar{t})}{\sum _{t=1}^{12}{(t-\bar{t})^2}}. \end{aligned}$$

(4)

$\beta ^{cg}_{x}$ in Eq. (4) may be interpreted as the mean growth of the mortality improvement rate for age group x, country c and gender g over a 5-year period assuming a linear trend. Equation (4) arguably produces more reliable results than computing the mean rate of increase between the starting and end points (akin to the maximum likelihood estimate of the drift parameter of a random walk with drift), since it takes all data points into account and is less sensitive to outliers at the two ends of the data series.

To determine the degree to which rotation has taken place (if at all) for a given country and gender, it has to be examined whether the acceleration of mortality decline has been more pronounced at advanced ages than in the earlier and middle stages of life (possibly characterized by deceleration). In other words, the degree of association between the variables acceleration and age needs to be measured using a plausible statistical technique. As age group x is an ordinal variable,⁷ and additionally, the association need not be linear for the rotation to take place, the popular Spearman’s $\rho$ for rank correlation (computed between the variables age group and acceleration) is chosen as the measure of rotation. Furthermore, as population sizes vary significantly by age group, and more populous age groups should arguably have higher importance in determining the degree of rotation, a commonly used, weighted version of Spearman’s $\rho$ (Pinto da Costa 2015) is used, with the respective average population sizes $P_{x_i}^{cg}$ over the period 1990–2015⁸ as weights:

$$\begin{aligned} \begin{aligned} \rho ^{cg}=\frac{\sum _{i=1}^{22}P_{x_i}^{cg}(\text {rank}(\beta ^{cg}_{x_i}) -\mu ^{cg})(i-\nu ^{cg})}{\sqrt{\sum _{i=1}^{22}P_{x_i}^{cg}(\text {rank} (\beta ^{cg}_{x_i})-\mu ^{cg})^2}\sqrt{\sum _{i=1}^{22}P_{x_i}^{cg}(i-\nu ^{cg})^2}} \\ \quad ((c,g) \in \{c_1,c_2,\ldots ,c_{28}\} \times \{M,W\}), \end{aligned} \end{aligned}$$

(5)

where

$$\begin{aligned} \mu ^{cg}=\frac{\sum _{i=1}^{22} P_{x_i}^{cg} \text {rank}(\beta ^{cg}_{x_i})}{\sum _{i=1}^{22} P_{x_i}^{cg}} \quad \text {and} \quad \nu ^{cg}=\frac{\sum _{i=1}^{22} P_{x_i}^{cg} i}{\sum _{i=1}^{22} P_{x_i}^{cg}} \end{aligned}$$

are the weighted means (taken over all age groups) of the ranks⁹ of the acceleration rates and the age group indices, respectively.

Additionally, the one-sided z-test (Pinto da Costa 2015) with

$$\begin{aligned} H_0: \rho ^{cg} \le 0, \quad H_1: \rho ^{cg}>0 \quad ((c,g) \in \{c_1,c_2,\ldots ,c_{28}\} \times \{M,W\}). \end{aligned}$$

(6)

may be used to test whether degrees of rotation are significantly different from zero.

2.3 Correlations between degrees of rotation and other variables

It is worth examining which variables may predict degrees of rotation $\rho ^{cg}$. In this subsection, methods of determining the strengths of association between degrees of rotation and several variables are presented in detail. These associations will be examined in the European Union as a whole, and additionally, within the former Eastern¹⁰ and Western blocs separately. The reason for handling these two groups of countries separately is to avoid Simpson’s paradox, which might result from the very different paths of demographic, economic and social development of the two former blocs of countries, especially between 1950 and 1990.

The relationship between degrees of rotation $\rho ^{cg}$ and gender within bloc $b \in \{EU, West, East\}$ may be examined by computing and comparing the mean degrees of rotation by gender (weighted by population counts in order to reflect the relative importances of various countries):

$$\begin{aligned} \rho ^b(g)=\frac{\sum _{c \in b}{\rho ^{cg}P^{cg}}}{\sum _{c \in b} P^{cg}}. \end{aligned}$$

(7)

Differences in mean degrees of rotation between the two genders may be tested for significance using the elementary paired-samples t test with

$$\begin{aligned} H_0: \mathbb {E}[\rho ^{b}(M)]=\mathbb {E}[\rho ^{b}(W)], \quad H_1: \mathbb {E}[\rho ^{b}(M)] \ne \mathbb {E}[\rho ^{b}(W)] \quad (b \in \{EU, West, East\}),\nonumber \\ \end{aligned}$$

(8)

weighted by population counts of the countries.

Additionally, differences in mean degrees of rotation between the two former political blocs may also be investigated separately for men and women by comparing the quantities defined by Eq. (7). To test whether the differences between the two halves of the European Union are significant, the basic independent-samples t test¹¹

$$\begin{aligned} H_0: \mathbb {E}[\rho ^{West}(g)]=\mathbb {E}[\rho ^{East}(g)], \quad H_1: \mathbb {E}[\rho ^{West}(g)] \ne \mathbb {E}[\rho ^{East}(g)] \quad (g \in \{M,W\})\nonumber \\ \end{aligned}$$

(9)

may be performed, again weighted by population sizes.

Li et al. (2013) state that rotation is more prevalent in low-mortality countries, and therefore they recommend that the process of rotation in the rotated variant of the Lee–Carter model should only start after the life expectancy at birth has reached a certain threshold (more specifically, they recommend the threshold of 80 years).

To examine the empirical validity of this statement separately for men and women, the strength of the association between degrees of rotation $\rho ^{cg}$ and mean life expectancies at birth $e_0^{cg}$ (over the period between 1950 and 2015) is measured using Spearman’s $\rho$ statistic, weighted by mean population sizes $P^{cg}$¹². The choice of Spearman’s $\rho$ is motivated by the fact that the relationship need not be linear, and weighting is applied since population sizes are highly heterogeneous, and countries with small populations should arguably have less importance in determining the strength of the association.

Additionally, to determine which other demographic variables degrees of rotation may depend on, the relationship between degrees of rotation $\rho ^{cg}$ and

• increments of life expectancies at birth between the periods 1950–1955 and 2010–2015, denoted by $\varDelta e^{cg}_0$, as well as

• remaining life expectancies at the age of 60 years,¹³ denoted by $e^{cg}_{60}$

are examined, again by computing Spearman’s $\rho$ statistic between the variables of interest, weighted by mean population sizes $P^{cg}$, by the same argument that more populous countries ought to have more influence on these measures of association.

The reason for choosing $\varDelta e^{cg}_0$ is that there used to be significant differences in life expectancies in the 1950s and the patterns of improvements have been different in various countries, while $e^{cg}_{60}$ is another variable of interest because pension providers might only be interested in forecasts for higher ages.

In general, the strength of the association between degrees of rotation $\rho$ on the one hand and one of the indicators $I \in \{e_0, \varDelta e_0, e_{60} \}$ on the other hand, inside bloc $b \in \{EU, West, East \}$ for gender $g \in \{M,W\}$ may be measured as

$$\begin{aligned} \rho ^{bg}(I) =\frac{\sum _{c \in b} P^{cg}(\text {rank}(\rho ^{cg})-\alpha ^{g})(\text {rank}(I^{cg})-\beta ^{g})}{\sqrt{\sum _{c \in b} P^{cg}(\text {rank}(\rho ^{cg})-\alpha ^{g})^2}\sqrt{\sum _{c \in b} P^{cg}(\text {rank}(I^{cg})-\beta ^{g})^2}}, \end{aligned}$$

(10)

where

$$\begin{aligned} \alpha ^{g}=\frac{\sum _{c \in b} P^{cg} \text {rank}(\rho ^{cg})}{\sum _{c \in b} P^{cg}} \quad \text {and} \quad \beta ^{g}=\frac{\sum _{c \in b} P^{cg} \text {rank}(I^{cg})}{\sum _{c \in b} P^{cg}} \end{aligned}$$

are the weighted means (taken over all members of the selected group of countries) of the ranks¹⁴ of the degrees of rotation and the selected indicators, respectively.

To test whether the measures of association $\rho ^{bg}(I)$ defined by Eq. (10) significantly differ from zero, p values of the one-sided z-test (Pinto da Costa 2015) with

$$\begin{aligned} H_0: \rho ^{bg}(I) \le 0, \quad H_1: \rho ^{bg}(I) >0 \quad (b \in \{EU, West, East\}, g \in \{M,W\}) \end{aligned}$$

will be computed and evaluated for significance throughout the rest of this paper.

3 Results

3.1 Degrees of rotation by country and gender

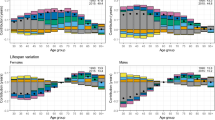
Figure 2 displays degrees of rotation by country and gender, as defined by Eq. (5), alongside the critical values at the 5% and 1% significance levels of the test of the hypotheses defined by Eq. (6). Table 5 in the Appendix contains the exact numeric values of $\rho ^{cg}$ as well as the p values of the above test by country and gender.

Fig. 2

Degrees of rotation (measured by Spearman’s $\rho$) by country and gender (top: men, bottom: women). The dashed and dotted-dashed lines denote the one-sided critical values at the 5% and 1% significance levels, respectively

Evidence for rotation is significant at the $5\%$ level in 19 European Union member states for women and 14 countries for men, and only in 11 countries (out of 28) for both genders, which suggests that rotation of the age pattern of mortality decline has been far from universal between 1950 and 2015.¹⁵

Apparently, no statistically significant rotation took place in case of either gender in 6 countries (Belgium, Croatia, Denmark, France, Luxembourg and Romania). On the other hand, degrees of rotation are very strongly significant (with $p<0.001$) for both genders in 6 other EU member states (Bulgaria, Cyprus, Finland, Greece, Poland and Slovakia), with the strongest evidence ($\rho \approx 1$ for both men and women) in Cyprus.

For the sake of illustration, three selected countries with very different rotation profiles are examined visually in Fig. 3 in more detail: namely, Cyprus, where evidence for rotation is the strongest for both genders, Denmark, where $\rho$ is negative for both men and women, indicating a slight yet somewhat surprising “anti-rotation”, and Germany, the most populous EU member state, which demonstrates weak (if any) evidence for rotation.

Fig. 3

Acceleration rates by age group for men (left) and women (right) in Cyprus (top), Denmark (middle) and Germany (bottom), along with the corresponding LOESS curves. The sizes of the bubbles are proportional to the populations of the corresponding age groups

The visual pattern is almost perfect in Cyprus, where acceleration rates start from the negative range at age 0, and increase with age thereafter, reaching the positive range around age 40 for men and 20 for women. The weak negative trends in Denmark and the similarly weak positive rotation in Germany are also visible in Fig. 3. It should be noted that the acceleration rates $\rho$ are weighted by population, which is represented by the sizes of the bubbles in Fig. 3. Recognizing the trends with the naked eye is facilitated by LOESS (LOcal regrESSion, a flexible generalization of both moving averages and polynomial regression, Cleveland and Devlin 1988) smoothing curves. The theoretical assumption of time-invariant improvements, which is widely used due to the popularity of the Lee–Carter model, would correspond to horizontal lines at zero acceleration.

Fig. 4

Rotation of the age pattern of mortality decline for men (left) and women (right) in Cyprus. The solid LOESS curve approximates the pattern of improvement between 1950 and 1960, while the dashed curve displays the new pattern between 2005 and 2015. The sizes of the bubbles are proportional to the populations of the corresponding age groups

The textbook case of Cyprus is further illustrated by Fig. 4, where the pattern of mortality improvements gradually shifted from the solid LOESS curve (1950–1960) to the dashed one (2005–2015). The size of the shift is a nearly perfectly monotone increasing function of age. Charts like Fig. 4 for Bulgaria, Finland, Greece, Poland and Slovakia yield comparable (even if somewhat more subtle) results, whereas similar plots for Denmark, France and Luxembourg display weak, barely recognizable tendencies of a clockwise anti-rotation, as captured by the negative values of $\rho ^{cg}$.

3.2 Mean degrees of rotation by gender and former political bloc

Table 1 contains weighted mean degrees of rotation by gender and country group, as defined by Eq. (7). As the weighted mean degree of rotation for women is more than twice as high as the one for men in the European Union as a whole, the results suggest that rotation was considerably more prevalent in female populations than among men between 1950 and 2015. According to the paired-samples t test of the hypotheses defined by Eq. (8), the differences between weighted mean degrees of rotation of men and women are statistically significant in the European Union as a whole as well as within both former political blocs.

On the other hand, even though Eastern member states apparently display higher mean degrees of rotation than coutries in the former Western bloc for both men and women, the differences between these groups are not statistically significant in case of either gender according to the t test with hypotheses defined by Eq. (9).¹⁶

Table 1 Weighted mean degrees of rotation by gender and differences between the two genders, with corresponding p values

3.3 Degrees of rotation by life expectancies at birth

Li et al. (2013) state that the rotation of the age pattern of mortality decline is more prevalent in low-mortality countries, and suggest that rotation should only start in their model once a high enough level of the life expectancy at birth (specifically, 80 years) has been reached.

In contrast to this assumption, several European Union member countries display strong evidence in favor of a rotation for both men and women throughout the period between 1950 and 2015, as demonstrated by Fig. 2, even though in many cases their life expectancies at birth had still not reached 80 years by 2015 for either males or females (Bulgaria and Slovakia, for example), and numerous other member states with very high life expectancies at birth display no sign of rotation at all (or even to the contrary, such as Denmark and France).

Figure 5 examines whether rotation has indeed been more prevalent in countries with higher life expectancies at birth. It is apparent in the top row of Fig. 5 that there is no significant positive trend for either men or women in the European Union as a whole: on the contrary, the linear regression lines have slightly negative slopes, and are nearly horizontal. Based on this figure, the statement of Li et al. (2013) about the relationship between degrees of rotation and life expectancies at birth may hold for Western European men and citizens of both sexes from the former Eastern bloc.

Fig. 5

Degrees of rotation $\rho ^{cg}$ as functions of mean life expectancies at birth $e_0$ between 1950 and 2015 for men (left) and women (right), in the EU as a whole (top), the former Western bloc (middle) and the former Eastern bloc (bottom). The solid straight lines are linear regression estimates. The sizes of the bubbles are proportional to the (male and female) mid-year populations of the corresponding countries in 2015

Beyond visual inspection, Table 2 summarizes the strengths of assocations $\rho ^{bg}(e_0)$, as defined by Eq. (10), between degrees of rotation $\rho ^{cg}$ and life expectancies at birth $e^{cg}_0$ alongside their associated p values. Table 2 indicates that the assumption of Li et al. (2013) only holds among former Eastern bloc countries, and by contrast, degrees of rotation are largely unrelated to life expectancies at birth within the European Union in general and among Western member states in particular.¹⁷

Table 2 Strengths of association $\rho ^{bg}(e_0)$ between degrees of rotation and mean life expectancies at birth among all, only Western and only Eastern member states of the European Union, by gender, with one-sided significance levels

3.4 Degrees of rotation by increments of life expectancies at birth

In a similar fashion, Table 3 displays the strengths of assocations $\rho ^{bg}(\varDelta e_0)$, as defined by Eq. (10), between degrees of rotation $\rho ^{cg}$ and increments of life expectancies at birth $\varDelta e^{cg}_0$ as well as the corresponding p values. It may be inferred from Table 3 that degrees of rotation among men are uncorrelated with increments of life expectancies at birth, while the associations are significant among women, but only in the European Union as a whole and among Western member states, and not inside the former Eastern bloc.

Table 3 Strengths of association $\rho (\varDelta e_0)$ between degrees of rotation and life expectancy improvements at birth among all, only Western and only Eastern member states of the European Union, by gender, with one-sided significance levels

3.5 Degrees of rotation by life expectancies at the age of 60 years

Finally, Table 4 indicates that degrees of rotation are universally unrelated to remaining life expectancies at age 60 (except for perhaps some very weak evidence in favor of a positive relationship among Eastern European men).

Table 4 Strengths of association $\rho (e_{60})$ between degrees of rotation and remaining life expectancies at age 60 among all, only Western and only Eastern member states of the European Union, by gender, with one-sided significance levels

4 Conclusions

Based on detailed data from the period between 1950 and 2015 for both genders and all 28 European Union member states, along with a relatively simple nonparametric, data-driven methodology using only popular, well-known statistical techniques, it is clear that the rotation of the age pattern of mortality improvements has only taken place in part of the 28 members, with only 11 countries displaying statistically significant evidence for rotation at the 5% level in case of both genders, while apparently no rotation at all (or even on the contrary, an anti-rotation) has occurred in a number of EU countries.

The results indicate that the rotation of the age pattern of mortality decline has been notably more prevalent among women than in male populations, in the EU as a whole as well as within both the former Eastern and Western blocs. This difference has been more significant in the Western half of the Union.

Contrary to Li et al. (2013), the presence and strength of the rotation phenomenon appear to be largely unrelated to mean life expectancies at birth in the European Union as a whole: positive and negative cases appear among both low- and high-mortality countries, and the strength of the assocation between these two variables is apparently statistically negligible. On the other hand, there is significant evidence for a positive relationship between degrees of rotation and life expectancies at birth, as noted by Li et al. (2013), among member states that used to be part of the Eastern Bloc during the Cold War.

Instead of life expectancies at birth, increments of these quantities between the beginning and the end of the observation period appear to be better predictors of the degrees of rotation in the case of women in the EU as a whole and the former Western bloc, which has not been noted in the literature.

The questions why the rotation of the age pattern of mortality decline has only taken place in part of the European Union and why it has been more noticeable in time series of female mortality rates deserve closer examination. Most likely, the explanation has to do with the way advances in medicine, lifestyle and nutrition among the elderly have been more prevalent in some countries than in others, especially among women. Unfortunately, a more thorough investigation of the causes of these findings falls outside the scope of this paper, as it would require an interdisciplinary approach transcending the purely statistical analysis presented here.

It would be desirable to create a multivariate model that explains degrees of rotation using several predictors simultaneously, however, it would require a much larger set of (possibly all) countries as observations in order to produce statistically significant effects.

As the rotation phenomenon may jeopardize the reliability of mortality forecasts for pension schemes as well as life and health insurers, which may lead to severe financial consequences, it is essential to be aware of the possibility of its presence and apply appropriate forecasting procedures that take it into consideration, whenever necessary.

As the immensely popular Lee and Carter (1992) mortality forecasting model ignores rotation, it is advisable to use the particularly promising Li et al. (2013) variant of the original method whenever there is evidence for rotation in the data series. This model variant incorporates a smooth rotation into forecasts, however, it is somewhat inflexible, as the proposed starting point (the age of 80 years) and the speed of the rotation (controlled by the exponent 0.5) are externally given by the authors and are not determined by past data. Making these parameters endogenous, possibly by extending and operationalizing the rotation as presented in this paper, would definitely increase the practical applicability of this excellent method even further.

Appendix

see Table 5

Table 5 Degrees of rotation $\rho ^{cg}$ by country and gender and one-sided p values